Systematic Evaluation of Different Infrastructure Systems for Tsunami Defense in Sendai City
Abstract
:1. Introduction
2. Methods
2.1. Numerical Tsunami Simulation
2.2. Tsunami Source Model
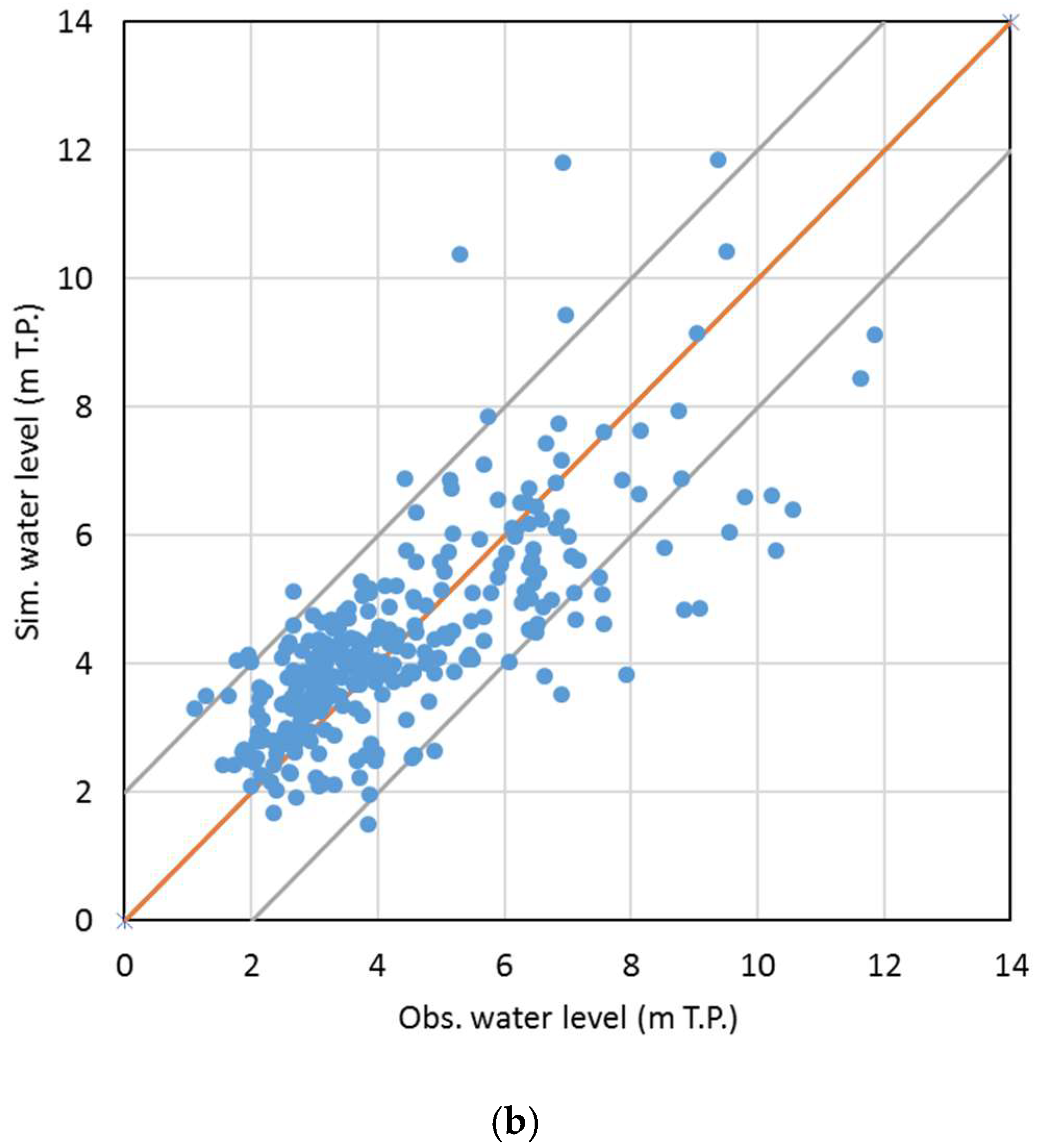
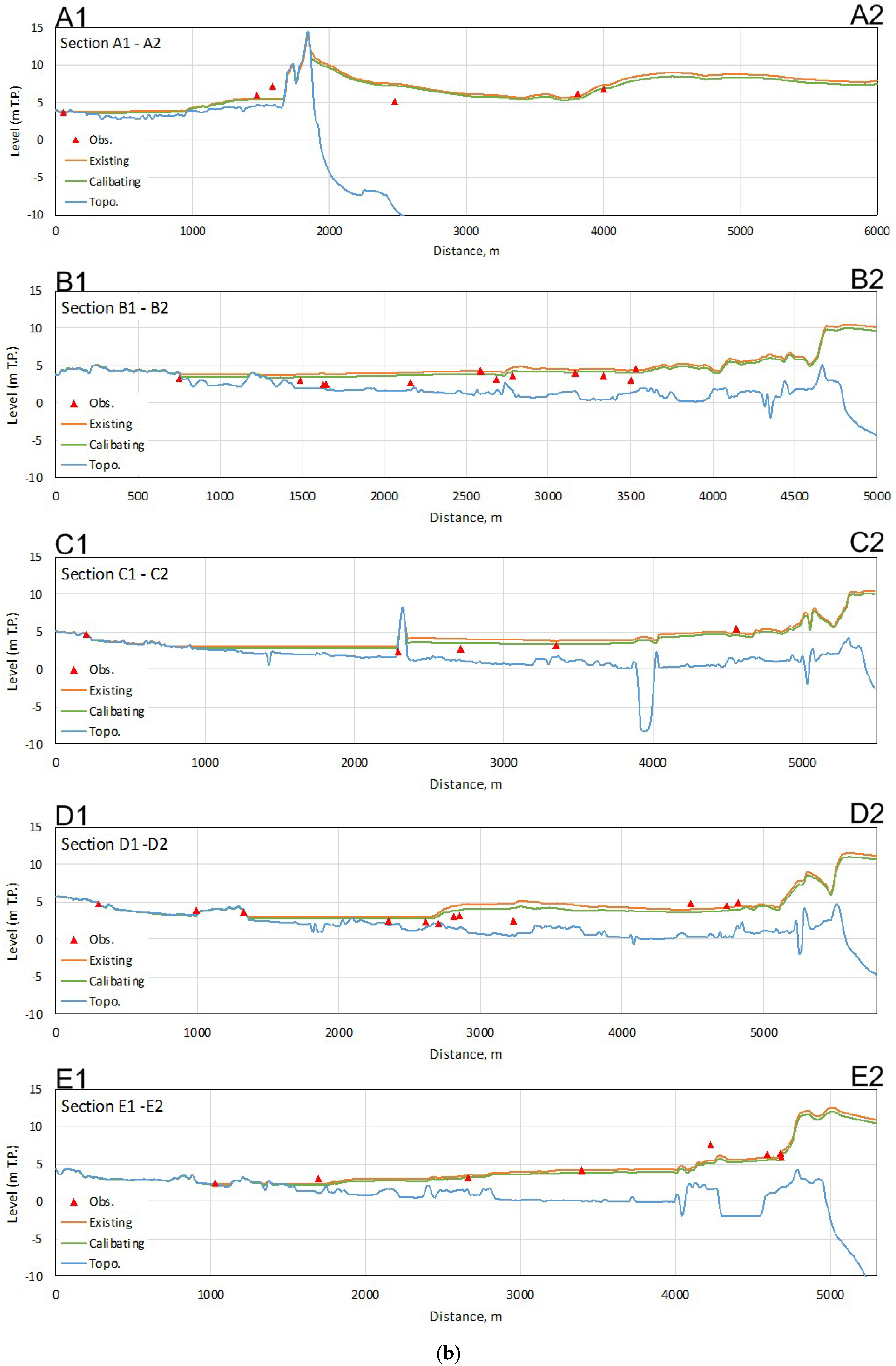
2.3. Calibration and Validation of Tsunami Model
2.4. Tsunami Simulation of the Multi-Infrastructure Scenario
3. Results and Discussion
3.1. Calibration and Validation Results
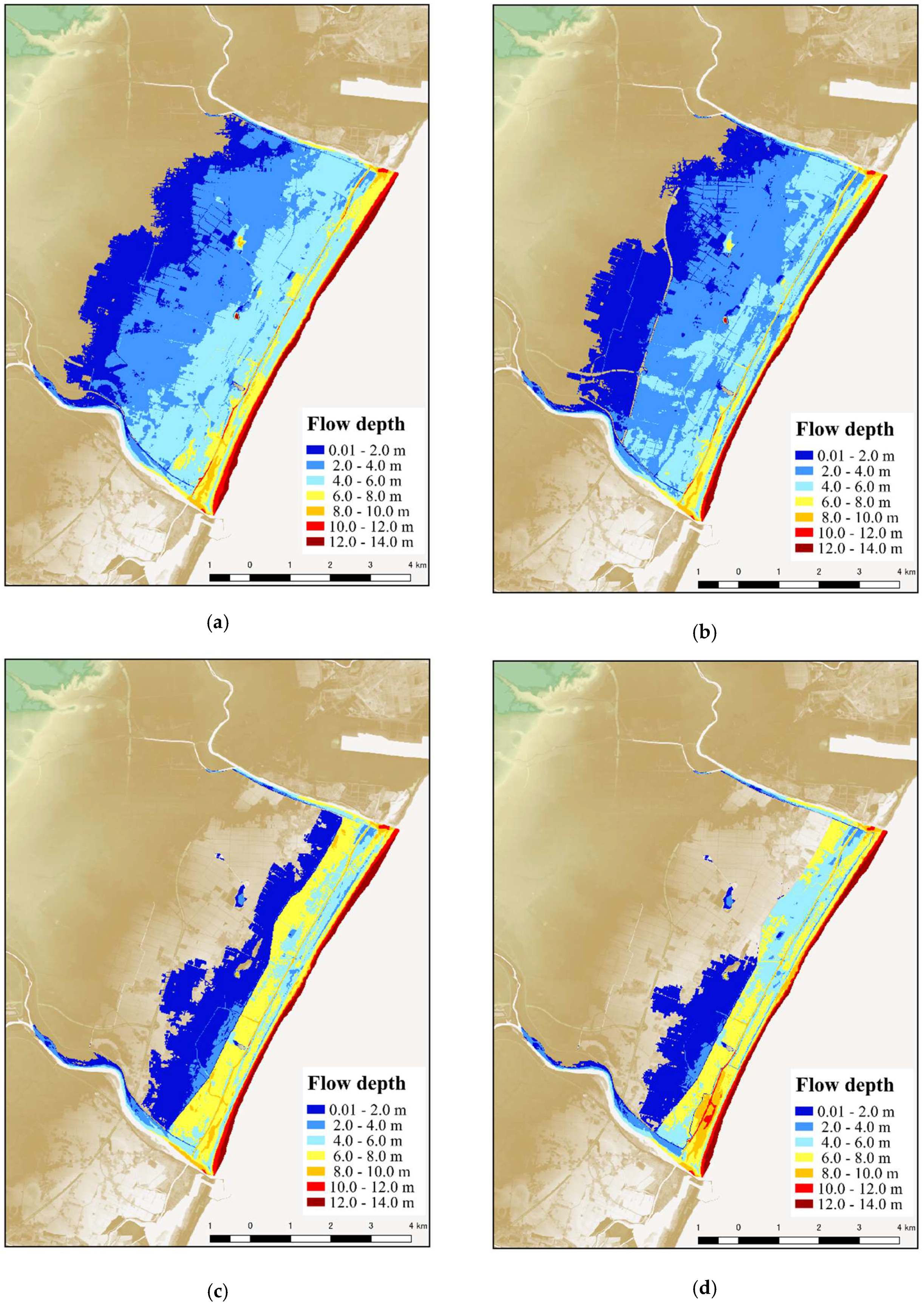
3.2. Inundation Results of the Tsunami Simulation for Each Scenario
3.3. Performances of Several Combinations of Multilayered Structures
3.4. Performances of the Existing and Reconstructed Structural Measures against the 2011 Tsunami
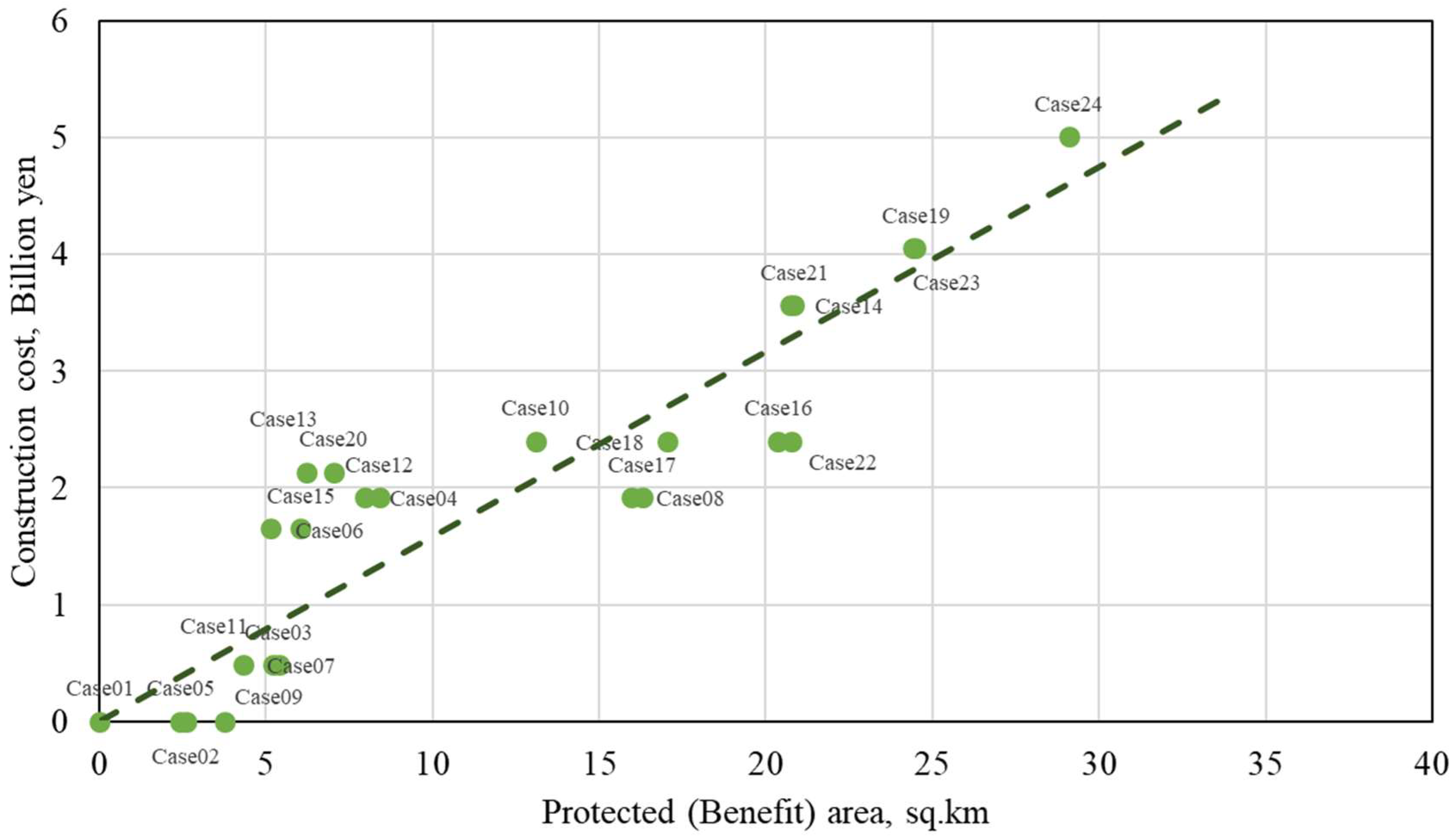
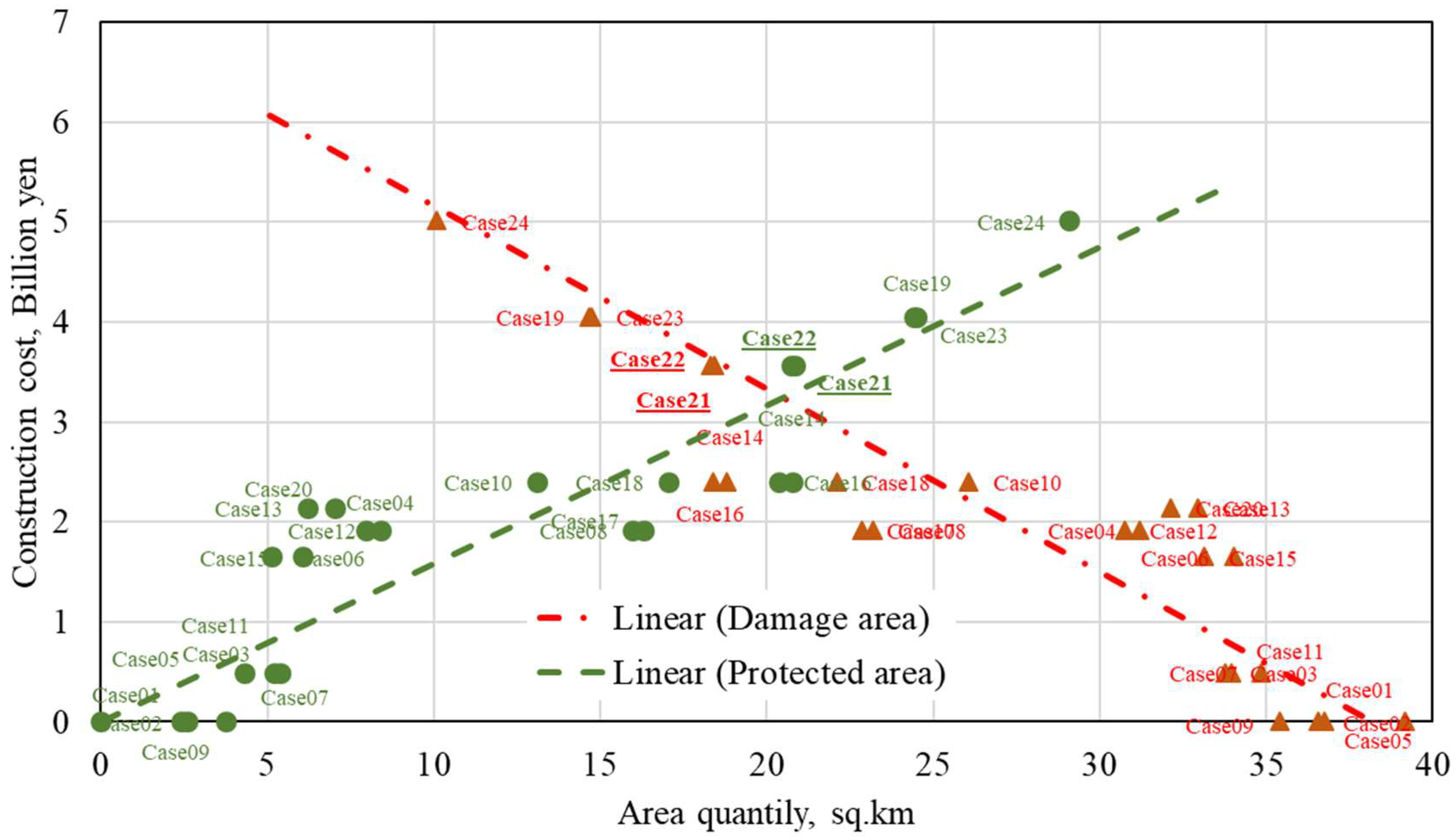
3.5. Construction Cost Perspectives of the Multilayered Countermeasures
3.6. Performance of Multilayered Structures from an Economic Construction Cost Perspective
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Geospatial Information Authority of Japan (GSI). Available online: http://www.gsi.go.jp/ (accessed on 14 March 2011).
- Koshimura, S.; Hayashi, S.; Gokon, H. The impact of the 2011 Tohoku earthquake tsunami disaster and implications to the reconstruction. Soils Found. 2014, 54, 560–572. [Google Scholar] [CrossRef]
- Mori, N.; Takahashi, T. The 2011 Tohoku Earthquake Tsunami Joint Survey Group. Nationwide post event survey and analysis of the 2011 Tohoku earthquake tsunami. Coast. Eng. J. 2012, 54, 125001. [Google Scholar] [CrossRef]
- Lacharote, P.; Leelawat, N.; Suppasri, A.; Thamarax, P.; Imamura, F. Estimation of fatality ratios and investigation of influential factors in the 2011 Great East Japan Tsunami. Int. J. Disaster Risk Reduct. 2017, 29, 37–54. [Google Scholar] [CrossRef]
- Suppasri, A.; Koshimura, S.; Imai, K.; Mas, E.; Gokon, H.; Muhari, A.; Imamura, F. Damage characteristic and field survey of the 2011 Great East Japan tsunami in Miyagi prefecture. Coast. Eng. J. 2012, 54, 1250005. [Google Scholar] [CrossRef]
- National Police Agency. Report of the Damage Caused by the 2011 Tohoku Earthquake and Tsunami. Available online: http://www.npa.go.jp/archive/keibi/biki/higaijokyo.pdf (accessed on 9 December 2016). (In Japanese)
- Ministry of Finance Japan, 2011. Japan’s Fiscal Condition. Available online: www.mof.go.jp/english/budget/budget/ (accessed on 20 December 2011).
- Ministry of Land, Infrastructure, Transport and Tourism (MLIT). 2011. Available online: http://www.mlit.go.jp/common/000138154.pdf (accessed on 3 March 2014).
- Liu, P.L.F.; Cho, Y.S.; Yoon, S.B.; Seo, S.N. Numerical Simulation of the 1960 Chilean Tsunami Propagation and Inundation as Hilo, Hawaii; Recent Development in Tsunami Research; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1994; pp. 99–115. [Google Scholar]
- Liu, P.L.F.; Woo, S.B.; Cho, Y.S. Computer Programe for Tsunami Propagation and Inundation; Technical Report; Cornell University: Ithaca, NY, USA, 1998. [Google Scholar]
- Titov, V.; Synolakis, C.E. Numerical Modeling of Tidal Wave Run-up. J. Waterw. Port Coast. Ocean Eng. 1998, 124, 157–171. [Google Scholar] [CrossRef]
- Imamura, F. Review of tsunami simulation with a finite difference method. In Long-Wave Runup Models; World Scientific Pub Co Inc.: Singapore, 1995; pp. 25–42. [Google Scholar]
- Jais wal, R.K.; Singh, A.P.; Rastogi, B.K. Simulation of the Arabian Sea tsunami propagation generated due to 1945 Makran earthquake and its effect on the western parts of Gujarat, India. Nat. Hazards 2008, 48, 245–248. [Google Scholar] [CrossRef]
- Usha, T.; Ramana Murthy, M.V.; Murthy, N.T.; Murty, T.S. Vulnerability Assessment of Car Nicobar to Tsunami Hazard using Numerical Model. Sci. Tsunami Hazards 2009, 28, 15–34. [Google Scholar]
- Chenthamil Selvan, S.; Kankara, R.S. Tsunami model simulation for 26 December 2004 and its effect on Koodankulam region of Tamil Nadu Coast. Int. J. Ocean Clim. Syst. 2016, 7, 62–69. [Google Scholar] [CrossRef]
- Koshimura, S.; Oie, T.; Yanagisa, H.; Imamura, F. Developing fragility curves for tsunami damage estimation using numerical and post-tsunami data from Banda Aceh, Indonesia. Coast. Eng. J. 2009, 51, 234–273. [Google Scholar] [CrossRef]
- Yamashita, K.; Sugawara, D.; Takahashi, T.; Imamura, F.; Saito, Y.; Imato, Y.; Kai, T.; Uehara, H. Numerical simulation of large-scale sediment transport caused by the 2011 Tohoku Earthquake Tsunami in Hirota Bay, Southern Sanriku Coast. Coast. Eng. J. 2016, 58, 1640015. [Google Scholar] [CrossRef]
- Sugawara, D.; Goto, K. Numerical modeling of the 2011 Tohoku-oki tsunami in the offshore and onshore of Sendai Plain, Japan. Sediment. Geol. 2012, 282, 110–123. [Google Scholar] [CrossRef]
- Oishi, Y.; Imamura, F.; Sugawara, D. Near-field tsunami inundation forecast using the parallel TUNAMI-N2 model: Application to the 2011 Tohoku-Oki earthquake combined with source inversions. Geophys. Res. Lett. 2015, 42, 1083–1091. [Google Scholar] [CrossRef]
- Sato, S. Characteristics of the 2011 Tohoku Tsunami and introduction of two level tsunamis for tsunami disaster mitigation. Proc. Jpn. Acad. Ser. B Phys. Biol. Sci. 2015, 91, 262–272. [Google Scholar] [CrossRef] [PubMed]
- Vana Tsimopoulou, J.K.V.; Sebastiaan, M.K.; Jonkman, N. Cost-Efficient Design of Multilayer Safety Systems against Large-Scale Coastal Disasters, 1st ed.; Elsevier Inc.: Oxford, UK, 2015. [Google Scholar]
- Tsimopoulou, V.; Jonkman, S.N.; Kolen, B.; Maaskant, B.; Mori, N.; Yasuda, T. A multi-layered safety perspective on the tsunami disaster in Tohoku, Japan. In Proceedings of the Flood Risk 2012 Conference, Rotterdam, The Netherlands, 19–23 November 2012; pp. 1–10. [Google Scholar]
- Khew, Y.T.J.; Jarzebski, M.P.; Dyah, F.; San Carlos, R.; Gu, J.; Esteban, M.; Aránguiz, R.; Akiyama, T. Assessment of social perception on the contribution of hard-infrastructure for tsunami mitigation to coastal community resilience after the 2010 tsunami: Greater Concepcion area, Chile. Int. J. Disaster Risk Reduct. 2015, 13, 324–333. [Google Scholar] [CrossRef]
- Takagi, H.; Bricker, J.D. Assessment of the effectiveness of general breakwaters in reducing tsunami inundation in Ishinimaki. Coast. Eng. J. 2014, 56, 1–21. [Google Scholar] [CrossRef]
- Samawasekara, R.S.M.; Sasaki, J.; Esteban, M. Assessment of the co-benefits of structures in coastal areas for tsunami mitigation and improving community resilience in Sri Lanka. Int. J. Disaster Risk Reduct. 2015, 13, 324–333. [Google Scholar] [CrossRef]
- Suppasri, A.; Latcharote, P.; Bricker, J.D.; Leelawat, N.; Hayashi, A.; Yamashita, K.; Makinoshima, F.; Roeber, V.; Imamura, F. Improvement of tsunami countermeasures based on lessons from the 2011 great east japan earthquake and tsunami -Situation after five years. Coast. Eng. J. 2016, 58, 1640011. [Google Scholar] [CrossRef]
- Strusińska-Correia, A. Tsunami mitigation in Japan after the 2011 Tōhoku Tsunami. Int. J. Disaster Risk Reduct. 2017, 22, 397–411. [Google Scholar] [CrossRef]
- Sendai City, Sendai City Earthquake Disaster Reconstruction Plan, Digest Version. Available online: https://www.city.sendai.jp/shinsaifukko/shise/daishinsai/fukko/kanren/kekaku/documents/english14511_cover-p2.pdf (accessed on 5 February 2018).
- Okada, Y. Surface deformation due to shear and tensile faults in a half-space. Bull. Seismol. Soc. Am. 1985, 75, 1135–1154. [Google Scholar]
- Imamura, F.; Koshimura, S.; Murashima, Y.; Akita, Y.; Shintani, Y. The Tsunami Source Model of the 2011 Tohoku Earthquake (ver.1.2). Available online: http://www.tsunami.civil.tohoku.ac.jp/hokusai3/J/events/tohoku_2011/model/dcrc_ver1.2.pdf (accessed on 25 April 2012).
- The 2011 Tohoku Earthquake Tsunami Joint Survey (TTJS) Group. Nationwide field survey of the 2011 off the Pacific coast of Tohoku earthquake tsunami. J. Jpn. Soc. Civ. Eng. 2011, 67, 63–66. [Google Scholar]
- Aida, I. Reliability of a tsunami source model derived from fault parameters. J. Phys. Earth 1978, 26, 57–73. [Google Scholar] [CrossRef]
- Suppasri, A.; Koshimura, S.; Imamura, F. Developing tsunami fragility curves based on the satellite remote sensing and the numerical modeling of the 2004 Indian Ocean tsunami in Thailand. Nat. Hazards Earth Syst. Sci. 2011, 11, 173–189. [Google Scholar] [CrossRef]
- Ines, A.V.M.; Hansen, J.W. Bias correction of daily GCM rainfall for crop simulation studies. J. Agric. For. Meteorol. 2006, 138, 44–53. [Google Scholar] [CrossRef]
- Acharya, N.; Chattopadhyay, S.; Mohanty, U.C.; Dasha, S.K.; Sahooc, L.N. On the bias correction of general circulation model output for Indian Summer Monsoon. J. Meteorol. Appl. 2013, 20, 349–356. [Google Scholar] [CrossRef]
- Asadullah, A.; Mcintyre, N.E.I.L.; Kigobe, M.A.X. Evaluation of five satellite products for estimation of rainfall over Uganda. Hydrol. Sci. J. 2010, 53, 1137–1150. [Google Scholar] [CrossRef]
- Pakoksung, K. Runoff Analysis Using Satellite Data for Regional Flood Assessment; Spatial and Time Series Bias Correction of Satellite Data. Ph.D. Thesis, Kochi University of Technology, Kami, Japan, 23 September 2016; p. 132. [Google Scholar]
- Hayashi, S.; Koshimura, S. The 2011 Tohoku tsunami flow velocity estimation by the aerial video analysis and numerical modeling. J. Disaster Res. 2013, 8, 561–572. [Google Scholar] [CrossRef]
- Geospatial Information Authority of Japan (GSI). On Estimation of Flooded Area by the 2011 Tsunami. Available online: www.gsi.go.jp/common/000059939.pdf (accessed on 5 May 2013). (In Japanese)
- Research and Statistics Department Minister’s Secretariat, Ministry of Economic, Trade and Industry (METI), Japan. Available online: http://www.meti.go.jp/english/statistics/tyo/tiikiio/index.html (accessed on 5 February 2018).
- Leng, L. Health Economic Evaluation: A Primer for Healthcare Professionals. Prim. Health Care 2016, 6, 223. [Google Scholar] [CrossRef]
- Locke, J. Some Considerations of the Consequences of Lowering the Interest and Raising the Value of Money. Available online: http://la.utexas.edu/users/hcleaver/368/368LockeSomeConsiderationsAlltable.pdf (accessed on 5 February 2018).
- Denham-Steuart, J. Inquiry into the Principles of Political Economy. Published in The Strand. 1767. Available online: https://www.marxists.org/reference/subject/economics/steuart/index.htm (accessed on 27 October 2014).
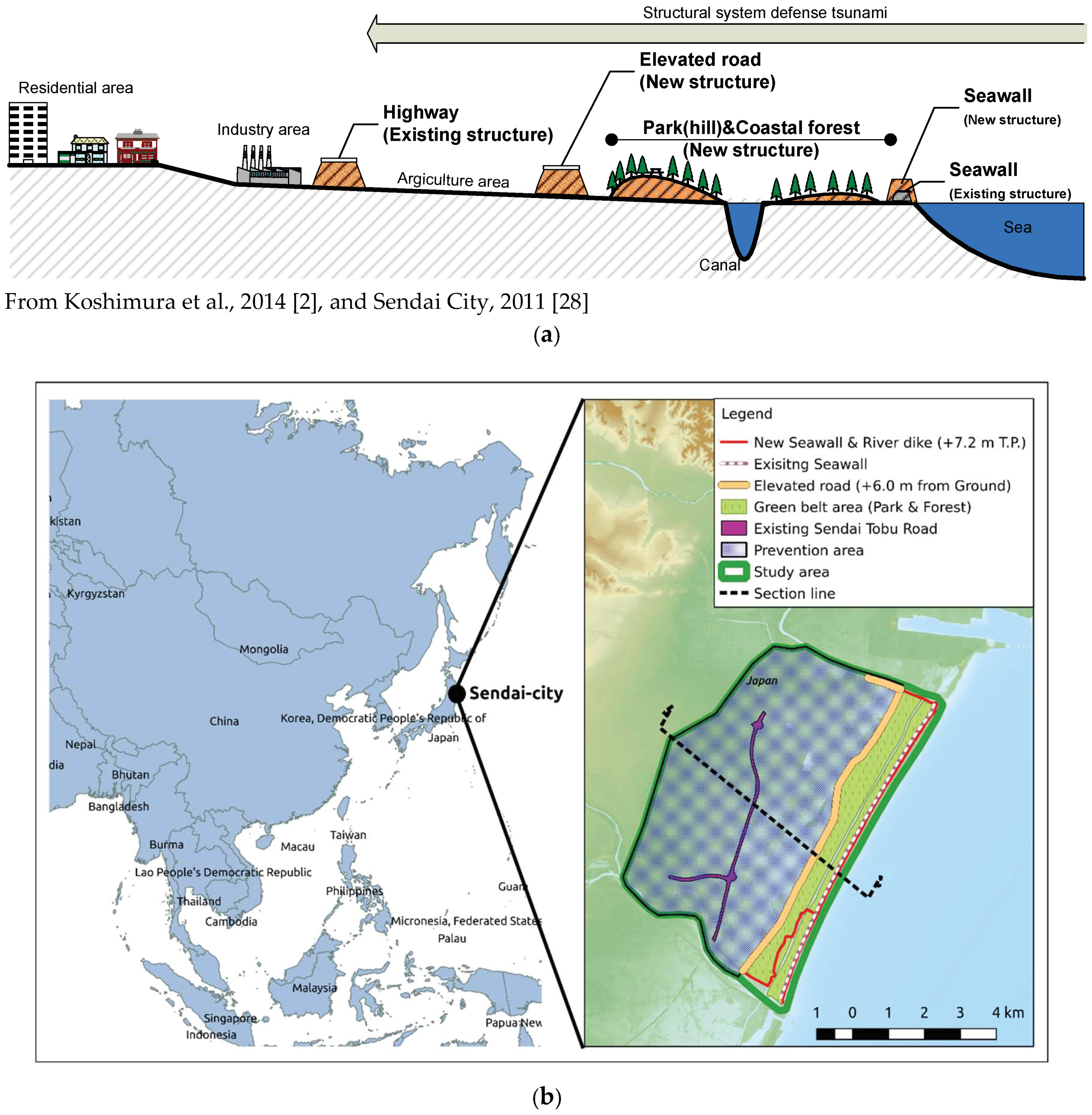
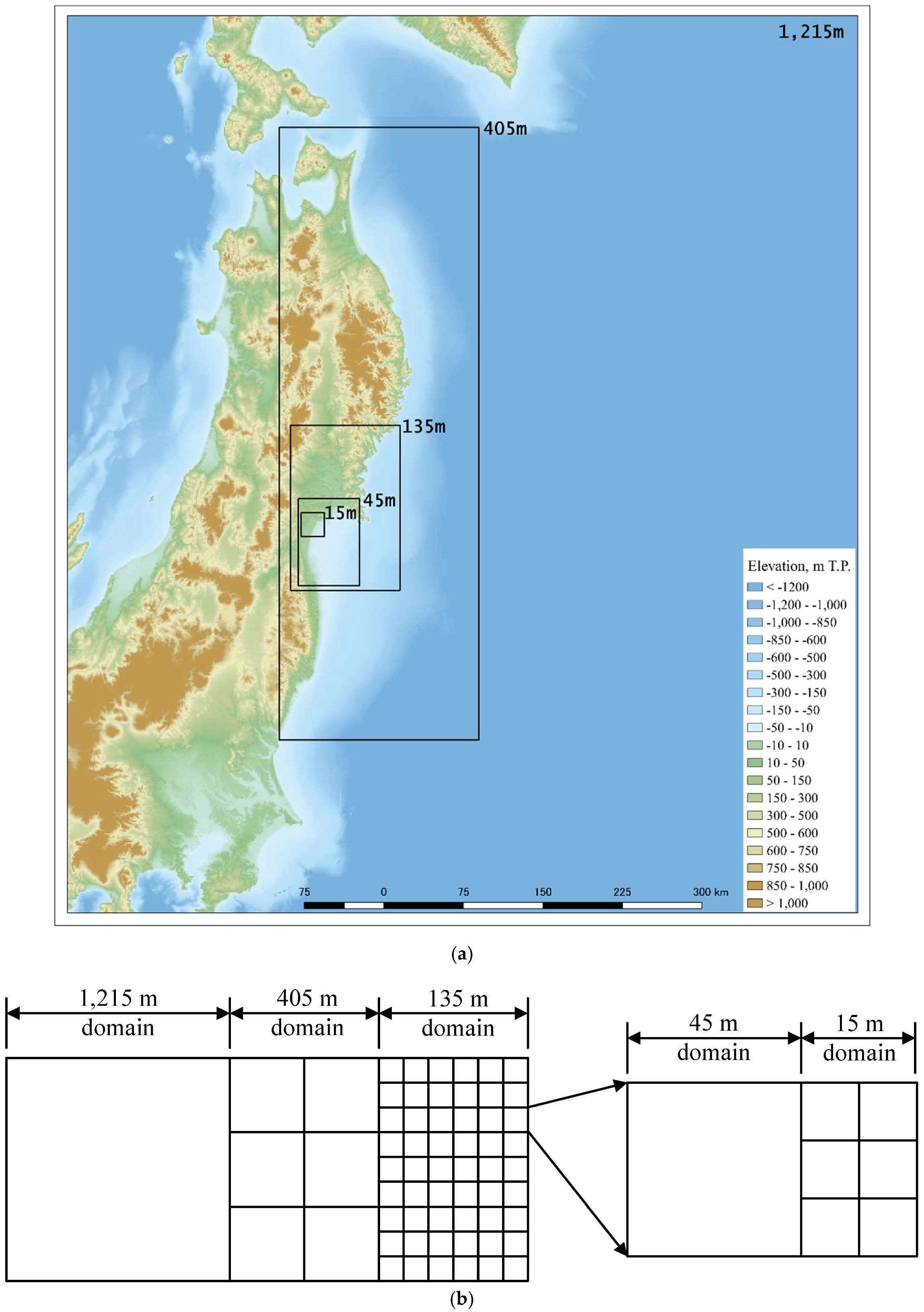
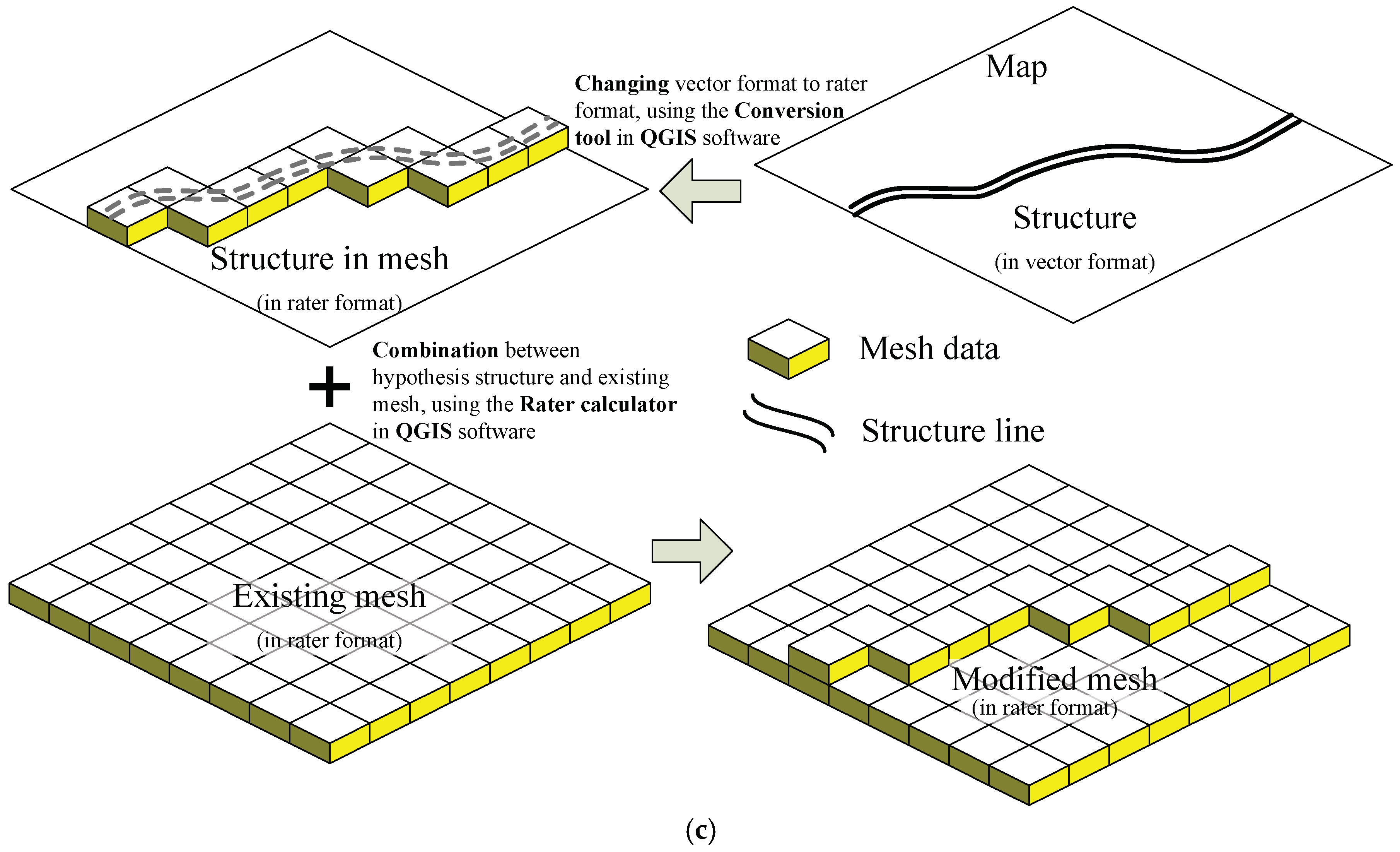
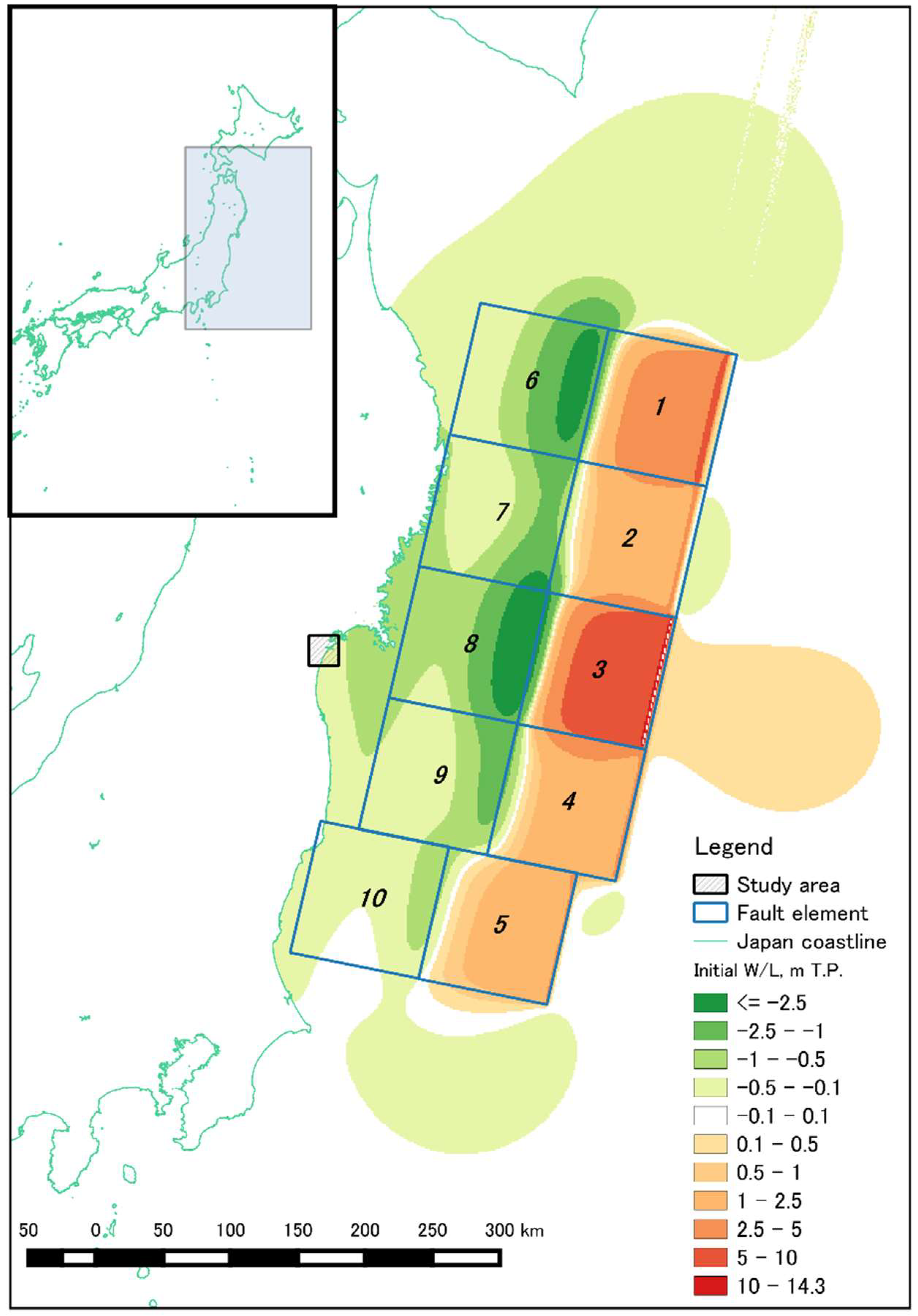
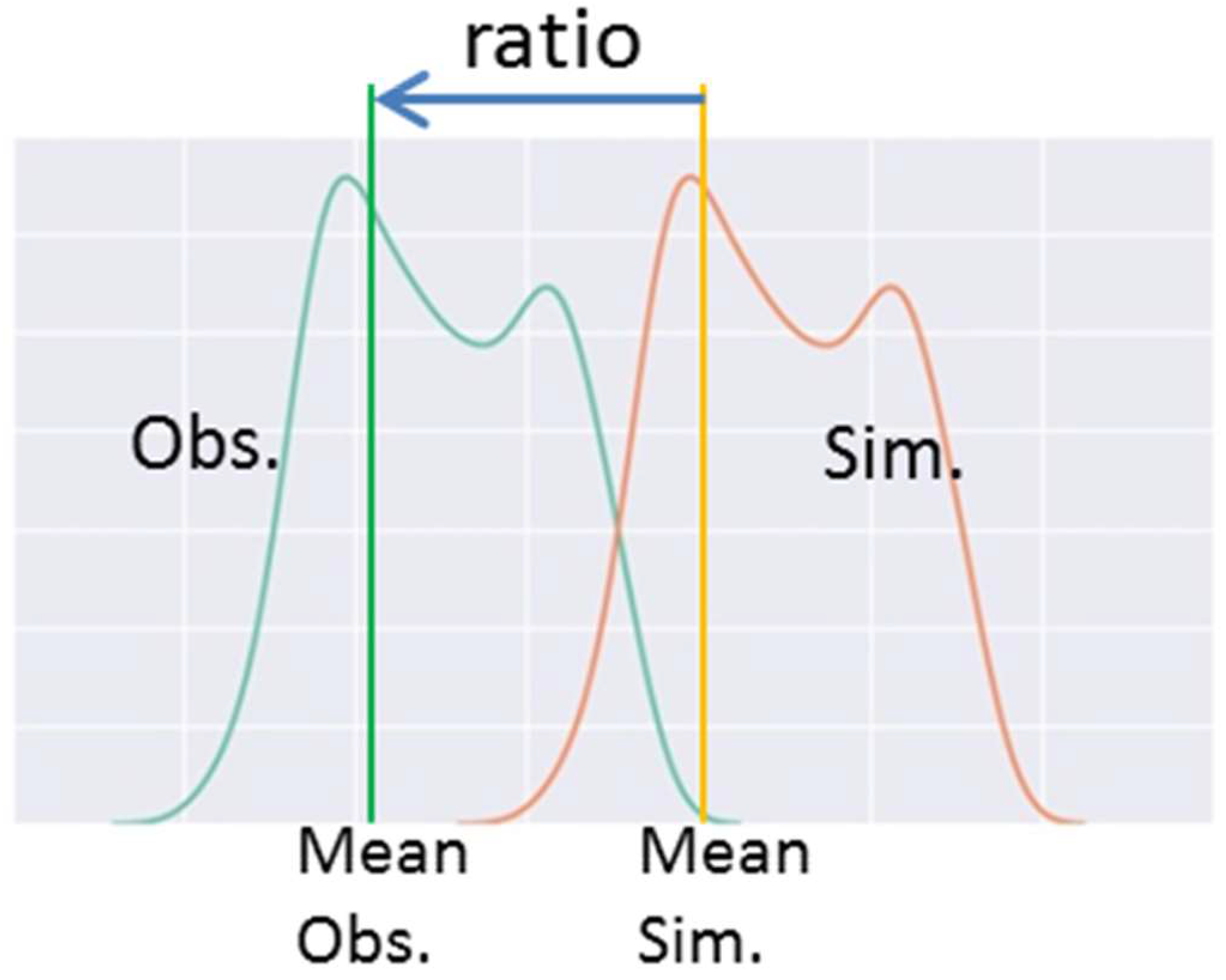
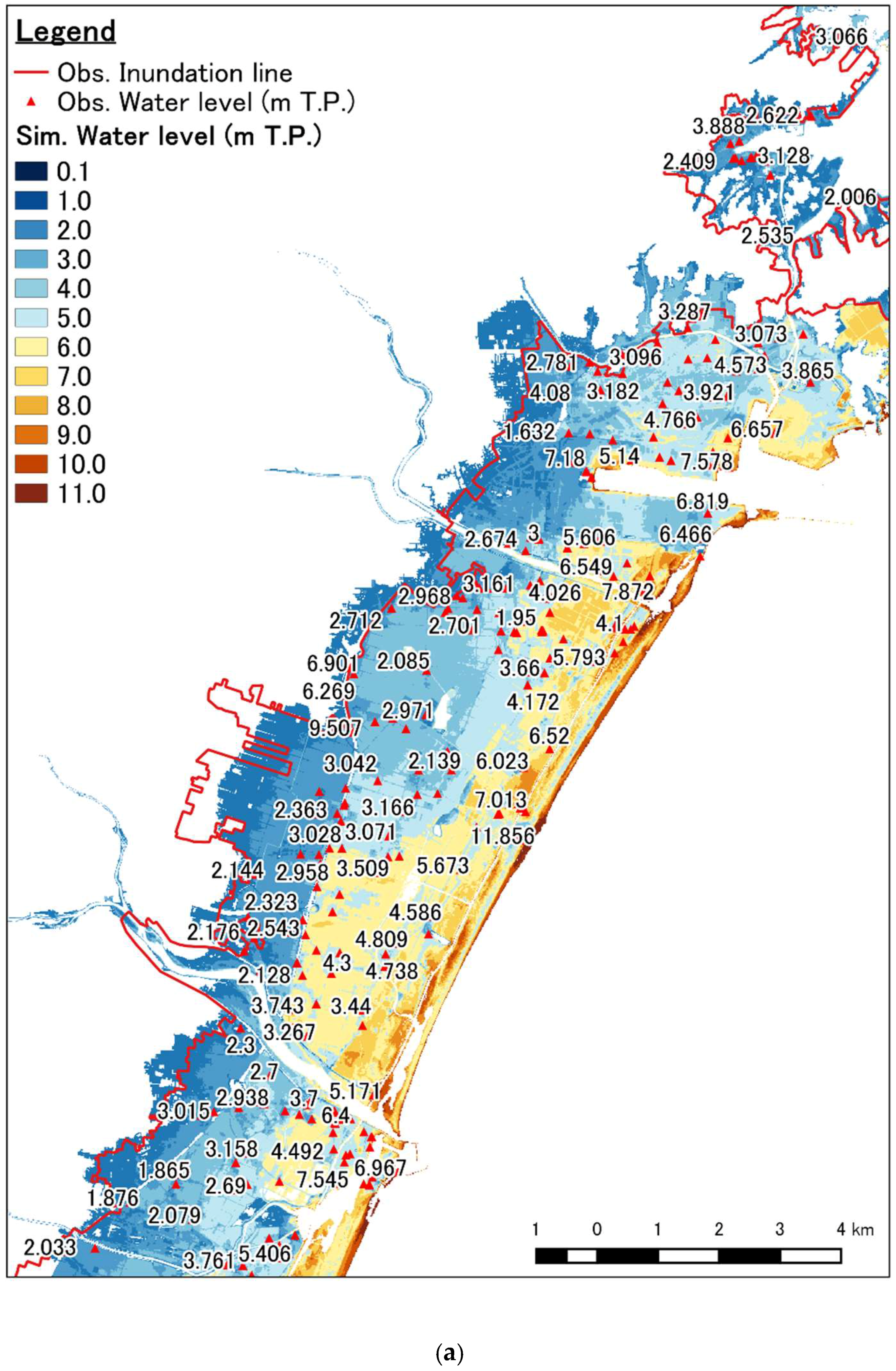
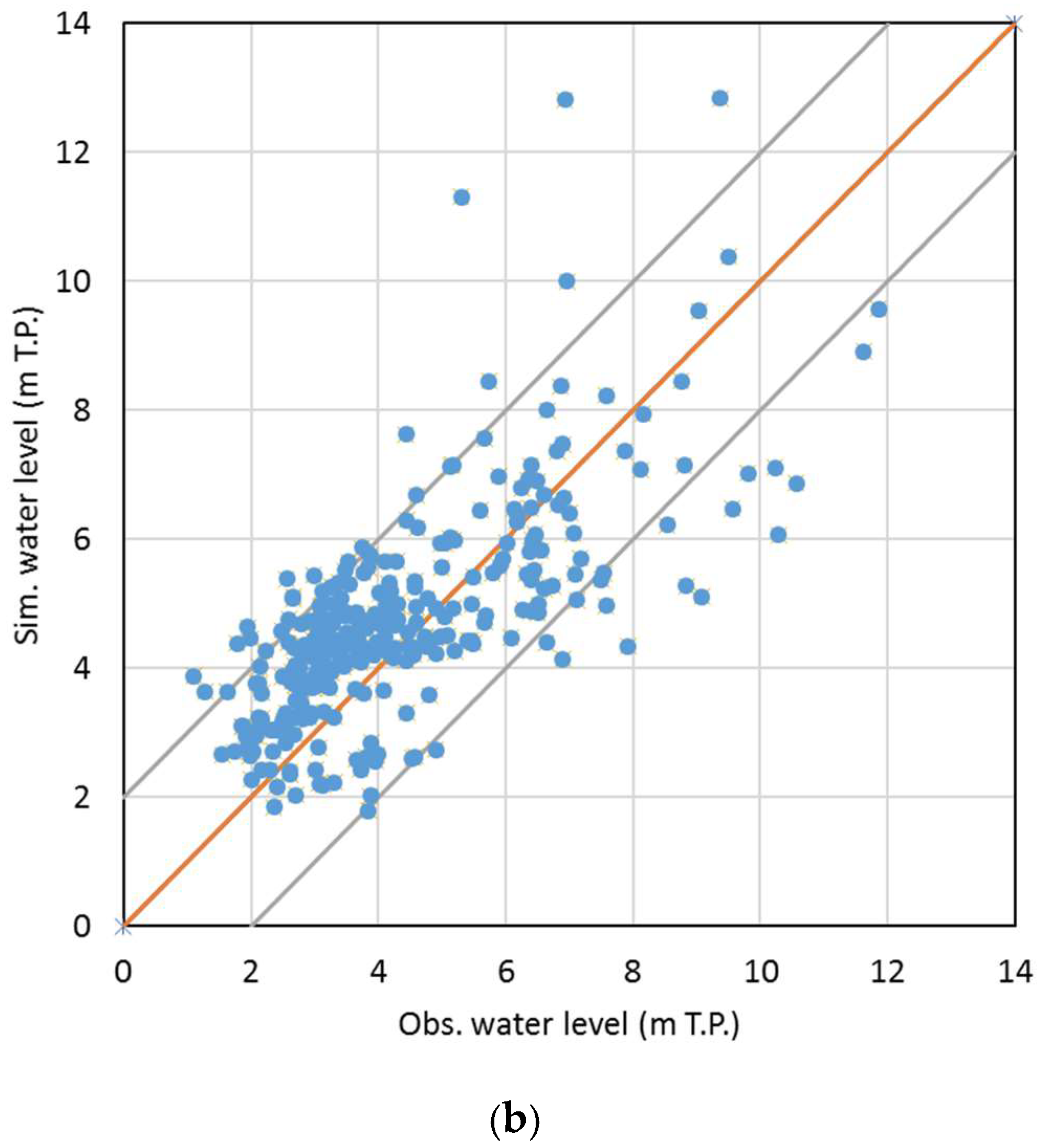
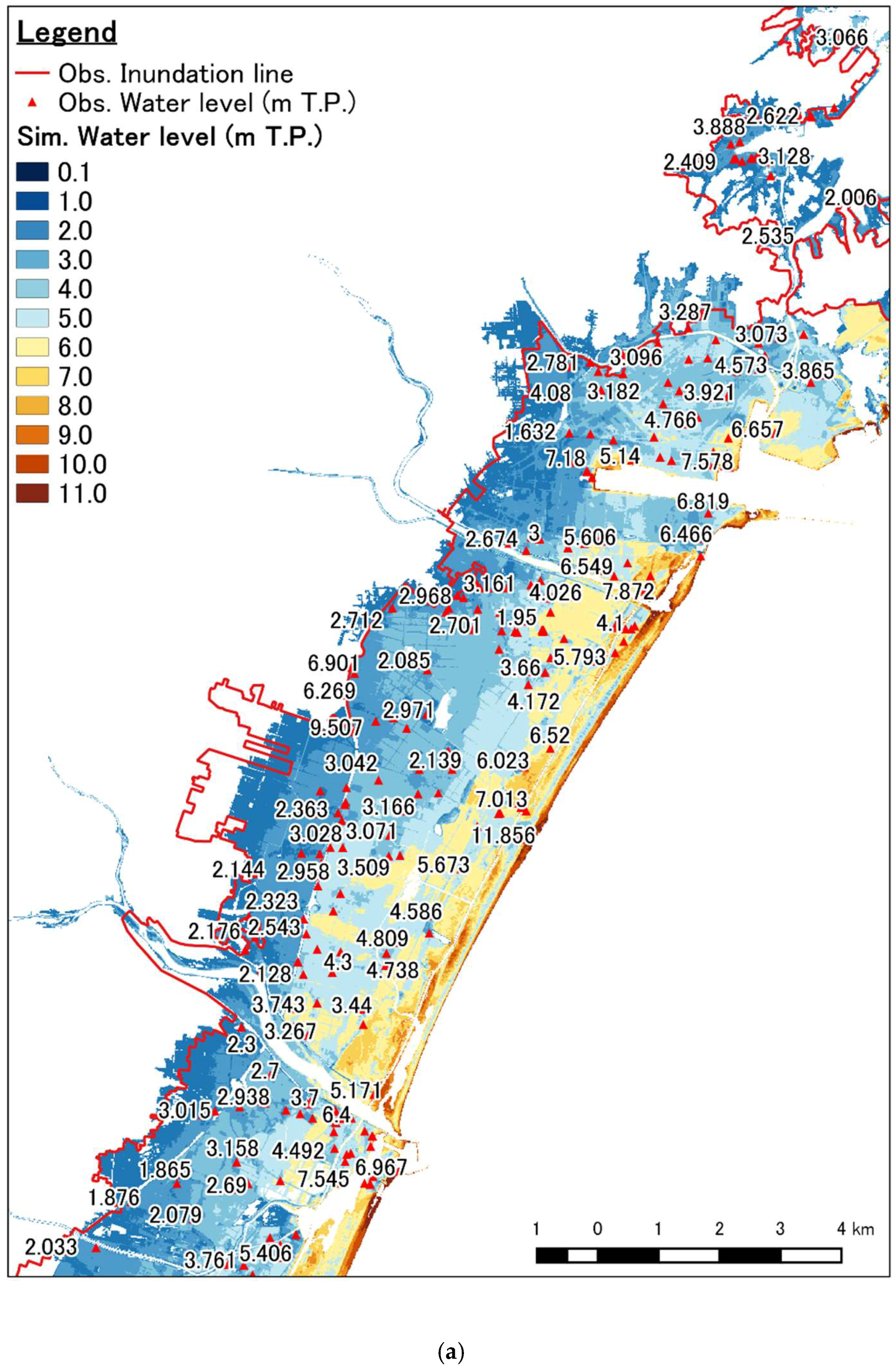
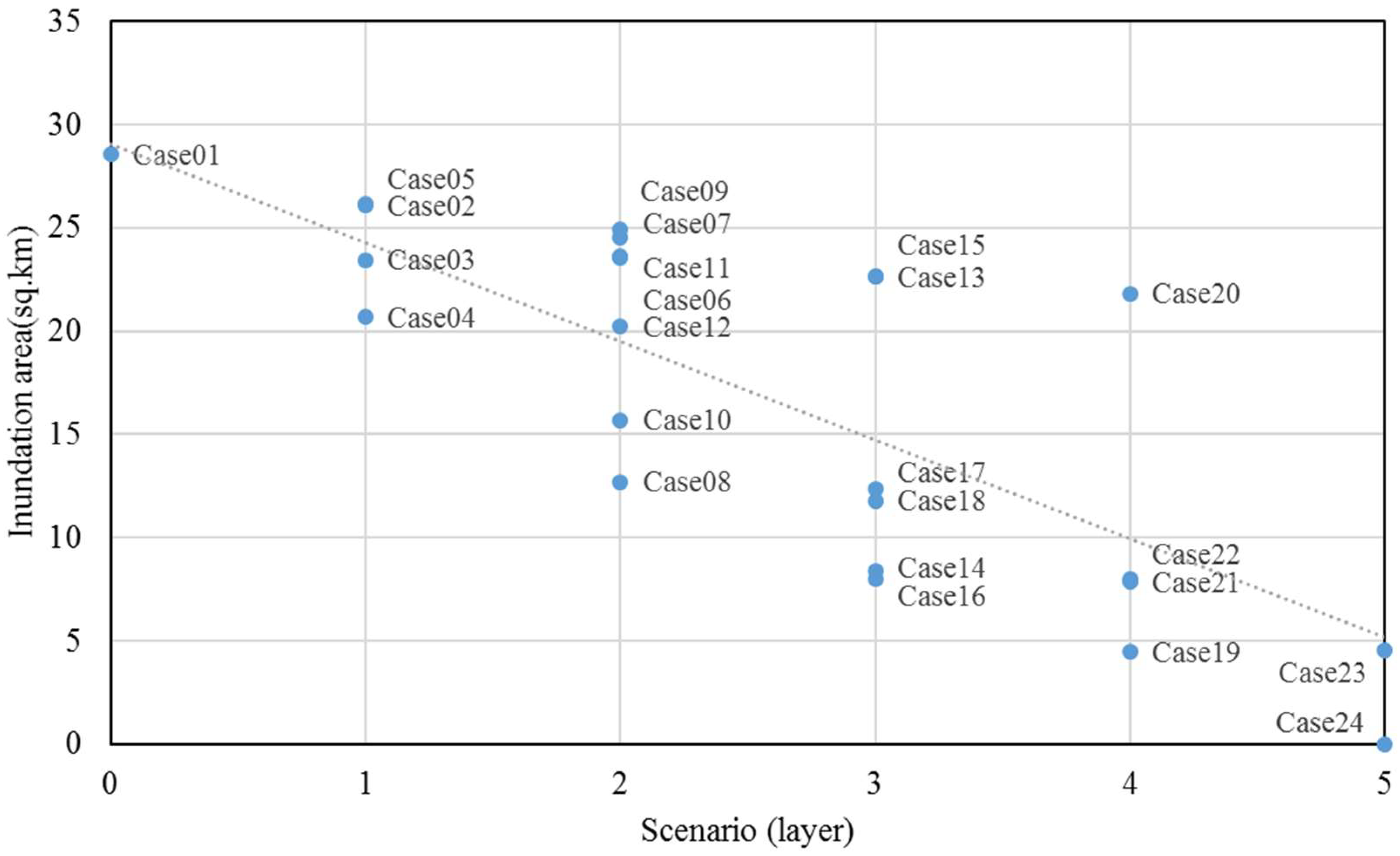
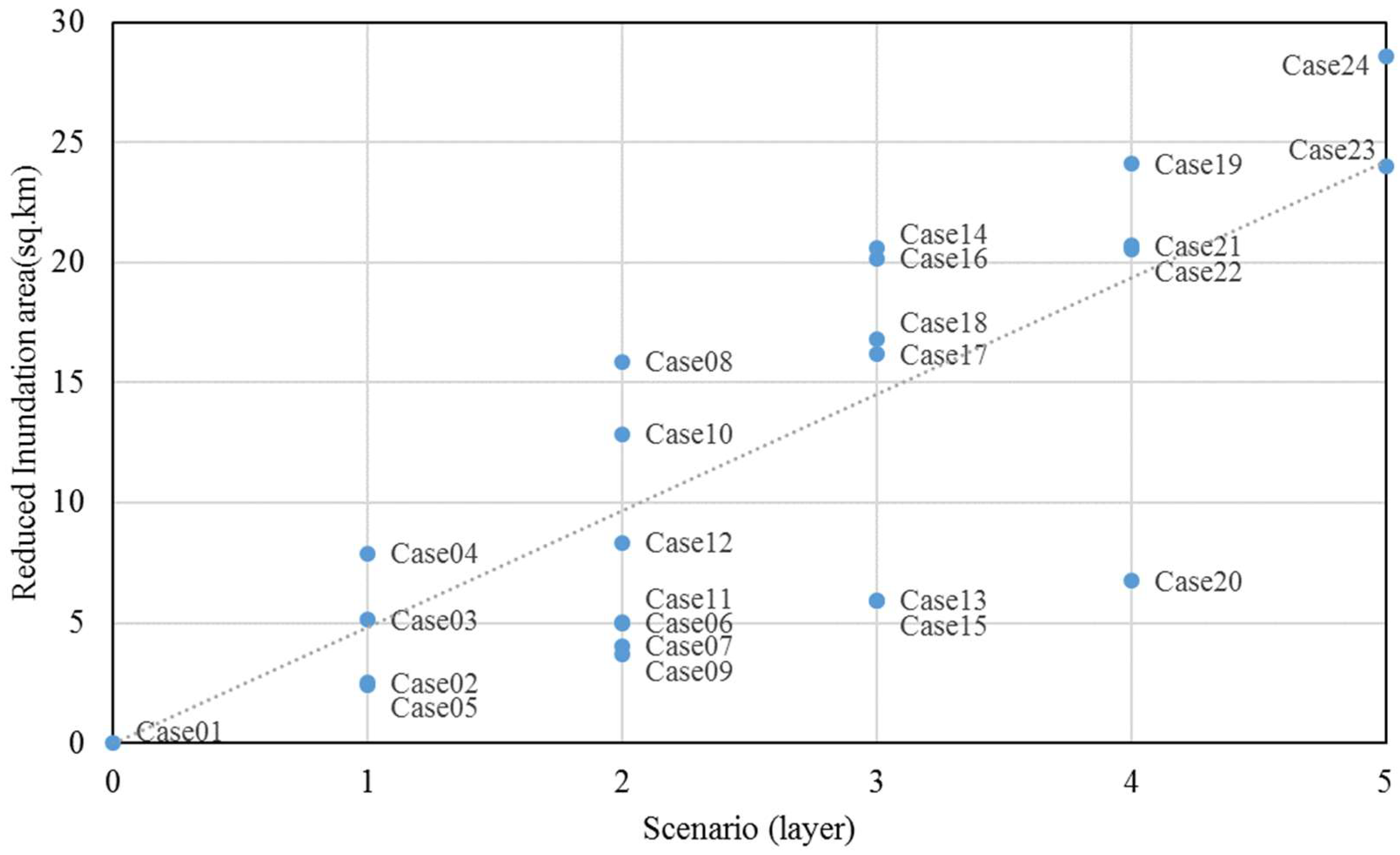
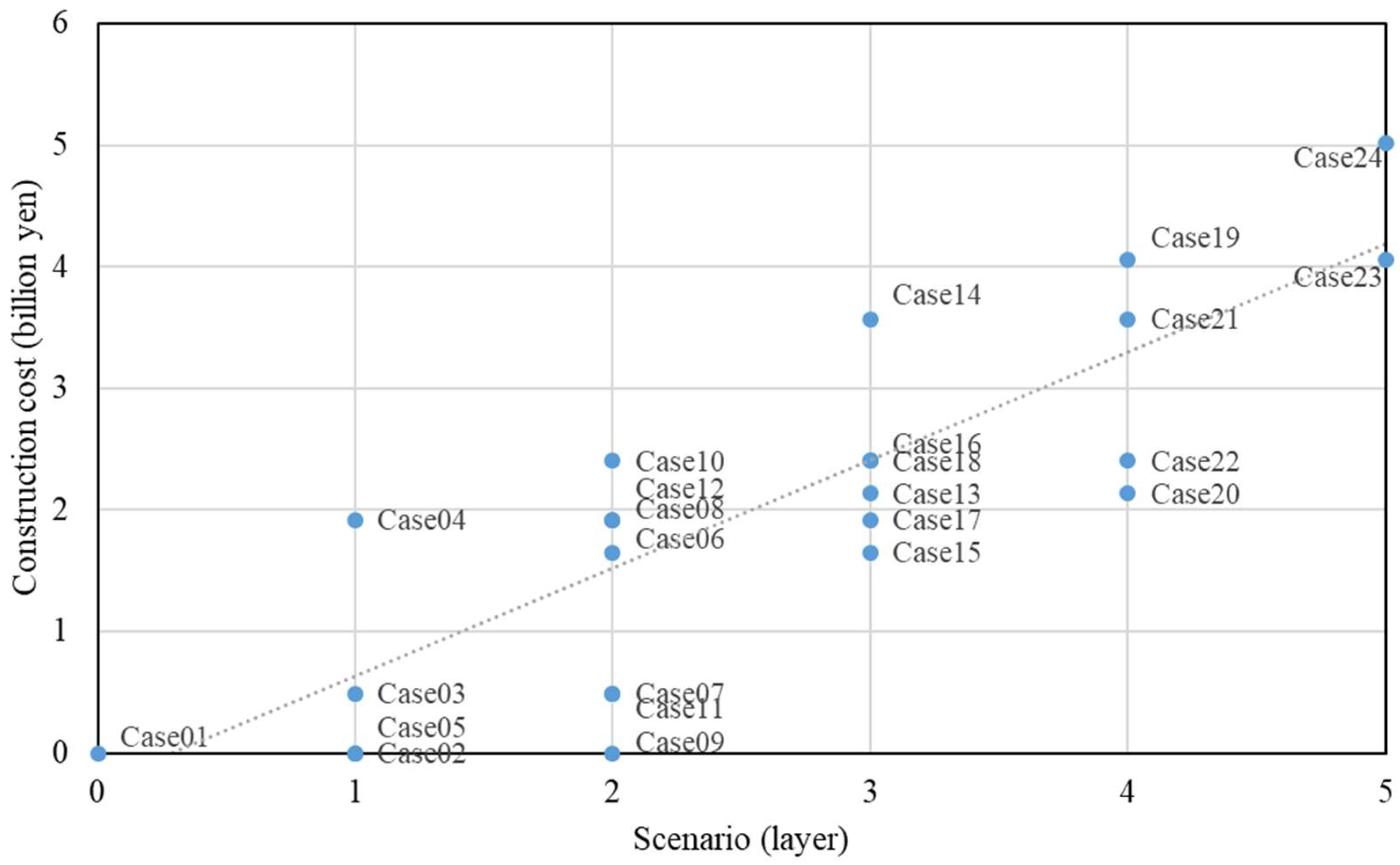

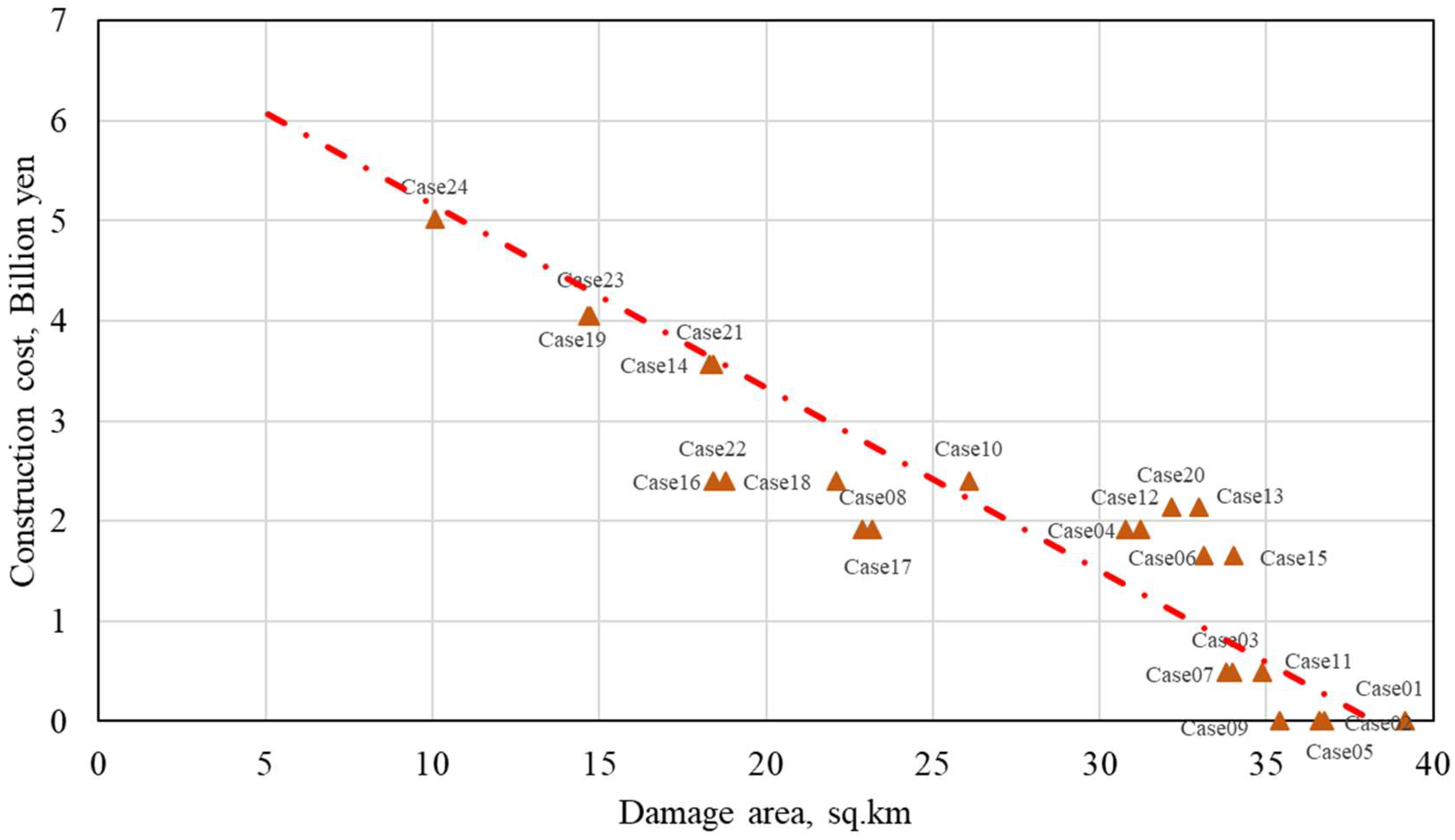
| Scenario | Case | Description |
|---|---|---|
| 0 layer | 01 | Non-structure |
| 1 layer | 02 | Existing seawall |
| 03 | Greenbelt | |
| 04 | Elevated road | |
| 05 | Existing highway | |
| 2 layers | 06 | Existing seawall + New seawall |
| 07 | Existing seawall + Greenbelt | |
| 08 | Existing seawall + Elevated road | |
| 09 | Existing seawall + Existing highway | |
| 10 | Greenbelt + Elevated road | |
| 11 | Greenbelt + Existing highway elevation | |
| 12 | Elevated road + Existing highway | |
| 3 layers | 13 | Existing seawall + New seawall + Greenbelt |
| 14 | Existing seawall + New seawall + Elevated road | |
| 15 | Existing seawall + New seawall + Existing highway | |
| 16 | Existing seawall + Greenbelt + Elevated road | |
| 17 | Existing seawall + Elevated road + Existing highway | |
| 18 | Greenbelt + Elevated road + Existing highway | |
| 4 layers | 19 | Existing seawall + New seawall + Greenbelt + Elevated road |
| 20 | Existing seawall + New seawall + Greenbelt + Existing highway | |
| 21 | Existing seawall + New seawall + Elevated road + Existing highway | |
| 22 | Existing seawall + Greenbelt + Elevated road + Existing highway | |
| 5 layers | 23 | Existing seawall + New seawall + Greenbelt + Elevated road (overflow) + Existing highway |
| 24 | Existing seawall + New seawall + Greenbelt + Elevated road (no-overflow) + Existing highway |
| Scenario (Layer) | Case | Inundation Area in Each Flow Depth Range, sq. km | ||||
|---|---|---|---|---|---|---|
| 0.01–2 m | 2–4 m | 4–6 m | 6–8 m | 8–10 m | ||
| 0 | 01 | 0.323 | 8.492 | 13.272 | 6.455 | 0.018 |
| 1 | 02 | 0.271 | 11.562 | 11.962 | 2.272 | 0.000 |
| 03 | 0.325 | 13.928 | 8.420 | 0.753 | 0.000 | |
| 04 | 0.358 | 12.456 | 7.497 | 0.351 | 0.000 | |
| 05 | 0.350 | 7.826 | 9.242 | 8.670 | 0.045 | |
| 2 | 06 | 0.290 | 13.379 | 9.454 | 0.424 | 0.000 |
| 07 | 0.240 | 12.907 | 10.221 | 1.142 | 0.000 | |
| 08 | 0.479 | 10.085 | 2.125 | 0.000 | 0.000 | |
| 09 | 0.316 | 9.646 | 11.985 | 2.944 | 0.000 | |
| 10 | 0.608 | 11.151 | 3.927 | 0.019 | 0.000 | |
| 11 | 0.218 | 9.727 | 10.910 | 2.736 | 0.000 | |
| 12 | 0.336 | 11.491 | 8.033 | 0.351 | 0.000 | |
| 3 | 13 | 0.353 | 14.705 | 7.198 | 0.375 | 0.000 |
| 14 | 0.433 | 6.855 | 0.691 | 0.000 | 0.000 | |
| 15 | 0.251 | 11.925 | 10.051 | 0.424 | 0.000 | |
| 16 | 0.419 | 7.380 | 0.605 | 0.000 | 0.000 | |
| 17 | 0.431 | 9.817 | 2.125 | 0.000 | 0.000 | |
| 18 | 0.350 | 9.683 | 1.743 | 0.000 | 0.000 | |
| 4 | 19 | 0.218 | 4.024 | 0.229 | 0.000 | 0.000 |
| 20 | 0.309 | 13.715 | 7.596 | 0.203 | 0.000 | |
| 21 | 0.395 | 6.776 | 0.691 | 0.000 | 0.000 | |
| 22 | 0.373 | 7.080 | 0.547 | 0.000 | 0.000 | |
| 5 | 23 | 0.221 | 4.083 | 0.235 | 0.000 | 0.000 |
| 24 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | |
| Structure | Unit Cost | Quantity | Cost (Billion yen) | ||
|---|---|---|---|---|---|
| Elevated road | 0.19 | billion yen/km | 10.20 | km | 1.92 |
| New seawall | 0.14 | billion yen/km | 1.65 | km | 1.65 |
| Greenbelt | 1.00 | million yen/hectare | 486.00 | hectare | 0.49 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pakoksung, K.; Suppasri, A.; Imamura, F. Systematic Evaluation of Different Infrastructure Systems for Tsunami Defense in Sendai City. Geosciences 2018, 8, 173. https://doi.org/10.3390/geosciences8050173
Pakoksung K, Suppasri A, Imamura F. Systematic Evaluation of Different Infrastructure Systems for Tsunami Defense in Sendai City. Geosciences. 2018; 8(5):173. https://doi.org/10.3390/geosciences8050173
Chicago/Turabian StylePakoksung, Kwanchai, Anawat Suppasri, and Fumihiko Imamura. 2018. "Systematic Evaluation of Different Infrastructure Systems for Tsunami Defense in Sendai City" Geosciences 8, no. 5: 173. https://doi.org/10.3390/geosciences8050173
APA StylePakoksung, K., Suppasri, A., & Imamura, F. (2018). Systematic Evaluation of Different Infrastructure Systems for Tsunami Defense in Sendai City. Geosciences, 8(5), 173. https://doi.org/10.3390/geosciences8050173







