Site Effect Assessment of the Gros-Morne Hill Area in Port-au-Prince, Haiti, Part A: Geophysical-Seismological Survey Results
Abstract
:1. Introduction
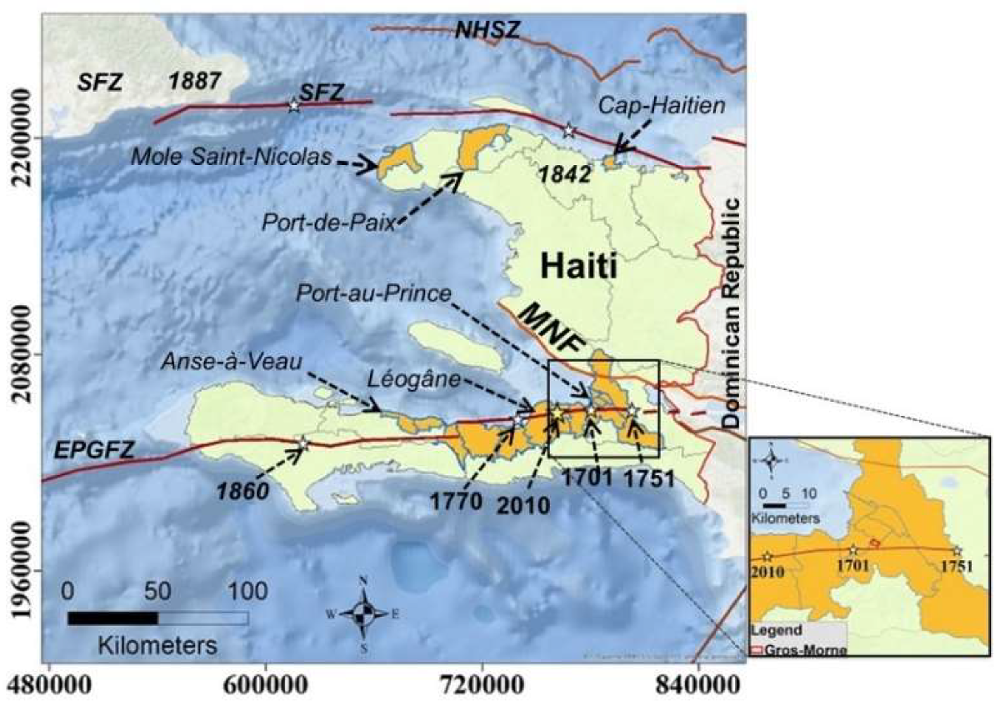
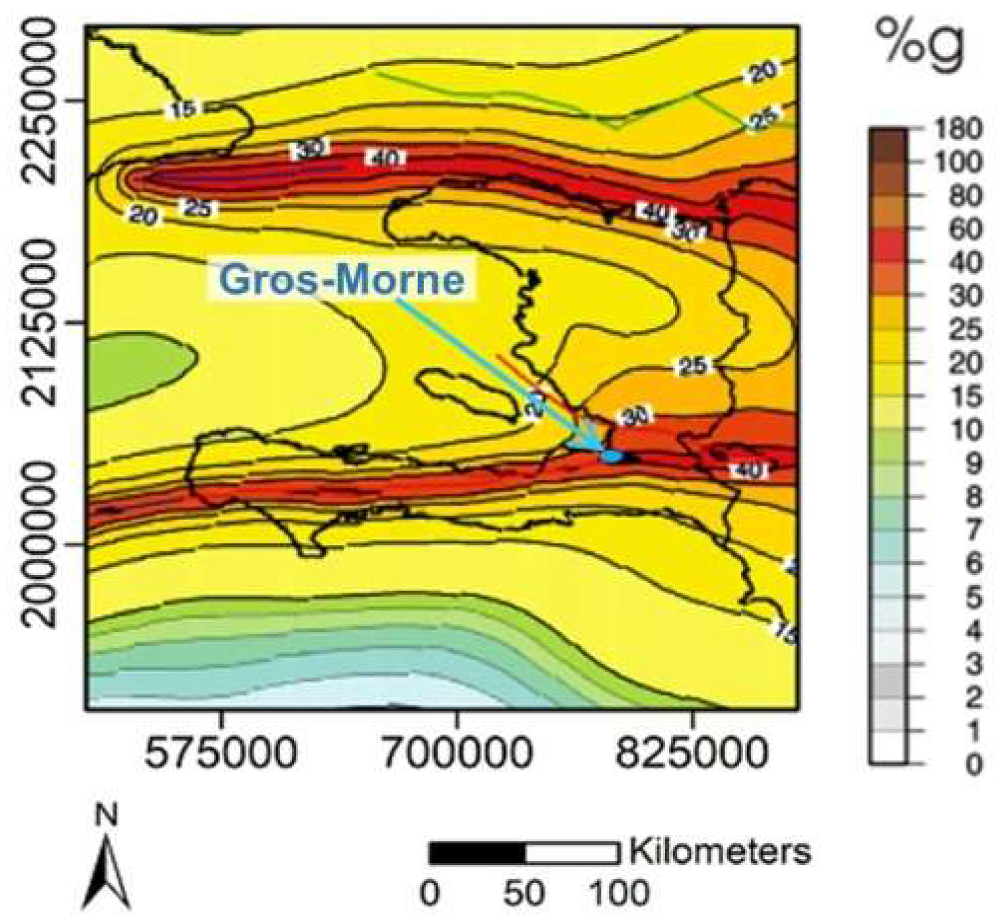
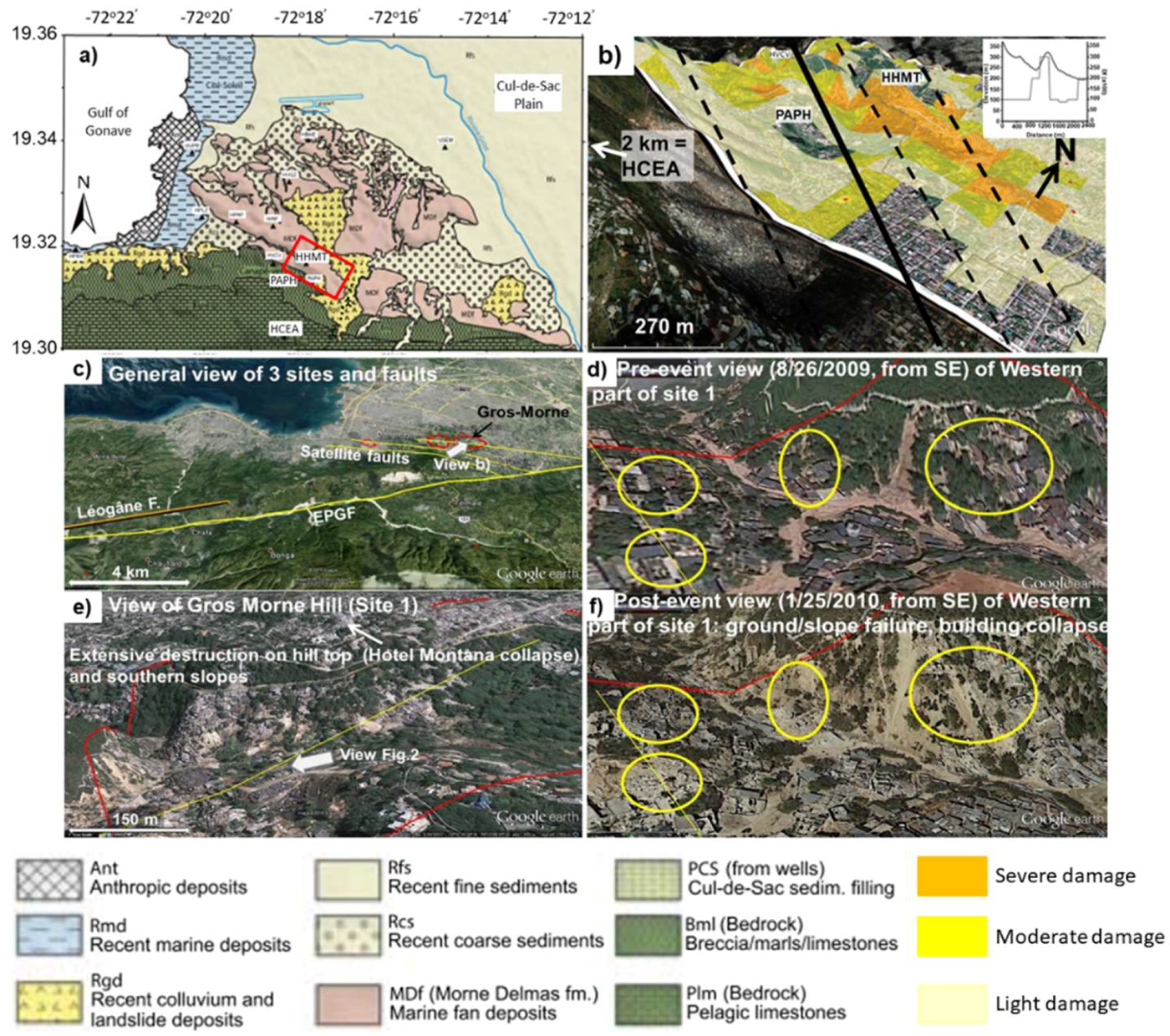
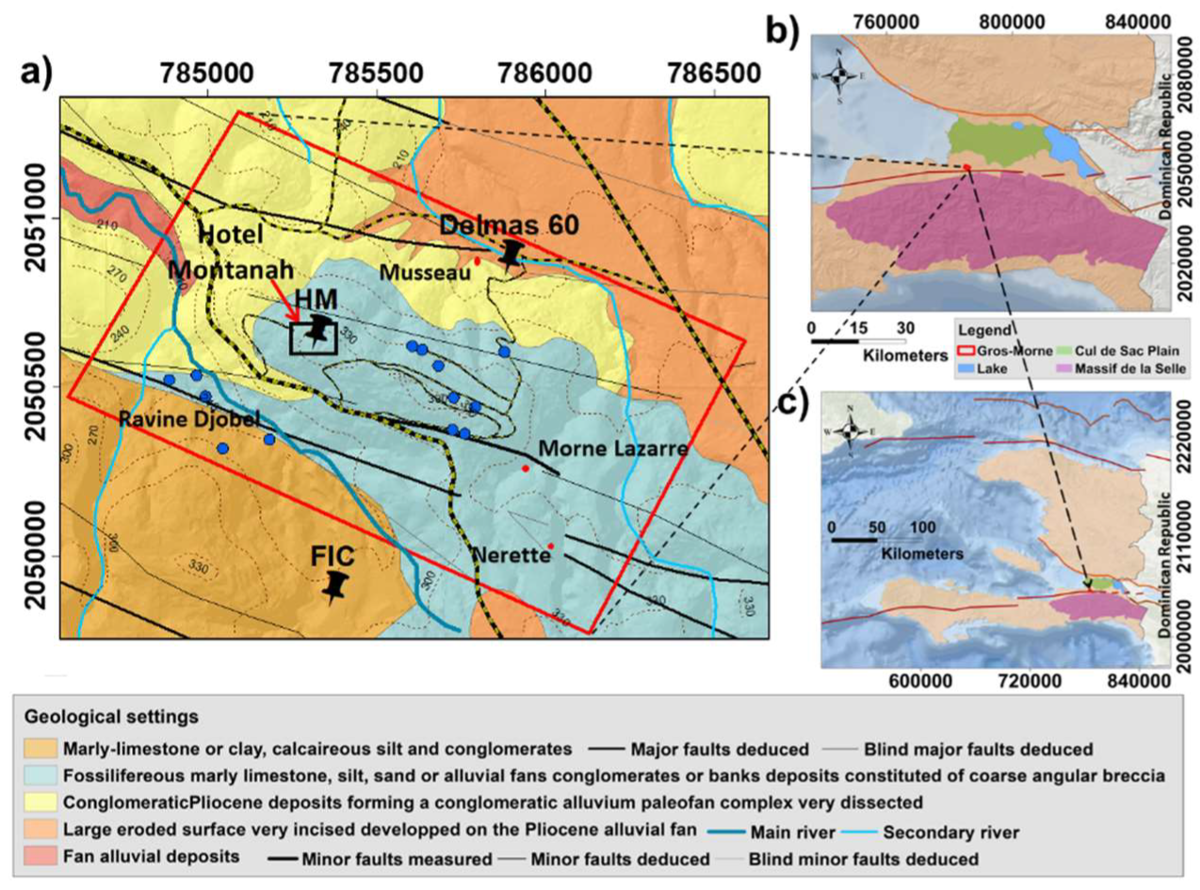
2. The Gros-Morne Hill: Geological and Tectonic Setting
3. Geophysical Investigations
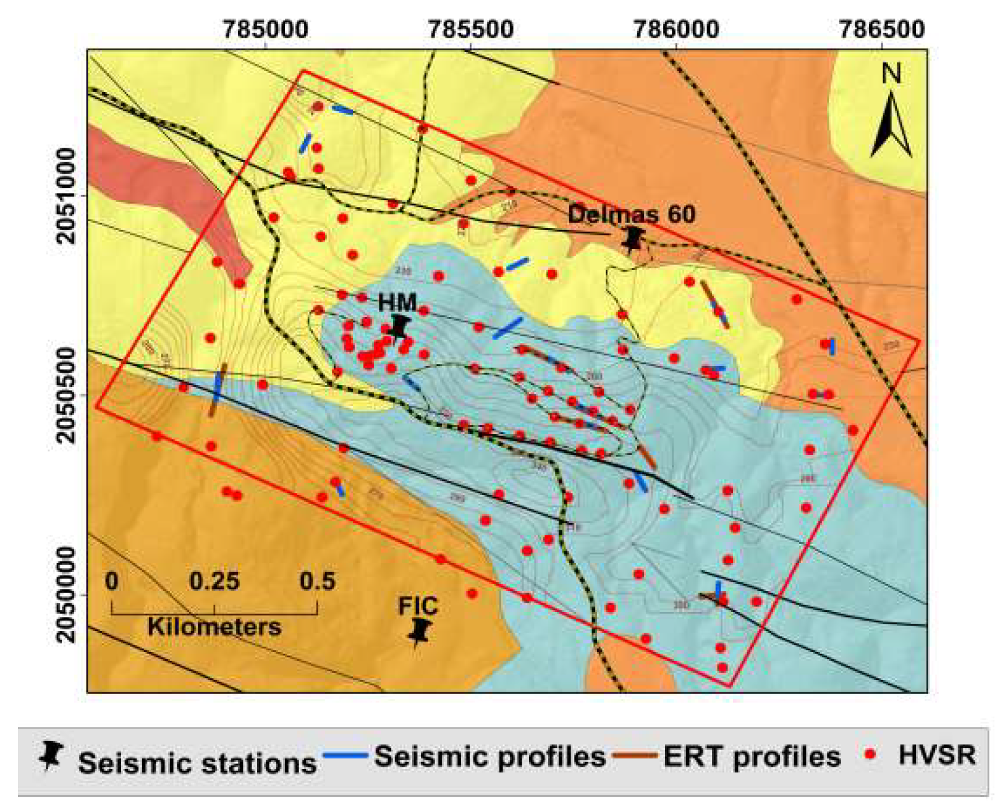
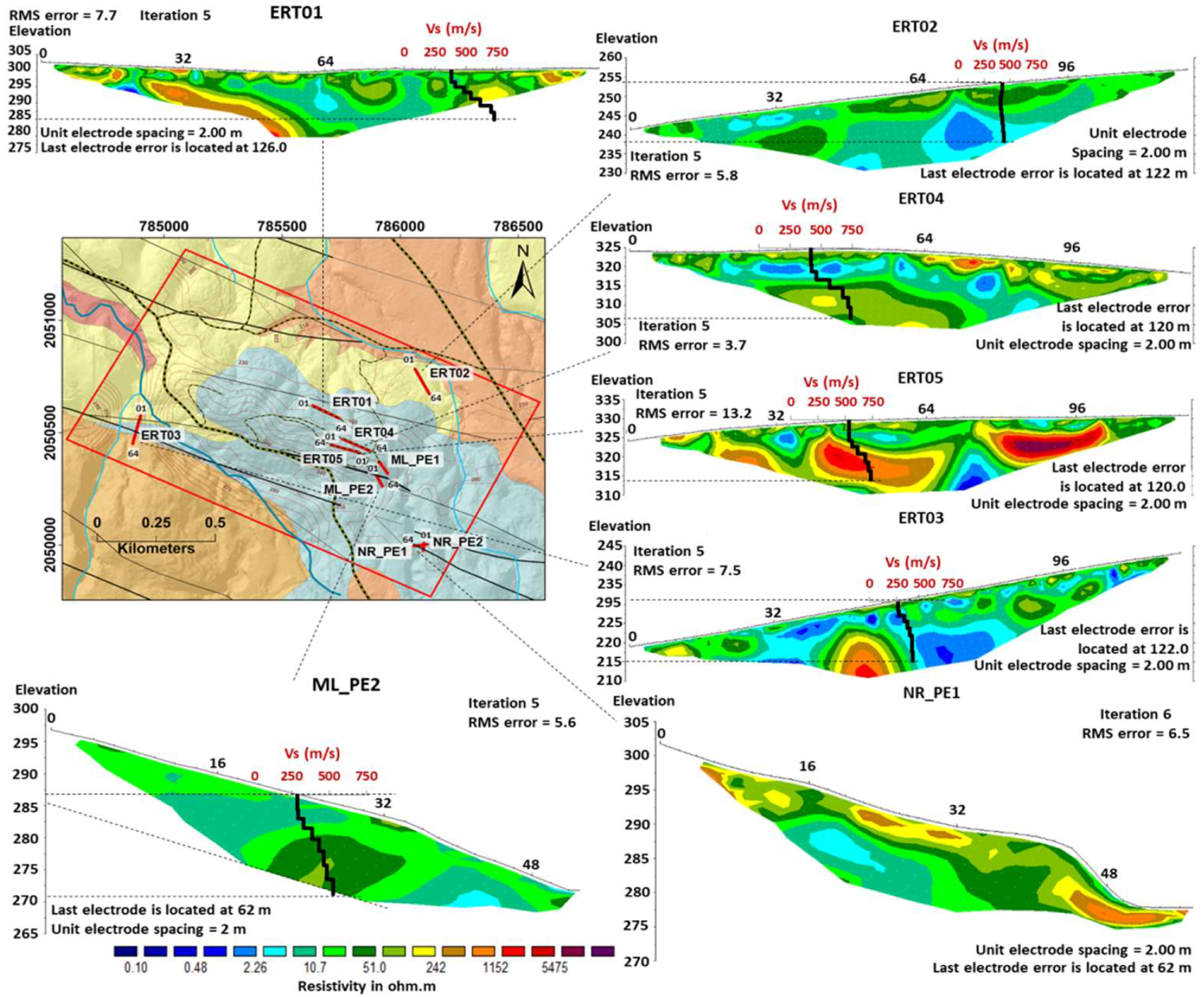
3.1. Electrical Resistivity Tomography Measurements
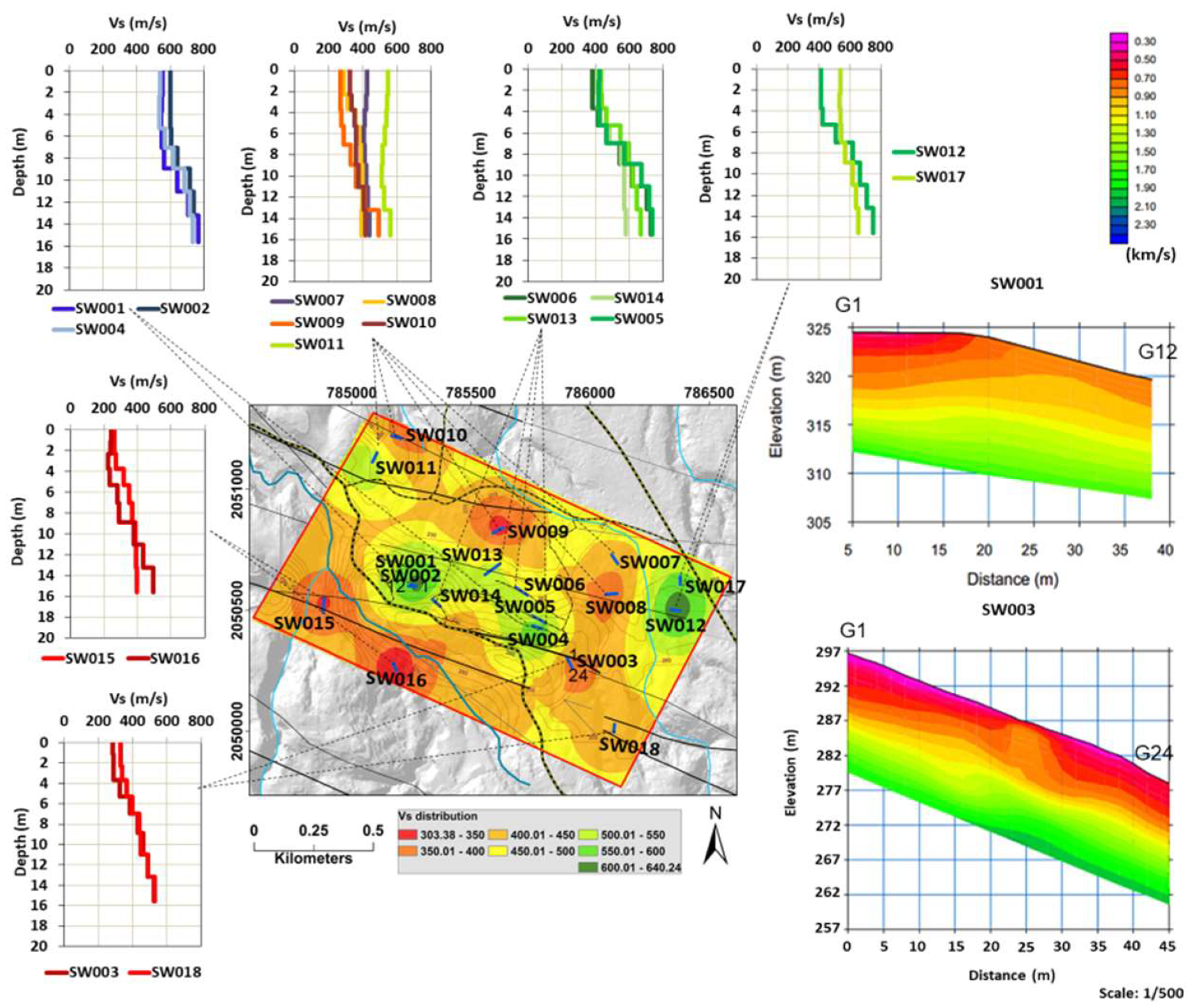
3.2. Seismic Surveys
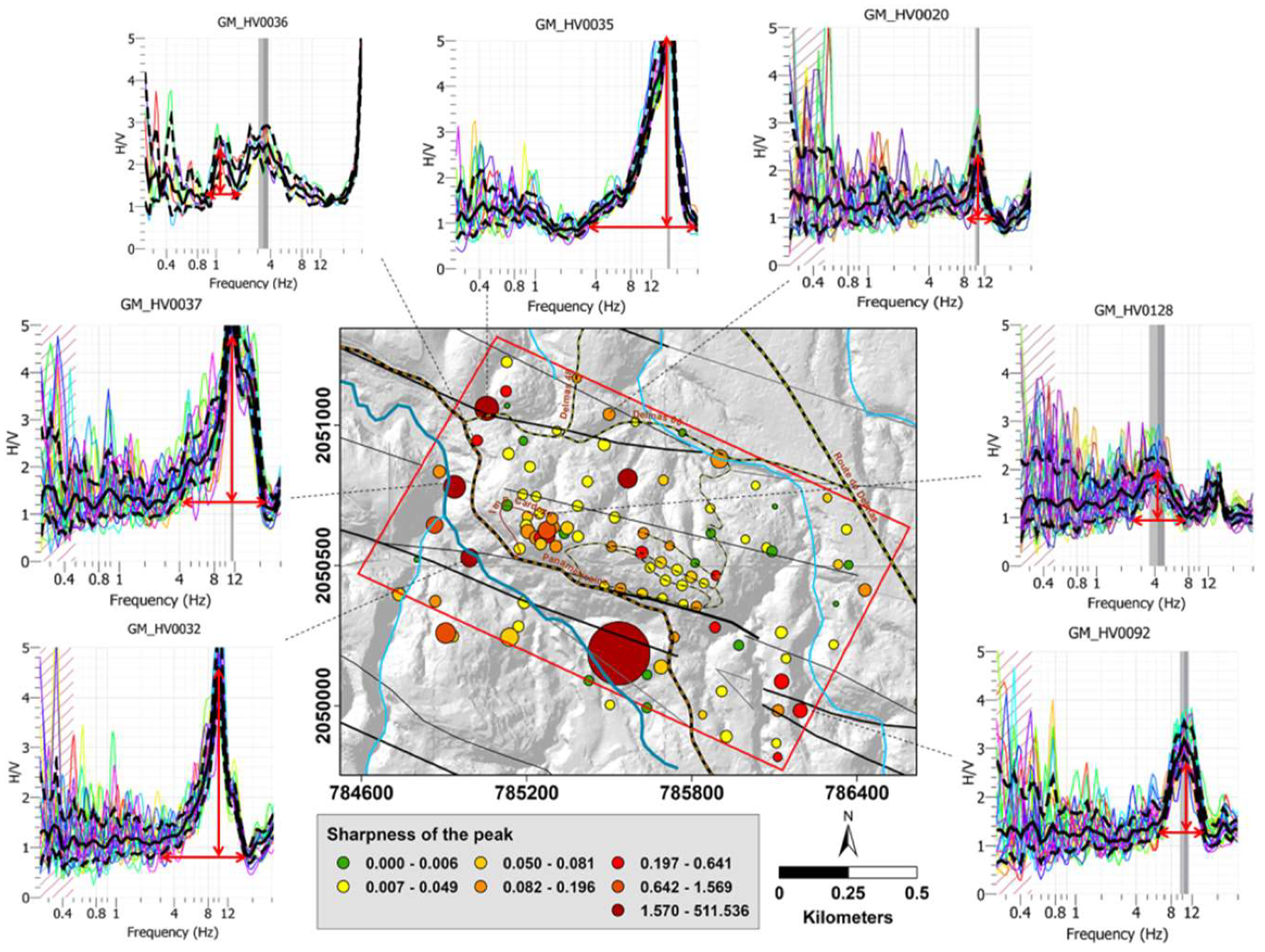
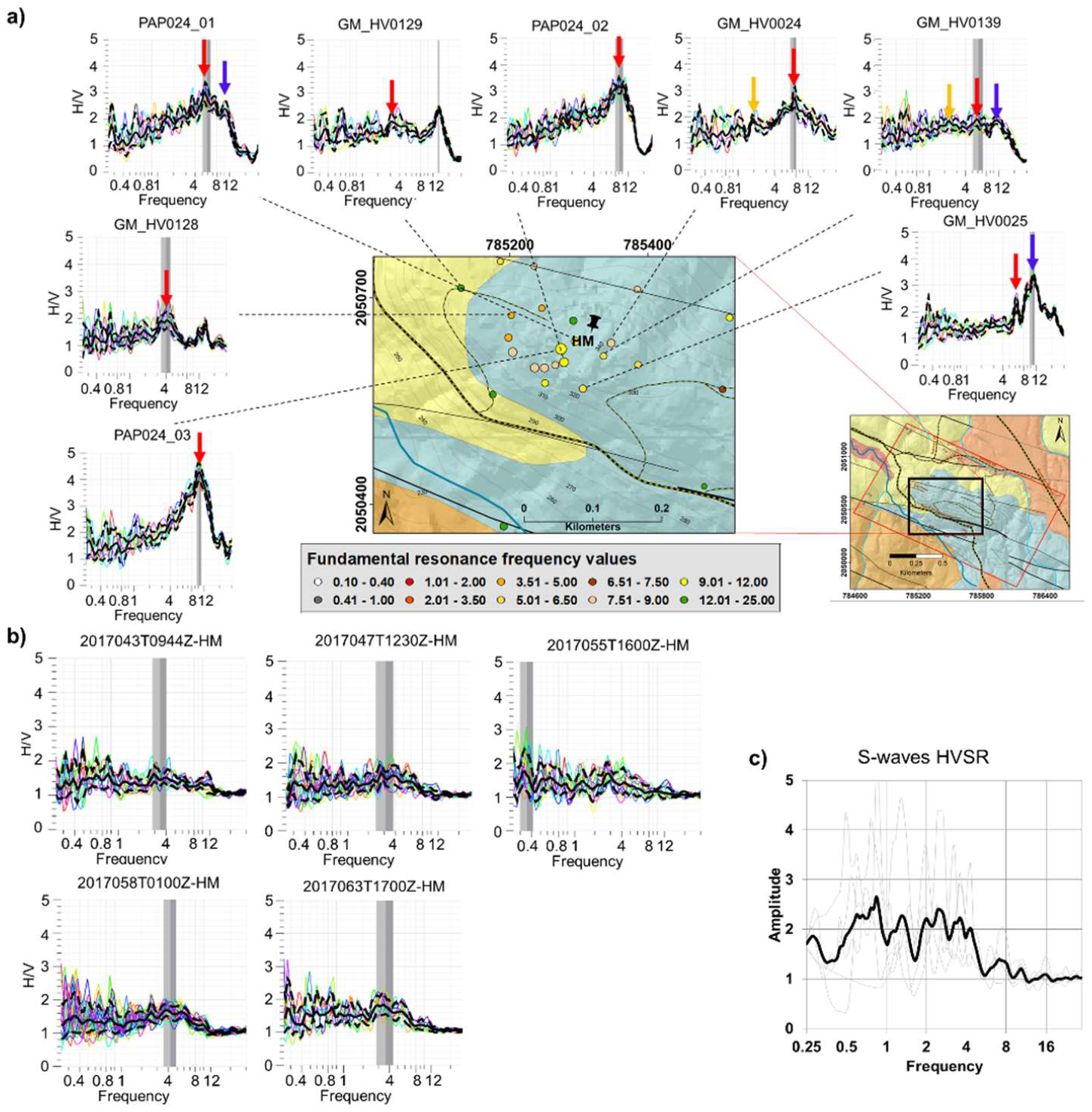
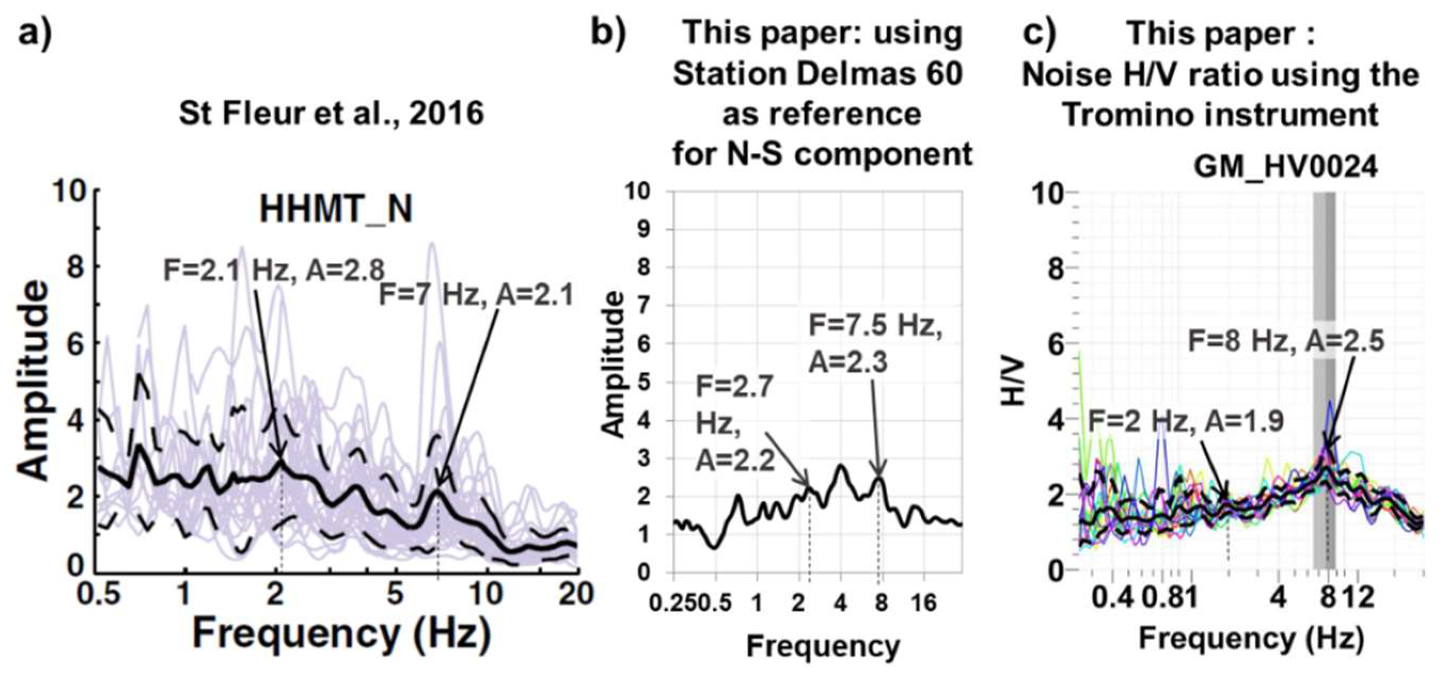
3.3. HVSR Measurements
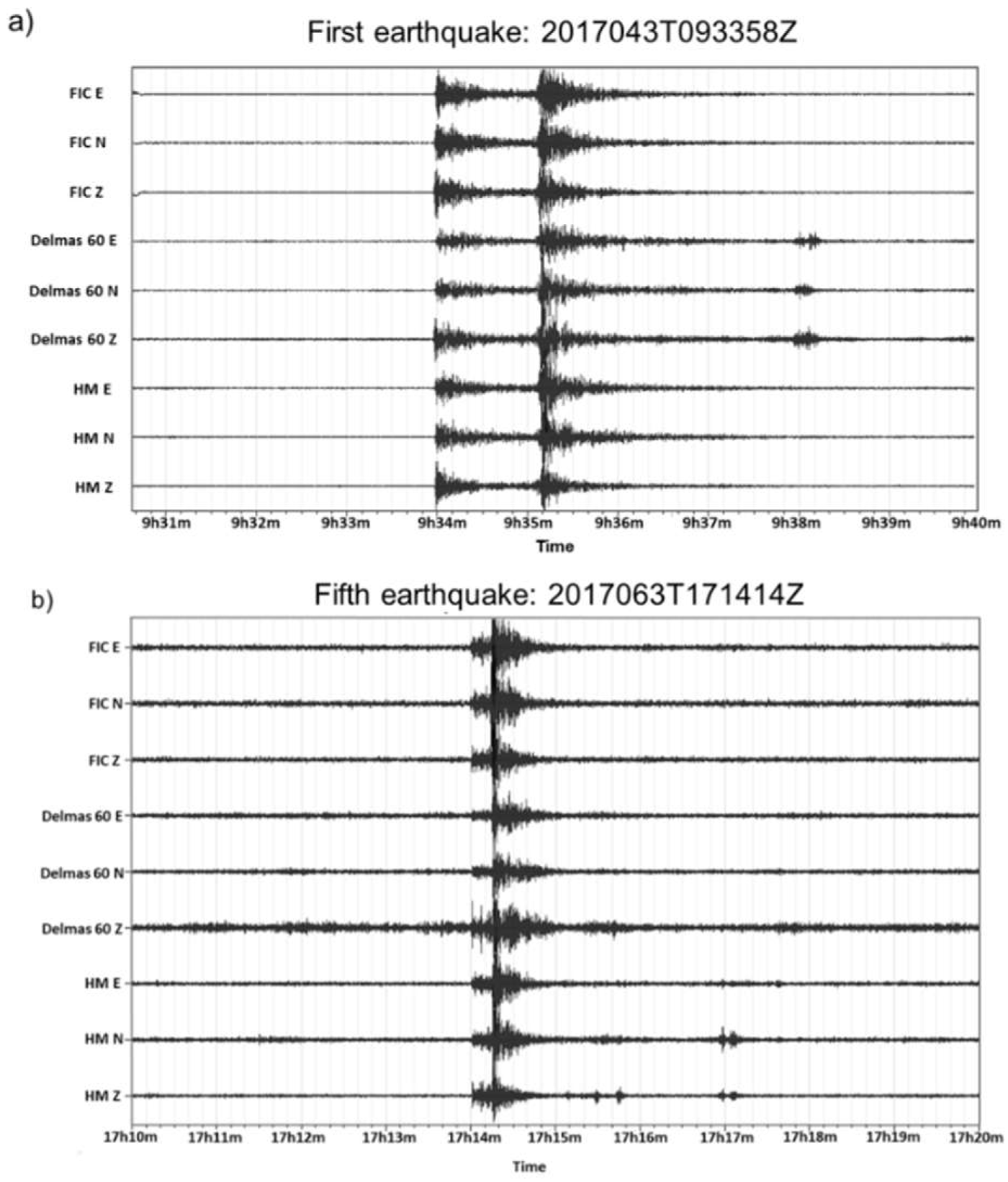
3.4. Earthquake Recordings
4. Data Processing and Results
4.1. ERT Surveys
4.2. Seismic Surveys
4.3. HVSR Results
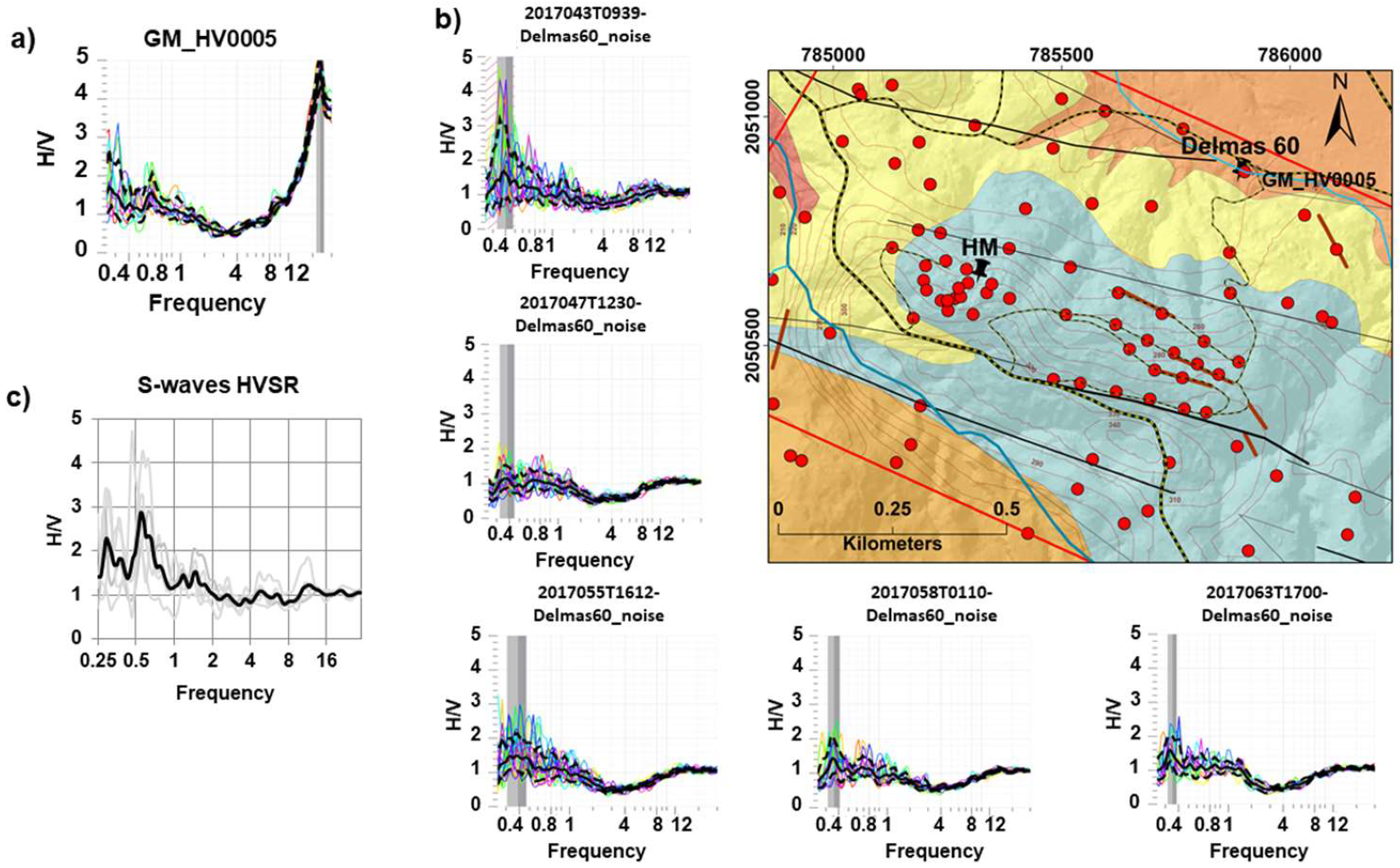
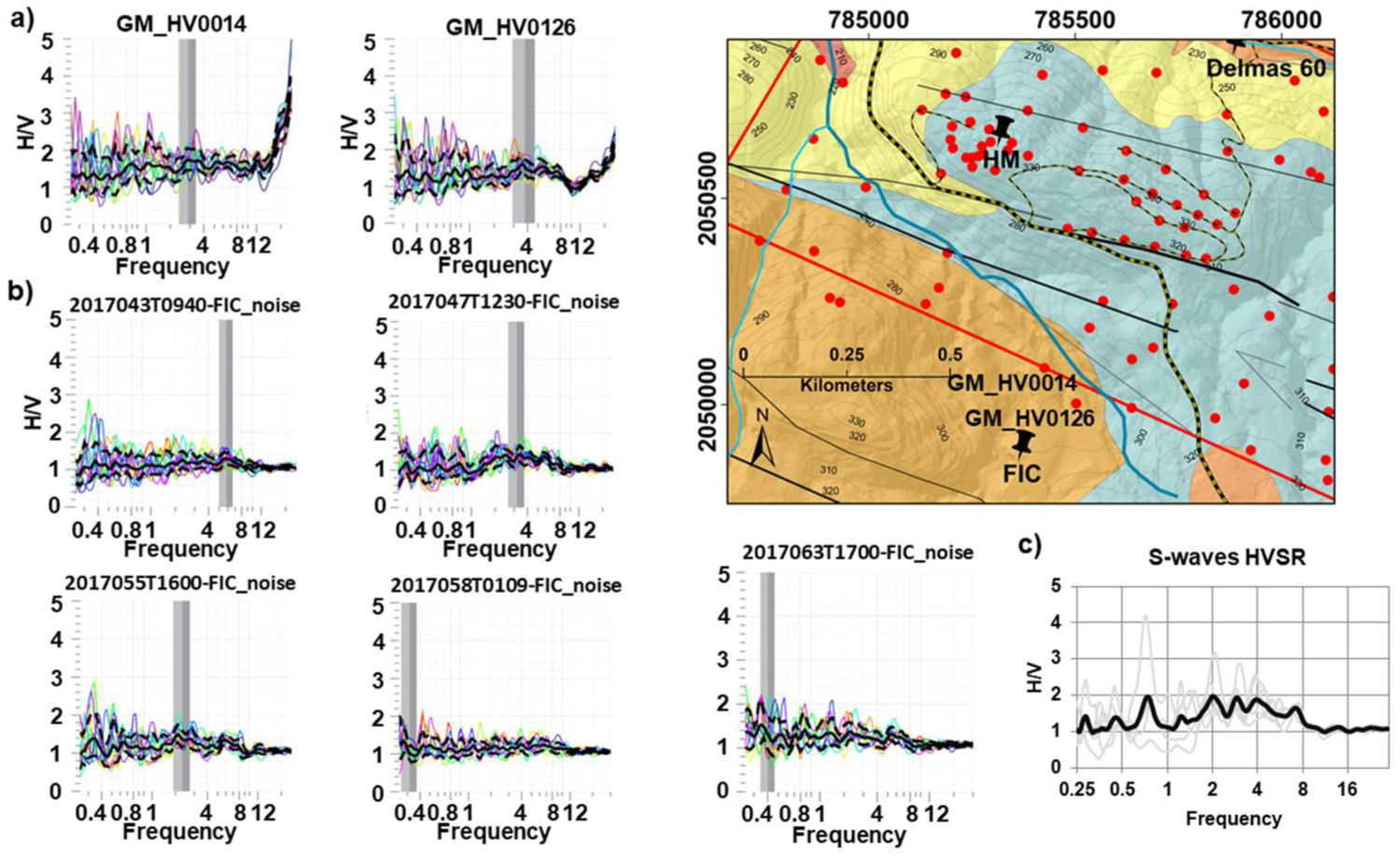
4.4. Earthquake Data
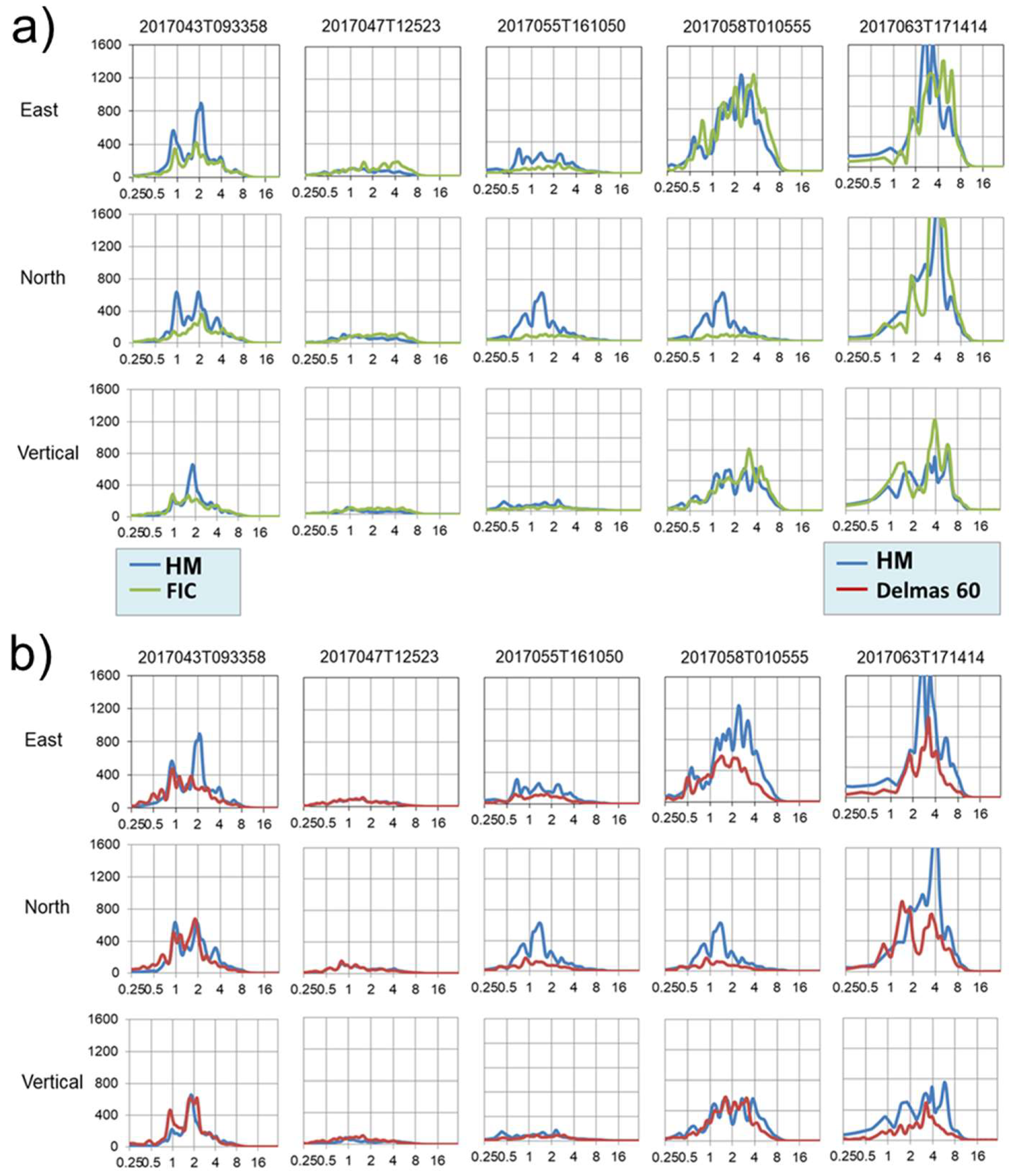
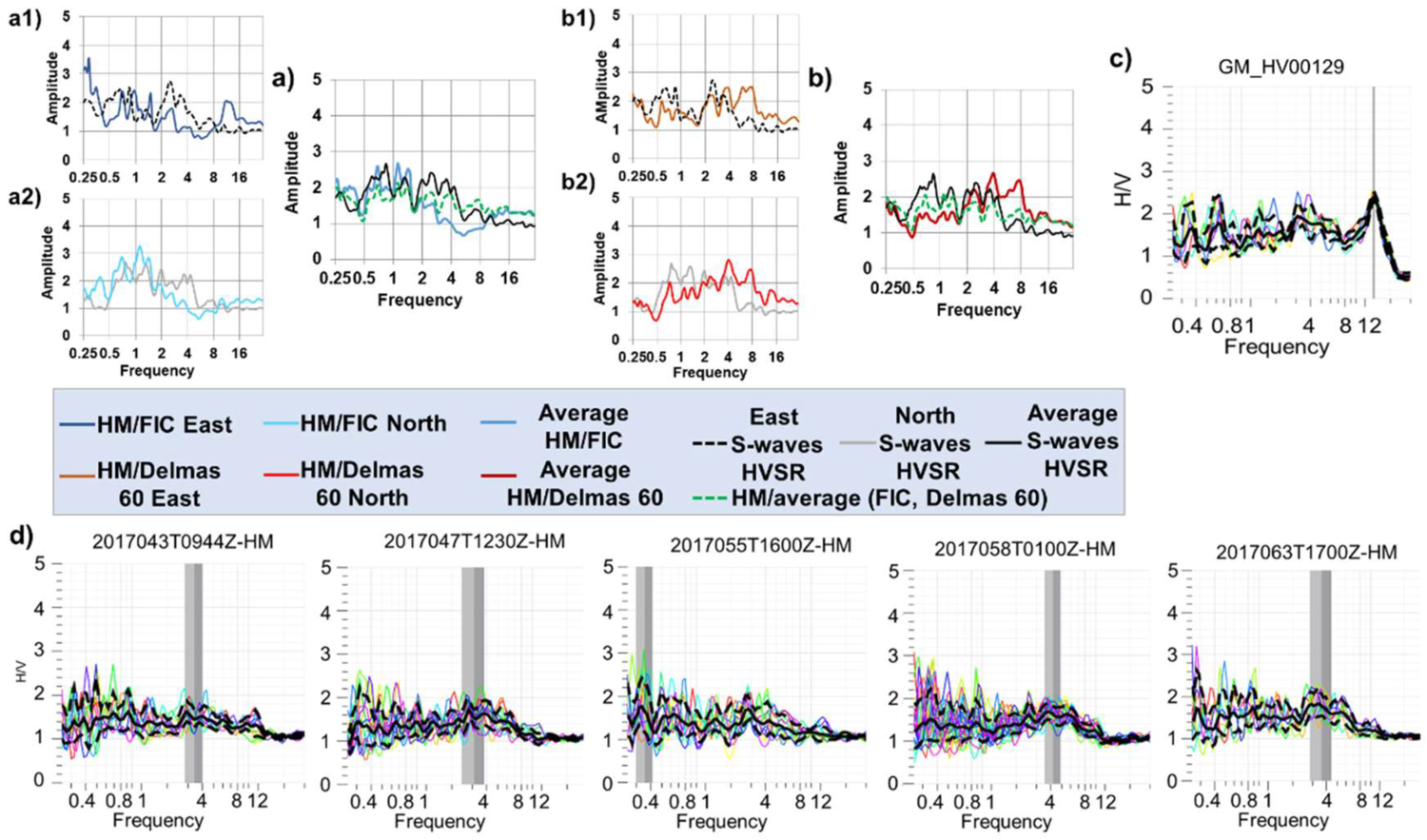
4.4.1. S-Waves HVSR Results
4.4.2. SSR Results
5. Discussion
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix
References
- Frankel, A.; Harmsen, S.; Mueller, C.; Calais, E.; Haase, J. Seismic hazard maps for Haiti. Earthq. Spectra 2011, 27 (Suppl. 1), 23–41. [Google Scholar] [CrossRef]
- Shedlock, K.M.; Tanner, J.G. Seismic hazard map of the western hemisphere. Ann. Geofis. 1999, 42, 1199–1214. [Google Scholar]
- Symithe, S.; Calais, E. Present-day shortening in Southern Haiti from GPS measurements and implications for seismic hazard. Tectonophysics 2016, 679, 117–124. [Google Scholar] [CrossRef]
- Bilham, R. Lessons from the Haiti earthquake. Nature 2010, 463, 878–879. [Google Scholar] [CrossRef] [PubMed]
- Hough, S.E.; Altidor, J.R.; Anglade, D.; Given, D.; Janvier, M.G.; Maharrey, J.Z.; Meremonte, M.; Mildor, B.S.-L.; Prepetit, C.; Yong, A. Localized damage caused by topographic amplification during the 2010 M7.0 Haiti earthquake. Nat. Geosci. 2010, 3, 778–782. [Google Scholar] [CrossRef]
- Assimaki, D.; Jeong, S. Ground-motion observations at Hotel Montana during the M 7.0 2010 Haiti earthquake: Topography or soil amplification? Bull. Seismol. Soc. Am. 2013, 103, 2577–2590. [Google Scholar] [CrossRef]
- Saint-Fleur, S.; Bertrand, E.; Courboulex, F.; De Lépinay, B.M.; Deschamps, A.; Hough, S.; Cultrera, G.; Boisson, D.; Prépetit, C. Site effects in Port-au-Prince (Haiti) from the analysis of spectral ratio and numerical simulations. Bull. Seismol. Soc. Am. 2016, 106, 1298–1315. [Google Scholar] [CrossRef]
- Grelle, G.; Wood, C.; Bonito, L.; Sappa, G.; Reveillino, P.; Rahimi, S.; Guadagno, F.M. A reliable computerized litho-morphometric model for development of 3D maps of Topographic Aggravation Factor (TAF): The cases of East Mountain (Utah, USA) and Port-au-Prince (Haiti). Bull. Earthq. Eng. 2017. [Google Scholar] [CrossRef]
- Calais, E.; Freed, A.; Mattioli, G.; Amelung, F.; Jónsson, S.; Jansma, P.; Hong, S.-H.; Dixon, T.; Prépetit, C.; Momplaisir, R. Transpressional rupture of an unmapped fault during the 2010 Haiti earthquake. Nat. Geosci. 2010, 3, 794–799. [Google Scholar] [CrossRef]
- Terrier, M.; Bialkowski, A.; Nachbaur, A.; Prépetit, C.; Joseph, Y.F. Revision of the geological context of the Port-au-Prince metropolitan area, Haiti: Implications for slope failures and seismic hazard assessment. Nat. Hazards Earth Syst. Sci. 2014, 14, 2577–2587. [Google Scholar] [CrossRef]
- Butterlin, J. Géologie Générale de la République d’Haïti; Travaux et Mémoires; Institut des Hautes Études de l’Amérique Latine: Paris, France, 1960; Volume 6, p. 194. [Google Scholar]
- Bourgueil, B.; Andreieff, P.; Lasnier, J.; Gonnard, R.; Le Métour, J.; Rançon, J.-P. Synthèse Géologique de la République d’Haïti: Volume I-Géologie; ATN/SF 2506 HA; Bureau Des Mines et de l’Énergie: Port-au-Prince, Haïti, 1988; Volume 1, p. 332. [Google Scholar]
- Boisson, D.; Momplaisir, R.B.-A. Carte Géologique d’Haïti, 1/250000ème; Bureau des Mines et de l’Energie: Port-au-Prince, Haïti, 1988. [Google Scholar]
- Bachhuber, J.L.; Rathje, E.M.; Cox, B.R.; Kottke, A.; Wood, C.; Dulberg, R.A.; GEER Team. Haiti Geologic UNOSAT Damage Map; GEER Team: Port-au-Prince, Haiti, 2010. [Google Scholar]
- Ministry of Agriculture Water Resources and Rural Development. Ministère de l’Agriculture des Ressources Naturelles et du Développement Rural. Service des Ressources en Eau; Carte Hyrogéologique de la République d’Haïti. Echelle 1/250000; 1990.
- Galli, P.A.C.; Giocoli, A.; Peronace, E.; Piscitelli, S.; Quadrio, B.; Bellanova, J. Integrated near surface geophysics across the active Mount Marzano Fault System (southern Italy): Seismogenic hints. Int. J. Earth Sci. 2014, 103, 315–325. [Google Scholar] [CrossRef]
- Nogoshi, M.; Igarashi, T. On the propagation characteristics ofmicrotremor. J. Seismol. Soc. Jpn. 1970, 23, 264–280. [Google Scholar]
- Nakamura, Y.A. Method for Dynamic Characteristics Estimation of Subsurface Using Microtremor on the Ground Surface; Quarterly Report; Railway Technical Research Institute: Tokyo, Japan, 1989; Volume 30, pp. 25–33. [Google Scholar]
- Bonnefoy-Claudet, S.; Cornou, C.; Bard, P.Y.; Cotton, F.; Moczo, P.; Kristek, J.; Fäh, D. H/V ratio: A tool for site effects evaluation. Results from 1-D noise simulations. Geophys. J. Int. 2006, 167, 827–837. [Google Scholar] [CrossRef]
- Lachet, C.; Bard, P.Y. Numerical and Theoretical Investigations on the Possibilities and Limitations of Nakamura’s Technique. J. Phys. Earth 1994, 42, 377–397. [Google Scholar] [CrossRef]
- Borcherdt, R.D. Effects of local geological geology on ground motion near the San Francisco. Bull. Seismol. Soc. Am. 1970, 60, 29–61. [Google Scholar]
- Laurendeau, A.; Courboulex, F.; Bonilla, L.F.; Alvarado, A.; Naya, V.A.; Guéguen, P.; Mercerat, E.D.; Singaucho, J.C.; Bertrand, E.; Perrault, M.; et al. Low-Frequency Seismic Amplification in the Quito Basin (Ecuador) Revealed by Accelerometric Recordings of the RENAC Network. Bull. Seismol. Soc. Am. 2017, 107, 2917–2926. [Google Scholar] [CrossRef]
- Loke, M.H. Tutorial: 2-D and 3-D Electrical Imaging Survey. 2011. Available online: https://pangea.stanford.edu/research/groups/sfmf/docs/DCResistivity_Notes.pdf (accessed on 20 April 2018).
- Wathelet, M. GEOPSY Geophysical Signal Database for Noise Array Processing. Software, LGIT, Grenoble. 2005. Available online: www.geopsy.org (accessed on 20 April 2018).
- Konno, K.; Ohmachi, T. Ground-Motion Characteristics Estimated from Spectral Ratio between Horizontal and Vertical Components of Microtremor. Bull. Seismol. Soc. Am. 1998, 88, 228–241. [Google Scholar]
- Bard, P.; the SESAME-Team. Guidelines for the Implementation of the H/V Spectral Ratio Technique on Ambient Vibrations: Measurements, Processing, and Interpretations, SESAME European Research Project Report: European Commission – Research General Directorate Project No. EVG1-CT-2000-00026 SESAME. 2004; 62. Available online: ftp://ftp.geo.uib.no/pub/seismo/SOFTWARE/SESAME/USER-GUIDELINES/SESAME-HV-User-Guidelines.pdf(accessed on 20 April 2018).
- Soutmans, T. Application de la Méthode Microsismique H/V Aux Études de Sites de Stockage de Déchets à LUBUMBASHI (République Démocratique du Congo) et de Glissements de Terrain Dans la Vallée de Maily-Say (République du Kirghizistan). Master Thesis, University of Liege, Liège, Belgium, 2010; p. 110. [Google Scholar]
- Geli, L.; Bard, P.Y.; Jullien, B. The effect of topography on earthquake ground motion: A review and new results. Bull. Seismol. Soc. Am. 1988, 78, 42–63. [Google Scholar]
- Cox, B.R.; Bachhuber, J.; Rathje, E.; Wood, C.M.; Dulberg, R.; Kottke, A.; Olson, S.M. Shear wave velocity-and geology-based seismic microzonation of Port-au-Prince, Haiti. Earthq. Spectra 2011, 27, 67–92. [Google Scholar] [CrossRef]
- Massa, M.; Barani, S.; Lovati, S. Overview of topographic effects based on experimental observations: Meaning, causes and possible interpretations. Geophys. J. Int. 2014, 197, 1537–1550. [Google Scholar] [CrossRef]
- Ulysse, S.; Boisson, D.; Prépetit, C.; Havenith, H.B. Site Effect Assessment of the Gros-Morne Hill Area in Port-au-Prince, Hait, Part B: Mapping and Modelling Results. Geosciences 2018, in press. [Google Scholar]


| Julian Day | Date | Time (UTC) | Latitude | Longitude | Depth (km) | Magnitude | Location |
|---|---|---|---|---|---|---|---|
| 43 | 12 February 2017 | 9:33:58 | - | - | - | - | - |
| 47 | 16 February 2017 | 12:52:39 | 18.763 | 69.403 | 101.9 | 4.6 | Dominican Republic |
| 55 | 24 February 2017 | 16:10:50 | - | - | - | - | - |
| 58 | 27 February 2017 | 1:05:26 | 18.997 | 70.019 | 73.4 | 4.5 | Dominican Republic |
| 63 | 4 March 2017 | 17:14:14 | - | - | - | - | - |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ulysse, S.; Boisson, D.; Prépetit, C.; Havenith, H.-B. Site Effect Assessment of the Gros-Morne Hill Area in Port-au-Prince, Haiti, Part A: Geophysical-Seismological Survey Results. Geosciences 2018, 8, 142. https://doi.org/10.3390/geosciences8040142
Ulysse S, Boisson D, Prépetit C, Havenith H-B. Site Effect Assessment of the Gros-Morne Hill Area in Port-au-Prince, Haiti, Part A: Geophysical-Seismological Survey Results. Geosciences. 2018; 8(4):142. https://doi.org/10.3390/geosciences8040142
Chicago/Turabian StyleUlysse, Sophia, Dominique Boisson, Claude Prépetit, and Hans-Balder Havenith. 2018. "Site Effect Assessment of the Gros-Morne Hill Area in Port-au-Prince, Haiti, Part A: Geophysical-Seismological Survey Results" Geosciences 8, no. 4: 142. https://doi.org/10.3390/geosciences8040142
APA StyleUlysse, S., Boisson, D., Prépetit, C., & Havenith, H.-B. (2018). Site Effect Assessment of the Gros-Morne Hill Area in Port-au-Prince, Haiti, Part A: Geophysical-Seismological Survey Results. Geosciences, 8(4), 142. https://doi.org/10.3390/geosciences8040142






