Generating Observation-Based Snow Depletion Curves for Use in Snow Cover Data Assimilation
Abstract
1. Introduction
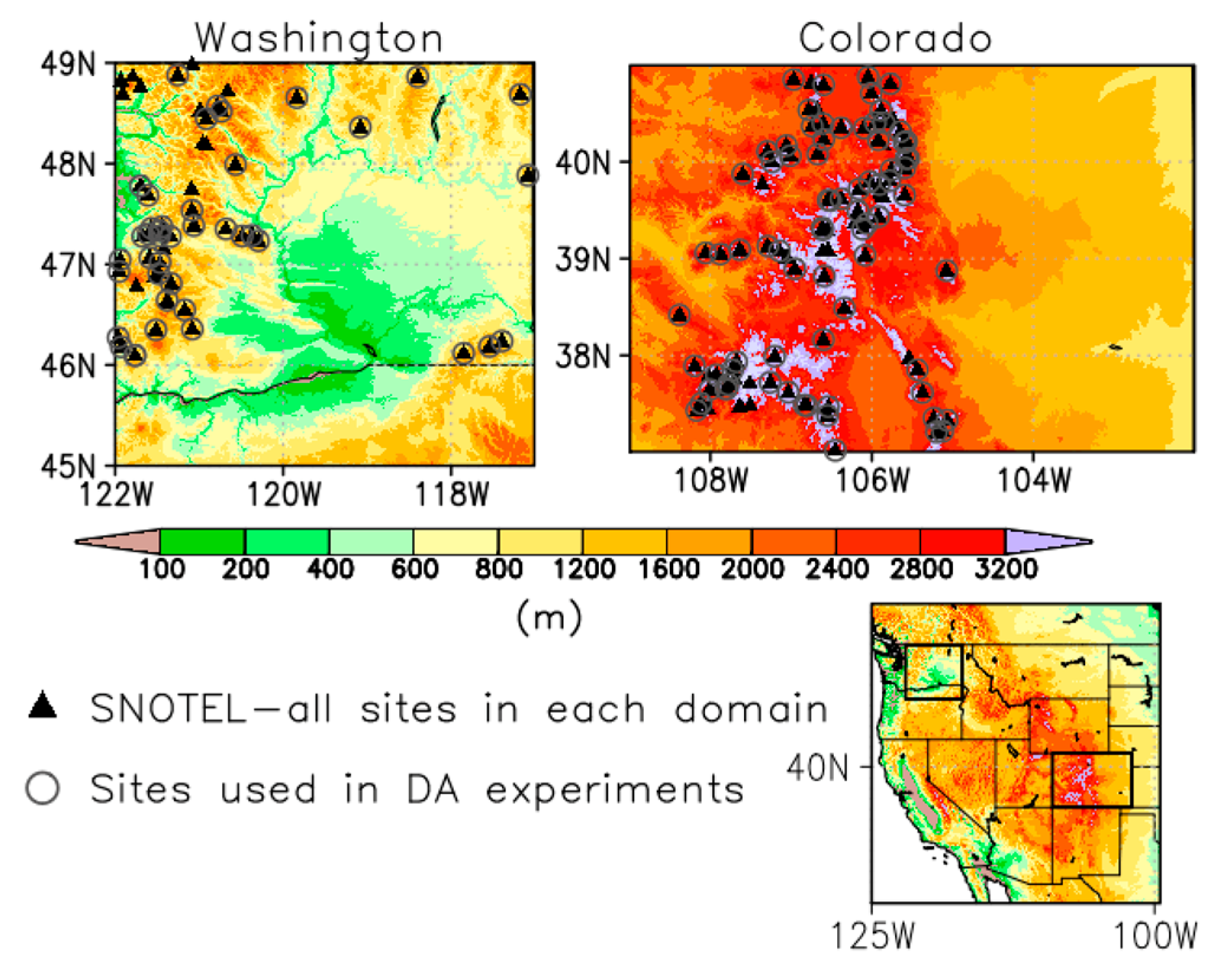
2. Study Area
3. Data and Model Sources
3.1. Observational Datasets Used
3.2. Land Surface Model Description and Setup
3.3. Data Assimilation Method and Experiment Setup
4. Methods
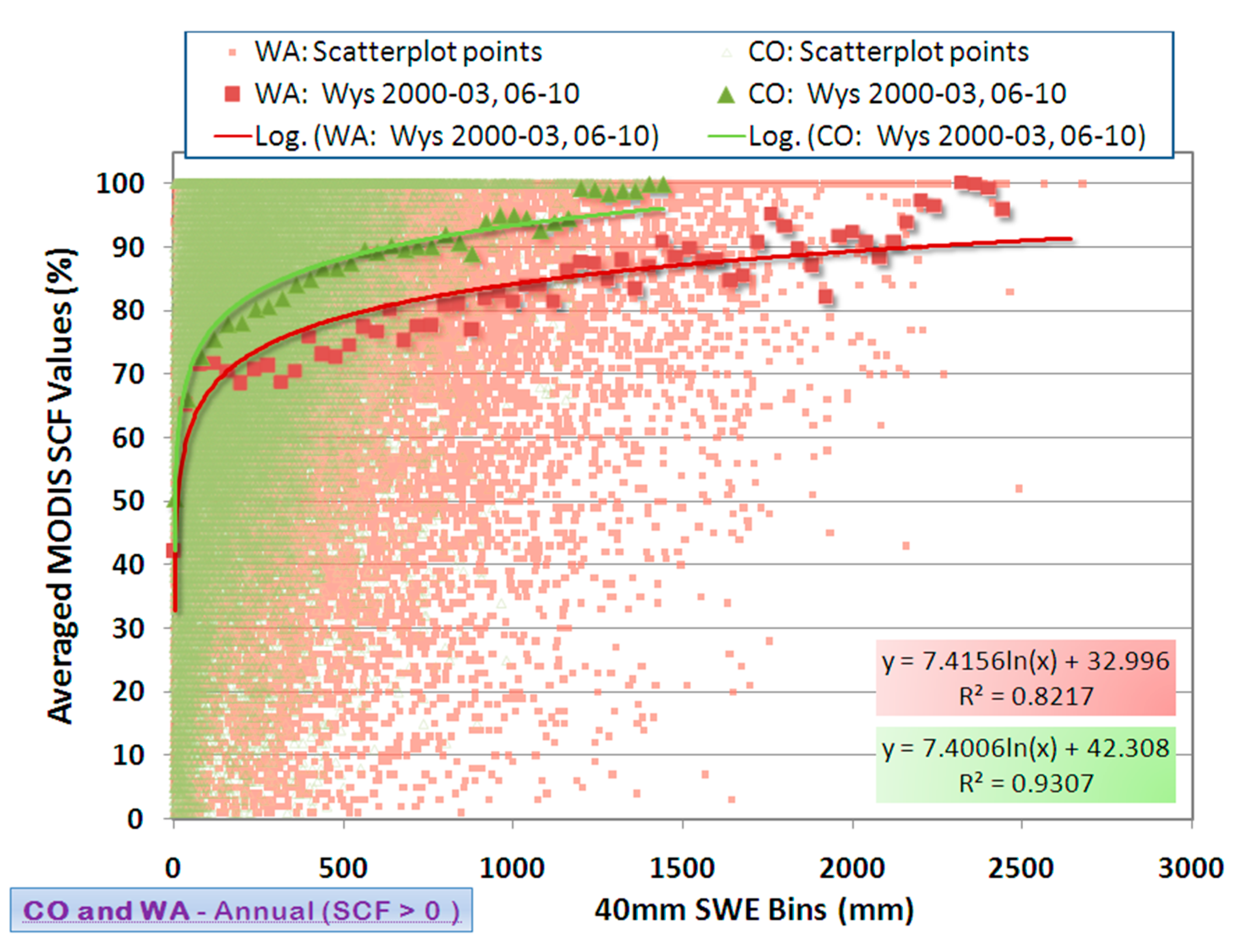
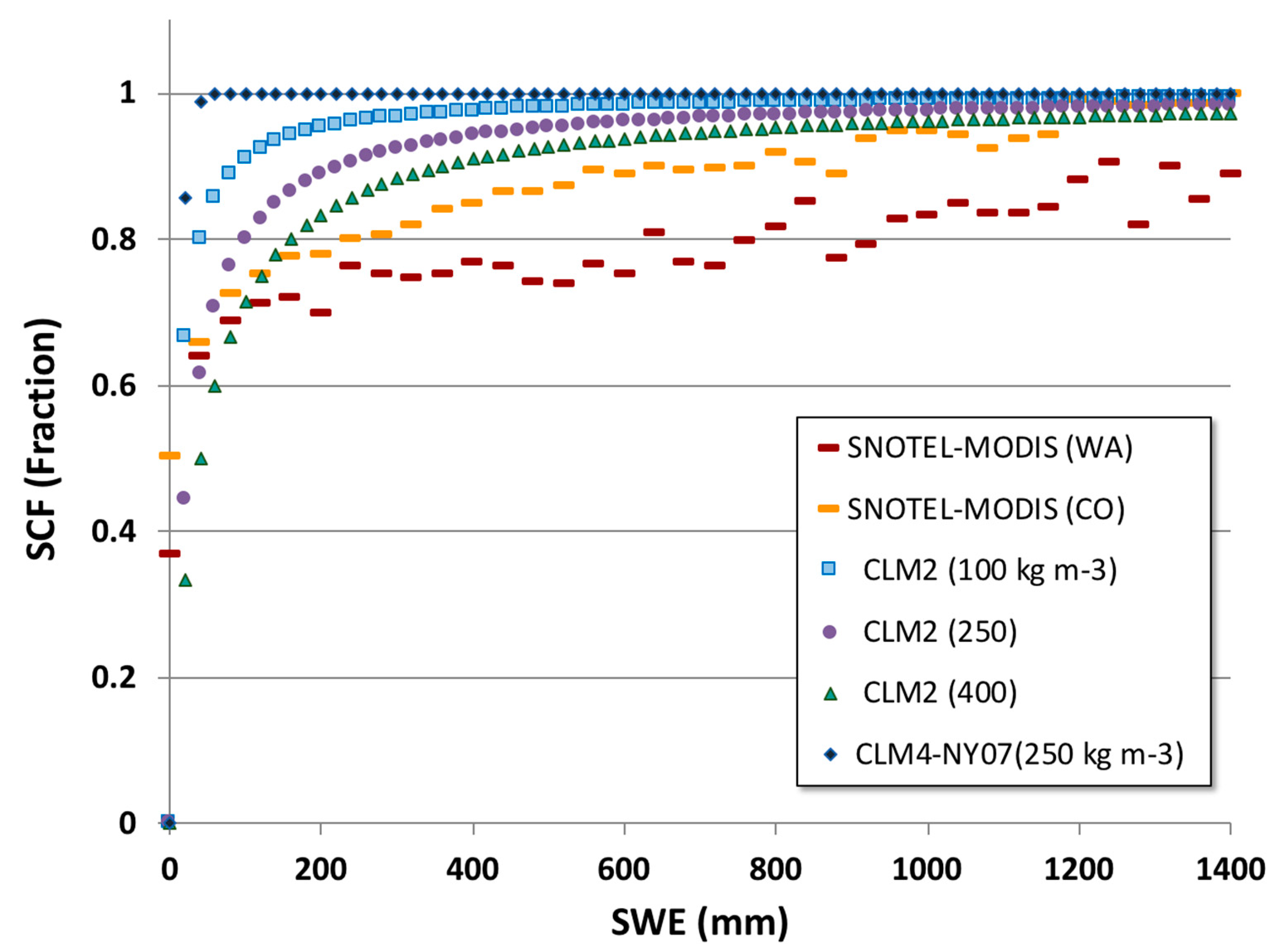
4.1. Deriving the Snow Depletion Curves from Snow Observations
4.2. Applying the New Snow Depletion Curves as Observation Operators
4.3. Generating Temporal and Physiographic Varying Snow Depletion Curves
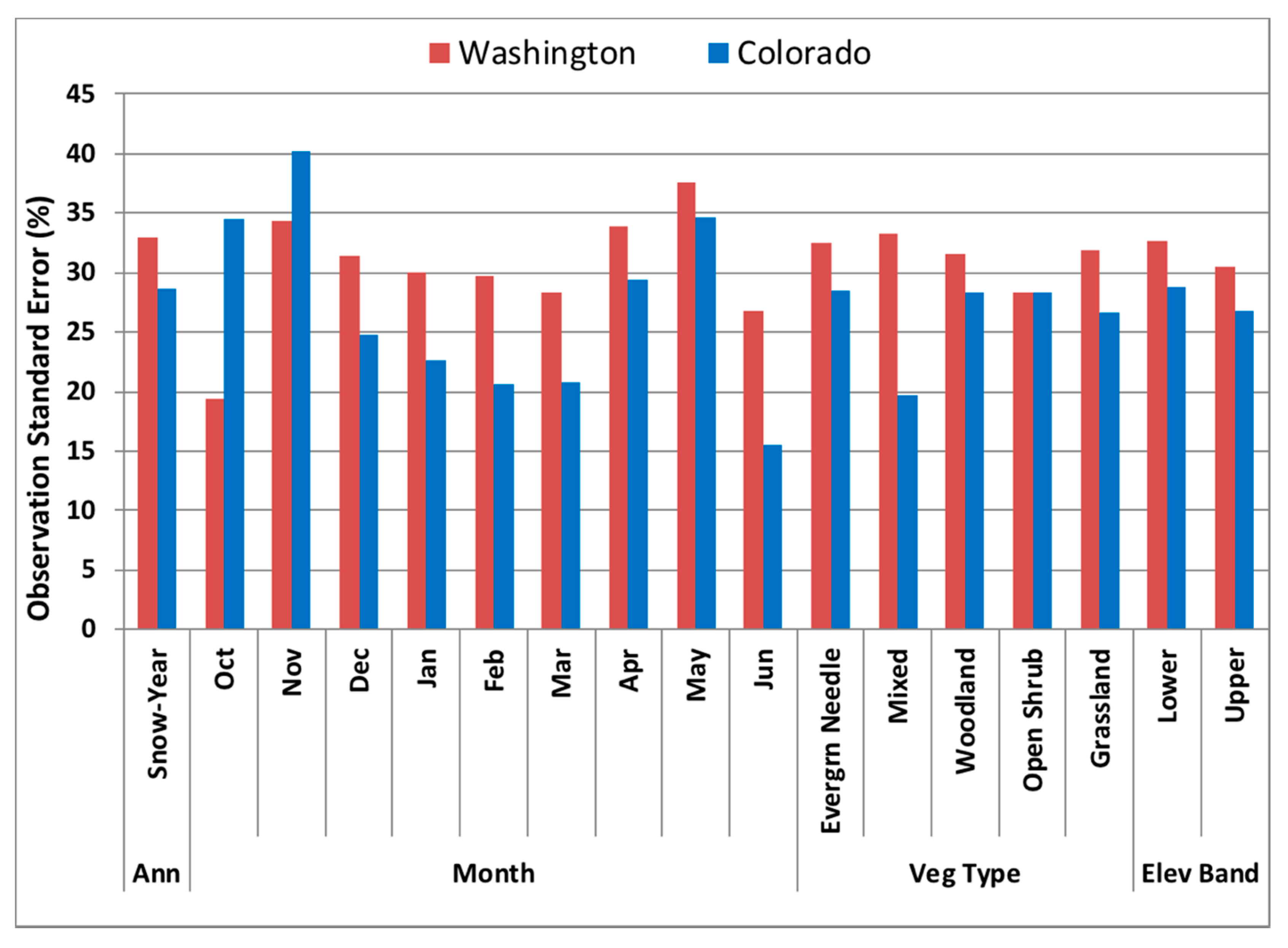
4.4. Estimating the Observational Standard Errors
5. Results
5.1. Applying the SDC Observation Operators to the Data Assimilation Experiments
5.2. Annual- vs. Varying Conditions based Observation Operators
6. Discussion
7. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Qu, X.; Hall, A. Assessing Snow Albedo Feedback in Simulated Climate Change. J. Clim. 2006, 19, 2617–2630. [Google Scholar] [CrossRef]
- Fassnacht, S.R.; Sexstone, G.A.; Kashipazha, A.H.; Lopez-Moreno, J.I.; Jasinski, M.F.; Kampf, S.K.; Von Thaden, B.C. Deriving snow-cover depletion curves for different spatial scales from remote sensing and snow telemetry data. Hydrol. Process. 2016, 30, 1708–1717. [Google Scholar] [CrossRef]
- Driscoll, J.M.; Hay, L.E.; Bock, A. Spatiotemporal Variability of Snow Depletion Curves Derived from SNODAS for the Conterminous United States, 2004–2013. J. Am. Water Resour. Assoc. 2017, 53, 655–666. [Google Scholar] [CrossRef]
- Liston, G.E. Representing subgrid snow cover heterogeneities in regional and global models. J. Clim. 2004, 17, 1381–1397. [Google Scholar] [CrossRef]
- Anderson, E.A. National Weather Service River Forecast System: Snow Accumulation and Ablation Model; NWS HYDRO-17; NOAA Technical Memorandum; NOAA: Silver Spring, MD, USA, 1973.
- Donald, J.R.; Soulis, E.D.; Kouwen, N.; Pietroniro, A. A land cover-based snow cover representation for distributed hydrologic-models. Water Resour. Res. 1995, 31, 995–1009. [Google Scholar] [CrossRef]
- Kolberg, S.A.; Gottschalk, L. Updating of snow depletion curve with remote sensing data. Hydrol. Process. 2006, 20, 2363–2380. [Google Scholar] [CrossRef]
- Shamir, E.; Georgakakos, K.P. Estimating snow depletion curves for American River basins using distributed snow modeling. J. Hydrol. 2007, 334, 162–173. [Google Scholar] [CrossRef]
- DeBeer, C.M.; Pomeroy, J.W. Influence of snowpack and melt energy heterogeneity on snow cover depletion and snowmelt runoff simulation in a cold mountain environment. J. Hydrol. 2017, 553, 199–213. [Google Scholar] [CrossRef]
- Andreadis, K.M.; Lettenmaier, D.P. Assimilating remotely sensed snow observations into a macroscale hydrology model. Adv. Water Resour. 2006, 29, 872–886. [Google Scholar] [CrossRef]
- Kolberg, S.; Rue, H.; Gottschalk, L. A Bayesian spatial assimilation scheme for snow coverage observations in a gridded snow model. Hydrol. Earth Syst. Sci. 2006, 10, 369–381. [Google Scholar] [CrossRef]
- Zaitchik, B.; Rodell, M. Forward-looking assimilation of MODIS-derived snow-covered area into a land surface model. J. Hydrometeorol. 2009, 10, 130–148. [Google Scholar] [CrossRef]
- Su, H.; Yang, Z.-L.; Niu, G.-Y.; Dickinson, R.E. Enhancing the estimation of continental-scale snow water equivalent by assimilation MODIS snow cover with the ensemble Kalman filter. J. Geophys. Res. 2008, 113, D08120. [Google Scholar] [CrossRef]
- De Lannoy, G.J.M.; Reichle, R.H.; Arsenault, K.R.; Houser, P.R.; Kumar, S.; Verhoest, N.E.C.; Pauwels, V.R.N. Multiscale assimilation of Advanced Microwave Scanning Radiometer-EOS snow water equivalent and Moderate Resolution Imaging Spectroradiometer snow cover fraction observations in northern Colorado. Water Resour. Res. 2012, 48, W01522. [Google Scholar] [CrossRef]
- Arsenault, K.R.; Houser, P.R.; De Lannoy, G.J.M.; Dirmeyer, P.A. Impacts of snow cover fraction data assimilation on modeled energy and moisture budgets. J. Geophys. Res. Atmos. 2013, 118, 7489–7504. [Google Scholar] [CrossRef]
- Zhang, Y.-F.; Hoar, T.J.; Yang, Z.-L.; Anderson, J.L.; Toure, A.M.; Rodell, M. Assimilation of MODIS snow cover through the Data Assimilation Research Testbed and the Community Land Model version 4. J. Geophys. Res. Atmos. 2014, 119, 7091–7103. [Google Scholar] [CrossRef]
- Xu, J.; Zhang, F.; Shu, H.; Zhong, K. Improvement of the Snow Depth in the Common Land Model by Coupling a Two-Dimensional Deterministic Ensemble Model with a Variational Hybrid Snow Cover Fraction Data Assimilation Scheme and a New Observation Operator. J. Hydrometeorol. 2017, 18, 119–138. [Google Scholar] [CrossRef]
- Clark, M.P.; Slater, A.G.; Barrett, A.P.; Hay, L.E.; McCabe, G.J.; Rajagopalan, B.; Leavesley, G.H. Assimilation of snow-covered area information into hydrologic and land-surface models. Adv. Water Resour. 2006, 29, 1209–1221. [Google Scholar] [CrossRef]
- Thirel, G.; Salamon, P.; Burek, P.; Kalas, M. Assimilation of MODIS snow cover area data in a distributed hydrological model using the particle filter. Remote Sens. 2013, 5, 5825–5850. [Google Scholar] [CrossRef]
- Niu, G.-Y.; Yang, Z.-L. An observation-based formulation of snow cover fraction and its evaluation over large North American river basins. J. Geophys. Res. 2007, 112, D21101. [Google Scholar] [CrossRef]
- Salomonson, V.V.; Appel, I. Estimating fractional snow cover from MODIS using the normalized difference snow index. Remote Sens. Environ. 2004, 89, 351–360. [Google Scholar] [CrossRef]
- Hall, D.K.; Riggs, G.A. Accuracy Assessment of the MODIS snow products. Hydrol. Process. 2007, 21, 1534–1547. [Google Scholar] [CrossRef]
- Salomonson, V.V.; Appel, I. Development of the Aqua MODIS NDSI fractional snow cover algorithm and validation results. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1747–1756. [Google Scholar] [CrossRef]
- Hall, D.K.; Riggs, G.A. MODIS/Terra Snow Cover Daily L3 Global 500 m Grid, Version 5; NASA National Snow and ICE Data Center Distributed Active Archive Center: Boulder, CO, USA, 2011. [CrossRef]
- Parajka, J.; Holko, L.; Kostka, Z.; Bloschl, G. MODIS snow cover mapping accuracy in a small mountain catchment—Comparison between open and forest sites. Hydrol. Earth Syst. Sci. 2012, 16, 2365–2377. [Google Scholar] [CrossRef]
- Dwyer, J.; Schmidt, G. The MODIS Reprojection Tool. In Earth Science Satellite Remote Sensing; Qu, J.J., Gao, W., Kafatos, M., Murphy, R.E., Salomonson, V.V., Eds.; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- National Climatic Data Center. Data Documentation for Dataset 6430 (DSI-6430), USDA/NRCS SNOTEL—Daily Data; Text Reports; NCDC: Asheville, NC, USA, 2002.
- Pan, M.; Sheffield, J.; Wood, E.F.; Mitchell, K.E.; Houser, P.R.; Schaake, J.C.; Robock, A.; Lohmann, D.; Cosgrove, B.; Duan, Q.; et al. Snow process modeling in the North American Land Data Assimilation System (NLDAS): 2. Evaluation of model simulated snow water equivalent. J. Geophys. Res. 2003, 108. [Google Scholar] [CrossRef]
- Serreze, M.C.; Clark, M.P.; Armstrong, R.L.; McGinnis, D.A.; Pulwarty, R.S. Characteristics of the western United States snowpack from snowpack telemetry (SNOTEL) data. Water Resour. Res. 1999, 35, 2145–2160. [Google Scholar] [CrossRef]
- Bonan, G.B.; Oleson, K.W.; Vertenstein, M.; Levis, S.; Zeng, X.; Dai, Y.; Dickinson, R.E.; Yang, Z.-L. The land surface climatology of the Community Land Model coupled to the NCAR Community Climate Model. J. Clim. 2002, 15, 3123–3149. [Google Scholar] [CrossRef]
- Dai, Y.; Zeng, X.; Dickinson, R.E.; Baker, I.; Bonan, G.B.; Bosilovich, M.G.; Denning, A.S.; Dirmeyer, P.A.; Houser, P.R.; Niu, G.; et al. The Common Land Model. Bull. Am. Meteorol. Soc. 2003, 84, 1013–1023. [Google Scholar] [CrossRef]
- Oleson, K.W.; Dai, Y.; Bonan, G.; Bosilovich, M.; Dickinson, R.; Dirmeyer, P.; Hoffman, F.; Houser, P.; Levis, S.; Niu, G.-Y.; et al. Technical Description of the Community Land Model (CLM); NCAR Technical Note; NCAR/TN-461+STR; Center for Atmospheric Research: Boulder, CO, USA, 2004. [Google Scholar]
- Kumar, S.V.; Peters-Lidard, C.D.; Tian, Y.; Houser, P.R.; Geiger, J.; Olden, S.; Lighty, L.; Eastman, J.L.; Doty, B.; Dirmeyer, P.; et al. Land Information System—An Interoperable Framework for High Resolution Land Surface Modeling. Environ. Model. Softw. 2006, 21, 1402–1415. [Google Scholar] [CrossRef]
- Anderson, E.A. A Point Energy and Mass Balance Model of a Snow Cover; NOAA Technical Report NWS 19; Office of Hydrology, National Weather Service: Silver Spring, MD, USA, 1976.
- Jordan, R. A One-Dimensional Temperature Model for a Snow Cover: Technical Documentation for SNTHERM.89; Special Report 91-16; U.S. Army Cold Regions Research and Engineering Laboratory: Hanover, NH, USA, 1991. [Google Scholar]
- Dai, Y.; Zeng, Q. A land surface model (IAP94) for climate studies. Part I: Formulation and validation in off-line experiments. Adv. Atmos. Sci. 1997, 14, 433–460. [Google Scholar]
- Feng, X.; Sahoo, A.; Arsenault, K.; Houser, P.; Luo, Y.; Troy, T.J. The Impact of Snow Model Complexity at Three CLPX Sites. J. Hydrometeorol. 2008, 9, 1464–1481. [Google Scholar] [CrossRef]
- Rutter, N.; Essery, R.; Pomeroy, J.; Altimir, N.; Andreadis, K.; Baker, I.; Barr, A.; Bartlett, P.; Boone, A.; Deng, H.; et al. Evaluation of forest snow process models (SnowMIP2). J. Geophys. Res. 2009, 114, D06111. [Google Scholar] [CrossRef]
- Wang, A.; Zeng, X. Improving the treatment of vertical snow burial fraction over short vegetation in the NCAR CLM3. Adv. Atmos. Sci. 2009, 26, 877–886. [Google Scholar] [CrossRef]
- Cosgrove, B.A.; Lohmann, D.; Mitchell, K.E.; Houser, P.R.; Wood, E.F.; Schaake, J.C.; Robock, A.; Marshall, C.; Sheffield, J.; Duan, Q.; et al. Real-time and retrospective forcing in the North American Land Data Assimilation System (NLDAS) project. J. Geophys. Res. 2003, 108, 8842. [Google Scholar] [CrossRef]
- Friedl, M.A.; McIver, D.K.; Hodges, J.C.F.; Zhang, X.Y.; Muchoney, D.; Strahler, A.H.; Woodcock, C.E.; Gopal, S.; Schneider, A.; Cooper, A.; et al. Global land cover classification at 1km spatial resolution using a classification tree approach. Remote Sens. Environ. 2002, 83, 287–302. [Google Scholar] [CrossRef]
- Reichle, R.H.; McLaughlin, D.B.; Entekhabi, D. Hydrologic data assimilation with the Ensemble Kalman filter. Mon. Weather Rev. 2002, 130, 103–114. [Google Scholar] [CrossRef]
- Reichle, R.H.; Bosilovich, M.G.; Crow, W.T.; Koster, R.D.; Kumar, S.V.; Mahanama, S.P.P.; Zaitchik, B.F. Recent Advances in Land Data Assimilation at the NASA Global Modeling and Assimilation Office. In Data Assimilation for Atmospheric, Oceanic and Hydrologic Applications; Park, S.K., Xu, L., Eds.; Springer: New York, NY, USA, 2009; pp. 407–428. [Google Scholar] [CrossRef]
- Kumar, S.V.; Reichle, R.H.; Peters-Lidard, C.D.; Koster, R.D.; Zhan, X.; Crow, W.T.; Eylander, J.B.; Houser, P.R. A land surface data assimilation framework using the land information system: Description and applications. Adv. Water Resour. 2008, 31, 1419–1432. [Google Scholar] [CrossRef]
- Bowling, L.C.; Pomeroy, J.W.; Lettenmaier, D.P. Parameterization of blowing-snow sublimation in a macroscale hydrology model. J. Hydrometeorol. 2004, 5, 745–762. [Google Scholar] [CrossRef]
- Jacko, J.A.; Stephanidis, C. (Eds.) Human-Computer Interaction: Theory and Practice; Lawrence Erlbaum and Associates: Mahwah, NJ, USA, 2003. [Google Scholar]
- Seo, H.; Miller, A.J.; Roads, J.O. The Scripps Coupled Ocean-Atmosphere Regional (SCOAR) Model, with Applications in the Eastern Pacific Sector. J. Clim. 2007, 20, 381–402. [Google Scholar] [CrossRef]
- Jost, G.; Weiler, M.; Gluns, D.R.; Alila, Y. The influence of forest and topography on snow accumulation and melt at the watershed-scale. J. Hydrol. 2007, 347, 101–115. [Google Scholar] [CrossRef]
- Anderton, S.P.; White, S.M.; Alvera, B. Evaluation of spatial variability in snow water equivalent for a high mountain catchment. Hydrol. Process. 2004, 18, 435–453. [Google Scholar] [CrossRef]
- Molotch, N.P.; Margulis, S.A. Estimating the distribution of snow water equivalent using remotely sensed snow cover data and a spatially distributed snowmelt model: A multi-resolution, multi-sensor comparison. Adv. Water Res. 2008, 31, 1503–1514. [Google Scholar] [CrossRef]
- Crow, W.T.; Ryu, D. A new data assimilation approach for improving runoff prediction using remotely-sensed soil moisture retrievals. Hydrol. Earth Syst. Sci. 2009, 13, 1–16. [Google Scholar] [CrossRef]
- Whitaker, J.S.; Hamill, T.M.; Wei, X.; Song, Y.; Toth, Z. Ensemble data assimilation with the NCEP Global Forecast System. Mon. Weather Rev. 2008, 136. [Google Scholar] [CrossRef]
- Déry, S.J.; Salomonson, V.V.; Stieglitz, M.; Hall, D.K.; Appel, I. An approach to using snow areal depletion curves inferred from MODIS and its application to land surface modelling in Alaska. Hydrol. Process. 2005, 19, 2755–2774. [Google Scholar] [CrossRef]
- Xu, L.; Dirmeyer, P. Snow-atmosphere coupling strength. Part I: Effect of model biases. J. Hydrometeorol. 2013, 14, 389–403. [Google Scholar] [CrossRef]
- Dong, J.; Peters-Lidard, C. On the relationship between temperature and MODIS snow cover retrieval errors in the Western U.S. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2010, 3, 132–140. [Google Scholar] [CrossRef]
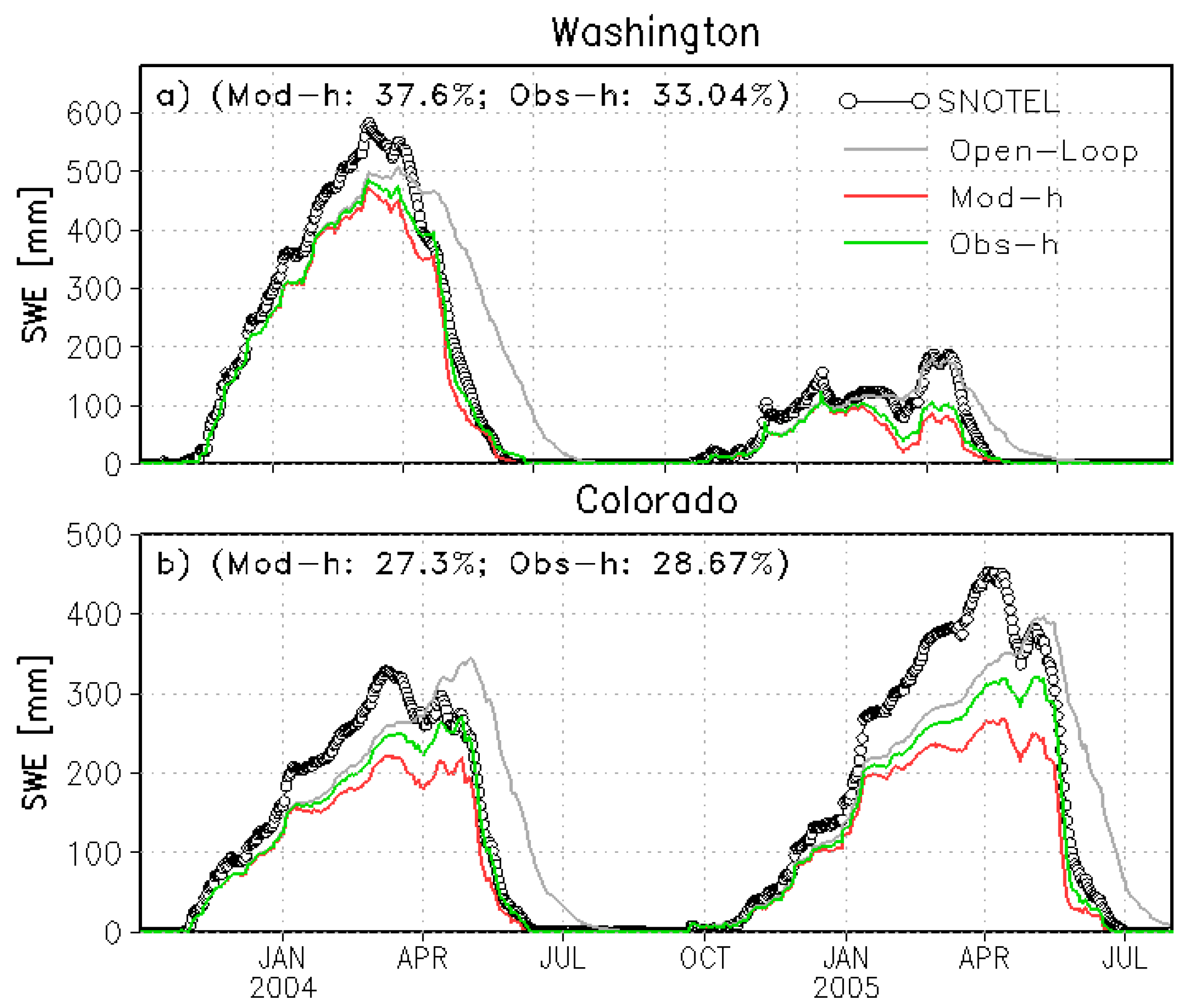
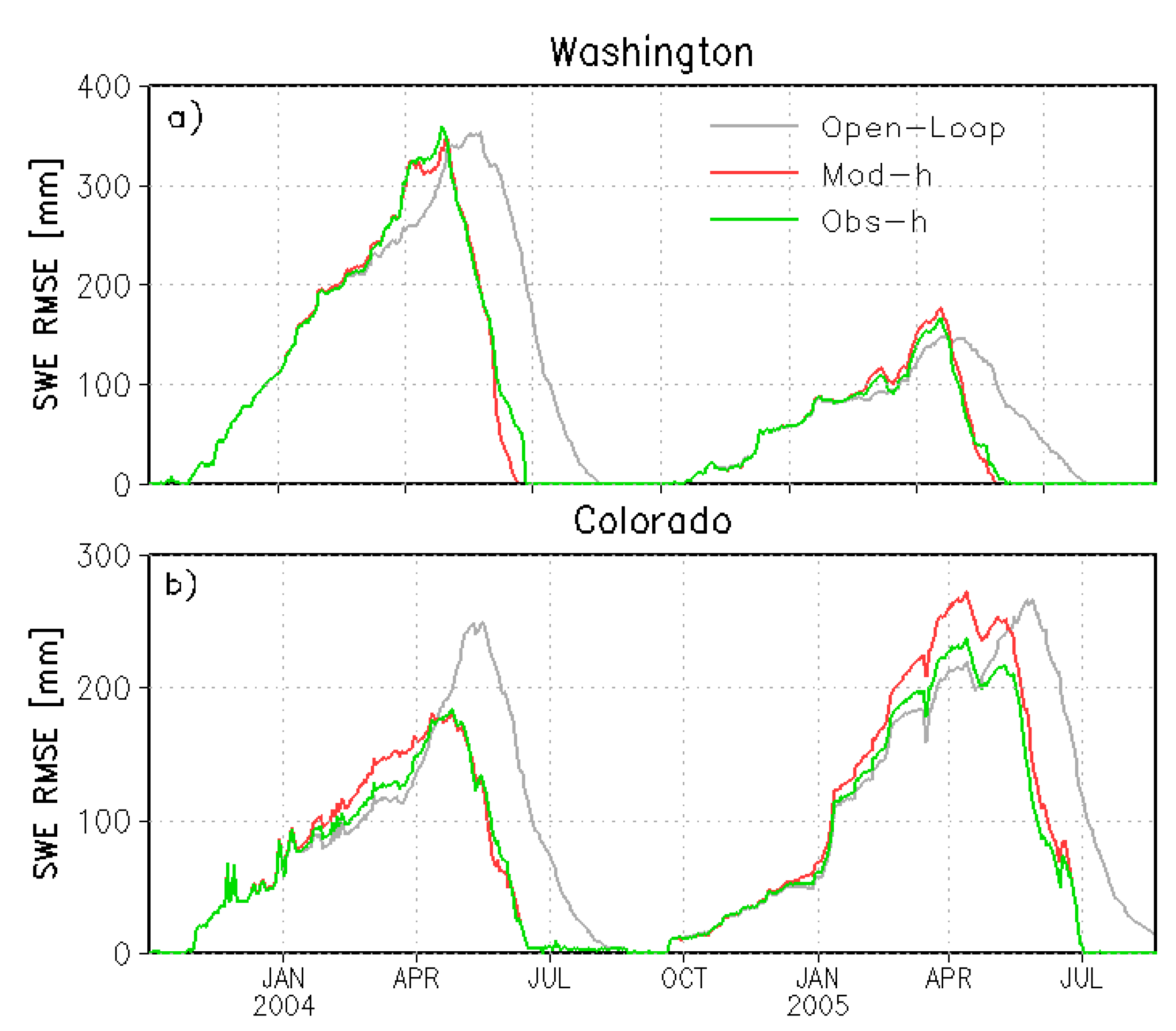
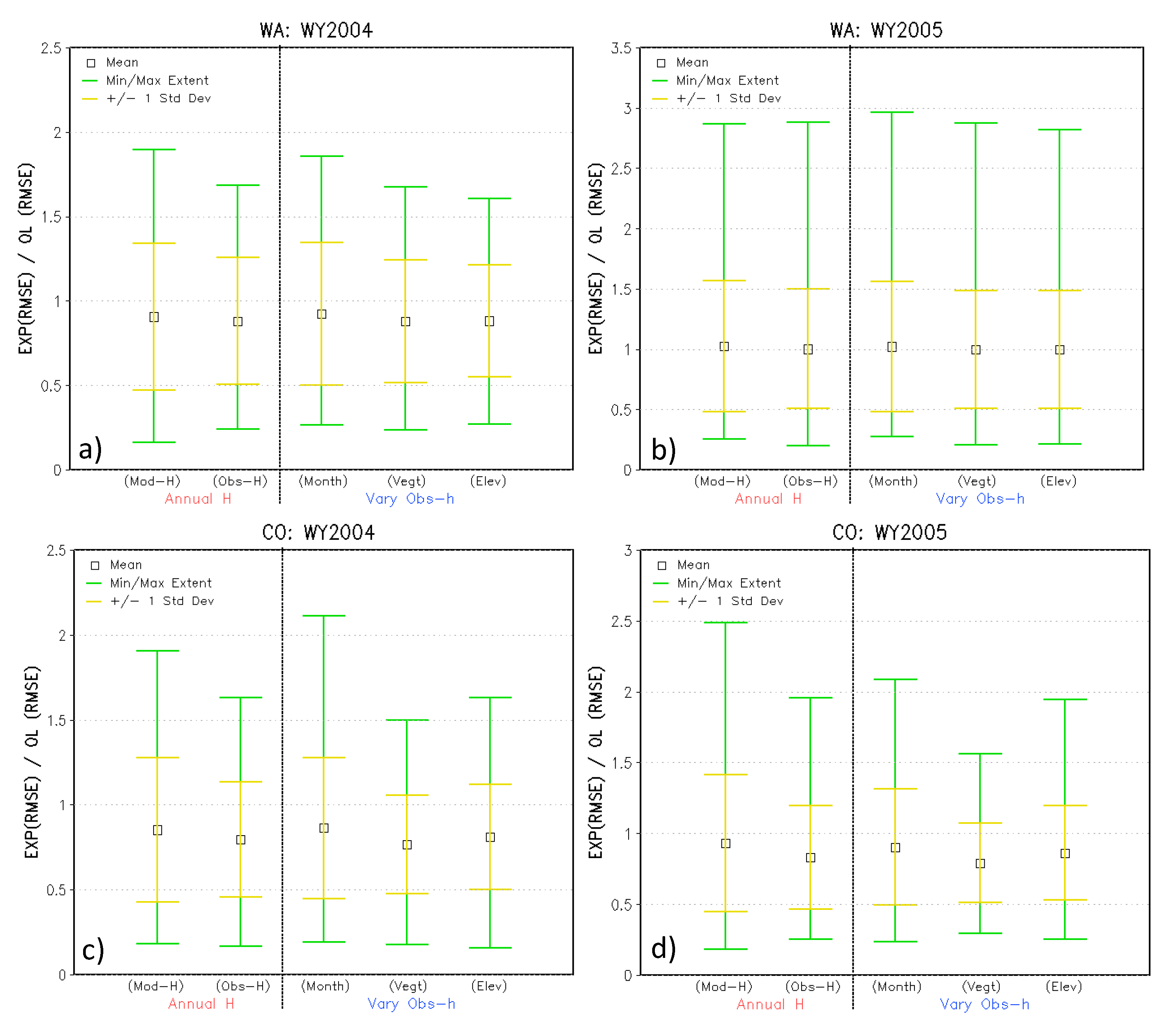
| Experiment Name | Description |
|---|---|
| Open-loop (OL) | The baseline ensemble model experiment with no snow cover assimilation performed. |
| EnKF: Model-h | Snow cover assimilation using EnKF and the default model-based SDC as the observation operator. |
| EnKF: Annual obs-h | Snow cover assimilation using EnKF and the annual observation-based SDC as the observation operator. |
| EnKF: Month-based obs-h | Snow cover assimilation using EnKF and the monthly-varying, observation-based SDCs as the observation operator. |
| EnKF: Vegetation-based obs-h | Snow cover assimilation using EnKF and the vegetation-type, observation-based SDCs as the observation operator. |
| EnKF: Elevation band-based obs-h | Snow cover assimilation using EnKF and the elevation-band, observation-based SDCs as the observation operator. |
| Observation Operator Comparison Statistics | ||||||||
|---|---|---|---|---|---|---|---|---|
| Average | SD | RMSE | Correl | Average | SD | RMSE | Correl | |
| (mm) | (mm) | (mm) | (-) | (mm) | (mm) | (mm) | (-) | |
| WA (40 Sites) | 2004 | 2005 | ||||||
| Observations | 221.85 | 216.19 | - | - | 61.19 | 66.56 | - | - |
| Open-loop | 247.01 | 188.17 | 168.22 | 0.79 | 64.30 | 61.14 | 65.09 | 0.74 |
| EnKF: Model-h | 183.54 | 184.21 | 138.54 | 0.87 | 34.62 | 40.38 | 60.29 | 0.75 |
| EnKF: Annual obs-h | 194.09 | 191.40 | 140.13 | 0.87 | 40.11 | 45.38 | 57.46 | 0.75 |
| EnKF: Month obs-h | 191.09 | 191.31 | 145.33 | 0.85 | 37.27 | 42.89 | 58.29 | 0.74 |
| EnKF: Veg. obs-h | 195.79 | 192.18 | 140.28 | 0.87 | 40.60 | 45.77 | 57.31 | 0.75 |
| EnKF: Elev. obs-h | 199.91 | 193.46 | 142.41 | 0.87 | 40.80 | 46.07 | 57.83 | 0.75 |
| CO (78 Sites) | 2004 | 2005 | ||||||
| Observations | 132.74 | 127.26 | - | - | 187.20 | 168.07 | - | - |
| Open-loop | 143.75 | 115.63 | 107.00 | 0.72 | 180.14 | 132.52 | 127.97 | 0.79 |
| EnKF: Model-h | 94.01 | 92.34 | 81.57 | 0.89 | 119.57 | 109.58 | 116.57 | 0.89 |
| EnKF: Annual obs-h | 108.00 | 105.82 | 79.24 | 0.88 | 139.72 | 127.99 | 103.69 | 0.91 |
| EnKF: Month obs-h | 111.15 | 109.82 | 86.21 | 0.86 | 145.82 | 134.43 | 109.96 | 0.89 |
| EnKF: Veg. obs-h | 114.26 | 111.18 | 76.91 | 0.88 | 147.93 | 134.33 | 99.51 | 0.91 |
| EnKF: Elev. obs-h | 112.60 | 109.71 | 81.74 | 0.87 | 144.87 | 132.64 | 108.19 | 0.90 |
| Normalized Innovation Analysis | ||||||||
|---|---|---|---|---|---|---|---|---|
| WA | CO | |||||||
| 2004 | 2005 | 2004 | 2005 | |||||
| Experiment | Mean | SD | Mean | SD | Mean | SD | Mean | SD |
| CLM2 mod-h | −0.43 | 0.89 | −0.39 | 0.81 | −0.43 | 0.92 | −0.37 | 0.87 |
| Annual obs-h | −0.41 | 0.99 | −0.57 | 0.95 | −0.42 | 0.98 | −0.34 | 0.94 |
| Monthly obs-h | −0.41 | 0.97 | −0.59 | 0.98 | −0.38 | 1.02 | −0.31 | 0.93 |
| Veg. obs-h | −0.41 | 1.02 | −0.58 | 0.95 | −0.39 | 1.01 | −0.30 | 0.97 |
| Elev. obs-h | −0.41 | 1.00 | −0.57 | 0.95 | −0.41 | 1.02 | −0.32 | 0.99 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arsenault, K.R.; Houser, P.R. Generating Observation-Based Snow Depletion Curves for Use in Snow Cover Data Assimilation. Geosciences 2018, 8, 484. https://doi.org/10.3390/geosciences8120484
Arsenault KR, Houser PR. Generating Observation-Based Snow Depletion Curves for Use in Snow Cover Data Assimilation. Geosciences. 2018; 8(12):484. https://doi.org/10.3390/geosciences8120484
Chicago/Turabian StyleArsenault, Kristi R., and Paul R. Houser. 2018. "Generating Observation-Based Snow Depletion Curves for Use in Snow Cover Data Assimilation" Geosciences 8, no. 12: 484. https://doi.org/10.3390/geosciences8120484
APA StyleArsenault, K. R., & Houser, P. R. (2018). Generating Observation-Based Snow Depletion Curves for Use in Snow Cover Data Assimilation. Geosciences, 8(12), 484. https://doi.org/10.3390/geosciences8120484





