Simulations of Moisture Gradients in Wood Subjected to Changes in Relative Humidity and Temperature Due to Climate Change
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Data
2.2. Simplified Theoretical Analysis
Simplified Analysis—Step-Change, Periodic Variation and Time Varying Moisture Diffusivity
2.3. WUFI® Pro Simulation Method
3. Impact of Future Climate Change on Wood
3.1. Hygrothermal Simulations of Future Climatic Conditions in Two Generic Buildings
3.2. Hygrothermal Simulations of Future Climate Conditions in Roggerdorf Church
4. Results
4.1. Comparison of the WUFI® Pro and the Simplified Model
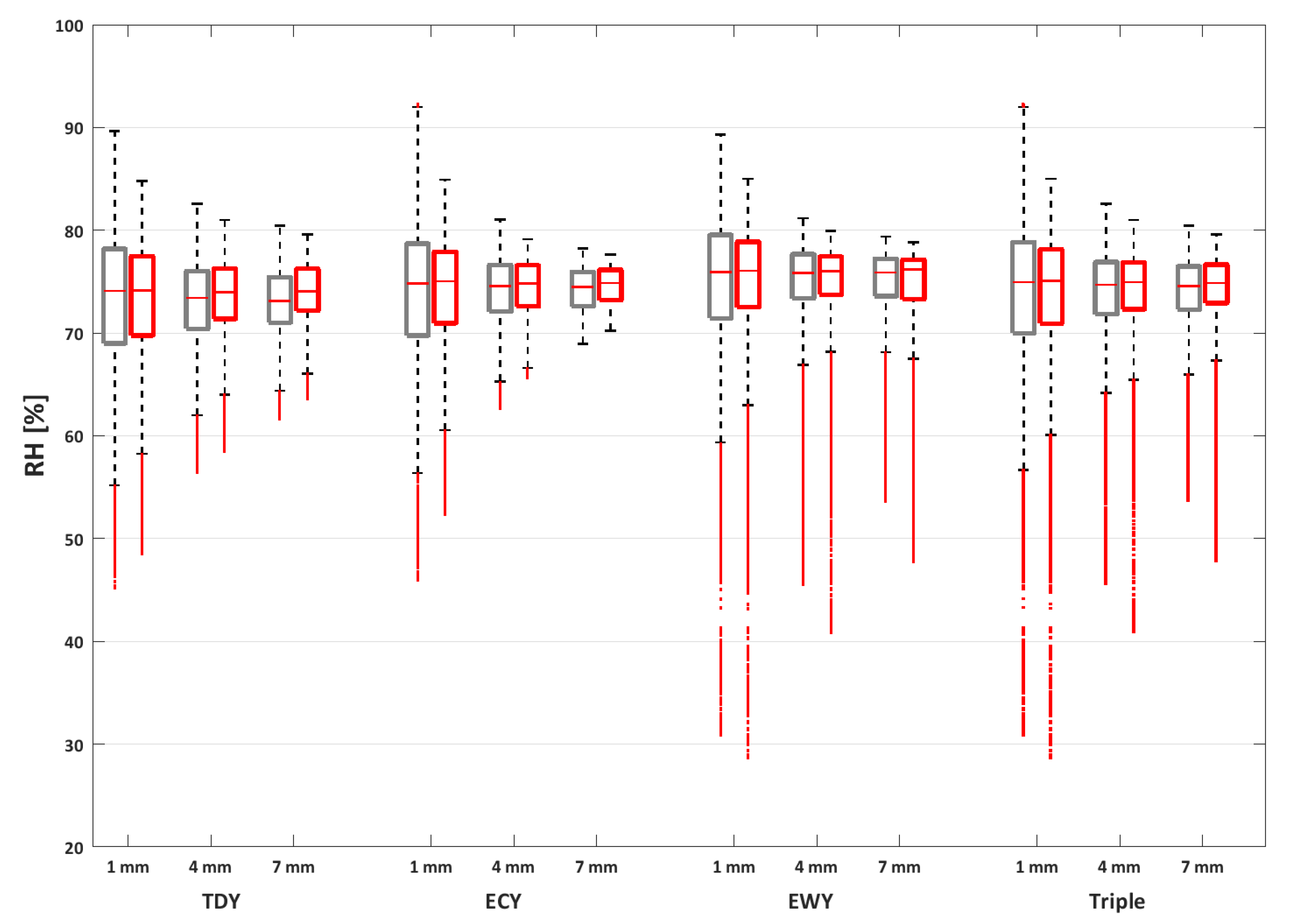
4.2. The Effect on Wood Using Hygrothermal Simulations of Future Climatic Conditions
5. Discussion
6. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Sabbioni, C. Noahs Ark Report Summary: Final Report Summary—Noahs Ark (Global Climate Change Impact on Built Heritage and Cultural Landscapes). 2011. Available online: https://cordis.europa.eu/result/rcn/47770_en.html (accessed on 8 April 2017).
- Anthem Press. The Atlas of Climate Change Impact on European Cultural Heritage: Scientific Analysis and Management Strategies; Sabbioni, C., Brimblecombe, P., Cassar, M., Eds.; Anthem Press: London, UK, 2012. [Google Scholar]
- Leissner, J.; Kilian, R.; Kotova, L.; Jacob, D.; Mikolajewicz, U.; Broström, T.; Ashley-Smith, J.; Schellen, H.L.; Martens, M.; van Schijndel, J.; et al. Climate for Culture: Assessing the impact of climate change on the future indoor climate in historic buildings using simulations. Herit. Sci. 2015, 3, 1–15. [Google Scholar] [CrossRef]
- Sustainable Energy Communities in Historic URBan Areas (SECHURBA). Available online: https://ec.europa.eu/energy/intelligent/projects/en/projects/sechurba#partners (accessed on 27 July 2018).
- EFFESUS. Available online: http://www.effesus.eu/ (accessed on 27 July 2018).
- Environmental Guidelines: IIC and ICOM-CC Declaration. 2014. Available online: https://www.iiconservation.org/node/5168 (accessed on 10 November 2014).
- Netherlands Organisation for Scientific Research. The Conservation of Panel Paintings and Related Objects: Research Agenda 2014–2020; Kos, N., van Duin, P., Eds.; Netherlands Organisation for Scientific Research (NWO): The Hague, The Netherlands, 2014. Available online: https://rkd.nl/en/explore/library/288805 (accessed on 13 June 2017).
- Engelund, E.T.; Garbrecht Thygesen, L.; Svensson, S.; Hill, C.A.S. A critical discussion of the physics of wood–water interactions. Wood Sci. Technol. 2013, 47, 141–161. [Google Scholar] [CrossRef] [Green Version]
- Bylund Melin, C. Wooden Objects in Historic Buildings: Effects of Dynamic Relative Humidity and Temperature. Ph.D. Thesis, University of Gothenburg, Gothenburg, Sweden, January 2018. [Google Scholar]
- Dai, G.; Ahmet, K. Long-term monitoring of timber moisture content below the fiber saturation point using wood resistance sensors. For. Prod. J. 2001, 51, 52–58. [Google Scholar]
- Brischke, C.; Rapp, A.O.; Bayerbach, R. Measurement system for long-term recording of wood moisture content with internal conductively glued electrodes. Build. Environ. 2008, 43, 1566–1574. [Google Scholar] [CrossRef]
- Fredriksson, M.; Wadsö, L.; Johansson, P. Small resistive wood moisture sensors: A method for moisture content determination in wood structures. Eur. J. Wood Wood Prod. 2013, 71, 515–524. [Google Scholar] [CrossRef]
- Isaksson, T.; Thelandersson, S. Experimental investigation on the effect of detail design on wood moisture content in outdoor above ground applications. Build. Environ. 2013, 59, 239–249. [Google Scholar] [CrossRef]
- Fredriksson, M.; Claesson, J.; Wadsö, L. The Influence of specimen size and distance to a surface on resistive moisture content measurements in wood. Math. Probl. Eng. 2015, 2015, 1–7. [Google Scholar] [CrossRef]
- Bylund Melin, C.; Gebäck, T.; Heintz, A.; Bjurman, J. Monitoring dynamic moisture gradients in wood using inserted relative humidity and temperature sensors. E-Preserv. Sci. 2016, 13, 7–14. Available online: http://www.morana-rtd.com/e-preservationscience/2016/ePS_2016_a2_Bylund_Melin.pdf (accessed on 17 March 2018).
- Bylund Melin, C.; Bjurman, J. Moisture gradients in wood subjected to RH and temperatures simulating indoor climate variations as found in museums and historic buildings. J. Cult. Herit. 2017, 25, 157–162. [Google Scholar] [CrossRef]
- IPCC. Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013. [Google Scholar]
- Nik, V.M.; Kalagasidis, A.S.; Kjellström, E. Statistical methods for assessing and analysing the building performance in respect to the future climate. Build. Environ. 2012, 53, 107–118. [Google Scholar] [CrossRef]
- Nik, V.M.; Kalagasidis, A.S.; Kjellström, E. Assessment of hygrothermal performance and mould growth risk in ventilated attics in respect to possible climate changes in Sweden. Build. Environ. 2012, 55, 96–109. [Google Scholar] [CrossRef]
- Nik, V.M. Making energy simulation easier for future climate—Synthesizing typical and extreme weather data sets out of regional climate models (RCMs). Appl. Energy 2016, 177, 204–226. [Google Scholar] [CrossRef]
- Nik, V.M. Application of typical and extreme weather data sets in the hygrothermal simulation of building components for future climate—A case study for a wooden frame wall. Energy Build. 2017, 154, 30–45. [Google Scholar] [CrossRef]
- Leissner, J. The Impact of Climate Change on Historic Buildings and Cultural Property. In UNESCO Today; Deutsche UNESCO-Kommission: Bonn, Germany, 2011; pp. 44–45. [Google Scholar]
- Bertolin, C.; Camuffo, D.; Leissner, J.; Antretter, F.; Winkler, M.; van Schijndel, A.W.M.; Schellen, H.L.; Kotova, L.; Mikolajewicz, U.; Brostrom, T.; et al. Results of the EU project Climate for Culture: Future climate-induced risks to historic buildings and their interiors. In Proceeding of the 2nd Annual SISC Conference, Venice, Italy, 29–30 September 2014. [Google Scholar]
- Hagentoft, C.-E.; Kalagasidis, A.S.; Adl-Zarrabi, B.; Roels, S.; Carmeliet, J.; Hens, H.; Grunewald, J.; Funk, M.; Becker, R.; Shamir, D.; et al. Assessment method of numerical prediction models for combined heat, air and moisture transfer in building components: Benchmarks for one-dimensional cases. J. Therm. Envel. Build. Sci. 2004, 27. [Google Scholar] [CrossRef]
- Hagentoft, C.-E. Introduction to Building Physics; Studentlitteratur: Lund, Sweden, 2001; ISBN 91-44-01896-7. [Google Scholar]
- Künzel, H. Verfahren zur ein- und Zweidimensionalen Berechnung des Gekoppelten Wärme- und Feuchtetransports in Bauteilen mit Einfachen Kennwerten. Ph.D. Thesis, Universität Stuttgart, Stuttgart, Germany, July 1994. (In German). [Google Scholar]
- Holl, K.K. Der Einfluss von Klimaschwankungen auf Kunstwerke im historischen Kontext. Untersuchung des Schadensrisikos Anhand von Restauratorischer Zustandsbewertung, Laborversuchen und Simulation. Ph.D. Thesis, Technical University, Munich, Germany, July 2016. (In German). [Google Scholar]
- Nik, V.M. Hygrothermal Simulations of Buildings Concerning Uncertainties of the Future Climate. Ph.D. Thesis, Chalmers University of Technology, Gothenburg, Sweden, May 2012. [Google Scholar]
- Samuelsson, P.; Gollvik, S.; Jansson, C.; Kupiainen, M.; Kourzeneva, E.; van de Berg, W.J. The Surface Processes of the Rossby Centre Regional Atmospheric Climate Model (RCA4); Swedish Meteorological and Hydrological Institute (SMHI): Norrköping, Sweden, 2015.
- Nik, V.M. Climate Simulation of An Attic Using Future Weather Data Sets—Statistical Methods for Data Processing and Analysis; Chalmers University of Technology: Gothenburg, Sweden, March 2010. [Google Scholar]
- Jacob, D.; Mikolajewicz, U.; Kotova, L. Climate for Culture—WP1: Assessment Report on Climate Evolution Scenarios Relevant for the Selected Regions; Deliverable 1.1, Internal Project Report; Danish Meteorological Institute: Copenhagen, Denmark, 2002. [Google Scholar]
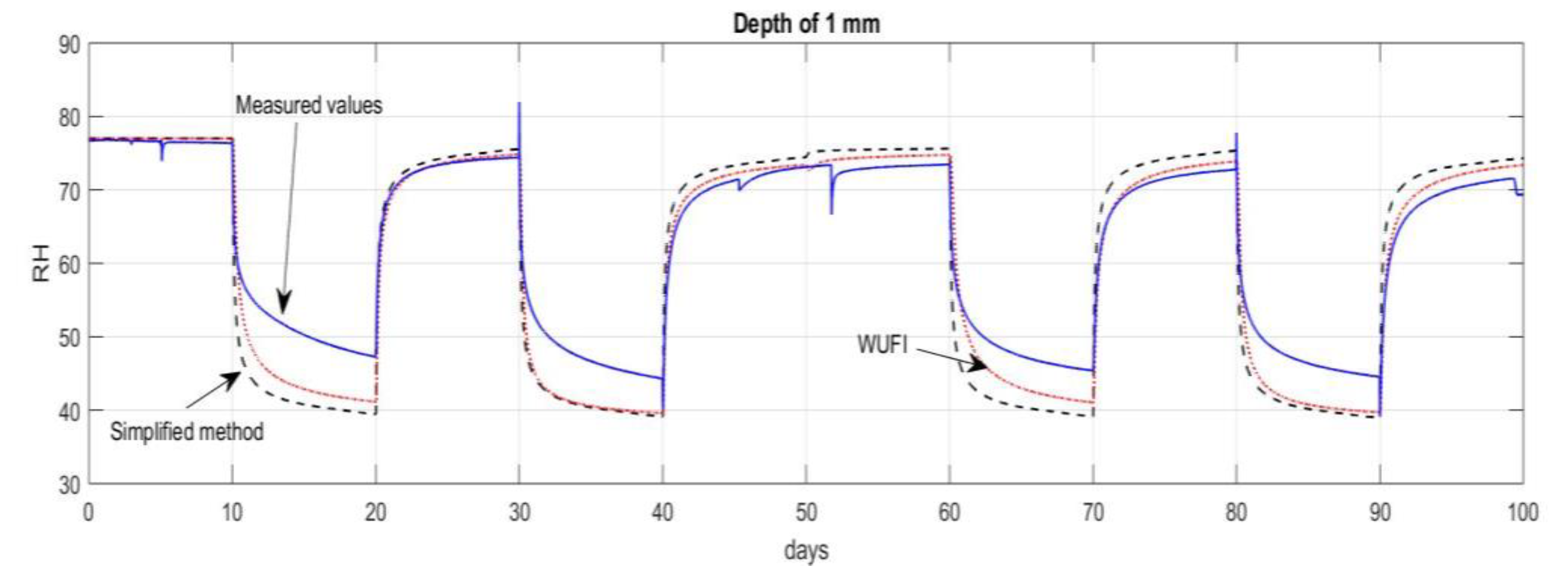
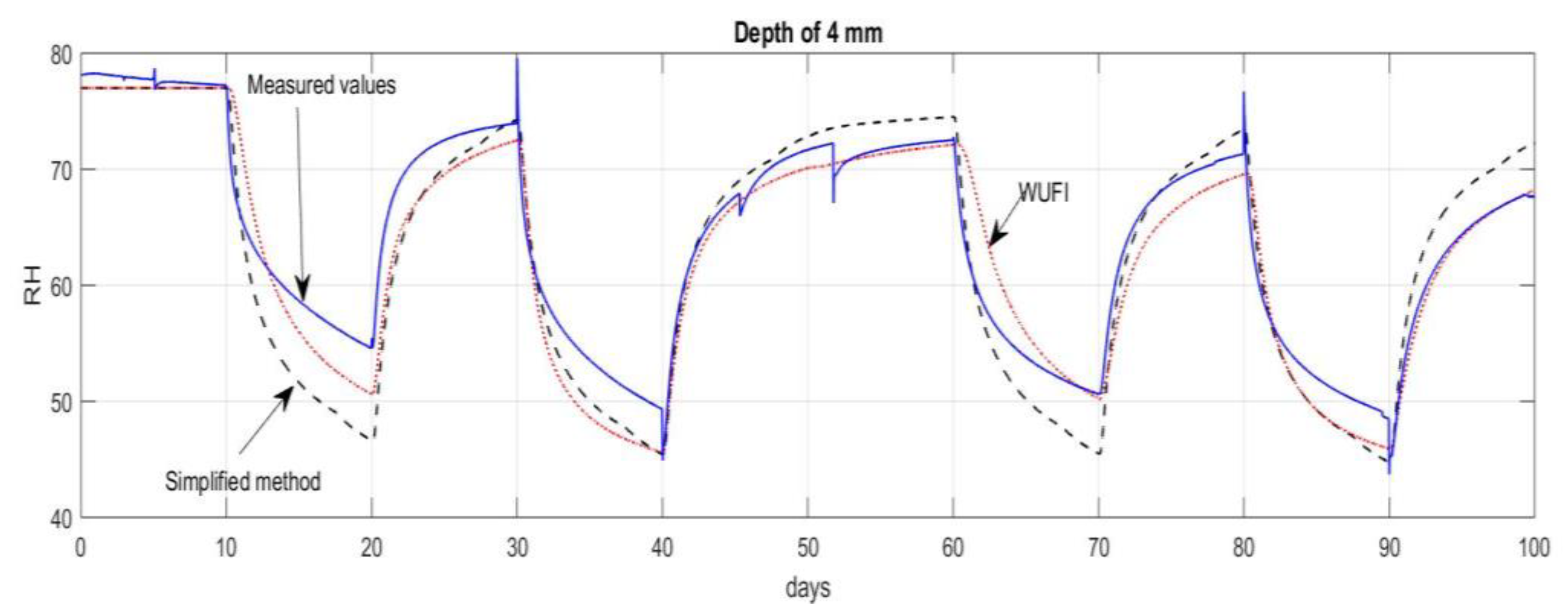
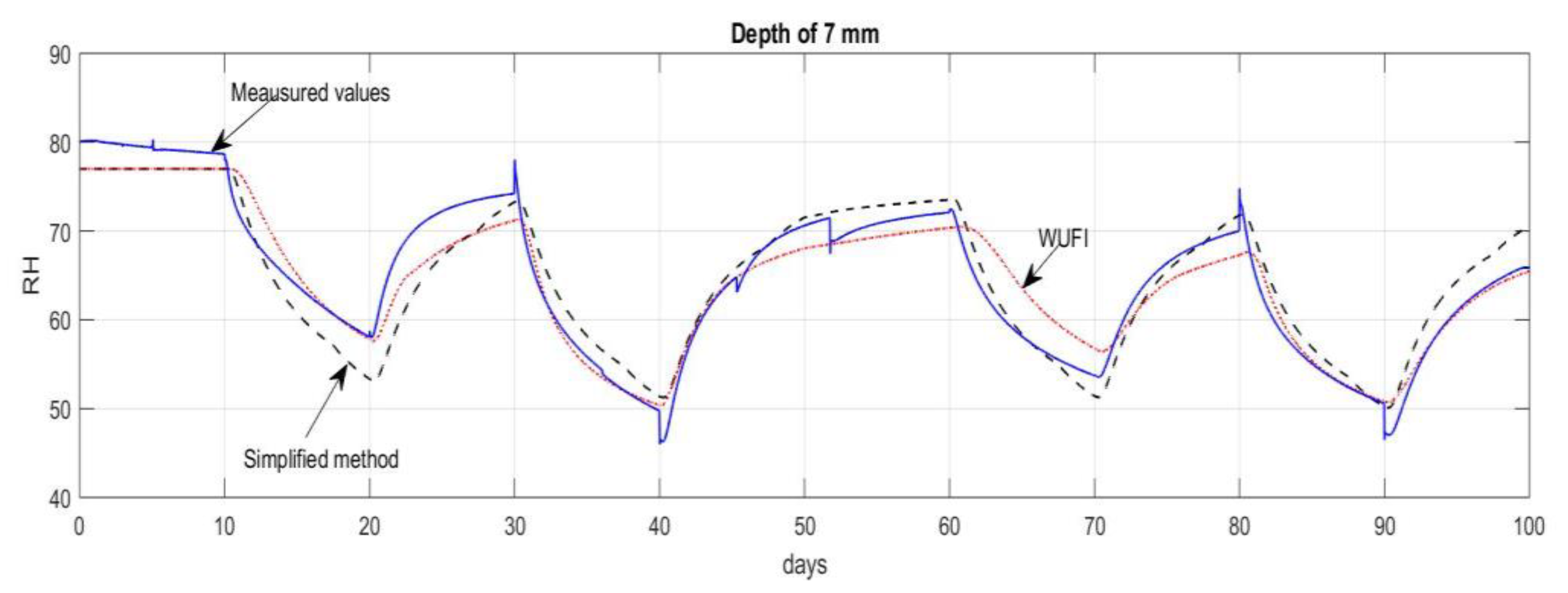
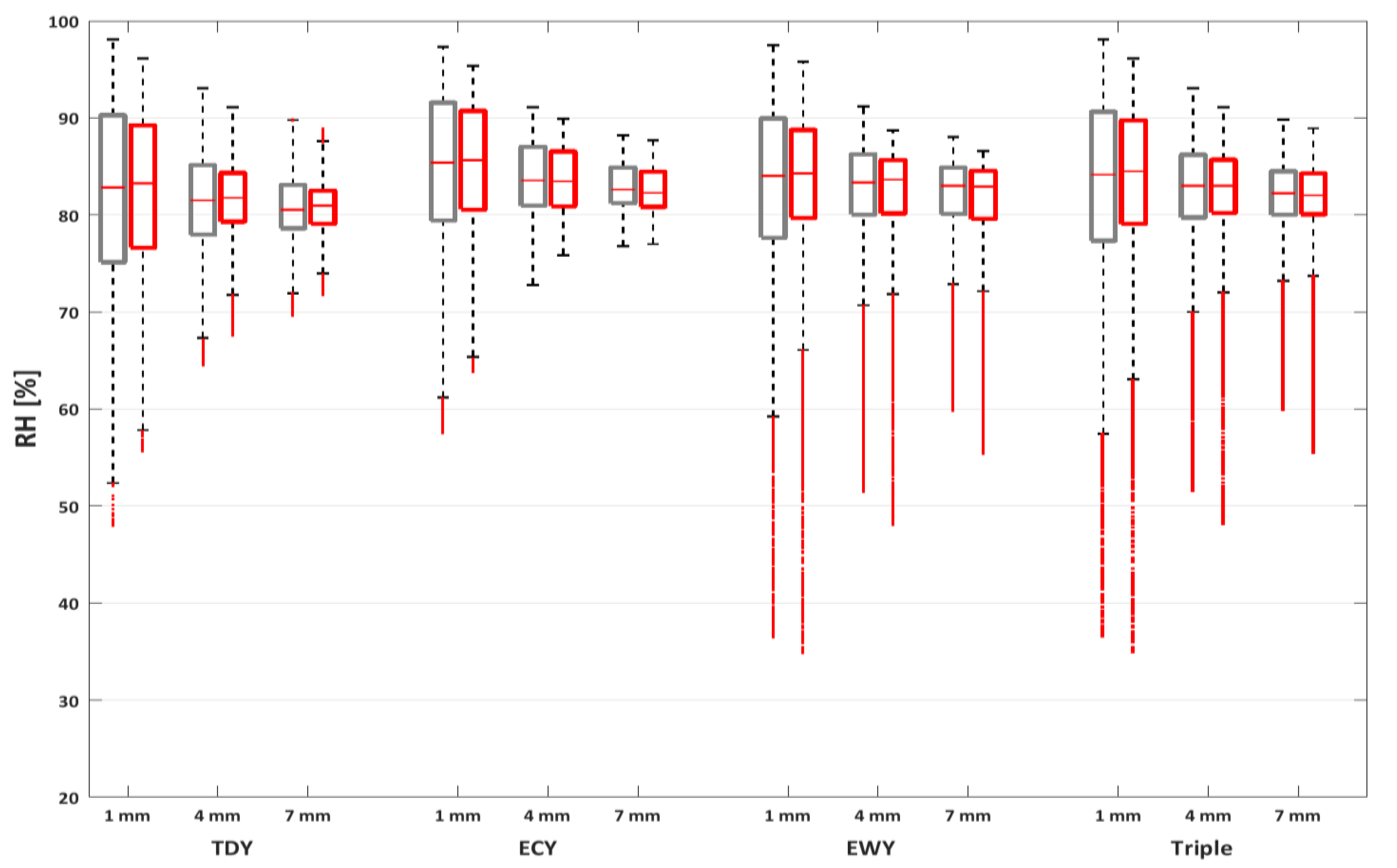
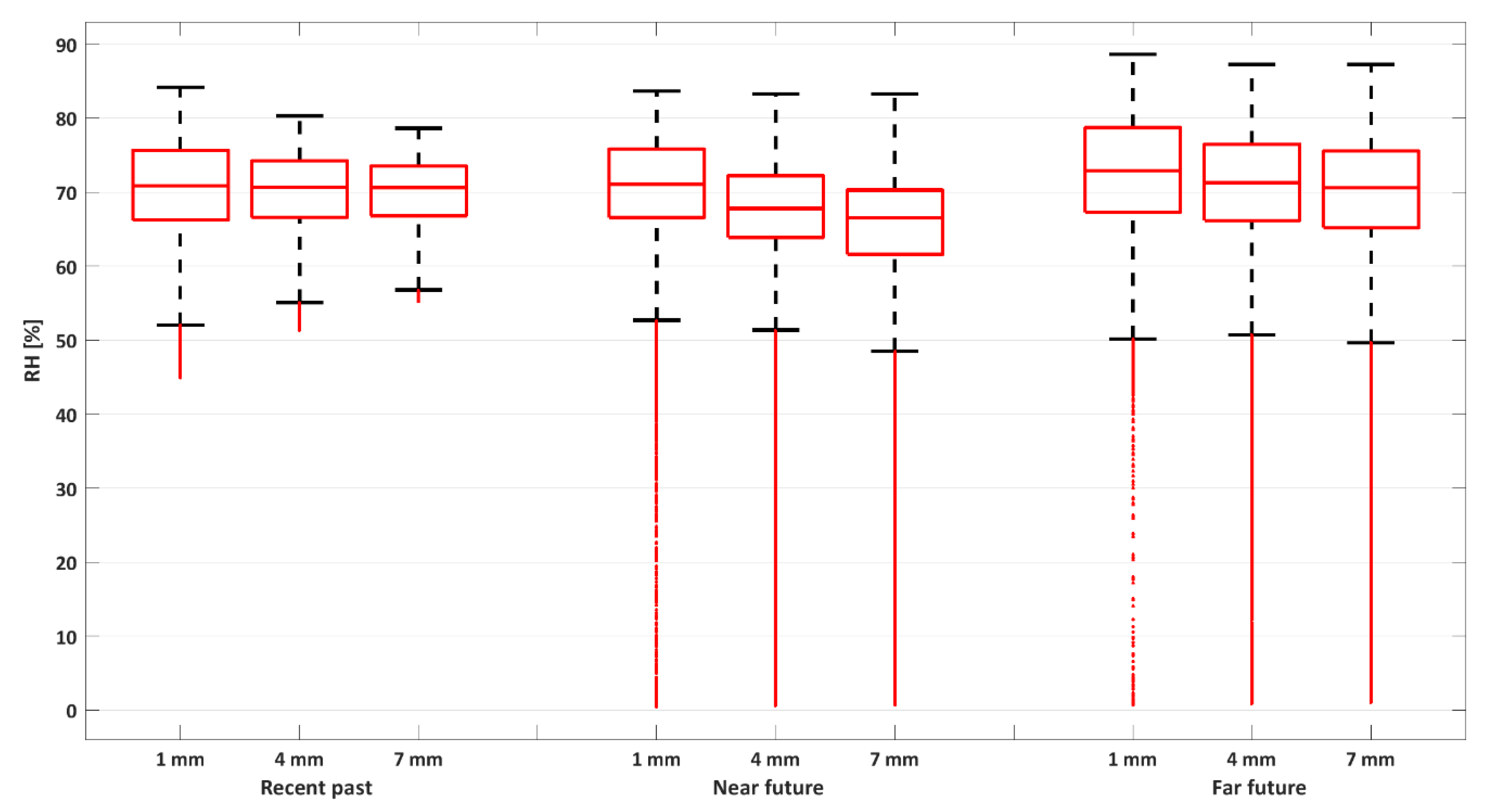
| The Simplified Model | WUFI® Pro Simulations | |||
|---|---|---|---|---|
| Depth (mm) | Average Difference (%) | Standard Deviation (%) | Average Difference (%) | Standard Deviation (%) |
| 1 mm | 1.6 | 4.9 | 1.6 | 3.4 |
| 4 mm | 1.1 | 3.2 | 1.2 | 2.5 |
| 7 mm | 0.1 | 2.9 | 0.3 | 2.5 |
| Gothenburg (One Year) | Bavaria (30 Years) | ||||
|---|---|---|---|---|---|
| Temperature (°C) | Relative Humidity (%) | Temperature (°C) | Relative Humidity (%) | ||
| TDY | 9.109 | 82.98 | Recent past | 9.8 | 70.4 |
| ECY | 4.131 | 85.08 | Near future | 10.6 | 71.2 |
| EWY | 13.54 | 84.15 | Far future | 11.6 | 72.1 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bylund Melin, C.; Hagentoft, C.-E.; Holl, K.; Nik, V.M.; Kilian, R. Simulations of Moisture Gradients in Wood Subjected to Changes in Relative Humidity and Temperature Due to Climate Change. Geosciences 2018, 8, 378. https://doi.org/10.3390/geosciences8100378
Bylund Melin C, Hagentoft C-E, Holl K, Nik VM, Kilian R. Simulations of Moisture Gradients in Wood Subjected to Changes in Relative Humidity and Temperature Due to Climate Change. Geosciences. 2018; 8(10):378. https://doi.org/10.3390/geosciences8100378
Chicago/Turabian StyleBylund Melin, Charlotta, Carl-Eric Hagentoft, Kristina Holl, Vahid M. Nik, and Ralf Kilian. 2018. "Simulations of Moisture Gradients in Wood Subjected to Changes in Relative Humidity and Temperature Due to Climate Change" Geosciences 8, no. 10: 378. https://doi.org/10.3390/geosciences8100378
APA StyleBylund Melin, C., Hagentoft, C.-E., Holl, K., Nik, V. M., & Kilian, R. (2018). Simulations of Moisture Gradients in Wood Subjected to Changes in Relative Humidity and Temperature Due to Climate Change. Geosciences, 8(10), 378. https://doi.org/10.3390/geosciences8100378






