Microlensing Searches for Exoplanets
Abstract
1. Introduction
1.1. Discovering Exoplanets
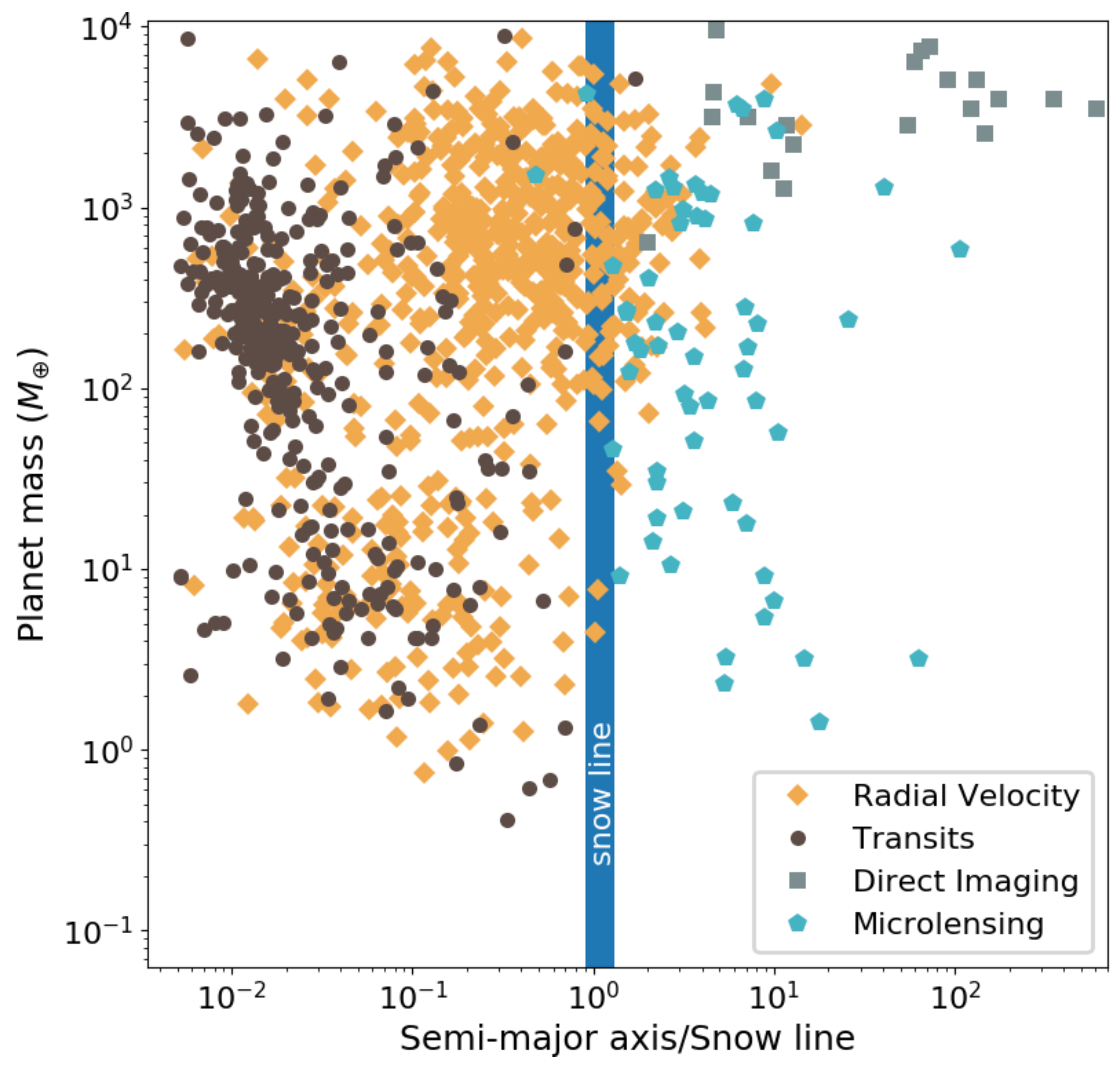
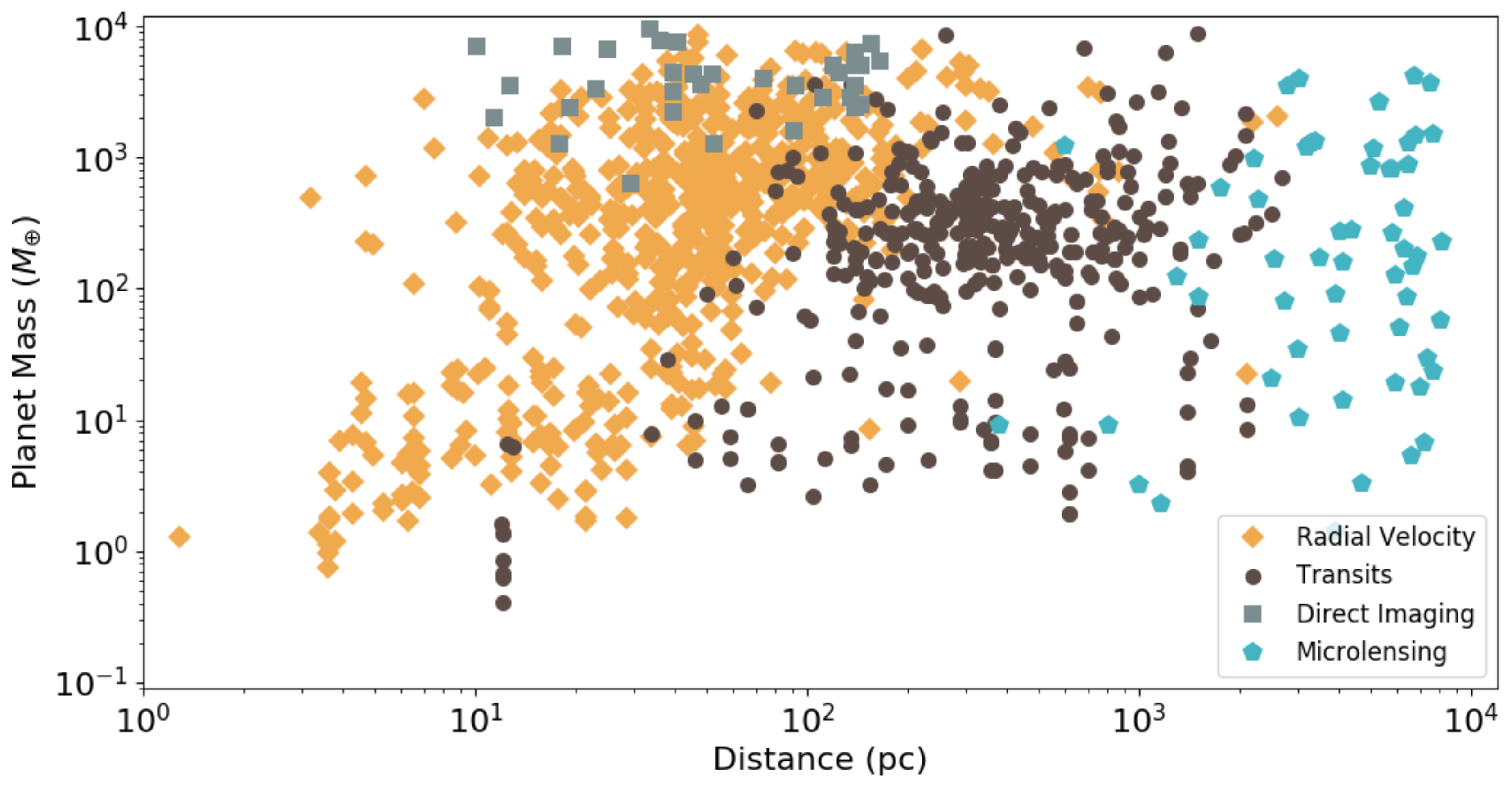
- Radial velocity detects planets by measuring the periodic shifting of spectral lines on the stellar spectrum that is induced by the orbital motion of the planet around the host star. Discoveries from radial velocity surveys over the past 20 years provide the first evidence that the incidence of giant planets increases with increasing stellar mass, at least for planets with short orbital periods [7]. Although the radial velocity method has been remarkably successful in identifying planets near their hosts, discoveries of giant planets beyond 1 AU for low-mass stars have been comparatively few [8] because detecting planets at larger orbital distances requires mission lifetimes that span several years to decades.
- Transit surveys, from the ground and from space, identify exoplanets with near edge-on orbits that pass in front of their host stars causing them to appear dimmer for the duration of the event. The most successful of these surveys to date has been the Kepler space mission [9], having found hundreds of large and small planets out to ∼1 AU from their hosts and thousands of candidates. Although its primary mission was suspended in 2013 due to the failure of two reaction wheels, without which the telescope could not point accurately, it provided strong evidence that terrestrial planets are far more numerous than gas giants for periods less than 85 days [10].
- Astrometry involves very precise measurements of a star’s position in the sky over a long period of time. If the star has planets orbiting it, then minute periodic shifts in its measured position could be detectable. The difficulty lies in extracting such highly accurate measurements, because the expected shifts are minuscule. This is the reason that no astrometric planet candidates have been confirmed to date. The Gaia space mission may change all that. It launched on 19 December 2013, and it is estimated it will discover thousands of planets in its expected 5-to-10-year lifetime [11]. It is worth noting that the strength of the astrometric signal is inversely proportional to the distance of the planet and its host star from the Earth.
- Pulsar timing provided the first successful exoplanet detections around Pulsars in 1992 [12]. Pulsars are rapidly rotating neutron stars; they are the superdense stellar remnants of supernova explosions in the distant past. The beam of electromagnetic radiation they emit as they rotate is detected on the Earth as it sweeps by, and is recorded as a highly regular and ultra-precise pulsation signal. Planets orbiting the pulsar reveal themselves through irregularities in the arrival time of the pulses.
- Direct imaging is the only method aiming to visually isolate an exoplanet from its host star. Through high-contrast imaging using adaptive optic systems on large telescopes, massive exoplanets orbiting at the outer reaches of their systems have been discovered [13]. Only those planets that lie very far from their host star can be found with this method, because a star will outshine any nearby planets by a billion times in the optical part of the spectrum.
- Microlensing, in many ways the odd one out, is the topic of this review. It discovers planets by measuring characteristic variations in the brightness of a background star generated by the gravity of intervening objects along the line of sight.
1.2. What Is Microlensing?
2. Microlensing Basics
2.1. Single Lens
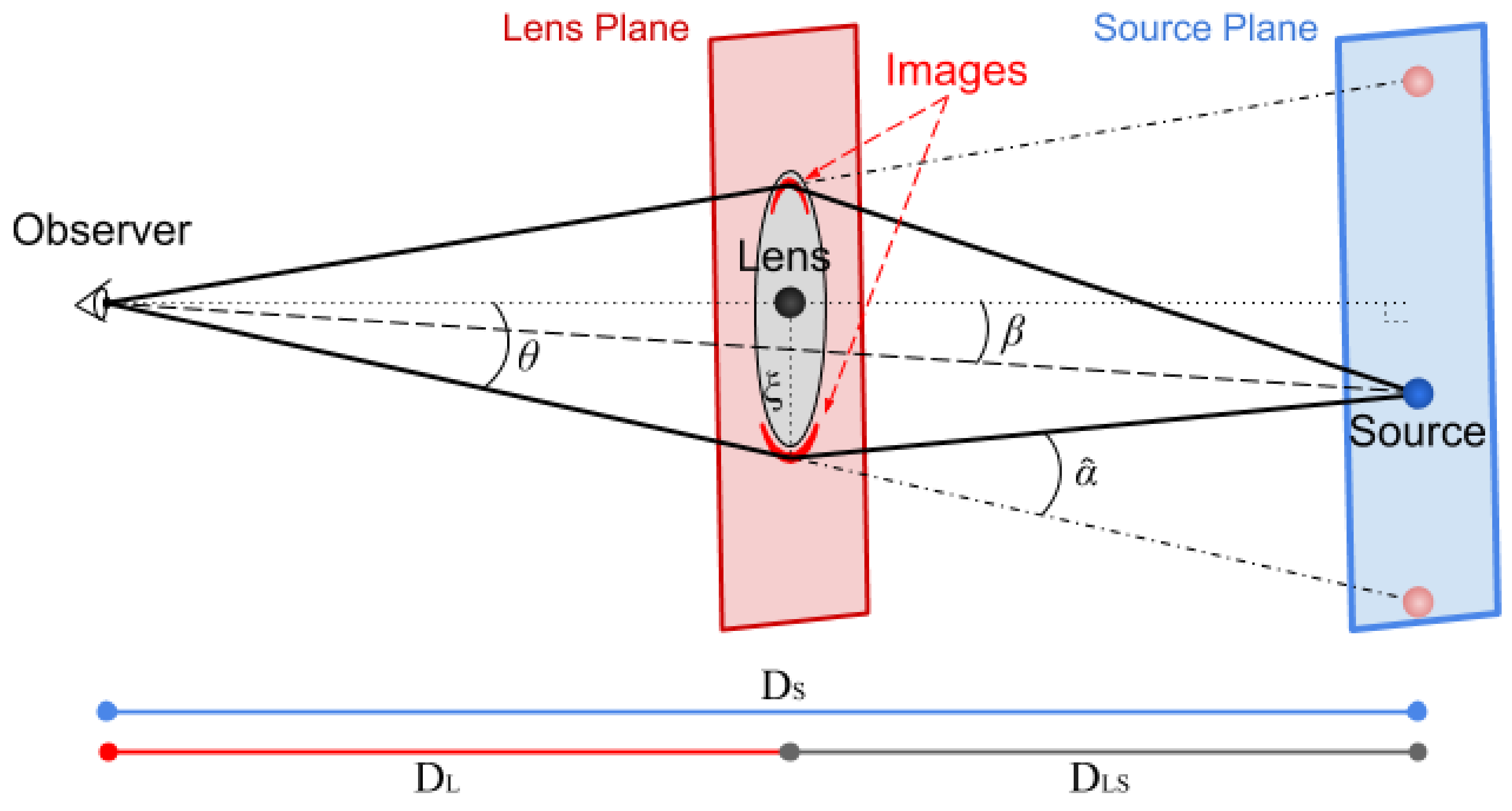
2.1.1. The Deflection Angle
2.1.2. The Lens Equation
2.1.3. The Einstein Radius
2.1.4. Image Positions
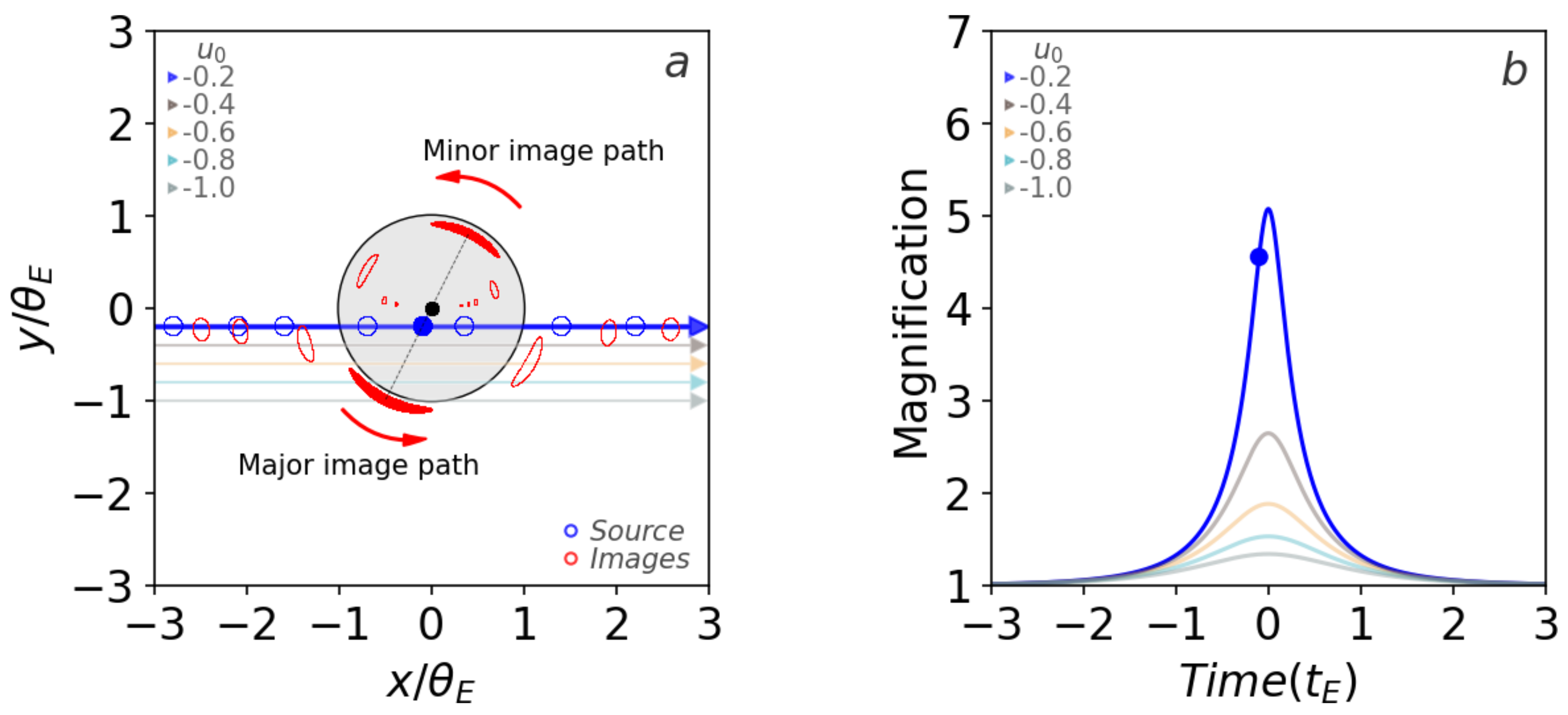
2.1.5. Magnification
2.1.6. Microlensing Timescales
2.1.7. The Optical Depth
2.2. Higher-Order Effects
2.2.1. Blending
2.2.2. Parallax
2.2.3. Finite Source
2.2.4. Binary Source
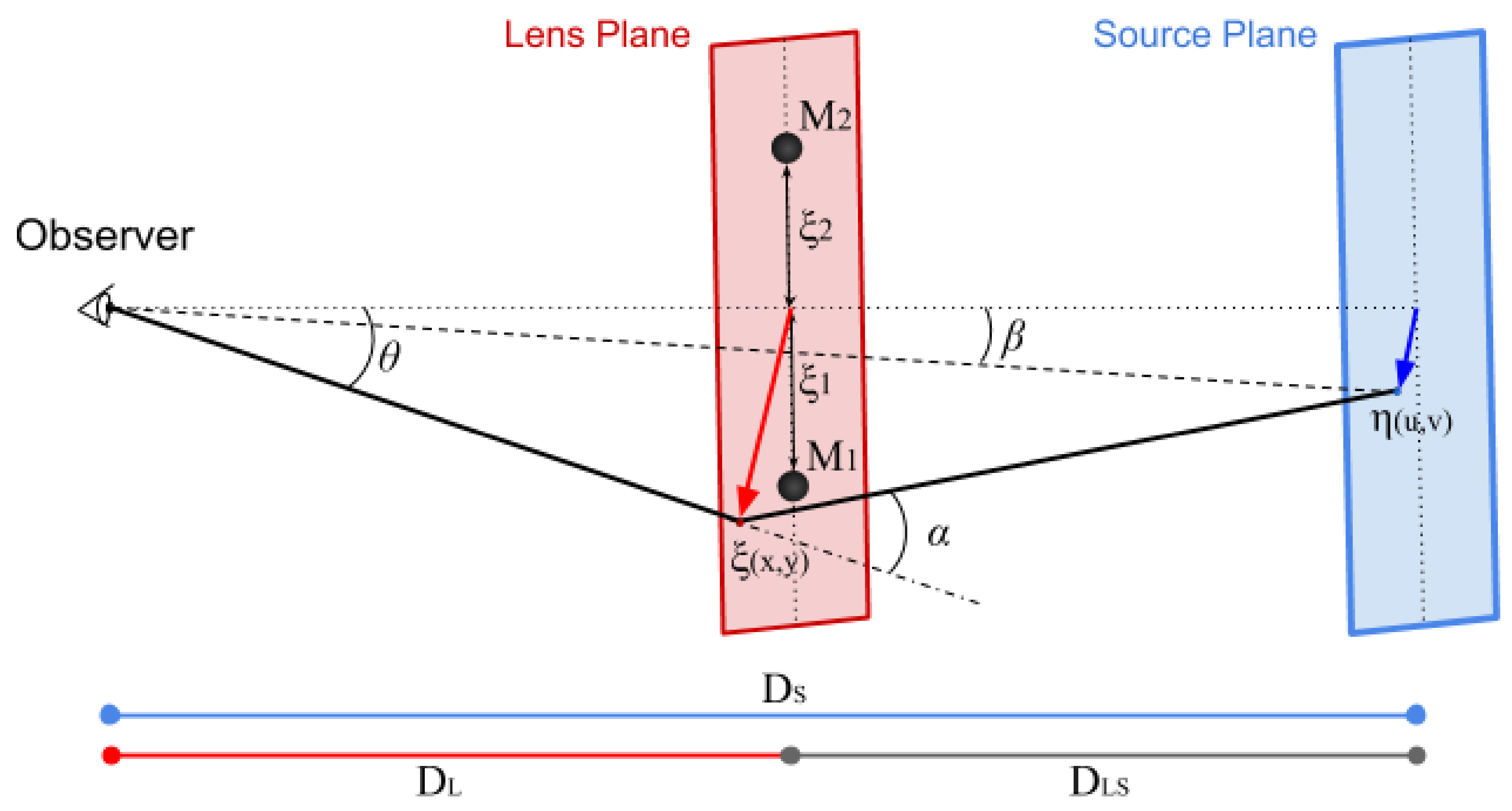
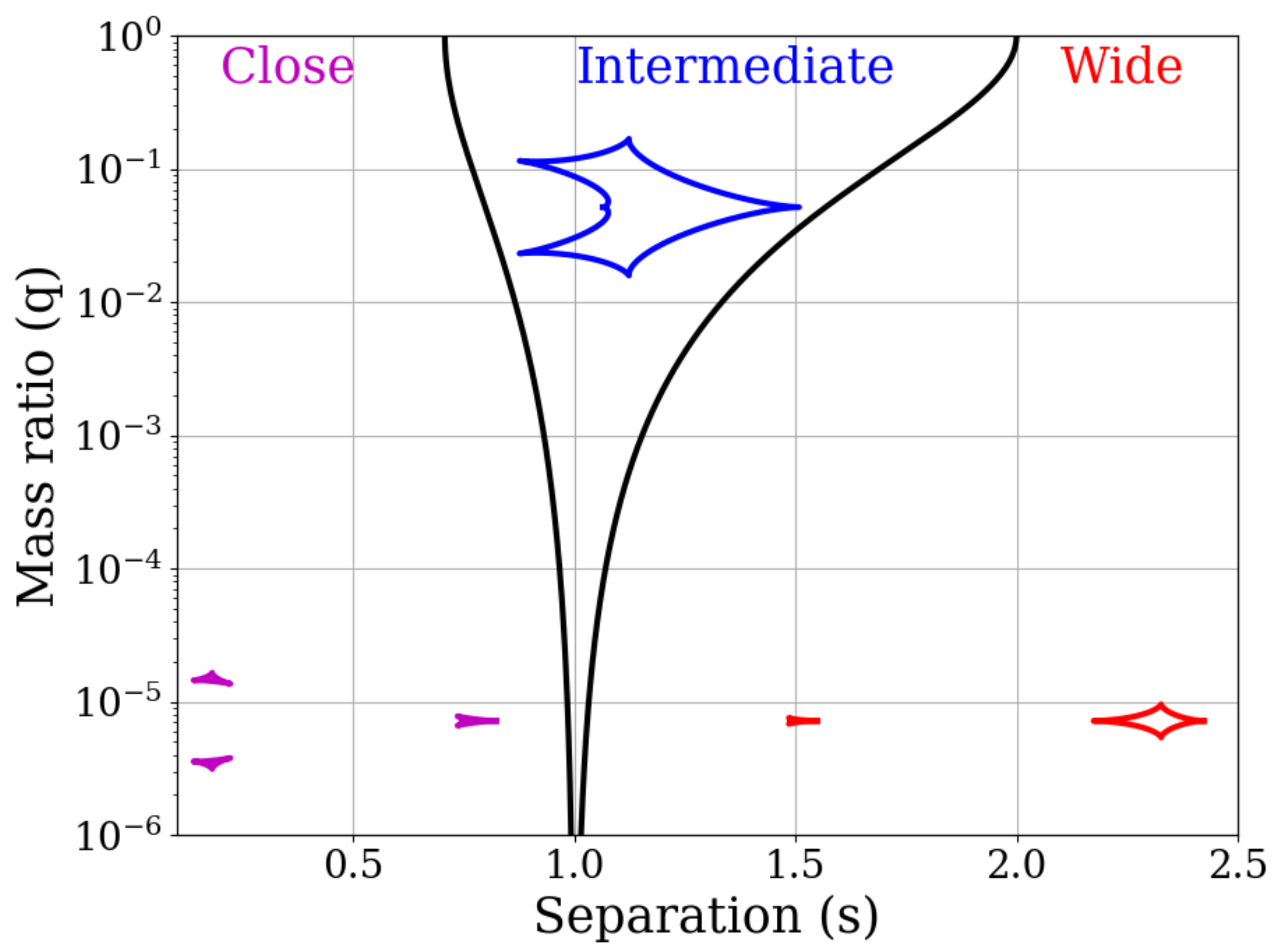
2.3. Binary Lens
2.4. The Magnification and Image Positions for the Binary Lens
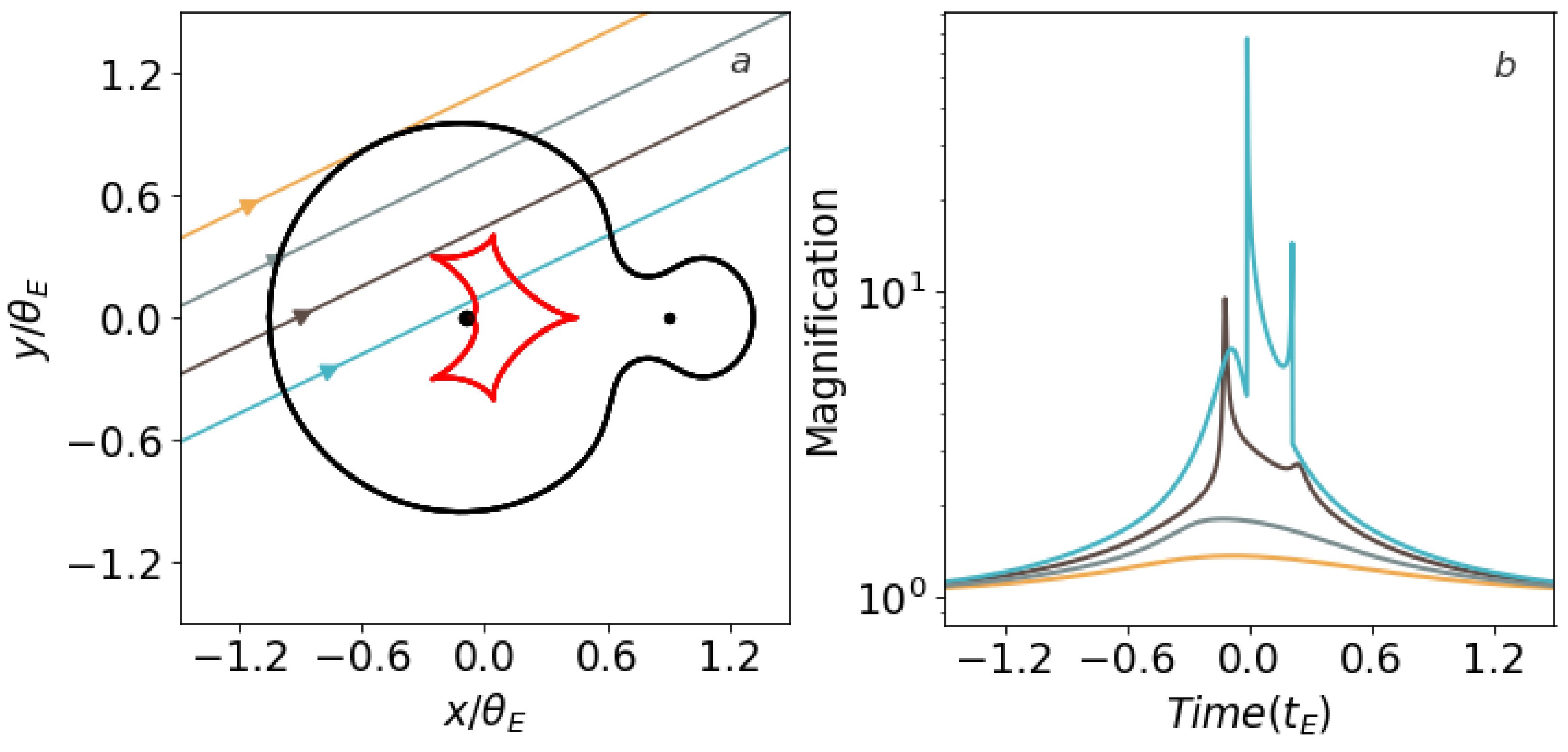
2.5. Critical Curves and Caustics
2.6. Binary Light Curve Degeneracies
2.7. Higher-Order Effects for Binary Lenses: Orbital Motion
2.8. Finding Planets
3. Microlensing Observations in Practice
3.1. Surveys and Follow-Up
3.2. Real-Time Modeling
3.3. Second-Generation Surveys
3.4. From Digital Images to Light Curves
4. Results from Microlensing
4.1. Highlights
4.1.1. A Cold Super-Earth Orbiting an M-Dwarf Star
4.1.2. A Jupiter-Saturn Analog
4.1.3. Limits on the Frequency of Planets
5. Strengths and Weaknesses of the Microlensing Method
5.1. Weaknesses
- The probability of observing planet-lensing events is low, ∼ per star. In practice, this does not constitute a problem because surveys monitor about a billion stars regularly and there are ∼3–5 new microlensing planets discovered every year.
- Planetary anomalies last only a few hours for Earths and a few days for Jupiters. Dozens of telescopes around the world coordinate their efforts to provide high-cadence observations of even the briefest anomalies.
- Microlensing planets are too far away and are not good targets for searching for life with next-generation space missions. Although these planets cannot be the studied further, they provide the missing piece of the puzzle when it comes to understanding how planetary systems form and evolve: what happens beyond the snow line.
- Microlensing events are one-off occurrences, with no possibility of observing them again. Yet their light curves are observed from dozens of telescopes around the world, providing independent confirmation of the features detected. They are typically very well sampled, so anomalies can be well constrained.
- It cannot find planets very close (≲0.4 AU) or too far (≳100 AU) from their host stars. Those regimes are better explored by transits, radial velocity and direct imaging. Microlensing is uniquely capable of exploring intermediate distances.
5.2. Strengths
- It does not have a bias for nearby stars, thus it explores the true Galactic population of planets.
- It does not have a bias for the type of host star and can equally well find planets around brown or red-dwarf stars, main-sequence stars, stellar remnants, or event detect planets that have been ejected from their systems and are no longer gravitationally bound to their stars.
- It does not require many years of observations to discover a planet. The typical microlensing event lasts for less than a month and provides a ‘snapshot’ of the system, with a good chance of revealing any planets close to the Einstein ring of the lens.
- It is very cheap in terms of the resources it requires, as it doesn’t rely on having access to massive telescopes. 1m-class telescopes are routinely used for the observations, and for the brighter events even smaller amateur telescopes have contributed useful data.
- It is sensitive to Earth-mass planets from ground-based observations.
- It is uniquely capable of finding planets at and beyond the snow line of their host stars.
6. Future Prospects
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| CCD | Charge-coupled device |
| AU | Astronomical unit. The average distance between the Sun and the Earth |
| WFIRST | Wide Field Infrared Survey Telescope |
| PSPL | Point source - Point lens |
| MACHO | Massive compact halo object |
| MOA | Microlensing observations in astrophysics |
| OGLE | Optical gravitational lensing experiment |
| KMTNet | Korea Microlensing Telescope Network |
| CCD | Charge-Coupled Device |
| EMCCD | Electron Multiplying Charge Coupled Device |
| VLTI | Very Large Telescope Interferometer |
| PIONIER | Precision Integrated-Optics Near-infrared Imaging ExpeRiment |
| GRAVITY | a VLTI instrument for precision astrometry and interferometric imaging |
References
- Ford, E.B. Architectures of planetary systems and implications for their formation. Proc. Natl. Acad. Sci. USA 2014, 111, 12616–12621. [Google Scholar] [CrossRef] [PubMed]
- Kley, W.; Nelson, R.P. Planet-Disk Interaction and Orbital Evolution. Annu. Rev. Astron. Astrophys. 2012, 50, 211–249. [Google Scholar] [CrossRef]
- De Wit, J.; Wakeford, H.R.; Lewis, N.K.; Delrez, L.; Gillon, M.; Selsis, F.; Leconte, J.; Demory, B.O.; Bolmont, E.; Bourrier, V.; et al. Atmospheric reconnaissance of the habitable-zone Earth-sized planets orbiting TRAPPIST-1. Nat. Astron. 2018, 2, 214–219. [Google Scholar] [CrossRef]
- Anglada-Escudé, G.; Amado, P.J.; Barnes, J.; Berdiñas, Z.M.; Butler, R.P.; Coleman, G.A.L.; de La Cueva, I.; Dreizler, S.; Endl, M.; Giesers, B.; et al. A terrestrial planet candidate in a temperate orbit around Proxima Centauri. Nature 2016, 536, 437–440. [Google Scholar] [CrossRef] [PubMed]
- Lecar, M.; Podolak, M.; Sasselov, D.; Chiang, E. On the Location of the Snow Line in a Protoplanetary Disk. Astrophys. J. 2006, 640, 1115–1118. [Google Scholar] [CrossRef]
- Min, M.; Dullemond, C.P.; Kama, M.; Dominik, C. The thermal structure and the location of the snow line in the protosolar nebula: Axisymmetric models with full 3-D radiative transfer. Icarus 2011, 212, 416–426. [Google Scholar] [CrossRef]
- Cumming, A.; Butler, R.P.; Marcy, G.W.; Vogt, S.S.; Wright, J.T.; Fischer, D.A. The Keck Planet Search: Detectability and the Minimum Mass and Orbital Period Distribution of Extrasolar Planets. Publ. ASP 2008, 120, 531. [Google Scholar] [CrossRef]
- Montet, B.T.; Crepp, J.R.; Johnson, J.A.; Howard, A.W.; Marcy, G.W. The TRENDS High-contrast Imaging Survey. IV. The Occurrence Rate of Giant Planets around M Dwarfs. Astrophys. J. 2014, 781, 28. [Google Scholar] [CrossRef]
- Batalha, N.M.; Rowe, J.F.; Bryson, S.T.; Barclay, T.; Burke, C.J.; Caldwell, D.A.; Christiansen, J.L.; Mullally, F.; Thompson, S.E.; Brown, T.M.; et al. Planetary Candidates Observed by Kepler. III. Analysis of the First 16 Months of Data. Astrophys. J. 2013, 204, 24. [Google Scholar] [CrossRef]
- Fressin, F.; Torres, G.; Charbonneau, D.; Bryson, S.T.; Christiansen, J.; Dressing, C.D.; Jenkins, J.M.; Walkowicz, L.M.; Batalha, N.M. The False Positive Rate of Kepler and the Occurrence of Planets. Astrophys. J. 2013, 766, 81. [Google Scholar] [CrossRef]
- Perryman, M.; Hartman, J.; Bakos, G.Á.; Lindegren, L. Astrometric Exoplanet Detection with Gaia. Astrophys. J. 2014, 797, 14. [Google Scholar] [CrossRef]
- Wolszczan, A.; Frail, D.A. A planetary system around the millisecond pulsar PSR1257 + 12. Nature 1992, 355, 145–147. [Google Scholar] [CrossRef]
- Macintosh, B.; Graham, J.R.; Barman, T.; De Rosa, R.J.; Konopacky, Q.; Marley, M.S.; Marois, C.; Nielsen, E.L.; Pueyo, L.; Rajan, A.; et al. Discovery and spectroscopy of the young jovian planet 51 Eri b with the Gemini Planet Imager. Science 2015, 350, 64–67. [Google Scholar] [CrossRef] [PubMed]
- Mayor, M.; Marmier, M.; Lovis, C.; Udry, S.; Ségransan, D.; Pepe, F.; Benz, W.; Bertaux, J.; Bouchy, F.; Dumusque, X.; et al. The HARPS search for southern extra-solar planets XXXIV. Occurrence, mass distribution and orbital properties of super-Earths and Neptune-mass planets. arXiv, 2011; arXiv:1109.2497. [Google Scholar]
- Cassan, A.; Kubas, D.; Beaulieu, J.P.; Dominik, M.; Horne, K.; Greenhill, J.; Wambsganss, J.; Menzies, J.; Williams, A.; Jørgensen, U.G.; et al. One or more bound planets per Milky Way star from microlensing observations. Nature 2012, 481, 167–169. [Google Scholar] [CrossRef] [PubMed]
- Ida, S.; Lin, D.N.C.; Nagasawa, M. Toward a Deterministic Model of Planetary Formation. VII. Eccentricity Distribution of Gas Giants. Astrophys. J. 2013, 775, 42. [Google Scholar] [CrossRef]
- Suzuki, D.; Bennett, D.P.; Sumi, T.; Bond, I.A.; Rogers, L.A.; Abe, F.; Asakura, Y.; Bhattacharya, A.; Donachie, M.; Freeman, M.; et al. The Exoplanet Mass-ratio Function from the MOA-II Survey: Discovery of a Break and Likely Peak at a Neptune Mass. Astrophys. J. 2016, 833, 145. [Google Scholar] [CrossRef]
- Einstein, A. Über den Einfluß der Schwerkraft auf die Ausbreitung des Lichtes. Ann. Phys. 1911, 340, 898–908. [Google Scholar] [CrossRef]
- Einstein, A. Erklarung der Perihelionbewegung der Merkur aus der allgemeinen Relativitatstheorie. Sitzungsber. Preuss. Akad. Wiss. 1915, 47, 831–839. [Google Scholar]
- Dyson, F.W.; Eddington, A.S.; Davidson, C. A Determination of the Deflection of Light by the Sun’s Gravitational Field, from Observations Made at the Total Eclipse of May 29, 1919. Philos. Trans. R. Soc. Lond. Ser. A 1920, 220, 291–333. [Google Scholar] [CrossRef]
- Einstein, A. Lens-Like Action of a Star by the Deviation of Light in the Gravitational Field. Science 1936, 84, 506–507. [Google Scholar] [CrossRef] [PubMed]
- Renn, J.; Sauer, T.; Stachel, J. The origin of gravitational lensing: A postscript to Einstein’s 1936 Science paper. Science 1997, 275, 184–186. [Google Scholar] [CrossRef] [PubMed]
- Kiraga, M.; Paczynski, B. Gravitational microlensing of the Galactic bulge stars. Astrophys. J. Lett. 1994, 430, L101–L104. [Google Scholar] [CrossRef]
- Udalski, A.; Szymanski, M.; Stanek, K.Z.; Kaluzny, J.; Kubiak, M.; Mateo, M.; Krzeminski, W.; Paczynski, B.; Venkat, R. The Optical Gravitational Lensing Experiment. The Optical Depth to Gravitational Microlensing in the Direction of the Galactic Bulge. Acta Astron. 1994, 44, 165–189. [Google Scholar]
- Peale, S.J. On Microlensing Event Rates and Optical Depth toward the Galactic Center. Astrophys. J. 1998, 509, 177–191. [Google Scholar] [CrossRef]
- Sumi, T.; Bennett, D.P.; Bond, I.A.; Abe, F.; Botzler, C.S.; Fukui, A.; Furusawa, K.; Itow, Y.; Ling, C.H.; Masuda, K.; et al. The Microlensing Event Rate and Optical Depth toward the Galactic Bulge from MOA-II. Astrophys. J. 2013, 778, 150. [Google Scholar] [CrossRef]
- Kim, S.L.; Lee, C.U.; Park, B.G.; Kim, D.J.; Cha, S.M.; Lee, Y.; Han, C.; Chun, M.Y.; Yuk, I. KMTNET: A Network of 1.6 m Wide-Field Optical Telescopes Installed at Three Southern Observatories. J. Korean Astron. Soc. 2016, 49, 37–44. [Google Scholar] [CrossRef]
- Udalski, A.; Szymański, M.K.; Szymański, G. OGLE-IV: Fourth Phase of the Optical Gravitational Lensing Experiment. Acta Astron. 2015, 65, 1–38. [Google Scholar]
- Poleski, R. Empirical microlensing event rates predicted by a phenomenological model. Mon. Not. R. Astron. Soc. 2016, 455, 3656–3661. [Google Scholar] [CrossRef]
- Ban, M.; Kerins, E.; Robin, A.C. The microlensing rate and distribution of free-floating planets towards the Galactic bulge. Astron. Astrophys. 2016, 595, A53. [Google Scholar] [CrossRef]
- Schneider, P.; Ehlers, J.; Falco, E.E. Gravitational Lenses; Springer: Berlin/Heidelberg, Germany, 1992; p. 112. [Google Scholar] [CrossRef]
- Dominik, M. Studying planet populations by gravitational microlensing. Gen. Relat. Gravit. 2010, 42, 2075–2100. [Google Scholar] [CrossRef]
- Mao, S. Astrophysical applications of gravitational microlensing. Res. Astron. Astrophys. 2012, 12, 947–972. [Google Scholar] [CrossRef]
- Gaudi, B.S. Microlensing Surveys for Exoplanets. Ann. Rev. Astron. Astrophys. 2012, 50, 411–453. [Google Scholar] [CrossRef]
- Wambsganss, J. Gravitational Lensing in Astronomy. Living Rev. Relat. 1998, 1, 12. [Google Scholar] [CrossRef] [PubMed]
- The OGLE Project. Optical Gravitational Lensing Experiment. 2018. Available online: http://ogle.astrouw.edu.pl/ (accessed on 29 September 2018).
- The MOA Project. Microlensing Observations in Astrophysics. 2018. Available online: http://www.phys.canterbury.ac.nz/moa/ (accessed on 29 September 2018).
- The KMTNet Project. Korea Microlensing Telescope Network. 2018. Available online: http://kmtnet.kasi.re.kr/kmtnet-eng/ (accessed on 29 September 2018).
- Paczynski, B. Gravitational microlensing by the galactic halo. Astrophys. J. 1986, 304, 1–5. [Google Scholar] [CrossRef]
- Horne, K.; Snodgrass, C.; Tsapras, Y. A metric and optimization scheme for microlens planet searches. Mon. Not. RAS 2009, 396, 2087–2102. [Google Scholar] [CrossRef]
- Hundertmark, M.; Street, R.A.; Tsapras, Y.; Bachelet, E.; Dominik, M.; Horne, K.; Bozza, V.; Bramich, D.M.; Cassan, A.; D’Ago, G.; et al. RoboTAP: Target priorities for robotic microlensing observations. Astron. Astrophys. 2018, 609, A55. [Google Scholar] [CrossRef]
- Paczynski, B. Gravitational microlensing of the Galactic bulge stars. Astrophys. J. Lett. 1991, 371, L63–L67. [Google Scholar] [CrossRef]
- Wood, A.; Mao, S. Optical depths and time-scale distributions in Galactic microlensing. Mon. Not. RAS 2005, 362, 945–951. [Google Scholar] [CrossRef]
- Wyrzykowski, Ł.; Rynkiewicz, A.E.; Skowron, J.; Kozłowski, S.; Udalski, A.; Szyma´ nski, M.K.; Kubiak, M.; Soszy´ nski, I.; Pietrzy ´ nski, G.; Poleski, R.; et al. OGLE-III Microlensing Events and the Structure of the Galactic Bulge. Astrophys. J. 2015, 216, 12. [Google Scholar] [CrossRef]
- Tsapras, Y.; Hundertmark, M.; Wyrzykowski, Ł.; Horne, K.; Udalski, A.; Snodgrass, C.; Street, R.; Bramich, D.M.; Dominik, M.; Bozza, V.; et al. The OGLE-III planet detection efficiency from six years of microlensing observations (2003–2008). Mon. Not. RAS 2016, 457, 1320–1331. [Google Scholar] [CrossRef]
- Paczynski, B. Gravitational microlensing at large optical depth. Astrophys. J. 1986, 301, 503–516. [Google Scholar] [CrossRef]
- Paczynski, B. Gravitational Microlensing in the Local Group. Ann. Rev. Astron. Astrophys. 1996, 34, 419–460. [Google Scholar] [CrossRef]
- Mao, S.; Paczynski, B. Mass Determination with Gravitational Microlensing. Astrophys. J. 1996, 473, 57. [Google Scholar] [CrossRef]
- Popowski, P.; Griest, K.; Thomas, C.L.; Cook, K.H.; Bennett, D.P.; Becker, A.C.; Alves, D.R.; Minniti, D.; Drake, A.J.; Alcock, C.; et al. Microlensing Optical Depth toward the Galactic Bulge Using Clump Giants from the MACHO Survey. Astrophys. J. 2005, 631, 879–905. [Google Scholar] [CrossRef]
- Alcock, C.; Allsman, R.A.; Alves, D.R.; Axelrod, T.S.; Becker, A.C.; Bennett, D.P.; Cook, K.H.; Drake, A.J.; Freeman, K.C.; Geha, M.; et al. The MACHO Project: Microlensing Optical Depth toward the Galactic Bulge from Difference Image Analysis. Astrophys. J. 2000, 541, 734–766. [Google Scholar] [CrossRef]
- Sumi, T.; Penny, M.T. Possible Solution of the Long-standing Discrepancy in the Microlensing Optical Depth toward the Galactic Bulge by Correcting the Stellar Number Count. Astrophys. J. 2016, 827, 139. [Google Scholar] [CrossRef]
- Moniez, M. Microlensing as a probe of the Galactic structure: 20 years of microlensing optical depth studies. Gen. Relat. Gravit. 2010, 42, 2047–2074. [Google Scholar] [CrossRef]
- Ryu, Y.H.; Chang, H.Y.; Park, M.G.; Lee, K.W. Microlensing Optical Depth Revisited with Recent Star Counts. Astrophys. J. 2008, 689, 1078–1083. [Google Scholar] [CrossRef]
- Ingrosso, G.; Calchi Novati, S.; de Paolis, F.; Jetzer, P.; Nucita, A.A.; Scarpetta, G.; Strafella, F. A new analysis of the MEGA M 31 microlensing events. Astron. Astrophys. 2007, 462, 895–902. [Google Scholar] [CrossRef]
- Tsapras, Y.; Carr, B.J.; Weston, M.J.; Kerins, E.; Baillon, P.; Gould, A.; Paulin-Henriksson, S. The POINT-AGAPE survey: Comparing automated searches of microlensing events towards M31. Mon. Not. RAS 2010, 404, 604–628. [Google Scholar] [CrossRef]
- Calchi Novati, S. Pixel lensing. Microlensing towards M31. Gen. Relat. Gravit. 2010, 42, 2101–2126. [Google Scholar] [CrossRef]
- Han, C.; Hwang, K.H.; Ryu, Y.H. Correlations Between Planetary Microlensing Parameters. Astrophys. J. 2010, 720, 409–414. [Google Scholar] [CrossRef]
- Smith, M.C.; Woźniak, P.; Mao, S.; Sumi, T. Blending in gravitational microlensing experiments: Source confusion and related systematics. Mon. Not. RAS 2007, 380, 805–818. [Google Scholar] [CrossRef]
- Thomas, C.L.; Griest, K. Fitting Photometry of Blended Microlensing Events. Astrophys. J. 2006, 640, 299–307. [Google Scholar] [CrossRef]
- Han, C. Analytic relations between the observed gravitational microlensing parameters with and without the effect of blending. Mon. Not. RAS 1999, 309, 373–378. [Google Scholar] [CrossRef]
- Beaulieu, J.P.; Bennett, D.P.; Batista, V.; Fukui, A.; Marquette, J.B.; Brillant, S.; Cole, A.A.; Rogers, L.A.; Sumi, T.; Abe, F.; et al. Revisiting the Microlensing Event OGLE 2012-BLG-0026: A Solar Mass Star with Two Cold Giant Planets. Astrophys. J. 2016, 824, 83. [Google Scholar] [CrossRef]
- Koshimoto, N.; Shvartzvald, Y.; Bennett, D.P.; Penny, M.T.; Hundertmark, M.; Bond, I.A.; Zang, W.C.; Henderson, C.B.; Suzuki, D.; Rattenbury, N.J.; et al. MOA-2016-BLG-227Lb: A Massive Planet Characterized by Combining Light-curve Analysis and Keck AO Imaging. Astron. J. 2017, 154, 3. [Google Scholar] [CrossRef]
- Beaulieu, J.P.; Batista, V.; Bennett, D.P.; Marquette, J.B.; Blackman, J.W.; Cole, A.A.; Coutures, C.; Danielski, C.; Dominis Prester, D.; Donatowicz, J.; et al. Combining Spitzer Parallax and Keck II Adaptive Optics Imaging to Measure the Mass of a Solar-like Star Orbited by a Cold Gaseous Planet Discovered by Microlensing. Astron. J. 2018, 155, 78. [Google Scholar] [CrossRef]
- Grieger, B.; Kayser, R.; Refsdal, S. A parallax effect due to gravitational micro-lensing. Nature 1986, 324, 126. [Google Scholar] [CrossRef]
- Gould, A. Extending the MACHO search to about 10 exp 6 solar masses. Astrophys. J. 1992, 392, 442–451. [Google Scholar] [CrossRef]
- Alcock, C.; Allsman, R.A.; Alves, D.; Axelrod, T.S.; Bennett, D.P.; Cook, K.H.; Freeman, K.C.; Griest, K.; Guern, J.; Lehner, M.J.; et al. First Observation of Parallax in a Gravitational Microlensing Event. Astrophys. J. Lett. 1995, 454, L125. [Google Scholar] [CrossRef]
- Gould, A. Resolution of the MACHO-LMC-5 Puzzle: The Jerk-Parallax Microlens Degeneracy. Astrophys. J. 2004, 606, 319–325. [Google Scholar] [CrossRef]
- Gould, A.; Horne, K. Kepler-like Multi-plexing for Mass Production of Microlens Parallaxes. Astrophys. J. Lett. 2013, 779, L28. [Google Scholar] [CrossRef]
- Calchi Novati, S.; Gould, A.; Udalski, A.; Menzies, J.W.; Bond, I.A.; Shvartzvald, Y.; Street, R.A.; Hundertmark, M.; Beichman, C.A.; Yee, J.C.; et al. Pathway to the Galactic Distribution of Planets: Combined Spitzer and Ground-Based Microlens Parallax Measurements of 21 Single-Lens Events. Astrophys. J. 2015, 804, 20. [Google Scholar] [CrossRef]
- Yee, J.C.; Udalski, A.; Calchi Novati, S.; Gould, A.; Carey, S.; Poleski, R.; Gaudi, B.S.; Pogge, R.W.; Skowron, J.; Kozłowski, S.; et al. First Space-based Microlens Parallax Measurement of an Isolated Star: Spitzer Observations of OGLE-2014-BLG-0939. Astrophys. J. 2015, 802, 76. [Google Scholar] [CrossRef]
- Bennett, D. Magellanic Cloud gravitational microlensing results: What do they mean? Phys. Rep. 1998, 307, 97–106. [Google Scholar] [CrossRef]
- An, J.H.; Albrow, M.D.; Beaulieu, J.P.; Caldwell, J.A.R.; DePoy, D.L.; Dominik, M.; Gaudi, B.S.; Gould, A.; Greenhill, J.; Hill, K.; et al. First Microlens Mass Measurement: PLANET Photometry of EROS BLG-2000-5. Astrophys. J. 2002, 572, 521–539. [Google Scholar] [CrossRef]
- Lee, C.H.; Seitz, S.; Riffeser, A.; Bender, R. Finite-source and finite-lens effects in astrometric microlensing. Mon. Not. RAS 2010, 407, 1597–1608. [Google Scholar] [CrossRef]
- Lee, C.H.; Riffeser, A.; Seitz, S.; Bender, R. Finite-Source Effects in Microlensing: A Precise, Easy to Implement, Fast, and Numerically Stable Formalism. Astrophys. J. 2009, 695, 200–207. [Google Scholar] [CrossRef]
- Dominik, M. Adaptive contouring-an efficient way to calculate microlensing light curves of extended sources. Mon. Not. RAS 2007, 377, 1679–1688. [Google Scholar] [CrossRef]
- Dominik, M. A robust and efficient method for calculating the magnification of extended sources caused by gravitational lenses. Astron. Astrophys. 1998, 333, L79–L82. [Google Scholar]
- Griest, K.; Hu, W. Effect of binary sources on the search for massive astrophysical compact halo objects via microlensing. Astrophys. J. 1992, 397, 362–380. [Google Scholar] [CrossRef]
- Gaudi, B.S. Distinguishing Between Binary-Source and Planetary Microlensing Perturbations. Astrophys. J. 1998, 506, 533–539. [Google Scholar] [CrossRef]
- Han, C. Astrometric Method for Breaking the Photometric Degeneracy between Binary-Source and Planetary Microlensing Perturbations. Astrophys. J. 2002, 564, 1015–1018. [Google Scholar] [CrossRef]
- Dominik, M. Where are the binary source galactic microlensing events? Astron. Astrophys. 1998, 333, 893–896. [Google Scholar]
- Han, C.; Jeong, Y. Where are the binary source gravitational microlensing events? II. Mon. Not. RAS 1998, 301, 231–234. [Google Scholar] [CrossRef]
- Liebig, C.; D’Ago, G.; Bozza, V.; Dominik, M. The complete catalogue of light curves in equal-mass binary microlensing. Mon. Not. RAS 2015, 450, 1565–1584. [Google Scholar] [CrossRef]
- Bourassa, R.R.; Kantowski, R.; Norton, T.D. The Spheroidal Gravitational Lens. Astrophys. J. 1973, 185, 747–756. [Google Scholar] [CrossRef]
- Schneider, P.; Weiss, A. The two-point-mass lens - Detailed investigation of a special asymmetric gravitational lens. Astron. Astrophys. 1986, 164, 237–259. [Google Scholar]
- Witt, H.J. Investigation of high amplification events in light curves of gravitationally lensed quasars. Astron. Astrophys. 1990, 236, 311–322. [Google Scholar]
- Rhie, S.H. Infimum Microlensing Amplification of the Maximum Number of Images of n-Point Lens Systems. Astrophys. J. 1997, 484, 63–69. [Google Scholar] [CrossRef]
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. Numerical Recipes in C++: The Art of Scientific Computing; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Skowron, J.; Gould, A. General Complex Polynomial Root Solver and Its Further Optimization for Binary Microlenses. arXiv, 2012; arXiv:1203.1034. [Google Scholar]
- Rhie, S.H. n-point Gravitational Lenses with 5(n-1) Images. arXiv, 2003; arXiv:astro-ph/0305166. [Google Scholar]
- Erdl, H.; Schneider, P. Classification of the multiple deflection two point-mass gravitational lens models and application of catastrophe theory in lensing. Astron. Astrophys. 1993, 268, 453–471. [Google Scholar]
- Han, C. Properties of Planetary Caustics in Gravitational Microlensing. Astrophys. J. 2006, 638, 1080–1085. [Google Scholar] [CrossRef]
- Cassan, A. An alternative parameterisation for binary-lens caustic-crossing events. Astron. Astrophys. 2008, 491, 587–595. [Google Scholar] [CrossRef]
- Gaudi, B.S. Microlensing by Exoplanets. In Exoplanets; Seager, S., Ed.; University of Arizona Press: Tucson, AZ, USA, 2010; pp. 79–110. [Google Scholar]
- Bozza, V.; Mancini, L.; Sozzetti, A. Methods of Detecting Exoplanets; Astrophysics and Space Science Library: Berlin, Germany, 2016; Volume 428. [Google Scholar] [CrossRef]
- Gaudi, B.S.; Gould, A. Planet Parameters in Microlensing Events. Astrophys. J. 1997, 486, 85–99. [Google Scholar] [CrossRef]
- Dominik, M. Ambiguities in FITS of observed binary lens galactic microlensing events. Astron. Astrophys. 1999, arXiv:[astro-ph/9703003]341, 943–953. [Google Scholar]
- Dominik, M. Parameter degeneracies and (un)predictability of gravitational microlensing events. Mon. Not. RAS 2009, 393, 816–821. [Google Scholar] [CrossRef]
- Dominik, M. The binary gravitational lens and its extreme cases. Astron. Astrophys. 1999, 349, 108–125. [Google Scholar]
- Skowron, J.; Ryu, Y.H.; Hwang, K.H.; Udalski, A.; Mrǎłz, P.; Kozłowski, S.; Soszyński, I.; Pietrukowicz, P.; Szymański, P.K.; Poleski, R.; et al. OGLE-2017-BLG-0373Lb: A Jovian Mass-Ratio Planet Exposes A New Accidental Microlensing Degeneracy. Acta Astron. 2018, 68, 43–61. [Google Scholar]
- Dominik, M. Galactic microlensing with rotating binaries. Astron. Astrophys. 1998, 329, 361–374. [Google Scholar]
- Albrow, M.D.; Beaulieu, J.P.; Caldwell, J.A.R.; Dominik, M.; Gaudi, B.S.; Gould, A.; Greenhill, J.; Hill, K.; Kane, S.; Martin, R.; et al. Detection of Rotation in a Binary Microlens: PLANET Photometry of MACHO 97-BLG-41. Astrophys. J. 2000, 534, 894–906. [Google Scholar] [CrossRef]
- Bachelet, E.; Shin, I.G.; Han, C.; Fouqué, P.; Gould, A.; Menzies, J.W.; Beaulieu, J.P.; Bennett, D.P.; Bond, I.A.; Dong, S.; et al. MOA 2010-BLG-477Lb: Constraining the Mass of a Microlensing Planet from Microlensing Parallax, Orbital Motion, and Detection of Blended Light. Astrophys. J. 2012, 754, 73. [Google Scholar] [CrossRef]
- Park, H.; Udalski, A.; Han, C.; Gould, A.; Beaulieu, J.P.; Tsapras, Y.; Szymański, M.K.; Kubiak, M.; Soszyński, I.; Pietrzyński, G.; et al. Gravitational Binary-lens Events with Prominent Effects of Lens Orbital Motion. Astrophys. J. 2013, 778, 134. [Google Scholar] [CrossRef]
- Shin, I.G.; Udalski, A.; Han, C.; Gould, A.; Dominik, M.; Fouqué, P.; Kubiak, M.; Szymański, M.K.; Pietrzyńki, G.; Soszyński, I.; et al. OGLE-2005-BLG-018: Characterization of Full Physical and Orbital Parameters of a Gravitational Binary Lens. Astrophys. J. 2011, 735, 85. [Google Scholar] [CrossRef]
- Shin, I.G.; Han, C.; Choi, J.Y.; Udalski, A.; Sumi, T.; Gould, A.; Bozza, V.; Dominik, M.; Fouqué, P.; Horne, K.; et al. Characterizing Low-mass Binaries from Observation of Long-timescale Caustic-crossing Gravitational Microlensing Events. Astrophys. J. 2012, 755, 91. [Google Scholar] [CrossRef]
- Gaudi, B.S.; Albrow, M.D.; An, J.; Beaulieu, J.P.; Caldwell, J.A.R.; DePoy, D.L.; Dominik, M.; Gould, A.; Greenhill, J.; Hill, K.; et al. Microlensing Constraints on the Frequency of Jupiter-Mass Companions: Analysis of 5 Years of PLANET Photometry. Astrophys. J. 2002, 566, 463–499. [Google Scholar] [CrossRef]
- Tsapras, Y.; Horne, K.; Kane, S.; Carson, R. Microlensing limits on numbers and orbits of extrasolar planets from the 1998–2000 OGLE events. Mon. Not. RAS 2003, 343, 1131–1144. [Google Scholar] [CrossRef]
- Gould, A.; Dong, S.; Gaudi, B.S.; Udalski, A.; Bond, I.A.; Greenhill, J.; Street, R.A.; Dominik, M.; Sumi, T.; Szymański, M.K.; et al. Frequency of Solar-like Systems and of Ice and Gas Giants Beyond the Snow Line from High-magnification Microlensing Events in 2005–2008. Astrophys. J. 2010, 720, 1073–1089. [Google Scholar] [CrossRef]
- Griest, K.; Safizadeh, N. The Use of High-Magnification Microlensing Events in Discovering Extrasolar Planets. Astrophys. J. 1998, 500, 37–50. [Google Scholar] [CrossRef]
- Peale, S.J. Probability of Detecting a Planetary Companion during a Microlensing Event. Astrophys. J. 2001, 552, 889–911. [Google Scholar] [CrossRef]
- Han, C.; Chang, H.Y.; An, J.H.; Chang, K. Properties of microlensing light curve anomalies induced by multiple planets. Mon. Not. RAS 2001, 328, 986–992. [Google Scholar] [CrossRef]
- Han, C. Analysis of Microlensing Light Curves Induced by Multiple-Planet Systems. Astrophys. J. 2005, 629, 1102–1109. [Google Scholar] [CrossRef]
- Rattenbury, N.J.; Bond, I.A.; Skuljan, J.; Yock, P.C.M. Planetary microlensing at high magnification. Mon. Not. RAS 2002, 335, 159–169. [Google Scholar] [CrossRef]
- Udalski, A.; Szymanski, M.; Kaluzny, J.; Kubiak, M.; Mateo, M. The Optical Gravitational Lensing Experiment. Acta Astron. 1992, 42, 253–284. [Google Scholar]
- Alard, C.; Guibert, J.; Bienayme, O.; Valls-Gabaud, D.; Robin, A.C.; Terzan, A.; Bertin, E. The DUO programme: First results of a microlensing investigation of the Galactic disk and bulge conducted with the ESO Schmidt telescope. Messenger 1995, 80, 31–34. [Google Scholar]
- Alcock, C.; Allsman, R.A.; Alves, D.; Axelrod, T.S.; Becker, A.C.; Bennett, D.P.; Cook, K.H.; Freeman, K.C.; Griest, K.; Guern, J.; et al. The MACHO Project: Limits on Planetary Mass Dark Matter in the Galactic Halo from Gravitational Microlensing. Astrophys. J. 1996, 471, 774. [Google Scholar] [CrossRef]
- Renault, C.; Afonso, C.; Aubourg, E.; Bareyre, P.; Bauer, F.; Brehin, S.; Coutures, C.; Gaucherel, C.; Glicenstein, J.F.; Goldman, B.; et al. Observational limits on MACHOS in the Galactic Halo. Astron. Astrophys. 1997, 324, L69–L72. [Google Scholar]
- Mao, S.; Paczynski, B. Gravitational microlensing by double stars and planetary systems. Astrophys. J. Lett. 1991, 374, L37–L40. [Google Scholar] [CrossRef]
- Gould, A.; Loeb, A. Discovering planetary systems through gravitational microlenses. Astrophys. J. 1992, 396, 104–114. [Google Scholar] [CrossRef]
- Udalski, A.; Szymanski, M.; Kaluzny, J.; Kubiak, M.; Mateo, M.; Krzeminski, W.; Paczynski, B. The Optical Gravitational Lensing Experiment. The Early Warning System: Real Time Microlensing. Acta Astron. 1994, 44, 227–234. [Google Scholar]
- Pratt, M.R.; Alcock, C.; Allsman, R.A.; Alves, D.; Axelrod, T.S.; Becker, A.; Bennett, D.P.; Cook, K.H.; Freeman, K.C.; Griest, K.; et al. Real-time Detection of Gravitational Microlensing. arXiv, 1995; arXiv:astro-ph/9508039. [Google Scholar]
- Albrow, M.; Beaulieu, J.P.; Birch, P.; Caldwell, J.A.R.; Kane, S.; Martin, R.; Menzies, J.; Naber, R.M.; Pel, J.W.; Pollard, K.; et al. The 1995 Pilot Campaign of PLANET: Searching for Microlensing Anomalies through Precise, Rapid, Round-the-Clock Monitoring. Astrophys. J. 1998, 509, 687–702. [Google Scholar] [CrossRef]
- Yoo, J.; DePoy, D.L.; Gal-Yam, A.; Gaudi, B.S.; Gould, A.; Han, C.; Lipkin, Y.; Maoz, D.; Ofek, E.O.; Park, B.G.; et al. OGLE-2003-BLG-262: Finite-Source Effects from a Point-Mass Lens. Astrophys. J. 2004, 603, 139–151. [Google Scholar] [CrossRef]
- Burgdorf, M.J.; Bramich, D.M.; Dominik, M.; Bode, M.F.; Horne, K.D.; Steele, I.A.; Rattenbury, N.; Tsapras, Y. Exoplanet detection via microlensing with RoboNet-1.0. Planet. Space Sci. 2007, 55, 582–588. [Google Scholar] [CrossRef]
- Tsapras, Y.; Street, R.; Horne, K.; Snodgrass, C.; Dominik, M.; Allan, A.; Steele, I.; Bramich, D.M.; Saunders, E.S.; Rattenbury, N.; et al. RoboNet-II: Follow-up observations of microlensing events with a robotic network of telescopes. Astron. Nachr. 2009, 330, 4. [Google Scholar] [CrossRef]
- Dominik, M.; Jørgensen, U.G.; Rattenbury, N.J.; Mathiasen, M.; Hinse, T.C.; Calchi Novati, S.; Harpsøe, K.; Bozza, V.; Anguita, T.; Burgdorf, M.J.; et al. Realisation of a fully-deterministic microlensing observing strategy for inferring planet populations. Astron. Nachr. 2010, 331, 671. [Google Scholar] [CrossRef]
- Han, C. Criteria in the Selection of Target Events for Planetary Microlensing Follow-up Observations. Astrophys. J. 2007, 661, 1202–1207. [Google Scholar] [CrossRef]
- Abe, F.; Airey, C.; Barnard, E.; Baudry, J.; Botzler, C.; Douchin, D.; Freeman, M.; Larsen, P.; Niemiec, A.; Perrott, Y.; et al. Extending the planetary mass function to Earth mass by microlensing at moderately high magnification. Mon. Not. RAS 2013, 431, 2975–2985. [Google Scholar] [CrossRef]
- Dominik, M.; Albrow, M.D.; Beaulieu, J.P.; Caldwell, J.A.R.; DePoy, D.L.; Gaudi, B.S.; Gould, A.; Greenhill, J.; Hill, K.; Kane, S.; et al. The PLANET microlensing follow-up network: Results and prospects for the detection of extra-solar planets. Planet. Space Sci. 2002, 50, 299–307. [Google Scholar] [CrossRef]
- Tsapras, Y.; Horne, K.; Carson, R.; Alvarez, J.M.; Batcheldor, D.; Graham, A.W.; James, P.A.; Knapen, J.; Quaintrell, H.; Gonzalez Serrano, I.; et al. Constraints on Jupiters from observations of Galactic bulge microlensing events during 2000. Mon. Not. RAS 2002, 337, 41–48. [Google Scholar] [CrossRef]
- Dominik, M.; Rattenbury, N.J.; Allan, A.; Mao, S.; Bramich, D.M.; Burgdorf, M.J.; Kerins, E.; Tsapras, Y.; Wyrzykowski, Ł. An anomaly detector with immediate feedback to hunt for planets of Earth mass and below by microlensing. Mon. Not. RAS 2007, 380, 792–804. [Google Scholar] [CrossRef]
- Dominik, M.; Horne, K.; Allan, A.; Rattenbury, N.J.; Tsapras, Y.; Snodgrass, C.; Bode, M.F.; Burgdorf, M.J.; Fraser, S.N.; Kerins, E.; et al. ARTEMiS (Automated Robotic Terrestrial Exoplanet Microlensing Search): A possible expert-system based cooperative effort to hunt for planets of Earth mass and below. Astrono. Nachr. 2008, 329, 248. [Google Scholar] [CrossRef]
- Bachelet, E.; Bramich, D.M.; Han, C.; Greenhill, J.; Street, R.A.; Gould, A.; D’Ago, G.; AlSubai, K.; Dominik, M.; Figuera Jaimes, R.; et al. Red Noise Versus Planetary Interpretations in the Microlensing Event Ogle-2013-BLG-446. Astrophys. J. 2015, 812, 136. [Google Scholar] [CrossRef]
- Bozza, V. Microlensing with an advanced contour integration algorithm: Green’s theorem to third order, error control, optimal sampling and limb darkening. Mon. Not. RAS 2010, 408, 2188–2200. [Google Scholar] [CrossRef]
- Ryu, Y.H.; Han, C.; Hwang, K.H.; Street, R.; Udalski, A.; Sumi, T.; Fukui, A.; Beaulieu, J.P.; Gould, A.; Dominik, M.; et al. OGLE-2009-BLG-092/MOA-2009-BLG-137: A Dramatic Repeating Event with the Second Perturbation Predicted by Real-time Analysis. Astrophys. J. 2010, 723, 81–88. [Google Scholar] [CrossRef]
- Bozza, V.; Dominik, M.; Rattenbury, N.J.; Jørgensen, U.G.; Tsapras, Y.; Bramich, D.M.; Udalski, A.; Bond, I.A.; Liebig, C.; Cassan, A.; et al. OGLE-2008-BLG-510: First automated real-time detection of a weak microlensing anomaly-brown dwarf or stellar binary? Mon. Not. RAS 2012, 424, 902–918. [Google Scholar] [CrossRef]
- Bachelet, E.; Norbury, M.; Bozza, V.; Street, R. pyLIMA: An Open-source Package for Microlensing Modeling. I. Presentation of the Software and Analysis of Single-lens Models. Astron. J. 2017, 154, 203. [Google Scholar] [CrossRef]
- Poleski, R.; Yee, J. Microlensing model fitting with MulensModel. arXiv, 2018; arXiv:1803.01003. [Google Scholar]
- Ranc, C.; Cassan, A. muLAn: Gravitational MICROlensing Analysis Software. 2018. Available online: https://github.com/muLAn-project/muLAn/ (accessed on 29 September 2018).
- Sako, T.; Sekiguchi, T.; Sasaki, M.; Okajima, K.; Abe, F.; Bond, I.A.; Hearnshaw, J.B.; Itow, Y.; Kamiya, K.; Kilmartin, P.M.; et al. MOA-cam3: A wide-field mosaic CCD camera for a gravitational microlensing survey in New Zealand. Exp. Astron. 2008, 22, 51–66. [Google Scholar] [CrossRef]
- The OGLE Project. OGLE-IV 32-chip Mosaic Camera. 2010. Available online: http://ogle.astrouw.edu.pl/main/OGLEIV/mosaic.html (accessed on 29 September 2018).
- Muraki, Y.; Han, C.; Bennett, D.P.; Suzuki, D.; Monard, L.A.G.; Street, R.; Jorgensen, U.G.; Kundurthy, P.; Skowron, J.; Becker, A.C.; et al. Discovery and Mass Measurements of a Cold, 10 Earth Mass Planet and Its Host Star. Astrophys. J. 2011, 741, 22. [Google Scholar] [CrossRef]
- Miyake, N.; Sumi, T.; Dong, S.; Street, R.; Mancini, L.; Gould, A.; Bennett, D.P.; Tsapras, Y.; Yee, J.C.; Albrow, M.D.; et al. A Sub-Saturn Mass Planet, MOA-2009-BLG-319Lb. Astrophys. J. 2011, 728, 120. [Google Scholar] [CrossRef]
- Kains, N.; Street, R.A.; Choi, J.Y.; Han, C.; Udalski, A.; Almeida, L.A.; Jablonski, F.; Tristram, P.J.; Jørgensen, U.G.; Szymański, M.K.; et al. A giant planet beyond the snow line in microlensing event OGLE-2011-BLG-0251. Astron. Astrophys. 2013, 552, A70. [Google Scholar] [CrossRef]
- Tsapras, Y.; Choi, J.Y.; Street, R.A.; Han, C.; Bozza, V.; Gould, A.; Dominik, M.; Beaulieu, J.P.; Udalski, A.; Jørgensen, U.G.; et al. A Super-Jupiter Orbiting a Late-type Star: A Refined Analysis of Microlensing Event OGLE-2012-BLG-0406. Astrophys. J. 2014, 782, 48. [Google Scholar] [CrossRef]
- Kim, S.L.; Park, B.G.; Lee, C.U.; Kappler, L.; Kappler, N.; Poteet, W.; Cauthen, H.; Blanco, D.; Buchroeder, R.; Teran, J.; et al. Wide-field telescope design for the KMTNet project. In Proceedings of the Techniques and Instrumentation for Detection of Exoplanets V, San Diego, CA, USA, 15 September 2011. [Google Scholar] [CrossRef]
- Henderson, C.B.; Gaudi, B.S.; Han, C.; Skowron, J.; Penny, M.T.; Nataf, D.; Gould, A.P. Optimal Survey Strategies and Predicted Planet Yields for the Korean Microlensing Telescope Network. Astrophys. J. 2014, 794, 52. [Google Scholar] [CrossRef]
- Martinez, P.; Klotz, A.; Demers, A.; Léna, F.B.P. A Practical Guide to CCD Astronomy; Cambridge University Press: Cambridge, UK, 1997; p. 263. [Google Scholar]
- Howell, S.B. Handbook of CCD Astronomy; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Mighell, K.J. CCD Aperture Photometry. Precis. CCD Photom. 1999, 189, 50. [Google Scholar]
- Heasley, J.N. Point-Spread Function Fitting Photometry. Precis. CCD Photom. 1999, 189, 56. [Google Scholar]
- Tomaney, A.B.; Crotts, A.P.S. Expanding the Realm of Microlensing Surveys with Difference Image Photometry. Astron. J. 1996, 112, 2872. [Google Scholar] [CrossRef]
- Alard, C.; Lupton, R.H. A Method for Optimal Image Subtraction. Astrophys. J. 1998, 503, 325–331. [Google Scholar] [CrossRef]
- Alard, C. Analysis of the OGLE microlensing candidates using the image subtraction method. Astron. Astrophys. 1999, 343, 10–18. [Google Scholar]
- Bramich, D.M. A new algorithm for difference image analysis. Mon. Not. RAS 2008, 386, L77–L81. [Google Scholar] [CrossRef]
- Albrow, M.D.; Horne, K.; Bramich, D.M.; Fouqué, P.; Miller, V.R.; Beaulieu, J.P.; Coutures, C.; Menzies, J.; Williams, A.; Batista, V.; et al. Difference imaging photometry of blended gravitational microlensing events with a numerical kernel. Mon. Not. RAS 2009, 397, 2099–2105. [Google Scholar] [CrossRef]
- Bramich, D.M.; Horne, K.; Albrow, M.D.; Tsapras, Y.; Snodgrass, C.; Street, R.A.; Hundertmark, M.; Kains, N.; Arellano Ferro, A.; Figuera, J.R.; et al. Difference image analysis: Extension to a spatially varying photometric scale factor and other considerations. Mon. Not. RAS 2013, 428, 2275–2289. [Google Scholar] [CrossRef]
- Gaudi, B.S.; Bennett, D.P.; Udalski, A.; Gould, A.; Christie, G.W.; Maoz, D.; Dong, S.; McCormick, J.; Szymański, M.K.; Tristram, P.J.; et al. Discovery of a Jupiter/Saturn Analog with Gravitational Microlensing. Science 2008, 319, 927. [Google Scholar] [CrossRef] [PubMed]
- Han, C.; Udalski, A.; Choi, J.Y.; Yee, J.C.; Gould, A.; Christie, G.; Tan, T.G.; Szymański, M.K.; Kubiak, M.; Soszyński, I. The Second Multiple-planet System Discovered by Microlensing: OGLE-2012-BLG-0026Lb, c A Pair of Jovian Planets beyond the Snow Line. Astrophys. J. Lett. 2013, 762, L28. [Google Scholar] [CrossRef]
- Bennett, D.P.; Rhie, S.H.; Udalski, A.; Gould, A.; Tsapras, Y.; Kubas, D.; Bond, I.A.; Greenhill, J.; Cassan, A.; Rattenbury, N.J.; et al. The First Circumbinary Planet Found by Microlensing: OGLE-2007-BLG-349L(AB)c. Astron. J. 2016, 152, 125. [Google Scholar] [CrossRef]
- Bennett, D.P.; Batista, V.; Bond, I.A.; Bennett, C.S.; Suzuki, D.; Beaulieu, J.P.; Udalski, A.; Donatowicz, J.; Bozza, V.; Abe, F.; et al. MOA-2011-BLG-262Lb: A Sub-Earth-Mass Moon Orbiting a Gas Giant Primary or a High Velocity Planetary System in the Galactic Bulge. Astrophys. J. 2014, 785, 155. [Google Scholar] [CrossRef]
- Hwang, K.H.; Udalski, A.; Bond, I.A.; Albrow, M.D.; Chung, S.J.; Gould, A.; Han, C.; Jung, Y.K.; Ryu, Y.H.; Shin, I.G.; et al. OGLE-2015-BLG-1459L: The Challenges of Exo-moon Microlensing. Astron. J. 2018, 155, 259. [Google Scholar] [CrossRef]
- NASA Exoplanet Archive. NASA Exoplanet Archive. 2018. Available online: https://exoplanetarchive.ipac.caltech.edu/ (accessed on 29 September 2018).
- The Extrasolar Planets Encyclopaedia. The Extrasolar Planets Encyclopaedia. 2018. Available online: http://exoplanet.eu/ (accessed on 29 September 2018).
- Spiegel, D.S.; Burrows, A.; Milsom, J.A. The Deuterium-burning Mass Limit for Brown Dwarfs and Giant Planets. Astrophys. J. 2011, 727, 57. [Google Scholar] [CrossRef]
- Daflon, S.; Cunha, K. Galactic Metallicity Gradients Derived from a Sample of OB Stars. Astrophys. J. 2004, 617, 1115–1126. [Google Scholar] [CrossRef]
- Gonzalez, G. The stellar metallicity-giant planet connection. Mon. Not. RAS 1997, 285, 403–412. [Google Scholar] [CrossRef]
- Valenti, J.A.; Fischer, D.A. Relationship between giant planet frequency and stellar metallicity. Phys. Scr. Vol. T 2008, 130, 014003. [Google Scholar] [CrossRef]
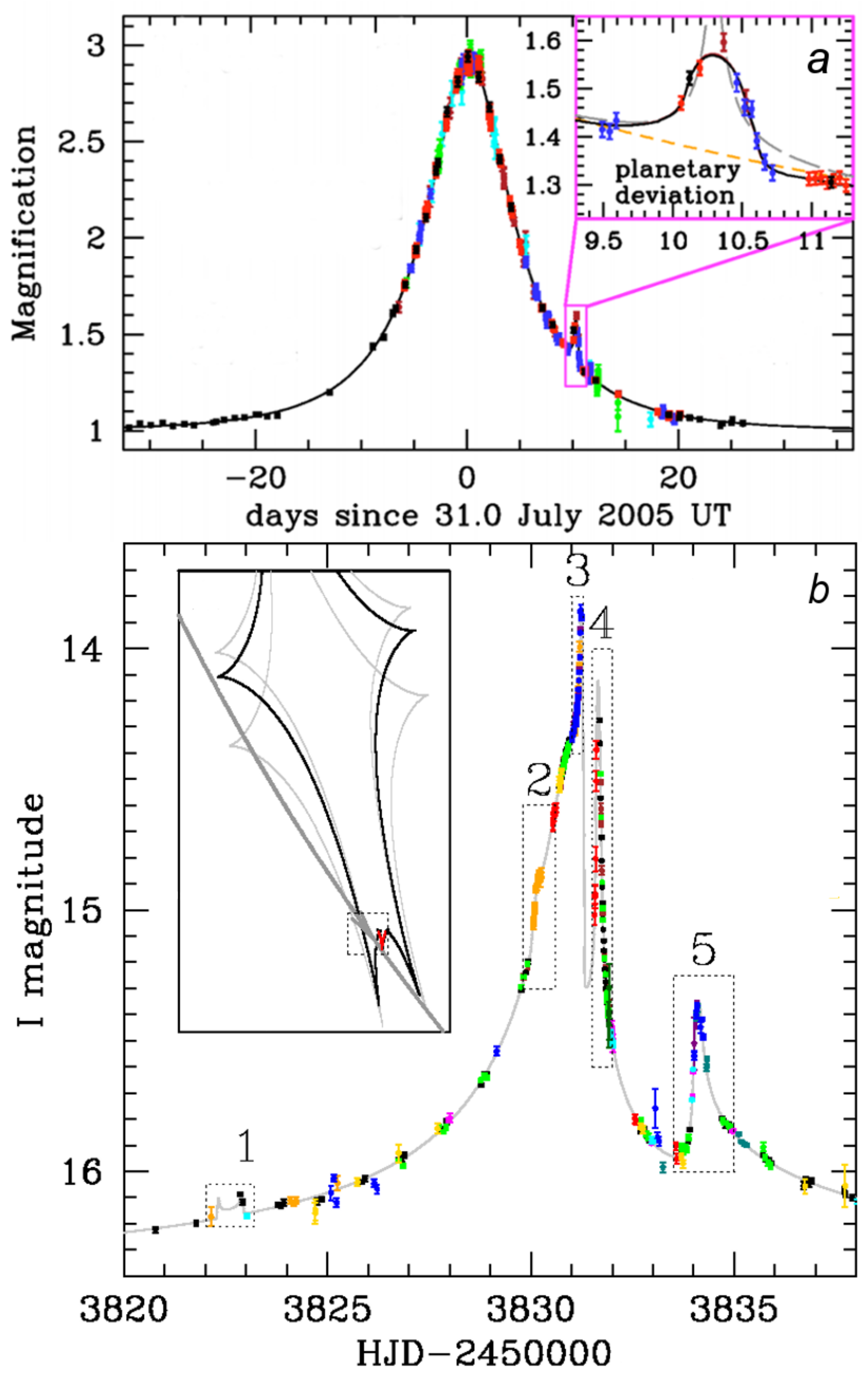
- Beaulieu, J.P.; Bennett, D.P.; Fouqué, P.; Williams, A.; Dominik, M.; Jørgensen, U.G.; Kubas, D.; Cassan, A.; Coutures, C.; Greenhill, J.; et al. Discovery of a cool planet of 5.5 Earth masses through gravitational microlensing. Nature 2006, 439, 437–440. [Google Scholar] [CrossRef] [PubMed]
- Laughlin, G.; Bodenheimer, P.; Adams, F.C. The Core Accretion Model Predicts Few Jovian-Mass Planets Orbiting Red Dwarfs. Astrophys. J. Lett. 2004, 612, L73–L76. [Google Scholar] [CrossRef]
- Bennett, D.P.; Rhie, S.H.; Nikolaev, S.; Gaudi, B.S.; Udalski, A.; Gould, A.; Christie, G.W.; Maoz, D.; Dong, S.; McCormick, J.; et al. Masses and Orbital Constraints for the OGLE-2006-BLG-109Lb,c Jupiter/Saturn Analog Planetary System. Astrophys. J. 2010, 713, 837–855. [Google Scholar] [CrossRef]
- Albrow, M.D.; Beaulieu, J.P.; Caldwell, J.A.R.; DePoy, D.L.; Dominik, M.; Gaudi, B.S.; Gould, A.; Greenhill, J.; Hill, K.; Kane, S.; et al. Limits on Stellar and Planetary Companions in Microlensing Event OGLE-1998-BUL-14. Astrophys. J. 2000, 535, 176–189. [Google Scholar] [CrossRef]
- Sumi, T.; Bennett, D.P.; Bond, I.A.; Udalski, A.; Batista, V.; Dominik, M.; Fouqué, P.; Kubas, D.; Gould, A.; Macintosh, B.; et al. A Cold Neptune-Mass Planet OGLE-2007-BLG-368Lb: Cold Neptunes Are Common. Astrophys. J. 2010, 710, 1641–1653. [Google Scholar] [CrossRef]
- Dominik, M. Planetary mass function and planetary systems. Mon. Not. RAS 2011, 411, 2–8. [Google Scholar] [CrossRef]
- Udalski, A.; Ryu, Y.H.; Sajadian, S.; Gould, A.; Mróz, P.; Poleski, R.; Szymański, M.K.; Skowron, J.; Soszyński, I.; Kozłowski, S.; et al. OGLE-2017-BLG-1434Lb: Eighth q<1x10e-4 Mass-Ratio Microlens Planet Confirms Turnover in Planet Mass-Ratio Function. Acta Astron. 2018, 68, 1–42. [Google Scholar]
- Snodgrass, C.; Horne, K.; Tsapras, Y. The abundance of Galactic planets from OGLE-III 2002 microlensing data. Mon. Not. RAS 2004, 351, 967–975. [Google Scholar] [CrossRef]
- Shvartzvald, Y.; Maoz, D.; Udalski, A.; Sumi, T.; Friedmann, M.; Kaspi, S.; Poleski, R.; Szymański, M.K.; Skowron, J.; Kozłowski, S.; et al. The frequency of snowline-region planets from four years of OGLE-MOA-Wise second-generation microlensing. Mon. Not. RAS 2016, 457, 4089–4113. [Google Scholar] [CrossRef]
- Bennett, D.P.; Rhie, S.H. Simulation of a Space-based Microlensing Survey for Terrestrial Extrasolar Planets. Astrophys. J. 2002, 574, 985–1003. [Google Scholar] [CrossRef]
- Green, J.; Schechter, P.; Baltay, C.; Bean, R.; Bennett, D.; Brown, R.; Conselice, C.; Donahue, M.; Fan, X.; Gaudi, B.S.; et al. Wide-Field InfraRed Survey Telescope (WFIRST) Final Report. arXiv, 2012; arXiv:1208.4012. [Google Scholar]
- Barclay, T.; Quintana, E.V.; Raymond, S.N.; Penny, M.T. The Demographics of Rocky Free-floating Planets and their Detectability by WFIRST. Astrophys. J. 2017, 841, 86. [Google Scholar] [CrossRef]
- Paczyński, B. Gravitational Microlensing with the Space Interferometry Mission. Astrophys. J. Lett. 1998, 494, L23–L26. [Google Scholar] [CrossRef]
- Safizadeh, N.; Dalal, N.; Griest, K. Astrometric Microlensing as a Method of Discovering and Characterizing Extrasolar Planets. Astrophys. J. 1999, 522, 512–517. [Google Scholar] [CrossRef]
- Dominik, M.; Sahu, K.C. Astrometric Microlensing of Stars. Astrophys. J. 2000, 534, 213–226. [Google Scholar] [CrossRef]
- Honma, M. Detecting Galactic MACHOs with VERA through Astrometric Microlensing of Distant Radio Sources. Publ. ASJ 2001, 53, 233–241. [Google Scholar] [CrossRef]
- Han, C.; Chun, M.S.; Chang, K. Astrometric Properties of Gravitational Binary-Microlens Events and Their Applications. Astrophys. J. 1999, 526, 405–410. [Google Scholar] [CrossRef]
- Paczynski, B. The Masses of Nearby Dwarfs Can Be Determined with Gravitational Microlensing. Acta Astron. 1995, 45, 345–348. [Google Scholar]
- Salim, S.; Gould, A. Nearby Microlensing Events: Identification of the Candidates for theSpace Interferometry Mission. Astrophys. J. 2000, 539, 241–257. [Google Scholar] [CrossRef]
- Proft, S.; Demleitner, M.; Wambsganss, J. Prediction of astrometric microlensing events during the Gaia mission. Astron. Astrophys. 2011, 536, A50. [Google Scholar] [CrossRef]
- Klüter, J.; Bastian, U.; Demleitner, M.; Wambsganss, J. Ongoing astrometric microlensing events of two nearby stars. Astron. Astrophys. 2018, 615, L11. [Google Scholar] [CrossRef]
- Klüter, J.; Bastian, U.; Demleitner, M.; Wambsganss, J. Prediction of Astrometric Microlensing Events from Gaia DR2 Proper Motions. arXiv, 2018; arXiv:1807.11077. [Google Scholar]
- Bramich, D.M.; Nielsen, M.B. An almanac of predicted microlensing events for the 21st century. arXiv, 2018; arXiv:1806.10003. [Google Scholar]
- Delplancke, F.; Górski, K.M.; Richichi, A. Resolving gravitational microlensing events with long-baseline optical interferometry. Prospects for the ESO Very Large Telescope Interferometer. Astron. Astrophys. 2001, 375, 701–710. [Google Scholar] [CrossRef]
- Cassan, A.; Ranc, C. Interferometric observation of microlensing events. Mon. Not. RAS 2016, 458, 2074–2079. [Google Scholar] [CrossRef]
- Mackay, C. High-efficiency lucky imaging. Mon. Not. RAS 2013, 432, 702–710. [Google Scholar] [CrossRef]
- Sajadian, S.; Rahvar, S.; Dominik, M.; Hundertmark, M. The advantages of using a Lucky Imaging camera for observations of microlensing events. Mon. Not. RAS 2016, 458, 3248–3259. [Google Scholar] [CrossRef]
- Mackay, C.; Dominik, M.; Steele, I.A.; Snodgrass, C.; Jørgensen, U.G.; Skottfelt, J.; Stefanov, K.; Carry, B.; Braga-Ribas, F.; Doressoundiram, A.; et al. GravityCam: Wide-Field High-Resolution High-Cadence Imaging Surveys in the Visible from the Ground. arXiv, 2017; arXiv:1709.00244. [Google Scholar]

© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tsapras, Y. Microlensing Searches for Exoplanets. Geosciences 2018, 8, 365. https://doi.org/10.3390/geosciences8100365
Tsapras Y. Microlensing Searches for Exoplanets. Geosciences. 2018; 8(10):365. https://doi.org/10.3390/geosciences8100365
Chicago/Turabian StyleTsapras, Yiannis. 2018. "Microlensing Searches for Exoplanets" Geosciences 8, no. 10: 365. https://doi.org/10.3390/geosciences8100365
APA StyleTsapras, Y. (2018). Microlensing Searches for Exoplanets. Geosciences, 8(10), 365. https://doi.org/10.3390/geosciences8100365




