Development of a Distributed Hydrologic Model for a Region with Fragipan Soils to Study Impacts of Climate on Soil Moisture: A Case Study on the Obion River Watershed in West Tennessee
Abstract
1. Introduction
2. Materials and Methods
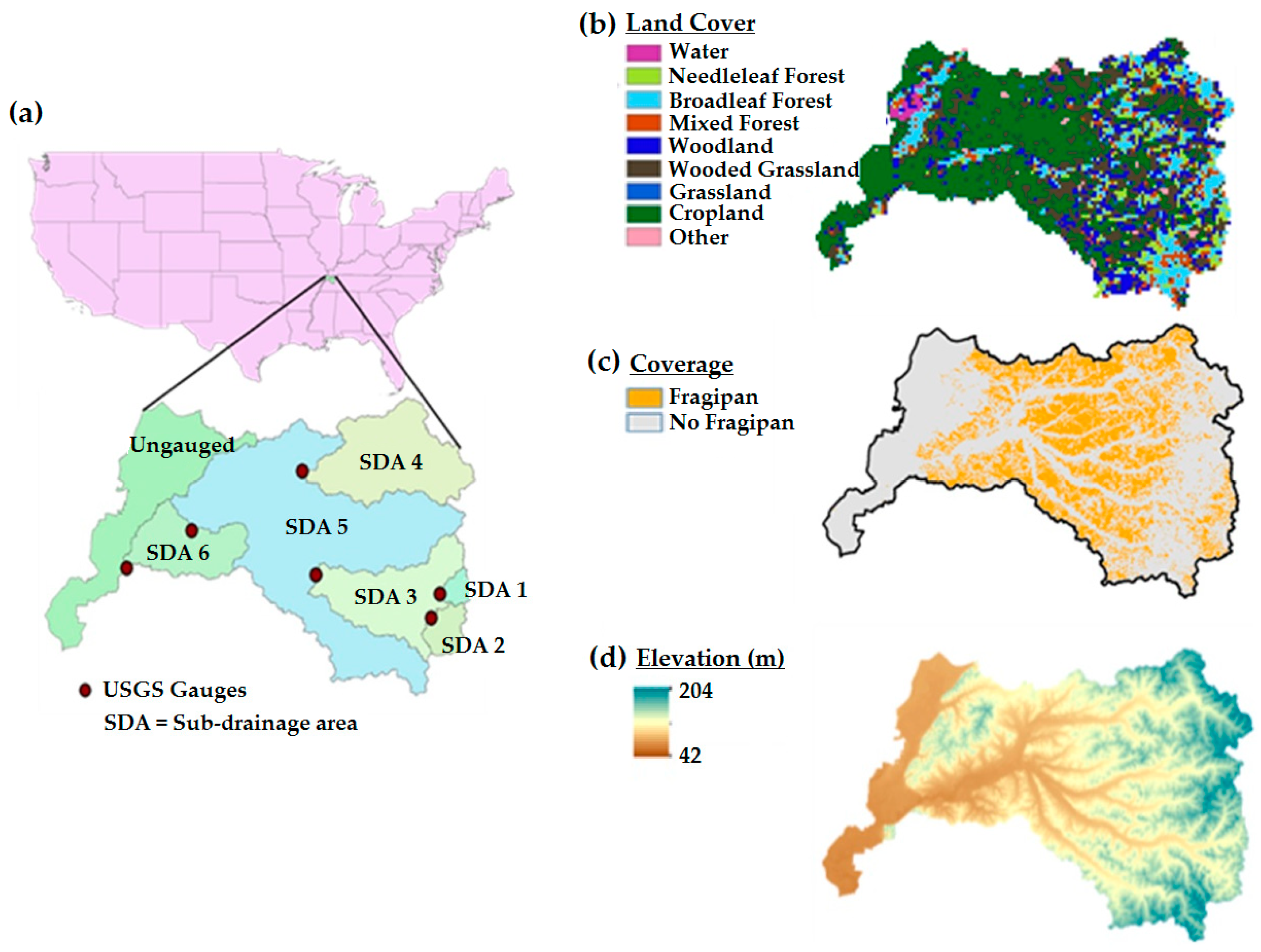
2.1. Study Area
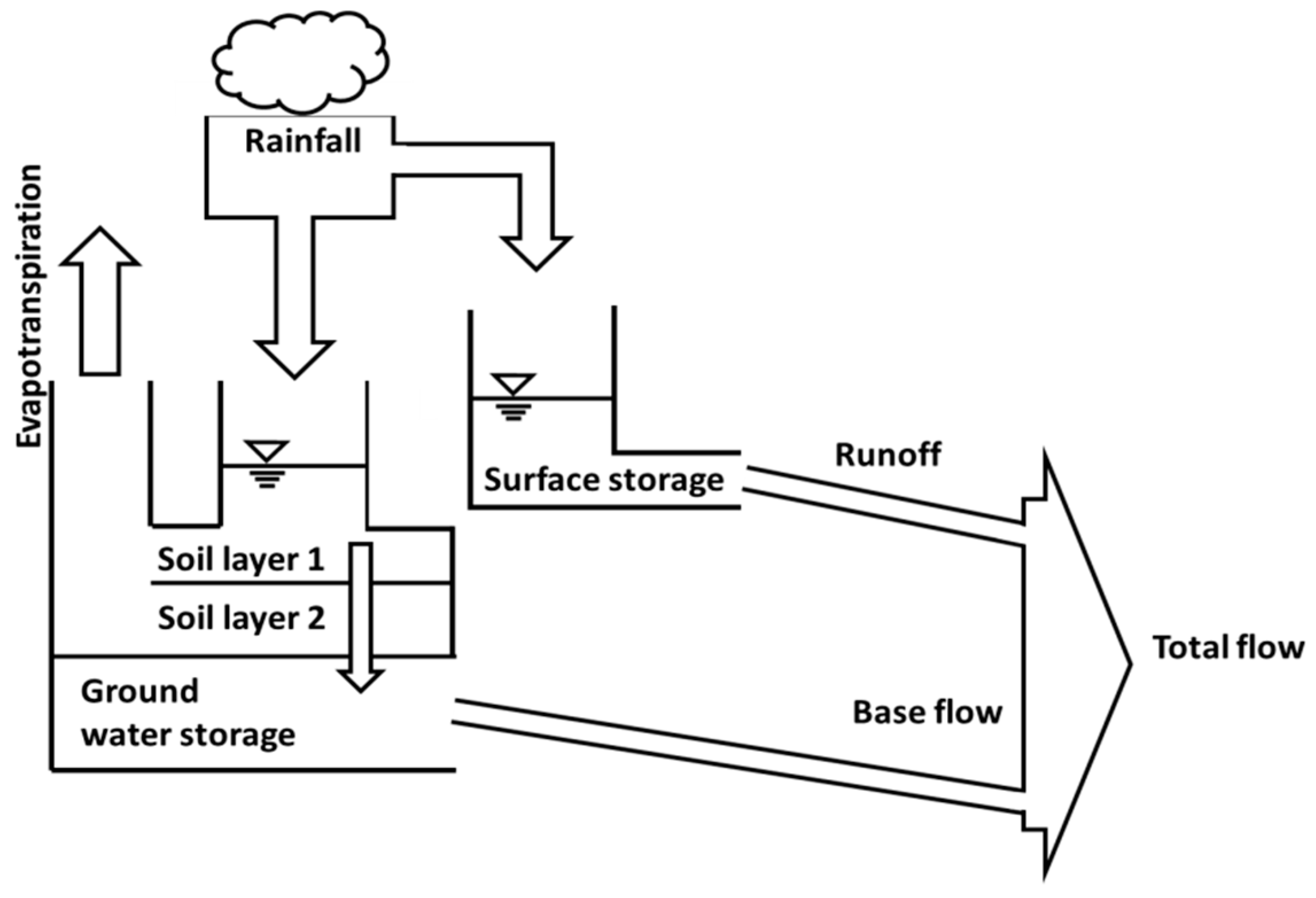
2.2. Hydrologic Model
2.3. Data Sources
2.4. Model Calibration & Validation
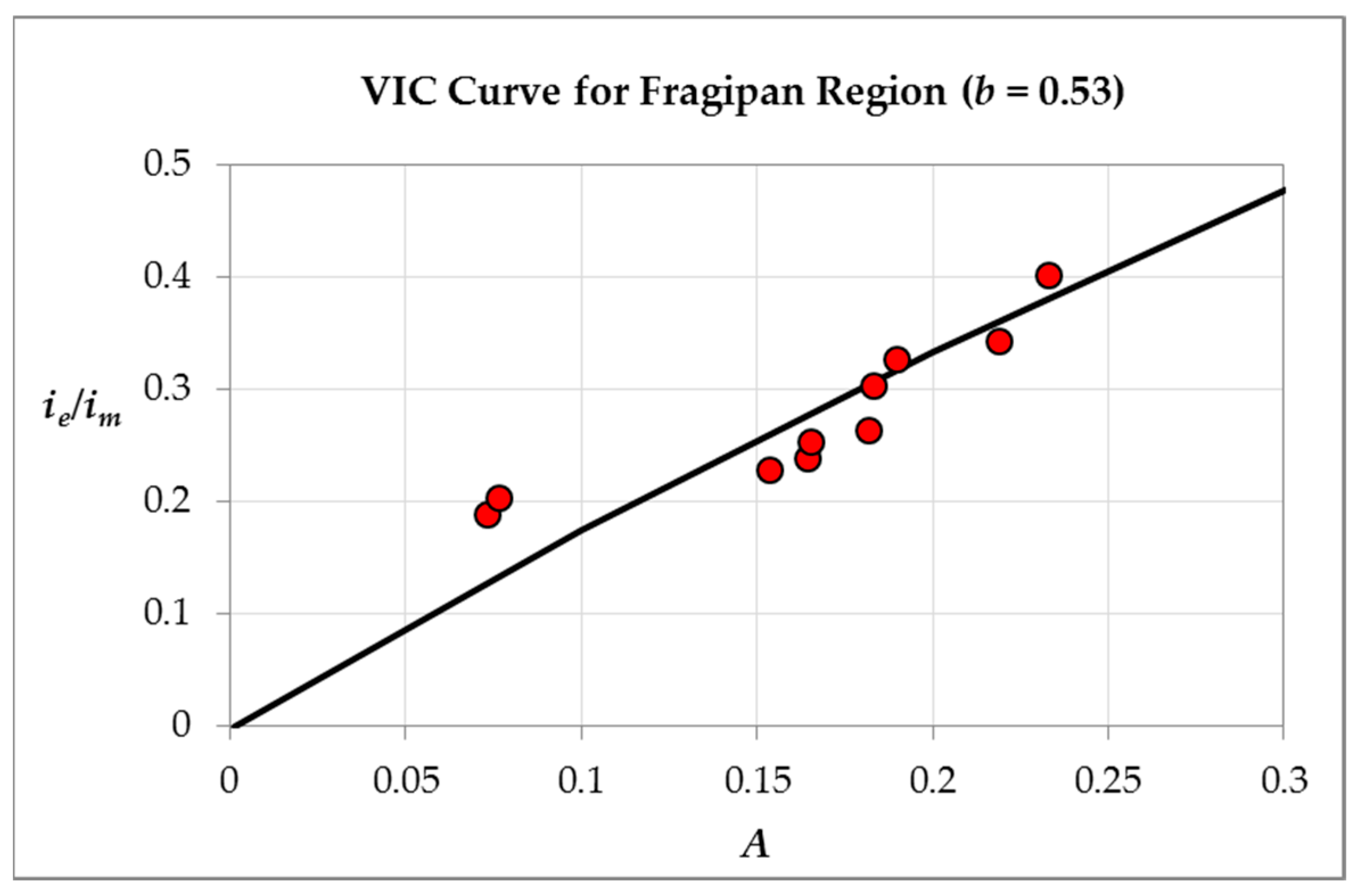
2.4.1. Selection of Calibration Parameters
2.4.2. Estimation of Calibration Parameters
3. Results
3.1. Model Calibration
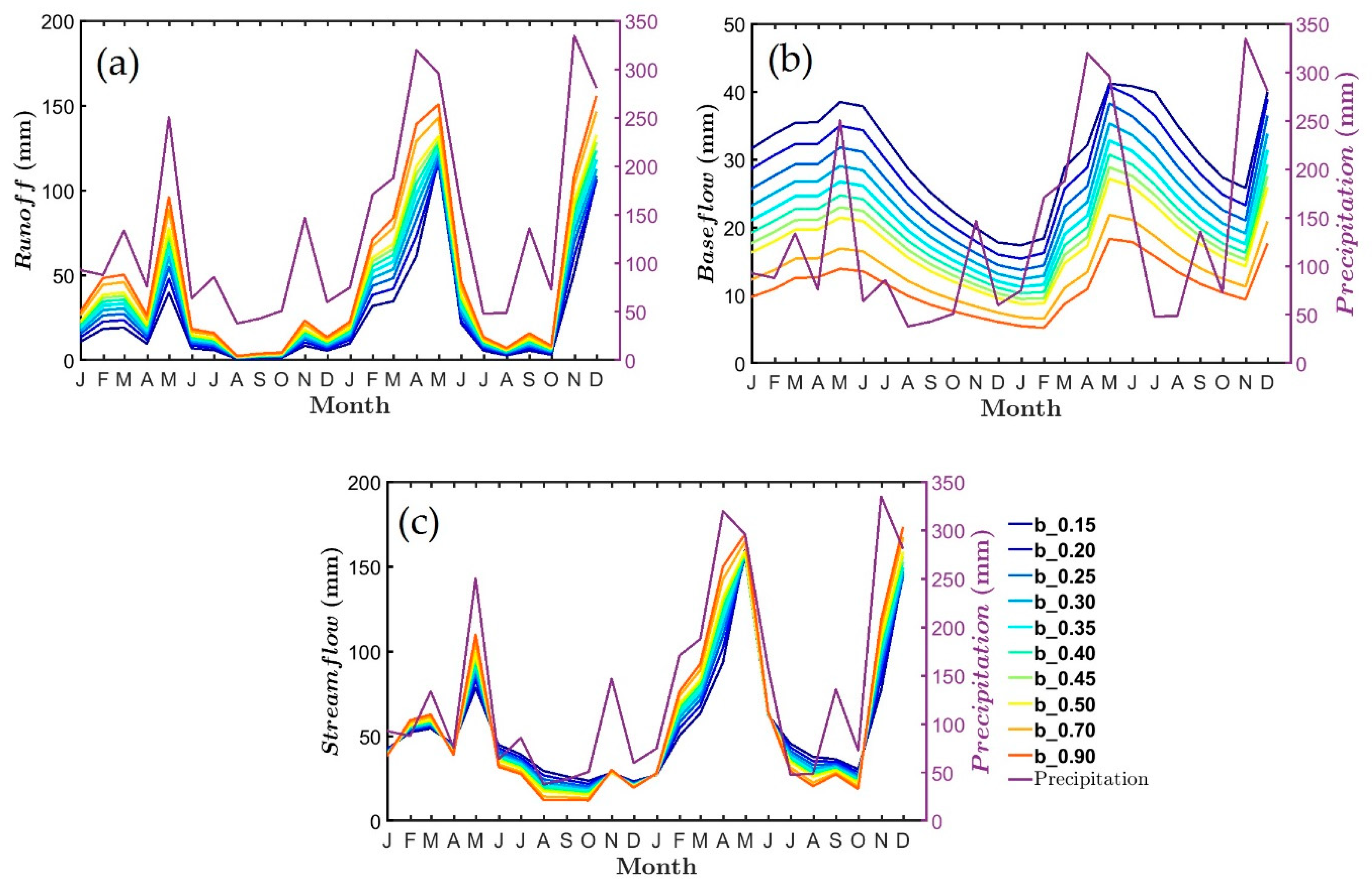
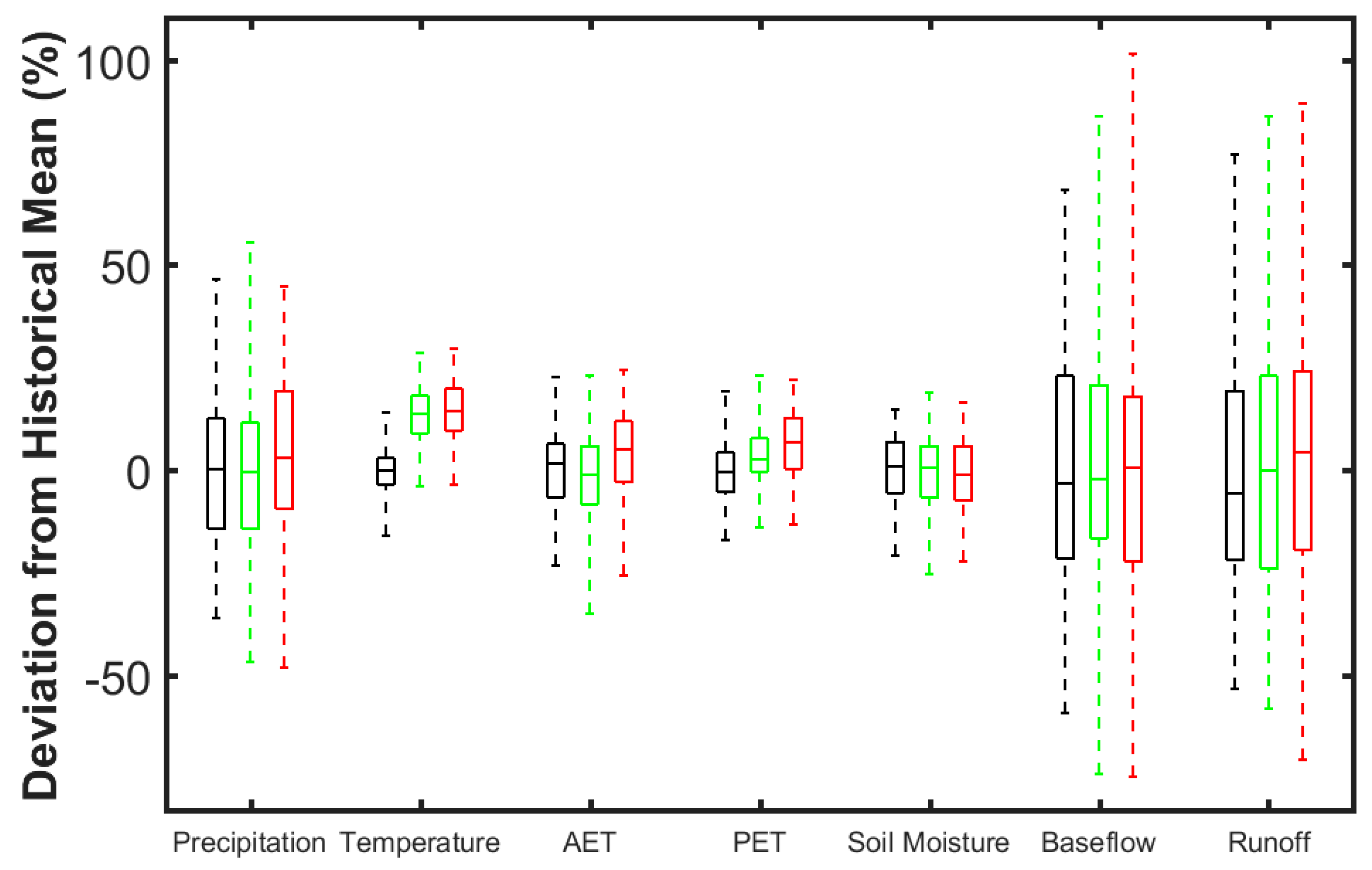
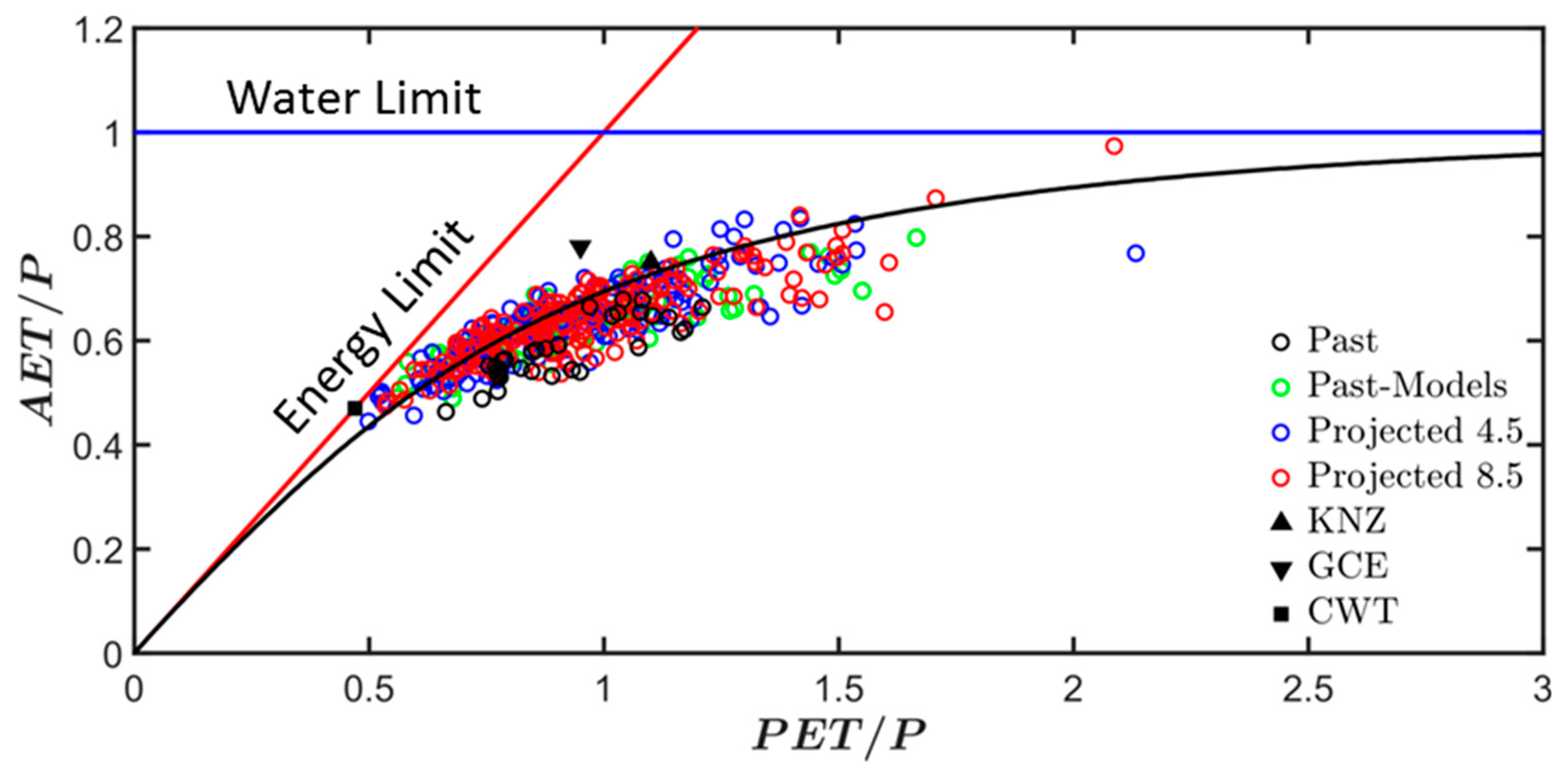
3.2. Climate Impact on the Obion River Watershed Water Budget
- Resistance (or responsivity), which measures the degree to which streamflow is synchronized with precipitation, and;
- Resilience (or elasticity), which measures the degree to which a watershed can return to normal functioning following perturbations.
4. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Article | Model Size | Value | Definition | Method |
|---|---|---|---|---|
| Zhao et al. [72] | N/A | 0.2–0.4 | Topographic factor, denoting non-uniformity of distribution of soil moisture storage. b = 0.2–0.4 for mountainous and hilly areas. | First estimated directly from observed hydrological data and then calibrated in the computation routine |
| Zhao [73] | N/A | 0.1–0.4 | Defines the non-uniformity of the surface conditions. (<10 km2), b = 0.1 and basins (<1000 s km2), b = 0.4. As x moves down the curve, it implies a redistribution of soil moisture during the drying period, with water flowing from the more elevated parts of the sub-basin to the lower parts. | Experience |
| Dumenil and Todini [74] | 600 km × 600 km | 0.01–0.5 | Parameter b is a function of orography only | Orography correction to represent steep orography |
| Wood et al. [15] | 767 km2 | 0.01–10; 0.085–0.129 | Shape parameter. Acknowledges that model assumes infiltration capacities vary within an area due to variations in topography, soil, and vegetation. | Sensitivity Analysis Estimated |
| Liang [14] | 11.7 km2 | 0.008 | Infiltration shape parameter | Estimated from streamflow, precipitation, and maximum/minimum temperature through calibration. |
| Kalma et al. [75] | 26 km2 | 4 | Empirical parameter | Assumed that they had a set of total storage capacity values. The cumulative frequency of these values were plotted and then was fit with different values of b by trial and error. |
| Zhao and Liu [76] | N/A | 0.1–2 | b varies from 0.1–0.4 when spatial scale is within thousands of square kilometers. b increases significantly to 1 or 2 even more when modeling area is over tens of thousands of square kilometers. b reflects the pattern of land surface characteristics (<100 km2) and heterogeneity of the land surface and distribution of rainfall (<1000 s km2) | Experience and through calibration of precipitation and streamflow. |
| Sivapalan and Woods [10] | N/A | 4.03 | Empirical parameter | Through fitting a distribution of soil depths obtained through field observations. |
| Liang et al. [46] | N/A | 0.01–0.5—Based off range from Todini 1992 | Infiltration shape parameter which is a measure of the spatial variability of the infiltration capacity. | Estimated using hydrologic information (especially streamflow). If no information is present, determine based on past calibration experience. |
| Abdulla et al. [58] | 1 × 1 degree | 0–0.4 | Infiltration parameter | Estimated using the Shuffled Complex Evolution search method where the objective function was the sum of squared differences between the simulated and observed streamflow. This was then spatially interpolated to derive b values across the basin. |
| Lohmann et al. [18] | 1/6 degree = 18 km | 0.12–0.16 | Infiltration capacity shape parameter | Calibrated through requiring direct runoff to approximately equal the fast flow from the routing model in VIC. |
| Jayawardena and Zhou [77] | 131 km2 | 13.186 (single parabolic curve) | Measures the non-uniformity of the spatial distribution of the soil moisture storage capacity over the catchment. | Calibrated using daily hydrological data |
| Nijssen et al. [78] | 1 degree 0.5 degree | 0.1–0.25 | Infiltration parameter | Estimated manually by comparing naturalized monthly streamflow hydrographs with modeled monthly hydrographs at key locations. |
| Liang and Xie, [79] | 1/8 degree cells | 0.1–0.5 | Soil moisture capacity shape parameter, which is a measure of the spatial variability of the soil moisture capacity, defined as the maximum amount of water that can be stored in the upper layer of the soil column. It is a surrogate for spatial heterogeneity of soil properties. | Sensitivity Analysis Meant to represent moderate infiltration capabilities. |
| Woolridge et al. [80] | Lumped—1260 km2 Distributed | 3.68–5.32; 2.069–7.20 | Model parameter giving the concave up shape for values less than one and convex up for values greater than one. | Optimized from rainfall-runoff data |
| Huang and Liang [20] | N/A | 0–13.5, however, only kept values 0–5 | Controls the shape of the spatial distribution of soil moisture capacity over a study area, and thus plays a significant role in describing the heterogeneity of soil moisture capacity over the study area. Derived from STATSGO data. | Estimated from STATSGO database. Estimated by fitting distribution of calculated soil moisture capacity of each soil column (soil moisture capacity = total soil depth × soil porosity). |
| Xie and Yuan [59] | 32–370 km2 (treated as lumped units) | 0.15–0.45 | Infiltration parameter which controls the amount of water that can infiltrate into the soil. | Calibration between observed and modeled hydrograph |
| Xie and Yuan et al. [81] | 50 km2 | 0–10 | Infiltration parameter which controls the amount of water that can infiltrate into the soil. | Calibration using streamflow |
| Chen et al. [82] | N/A | 0–larger | Represents the spatial heterogeneity of spatial field capacity (b = 0 for uniform distribution and large for significant spatial variation) | Calibration using streamflow and precipitation data. |
| Oubeidillah et al. [9] | 4 km × 4 km | 0.001–0.8 | Variable infiltration curve parameter | Calibration of modeled streamflow against USGS Water Watch data for each HUC8 in CONUS |
References
- Rodriguez-Iturbe, I.; Porporato, A. Ecohydrology of Water-Controlled Ecosystems: Soil Moisture and Plant Dynamics, 1st ed.; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Al-Kaisi, M.M.; Elmore, R.W.; Guzman, J.G.; Hanna, H.M.; Hart, C.E.; Helmers, M.J.; Hodgson, E.W.; Lenssen, A.W.; Mallarino, A.P.; Robertson, A.E.; et al. Drought impact on crop production and the soil environment: 2012 experiences from Iowa. J. Soil Water Conserv. 2013, 68, 19A–24A. [Google Scholar] [CrossRef]
- Pack, D.; Robinson, K. About $300 Million in Indiana Crops’ Value Lost to Flooding so Far; Purdue University Agricultural News: Purdue, IN, USA, 2015. [Google Scholar]
- Ramírez, J.A.; Finnerty, B. Precipitation and water-table effects on agricultural production and economics. J. Irrig. Drain Eng. 1996, 122, 164–171. [Google Scholar] [CrossRef]
- Clark, C.D.; Harden, C.; Park, W.; Schwartz, J.; Ellis, C.; McKnight, J.; Betterton, E.; Tracy, H.; VanCor, K. The Water-Energy Nexus in East Tennessee; White Paper; University of Tennessee: Knoxville, TN, USA, 2013. [Google Scholar]
- Ingram, K.T.; Dow, K.; Carter, L.; Anderson, J. Climate of the Southeast United States: Variability, Change, Impacts, and Vulnerability; Island Press: Washington, DC, USA, 2013. [Google Scholar]
- McCuen, R.H.; Snyder, W.M. Hydrologic Modeling. Statistical Methods and Applications; Prentice-Hall: Englewood Cliffs, NJ, USA, 1986. [Google Scholar]
- Hejazi, M.I.; Moglen, G.E. The effect of climate and land use change on flow duration in the Maryland Piedmont region. Hydrol. Process. 2008, 22, 4710–4722. [Google Scholar] [CrossRef]
- Oubeidillah, A.A.; Kao, S.C.; Ashfaq, M.; Naz, B.S.; Tootle, G. A large-scale, high-resolution hydrological model parameter data set for climate change impact assessment for the conterminous US. Hydrol. Earth Syst. Sci. 2014, 18, 67–84. [Google Scholar] [CrossRef]
- Sivapalan, M.; Woods, R.A. Evaluation of the effects of general circulation models’ subgrid variability and patchiness of rainfall and soil moisture on land surface water balance fluxes. Hydrol. Process. 1995, 9, 697–717. [Google Scholar] [CrossRef]
- Aggarwal, S.P.; Garg, V.; Gupta, P.K.; Nikam, B.R.; Thakur, P.K.; Roy, P.S. Run-off potential assessment over Indian landmass: A macro-scale hydrological modelling approach. Curr. Sci. 2013, 104, 950–959. [Google Scholar]
- Wang, G.Q.; Zhang, J.Y.; Jin, J.L.; Pagano, T.C.; Calow, R.; Bao, Z.X.; Liu, C.S.; Liu, Y.L.; Yan, X.L. Assessing water resources in China using PRECIS projections and a VIC model. Hydrol. Earth Syst. Sci. 2012, 16, 231–240. [Google Scholar] [CrossRef]
- Houborg, R.; Rodell, M.; Li, B.; Reichle, R.; Zaitchik, B.F. Drought indicators based on model-assimilated Gravity Recovery and Climate Experiment (GRACE) terrestrial water storage observations. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Liang, X.; Lettenmaier, D.P.; Wood, E.F.; Burges, S.J. A simple hydrologically based model of land surface water and energy fluxes for general circulation models. J. Geophys. Res. Atmos. 1994, 99, 14415–14428. [Google Scholar] [CrossRef]
- Wood, E.F.; Lettenmaier, D.P.; Zartarian, V.G. A land-surface hydrology parameterization with subgrid variability for general circulation models. J. Geophys. Res. 1992, 97, 2717–2728. [Google Scholar] [CrossRef]
- Bowling, L.C.; Lettenmaier, D.P. Modeling the Effects of Lakes and Wetlands on the Water Balance of Arctic Environments. J. Hydrometeorol. 2010, 11, 276–295. [Google Scholar] [CrossRef]
- Bohn, T.J.; Livneh, B.; Oyler, J.W.; Running, S.W.; Nijssen, B.; Lettenmaier, D.P. Global evaluation of MTCLIM and related algorithms for forcing of ecological and hydrological models. Agric. For. Meteorol. 2013, 176, 38–49. [Google Scholar] [CrossRef]
- Lohmann, D.; Mitchell, K.E.; Houser, P.R.; Wood, E.F.; Schaake, J.C.; Robock, A.; Cosgrove, B.A.; Sheffield, J.; Duan, Q.Y.; Luo, L.F.; et al. Streamflow and water balance intercomparisons of four land surface models in the North American Land Data Assimilation System project. J. Geophys. Res. 2004, 109. [Google Scholar] [CrossRef]
- Troy, T.J.; Wood, E.F.; Sheffield, J. An efficient calibration method for continental-scale land surface modeling. Water Resour. Res. 2008, 44, 1–13. [Google Scholar] [CrossRef]
- Huang, M.; Liang, X.; Liang, Y. A transferability study of model parameters for the Variable Infiltration Capacity land surface scheme. J. Geophys. Res. 2003, 108. [Google Scholar] [CrossRef]
- Peterson, J.R.; Hamlett, J.M. Hydrologic Calibration of the Swat Model in a Watershed Containing Fragipan Soils. J. Am. Water Resour. Assoc. 1998, 34, 531–544. [Google Scholar] [CrossRef]
- Bockheim, J.G.; Hartemink, A.E. Soils with fragipans in the USA. Catena 2013, 104, 233–242. [Google Scholar] [CrossRef]
- Lin, H.; Bouma, J.; Wilding, L.P.; Richardson, J.L.; Kutílek, M.; Nielsen, D.R. Advances in Hydropedology. Adv. Agron. 2005, 85, 1–89. [Google Scholar]
- Soil Conservation Service, U.S. Departments of Agriculture. Soil Taxonomy—A Basic System of Soil Classification for Making and Interpreting Soil Surveys. Geological Magazine; USDA-NRCS Agricultural Handbook No. 436; U.S. Government Printing Office: Washington, DC, USA, 1999.
- Duan, Q.; Sorooshian, S.; Gupta, V. Effective and efficient global optimization for conceptual rainfall-runoff models. Water Resour. Res. 1992, 28, 1015–1031. [Google Scholar] [CrossRef]
- Beven, K.J. Prophecy, reality and uncertainty in distributed hydrological modelling. Adv. Water Resour. 1993, 16, 41–51. [Google Scholar] [CrossRef]
- Beven, K.J.; Freer, J. Equifinality, data assimilation, and uncertainty estimation in mechanistic modelling of complex environmental systems using the GLUE methodology. J. Hydrol. 2001, 249, 11–29. [Google Scholar] [CrossRef]
- Beven, K. A manifesto for the equifinality thesis. J. Hydrol. 2005, 320, 18–36. [Google Scholar] [CrossRef]
- Lüdtke, S.; Apel, H.; Nied, M.; Carl, P.; Merz, B. Reducing equifinality of hydrological models by integrating Functional Streamflow Disaggregation. In Proceedings of the EGU General Assembly Conference Abstracts, Vienna, Austria, 27 April–2 May 2014; Volume 16. [Google Scholar]
- Horton, R. Approach toward a Physical Interpretation of Infiltration-Capacity. Soil Sci. Soc. Am. J. 1941, 5, 399–417. [Google Scholar] [CrossRef]
- Pimentel, D.; Hall, C.W. Food and Energy Resources; Academic Press: Orlando, FL, USA, 2012. [Google Scholar]
- Locke, M.A.; Tyler, D.D.; Gaston, L.A. Soil and water conservation in the mid south united states lessons learned and a look to the future. Soil Water Conserv. Adv. 2010, 60, 201–236. [Google Scholar]
- Buntley, G.J.; Daniels, R.B.; Gamble, E.E.; Brown, W.T. Fragipan horizons in soils of the Memphis-Loring-Grenada sequence in West Tennessee. Soil Sci. Soc. Am. J. 1977, 41, 400–407. [Google Scholar] [CrossRef]
- Van Muysen, W.; Govers, G.; Van Oost, K.; Van Rompaey, A. The effect of tillage depth, tillage speed, and soil condition on chisel tillage erosivity. J. Soil Water Conserv. 2000, 55, 355–364. [Google Scholar]
- Delgado, J.A.; Nearing, M.A.; Rice, C.W. Conservation Practices for Climate Change Adaptation. Adv. Agron. 2013, 121, 47–115. [Google Scholar]
- Wachendorf, C.; Stuelpnagel, R.; Wachendorf, M. Influence of land use and tillage depth on dynamics of soil microbial properties, soil carbon fractions and crop yield after conversion of short-rotation coppices. Soil Use Manag. 2017, 33, 379–388. [Google Scholar] [CrossRef]
- McDaniel, P.A.; Regan, M.P.; Brooks, E.; Boll, J.; Barndt, S.; Falen, A.; Young, S.K.; Hammel, J.E. Linking fragipans, perched water tables, and catchment-scale hydrological processes. Catena 2008, 73, 166–173. [Google Scholar] [CrossRef]
- Hamman, J.J.; Nijssen, B.; Bohn, T.J.; Gergel, D.R.; Mao, Y. The Variable Infiltration Capacity model version 5 (VIC-5): Infrastructure improvements for new applications and reproducibility. Geosci. Model Dev. 2018, 11, 3481–3496. [Google Scholar] [CrossRef]
- Hamlet, A.F.; Lettenmaier, D.P. Effects of 20th century warming and climate variability on flood risk in the western US. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- Sheffield, J.; Andreadis, K.M.; Wood, E.F.; Lettenmaier, D.P. Global and continental drought in the second half of the twentieth century: Severity–area–duration analysis and temporal variability of large-scale events. J. Clim. 2009, 22, 1962–1981. [Google Scholar] [CrossRef]
- Zhu, C.; Leung, L.R.; Gochis, D.; Qian, Y.; Lettenmaier, D.P. Evaluating the influence of antecedent soil moisture on variability of the North American Monsoon precipitation in the coupled MM5/VIC modeling system. J. Adv. Model. Earth Syst. 2009, 1. [Google Scholar] [CrossRef]
- Tan, A.; Adam, J.C.; Lettenmaier, D.P. Change in spring snowmelt timing in Eurasian Arctic rivers. J. Geophys. Res. Atmos. 2011, 116. [Google Scholar] [CrossRef]
- Livneh, B.; Rosenberg, E.A.; Lin, C.; Nijssen, B.; Mishra, V.; Andreadis, K.M.; Maurer, E.P.; Lettenmaier, D.P. A long-term hydrologically based dataset of land surface fluxes and states for the conterminous United States: Update and extensions. J. Clim. 2013, 26, 9384–9392. [Google Scholar] [CrossRef]
- Nijssen, B.; Bowling, L.C.; Lettenmaier, D.P.; Clark, D.B.; El Maayar, M.; Essery, R.; Goers, S.; Gusev, Y.M.; Habets, F.; Van Den Hurk, B.; et al. Simulation of high latitude hydrological processes in the Torne-Kalix basin: PILPS Phase 2(e) 2: Comparison of model results with observations. Glob. Planet. Chang. 2003, 38, 31–53. [Google Scholar] [CrossRef]
- Wood, E.F.; Lettenmaier, D.P.; Liang, X.; Lohmann, D.; Boone, A.; Chang, S.; Chen, F.; Dai, Y.; Dickinson, R.E.; Duan, Q.; et al. The project for intercomparison of land-surface parameterization schemes (PILPS) phase 2(c) Red-Arkansas River basin experiment: 1. Experiment description and summary intercomparisons. Glob. Planet. Chang. 1998, 19, 115–135. [Google Scholar] [CrossRef]
- Liang, X.; Wood, E.F.; Lettenmaier, D.P. Surface soil moisture parameterization of the VIC-2L model: Evaluation and modification. Glob. Planet. Chang. 1996, 13, 195–206. [Google Scholar] [CrossRef]
- Senay, G.B.; Bohms, S.; Singh, R.K.; Gowda, P.H.; Velpuri, N.M.; Alemu, H.; Verdin, J.P. Operational evapotranspiration mapping using remote sensing and weather datasets: A new parameterization for the SSEB approach. J. Am. Water Res. Assoc. 2013, 49, 577–591. [Google Scholar] [CrossRef]
- Thornton, P.E.; Running, S.W.; White, M.A. Generating surfaces of daily meteorological variables over large regions of complex terrain. J. Hydrol. 1997, 190, 214–251. [Google Scholar] [CrossRef]
- Taylor, K.E.; Stouffer, R.J.; Meehl, G.A. An Overview of CMIP5 and the Experiment Design. Bull. Am. Meteorol. Soc. 2012, 93, 485–498. [Google Scholar] [CrossRef]
- Van Vuuren, D.P.; Edmonds, J.; Kainuma, M.; Riahi, K.; Thomson, A.; Hibbard, K.; Hurtt, G.C.; Kram, T.; Krey, V.; Lamarque, J.F.; et al. The representative concentration pathways: An overview. Clim. Chang. 2011, 109, 5–31. [Google Scholar] [CrossRef]
- Cosby, B.J.; Hornberger, G.M.; Clapp, R.B.; Ginn, T.R. A Statistical Exploration of the Relationships of Soil Moisture Characteristics to the Physical Properties of Soils. Water Resour. Res. 1984, 20, 682–690. [Google Scholar] [CrossRef]
- Chawla, I.; Mujumdar, P.P. Isolating the impacts of land use and climate change on streamflow. Hydrol. Earth Syst. Sci. 2015, 19, 3633–3651. [Google Scholar] [CrossRef]
- Miller, D.A.; White, R.A. A conterminous United States multilayer soil characteristics dataset for regional climate and hydrology modeling. Earth Interact. 1998, 2, 1–26. [Google Scholar] [CrossRef]
- Gao, H.; Tang, Q.; Shi, X.; Zhu, C.; Bohn, T. Water budget record from Variable Infiltration Capacity (VIC) model. In Algorithm Theoretical Basis Document for Terrestrial Water Cycle Data Records; Faculty of Science and Technology, Lancaster Environment Centre: Lancaster, UK, 2010; pp. 120–173. [Google Scholar]
- Gburek, W.J.; Needelman, B.A.; Srinivasan, M.S. Fragipan controls on runoff generation: Hydropedological implications at landscape and watershed scales. Geoderma 2006, 131, 330–344. [Google Scholar] [CrossRef]
- Maidment, D.R. Handbook of Hydrology; McGraw Hill: New York, NY, USA, 1993. [Google Scholar]
- Ramcharan, A.; Hengl, T.; Nauman, T.; Brungard, C.; Waltman, S.; Wills, S.; Thompson, J. Soil property and class maps of the conterminous United States at 100-meter spatial resolution. Soil Sci. Soc. Am. J. 2018, 82. [Google Scholar] [CrossRef]
- Abdulla, F.A.; Lettenmaier, D.P.; Wood, E.F.; Smith, J.A. Application of a macroscale hydrologic model to estimate the water balance of the Arkansas-Red River Basin. J. Geophys. Res. Atmos. 1996, 101, 7449–7459. [Google Scholar] [CrossRef]
- Xie, Z.; Yuan, F. A parameter estimation scheme of the land surface model VIC using the MOPEX databases. IAHS Publ. 2006, 307, 169–179. [Google Scholar]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models: Part 1. A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Binger, R.L.; Harmel, R.D.; Veith, T. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Wu, Z.; Lu, G.; Wen, L.; Lin, C.; Zhang, J.; Yang, Y. Thirty-Five Year (1971–2005) Simulation of Daily Soil Moisture Using the Variable Infiltration Capacity Model over China. Atmos. Ocean 2007, 45, 37–45. [Google Scholar] [CrossRef]
- Yang, G.; Bowling, L.C.; Cherkauer, K.A.; Pijanowski, B.C.; Niyogi, D. Hydroclimatic response of watersheds to urban intensity—An Observational and modeling based analysis for the White River basin, Indiana. J. Hydrometeorol. 2010, 11, 122–138. [Google Scholar] [CrossRef]
- Hanson, P.J.; Weltzin, J.F. Drought disturbance from climate change: Repsonse of United States forests. Sci. Total Enivron. 2000, 262, 205–220. [Google Scholar] [CrossRef]
- Parr, D.T. Understanding the Hydrological Impacts of Climate Variability and Climate Change Based on Numerical Modeling and Observations. Ph.D. Thesis, University of Connecticut, Storrs, CT, USA, 2015. [Google Scholar]
- Jung, M.; Reichstein, M.; Ciais, P.; Seneviratne, S.I.; Sheffield, J.; Goulden, M.L.; Bonan, G.; Cescatti, A.; Chen, J.; De Jeu, R.; et al. Recent decline in the global land evapotranspiration trend due to limited moisture supply. Nature 2010, 467, 951–954. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.K.; Schilling, K.E. Effects of land cover on water table, soil moisture, evapotranspiration, and groundwater recharge: A Field observation and analysis. J. Hydrol. 2006, 319, 328–338. [Google Scholar] [CrossRef]
- Budyko, M.I.; Miller, D.H. Climate and Life; Academic Press: New York, NY, USA, 1974. [Google Scholar]
- Carey, S.K.; Tetzlaff, D.; Seibert, J.; Soulsby, C.; Buttle, J.; Laudon, H.; McDonnell, J.; McGuire, K.; Caissie, D.; Shanley, J.; et al. Inter-comparison of hydro-climatic regimes across northern catchments: Synchronicity, resistance and resilience. Hydrol. Process. 2010, 24, 3591–3602. [Google Scholar] [CrossRef]
- Bohac, C.E.; Bowen, A.K. Water Use in the Tennessee Valley for 2010 and Projected Use in 2035; Tennessee Valley Authority: Chattanooga, TN, USA, 2012. [Google Scholar]
- USDA. Farm and Ranch Irrigation Survey; U.S. Department of Agriculture: Washington, DC, USA, 2013.
- Zhao, R.; Zuang, Y.; Fang, L.; Liu, X.; Zhang, Q. The Xinanjiang model. Hydrol. Forecast. 1980, 129, 351–356. [Google Scholar]
- Zhao, R.-J. The Xinanjiang model applied in China. J. Hydrol. 1992, 135, 371–381. [Google Scholar]
- Dümenil, L.; Todini, E. A Rainfall Runoff Scheme for Use in the Hamburg Climate Model. In Advances in Theoretical Hydrology, a Tribute to James Dooge, European Geophysical Society Series of Hydrological Sciences; O’Kane, J.P., Ed.; Elsevier: Amsterdam, The Netherlands, 1992; pp. 129–157. [Google Scholar]
- Kalma, J.D.; Bates, B.C.; Woods, R.A. Predicting catchment-scale soil moisture status with limited field measurements. Hydrol. Process. 1995, 9, 445–467. [Google Scholar] [CrossRef]
- Zhao, R.J.; Liu, R.X. The Xinjiang model. In Computer Models of Watershed Hydrology; Singh, V.P., Ed.; Water Resour. Publ.: Highlands Ranch, CO, USA, 1995. [Google Scholar]
- Jayawardena, A.W.; Zhou, M.C. A modified spatial soil moisture storage capacity distribution curve for the Xinanjiang model. J. Hydrol. 2000, 227, 93–113. [Google Scholar] [CrossRef]
- Nijssen, B.; Schnur, R.; Lettenmaier, D.P. Global retrospective estimation of soil moisture using the Variable Infiltration Capacity land surface model, 1980–93. J. Clim. 2001, 14, 1790–1808. [Google Scholar] [CrossRef]
- Liang, X.; Xie, Z. A new surface runoff parameterization with subgrid-scale soil heterogeneity for land surface models. Adv. Water Resour. 2001, 24, 1173–1193. [Google Scholar] [CrossRef]
- Wooldridge, S.; Kalma, J.; Kuczera, G. Parameterisation of a simple semi-distributed model for assessing the impact of land-use on hydrologic response. J. Hydrol. 2001, 254, 16–32. [Google Scholar] [CrossRef]
- Xie, Z.H.; Yuan, F.; Duan, Q.Y.; Zheng, J.; Liang, M.L.; Chen, F. Regional parameter estimation of the VIC land surface model: Methodology and application to river basins in China. J. Hydrometeorol. 2007, 8, 447–468. [Google Scholar] [CrossRef]
- Chen, X.; Chen, Y.D.; Xu, C. A distributed monthly hydrological model for integrating spatial variations of basin topography and rainfall. Hydrol. Process. 2007, 21, 242–252. [Google Scholar] [CrossRef]
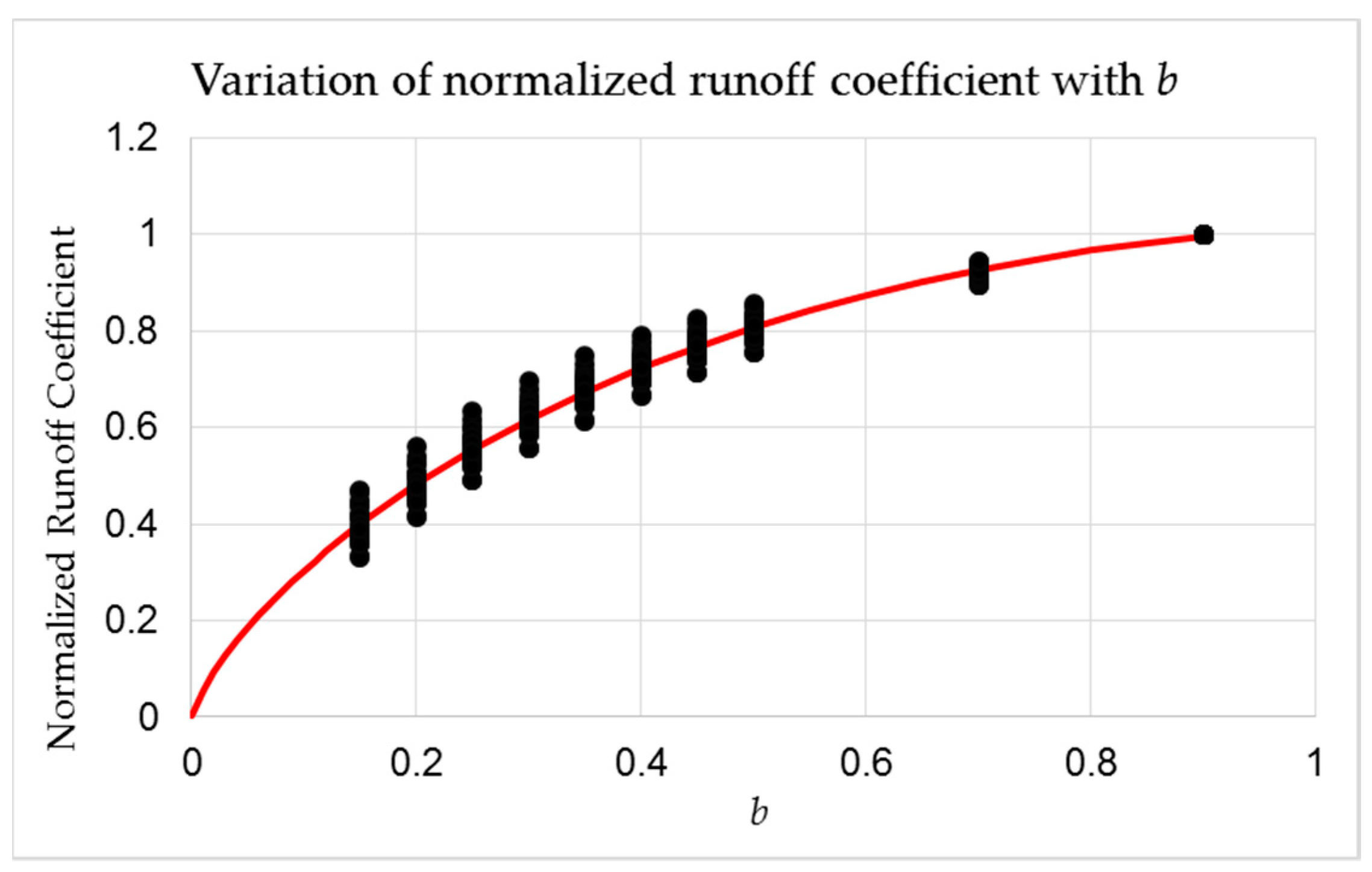
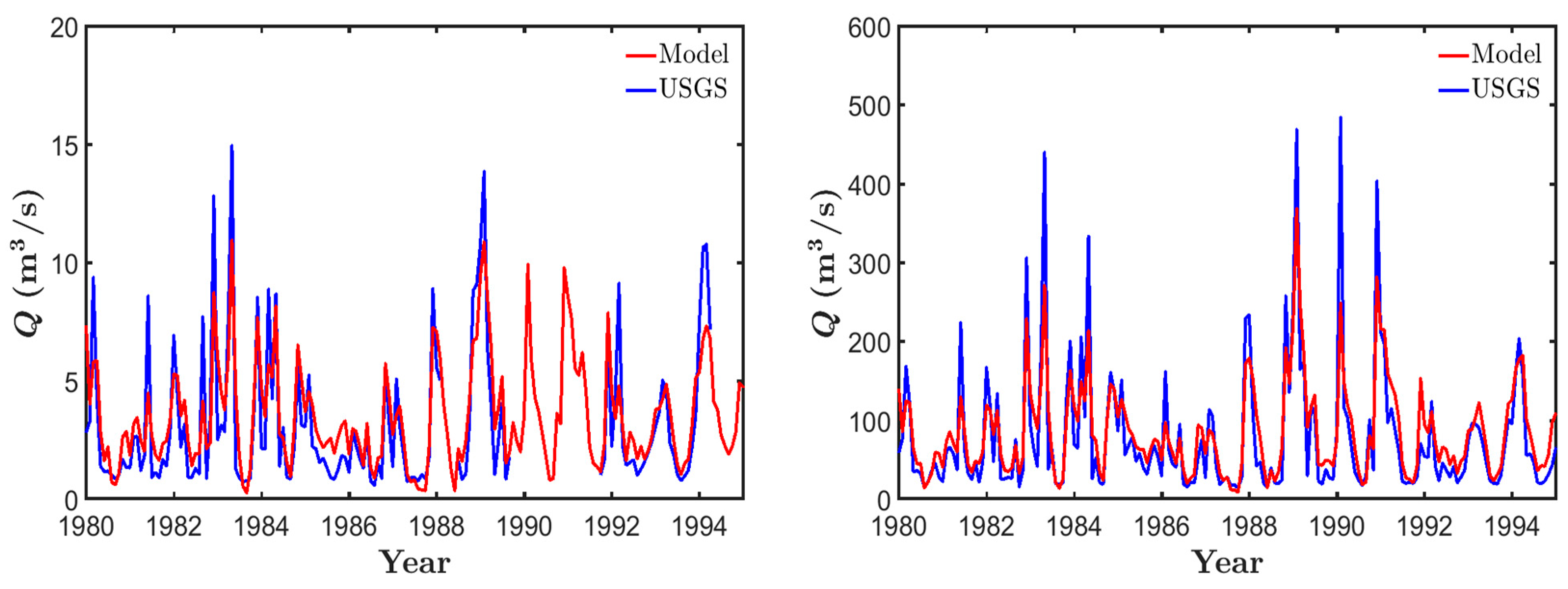
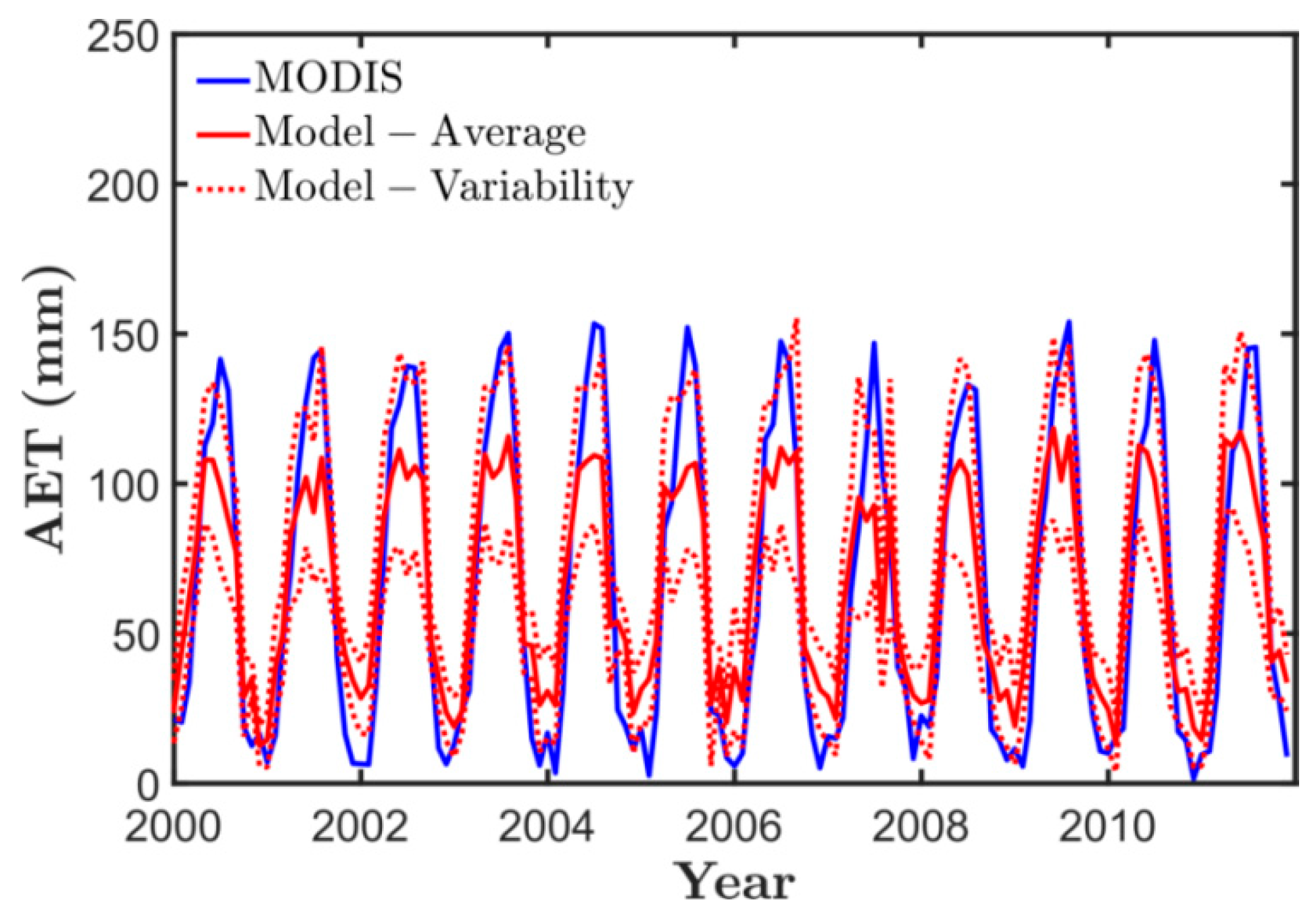
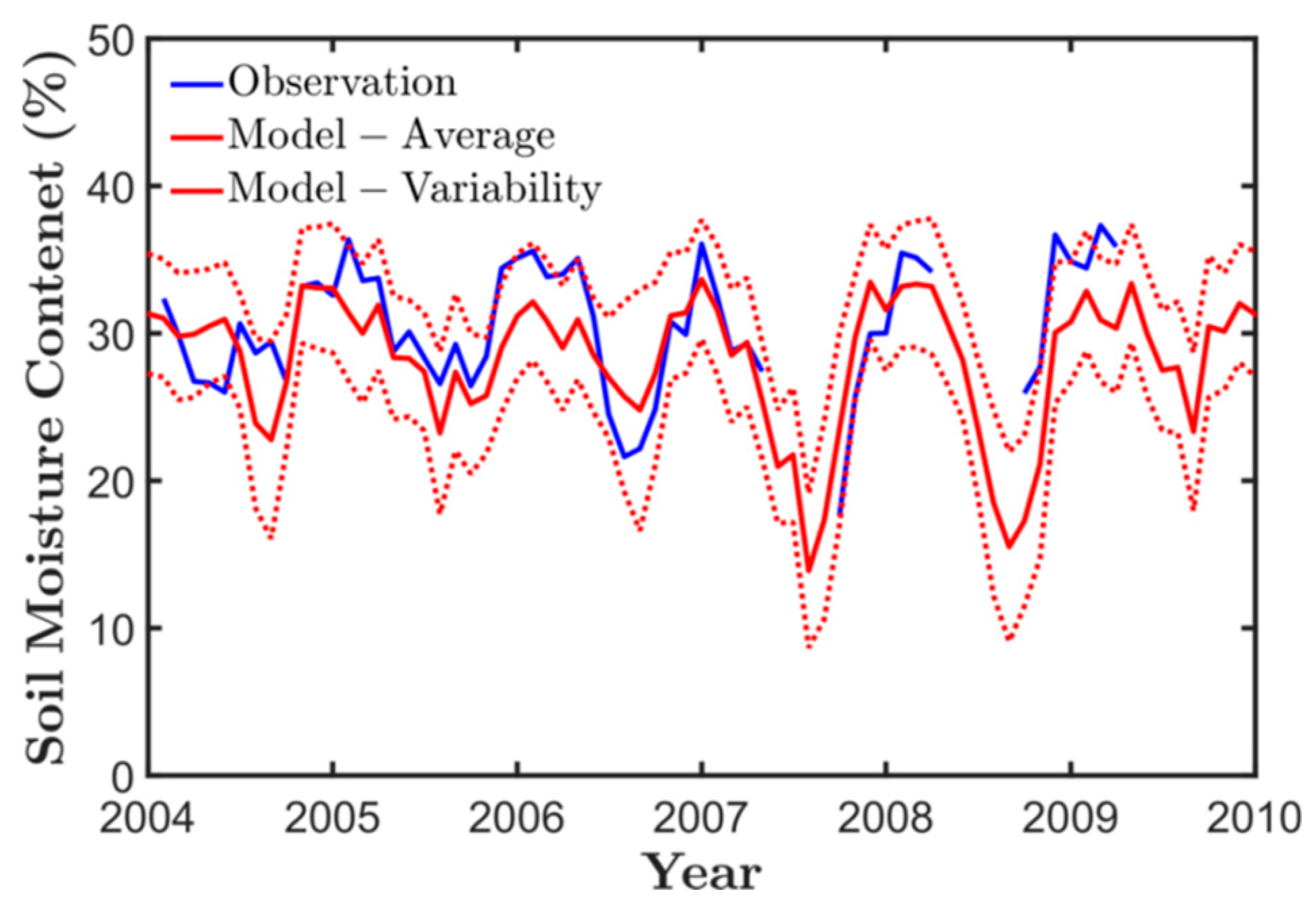
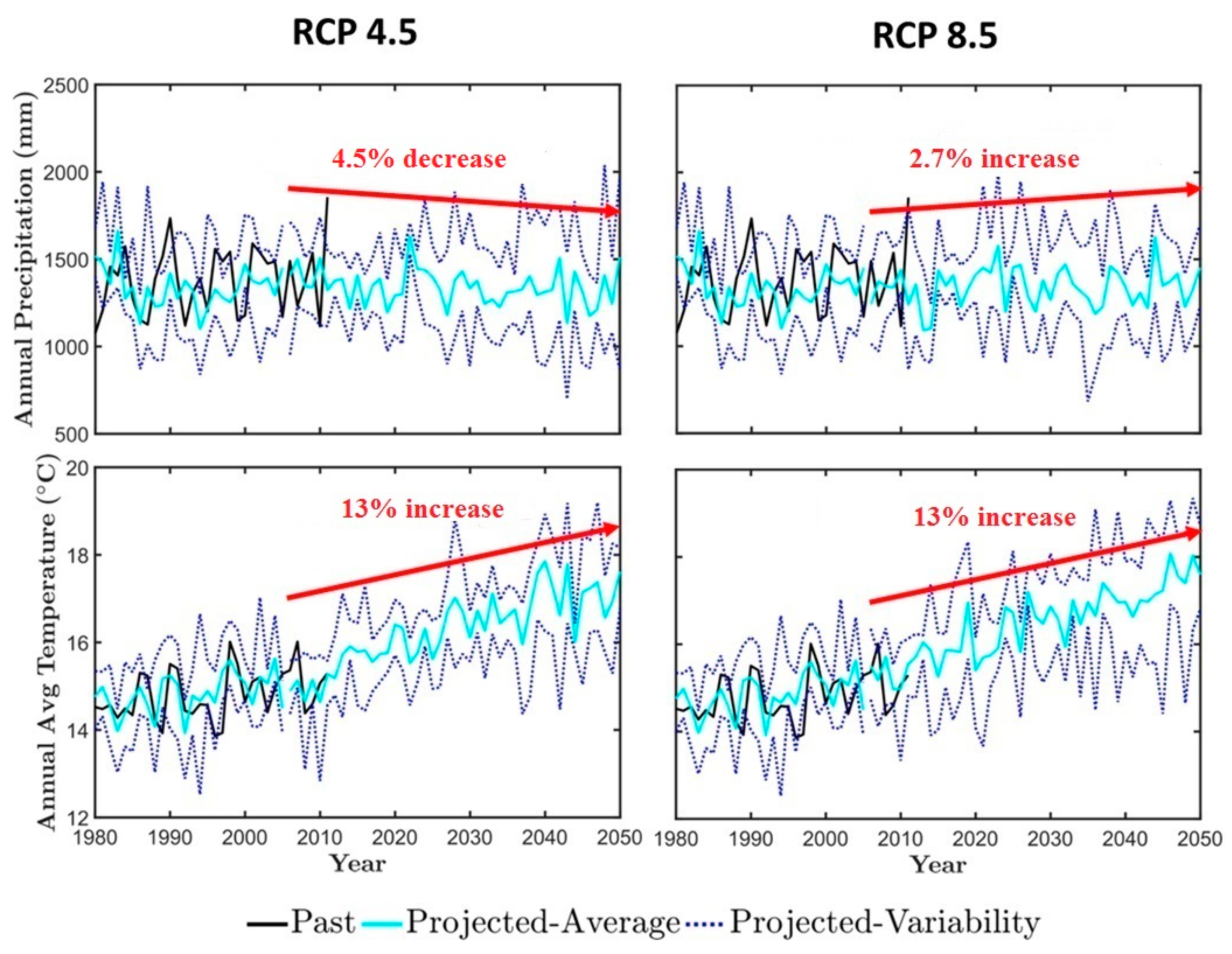
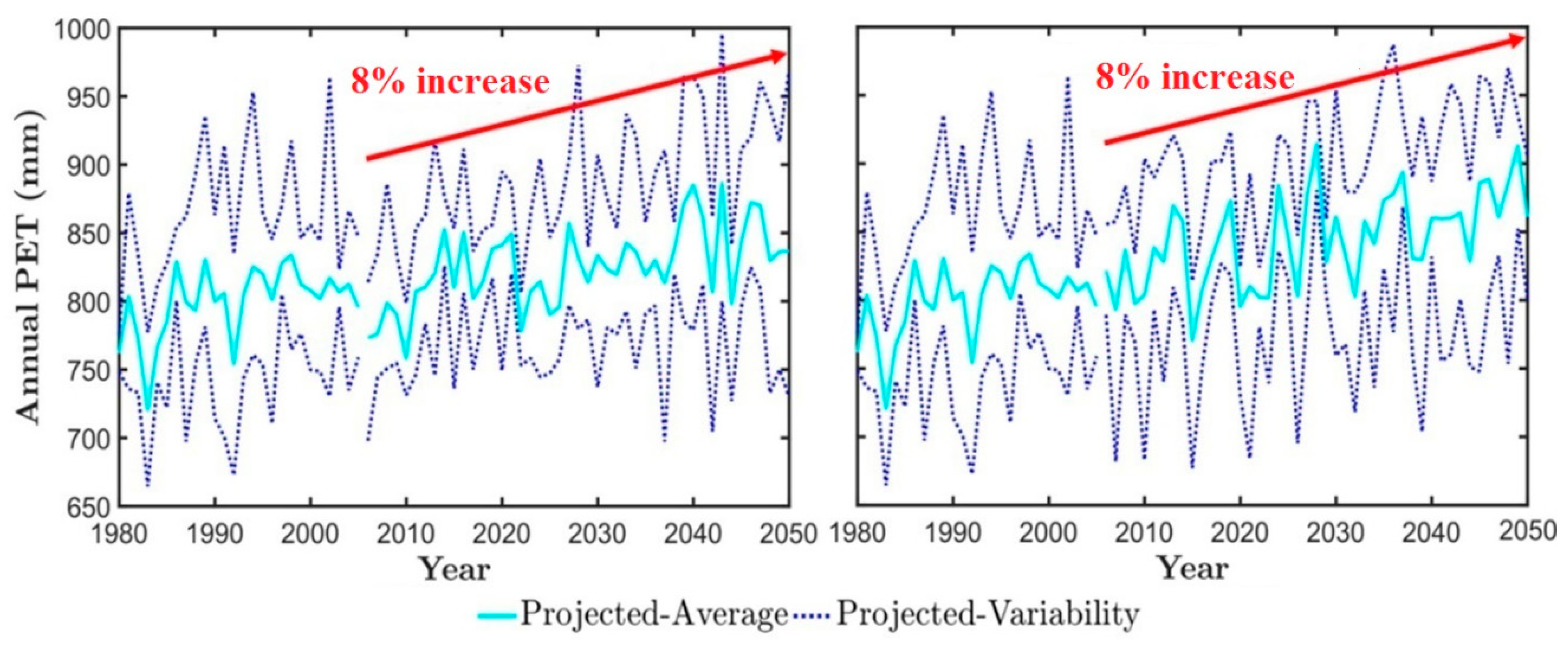
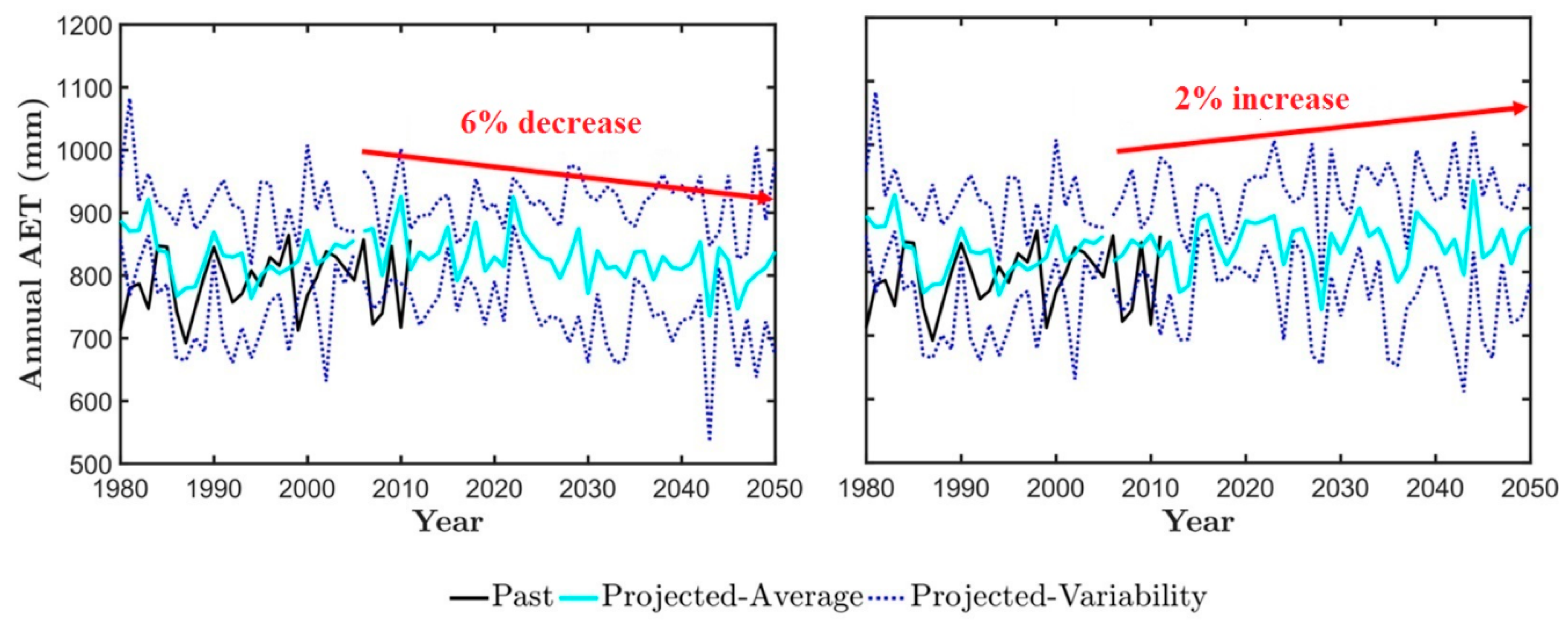
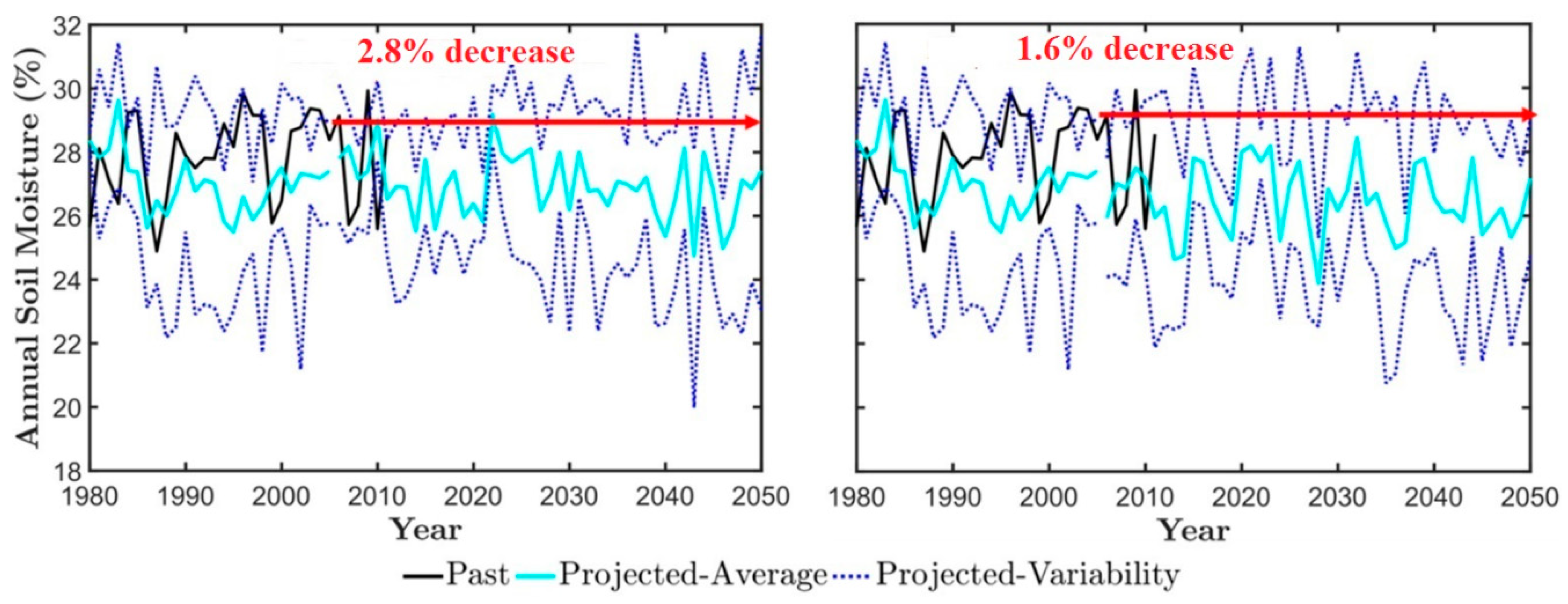
| Parameter | Allowed Range | Unit | Determination in This Study | Selected Values for Calibration |
|---|---|---|---|---|
| b | 0.001–1.00 | - | Horton model, effective soil moisture approach | - |
| Ds | 0.001–1.00 | - | Calibrated | 0.1–0.9 |
| Dsmax | 0.100–50.00 | mm/d | Ksat × Slope 2 | - |
| Ws3 | 0.200–1.00 | - | Calibrated | 0.5–0.9 |
| Layer 2 Depth | 0.1–3.0 | m | Constant | - |
| Layer 3 Depth | 0.1–3.0 | m | Sensitivity Analysis | - |
| Exp | 0.1–30.00 | - | 3 + 2b1 4 | - |
| Study | Watershed Area | Cell Size | Time Step | Region | Soil Order 1 | Fragipan | Hydrological Regime | Land Cover | b | Ds | Ws |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Liang et al. [14] | 11.7 km2 | 15 km | Daily | King Creek, Kansas | Mollisols | No | Semiarid | Tall Grass | 0.008 | 7.7 × 10−5 | 0.96 |
| Abdulla et al. [58] | 6 × 105 km2 | 1 degree | Daily | Arkansas-Red River (US Southern Great Plains) | Utisols, Alfisols, Mollisols | Yes, on eastern side of basin | Arid to Humid | Grass, Shrub, Woodland, Forest, Alpine | 0.0–0.4 | - | - |
| Troy et al. [19] | Cell-Based | 1/8 degree | 12 h | Northwest Tennessee | Alfisols | Yes | Sub-humid to Humid | Crop, Grass | 0.2–0.5 | - | - |
| Xie and Yuan [59] | 43–371 km2 | Each watershed treated as one cell | Hourly | France (12 Watersheds) | Alfisols, Inceptisols | Yes, on eastern side of France | Humid | Forest, Woodland, Grass, Shrub, Crop | 0.15–0.45 | 0.02 | 0.8 |
| Chawla and Mujumdar [52] | 9 × 104 km2 | 1/2 degree | Daily | Midstream Upper Ganga Basin, India | Lithosols, Cambisols, Regosols, Gleysols, Fluvisols | No | subequatorial monsoon climate with sufficient moistening | Forest, Crop | 0.044 | 0.0004 | 0.62 |
| SDA | Ds | Ws | NSE Coef. | Relative Bias | USGS Station |
|---|---|---|---|---|---|
| 1 | 0.9 | 0.9 | 0.71 | 0.23 | 07024200 |
| 2 | 0.9 | 0.9 | 0.74 | 0.10 | 07024300 |
| 3 | 0.9 | 0.9 | 0.67 | 0.32 | 07024500 |
| 4 | 0.1 | 0.5 | 0.75 | 0.04 | 07025400 |
| 5 | 0.9 | 0.9 | 0.73 | 0.12 | 07026040 |
| 6 | 0.9 | 0.9 | 0.73 | 0.16 | 07026300 |
| Parameter | Mean | Standard Dev. | T-Test | F-Test | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Past | RCP 4.5 | RCP 8.5 | Past | RCP 4.5 | RCP 8.5 | RCP 4.5 | RCP 8.5 | RCP 4.5 | RCP 8.5 | |||||
| Result | p-Value | Result | p-Value | Result | p-Value | Result | p-Value | |||||||
| Precipitation (mm) | 1308 | 1316 | 1350 | 231 | 278 | 254 | 0 | 0.84 | 0 | 0.28 | 0 | 0.10 | 0 | 0.40 |
| Temperature (°C) | 14.91 | 16.93 | 17.09 | 0.84 | 1.01 | 1.17 | 1 | 2 × 10−28 | 1 | 2 × 10−27 | 0 | 1 × 10−1 | 1 | 4 × 10−3 |
| AET (mm) | 820 | 812 | 851 | 81 | 90 | 89 | 0 | 0.57 | 0 | 0.02 | 0 | 0.33 | 0 | 0.40 |
| PET (mm) | 809 | 840 | 860 | 57 | 63 | 67 | 1 | 9 × 10−4 | 1 | 5 × 10−7 | 0 | 4 × 10−1 | 0 | 2 × 10−1 |
| Soil Moisture (%) | 26.7 | 26.7 | 26.4 | 2.3 | 2.4 | 2.4 | 0 | 0.95 | 0 | 0.41 | 0 | 0.67 | 0 | 0.62 |
| Baseflow (mm) | 303 | 311 | 303 | 89 | 98 | 97 | 0 | 0.59 | 0 | 0.97 | 0 | 0.35 | 0 | 0.41 |
| Runoff (mm) | 185 | 191 | 192 | 52 | 65 | 58 | 0 | 0.50 | 0 | 0.39 | 0 | 0.05 | 0 | 0.35 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghaneeizad, S.; Papanicolaou, A.; Abban, B.; Wilson, C.; Giannopoulos, C.; Lambert, D.; Walker, F.; Hawkins, S. Development of a Distributed Hydrologic Model for a Region with Fragipan Soils to Study Impacts of Climate on Soil Moisture: A Case Study on the Obion River Watershed in West Tennessee. Geosciences 2018, 8, 364. https://doi.org/10.3390/geosciences8100364
Ghaneeizad S, Papanicolaou A, Abban B, Wilson C, Giannopoulos C, Lambert D, Walker F, Hawkins S. Development of a Distributed Hydrologic Model for a Region with Fragipan Soils to Study Impacts of Climate on Soil Moisture: A Case Study on the Obion River Watershed in West Tennessee. Geosciences. 2018; 8(10):364. https://doi.org/10.3390/geosciences8100364
Chicago/Turabian StyleGhaneeizad, Seyed, Athanasios (Thanos) Papanicolaou, Benjamin Abban, Christopher Wilson, Christos Giannopoulos, Dayton Lambert, Forbes Walker, and Shawn Hawkins. 2018. "Development of a Distributed Hydrologic Model for a Region with Fragipan Soils to Study Impacts of Climate on Soil Moisture: A Case Study on the Obion River Watershed in West Tennessee" Geosciences 8, no. 10: 364. https://doi.org/10.3390/geosciences8100364
APA StyleGhaneeizad, S., Papanicolaou, A., Abban, B., Wilson, C., Giannopoulos, C., Lambert, D., Walker, F., & Hawkins, S. (2018). Development of a Distributed Hydrologic Model for a Region with Fragipan Soils to Study Impacts of Climate on Soil Moisture: A Case Study on the Obion River Watershed in West Tennessee. Geosciences, 8(10), 364. https://doi.org/10.3390/geosciences8100364