A New Degassing Model to Infer Magma Dynamics from Radioactive Disequilibria in Volcanic Plumes
Abstract
:1. Introduction
2. Short-Lived Radioactivity Measurements in Mount Etna Plume
2.1. Field Description and Sampling Techniques
2.2. Analytical Techniques
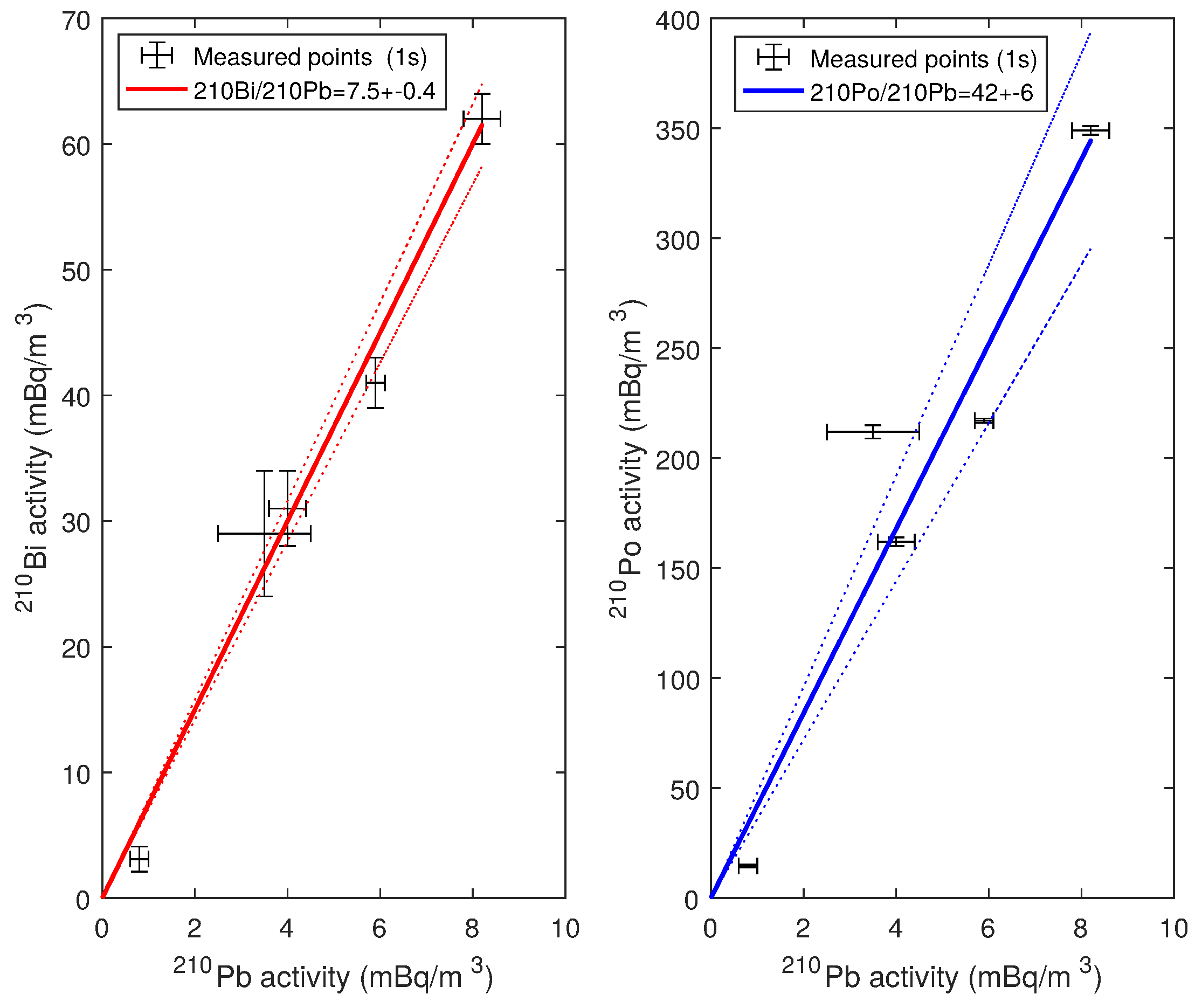
2.3. Analytical Results
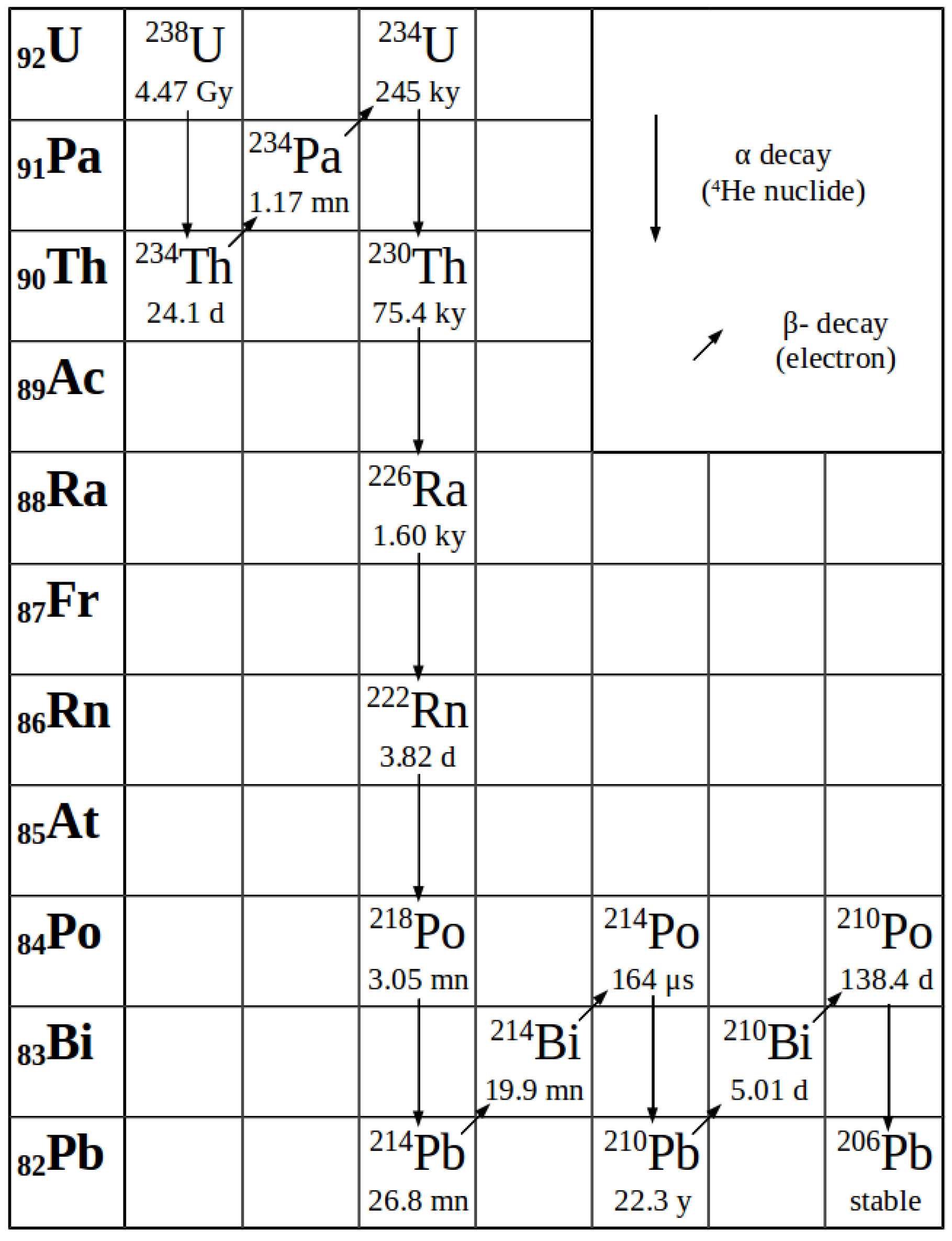
3. Modelling of Radionuclide Degassing and 210Pb-210Bi-210Po Radioactive Disequilibria in Volcanic Plumes
3.1. 222Rn Enrichments in Volcanic Gases: Towards a New Degassing Model for Short-Lived Radionuclides
3.2. Radioactive Disequilibria in Gases at the Time of Exsolution
3.2.1. Specific Case of 222Rn Exsolution
3.2.2. 222Rn-210Pb-210Bi-210Po Fractionation upon Exsolution
3.3. Gas Phase Transfer towards the Surface: Radioactive Decay within Gas Bubbles
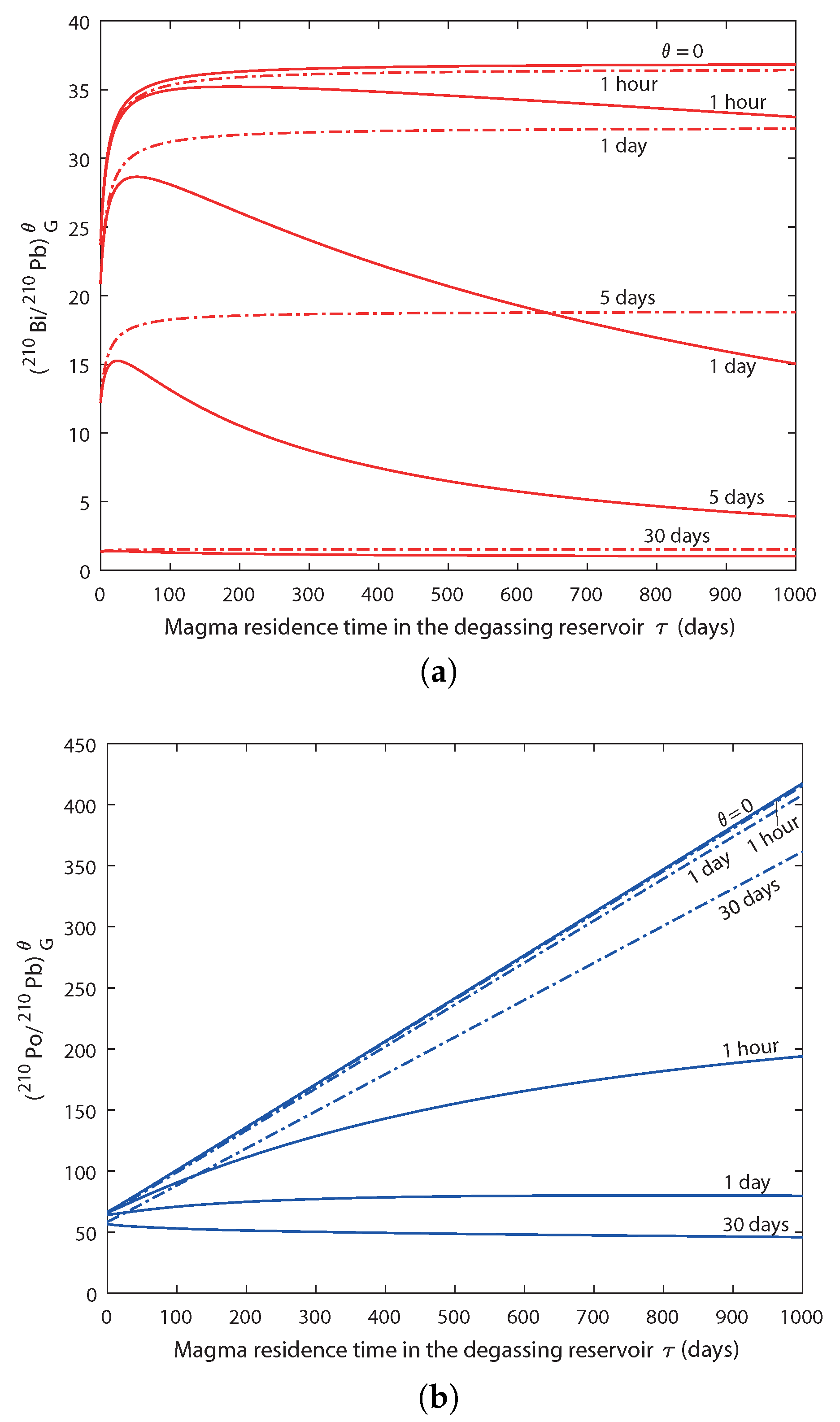
3.4. Results and Discussion
4. Model Application
4.1. Estimation of Input Paramaters
4.1.1. Volatile Weight Fraction
4.1.2. Fraction of Degassed Radon f
4.1.3. Volatilities of Lead, Bismuth and Polonium (Emanation Coefficients and Gas-Melt Partitioning Coefficients D)
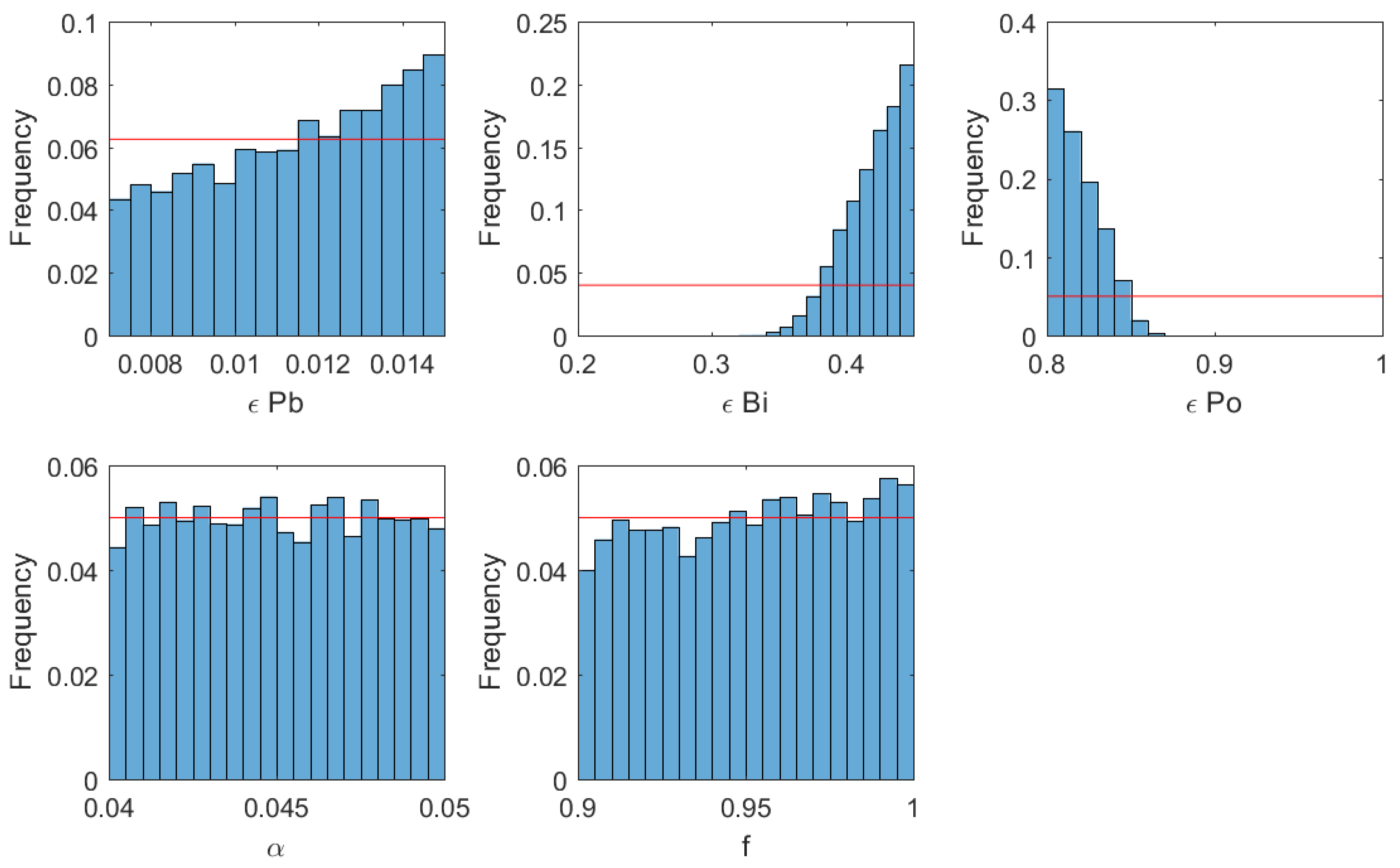
4.2. Inversion of the Model
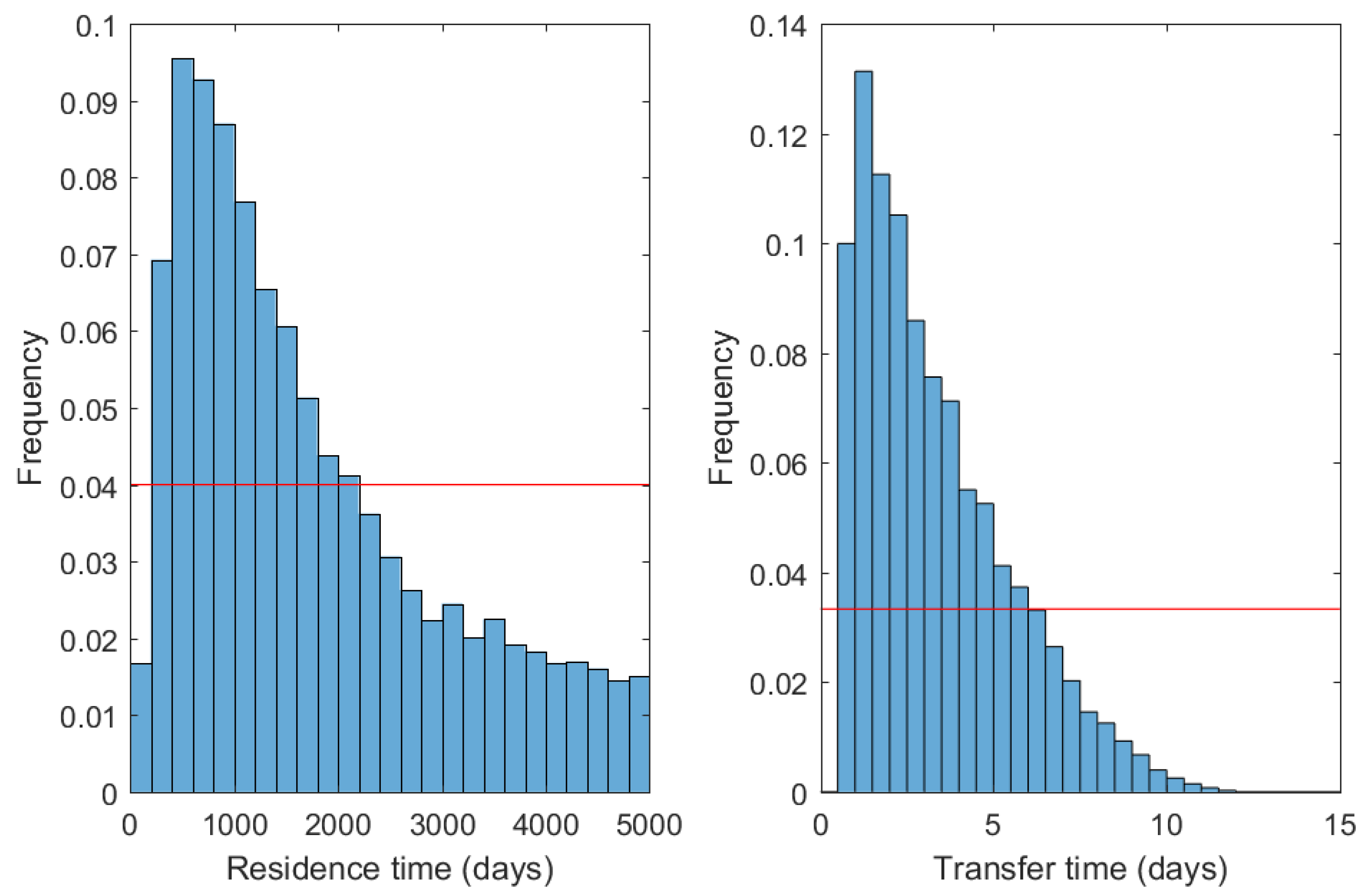
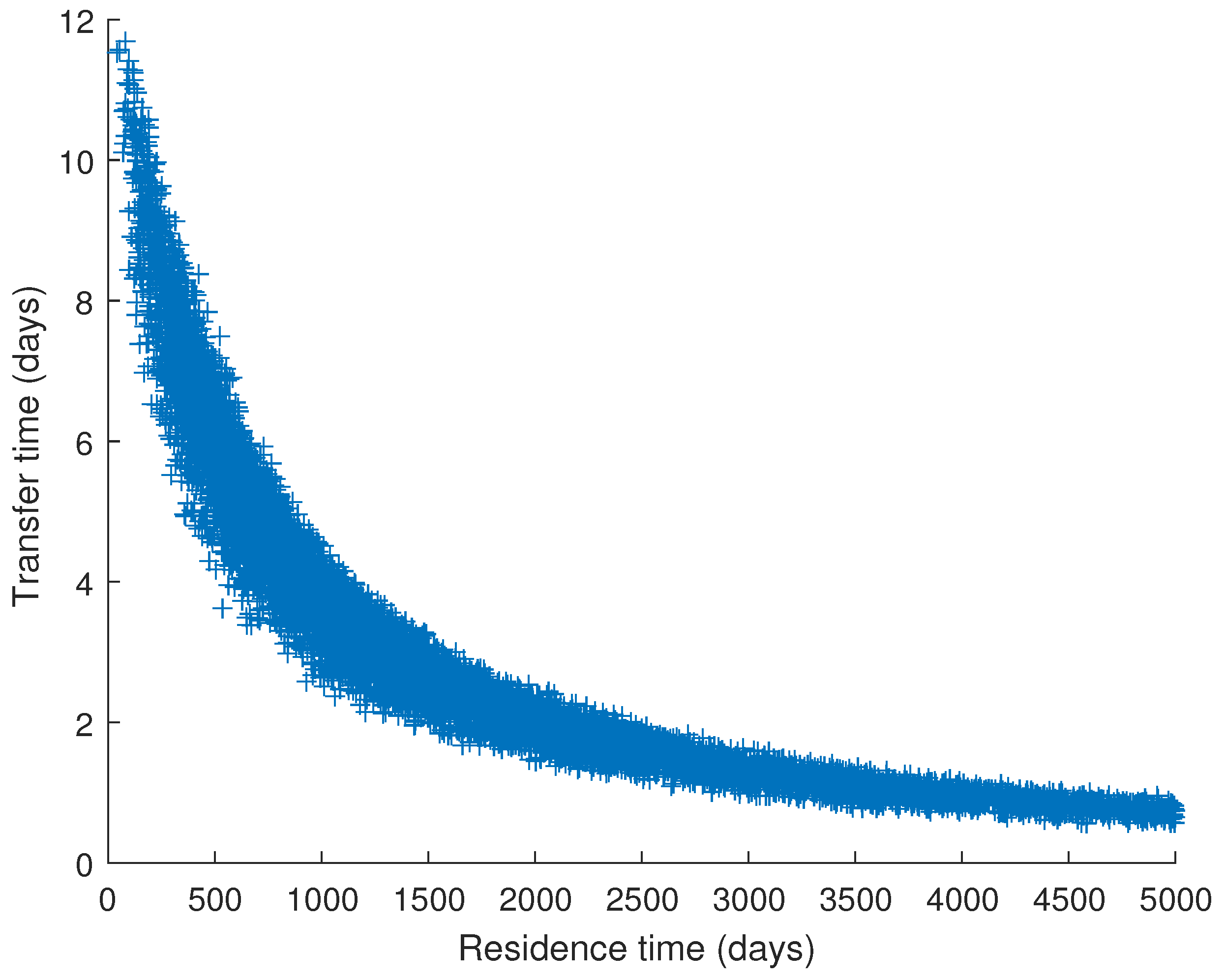
4.2.1. Methodology
- each parameter (see Table 2) is chosen randomly in its range of variation according to an uniform law.
- the residence time and the transfer time are also chosen randomly (between 0 and 5000 days for , and between 0 and 15 days for ). The upper limit for is in agreement with the order of magnitude of Mount Etna magma residence time in shallow reservoirs: a few tens of years in Condomines et al. [45], one year in Armienti et al. [46]. The upper limit for is coherent with maximum estimates of the gas phase transfer time at Mount Etna [14].
- radioactive disequilibria in the gas phase are computed according to the model equations.
- if the computed values match the measured ones, then the set of parameters and the dynamic variables ( and ) are stored in a database.
- these operations are repeated until a statistically relevant database (here 10,000 elements) is built. If enough combinations of parameters are simulated, the parameter space is sampled without any important gap.
4.2.2. Discussion of Results and Implications for Magma Dynamics at Mount Etna
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
Appendix B
References
- Caltabiano, T.; Burton, M.; Giammanco, S.; Allard, P.; Bruno, N.; Mure, F.; Romano, R. Volcanic gas emissions from the summit craters and flanks of Mt. Etna, 1987–2000. In Mt. Etna: Volcano Laboratory; Wiley: Hoboken, NJ, USA, 2004; pp. 111–128. [Google Scholar]
- Wallace, P.J. Volatiles in subduction zone magmas: Concentrations and fluxes based on melt inclusion and volcanic gas data. J. Volcanol. Geotherm. Res. 2005, 140, 217–240. [Google Scholar] [CrossRef]
- Shinohara, H. Excess degassing from volcanoes and its role on eruptive and intrusive activity. Rev. Geophys. 2008, 46. [Google Scholar] [CrossRef]
- Allard, P. Endogenous magma degassing and storage at Mount Etna. Geophys. Res. Lett. 1997, 24, 2219–2222. [Google Scholar] [CrossRef]
- Bonaccorso, A.; Bonforte, A.; Currenti, G.; Negro, C.D.; Stefano, A.D.; Greco, F. Magma storage, eruptive activity and flank instability: Inferences from ground deformation and gravity changes during the 1993–2000 recharging of Mt. Etna volcano. J. Volcanol. Geotherm. Res. 2011, 200, 245–254. [Google Scholar] [CrossRef]
- Sharma, K.; Blake, S.; Self, S.; Krueger, A.J. SO2 emissions from basaltic eruptions, and the excess sulfur issue. Geophys. Res. Lett. 2004, 31, L13612. [Google Scholar] [CrossRef]
- Steffke, A.M.; Harris, A.J.; Burton, M.; Caltabiano, T.; Salerno, G.G. Coupled use of COSPEC and satellite measurements to define the volumetric balance during effusive eruptions at Mt. Etna, Italy. J. Volcanol. Geotherm. Res. 2011, 205, 47–53. [Google Scholar] [CrossRef]
- Schiano, P.; Clocchiatti, R.; Ottolini, L.; Busa, T. Transition of Mount Etna lavas from a mantle-plume to an island-arc magmatic source. Nature 2001, 412, 900–904. [Google Scholar] [CrossRef] [PubMed]
- Kazahaya, K.; Shinohara, H.; Saito, G. Excessive degassing of Izu-Oshima volcano: Magma convection in a conduit. Bull. Volcanol. 1994, 56, 207–216. [Google Scholar] [CrossRef]
- Stevenson, D.S.; Blake, S. Modelling the dynamics and thermodynamics of volcanic degassing. Bull. Volcanol. 1998, 60, 307–317. [Google Scholar] [CrossRef]
- Beckett, F.; Burton, M.; Mader, H.; Phillips, J.; Polacci, M.; Rust, A.; Witham, F. Conduit convection driving persistent degassing at basaltic volcanoes. J. Volcanol. Geotherm. Res. 2014, 283, 19–35. [Google Scholar] [CrossRef]
- Ferlito, C.; Coltorti, M.; Lanzafame, G.; Giacomoni, P.P. The volatile flushing triggers eruptions at open conduit volcanoes: Evidence from Mount Etna volcano (Italy). Lithos 2014, 184, 447–455. [Google Scholar] [CrossRef]
- Moretti, R.; Métrich, N.; Arienzo, I.; Renzo, V.D.; Aiuppa, A.; Allard, P. Degassing vs. eruptive styles at Mt. Etna volcano (Sicily, Italy). Part I: Volatile stocking, gas fluxing, and the shift from low-energy to highly explosive basaltic eruptions. Chem. Geol. 2017. [Google Scholar] [CrossRef]
- Lambert, G.; Le Cloarec, M.F.; Ardouin, B.; Le Roulley, J.C. Volcanic emission of radionuclides and magma dynamics. Earth Planet. Sci. Lett. 1985, 76, 185–192. [Google Scholar] [CrossRef]
- Gauthier, P.J.; Le Cloarec, M.F.; Condomines, M. Degassing processes at Stromboli volcano inferred from short-lived disequilibria (210Pb–210Bi–210Po) in volcanic gases. J. Volcanol. Geotherm. Res. 2000, 102, 1–19. [Google Scholar] [CrossRef]
- Lambert, G.; Bristeau, P.; Polian, G. Emission and enrichments of radon daughters from Etna volcano magma. Geophys. Res. Lett. 1976, 3, 724–726. [Google Scholar] [CrossRef]
- Pennisi, M.; Le Cloarec, M.F.; Lambert, G.; Le Roulley, J.C. Fractionation of metals in volcanic emissions. Earth Planet. Sci. Lett. 1988, 88, 284–288. [Google Scholar] [CrossRef]
- Le Cloarec, M.F.; Pennisi, M.; Ardouin, B.; Le Roulley, J.C.; Lambert, G. Relationship between gases and volcanic activity of Mount Etna in 1986. J. Geophys. Res. Solid Earth 1988, 93, 4477–4484. [Google Scholar] [CrossRef]
- Le Cloarec, M.F.; Pennisi, M. Radionuclides and sulfur content in Mount Etna plume in 1983–1995: New constraints on the magma feeding system. J. Volcanol. Geotherm. Res. 2001, 108, 141–155. [Google Scholar] [CrossRef]
- Allard, P.; Aiuppa, A.; Bani, P.; Métrich, N.; Bertagnini, A.; Gauthier, P.J.; Shinohara, H.; Sawyer, G.; Parello, F.; Bagnato, E.; et al. Prodigious emission rates and magma degassing budget of major, trace and radioactive volatile species from Ambrym basaltic volcano, Vanuatu island Arc. J. Volcanol. Geotherm. Res. 2016, 322, 119–143. [Google Scholar] [CrossRef]
- Gauthier, P.J.; Sigmarsson, O.; Gouhier, M.; Haddadi, B.; Moune, S. Elevated gas flux and trace metal degassing from the 2014–2015 fissure eruption at the Bárðarbunga volcanic system, Iceland. J. Geophys. Res. Solid Earth 2016, 121, 1610–1630. [Google Scholar] [CrossRef]
- Le Cloarec, M.F.; Lambert, G.; Le Guern, F.; Ardouin, B. Echanges de matériaux volatils entre phase solide, liquide et gazeuse au cours de l’éruption de l’Etna de 1983. Comptes-Rendus des Séances de l’Académie des Sciences. Série 2, Mécanique-Physique, Chimie, Sciences de l’univers, Sciences de la terre 1984, 298, 805–808. (In French) [Google Scholar]
- Le Cloarec, M.F.; Lambert, G.; Ardouin, B. Isotopic enrichment of 210Pb in gaseous emission from Mount Etna (Sicily). Chem. Geol. 1988, 70, 128. [Google Scholar] [CrossRef]
- Behncke, B.; Branca, S.; Corsaro, R.A.; Beni, E.D.; Miraglia, L.; Proietti, C. The 2011–2012 summit activity of Mount Etna: Birth, growth and products of the new SE crater. J. Volcanol. Geotherm. Res. 2014, 270, 10–21. [Google Scholar] [CrossRef]
- Geryes, T.; Monsanglant-Louvet, C. Determination of correction factors for alpha activity measurements in the environment (conditions of high dust loading). Radiat. Prot. Dosim. 2010, 144, 659–662. [Google Scholar] [CrossRef] [PubMed]
- Mather, T.A. Volcanoes and the environment: Lessons for understanding Earth’s past and future from studies of present-day volcanic emissions. J. Volcanol. Geotherm. Res. 2015, 304, 160–179. [Google Scholar] [CrossRef]
- Gill, J.; Williams, R.; Bruland, K. Eruption of basalt and andesite lava degasses 222Rn and 210Po. Geophys. Res. Lett. 1985, 12, 17–20. [Google Scholar] [CrossRef]
- Reagan, M.; Tepley, F.J.; Gill, J.B.; Wortel, M.; Hartman, B. Rapid time scales of basalt to andesite differentiation at Anatahan volcano, Mariana Islands. J. Volcanol. Geotherm. Res. 2005, 146, 171–183. [Google Scholar] [CrossRef]
- Sigmarsson, O.; Condomines, M.; Gauthier, P.J. Excess 210Po in 2010 Eyjafjallajökull tephra (Iceland): Evidence for pre-eruptive gas accumulation. Earth Planet. Sci. Lett. 2015, 427, 66–73. [Google Scholar] [CrossRef]
- Girard, G.; Reagan, M.K.; Sims, K.W.W.; Thornber, C.R.; Waters, C.L.; Phillips, E.H. 238U–230Th–226Ra–210Pb–210Po Disequilibria Constraints on Magma Generation, Ascent, and Degassing during the Ongoing Eruption of Kīlauea. J. Petrol. 2017, 58, 1199–1226. [Google Scholar] [CrossRef]
- Gauthier, P.J.; Le Cloarec, M.F. Variability of alkali and heavy metal fluxes released by Mt. Etna volcano, Sicily, between 1991 and 1995. J. Volcanol. Geotherm. Res. 1998, 81, 311–326. [Google Scholar] [CrossRef]
- Aiuppa, A.; Dongarrà, G.; Valenza, M.; Federico, C.; Pecoraino, G. Degassing of trace volatile metals during the 2001 eruption of Etna. In Volcanism and the Earth’s Atmosphere; Wiley: Hoboken, NJ, USA, 2003; pp. 41–54. [Google Scholar]
- Kayzar, T.M.; Cooper, K.M.; Reagan, M.K.; Kent, A.J. Gas transport model for the magmatic system at Mount Pinatubo, Philippines: Insights from (210Pb)/(226Ra). J. Volcanol. Geotherm. Res. 2009, 181, 124–140. [Google Scholar] [CrossRef]
- Condomines, M.; Sigmarsson, O.; Gauthier, P. A simple model of 222Rn accumulation leading to 210Pb excesses in volcanic rocks. Earth Planet. Sci. Lett. 2010, 293, 331–338. [Google Scholar] [CrossRef]
- Berlo, K.; Turner, S. 210Pb-226Ra disequilibria in volcanic rocks. Earth Planet. Sci. Lett. 2010, 296, 155–164. [Google Scholar] [CrossRef]
- Reagan, M.; Turner, S.; Handley, H.; Turner, M.; Beier, C.; Caulfield, J.; Peate, D. 210Pb-226Ra disequilibria in young gas-laden magmas. Sci. Rep. 2017, 7, 45186. [Google Scholar] [CrossRef] [PubMed]
- Gauthier, P.J.; Condomines, M. 210Pb–226Ra radioactive disequilibria in recent lavas and radon degassing: Inferences on the magma chamber dynamics at Stromboli and Merapi volcanoes. Earth Planet. Sci. Lett. 1999, 172, 111–126. [Google Scholar] [CrossRef]
- Bateman, H. The solution of a system of differential equations occurring in the theory of radioactive transformations. Proc. Camb. Philos. Soc. 1910, 15, 423–427. [Google Scholar]
- Moral, L.; Pacheco, A. Algebraic approach to the radioactive decay equations. Am. J. Phys. 2003, 71, 684–686. [Google Scholar] [CrossRef]
- Gauthier, P.J.; Condomines, M.; Hammouda, T. An experimental investigation of radon diffusion in an anhydrous andesitic melt at atmospheric pressure: Implications for radon degassing from erupting magmas. Geochim. Cosmochim. Acta 1999, 63, 645–656. [Google Scholar] [CrossRef]
- Métrich, N.; Allard, P.; Spilliaert, N.; Andronico, D.; Burton, M. 2001 flank eruption of the alkali- and volatile-rich primitive basalt responsible for Mount Etna’s evolution in the last three decades. Earth Planet. Sci. Lett. 2004, 228, 1–17. [Google Scholar] [CrossRef]
- Spilliaert, N.; Métrich, N.; Allard, P. S–Cl–F degassing pattern of water-rich alkali basalt: Modelling and relationship with eruption styles on Mount Etna volcano. Earth Planet. Sci. Lett. 2006, 248, 772–786. [Google Scholar] [CrossRef]
- Sato, K.; Sato, J. Estimation of gas-releasing efficiency of erupting magma from 226Ra–222Rn disequilibrium. Nature 1977, 266, 439–440. [Google Scholar] [CrossRef]
- Sato, K.; Kaneoka, I.; Sato, J. Rare-gas releasing experiments and Rn degassing from erupting magma. Geochem. J. 1980, 14, 91–94. [Google Scholar] [CrossRef]
- Condomines, M.; Tanguy, J.C.; Michaud, V. Magma dynamics at Mt Etna: Constraints from U-Th-Ra-Pb radioactive disequilibria and Sr isotopes in historical lavas. Earth Planet. Sci. Lett. 1995, 132, 25–41. [Google Scholar] [CrossRef]
- Armienti, P.; Pareschi, M.; Innocenti, F.; Pompilio, M. Effects of magma storage and ascent on the kinetics of crystal growth. Contrib. Mineral. Petrol. 1994, 115, 402–414. [Google Scholar] [CrossRef]
- Allard, P.; Behncke, B.; D’Amico, S.; Neri, M.; Gambino, S. Mount Etna 1993–2005: Anatomy of an evolving eruptive cycle. Earth-Sci. Rev. 2006, 78, 85–114. [Google Scholar] [CrossRef]

| Sample | Date and time | Volume (m3) | 210Pb | 210Bi | 210Po |
|---|---|---|---|---|---|
| Atmospheric blank | 11/05/2015 12:00 | 3.9 | bdl | bdl | bdl |
| TDF1 | 12/05/2015 12:07 | 3.9 | bdl | bdl | bdl |
| TDF2 | 13/05/2015 11:04 | 6.6 | 0.8 ± 0.2 | 3.1 ± 1 | 14.6 ± 0.7 |
| TDF3 | 13/05/2015 12:15 | 6.6 | bdl | bdl | bdl |
| TDF4 | 14/05/2015 10:51 | 1.7 | 3.5 ± 1.0 | 29 ± 5 | 212 ± 3 |
| TDF5A | 14/05/2015 11:38 | 3.9 | 4.0 ± 0.4 | 31 ± 3 | 162 ± 2 |
| TDF5B | 14/05/2015 11:38 | 3.0 | 8.2 ± 0.4 | 62 ± 2 | 349± 2 |
| TDF6 | 14/05/2015 12:31 | 6.6 | 5.9 ± 0.2 | 41 ± 2 | 217 ± 1 |
| Parameter | Range | References |
|---|---|---|
| (wt.%) | 4–5 | Métrich et al. [41], Spilliaert et al. [42] |
| f | 0.9–1 | Gill et al. [27], Gauthier et al. [40], Sato and Sato [43], Sato et al. [44] |
| (%) | 0.7–1.5 | Lambert et al. [14], Mather [26] |
| (%) | 20–45 | Lambert et al. [14], Pennisi et al. [17] |
| (%) | 80–100 | Le Cloarec et al. [22], Gill et al. [27], Reagan et al. [28], Girard et al. [30] |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Terray, L.; Gauthier, P.-J.; Salerno, G.; Caltabiano, T.; La Spina, A.; Sellitto, P.; Briole, P. A New Degassing Model to Infer Magma Dynamics from Radioactive Disequilibria in Volcanic Plumes. Geosciences 2018, 8, 27. https://doi.org/10.3390/geosciences8010027
Terray L, Gauthier P-J, Salerno G, Caltabiano T, La Spina A, Sellitto P, Briole P. A New Degassing Model to Infer Magma Dynamics from Radioactive Disequilibria in Volcanic Plumes. Geosciences. 2018; 8(1):27. https://doi.org/10.3390/geosciences8010027
Chicago/Turabian StyleTerray, Luca, Pierre-J. Gauthier, Giuseppe Salerno, Tommaso Caltabiano, Alessandro La Spina, Pasquale Sellitto, and Pierre Briole. 2018. "A New Degassing Model to Infer Magma Dynamics from Radioactive Disequilibria in Volcanic Plumes" Geosciences 8, no. 1: 27. https://doi.org/10.3390/geosciences8010027
APA StyleTerray, L., Gauthier, P.-J., Salerno, G., Caltabiano, T., La Spina, A., Sellitto, P., & Briole, P. (2018). A New Degassing Model to Infer Magma Dynamics from Radioactive Disequilibria in Volcanic Plumes. Geosciences, 8(1), 27. https://doi.org/10.3390/geosciences8010027








