Preliminary Validation of a Novel Method for the Assessment of Effective Stress State in Partially Saturated Soils by Cone Penetration Tests

Abstract

A proper assessment of the soil effective stress state is crucial in many cases to identify a potential geological/geotechnical hazard as shallow landslides or failure of levees that may have a significant impact on human activities and development. This paper is aimed at validating a methodology for the expeditious and economic determination of effective stress state in the vadose zone recently proposed by Lo Presti et al. in 2016. The method is based on the interpretation of cone penetration tests (CPTu). Its validation was carried out by comparing the CPTu predicted values of suction against the measured ones in a well-documented and monitored site. The comparison also includes the prediction of suction that was obtained by using the so-called Modified Kovacs model (MK). Moreover, additional data of water content and saturation degree from another site were used to predict the suction by using the MK model. These values of suction were compared with those inferred by the CPTu.

1. Introduction

Traditional soil mechanics mainly considers fully saturated or dry soils. The interest in partially saturated soils or soils saturated by capillarity is quite recent and still under development. Indeed, notwithstanding the early formulation by Bishop [1] of the effective stress principle for partially saturated soils, in practice, the effects of partial saturation are mainly neglected or rarely applied.

The difficulty in assessing the in situ saturation degree and/or to obtain reliable measurements of suction, as well as the continuous variation of these parameters is the main reason of the limited use in practice of the huge knowledge that has been gained in recent years on the “soil mechanics of partially saturated soils”.

Anyway, a correct estimate of suction or in situ effective stress state is extremely important in many cases. As an example, suction can improve significantly the response of a laterally loaded pile foundation, which is mainly affected by the shallower soil layers. To capture the actual load-deflection curves of some lateral load tests on single pile, Stacul et al. [2] developed an analysis method that considers the increase of both stiffness and resistance in partially saturated soil conditions. Other examples are represented by shallow landslides and failures of levee systems: before the triggering event, soils of interest are usually unsaturated. The quick increase of saturation degree and the development of positive values of pore pressure are the most important causes for shallow landslide and triggering of levee-failure [3,4].

Lo Presti et al. [5] proposed a method for assessing the effective stress state for clayey soils by an appropriate interpretation of CPTu tests. Such a method is briefly described in Section 2.

The method is based on the consideration that the tip resistance strongly depends on the water content in the case of fine-grained soils. Therefore, as known, the tip resistance may be very high in the desiccated crust and even in the vadose zone saturated by capillarity.

The suction effect, in fact, has a significant influence on the cone penetration resistance through suction hardening and its contribution to the effective stress state, as observed recently in the work of Yang and Russell [6]. In [6] Lyell silty sand was tested in a calibration chamber, and Yang and Russell highlighted that further studies are necessary for a wide range of unsaturated soil types to generalise CPT interpretation methods.

The typical trend of the tip resistance within a partially saturated clayey soil is shown in Figure 1. This figure shows the tip resistance for two tests carried out at the same location with two different water table depths [5,7]. The deposit was homogeneous and on the basis of laboratory testing on undisturbed samples retrieved from the first three meters was mainly classified as CL (low plasticity clay) to CH (high plasticity clay) according to the USCS classification system. The water table was found at a depth of 3.5 m during the wet season (June 2001) and at a depth of 5 m during the dry season (September 2001). Despite the homogeneity of the deposit, it can be observed that the tip resistance (q_c) is influenced to a great extent by the water table depth (due to suction) so that q_c increases from 1–2 MPa to 3–4 MPa in the vadose zone above the water table (Figure 1). As can be observed, such an increase is higher during the dry season.

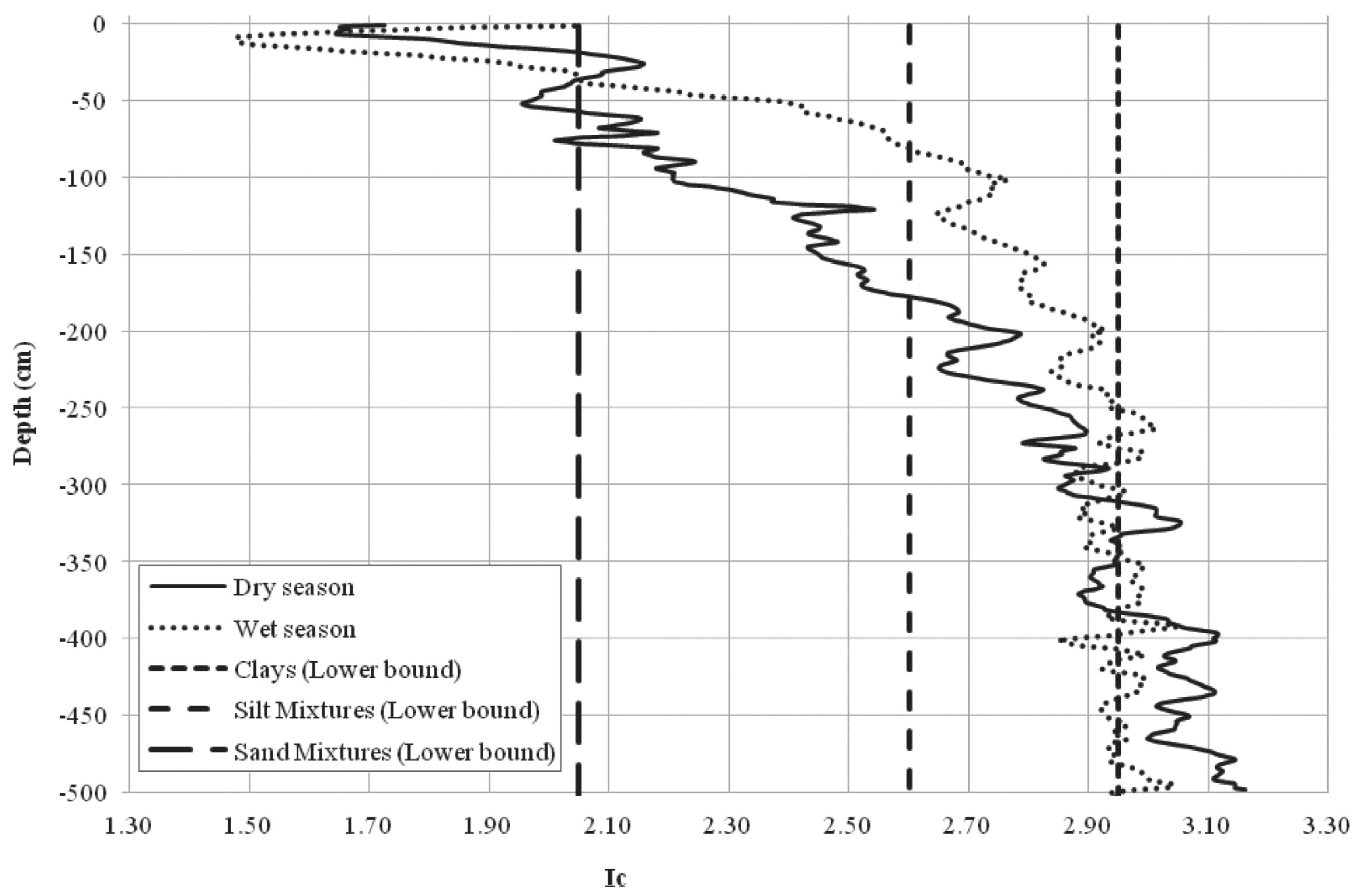
The effect of suction is evident even in terms of soil classification index (I_c) values (Figure 2). I_c can be inferred by CPTu tests data as described in Robertson [8], Jefferies and Davies [9] and Robertson and Wride [10]. In particular, the I_c index of Figure 2, was computed according to the normalized classification system by Robertson and Wride [10]. As far as the I_c index is concerned, the values decrease from about 3.0 at the water table depth to about 2.0 at a depth of 50 cm. In terms of SBTn (i.e., normalized Soil Behavior Type [10]) classes, silts and sand mixtures become predominant instead of OC stiff clay.

This paper is aimed at validating this recently proposed methodology. Its preliminary validation was carried out by comparing the CPTu predicted values of suction against the measured ones in a well-documented and monitored site.

2. Method

The method applicability requires that the soil is homogeneous, and the water table known. Moreover, the CPTu should be performed down to a depth below the water table. Were these hypotheses respected, the I_c value below the water table is assumed as a target one and the lower I_c values above the water table are corrected by changing the vertical effective stress according to Equations (1)–(4) [8,9,10].

$$Q_{tn}=\left(\frac{q_t-{\sigma }_{v0}}{{\sigma }_{atm}}\right)\cdot {\left(\frac{{\sigma }_{atm}}{{\sigma }_{v0}^{\prime }}\right)}^n$$

(1)

$$n=0.381\cdot I_c+0.05\cdot \left(\frac{{\sigma }_{v0}^{\prime }}{{\sigma }_{atm}}\right)-0.15$$

(2)

$$F=\frac{f_s}{q_t-{\sigma }_{v0}}\cdot 100$$

(3)

$$I_c=\sqrt{{\left(3.47-\log Q_{tn}\right)}^2+{\left(\log F+1.22\right)}^2}$$

(4)

where Q_tn = normalized tip resistance; q_t = total tip resistance; σ_v0 = total vertical stress of the soil; σ_atm = reference pressure, equal to (1) atm (=98 kPa); n = stress exponent expressed as a function of the classification index; σ’_v0 = effective vertical stress of the soil; F = normalized friction ratio; fs = sleeve friction.

In case of fine-grained soils, the stress exponent (n) is approximately equal to (1), thus once defined the I_c target (I_c,t) value the corresponding effective vertical stress (σ’_v0) can be easily evaluated according to Equation (5).

$${\sigma }_{v0}^{\prime }=\frac{q_t-{\sigma }_{v0}}{{10}^{3.47-\sqrt{I_{c,t}^2-{\left(\log F+1.22\right)}^2}}}$$

(5)

Once obtained the effective vertical stress value, the relationship (Equation (6)) proposed by Bishop [1] can be used to estimate the matric suction.

$${\sigma }_{v0}^{\prime }=\left({\sigma }_{v0}-u_a\right)+\chi \cdot \left(u_a-u_w\right)$$

(6)

where u_a = air pressure; u_w = water pressure; χ = effective stress parameter that is expressed as a function of the degree of saturation (S_r); and suction ψ is equal to u_a − u_w.

Suction can be evaluated according to Equation (6) rewritten in the following way (Equation (7)):

$$\psi =\frac{{\sigma }_{v0}^{\prime }-{\sigma }_{v0}+u_a}{\chi }$$

(7)

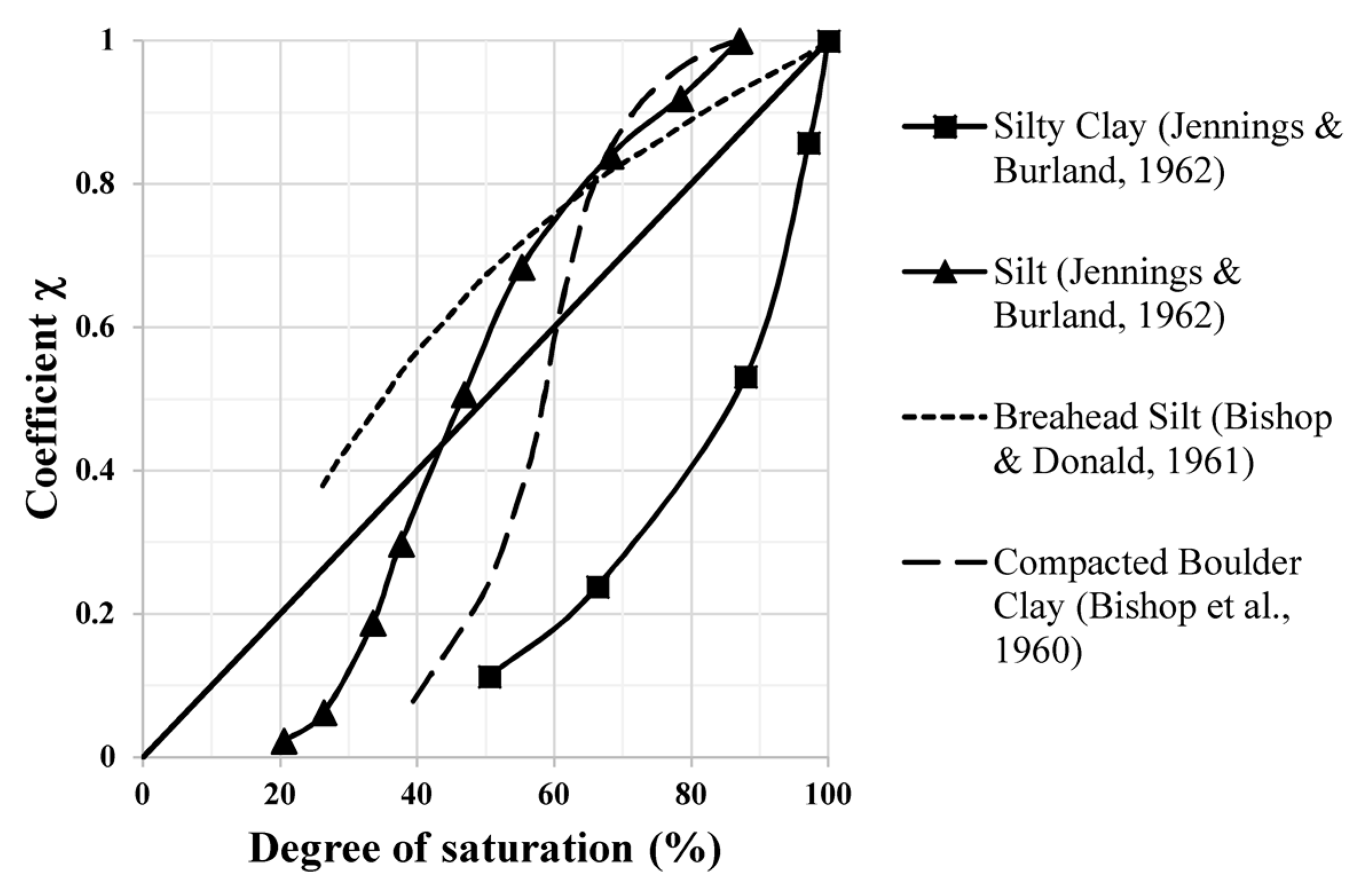
In order to properly use Equation (7) the value of χ should be assessed on the basis of the actual degree of saturation of the soil layers above the water table. The relationship between χ and S_r (Figure 3) is available in literature for different soil types (e.g., [11,12,13]). More recently, Konrad and Lebeau [14] related the effective stress parameter (χ) to an effective degree of saturation, which is linked to the capillary component of water retention. Nevertheless, the applicability of the methodology developed in [14] has been validated for non-plastic soils.

The MK-model (Modified-Kovacs model), as proposed by Aubertin et al. [15,16] (see also Mbonimpa et al. [17,18]), was also used for estimating suction (ψ) on the basis of the measured liquid limit (w_L), void ratio (e) and degree of saturation (S_r) in the shallower soil layers. The MK-model makes use of a parameter defined as the equivalent capillary rise (h_c0) in the porous medium and is calculated using the expression for the rise of water in a capillary tube with a diameter d.

For the sake of convenience, the expression to estimate the equivalent capillary rise in cohesive/plastic soils is reported below (Equation (8), [16]):

$$h_{c0}(cm)=\frac{0.15{\rho }_s}{e}{w}_L^{1.45}$$

(8)

where ρ_s = soil grain density (kg/m³); e = void ratio (−); w_L = liquid limit (%). The MK-model uses h_c0 as a reference parameter to define the relationship between the degree of saturation (S_r) and the matric suction (ψ). The model considers that water is held by capillary forces, responsible for capillary saturation (S_c), and by adhesive forces, causing saturation by adhesion (S_a). The relationship proposed in the MK-model is written as in Equation (9) [16]:

$$S_r=S_c+S_a\left(1-S_c\right)$$

(9)

The contribution of the capillary and the adhesion components to the total degree of saturation (S_r) is defined as a function of h_c0 and ψ using Equations (10)–(12) [16].

$$S_c=1-{\left[{\left(h_{c0}/\psi \right)}^2+1\right]}^m\exp \left[-m\cdot {\left(h_{c0}/\psi \right)}^2\right]$$

(10)

$$S_a=a_c\cdot \left[1-\frac{\ln \left(1+\psi /{\psi }_r\right)}{\ln \left(1+{\psi }_0/{\psi }_r\right)}\right]\cdot \frac{{\left(h_{c0}/{\psi }_n\right)}^{2/3}}{e^{1/3}\cdot {\left(\psi /{\psi }_n\right)}^{1/6}}$$

(11)

$${\psi }_r=0.86\cdot {\left(\frac{0.15{\rho }_s}{e}\right)}^{1.2}{w}_L^{1.74}$$

(12)

where for cohesive/plastic soils m and a_c = model constants that can be assumed equal to 3 × 10⁻⁵ and 7 × 10⁻⁴, respectively; ψ_r = suction at residual water content (Equation (12)); ψ₀ = suction value corresponding approximately to complete dryness, in the MK-model is assumed equal to 10⁷ cm; ψ_n = a normalization parameter and equal to 1 cm when ψ is given in cm, and corresponding to 10⁻³ atm.

The assessment of suction (ψ) is carried out following these steps:

• compute the equivalent capillary rise (h_c0) using ρ_s, e and w_L measured in situ (Equation (8));
• compute S_c and S_a assuming a trial value for the unknown suction ψ using Equations (10) and (11);
• compute S_r with Equation (9);
• repeat steps 2 and 3 assuming different values for the suction ψ in order to obtain a degree of saturation (S_r) approximately equal to that measured in the test site.

3. Test Sites

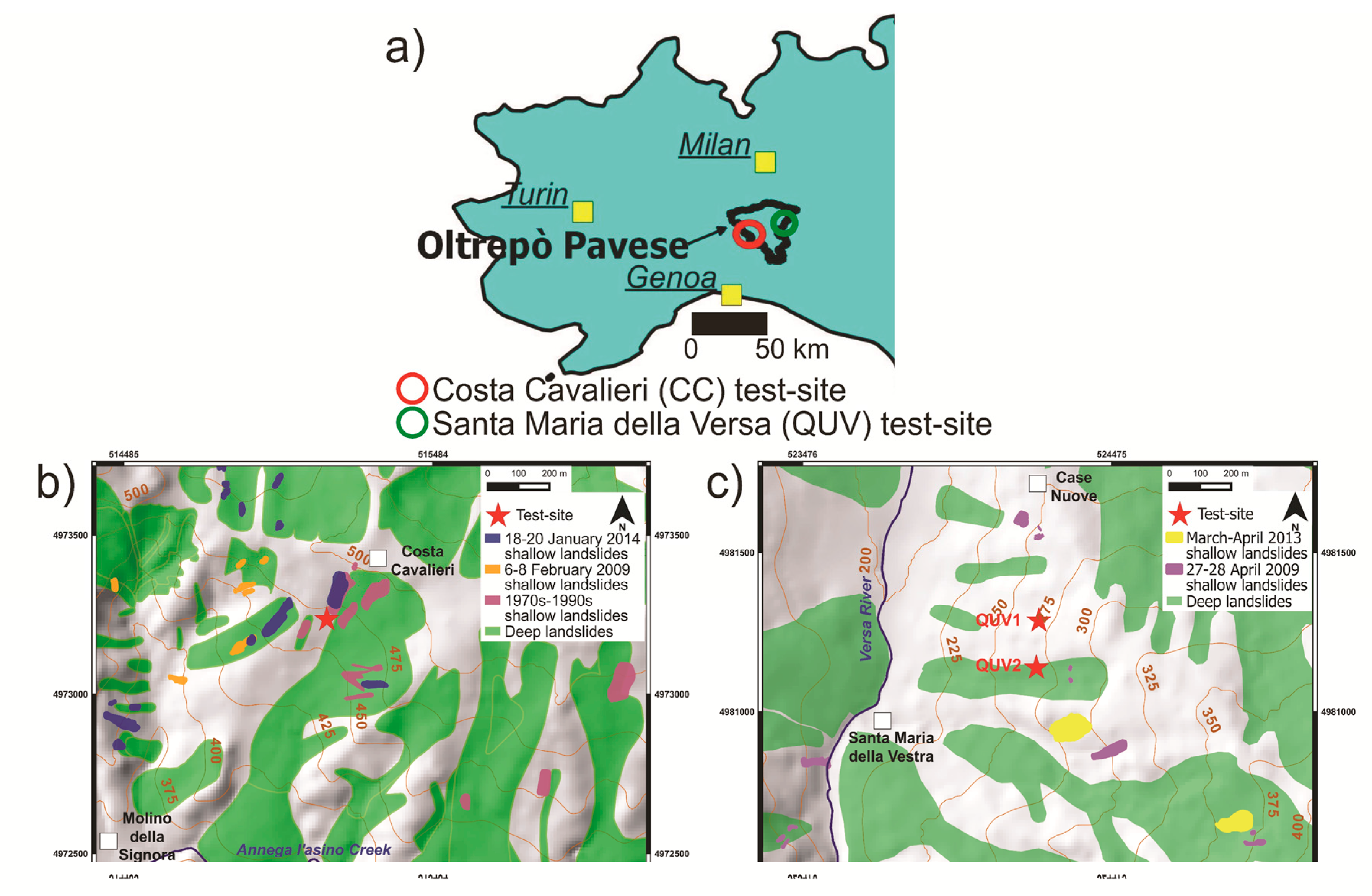
Two test sites were considered. Both are located in Oltrepò Pavese, a hilly region of northern Apennines, in northwestern Italy (Figure 4a). The analyzed soils consist of colluvial soils deriving from the weathering of clay bedrock.

The first site (Figure 4b) is named Costa Cavalieri (CC) and it is located on a low-medium topographic gradient slope (7–18°). The slope elevation ranges from 460 to 500 m a.s.l. A cultivation of alfalfa grass entirely covers the slope. The bedrock is composed of a clayey melange, with scattered calcareous and marly blocks. Due to the very low permeability of these materials, deep water tables are only seasonally present along the hillslopes inside bedrock levels; perched water table also develops seasonally.

Five main soil horizons were identified in the colluvial cover, thick 2 m (

Table 1. Selected geotechnical and physical properties of Costa Cavalieri test-site soil and weathered bedrock ¹.

Type	D (m)	Sa (%)	S (%)	C (%)	CaCO3 (%)	wL (%)	PI (%)
A-cc	0.2	2.3	42.2	54.5	9.8	69.2	49.3
B-cc	0.4	2.2	39.7	57.5	9.8	71.3	53.1
C-cc	0.9	2.3	45.7	51.5	13.7	73.9	53.6
D-cc	1.2	3.2	46.8	47.5	26.7	65.5	45.6
E-cc	1.7	0.7	42.2	57.0	0.0	73.4	51.1

¹ D: depth; Sa: sand; S: silt; C: clay; CaCO₃ carbonate content; w_L: liquid limit; PI: plasticity index.

). These levels were named with subsequent letters, from A to E, according to their position in the soil profile. The weathered bedrock (WB) is composed of more compacted clays and was identified at 2 m from the ground surface. All the tests for the soil characterization were carried out according to the Recommendation by the Italian Geotechnical Society [19] and the ASTM Standards.

In the first 1.44 m from the surface, the soil is characterized by a high amount of carbonate in the profile (9.8–13.7%). Moreover, there is the presence of a calcic horizon, rich in carbonate concretions (D-cc level), where the carbonates reach values of 26.7% (Table 1). Instead, E-cc level, below the calcic horizon, does not present carbonate in the soil matrix. An X-ray diffraction analysis on tout-venant revealed that all the soil levels have a high content in mica and in smectite, both generally in the range between 25 and 40%. D-cc level showed an abundance in carbonate minerals (37%), confirming the presence of the calcic horizon.

On the basis of the grain-size distribution (Table 1), soil horizons are very similar. Clay is the most abundant grain size class, ranging in a narrow path between 47.5 and 57.5%. Silt is also in a narrow range between 39.7 and 46.9%. Sand and gravel contents are very low in all the soil levels, keeping between 0 and 3.2%. According to USCS classification, soil horizons are highly plastic soils (CH), with liquid limit (w_L) ranging from 65.5 to 73.4% and plasticity index (PI) between 45.6 and 53.6% (Table 1). Unit weight (γ) is rather steady along the soil profile, ranging between 18.6 and 19.1 kN/m³.

Oedometric tests, performed on undisturbed samples collected in B-cc and C-cc horizons, showed that all the soil levels are over-consolidated. Peak shear strength parameters were obtained for C-cc horizon through a direct-shear test. Peak friction angle (φ′) is about 14°, while effective cohesion (c′) is of 15 kPa.

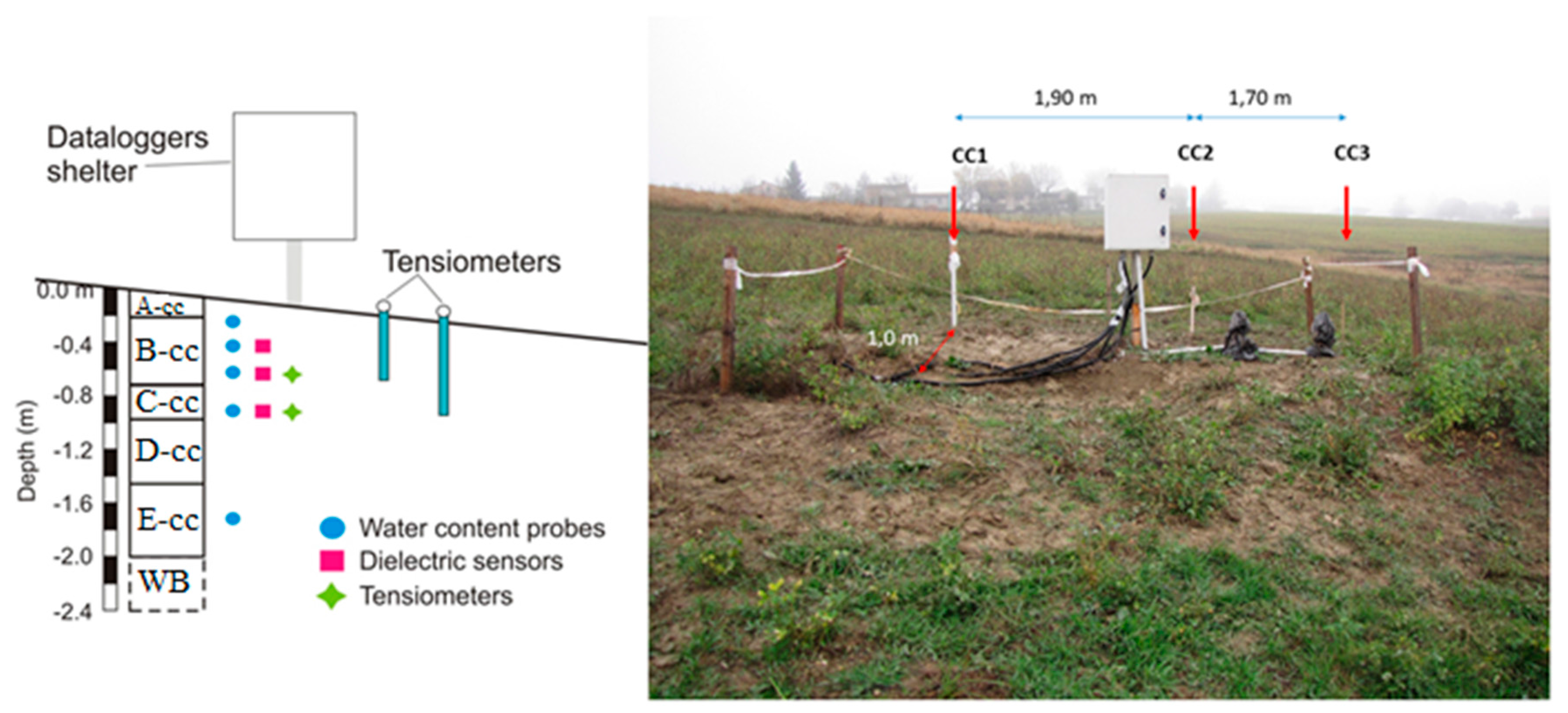
In this site a hydrological monitoring station (Figure 5) was installed since 27 November 2015 (Bordoni et al. [20]). Data were recorded every 10 min. The monitoring station included water content probes, tensiometers and dielectric sensors. GS3 probes (Decagon Devices Inc., Pullman, WA, USA) were installed at 0.2, 0.4, 0.6, 0.9 and 1.7 m from the ground surface for the measure of the water content. A combination of different devices was used for measuring pore water pressure: two tensiometers (T4e UMS GmbH) and three dielectric sensors (MPS-6 Decagon Devices) were installed at 0.4, 0.6 and 0.9 m from ground level. Tensiometers were installed to measure pore water pressures higher than −101 kPa, while the other pore water pressure devices allow to measure pore water pressures lower than −101 kPa (Bittelli et al. [21]). The monitoring system was equipped with a datalogger (DL-6te, EM-50) powered by batteries.

The second site (Figure 4c) is named Santa Maria della Versa (QUV); it is a western-facing slope also characterized by low-medium topographic gradient (8°). The slope elevation ranges from 260 to 270 m a.s.l. Vineyards entirely cover the slope.

The bedrock consists of a flysch i.e., medium to thickly stratified limestones and marly limestones. The water table is at 3.5 m depth. Soil classification (

Table 2. Selected geotechnical and physical properties of Santa Maria della Versa test-site soil and weathered bedrock ¹.

Type	D (m)	Sa (%)	S (%)	C (%)	wL (%)	PI (%)
QUV1	0.00–0.45	5.8	34.8	52.5	-	-
QUV1	0.45–0.80	6.0	37.8	55.0	71.3	51.6
QUV1	0.80–1.70	2.9	50.0	46.5	-	-
QUV2	0.00–0.40	4.9	25.6	66.8	-	-
QUV2	0.65–0.75	2.1	29.9	66.5	-	-
QUV2	0.75–1.15	3.7	36.8	58.0	84.3	62.2

¹ D: depth; Sa: sand; S: silt; C: clay; w_L: liquid limit; PI: plasticity index.

) was carried out on samples extracted from two open pits made in the test-site (named QUV1 and QUV2), at depth not greater than about 1.7 m.

Colluvial soils above the bedrock levels were characterized as Costa Cavalieri soils. The soil is rich in clayey minerals, as confirmed by the abundance in clay particles and by a series of shrinkage cracks present during the samplings.

On the basis of the grain-size distribution (Table 2), soil horizons are very similar in depth and between the two sites. Clay is generally the most abundant grain size class, ranging in a path between 46.5 and 66.8%. Silt is also in a range between 25.6 and 50.0%. Sand and gravel contents are very low in all the soil levels, keeping between 0 and 6.0%.

According to USCS classification, soil horizons are highly plastic soils (CH), with liquid limit (w_L) ranging from 71.3 to 84.3% and plasticity index (PI) between 51.6 and 61.2% (Table 2). Unit weight (γ) is rather steady along the soil profile, ranging between 17.9 and 20.1 kN/m³.

CPTu tests were carried out close to the QUV1 and QUV2 open pits, through a Pagani Penetrometer model TG63-150kN and according to ASTM D5778 [22]; the acquisition system/data logger was TGAS-08. Silicone oil was used for saturation of the filter. Bronze Filter saturation process was done previously using a professional vacuum pump for 24 h at Pagani Company.

The CPTu tests were carried out at CC site after a very dry period in November 2017 (

Table 3. In situ characteristics of Costa Cavalieri test-site (9 November 2017) ¹.

Depth (m)	W (m3/m3)	Sr (%)	uw (kPa)
0.2	0.402	80	-
0.4	0.251	55	−21.0
0.6	0.187	41	−1520.6
0.9	0.255	56	−1653.2
1.7	0.265	61	−1250

¹ w: water content; S_r: saturation degree; u_w: pore water pressure.

). Anyway, 77.2 mm of rain have fallen in 5 days just before the execution of the tests. It is worth noting that this event was the most intense of the 2017. This year was in fact characterized by a strong dryness, testified by a low amount of rain fallen (406 mm of cumulated rainfall, equal to 57% of the average amount of cumulated rainfall for this area). CPTu tests at QUV were also carried out in a very dry period in between July and August 2017.

Table 3 and

Table 4. In situ characteristics of Santa Maria della Versa test-site (25 August 2017) ¹.

Pit	Depth (m)	E (−)	W (%)	γ (kN/m3)	γd (kN/m3)	θs (%)	Sr (%)
QUV1	−0.14	0.67	18.10	19.38	15.88	25.21	71.78
QUV1	−0.27	0.81	18.12	17.93	14.69	30.39	59.62
QUV1	−0.32	0.72	20.52	19.37	15.40	27.20	75.44
QUV1	−0.37	0.70	20.84	19.70	15.60	26.38	78.97
QUV1	−0.50	0.79	20.93	18.70	14.79	29.88	70.05
QUV1	−0.55	0.82	20.82	18.38	14.55	30.97	67.24
QUV1	−0.60	0.80	19.96	18.44	14.76	29.95	66.65
QUV1	−0.70	0.73	20.44	19.23	15.30	27.62	73.99
QUV1	−0.80	0.71	19.38	19.23	15.50	26.72	72.54
QUV1	−0.90	0.70	18.92	19.20	15.57	26.49	71.41
QUV1	−1.00	0.70	19.46	19.31	15.55	26.55	73.28
QUV1	−1.10	0.67	17.83	19.36	15.91	25.10	71.06
QUV1	−1.15	0.70	18.75	19.20	15.60	26.37	71.12
QUV1	−1.40	0.65	19.80	19.98	16.02	24.68	80.22
QUV1	−1.45	0.63	18.96	20.07	16.26	23.75	79.84
QUV1	−1.60	0.79	20.71	18.72	14.84	29.67	69.81
QUV2	−0.10	0.77	18.97	18.51	15.00	28.90	65.66
QUV2	−0.20	0.86	21.56	18.13	14.22	32.57	66.20
QUV2	−0.30	0.78	19.97	18.58	14.87	29.50	67.69
QUV2	−0.40	0.89	25.95	18.99	14.06	33.38	77.73
QUV2	−0.50	0.83	25.28	19.42	14.51	31.17	81.10
QUV2	−0.60	0.81	23.20	19.04	14.63	30.62	75.76
QUV2	−0.70	0.82	22.97	18.90	14.56	30.95	74.22
QUV2	−0.80	0.81	21.39	18.63	14.64	30.55	70.03
QUV2	−0.90	0.85	23.26	18.68	14.33	32.03	72.64
QUV2	−1.00	0.94	23.93	17.94	13.65	35.51	67.37

¹ e: void ratio; w: water content; γ: unit weight; γ_d: dry unit weight; θ_s: saturation water content; S_r: saturation degree.

respectively summarize the saturation degree with depth at CC and QUV, as estimated at the time CPTu were performed.

As far as the CC site is concerned three different ψ values were obtained: (a) from measurements; (b) from CPTu interpretation; (c) from application of the MK model as a predictive tool. In the case of QUV site the direct in situ measurements are missing.

4. Results

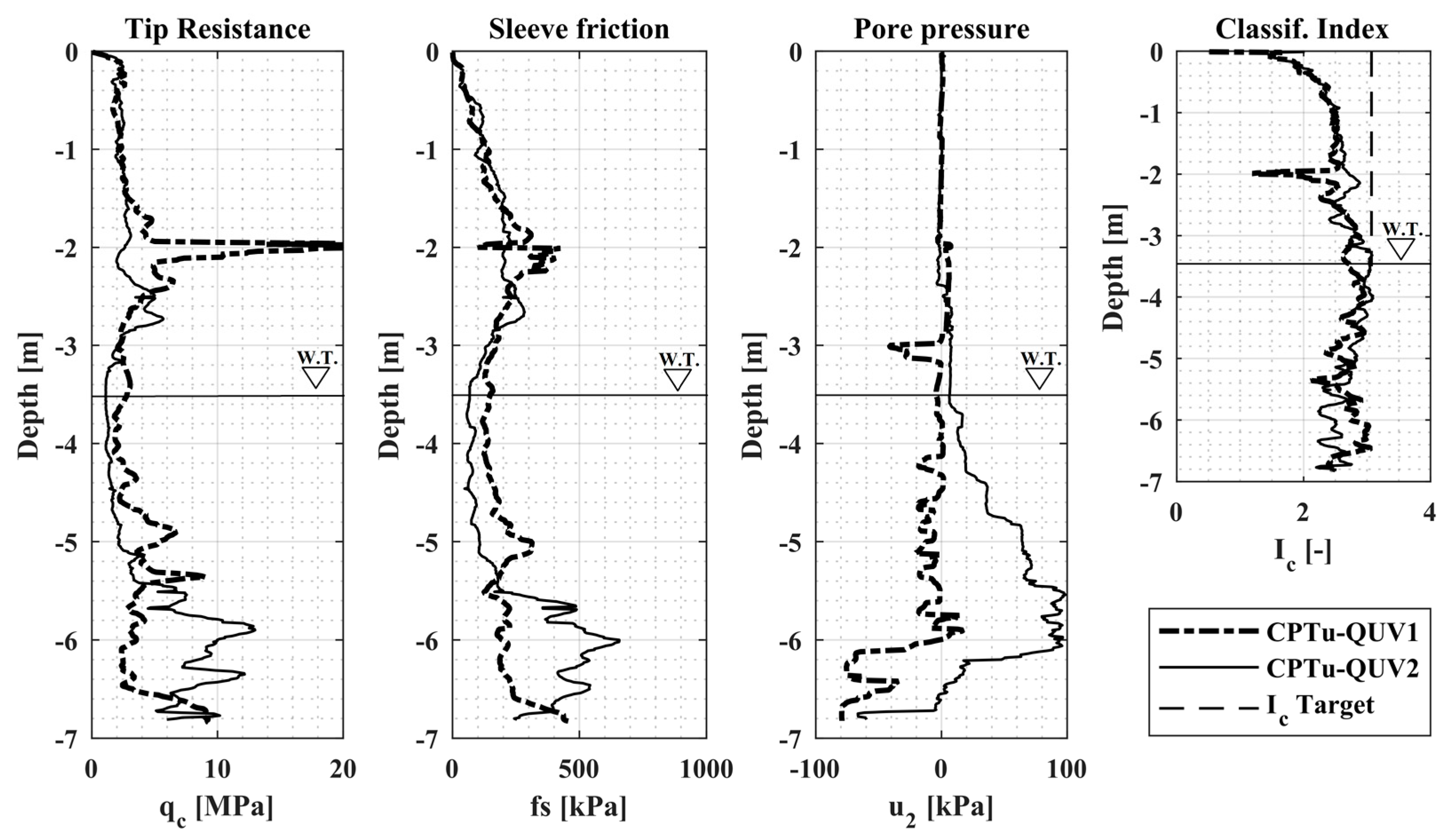
Figure 6 summarizes the results of CPTu at CC site. The Figure also shows the selected I_c target and I_c values as obtained from CPTu interpretation.

For the test sites “CC” and “QUV” the average degree of saturation (at the time of CPTu tests) in the first 2 m was equal to 55% and 70%, respectively. Considering that the soils were classified as silty clays the best estimate of χ (Figure 3) led to values ranging in between 0.2 and 0.25 (depending on the saturation degree). These values were used in the Bishop equation (Equation (7)).

Therefore, it was possible to estimate the values of suction according to the previously described methods and to compare these estimated values to the measured ones (Figure 7).

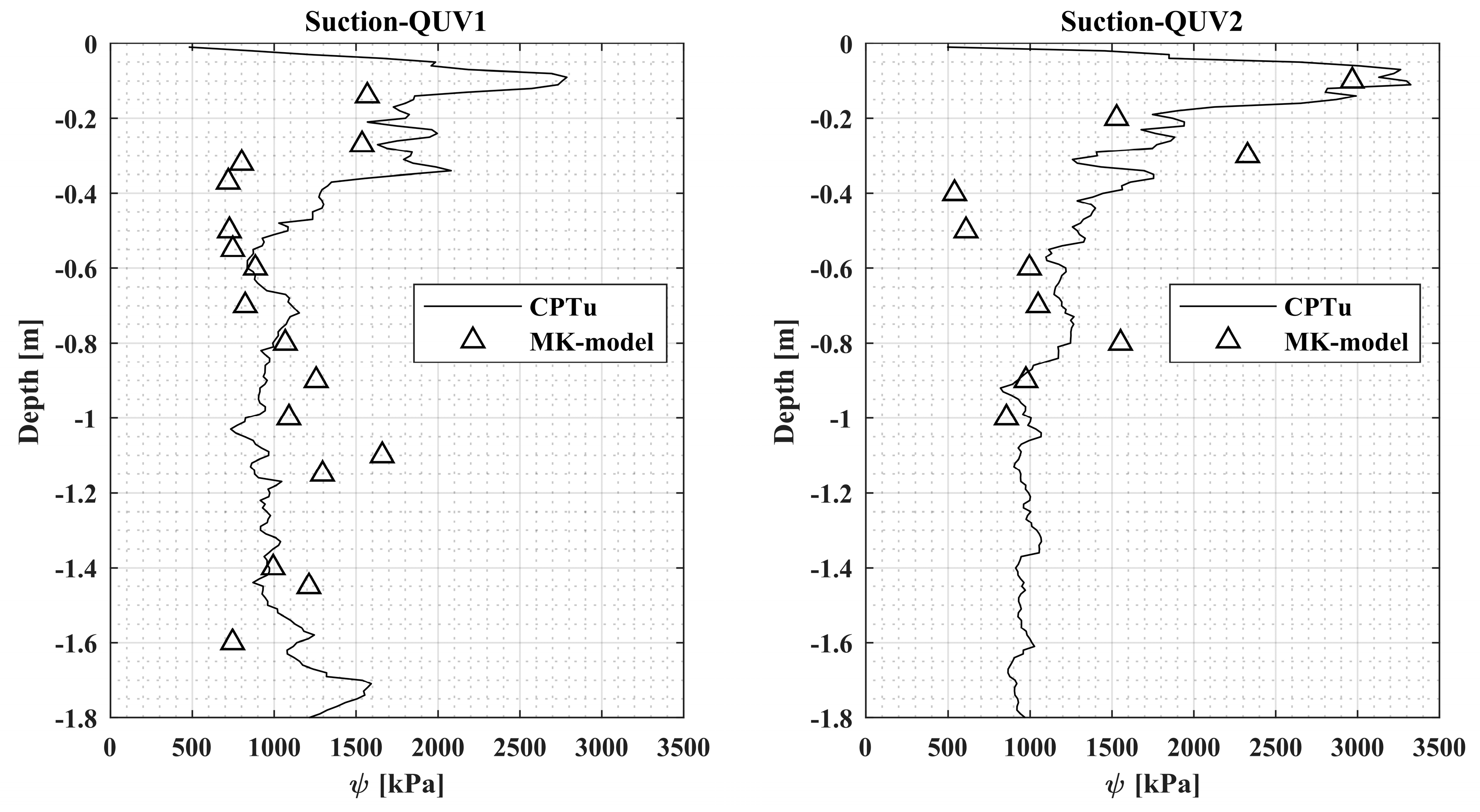
The measured values of suction and those inferred by means of the MK method and from re-interpretation of CPTu are in very good agreement.

Some increase in suction values around depth of 1.6 m in CC1 and CC2 (Figure 7) is predicted using the CPTu-based method. Nevertheless, this is simply due to the locally high tip resistance (q_c) values in CPTu-CC1 and CPTu-CC2 at a depth approximately equal to 1.6 m (heterogeneous layer). The same does not happen in CPTu-CC3 case.

Moreover, both the considered methods are capable of perfectly miming the trend of suction with an important reduction in the shallower part because of the raining during few days before CPTu testing.

Similar observations can be done as far as the CPTu tests at QUV site are concerned. In this case, the CPTu-based suction values mimic those predicted by the MK model but exhibit some discrepancies especially at depths in between 0.3 and 1.0 m (Figure 8 and Figure 9). Unfortunately, the experimental measurement of suction at QUV site was not available and therefore it was not possible to establish if such discrepancies depend on limitations in the use of the MK model or of the proposed method.

It is important to stress that the proposed CPTu-based method directly assesses the effective stress state. As an alternative Khalili and Khabbaz [23] proposed a relationship for the estimate of χ parameter as a function of the ratio between the matric suction and the air entry value. On the other hand, Lu et al. [24] proposed a closed-form equation for the evaluation of the effective stress as a function of the matric suction and the Van Genuchten’s model parameters [25]. Unfortunately, these methods could not be applied to the present case studies because the necessary parameters were not available. Additionally, soil types validating the methods in [23,24] are very different than the silty-clay mixtures of the present study.

5. Conclusions

This paper presented a method for the determination of effective stress state in the vadose zone based on the interpretation of piezocone tests (CPTu). The preliminary validation was carried out by comparing the CPTu predicted values of suction against those measured in a monitored site and those predicted by using the so-called Modified Kovacs model (MK).

The values of suction obtained using the CPTu method were assessed based on the soil type and the measured degree of saturation, applying the effective stress equation for partly saturated soils proposed by Bishop.

Despite that future research appears necessary to fully validate the proposed methodology. The obtained results are really encouraging and suggest that the proposed method based on the CPTu re-interpretation could be an expeditious and economic tool for the estimate of the in situ effective stress state in fine-grained soil deposits. A proper assessment of the latter is crucial in many cases to identify potential geological/geotechnical hazards as shallow landslides or failure of levees. In particular, the method is proposed for the shallow part of homogeneous clayey deposits.

If the proposed method is applied to evaluate the soil effective stress state the knowledge of the saturation degree is not required. In this case only the water table position and the results from CPTu tests (that can be carried out very easily and quickly) are required. Nevertheless, the knowledge of the saturation degree is necessary to estimate suction by using the “effective stress parameter (χ) vs. degree of saturation” relationships available in literature for specific soil types.

At the same time, the good performance of both the MK model and the relationship between the degree of saturation and the effective stress parameter (χ) of the Bishop equation are confirmed by the data shown.