Earthquake Magnitude and Shaking Intensity Dependent Fragility Functions for Rapid Risk Assessment of Buildings
Abstract
:1. Introduction
2. Materials and Methods
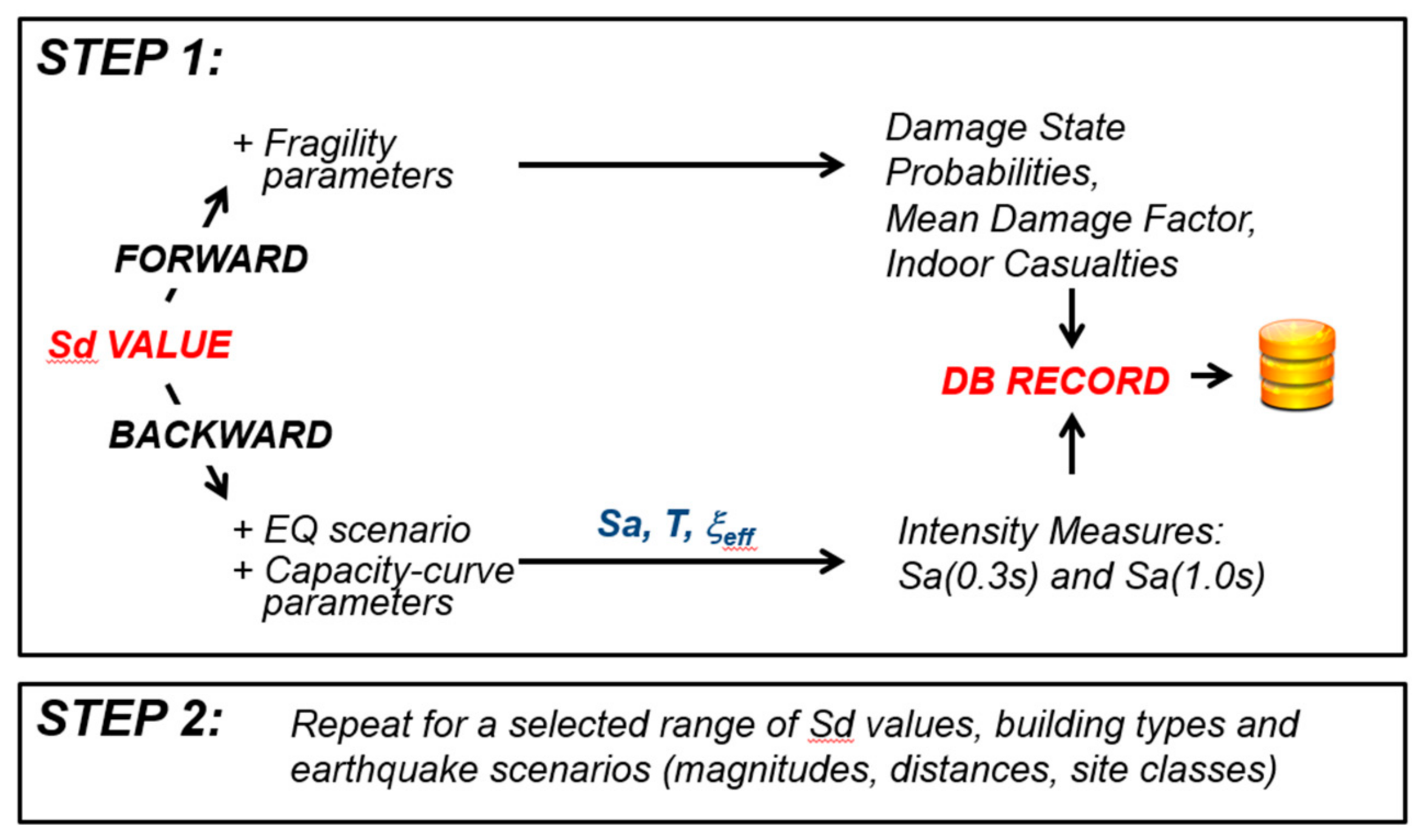
2.1. Background of the Methodology
2.2. Database of Damage State Probabilities
2.3. Optimization of Building Inventories
2.3.1. Inventory Scheme with 53 Most Frequent Building Classes
2.3.2. Reduced Inventory Scheme with 24 Combined Building Classes
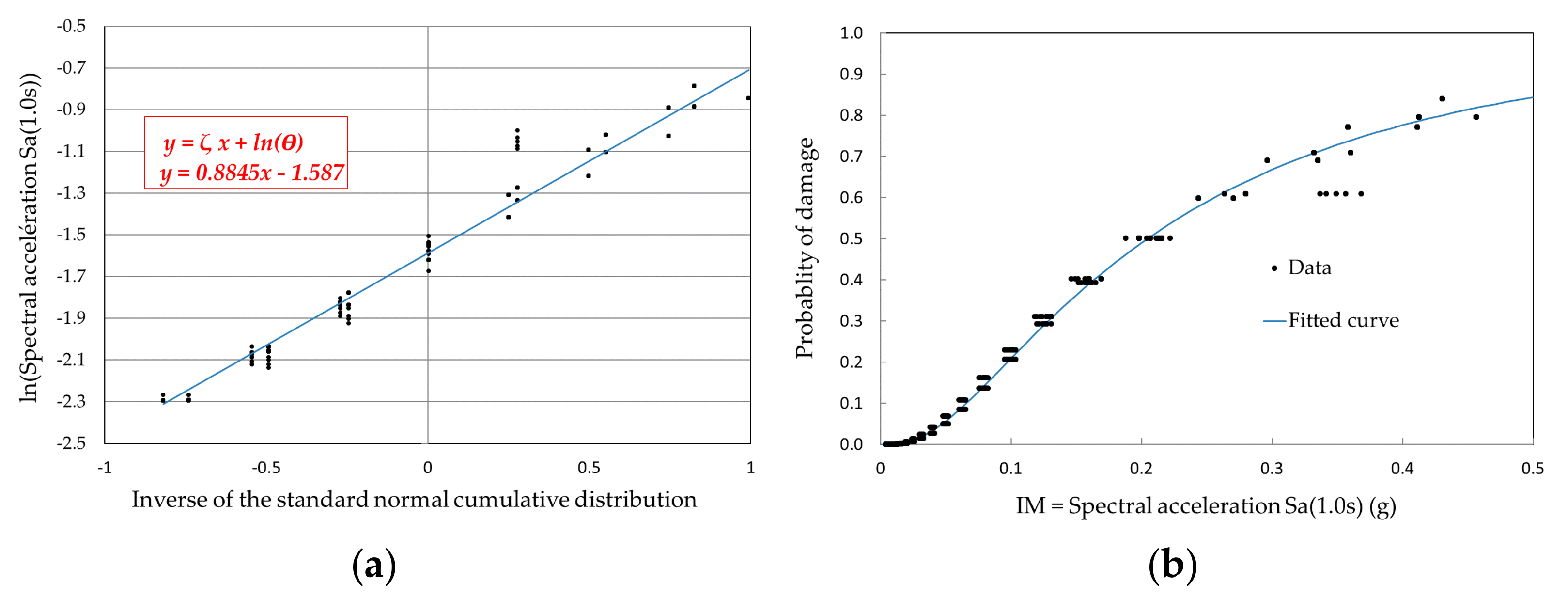
2.4. Fitting Implicit Fragility Curves for Single IM
3. Results
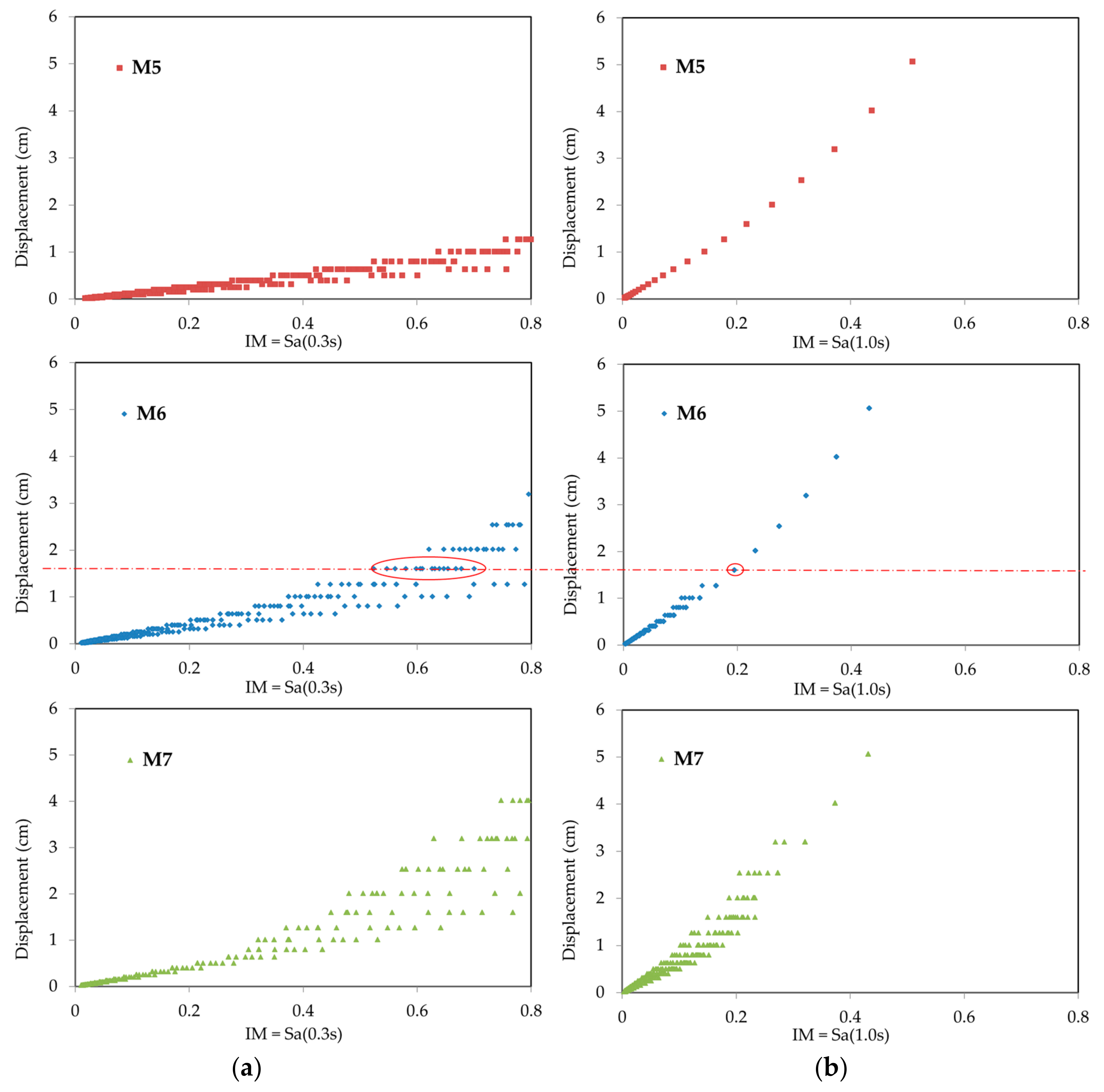
3.1. Selecting Single Intensity Measure
3.2. Sensitivity of Implicit Fragility Functions to Epicentral Distance and Site Class
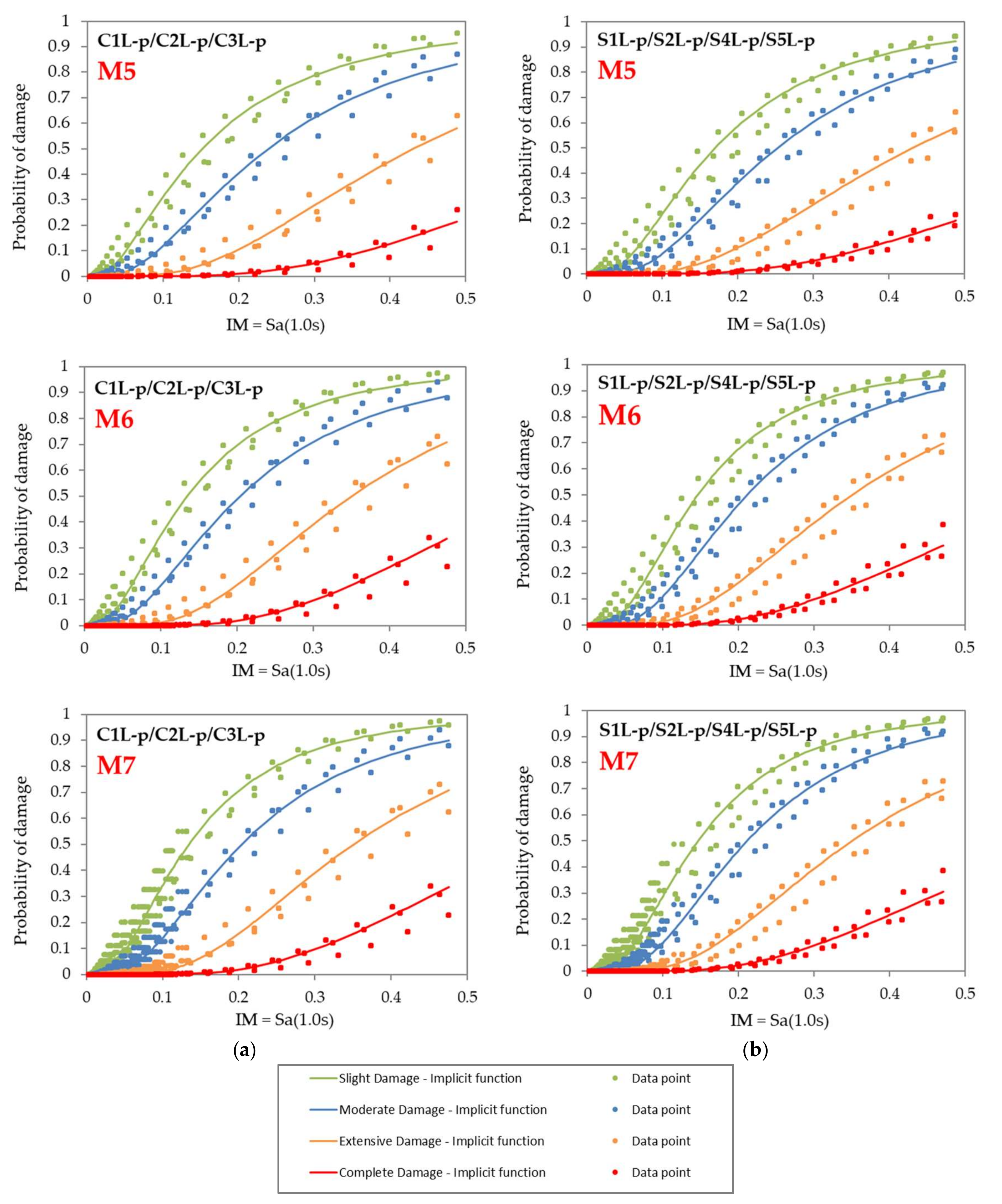
3.3. Implicit Fragility Fucntions for Simplified Building Classification
- group building classes with similar material, same height range and same code level;
- group building classes for which the lateral force resisting system is difficult to identify with visual screening;
- keep separate the building classes of the same structural system that can be easily identified knowing the height, year of construction or occupancy, information available in municipal property assessment database.
- S3: these light frames low rise are mostly used for agricultural structures, industrial factories, and warehouses and can be easily identified from occupancy and height.
- W1 and W2: these wood building classes can be identified by the occupancy as W1 are light wood frame single- or multiple-family dwellings of one or more stories in height and W2 are wood frame commercial and industrial buildings with a floor area larger than 5000 square feet.
- URM: unreinforced masonry building class can be easily identified by visual screening.
4. Discussion
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
| Material | Description/Lateral Force Resisting System | Label | No. | Height Subclasses 1 |
|---|---|---|---|---|
| Wood buildings | Light wood frame single- or multiple-family dwellings of one or more stories in height | W1 | 1 | W1 |
| Wood frame commercial and industrial buildings with a floor area larger than 5000 square feet | W2 | 2 | W2 | |
| Steel buildings | Steel moment frame | S1 | 3 | S1L |
| 4 | S1M | |||
| 5 | S1H | |||
| Steel braced frame | S2 | 6 | S2L | |
| 7 | S2M | |||
| 8 | S2H | |||
| Steel light frame | S3 | 9 | S3 | |
| Steel frame with cast in place concrete shear walls | S4 | 10 | S4L | |
| 11 | S4M | |||
| 12 | S4H | |||
| Steel frame with unreinforced masonry infill walls | S5 | 13 | S5L | |
| 14 | S5M | |||
| 15 | S5H | |||
| Concrete Buildings | Concrete moment frame | C1 | 16 | C1L |
| 17 | C1M | |||
| 18 | C1H | |||
| Concrete shear walls | C2 | 19 | C2L | |
| 20 | C2M | |||
| 21 | C2H | |||
| Concrete frame with unreinforced masonry infill walls | C3 | 22 | C3L | |
| 23 | C3M | |||
| 24 | C3H | |||
| Precast concrete buildings | Precast concrete tilt-up walls | PC1 | 25 | PC1 |
| Precast concrete frames with concrete shear walls | PC2 | 26 | PC2L | |
| 27 | PC2M | |||
| 28 | PC2H | |||
| Reinforced masonry buildings | Reinforced masonry bearing walls with wood or metal deck diaphragms | RM1 | 29 | RM1L |
| 30 | RM1M | |||
| Reinforced masonry bearing walls with precast concrete diaphragms | RM2 | 31 | RM2L | |
| 32 | RM2M | |||
| 33 | RM2H | |||
| Unreinforced masonry buildings | Unreinforced masonry bearing walls | URM | 34 | URML |
| 35 | URMM | |||
| Mobil homes | Mobil homes | MH | 36 | MH |
| Building Class | Slight Damage | Moderate Damage | Extensive Damage | Complete Damage | ||||
|---|---|---|---|---|---|---|---|---|
| Median | St. Dev. | Median | St. Dev. | Median | St. Dev. | Median | St. Dev. | |
| C1L_p + C2L_p + C3L_p | 0.15 | 0.85 | 0.24 | 0.74 | 0.43 | 0.61 | 0.77 | 0.58 |
| C1M_p + C2M_p + C3M_p | 0.17 | 0.68 | 0.27 | 0.63 | 0.50 | 0.58 | 0.90 | 0.61 |
| C1H_p + C2H_p + C3H_p | 0.13 | 0.69 | 0.21 | 0.68 | 0.48 | 0.80 | 0.96 | 0.79 |
| C1L_l + C2L_l + C3L_l | 0.21 | 0.82 | 0.33 | 0.73 | 0.59 | 0.57 | 1.07 | 0.61 |
| C1M_l + C2M_l + C3M_l | 0.23 | 0.69 | 0.35 | 0.63 | 0.67 | 0.59 | 1.40 | 0.72 |
| C1H_l + C2H_l + C3H_l | 0.17 | 0.67 | 0.29 | 0.72 | 0.60 | 0.74 | 1.33 | 0.82 |
| S1L_p + S2L_p + S4L_p + S5L_p | 0.17 | 0.74 | 0.25 | 0.66 | 0.43 | 0.61 | 0.79 | 0.59 |
| S1M_p + S2M_p + S4M_P + S5M_p | 0.17 | 0.66 | 0.26 | 0.60 | 0.50 | 0.66 | 0.97 | 0.70 |
| S1H_p + S2H_p + S4H_p | 0.14 | 0.73 | 0.22 | 0.70 | 0.54 | 0.86 | 1.29 | 0.86 |
| S1L_l + S2L_l + S4L_l + S5L_l | 0.23 | 0.74 | 0.32 | 0.67 | 0.52 | 0.53 | 0.89 | 0.53 |
| S1M_l + S2M_l + S4M_l + S5M_l | 0.24 | 0.65 | 0.34 | 0.63 | 0.60 | 0.56 | 1.44 | 0.79 |
| S1H_l + S2H_l + S4H_l + S5H_l | 0.18 | 0.72 | 0.29 | 0.70 | 0.66 | 0.78 | 1.37 | 0.84 |
| Building Class | Slight Damage | Moderate Damage | Extensive Damage | Complete Damage | ||||
|---|---|---|---|---|---|---|---|---|
| Median | St. Dev. | Median | St. Dev. | Median | St. Dev. | Median | St. Dev. | |
| C1L_p + C2L_p + C3L_p | 0.13 | 0.77 | 0.20 | 0.70 | 0.35 | 0.56 | 0.60 | 0.53 |
| C1M_p + C2M_p + C3M_p | 0.15 | 0.64 | 0.23 | 0.60 | 0.41 | 0.53 | 0.73 | 0.59 |
| C1H_p + C2H_p + C3H_p | 0.12 | 0.63 | 0.19 | 0.62 | 0.37 | 0.65 | 0.73 | 0.68 |
| C1L_l + C2L_l + C3L_l | 0.18 | 0.71 | 0.26 | 0.66 | 0.44 | 0.53 | 0.74 | 0.53 |
| C1M_l + C2M_l + C3M_l | 0.19 | 0.60 | 0.29 | 0.56 | 0.51 | 0.53 | 1.09 | 0.69 |
| C1H_l + C2H_l + C3H_l | 0.16 | 0.60 | 0.25 | 0.67 | 0.51 | 0.74 | 1.06 | 0.78 |
| S1L_p + S2L_p + S4L_p + S5L_p | 0.15 | 0.69 | 0.21 | 0.61 | 0.35 | 0.57 | 0.63 | 0.58 |
| S1M_p + S2M_p + S4M_P + S5M_p | 0.16 | 0.58 | 0.22 | 0.56 | 0.39 | 0.57 | 0.68 | 0.61 |
| S1H_p + S2H_p + S4H_p | 0.13 | 0.68 | 0.20 | 0.63 | 0.41 | 0.68 | 0.77 | 0.64 |
| S1L_l + S2L_l + S4L_l + S5L_l | 0.18 | 0.65 | 0.27 | 0.59 | 0.42 | 0.49 | 0.79 | 0.57 |
| S1M_l + S2M_l + S4M_l + S5M_l | 0.19 | 0.58 | 0.28 | 0.56 | 0.49 | 0.54 | 0.81 | 0.56 |
| S1H_l + S2H_l + S4H_l + S5H_l | 0.17 | 0.63 | 0.26 | 0.65 | 0.52 | 0.67 | 1.11 | 0.77 |
| Building Class | Slight Damage | Moderate Damage | Extensive Damage | Complete Damage | ||||
|---|---|---|---|---|---|---|---|---|
| Median | St. Dev. | Median | St. Dev. | Median | St. Dev. | Median | St. Dev. | |
| S3-l | 0.14 | 0.85 | 0.21 | 0.73 | 0.40 | 0.65 | 0.70 | 0.50 |
| S3-p | 0.11 | 0.95 | 0.17 | 0.79 | 0.32 | 0.72 | 0.59 | 0.53 |
| URML-l | 0.14 | 0.97 | 0.27 | 0.96 | 0.60 | 0.95 | 1.42 | 0.96 |
| URML-p | 0.11 | 1.15 | 0.22 | 1.12 | 0.46 | 1.00 | 1.08 | 1.02 |
| URMM-l | 0.16 | 0.89 | 0.28 | 0.75 | 0.56 | 0.62 | 1.21 | 0.71 |
| URMM-p | 0.12 | 0.95 | 0.22 | 0.79 | 0.44 | 0.64 | 0.81 | 0.60 |
| W1-l | 0.21 | 0.95 | 0.53 | 1.00 | 1.68 | 1.04 | 4.24 | 1.01 |
| W1-m | 0.21 | 0.93 | 0.59 | 0.96 | 2.06 | 0.99 | 5.69 | 1.16 |
| W1-p | 0.16 | 1.00 | 0.38 | 0.98 | 1.08 | 1.00 | 2.20 | 0.93 |
| W2-l | 0.27 | 0.83 | 0.55 | 0.72 | 1.26 | 0.66 | 2.43 | 0.74 |
| W2-m | 0.33 | 0.92 | 0.84 | 0.99 | 2.36 | 0.92 | 4.67 | 0.83 |
| W2-p | 0.20 | 0.84 | 0.40 | 0.74 | 0.89 | 0.64 | 1.53 | 0.66 |
| Building Class | Slight Damage | Moderate Damage | Extensive Damage | Complete Damage | ||||
|---|---|---|---|---|---|---|---|---|
| Median | St. Dev. | Median | St. Dev. | Median | St. Dev. | Median | St. Dev. | |
| S3-l | 0.13 | 0.76 | 0.18 | 0.72 | 0.33 | 0.61 | 0.60 | 0.51 |
| S3-p | 0.10 | 0.84 | 0.14 | 0.74 | 0.26 | 0.64 | 0.48 | 0.54 |
| URML-l | 0.13 | 0.92 | 0.24 | 0.87 | 0.50 | 0.86 | 1.01 | 0.81 |
| URML-p | 0.10 | 1.05 | 0.19 | 0.98 | 0.38 | 0.87 | 0.80 | 0.90 |
| URMM-l | 0.14 | 0.77 | 0.25 | 0.69 | 0.48 | 0.58 | 0.82 | 0.58 |
| URMM-p | 0.11 | 0.87 | 0.20 | 0.72 | 0.36 | 0.55 | 0.65 | 0.56 |
| W1-l | 0.19 | 0.89 | 0.44 | 0.88 | 1.21 | 0.92 | 2.39 | 0.83 |
| W1-m | 0.21 | 0.87 | 0.54 | 0.90 | 1.73 | 0.93 | 4.49 | 1.09 |
| W1-p | 0.16 | 0.97 | 0.34 | 0.89 | 0.82 | 0.85 | 1.91 | 0.90 |
| W2-l | 0.22 | 0.75 | 0.43 | 0.65 | 0.91 | 0.60 | 1.51 | 0.62 |
| W2-m | 0.28 | 0.78 | 0.62 | 0.84 | 1.68 | 0.84 | 2.75 | 0.70 |
| W2-p | 0.18 | 0.76 | 0.34 | 0.66 | 0.68 | 0.57 | 1.26 | 0.63 |
References
- GEM (Global Earthquake Model). Openquake Platform. Pavia, Italy. Available online: https://github.com/gem/oq-platform (accessed on 9 November 2017).
- NORSAR. Risk Analysis Software—The SELENA-RISe Open Risk Package. Kjeller, Norway. Available online: selena.sourceforge.net (accessed on 8 January 2018).
- FEMA-NIBS. HAZUS-MH 2.1: Multi-Hazard Loss Estimation Methodology Earthquake Model; User Manual; Federal Emergency Management Agency, National Institute of Building Science: Washington, DC, USA, 2012; 863p. [Google Scholar]
- GFDRR (Global Facility for Disaster Reduction and Recovery). Understanding Risk—Review of Open Source and Open Access Software Packages Available to Quantify Risk from Natural Hazards; International Bank for Reconstruction and Development/International Development Association of The World Bank: Washington, DC, USA, 2014; 67p. [Google Scholar]
- Wald, D.J.; Jaiswal, K.S.; Marano, K.D.; Bausch, D.B.; Hearne, M.G. PAGER—Rapid Assessment of an Earthquake’s Impact; Fact Sheet 2010–3036; U.S. Geological Survey: Reston, VA, USA, 2011; 4p. [Google Scholar]
- Coburn, A.W.; Spence, R.J.S. Earthquake Protection, 2nd ed.; John Wiley & Sons: Chichester, UK, 2002. [Google Scholar]
- Kircher, C.A.; Nassar, A.A.; Kustu, O.; Holmes, W.T. Development of building damage functions for earthquake loss estimation. Earthq. Spectra 1997, 13, 663–682. [Google Scholar] [CrossRef]
- Mouroux, P.; Le Brun, B. Presentation of RISK-UE project. Bull. Earthq. Eng. 2006, 4, 323–339. [Google Scholar] [CrossRef]
- Rota, M.; Penna, A.; Strobbia, C.L. Processing Italian damage data to derive typological fragility curves. Soil Dyn. Earthq. Eng. 2008, 28, 933–947. [Google Scholar] [CrossRef]
- Nastev, N.; Nollet, M.-J.; Abo El Ezz, A.; Smirnoff, A.; Ploeger, S.K.; McGrath, H.; Sawada, M.; Stefanakis, E.; Parent, M. Methods and tools for natural hazard risk analysis in Eastern Canada—Use of knowledge to understand vulnerability and implement mitigation measures. ASCE Nat. Hazards Rev. 2015, 18, B4015002. [Google Scholar] [CrossRef]
- NRC (National Research Council). National Building Code of Canada 2015; Associate Committee on the National Building Code, National Research Council: Ottawa, ON, Canada, 2017. [Google Scholar]
- Atkinson, G.M.; Boore, D.M. Earthquake ground-motion prediction equations for eastern North America. Bull. Seismol. Soc. Am. 2006, 96, 2181–2205. [Google Scholar] [CrossRef]
- Atkinson, G.M.; Adams, J. Ground motion prediction equations for application to the 2015 Canadian national seismic hazard maps. Can. J. Civ. Eng. 2013, 40, 988–998. [Google Scholar] [CrossRef]
- Boore, D.M.; Joyner, W.B.; Fumal, T.E. Equations for estimating horizontal response spectra and peak acceleration from Western North American earthquakes: A summary of recent work. Seismol. Res. Lett. 1997, 68, 128–153. [Google Scholar] [CrossRef]
- Abo El Ezz, A.; Nollet, M.-J.; Nastev, M. Seismic fragility assessment of low-rise stone masonry buildings. Earthq. Eng. Eng. Vib. 2013, 12, 87–97. [Google Scholar] [CrossRef]
- Lagomarsino, S.; Giovinazzi, S. Macroseismic and mechanical models for the vulnerability and damage assessment of current buildings. Bull. Earthq. Eng. 2006, 4, 415–443. [Google Scholar] [CrossRef]
- Karbassi, A.; Nollet, M.J. Performance-based seismic vulnerability evaluation of masonry buildings using Applied Element Method in a nonlinear dynamic-based analytical procedure. Earthq. Spectra 2013, 29, 399–426. [Google Scholar] [CrossRef]
- Freeman, S.A. The Capacity Spectrum Method as a Tool for Seismic Design. In Proceedings of the 11th European Conference on Earthquake Engineering, Paris, France, 6–11 September 1998. [Google Scholar]
- Freeman, S.A. Review of the development of the capacity spectrum method. ISET J. Earthq. Technol. 2004, 41, 1–13. [Google Scholar]
- Mahaney, A.; Paret, T.F.; Kehoe, B.E.; Freeman, S.A. The Capacity Spectrum Method for Evaluating Structural Response during the Loma Prieta Earthquake. In Proceedings of the 1993 United States National Earthquake Conference, Memphis, TN, USA, 2–5 May 1993; Volume 2, pp. 501–510. [Google Scholar]
- Porter, K.A. Cracking an open safe: HAZUS vulnerability functions in terms of structure-independent spectral acceleration. Earthq. Spectra 2009, 25, 361–378. [Google Scholar] [CrossRef]
- Abo El Ezz, A.; Nollet, M.-J.; Nastev, M. Methodology for Rapid Assessment of Seismic Damage to Buildings in Canadian Settings; Open File 7450; Geological Survey of Canada: Ottawa, ON, Canada, 2014; 41p. [Google Scholar]
- FEMA-NIBS. HAZUS-MH 2.1: Multi-Hazard Loss Estimation Methodology Earthquake Model; Technical Manual; Federal Emergency Management Agency, National Institute of Building Science: Washington, DC, USA, 2012; 718p. [Google Scholar]
- NRC. Manual for Screening of Buildings for Seismic Investigation; Institute for Research in Construction, National Research Council: Ottawa, ON, Canada, 1992. [Google Scholar]
- Ventura, C.E.; Finn, W.L.; Onur, T.; Blanquera, A.; Rezai, M. Regional seismic risk in British Columbia—classification of buildings and development of damage probability functions. Can. J. Civil. Eng. 2005, 32, 372–387. [Google Scholar] [CrossRef]
- Nollet, M.J.; Désilets, C.; Abo-El-Ezz, A.; Nastev, M. Approche Méthodologique D’inventaire de Bâtiments Pour les Études de Risque Sismique en Milieu Urbain: Ville de Québec, Arrondissement La Cité-Limoilou; Open File 7260; Geological Survey of Canada: Ottawa, ON, Canada, 2013; 93p. [Google Scholar]
- Uva, G.; Sanjust, C.A.; Casolo, S.; Mezzina, M. ANTAEUS Project for the Regional Vulnerability Assessment of the Current Building Stock in Historical Centers. Int. J. Arch. Heritage 2016, 10, 20–43. [Google Scholar] [CrossRef]
- Rossetto, T.; Elnashai, A. Derivation of vulnerability functions for European-type RC structures based on observational data. Eng. Struct. 2003, 25, 1241–1263. [Google Scholar] [CrossRef]
- Moehle, J.; Deierlein, G.G. A framework methodology for performance-based earthquake engineering. In Proceedings of the 13th World Conference on Earthquake Engineering, Vancouver, BC, Canada, 1–6 August 2004. [Google Scholar]
- Kircher, C.A.; Whitman, R.; Holmes, W.T. Hazus earthquake loss estimation methods. Nat. Hazards Rev. 2006, 7, 45–59. [Google Scholar] [CrossRef]
- ATC. Seismic Evaluation and Retrofit of Concrete Buildings: ATC-40; Applied Technology Council: Redwood City, CA, USA, 1996. [Google Scholar]
- Paxton, B.; Elwood, K.J.; Ingham, J.M. Empirical Damage Relationships and Benefit-Cost Analysis for the Seismic Retrofit of URM Buildings. Earthq. Spectra 2017, 33, 1053–1074. [Google Scholar] [CrossRef]
- Di Sarno, L. Effects of multiple earthquakes on inelastic structural response. Eng. Struct. 2013, 56, 673–681. [Google Scholar] [CrossRef]
- Goda, K.; Taylor, C.A. Effects of aftershocks on peak ductility demand due to strong ground motion records from shallow crustal earthquakes. Earthq. Eng. Struct. Dyn. 2012, 41, 2311–2330. [Google Scholar] [CrossRef]
- Li, Q.; Ellingwood, B.R. Performance evaluation and damage assessment of steel frame buildings under main shock-aftershock earthquake sequences. Earthq. Eng. Struct. Dyn. 2007, 36, 405–427. [Google Scholar] [CrossRef]
- Applied Technology Council (ATC). Rapid Visual Screening of Buildings for Potential Seismic Hazards: A Handbook (FEMA P-154), 3rd ed.; Applied Technology Council: Redwood City, CA, USA, 2015. [Google Scholar]

| Material | Description/Lateral Force Resisting System | Label | Height | Code Level |
|---|---|---|---|---|
| Wood buildings | Light wood frame single- or multiple-family dwellings of one or more stories in height | W1 | Low-rise | Pre-code Low-code Medium-code |
| Wood frame commercial and industrial buildings with a floor area larger than 5000 square feet | W2 | Low-rise | Pre-code Low-code Medium-code | |
| Steel buildings | Steel moment frame | S1 | Low-rise Medium-rise High-rise | Pre-code Low-code |
| Steel braced frame | S2 | Low-rise Medium-rise High-rise | Pre-code Low-code | |
| Steel light frame | S3 | Low-rise | Pre-code Low-code | |
| Steel frame with cast in place concrete shear walls | S4 | Low-rise Medium-rise High-rise | Pre-code Low-code | |
| Steel frame with unreinforced masonry infill walls | S5 | Low-rise Medium-rise High-rise 1 | Pre-code Low-code | |
| Concrete Buildings | Concrete moment frame | C1 | Low-rise Medium-rise High-rise | Pre-code Low-code |
| Concrete shear walls | C2 | Low-rise Medium-rise High-rise | Pre-code Low-code | |
| Concrete frame with unreinforced masonry infill walls | C3 | Low-rise Medium-rise High-rise | Pre-code Low-code | |
| Unreinforced masonry buildings | Unreinforced masonry bearing walls | URM | Low-rise Medium-rise | Pre-code Low-code |
| Earthquake Scenarios | Damage State | Maximum MAAD | Building Class |
|---|---|---|---|
| M5, all distances and all site classes | Slight | 2.91% | S3-p |
| Moderate | 1.77% | S3-p | |
| Extensive | 0.78% | S3-p | |
| Complete | 0.28% | S3-p | |
| M6, all distances and all site classes | Slight | 3.17% | S3-p |
| Moderate | 1.96% | S3-p | |
| Extensive | 0.86% | S3-p | |
| Complete | 0.33% | S3-p | |
| M7, all distances and all site classes | Slight | 3.43% | URML-p |
| Moderate | 1.96% | S3-p | |
| Extensive | 0.86% | S3-p | |
| Complete | 0.33% | S3-p |
| Material | Description/Lateral Force Resisting System | Label | Height | Code Level 1 |
|---|---|---|---|---|
| Wood buildings | Light wood frame single- or multiple-family dwellings of one or more stories in height | W1 | Low-rise | Pre-code Low-code Medium-code |
| Wood frame commercial and industrial buildings with a floor area larger than 5000 square feet | W2 | Low-rise | Pre-code Low-code Medium-code | |
| Steel buildings | Steel moment frame (S1), Steel braced frame (S2), Steel frame with cast in place concrete shear walls (S4), Steel frame with unreinforced masonry infill walls (S5) | S | Low-rise Medium-rise High-rise | Pre-code Low-code |
| Steel light frame | S3 | Low-rise | Pre-code Low-code | |
| Concrete Buildings | Concrete moment frame (C1), Concrete shear walls (C2), Concrete frame with unreinforced masonry infill walls (C3) | C | Low-rise Medium-rise High-rise | Pre-code Low-code |
| Unreinforced masonry buildings | Unreinforced masonry bearing walls | URM | Low-rise Medium-rise | Pre-code Low-code |
| Earthquake Scenarios | Damage State | Maximum MAAD | Building Group |
|---|---|---|---|
| M5 all distances and all site classes | Slight | 3.58% | C1L-l + C2L-l + C3L-l |
| Moderate | 2.30% | S1L-l + S2L-l+ S4L-l + S5L-l | |
| Extensive | 1.71% | C1L-l + C2L-l + C3L-l | |
| Complete | 0.62% | C1H-p + C2H-p + C3H-p | |
| M6 all distances and all site classes | Slight | 3.33% | C1L-p + C2L-p + C3L-p |
| Moderate | 2.37% | C1H-p + C2H-p + C3H-p | |
| Extensive | 1.88% | C1H-p + C2H-p + C3H-p | |
| Complete | 0.93% | C1H-p + C2H-p + C3H-p | |
| M7 all distances and all site classes | Slight | 3.12% | C1L-p + C2L-p + C3L-p |
| Moderate | 2.37% | C1H-p + C2H-p + C3H-p | |
| Extensive | 1.88% | C1H-p + C2H-p + C3H-p | |
| Complete | 0.93% | C1H-p + C2H-p + C3H-p |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nollet, M.-J.; Abo El Ezz, A.; Surprenant, O.; Smirnoff, A.; Nastev, M. Earthquake Magnitude and Shaking Intensity Dependent Fragility Functions for Rapid Risk Assessment of Buildings. Geosciences 2018, 8, 16. https://doi.org/10.3390/geosciences8010016
Nollet M-J, Abo El Ezz A, Surprenant O, Smirnoff A, Nastev M. Earthquake Magnitude and Shaking Intensity Dependent Fragility Functions for Rapid Risk Assessment of Buildings. Geosciences. 2018; 8(1):16. https://doi.org/10.3390/geosciences8010016
Chicago/Turabian StyleNollet, Marie-José, Ahmad Abo El Ezz, Oliver Surprenant, Alex Smirnoff, and Miroslav Nastev. 2018. "Earthquake Magnitude and Shaking Intensity Dependent Fragility Functions for Rapid Risk Assessment of Buildings" Geosciences 8, no. 1: 16. https://doi.org/10.3390/geosciences8010016
APA StyleNollet, M.-J., Abo El Ezz, A., Surprenant, O., Smirnoff, A., & Nastev, M. (2018). Earthquake Magnitude and Shaking Intensity Dependent Fragility Functions for Rapid Risk Assessment of Buildings. Geosciences, 8(1), 16. https://doi.org/10.3390/geosciences8010016





