Geomagnetic Signatures of Moderate Earthquakes from Kumaun Himalaya, India
Abstract
1. Introduction
1.1. Seismotectonics of Uttarakhand and Western Nepal
1.2. Electromagnetic Signatures of Earthquake Processes
2. Data
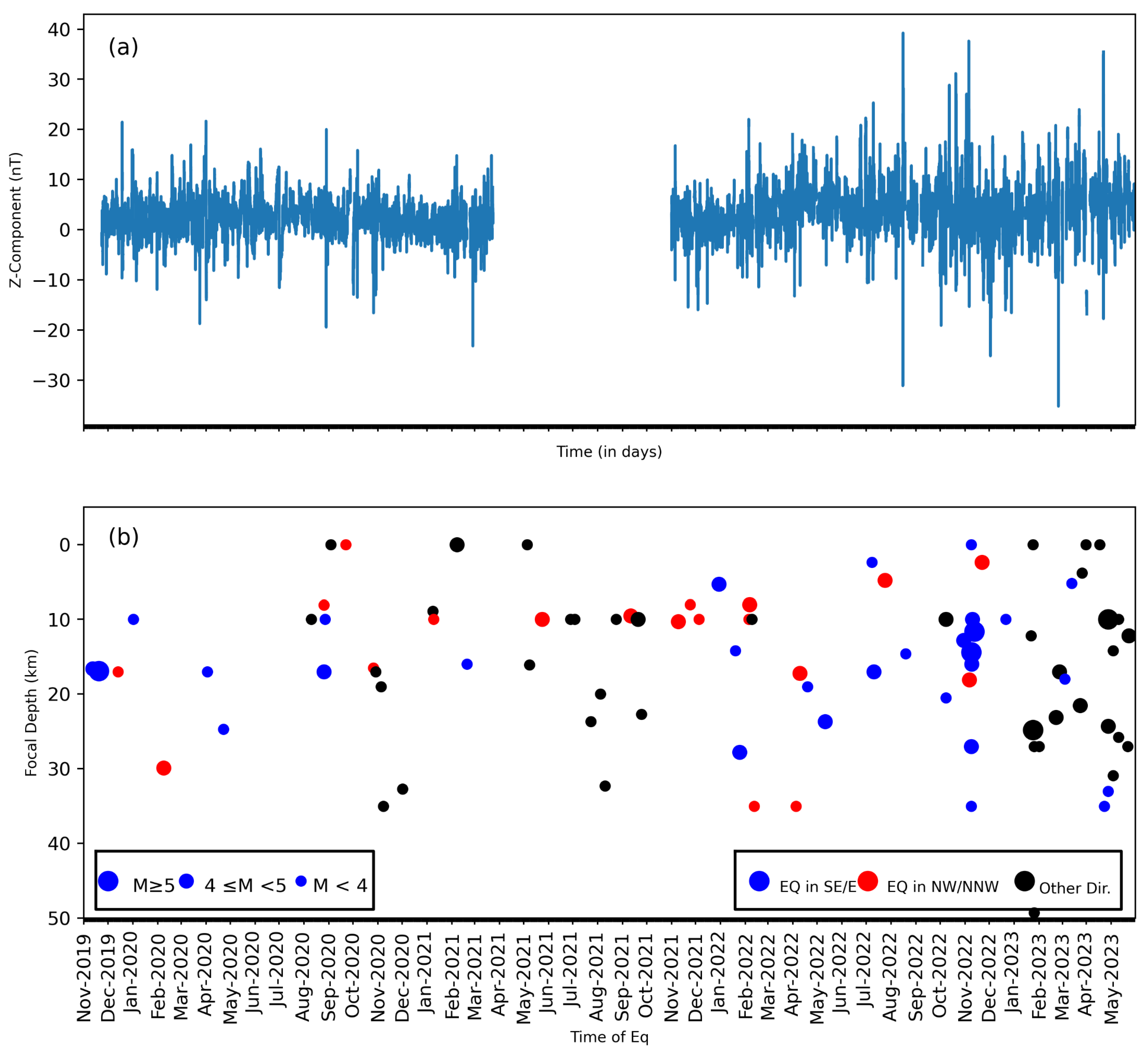
2.1. Geomagnetic Data
2.2. Earthquake Data
3. Approach Chosen for Data Analysis
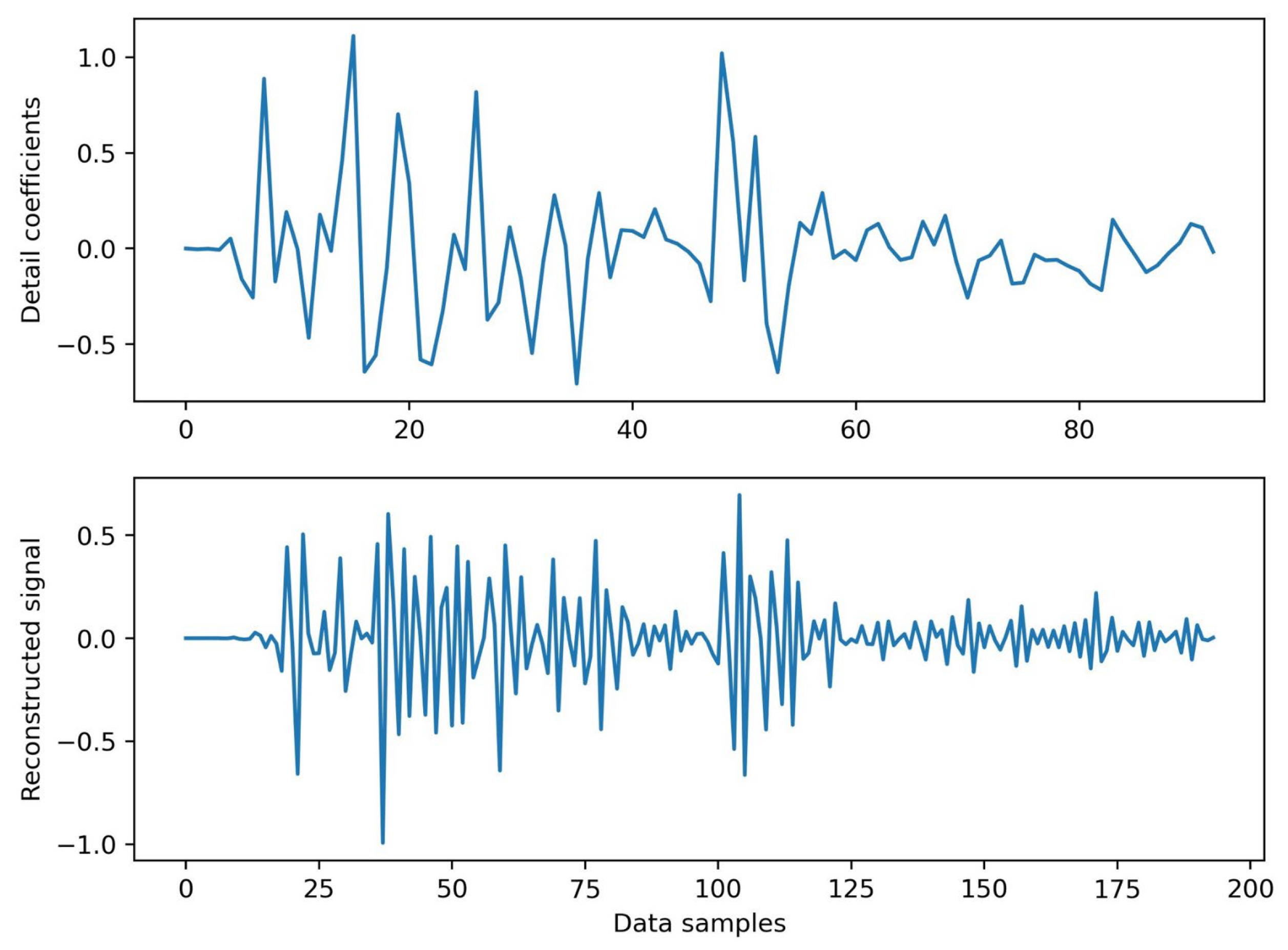
3.1. Energy in the ULF Signal from DWT
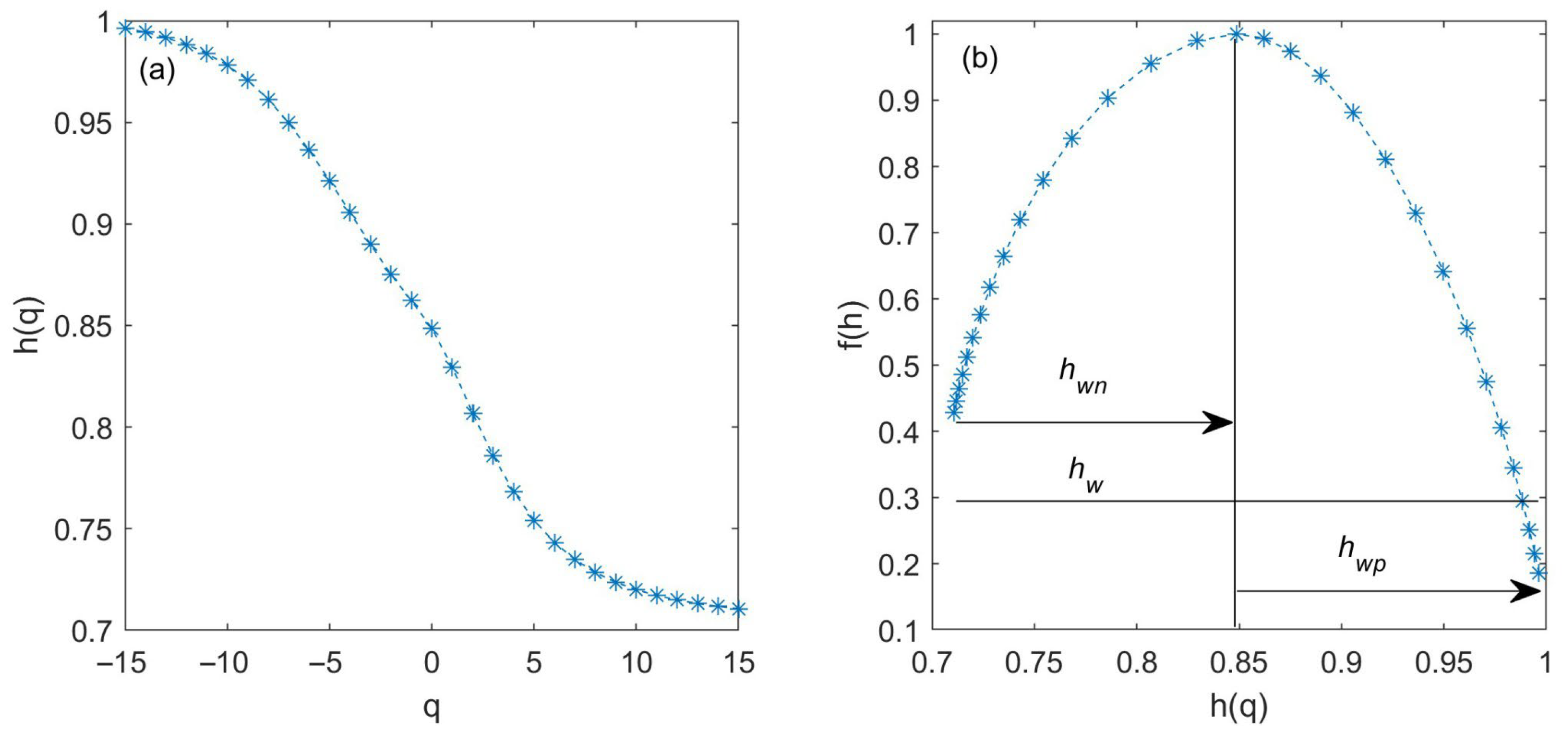
3.2. Multifractal Computations of the Geomagnetic Signal
4. Results
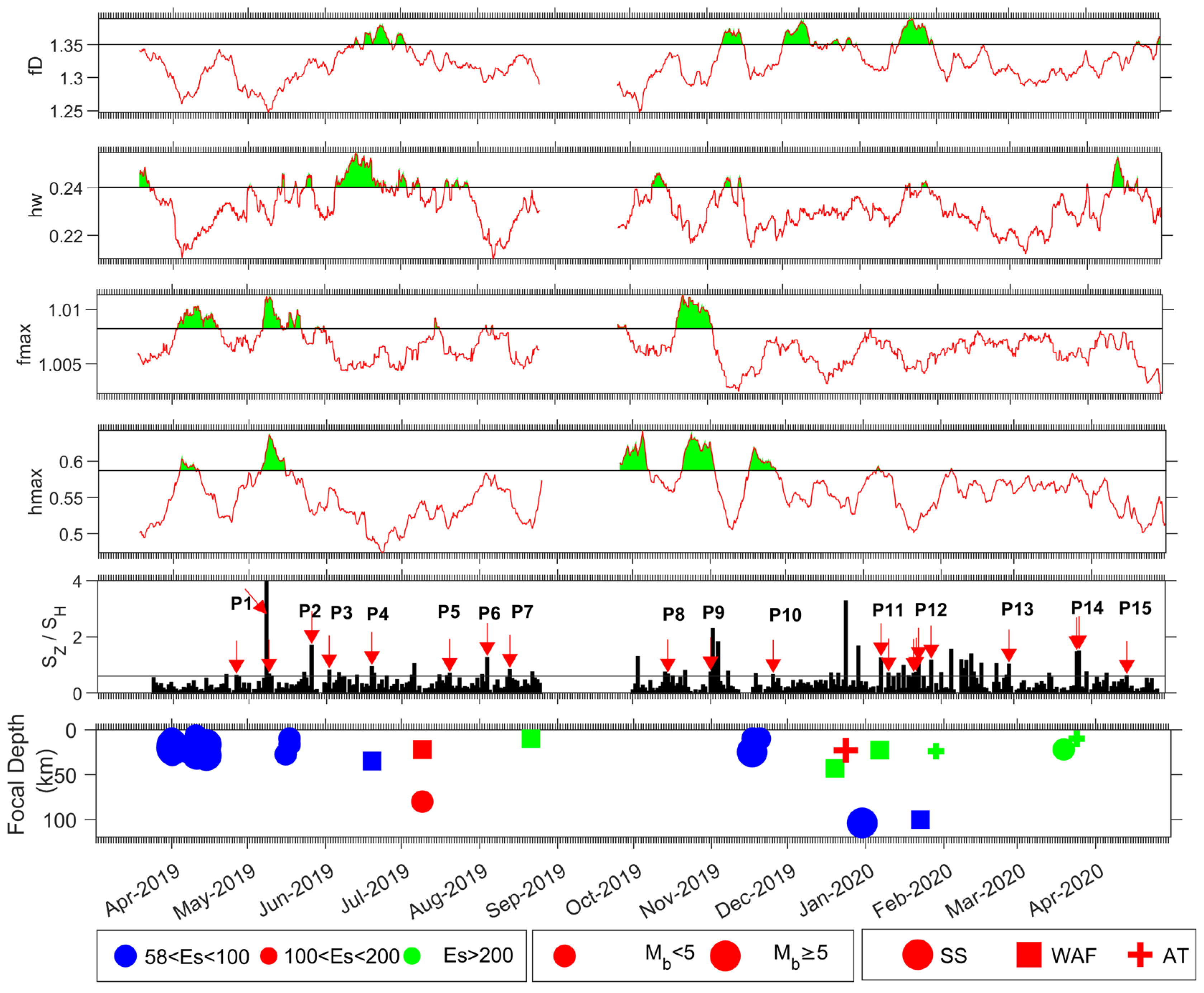
4.1. Results from the DWT
4.2. Results from the Multifractal Analysis
5. Discussion
6. Conclusions
- This study shows that the moderate earthquakes in eastern Kumaun and western Nepal have signatures of high-energy ULF emissions and high-frequency components in multifractal parameters. The earthquakes to the west and north are associated with moderate ULF emissions and a low-frequency component of fractal parameters.
- As electromagnetic emissions are affected by several mechanisms like stress concentration and the presence of fluids or other conductors, these differences reflect variations in structural and geological configurations, as well as differences in earthquake mechanisms.
- The SEM signatures of moderate earthquakes from the Andaman–Nicobar subduction zone have different characteristics compared to the current study. This implies that the chosen SEM parameters are sensitive indicators of the underlying processes. It also means that a compilation of many studies of moderate earthquakes in different tectonic regimes can lead to robust models of these signatures vis-à-vis seismo-tectonic processes.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Aitchison, J.C.; Ali, J.R.; Davis, A.M. When and where did India and Asia collide? J. Geophys. Res. Solid Earth 2007, 112, B0542. [Google Scholar] [CrossRef]
- Gansser, A. The geodynamic history of the Himalaya. In Zagros Hindu Kush Himalaya Geodynamic Evolution; American Geophysical Union: Washington, DC, USA, 1981; Volume 3, pp. 111–121. [Google Scholar]
- Lavé, J.; Avouac, J.P. Fluvial incision and tectonic uplift across the Himalayas of central Nepal. J. Geophys. Res. Solid Earth 2001, 106, 26561–26591. [Google Scholar] [CrossRef]
- Bilham, R. Himalayan earthquakes: A review of historical seismicity and early 21st century slip potential. Geol. Soc. Lond. Spec. Publ. 2019, 483, 423–482. [Google Scholar] [CrossRef]
- Gupta, H.; Gahalaut, V.K. Seismotectonics and large earthquake generation in the Himalayan region. Gondwana Res. 2014, 25, 204–213. [Google Scholar] [CrossRef]
- Angster, S.; Fielding, E.J.; Wesnousky, S.; Pierce, I.; Chamlagain, D.; Gautam, D.; Upreti, B.N.; Kumahara, Y.; Nakata, T. Field reconnaissance after the 25 April 2015 M 7.8 Gorkha earthquake. Seismol. Res. Lett. 2015, 86, 1506–1513. [Google Scholar] [CrossRef]
- Rajendran, C.P.; Sanwal, J.; John, B.; Anandasabari, K.; Rajendran, K.; Kumar, P.; Jaiswal, M.; Chopra, S. Footprints of an elusive mid-14th century earthquake in the central Himalaya: Consilience of evidence from Nepal and India. Geol. J. 2019, 54, 2829–2846. [Google Scholar] [CrossRef]
- Shanker, D.; Paudyal, H.; Singh, H.N. Discourse on seismotectonics of Nepal Himalaya and vicinity: Appraisal to earthquake hazard. Geosciences 2011, 1, 1–15. [Google Scholar]
- Kanaujia, J.; Ravi Kumar, M.; Sunilkumar, T.C.; Naresh, B.; Devi, A.; Vijayaraghavan, R.; Suresh, G.; Saha, S.; Srinivas, D.; Solomon Raju, P. Nature of the Himalayan Seismicity Belt in the Garhwal–Kumaun Segment and its tectonic implications. Seismol. Res. Lett. 2024, 95, 2386–2398. [Google Scholar] [CrossRef]
- Yadav, R.K.; Gahalaut, V.K.; Bansal, A.K.; Sati, S.P.; Catherine, J.; Gautam, P.; Kumar, K.; Rana, N. Strong seismic coupling underneath Garhwal–Kumaun region, NW Himalaya, India. Earth Planet. Sci. Lett. 2019, 506, 8–14. [Google Scholar] [CrossRef]
- Ohta, K.; Watanabe, N.; Hayakawa, M. The observation of ULF emissions at Nakatsugawa in possible association with the 2004 Mid Niigata Prefecture earthquake. Earth Planets Space 2005, 57, 1103–1108. [Google Scholar] [CrossRef]
- Pulinets, S.; Ouzounov, D. Lithosphere–Atmosphere–Ionosphere Coupling (LAIC) model—An unified concept for earthquake precursors validation. J. Asian Earth Sci. 2011, 41, 371–382. [Google Scholar] [CrossRef]
- Molchanov, O.A.; Hayakawa, M.; Oudoh, T.; Kawai, E. Precursory effects in the subionospheric VLF signals for the Kobe earthquake. Phys. Earth Planet. Inter. 1998, 105, 239–248. [Google Scholar] [CrossRef]
- Liu, J.Y.; Chen, C.H.; Chen, Y.I.; Yen, H.Y.; Hattori, K.; Yumoto, K. Seismo-geomagnetic anomalies and M ≥ 5.0 earthquakes observed in Taiwan during 1988–2001. Phys. Chem. Earth Parts A/B/C 2006, 31, 215–222. [Google Scholar] [CrossRef]
- Lei, Y.; Jiao, L.; Chen, H. Possible correlation between the vertical component of lithospheric magnetic field and continental seismicity. Earth Planets Space 2018, 70, 179. [Google Scholar] [CrossRef]
- Chen, C.H.; Liu, J.Y.; Lin, P.Y.; Yen, H.Y.; Hattori, K.; Liang, W.T.; Chen, Y.I.; Yeh, Y.H.; Zeng, X. Pre-seismic geomagnetic anomaly and earthquake location. Tectonophysics 2010, 489, 240–247. [Google Scholar] [CrossRef]
- Fujinawa, Y.; Takahashi, K.; Noda, Y.; Iitaka, H.; Yazaki, S. Remote detection of the electric field change induced at the seismic wave front from the start of fault rupturing. Int. J. Geophys. 2011, 1, 752193. [Google Scholar] [CrossRef][Green Version]
- Takla, E.M.; Yumoto, K.; Liu, J.Y.; Kakinami, Y.; Uozumi, T.; Abe, S.; Ikeda, A. Anomalous geomagnetic variations possibly linked with the Taiwan earthquake (Mw = 6.4) on 19 December 2009. Int. J. Geophys. 2011, 1, 848467. [Google Scholar] [CrossRef]
- Takla, E.M. Local time dependence of earthquakes occurrence and its possible connection with geomagnetic diurnal variations. NRIAG J. Astron. Geophys. 2022, 11, 132–141. [Google Scholar] [CrossRef]
- Fidani, C. The central Italy electromagnetic network and the 2009 L’Aquila earthquake: Observed electric activity. Geosciences 2011, 1, 3–25. [Google Scholar] [CrossRef]
- Fidani, C.; Orsini, M.; Iezzi, G.; Vicentini, N.; Stoppa, F. Electric and magnetic recordings by Chieti CIEN Station during the intense 2016–2017 seismic swarms in Central Italy. Front. Earth Sci. 2020, 8, 536332. [Google Scholar] [CrossRef]
- Xu, G.; Han, P.; Huang, Q.; Hattori, K.; Febriani, F.; Yamaguchi, H. Anomalous behaviors of geomagnetic diurnal variations prior to the 2011 off the Pacific coast of Tohoku earthquake (Mw9.0). J. Asian Earth Sci. 2013, 77, 59–65. [Google Scholar] [CrossRef]
- Han, P.; Hattori, K.; Xu, G.; Ashida, R.; Chen, C.H.; Febriani, F.; Yamaguchi, H. Further investigations of geomagnetic diurnal variations associated with the 2011 off the Pacific coast of Tohoku earthquake (Mw 9.0). J. Asian Earth Sci. 2015, 114, 321–326. [Google Scholar] [CrossRef]
- Han, P.; Hattori, K.; Huang, Q.; Hirooka, S.; Yoshino, C. Spatiotemporal characteristics of the geomagnetic diurnal variation anomalies prior to the 2011 Tohoku earthquake (Mw 9.0) and the possible coupling of multiple pre-earthquake phenomena. J. Asian Earth Sci. 2016, 129, 13–21. [Google Scholar] [CrossRef]
- Yao, X.; Feng, Z.; Teng, Y.; Wang, Y.; Zheng, Q. Geomagnetic variations associated with strong earthquakes in Yunnan area. Open J. Earthq. Res. 2017, 6, 228. [Google Scholar] [CrossRef][Green Version]
- Bulusu, J.; Arora, K.; Singh, S.; Edara, A. Simultaneous electric, magnetic and ULF anomalies associated with moderate earthquakes in Kumaun Himalaya. Nat. Hazards 2023, 116, 3925–3955. [Google Scholar] [CrossRef]
- Prajapati, R.; Arora, K. Fractal analysis of geomagnetic data to decipher pre-earthquake process in Andaman-Nicobar region, India. Nonlinear Process. Geophys. Discuss. 2024, 32, 1–21. [Google Scholar]
- Wang, Z.; Ni, Z.; Chen, S.; Su, S.; Yuan, J. Characteristics of Local Geomagnetic Field Variations and the Tectonic Stress Field Adjacent to the 21 May 2021, Ms 6.4 Yangbi Earthquake, Yunnan, China. Appl. Sci. 2022, 12, 1005. [Google Scholar] [CrossRef]
- Dologlou, E. Possible relationship between Seismic Electric Signals (SES) lead time and earthquake stress drop. Proc. Jpn. Acad. Ser. B 2008, 84, 117–122. [Google Scholar] [CrossRef]
- Freund, F. Pre-earthquake signals: Underlying physical processes. J. Asian Earth Sci. 2011, 41, 383–400. [Google Scholar] [CrossRef]
- Freund, F.; Pilorz, S. Electric currents in the Earth crust and the generation of pre-earthquake ULF signals. Front. Earthq. Predict. Stud. 2012, 464–508. [Google Scholar]
- Helman, D.S. Earth electricity: A review of mechanisms which cause telluric currents in the lithosphere. Ann. Geophys. 2013, 56, G0564. [Google Scholar]
- Helman, D.S. Seismic electric signals (SES) and earthquakes: A review of an updated VAN method and competing hypotheses for SES generation and earthquake triggering. Phys. Earth Planet. Inter. 2020, 302, 106484. [Google Scholar] [CrossRef]
- Scoville, J.; Heraud, J.; Freund, F. Pre-earthquake magnetic pulses. Nat. Hazards Earth Syst. Sci. 2015, 15, 1873–1880. [Google Scholar] [CrossRef]
- Tsutsui, M. Behaviors of electromagnetic waves directly excited by earthquakes. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1961–1965. [Google Scholar] [CrossRef]
- Ida, Y.; Hayakawa, M.; Adalev, A.; Gotoh, K. Multifractal analysis for the ULF geomagnetic data during the 1993 Guam earthquake. Nonlinear Process. Geophys. 2005, 12, 157–162. [Google Scholar] [CrossRef]
- Potirakis, S.M.; Hayakawa, M.; Schekotov, A. Fractal analysis of the ground-recorded ULF magnetic fields prior to the 11 March 2011 Tohoku earthquake (MW = 9): Discriminating possible earthquake precursors from space-sourced disturbances. Nat. Hazards 2017, 85, 59–86. [Google Scholar] [CrossRef]
- Hattori, K. ULF geomagnetic changes associated with large earthquakes. Terr. Atmos. Ocean. Sci. 2004, 15, 329–360. [Google Scholar] [CrossRef]
- Hattori, K.; Takahashi, I.; Yoshino, C.; Isezaki, N.; Iwasaki, H.; Harada, M.; Kawabata, K.; Kopytenko, E.; Kopytenko, Y.; Maltsev, P.; et al. ULF geomagnetic field measurements in Japan and some recent results associated with Iwateken Nairiku Hokubu earthquake in 1998. Phys. Chem. Earth Parts A/B/C 2004, 29, 481–494. [Google Scholar] [CrossRef]
- Hattori, K.; Han, P.; Huang, Q. Global variation of ULF geomagnetic fields and detection of anomalous changes at a certain observatory using reference data. Electr. Eng. 2013, 182, 9–18. [Google Scholar] [CrossRef]
- Han, P.; Hattori, K.; Hirokawa, M.; Zhuang, J.; Chen, C.H.; Febriani, F.; Yamaguchi, H.; Yoshino, C.; Liu, J.Y.; Yoshida, S. Statistical analysis of ULF seismomagnetic phenomena at Kakioka, Japan, during 2001–2010. J. Geophys. Res. Space Phys. 2014, 119, 4998–5011. [Google Scholar] [CrossRef]
- Warden, S.; MacLean, L.; Lemon, J.; Schneider, D. Statistical analysis of pre-earthquake electromagnetic Anomalies in the ULF Range. J. Geophys. Res. Space Phys. 2020, 125, e2020JA027955. [Google Scholar] [CrossRef]
- Chavez, O.; Millan-Almaraz, J.R.; Pérez-Enríquez, R.; Arzate-Flores, J.A.; Kotsarenko, A.; Cruz-Abeyro, J.A.; Rojas, E. Detection of ULF geomagnetic signals associated with seismic events in Central Mexico using Discrete Wavelet Transform. Nat. Hazards Earth Syst. Sci. 2010, 10, 2557–2564. [Google Scholar] [CrossRef]
- Hayakawa, M.; Ito, T.; Smirnova, N. Fractal analysis of ULF geomagnetic data associated with the Guam earthquake on August 8, 1993. Geophys. Res. Lett. 1999, 26, 2797–2800. [Google Scholar] [CrossRef]
- Smirnova, N.; Hayakawa, M.; Gotoh, K.; Volobuev, D. Scaling characteristics of ULF geomagnetic fields at the Guam seismoactive area and their dynamics in relation to the earthquake. Nat. Hazards Earth Syst. Sci. 2001, 1, 119–126. [Google Scholar] [CrossRef]
- Gotoh, K.; Hayakawa, M.; Smirnova, N. Fractal analysis of the ULF geomagnetic data obtained at Izu Peninsula, Japan in relation to the nearby earthquake swarm of June–August 2000. Nat. Hazards Earth Syst. Sci. 2003, 3, 229–236. [Google Scholar] [CrossRef]
- Smirnova, N.A.; Kiyashchenko, D.A.; Troyan, V.N.; Hayakawa, M. Multifractal approach to study the earthquake precursory signatures using the ground-based observations. Rev. Appl. Phys. 2013, 2, 58–67. [Google Scholar]
- Hattori, K.; Serita, A.; Yoshino, C.; Hayakawa, M.; Isezaki, N. Singular spectral analysis and principal component analysis for signal discrimination of ULF geomagnetic data associated with 2000 Izu Island Earthquake Swarm. Phys. Chem. Earth Parts A/B/C 2006, 31, 281–291. [Google Scholar] [CrossRef]
- Jach, A.; Kokoszka, P.; Sojka, J.; Zhu, L. Wavelet-based index of magnetic storm activity. J. Geophys. Res. Space Phys. 2006, 111, A09215. [Google Scholar] [CrossRef]
- Jaffard, S. Pointwise regularity associated with function spaces and multifractal analysis. Banach Cent. Publ. 2006, 72, 93. [Google Scholar]
- Serrano, E.; Figliola, A. Wavelet leaders: A new method to estimate the multifractal singularity spectra. Phys. A Stat. Mech. Appl. 2009, 388, 2793–2805. [Google Scholar] [CrossRef]
- Wendt, H.; Abry, P.; Jaffard, S. Bootstrap for empirical multifractal analysis. IEEE Signal Process. Mag. 2007, 24, 38–48. [Google Scholar] [CrossRef]
- Lashermes, B.; Jaffard, S.; Abry, P. Wavelet leader based multifractal analysis. In Proceedings of the (ICASSP’05) IEEE International Conference on Acoustics, Speech, and Signal Processing 2005, Philadelphia, PA, USA, 23–23 March 2005; Volume 4, pp. iv/161–iv/164. [Google Scholar]
- Wendt, H. Contributions of Wavelet Leaders and Bootstrap to Multifractal Analysis: Images, Estimation Performance, Dependence Structure and Vanishing Moments. Confidence Intervals and Hypothesis Tests. Ph.D. Thesis, Ecole Normale Supérieure de Lyon-ENS LYON, Lyon, France, 2008. [Google Scholar]
- Arora, K.; Prajapati, R. Patterns of Seismo-Electromagnetic Signatures of Moderate Earthquakes in Diverse Tectonic Settings. J. Geol. Soc. India 2025, 101, 815–820. [Google Scholar] [CrossRef]
- Harris, R.O. Geodynamic patterns of ophiolites and marginal basins in the Indonesian and New Guinea regions. Geol. Soc. Lond. Spec. Publ. 2003, 218, 481–505. [Google Scholar] [CrossRef]
- Moeremans, R.; Singh, S.C.; Mukti, M.; McArdle, J.; Johansen, K. Seismic images of structural variations along the deformation front of the Andaman–Sumatra subduction zone: Implications for rupture propagation and tsunamigenesis. Earth Planet. Sci. Lett. 2014, 386, 75–85. [Google Scholar] [CrossRef]
- Mukhopadhyay, B. Clusters of moderate size earthquakes along Main Central Thrust (MCT) in Himalaya. Int. J. Geosci. 2011, 2, 318. [Google Scholar] [CrossRef]
- Gao, Y.; Wang, D.; Wen, J.; Hu, H.; Chen, X.; Yao, C. Electromagnetic responses to an earthquake source due to the motional induction effect in a 2-D layered model. Geophys. J. Int. 2019, 219, 563–593. [Google Scholar] [CrossRef]
- Mandal, P.; Prathigadapa, R.; Srinivas, D.; Saha, S.; Saha, G. Evidence of structural segmentation of the Uttarakhand Himalaya and its implications for earthquake hazard. Sci. Rep. 2023, 13, 2079. [Google Scholar] [CrossRef]
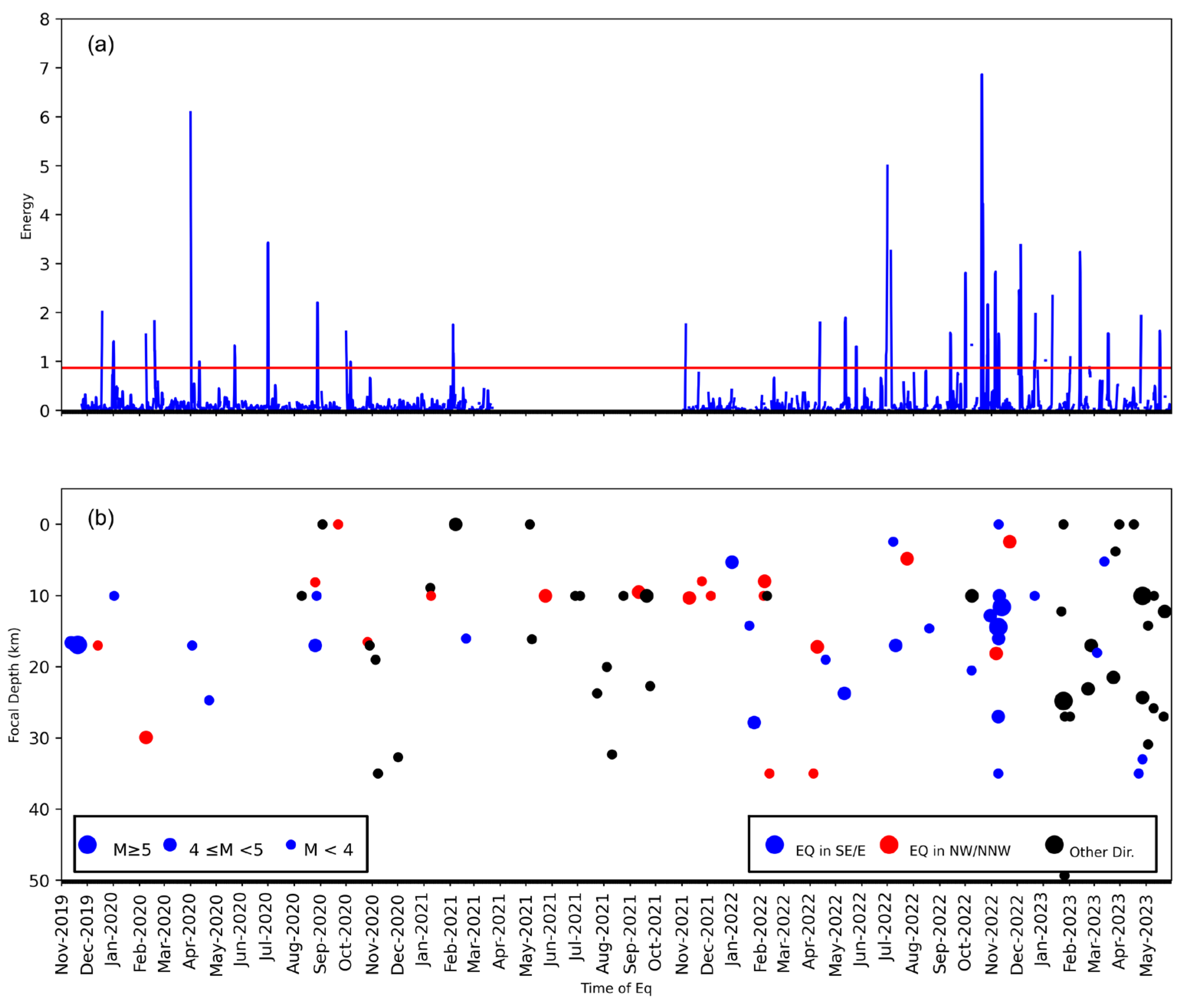
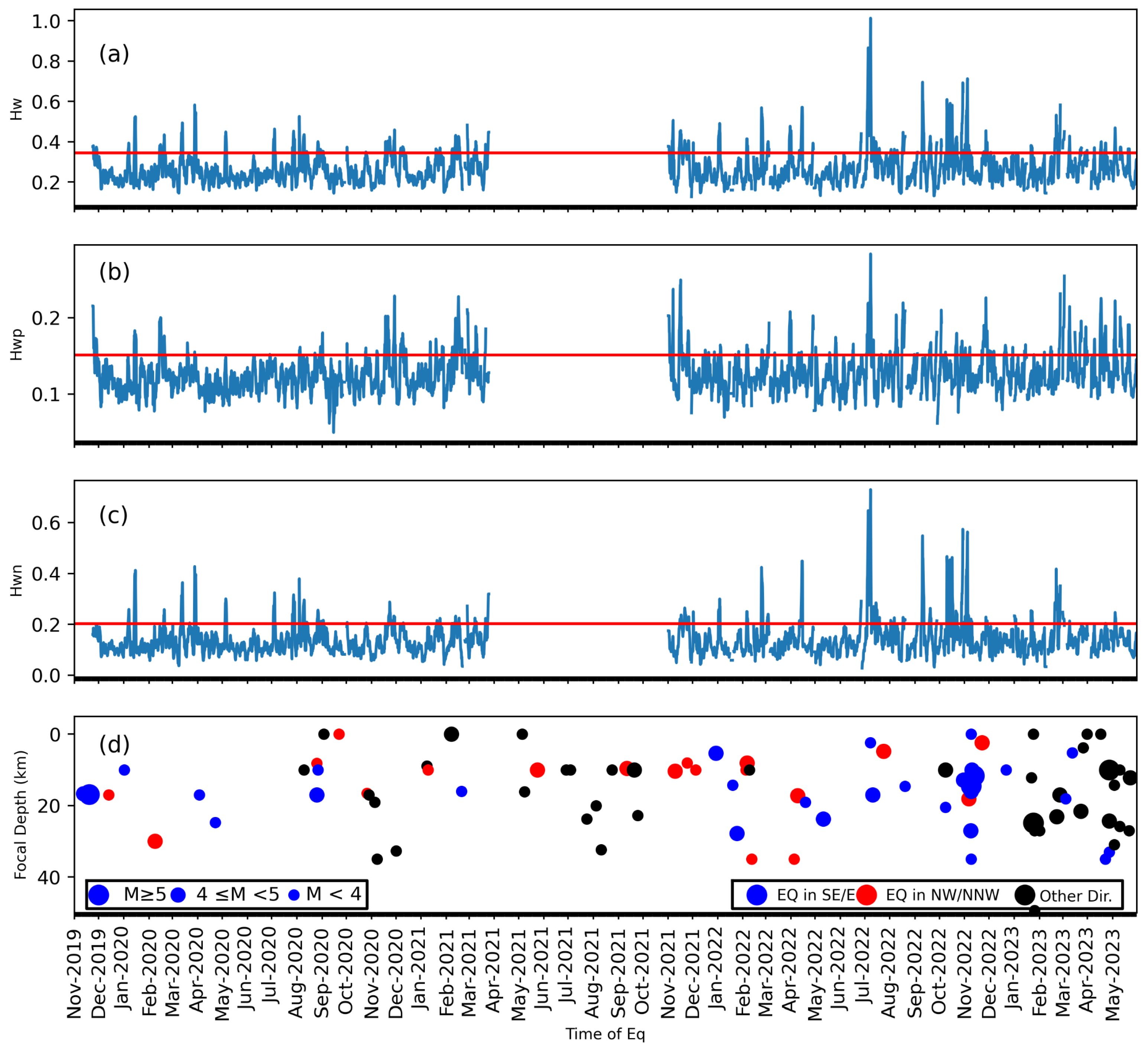
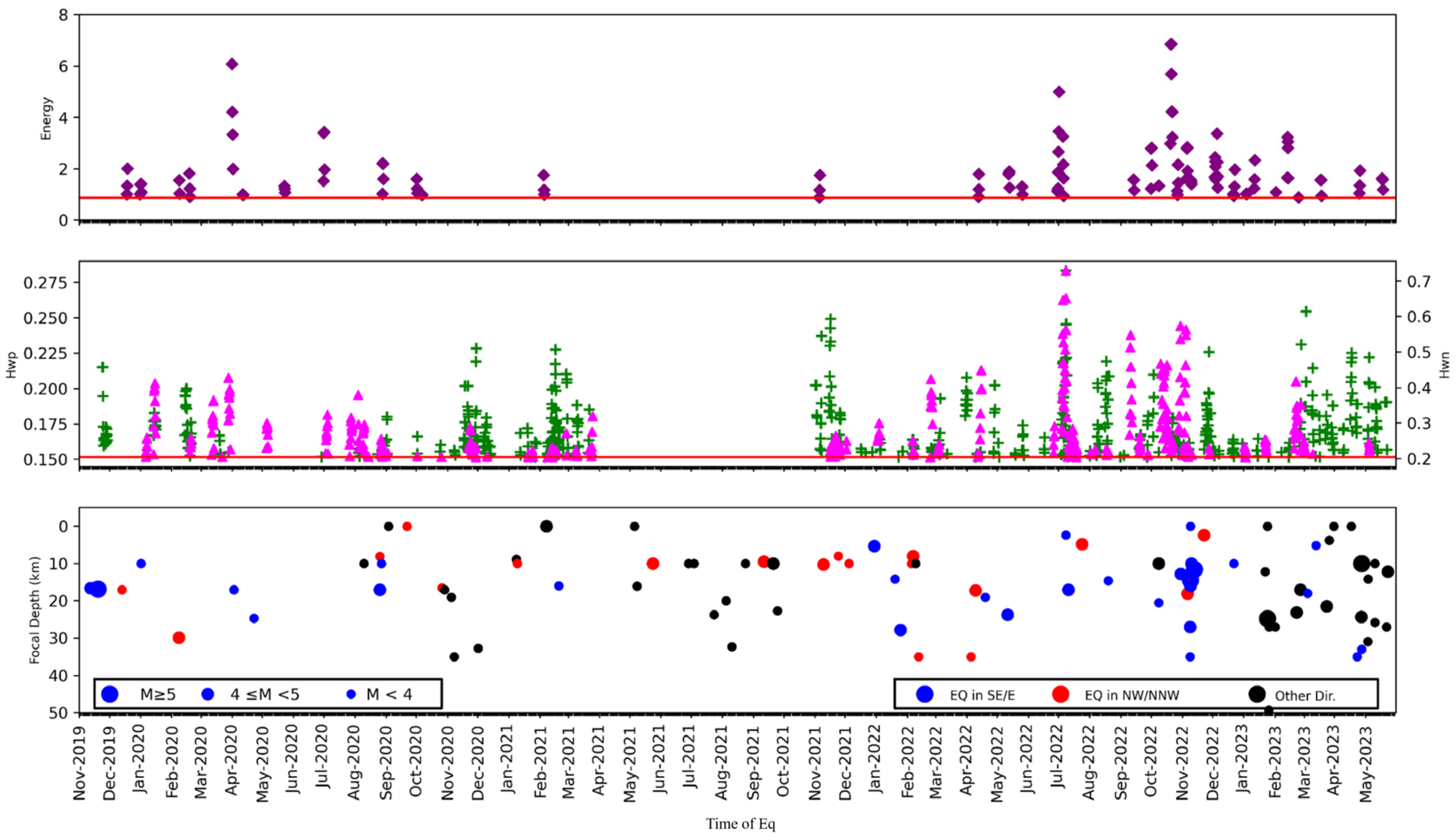
| Date | fD (km) | Mag. | Ep_Dist | Azimuth /Fault | DWT Response | Amplitude /ULF Energy | Fractal Response | Remarks |
|---|---|---|---|---|---|---|---|---|
| 12-11-2019 | 16.6 | 4.4 | 26.77 | E/MCT | Data sort | -- | -- | Prior data are not available |
| 19-11-2019 | 16.9 | 5.3 | 142.93 | SE/MCT | Data sort | -- | -- | Prior data are not available |
| 13-12-2019 | 17 | 3.8 | 71.98 | NW/MCT | Data sort | -- | -- | Prior data are not available |
| 01-01-2020 | 10 | 3.6 | 78.25 | SE/MCT | 30-Dec-2019 1 prior | 2.10, 1.35 | Higher amplitude for SE Eq | |
| 08-02-2020 | 29.9 | 4.6 | 3.22 | Over_st/MCT | 7 Feb-2020 1 prior | 1.64 | 14–16 Jan; 15 d priors,, , | Smaller amp./ also appear with and Hw due to large mag. and smallest Ep_dist. |
| 02-04-2020 | 17 | 3.9 | 117.87 | SE/MCT | 31 Mar–01 Apr; 2 prior | 6.21 | 28–29 Mar; 4 prior, , (dom);12–13 Mar; 15 d prior, , | Large amp/, for SE Eq |
| 22-04-2020 | 24.7 | 3.6 | 126.24 | SE/SAT | Nil | Nil | No corresponding SEM signatures | |
| 09-08-2020 | 10 | 3.6 | 114.63 | NNE/Unkn. | 3–4 Aug, 5 d prior, , ; 28–29 Jul, 11 d prior, , ; simul., and | |||
| 25-08-2020 | 8.1 | 3.5 | 116.42 | NW/MCT | No corresponding signature, possibly due to SE Eq together | |||
| 25-08-2020 | 17 | 4.2 | 116.88 | SE/MCT | Same as above | |||
| 27-08-2020 | 10 | 3.8 | 87.88 | SSE/MCT | 1 d post; | 2.16 | 1 d post; and ; | Eq. in southern region; large and appear |
| 03-09-2020 | 0 | 3.5 | 152.70 | S/Unkn | 6 prior; | 2.16 | 8 prior, , | Same as above |
| 21-09-2020 | 0 | 3.6 | 196.87 | NW/STDS | nil | nil | No corresponding signature | |
| 26-10-2020 | 16.5 | 3.9 | 247.42 | NW/Unkn | nil | nil | No corresponding signature, possibly due to subsequent Eqs in different directions | |
| 28-10-2020 | 17 | 3.8 | 118.20 | SW/MCT | nil | nil | Same as above remark | |
| 04-11-2020 | 19 | 3.5 | 86.93 | SW/MCT | nil | nil | Same as above remark | |
| 07-11-2020 | 35 | 3.5 | 84.18 | NE/Unkn | nil | nil | Same as above remark | |
| 01-12-2020 | 32.7 | 3.7 | 189.16 | W/HFT | 27–30 Nov, 4 d prior, ; | |||
| 08-01-2021 | 8.9 | 3.6 | 16.03 | Over_st/MCT | nil | 6–10 ; ~30 d prior | Not considered as an SEM signature due to unusual and large duration (~5 days) before Eq | |
| 09-01-2021 | 10 | 3.8 | 162.45 | NW/MCT | nil | No corresponding signatures | ||
| 07-02-2021 | 0 | 4.3 | 90.90 | NE/Unkn | 4 Feb, 3 d prior | 1.81 | 25 Jan ; 12 d prior | No corresponding signatures |
| 19-02-2021 | 16 | 3.6 | 19.75 | SSE/overst /MCT | 12–17 , , 7 d prior | SE earthquake; and | ||
| 05-05-2021 | 0 | 3.5 | 71.36 | Data gap | ||||
| 08-05-2021 | 16.1 | 3.5 | 57.13 | Data gap | ||||
| 23-05-2021 | 10 | 4.2 | 114.71 | Data gap | ||||
| 28-06-2021 | 10 | 3.8 | 7.806 | Data gap | ||||
| 02-07-2021 | 10 | 3.9 | 158.15 | Data gap | ||||
| 23-07-2021 | 23.7 | 3.6 | 146.38 | Data gap | ||||
| 04-08-2021 | 20 | 3.5 | 228.91 | Data gap | ||||
| 10-08-2021 | 32.3 | 3.6 | 197.34 | Data gap | ||||
| 23-08-2021 | 10 | 3.7 | 119.28 | Data gap | ||||
| 11-09-2021 | 9.5 | 4.6 | 83.70 | Data gap | ||||
| 20-09-2021 | 10 | 4.3 | 81.71 | Data gap | ||||
| 24-09-2021 | 22.7 | 3.6 | 41.39 | Data gap | ||||
| 09-11-2021 | 10.3 | 4.6 | 244.65 | NW/Unkn | 5–6 Nov, 4 d prior | 1.81 | 5–6 Nov, 4 prior, , | Small amp./ , for NE Eq |
| 24-11-2021 | 8 | 3.6 | 241.28 | NW/Unkn | 15–17 Nov, 9 prior, (strong), | Only and for NE Eq | ||
| 04-12-2021 | 10 | 3.8 | 131.09 | NW/MCT | nil | 15–17 Nov, 18 prior, (strong), | Only and for NE Eq | |
| 29-12-2021 | 5.3 | 4.4 | 58.15 | SE/MCT | nil | nil | No corresponding signature for SEE Eq | |
| 19-01-2022 | 14.2 | 3.6 | 93.88 | SE/MCT | 2–3 Jan , 17 d prior | Only , and component for SE Eq | ||
| 24-01-2022 | 27.8 | 4.1 | 42.33 | SE/MCT | -- | - | - | - |
| 04-02-2022 | 10 | 3.5 | 208.31 | NW/Unkn | 5–6 Feb, h-all, 1 d post | extra with and correspond to 4 subsequent Eqs in northern direction | ||
| 06-02-2022 | 8 | 4 | 245.54 | NW/STDS | 5–6 Feb, h-all, 1 d prior | For above comment | ||
| 09-02-2022 | 10 | 3.5 | 130.00 | NE/Unkn | 5–6 Feb, h-all, 4 d prior | For above comment | ||
| 11-02-2022 | 35 | 3.8 | 126.94 | NW/MCT | 5–6 Feb, h-all, 6 d prior | For above comment | ||
| 05-04-2022 | 35 | 3.8 | 146.75 | NNW/Unkn | nil | nil | 30–31 Mar, , , 6 d prior | no amp; and for NW Eq; for next Eq also |
| 09-04-2022 | 17.2 | 4.3 | 191.46 | NW/MCT | nil | nil | 30–31 Mar, , | Above remark same |
| 19-04-2022 | 19 | 3.5 | 75.02 | SE/MCT | 12–13 Apr, 7 d prior | 1.81 | 14–15 Apr, 5 d prior, (strong), | small amp, and for SE Eq due to small magnitude |
| 11-05-2022 | 23.7 | 4.8 | 49.55 | SE/MCT | 12 May, 1 d post; 25 May, 14 d prior | 1.99 | 24–25 May, 13 d prior, | small amplitude, only for SE Eq due to large magnitude of Eq |
| 08-07-2022 | 2.4 | 3.9 | 15.08 | Over_stE/ MCT | 29 Jun–5 Jul, 10 d prior | 5.4 | 3–8 Jul, 5 d prior, h-all | moderate magnitude; large amp. and hall, unique from other SE Eq possibilities due to more eastern Eq and moderate magnitude |
| 10-07-2022 | 17 | 4 | 93.84 | SE/MCT | 29 Jun–5 Jul, 12 d prior | 5.40 | 3–8 Jul, 7 d prior, h-all | |
| 24-07-2022 | 4.8 | 4 | 161.2 | NW/MCT | 29 Jun–5 Jul, 26 d prior | 5.4 | 3–8 Jul, 21 d prior, h-all | not considered for SEM due to unusually large number of prior days |
| 19-08-2022 | 14.6 | 3.7 | 24.65 | Overst_SE/ MCT | nil | 8 Aug, 11 prior, ; 15–20 Aug, 4 d prior, (strong) | no amp., and SEM anomaly for SE Eq due to small mag Eq | |
| 08-10-2022 | 20.5 | 3.7 | 16.72 | Overst_SE/ MCT | 31 Sep–1 Oct, 9 d prior | 2.8 | 2–5 Oct, 6 d prior; 10–16, , 2 d post | large amp.; SE Eq, small to large mag. Eq, also present with and , possibly due to more eastern Eqs present (for mod and large mag. Eqs) |
| 08-10-2022 | 10 | 4.9 | 39.07 | ESE/MCT | 31 Sep–1 Oct, 9 d prior | 2.8 | 2–5 Oct, 6 d prior; 10–16, , 2 d post | |
| 09-10-2022 | 10 | 3.6 | 179.4 | NE/Unkn | 31 Sep–1 Oct, 10 d prior | 2.8 | 2–5 Oct, 7 d prior; 10–16, , 3 d post | |
| 30-10-2022 | 12.8 | 4.4 | 121.4 | SEE/MCT | 20–22 Oct, 8 d prior; 28 Oct, 2 prior | 6.91, 2.10 | 2–5 Oct, 28 d prior; 10–16, , 20 d prior; 28–30 Oct,2 d prior, | large amp., mod mag., also present with and Eqs, possibly due to more eastern Eqs being present |
| 06-11-2022 | 18.1 | 4.5 | 152.6 | NW/MCT | 5–6 Nov, 1 prior, | 2.86 | 3–4 Nov, 3 d prior, (strong), , | not considered for this Eq due to subsequent dominant Eq in SE direction |
| 08-11-2022 | 27 | 4.7 | 152.4 | SEE/MCT | 5–6 Nov, 3 prior, | 2.86 | 3–4 Nov, 5 d prior, (strong), , | |
| 08-11-2022 | 35 | 3.5 | 149.4 | SE/MBT | 5–6 Nov, 3 prior, | 2.86 | 3–4 Nov, 5 d prior, (strong), , | |
| 08-11-2022 | 14.4 | 5.9 | 143.2 | SE/MCT | 5–6 Nov, 3 prior, | 2.86 | 3–4 Nov, 5 d prior, (strong), , | small to mod. mag. Eq in SE directionLarge amp, and Hw present for SE Eqs |
| 08-11-2022 | 10 | 3.8 | 105.9 | SE/MCT | 5–6 Nov, 3 prior, | 2.86 | 3–4 Nov, 5 d prior, (strong), , | |
| 08-11-2022 | 0 | 3.6 | 172.4 | SE/MCT/STDS | 5–6 Nov, 3 prior, | 2.86 | 3–4 Nov, 5 d prior, (strong), , | |
| 09-11-2022 | 16 | 4.2 | 32.04 | stsn SE/MCT | 9 Nov. Simultaneous | 1.58 | 3–4 Nov, 6 d prior, (strong), , | small amp, mod. magnitude Eq; and for SE Eq |
| 09-11-2022 | 10 | 4.1 | 163.0 | SE/MBT | 9 Nov. Simultaneous | 1.58 | 3–4 Nov, 6 d prior, (strong), | |
| 12-11-2022 | 11.6 | 5.3 | 142.5 | SE/MCT | 9 Nov. 3 d prior | 1.58 | 3–4 Nov, 9 d prior, (strong), , | |
| 22-01-2023 | 12.2 | 3.5 | 26.41285188 | SEE/MCT | 3 Jan, 13–14 Jan | 1.56, 3 | 30 Dec–2 Jan, and ; 13–14 hwp; 21–24 | small to mod amp.; , —very small to mod. small mag. Eq |
| 24-01-2023 | 24.8 | 5.6 | 175.1345405 | SEE/MCT | 3 Jan, 13–14 Jan | 1.56, 3 | 30 Dec–2 Jan, and 13–14 hwp; 21–24 hwn | small to mod amp; , —very small to mod. mag. Eq |
| 24-01-2023 | 0 | 3.6 | 160.9061784 | NEE/STDS | 3 Jan, 13–14 Jan | 1.56, 3 | 30 Dec–2 Jan, and ; 13–14 hwp; 21–24 hwn | small to mod amp; , —very small to mod. small mag. Eq |
| 25-01-2023 | 49.3 | 3.6 | 171.3197248 | SEE/MCT | 3 Jan, 13–14 Jan | 1.56, 3 | 30 Dec–2 Jan, and ; 13–14 hwp; 21–24 | small to mod amp; , —very small to mod. small mag Eq |
| 26-01-2023 | 27 | 3.5 | 148.1686039 | SEE/MCT | 3 Jan, 13–14 Jan | 1.56, 3 | 30 Dec–2 Jan, and ; 13–14 hwp;21–24 | small to mod amp; , —very small to mod. small mag. Eq |
| 01-02-2023 | 27 | 3.5 | 174.3250963 | SEE/MCT | 01-Feb | 1.51 | ---- | small amp, small mag. Eq |
| 22-02-2023 | 23.1 | 4.7 | 174.4369709 | SEE/MCT | 15–18 Feb, | 4 | 15–18 Feb ; 21–24 | large mag., , hwn (mod), mod. mag. Eq |
| 26-02-2023 | 17 | 4 | 115.7151921 | SEE/unknown | --- | 25–26, Feb , | (mod), (strong), mod. mag. Eq | |
| 03-03-2023 | 18 | 3.7 | 147.893641 | SE/Unknown | --- | 1–3 Mar | (strong), small mag. Eq | |
| 13-03-2023 | 5.2 | 3.7 | 214.5163843 | SE/Unknown | --- | 8–12 Mar | (strong), small mag. Eq | |
| 24-03-2023 | 21.5 | 4 | 185.9171992 | SEE/MCT | 16–17 mar | 2.8 | 23–25 Mar, | mod amp, (mod), mod. mag. Eq |
| 26-03-2023 | 3.8 | 3.7 | 174.9520327 | SEE/MCT | 16–17 mar | 2.8 | 23–25 Mar, | mod amp, (mod), small mag. Eq |
| 31-03-2023 | 0 | 3.8 | 180.7622673 | NEE/STDS | 28–31 Mar, | (strong), small mag. Eq | ||
| 17-04-2023 | 0 | 3.6 | 252.3814862 | NE/MCT | --- | 8–10 Apr, ; 15–18 Apr | (strong), small mag. Eq | |
| 23-04-2023 | 35 | 3.5 | 177.0987389 | SE/HFT | --- | 8–10 Apr, 15–18 Apr | (strong), small mag. Eq | |
| 27-04-2023 | 24.3 | 4.4 | 161.6058988 | SEE/MCT | 22–24 Apr | 2.2 | 21–23 | mod amp, (mod), mod mag. Eq |
| 27-04-2023 | 10 | 5.1 | 168.7926929 | SEE/MCT | 22–24 Apr | 2.2 | 21–23 | mod amp, (mod), large mag. Eq |
| 27-04-2023 | 33 | 3.6 | 147.0693867 | East/STDS | 22–24 Apr | 2.2 | 21–23 | mod amp, (mod), large mag. Eq |
| 28-04-2023 | 10 | 4.2 | 131.4541371 | SEE/MCT | 22–24 Apr | 2.2 | 21–23 | mod amp, (mod), mod mag. Eq |
| 01-05-2023 | 68.5 | 3.5 | 191.3260161 | SEE/MCT | --- | 1–5 May , small | (strong), small mag. Eq | |
| 04-05-2023 | 30.9 | 3.6 | 87.50638019 | NE/MCT | --- | 1–5 May , small | (strong), small mag. Eq | |
| 04-05-2023 | 14.2 | 3.7 | 163.273757 | SEE/MCT | --- | 1–5 May , small | (strong), small mag. Eq | |
| 10-05-2023 | 25.8 | 3.8 | 155.5813625 | SEE/MCT | --- | 9–12 | (mod), small mag. Eq | |
| 11-05-2023 | 10 | 3.6 | 55.14957113 | SEE/MCT | --- | 9–12 | (mod), small mag. Eq | |
| 22-05-2023 | 27 | 3.5 | 157.1302744 | SEE/MCT | 16–14 May | 1.53 | 19–21 | small mag, (mod), small mag. Eq |
| 23-05-2023 | 12.2 | 4.2 | 132.3489941 | SEE/MCT | 16–14 May | 1.53 | 19–21 | small mag, (mod), mod mag. Eq |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Prajapati, R.; Arora, K. Geomagnetic Signatures of Moderate Earthquakes from Kumaun Himalaya, India. Geosciences 2025, 15, 365. https://doi.org/10.3390/geosciences15090365
Prajapati R, Arora K. Geomagnetic Signatures of Moderate Earthquakes from Kumaun Himalaya, India. Geosciences. 2025; 15(9):365. https://doi.org/10.3390/geosciences15090365
Chicago/Turabian StylePrajapati, Rahul, and Kusumita Arora. 2025. "Geomagnetic Signatures of Moderate Earthquakes from Kumaun Himalaya, India" Geosciences 15, no. 9: 365. https://doi.org/10.3390/geosciences15090365
APA StylePrajapati, R., & Arora, K. (2025). Geomagnetic Signatures of Moderate Earthquakes from Kumaun Himalaya, India. Geosciences, 15(9), 365. https://doi.org/10.3390/geosciences15090365





