State-of-the-Art Review and Prospect of Modelling the Dynamic Fracture of Rocks Under Impact Loads and Application in Blasting
Abstract
1. Introduction
2. Peculiarities of Dynamic Fracture of Rocks Under Impact Loads
3. State-of-the-Art Review of Modelling Rock Dynamic Fracture and Blasting with Various Computational Mechanics Methods
3.1. Modelling Dynamic Fracture in Rock Dynamic Experiments Using Finite Element Method
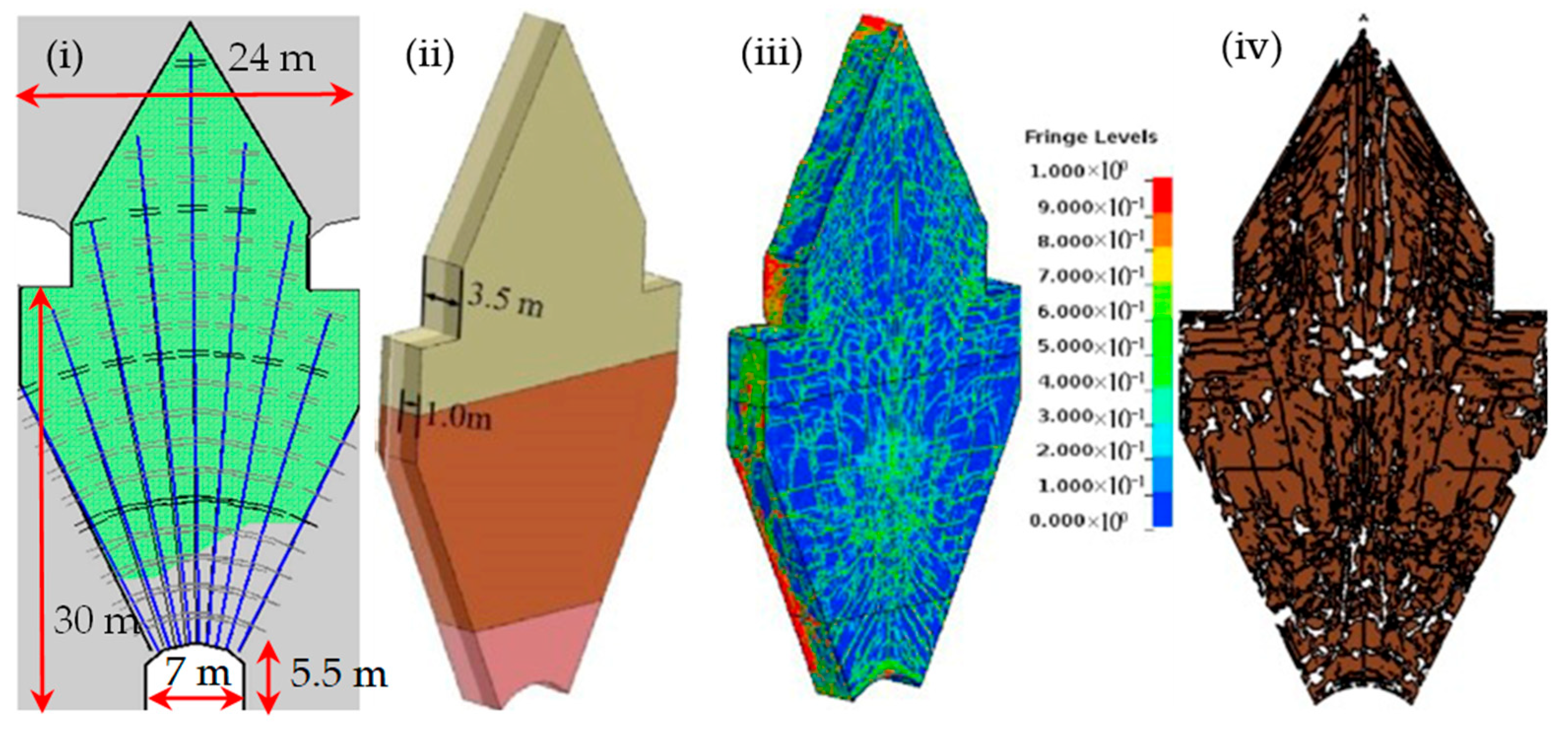
3.2. Modelling Dynamic Fracture in Rock Blasting Using Finite Element Method
3.3. Modelling Dynamic Fracture in Dynamic Tests Using Discrete Element Method
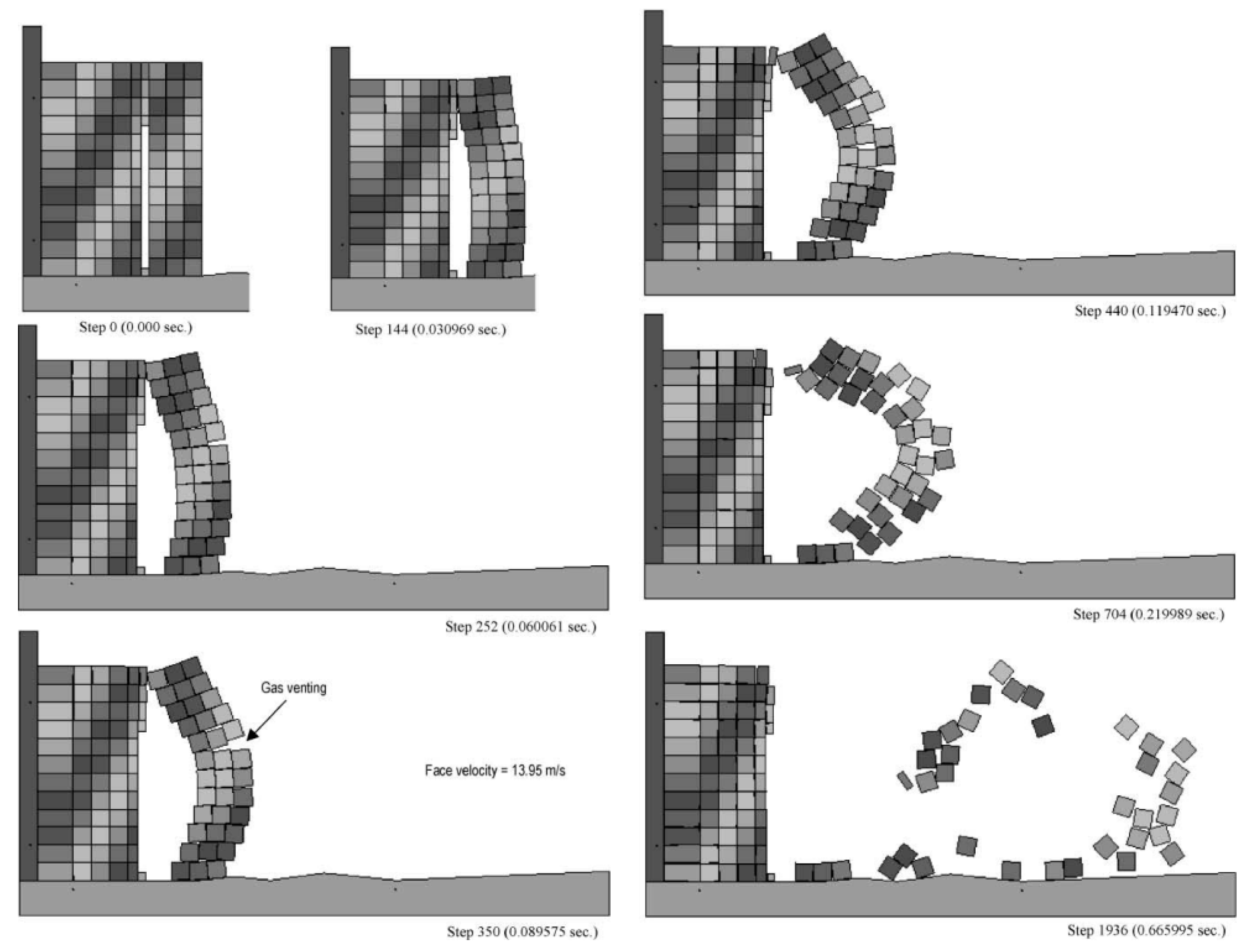
3.4. Modelling Dynamic Fracture in Rock Blasting Using the Discrete Element Method
3.5. Modelling Dynamic Fracture Using the Combined Finite–Discrete Element Method
3.5.1. Review of the Development of the Combined Finite–Discrete Element Method
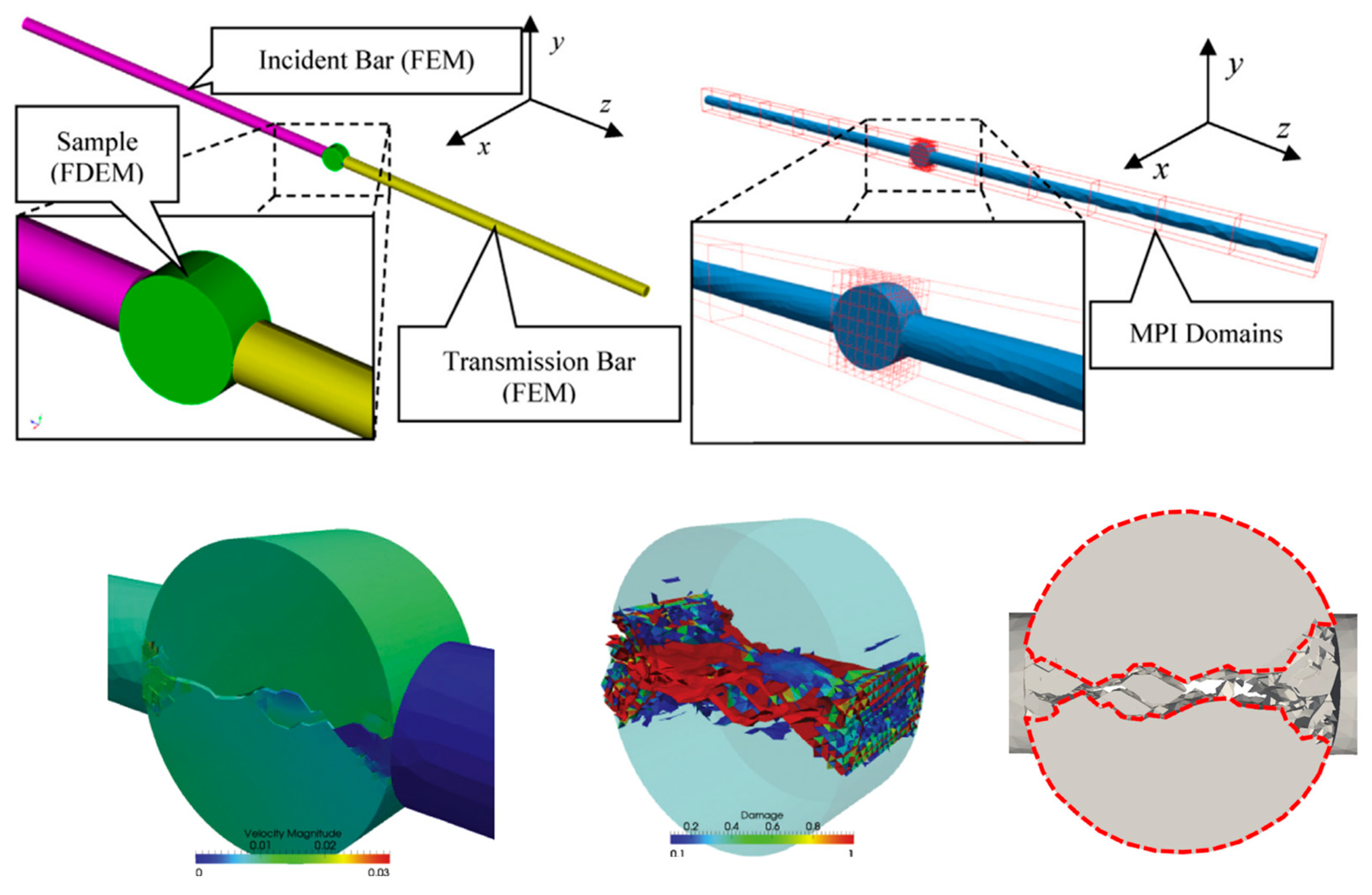
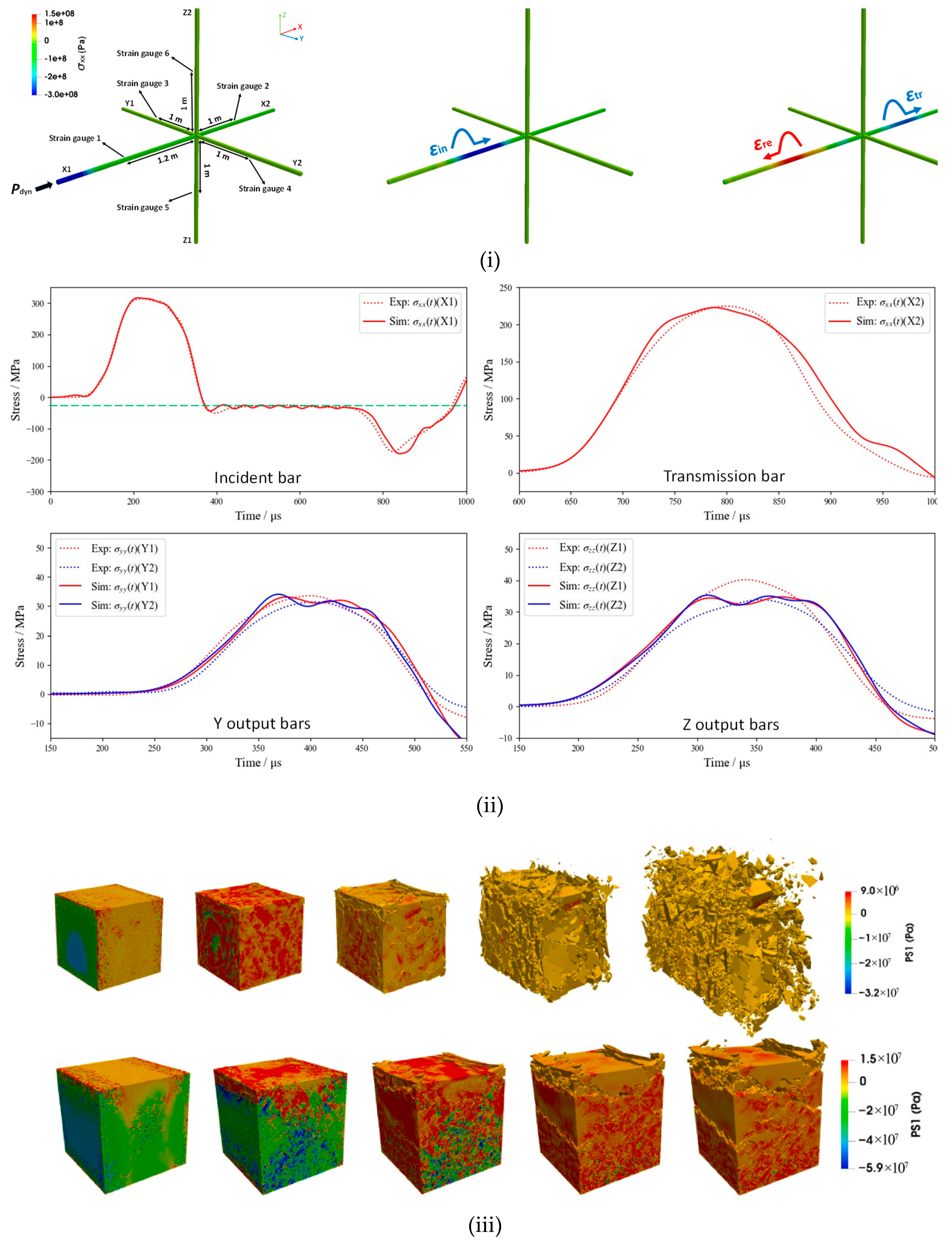
3.5.2. Review of Modelling Dynamic Fracture in Rock Dynamic Tests Using FDEM
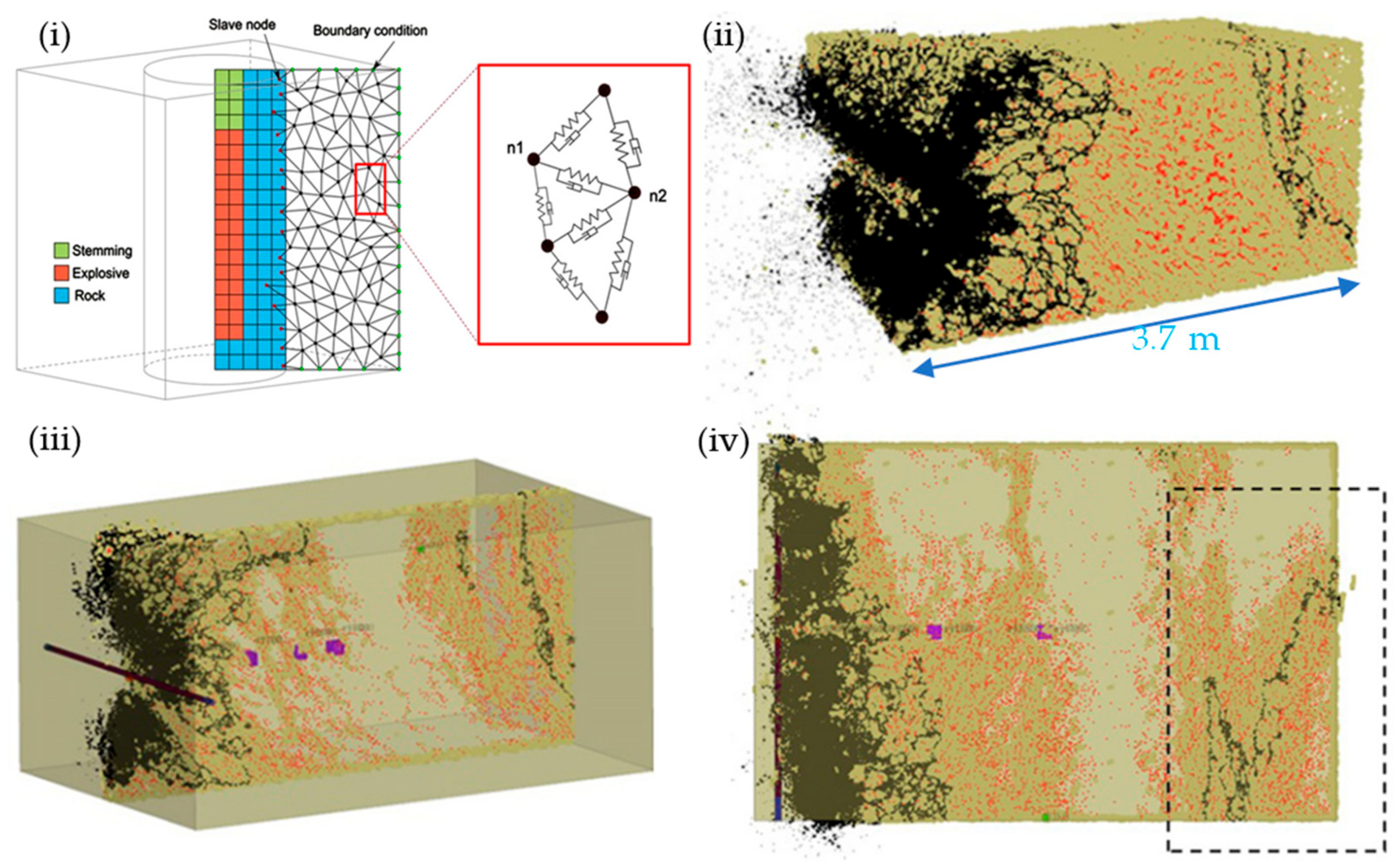
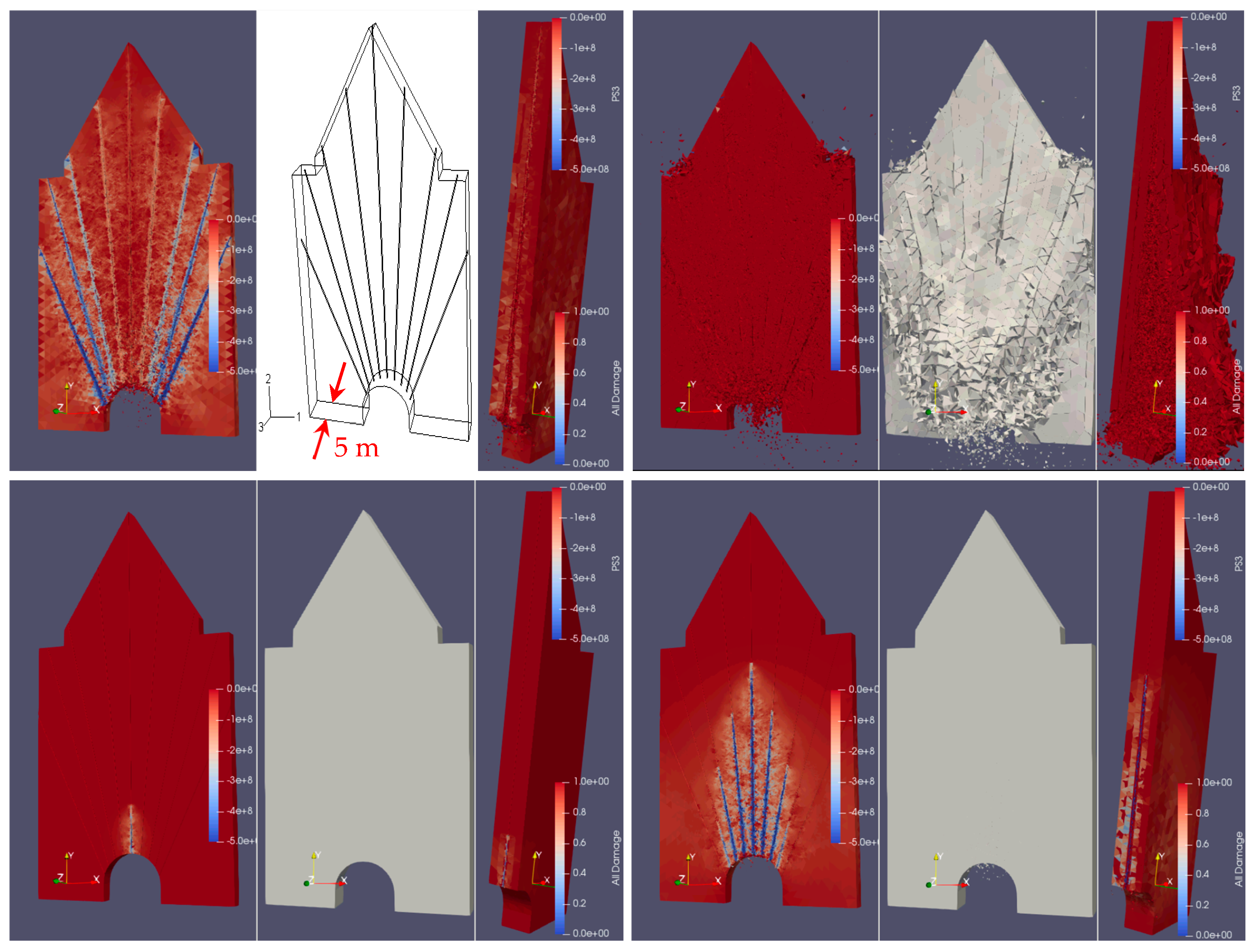
3.5.3. Review of Modelling Rock Dynamic Fracture by Blasting Using FDEM
3.6. Modelling Rock Dynamic Fracture and Blasting Using Other Numerical Methods
4. Discussions and Prospects of Modelling Rock Dynamic Fractures and Blasting
4.1. Discussions and Research Gaps in Modelling Rock Dynamic Fracture
4.1.1. Research Gaps in Modelling the Dynamic Properties of Rocks and Discontinuities
4.1.2. Research Gaps in Modelling the Heterogeneity of Rocks Under Dynamic Loads
4.1.3. Research Gaps in Modelling Existing Discontinuities and New Fractures in 3D
4.1.4. Research Gaps in Modelling the Detonation of Explosives and Detonation-Induced Gas Flow Through Fracturing Rock Mass
4.1.5. Research Gaps in Modelling the Multiphysical Coupling Process in Rock Blasting
4.2. Hybrid Finite-Discrete Element Method (HFDEM) for Modelling Rock Dynamic Fracture and Its Application in Rock Blasting
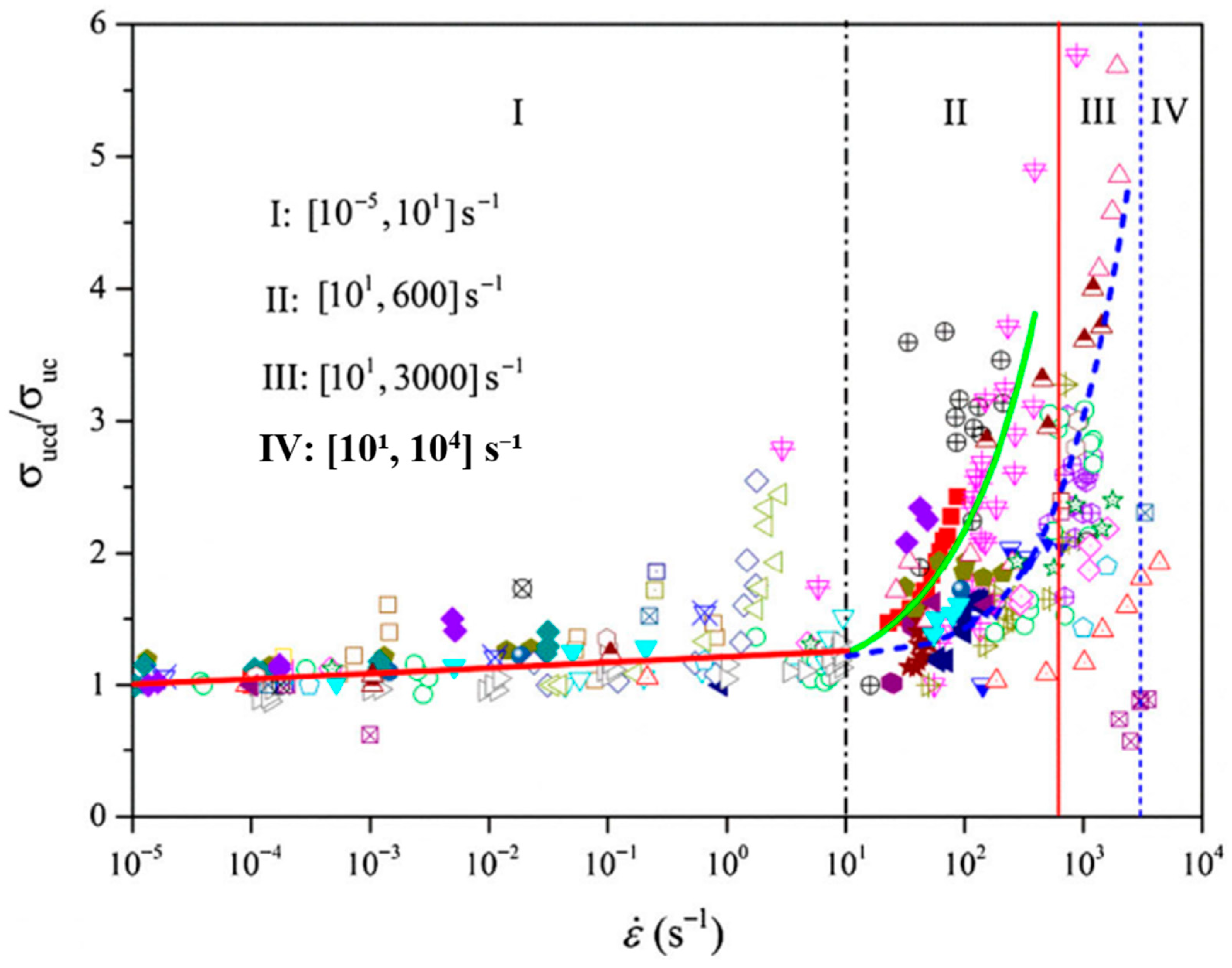
4.2.1. Modelling Loading Rate Effects on Rock Dynamic Behaviour
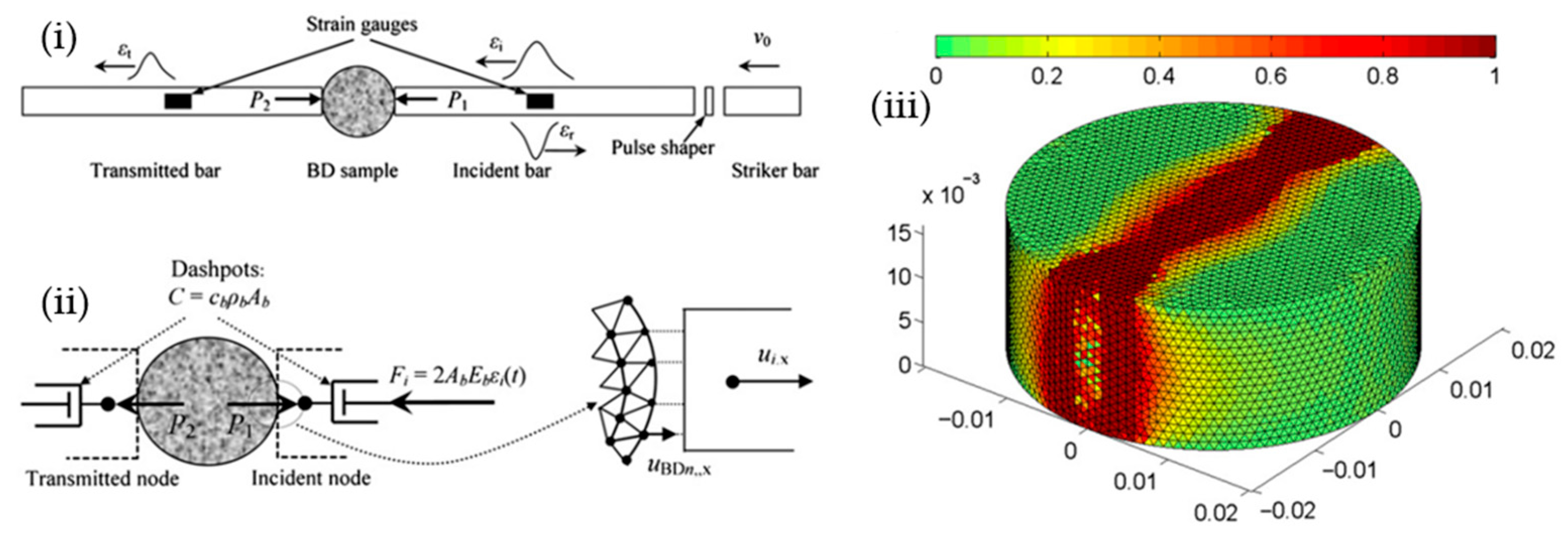
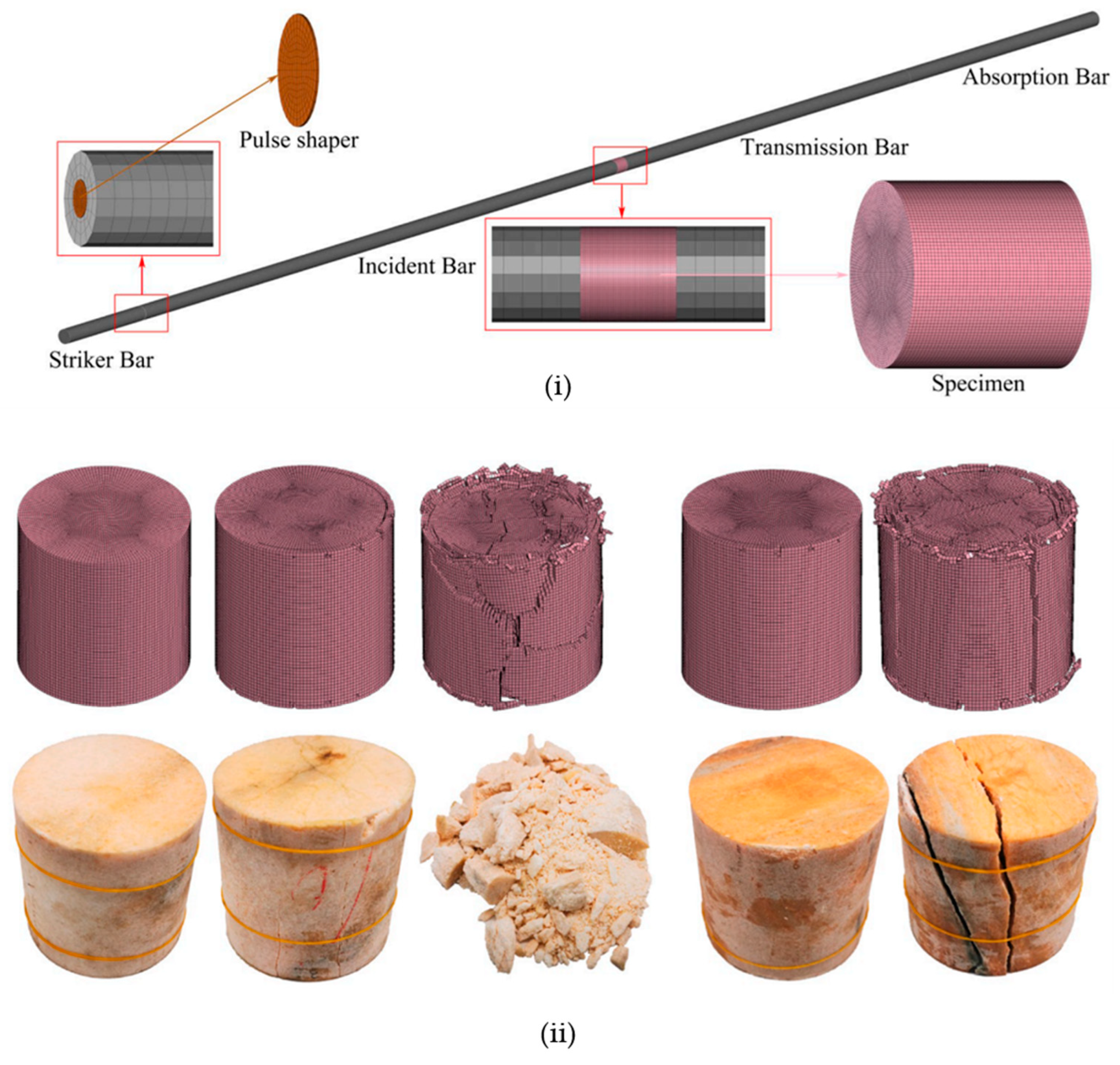
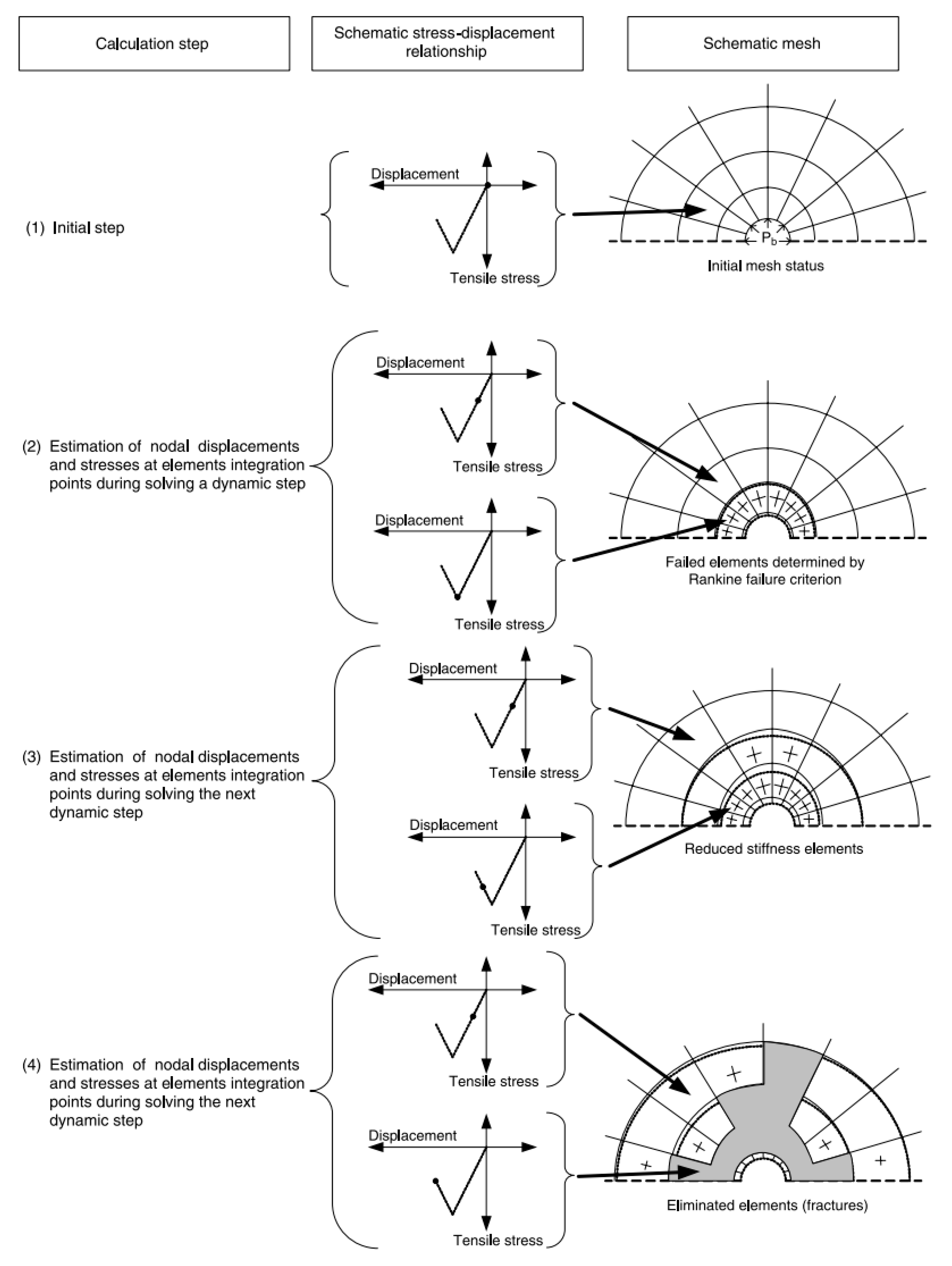
4.2.2. Modelling Stress Wave Propagation, Reflection and Absorbing as Well as Stress Wave-Induced Fracture
4.2.3. Modelling Explosive–Rock Interaction Including Detonation-Induced Gas Expansion and Flow Through Fracturing Rock
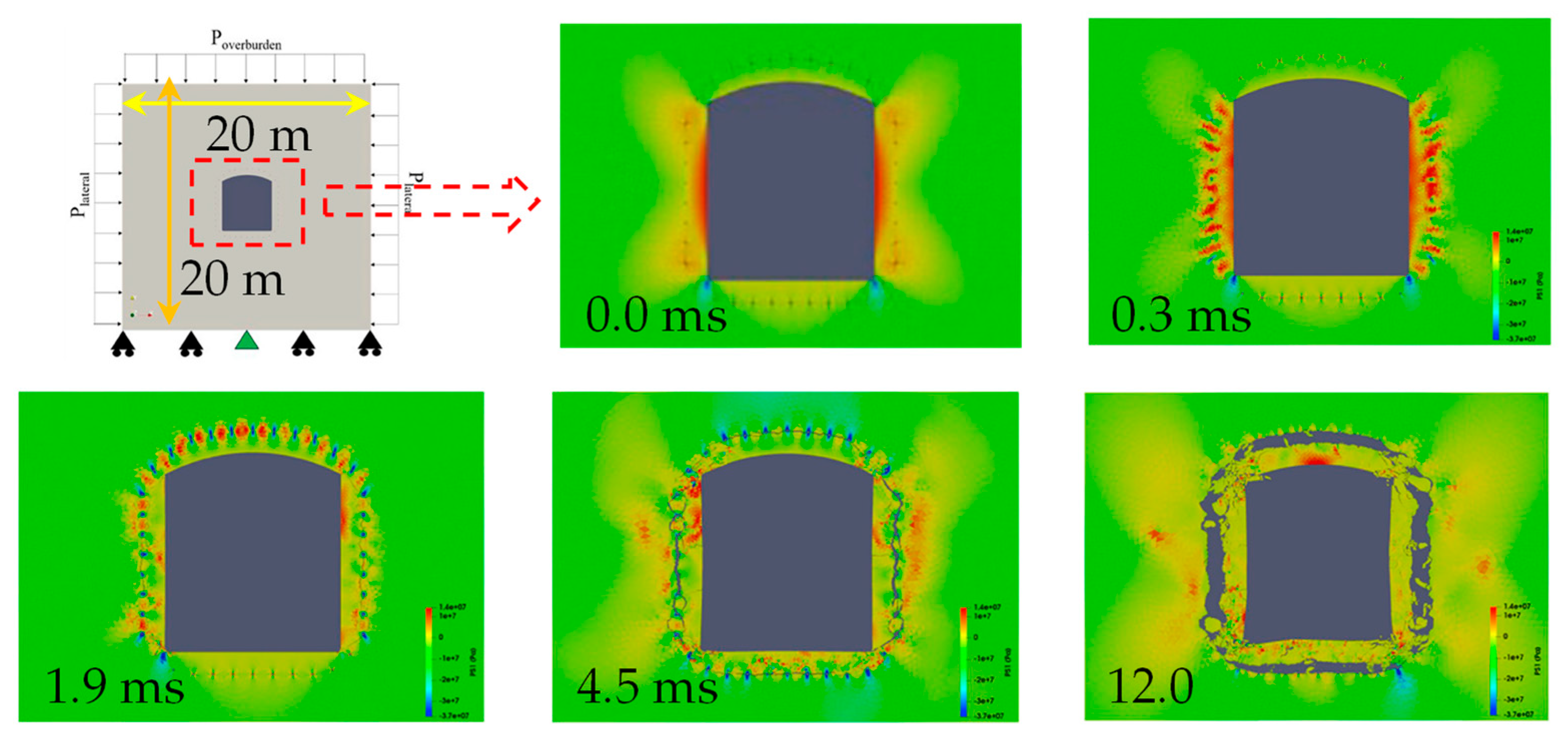
4.2.4. Modelling Dynamic Fracturing Under Coupled Static and Dynamic Conditions
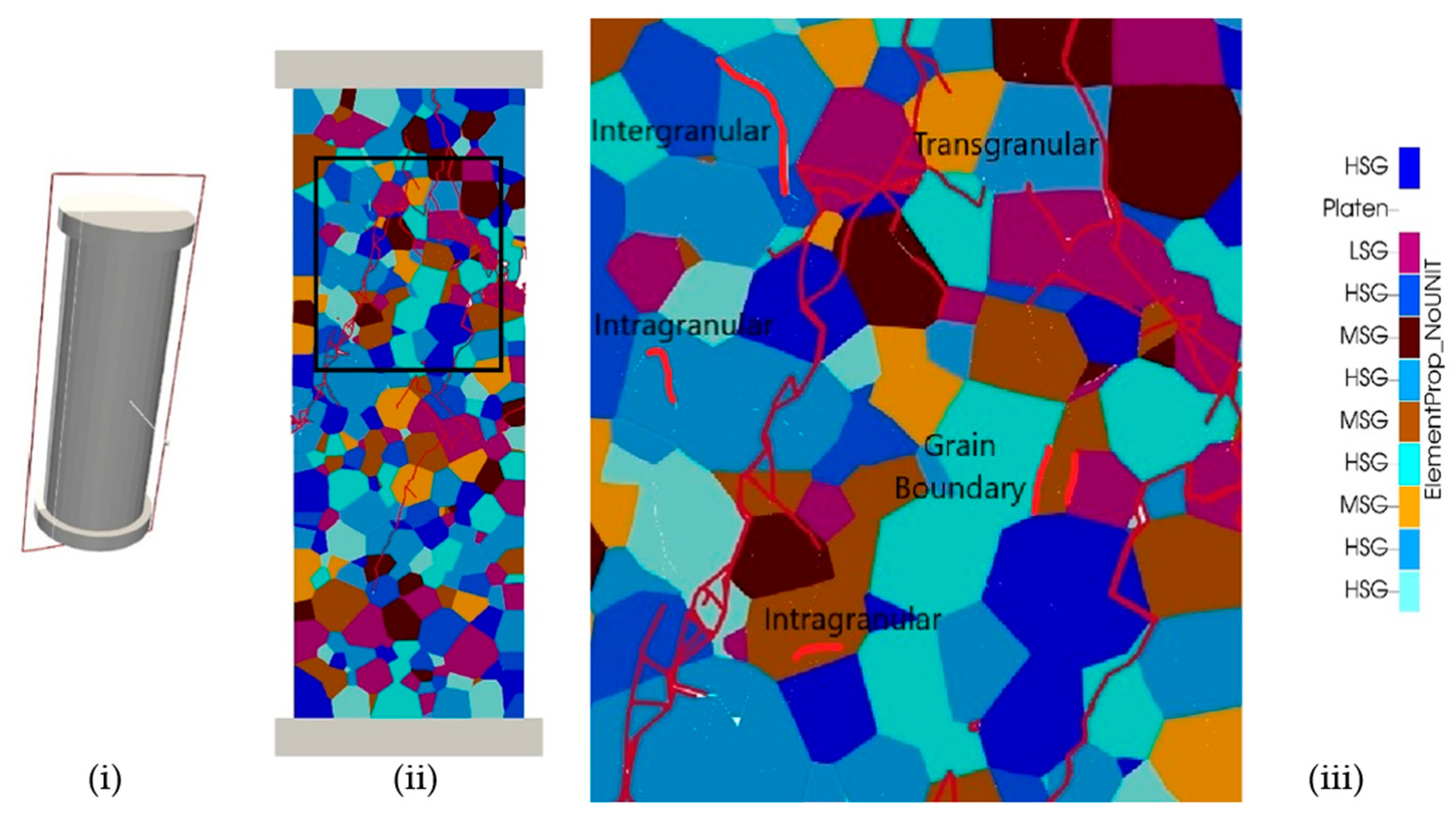
4.2.5. Modelling the Dynamic Fracture of Heterogeneous Rock and Rock Mass with Pre-Existing Discrete Fracture Network
4.2.6. Modelling Dynamic Fracture-Induced Fragment Size Distribution
4.3. Future Directions for Modelling Rock Dynamic Fracture and a Systematic Numerical Modelling Approach for Rock Blasting
- Multi-scale modelling: Multi-scale modelling effectively bridges the gap between microscopic rock fracturing behavior and large-scale engineering applications. It encompasses hierarchical and concurrent multi-scale modellings [8]. Hierarchical multi-scale modelling establishes connections from micro-scale to broader continuum mechanics models, enhancing our comprehension of rock dynamic fracturing over various scales [198]. Concurrent multi-scale methods, on the other hand, simulate multiple scales at once in a single model, enabling precise insights into complex processes like dynamic crack propagation, where interactions between scales are essential [8].
- Multi-physics coupled or interaction modelling: Rock dynamic fracture and rock blasting involve complex interactions between thermal (T), mechanical (M), hydraulic (H) and chemical (C) processes. THMC models remain a challenging task to develop accurate but effective computational models. This challenge is especially evident when tackling issues that encompass long temporal scales or vast spatial regions. Thus, advanced numerical methods are required to accurately represent the complex interactions among diverse physical processes, such as the examination of dynamic damage-permeability coupling [122] and the more intricate dynamic interactions between rock masses and fluids within the realm of fluid-structure interaction [151,152,153,171,196].
- Hybrid modelling: FDEM, including HFDEM, has demonstrated that the integration of FEM with DEM facilitates a more thorough representation of rock dynamic fracturing behavior under varying loading conditions. Thus, the evolution of hybrid continuous/discontinuous methods signifies the most notable enhancement in computational modelling capabilities, integrating various computational techniques to tackle rock dynamic fracture issues. In order to overcome the shortcomings of each numerical technique, the hybrid methods combine their best features.
- High-performance modelling: 3D numerical modelling of rock dynamic fracture is extremely computationally intensive, especially for large engineering applications. Parallel computation has provided a critical alternative for high-performance modelling in terms of both hardware scale and computational efficiency and has revolutionized rock dynamic fracturing simulations, as demonstrated by various CPU and GPU-based parallelization of FDEM with Message Passing Interface (MPI), OpenMP, OpenCL and CUDA reviewed in Section 3.5.1. Heterogeneous CPU-GPU hybrid parallelization combines multiple parallelization strategies and heterogeneous computing resources, which enable large-scale high-performance modelling in the future.
- AI-enhanced modelling: The incorporation of artificial intelligence (AI) techniques has emerged as a viable option for modelling rock dynamic fracturing. This novel method delves into the potential of integrating machine learning into numerical simulations for more effective and accurate modeling of rock dynamic fracturing behaviors. These avenues include creating surrogate models or optimizing computational parameters [8].
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, Q.B.; Zhao, J. A review of dynamic experimental techniques and mechanical behaviour of rock materials. Rock. Mech. Rock. Eng. 2014, 47, 1411–1478. [Google Scholar] [CrossRef]
- Mohammadnejad, M.; Liu, H.Y.; Chan, A.; Dehkhoda, S.; Fukuda, D. An overview on advances in computational fracture mechanics of rock. Geosyst. Eng. 2021, 24, 206–229. [Google Scholar] [CrossRef]
- An, H.M.; Liu, H.Y.; Han, H.; Zheng, X.; Wang, X.G. Hybrid finite-discrete element modelling of dynamic fracture and resultant fragment casting and muck-piling by rock blast. Comput. Geotech. 2017, 81, 322–345. [Google Scholar] [CrossRef]
- Lindholm, U.S. High strain rate tests. In Techniques of Metals Research; Bunsmah, R.F., Ed.; Wiley & Sons: Hoboken, NJ, USA, 1971; Volume V, Part l. [Google Scholar]
- Field, J.E.; Walley, T.M.; Proud, W.G.; Goldrein, H.T.; Siviour, C.R. Review of experimental techniques for high rate deformation and shock studies. Int. J. Impact Eng. 2004, 30, 725–775. [Google Scholar] [CrossRef]
- Ramesh, K.T. High rates and impact experiments. In Handbook of Experimental Solid Mechanics; Springer: Boston, MA, USA, 2008; p. 933. [Google Scholar] [CrossRef]
- Zhang, Z.X. Rock Fracture and Blasting: Theory and Applications; Elsevier: Amsterdam, The Netherlands, 2016. [Google Scholar]
- He, M.; Wang, L.G.; Yao, W.; Dang, W.; Wang, Z. AI for Rock Dynamics; Spring Nature: Berlin/Heidelberg, Germany, 2025. [Google Scholar] [CrossRef]
- Liu, X.; Chen, J.; Zhao, Z.; Lan, H.; Liu, F. Simulating seismic wave propagation in viscoelastic media with an irregular free surface. Pure Appl. Geophys. 2018, 175, 3419–3439. [Google Scholar] [CrossRef]
- Che, A.; Yang, H.; Wang, B. Wave propagations through jointed rock masses and their effects on stability of slopes. Eng. Geol. 2016, 201, 45–56. [Google Scholar] [CrossRef]
- Johansson, D.; Ouchterlony, F. Shock wave interactions in rock blasting: The use of short delays to improve fragmentation in model-scale. Rock. Mech. Rock. Eng. 2013, 46, 1–18. [Google Scholar] [CrossRef]
- Zhang, Y.; Gu, Y.; Fan, L.; Zhao, G.F.; Rui, F. Parametric simulation of stress wave propagation affected by high-temperature damage in rocks using a coupled DLSM-DDA method. Rock. Mech. Rock. Eng. 2025, 58, 6539–6555. [Google Scholar] [CrossRef]
- Rabczuk, T.; Bordas, S.; Zi, G. Editorial: Computational methods for fracture. Math. Probl. Eng. 2014, 593041. [Google Scholar] [CrossRef]
- Dai, F.; Chen, R.; Xia, K. A semi-circular bend technique for determining dynamic fracture toughness. Exp. Mech. 2010, 50, 783–791. [Google Scholar] [CrossRef]
- Qian, Q.; Zhou, X. Quantitative analysis of rockburst for surrounding rocks and zonal disintegration mechanism in deep tunnels. J. Rock. Mech. Geotech. Eng. 2011, 3, 1–9. [Google Scholar] [CrossRef]
- Wang, Y.; Tonon, F. Dynamic validation of a discrete element code in modeling rock fragmentation. Int. J. Rock. Mech. Min. Sci. 2011, 48, 535–545. [Google Scholar] [CrossRef]
- Zou, C.; Li, H. Combined numerical and experimental studies on the dynamic and quasi-static failure modes of brittle rock. Int. J. Rock. Mech. Min. Sci. 2021, 148, 104957. [Google Scholar] [CrossRef]
- Green, S.J.; Perkins, R.D. Uniaxial compression tests at varying strain rates on three geologic materials. In Proceedings of the 10th U.S. Symposium on Rock Mechanics (USRMS), Austin, TX, USA, 20–22 May 1968; p. ARMA-68-0035. [Google Scholar]
- Kumar, A. The effect of stress rate and temperature on the strength of basalt and granite. Geophysics 1968, 33, 501–510. [Google Scholar] [CrossRef]
- Chong, K.P.; Hoyt, P.M.; Smith, J.W.; Paulsen, B.Y. Effects of strain rate on oil shale fracturing. Int. J. Rock. Mech. Min. Sci. Geomech. Abstr. 1980, 17, 35–43. [Google Scholar] [CrossRef]
- Zhao, J. Applicability of Mohr–Coulomb and Hoek–Brown strength criteria to the dynamic strength of brittle rock. Int. J. Rock. Mech. Min. Sci. 2000, 37, 1115–1121. [Google Scholar] [CrossRef]
- Chen, C.H.; Chen, C.S.; Wu, J.H. Fracture toughness analysis on cracked ring disks of anisotropic rock. Rock Mech. Rock. Eng. 2008, 41, 539–562. [Google Scholar] [CrossRef]
- Ouchterlony, F. Suggested methods for determining the fracture toughness of rock. Int. J. Rock. Mech. Min. 1988, 25, 71–96. [Google Scholar] [CrossRef]
- Fowell, R.J. Suggested method for determining mode I fracture toughness using cracked chevron notched Brazilian disc (CCNBD) specimens. Int. J. Rock. Mech. Min. 1995, 32, 57–64. [Google Scholar] [CrossRef]
- Wang, Q.; Jia, X.; Kou, S.; Zhang, Z.X.; Linqvist, P.A. More accurate stress intensity factor derived by finite element analysis for the ISRM suggested rock fracture toughness specimen—CCNBD. Int. J. Rock. Mech. Min. Sci. 2003, 40, 233–241. [Google Scholar] [CrossRef]
- Kuruppu, M.D.; Obara, Y.; Ayatollahi, M.R.; Chong, K.P.; Funatsu, T. ISRM-Suggested method for determining the mode I static fracture toughness using semi-circular bend specimen. Rock. Mech. Rock. Eng. 2014, 47, 267–274. [Google Scholar] [CrossRef]
- Zhang, Z.X.; Kou, S.Q.; Yu, J.; Yu, Y.; Jiang, L.G.; Lindqvist, P.A. Effects of loading rate on rock fracture. Int. J. Rock. Mech. Min. 1999, 36, 597–611. [Google Scholar] [CrossRef]
- Zhang, Z.X.; Kou, S.Q.; Jiang, L.G.; Lindqvist, P.A. Effects of loading rate on rock fracture: Fracture characteristics and energy partitioning. Int. J. Rock. Mech. Min. 2000, 37, 745–762. [Google Scholar] [CrossRef]
- Kalthoff, J.F. Fracture behavior under high rates of loading. Eng. Fract. Mech. 1986, 23, 289–298. [Google Scholar] [CrossRef]
- Kim, Y.; Chao, Y. Effect of loading rate on dynamic fracture initiation toughness of brittle materials. Int. J. Fract. 2007, 145, 195–204. [Google Scholar] [CrossRef]
- Nie, H.; Ma, W.; Wang, K.; Ren, J.; Cao, J.; Dang, W. A review of dynamic multiaxial experimental techniques. Rev. Sci. Instrum. 2020, 91, 111501. [Google Scholar] [CrossRef]
- Li, X.; Gong, F.; Tao, M.; Dong, L.; Du, K.; Ma, C.; Zhou, Z.; Yin, T. Failure mechanism and coupled static-dynamic loading theory in deep hard rock mining: A review. J. Rock. Mech. Geotech. Eng. 2017, 9, 767–782. [Google Scholar] [CrossRef]
- Luo, H.; Gong, H.; Luo, Y.; Xia, D.; Zhang, X.; Li, X. The macroscopic and microscopic fatigue failure mechanisms of high temperature thermally damaged granite under cyclic impact loading. Geothermics 2025, 121, 103047. [Google Scholar] [CrossRef]
- Zheng, Z.; Li, R.; Li, S.; Lu, G.; Zhang, Q.; Qiu, S. A novel dynamic fractional mechanical model for rock fracture under true triaxial static-dynamic combined loading and its engineering application. Rock. Mech. Rock. Eng. 2024, 57, 9343–9369. [Google Scholar] [CrossRef]
- Jing, L.; Hudson, J.A. Numerical methods in rock mechanics. Int. J. Rock. Mech. Min. Sci. 2002, 39, 409–427. [Google Scholar] [CrossRef]
- Lisjak, A.; Grasselli, G. A review of discrete modelling techniques for fracturing processes in discontinuous rock masses. J. Rock. Mech. Geotech. Eng. 2014, 6, 301–314. [Google Scholar] [CrossRef]
- Preece, D.; Thorne, B.; Baer, M.; Swegle, J. Computer Simulation of Rock Blasting: A Summary of Work from 1987 Through 1993; SAND94-1027; Sandia National Laboratories: Albuquerque, NM, USA, 1994. [Google Scholar]
- Latham, J.P.; Lu, P. Development of an assessment system for the blastability of rock masses. Int. J. Rock. Mech. Min. Sci. 1999, 36, 41–55. [Google Scholar] [CrossRef]
- Bittencourt, T.N.; Wawrzynek, P.A.; Ingraffea, A.R.; Sousa, J.L. Quasi-automatic simulation of crack propagation for 2D LEFM problems. Eng. Fract. Mech. 1996, 55, 321–334. [Google Scholar] [CrossRef]
- Song, J.H. Computations of the Dynamic Fracture of Quasi-Brittle Plane and Shell Structures by the Extended Finite Element Method. Ph.D. Thesis, Northwestern University, Evanston, IL, USA, 2012. [Google Scholar]
- Tang, C. Numerical simulation of progressive rock failure and associated seismicity. Int. J. Rock. Mech. Min. Sci. 1997, 34, 249–261. [Google Scholar] [CrossRef]
- Liu, H.Y.; Kou, S.Q.; Lindqvist, P.A.; Tang, C.A. Numerical simulation of the rock fragmentation process induced by indenters. Int. J. Rock. Mech. Min. Sci. 2002, 39, 491–505. [Google Scholar] [CrossRef]
- Saksala, T. Damage–viscoplastic consistency model with a parabolic cap for rocks under low-velocity impact loading. Int. J. Numer. Anal. Meth. Geomech. 2010, 34, 1362–1386. [Google Scholar] [CrossRef]
- Rabczuk, T. Computational methods for fracture in brittle and quasi-brittle solids: State-of-the-art review and future perspectives. Appl. Math. 2013, 2013, 849231. [Google Scholar] [CrossRef]
- Song, J.H.; Wang, H.; Belytschko, T. A comparative study on finite element methods for dynamic fracture. Comput. Mech. 2008, 42, 239–250. [Google Scholar] [CrossRef]
- Li, Q.; Li, Q.; Cao, H.; Wu, J.; Wang, F.; Wang, Y. The crack propagation behaviour of CO2 fracturing fluid in unconventional low permeability reservoirs; factor analysis and mechanism revelation. Process 2025, 13, 159. [Google Scholar] [CrossRef]
- Li, Q.; Li, Y.; Cheng, Y.; Li, Q.; Wang, F.; Wei, J.; Liu, Y.; Zhang, C.; Song, B.; Yan, C.; et al. Numerical simulation of fracture reorientation during hydraulic fracturing in perforated horizontal well in shale reservoirs. Energy Sources Part. A Recovery Util. Environ. Eff. 2018, 40, 1807–1813. [Google Scholar] [CrossRef]
- Belytschko, T.; Black, T. Elastic crack growth in finite elements with minimal remeshing. Int. J. Numer. Meth. Eng. 1999, 45, 601–620. [Google Scholar] [CrossRef]
- Moës, N.; Dolbow, J.; Belytschko, T. A finite element method for crack growth without remeshing. Int. J. Numer. Meth. Eng. 1999, 46, 131–150. [Google Scholar] [CrossRef]
- Yu, T.T. The extended finite element method (XFEM) for discontinuous rock masses. Eng. Comput. 2011, 28, 340–369. [Google Scholar] [CrossRef]
- Zhang, Y.L.; Feng, X.T. Extended finite element simulation of crack propagation in fractured rock masses. Mater. Res. Innov. 2011, 15, 1–3. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, H.; Lin, H.; Zhao, Y.; Liu, Y. Fracture behaviour of central-flawed rock plate under uniaxial compression. Theor. Appl. Fract. Mech. 2020, 106, 102503. [Google Scholar] [CrossRef]
- Zhuang, X.; Chun, J.; Zhu, H. A comparative study on unfilled and filled crack propagation for rock-like brittle material. Theor. Appl. Fract. Mech. 2014, 72, 110–120. [Google Scholar] [CrossRef]
- Xie, Y.; Cao, P.; Liu, J.; Dong, L. Influence of crack surface friction on crack initiation and propagation: A numerical investigation based on extended finite element method. Comput. Geotech. 2016, 74, 1–14. [Google Scholar] [CrossRef]
- Oñate, E.; Idelsohn, S.R.; Del Pin, F.; Aubry, R. The particle finite element method—An overview. Int. J. Comput. Methods 2004, 1, 267–307. [Google Scholar] [CrossRef]
- Cremonesi, M.; Franci, A.; Idelsohn, S.; Oñate, E. A state of the art review of the particle finite element method (PFEM). Arch. Comput. Methods Eng. 2020, 27, 1709–1735. [Google Scholar] [CrossRef]
- Zhou, L.; Zhu, Z.; Qiu, H.; Zhang, X.; Lang, L. Study of the effect of loading rates on crack propagation velocity and rock fracture toughness using cracked tunnel specimens. Int. J. Rock. Mech. Min. Sci. 2018, 112, 25–34. [Google Scholar] [CrossRef]
- Zhou, Q.; Zhu, Z.; Wang, X.; Zhou, J.; Lang, L.; Zhang, X. The effect of a pre-existing crack on a running crack in brittle material under dynamic loads. Fatigue Fract. Eng. Mater. Struct. 2019, 42, 2544–2557. [Google Scholar] [CrossRef]
- Hughes, M.L.; Tedesco, J.W.; Ross, C.A. Numerical analysis of high strain rate splitting-tensile tests. Comput. Struct. 1993, 47, 653–671. [Google Scholar] [CrossRef]
- Zhu, W.C.; Tang, C.A. Micromechanical model for simulating the fracture process of rock. Rock. Mech. Rock. Eng. 2004, 37, 25–56. [Google Scholar] [CrossRef]
- Zhou, X.Q.; Hao, H. Mesoscale modelling of concrete tensile failure mechanism at high strain rates. Comput. Struct. 2008, 86, 2013–2026. [Google Scholar] [CrossRef]
- Saksala, T.; Hokka, M.; Kuokkala, V.T.; Mäkinen, J. Numerical modeling and experimentation of dynamic Brazilian disc test on Kuru granite. Int. J. Rock. Mech. Min. Sci. 2013, 59, 128–138. [Google Scholar] [CrossRef]
- Wang, X.; Liu, Z.; Gao, X.; Li, P.; Dong, B. Dynamic characteristics and fracture process of marble under repeated impact loading. Eng. Fract. Mech. 2022, 276, 108926. [Google Scholar] [CrossRef]
- Thorne, B.J. A Damage Model for Rock Fragmentation and Comparison of Calculations with Blasting Experiments in Granite; Report No. SAND-90-1389; Sandia National Laboratories: Albuquerque, NM, USA, 1990. [Google Scholar] [CrossRef][Green Version]
- Cho, S.H.; Kaneko, K. Influence of the applied pressure waveform on the dynamic fracture processes in rock. Int. J. Rock. Mech. Min. Sci. 2004, 41, 771–784. [Google Scholar] [CrossRef]
- Liu, H.; Kou, S.; Lindqvist, P.A.; Tang, C.A. Numerical Modelling of Crack Propagation by Blast in TASQ Tunnel of Aspo Hard Rock Laboratory; SKB Project: Stockholm, Sweden, 2005. [Google Scholar][Green Version]
- Rouabhi, A.; Tijani, M.; Moser, P.; Goetz, D. Continuum modelling of dynamic behaviour and fragmentation of quasi-brittle materials: Application to rock fragmentation by blasting. Int. J. Numer. Anal. Methods Geomech. 2005, 29, 729–749. [Google Scholar] [CrossRef]
- Liu, H.; Kou, S.Q.; Lindqvist, P.A.; Zhang, Z.X. Numerical simulation of production blasting in sublevel caving. APS Blasting 2007, 1, 23–30. [Google Scholar]
- Wang, Z.L.; Li, Y.C.; Shen, R.F. Numerical simulation of tensile damage and blast crater in brittle rock due to underground explosion. Int. J. Rock. Mech. Min. Sci. 2007, 44, 730–738. [Google Scholar] [CrossRef]
- Wang, Z.; Li, Y.; Wang, J.G. A method for evaluating dynamic tensile damage of rock. Eng. Fract. Mech. 2008, 75, 2812–2825. [Google Scholar] [CrossRef]
- Ma, G.W.; An, X.M. Numerical simulation of blasting-induced rock fractures. Int. J. Rock. Mech. Min. Sci. 2008, 45, 966–975. [Google Scholar] [CrossRef]
- Wei, X.Y.; Zhao, Z.Y.; Gu, J. Numerical simulations of rock mass damage induced by underground explosion. Int. J. Rock. Mech. Min. Sci. 2009, 46, 1206–1213. [Google Scholar] [CrossRef]
- Sjöberg, J.; Schill, M.; Hilding, D.; Yi, C.; Nyberg, U.; Johansson, D. Computer simulations of blasting with precise initiation. In ISRM International Symposium—EUROCK; OnePetro: Richardson, TX, USA, 2012. [Google Scholar][Green Version]
- Saharan, M.R.; Mitri, H.S. Numerical procedure for dynamic simulation of discrete fractures due to blasting. Rock. Mech. Rock. Eng. 2008, 41, 641–670. [Google Scholar] [CrossRef]
- Zhu, Z.; Mohanty, B.; Xie, H. Numerical investigation of blasting-induced crack initiation and propagation in rocks. Int. J. Rock. Mech. Min. Sci. 2007, 44, 412–424. [Google Scholar] [CrossRef]
- Zhu, Z. Numerical prediction of crater blasting and bench blasting. Int. J. Rock. Mech. Min. Sci. 2009, 46, 1088–1096. [Google Scholar] [CrossRef]
- Liang, W.M.; Liu, H.Y.; Yang, X.L.; Williams, D.J. Effects of decoupled charge blasting on rock fragmentation efficiency. In Proceedings of the 12th ISRM Congress, Beijing, China, 16–21 October 2011; p. ISRM-12CONGRESS-2011-222. [Google Scholar][Green Version]
- Zhang, Z.X.; Wimmer, M. A case study of dividing a single blast into two parts in sublevel caving. Int. J. Rock. Mech. Min. Sci. 2018, 104, 84–93. [Google Scholar] [CrossRef]
- Yi, C.; Sjöberg, J.; Johansson, D. Numerical modelling for blast-induced fragmentation in sublevel caving mines. Tunn. Undergr. Space Technol. 2017, 68, 167–173. [Google Scholar] [CrossRef]
- Bird, R.; Paluszny, A.; Thomas, R.N.; Zimmerman, R.W. Modelling of fracture intensity increase due to interacting blast waves in three-dimensional granitic rocks. Int. J. Rock. Mech. Min. Sci. 2023, 162, 105279. [Google Scholar] [CrossRef]
- Zhang, F.; Yang, L.; Hu, Y.; Ma, J.; Liu, N.; Yang, R. Experimental and numerical study on mechanical response mechanism of granite under coupled confining pressure and blasting load. Rock. Mech. Rock. Eng. 2025, 58, 1617–1637. [Google Scholar] [CrossRef]
- Potyondy, D.O.; Cundall, P.A. A bonded-particle model for rock. Int. J. Rock. Mech. Min. Sci. 2004, 41, 1329–1364. [Google Scholar] [CrossRef]
- Itasca Consulting Group, Inc. PFC2D (Particle Flow Code in 2 Dimensions); Version 5.0; Itasca: Minneapolis, MN, USA, 2008. [Google Scholar][Green Version]
- Itasca Consulting Group, Inc. PFC3D (Particle Flow Code in 3 Dimensions); Version 4.0; ICG: Minneapolis, MN, USA, 2008. [Google Scholar][Green Version]
- Potyondy, D.O. The bonded-particle model as a tool for rock mechanics research and application: Current trends and future directions. Geosyst Eng. 2015, 18, 1–28. [Google Scholar] [CrossRef]
- Yan, Z.; Wilkinson, S.K.; Stitt, E.H.; Marigo, M.J. Discrete element modelling (DEM) input parameters: Understanding their impact on model predictions using statistical analysis. Comput. Part. Mech. 2015, 2, 283–299. [Google Scholar] [CrossRef]
- Richter, C.; Rößler, T.; Kunze, G.; Katterfeld, A.; Will, F. Development of a standard calibration procedure for the DEM parameters of cohesionless bulk materials—Part II: Efficient optimization-based calibration. Powder Technol. 2020, 360, 967–976. [Google Scholar] [CrossRef]
- Xue, B.; Que, Y.; Pei, J.; Ma, X.; Wang, D.; Yuan, Y.; Zhang, H. A state-of-the-art review of discrete element method for asphalt mixtures: Model generation methods, contact constitutive models and application directions. Constr. Build. Mater. 2024, 414, 134842. [Google Scholar] [CrossRef]
- Potyondy, D.O. A flat-jointed bonded-particle material for hard rock. In Proceedings of the 46th U.S. Rock Mechanics/Geomechanics Symposium, Chicago, IL, USA, 24–27 June 2012; p. ARMA-2012-501. [Google Scholar][Green Version]
- Sun, W.; Wu, S.C.; Zhou, Y.; Zhou, J.X. Comparison of crack processes in single-flawed rock-like material using two bonded–particle models under compression. Arab. J. Geosci. 2019, 12, 156. [Google Scholar] [CrossRef]
- Li, X.; Zou, Y.; Zhou, Z. Numerical simulation of the rock SHPB test with a special shape striker based on the discrete element method. Rock. Mech. Rock. Eng. 2014, 47, 1693–1709. [Google Scholar] [CrossRef]
- Hu, W.R.; Liu, K.; Potyondy, D.O.; Zhang, Q.B. 3D continuum-discrete coupled modelling of triaxial Hopkinson bar tests on rock under multiaxial static-dynamic loads. Int. J. Rock. Mech. Min. Sci. 2020, 134, 104448. [Google Scholar] [CrossRef]
- Kozicki, J.; Donzé, F.V. A new open-source software developed for numerical simulations using discrete modeling methods. Comput. Methods Appl. Mech. Eng. 2008, 197, 4429–4443. [Google Scholar] [CrossRef]
- Frédéric, D.; Magnier, S.A. Formulation of a 3-D numerical model of brittle behaviour. Geophys. J. Int. 1995, 122, 790–802. [Google Scholar] [CrossRef]
- Donzé, F.; Magnier, S.A. Spherical discrete element code. Discret. Elem. Proj. Rep. 1997, 2, 1309–1323. [Google Scholar]
- Karatela, E.; Taheri, A. Three-dimensional hydro-mechanical model of borehole in fractured rock mass using discrete element method. J. Nat. Gas. Sci. Eng. 2018, 53, 263–275. [Google Scholar] [CrossRef]
- Mohammadnejad, M. Advanced FDEM Modelling of Rock Fracture Process and Applications in Rock Cutting. Ph.D. Thesis, University of Tasmania, Tasmania, Australia, 2020. [Google Scholar][Green Version]
- Preece, D.S. A Numerical Study of Bench Blast Row Delay Timing and Its Influence on Percent-Cast; SAND-93-2566C; CONF-940506-2; Sandia National Labs: Albuquerque, NM, USA, 1993. [Google Scholar][Green Version]
- Song, J.; Kim, K. Micromechanical modeling of the dynamic fracture process during rock blasting. Int. J. Rock. Mech. Min. Sci. Geomech. Abstr. 1996, 33, 387–394. [Google Scholar] [CrossRef]
- Potyondy, D.O.; Cundall, P.A.; Lee, C.A. Modelling rock using bonded assemblies of circular particles. In Proceedings of the 2nd North American Rock Mechanics Symposium, Montreal, Quebec, Canada, 19–21 June 1996; p. ARMA-96. [Google Scholar][Green Version]
- Donze, F.V.; Bouchez, J.; Magnier, S.A. Modelling fractures in rock blasting. Int. J. Rock. Mech. Min. Sci. 1997, 34, 1153–1163. [Google Scholar] [CrossRef]
- Mortazavi, A.; Katsabanis, P.D. Modelling burden size and strata dip effects on the surface blasting process. Int. J. Rock. Mech. Min. Sci. 2001, 38, 481–498. [Google Scholar] [CrossRef]
- Zhao, X.; Zhao, J.; Cai, J.; Hefny, A.M. UDEC modelling on wave propagation across fractured rock masses. Comput. Geotech. 2008, 35, 97–104. [Google Scholar] [CrossRef]
- Saiang, D. Stability analysis of the blast-induced damage zone by continuum and coupled continuum–discontinuum methods. Eng. Geol. 2010, 116, 1–11. [Google Scholar] [CrossRef]
- Ning, Y.; Yang, J.; An, X.; Ma, G. Modelling rock fracturing and blast-induced rock mass failure via advanced discretisation within the discontinuous deformation analysis framework. Comput. Geotech. 2011, 38, 40–49. [Google Scholar] [CrossRef]
- Ning, Y.; Yang, J.; Ma, G.; Chen, P. Modelling rock blasting considering explosion gas penetration using discontinuous deformation analysis. Rock. Mech. Rock. Eng. 2011, 44, 483–490. [Google Scholar] [CrossRef]
- Onederra, I.A.; Furtney, J.K.; Sellers, E.; Iverson, S. Modelling blast induced damage from a fully coupled explosive charge. Int. J. Rock. Mech. Min. Sci. 2013, 58, 73–84. [Google Scholar] [CrossRef]
- Fakhimi, A.; Lanari, M. DEM–SPH simulation of rock blasting. Comput. Geotech. 2014, 55, 158–164. [Google Scholar] [CrossRef]
- Lak, M.; Fatehi Marji, M.; Yarahamdi Bafghi, A.R.; Abdollahipour, A. Discrete element modeling of explosion-induced fracture extension in jointed rock masses. J. Min. Environ. 2019, 10, 125–138. [Google Scholar]
- Ding, C.; Yang, R.; Zheng, C.; Yang, L.; He, S.; Feng, C. Numerical analysis of deep hole multi-stage cut blasting of vertical shaft using a continuum-based discrete element method. Arab. J. Geosci. 2021, 14, 1086. [Google Scholar] [CrossRef]
- Munjiza, A. The Combined Finite-Discrete Element Method; Wiley: Chichester, UK, 2004. [Google Scholar][Green Version]
- Rougier, E.; Knight, E.E.; Broome, S.T.; Sussman, A.J.; Munjiza, A. Validation of a three-dimensional finite-discrete element method using experimental results of the split Hopkinson pressure bar test. Int. J. Rock. Mech. Min. Sci. 2014, 70, 101–108. [Google Scholar] [CrossRef]
- Liu, H.Y.; Kang, Y.M.; Lin, P. Hybrid finite–discrete element modeling of geomaterials fracture and fragment muck-piling. Int. J. Geotech. Eng. 2015, 9, 115–131. [Google Scholar] [CrossRef]
- Yan, C.; Zheng, H. FDEM-flow3D: A 3D hydro-mechanical coupled models considering the pore seepage of rock matrix for simulating three-dimensional hydraulic fracturing. Comput. Geotech. 2017, 81, 212–228. [Google Scholar] [CrossRef]
- Lisjak, A.; Kaifosh, P.; Tatone, B.; Mahabadi, O.; Grasselli, G. A 2D fully-coupled hydro-mechanical FDEM formulation for modelling fracturing processes in discontinuous porous rock masses. Comput. Geotech. 2017, 81, 1–18. [Google Scholar] [CrossRef]
- Klerck, P.A.; Sellers, E.J.; Owen, D.R.J. Discrete fracture in quasi-brittle materials under compressive and tensile stress states. Comput. Methods Appl. Mech. Eng. 2004, 193, 3035–3056. [Google Scholar] [CrossRef]
- Xiang, J.; Munjiza, A.; Latham, J.P. Finite strain, finite rotation quadratic tetrahedral element for the combined finite–discrete element method. Int. J. Numer. Meth Eng. 2009, 79, 946–978. [Google Scholar] [CrossRef]
- Munjiza, A.; Xiang, J.; Garcia, X.; Latham, J.P.; D’Albano, G.S.; John, N.W.M. The virtual geoscience workbench, VGW: Open source tools for discontinuous systems. Particuology 2010, 8, 100–105. [Google Scholar] [CrossRef]
- Mahabadi, O.K.; Lisjak, A.; Munjiza, A.; Grasselli, G. Y-Geo: New combined finite-discrete element numerical code for geomechanical applications. Int. J. Geomech. 2012, 12, 676–688. [Google Scholar] [CrossRef]
- Knight, E.E.; Rougier, E.; Lei, Z.; Euser, B.; Chau, V.; Boyce, S.H.; Gao, K.; Okubo, K.; Froment, M. HOSS: An implementation of the combined finite-discrete element method. Comp. Part. Mech. 2020, 7, 765–787. [Google Scholar] [CrossRef]
- Mahabadi, O.K.; Lisjak, A.; He, L.; Tatone, B.S.A.; Kaifosh, P.; Grasselli, G. Development of a new fully-parallel finite-discrete element code: Irazu. In Proceedings of the 50th U.S. Rock Mechanics/Geomechanics Symposium, Houston, TX, USA, 26–29 June 2016; p. ARMA-2016-516. [Google Scholar] [CrossRef]
- Yan, C.; Zheng, H.; Sun, G.; Ge, X. Combined finite-discrete element method for simulation of hydraulic fracturing. Rock. Mech. Rock. Eng. 2016, 49, 1389–1410. [Google Scholar] [CrossRef]
- Lei, Z.; Rougier, E.; Knight, E.E.; Munjiza, A. A framework for grand scale parallelization of the combined finite discrete element method in 2D. Comput. Part. Mech. 2014, 1, 307–319. [Google Scholar] [CrossRef]
- Hamdi, P.; Stead, D.; Elmo, D. Damage characterization during laboratory strength testing: A 3D-finite-discrete element approach. Comput. Geotech. 2014, 60, 33–46. [Google Scholar] [CrossRef]
- Xiang, J.; Latham, J.P. Algorithms and capabilities of solidity to simulate interactions and packing of complex shapes. In Simulations in Bulk Solids Handling: Applications of DEM and Other Methods; John Wiley & Sons: Hoboken, NJ, USA, 2013; pp. 231–246. [Google Scholar] [CrossRef]
- Guo, N.; Zhao, J. A coupled FEM/DEM approach for hierarchical multiscale modelling of granular media. Int. J. Numer. Meth Eng. 2014, 99, 789–818. [Google Scholar] [CrossRef]
- Guo, N.; Zhao, J. Parallel hierarchical multiscale modelling of hydro-mechanical problems for saturated granular soils. Comput. Methods Appl. Mech. Eng. 2016, 305, 37–61. [Google Scholar] [CrossRef]
- Wu, H.; Guo, N.; Zhao, J. Multiscale modeling and analysis of compaction bands in high-porosity sandstones. Acta Geotech. 2018, 13, 575–599. [Google Scholar] [CrossRef]
- Wu, H.; Zhao, J.; Guo, N. Multiscale insights into borehole instabilities in high-porosity sandstones. J. Geophys. Res: Solid. Earth 2018, 123, 3450–3473. [Google Scholar] [CrossRef]
- Munshi, A.; Gaster, B.; Mattson, T.G.; Ginsburg, D. OpenCL Programming Guide; Pearson Education: London, UK, 2011. [Google Scholar]
- Nvidia Corporation. NVIDIA CUDA C Programming Guide, Version 4.0; Nvidia: Santa Clara, CA, USA, 2011. [Google Scholar]
- Lisjak, A.; Mahabadi, O.K.; He, L.; Tatone, B.S.A.; Kaifosh, P.; Haque, S.A.; Grasselli, G. Acceleration of a 2D/3D finite-discrete element code for geomechanical simulations using general purpose GPU computing. Comput. Geotech. 2018, 100, 84–96. [Google Scholar] [CrossRef]
- Fukuda, D.; Mohammadnejad, M.; Liu, H.Y.; Dehkhoda, S.; Chan, A.; Cho, S.H.; Fujii, Y. Development of a GPGPU-parallelized hybrid finite-discrete element method for modeling rock fracture. Int. J. Numer. Anal. Methods Geomech. 2019, 43, 1797–1824. [Google Scholar] [CrossRef]
- Fukuda, D.; Mohammadnejad, M.; Liu, H.Y.; Zhang, Q.; Zhao, J.; Dehkhoda, S.; Fujii, Y. Development of a 3D hybrid finite-discrete element simulator based on GPGPU-parallelized computation for modelling rock fracturing under quasi-static and dynamic loading conditions. Rock. Mech. Rock. Eng. 2020, 53, 1079–1112. [Google Scholar] [CrossRef]
- Liu, H.; Liu, Q.; Ma, H.; Fish, J. A novel GPGPU-parallelized contact detection algorithm for combined finite-discrete element method. Int. J. Rock. Mech. Min. Sci. 2021, 144, 104782. [Google Scholar] [CrossRef]
- Lei, Y.; Liu, Q.; Liu, H. Developing a memory-efficient GPGPU-parallelized contact detection algorithm for 3D engineering-scale FDEM simulations. Comput. Geotech. 2025, 179, 107031. [Google Scholar] [CrossRef]
- Mahabadi, O.K.; Cottrell, B.E.; Grasselli, G. An example of realistic modelling of rock dynamics problems: FEM/DEM simulation of dynamic Brazilian test on Barre granite. Rock. Mech. Rock. Eng. 2010, 43, 707–716. [Google Scholar] [CrossRef]
- Osthus, D.; Godinez, H.C.; Rougier, E.; Srinivasan, G. Calibrating the stress-time curve of a combined finite-discrete element method to a Split Hopkinson Pressure Bar experiment. Int. J. Rock. Mech. Min. Sci. 2018, 106, 278–288. [Google Scholar] [CrossRef]
- Fukuda, D.; Liu, H.Y.; Zhang, Q.; Zhao, J.; Kodama, J.I.; Fujii, Y.; Chan, A.H.C. Modelling of dynamic rock fracture process using the finite-discrete element method with a novel and efficient contact activation scheme. Int. J. Rock. Mech. Min. Sci. 2021, 138, 104645. [Google Scholar] [CrossRef]
- Wu, D.; Li, H.; Fukuda, D.; Liu, H. Development of a finite-discrete element method with finite-strain elasto-plasticity and cohesive zone models for simulating the dynamic fracture of rocks. Comput. Geotech. 2023, 156, 105271. [Google Scholar] [CrossRef]
- Mohammadnejad, M.; Dehkhoda, S.; Fukuda, D.; Liu, H.; Chan, A. GPGPU-parallelised hybrid finite-discrete element modelling of rock chipping and fragmentation process in mechanical cutting. J. Rock. Mech. Geotech. Eng. 2020, 12, 310–325. [Google Scholar] [CrossRef]
- Li, Y.; Chen, Z.; Ye, Y.; Yang, Y. Combined finite-discrete element method for modelling the interaction between single PDC cutter and brittle rock. J. Pet. Sci. Eng. 2021, 207, 109133. [Google Scholar] [CrossRef]
- Huang, A.; Wei, G.; Zou, Y.; Zou, J.; Deng, R.; Ye, B. Numerical simulation of rock breaking by PDC cutter with finite-discrete-infinite element method. Geoenergy Sci. Eng. 2023, 225, 211725. [Google Scholar] [CrossRef]
- Liu, W.; Deng, H.; Zhu, X.; Lv, Y.; Luo, Y. The rock cutting simulation of heterogeneous granite using FDEM method. Petroleum 2023, 11, 1–12. [Google Scholar] [CrossRef]
- Yang, X.; Xiang, J.; Naderi, S.; Wang, Y.; Aising, J.; Ugarte, I.; Latham, J.P. Multi-criteria validation of hi-fidelity numerical model of impact breakage: Towards next generation percussion drill simulation. Int. J. Rock. Mech. Min. Sci. 2025, 191, 106125. [Google Scholar] [CrossRef]
- Naderi, S.; Gerbaud, L.; Velmurugan, N.; Xiang, J.; Yang, X.; Aising, J.; Chambres, C.; Latham, J.P. A study of rock breakage under exxtreme submerged confining pressure: Can DTH hammer drilling deliver. Rock Mech Rock Eng 2025, 1–23. [Google Scholar] [CrossRef]
- Munjiza, A.; Latham, J.P.; Andrews, K.R.F. Detonation gas model for combined finite-discrete element simulation of fracture and fragmentation. Int. J. Numer. Meth Eng. 2000, 49, 1495–1520. [Google Scholar] [CrossRef]
- Han, H.; Fukuda, D.; Liu, H.Y.; Fathi, S.E.; Sellers, E.; Liu, T.; Chan, A.H.C. FDEM modelling of rock fracture and fragmentation induced by contour blasting during tunnelling with high horizontal in-situ stress. Int. J. Rock. Mech. Min. Sci. 2020, 127, 104214. [Google Scholar] [CrossRef]
- Han, H.; Fukuda, D.; Liu, H.; Salmi, E.F.; Sellers, E.; Liu, T.; Chan, A. FDEM simulation of rock damage evolution induced by contour blasting in the bench of tunnel at deep depth. Tunn. Undergr. Space Technol. 2020, 103, 103495. [Google Scholar] [CrossRef]
- Han, H.; Fukuda, D.; Xie, J.; Salmi, E.F.; Sellers, E.; Liu, H.; Chan, A. Rock dynamic fracture by destress blasting and application in controlling rockbursts in deep underground. Comput. Geotech. 2023, 155, 105228. [Google Scholar] [CrossRef]
- Yang, P.; Xiang, J.; Chen, M.; Fang, F.; Pavlidis, D.; Latham, J.P.; Pain, C. The immersed-body gas-solid interaction model for blast analysis in fractured solid media. Int. J. Rock. Mech. Min. Sci. 2017, 91, 119–132. [Google Scholar] [CrossRef]
- Yang, P.; Lei, Q.; Xiang, J.; Latham, J.P.; Pain, C. Numerical simulation of blasting in confined fractured rocks using an immersed-body fluid-solid interaction model. Tunn. Undergroud Space Technol. 2020, 98, 103352. [Google Scholar] [CrossRef]
- Munjiza, A.; Rougier, E.; Lei, Z.; Knight, E.E. FSIS: A novel fluid-solid interaction solver for fracturing and fragmenting solids. Comput. Part. Mech. 2020, 7, 789–805. [Google Scholar] [CrossRef]
- Lu, A.; Yang, P.; Lu, W.; Li, X.; Lin, X.; Luo, S.; Huang, S.; Grasselli, G. Crack propagation mechanism of smooth blasting holes for tunnel excavation under high in-situ stress. Eng. Frac Mech. 2024, 304, 110144. [Google Scholar] [CrossRef]
- Raghavaraju, R.; Mohanty, B. Experimental and numerical study on the transmitted shock wave from a blasthole. In Proceedings of the14th International Symposium on Rock Fragmentation by Blasting (FRAGBLAST14), Antalya, Türkiye, 7–10 April 2025; pp. 217–227. [Google Scholar]
- Lei, Z.; Rougier, E.; Knight, E.E. Block caving induced instability analysis using FDEM. In Proceedings of the 47th U.S. Rock Mechanics/Geomechanics Symposium, San Francisco, California, 23–26 June 2013; p. ARMA 13-703. [Google Scholar]
- Liu, H.; Fukuda, D.; Han, H. Development and application of a three-dimensional GPGPU-parallelized FDEM for modelling rock fragmentation by blast. IOP Conf. Ser. Earth Environ. Sci. 2021, 861, 032027. [Google Scholar] [CrossRef]
- Wu, D.; Fukuda, D.; Min, G.; Li, H.; Liu, H.; Ogata, S.; Zhang, Q. Development of a GPGPU-parallelized 3-D FDEM with a novel and simple implementation of extrinsic cohesive zone model. Comput. Geotech. 2024, 174, 106643. [Google Scholar] [CrossRef]
- Banadaki, M.M.D. Stress-Wave Induced Fracture in Rock due to Explosive Action; University of Toronto: Toronto, ON, Canada, 2010. [Google Scholar]
- Lisjak, A.; Hinkey, J.; Andersen, J.; Mahabadi, O.; Detournay, E.; Araujo, E.; Rimmelin, R. Development of a novel dynamic wellbore fracturing technology by integrating full-scale experimental testing and FDEM numerical simulations. Rock. Mech. Rock. Eng. 2024. [Google Scholar] [CrossRef]
- Fang, Z.; Harrison, J.P. Numerical analysis of progressive fracture and associated behaviour of mine pillars by use of a local degradation model. Min. Technol. 2002, 111, 59–72. [Google Scholar] [CrossRef]
- Fu, J.W.; Zhang, X.Z.; Zhu, W.S.; Chen, K.; Guan, J.F. Simulating progressive failure in brittle jointed rock masses using a modified elastic-brittle model and the application. Eng. Fract. Mech. 2017, 178, 212–230. [Google Scholar] [CrossRef]
- Guo, S.; Qi, S.; Zou, Y.; Zheng, B. Numerical studies on the failure process of heterogeneous brittle rocks or rock-like materials under uniaxial compression. Materials 2017, 10, 378. [Google Scholar] [CrossRef]
- Shen, B.; Stephansson, O.; Rinne, M. Modelling Rock Fracturing Processes; Springer: Dordrecht, The Netherlands, 2014. [Google Scholar]
- Pramanik, R.; Deb, D. SPH procedures for modeling multiple intersecting discontinuities in geomaterial. Int. J. Numer. Anal. Methods Geomech. 2015, 39, 343–367. [Google Scholar] [CrossRef]
- Lu, W.; Leng, Z.; Chen, M.; Yan, P.; Hu, Y. A modified model to calculate the size of the crushed zone around a blast-hole. J. South. Afr. Inst. Min. Metall. 2016, 116, 412–422. [Google Scholar] [CrossRef]
- Li, Y.; Hu, S.; Sun, X.; Stan, M. A review: Applications of the phase field method in predicting microstructure and property evolution of irradiated nuclear materials. NPJ Comput. Mater. 2017, 3, 16. [Google Scholar] [CrossRef]
- Sargado, J.M.L.; Keilegavlen, E.; Berre, I.; Nordbotten, J.M. High-accuracy phase-field models for brittle fracture based on a new family of degradation functions. J. Mech. Phys. Solids 2017, 111, 458–489. [Google Scholar] [CrossRef]
- Lai, X.; Liu, L.; Li, S.; Zeleke, M.; Liu, Q.; Wang, Z. A non-ordinary state-based peridynamics modelling of fracture in quasi-brittle materials. Int. J. Impact Eng. 2018, 111, 130–146. [Google Scholar] [CrossRef]
- Zhu, F.; Zhao, J. Peridynamic modelling of blasting induced rock fractures. J. Mech. Phys. Solids 2021, 153, 104469. [Google Scholar] [CrossRef]
- Zheng, Y.; Yan, C. A coupled FDEM-SPH model for simulating problems of fluid-solid interaction. Int. J. Num. Analy. Meth. Geomech. 2025, 1–20. [Google Scholar] [CrossRef]
- Zhang, Y.; Wong, L.N.Y. A review of numerical techniques approaching microstructures of crystalline rocks. Comput. Geosci. 2018, 115, 167–187. [Google Scholar] [CrossRef]
- Munjiza, A.A.; Knight, E.E.; Rougier, E. Computational Mechanics of Discontinua; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar] [CrossRef]
- Liu, H.Y. Hybrid finite-discrete element modelling of dynamic fracture of rocks with various geometries. Appl. Mech. Mater. 2012, 256, 183–186. [Google Scholar] [CrossRef]
- Liu, H.Y.; Han, H.; An, H.M.; Shi, J.J. Hybrid finite-discrete element modelling of asperity degradation and gouge grinding during direct shearing of rough rock joints. Int. J. Coal Sci. Technol. 2016, 3, 295–310. [Google Scholar] [CrossRef]
- Mohammadnejad, M.; Fukuda, D.; Liu, H.Y.; Dehkhoda, S.; Chan, A. GPGPU-parallelized 3D combined finite–discrete element modelling of rock fracture with adaptive contact activation approach. Comp. Part. Mech. 2020, 7, 849–867. [Google Scholar] [CrossRef]
- Yahaghi, J.; Liu, H.; Chan, A.; Fukuda, D. Development of a three-dimensional grain-based combined finite-discrete element method to model the failure process of fine-grained sandstones. Comput. Geotech. 2023, 153, 105065. [Google Scholar] [CrossRef]
- Han, H.; Fukuda, D.; Liu, H.; Zhang, Q.; Zhao, J.; Wu, D.; Chan, A. Modelling dynamic fracture and fragmentation of rocks under multiaxial coupled static and dynamic loads with a parallelised 3D FDEM. Comput. Geotech. 2024, 172, 106483. [Google Scholar] [CrossRef]
- Han, H.; Liu, X.; Liu, H.; Fukuda, D.; Zeng, L.; Xiong, Z.; Chan, A. Analysis of Step-Path Failure Mechanisms in Rock Slopes with En-Echelon Joints Based on FDEM Simulation. Simul. Model. Pract. Theory 2025, 142, 103138. [Google Scholar] [CrossRef]
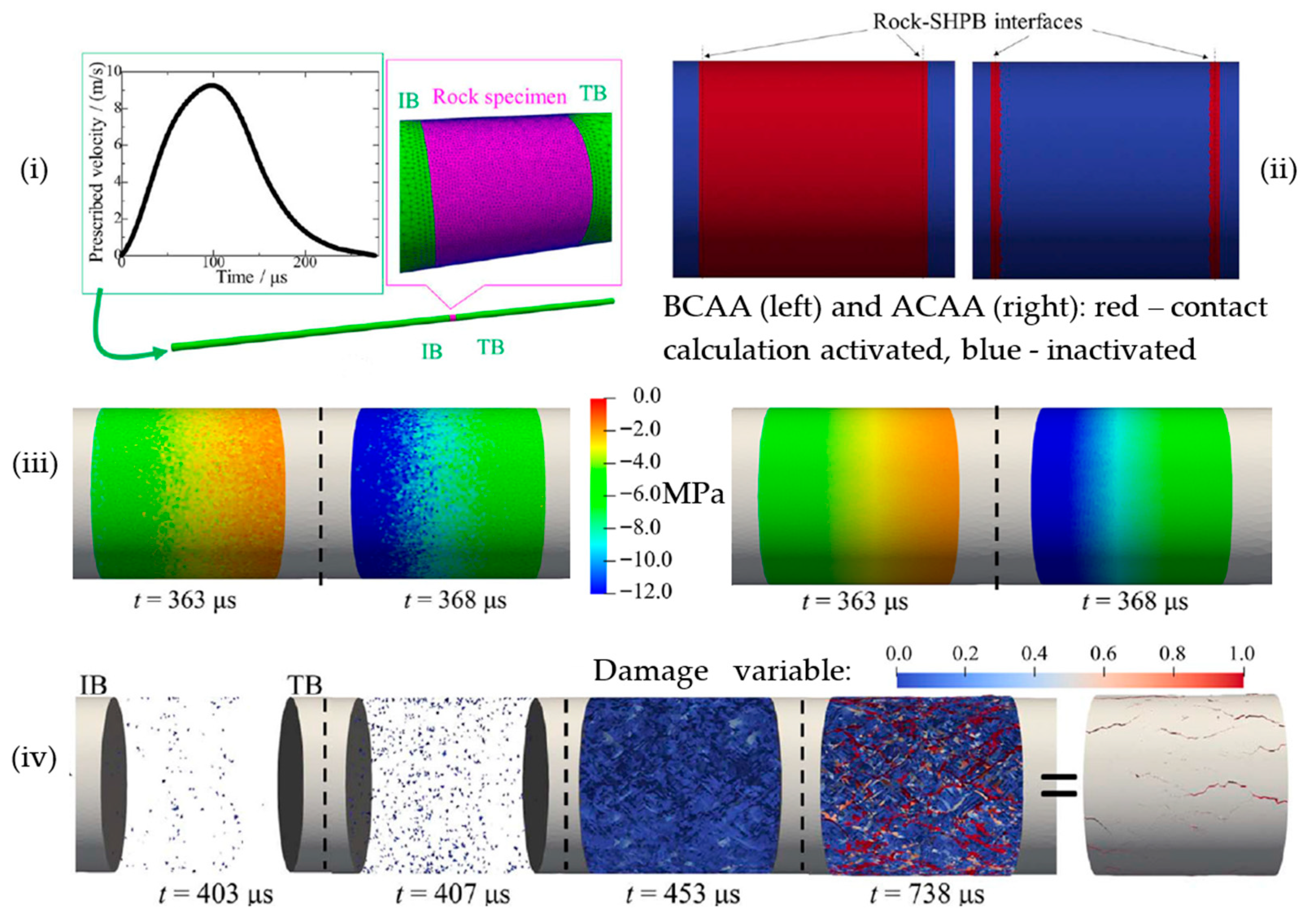
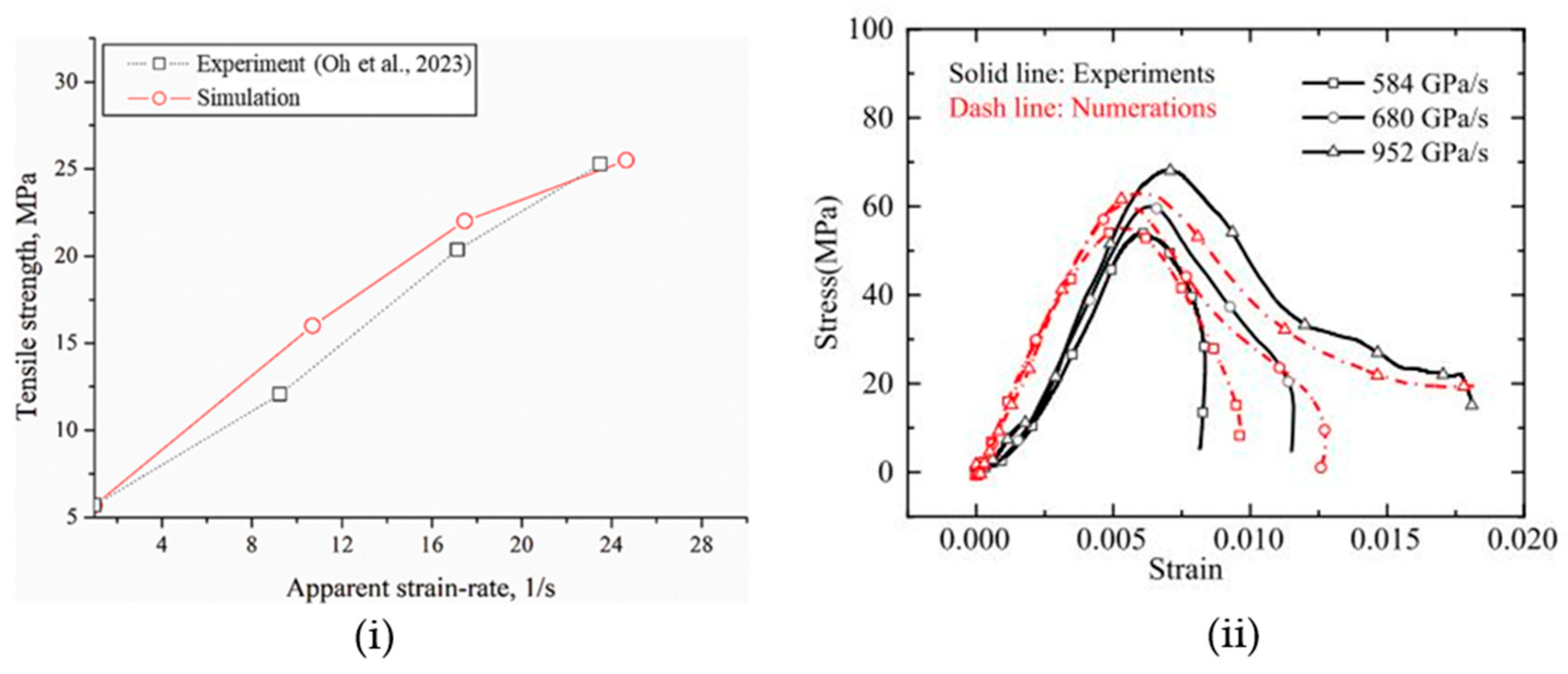
- Min, G.; Fukuda, D.; Oh, S.; Liu, H.; Cho, S. Verification of Spalling Tensile Strength of Rocks using 3D GPGPU-accelerated Hybrid FEM/DEM. IOP Conf. Ser. Earth Environ. Sci. 2023, 1124, 012117. [Google Scholar] [CrossRef]
- Yan, Y.; Li, J.; Fukuda, D.; Liu, H. Experimental and numerical studies on dynamic fracturing behavior of roughly jointed rock. Comput. Part. Mech. 2024, 11, 1715–1734. [Google Scholar] [CrossRef]
- Yang, X.; Xiang, J.; Latham, J.P.; Naderi, S.; Wang, Y. Cracking and fragmentation in percussive drilling: Insight from FDEM simulation. J. Rock. Mech. Geotech. Eng. 2025, in press. [CrossRef]
- Lysmer, J.; Kuhlemeyer, R.L. Finite dynamic model for infinite media. J. Eng. Mech. Div. 1969, 95, 859–877. [Google Scholar] [CrossRef]
- Cunningham, C. Blasthole Pressure: What it really means and how we should use it. Proc. Annu. Conf. Explos. Blasting Tech. 2006, 32, 255. [Google Scholar]
- Olsson, M.; Niklasson, B.; Wilson, L.; Andersson, C.; Christiansson, R. Äspö HRL: Experiences of Blasting of the TASQ Tunnel; SKB-R--04-73; Swedish Nuclear Fuel and Waste Management Co.: Solna, Sweden, 2004. [Google Scholar]
- Starfield, A.M. Strain wave theory in rock blasting. In Proceedings of the The 8th U.S. Symposium on Rock Mechanics (USRMS), Minneapolis, MN, USA, 15–17 September 1966; p. ARMA-66-0538. [Google Scholar]
- Rossmanith, H.P.; Kouzniak, N. Supersonic detonation in rock mass—Part 2: Particle displacements and velocity fields for single and multiple non-delayed and delayed detonating blastholes. Fragblast 2004, 8, 95–117. [Google Scholar] [CrossRef]
- Mitelman, A.; Elmo, D. Modelling of blast-induced damage in tunnels using a hybrid finite-discrete numerical approach. J. Rock. Mech. Geotech. Eng. 2014, 6, 565–573. [Google Scholar] [CrossRef]
- Liu, K.; Zhang, Q.B.; Wu, G.; Li, J.C.; Zhao, J. Dynamic mechanical and fracture behaviour of sandstone under multiaxial loads using a triaxial Hopkinson bar. Rock. Mech. Rock. Eng. 2019, 52, 2175–2195. [Google Scholar] [CrossRef]
- Daehnke, A.; Rossmanith, H.P.; Napier, J.A.L. Gas pressurisation of blast-induced conical cracks. Int. J. Rock. Mech. Min. Sci. 1997, 34, 263.e1–263.e17. [Google Scholar] [CrossRef]
- Ruest, M.R. Numerical Methods for Simulating the Flow of Detonation Products Within an Explicit Fracture Network Formed by the Coalescence of Cracks During Blasting. Ph.D. Thesis, The University of Queensland, Brisbane, Australian, 2008. [Google Scholar] [CrossRef]
- Furtney, J.K.; Sellers, E.; Onederra, I. Simple models for the complex process of rock blasting. In Rock Fragmentation by Blasting; CRC Press: Boca Raton, Florida, USA, 2012; pp. 40–47. [Google Scholar] [CrossRef]
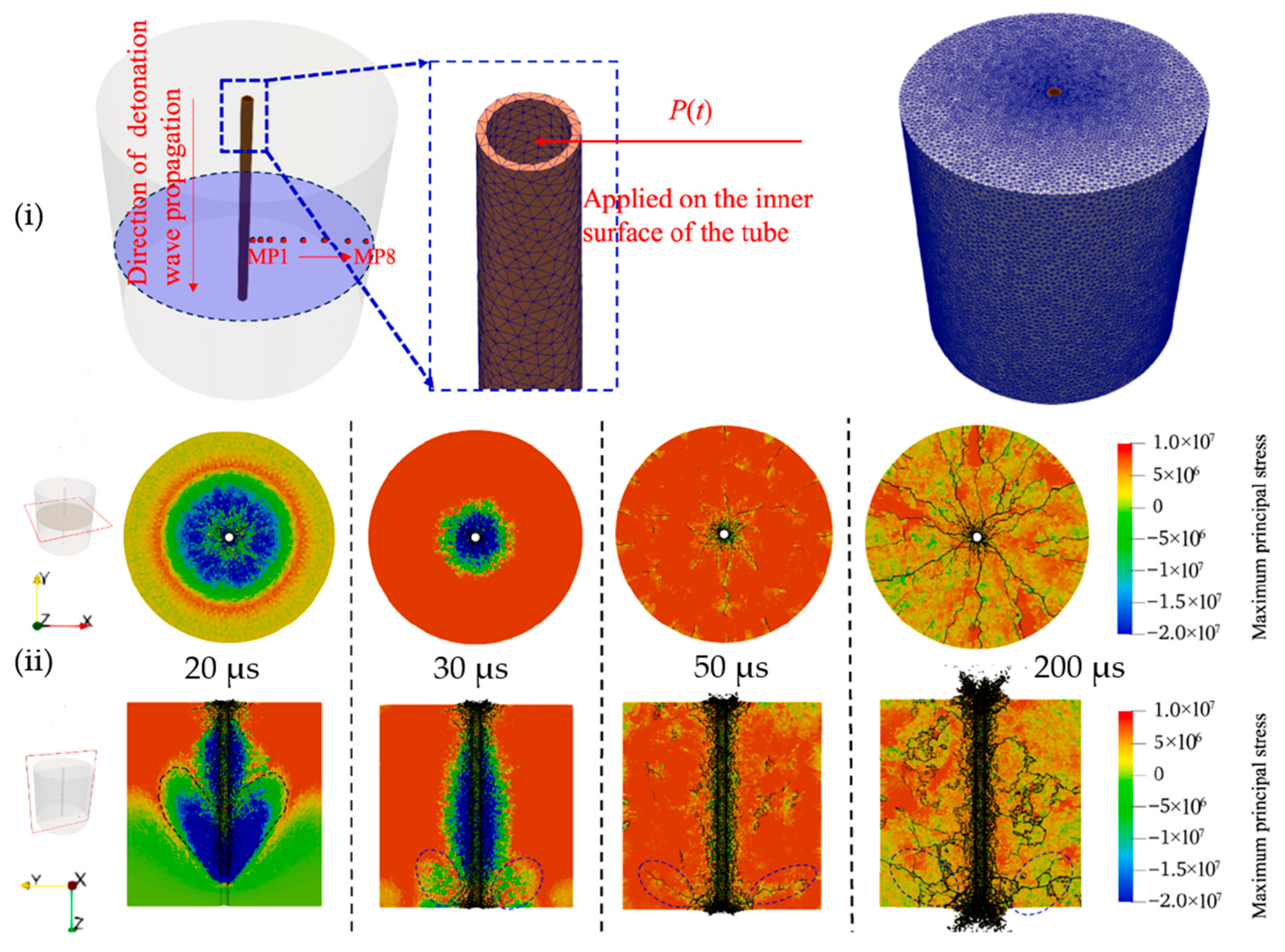
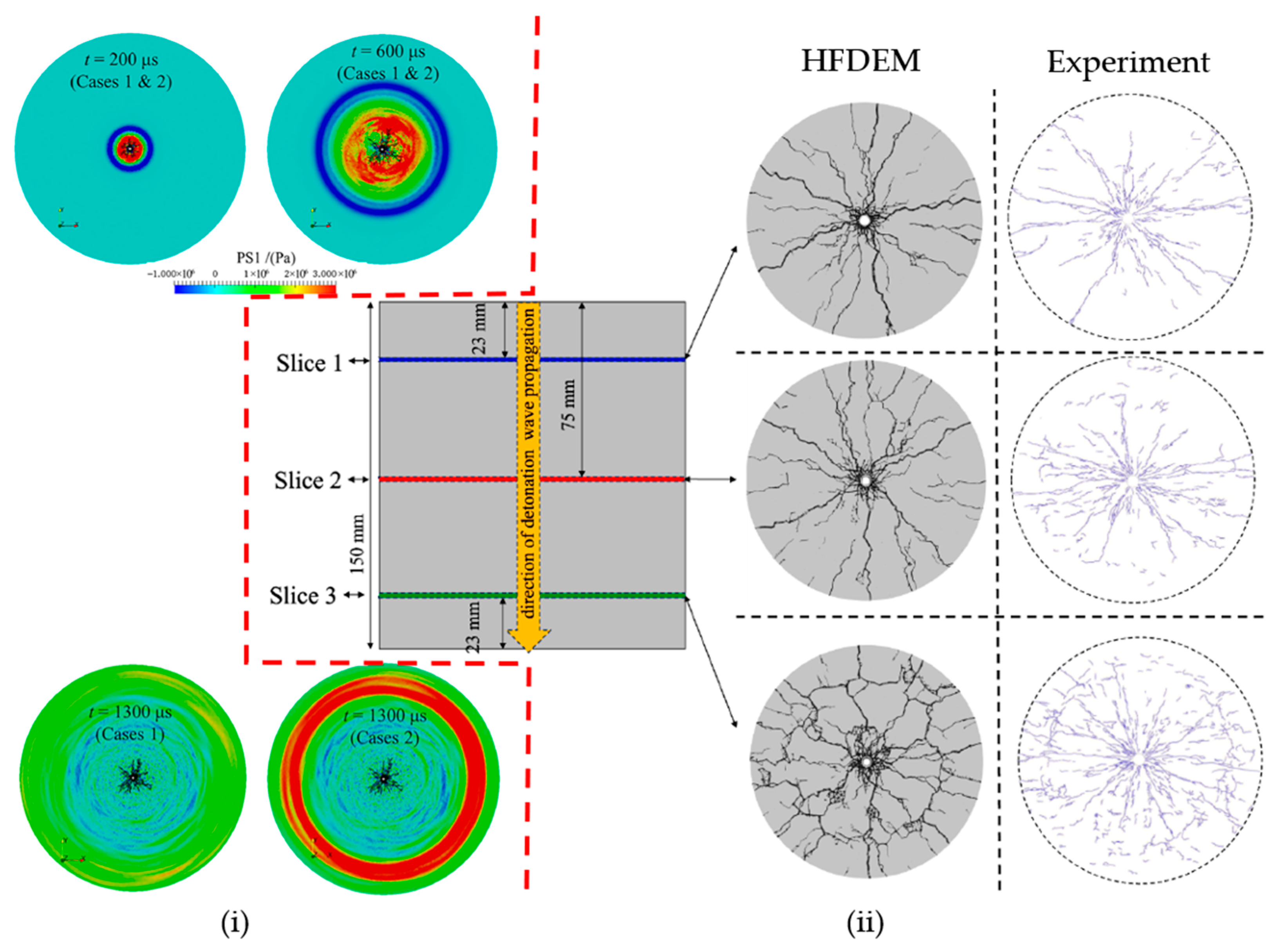
- Kamran, M.; Liu, H.; Fukuda, D.; Wu, D.; Min, G.; Salmi, E.F.; Sellers, E.; Chan, A. 3D Hybrid Finite-Discrete Element Modelling of Dynamic Fracture Induced by Controlled Blasting. In Proceedings of the 14th International Symposium on Rock Fragmentation by Blasting (FRAGBLAST 2025), Antalya, Turkey 7–10 April 2025. [Google Scholar]
- Nilson, R.H.; Proffer, W.J.; Duff, R.E. Modelling of gas-driven fractures induced by propellant combustion within a borehole. Int. J. Rock. Mech. Min. Sci. Geomech. Abstr. 1985, 22, 3–19. [Google Scholar] [CrossRef]
- Goodarzi, M.; Mohammadi, S.; Jafari, A. Numerical analysis of rock fracturing by gas pressure using the extended finite element method. Pet. Sci. 2015, 12, 304–315. [Google Scholar] [CrossRef]
- Fukuda, D.; Tashiro, O.; Ikawa, W.; Min, G.; Takahashi, Y.; Saburi, T.; Kubota, S. Development of a coupled numerical simulator incorporating key processes in rock blasting with the help of high-performance computing. In Proceedings of the 14th International Symposium on Rock Fragmentation by Blasting (FRAGBLAST 2025), Antalya, Türkiye, 7–10 April 2025. [Google Scholar]
- Quey, R.; Dawson, P.R.; Barbe, F. Large-scale 3D random polycrystals for the finite element method: Generation, meshing and remeshing. Comput. Methods Appl. Mech. Eng. 2011, 200, 1729–1745. [Google Scholar] [CrossRef]
- Kong, L.; Xie, H.; Li, C. Traction-based microplane model for charactering the progressive failure of rock-like material. J. Mech. Phys. Solids 2025, 194, 105910. [Google Scholar] [CrossRef]
- Jing, L. A review of techniques, advances and outstanding issues in numerical modelling for rock mechanics and rock engineering. Int. J. Rock. Mech. Min. Sci. 2003, 40, 283–353. [Google Scholar] [CrossRef]
- Wang, J.; Apel, D.B.; Pu, Y.; Hall, R.; Wei, C.; Sepehri, M. Numerical modelling for rockbursts: A state-of-the-art review. J. Rock. Mech. Geotech. Eng. 2021, 13, 457–478. [Google Scholar] [CrossRef]

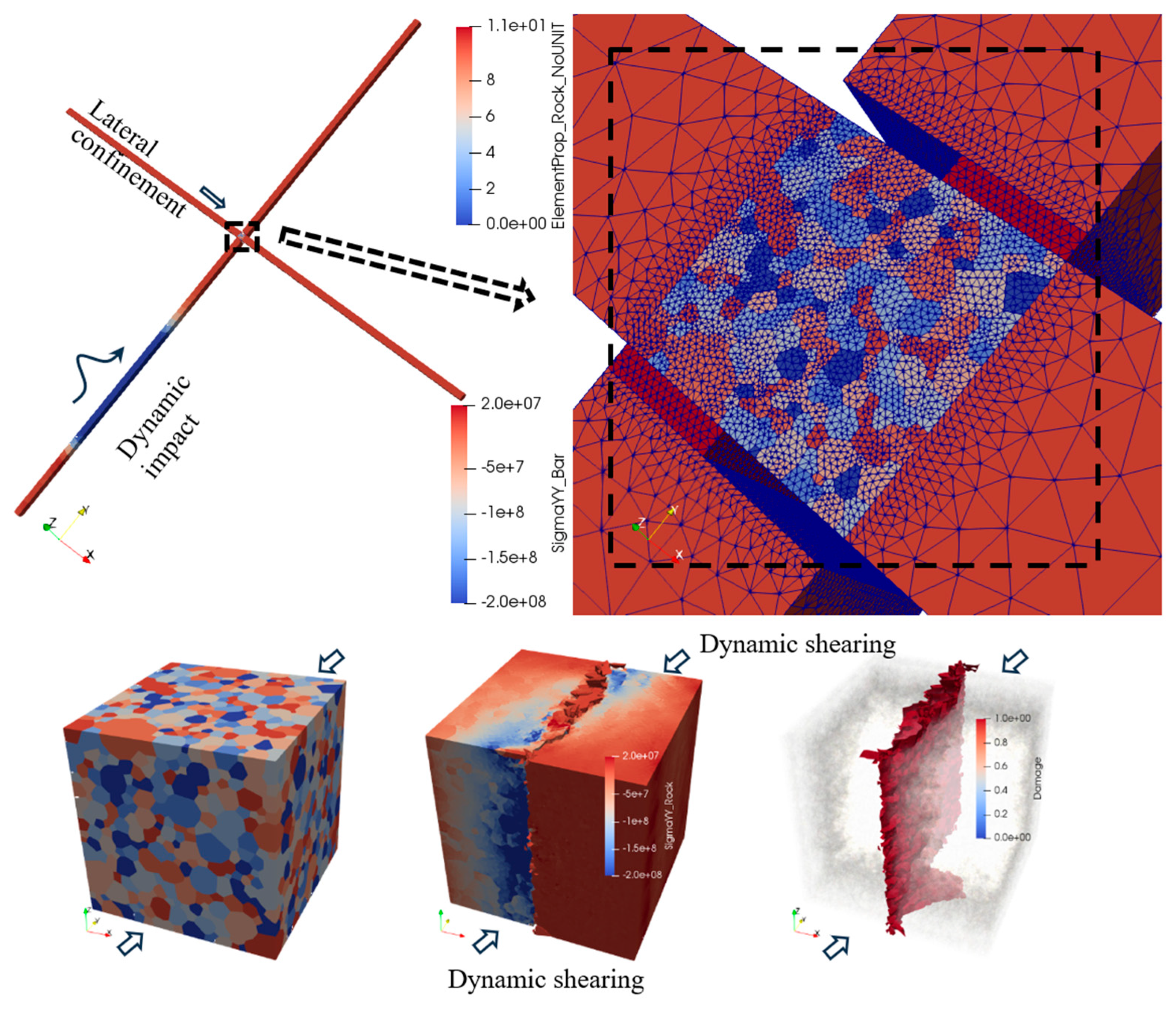
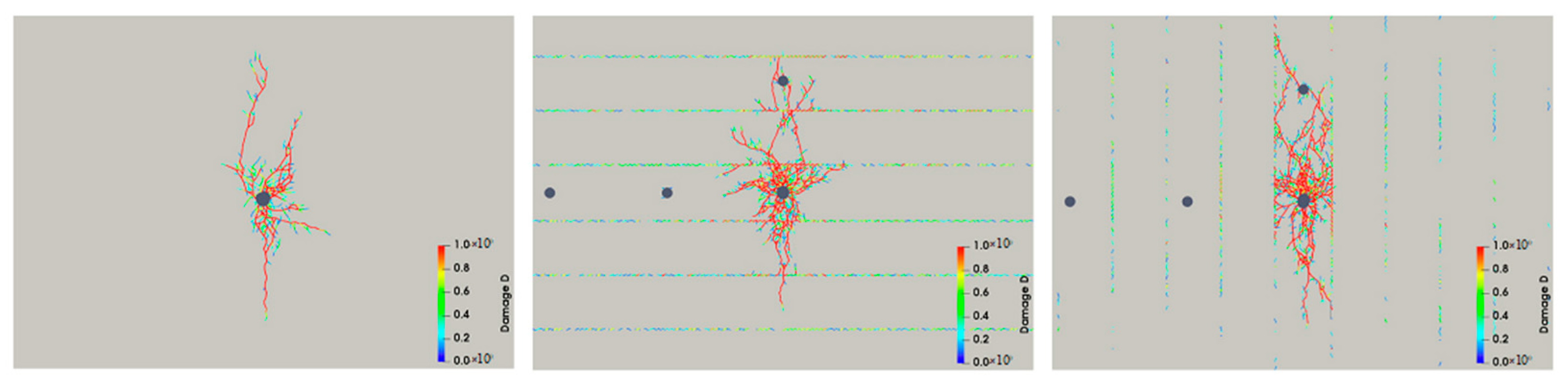


| Types | Positive Aspects | Negative Aspects |
|---|---|---|
| Static fracture | Fracture frequently displays distinct patterns, allowing for quite accurate predictions | Fracture can take a considerable amount of time to develop |
| Static loads allow for a better regulated mode of rock failure Feasible to employ mitigation strategies to prevent or control rock fractures given the gradual nature of static loads Insignificant to loading rates | May not completely convey the conditions that rock experiences in real-world scenarios Fractures may have limited capacity to accommodate localized variations in rock properties or structural vulnerabilities | |
| Dynamic fracture | Offer more accurate representation of abrupt and dynamic occurrences, such as rockfall, rockburst or blasting | Frequently extremely unpredictable due to the complexity of dynamic events and continuously changing interactions |
| Fail abruptly without any warning, which can facilitate the efficient removal or fragmentation of boulders in mining and construction Failure process is sensitive to localized variations in rock properties | Typically sudden and unexpected Strong loading rate-dependent |
| Methods (Code and Literature) | Positive Aspects | Negative Aspects |
|---|---|---|
| FEM | Implicit and explicit algorithms for distinct static and dynamic processes, respectively | Complex and difficult to model granular properties and contact mechanics |
| ADINA [59] (ABAQUS) [62,74] (LS-DYNA) [63,68,69,70,71,79] (AUTODYN) [61,75,76,77] (XFEM) [40,48,49] (PFEM) [55,56] (RFPA) [60,66] (Others) [80] | Capture complex Multiphysics behavior Easy to be combined with other numerical techniques to solve complex problems Inherent scale independence Allow rapid analysis of stress concentration zones, deformation pattern and associated design implications Easily handle material heterogeneity and geometric nonlinearity Model the complex mechanical behavior in rock and rock mass by incorporating diverse constitutive models Able to simultaneously simulate high strain rate, strain hardening and damage softening as well as confining pressures Suitable for small deformation | Challenging to model discontinuous behavior and not suitable for highly jointed-blocky media Post-processing method is needed to transfer damage to fracture/fragmentation, which is somewhat arbitrary, and hence a strong background in numerical analysis is crucial Difficult to understand the behaviour of individual cracks Calculation time increases exponentially with number of elements, especially in the case of implicit integration Input limitations due to the difficulty in determining certain critical parameters |
| DEM | Able to model complicated interactions | Computationally expensive |
| (PFC) [91,92,104] (UDEC/3DEC) [96,103] (DDA) [102,105,106] (Yade) [93,94,95] (HSBM) [107] (DFN) [109] (CDEM) [110] | Easy to model jointed rock systems Able to mimic granular flow, collision and compaction Able to describe bulk material behavior through its microstructure Allow large deformation and detachment of blocks | Small time step and continuous changing contact detection Limited ability to capture high-speed impact or fluidized flows Unclear relationship between micro- and macro-properties, which makes parameter calibration process laborious (PFC) Crack trajectory is either predetermined or mesh dependent (UDEC/3DEC and DDA) |
| FDEM | Inherit all advantages of FEM and DEM | Overcome most disadvantages of FEM and DEM but computationally expensive |
| (Y2D) [111,147,155] (ELFEN) [116,124] (Y-Geo) [119,137,154] (Solidity) [145,151,152] (HOSS) [112,120,123,138,156] (HFDEM) [3,133,134,139,140,141,149,150,157,158] (Irazu) [121,132,160] (MultiFS) [123,171] (Others) [136,137] | Account for transition from continuum to discontinuum Become pure FEM before fracturing when extrinsic cohesive zone model is adopted Deformable, breakable and irregular-shaped discrete particles Simpler contact calculations than DEM | Parallelization is essential for large models and 3D models Need parameter calibrations There is a scarcity of data concerning contact properties and fracture mechanics characteristics Micro-cracking highly depends on the fracturing mechanism |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kamran, M.; Liu, H.; Fukuda, D.; Jia, P.; Min, G.; Chan, A. State-of-the-Art Review and Prospect of Modelling the Dynamic Fracture of Rocks Under Impact Loads and Application in Blasting. Geosciences 2025, 15, 314. https://doi.org/10.3390/geosciences15080314
Kamran M, Liu H, Fukuda D, Jia P, Min G, Chan A. State-of-the-Art Review and Prospect of Modelling the Dynamic Fracture of Rocks Under Impact Loads and Application in Blasting. Geosciences. 2025; 15(8):314. https://doi.org/10.3390/geosciences15080314
Chicago/Turabian StyleKamran, Muhammad, Hongyuan Liu, Daisuke Fukuda, Peng Jia, Gyeongjo Min, and Andrew Chan. 2025. "State-of-the-Art Review and Prospect of Modelling the Dynamic Fracture of Rocks Under Impact Loads and Application in Blasting" Geosciences 15, no. 8: 314. https://doi.org/10.3390/geosciences15080314
APA StyleKamran, M., Liu, H., Fukuda, D., Jia, P., Min, G., & Chan, A. (2025). State-of-the-Art Review and Prospect of Modelling the Dynamic Fracture of Rocks Under Impact Loads and Application in Blasting. Geosciences, 15(8), 314. https://doi.org/10.3390/geosciences15080314








