Integrated Capuchin Search Algorithm-Optimized Multilayer Perceptron for Robust and Precise Prediction of Blast-Induced Airblast in a Blasting Mining Operation
Abstract
1. Introduction
- PSO-ANN: uses particle swarm optimization to tune weights and biases but lacks CapSA’s multiphase search operators.
- MVRA: offers a transparent linear regression baseline.
- USBM predictor: depends on scaled distance and charge weight correlations.
2. Materials and Methods
2.1. Data Acquisition
2.2. Geology of the Area
- Lithology: The primary rock is a large granite with coarse grains that is part of the Gaborone Granite Complex. Moreover, the mineralogy of the area consists of equigranular Quartz, K-feldspar, plagioclase, and biotite with fresh exposures that are light grey to pinkish [37].
- Weathering and overburden profile: It consists of topsoil that is less than 1 m, characterized by aeolian silts, calcrete nodules, and sparse vegetation. The saprolite is between 1 m to 3 m, made of soft, clay-laden, orange-brown material with remnants of the original granitoid structure. In addition, saprock lies between 2 m to 5 m and it is made up of blocky, fractured granite corestones that are friable and micro-fractured. Moreover, the fresh granite lies deeper than 5 m and serves as the primary aggregate resource.
- Quarry bench geometry: The quarry has bench heights ranging from 8–10 m, while the bench angles are 70–75 degrees. Furthermore, berm widths are 3–5 m and act as catch benches for loose rocks. The overall depth of pit is more than fifty meters below the initial ground surface.
- Structural and discontinuity features: There are two main sets of joints in the quarry, which are subvertical NE-SW and steeply sloping NW-SE. The spacing between them is 1.5 m, and there are irregular vein-like intrusions of about less than 0.5 m thickness in some areas. Furthermore, it can be observed that the bench faces show different rock fracture intensities as shown in Figure 2.
- Hydrogeology and ground conditions: The quarry has poor natural drainage, which results in a buildup of rainfall and seepage in the lower benches, resulting in water pools. However, the operators use portable centrifugal pumps, which are rated between 5–10 horsepower, to pump water buildups to settling ponds and other natural drainage channels. Furthermore, regular dewatering is done to keep bench surfaces free of water, thus decreasing pore pressures around drillholes, and this leads to improved drilling efficiency while mitigating the risks of drill rig instability, bit slippage, and worker slips or falls. This level of water monitoring and pumping of buildups ensures secure and uninterrupted drilling.
2.3. Rock Mass Characterization
3. Proposed CapSA-MLP, PSO-ANN, MVRA, and the USBM Predictor Approaches for Predicting Blast-Induced Airblast
3.1. Capuchin Search Algorithm–Optimized Multilayer Perceptron
- Jump operator: With probability pjump capuchin executes a large random perturbation:where represents network hyperparameters and initial weights, and σjump is a scaling parameter that promotes prolonged exploration.
- Swing operator: as a substitute, with probability, Pswing, the capuchin advances toward the present global optimum via weighted vector shift:
- Climb operator: If neither Jump nor Swing is activated, the capuchin conducts a localized fine-tuning, defined as follows:where is a minor standard deviation that enables accurate weight and hyperparameter modifications to reduce RMSE.
3.2. Multivariate Regression Analysis (MVRA)
3.3. USBM Predictor
3.4. Rock Mass Strength Calculation
3.5. Implementation of CapSA-MLP, PSO-ANN, MVRA, and USBM Models
- Data segmentation and preprocessing: A total of 75 blasting datasets were randomly partitioned into training (80%) and testing (20%) sets. Also, additional independent validation of 15 new blasting datasets was set aside to be used for final model verification. No missing values were identified, as all parameters were obtained on site and determined through laboratory uniaxial compressive strength testing (RMS).
- CapSA-MLP: A feedforward multilayer perceptron architecture was employed with one hidden layer. The input layer included six neurons representing MCPD, RMS, HD, D, TEM, and NH, whereas the output layer featured a single neuron that generated the predicted airblast. A hyperbolic tangent sigmoid transfer function was applied in the hidden layer, while a linear transfer function was implemented in the output layer. Table 3 shows the statistics of the parameters used in developing CapSA-MLP models. Moreover, CapSA-MLP was set with a population size between 40 and 400 and allowed to run for a maximum of 200 iterations. Convergence was detected when the change in RMSE between successive iterations dropped below 1 × 10−4; at this moment, the search ended immediately. Lastly, it also stopped automatically after the 200th iteration.
- PSO-ANN: The total number of hidden neurons was set at the optimal value established by CapSA to provide a balanced comparison. The network comprised an input layer featuring six neurons (MCPD, RMS, HD, D, TEM, and NH) and an output layer containing one individual neuron that generated the estimated airblast. The hidden layer employed a hyperbolic tangent sigmoid activation function, while the output layer utilized a linear activation function. Table 5 shows the statistics of parameters used in developing the PSO models.
- MVRA: Applying Equation (6) to our dataset of blasts, the resultant equation for airblast is as follows:AB = 46.732 + 0.108NH + 0.019D + 1.591HD + 12.06RMS + 0.0099MCPD − 0.0011TEM
- USBM predictor: For this study, we adopted the commonly used USBM predictor, as seen in many previous studies. The values of H and −β of the USBM predictor were determined based on the training datasets. A simple linear regression analysis was performed on datasets, with a training-to-testing ratio of 80% to 20%. The USBM predictor Equation (6) was transformed into the usual form of a linear equation, y = mx + c, by applying logarithms to both sides of the equation. Taking the logarithm on both sides gives the USBM predictor (8):logP = logH − βlogSD
3.6. Performance Metrics
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Acronym | Full Form |
| RMS | Rock mass strength |
| CapSA-MLP | Capuchin search algorithm-optimized multilayer perceptron |
| PSO-ANN | Particle swarm optimized–artificial neural network |
| MVRA | Multivariate regression analysis |
| USBM | United States Bureau of Mines |
| MCPD | Maximum charge per delay |
| TEM | Total explosive mass |
| NH | Number of holes |
| HD | Hole depth |
| D | Monitoring distance |
| RQD | Rock quality designation |
| SVM | Support vector machine |
| GA | Genetic algorithm |
| ANFIS | Adaptive neuro-fuzzy inference system |
| ANN | Artificial neural network |
| ST | Stemming length |
| RD | Rock density |
| S | Spacing |
| BH | Bench height |
| B | Burden |
References
- Wharton, R.K.; Formby, S.A.; Merrifield, R. Airblast TNT Equivalence for a Range of Commercial Blasting Explosives. J. Hazard. Mater. 2000, 79, 31–39. [Google Scholar] [CrossRef] [PubMed]
- Wu, C.; Hao, H. Modeling of Simultaneous Ground Shock and Airblast Pressure on Nearby Structures from Surface Explosions. Int. J. Impact Eng. 2005, 31, 699–717. [Google Scholar] [CrossRef]
- Rodríguez, R.; Toraño, J.; Menéndez, M. Prediction of the Airblast Wave Effects near a Tunnel Advanced by Drilling and Blasting. Tunn. Undergr. Space Technol. 2007, 22, 241–251. [Google Scholar] [CrossRef]
- Drew, L.J.; Langer, W.H.; Sachs, J.S. Environmentalism and Natural Aggregate Mining. Nat. Resour. Res. 2002, 11, 19–28. [Google Scholar] [CrossRef]
- Dehghani, H.; Alimohammadnia, F. Estimation of Air Over-Pressure Using Bat Algorithm. Min. Scince 2021, 28, 77–92. [Google Scholar] [CrossRef]
- Mohamad, E.T.; Hajihassani, M.; Armaghani, D.; Marto, A. Simulation of Blasting-Induced Air Over-pressure by Means of Artificial Neural Networks. Int. Rev. Model. Simul. 2012, 5, 2501–2506. [Google Scholar]
- Stachura, V.J. Airblast and Ground Vibration Generation and Propagation from Contour Mine Blasting; Bureau of Mines: Washington, DC, USA, 1984. [Google Scholar]
- Stachura, V.J.; Siskind, D.E.; Engler, A.J. Airblast Instrumentation and Measurement Techniques from Surface Mine Blasting; Bureau of Mines: Washington, DC, USA, 1981. [Google Scholar]
- Siskind, D.E. Vibrations from Blasting; International Society of Explosives Engineers: Cleveland, OH, USA, 2002. [Google Scholar]
- Balkema, A. Rock Blasting Terms and Symbols; Rustan, A., Ed.; Balkema Publishers: Rotterdam, The Netherlands, 1998; ISBN 9780429190650. [Google Scholar]
- Kuzu, C.; Fisne, A.; Ercelebi, S.G. Operational and Geological Parameters in the Assessing Blast Induced Airblast-Overpressure in Quarries. Appl. Acoust. 2009, 70, 404–411. [Google Scholar] [CrossRef]
- Segarra, P.; Domingo, J.F.; López, L.M.; Sanchidrián, J.A.; Ortega, M.F. Prediction of near Field Overpres-sure from Quarry Blasting. Appl. Acoust. 2010, 71, 1169–1176. [Google Scholar] [CrossRef]
- Khandelwal, M.; Kankar, P.K. Prediction of Blast-Induced Air Overpressure Using Support Vector Ma-chine. Arab. J. Geosci. 2011, 4, 427–433. [Google Scholar] [CrossRef]
- Mohamad, T.E.; Jahed Armaghani, D.; Hasanipanah, M.; Murlidhar, B.R.; Alel, M.N.A. Estimation of Air-Overpressure Produced by Blasting Operation through a Neuro-Genetic Technique. Environ. Earth Sci. 2016, 75, 174. [Google Scholar] [CrossRef]
- Khandelwal, M.; Singh, T.N. Prediction of Blast Induced Air Overpressure in Opencast Mine. Noise Vib. Worldw. 2005, 36, 7–16. [Google Scholar] [CrossRef]
- Ureel, S.; Momayez, M. An Investigation of the Present and Future Testing Methods of Rock Abrasion Resistance. Int. J. Min. Eng. Miner. Process. 2014, 3, 10–19. [Google Scholar]
- Naiem, M.M.A.A. Correlation of Sandstone Rock Properties Obtained from Field and Laboratory Tests. Int. J. Civ. Struct. Eng. 2013, 4, 45–55. [Google Scholar]
- Priddy, K.; Keller, P.E. Artificial Neural Networks: An Introduction; SPIE Press: Bellingham, WA, USA, 2005. [Google Scholar]
- Adhikari, R.; Agrawal, R.K.; Adhikari, R. Effectiveness of PSO Based Neural Network for Seasonal Time Series Forecasting. In Proceedings of the Fifth Indian International Conference on Artificial Intelligence, Tumkur, India, 14–16 December 2011; Volume 3, pp. 231–244. [Google Scholar]
- Wang, X.G.; Tang, Z.; Tamura, H.; Ishii, M.; Sun, W.D. An Improved Backpropagation Algorithm to Avoid the Local Minima Problem. Neurocomputing 2004, 56, 455–460. [Google Scholar] [CrossRef]
- Kazemi, M.M.K.; Nabavi, Z.; Khandelwal, M. Prediction of Blast-Induced Air Overpressure Using a Hybrid Machine Learning Model and Gene Expression Programming (GEP): A Case Study from an Iron Ore Mine. AIMS Geosci. 2023, 9, 357–381. [Google Scholar] [CrossRef]
- Zhang, R.; Li, Y.; Gui, Y.; Zhou, J. Prediction of Blasting Induced Air-Overpressure Using a Radial Basis Function Network with an Additional Hidden Layer. Appl. Soft Comput. 2022, 127, 109343. [Google Scholar] [CrossRef]
- Zeng, J.; Jamei, M.; Nait Amar, M.; Hasanipanah, M.; Bayat, P. A Novel Solution for Simulating Air Over-pressure Resulting from Blasting Using an Efficient Cascaded Forward Neural Network. Eng. Comput. 2022, 38, 2069–2081. [Google Scholar] [CrossRef]
- Faradonbeh, R.S.; Armaghani, D.J.; Amnieh, H.B.; Mohamad, E.T. Prediction and Minimization of Blast-Induced Flyrock Using Gene Expression Programming and Firefly Algorithm. Neural Comput. Appl. 2018, 29, 269–281. [Google Scholar] [CrossRef]
- Jahed Armaghani, D.; Hasanipanah, M.; Tonnizam Mohamad, E. A Combination of the ICA-ANN Model to Predict Air-Overpressure Resulting from Blasting. Eng. Comput. 2016, 32, 155–171. [Google Scholar] [CrossRef]
- Hajihassani, M.; Jahed Armaghani, D.; Monjezi, M.; Mohamad, E.T.; Marto, A. Blast-Induced Air and Ground Vibration Prediction: A Particle Swarm Optimization-Based Artificial Neural Network Approach. Environ. Earth Sci. 2015, 74, 2799–2817. [Google Scholar] [CrossRef]
- Jahed Armaghani, D.; Hajihassani, M.; Sohaei, H.; Tonnizam Mohamad, E.; Marto, A.; Motaghedi, H.; Moghad-dam, M.R. Neuro-Fuzzy Technique to Predict Air-Overpressure Induced by Blasting. Arab. J. Geosci. 2015, 8, 10937–10950. [Google Scholar] [CrossRef]
- Khatir, A.; Capozucca, R.; Khatir, S.; Magagnini, E.; Cuong-Le, T. Enhancing Damage Detection Using Reptile Search Algorithm-Optimized Neural Network and Frequency Response Function. J. Vib. Eng. Technol. 2025, 13, 88. [Google Scholar] [CrossRef]
- Khatir, A.; Capozucca, R.; Khatir, S.; Magagnini, E.; Benaissa, B.; Le Thanh, C.; Abdel Wahab, M. A New Hybrid PSO-YUKI for Double Cracks Identification in CFRP Cantilever Beam. Compos. Struct. 2023, 311, 116803. [Google Scholar] [CrossRef]
- Ouadi, B.; Khatir, A.; Magagnini, E.; Mokadem, M.; Abualigah, L.; Smerat, A. Optimizing Silt Density Index Prediction in Water Treatment Systems Using Pressure-Based Gradient Boosting Hybridized with Salp Swarm Algorithm. J. Water Process Eng. 2024, 68, 106479. [Google Scholar] [CrossRef]
- Osmani, A.; Shamass, R.; Tsavdaridis, K.D.; Ferreira, F.P.V.; Khatir, A. Deflection Predictions of Tapered Cellular Steel Beams Using Analytical Models and an Artificial Neural Network. Buildings 2025, 15, 992. [Google Scholar] [CrossRef]
- Braik, M.; Sheta, A.; Al-Hiary, H. A Novel Meta-Heuristic Search Algorithm for Solving Optimization Problems: Capuchin Search Algorithm. Neural Comput. Appl. 2021, 33, 2515–2547. [Google Scholar] [CrossRef]
- Eker, E. Performance Evaluation of Capuchin Search Algorithm Through Non-Linear Problems, and Optimization of Gear Train Design Problem. Eur. J. Tech. 2023, 13, 142–149. [Google Scholar] [CrossRef]
- He, Z.; Armaghani, D.J.; Masoumnezhad, M.; Khandelwal, M.; Zhou, J.; Murlidhar, B.R. A Combination of Expert-Based System and Advanced Decision-Tree Algorithms to Predict Air-Overpressure Resulting from Quarry Blasting. Nat. Resour. Res. 2021, 30, 1889–1903. [Google Scholar] [CrossRef]
- Hosseini, S.; Poormirzaee, R.; Hajihassani, M. Application of Reliability-Based Back-Propagation Causality-Weighted Neural Networks to Estimate Air-Overpressure Due to Mine Blasting. Eng. Appl. Artif. Intell. 2022, 115, 105281. [Google Scholar] [CrossRef]
- Nguyen, H.; Bui, X.-N.; Drebenstedt, C.; Choi, Y. Enhanced Prediction Model for Blast-Induced Air Over-Pressure in Open-Pit Mines Using Data Enrichment and Random Walk-Based Grey Wolf Optimization–Two-Layer ANN Model. Nat. Resour. Res. 2024, 33, 943–972. [Google Scholar] [CrossRef]
- Mabogo, J.; Cotterill, D.K. The Gaborone Granite Complex: Petrology and Structure; Bulletin of the Geological Survey of Botswana: Gaborone, Botswana, 1989; Volume 23. [Google Scholar]
- Hoek, E.; Marinos, P.; Benissi, M. Applicability of the Geological Strength Index (GSI) Classification for Very Weak and Sheared Rock Masses. The Case of the Athens Schist Formation. Bull. Eng. Geol. Environ. 1998, 57, 151–160. [Google Scholar] [CrossRef]
- Dreyfus, G. Neural Networks: Methodology and Application; Springer: Berlin/Heidelberg, Germany, 2005; ISBN 3-540-22980-9. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; IEEE: New York, NY, USA, 1995; pp. 1942–1948. [Google Scholar]
- Lawal, A.I.; Aladejare, A.E.; Onifade, M.; Bada, S.; Idris, M.A. Predictions of Elemental Composition of Coal and Biomass from Their Proximate Analyses Using ANFIS, ANN and MLR. Int. J. Coal Sci. Technol. 2021, 8, 124–140. [Google Scholar] [CrossRef]
- Onifade, M.; Lawal, A.I.; Aladejare, A.E.; Bada, S.; Idris, M.A. Prediction of Gross Calorific Value of Solid Fuels from Their Proximate Analysis Using Soft Computing and Regression Analysis. Int. J. Coal Prep. Util. 2022, 42, 1170–1184. [Google Scholar] [CrossRef]
- Said, K.O.; Onifade, M.; Lawal, A.I.; Githiria, J.M. An Artificial Intelligence-Based Model for the Prediction of Spontaneous Combustion Liability of Coal Based on Its Proximate Analysis. Combust. Sci. Technol. 2021, 193, 2350–2367. [Google Scholar] [CrossRef]
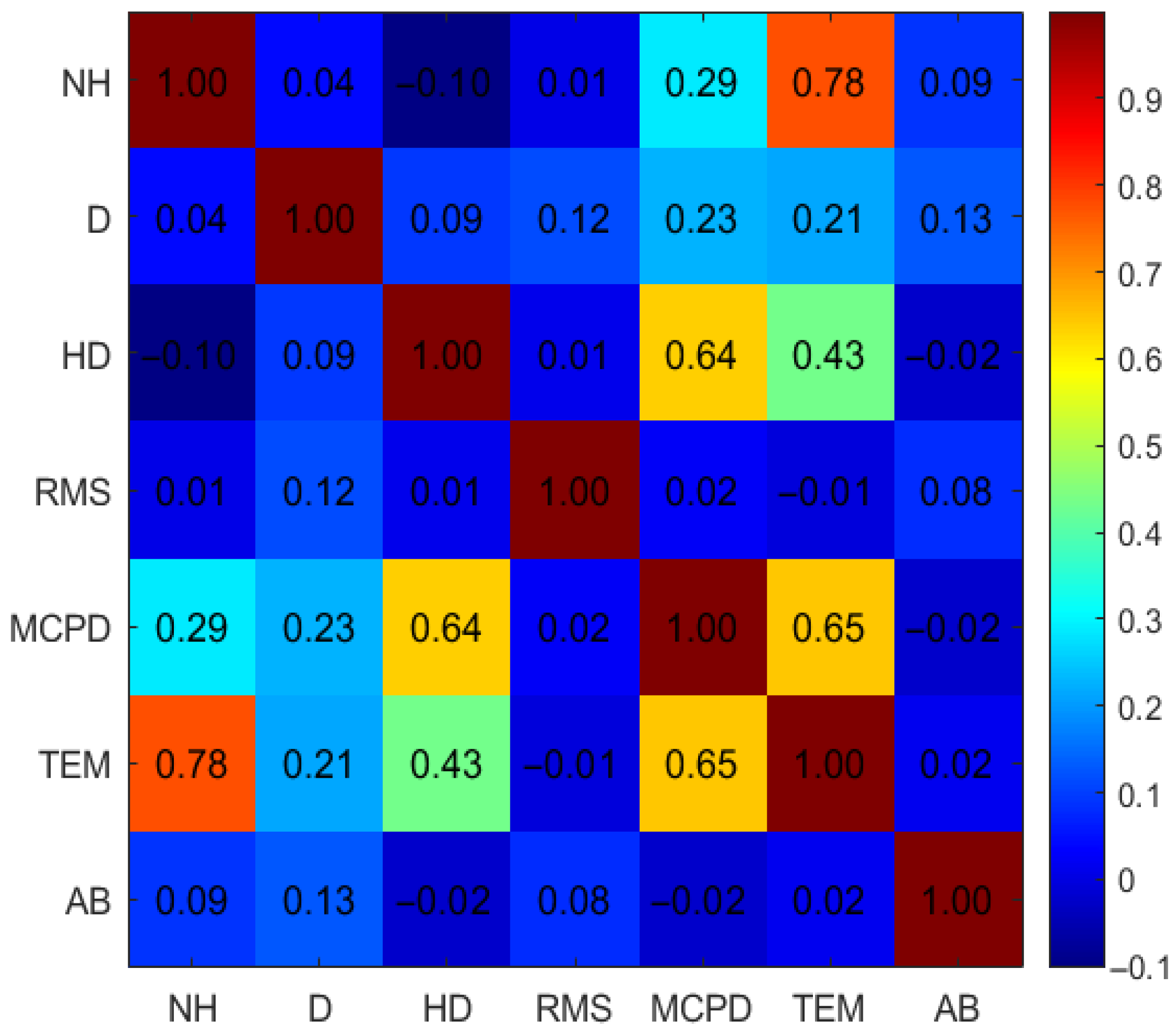








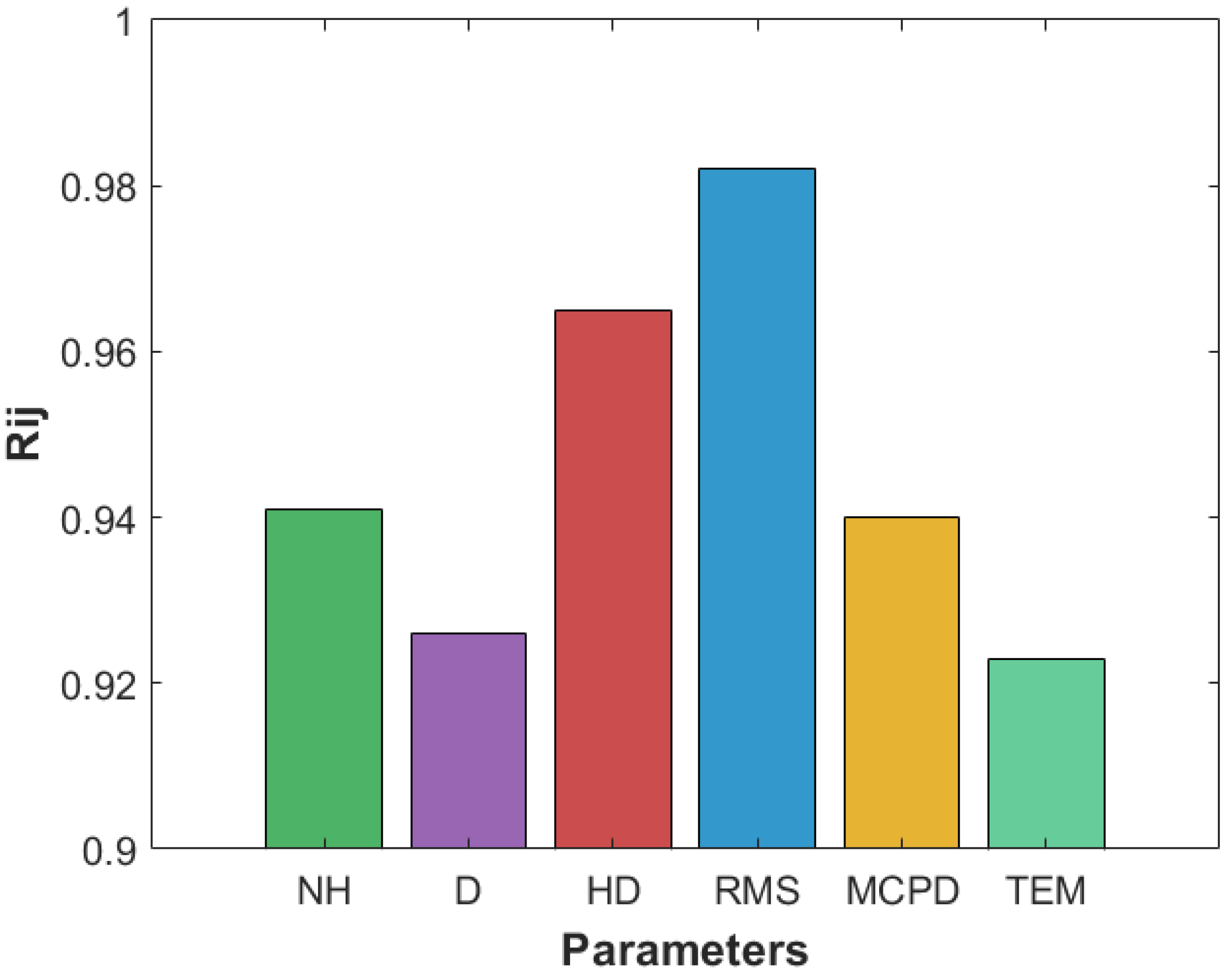
| Reference | Algorithm | Input Parameters | Number of Blasting Datasets |
|---|---|---|---|
| Kazemi et al., 2023 [21] | XGBoost optimized via grey wolf optimization (XGB-GWO) | MCPD, D, RQD, stemming length (ST), burden (B), and spacing (S) | 66 |
| Zhang et al., 2022 [22] | Radial basis function network with two hidden layers (RBF-2) | MCPD, D, rock density, bench height (BH), and HD | 76 |
| Zeng et al., 2021 [23] | Cascaded forward neural network trained via Levenberg–Marquardt | HD, powder factor (PF), TEM, ST, S, B, RQD, NH, and D | 62 |
| Faradonbeh et al., 2018 [24] | Gene programming (GP) and gene expression programming (GEP) | MCPD, D, B, S, ST, and BH | 97 |
| Armaghani et al., 2016 [25] | ICA-ANN (imperialist competitive algorithm-optimized ANN) | MCPD, D, B, ST, and BH | 70 |
| Hasanipanah et al., 2015 [26] | Adaptive neuro-fuzzy inference system (ANFIS) | MCPD, ST, B, RQD, and D | 77 |
| Hajihassani et al., 2015 [27] | Neuro-fuzzy (ANFIS) vs. standard ANN and multiple regression (MR) | MCPD, D, RQD, ST, B, and S | 38 |
| Parameter | NH | D | HD | RMS | MCPD | TEM | Airblast |
|---|---|---|---|---|---|---|---|
| Category | Input | Input | Input | Input | Input | Input | Output |
| Unit | m | m | Mpa | Kg | Kg | dB | |
| Minimum | 74 | 200 | 5.8 | 4.6 | 89.1 | 3742.5 | 81 |
| Maximum | 321 | 900 | 15.3 | 4.7 | 368.12 | 33,102.8 | 142 |
| Average | 196.45 | 371.07 | 11.48 | 4.4 | 229.79 | 15,674.72 | 126.59 |
| Parameters | Values |
|---|---|
| Hidden layers | 1 |
| Hidden neurons per layer | 14, 17, 18, 19, 20, 22, 23, 25, 26, 27 |
| Activation function | Hyperbolic tangent sigmoid |
| Learning rate (η) | 0.005–0.1 |
| Momentum (α) | 0.1–0.9 |
| L2 weight-decay (λ) (log10) | 1 × 10−6–1 × 10−3 |
| Dropout rate | 0.0–0.5 |
| Batch size | 30–70 |
| CapSA population size | 40–400 |
| CapSA local-search radius | 0.2–0.8 |
| Component | CapSA | PSO |
|---|---|---|
| Computation per cycle | Evaluates fitness for each capuchin and then applies leap, swing, and climb behaviors across all decision variables, carrying an extra constant overhead beyond the basic updates. | Evaluates fitness for each particle and then updates velocity and position across all decision variables, so that time grows with swarm size and problem dimension. |
| Memory requirements | Stores position data and a small set of behavioral parameters for each capuchin, resulting in similar linear growth with only modest additional memory usage. | Stores both position and velocity vectors for every particle, leading to linear growth in memory with respect to swarm size and variable count. |
| Convergence behavior | Employs multiple local-search operators that yield stronger refinement per cycle and can reach target accuracy in fewer overall cycles, despite a longer time per cycle. | Simple update rules foster broad exploration early on but often require more cycles to achieve fine-tuned solutions. |
| Parameters | Values |
|---|---|
| Hidden layers | 1 |
| Hidden neurons per layer | 14, 17, 18, 19, 20, 22, 23, 25, 26, 27 |
| Activation function | Hyperbolic-tangent sigmoid |
| Learning rate (η) | 0.005–0.1 |
| Momentum (α) | 0.1–0.9 |
| L2 weight-decay (λ) (log10) | 10−6–10−3 |
| Dropout rate | 0.0–0.5 |
| Batch size | 30–70 |
| PSO swarm size | 40–400 |
| Inertia weight (w) | 0.4–0.9 |
| Cognitive coefficient (c1) | 0.5–2.5 |
| Social coefficient (c2) | 0.5–3 |
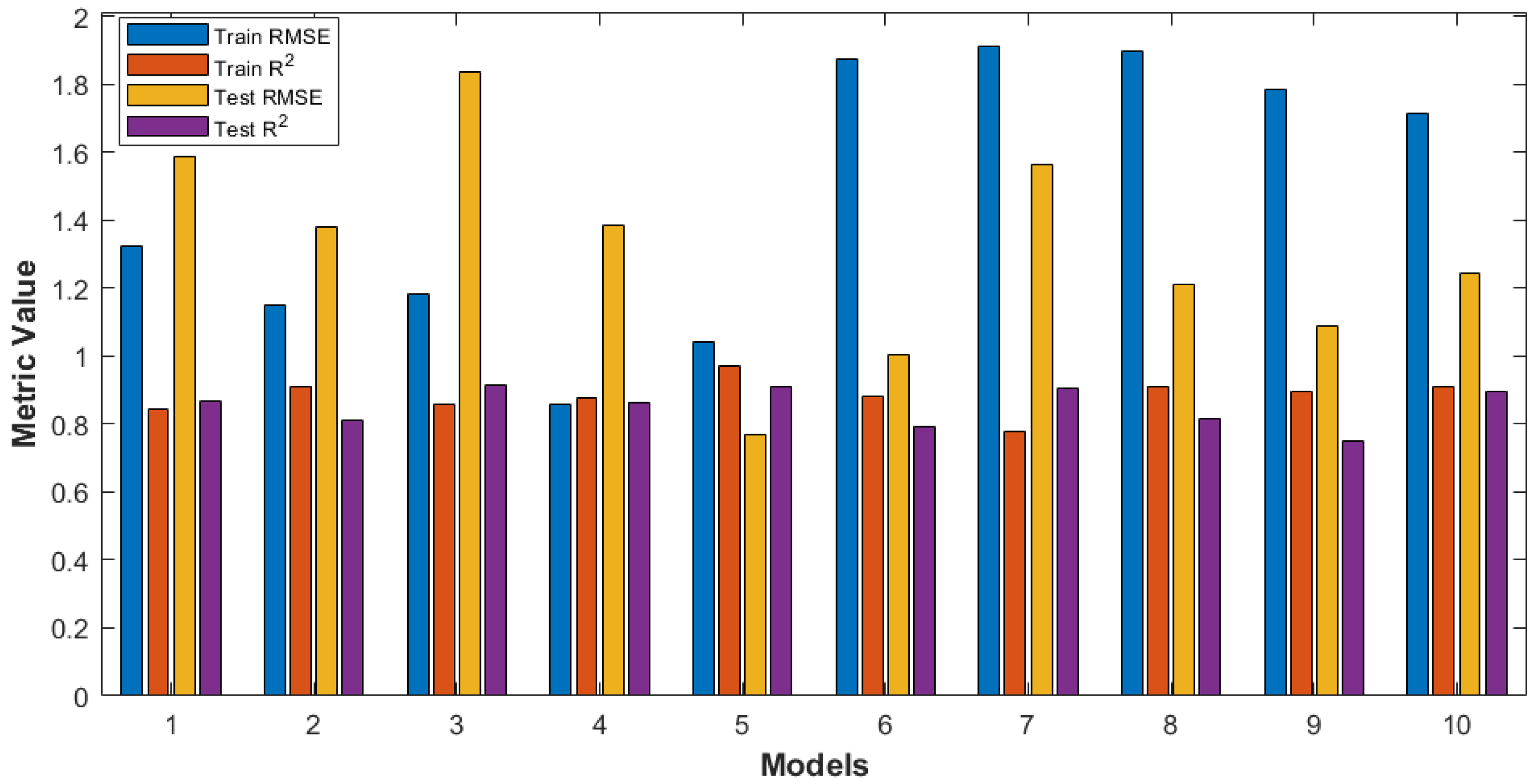
| Model | Hidden Neurons | Train RMSE | Train R2 | Test RMSE | Test R2 |
|---|---|---|---|---|---|
| 1 | 23 | 1.326 | 0.844 | 1.589 | 0.867 |
| 2 | 20 | 1.149 | 0.911 | 1.379 | 0.812 |
| 3 | 26 | 1.183 | 0.858 | 1.836 | 0.917 |
| 4 | 17 | 0.856 | 0.877 | 1.386 | 0.865 |
| 5 | 22 | 1.042 | 0.969 | 0.771 | 0.911 |
| 6 | 25 | 1.873 | 0.882 | 1.002 | 0.792 |
| 7 | 14 | 1.913 | 0.780 | 1.564 | 0.905 |
| 8 | 18 | 1.899 | 0.911 | 1.213 | 0.817 |
| 9 | 19 | 1.784 | 0.897 | 1.087 | 0.751 |
| 10 | 27 | 1.714 | 0.909 | 1.245 | 0.896 |
| Model | Hidden Neurons | Train RMSE | Train R2 | Test RMSE | Test R2 |
|---|---|---|---|---|---|
| 1 | 23 | 1.096 | 0.892 | 1.098 | 0.905 |
| 2 | 20 | 1.391 | 0.968 | 1.087 | 0.893 |
| 3 | 26 | 1.459 | 0.965 | 1.182 | 0.941 |
| 4 | 17 | 1.316 | 0.983 | 1.391 | 0.883 |
| 5 | 22 | 1.302 | 0.881 | 1.216 | 0.935 |
| 6 | 25 | 1.129 | 0.814 | 1.092 | 0.917 |
| 7 | 14 | 1.011 | 0.929 | 1.090 | 0.842 |
| 8 | 18 | 1.842 | 0.848 | 1.528 | 0.861 |
| 9 | 19 | 1.246 | 0.914 | 1.628 | 0.882 |
| 10 | 27 | 1.351 | 0.894 | 1.423 | 0.921 |
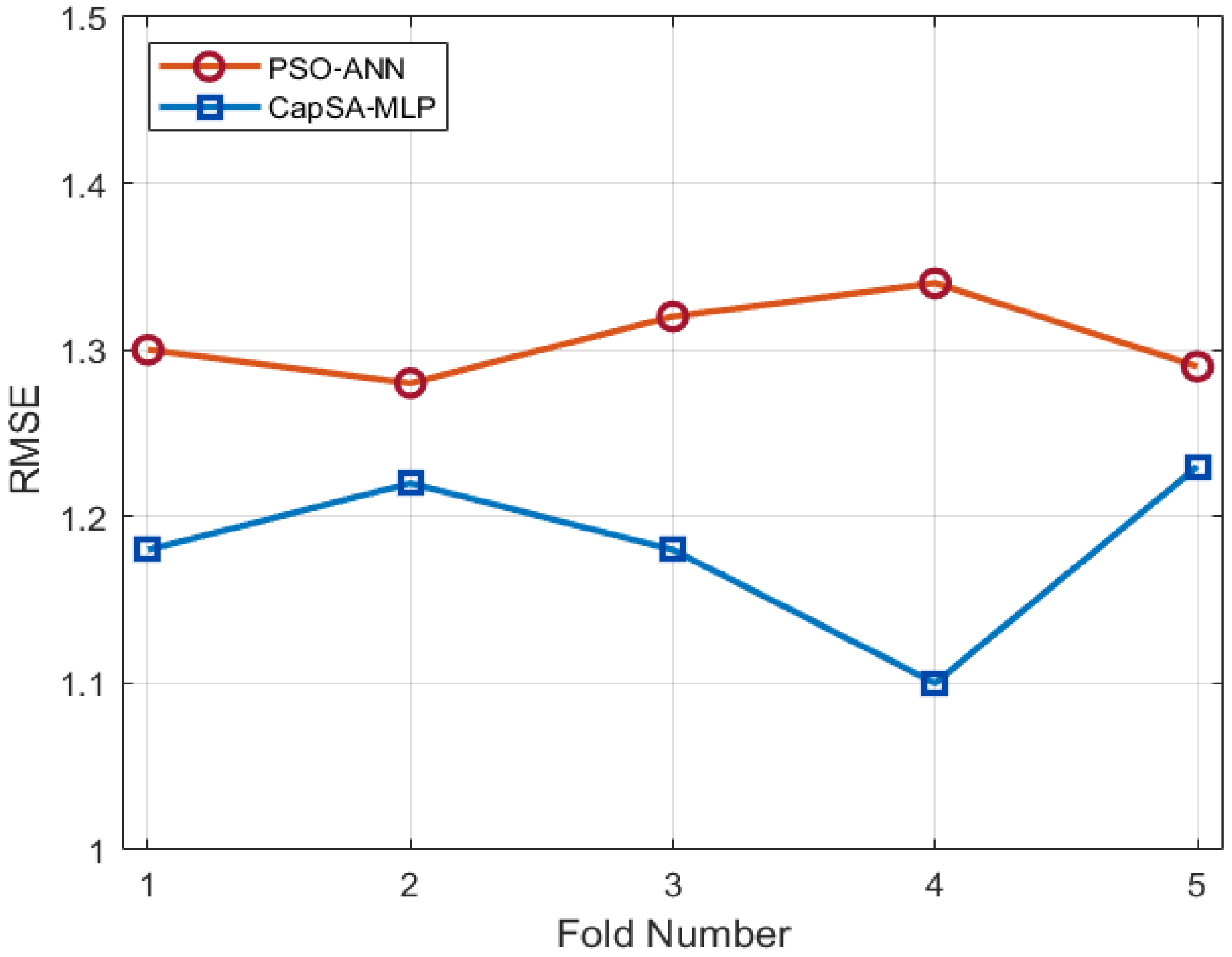
| Method | Hidden Neurons | Learning Rate (η) | Momentum (α) |
|---|---|---|---|
| CapSA-MLP | 26 | 0.069 | 0.480 |
| PSO-ANN | 22 | 0.025 | 0.650 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gaopale, K.; Sasaoka, T.; Hamanaka, A.; Shimada, H. Integrated Capuchin Search Algorithm-Optimized Multilayer Perceptron for Robust and Precise Prediction of Blast-Induced Airblast in a Blasting Mining Operation. Geosciences 2025, 15, 306. https://doi.org/10.3390/geosciences15080306
Gaopale K, Sasaoka T, Hamanaka A, Shimada H. Integrated Capuchin Search Algorithm-Optimized Multilayer Perceptron for Robust and Precise Prediction of Blast-Induced Airblast in a Blasting Mining Operation. Geosciences. 2025; 15(8):306. https://doi.org/10.3390/geosciences15080306
Chicago/Turabian StyleGaopale, Kesalopa, Takashi Sasaoka, Akihiro Hamanaka, and Hideki Shimada. 2025. "Integrated Capuchin Search Algorithm-Optimized Multilayer Perceptron for Robust and Precise Prediction of Blast-Induced Airblast in a Blasting Mining Operation" Geosciences 15, no. 8: 306. https://doi.org/10.3390/geosciences15080306
APA StyleGaopale, K., Sasaoka, T., Hamanaka, A., & Shimada, H. (2025). Integrated Capuchin Search Algorithm-Optimized Multilayer Perceptron for Robust and Precise Prediction of Blast-Induced Airblast in a Blasting Mining Operation. Geosciences, 15(8), 306. https://doi.org/10.3390/geosciences15080306






