Statistical Physics of Fissure Swarms and Dike Swarms
Abstract
1. Introduction
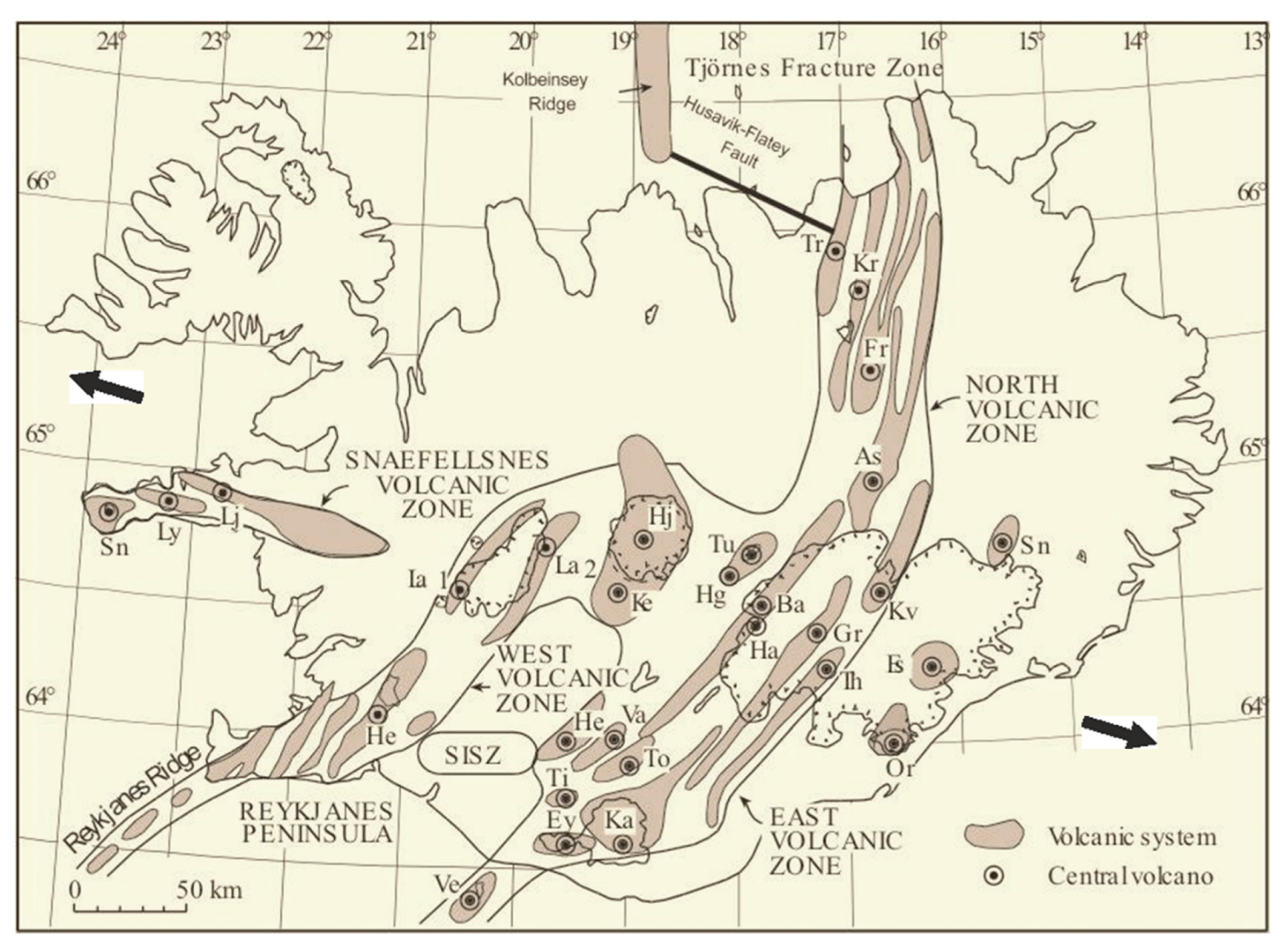
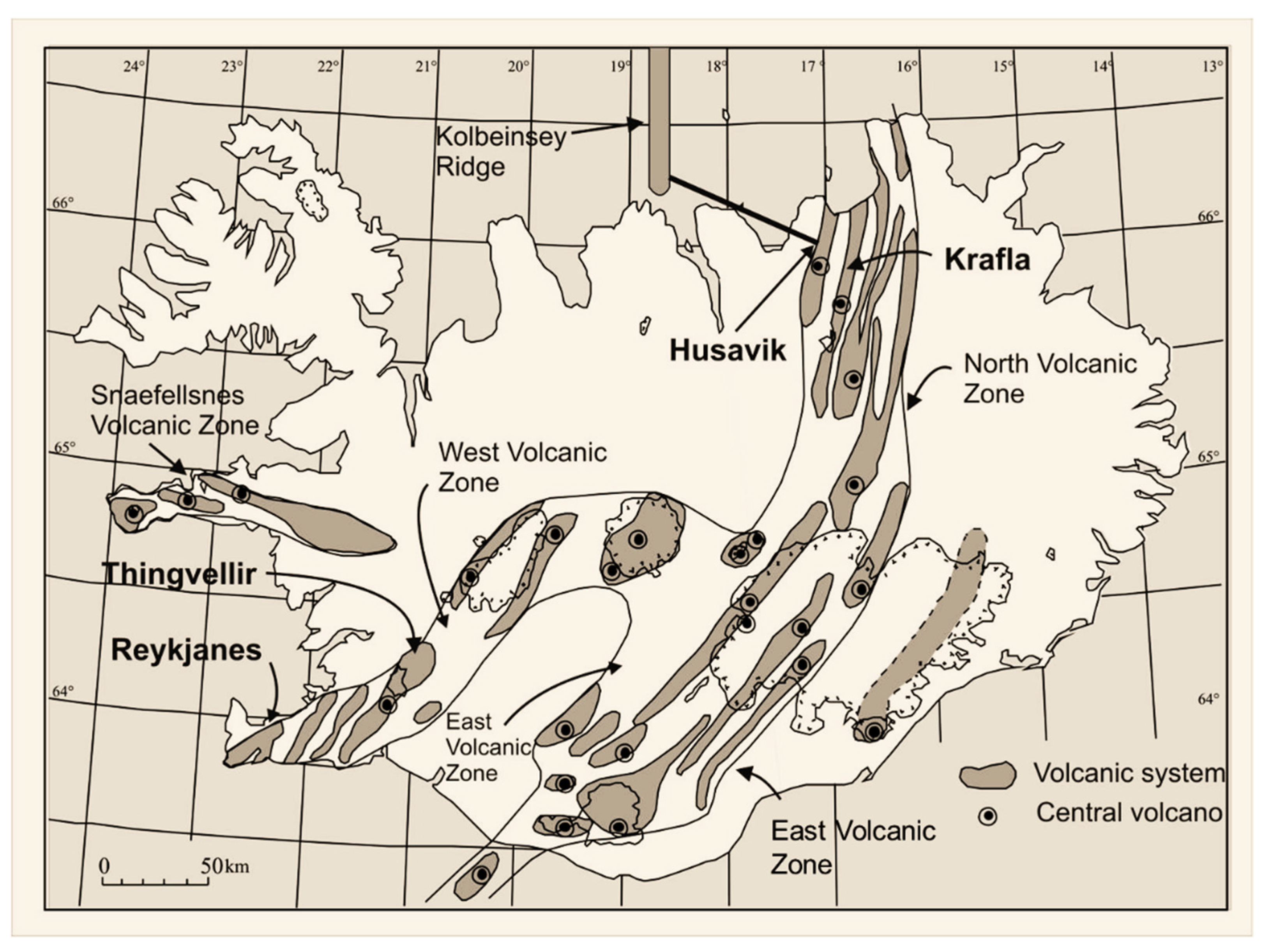
2. Basic Characteristics of Fissure Swarms and Dike Swarms
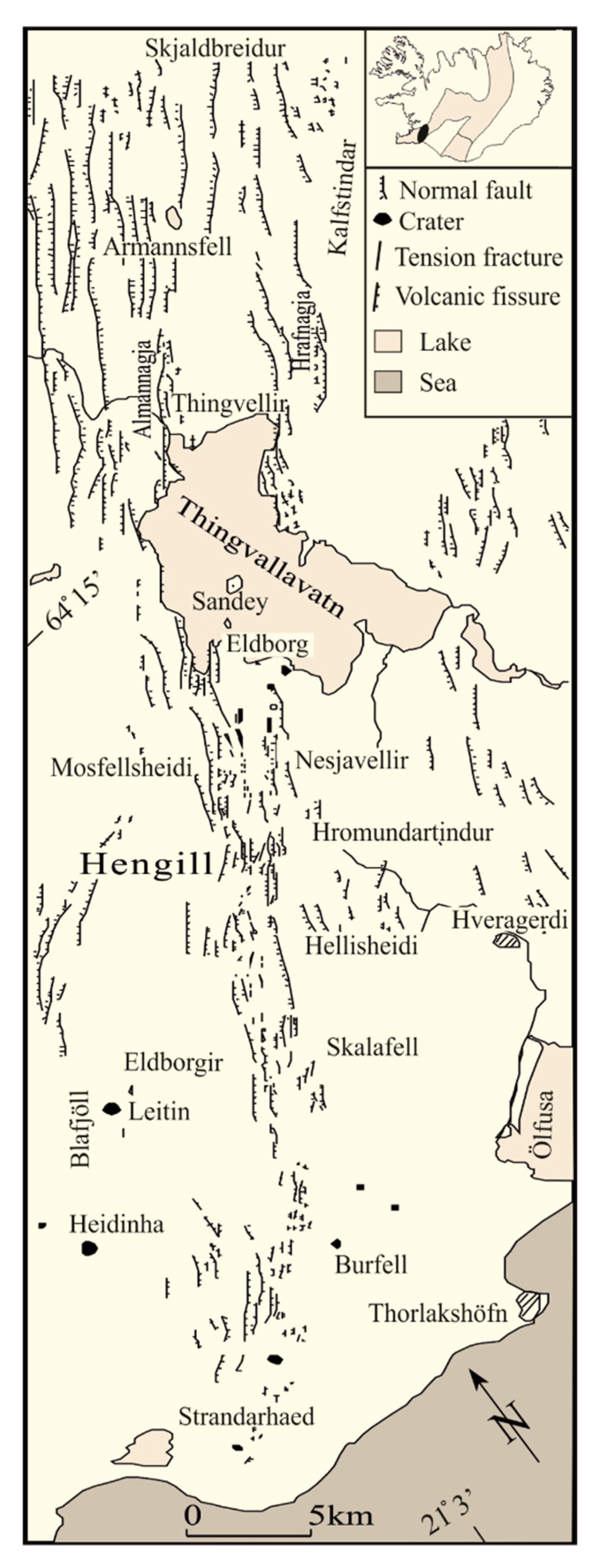
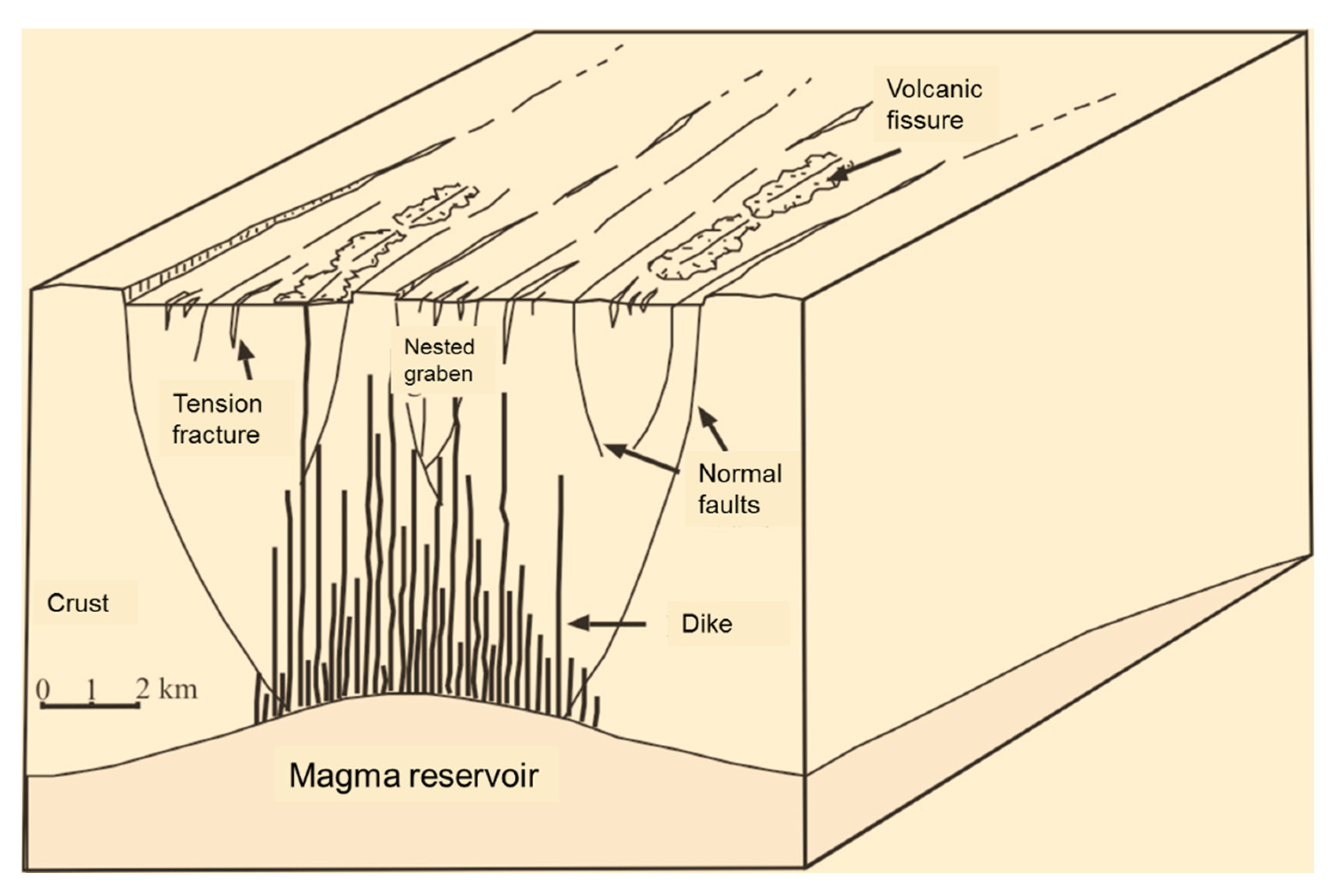
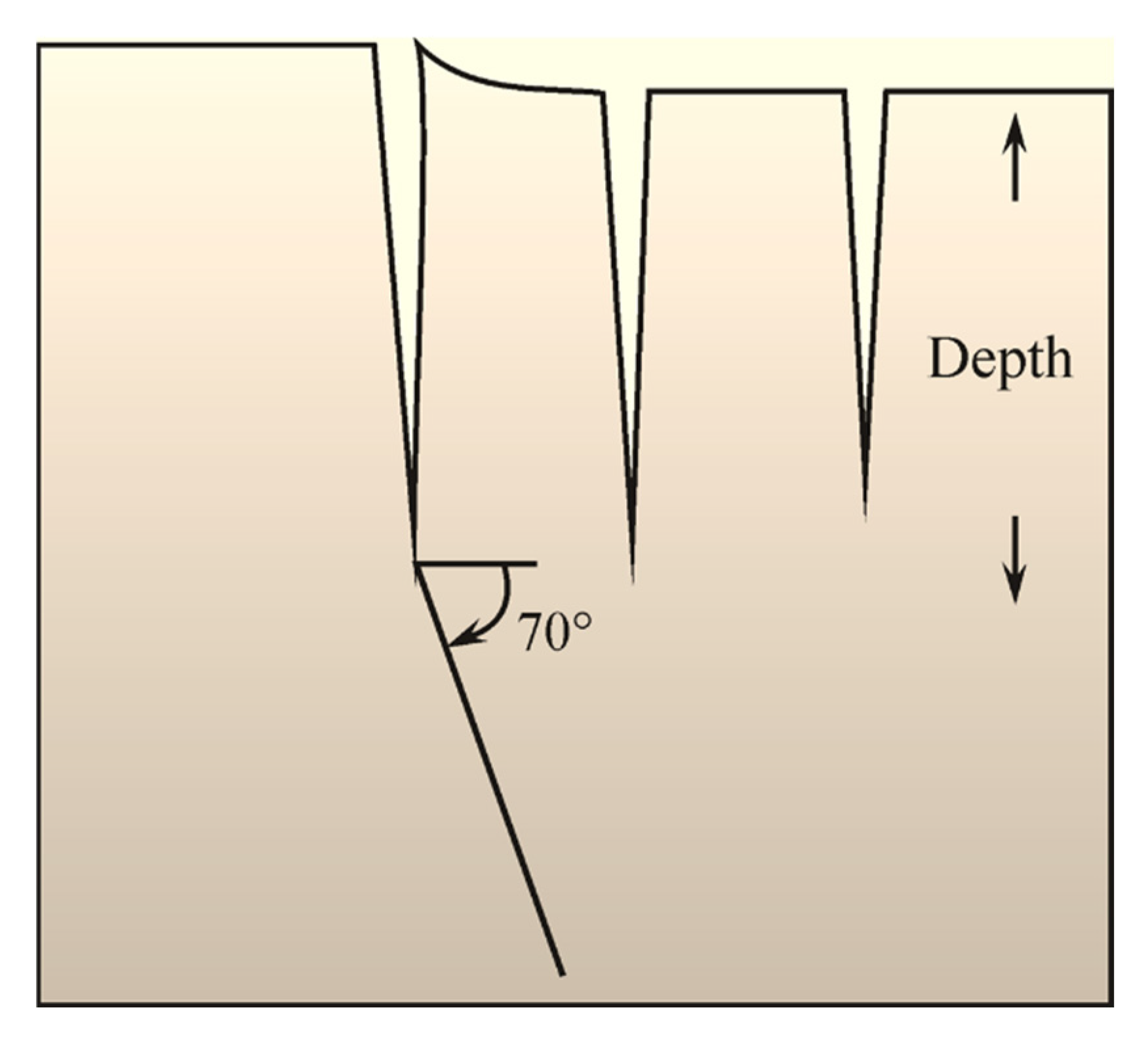
2.1. Fissure Swarms
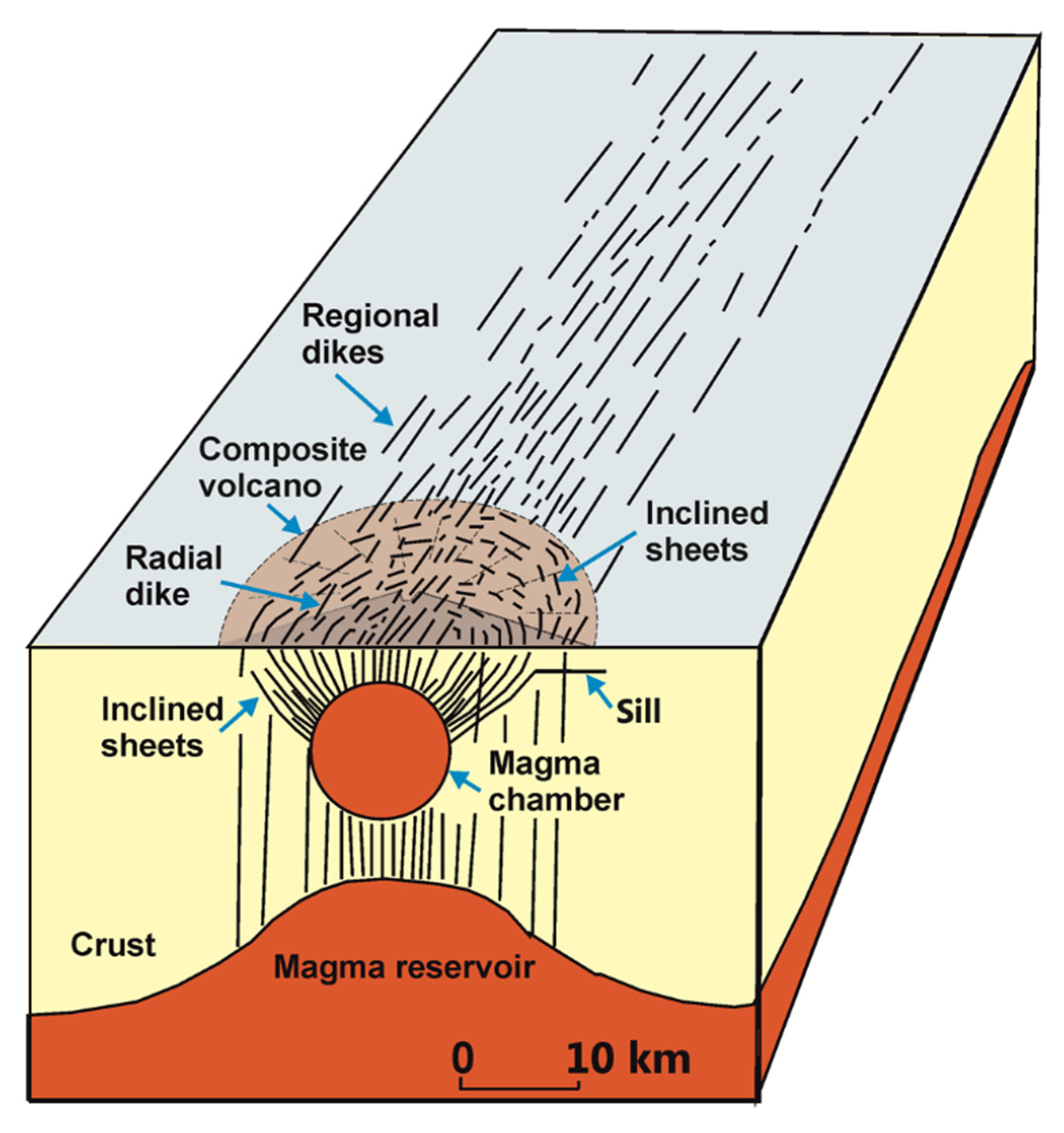
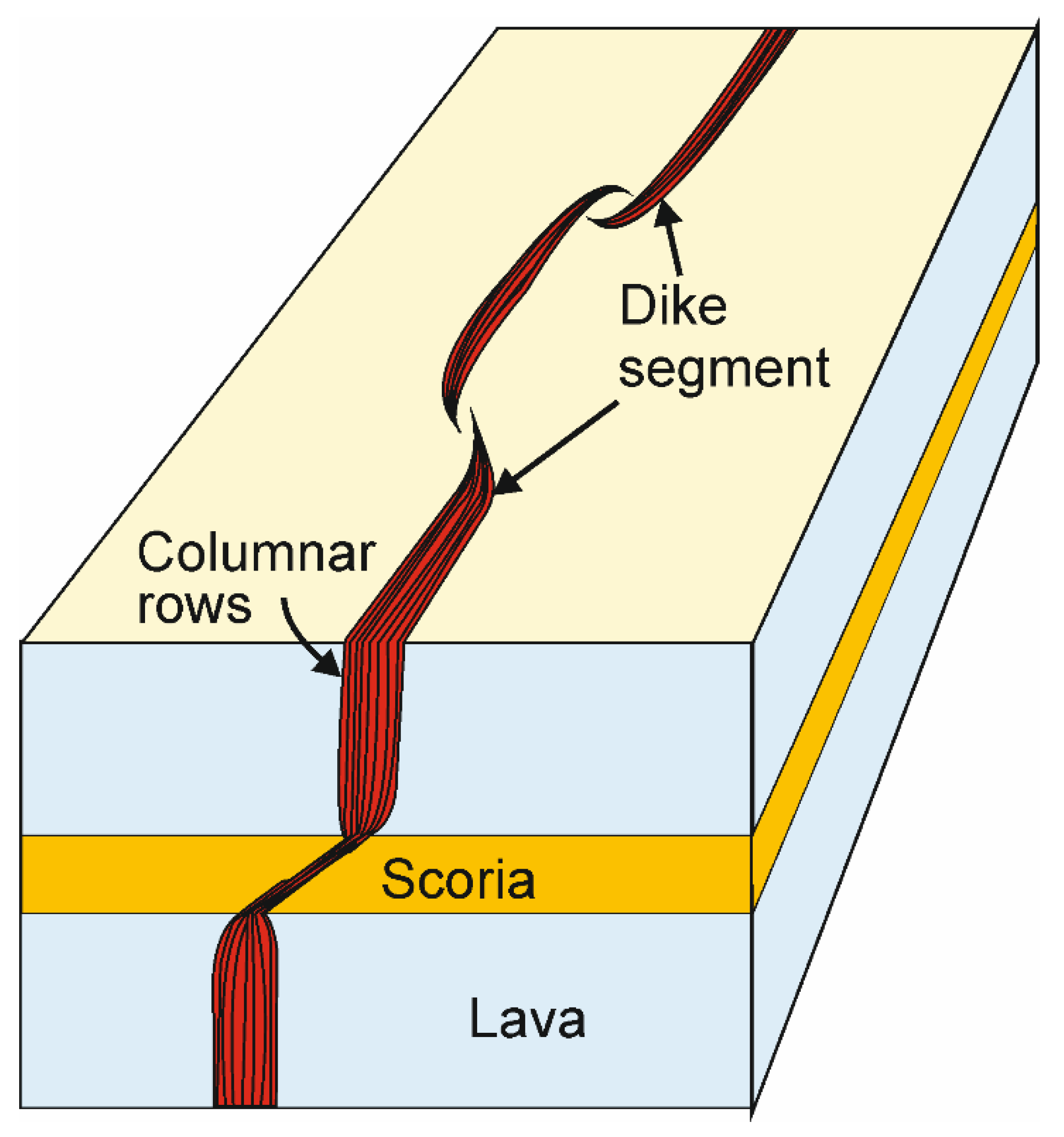
2.2. Dike Swarms

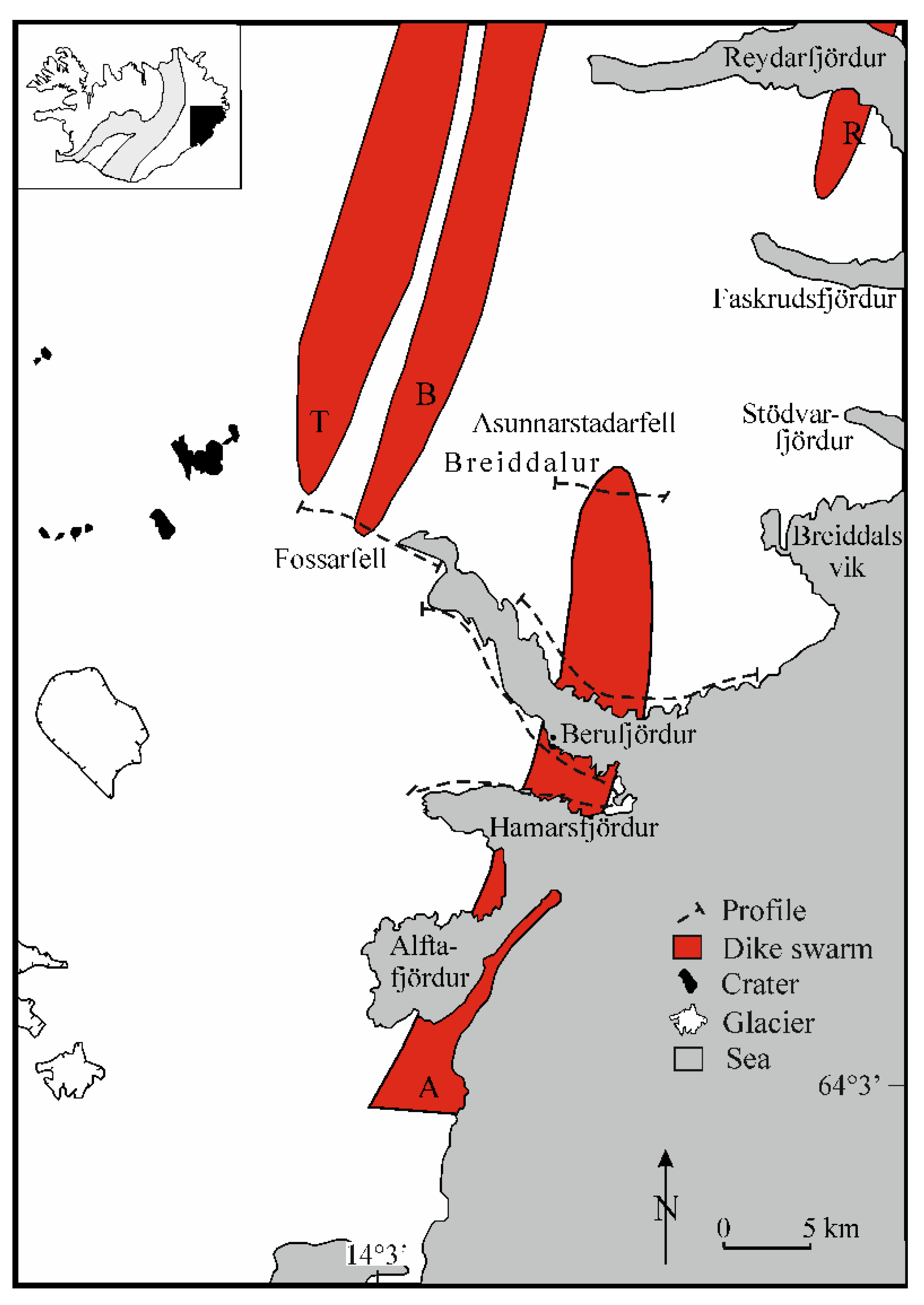

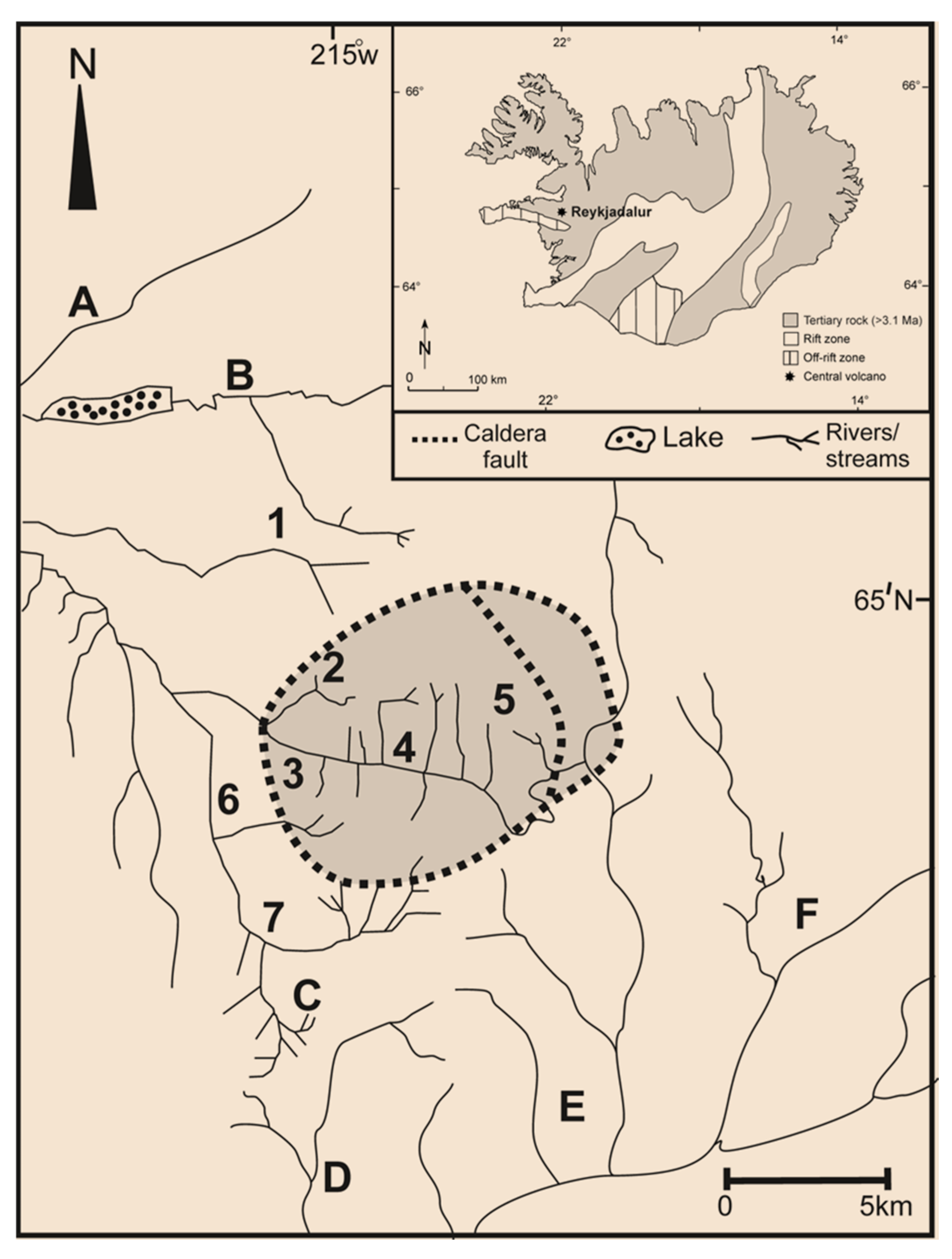
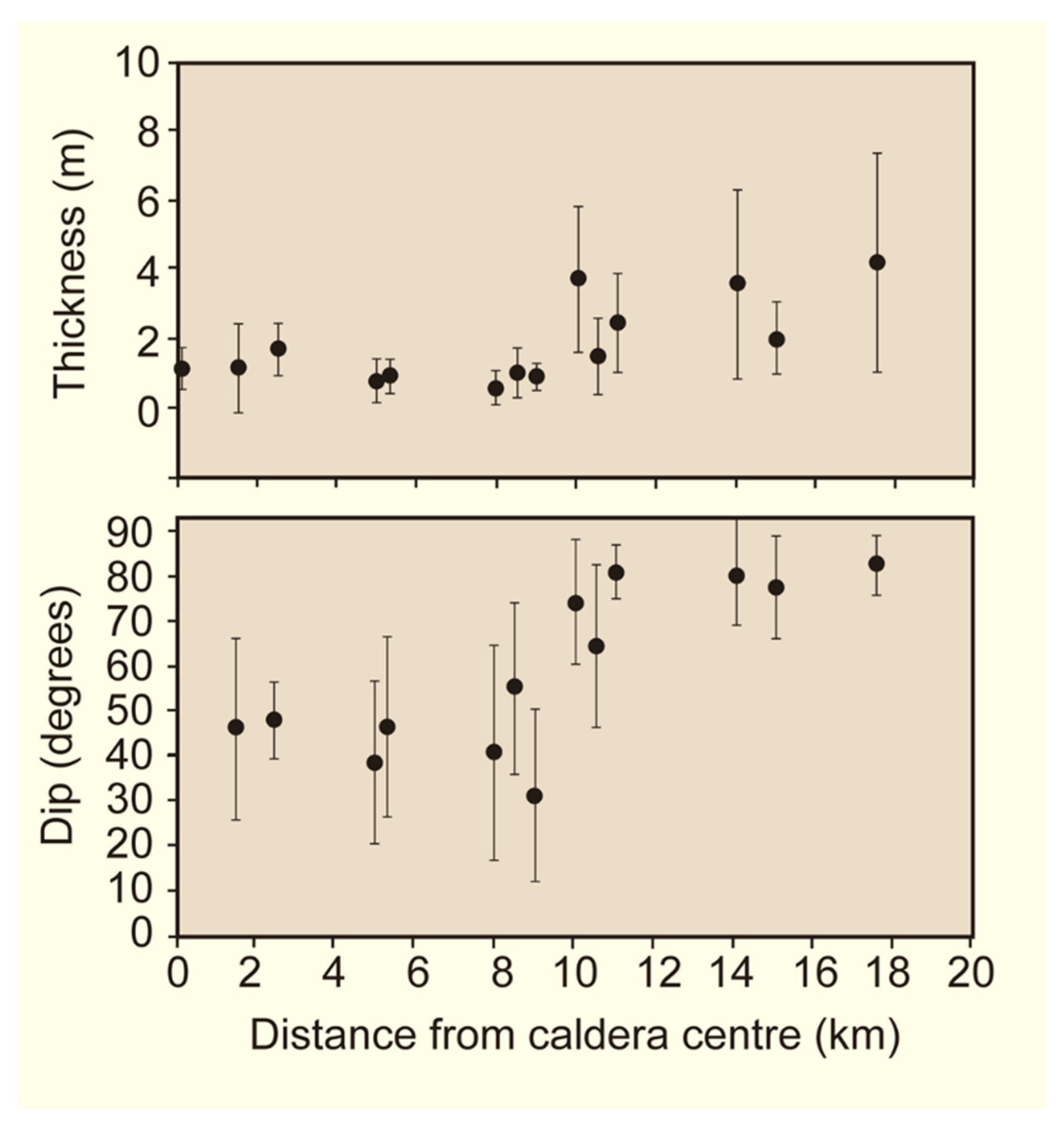
3. Size Distributions of Fissures and Dikes
3.1. Overview
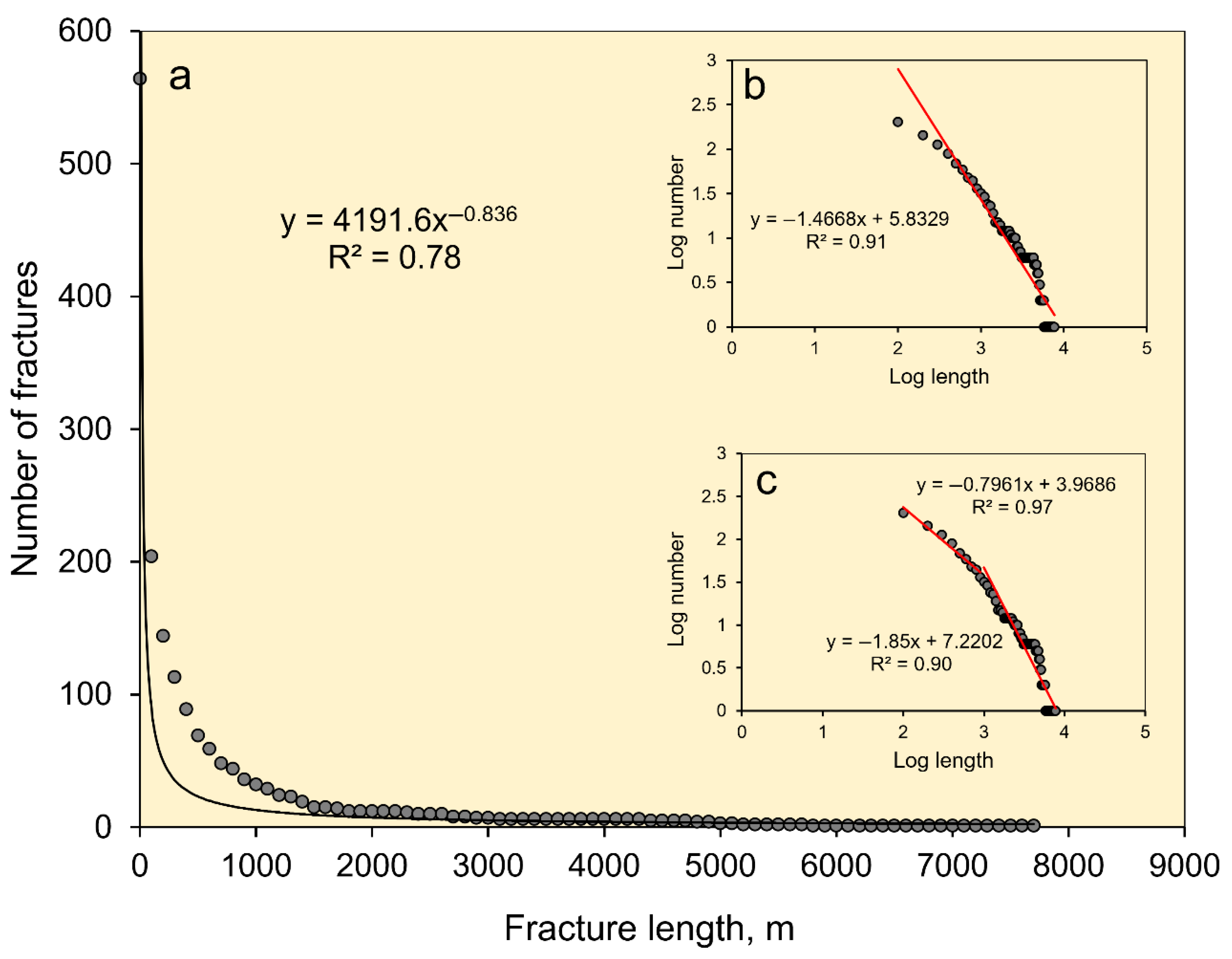
3.2. Power Laws
3.2.1. Tension Fractures and Normal Faults
3.2.2. Dikes
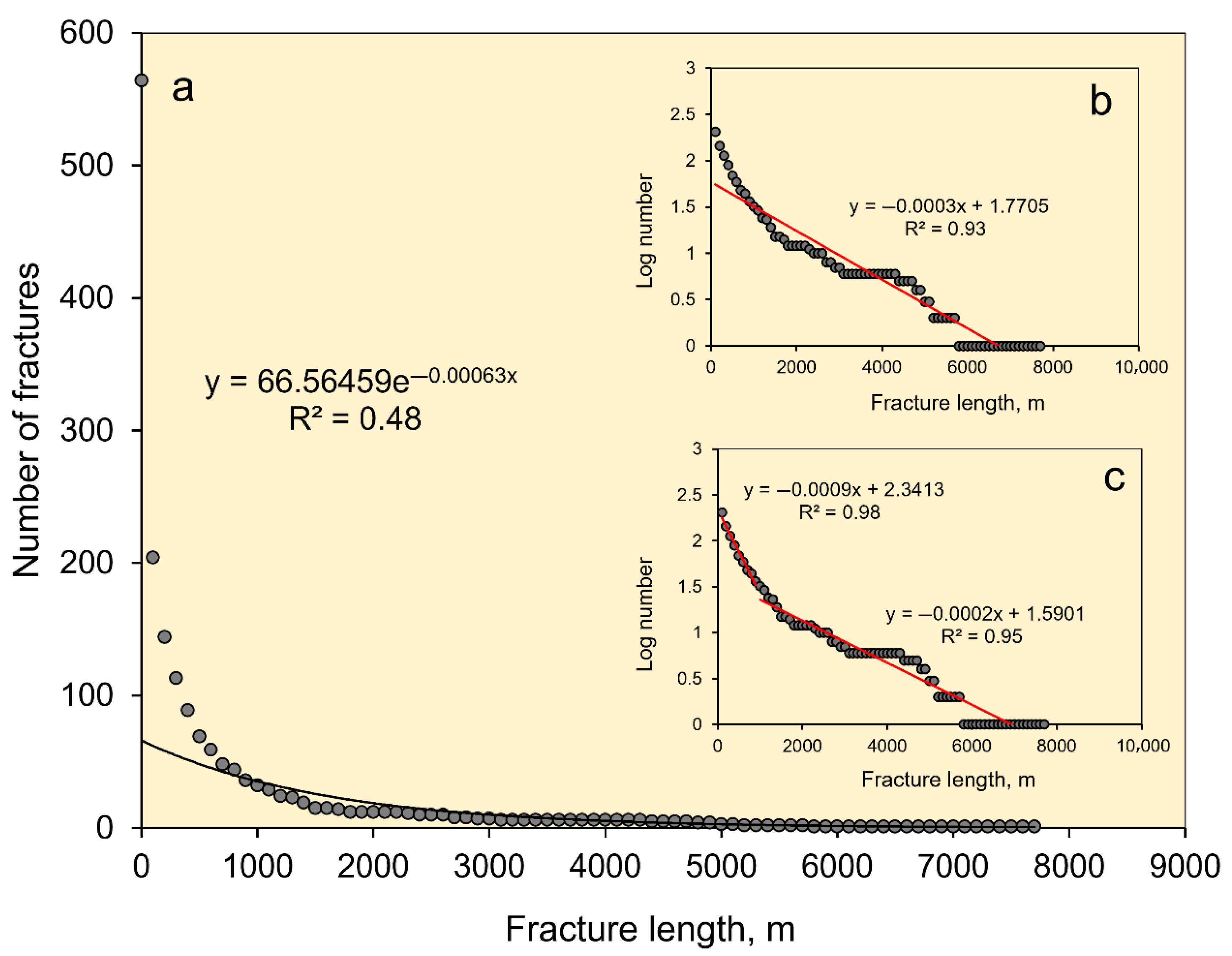
3.3. Exponential Laws
3.3.1. Tension Fractures and Normal Faults
3.3.2. Dikes
4. Theoretical Framework
5. Free Energy
6. Frequency Distributions
7. Relation Between Frequency Distribution, Free Energy, and Entropy
8. Energy Needed for Fracture Propagation
9. Entropy Results
9.1. Fissure Swarms
9.2. Dike Swarm
9.3. Explanation of the Entropies
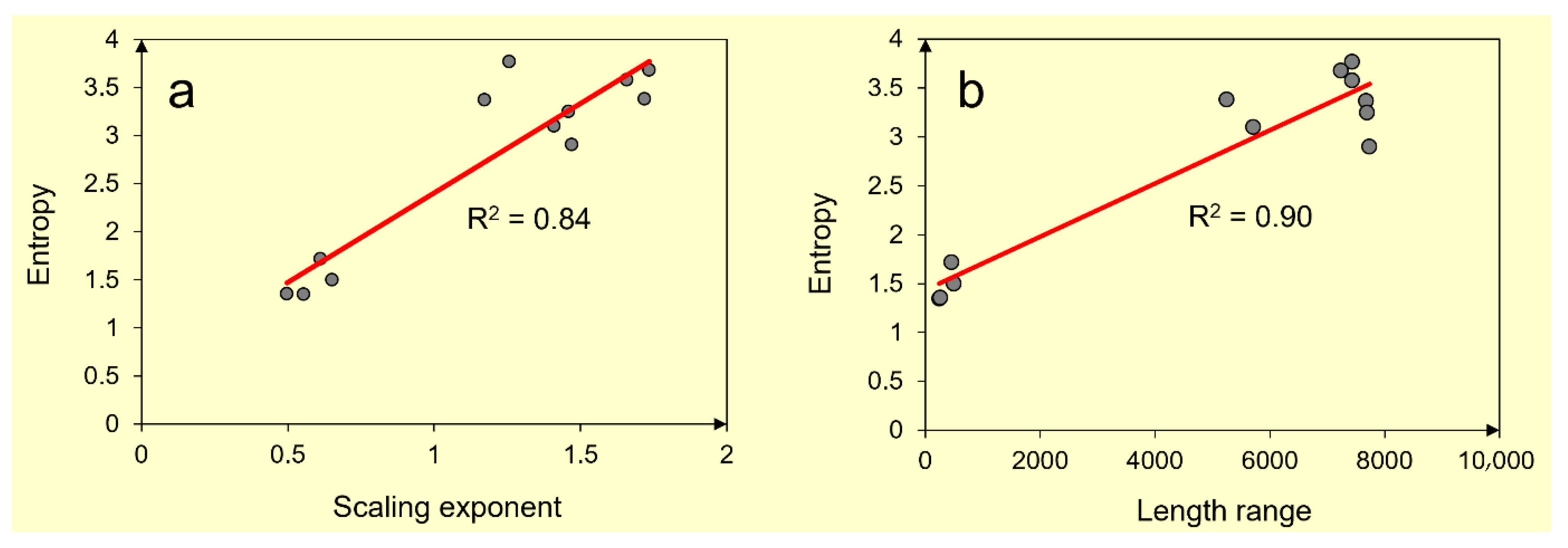
- The scaling exponent of the longer fissures/dikes in each swarm is always much larger than the scaling exponent of the shorter fissures/dikes and somewhat larger than that of all the fissures/dikes in that swarm. I suggest that this is primarily because the logarithm-transformation compresses the data. For example, the distance between 1 and 10 (0 and 1 on the logarithmic scale) is the same as the distance between 10 and 100 (1 and 2 on the logarithmic scale), or the distance been 100 and 1000 (2 and 3 on the logarithmic scale). Thus, the long-fissure/dike part (the tail) of the size distribution becomes compressed resulting in a steeper slope of that part than of the short-fissure/dike part. The steeper the slope, the higher is the scaling exponent.
- The calculated entropies of the long-fissure/dike parts of the sets are also much higher than those of the short-fissure/dike parts of the sets and, in fact, somewhat higher than those of the all the fissure/dikes in each particular swarm. I suggest that this is primarily because the long-fissure/dike parts—the tail parts of the size distributions—are those that are closest to being uniform distributions. Uniform statistical distributions, which for discrete data mean that all the bins with equal class limits (widths) are of the same height, have the highest entropy. By contrast, the bins of the short-fissure/dike parts of the distributions have widely different bin heights, that is, are peaked, and thus with low entropy. The size distributions of all the fissures/dikes in a swarm include both the peaked part (the short-fissure/dike part) of the distribution as well as the more uniform tail part (the long-fissure/dike part) and therefore have an entropy that is somewhat lower than that of the more uniform long-fissure/dike parts.
10. Application
10.1. Stress States as Microstates
10.2. Stress-Homogenisation
10.3. Energy for Large-Scale Fracture Propagation
11. Discussion and Conclusions
- Length-size distributions of 565 tectonic tension fractures and normal faults—referred together as fissures—located in Holocene fissure swarms in Iceland show reasonable to good fits both with negative power laws and negative exponential laws. Length-size distributions of basaltic dikes in regional swarms of Neogene (Tertiary) age in Iceland also show fits with negative power laws and negative exponential laws.
- Based on the calculated coefficient of determination (R2), the non-transformed fissure-length data show better fit with a power law (R2 = 0.78) than with an exponential law (R2 = 0.48). The single-line and double-line (regression) fits with the log-transformed (power law) and semi-log-transformed (exponential law) fissure-length data, however, are similar: for the various sets R2 ranges from 0.90 to 0.97 for the power laws and from 0.93 to 0.98 for the exponential laws.
- The non-transformed dike-length data show a much better fit with an exponential law (R2 = 0.91) than with a power law (R2 = 0.25). The single-line and double-line fits with the log-transformed (power law) and semi-log transformed (exponential law) dike-length data, while more similar than for the non-transformed data, also show differences. Thus, for the various sets R2 ranges from 0.89 to 0.97 for the power laws but from 0.96 to 0.99 for the exponential laws. Thus, the dike-length data generally fit a negative exponential law somewhat better than a negative power law.
- Using the thermodynamic concept of Helmholtz free energy and the statistical concept of a microstate as basis, the general equation for entropy, known as the Gibbs–Shannon entropy formula, is derived (Equation (42)). This formula is completely general and applies to any probability or statistical frequency distribution, including the length-size distributions of tension fractures, normal faults, and dikes.
- Using the interpretation that Gibbs–Shannon entropy is a measure of spreading in statistical size-distributions of dike and tectonic fracture populations, the entropies were calculated for 12 sets and subsets of tension fractures and normal faults (the fissures of the fissure swarms) and 3 sets and subsets of dikes (in the studied dike swarm). The results show that for the sets and subsets of fissures and dikes entropy is positively correlated with the scaling exponent and the length range of the power laws. This means that much of the variation in the calculated entropy of these sets and subsets can be explained in terms of the variation in these two parameters, namely length range and scaling exponent.
- The highest calculated entropies are those of the subsets of long fissures/dikes. It is proposed that these high entropies are because the long fissures/dikes constitute the tail parts of the length-size distributions. The tail parts are those where the size-distribution is closest to being uniform. Uniform distributions, which for discrete data such as here are characterised by all the bins (with the same class limits or widths) being of the same height, have the highest entropy.
- The length-size distributions of fissures and dikes are explained in terms of microstates and stress-homogenisation. Microstates refer to specific configurations of thermodynamic systems. Here they refer, first, to the bins in the statistical size distribution of the fissures and dikes and, second, to stress-state distribution in a rock body or a crustal segment. The probability of the occurrence of a given microstate depends on the energy associated with that state and follows a negative exponential distribution–Boltzmann distribution (Equations (21), (23) and (26)). The size distribution of local stress states within which the stress field is homogeneous is here supposed to follow a Boltzmann distribution, so that most of the local stress states control small volumes. Then it follows that the overall state of stress in a large body/crustal segment is, with its numerous but mostly small local stress states, highly heterogeneous. Thus, at any given moment the most probably overall state of stress in a large rock body/crustal segment is highly heterogeneous, favouring short fissures/dike segments.
- For a long fissure/dike to form, a large part of the hosting rock body/crustal segment must be stress-homogenised. This means that the state of stress within a large part of the rock body is everywhere favourable to a particular mechanical type of fracture, here either a fissure or a dike. Stress-homogenisation in a large rock volume located in a tectonically active area is reflected in slip on or opening of small fractures. Some fracture slip is aseismic, but there is generally considerable seismic activity associated with stress-homogenisation. Normally, the process takes considerable time, but the exact time depends on the rate of loading or energy input into the rock body and the mechanical properties of the body. If the rate is high and the mechanical properties of the body similar, then the stress-homogenisation may occur over a (geologically) short time. But at normal geological loading rates, such as associated with plate movements, the stress-homogenisation may take years, decades, or centuries.
- When large rock bodies/crustal segments become stress-homogenised so as to favour larger fissures/dikes, the frequency distributions tend to shift to the right (Figure 17, Figure 20, Figure 23 and Figure 24). This means that the tail parts of the size distributions becomes extended, that is, proportionally longer. Here it is suggested that shifts of this kind may contribute to the transformation of exponential laws into power laws. This follows because as longer fissures/dikes become proportionally more common (when larger rock bodies/crustal segments become stress-homogenised), then, for a negative exponential law, the tail becomes gradually more similar to that of a power law.
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gudmundsson, A. Volcanotectonics: Understanding the Structure, Deformation and Dynamics of Volcanoes; Cambridge University Press: Cambridge, UK, 2020. [Google Scholar]
- Gudmundsson, A. The propagation paths of fluid-driven fractures in layered and faulted rocks. Geol. Mag. 2022, 159, 1978–2001. [Google Scholar] [CrossRef]
- Gudmundsson, A. Rock Fractures in Geological Processes; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Griffith, A.A. The phenomena of rupture and flow in solids. Phil. Trans. Roy. Soc. Lond. 1920, A221, 163–198. [Google Scholar]
- Jaeger, J.C.; Cook, N.G.W. Fundamentals of Rock Mechanics, 3rd ed.; Chapman and Hall: London, UK, 1979. [Google Scholar]
- Tibaldi, A. Structure of volcano plumbing systems: A review of multi-parametric effects. J. Volcanol. Geotherm. Res. 2015, 298, 85–135. [Google Scholar] [CrossRef]
- Gudmundsson, A. Dynamics of volcanic systems in Iceland: Example of tectonism and volcanism at juxtaposed hotspot and mid-ocean ridge systems. Annu. Rev. Earth Planet. Sci. 2000, 28, 107–140. [Google Scholar] [CrossRef]
- Rickwood, P.C. The anatomy of a dyke and the determination of propagation and flow directions. In Mafic Dykes and Emplacement Mechanisms; Parker, A.J., Rickwood, P.C., Tucker, D.H., Eds.; Balkema: Rotterdam, The Netherlands, 1990; pp. 81–100. [Google Scholar]
- Ernst, R.E.; Grosfils, E.B.; Mege, D. Giant dike swarms: Earth, Venus, and Mars. Annu. Rev. Earth Planet. Sci. 2001, 29, 489–534. [Google Scholar] [CrossRef]
- Gudmundsson, A.; Friese, N.; Galindo, I.; Philipp, S.L. Dike-induced reverse faulting in a graben. Geology 2008, 36, 123–126. [Google Scholar] [CrossRef]
- Gudmundsson, A.; Pasquare, F.A.; Tibaldi, A. Dykes, sills, laccoliths, and inclined sheets in Iceland. In Physical Geology of Shallow Magmatic Systems: Dykes, Sills and Laccoliths; Breitkreuz, C., Rocchi, S., Eds.; Springer: Berlin/Heidelberg, Germany, 2018; pp. 363–376. [Google Scholar]
- Coleman, R.G. Ophiolites. In Ancient Oceanic Lithosphere? Springer: Berlin/Heidelberg, Germany, 1977. [Google Scholar]
- Nicolas, A. Structures of Ophiolites and Dynamics of Oceanic Lithosphere; Springer: Berlin/Heidelberg, Germany, 1989. [Google Scholar]
- Gudmundsson, A. How local stresses control magma-chamber ruptures, dyke injections, and eruptions in composite volcanoes. Earth-Sci. Rev. 2006, 79, 1–31. [Google Scholar] [CrossRef]
- Gautneb, H.; Gudmundsson, A. Effect of local and regional stress fields on sheet emplacement in West Iceland. J. Volcanol. Geotherm. Res. 1992, 51, 339–356. [Google Scholar] [CrossRef]
- Gudmundsson, A. Infrastructure and mechanics of volcanic systems in Iceland. Tectonophysics 1995, 64, 1–22. [Google Scholar] [CrossRef]
- Huges, I.G.; Hase, T.P.A. Measurements and Their Uncertainties; Oxford University Press: Oxford, UK, 2010. [Google Scholar]
- Gudmundsson, A. Tectonics of the Thingvellir fissure swarm, SW Iceland. J. Struct. Geol. 1987, 9, 61–69. [Google Scholar] [CrossRef]
- Gudmundsson, A. Geometry, formation and development of tectonic fractures on the Reykjanes Peninsula, Southwest Iceland. Tectonophysics 1987, 139, 295–308. [Google Scholar] [CrossRef]
- Xie, H. Fractals in Rock Mechanics, 2nd ed.; CRC Press/Balkema: Rotterdam, The Netherlands, 2020. [Google Scholar]
- Hatton, C.G.; Main, I.G.; Meredith, P.G. Non-universal scaling of fracture length and opening displacement. Nature 1994, 367, 160–162. [Google Scholar] [CrossRef]
- Turcotte, D.L. Fractals and Chaos in Geology and Geophysics, 2nd ed.; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Bour, O.; Davy, P. On the connectivity of three-dimensional fault networks. Water Resour. Res. 1998, 34, 2611–2622. [Google Scholar] [CrossRef]
- Berkowitz, B.; Bour, O.; Davi, P.; Odling, N. Scaling of fracture connectivity in geological formations. Geophys. Res. Lett. 2000, 27, 2061–2064. [Google Scholar] [CrossRef]
- Bonnet, E.; Bour, O.; Odling, N.E.; Davy, P.; Main, I.; Cowie, P.; Berkowitz, B. Scaling of fracture systems in geological media. Rev. Geophys. 2001, 39, 347–383. [Google Scholar] [CrossRef]
- Babiker, M.; Gudmundsson, A. The effects of dykes and faults on groundwater flow in an arid land: The Red Sea Hills, Sudan. J. Hydrol. 2004, 297, 256–273. [Google Scholar] [CrossRef]
- Nieto-Samaniego, A.F.; Alaniz-Alvarez, S.A.; Tolson, G.; Oleschko, K.; Korvin, G.; Xu, S.S.; Pérez-Venzor, J.A. Spatial distribution, scaling and self-similar behavior of fracture arrays in the Los Planes Fault, Baja California Sur, Mexico. Pure Appl. Geophys. 2005, 162, 805–826. [Google Scholar] [CrossRef]
- Gudmundsson, A.; Mohajeri, N. Relations between the scaling exponents, entropies, and energies of fracture networks. Bull. Geol. Soc. France 2013, 184, 377–387. [Google Scholar] [CrossRef]
- Gudmundsson, A.; De Guidi, G.; Scudero, S. Length–displacement scaling and fault growth. Tectonophysics 2013, 608, 1298–1309. [Google Scholar] [CrossRef]
- Mege, D.; Korme, T. Fissure eruption of flood basalts from statistical analysis of dyke fracture length. J. Volcanol. Geotherm. Res. 2004, 131, 77–92. [Google Scholar] [CrossRef]
- Ray, R.; Sheth, H.C.; Mallik, J. Structure and emplacement of the Nandurbar–Dhule mafic dyke swarm, Deccan Traps, and the tectonomagmatic evolution of flood basalts. Bull. Volcanol. 2007, 69, 537–551. [Google Scholar] [CrossRef]
- Patel, R.; Gadgil, R.; Sarma, D.S. Role of dyke geometry in understanding dyke-emplacement mechanisms and magma-chamber dynamics: A critical appraisal from the Chotanagpur Gneissic Complex, India. J. Volcanol. Geotherm. Res. 2021, 418, 107344. [Google Scholar] [CrossRef]
- Babiker, M.; Gudmundsson, A. Geometry, structure and emplacement of mafic dykes in the Red Sea Hills, Sudan. J. Afr. Earth. Sci. 2004, 38, 279–292. [Google Scholar] [CrossRef]
- Hollanda, M.H.B.M.; Archanjo, C.J.; Macêdo Filho, A.A.; Fossen, H. The Mesozoic Equatorial Atlantic Magmatic Province (EQUAMP): A New Large Igneous Province in South America. In Dyke Swarms of the World: A Modern Perspective; Srivastava, R.K., Ernst, R.E., Peng, P., Eds.; Springer: Berlin/Heidelberg, Germany, 2019; pp. 87–110. [Google Scholar]
- Gudmundsson, A. Form and dimensions of dykes in eastern Iceland. Tectonophysics 1983, 95, 295–307. [Google Scholar] [CrossRef]
- Becerril, L.; Galindo, I.; Gudmundsson, A.; Morales, J.M. Depth of origin of magma in eruptions. Sci. Rep. 2013, 3, 2762. [Google Scholar] [CrossRef]
- Masoud, A.A. Geometry and field relations disclose the emplacement dynamics of the SW Sinai Dyke Swarms (Egypt). J. Volcanol. Geotherm. Res. 2020, 395, 106831. [Google Scholar] [CrossRef]
- Biswas, S.K.; Saha, K.; Das, G.; Mondal, T.K. Estimation of magma overpressure from partially exposed dykes—A new approach. J. Struct. Geol. 2023, 168, 104822. [Google Scholar] [CrossRef]
- Gudmundsson, A. The geometry and growth of dykes. In Physics and Chemistry of Dykes; Baer, G., Heimann, A., Eds.; Balkema: Rotterdam, The Netherlands, 1995; pp. 23–34. [Google Scholar]
- Scudero, S.; De Guidi, G.; Gudmundsson, A. Size distributions of fractures, dykes, and eruptions on Etna, Italy: Implications for magma-chamber volume and eruption potential. Sci. Rep. 2019, 9, 4139. [Google Scholar] [CrossRef]
- Gudmundsson, A. Dyke emplacement at divergent plate boundaries. In Mafic Dykes and Emplacement Mechanisms; Parker, A.J., Rickwood, P.C., Tucker, D.H., Eds.; Balkema: Rotterdam, The Netherlands, 1990; pp. 47–62. [Google Scholar]
- Fjader, K.; Gudmundsson, A.; Forslund, T. Dikes, minor faults and mineral veins associated with a transform fault in North Iceland. J. Struct. Geol. 1994, 16, 109–119. [Google Scholar] [CrossRef]
- Villemin, T.; Bergerat, F.; Angelier, J.; Lacasse, C. Brittle deformation and fracture patterns on oceanic rift shoulders: The Esja peninsula, SW Iceland. J. Struct. Geol. 1994, 16, 1641–1654. [Google Scholar] [CrossRef]
- Jolly, R.J.H.; Sanderson, D.J. Variation in the form and distribution of dykes in the Mull swarm, Scotland. J. Struct. Geol. 1995, 17, 1543–1557. [Google Scholar] [CrossRef]
- Walker, G.P.L.; Eyre, P.R. Dike complexes in American Samoa. J. Volcanol. Geotherm. Res. 1995, 69, 241–254. [Google Scholar] [CrossRef]
- Walker, G.P.L.; Eyre, P.R.; Spengler, S.R.; Knight, M.D.; Kennedy, K. Congruent dyke-widths in large basaltic volcanoes. In Physics and Chemistry of Dykes; Baer, G., Heimann, A., Eds.; Balkema: Rotterdam, The Netherlands, 1995; pp. 35–40. [Google Scholar]
- Klausen, M.B. Similar dyke thickness variation across three volcanic rifts in the North Atlantic region: Implications for intrusion mechanisms. Lithos 2006, 92, 137–153. [Google Scholar] [CrossRef]
- Patel, R.; Shankar, R.; Sarma, D.S.; Panda, A. Geochemistry and petrogenesis of tholeiitic dykes from the Chotanagpur Gneissic Complex, Eastern India. J. Earth Sys. Sci. 2021, 130, 160. [Google Scholar] [CrossRef]
- Sneddon, I.N.; Lowengrub, M. Crack Problems in the Classical Theory of Elasticity; Wiley: New York, NY, USA, 1969. [Google Scholar]
- Gray, T.G.F. Handbook of Crack Opening Data; Abington Publishing: Cambridge, UK, 1992. [Google Scholar]
- Gudmundsson, A.; Homberg, C. Evolution of stress fields and faulting in seismic zones. Pure Appl. Geophys. 1999, 154, 257–280. [Google Scholar] [CrossRef]
- Ren, Y.; Geersen, J.; Grevemeyer, L. Impact of spreading rate and age-offset on oceanic transform fault morphology. Geophys. Res. Lett. 2022, 49, e2021GL096170. [Google Scholar] [CrossRef]
- Philipp, S.L. Geometry and formation of gypsum veins in mudstones at Watchet, Somerset, SW England. Geol. Mag. 2008, 145, 831–844. [Google Scholar] [CrossRef]
- Gudmundsson, A. Transport of geothermal fluids along dikes and fault zones. Energies 2022, 15, 7106. [Google Scholar] [CrossRef]
- Mohajeri, N.; Gudmundsson, A. Entropies and scaling exponents of street and fracture networks. Entropy 2012, 14, 800–833. [Google Scholar] [CrossRef]
- Clauset, A.; Chalizi, R.C.; Newman, M.E.J. Power-law distributions in empirical data. Soc. Industr. Appl. Math. 2009, 51, 661–703. [Google Scholar] [CrossRef]
- Gudmundsson, A. Formation and growth of normal faults at the divergent plate boundary in Iceland. Terra Nova 1992, 4, 464–471. [Google Scholar] [CrossRef]
- Rossi, M.J. Morphology and mechanism of eruption of postglacial lava shields in Iceland. Bull. Volcanol. 1996, 57, 530–540. [Google Scholar] [CrossRef]
- Andrew, R.E.B.; Gudmundsson, A. Distribution, structure, and formation of Holocene lava shields in Iceland. J. Volcanol. Geotherm. Res. 2007, 168, 137–154. [Google Scholar] [CrossRef]
- Thordarsson, T.; Hoskuldsson, A. Postglacial volcanism in Iceland. Jökull 2008, 58, 197–228. [Google Scholar] [CrossRef]
- Gudmundsson, A. The Glorious Geology of Iceland’s Golden Circle; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Atkins, A.G.; Mai, Y.W. Elastic and Plastic Fracture; Horwood: Chichester, UK, 1985. [Google Scholar]
- Gudmundsson, A. Tectonic aspects of dykes in northwestern Iceland. Jökull 1984, 34, 81–96. [Google Scholar] [CrossRef]
- Gudmundsson, A.; Bergerat, F.; Angelier, J. Off-rift and rift-zone palaeostresses in Northwest Iceland. Tectonophysics 1996, 255, 211–228. [Google Scholar] [CrossRef]
- Gudmundsson, A. Multiple dikes make eruptions easy. J. Volcanol. Geotherm. Res. 2025, 460, 108284. [Google Scholar] [CrossRef]
- Rice, J.R. Thermodynamics of the quasi-static growth of Griffith cracks. J. Mech. Phys. Solids 1978, 26, 61–78. [Google Scholar] [CrossRef]
- Stevens, R.N.; Guiu, F. Energy balance concepts in the physics of fracture. Proc. R. Soc. Lond. 1991, A435, 169–184. [Google Scholar]
- Wei, R.P. Fracture Mechanics: Integration of Mechanics, Material Science and Chemistry; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Gudmundsson, A.; Friese, N.; Andrew, R.; Philipp, S.L.; Ertl, G.; Letourneur, L. Effects of dyke emplacement and plate pull on mechanical interaction between volcanic systems and central volcanoes in Iceland. In Studies in Volcanology: The Legacy of George Walker; Thordarson, T., Self, S., Larsen, G., Rowland, S.K., Höskuldsson, A., Eds.; IAVCEI: Geneva, Switzerland, 2009; Volume 2, pp. 331–347. [Google Scholar]
- Fukuyama, E. (Ed.) Fault-Zone Properties and Earthquake Rupture Dynamics; Academic Press: Oxford, UK, 2009. [Google Scholar]
- Frisch, W.; Meschede, M.; Blakey, R. Plate Tectonics: Continental Drift and Mountain Building; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Yeats, R.S.; Sieh, K.; Allen, C.R. The Geology of Earthquakes; Oxford University Press: Oxford, UK, 1997. [Google Scholar]
- Sommerfeld, A. Thermodynamics and Statistical Mechanics; Academic Press: New York, NY, USA, 1964. [Google Scholar]
- Widom, B. Statistical Mechanics; Cambridge University Press: New York, NY, USA, 2002. [Google Scholar]
- Panagiotopoulos, A.Z. Essential Thermodynamics; Drios Press: Princeton, NJ, USA, 2012. [Google Scholar]
- Anderson, T.L. Fracture Mechanics, 3rd ed.; Taylor and Francis: London, UK, 2005. [Google Scholar]
- Bao, T.F.; Peng, Y.; Cong, P.J.; Wang, J.L. Analysis of crack propagation in concrete structures with structural information entropy. Sci. China Technol. Sci. 2010, 53, 1943–1948. [Google Scholar] [CrossRef]
- Naderi, M.; Amiri, M.; Khonsari, M.M. On the thermodynamic entropy of fatigue fracture. Proc. Roy. Soc. Lond. 2010, A466, 423–438. [Google Scholar] [CrossRef]
- Kilburn, C.R.J. Forecasting volcanic eruptions: Beyond the failure forecast method. Front. Earth Sci. 2018, 6, 133. [Google Scholar] [CrossRef]
- Satow, C.; Gudmundsson, A.; Gertisser, R.; Ramsey, C.B.; Bazargan, M.; Pyle, D.M.; Wulf, S.; Miles, A.J.; Hardiman, M. Eruptive activity of the Santorini Volcano controlled by sea-level rise and fall. Nat. Geosci. 2021, 14, 586–592. [Google Scholar] [CrossRef]
- Gudmundsson, A. The effects of stress gradients on faulting and dike emplacement, with applications to Santorini and Iceland. In The Role of Tectonics on the Emergence and Evolution of Volcanic Features with Particular Reference to the to the Mediterranean Region; Papanikolaou, D., Ed.; Geological Society, London, Special Publications; The Geological Society of London: London, UK, 2025; in press. [Google Scholar]
- Gudmundsson, A.; Simmenes, T.H.; Larsen, B.; Philipp, S.L. Effects of internal structure and local stresses on fracture propagation, deflection, and arrest in fault zones. J. Struct. Geol. 2010, 32, 1643–1655. [Google Scholar] [CrossRef]
- Blundell, S.J.; Blundell, K.M. Concepts in Thermal Physics; Oxford University Press: Oxford, UK, 2006. [Google Scholar]
- Swendsen, R.H. An Introduction to Statistical Mechanics and Thermodynamics, 2nd ed.; Oxford University Press: Oxford, UK, 2019. [Google Scholar]
- Hobé, A.; Bazargan, M.; Selek, B.; Tryggvason, A.; Alofe, E.; Gudmundsson, A. Tomographic and volcanotectonic controls on the 2021–2023 Fagradalsfjall eruptions, Iceland. Sci. Rep. 2025, 15, 16455. [Google Scholar] [CrossRef]
- Bjornsson, A. Dynamics of crustal rifting in NE Iceland. J. Geophys. Res. 1985, 90, 10151–10162. [Google Scholar] [CrossRef]
- Sigmundsson, F.; Parks, M.; Hooper, A.; Geirsson, H.; Vogfjörd, K.S.; Drouin, V.; Ófeigsson, B.G.; Hreinsdóttir, S.; Hjaltadóttir, S.; Jónsdóttir, K.; et al. Deformation and seismicity decline before the 2021 Fagradalsfjall eruption. Nature 2022, 609, 523–528. [Google Scholar] [CrossRef]
- De Pascale, G.P.; Fischer, T.J.; Moreland, W.M.; Geirsson, H.; Hrubcová, P.; Drouin, V.; Forester, D.; Payet-Clerc, M.; da Silveira, D.B.; Vlček, J.; et al. On the move: 2023 observations on real time graben formation, Grindavik, Iceland. Geophys. Res. Lett. 2024, 51, e2024GL110150. [Google Scholar] [CrossRef]
- Rundle, J.B.; Turcotte, D.L.; Shcherbakov, R.; Klein, W.; Sammis, C. Statistical physics approach to understanding the multiscale dynamics of earthquake fault systems. Rev. Geophys. 2003, 41, 4. [Google Scholar] [CrossRef]
- Main, I. Statistical physics, seismogenesis, and seismic hazard. Rev. Geophys. 1996, 34, 433–462. [Google Scholar] [CrossRef]
- Andrew, R.E.B.; Gudmundsson, A. Volcanoes as elastic inclusions: Their effects on the propagation of dykes, volcanic fissures, and volcanic zones in Iceland. J. Volcanol. Geotherm. Res. 2008, 177, 1045–1054. [Google Scholar] [CrossRef]
- Qu, J.; Cherkaoui, M. Fundamentals of Micromechanics of Solids; Wiley: New York, NY, USA, 2006. [Google Scholar]
- Yin, H.; Zhao, Y. Introduction to the Micromechanics of Composite Materials; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Morad, D.; Lyakhovsky, V.; Hatzor, Y.H.; Sagy, A. Stress heterogeneity and the onset of faulting along geometrically irregular faults. Geophys. Res. Lett. 2022, 49, e2021GL097591. [Google Scholar] [CrossRef]
- Mika Liao, Y.W.; Fry, B.; Howell, A.; Williams, C.A.; Nicol, A.; Rollins, C. The role of heterogeneous stress in earthquake cycle models of the Hikurangi–Kermadec subduction zone. Geophys. J. Int. 2024, 239, 574–590. [Google Scholar] [CrossRef]
- Schoenball, M.; Davatzes, N.C. Quantifying the heterogeneity of the tectonic stress field using borehole data. J. Geophys. Res. 2017, 122, 6737–6756. [Google Scholar] [CrossRef]
- Huang, Y.; Ide, S.; Kato, A.; Yoshida, K.; Jiang, C.; Zhai, P. Fault material heterogeneity controls deep interplate earthquakes. Sci. Advan. 2025, 11, eadr9353. [Google Scholar] [CrossRef]
- Li, M.; Niemeijer, A.; van Dinther, Y. Earthquake nucleation and slip behavior altered by stochastic normal stress heterogeneity. J. Geophys. Res. 2024, 130, e2024JB029857. [Google Scholar] [CrossRef]









| Fracture and Dike Data | ||||
|---|---|---|---|---|
| Population | Number | Length Range (m) | ||
| Reykjanes | 120 | 40–5750 | γ = 1.410 | 3.098 |
| 40–500 | γ = 0.612 | 1.716 | ||
| 500–5750 | γ = 1.720 | 3.38 | ||
| Thingvellir | 101 | 57–7736 | γ = 1.173 | 3.369 |
| 57–300 | γ = 0.554 | 1.347 | ||
| 300–7736 | γ = 1.257 | 3.766 | ||
| Reykjanes- Thingvellir | 221 | 40–7736 | γ = 1.460 | 3.246 |
| 40–300 | γ = 0.497 | 1.353 | ||
| 300–7736 | γ = 1.659 | 3.578 | ||
| All fracture data | 565 | 0.1–7736 | γ = 1.471 | 2.902 |
| 0.1–500 | γ = 0.652 | 1.497 | ||
| 500–7736 | γ = 1.735 | 3.676 | ||
| Dikes | 1041 | 26–8948 | γ = 1.772 | 3.117 |
| 26–1000 | γ = 0.339 | 2.225 | ||
| 1000–8948 | γ = 2.720 | 3.397 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gudmundsson, A. Statistical Physics of Fissure Swarms and Dike Swarms. Geosciences 2025, 15, 301. https://doi.org/10.3390/geosciences15080301
Gudmundsson A. Statistical Physics of Fissure Swarms and Dike Swarms. Geosciences. 2025; 15(8):301. https://doi.org/10.3390/geosciences15080301
Chicago/Turabian StyleGudmundsson, Agust. 2025. "Statistical Physics of Fissure Swarms and Dike Swarms" Geosciences 15, no. 8: 301. https://doi.org/10.3390/geosciences15080301
APA StyleGudmundsson, A. (2025). Statistical Physics of Fissure Swarms and Dike Swarms. Geosciences, 15(8), 301. https://doi.org/10.3390/geosciences15080301





