Real-Time Foreshock–Aftershock–Swarm Discrimination During the 2025 Seismic Crisis near Santorini Volcano, Greece: Earthquake Statistics and Complex Networks
Abstract
1. Introduction


2. Materials and Methods
2.1. Seismotectonic and Volcanic Setting
2.2. Discrimination of Foreshocks from Other Earthquake Clusters
2.3. Research Strategy
2.4. Earthquake Data
2.5. Research Methods
2.5.1. Catalog Completeness
2.5.2. Space–Time Seismicity Distribution Using Complex Networks
2.5.3. Frequency–Magnitude Distribution
3. Results
3.1. Background Seismicity
3.2. Analysis of the 2025 Cluster
3.2.1. Earthquake Catalog Completeness
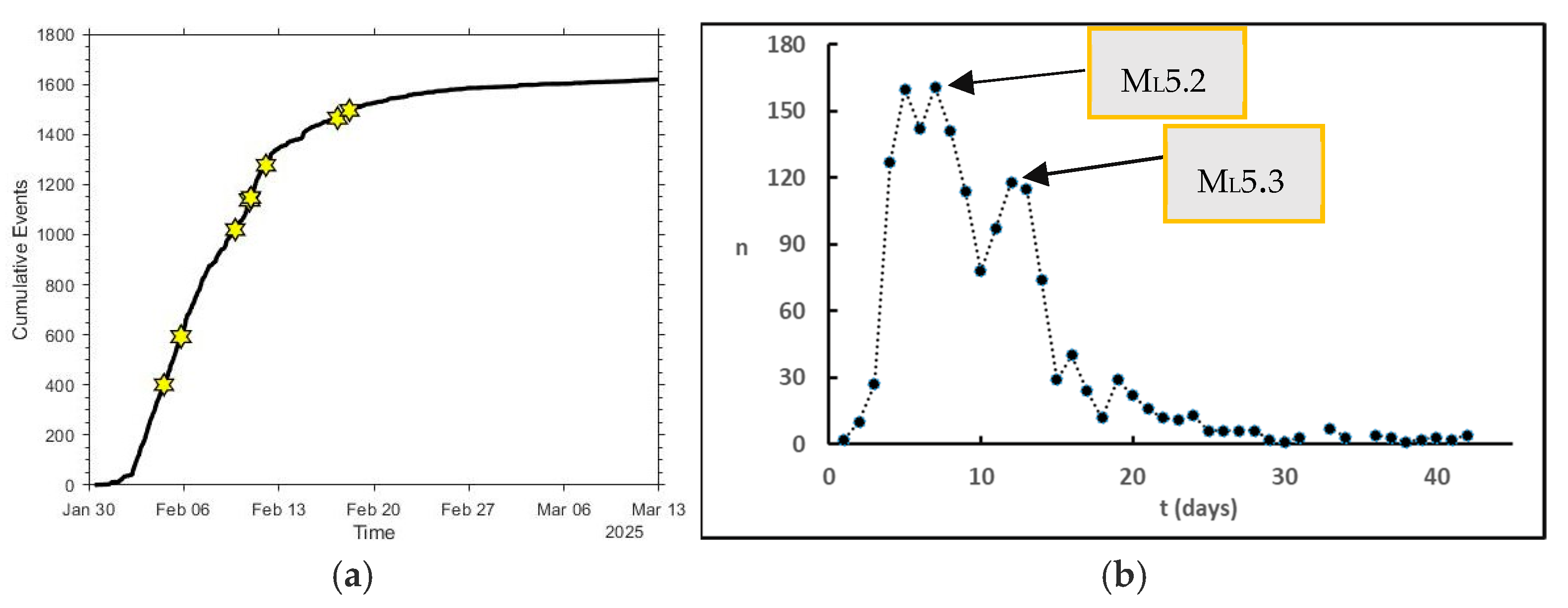
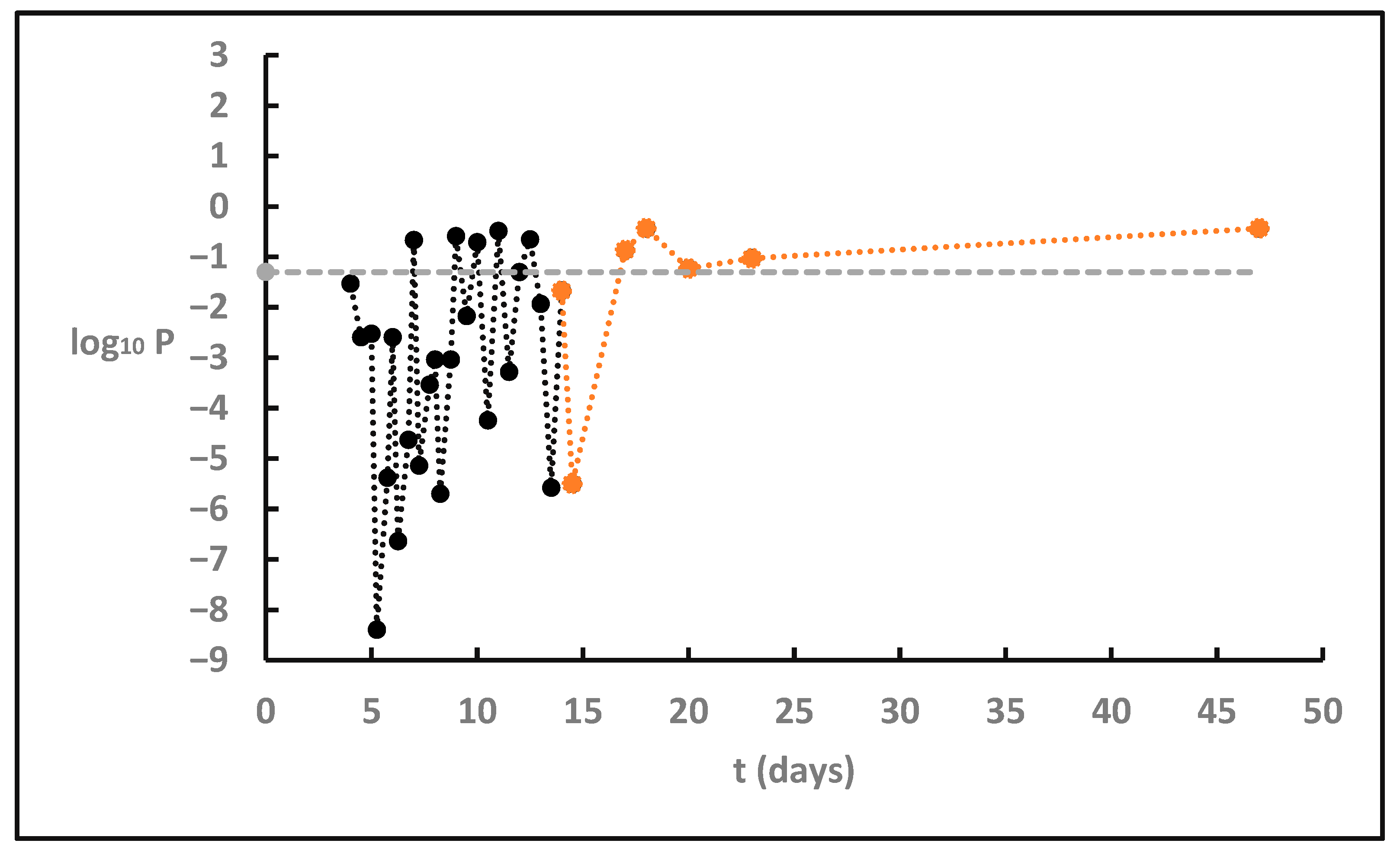
3.2.2. Temporal Variation
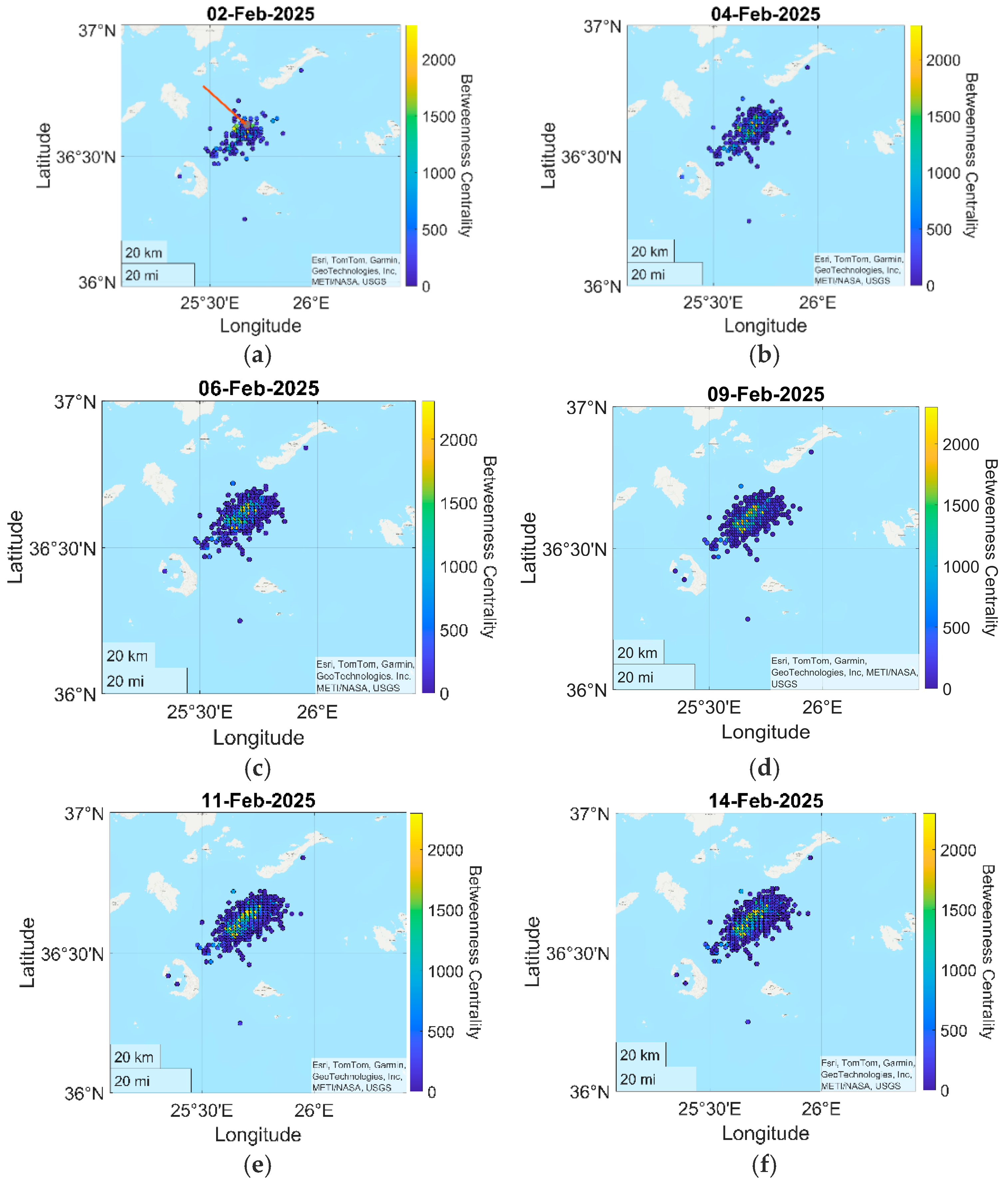
3.2.3. Spatial Variation
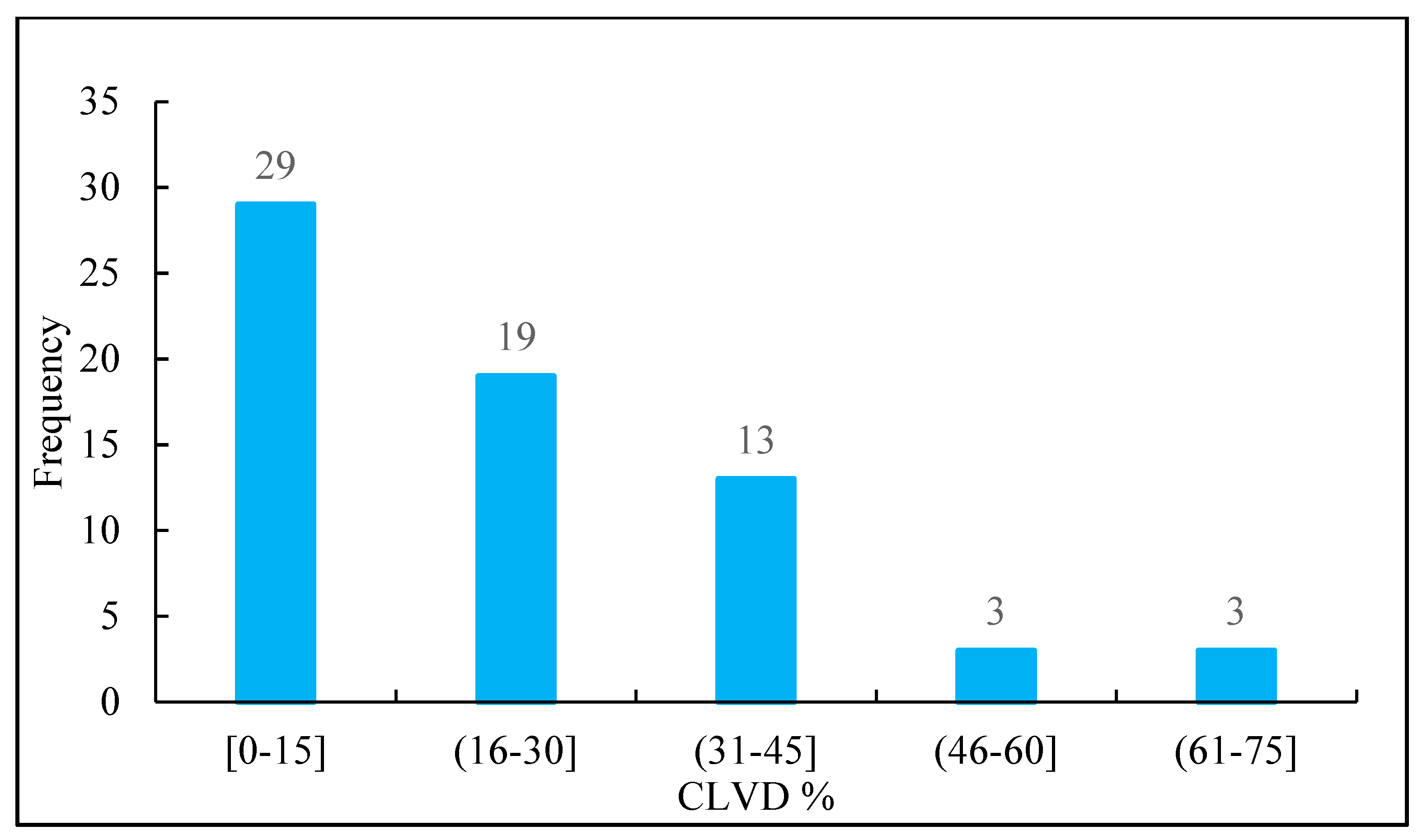
3.2.4. b-Value Variation
4. Discussion

5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Correction Statement
Appendix A
References
- Papadopoulos, G.A.; Charalampakis, M.; Fokaefs, A.; Minadakis, G. Strong foreshock signal preceding the L’Aquila (Italy) earthquake (Mw6.3) of 6 April 2009. Nat. Hazards Earth Syst. Sci. 2010, 10, 19–24. [Google Scholar] [CrossRef]
- Gulia, L.; Wiemer, S. Real-time discrimination of earthquake foreshocks and aftershocks. Nature 2019, 574, 193–199. [Google Scholar] [CrossRef]
- Dascher-Cousineau, K.; Lay, T.; Brodsky, E.E. Two Foreshock Sequences Post Gulia and Wiemer. Seismol. Res. Lett. 2020, 91, 2843–2850. [Google Scholar] [CrossRef]
- Druitt, T.; Mellors, R.; Pyle, D.; Sparks, R. Explosive volcanism on Santorini, Greece. Geol. Mag. 1989, 126, 95–126. [Google Scholar] [CrossRef]
- Friedrich, W.L. Fire in the Sea; Cambridge University Press: Cambridge, UK, 2000; 258p. [Google Scholar]
- McCoy, F.W.; Heiken, G. (Eds.) The Late-Bronze Age explosive eruption of Thera (Santorini), Greece: Regional and local effects. In Volcanic Hazards and Disasters in Human Antiquity; Geological Society of America: Boulder, Colorado, 2000. [Google Scholar] [CrossRef]
- Galanopoulos, A. The damaging shocks and the earthquake potential of Greece. Ann. Geol. Pays Hellen. 1982, 30, 648–724, (In Greek with English Abstract). [Google Scholar]
- Papadopoulos, G.A.; Pavlides, S.B. The large 1956 earthquake in the South Aegean: Macroseismic field configuration, faulting, and neotectonics of Amorgos Island. Earth Planet. Sci. Lett. 1992, 113, 383–396. [Google Scholar] [CrossRef]
- Papadopoulos, G.A. Tsunamis in the European-Mediterranean Region-From Historical Record to Risk Mitigation; Elsevier: Amsterdam, The Netherlands, 2016; 271p. [Google Scholar]
- McClusky, S.; Balassanian, S.; Barka, A.; Demir, C.; Ergintav, S.; Georgiev, I.; Gurkan, O.; Hamburger, M.; Hurst, K.; Kahle, H.; et al. Global Positioning System constraints on plate kinematics and dynamics in the eastern Mediterranean and Caucasus. J. Geophys. Res. 2000, 105, 5695–5719. [Google Scholar] [CrossRef]
- Bocchini, G.M.; Brüstle, A.; Becker, D.; Meier, T.; van Keken, P.E.; Ruscic, M.; Papadopoulos, G.A.; Rische, M.; Friederich, W. Tearing, segmentation, and backstepping subduction in the Aegean: New insights from seismicity. Tectonophysics 2018, 734–735, 96–118. [Google Scholar] [CrossRef]
- International Seismological Centre. The ISC-GEM Global Instrumental Earthquake Catalogue, Version 11.0-Released on 2024-06-25. Available online: http://www.isc.ac.uk/iscgem/download.php (accessed on 6 May 2025).
- Makropoulos, K.; Kaviris, G.; Kouskouna, V. An updated and extended earthquake catalogue for Greece and adjacent areas since 1900. Nat. Hazards Earth Syst. Sci. 2012, 12, 1425–1430. [Google Scholar] [CrossRef]
- GCMT: Global CMT Catalog. Available online: https://www.globalcmt.org/CMTsearch.html (accessed on 6 May 2025).
- Brüstle, A.; Friederich, W.; Meier, T.; Gross, C. Focal mechanism and depth of the 1956 Amorgos twin earthquakes from waveform matching of analogue seismograms. Solid Earth 2014, 5, 1027–1044. [Google Scholar] [CrossRef]
- EMODnet Digital Bathymetry (DTM 2024). EMODnet Bathymetry Consortium. Available online: https://sextant.ifremer.fr/record/cf51df64-56f9-4a99-b1aa-36b8d7b743a1/ (accessed on 20 April 2025).
- Papathoma-Köhle, M. Letter to the Editor: Latest earthquakes in Santorini reveal the need for a multi-hazard and multi-vulnerability approach to disaster risk reduction. Nat. Hazards 2025, 121, 11215–11220. [Google Scholar] [CrossRef]
- Ganas, A. NOAFAULTS KMZ Layer Version 5.0 (V5.0) [Data Set]. Zenodo 2023. Available online: https://zenodo.org/records/8075517 (accessed on 20 April 2025).
- McKenzie, D. Active tectonics of the Alpine-Himalayan belt: The Aegean Sea and surrounding regions. Geophys. J. R. Astron. Soc. 1978, 55, 217–254. [Google Scholar] [CrossRef]
- Kapetanidis, V.; Kassaras, I. Contemporary crustal stress of the Greek region deduced from earthquake focal mechanisms. J. Geodyn. 2019, 123, 55–82. [Google Scholar] [CrossRef]
- Minoura, K.; Imamoura, F.; Kuran, U.; Nakamura, T.; Papadopoulos, G.A.; Takahashi, T.; Yalciner, A.C. Discovery of Minoan tsunami deposits. Geology 2000, 28, 59–62. [Google Scholar] [CrossRef]
- Vougioukalakis, G.; Sbrana, A.; Mitropoulos, D. The 1649–50 Kolumbo submarine volcano activity, Santorini, Greece. In The European Laboratory Volcanoes: Workshop Proceedings; Barberi, F., Casale, R., Fratta, M., Eds.; European Science Commission: Luxembourg, 1995; pp. 189–192. [Google Scholar]
- Dominey-Howes, D.T.M.; Papadopoulos, G.A.; Dawson, A.G. Geological and historical investigation of the 1650 Mt. Columbo (Thera Island) eruption and tsunami, Aegean Sea, Greece. Nat. Hazards 2000, 21, 83–96. [Google Scholar] [CrossRef]
- Galanopoulos, A.G. The seismic sea wave of 9 July 1956. Prakt. Akad. Athens 1957, 32, 90–101, (In Greek with English Abstract). [Google Scholar]
- Ambraseys, N.N. The seismic sea wave of 9 July 1956 in the Greek Archipelago. J. Geophys. Res. 1960, 65, 1257–1265. [Google Scholar] [CrossRef]
- Papadopoulos, G.A.; Imamura, F.; Minoura, K.; Takahashi, T.; Karakatsanis, S.; Fokaefs, A.; Orfanogiannaki, K.; Daskalaki, E.; Diakogianni, G. The 9 July 1956 large tsunami in the south Aegean Sea: Compilation of a data basis and re-evaluation. In Proceedings of the 22nd International IUGG Tsunami Symposium, Chania, Greece, 27–29 June 2005; pp. 173–180. [Google Scholar]
- Okal, E.A.; Synolakis, C.E.; Uslu, B.; Kalligeris, N.; Voukouvalas, E. The 1956 earthquake and tsunami in Amorgos, Greece. Geophys. J. Internat. 2009, 178, 1533–1554. [Google Scholar] [CrossRef]
- Papadopoulos, G.A.; Gràcia, E.; Urgeles, R.; Sallares, V.; De Martini, P.M.; Pantosti, D.; González, M.; Yalciner, A.C.; Mascle, J.; Sakellariou, D.; et al. Historical and pre-historical tsunamis in the Mediterranean and its connected seas: Geological signatures, generation mechanisms and coastal impacts. Mar. Geol. 2014, 354, 81–109. [Google Scholar] [CrossRef]
- Perissoratis, C.; Papadopoulos, G.A. Sediment instability and slumping in the southern Aegean Sea and the case history of the 1956 tsunami. Mar. Geol. 1999, 161, 287–305. [Google Scholar] [CrossRef]
- Nomikou, P.; Hübscher, C.; Papanikolaou, D.; Farangitakis, G.P.; Ruhnau, M.; Lampridou, D. Expanding extension, subsidence and lateral segmentation within the Santorini-Amorgos basins during Quaternary: Implications for the 1956 Amorgos events, central-south Aegean Sea, Greece. Tectonophysics 2017, 722, 138–153. [Google Scholar] [CrossRef]
- Leclerc, F.; Palagonia, S.; Feuillet, N.; Nomikou, P.; Lampridou, D.; Barrière, P.; Dano, A.; Ochoa, E.; Gracias, N.; Escartin, J. Large seafloor rupture caused by the 1956 Amorgos tsunamigenic earthquake, Greece. Commun. Earth Environ. 2024, 5, 663. [Google Scholar] [CrossRef]
- Papazachos, B.C.; Delibasis, N.D. Tectonic stress field and seismic faulting in the area of Greece. Tectonophysics 1969, 7, 231–255. [Google Scholar] [CrossRef]
- Ritsema, A.R. Earthquake mechanisms of the Balkan region. R. Neth. Meteorol. Inst. Sci. Rep. 1974, 74, 97. [Google Scholar]
- Shirokova, E.I. Stress pattern and probable motion in the earthquake loci of the Asia-Mediterranean seismic belt. In Elastic Strain Field of the Earth and Mechanisms of Earthquake Sources; Balakina, L.M., Misharina, L.A., Vvedenskaya, A.V., Eds.; Nauka: Moscow, Russia, 1972. [Google Scholar]
- Tsampouraki-Kraounaki, K.; Sakellariou, D.; Rousakis, G.; Morfis, I.; Panagiotopoulos, I.; Livanos, I.; Manta, K.; Paraschos, F.; Papatheodorou, G. The Santorini-Amorgos Shear Zone: Evidence for Dextral Transtension in the South Aegean Back-Arc Region, Greece. Geosciences 2021, 11, 216. [Google Scholar] [CrossRef]
- Bohnhoff, M.; Rische, M.; Meier, T.; Becker, D.; Stavrakakis, G.; Harjes, H.-P. Microseismic activity in the Hellenic Volcanic Arc, Greece, with emphasis on the seismotectonic setting of the Santorini-Amorgos zone. Tectonophysics 2006, 423, 17–33. [Google Scholar] [CrossRef]
- Hufstetler, R.S.; Hooft, E.E.E.; Toomey, D.R.; VanderBeek, B.P.; Papazachos, C.B.; Chatzis, N. Seismic structure of the mid to upper crust at the Santorini-Kolumbo magma system from joint earthquake and active source Vp-Vs tomography. Geochem. Geophys. Geosyst. 2025, 26, e2024GC012022. [Google Scholar] [CrossRef]
- Papadimitriou, P.; Kapetanidis, V.; Karakonstantis, A.; Kaviris, G.; Voulgaris, N.; Makropoulos, K. The Santorini Volcanic Complex: A detailed multi-parameter seismological approach with emphasis on the 2011–2012 unrest period. J. Geodyn. 2015, 85, 32–57. [Google Scholar] [CrossRef]
- Mogi, K. Some discussion on aftershocks, foreshocks and earthquake swarms—The fracture of a semi-infinite body caused by an inner stress origin and its relation to the earthquake phenomena (3rd paper). Bull. Earthq. Res. Inst. Univ. Tokyo 1963, 41, 615–658. [Google Scholar]
- Mogi, K. Earthquake Prediction, 1st ed.; Academic Press: Tokyo, Japan, 1985; 355p. [Google Scholar]
- Ogata, Y.; Utsu, T.; Katsura, K. Statistical discrimination of foreshocks from other earthquake clusters. Geophys. J. Int. 1996, 127, 17–30. [Google Scholar] [CrossRef]
- Van der Elst, N.J. b-positive: A robust estimator of aftershock magnitude distribution in transiently incomplete catalogs. J. Geophys. Res. 2021, 126, e2020JB021027. [Google Scholar] [CrossRef]
- Ishimoto, M.; Iida, K. Observations of earthquakes registered with the microseismograph constructed recently. Bull. Earthq. Res. Inst. Univ. Tokyo 1939, 17, 443–478. [Google Scholar]
- Gutenberg, B.; Richter, C. Frequency of earthquakes in California. Bull. Seism. Soc. Am. 1944, 34, 185–188. [Google Scholar] [CrossRef]
- Frohlich, C.; Davis, S.D. Teleseismic b values; or, much ado about 1.0. J. Geophys. Res. 1993, 98, 631–644. [Google Scholar] [CrossRef]
- Schorlemmer, D.; Wiemer, S.; Wyss, M. Variations in earthquake-size distribution across different stress regimes. Nature 2005, 437, 539–542. [Google Scholar] [CrossRef]
- Scholz, C.H. Microfractures, Aftershocks, and Seismicity. Bull. Seism. Soc. Am. 1968, 58, 1117–1130. [Google Scholar]
- Enescu, B.; Ito, K. The 1998 Hida Mountain, Central Honshu, Japan, earthquake swarm: Double-difference event relocation, frequency-magnitude distribution and Coulomb stress changes. Tectonophysics 2005, 409, 147–157. [Google Scholar] [CrossRef]
- Abercrombie, R.E.; Mori, J. Occurrence patterns of foreshocks to large earthquakes in the western United States. Nature 1996, 381, 303–307. [Google Scholar] [CrossRef]
- Yamashita, T. Simulation of seismicity due to fluid migration in a fault zone. Geophys. J. Int. 1998, 132, 674–686. [Google Scholar] [CrossRef]
- Olami, Z.; Feder, H.; Christensen, K. Self-organized criticality in a continuous, non-conservative cellular automaton modeling earthquakes. Phys. Rev. Lett. 1992, 68, 1244–1247. [Google Scholar] [CrossRef]
- Avlonitis, Μ.; Papadopoulos, G.A. Foreshocks and b-value: Bridging macroscopic observations to source mechanical considerations. Pure Appl. Geophys. 2014, 171, 2569–2580. [Google Scholar] [CrossRef]
- Suyehiro, S.; Sekiya, H. Foreshocks and earthquake prediction. Tectonophysics 1972, 14, 219–225. [Google Scholar] [CrossRef]
- Papazachos, B.C. Foreshocks and earthquake prediction. Tectonophysics 1975, 28, 213–226. [Google Scholar] [CrossRef]
- Ishida, M.; Kanamori, H. The foreshock activity of the 1971 San Fernando earthquake. California. Bull. Seism. Soc. Am. 1978, 68, 1265–1279. [Google Scholar] [CrossRef]
- Kagan, Y.; Knopoff, L. Statistical study of the occurrence of shallow earthquakes. Geophys. J. R. Astron. Soc. 1978, 55, 67–86. [Google Scholar] [CrossRef]
- Jones, L.M.; Molnar, P. Some characteristics of foreshocks and their possible relationship to earthquake prediction and premonitory slip on faults. J. Geophys. Res. 1979, 84, 3596–3608. [Google Scholar] [CrossRef]
- Maeda, K. Time distribution of immediate foreshocks obtained by a stacking method. Pure Appl. Geophys. 1999, 155, 381–394. [Google Scholar] [CrossRef]
- Yamaoka, K.; Ooida, T.; Ueda, Y. Detailed distribution of accelerating foreshocks before a M 5.1 earthquake in Japan. Pure Appl. Geophys. 1999, 155, 335–353. [Google Scholar] [CrossRef]
- Papadopoulos, G.A.; Drakatos, G.; Plessa, A. Foreshock activity as a precursor of strong earthquakes in Corinthos Gulf, Central Greece. Phys. Chem. Earth 2000, 25, 239–245. [Google Scholar] [CrossRef]
- Raykova, P.; Solakov, D.; Simeonova, S. A statistical study of the MW5.3 Valandovo (northern Macedonia) earthquake seismic sequence. Boll. Geofis. Teor. Appl. 2019, 60, 443–456. [Google Scholar]
- Matsumoto, S.; Iio, Y.; Sakai, S.; Kato, A. Strength dependency of frequency–magnitude distribution in earthquakes and implications for stress state criticality. Nat. Commun. 2024, 15, 4957. [Google Scholar] [CrossRef]
- Wetzler, N.; Lay, T.; Brodsky, E.E. Global Characteristics of Observable Foreshocks for Large Earthquakes. Seismol. Res. Lett. 2023, 94, 2313–2325. [Google Scholar] [CrossRef]
- Bressan, G.; Barnaba, C.; Peresan, A.; Rossi, G. Anatomy of seismicity clustering from parametric space-time analysis. Phys. Earth Planet. Inter. 2021, 320, 106787. [Google Scholar] [CrossRef]
- Mogi, K. The fracture of a semi-infinite body caused by an inner stress origin and its relation to the earthquake phenomena (2nd paper). Bull. Earthq. Res. Inst. Univ. Tokyo 1963, 41, 595–614. [Google Scholar]
- Yamashita, F.; Fukuyama, E.; Xu, S.; Kawakata, H.; Mizoguchi, K.; Takizawa, S. Two end-member earthquake preparations illuminated by foreshock activity on a meter-scale laboratory fault. Nat. Commun. 2021, 12, 4302. [Google Scholar] [CrossRef]
- Hainzl, S.; Zoller, G.; Kurths, J. Similar power laws for foreshock and aftershock sequences in a spring-block model for earthquakes. J. Geophys. Res. 1999, 104, 7243–7253. [Google Scholar] [CrossRef]
- Lei, X.; Li, S.; Liu, L. Seismic b-Value for Foreshock AE Events Preceding Repeated Stick-Slips of Pre-Cut Faults in Granite. Appl. Sci. 2018, 8, 2361. [Google Scholar] [CrossRef]
- Dong, L.; Zhang, L.; Liu, H.; Du, K.; Liu, X. Acoustic Emission b Value Characteristics of Granite under True Triaxial Stress. Mathematics 2022, 10, 451. [Google Scholar] [CrossRef]
- Main, I. Apparent breaks in scaling in the earthquake cumulative frequency-magnitude distribution: Fact or artifact? Bull. Seism. Soc. Am. 2000, 90, 86–97. [Google Scholar] [CrossRef]
- Yamashita, T.; Knopoff, L. A model of foreshock occurrence. Geophys. J. Int. 2007, 96, 389–399. [Google Scholar] [CrossRef]
- Ito, R.; Kaneko, Y. Physical mechanism for a temporal decrease of the Gutenberg-Richter b-value prior to a large earthquake. J. Geophys. Res. 2023, 128, e2023JB027413. [Google Scholar] [CrossRef]
- Papadopoulos, G.A.; Latoussakis, I.; Daskalaki, E.; Diakogianni, G.; Fokaefs, A.; Kolligri, M.; Liadopoulou, K.; Orfanogiannaki, K.; Pirentis, A. The East Aegean Sea strong earthquake sequence of October-November 2005: Lessons learned for earthquake prediction from foreshocks. Nat. Hazards Earth Syst. Sci. 2006, 6, 895–901. [Google Scholar] [CrossRef]
- Triantafyllou, I.; Karavias, A.; Koukouvelas, I.; Papadopoulos, G.A.; Parcharidis, I. The Crete Isl. (Greece) Mw6.0 Earthquake of 27 September 2021: Expecting the Unexpected. GeoHazards 2022, 3, 106–124. [Google Scholar] [CrossRef]
- Engdahl, E.R.; Kisslinger, C. Seismological Precursors to a Magnitude Earthquake in the Central Aleutian Islands. J. Phys. Earth 1977, 25, 243–250. [Google Scholar] [CrossRef]
- Chen, Y.; Liu, J.; Ge, H. Pattern Characteristics of Foreshock Sequences. Pure Appl. Geophys. 1999, 155, 395–408. [Google Scholar] [CrossRef]
- Kato, A.; Obara, K.; Igarashi, T.; Tsuruoka, H.; Nakagawa, S.; Hirata, N. Propagation of slow slip leading up to the 2011 Mw 9.0 Tohoku-Oki earthquake. Science 2012, 335, 705–708. [Google Scholar] [CrossRef]
- Lippiello, E.; Marzocchi, W.; De Arcangelis, L.; Godano, C. Spatial organization of foreshocks as a tool to forecast large earthquakes. Sci. Rep. 2012, 2, 846. [Google Scholar] [CrossRef] [PubMed]
- Papadopoulos, G.A.; Minadakis, G. Foreshock Patterns Preceding Great Earthquakes in the Subduction Zone of Chile. In Geodynamics of the Latin American Pacific Margin; Springer Nature: Berlin/Heidelberg, Germany, 2016. [Google Scholar] [CrossRef]
- Kato, A.; Fukuda, J.; Nakagawa, S.; Obara, K. Foreshock migration preceding the 2016 Mw7.0 Kumamoto earthquake, Japan. Geophys. Res. Lett. 2016, 43, 8945–8953. [Google Scholar] [CrossRef]
- Papadopoulos, G.A.; Agalos, A.; Minadakis, G.; Triantafyllou, I.; Krassakis, P. Short-Term Foreshocks as Key Information for Mainshock Timing and Rupture: The Mw6.8 25 October 2018 Zakynthos Earthquake, Hellenic Subduction Zone. Sensors 2020, 20, 5681. [Google Scholar] [CrossRef]
- Suzuki, T.; Matsukawa, H. Self-organized first-order transition from foreshock to mainshock in earthquake sequences induced by heat, fluid pressure, and porosity. Eur. Phys. J. 2025, 98, 67. [Google Scholar] [CrossRef]
- Peng, Z.; Lei, X. Physical mechanisms of earthquake nucleation and foreshocks: Cascade triggering, aseismic slip, or fluid flows? Earthq. Res. Adv. 2024, 5, 100349. [Google Scholar] [CrossRef]
- Utsu, T.; Ogata, Y.; Matsuura, R. The centenary of the Omori formula for a decay law of aftershocks activity. J. Phys. Earth 1995, 43, 1–33. [Google Scholar] [CrossRef]
- Ogata, Y.; Katsura, K. Comparing foreshock characteristics and foreshock forecasting in observed and simulated earthquake catalogs. J. Geophys. Res. 2014, 119, 8457–8477. [Google Scholar] [CrossRef]
- Tamaribuchi, K.; Yagi, Y.; Enescu, B.; Hirano, S. Characteristics of foreshock activity inferred from the JMA earthquake catalog. Earth Planets Space 2018, 70, 90. [Google Scholar] [CrossRef]
- Tormann, T.; Enescu, B.; Woessner, J.; Wiemer, S. Randomness of megathrust earthquakes implied by rapid stress recovery after the Japan earthquake. Nat. Geosci. 2015, 8, 152–158. [Google Scholar] [CrossRef]
- Tormann, T.; Wiemer, S.; Metzger, S.; Michael, A.; Hardebeck, J.L. Size distribution of Parkfield’s microearthquakes reflects changes in surface creep rate. Geophys. J. Int. 2013, 193, 1474–1478. [Google Scholar] [CrossRef]
- Tormann, T.; Wiemer, S.; Mignan, A. Systematic survey of high-resolution b value imaging along Californian faults: Inference on asperities. J. Geophys. Res. 2014, 119, 2029–2054. [Google Scholar] [CrossRef]
- Wiemer, S.; Wyss, M. Mapping spatial variability of the frequency-magnitude distribution of earthquakes. Adv. Geo-Phys. 2002, 45, 259–302. [Google Scholar] [CrossRef]
- Wiemer, S.; Katsumata, K. Spatial variability of seismicity parameters in aftershock zones. J. Geophys. Res. 1999, 104, 13135–13151. [Google Scholar] [CrossRef]
- McNutt, S.R. Seismic monitoring and eruption forecasting of volcanoes: A review of the state-of-the-art and case histories. In Monitoring and Mitigation of Volcano Hazards; Scarpa, R., Tilling, R.I., Eds.; Springer: Berlin/Heidelberg, Germany, 1996; pp. 99–146. [Google Scholar] [CrossRef]
- Hamdache, M.; Peláez, J.A.; Henares, J.; Damerdji, Y.; Sawires, R. Analysis of the 2012–2013 Torreperogil-Sabiote seismic swarm. Phys. Chem. Earth 2016, 95, 101–112. [Google Scholar] [CrossRef]
- Stankova, J.; Bilek, S.L.; Rowe, C.A.; Aster, R.C. Characteristics of the October 2005 Microearthquake Swarm and Reactivation of Similar Event Seismic Swarms over Decadal Time Periods near Socorro, New Mexico. Bull. Seismol. Soc. Am. 2008, 98, 93–105. [Google Scholar] [CrossRef]
- Yamashita, T. Pore Creation due to Fault Slip in a Fluid-permeated Fault Zone and its Effect on Seismicity: Generation Mechanism of Earthquake Swarm. Pure Appl. Geophys. 1999, 155, 625–647. [Google Scholar] [CrossRef]
- Shapiro, S.A.; Dinske, C. Scaling of seismicity induced by nonlinear fluid-rock interaction. J. Geophys. Res. 2009, 114, 1–14. [Google Scholar] [CrossRef]
- Naoi, M.; Nakatani, M.; Horiuchi, S.; Yabe, Y.; Philipp, J.; Kgarume, T.; Morema, G.; Khambule, S.; Masakale, T.; Ribeiro, L.; et al. Frequency-Magnitude Distribution of −3.7≤ Mw≤ 1 Mining-Induced Earthquakes Around a Mining Front and b Value In-variance with Post-Blast Time. Pure Appl. Geophys. 2014, 171, 2665–2684. [Google Scholar] [CrossRef]
- Papadopoulos, G.A.; Minadakis, G.; Orfanogiannaki, K. Short-Term Foreshocks and Earthquake Prediction. In Atmospheric and Ionospheric Electromagnetic Phenomena Associated with Earthquakes; Ouzounov, D., Pulinets, S., Hattori, K., Taylor, P., Freund, F., Eds.; AGU Geophysical Monograph Series, 1st ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2018; pp. 127–147. [Google Scholar] [CrossRef]
- Triantafyllou, I.; Papadopoulos, G.A. A Unique Seismic Cluster near Santorini, Greece, very Likely a Foreshock Sequence. Report, European-Mediterranean Seismological Centre, Uploaded on 6 February 2025, 3p. Available online: https://www.emsc-csem.org/Special_reports/ (accessed on 20 April 2025).
- Triantafyllis, N.; Venetis, I.E.; Fountoulakis, I.; Pikoulis, E.-V.; Sokos, E.; Evangelidis, C.-P. Gisola: A High-Performance Computing Application for Real-Time Moment Tensor Inversion. Seismol. Res. Lett. 2021, 93, 957–966. [Google Scholar] [CrossRef]
- Wiemer, S. A software package to analyze seismicity: ZMAP. Seismol. Res. Lett. 2001, 72, 374–383. [Google Scholar] [CrossRef]
- Abe, S.; Suzuki, N. Scale-free network of earthquakes. Europhys. Lett. 2004, 65, 581–586. [Google Scholar] [CrossRef]
- Abe, S.; Suzuki, N. Dynamical evolution of clustering in complex network of earthquakes. Eur. Phys. J. B 2007, 59, 93–97. [Google Scholar] [CrossRef]
- Baiesi, M.; Paczuski, M. Scale-free networks of earthquakes and aftershocks. Phys. Rev. E 2004, 69, 066106. [Google Scholar] [CrossRef] [PubMed]
- Baiesi, M.; Paczuski, M. Complex networks of earthquakes and aftershocks. Nonlinear Process. Geophys. 2005, 12, 47–56. [Google Scholar] [CrossRef]
- Barrat, A.; Barthélemy, M.; Vespignani, A. Dynamical Processes on Complex Networks; Cambridge University Press: Cambridge, UK, 2008; 361p. [Google Scholar]
- Daskalaki, E.; Papadopoulos, G.A.; Spiliotis, K.; Siettos, C. Analysing the topology of seismicity in the Hellenic arc using complex networks. J. Seismol. 2014, 18, 37–46. [Google Scholar] [CrossRef]
- Chorozoglou, D.; Kugiumtzis, D.; Papadimitriou, E. Testing the structure of earthquake networks from multivariate time series of successive main shocks in Greece. Phys. A 2018, 499, 28–39. [Google Scholar] [CrossRef]
- Daskalaki, E.; Spiliotis, K.; Siettos, C.; Minadakis, G.; Papadopoulos, G.A. Foreshocks and short-term hazard assessment of large earthquakes using complex networks: The case of the 2009 L’Aquila earthquake. Nonlinear Process. Geophys. 2016, 23, 241–256. [Google Scholar] [CrossRef]
- Newman, M. Networks: An Introduction; Oxford University Press: Oxford, UK, 2010. [Google Scholar] [CrossRef]
- Aki, K. Maximum likelihood estimates of b in the formula log N = a − bM and its confidence limits. Bull. Earthq. Res. Inst. Univ. Tokyo 1965, 43, 237–239. [Google Scholar]
- Utsu, T. A method for determining the value of b in a formula log N = a − bM showing the magnitude-frequency relation for earthquakes. Geophys. Bull. Hokkaido Univ. 1965, 13, 99–103. (In Japanese) [Google Scholar]
- Utsu, T. Representation and analysis of the earthquake size distribution: A historical review and some new approaches. Pure Appl. Geophys. 1992, 155, 509–535. [Google Scholar] [CrossRef]
- Aki, K. Characterization of barriers on an earthquake fault. J. Geophys. Res. 1979, 84, 6140–6148. [Google Scholar] [CrossRef]
- Omori, F. On the aftershocks of earthquakes. J. Coll. Sci. Imp. Univ. Tokyo 1894, 7, 111–200. [Google Scholar]
- Jordan, T.H.; Chen, Y.-T.; Gasparini, P.; Madariaga, R.; Main, I.; Marzocchi, W.; Papadopoulos, G.; Sobolev, G.; Yamaoka, K.; Zschau, J. Operational earthquake forecasting—state of knowledge and guidelines for utilization. Ann. Geophys. 2011, 54, 315–391. [Google Scholar] [CrossRef]
- Demichelis, A.; Ongaro, M. Public understanding and scientific uncertainty: The communication of risk in the L’Aquila earthquake. AIMS Geosci. 2024, 10, 540–552. [Google Scholar] [CrossRef]
- Institute of Geodynamics, National Observatory of Athens. Observations and Preliminary Results on the Seismic Sequence Between Santorini and Amorgos; Updated Version 25 March 2025; 30p. Available online: https://www.emsc.eu/Special_reports/?id=351 (accessed on 20 April 2025).
- Stein, S.; Wysession, M. An Introduction to Seismology, Earthquakes, and Earth Structure; Blackwell Publishing: Malden, MA, USA, 2003; 498p. [Google Scholar]
- Vollmer, F.W. Orient: Directional Data Analysis Software. 2024. Available online: https://vollmerf.github.io/orient/ (accessed on 20 April 2025).
- Lohman, R.B.; McGuire, J.J. Earthquake swarms driven by aseismic creep in the Salton Trough, California. J. Geophys. Res. 2007, 112, B04405. [Google Scholar] [CrossRef]
- Dziak, R.P.; Fox, C.-G. The January 1998 earthquake swarm at Axial Volcano, Juan de Fuca Ridge: Hydroacoustic evidence of seafloor volcanic activity. Geophys. Res. Lett. 1999, 26, 3429–3432. [Google Scholar] [CrossRef]
- Madarieta-Txurruka, A.; González-Castillo, L.; Peláez, J.A.; Catalán, M.; Henares, J.; Gil, A.J.; Lamas-Fernández, F.; Galindo-Zaldívar, J. The role of faults as barriers in confined seismic sequences: 2021 seismicity in the Granada Basin (Betic Cordillera). Tectonics 2022, 41, e2022TC007481. [Google Scholar] [CrossRef]
- Shaw, B.E. Generalized Omori law for aftershocks and foreshocks from a simple dynamics. Geophys. Res. Lett. 1993, 20, 907–910. [Google Scholar] [CrossRef]
- Im, K.; Avouac, J.-P. Cascading foreshocks, aftershocks and earthquake swarms in a discrete fault network. Geophys. J. Int. 2023, 235, 831–852. [Google Scholar] [CrossRef]
- Briole, P.; Ganas, A.; Elias, P.; Sakkas, V. Santorini Seismo-Volcanic Event: GNSS Time Series and Preliminary Models; Updated Version 13 February 2025; 11p. Available online: https://www.emsc-csem.org/Files/event/1765158/20250209-santorini-gnss-time-series.pdf (accessed on 20 April 2025).
- Alatza, S.; Papoutsis, I.; Paradissis, D.; Kontoes, C.; Papadopoulos, G.A. Multi-temporal InSAR analysis for monitoring ground deformation in Amorgos Island, Greece. Sensors 2020, 20, 338. [Google Scholar] [CrossRef] [PubMed]
- Kato, A.; Ben-Zion, Y. The generation of large earthquakes. Nat. Rev. Earth Environ. 2021, 2, 26–39. [Google Scholar] [CrossRef]
- McLaskey, G.C. Earthquake initiation from laboratory observations and implications for foreshocks. J. Geophys. Res. 2019, 124, 2882–2904. [Google Scholar] [CrossRef]
- Cattania, C.; Segall, P. Precursory slow slip and foreshocks on rough faults. J. Geophys. Res. 2021, 126, e2020JB020430. [Google Scholar] [CrossRef]












Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Triantafyllou, I.; Papadopoulos, G.A.; Siettos, C.; Spiliotis, K. Real-Time Foreshock–Aftershock–Swarm Discrimination During the 2025 Seismic Crisis near Santorini Volcano, Greece: Earthquake Statistics and Complex Networks. Geosciences 2025, 15, 300. https://doi.org/10.3390/geosciences15080300
Triantafyllou I, Papadopoulos GA, Siettos C, Spiliotis K. Real-Time Foreshock–Aftershock–Swarm Discrimination During the 2025 Seismic Crisis near Santorini Volcano, Greece: Earthquake Statistics and Complex Networks. Geosciences. 2025; 15(8):300. https://doi.org/10.3390/geosciences15080300
Chicago/Turabian StyleTriantafyllou, Ioanna, Gerassimos A. Papadopoulos, Constantinos Siettos, and Konstantinos Spiliotis. 2025. "Real-Time Foreshock–Aftershock–Swarm Discrimination During the 2025 Seismic Crisis near Santorini Volcano, Greece: Earthquake Statistics and Complex Networks" Geosciences 15, no. 8: 300. https://doi.org/10.3390/geosciences15080300
APA StyleTriantafyllou, I., Papadopoulos, G. A., Siettos, C., & Spiliotis, K. (2025). Real-Time Foreshock–Aftershock–Swarm Discrimination During the 2025 Seismic Crisis near Santorini Volcano, Greece: Earthquake Statistics and Complex Networks. Geosciences, 15(8), 300. https://doi.org/10.3390/geosciences15080300






