Evaluating Time Series Models for Monthly Rainfall Forecasting in Arid Regions: Insights from Tamanghasset (1953–2021), Southern Algeria
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Dataset
Precipitations
2.3. Classical Forecasting Methods
2.3.1. Autoregressive Integrated Moving Average (ARIMA)
2.3.2. ETS: Trend Component (T), a Seasonal Component (S), and an Error Term (E)
2.3.3. STL Decomposition Followed by the ETS Forecasting Model
2.3.4. Neural Network Autoregressive (NNAR) Model
2.3.5. TBATS Model: A State Space Approach for Complex Seasonal Time Series Forecasting
2.3.6. Performance Evaluation Metrics
3. Results
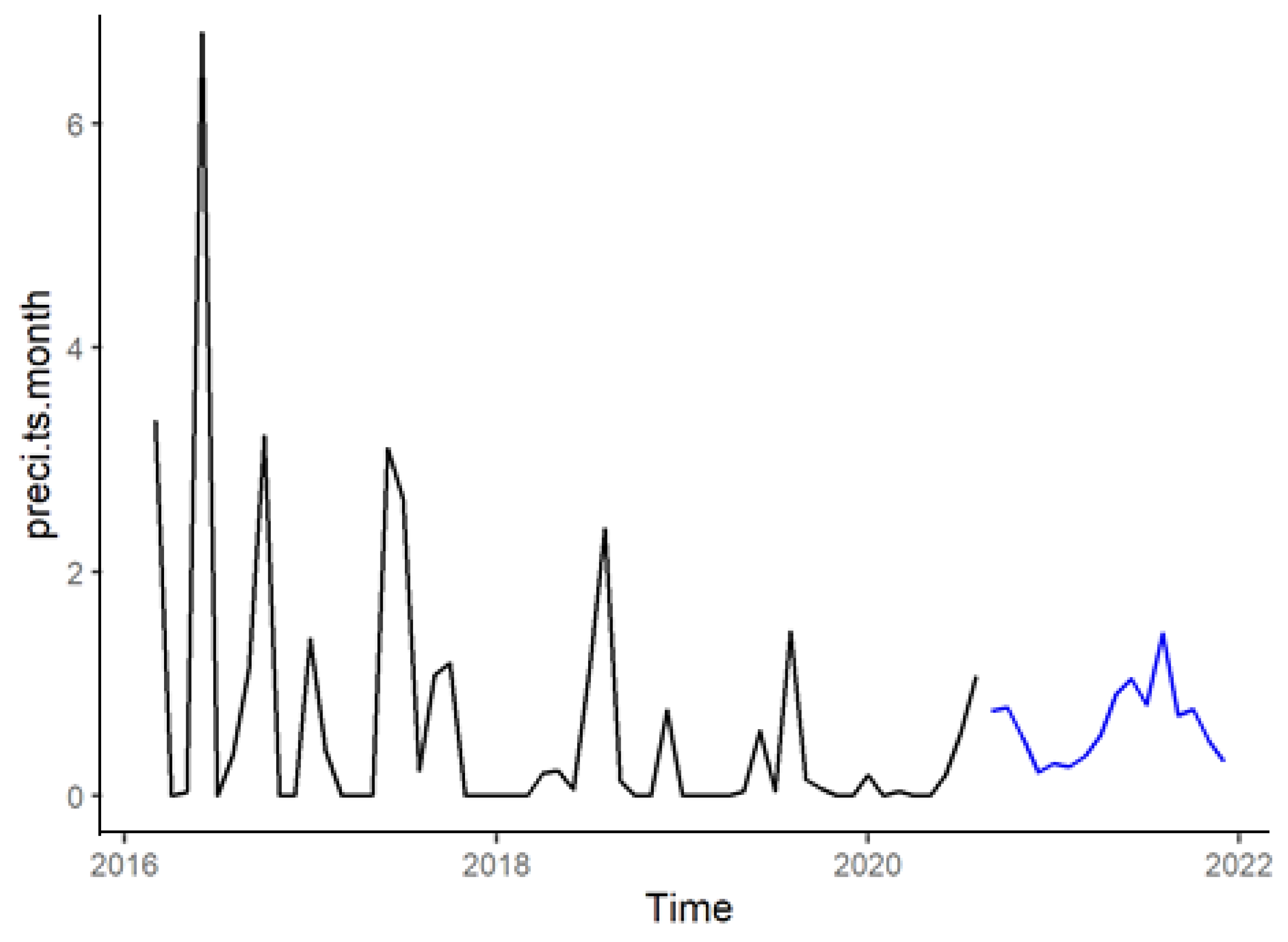
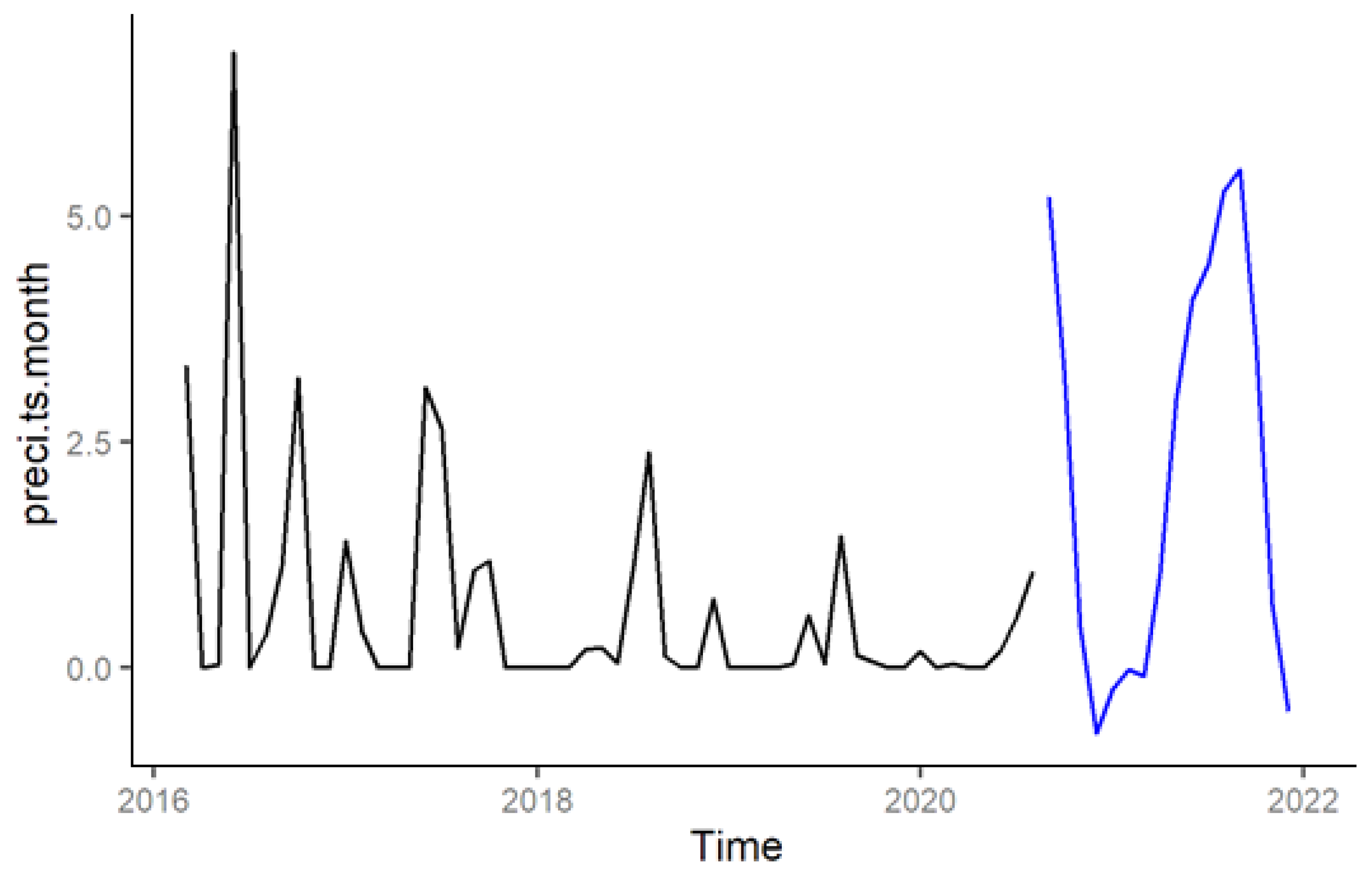
3.1. ARIMA Model for Statistical Forecasting of Monthly Precipitation
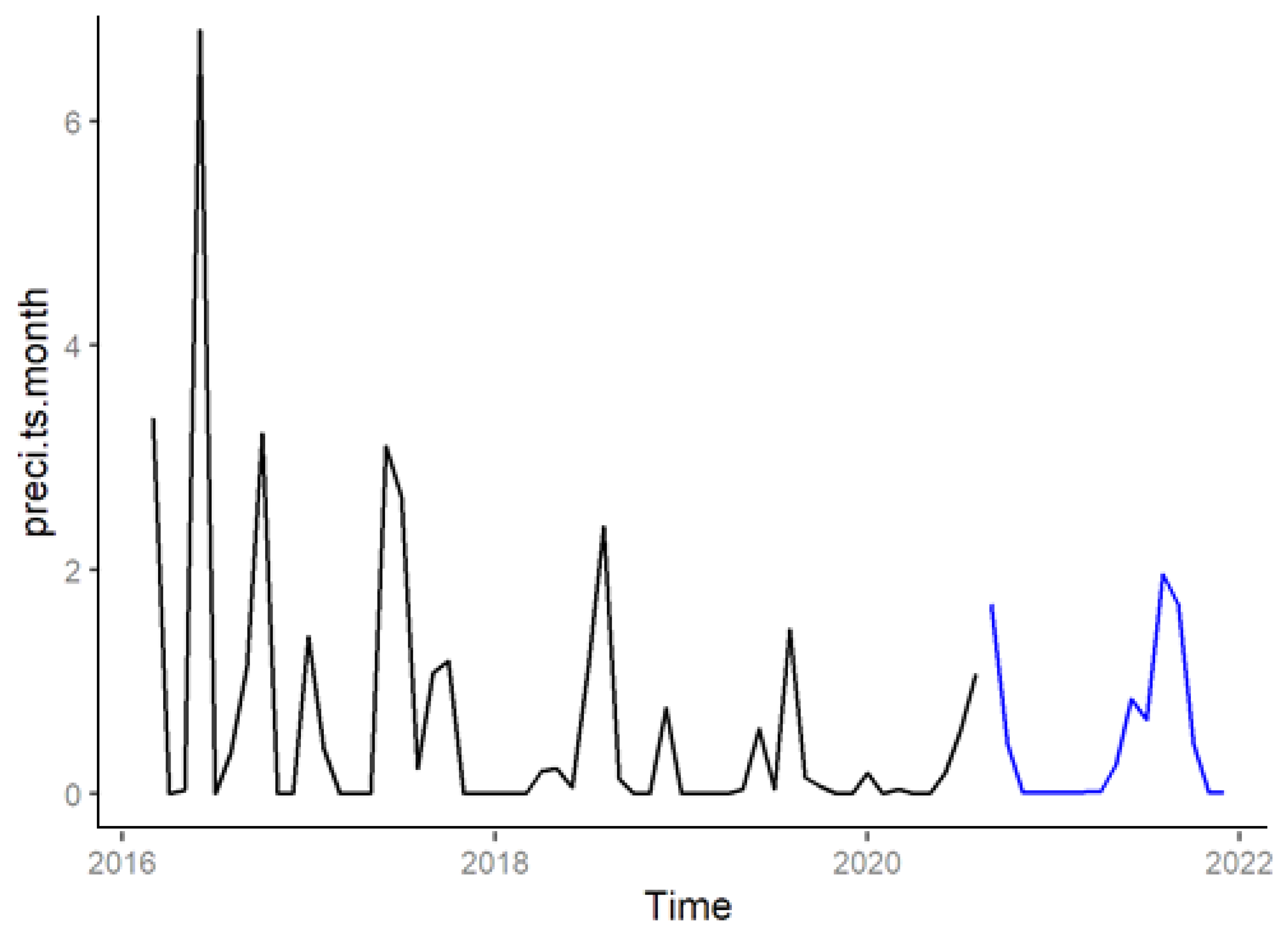
3.2. ETS for Forecasting Monthly Precipitation at Tamanghasset Station
3.3. STL Decomposition of Monthly Precipitation at Tamanghasset Station
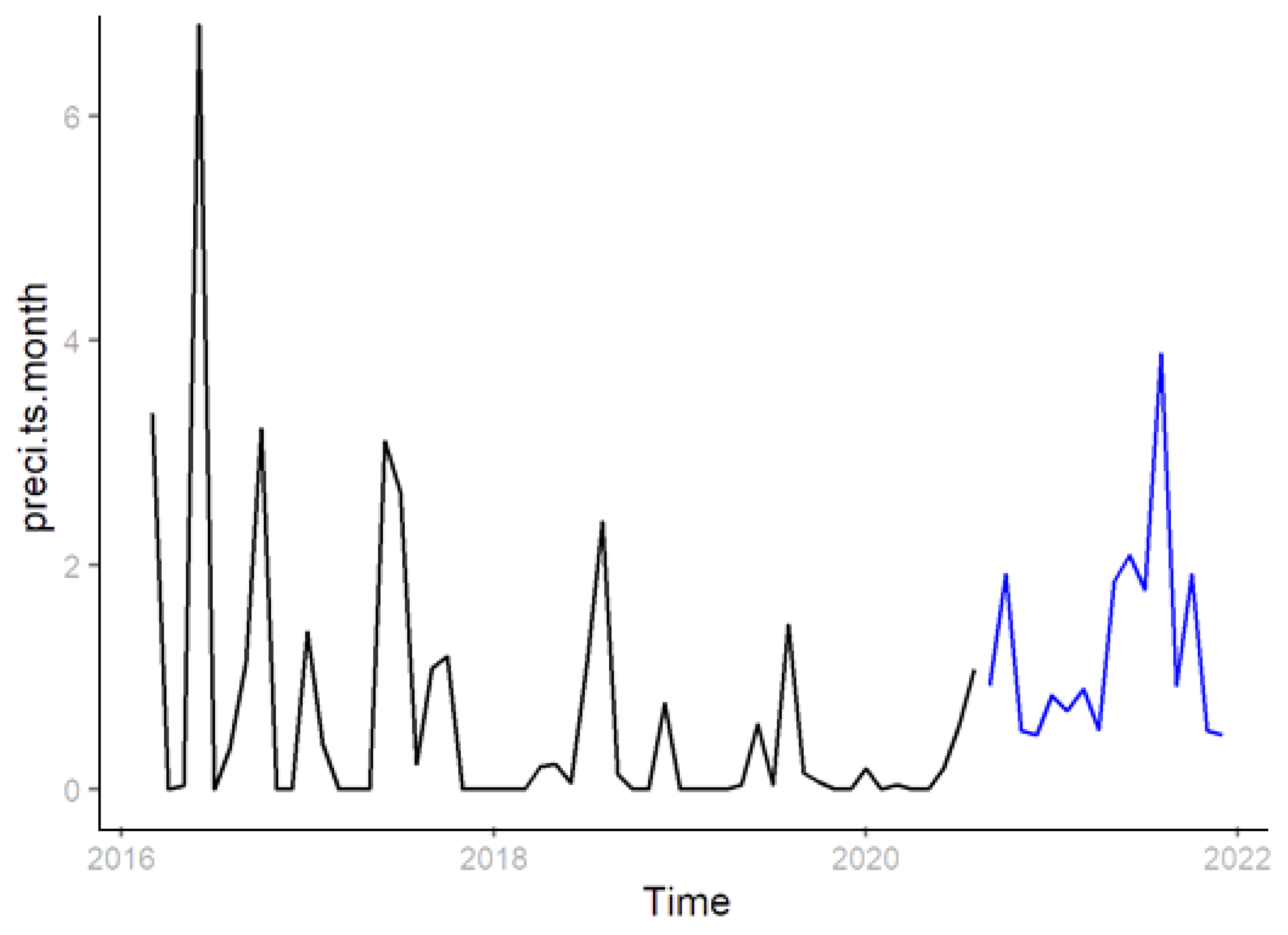
3.4. Forecasting Monthly Precipitation Using the NNAR Model
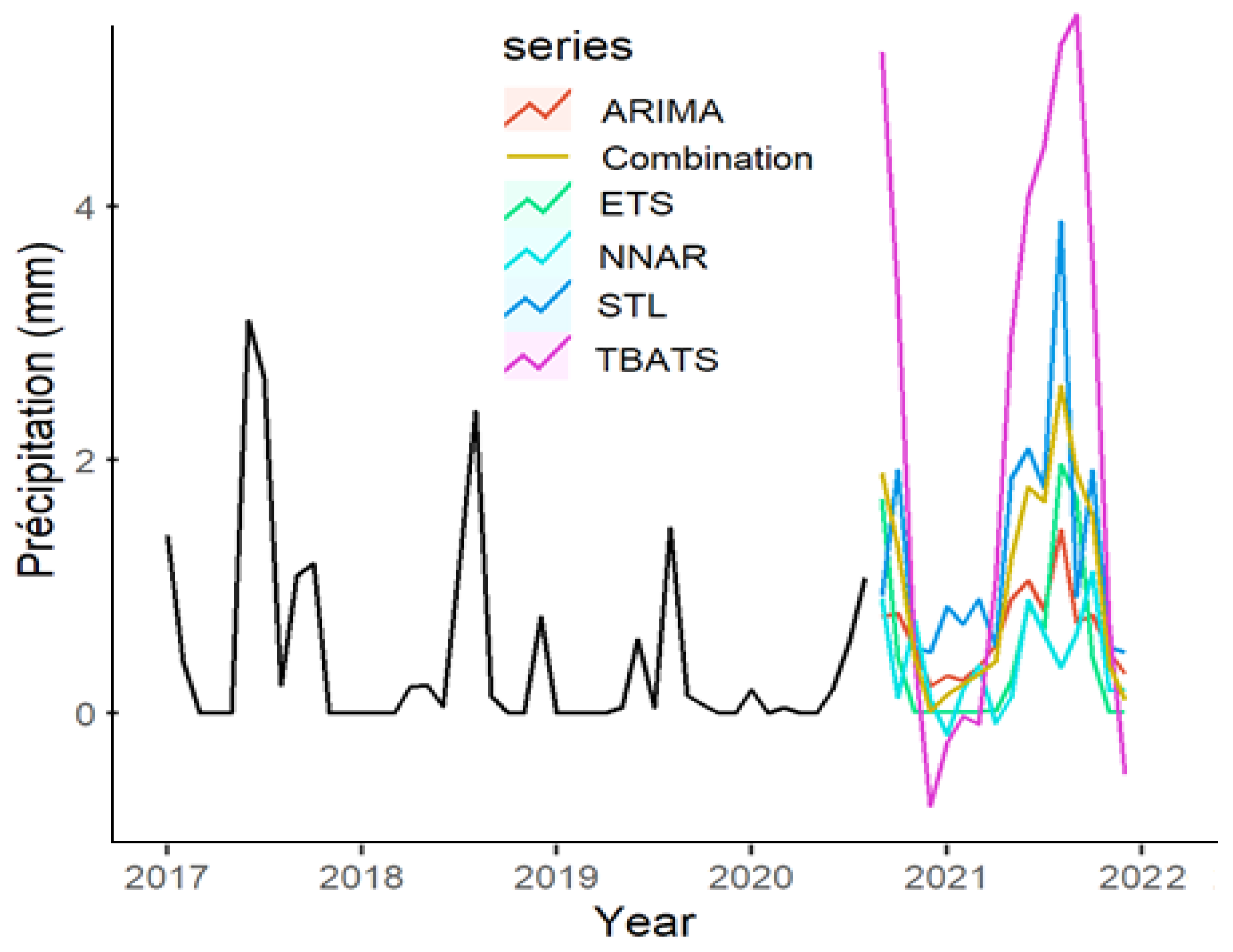
3.5. Selection of the Optimal Models Based on RMSE and MAPE Metrics
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Watson, F.; Austin, P. Physiology of human fluid balance. Anaesth. Intensiv. Care Med. 2021, 22, 644–651. [Google Scholar] [CrossRef]
- Ma, R.; Han, J.; Alrowais, R.; Zhou, J.; Li, R. Atmospheric water as alternative and universal resources: From the energy perspective. Nano Energy 2025, 140, 111012. [Google Scholar] [CrossRef]
- Jahan Rakib, M.R.; Mohiuddin, M.; Al Masud, M.A.; Murshed, M.F.; Senapathi, V.; Islam, M.A.; Jakariya, M. Exploring the impact of microplastics in groundwater on human health: A comprehensive review. Curr. Opin. Environ. Sci. Health 2025, 44, 100605. [Google Scholar] [CrossRef]
- Ahmed, A.A.; Sayed, S.; Abdoulhalik, A.; Moutari, S.; Oyedele, L. Applications of machine learning to water resources management: A review of present status and future opportunities. J. Clean. Prod. 2024, 441, 140715. [Google Scholar] [CrossRef]
- Chahid, M.; Stitou El Messari, J.E.; Hilal, I.; Aqnouy, M. Application of the DRASTIC-LU/LC method combined with machine learning models to assess and predict the vulnerability of the Rmel aquifer (Northwest, Morocco). Groundw. Sustain. Dev. 2024, 27, 101345. [Google Scholar] [CrossRef]
- Latif, S.D.; Mohammed, D.O.; Jaafar, A. Developing an innovative machine learning model for rainfall prediction in a semi-arid region. J. Hydroinform. 2024, 26, 904–914. [Google Scholar] [CrossRef]
- Ahmadov, E. Water resources management to achieve sustainable development in Azerbaijan. Sustain. Futures 2020, 2, 100030. [Google Scholar] [CrossRef]
- En-nagre, K.; Aqnouy, M.; Bouadila, A.; Et-Takaouym, C.; Chahid, M.; Bouizrou, I.; Hilal, I.; Stitou El Messari, J.E.; Tariq, A. Assessment of Three Satellite Precipitation Products for Hydrological Studies in a Data-Scarce Context: Ouarzazate Basin, Southern Morocco. Nat. Hazards Res. 2025, in press. [CrossRef]
- Et-Takaouy, C.; Aqnouy, M.; Boukholla, A.; Stitou El Messari, J.E. Exploring the spatio-temporal variability of four satellite-based precipitation products (SPPs) in northern Morocco: A comparative study of complex climatic and topographic conditions. Mediterr. Geosci. Rev. 2024, 6, 123–144. [Google Scholar] [CrossRef]
- Akram, M.; Hamid, A. A comprehensive review on water balance. Biomed. Prev. Nutr. 2013, 3, 193–195. [Google Scholar] [CrossRef]
- Aqnouy, M.; Ommane, Y.; Ouallali, A.; Gourfi, A.; Ayele, G.T.; El Yousfi, Y.; Bouizrou, I.; Stitou El Messari, J.E.; Zettam, A.; Melesse, A.M.; et al. Evaluation of TRMM 3B43 V7 precipitation data in varied Moroccan climatic and topographic zones. Mediterr. Geosci. Rev. 2024, 6, 159–175. [Google Scholar] [CrossRef]
- Yang, T.-H.; Liu, W.-C. A general overview of the risk-reduction strategies for floods and droughts. Sustainability 2020, 12, 2687. [Google Scholar] [CrossRef]
- Morante-Carballo, F.; Montalván-Burbano, N.; Quiñonez-Barzola, X.; Jaya-Montalvo, M.; Carrión-Mero, P. What Do We Know about Water Scarcity in Semi-Arid Zones? A Global Analysis and Research Trends. Water 2022, 14, 2685. [Google Scholar] [CrossRef]
- Wang, M.; Chen, Y.; Li, J.; Zhao, Y. Spatiotemporal evolution and driving force analysis of drought characteristics in the Yellow River Basin. Ecol. Indic. 2025, 170, 113007. [Google Scholar] [CrossRef]
- Zaerpour, M.; Hatami, S.; Ballarin, A.S.; Knoben, W.J.M.; Papalexiou, S.M.; Pietroniro, A.; Clark, M.P. Impacts of agriculture and snow dynamics on catchment water balance in the U.S. and Great Britain. Commun. Earth Environ. 2024, 5, 733. [Google Scholar] [CrossRef] [PubMed]
- Bista, S.; Baniya, R.; Sharma, S.; Ghimire, G.R.; Panthi, J.; Prajapati, R.; Thapa, B.R.; Talchabhadel, R. Hydrologic applicability of satellite-based precipitation estimates for irrigation water management in the data-scarce region. J. Hydrol. 2024, 636, 131310. [Google Scholar] [CrossRef]
- Bouizrou, I.; Bouadila, A.; Aqnouy, M.; Gourfi, A. Assessment of remotely sensed precipitation products for climatic and hydrological studies in arid to semi-arid data-scarce region, central-western Morocco. Remote Sens. Appl. Soc. Environ. 2023, 30, 100976. [Google Scholar] [CrossRef]
- Deng, Y.; Wang, X.; Ruan, H.; Lin, J.; Chen, X.; Chen, Y.; Duan, W.; Deng, H. The magnitude and frequency of detected precipitation determine the accuracy performance of precipitation data sets in the high mountains of Asia. Sci. Rep. 2024, 14, 17251. [Google Scholar] [CrossRef] [PubMed]
- Sham, F.A.F.; El-Shafie, A.; Jaafar, W.Z.W.; S, A.; Sherif, M.; Ahmed, A.N. Advances in AI-based rainfall forecasting: A comprehensive review of past, present, and future directions with intelligent data fusion and climate change models. Results Eng. 2025, 27, 105774. [Google Scholar] [CrossRef]
- Alsumaiei, A.A. Long-term rainfall forecasting in arid climates using artificial intelligence and statistical recurrent models. J. Eng. Res. 2024, 13, 1594–1602. [Google Scholar] [CrossRef]
- Higuera Roa, O.; Cotti, D.; Aste, N.; Bustillos-Ardaya, A.; Schneiderbauer, S.; Tourino Soto, I.; Román-Dañobeytia, F.; Walz, Y. Deriving targeted intervention packages of nature-based solutions for climate change adaptation and disaster risk reduction: A geospatial multi-criteria approach for building resilience in the Puna region, Peru. Nat.-Based Solut. 2023, 4, 100090. [Google Scholar] [CrossRef]
- He, R.; Zhang, L.; Chew, A.W.Z. Modeling and predicting rainfall time series using seasonal-trend decomposition and machine learning. Knowl.-Based Syst. 2022, 251, 109125. [Google Scholar] [CrossRef]
- Ayiah-Mensah, F.; Bosson-Amedenu, S.; Baah, E.M.; Addor, J.A. Advancements in seasonal rainfall forecasting: A seasonal auto-regressive integrated moving average model with outlier adjustments for Ghana’s Western Region. Sci. Afr. 2025, 28, e02632. [Google Scholar] [CrossRef]
- Effrosynidis, D.; Spiliotis, E.; Sylaios, G.; Arampatzis, A. Time series and regression methods for univariate environmental forecasting: An empirical evaluation. Sci. Total Environ. 2023, 875, 162580. [Google Scholar] [CrossRef] [PubMed]
- Madi, H.; Bedjaoui, A.; Elhoussaoui, A.; Elbakai, L.O.; Bounaama, A. Flood Vulnerability Mapping and Risk Assessment Using Hydraulic Modeling and GIS in Tamanrasset Valley Watershed, Algeria. J. Ecol. Eng. 2023, 24, 35–48. [Google Scholar] [CrossRef] [PubMed]
- Monjo, R.; Meseguer-Ruiz, O. Review: Fractal Geometry in Precipitation. Atmosphere 2024, 15, 135. [Google Scholar] [CrossRef]
- Chahid, M.; Hilal, I.; En-Nagre, K.; Et-Takaouy, C.; El Messari, J.E.S.; Aqnouy, M. Assessment and modeling of the hydrochemical evolution of the Rmel aquifer (NW Morocco): Geostatistical approaches and machine learning for sustainable management. Mediterr. Geosci. Rev. 2025, 7, 341–362. [Google Scholar] [CrossRef]
- Chahid, M.; Hilal, I.; Et-Takaouy, C.; En-Nagre, K.; Stitou El Messari, J.E.; Mansour, M.R.A.; Aqnouy, M. Comparison of groundwater pollution vulnerability assessments via the DRASTIC-LU and DRASTIC-LU-NO3− methods in the Ouled Ogbane aquifer, Northwest Morocco. Environ. Sci. Pollut. Res. 2025, 32, 16261–16279. [Google Scholar] [CrossRef] [PubMed]
- Hurtado, A.R.; Díaz-Cano, E.; Berbel, J. The paradox of success: Water resources closure in Axarquia (southern Spain). Sci. Total Environ. 2024, 946, 174318. [Google Scholar] [CrossRef] [PubMed]
- Khacheba, R.; Cherfaoui, M.; Hartani, T.; Drouiche, N. The nexus approach to water–energy–food security: An option for adaptation to climate change in Algeria. Desalin. Water Treat. 2018, 131, 30–33. [Google Scholar] [CrossRef]
- Gastineau, R.; Hamedi, C.; Baba Hamed, M.B.; Abi-Ayad, S.M.E.A.; Bąk, M.; Lemieux, C.; Turmel, M.; Dobosz, S.; Wróbel, R.J.; Kierzek, A.; et al. Morphological and molecular identification reveals that waters from an isolated oasis in Tamanrasset (extreme South of Algerian Sahara) are colonized by opportunistic and pollution-tolerant diatom species. Ecol. Indic. 2021, 121, 107104. [Google Scholar] [CrossRef]
- Sahnoune, F.; Belhamel, M.; Zelmat, M.; Kerbachi, R. Climate change in Algeria: Vulnerability and strategy of mitigation and adaptation. Energy Procedia 2013, 36, 1286–1294. [Google Scholar] [CrossRef]
- Hadj Arab, A.; Chenlo, F.; Benghanem, M. Loss-of-load probability of photovoltaic water pumping systems. Sol. Energy 2004, 76, 713–723. [Google Scholar] [CrossRef]
- Chaulagain, S.; Lamichhane, M.; Chaulagain, U. A review of current trends, challenges, and future perspectives in machine learning applications to water resources in Nepal. J. Hazard. Mater. Adv. 2025, 18, 100678. [Google Scholar] [CrossRef]
- Olawade, D.B.; Wada, O.Z.; Ige, A.O.; Egbewole, B.I.; Olojo, A.; Oladapo, B.I. Artificial intelligence in environmental monitoring: Advancements, challenges, and future directions. Hyg. Environ. Health Adv. 2024, 12, 100114. [Google Scholar] [CrossRef]
- Bolan, S.; Padhye, L.P.; Jasemizad, T.; Govarthanan, M.; Karmegam, N.; Wijesekara, H.; Amarasiri, D.; Hou, D.; Zhou, P.; Biswal, B.K.; et al. Impacts of climate change on the fate of contaminants through extreme weather events. Sci. Total Environ. 2024, 909, 168388. [Google Scholar] [CrossRef] [PubMed]
- Judge, G.G.; Hill, R.C.; Griffiths, W.E.; Lutkepohl, H.; Lee, T. Introduction to the Theory and Practice of Econometrics, 2nd ed.; John Wiley: New York, NY, USA, 1988; pp. xxxv + 1024. ISBN 0-471-62414-4. [Google Scholar]
- Box, G.E.P.; Jenkins, G.M. Time Series Analysis, Forecasting and Control, Revised ed.; Holden-Day: San Francisco, CA, USA, 1994. [Google Scholar]
- Jofipasi, C.A.; Miftahuddin, M.; Sofyan, H. Selection for the best ETS (error, trend, seasonal) model to forecast weather in the Aceh Besar District. IOP Conf. Ser. Mater. Sci. Eng. 2018, 352, 012055. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Khandakar, Y. Automatic time series forecasting: The forecast package for R. J. Stat. Softw. 2008, 27, 1–22. [Google Scholar] [CrossRef]
- Tealab, A.; Hefny, H.; Badr, A. Forecasting of nonlinear time series using ANN. Future Comput. Inform. J. 2017, 2, 39–47. [Google Scholar] [CrossRef]
- Thoplan, R. Random Forests for Poverty Classification. Int. J. Sci. Basic Appl. Res. 2014, 17, 252–259. [Google Scholar]
- Perone, G. Comparison of ARIMA, ETS, NNAR, TBATS and hybrid models to forecast the second wave of COVID-19 hospitalizations in Italy. Eur. J. Health Econ. 2022, 23, 917–940. [Google Scholar] [CrossRef] [PubMed]
- Talkhi, N.; Akhavan Fatemi, N.; Ataei, Z.; Jabbari Nooghabi, M. Modeling and forecasting number of confirmed and death caused COVID-19 in IRAN: A comparison of time series forecasting methods. Biomed. Signal Process. Control 2021, 66, 102494. [Google Scholar] [CrossRef] [PubMed]
- de Livera, A.M.; Hyndman, R.J.; Snyder, R.D. Forecasting time series with complex seasonal patterns using exponential smoothing. J. Am. Stat. Assoc. 2011, 106, 1513–1527. [Google Scholar] [CrossRef]
- Kim, S.; Kim, H. A new metric of absolute percentage error for intermittent demand forecasts. Int. J. Forecast. 2016, 32, 669–679. [Google Scholar] [CrossRef]
- Arumugam, P.; Saranya, R. Outlier Detection and Missing Value in Seasonal ARIMA Model Using Rainfall Data. Mater. Today Proc. 2018, 5, 1791–1799. [Google Scholar] [CrossRef]
- Bari, S.H.; Rahman, M.T.; Hussain, M.M.; Ray, S. Forecasting Monthly Precipitation in Sylhet City Using ARIMA Model. Civ. Environ. Res. 2015, 7, 69–77. [Google Scholar]
- Dahiya, P.; Kumar, M.; Manhas, S.; Saini, A.; Yadav, S.K.; Sirohi, S.; Kamboj, M.; Khichar, M.L.; Mishra, E.P.; Sharma, V.; et al. Time series study of climate variables utilising a seasonal ARIMA technique for the Indian states of Punjab and Haryana. Discov. Appl. Sci. 2024, 6, 650. [Google Scholar] [CrossRef]
- Abd-Elhamid, H.F.; El-Dakak, A.M.; Zeleňáková, M.; K, S.O.; Mahdy, M.; Abd El Ghany, S.H. Rainfall forecasting in arid regions in response to climate change using ARIMA and remote sensing. Geomat. Nat. Hazards Risk 2024, 15, 2347414. [Google Scholar] [CrossRef]
- Parviz, L.; Ghorbanpour, M. Assimilation of PSO and SVR into an improved ARIMA model for monthly precipitation forecasting. Sci. Rep. 2024, 14, 12107. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.; Kim, H.; Kim, H.G.; Lee, D.; Yoon, S. A comprehensive survey of deep learning for time series forecasting: Architectural diversity and open challenges. Artif. Intell. Rev. 2025, 58, 216. [Google Scholar] [CrossRef]
- Ray, S.S.; Verma, R.K.; Singh, A.; Myung, S.; Park, Y.I.; Kim, I.C.; Lee, H.K.; Kwon, Y.-N. Exploration of time series model for predictive evaluation of long-term performance of membrane distillation desalination. Process Saf. Environ. Prot. 2022, 160, 1–12. [Google Scholar] [CrossRef]
- Sangeetha, S.K.B.; Mathivanan, S.K.; Rajadurai, H.; Cho, J.; Easwaramoorthy, S.V. A multi-modal geospatial–temporal LSTM based deep learning framework for predictive modeling of urban mobility patterns. Sci. Rep. 2024, 14, 31579. [Google Scholar]
- Sanchez-Vazquez, M.J.; Nielen, M.; Gunn, G.J.; Lewis, F.I. Using seasonal-trend decomposition based on loess (STL) to explore temporal patterns of pneumonic lesions in finishing pigs slaughtered in England, 2005–2011. Prev. Vet. Med. 2012, 104, 65–73. [Google Scholar] [CrossRef] [PubMed]
- Apaydin, H.; Taghi Sattari, M.; Falsafian, K.; Prasad, R. Artificial intelligence modelling integrated with Singular Spectral analysis and Seasonal-Trend decomposition using Loess approaches for streamflow predictions. J. Hydrol. 2021, 600, 126506. [Google Scholar] [CrossRef]
- Lem, K.H. The STL-ARIMA approach for seasonal time series forecast: A preliminary study. ITM Web Conf. 2024, 67, 01008. [Google Scholar] [CrossRef]
- Trull, O.; García-Díaz, J.C.; Peiró-Signes, A. Multiple seasonal STL decomposition with discrete-interval moving seasonalities. Appl. Math. Comput. 2022, 433, 127398. [Google Scholar] [CrossRef]
- Khalek, M.A.; Ali, M.A. Comparative Study of Wavelet-SARIMA and Wavelet-NNAR Models for Groundwater Level in Rajshahi District. IOSR J. Environ. Sci. 2016, 10, 1–15. [Google Scholar]
- Ahmar, A.S.; Singh, P.K.; Ruliana, R.; Pandey, A.K.; Gupta, S. Comparison of ARIMA, SutteARIMA, and Holt-Winters, and NNAR Models to Predict Food Grain in India. Forecasting 2023, 5, 138–152. [Google Scholar] [CrossRef]
- Saranya, M.S.; Vinish, V.N. A comparative evaluation of streamflow prediction using the SWAT and NNAR models in the Meenachil River Basin of Central Kerala, India. Water Sci. Technol. 2023, 88, 2002–2018. [Google Scholar] [CrossRef] [PubMed]
- Ray, M.; Sahoo, K.C.; Abotaleb, M.; Ray, S.; Sahu, P.K.; Mishra, P.; GhaziAlKhatib, A.; SankarDas, S.; Jain, V.; Balloo, R. Modeling and forecasting meteorological factors using BATS and TBATS models for the Keonjhar district of Orissa. Mausam 2022, 73, 555–564. [Google Scholar] [CrossRef]

| Seasonal Component | |||
|---|---|---|---|
| N (None) | A (Additive) | M (Multiplicative) | |
| N (None) | N (None) | Na | NM |
| A (Additive) | AN | AA | AM |
| Ad (Additive Damped) | AdN | AdA | AdM |
| M (Multiplicative) | MN | MA | MM |
| Model | Model | Model |
|---|---|---|
| ETS (M, M, N) | ETS (A, M, A) | ETS (M, N, M) |
| ETS (M, A, N) | ETS (A, Md, N) | ETS (M, N, A) |
| ETS (M, A, M) | ETS (A, Md, M) | ETS (M, N, N) |
| ETS (A, M, N) | ETS (A, N, A) | ETS (M, A, A) |
| ETS (A, N, N) | ETS (M, Ad, M) | ETS (A, Ad, M) |
| ETS (A, A, M) | ETS (M, Ad, N) | ETS (M, M, A) |
| ETS (M, M, M) | ETS (M, Md, M) | ETS (A, A, A) |
| ETS (A, N, M) | ETS (A, Ad, N) | ETS (A, Ad, A) |
| ETS (A, A, N) | ETS (M, Md, A) | ETS (M, Ad, A) |
| ME | RMSE | MAE | MPE | MAPE | ACF1 | |
|---|---|---|---|---|---|---|
| ARIMA | 0.1177 | 8.854 | 4.975 | −3.586 | 149.4 | −0.03284 |
| ETS | −3.275 | 9.512 | 3.616 | −23,572 | 23,680 | 0.02456 |
| STL-ETS | 0.1806 | 8.004 | 4.524 | −1.418 | 146.7 | 0.0176 |
| NNAR | 0.005227 | 2.248 | 1.187 | 58.77 | 87.68 | −0.0007443 |
| TBATS | −0.2178 | 8.713 | 4.707 | 2.863 | 144.6 | −0.03078 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abderrahmane, B.; Chahid, M.; Aqnouy, M.; Milewski, A.M.; Lahcen, B. Evaluating Time Series Models for Monthly Rainfall Forecasting in Arid Regions: Insights from Tamanghasset (1953–2021), Southern Algeria. Geosciences 2025, 15, 273. https://doi.org/10.3390/geosciences15070273
Abderrahmane B, Chahid M, Aqnouy M, Milewski AM, Lahcen B. Evaluating Time Series Models for Monthly Rainfall Forecasting in Arid Regions: Insights from Tamanghasset (1953–2021), Southern Algeria. Geosciences. 2025; 15(7):273. https://doi.org/10.3390/geosciences15070273
Chicago/Turabian StyleAbderrahmane, Ballah, Morad Chahid, Mourad Aqnouy, Adam M. Milewski, and Benaabidate Lahcen. 2025. "Evaluating Time Series Models for Monthly Rainfall Forecasting in Arid Regions: Insights from Tamanghasset (1953–2021), Southern Algeria" Geosciences 15, no. 7: 273. https://doi.org/10.3390/geosciences15070273
APA StyleAbderrahmane, B., Chahid, M., Aqnouy, M., Milewski, A. M., & Lahcen, B. (2025). Evaluating Time Series Models for Monthly Rainfall Forecasting in Arid Regions: Insights from Tamanghasset (1953–2021), Southern Algeria. Geosciences, 15(7), 273. https://doi.org/10.3390/geosciences15070273










