Understanding Complex Hydraulic Heterogeneities in Crystalline Basement Aquifers Used as Drinking Water Sources
Abstract
1. Introduction
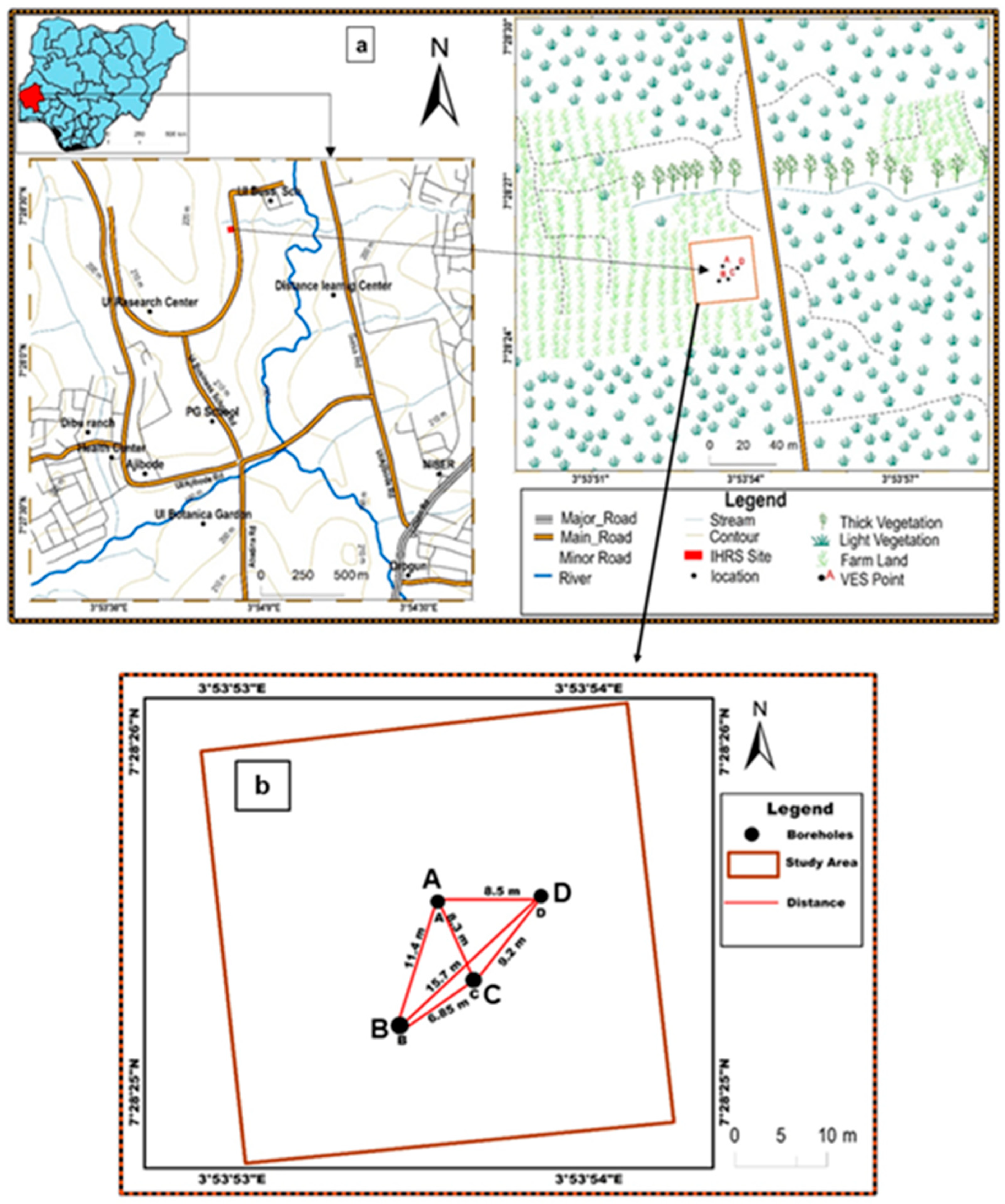
2. Study Site
3. Materials and Methods
3.1. Constant-Rate Pumping Test
3.2. Step Drawdown Tests
3.3. Recovery Tests
3.4. Tracer Test
4. Results
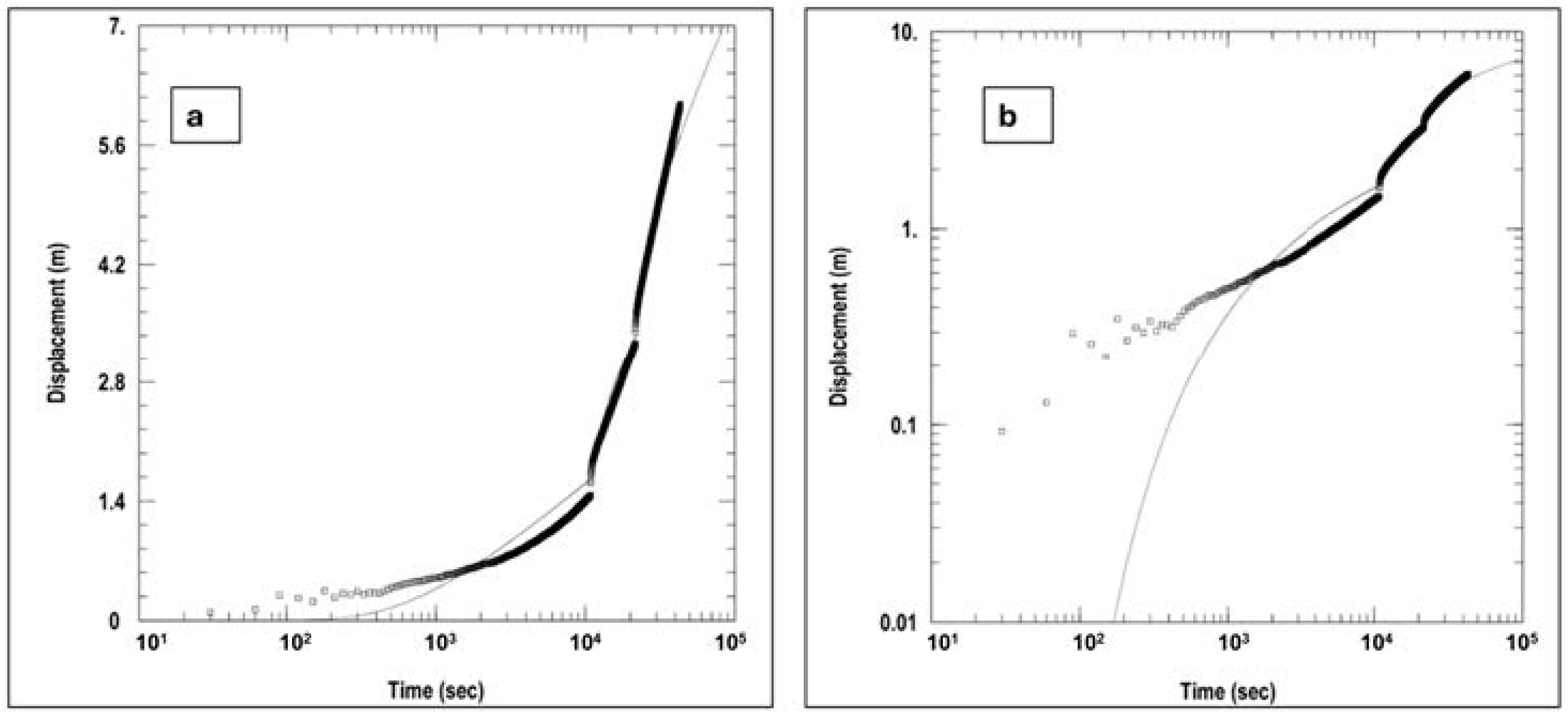
4.1. Constant Rate Pumping Tests
4.2. Step-Drawdown Pumping Test
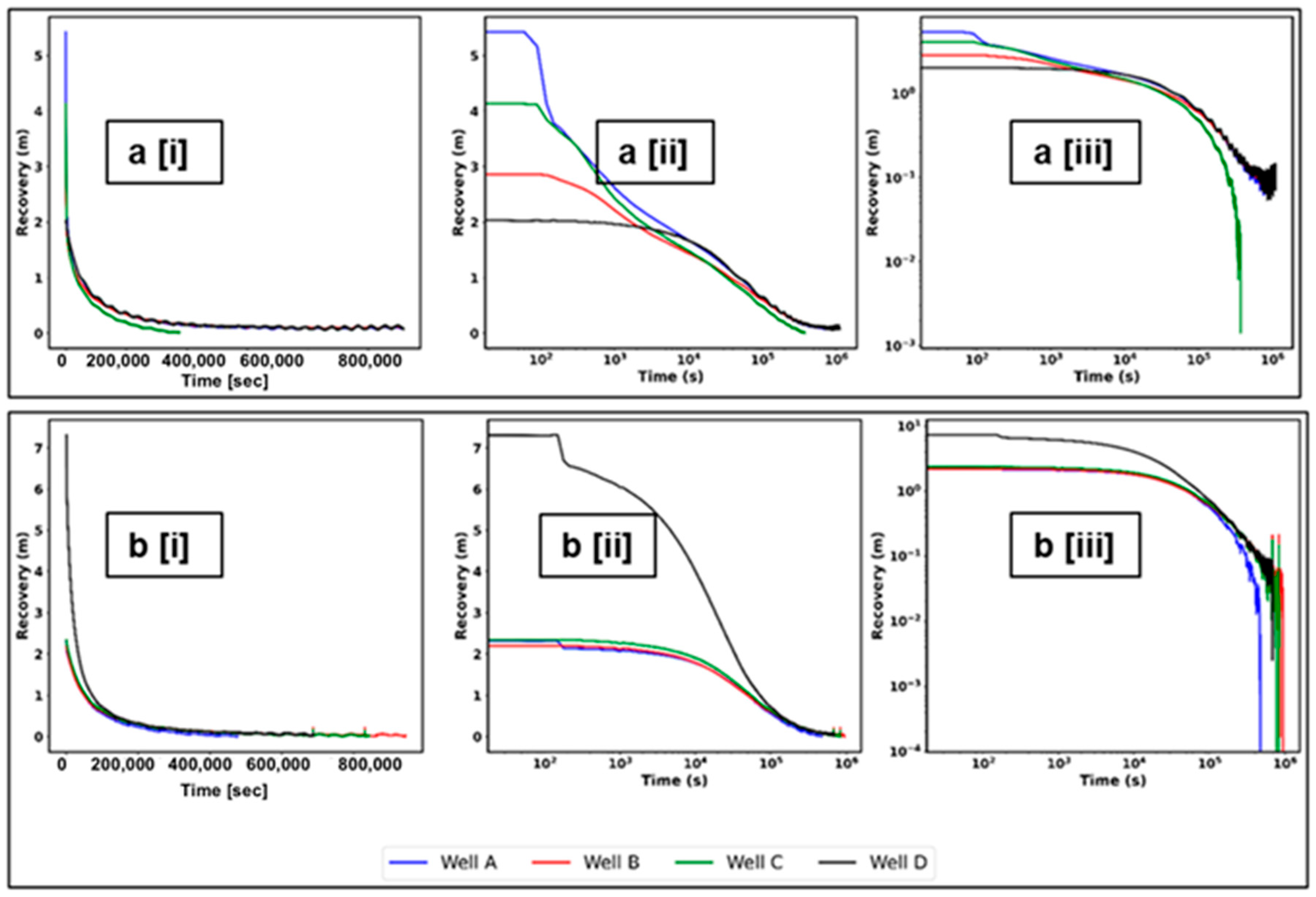
4.3. Recovery Test
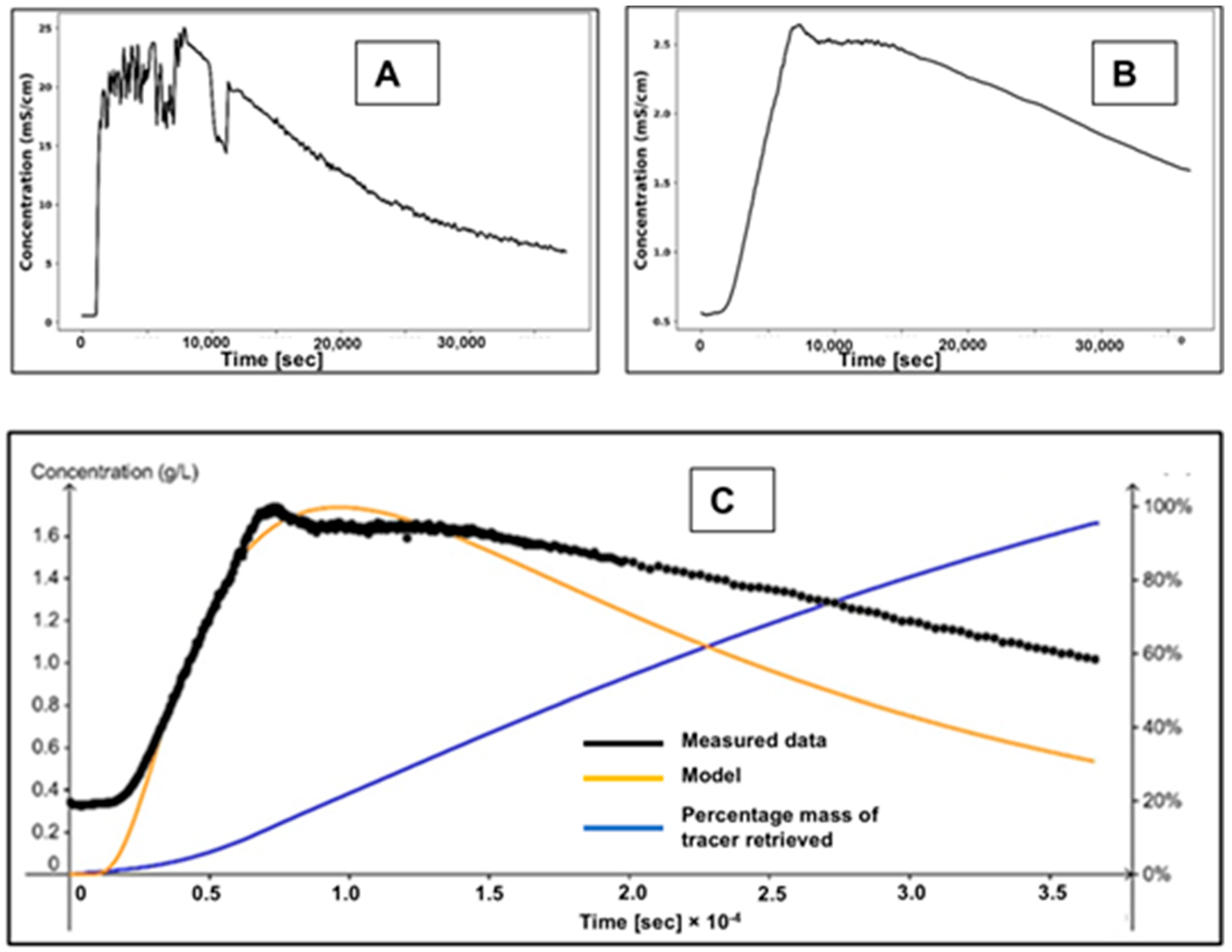
4.4. Tracer Test
5. Discussion
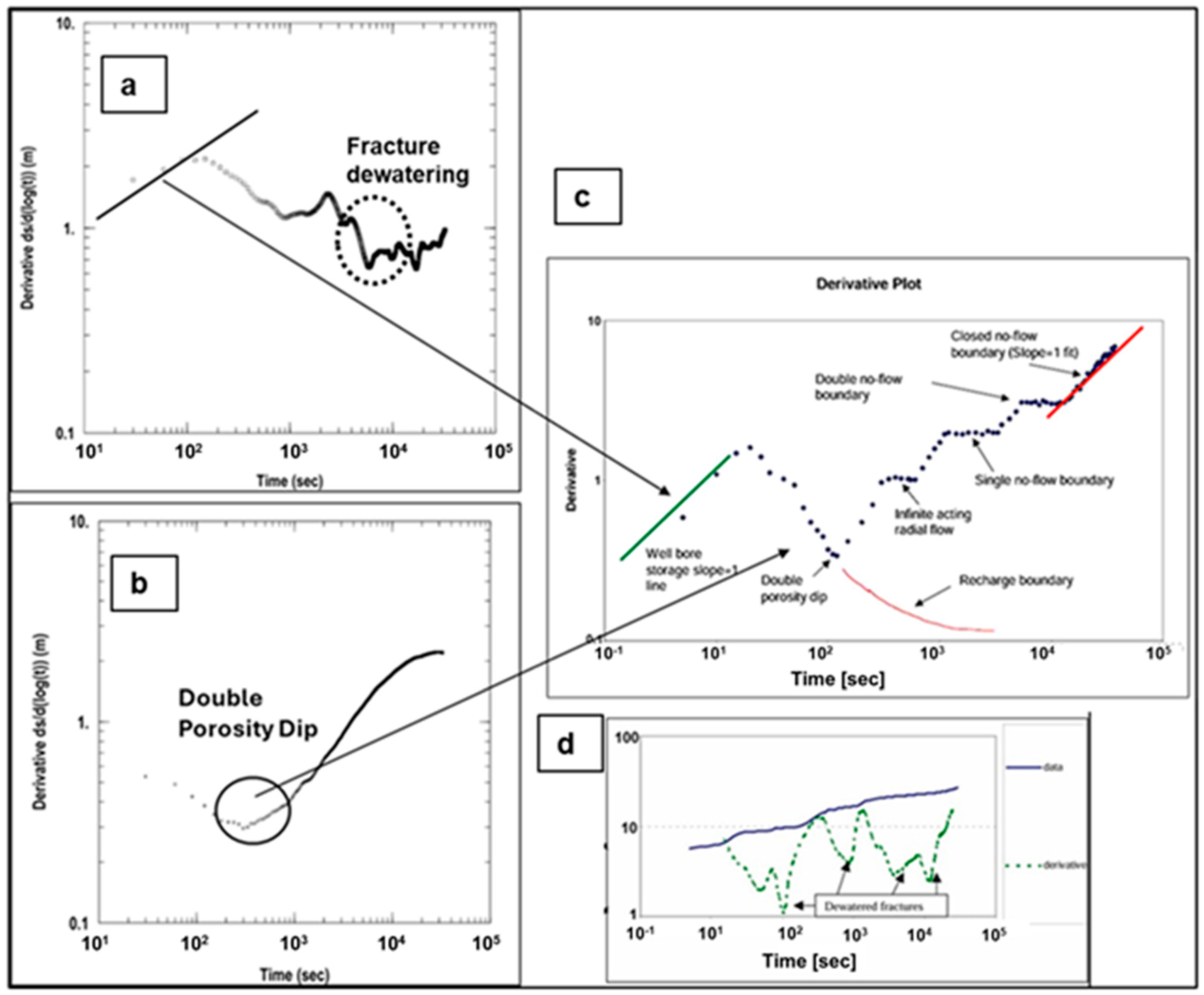
5.1. Aquifer Hydraulic Properties
5.2. Aquifer Connectivity
5.3. Well Yield and Sustainable Aquifer Use
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Abbott, B.W.; Baranov, V.; Mendoza-Lera, C.; Nikolakopoulou, M.; Harjung, A.; Kolbe, T.; Balasubramanian, M.N.; Vaessen, T.N.; Ciocca, F.; Campeau, A.; et al. Using multi-tracer inference to move beyond single-catchment ecohydrology. Earth-Sci. Rev. 2016, 160, 19–42. [Google Scholar] [CrossRef]
- Lachassagne, P.; Dewandel, B.; Wyns, R. Review: Hydrogeology of weathered crystalline/hard-rock aquifers—Guidelines for the operational survey and management of their groundwater resources. Hydrogeol. J. 2021, 29, 2561–2594. [Google Scholar] [CrossRef]
- Muchingami, I.; Chuma, C.; Gumbo, M.; Hlatywayo, D.; Mashingaidze, R. Review: Approaches to groundwater exploration and resource evaluation in the crystalline basement aquifers of Zimbabwe. Hydrogeol. J. 2019, 27, 915–928. [Google Scholar] [CrossRef]
- Doro, K.O.; Adegboyega, C.O.; Aizebeokhai, A.P.; Oladunjoye, M.A. The Ibadan Hydrogeophysics Research Site (IHRS)—An Observatory for Studying Hydrological Heterogeneities in A Crystalline Basement Aquifer in Southwestern Nigeria. Water 2023, 15, 433. [Google Scholar] [CrossRef]
- Neuman, S.P.; Blattstein, A.; Riva, M.; Tartakovsky, D.M.; Guadagnini, A.; Ptak, T. Type curve interpretation of late-time pumping test data in randomly heterogeneous aquifers. Water Resour. Res. 2007, 43, W10421. [Google Scholar] [CrossRef]
- Akurugu, B.A.; Chegbeleh, L.P.; Yidana, S.M. Characterisation of groundwater flow and recharge in crystalline basement rocks in the Talensi District, Northern Ghana. J. Afr. Earth Sci. 2020, 161, 103665. [Google Scholar] [CrossRef]
- Yidana, S.M.; Alfa, B.; Banoeng-Yakubo, B.; Obeng Addai, M. Simulation of groundwater flow in a crystalline rock aquifer system in Southern Ghana—An evaluation of the effects of increased groundwater abstraction on the aquifers using a transient groundwater flow model. Hydrol. Process. 2014, 28, 1084–1094. [Google Scholar] [CrossRef]
- Doro, K.O.; Ehosioke, S.; Aizebeokhai, A.P. Sustainable Soil and Water Resources Management in Nigeria: The Need for a Data-Driven Policy Approach. Sustainability 2020, 12, 4204. [Google Scholar] [CrossRef]
- Lachassagne, P.; Wyns, R.; Dewandel, B. The fracture permeability of hard rock aquifers is due neither to tectonics, nor to unloading, but to weathering processes. Terra Nova 2011, 23, 145–161. [Google Scholar] [CrossRef]
- Ofterdinger, U.; MacDonald, A.M.; Comte, J.-C.; Young, M.E. Groundwater in fractured bedrock environments: Managing catchment and subsurface resources—An introduction. Geol. Soc. 2019, 479, 1–9. [Google Scholar] [CrossRef]
- Wright, E.P. The hydrogeology of crystalline basement aquifers in Africa. Geol. Soc. Lond. Spec. Publ. 1992, 66, 1–27. [Google Scholar] [CrossRef]
- Maréchal, J.-C.; Dewandel, B.; Subrahmanyam, K. Use of hydraulic tests at different scales to characterize fracture network properties in the weathered-fractured layer of a hard rock aquifer. Water Resour. Res. 2004, 40, W11508. [Google Scholar] [CrossRef]
- Berkowitz, B. Characterizing flow and transport in fractured geological media: A review. Adv. Water Resour. 2002, 25, 861–884. [Google Scholar] [CrossRef]
- Neuman, S.P. Trends, prospects and challenges in quantifying flow and transport through fractured rocks. Hydrogeol. J. 2005, 13, 124–147. [Google Scholar] [CrossRef]
- Maréchal, J.-C.; Vouillamoz, J.-M.; Kumar, M.M.; Dewandel, B. Estimating aquifer thickness using multiple pumping tests. Hydrogeol. J. 2010, 18, 1787–1796. [Google Scholar] [CrossRef]
- Stober, I.; Bucher, K. Hydraulic properties of the crystalline basement. Hydrogeol. J. 2007, 15, 213–224. [Google Scholar] [CrossRef]
- Pradhan, R.M.; Singh, A.; Ojha, A.K.; Biswal, T.K. Structural controls on bedrock weathering in crystalline basement terranes and its implications on groundwater resources. Sci. Rep. 2022, 12, 11815. [Google Scholar] [CrossRef]
- Mézquita González, J.A.; Comte, J.-C.; Legchenko, A.; Ofterdinger, U.; Healy, D. Quantification of groundwater storage heterogeneity in weathered/fractured basement rock aquifers using electrical resistivity tomography: Sensitivity and uncertainty associated with petrophysical modelling. J. Hydrol. 2021, 593, 125637. [Google Scholar] [CrossRef]
- Chapman, M. Conceptualization and characterization of fractured-bedrock ground-water systems. In Enigmas of ground water in Crystalline Rocks. Problems and Solutions, Symposium Proceedings, 16 February 2001; Carolina Sections of the Association of Engineering Geologists and the American Institute of Professional Geologists: Raleigh, NC, USA, 2001. [Google Scholar]
- Harned, D.; Daniel, C., III. The transition zone between bedrock and regolith: Conduit for contamination? In Ground Water in the Piedmont, Proceedings of the Conference on Ground Water in the Piedmont of the Eastern United States, Charlotte, NC, USA, 16–18 October 1992; Daniel, C.C., White, R.K., III., Stone, P.A., Eds.; Clemson University: Clemson, SC, USA, 1992; pp. 336–348. [Google Scholar]
- National Academies of Sciences, Engineering, and Medicine; Division on Earth and Life Studies; Board on Earth Sciences and Resources; Committee on Subsurface Characterization, Modeling, Monitoring, and Remediation of Fractured Rock; Committee on Geological and Geotechnical Engineering. Characterization, Modeling, Monitoring, and Remediation of Fractured Rock; National Academies Press: Washington, DC, USA, 2020. [Google Scholar] [CrossRef]
- Nicolas, M. Impact of Heterogeneity on Natural and Managed Aquiferrecharge in Weathered Fractured Crystalline Rock Aquifers. Ph.D. Thesis, Université de Rennes, Rennes, France, 2019. [Google Scholar]
- Maréchal, J.-C.; Selles, A.; Dewandel, B.; Boisson, A.; Perrin, J.; Ahmed, S. An Observatory of Groundwater in Crystalline Rock Aquifers Exposed to a Changing Environment: Hyderabad, India. Vadose Zone J. 2018, 17, 180076. [Google Scholar] [CrossRef]
- Aizebeokhai, A.P.; Ogungbade, O.; Oyeyemi, K.D. Application of geoelectrical resistivity for delineating crystalline basement aquifers in Basiri, Ado-Ekiti, Southwestern Nigeria. Arab. J. Geosci. 2021, 14, 51. [Google Scholar] [CrossRef]
- Doro, K.O.; Leven, C.; Cirpka, O.A. Delineating subsurface heterogeneity at a loop of River Steinlach using geophysical and hydrogeological methods. Environ. Earth Sci. 2013, 69, 335–348. [Google Scholar] [CrossRef]
- Burbey, T.J.; Hisz, D.; Murdoch, L.C.; Zhang, M. Quantifying fractured crystalline-rock properties using well tests, earth tides and barometric effects. J. Hydrol. 2012, 414–415, 317–328. [Google Scholar] [CrossRef]
- Cirpka, O.A.; Leven, C.; Schwede, R.; Doro, K.; Bastian, P.; Ippisch, O.; Klein, O.; Patzelt, A. Tomography of the Earth’s Crust: From Geophysical Sounding to Real-Time Monitoring. In Geotechnologien Science Report No. 21; Weber, M., Münch, U., Eds.; Springer International Publishing: Cham, Germany, 2014; pp. 157–176. [Google Scholar]
- Butler, J.J., Jr.; Zhan, X. Hydraulic tests in highly permeable aquifers. Water Resour. Res. 2004, 40, W12402. [Google Scholar] [CrossRef]
- Doro, K.O.; Cirpka, O.A.; Leven, C. Tracer Tomography: Design Concepts and Field Experiments Using Heat as a Tracer. Groundwater 2015, 53, 139–148. [Google Scholar] [CrossRef]
- Leven, C.; Dietrich, P. What information can we get from pumping tests?-comparing pumping test configurations using sensitivity coefficients. J. Hydrol. 2006, 319, 199–215. [Google Scholar] [CrossRef]
- Maliva, R.G. Aquifer Characterization Techniques: Schlumberger Methods in Water Resources Evaluation Series No. 4; Springer International Publishing: Cham, Switzerland, 2016; p. 617. [Google Scholar]
- Dashti, Z.; Nakhaei, M.; Vadiati, M.; Karami, G.H.; Kisi, O. A literature review on pumping test analysis (2000–2022). Environ. Sci. Pollut. Res. 2023, 30, 9184–9206. [Google Scholar] [CrossRef] [PubMed]
- Kruseman, G.P.; De Ridder, N.A. Analysis and Evaluation of Pumping Test Data. International Institute for Land Reclamation and Improvement: Ageningen, The Netherlands, 2000; p. 372. [Google Scholar]
- Theis, C.V. The relation between the lowering of the Piezometric surface and the rate and duration of discharge of a well using ground-water storage. Eos Trans. Am. Geophys. Union 1935, 16, 519–524. [Google Scholar] [CrossRef]
- Chang, S.W.; Memari, S.S.; Clement, T.P. PyTheis—A Python Tool for Analyzing Pump Test Data. Water 2021, 13, 2180. [Google Scholar] [CrossRef]
- Cooper, H., Jr.; Jacob, C.E. A generalized graphical method for evaluating formation constants and summarizing well-field history. Eos Trans. Am. Geophys. Union 1946, 27, 526–534. [Google Scholar]
- Neuman, S.P. Effect of partial penetration on flow in unconfined aquifers considering delayed gravity response. Water Resour. Res. 1974, 10, 303–312. [Google Scholar] [CrossRef]
- Hammond, P.A.; Field, M.S. A reinterpretation of historic aquifer tests of two hydraulically fractured wells by application of inverse analysis, derivative analysis, and diagnostic plots. J. Water Resour. Prot. 2014, 6, 45306. [Google Scholar] [CrossRef][Green Version]
- Moench, A.F. Double-porosity models for a fissured groundwater reservoir with fracture skin. Water Resour. Res. 1984, 20, 831–846. [Google Scholar] [CrossRef]
- Barker, J. A generalized radial flow model for hydraulic tests in fractured rock. Water Resour. Res. 1988, 24, 1796–1804. [Google Scholar] [CrossRef]
- Wu, Y.-S.; Ye, M.; Sudicky, E.A. Fracture-Flow-Enhanced Matrix Diffusion in Solute Transport Through Fractured Porous Media. Transp. Porous Media 2010, 81, 21–34. [Google Scholar] [CrossRef]
- Lin, Y.C.; Yeh, H.D. A lagging model for describing drawdown induced by a constant-rate pumping in a leaky confined aquifer. Water Resour. Res. 2017, 53, 8500–8511. [Google Scholar] [CrossRef]
- Tamayo-Mas, E.; Bianchi, M.; Mansour, M. Impact of model complexity and multi-scale data integration on the estimation of hydrogeological parameters in a dual-porosity aquifer. Hydrogeol. J. 2018, 26, 1917–1933. [Google Scholar] [CrossRef]
- Chen, C.; Tao, Q.; Wen, Z.; Wörman, A.; Jakada, H. Step-drawdown test for identifying aquifer and well loss parameters in a partially penetrating well with irregular (non-linear increasing) pumping rates. J. Hydrol. 2022, 614, 128652. [Google Scholar] [CrossRef]
- Shekhar, S. An approach to interpretation of step drawdown tests. Hydrogeol. J. 2006, 14, 1018–1027. [Google Scholar] [CrossRef]
- An, H.; Ha, K.; Lee, E. Transient analysis of a step-drawdown test using a time-varying well-loss equation. Hydrogeol. J. 2022, 30, 303–314. [Google Scholar] [CrossRef]
- Randall, A.D.; Mills, A.C. Transmissivity Estimated from Brief Aquifer tests of domestic wells and compared with bedrock lithofacies and position on hillsides in the Appalachian Plateau of New York; US Geological Survey Scientific Investigations Report 2020-5087; US Geological Survey: Reston, VA, USA, 2020; 21p. [CrossRef]
- Viswanathan, H.S.; Ajo-Franklin, J.; Birkholzer, J.T.; Carey, J.W.; Guglielmi, Y.; Hyman, J.D.; Karra, S.; Pyrak-Nolte, L.J.; Rajaram, H.; Srinivasan, G.; et al. From Fluid Flow to Coupled Processes in Fractured Rock: Recent Advances and New Frontiers. Rev. Geophys. 2022, 60, e2021RG000744. [Google Scholar] [CrossRef]
- Wang, Y.; Zhan, H.; Huang, K.; He, L.; Wan, J. Identification of non-Darcian flow effect in double-porosity fractured aquifer based on multi-well pumping test. J. Hydrol. 2021, 600, 126541. [Google Scholar] [CrossRef]
- Leibundgut, C.; Maloszewski, P.; Külls, C. Tracers in Hydrology; John Wiley & Sons: West Sussex, UK, 2011; p. 434. [Google Scholar]
- Weight, W.D. Hydrogeology Field Manual, 2nd ed.; The McGraw-Hill Companies, Inc.: New York, NY, USA, 2008; p. 741. [Google Scholar]
- Bear, J.; Buchlin, J.-M. Modelling and Applications of Transport Phenomena in Porous Media; Springer: Dordrecht, The Netherland, 1991; p. 381. [Google Scholar]
- Cook, P.G. A Guide to Regional Groundwater Flow in Fractured Rock Aquifers; CSIRO Land and Water: Clayton, Australia, 2003. [Google Scholar]
- Pettenati, M.; Perrin, J.; Pauwels, H.; Ahmed, S. Simulating fluoride evolution in groundwater using a reactive multicomponent transient transport model: Application to a crystalline aquifer of Southern India. Appl. Geochem. 2013, 29, 102–116. [Google Scholar] [CrossRef]
- Huysmans, M.; Dassargues, A. Review of the use of Péclet numbers to determine the relative importance of advection and diffusion in low permeability environments. Hydrogeol. J. 2005, 13, 895–904. [Google Scholar] [CrossRef]
- Masciopinto, C.; Passarella, G.; Caputo, M.C.; Masciale, R.; De Carlo, L. Hydrogeological models of water flow and pollutant transport in karstic and fractured reservoirs. Water Resour. Res. 2021, 57, e2021WR029969. [Google Scholar] [CrossRef]
- Tsang, Y.W.; Tsang, C.F.; Neretnieks, I.; Moreno, L. Flow and tracer transport in fractured media: A variable aperture channel model and its properties. Water Resour. Res. 1988, 24, 2049–2060. [Google Scholar] [CrossRef]
- Becker, M.W.; Shapiro, A.M. Interpreting tracer breakthrough tailing from different forced-gradient tracer experiment configurations in fractured bedrock. Water Resour. Res. 2003, 39, 1024. [Google Scholar] [CrossRef]
- Haggerty, R.; Gorelick, S.M. Multiple-rate mass transfer for modeling diffusion and surface reactions in media with pore-scale heterogeneity. Water Resour. Res. 1995, 31, 2383–2400. [Google Scholar]
- Wang, L.; Yoon, S.; Zheng, L.; Wang, T.; Chen, X.; Kang, P.K. Flux exchange between fracture and matrix dictates late-time tracer tailing. J. Hydrol. 2023, 627, 130480. [Google Scholar] [CrossRef]
- Wu, H.; Wei, Y.; Zhang, K. Quantifying matrix diffusion effect on solute transport in subsurface fractured media. EGUsphere 2025, 2025, 1–23. [Google Scholar]
- Elueze, A. Geology of the precambrian schist belt in Ilesha area southwestern Nigeria. Geol. Surv. Nig 1988, 1988, 77–82. [Google Scholar]
- Jayeoba, A.; Oladunjoye, M.A. 2-D electrical resistivity tomography for groundwater exploration in hard rock terrain. Int. J. Sci. Technol. 2015, 4, 156–163. [Google Scholar]
- Olaojo, A.A.; Oladunjoye, M.A.; Sanuade, O.A. Geoelectrical assessment of polluted zone by sewage effluent in University of Ibadan campus southwestern Nigeria. Environ. Monit. Assess. 2018, 190, 24. [Google Scholar] [CrossRef]
- Rahaman, M. Recent advances in the study of the basement complex of Nigeria. In Pre Cambrian Geology of Nigeria; Geological Survey of Nigeria: Kaduna South, Nigeria, 1988; pp. 11–43. [Google Scholar]
- Dasho, O.A.; Ariyibi, E.A.; Adebayo, A.S.; Falade, S.C. Seismotectonic lineament mapping over parts of Togo-Benin-Nigeria shield. NRIAG J. Astron. Geophys. 2020, 9, 539–547. [Google Scholar] [CrossRef]
- Oladejo, O.; Adagunodo, T.; Sunmonu, L.; Adabanija, M.; Omeje, M.; Babarimisa, I.; Bility, H. Structural Analysis of Subsurface Stability Using Aeromagnetic Data: A case of Ibadan, Southwestern Nigeria; IOP Publishing: Bristol, UK, 2019; p. 012083. [Google Scholar]
- Doro, K.O.; Adegboyega, C.O.; Aizebeokhai, A.P.; Oladunjoye, M.A. Hydrological Variability in Crystalline Basement Aquifers—Insight from a First Hydrogeophysics Research Site in Nigeria. Water 2020, 1, 1–5. [Google Scholar]
- Oladunjoye, M.; Korode, I.; Adefehinti, A. Geoelectrical exploration for groundwater in crystalline basement rocks of Gbongudu community, Ibadan, southwestern Nigeria. Glob. J. Geol. Sci. 2019, 17, 25–43. [Google Scholar] [CrossRef]
- Balasubramanian, A. Procedure for conducting pumping tests. Indian Soc. Sci. Congr.-Trends Earth Sci. Res. 2017. Available online: https://www.researchgate.net/profile/A-Balasubramanian/publication/315662924_Procedure_for_Conducting_Pumping_Tests/links/58d93a3ba6fdccca1c4bf9df/Procedure-for-Conducting-Pumping-Tests.pdf (accessed on 20 November 2024).
- Dross, P. Technical Review: Practical Guidelines for Test Pumping in Water Wells; International Committee of the Red Cross: Geneva, Switzerland, 2011. [Google Scholar]
- Gross, E.L. Manual Pumping Test Method for Characterizing the Productivity of Drilled Wells Equipped with Rope Pumps; Michigan Technological University: Houghton, MI, USA, 2008. [Google Scholar]
- van Tonder, G.J.; Botha, J.F.; Chiang, W.H.; Kunstmann, H.; Xu, Y. Estimation of the sustainable yields of boreholes in fractured rock formations. J. Hydrol. 2001, 241, 70–90. [Google Scholar] [CrossRef]
- Novakowski, K.S. Analysis of pulse interference tests. Water Resour. Res. 1989, 25, 2377–2387. [Google Scholar] [CrossRef]
- Lescarboura, J.A.; Walther, H.C., Jr.; Wilson, P.L. Design and Analysis of Interference Tests. In Proceedings of the SPE California Regional Meeting, Ventura, CA, USA, 2–4 April 1975; p. SPE-5314. [Google Scholar] [CrossRef]
- Bourdet, D.; Ayoub, J.A.; Kniazeff, V.; Pirard, Y.M.; Whittle, T.M. Interpreting Well Tests in Fractured Reservoirs; World Oil: South Gate, CA, USA; pp. 77–78.
- Remson, I.; Lang, S. A pumping-test method for the determination of specific yield. Eos Trans. Am. Geophys. Union 1955, 36, 321–325. [Google Scholar]
- Gomo, M. On the Flow Characteristics (FC) method for estimating sustainable borehole yield. Water SA 2024, 50, 131–136. [Google Scholar] [CrossRef]
- van Tonder, G.; Kunstmann, H.; Xu, Y.; Fourie, F. Estimation of the sustainable yield of a borehole including boundary information, drawdown derivatives and uncertainty propagation. In Calibration and Reliability in Groundwater Modelling, Proceedings of the ModelCARE 99 Conference, Zurich, Switzerland, 20–23 September 1999; IAHS Publ. No. 265; IAHS (International Association of Hydrological Sciences): Wallingford, Oxfordshire, UK, 2000; pp. 367–376. [Google Scholar]
- Hantush, M.S.; Jacob, C.E. Non-steady radial flow in an infinite leaky aquifer. Eos Trans. Am. Geophys. Union 1955, 36, 95–100. [Google Scholar]
- Agarwal, R.G. A New Method to Account for Producing Time Effects When Drawdown Type Curves Are Used to Analyze Pressure Buildup and Other Test Data. In Proceedings of the 55th Annual Technical Conference and Exhibition, Dallas, TX, USA, 21–24 September 1980; p. SPE-9289-MS. [Google Scholar]
- Gutierrez, A.; Klinka, T.; Thiéry, D.; Buscarlet, E.; Binet, S.; Jozja, N.; Défarge, C.; Leclerc, B.; Fécamp, C.; Ahumada, Y.; et al. TRAC, a collaborative computer tool for tracer-test interpretation. EPJ Web Conf. 2013, 50, 03002. [Google Scholar] [CrossRef]
- Rorabaugh, M.I. Graphical and Theoretical Analysis of Step-Drawdown Test of Artesian Well; The American Society of Civil Engineers (ASCE): Reston, VA, USA, 1953; pp. 1–23. [Google Scholar]
- Singhal, B.B.S.; Gupta, R.P. Applied Hydrogeology of Fractured Rocks; Springer Science & Business Media: Cham, Switzerland, 2010. [Google Scholar]
- Chilton, P.J.; Foster, S.S. Hydrogeological characterisation and water-supply potential of basement aquifers in tropical Africa. Hydrogeol. J. 1995, 3, 36–49. [Google Scholar] [CrossRef]
- Taylor, R.; Howard, K. A tectono-geomorphic model of the hydrogeology of deeply weathered crystalline rock: Evidence from Uganda. Hydrogeol. J. 2000, 8, 279–294. [Google Scholar] [CrossRef]
- Acheampong, S.Y.; Hess, J.W. Hydrogeologic and hydrochemical framework of the shallow groundwater system in the southern Voltaian Sedimentary Basin, Ghana. Hydrogeol. J. 1998, 6, 527–537. [Google Scholar] [CrossRef]
- Blessent, D.; Therrien, R.; Gable, C.W. Large-scale numerical simulation of groundwater flow and solute transport in discretely-fractured crystalline bedrock. Adv. Water Resour. 2011, 34, 1539–1552. [Google Scholar] [CrossRef]
- Zhang, Y.; Green, C.T.; Tick, G.R. Peclet number as affected by molecular diffusion controls transient anomalous transport in alluvial aquifer–aquitard complexes. J. Contam. Hydrol. 2015, 177–178, 220–238. [Google Scholar] [CrossRef]
- Lapworth, D.; MacDonald, A.; Tijani, M.; Darling, W.; Gooddy, D.; Bonsor, H.; Araguás-Araguás, L. Residence times of shallow groundwater in West Africa: Implications for hydrogeology and resilience to future changes in climate. Hydrogeol. J. 2013, 21, 673–686. [Google Scholar] [CrossRef]

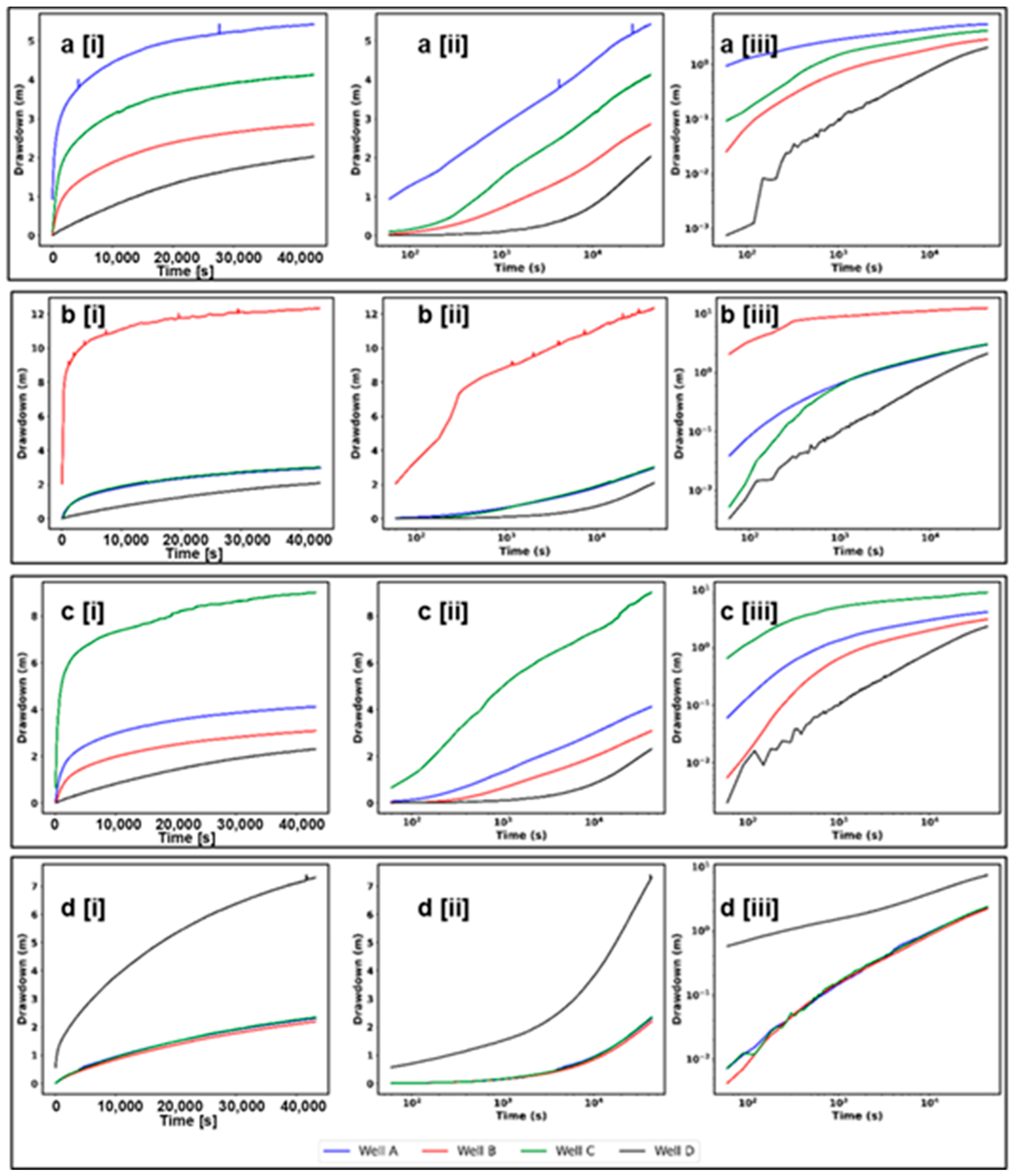


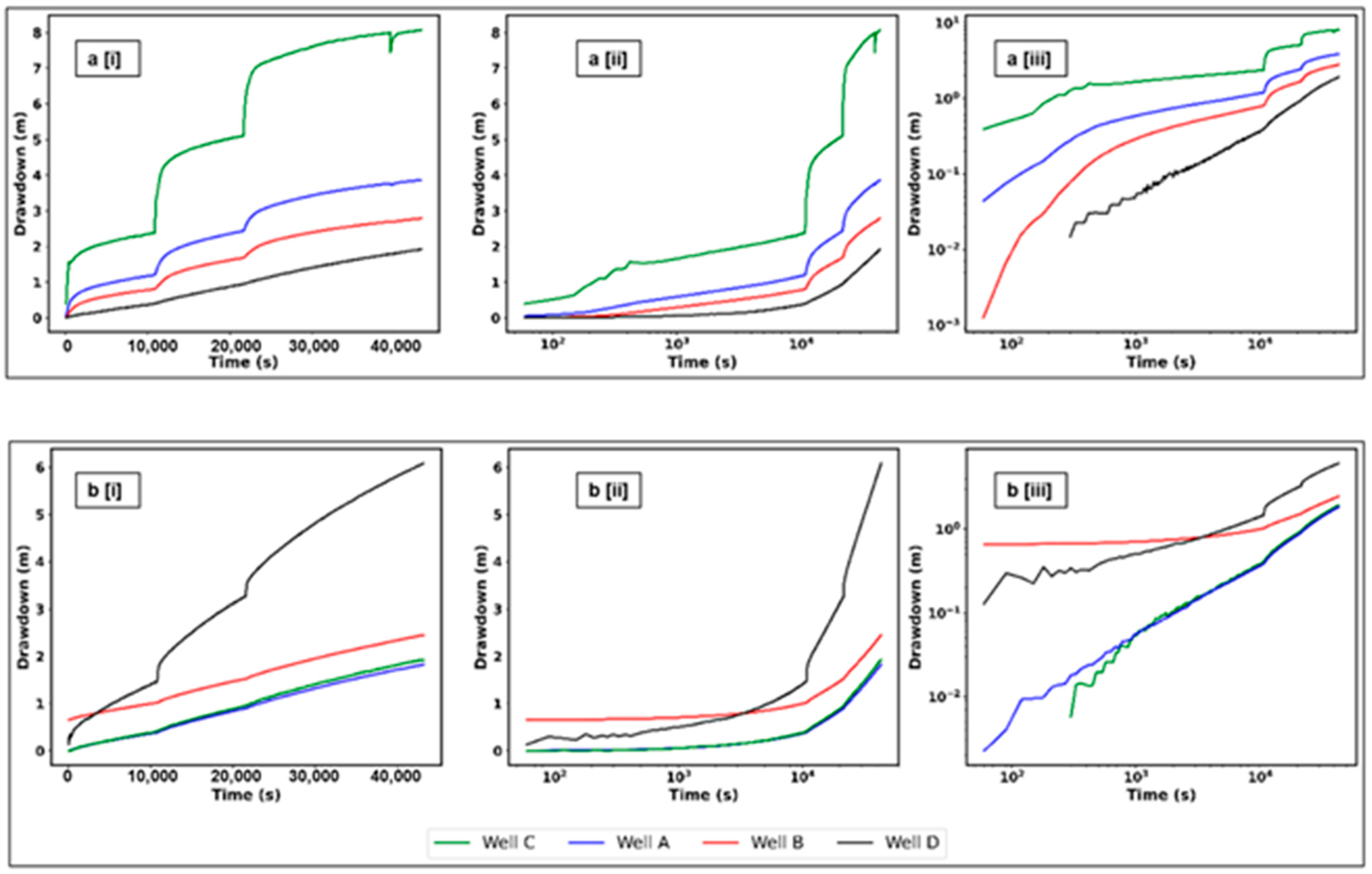
| Well Name | Status | Distance from Pumped Well (m) | 9 h Drawdown (m) | 12 h Drawdown (m) |
|---|---|---|---|---|
| A | Pumping | 0.00 | 4.94 | 5.43 |
| B | Observation | 11.40 | 2.48 | 2.86 |
| C | Observation | 8.30 | 3.63 | 4.13 |
| D | Observation | 8.50 | 1.63 | 2.03 |
| A | Observation | 11.40 | 2.73 | 2.96 |
| B | Pumping | 0.00 | 12.47 | 12.58 |
| C | Observation | 6.85 | 2.68 | 3.01 |
| D | Observation | 15.70 | 1.73 | 2.08 |
| A | Observation | 8.30 | 3.52 | 4.12 |
| B | Observation | 6.85 | 2.55 | 3.08 |
| C | Pumping | 0.00 | 7.22 | 9.00 |
| D | Observation | 9.20 | 1.28 | 2.31 |
| A | Observation | 8.50 | 1.77 | 2.31 |
| B | Observation | 15.70 | 1.74 | 2.19 |
| C | Observation | 9.20 | 1.86 | 2.34 |
| D | Pumping | 0.00 | 6.18 | 7.30 |
| Wells | Hydraulic Parameters | Pumping at Well A (9 h) | Pumping at Well D (9 h) | Pumping at Well C (9 h) | Pumping at Well B (9 h) | Pumping at Well B (12 h) | Pumping at Well C (12 h) | Pumping at Well D (12 h) | Pumping at Well A (12 h) |
|---|---|---|---|---|---|---|---|---|---|
| WELL A | Fracture Hydraulic Conductivity (m/s) | 6.57 × 10−6 | 1.23 × 10−6 | 2.43 × 10−6 | 2.97 × 10−6 | 2.99 × 10−6 | 3.22 × 10−6 | 6.41 × 10−7 | 1.00 × 10−5 |
| Matrix Hydraulic Conductivity (m/s) | 1.09 × 10−6 | 1.92 × 10−9 | 2.43 × 10−10 | 3.54 × 10−10 | 3.40 × 10−10 | 2.61 × 10−10 | 1.00 × 10−10 | 1.00 × 10−10 | |
| Fracture Specific Storage (m−1) | 2.46 × 10−4 | 2.30 × 10−6 | 2.77 × 10−7 | 3.03 × 10−7 | 3.15 × 10−7 | 2.14 × 10−7 | 1.96 × 10−6 | 1.08 × 10−4 | |
| Matrix Specific Storage (m−1) | 5.48 × 10−2 | 9.75 × 10−4 | 7.33 × 10−5 | 6.88 × 10−5 | 6.53 × 10−5 | 2.42 × 10−5 | 4.85 × 10−3 | 7.02 × 10−5 | |
| Transmissivity (m2/s) | 1.01 × 10−4 | 1.89 × 10−5 | 3.71 × 10−5 | 4.54 × 10−5 | 4.56 × 10−5 | 4.92 × 10−5 | 9.79 × 10−6 | 1.54 × 10−4 | |
| Flow Dimension (n) | 2.06 | 2.22 | 1.97 | 2.00 | 2.00 | 2.00 | 2.00 | 1.78 | |
| WELL B | Fracture Hydraulic Conductivity (m/s) | 3.82 × 10−6 | 3.64 × 10−6 | 2.64 × 10−6 | 3.53 × 10−6 | 3.54 × 10−6 | 3.17 × 10−6 | 7.85 × 10−7 | 1.66 × 10−5 |
| Matrix Hydraulic Conductivity (m/s) | 9.19 × 10−10 | 4.29 × 10−8 | 6.95 × 10−10 | 7.69 × 10−10 | 1.00 × 10−10 | 7.63 × 10−10 | 1.00 × 10−10 | 4.25 × 10−2 | |
| Fracture-Specific Storage | 5.78 × 10−7 | 5.07 × 10−5 | 2.06 × 10−5 | 4.60 × 10−6 | 1.09 × 10−6 | 1.89 × 10−5 | 6.35 × 10−7 | 4.51 × 10−5 | |
| Matrix Specific Storage | 9.19 × 10−5 | 1.16 × 10−4 | 2.23 × 10−4 | 1.00 × 10−10 | 1.00 × 10−10 | 1.20 × 10−4 | 5.40 × 10−4 | 1.16 × 10−10 | |
| Transmissivity (m2/s) | 1.06 × 10−4 | 1.01 × 10−4 | 7.30 × 10−5 | 9.75 × 10−5 | 9.77 × 10−5 | 8.70 × 10−5 | 2.17 × 10−5 | 2.53 × 10−4 | |
| Flow Dimension (n) | 2.35 | 2.00 | 2.00 | 2.00 | 2.00 | 2.00 | 2.00 | 1.71 | |
| WELL C | Fracture Hydraulic Conductivity (m/s) | 7.19 × 10−6 | 1.91 × 10−6 | 2.76 × 10−6 | 3.71 × 10−6 | 1.82 × 10−6 | 2.49 × 10−6 | 1.45 × 10−5 | 2.66 × 10−6 |
| Matrix Hydraulic Conductivity (m/s) | 1.87 × 10−10 | 8.06 × 10−9 | 7.67 × 10−9 | 1.43 × 10−9 | 1.45 × 10−10 | 1.00 × 10−10 | 6.14 × 10−2 | 1.00 × 10−10 | |
| Fracture-Specific Storage | 1.16 × 10−5 | 1.29 × 10−5 | 1.90 × 10−3 | 2.24 × 10−5 | 1.70 × 10−5 | 2.46 × 10−3 | 1.95 × 10−4 | 3.02 × 10−6 | |
| Matrix Specific Storage | 1.30 × 10−5 | 4.94 × 10−4 | 9.31 × 10−4 | 7.84 × 10−5 | 5.65 × 10−4 | 1.00 × 10−10 | 1.00 × 10−10 | 1.43 × 10−4 | |
| Transmissivity (m2/s) | 1.99 × 10−4 | 5.30 × 10−5 | 7.66 × 10−5 | 1.03 × 10−4 | 5.05 × 10−5 | 6.91 × 10−5 | 4.03 × 10−4 | 4.06 × 10−6 | |
| Flow Dimension (n) | 2.00 | 2.00 | 2.00 | 2.05 | 2.00 | 2.00 | 0.93 | ||
| WELL D | Fracture Hydraulic Conductivity (m/s) | 2.63 × 10−7 | 5.11 × 10−7 | 5.59 × 10−8 | 5.50 × 10−6 | 1.36 × 10−6 | 4.36 × 10−7 | 4.80 × 10−7 | 1.64 × 10−5 |
| Matrix Hydraulic Conductivity (m/s) | 3.52 × 10−10 | 1.00 × 10−00 | 1.71 × 10−10 | 6.70 × 10−5 | 1.00 × 10−10 | 1.13 × 10−10 | 4.04 × 10−1 | 1.42 × 10−5 | |
| Fracture-Specific Storage | 1.27 × 10−5 | 1.25 × 10−00 | 1.90 × 10−6 | 1.00 × 10−3 | 1.12 × 10−6 | 1.86 × 10−6 | 1.10 × 10−0 | 2.40 × 10−3 | |
| Matrix Specific Storage | 1.02 × 10−2 | 1.00 × 10−0 | 3.34 × 10−3 | 1.00 × 10−3 | 5.44 × 10−4 | 2.48 × 10−3 | 9.54 × 10−1 | 2.83 × 10−8 | |
| Transmissivity (m2/s) | 7.28 × 10−6 | 1.41 × 10−5 | 1.54 × 10−6 | 1.52 × 10−4 | 3.75 × 10−5 | 1.21 × 10−5 | 1.33 × 10−5 | 1.64 × 10−5 | |
| Flow Dimension (n) | 2.68 | 2.00 | 2.00 | 2.00 | 2.00 | 2.00 | 2.00 |
| Pumping Well | Extraction Well | A | B | C | D |
|---|---|---|---|---|---|
| A | Specific Yield (%) | 0.16% | 0.22% | 0.34% | |
| Distance from pumping well | 11.40 m | 8.30 m | 8.50m | ||
| Volume of material dewatered (m3) | 3426.80 m3 | 2427.60 m3 | 1575.90 m3 | ||
| Volume of water drained (L) | 38.84 L | 53.41 L | 53.58 L | ||
| B | Specific Yield (%) | 0.03% | 0.08% | 0.05% | |
| Distance from pumping well | 11.40 m | 6.85 m | 15.70 m | ||
| Volume of material dewatered (m3) | 16,358.75 m3 | 6295.01 m3 | 9494.89 m3 | ||
| Volume of water drained (L) | 50.71 L | 50.36 L | 47.48 L | ||
| C | Specific Yield (%) | 0.04% | 0.17% | 0.20% | |
| Distance from pumping well | 8.30 m | 6.85 m | 9.20 m | ||
| Volume of material dewatered (m3) | 12,448.40 m3 | 3075.70 m3 | 2595.83 m3 | ||
| Volume of water drained (L) | 49.79 L | 52.29 L | 51.93 L | ||
| D | Specific Yield (%) | 0.28% | 0.08% | 0.24% | |
| Distance from pumping well | 8.50 m | 15.70 m | 9.20 m | ||
| Volume of material dewatered (m3) | 1906.70 m3 | 6372.93 m3 | 2247.88 m3 | ||
| Volume of water drained (L) | 53.38 L | 50.98 L | 53.94 L |
| Well | Sustainable Yield | Number of Persons That Can Be Supplied |
|---|---|---|
| A | 1166.40 m3 at 0.45 L/s | 1555 People |
| B | 414.72 m3 at 0.16 L/s | 553 People |
| C | 803.52 m3 at 0.31 L/s | 1071 People |
| D | 984.96 m3 at 0.38 L/s | 1313 People |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Doro, K.O.; Olabode, P.I.; Adeniran, M.A.; Oladunjoye, M.A. Understanding Complex Hydraulic Heterogeneities in Crystalline Basement Aquifers Used as Drinking Water Sources. Geosciences 2025, 15, 239. https://doi.org/10.3390/geosciences15070239
Doro KO, Olabode PI, Adeniran MA, Oladunjoye MA. Understanding Complex Hydraulic Heterogeneities in Crystalline Basement Aquifers Used as Drinking Water Sources. Geosciences. 2025; 15(7):239. https://doi.org/10.3390/geosciences15070239
Chicago/Turabian StyleDoro, Kennedy O., Phebe I. Olabode, Margaret A. Adeniran, and Michael A. Oladunjoye. 2025. "Understanding Complex Hydraulic Heterogeneities in Crystalline Basement Aquifers Used as Drinking Water Sources" Geosciences 15, no. 7: 239. https://doi.org/10.3390/geosciences15070239
APA StyleDoro, K. O., Olabode, P. I., Adeniran, M. A., & Oladunjoye, M. A. (2025). Understanding Complex Hydraulic Heterogeneities in Crystalline Basement Aquifers Used as Drinking Water Sources. Geosciences, 15(7), 239. https://doi.org/10.3390/geosciences15070239






