Advancing the Prediction and Evaluation of Blast-Induced Ground Vibration Using Deep Ensemble Learning with Uncertainty Assessment
Abstract
1. Introduction
- Create a deep ensemble model that accurately predicts blast-induced PPV independent of regional characteristics and maintains high prediction accuracy across diverse quarry sites.
- Integrate uncertainty quantification into blast-induced PPV estimation and quantitatively assess the uncertainty associated with the model’s predictions, addressing a notable gap in the literature.
- Validate the performance of the proposed deep ensemble approach with conventional methods—such as the United States Bureau of Mines (USBM) empirical equation and a single DNN model—to verify the effectiveness of DNNs in this application.
- Provide a robust predictive tool that contributes to engineering solutions aimed at mitigating the severe environmental and structural impacts caused by blasting operations.
2. Materials and Methods
2.1. Empirical Model
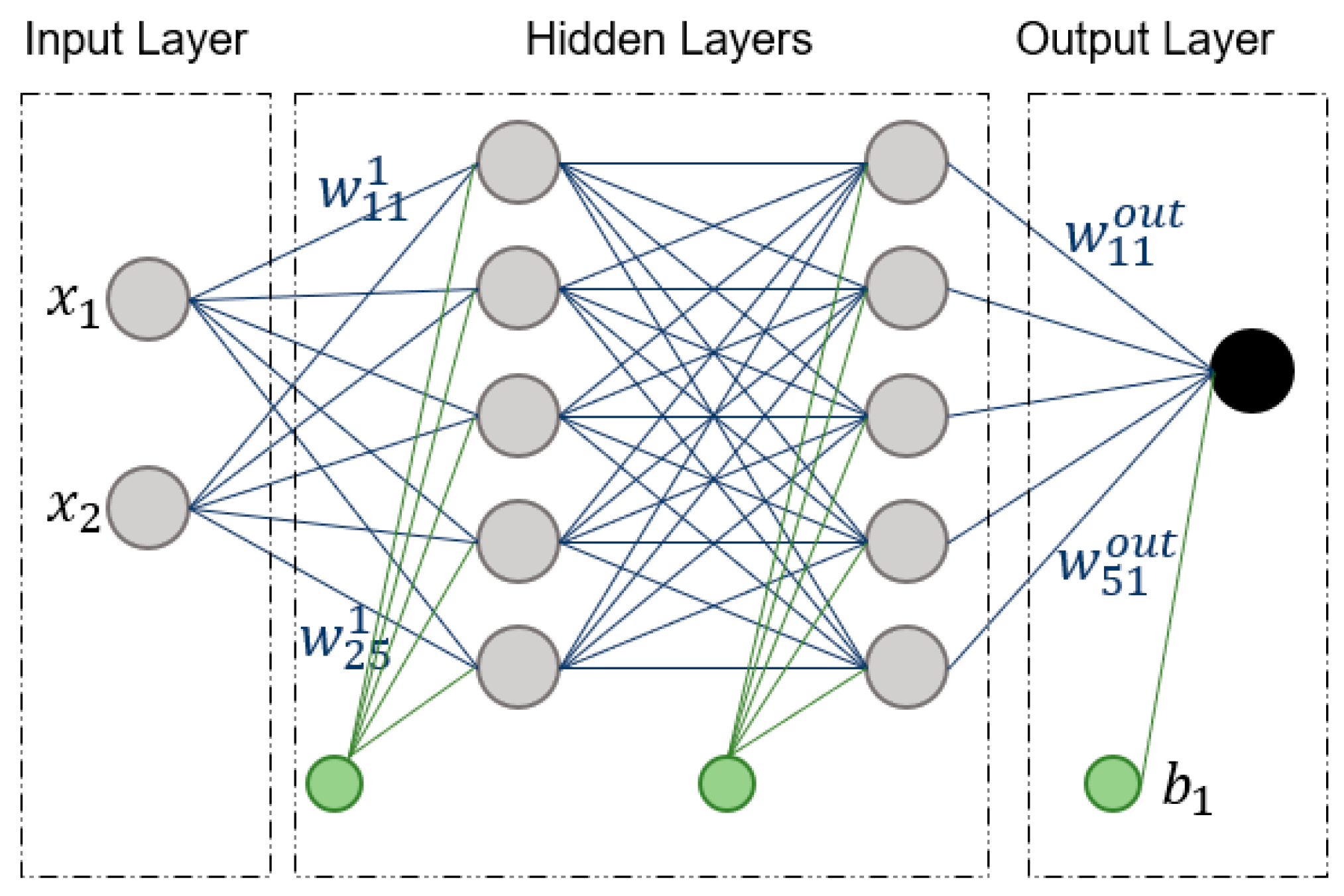
2.2. Deep Neural Network
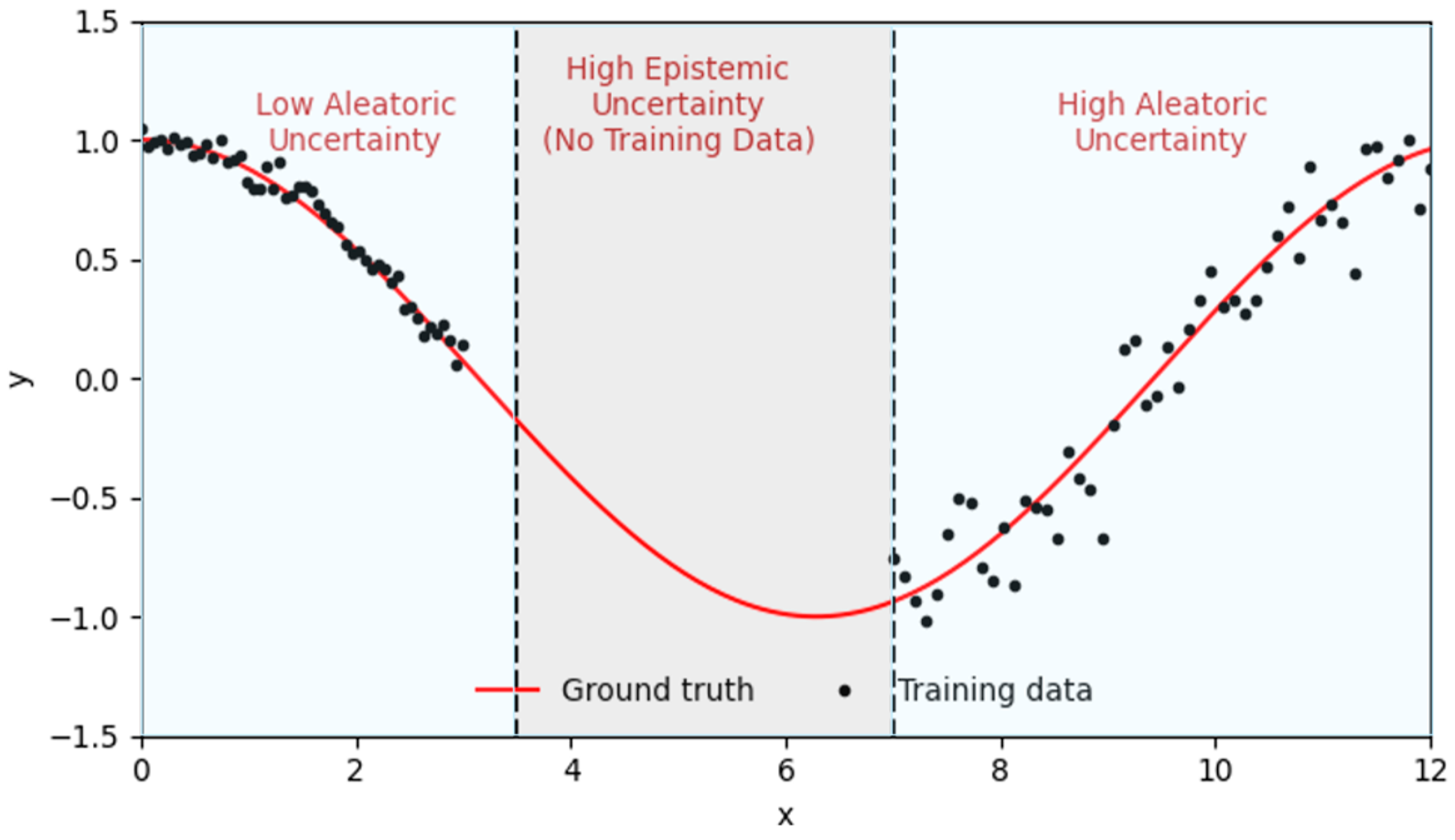
2.3. The Uncertainty Framework
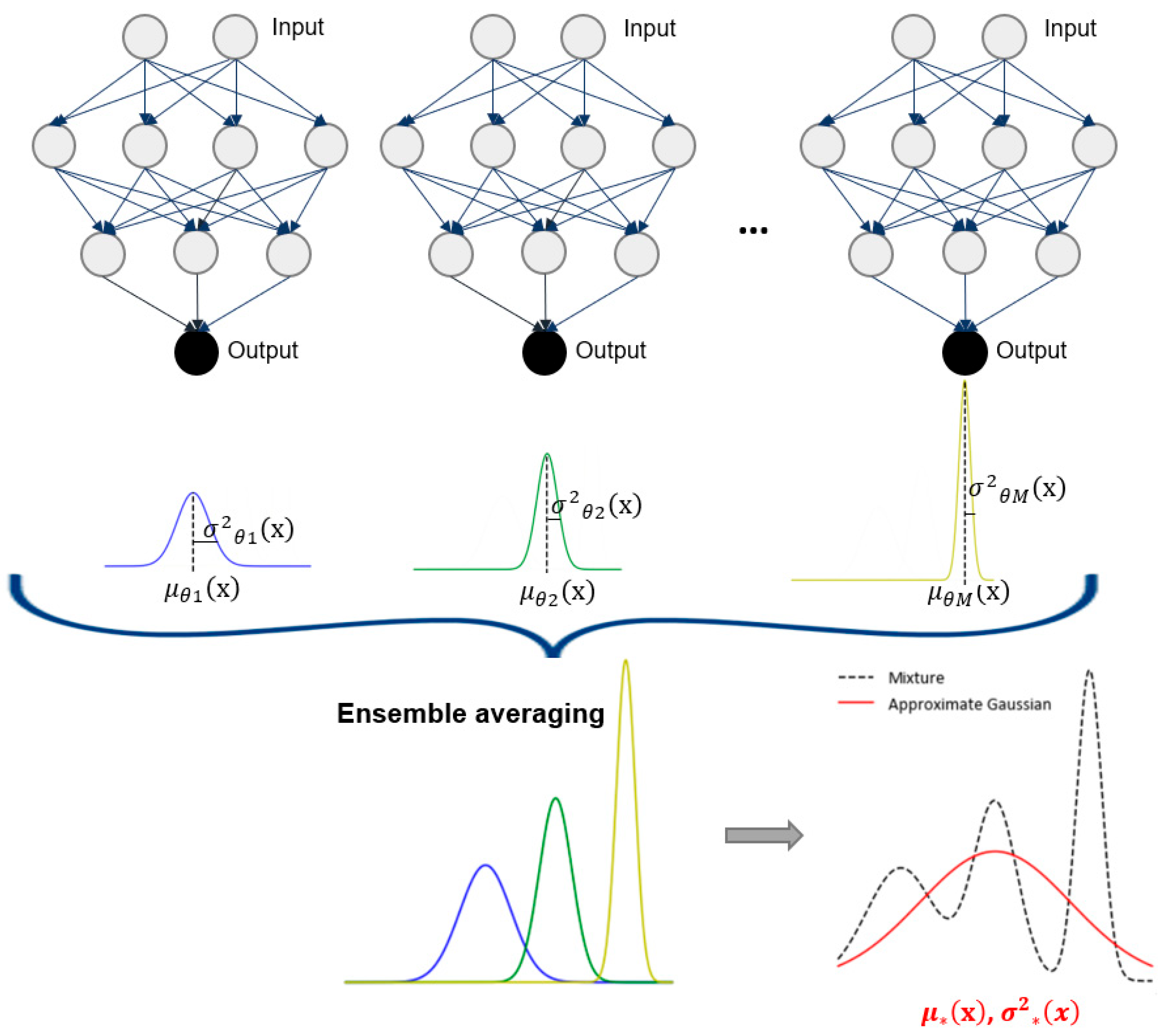
2.4. Deep Ensembles
3. Proposed Deep Ensemble Model for Predicting Blast-Induced PPV
3.1. Dataset Description
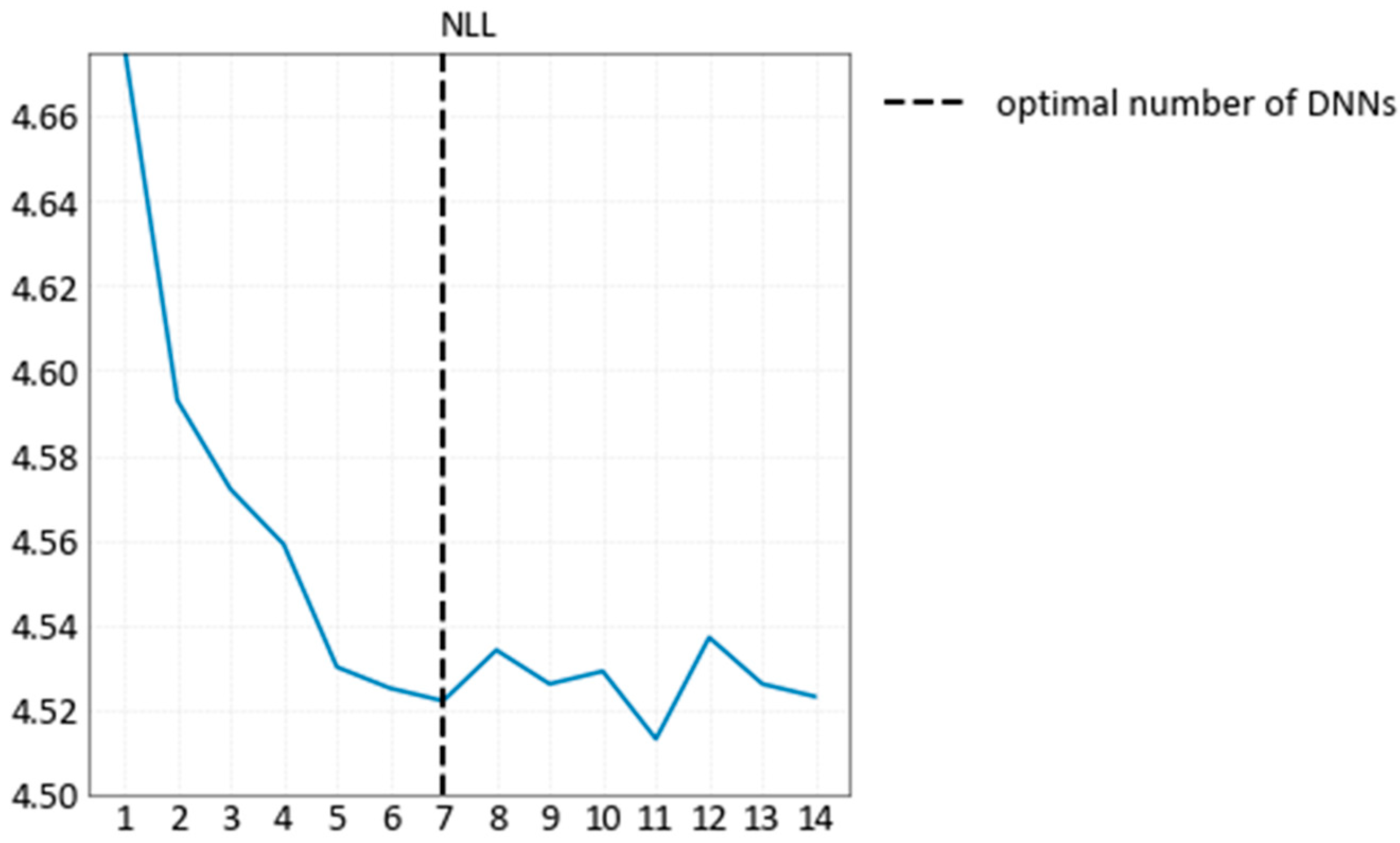
3.2. Deep Ensemble Training Procedure
4. Results and Discussion
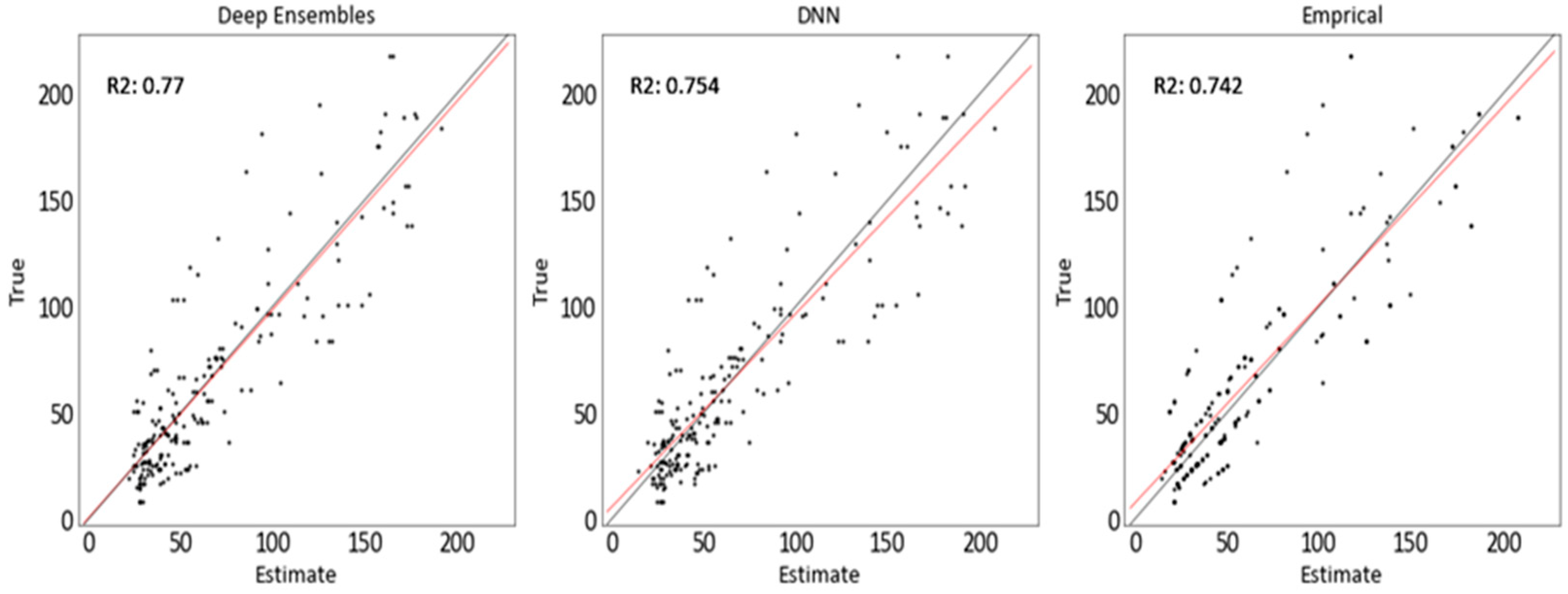
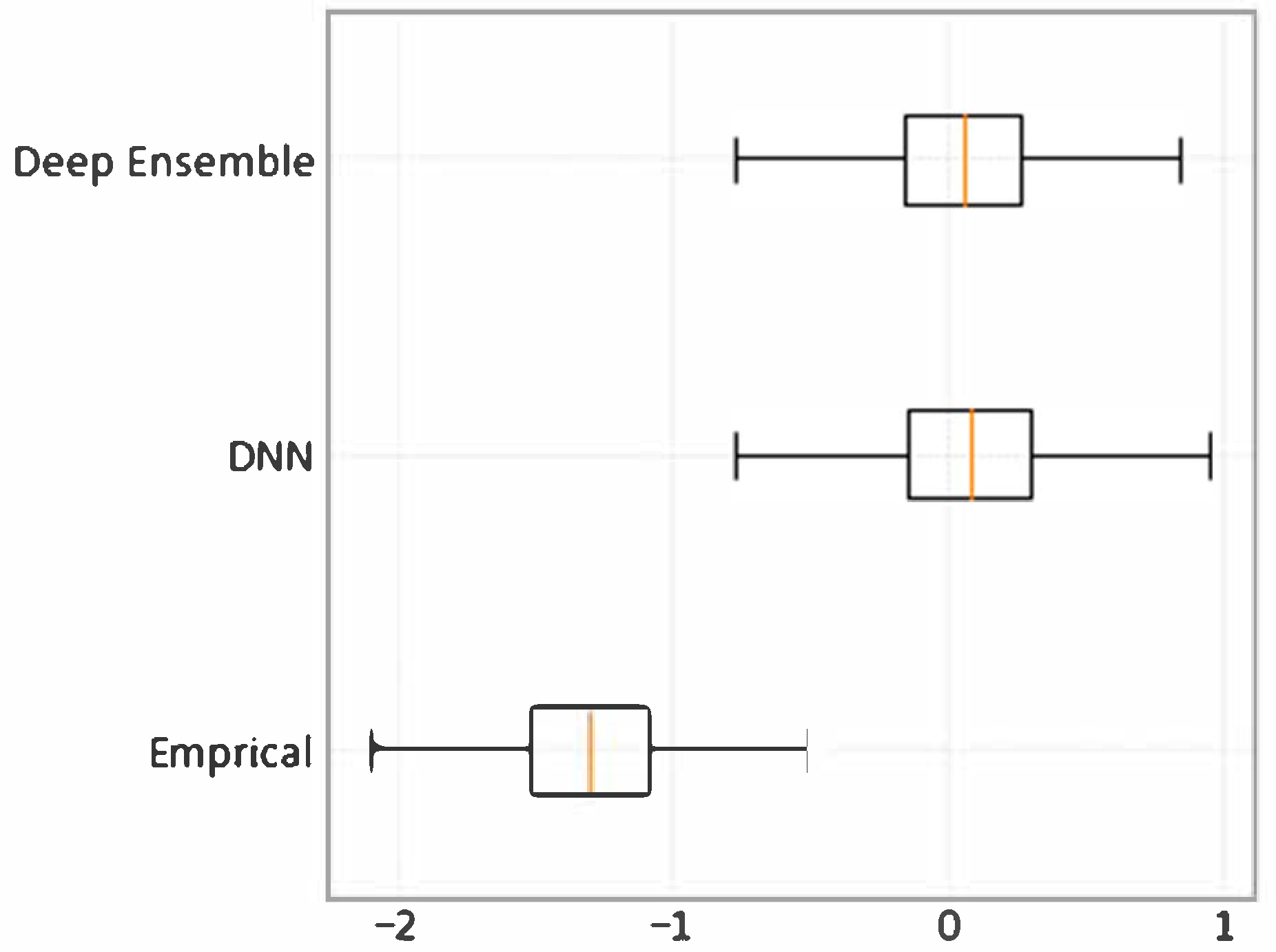
4.1. Model Verification and Evaluation
4.2. Evaluating the Developed PPV Predictive Models
5. Conclusions
- A deep ensemble model was developed that accurately estimates blast-induced PPV across diverse geological settings, demonstrating consistency and generalizability.
- Uncertainty quantification was successfully integrated into the modeling framework, achieving a 95% PICP and providing well-calibrated uncertainty estimates to support informed decision-making in blasting operations.
- The proposed deep ensemble approach was shown to outperform both the USBM equation and a single DNN model in terms of accuracy and uncertainty representation.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Acronym | Full Form | First Appearance (Page) |
|---|---|---|
| SC | Soft computing | p. 2 |
| PPV | Peak Particle Velocity | p. 2 |
| D | Distance from the blasting site | p. 2 |
| W | Charge weight per delay | p. 3 |
| ML | Machine learning | p. 3 |
| ABC | Artificial Bee Colony | p. 3 |
| ANN | Artificial Neural Networks | p. 3 |
| AN-FIS | Adaptive Neural Network Based on The Fuzzy Inference System | p. 3 |
| CART | Classification and Regression Tree | p. 3 |
| EO | Earthworm Optimization | p. 3 |
| FA | Firefly Algorithm | p. 3 |
| FCM | Fuzzy C-Means Clustering | p. 3 |
| FFA | Firefly Algorithm | p. 3 |
| FS | Feature Selection | p. 3 |
| GA | Genetic Algorithm | p. 3 |
| HHO | Harris Hawks Optimization | p. 3 |
| HKM | Hierarchical K-Means Clustering | p. 3 |
| ICA | Imperialist Competitive Algorithm | p. 3 |
| KNN | K-Nearest Neighbors | p. 3 |
| MAE | Mean Absolute Error | p. 3 |
| MAPE | Mean Absolute Percentage Error | p. 3 |
| MFA | Modified Firefly Algorithm | p. 3 |
| MR | Multiple Regression | p. 3 |
| PSO | Particle Swarm Optimization | p. 3 |
| DNN | Deep neural network | p. 3 |
| AI | Artificial intelligence | p. 4 |
| MC | Monte Carlo | p. 5 |
| USBM | United States Bureau of Mines | p. 6 |
| MLP | Multi-layer perceptron | p. 6 |
| MSE | The mean square error | p. 7 |
| NLL | Negative log-likelihood | p. 7 |
| GPS | Global positioning service | p. 10 |
| ANFO | Ammonium nitrate fuel oil | p. 10 |
| RMSE | Root mean of squared error | p. 12 |
| PI | Prediction intervals | p. 12 |
| PICP | Prediction interval coverage probability | p. 13 |
| MPIW | Mean prediction interval width | p. 13 |
References
- Uyar, G.G.; Aksoy, C.O. Comparative Review and Interpretation of the Conventional and New Methods in Blast Vibration Analyses. Geomech. Eng. 2019, 18, 545–554. [Google Scholar] [CrossRef]
- Bui, X.-N.; Nguyen, H.; Tran, Q.-H.; Nguyen, D.-A.; Bui, H.-B. Predicting Ground Vibrations Due to Mine Blasting Using a Novel Artificial Neural Network-Based Cuckoo Search Optimization. Nat. Resour. Res. 2021, 30, 2663–2685. [Google Scholar] [CrossRef]
- Murlidhar, B.R.; Kumar, D.; Jahed Armaghani, D.; Mohamad, E.T.; Roy, B.; Pham, B.T. A Novel Intelligent ELM-BBO Technique for Predicting Distance of Mine Blasting-Induced Flyrock. Nat. Resour. Res. 2020, 29, 4103–4120. [Google Scholar] [CrossRef]
- Ak, H.; Iphar, M.; Yavuz, M.; Konuk, A. Evaluation of Ground Vibration Effect of Blasting Operations in a Magnesite Mine. Soil. Dyn. Earthq. Eng. 2009, 29, 669–676. [Google Scholar] [CrossRef]
- Armaghani, D.J.; Momeni, E.; Abad, S.V.A.N.K.; Khandelwal, M. Feasibility of ANFIS Model for Prediction of Ground Vibrations Resulting from Quarry Blasting. Environ. Earth Sci. 2015, 74, 2845–2860. [Google Scholar] [CrossRef]
- Dindarloo, S.R. Peak Particle Velocity Prediction Using Support Vector Machines: A Surface Blasting Case Study. J. South. Afr. Inst. Min. Metall. 2015, 115, 637–643. [Google Scholar] [CrossRef]
- Khandelwal, M.; Armaghani, D.J.; Faradonbeh, R.S.; Yellishetty, M.; Majid, M.Z.A.; Monjezi, M. Classification and Regression Tree Technique in Estimating Peak Particle Velocity Caused by Blasting. Eng. Comput. 2017, 33, 45–53. [Google Scholar] [CrossRef]
- Haghnejad, A.; Ahangari, K.; Moarefvand, P.; Goshtasbi, K. Numerical Investigation of the Impact of Geological Discontinuities on the Propagation of Ground Vibrations. Geomech. Eng. 2018, 14, 545–552. [Google Scholar] [CrossRef]
- Singh, T.N.; Singh, V. An Intelligent Approach to Prediction and Controlground Vibration in Mines. Geotech. Geol. Eng. 2005, 23, 249–262. [Google Scholar] [CrossRef]
- Duvall, W.I.; Fogelson, D.E. Review of Criteria for Estimating Damage to Residences from Blasting Vibrations; Bureau of Mines: College Park, MD, USA, 1962. [Google Scholar]
- Ambraseys, N.H.A. Dynamic Behaviour of Rock Masses; John Wiley and Sons: Hoboken, NJ, USA, 1968. [Google Scholar]
- Langefors, U.K.B. The Modern Techniques of Rock Blasting; John Wiely and Sons Inc.: New York, NY, USA, 1978. [Google Scholar]
- Ghosh, A.; Daemen, J.K. A Simple New Blast Vibration Predictor of Ground Vibrations Induced Predictor. In Proceedings of the 24th U.S. Symposium on Rock Mechanics (USRMS), College Station, TX, USA, 20–23 June 1983. [Google Scholar]
- Roy, P.P. Vibration Control in an Opencast Mine Based on Improved Blast Vibration Predictors. Min. Sci. Technol. 1991, 12, 157–165. [Google Scholar] [CrossRef]
- Ak, H.; Konuk, A. The Effect of Discontinuity Frequency on Ground Vibrations Produced from Bench Blasting: A Case Study. Soil. Dyn. Earthq. Eng. 2008, 28, 686–694. [Google Scholar] [CrossRef]
- Simangunsong, G.M.; Wahyudi, S. Effect of Bedding Plane on Prediction Blast-Induced Ground Vibration in Open Pit Coal Mines. Int. J. Rock Mech. Min. Sci. 2015, 79, 1–8. [Google Scholar] [CrossRef]
- Iphar, M.; Yavuz, M.; Ak, H. Prediction of Ground Vibrations Resulting from the Blasting Operations in an Open-Pit Mine by Adaptive Neuro-Fuzzy Inference System. Environ. Geol. 2008, 56, 97–107. [Google Scholar] [CrossRef]
- Mohamadnejad, M.; Gholami, R.; Ataei, M. Comparison of Intelligence Science Techniques and Empirical Methods for Prediction of Blasting Vibrations. Tunn. Undergr. Space Technol. 2012, 28, 238–244. [Google Scholar] [CrossRef]
- Monjezi, M.; Ghafurikalajahi, M.; Bahrami, A. Prediction of Blast-Induced Ground Vibration Using Artificial Neural Networks. Tunn. Undergr. Space Technol. 2011, 26, 46–50. [Google Scholar] [CrossRef]
- Khandelwal, M. Evaluation and Prediction of Blast-Induced Ground Vibration Using Support Vector Machine. Int. J. Rock Mech. Min. Sci. 2010, 47, 509–516. [Google Scholar] [CrossRef]
- Saadat, M.; Khandelwal, M.; Monjezi, M. An ANN-Based Approach to Predict Blast-Induced Ground Vibration of Gol-E-Gohar Iron Ore Mine, Iran. J. Rock Mech. Geotech. Eng. 2014, 6, 67–76. [Google Scholar] [CrossRef]
- Hajihassani, M.; Jahed Armaghani, D.; Marto, A.; Tonnizam Mohamad, E. Ground Vibration Prediction in Quarry Blasting through an Artificial Neural Network Optimized by Imperialist Competitive Algorithm. Bull. Eng. Geol. Environ. 2015, 74, 873–886. [Google Scholar] [CrossRef]
- Amiri, M.; Bakhshandeh Amnieh, H.; Hasanipanah, M.; Mohammad Khanli, L. A New Combination of Artificial Neural Network and K-Nearest Neighbors Models to Predict Blast-Induced Ground Vibration and Air-Overpressure. Eng. Comput. 2016, 32, 631–644. [Google Scholar] [CrossRef]
- Azimi, Y.; Khoshrou, S.H.; Osanloo, M. Prediction of Blast Induced Ground Vibration (BIGV) of Quarry Mining Using Hybrid Genetic Algorithm Optimized Artificial Neural Network. Measurement 2019, 147, 106874. [Google Scholar] [CrossRef]
- Taheri, K.; Hasanipanah, M.; Golzar, S.B.; Majid, M.Z.A. A Hybrid Artificial Bee Colony Algorithm-Artificial Neural Network for Forecasting the Blast-Produced Ground Vibration. Eng. Comput. 2017, 33, 689–700. [Google Scholar] [CrossRef]
- Shang, Y.; Nguyen, H.; Bui, X.-N.; Tran, Q.-H.; Moayedi, H. A Novel Artificial Intelligence Approach to Predict Blast-Induced Ground Vibration in Open-Pit Mines Based on the Firefly Algorithm and Artificial Neural Network. Nat. Resour. Res. 2020, 29, 723–737. [Google Scholar] [CrossRef]
- Bayat, P.; Monjezi, M.; Rezakhah, M.; Armaghani, D.J. Artificial Neural Network and Firefly Algorithm for Estimation and Minimization of Ground Vibration Induced by Blasting in a Mine. Nat. Resour. Res. 2020, 29, 4121–4132. [Google Scholar] [CrossRef]
- Nguyen, H.; Drebenstedt, C.; Bui, X.-N.; Bui, D.T. Prediction of Blast-Induced Ground Vibration in an Open-Pit Mine by a Novel Hybrid Model Based on Clustering and Artificial Neural Network. Nat. Resour. Res. 2020, 29, 691–709. [Google Scholar] [CrossRef]
- Fişne, A.; Kuzu, C.; Hüdaverdi, T. Prediction of Environmental Impacts of Quarry Blasting Operation Using Fuzzy Logic. Environ. Monit. Assess. 2011, 174, 461–470. [Google Scholar] [CrossRef]
- Ghasemi, E.; Ataei, M.; Hashemolhosseini, H. Development of a Fuzzy Model for Predicting Ground Vibration Caused by Rock Blasting in Surface Mining. J. Vib. Control 2013, 19, 755–770. [Google Scholar] [CrossRef]
- Hasanipanah, M.; Faradonbeh, R.S.; Amnieh, H.B.; Armaghani, D.J.; Monjezi, M. Forecasting Blast-Induced Ground Vibration Developing a CART Model. Eng. Comput. 2017, 33, 307–316. [Google Scholar] [CrossRef]
- Bui, X.-N.; Jaroonpattanapong, P.; Nguyen, H.; Tran, Q.-H.; Long, N.Q. A Novel Hybrid Model for Predicting Blast-Induced Ground Vibration Based on k-Nearest Neighbors and Particle Swarm Optimization. Sci. Rep. 2019, 9, 13971. [Google Scholar] [CrossRef]
- Yu, Z.; Shi, X.; Zhou, J.; Chen, X.; Qiu, X. Effective Assessment of Blast-Induced Ground Vibration Using an Optimized Random Forest Model Based on a Harris Hawks Optimization Algorithm. Appl. Sci. 2020, 10, 1403. [Google Scholar] [CrossRef]
- Zhou, J.; Asteris, P.G.; Armaghani, D.J.; Pham, B.T. Prediction of Ground Vibration Induced by Blasting Operations through the Use of the Bayesian Network and Random Forest Models. Soil. Dyn. Earthq. Eng. 2020, 139, 106390. [Google Scholar] [CrossRef]
- Hasanipanah, M.; Monjezi, M.; Shahnazar, A.; Jahed Armaghani, D.; Farazmand, A. Feasibility of Indirect Determination of Blast Induced Ground Vibration Based on Support Vector Machine. Measurement 2015, 75, 289–297. [Google Scholar] [CrossRef]
- Sheykhi, H.; Bagherpour, R.; Ghasemi, E.; Kalhori, H. Forecasting Ground Vibration Due to Rock Blasting: A Hybrid Intelligent Approach Using Support Vector Regression and Fuzzy C-Means Clustering. Eng. Comput. 2018, 34, 357–365. [Google Scholar] [CrossRef]
- Chen, W.; Hasanipanah, M.; Nikafshan Rad, H.; Jahed Armaghani, D.; Tahir, M.M. A New Design of Evolutionary Hybrid Optimization of SVR Model in Predicting the Blast-Induced Ground Vibration. Eng. Comput. 2021, 37, 1455–1471. [Google Scholar] [CrossRef]
- Ding, Z.; Nguyen, H.; Bui, X.-N.; Zhou, J.; Moayedi, H. Computational Intelligence Model for Estimating Intensity of Blast-Induced Ground Vibration in a Mine Based on Imperialist Competitive and Extreme Gradient Boosting Algorithms. Nat. Resour. Res. 2020, 29, 751–769. [Google Scholar] [CrossRef]
- Zhang, X.; Nguyen, H.; Bui, X.-N.; Tran, Q.-H.; Nguyen, D.-A.; Bui, D.T.; Moayedi, H. Novel Soft Computing Model for Predicting Blast-Induced Ground Vibration in Open-Pit Mines Based on Particle Swarm Optimization and XGBoost. Nat. Resour. Res. 2020, 29, 711–721. [Google Scholar] [CrossRef]
- Nguyen, H.; Bui, X.-N.; Bui, H.-B.; Cuong, D.T. Developing an XGBoost Model to Predict Blast-Induced Peak Particle Velocity in an Open-Pit Mine: A Case Study. Acta Geophys. 2019, 67, 477–490. [Google Scholar] [CrossRef]
- Nguyen, H.; Choi, Y.; Monjezi, M.; Van Thieu, N.; Tran, T.-T. Predicting Different Components of Blast-Induced Ground Vibration Using Earthworm Optimisation-Based Adaptive Neuro-Fuzzy Inference System. Int. J. Min. Reclam. Environ. 2024, 38, 99–126. [Google Scholar] [CrossRef]
- Dumakor-Dupey, N.K.; Arya, S.; Jha, A. Advances in Blast-Induced Impact Prediction—A Review of Machine Learning Applications. Minerals 2021, 11, 601. [Google Scholar] [CrossRef]
- Zhu, C.; Xu, Y.; Wu, Y.; He, M.; Zhu, C.; Meng, Q.; Lin, Y. A Hybrid Artificial Bee Colony Algorithm and Support Vector Machine for Predicting Blast-Induced Ground Vibration. Earthq. Eng. Eng. Vib. 2022, 21, 861–876. [Google Scholar] [CrossRef]
- Yu, Z.; Shi, X.; Zhou, J.; Gou, Y.; Huo, X.; Zhang, J.; Armaghani, D.J. A New Multikernel Relevance Vector Machine Based on the HPSOGWO Algorithm for Predicting and Controlling Blast-Induced Ground Vibration. Eng. Comput. 2022, 38, 1905–1920. [Google Scholar] [CrossRef]
- Yuan, H.; Zou, Y.; Li, H.; Ji, S.; Gu, Z.; He, L.; Hu, R. Assessment of Peak Particle Velocity of Blast Vibration Using Hybrid Soft Computing Approaches. J. Comput. Des. Eng. 2025, 12, 154–176. [Google Scholar] [CrossRef]
- Nguyen, H.; Bui, X.-N.; Topal, E. Enhancing Predictions of Blast-Induced Ground Vibration in Open-Pit Mines: Comparing Swarm-Based Optimization Algorithms to Optimize Self-Organizing Neural Networks. Int. J. Coal Geol. 2023, 275, 104294. [Google Scholar] [CrossRef]
- Qiu, Y.; Zhou, J.; Khandelwal, M.; Yang, H.; Yang, P.; Li, C. Performance Evaluation of Hybrid WOA-XGBoost, GWO-XGBoost and BO-XGBoost Models to Predict Blast-Induced Ground Vibration. Eng. Comput. 2022, 38, 4145–4162. [Google Scholar] [CrossRef]
- Abdar, M.; Pourpanah, F.; Hussain, S.; Rezazadegan, D.; Liu, L.; Ghavamzadeh, M.; Fieguth, P.; Cao, X.; Khosravi, A.; Acharya, U.R.; et al. A Review of Uncertainty Quantification in Deep Learning: Techniques, Applications and Challenges. Inf. Fusion. 2021, 76, 243–297. [Google Scholar] [CrossRef]
- Dorjsembe, U.; Lee, J.H.; Choi, B.; Song, J.W. Sparsity Increases Uncertainty Estimation in Deep Ensemble. Computers 2021, 10, 54. [Google Scholar] [CrossRef]
- Gawlikowski, J.; Tassi, C.R.N.; Ali, M.; Lee, J.; Humt, M.; Feng, J.; Kruspe, A.; Triebel, R.; Jung, P.; Roscher, R.; et al. A Survey of Uncertainty in Deep Neural Networks. Artif. Intell. Rev. 2023, 56, 1513–1589. [Google Scholar] [CrossRef]
- Gal, Y.; Ghahramani, Z. Dropout as a Bayesian Approximation: Representing Model Uncertainty in Deep Learning. In Proceedings of the 33rd International Conference on Machine Learning, PMLR, New York, NY, USA, 19–24 June 2016. [Google Scholar]
- Lang, N.; Kalischek, N.; Armston, J.; Schindler, K.; Dubayah, R.; Wegner, J.D. Global Canopy Height Regression and Uncertainty Estimation from GEDI LIDAR Waveforms with Deep Ensembles. Remote Sens. Environ. 2022, 268, 112760. [Google Scholar] [CrossRef]
- IS-6922; Criteria for Safety and Design of Structures Subjected to under Ground Blast. Bureau of Indian Standards: New Delhi, India, 1973.
- Rodríguez, R.; de Marina, L.G.; Bascompta, M.; Lombardía, C. Determination of the Ground Vibration Attenuation Law from a Single Blast: A Particular Case of Trench Blasting. J. Rock Mech. Geotech. Eng. 2021, 13, 1182–1192. [Google Scholar] [CrossRef]
- Trippi, R.R.; Turban, E. Neural Networks in Finance and Investing: Using Artificial Intelligence to Improve Real World Performance; McGraw-Hill, Inc.: Chicago, IL, USA, 1992; ISBN 978-1-55738-452-2. [Google Scholar]
- Cheng, B.; Titterington, D.M. Neural Networks: A Review from a Statistical Perspective. Statist. Sci. 1994, 9, 2–30. [Google Scholar] [CrossRef]
- Haykin, S. Neural Networks and Learning Machines; Pearson Education: Chennai, India, 2009. [Google Scholar]
- Kanevski, M.; Timonin, V.; Pozdnukhov, A. Machine Learning for Spatial Environmental Data: Theory, Applications, and Software; EPFL Press: New York, NY, USA, 2009; ISBN 978-0-429-14781-4. [Google Scholar]
- Lakshminarayanan, B.; Pritzel, A.; Blundell, C. Simple and Scalable Predictive Uncertainty Estimation Using Deep Ensembles. In Proceedings of the Advances in Neural Information Processing Systems; Curran Associates, Inc.: Red Hook, NY, USA, 2017; Volume 30. [Google Scholar]
- Hammed, O.S.; Popoola, O.I.; Adetoyinbo, A.A.; Awoyemi, M.O.; Adagunodo, T.A.; Olubosede, O.; Bello, A.K. Peak Particle Velocity Data Acquisition for Monitoring Blast Induced Earthquakes in Quarry Sites. Data Brief. 2018, 19, 398–408. [Google Scholar] [CrossRef]
- Pearce, T.; Brintrup, A.; Zaki, M.; Neely, A. High-Quality Prediction Intervals for Deep Learning: A Distribution-Free, Ensembled Approach. In Proceedings of the 35th International Conference on Machine Learning, PMLR, Stockholm, Sweden, 10–15 July 2018; pp. 4075–4084. [Google Scholar]
- Papadopoulos, G.; Edwards, P.J.; Murray, A.F. Confidence Estimation Methods for Neural Networks: A Practical Comparison. IEEE Trans. Neural Netw. 2001, 12, 1278–1287. [Google Scholar] [CrossRef] [PubMed]
- Khosravi, A.; Nahavandi, S.; Creighton, D.; Atiya, A.F. Comprehensive Review of Neural Network-Based Prediction Intervals and New Advances. IEEE Trans. Neural Netw. 2011, 22, 1341–1356. [Google Scholar] [CrossRef] [PubMed]
- Zhu, X.; Vondrick, C.; Fowlkes, C.C.; Ramanan, D. Do We Need More Training Data? Int. J. Comput. Vis. 2016, 119, 76–92. [Google Scholar] [CrossRef]
- Kraus, M.; Feuerriegel, S.; Oztekin, A. Deep Learning in Business Analytics and Operations Research: Models, Applications and Managerial Implications. Eur. J. Oper. Res. 2020, 281, 628–641. [Google Scholar] [CrossRef]



| References | Dataset | Method | Location | Results |
|---|---|---|---|---|
| Khandelwal, 2010 [20] | 174 blast vibration records | SVM | Jayant opencast mine of Northern Coalfields Limited (NCL) | R2 0.960 |
| Saadat et al., 2014 [21] | 69 blasting operations | ANN | Gol-E-Gohar (GEG) iron mine, Iran | R2 of 0.957, and MSE of 0.000722 |
| Hajihassani et al., 2015 [22] | 95 blasting operations | ANN-ICA | Harapan Ramai granite quarry in Johor, Malaysia | R2 of 0.856 |
| Amiri et al., 2016 [23] | 75 blasting operations | ANN-KNN | Shur river dam, Iran | R2 of 0.95, and RMSE of 1.7 |
| Azimi et al., 2019 [24] | 70 blast vibration events | GA-ANN | Sungun Copper Mine site in Iran | R2 of 0.98, MAPE of 60.01, and RMSE of 3.0471 |
| Taheri et al., 2017 [25] | 89 blasting events | ABC-ANN | Miduk copper mine, Iran | R2 of 0.95 |
| Shang et al., 2020 [26] | 83 blasting events | FA-ANN | Tan Dong Hiep quarry mine, Vietnam | RMSE of 0.464, MAE of 0.356, and R2 of 0.966 |
| Bayat et al., 2020 [27] | 154 blasting events | ANN optimized by FA | Hozak limestone mine, Alborz state, Iran | R2 of 0.977 |
| Nguyen et al., 2020 [28] | 85 blasting events | HKM–ANN | North of Vietnam | RMSE of 0.554, and R2 of 0.983 |
| Fişne et al., 2011 [29] | 33 blast events | Fuzzy logic approach | Akdaglar Quarry, İstanbul, Türkiye | RMSE of 5.31. |
| Ghasemi et al., 2013 [30] | 120 blast events | Fuzzy logic model | Sarcheshmeh copper mine, Iran | R2 of 94.59, RMSE of 2.73, and MAPE of 23.25 |
| Hasanipanah et al., 2017 [31] | 86 blasting events | CART, MR | Miduk copper mine, Iran | R2 of 0.95, and RMSE of 0.17 |
| Bui et al., 2019 [32] | 152 blasting events | PSO-KNN | Deo Nai open-pit coal mine, North of Vietnam | RMSE of 0.797, R2 of 0.977, and MAE of 0.385 |
| Yu et al., 2020 [33] | 137 blasting events | HHO-RF | Tonglvshan open-cast mine, China | R2 of 0.94, MAE of 0.29, and RMSE of 0.34 |
| Zhou et al., 2020 [34] | 102 blasting operations | FS-RF | A blasting mine | R2 of 90.32 |
| Hasanipanah et al., 2015 [35] | 80 blasting operations | SVM | Bakhtiari Dam, Iran | R2 of 0.96 |
| Sheykhi et al., 2018 [36] | 120 blast events | FCM–SVR | Sarcheshmeh copper mine, Iran | R2 of 0.853, and RMSE of 1.80 |
| Chen et al., 2021 [37] | 95 blasting operations | MFA–SVR | Harapan Ramai granite quarry, Johor, Malaysia | R2 of 0.984, and RMSE of 0.614 |
| Ding et al., 2020 [38] | 136 blasting events | XGBoost optimized by ICA | Nui Beo openpit coal mine, Vietnam | RMSE of 0.736, R2 of 0.988, and MAE of 0.527 |
| Zhang et al., 2020 [39] | 175 blasting operations | PSO-XGBoost | Mine quarry in Vietnam | RMSE of 0.583, R2 of 0.968, and MAE of 0.346 |
| Nguyen et al., 2019 [40] | 146 blasting events | XGBoost | Deo Nai open-pit coal mine in Vietnam | RMSE of 1.742, and R2 of 0.952 |
| Nguyen et al., 2024 [41] | 200 blasting events | EO-ANFIS | 10 quarries in Nigeria | RMSE of 2.816, MAPE of 0.398, and R2 of 0.746 |
| D (m) | W (kg) | PPV (mm/s) | |
| mean | 775 | 1517.63 | 64.17 |
| std | 289.03 | 353.89 | 48.75 |
| min | 300 | 650 | 8 |
| 25% | 537.5 | 1250 | 28.14 |
| 50% | 775 | 1500 | 46.94 |
| 75% | 1012.5 | 1800 | 83.89 |
| max | 1250 | 2950 | 247.53 |
| Empirical | DNN | Deep Ensemble | |
| RMSE | 24.67 | 23.566 0.084 | 22.674 0.056 |
| 0.742 | 0.754 0.021 | 0.77 0.018 | |
| NLL | 100.68 | 4.596 0.148 | 4.44 0.092 |
| PICP | 0.91 | 0.9 0.036 | 0.95 0.021 |
| MPIW | 2.199 | 1.779 0.197 | 1.769 0.085 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bozkurt Keser, S.; Yavuz, M.; Erten, G.E. Advancing the Prediction and Evaluation of Blast-Induced Ground Vibration Using Deep Ensemble Learning with Uncertainty Assessment. Geosciences 2025, 15, 182. https://doi.org/10.3390/geosciences15050182
Bozkurt Keser S, Yavuz M, Erten GE. Advancing the Prediction and Evaluation of Blast-Induced Ground Vibration Using Deep Ensemble Learning with Uncertainty Assessment. Geosciences. 2025; 15(5):182. https://doi.org/10.3390/geosciences15050182
Chicago/Turabian StyleBozkurt Keser, Sinem, Mahmut Yavuz, and Gamze Erdogan Erten. 2025. "Advancing the Prediction and Evaluation of Blast-Induced Ground Vibration Using Deep Ensemble Learning with Uncertainty Assessment" Geosciences 15, no. 5: 182. https://doi.org/10.3390/geosciences15050182
APA StyleBozkurt Keser, S., Yavuz, M., & Erten, G. E. (2025). Advancing the Prediction and Evaluation of Blast-Induced Ground Vibration Using Deep Ensemble Learning with Uncertainty Assessment. Geosciences, 15(5), 182. https://doi.org/10.3390/geosciences15050182






