Application of LiDAR Differentiation and a Modified Savage–Hutter Model to Analyze Co-Seismic Landslides: A Case Study of the 2024 Noto Earthquake, Japan
Abstract
1. Introduction
1.1. Background
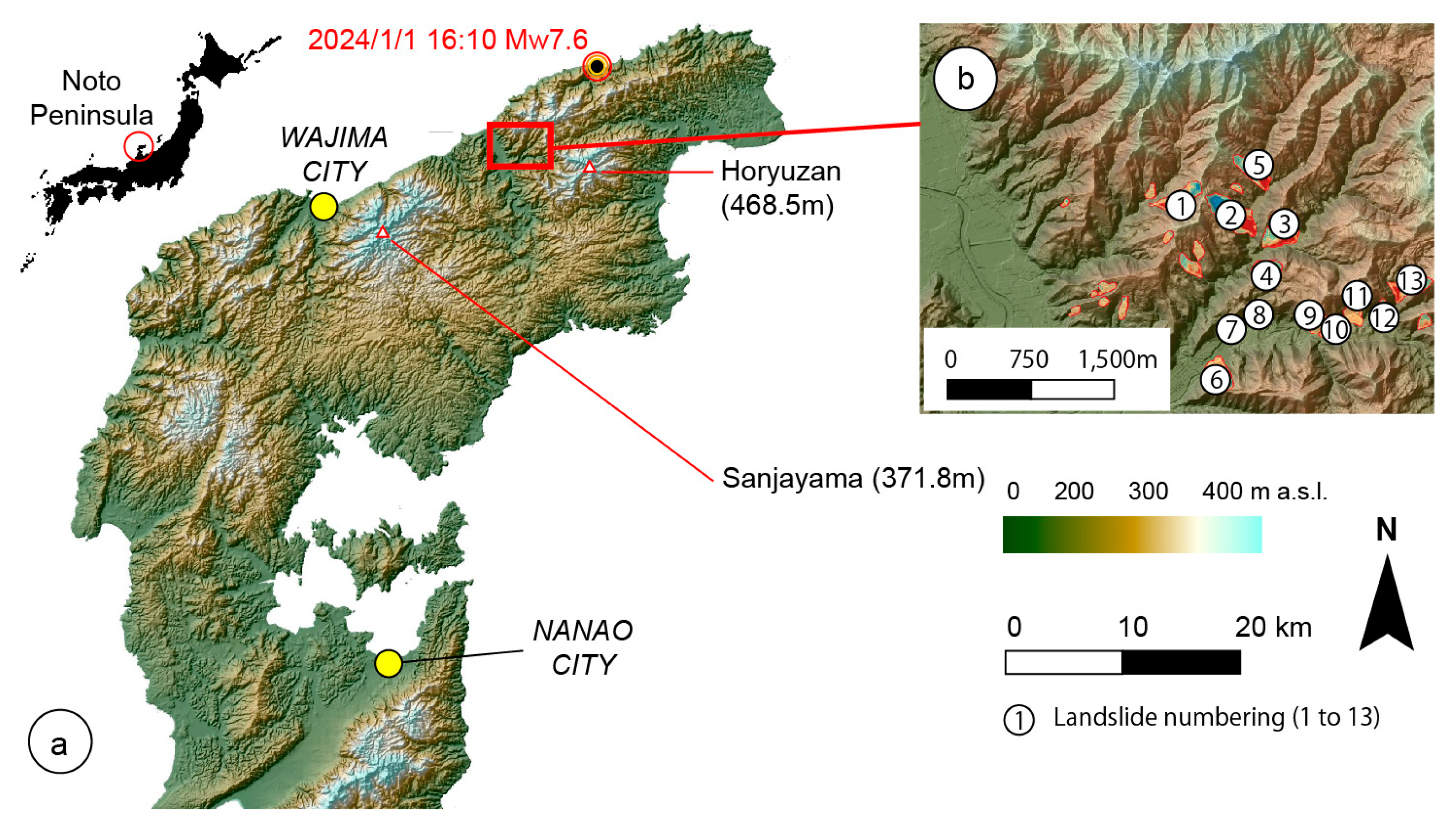
1.2. Research Location
2. Materials and Methods
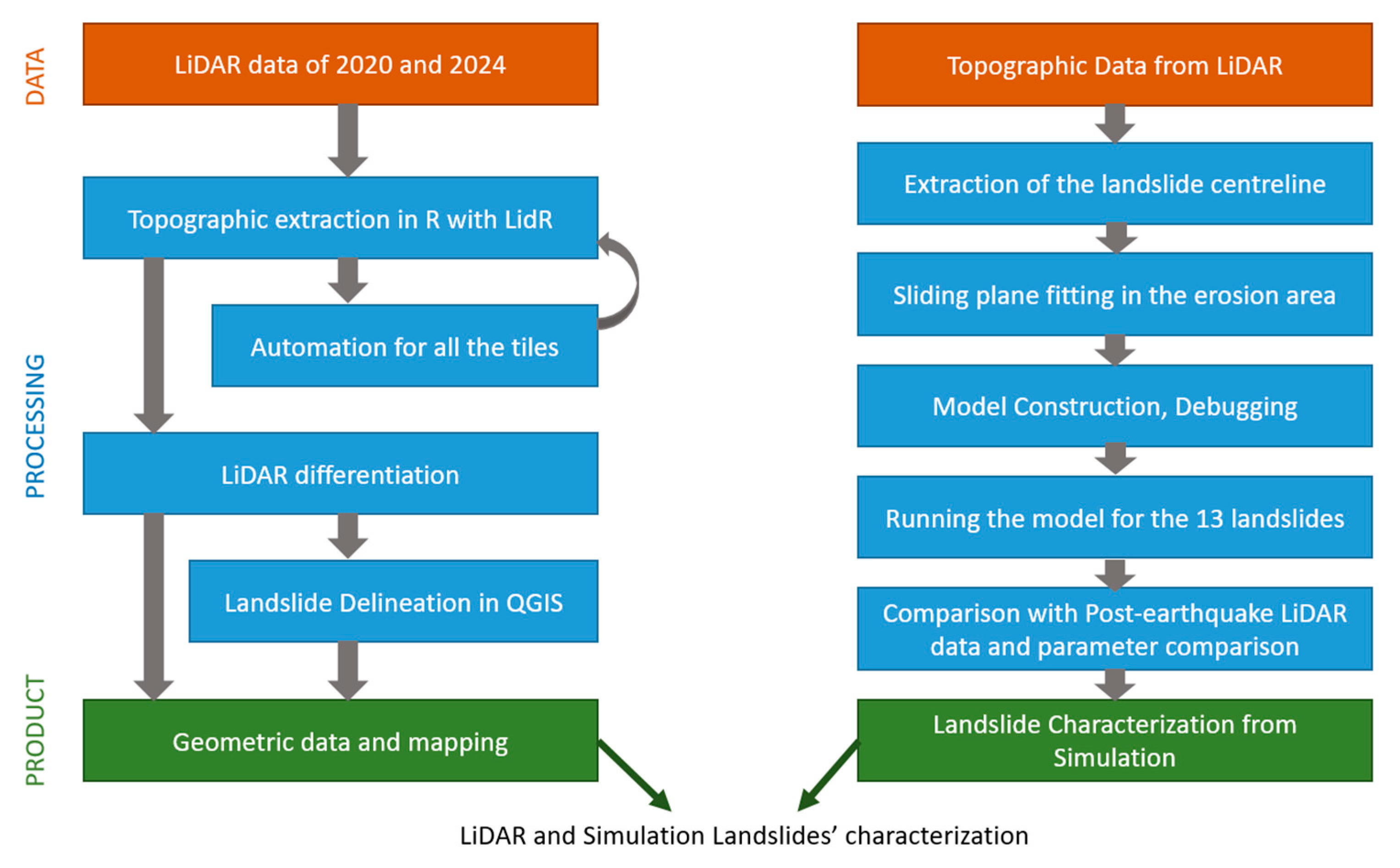
2.1. Pre- and Post-Earthquake LiDAR Analysis and Landslide Morphology Retrieval
2.2. Simulation Model
3. Results
3.1. Erosion and Deposition Analysis from LiDAR Differentiation
3.2. Simplified Savage–Hutter Landslides’ Simulations
4. Discussion
4.1. Main Findings
4.2. Implications for Methodological Developments
4.3. Implication for Hazard and Disaster Risk Reduction
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Newmark, N.M. Effects of earthquakes on dams and embankments. Geotechnique 1965, 15, 139–160. [Google Scholar] [CrossRef]
- Jibson, R.W.; Harp, E.L.; Michael, J.A. A method for producing digital probabilistic seismic landslide hazard maps. Eng. Geol. 2000, 58, 271–289. [Google Scholar] [CrossRef]
- Jibson, R.W. Regression models for estimating coseismic landslide displacement. Eng. Geol. 2007, 91, 209–218. [Google Scholar] [CrossRef]
- Moreno, M.; Steger, S.; Tanyas, H.; Lombardo, L. Modeling the area of co-seismic landslides via data-driven models: The Kaikoura example. Eng. Geol. 2023, 320, 107121. [Google Scholar] [CrossRef]
- Saputra, A.; Gomez, C.; Hadmoko, D.S.; Sartohadi, J. Coseismic landslide susceptibility assessment using geographic information system. Geoenviron. Disasters 2016, 3, 27. [Google Scholar] [CrossRef]
- Padrones, J.T.; Ramos, N.T.; Dimalanta, C.B.; Queano, K.L.; Faustino-Eslava, D.V.; Yumul, G.P., Jr.; Watanabe, K. Landslide Susceptibility Mapping in a Geologically Complex Terraine: A Case Study from Northwest Mindoro, Philippines. Manila J. Sci. 2017, 10, 25–44. [Google Scholar]
- Kuo, C.-Y.; Chang, K.-J.; Tsai, P.-W.; Wei, S.-K.; Chen, R.-F.; Dong, J.-J.; Yang, C.-M.; Chan, Y.-C.; Tai, Y.-C. Identification fo co-seismic ground motion due to fracturing and impact of the Tsaoling landslide, Taiwan. Eng. Geol. 2015, 196, 268–279. [Google Scholar] [CrossRef]
- Zhang, Y.; Xiao, Y.; Wang, B.; Tang, W.; Yu, P.; Wang, W.; Xu, P.; Buah, P.A. Directivity effect of the spatial distribution of co-seismic landslides affected by near-fault ground motions. Comput. Geotech. 2024, 170, 106263. [Google Scholar] [CrossRef]
- Ma, N.; Wang, G.; Kamai, T.; Doi, I.; Chigira, M. Amplification of seismic response of a large deep-seated landslide in Tokushima, Japan. Eng. Geol. 2019, 249, 218–234. [Google Scholar] [CrossRef]
- Chandra Pal, S.; Saha, A.; Chowdhuri, I.; Ruidas, D.; Chakrabortty, R.; Roy, P.; Shit, M. Earthquake hotspot and coldspot: Where, why and how? Geosystems Geoenviron. 2023, 2, 100130. [Google Scholar] [CrossRef]
- Zhai, C.; Chang, Z.; Li, S.; Chen, Z.; Xie, L. Quantitative identification of near-fault pulse-like ground motions based on energy. Bull. Seismol. Soc. Am. 2013, 103, 2591–2603. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, G.; Zheng, L.; Li, Y.; Wu, J. Effects of near-fault seismic loadings on run-out of large-scale landslide: A case study. Eng. Geol. 2013, 166, 216–236. [Google Scholar] [CrossRef]
- Hadmoko, D.S.; Lavigne, F.; Sartohadi, J.; Gomez, C.; Daryono, D. Spatio-temporal distribution of landslides in Java and the Triggering Factors. Forum Geogr. 2017, 31, 1–15. [Google Scholar] [CrossRef]
- Du, P.; Li, L.; Kopf, A.; Wang, D.; Chen, K.; Shi, H.; Wang, W.; Pan, X.; Hu, G.; Zhang, P. Earthquake-induced Submarine Landslides (EQISLs) and a comparison with their Terrestrial Counterparts: Insights from a New Database. Earth Sci. Rev. 2024, 261, 104634. [Google Scholar] [CrossRef]
- Zhu, S.; Shi, Y.; Lu, M.; Xie, F.R. Dynamic mechanisms of earthquake-triggered landslides. Sci. China Earth Sci. 2013, 56, 1769–1779. [Google Scholar] [CrossRef]
- Fan, X.; Scaringi, G.; West, A.J.; Westen, C.J.; Tanyas, H.; Hovius, N.; Hales, T.C.; Korup, O.; Zhang, Q.; Evans, S.G.; et al. Rain and small earthquakes maintain a slow-moving landslide in a persistent critical state. Nat. Commun. 2020, 11, 780. [Google Scholar] [CrossRef]
- Meunier, P.; Uchida, T.; Hovius, N. Landslide patterns reveal the sources of large earthquakes. Earth Planet. Sci. Lett. 2013, 363, 27–33. [Google Scholar] [CrossRef]
- Grant, R.R.; Culhane, N.K. Global Pattenrs of coseismic landslide runout mobility differ from aseismic landslide trends. Eng. Geol. 2025, 344, 107824. [Google Scholar] [CrossRef]
- Serva, L.; Vittori, E.; Comerci, V.; Esposito, E.; Guerrieri, L.; Michetti, A.M.; Mohammadiun, B.; Mahammadioun, G.C.; Porfido, S.; Tatevossian, R.E. Earthquake Hazard and the Environmental Seismic Intensity (ESI) Scale. Pure Appl. Geophys. 2016, 173, 1479–1515. [Google Scholar] [CrossRef]
- Ferrario, M.F. Landslides triggered by multiple earthquakes: Insights from the 2018 Lombok (Indonesia) events. Nat. Hazards 2019, 98, 572–592. [Google Scholar] [CrossRef]
- Koukouvelas, I.K.; Piper, D.J.W.; Katsonopoulou, D.; Kontopoulos, N.; Verroios, S.; Nikolakopous, K.; Zygouri, V. Earthquake-triggered landslides and mudflows: Was this the wave that engulfed Ancient Helike. Holocene 2020, 30, 1653–1668. [Google Scholar] [CrossRef]
- Keefer, D.K. Investigating Landslides caused by earthquakes—A historical review. Surv. Geophys. 2002, 23, 473–510. [Google Scholar] [CrossRef]
- Simonett, D.S. Landslide Distribution and Earthquakes in the Bevani and Toricelli mountain, New Guinea—A statistical Analysis. In Landform Studies from Australia and New Guinea; Jennings, J.N., Mabbutt, J.A., Eds.; Cambridge University Press: Cambridge, UK, 1967; pp. 64–84. [Google Scholar]
- You, T.L.; Hoose, S.N. Historical Ground Failures in Northern California Associated with Earthquakes; U.S. Geological Survey Professional Paper; USGS Publications Warehouse: Washington, USA, 1978; p. 993. [Google Scholar]
- Hancox, G.T.; Perrin, N.D.; Dellow, G.D. Earthquake-Induced Landsliding in New Zealand and Implications for MM Intensity and Seismic Hazard Assessment; GNS Client Report; Institute of Geological and Nuclear Sciences Ltd.: Lower Hutt, New Zealand, 1997; p. 43601B. [Google Scholar]
- Reichenbach, P.; Rossi, M.; Malamud, B.D.; Mihir, M.; Guzzetti, F. A review of statistically-based landslide susceptibility models. Earth Sci. Rev. 2018, 180, 60–91. [Google Scholar] [CrossRef]
- Shao, X.; Xu, C. Earthquake-induced landslides susceptibility assessment: A review of the state-of-the-art. Nat. Hazards Res. 2022, 3, 172–182. [Google Scholar] [CrossRef]
- Fan, X.; Yunus, A.P.; Scaringi, G.; Catani, F.; Subramanian, S.S.; Xu, Q.; Huang, R. Rapidly evolving controls of landslides after a strong earthquake and implications for hazard assessments. Geophys. Res. Lett. 2021, 48, e2020GL090509. [Google Scholar] [CrossRef]
- Gomez, C. Point Cloud Technologies for Geomorphologists, From Data Acquisition to Processing; Springer: Dordrecht, Switzerland, 2021. [Google Scholar]
- Gomez, C.; Allouis, T.; Lissak, C.; Hotta, N.; Shinohara, Y.; Hadmoko, D.S.; Vilimek, V.; Wassmer, P.; Lavigne, F.; Setiawan, A.; et al. High-Resolution Point-Cloud for Landslides in the 21st Century: From Data Acquisition to New Processing Concepts. In Understanding and Reducing Landslide Disaster Risk. WLF 2020. ICL Contribution to Landslide Disaster Risk Reduction; Arbanas, Ž., Bobrowsky, P.T., Konagai, K., Sassa, K., Takara, K., Eds.; Springer: Dordrecht, Switzerland, 2021; pp. 199–213. [Google Scholar] [CrossRef]
- Jebur, M.N.; Pradhan, B.; Tehrany, M.S. Optimization of landslide conditioning factors using very high-resolution airborne laser scanning (LiDAR) data at catchment scale. Remote Sens. Environ. 2014, 152, 150–165. [Google Scholar] [CrossRef]
- Gorum, T. Landslide recognition and mapping in a mixed forest environment from airborne LiDAR data. Eng. Geol. 2019, 258, 105155. [Google Scholar] [CrossRef]
- Shi, W.; Deng, S.; Xu, W. Extraction of multi-scale landslide morphological features based on local Gi* using airborne LiDAR-derived DEM. Geomorphology 2018, 303, 229–242. [Google Scholar] [CrossRef]
- Gomez, C.; Hotta, N. Deposits’ Morphology of the 2018 Hokkaido Iburi-Tobu Earthquake Mass Movements from LiDAR & Aerial Photographs. Remote Sens. 2021, 13, 3421. [Google Scholar] [CrossRef]
- Gomez, C. The 1 January 2024 Noto peninsula co-seismic landslides hazards: Preliminary results. AUC Geogr. 2024, 60, 3–10. [Google Scholar] [CrossRef]
- Gomez, C.; Purdie, H. UAV-based Photogrammetry and Geocomputing for Hazards and Disaster Risk Monitoring—A Review. Geoenviron. Disasters 2016, 3, 23. [Google Scholar] [CrossRef]
- Zhang, M.; Gomez, C.; Shinohara, Y.; Hotta, N. Drone LiDAR Occlusion Analysis and Simulation from Retrieved Pathways to Improve Ground Mapping of Forested Environments. Drones 2025, 9, 135. [Google Scholar] [CrossRef]
- Sestras, P.; Badea, G.; Badea, A.C.; Salagean, T.; Oniga, V.-E.; Rosca, S.; Bilasco, S.; Bruma, S.; Spalevic, V.; Kader, S.; et al. A novel method for landslide deformation monitoring by fusing UAV photogrammetry and LiDAR data based on each sensor’s mapping advantage in regards to terrain feature. Eng. Geol. 2025, 346, 107890. [Google Scholar] [CrossRef]
- Zhang, M.; Gomez, C.; Hotta, N.; Daikai, R.; Sawada, S.; Bradak, B. Tele-effect of Geomorphological Change on the Spatial Variability of the Precision of SfM-MVS 3D Point-cloud Models. AUC Geogr. 2025, in press. [Google Scholar] [CrossRef]
- Lin, A.F.; Wotherspoon, L. The use of global versus region-specific data for the prediction of co-seismic landslides. Eng. Geol. 2023, 327, 107335. [Google Scholar] [CrossRef]
- Fan, X.; Scaringi, G.; Korup, O.; Joshua West, A.; van Westen, C.J.; Tanyas, H.; Hovius, N.; Hales, T.C.; Jibson, R.W.; Allstadt, K.E.; et al. Earhtquake-induced chains of geologic hazards: Patterns, mechanisms, and impacts. Rev. Geophys. 2019, 57, 421–503. [Google Scholar] [CrossRef]
- Gallen, S.F.; Clark, M.K.; Godt, J.W.; Roback, K.; Niemi, N.A. Application and evaluation of a rapid response earthquake-triggered landslide model to the 25 April 2015 Mw 7.8 Gorkha earthquake, Nepal. Tectonophysics 2017, 714–715, 173–187. [Google Scholar] [CrossRef]
- Moghaddam, H.; Darbani, M.S.; Sadrara, A.; Hajirasouliha, I. Recommendation of new design spectra for Iran using modified Newmark method. Soil. Dyn. Earthqu Eng. 2023, 176, 108332. [Google Scholar] [CrossRef]
- Xuan, G.; Yue, G.; Wang, Y.; Wang, D. An edge-based smoothed finite element method combined with Newmark method for time domain acoustic wave scattering problem. Eng. Anal. Bound. Elem. 2024, 158, 182–198. [Google Scholar] [CrossRef]
- Ye, S.; Xue, T.; Wang, W. Multi-stage slope displacement analysis based on real-time dynamic Newmark slider method. Soil. Dyn. Earthqu Eng. 2023, 174, 108209. [Google Scholar] [CrossRef]
- Vanneschi, C.; Eyre, M.; Burda, J.; Zizka, L.; Francioni, M.; Cogga, J.S. Investigation of landslide failure mechanisms adjacent to lignite mining operations in North Bohemia (Czech Republic) through a limit equilibrium/finite element modelling approach. Geomorphology 2018, 320, 142–153. [Google Scholar] [CrossRef]
- A, H.; Wang, H.; Xu, W.; Shi, H.; Hou, J. Numerical estimation of river blockage and the whole lifecycle of landslide-generated impulse waves in mountain reservoirs using a hybrid DEM-SPH and SWEs method. Eng. Geol. 2025, 351, 108022. [Google Scholar] [CrossRef]
- Ali, Y.; Gugsa, T.H.; Raghuvanshi, T.K. GIS-based statistical analysis for landslide susceptibility evaluation and zonation mapping: A case from Blue Nile Gorge, Gohatsion-Dejen road corridor, Central Ethiopia. Environ. Challenges 2024, 16, 100968. [Google Scholar] [CrossRef]
- Yang, S.; Tan, J.; Luo, D.; Wang, Y.; Guo, X.; Zhu, Q.; Ma, C.; Xiong, H. Sample size effects on landslide susceptibility models: A comparative study of heuristic, statistical, machine learning, deep learning and ensemble learning models with SHAP analysis. Comput. Geosci. 2024, 193, 105723. [Google Scholar] [CrossRef]
- He, X.; Xu, C.; Qi, W.; Hunag, Y. Contrasting landslides distribution patterns and seismic rupture processes of 2014 Jinggu and Ludian earthquakes, China. Sci. Rep. 2024, 14, 28470. [Google Scholar] [CrossRef]
- Okuwaki, R.; Yagi, Y.; Murakami, A.; Fukahata, Y. A Multiplex Rupture Sequence Under Complex Fault Network Due To Preceding Earthquake Swarms During the 2024 Mw 7.5 Noto Peninsula, Japan, Earthquake. Geophys. Res. Lett. 2024, 51, e2024GL109224. [Google Scholar] [CrossRef]
- Kato, A. Implications of fault-valve behavior from immediate aftershocks following the 2023 Mj6.5 earthquake beneath the Noto Peninsula, central Japan. Geophys. Res. Lett. 2024, 51, e2023GL106444. [Google Scholar] [CrossRef]
- Liu, C.; Bai, Y.; Lay, T.; He, P.; Wen, Y.; Wei, X.; Xiong, N.; Xiong, X. Shallow crustal rupture in a major Mw 7.5 earthquake above a deep crustal seismic swarm along the Noto Peninsula in western Japan. Earth Planet. Sci. Lett. 2025, 648, 119107. [Google Scholar] [CrossRef]
- Malatesta, L.C.; Sueoka, S.; Kataoka, K.S.; Komatsu, T.; Tsukamoto, S.; Bruhat, L.; Olive, J.-A. Geology and Geomorphology of the Jan 1st 2024 Mw 7.6 Noto Peninsula Earthquake: Observations and context. In Proceedings of the EGU General Assembly 2024, Vienna, Austria, 14–19 April 2024. EGU24-15494. [Google Scholar] [CrossRef]
- Ozaki, M. 1:200,000 Geological Map of the Northern Part of the Noto Peninsula; Seamless Geoinformation Series of Japanese Coastal Zones, Northern Coastal Zone of Noto Peninsula; Geological Survey of Japan (GSJ): Tsukuba, Japan, 2010; p. S-1. [Google Scholar]
- Umeda, K.; Ninomiya, A.; Negi, T. Heat source for an amagmatic hydrothermal system, Noto Peninsula, Central Japan. J. Geophys. Res. 2009, 114, B01202. [Google Scholar] [CrossRef]
- Kaseno, Y. Geology of Southern Noto Peninsula, Central Japan, with reference to the Cenozoic history. Sci. Rep. Kanazawa Univ. 1963, 8-2, 541–568. [Google Scholar] [CrossRef]
- Zhang, W.; Qi, J.; Wan, P.; Wang, H.; Xie, D.; Wang, X.; Yan, G. An Easy-to-Use Airborne LiDAR Data Filtering Method based on Cloth Simulation. Remote Sens. 2024, 8, 501. [Google Scholar] [CrossRef]
- Liu, W.; He, S.-M.; OnYang, C.-J. Dynamic process simulation with a Savage–Hutter type model for the intrusion of landslide into river. J. Mount Sci. 2016, 13, 1265–1274. [Google Scholar] [CrossRef]
- Bouchut, F.; Mangeney-Castelnau, A.; Perthame, B.; Vilotte, J.-P. A new model of Saint Venant and Savage–Hutter type for gravity driven shallow water flows. Comptes Rendus Math. 2003, 336, 531–536. [Google Scholar] [CrossRef]
- Fernandez-Nieto, E.D.; Bouchut, F.; Dresch, D.; Castro Diaz, M.J.; Mangeney, A. A new Savage–Hutter type model for submarine avalanches and generated tsunami. J. Comput. Phys. 2008, 16, 7720–7754. [Google Scholar] [CrossRef]
- Gupta, K.; Satyam, N. Co-seismic landslide hazard assessment of Uttarakhand state (India) based on the modified Newmark model. J. Asian Earth Sci. 2022, 8, 100120. [Google Scholar] [CrossRef]
- Tang, Y.; Che, A.; Cao, Y.; Zhang, F. Risk assessment of seismic landslides based on the analysis of historical earthquake disaster characteristics. Bull. Eng. Geol. Environ. 2020, 79, 2271–2284. [Google Scholar] [CrossRef]
- Mreyen, A.-S.; Donati, D.; Elmo, D.; Donze, F.V.; Havenith, H.-B. Dynamic numerical modelling of co-seismic landslides using the 3D distinct element method: Insights from the Balta rockslide (Romania). Eng. Geol. 2022, 307, 106774. [Google Scholar] [CrossRef]
- Zhao, H.; Song, E.-X. A method for predicting co-seismic displacements of slopes for landslide hazard zonation. Soil. Dyn. Earthq. Eng. 2012, 40, 62–77. [Google Scholar] [CrossRef]



| Landslide Number | φ = 20° | φ = 25° | φ = 30° |
|---|---|---|---|
| 1 | 1.21/1.23 | 1.35/1.58 | 1.92/1.96 |
| 2 | 1.06/1.3 | 1.36/1.66 | 1.69/2.06 |
| 3 | 0.93/1.19 | 1.2/1.52 | 1.48/1.88 |
| 4 | 0.64/0.73 | 0.82/0.93 | 1.02/1.16 |
| 5 | 0.99/1.16 | 1.27/1.48 | 1.58/1.84 |
| 6 | 0.83/0.97 | 1.06/1.24 | 1.31/1.53 |
| 7 | 0.71/0.79 | 0.91/1.01 | 1.12/1.25 |
| 8 | 0.55/0.6 | 0.71/0.77 | 0.88/0.96 |
| 9 | 0.44/0.48 | 0.56/0.62 | 0.69/0.76 |
| 10 | 0.54/0.6 | 0.69/0.77 | 0.85/0.95 |
| 11 | 0.76/0.86 | 0.97/1.1 | 1.2/1.36 |
| 12 | 0.62/0.68 | 0.79/0.88 | 0.98/1.09 |
| 13 | 1.03/1.22 | 1.32/1.56 | 1.64/1.93 |
| Landslide Number | Prior-Earthquake | Post-Earthquake |
|---|---|---|
| 1 | 25.5 | 28.5 |
| 2 | 25 | 27.5 |
| 3 | 23.5 | 28 |
| 4 | 29.8 | 28.8 |
| 5 | 26.8 | 28.1 |
| 6 | 20 | 25 |
| 7 | 22.8 | 27.7 |
| 8 | 18 | 271 |
| 9 | 18.1 | 29.5 |
| 10 | 24 | 29.7 |
| 11 | 25.5 | 30.2 |
| 12 | 24.6 | 27.6 |
| 13 | 27.8 | 28.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gomez, C.; Hadmoko, D.S. Application of LiDAR Differentiation and a Modified Savage–Hutter Model to Analyze Co-Seismic Landslides: A Case Study of the 2024 Noto Earthquake, Japan. Geosciences 2025, 15, 180. https://doi.org/10.3390/geosciences15050180
Gomez C, Hadmoko DS. Application of LiDAR Differentiation and a Modified Savage–Hutter Model to Analyze Co-Seismic Landslides: A Case Study of the 2024 Noto Earthquake, Japan. Geosciences. 2025; 15(5):180. https://doi.org/10.3390/geosciences15050180
Chicago/Turabian StyleGomez, Christopher, and Danang Sri Hadmoko. 2025. "Application of LiDAR Differentiation and a Modified Savage–Hutter Model to Analyze Co-Seismic Landslides: A Case Study of the 2024 Noto Earthquake, Japan" Geosciences 15, no. 5: 180. https://doi.org/10.3390/geosciences15050180
APA StyleGomez, C., & Hadmoko, D. S. (2025). Application of LiDAR Differentiation and a Modified Savage–Hutter Model to Analyze Co-Seismic Landslides: A Case Study of the 2024 Noto Earthquake, Japan. Geosciences, 15(5), 180. https://doi.org/10.3390/geosciences15050180







