Study on Post-Stack Signal Denoising for Long-Offset Transient Electromagnetic Data Based on Combined Windowed Interpolation and Singular Spectrum Analysis
Abstract
1. Introduction
2. Denoising Process
2.1. Stacking
2.2. Windowed Interpolation
2.3. Singular Spectrum Analysis
- Embedding
- Singular Value Decomposition
- Grouping
- Diagonal Averaging
3. Verification of Denoising Effect
3.1. Effectiveness of Stacking Denoising
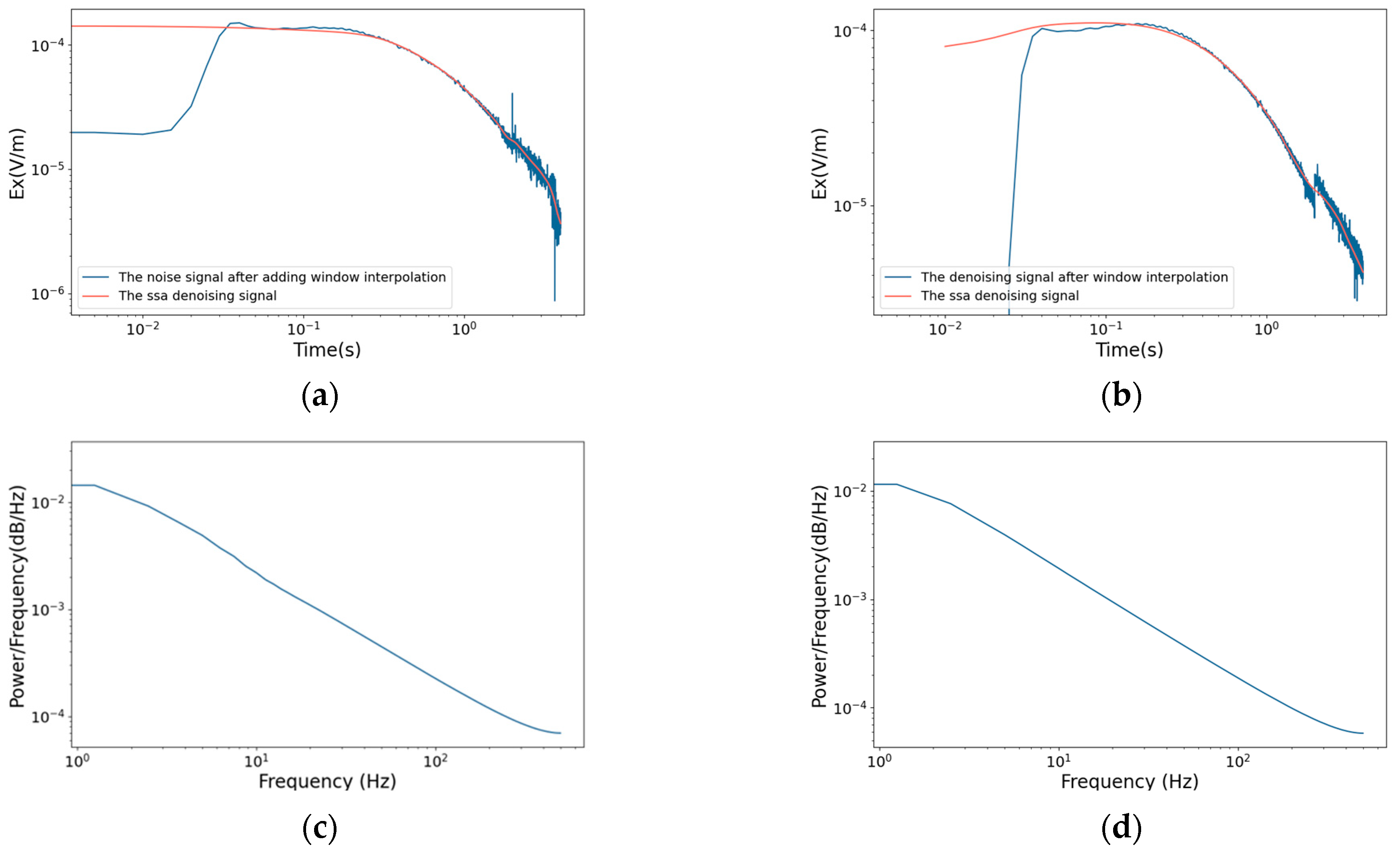
3.2. Effectiveness of Windowed Interpolation
3.3. Effectiveness of SSA
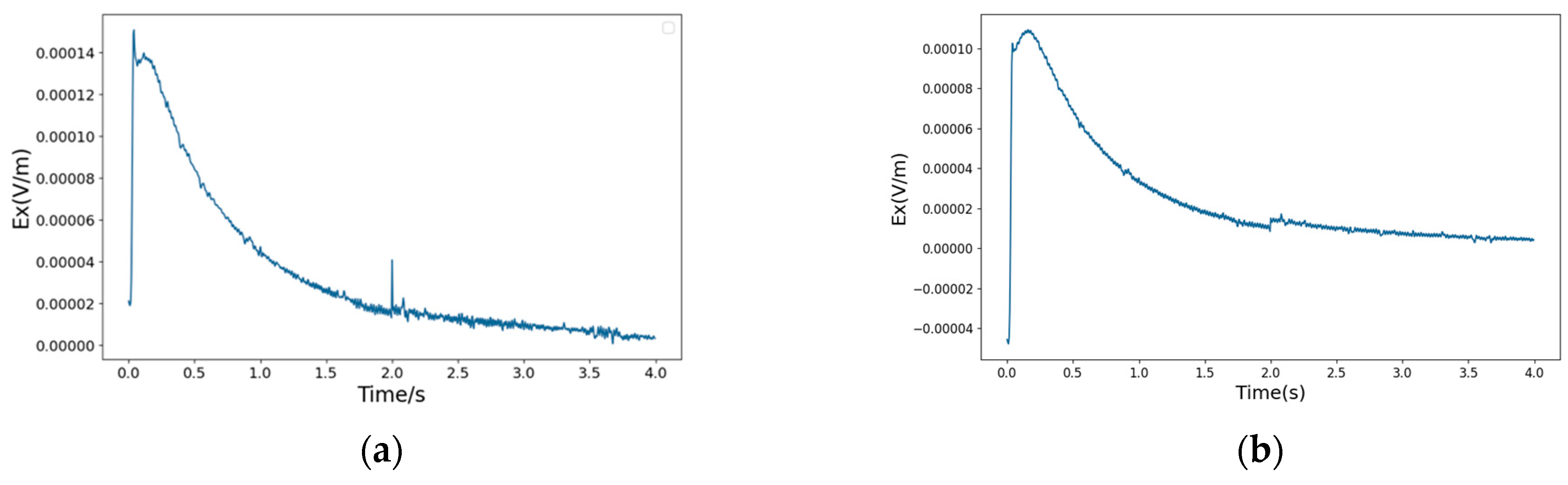
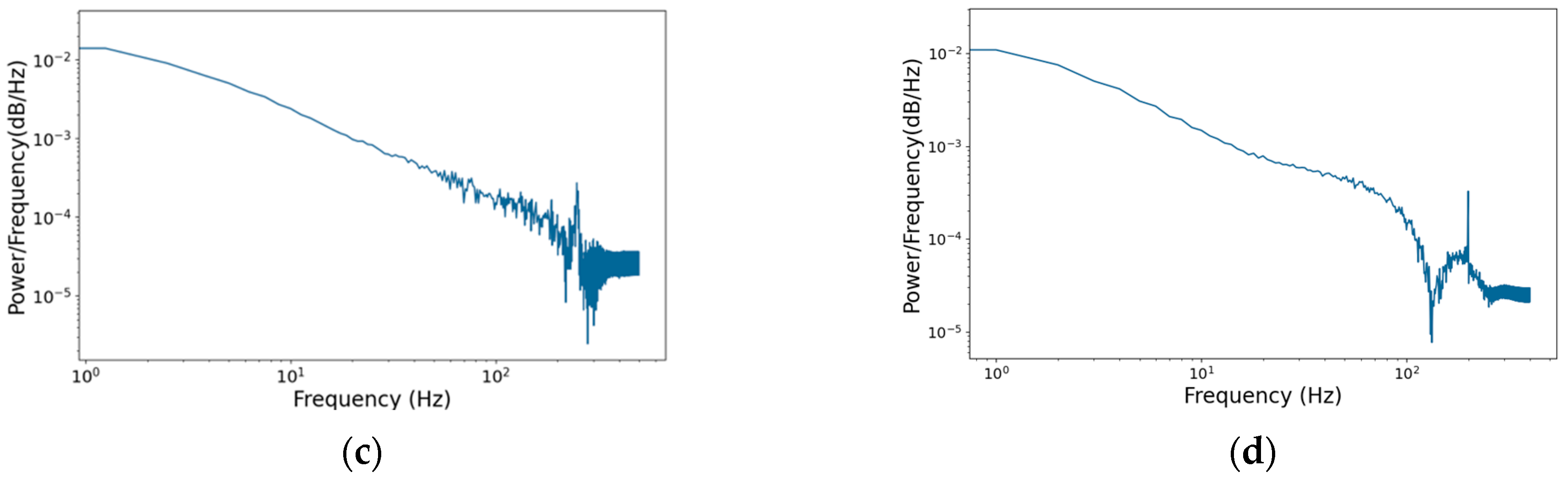
4. Denoising Processing of Field-Measured Data
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hördt, A.; Druskin, V.L.; Knizhnerman, L.A.; Strack, K.M. Interpretation of 3-D Effects in Long-Offset Transient Electromagnetic (LOTEM) Soundings in the Muensterland Area/Germany. Geophysics 1992, 57, 1127–1137. [Google Scholar] [CrossRef]
- Wu, X.; Xue, G.Q.; Xiao, P.; Rao, L.T.; Guo, R.; Fang, G.Y. Noise reduction technology of TEM using optimization of instrument sampling function. Chin. J. Geophys. 2017, 60, 3677–3684. [Google Scholar]
- Strack, K. Exploration with Deep Transient Electromagnetics; Elsevier Science Publishers B V: Amsterdam, The Netherlands, 1992. [Google Scholar]
- Macnae, J.C.; Lamontagne, Y.; West, G.F. Noise processing techniques for time-domain EM systems. Geophysics 1984, 49, 934–948. [Google Scholar]
- Ji, Y.; Wu, Q.; Wang, Y.; Lin, J.; Li, D.; Du, S.; Yu, S.; Guan, S. Noise reduction of grounded electrical source airborne transient electromagnetic data using an exponential fitting-adaptive Kalman filter. Explor. Geophys. 2018, 49, 243–252. [Google Scholar]
- Chen, K.; Pu, X.; Ren, Y.; Qiu, H.; Lin, F.; Zhang, S. TEMDNet: A novel deep denoising network for transient electromagnetic signal with signal-to-image transformation. IEEE Trans. Geosci. Remote Sens. 2020, 60, 1–18. [Google Scholar]
- Lin, F.; Chen, K.; Wang, X.; Cao, H.; Chen, D.; Chen, F. Denoising stacked autoencoders for transient electromagnetic signal denoising. Nonlinear Process. Geophys. 2019, 26, 13–23. [Google Scholar]
- Qi, T.; Wei, X.; Feng, G.; Zhang, F.; Zhao, D.; Guo, J. A method for reducing transient electromagnetic noise: Combination of variational mode decomposition and wavelet denoising algorithm. Measurement 2022, 198, 111420. [Google Scholar] [CrossRef]
- Zhang, X.; Li, W. Suppression of power frequency noise in vibration signals using windowed interpolation method. Noise Vib. Control 2022, 42, 142–147. [Google Scholar]
- Xu, Y.; Xie, X.; Zhou, L.; Xi, B.; Yan, L. Noise Characteristics and Denoising Methods of Long-Offset Transient Electromagnetic Method. Minerals 2023, 13, 1084. [Google Scholar] [CrossRef]
- Lu, C.; Xie, X.; Xu, Y. The research on denoising of long-offset transient electromagnetic stacked signals based on windowed interpolation and singular spectrum analysis integration. In Proceedings of the EMIW-2024, Beppu, Japan, 7–13 September 2024. [Google Scholar]
- Qi, C.; Wang, X. Harmonic parameter estimation based on interpolated FFT algorithm. J. Electr. Eng. 2003, 18, 92–95. [Google Scholar]
- Pan, W.; Qian, Y.; Zhou, E. Power harmonic measurement theory based on windowed interpolation FFT—(I) Window function study. J. Electr. Eng. 1994, 50–54. [Google Scholar] [CrossRef]
- Pan, W.; Qian, Y.; Zhou, E. Power harmonic measurement theory based on windowed interpolation FFT—(II) Double interpolation FFT theory. J. Electr. Eng. 1994, 53–56. [Google Scholar] [CrossRef]
- Qi, C.; Chen, L.; Wang, X. Accurate estimation of grid harmonic parameters using interpolated FFT algorithm. J. Zhejiang Univ. Eng. Ed. 2003, 37, 112–116. [Google Scholar]
- Jiang, Z.; Ding, Y. Generality and application characteristics of singular spectrum analysis. Acta Meteorol. Sin. 1998, 56, 736–745. [Google Scholar]
- Dai, H.; Xu, A.; Sun, W. Signal denoising method based on improved singular spectrum analysis. J. Beijing Inst. Technol. 2016, 36, 727–732. [Google Scholar]
- Zhigljavsky, A. Singular spectrum analysis for time series: Introduction to this special issue. Stat. Its Interface 2010, 3, 255–258. [Google Scholar] [CrossRef]
- Wang, X.; Yan, L.; Mao, Y.; Huang, X.; Xie, X.; Zhou, L. 3D forward modeling of long-offset transient electromagnetic under undulating topography. J. Jilin Univ. (Earth Sci. Ed.) 2022, 52, 754–766. [Google Scholar] [CrossRef]
- Yang, Y.; Li, D.; Tong, T.; Zhang, D.; Zhou, Y.; Chen, Y. Denoising controlled-source electromagnetic data using least-squares inversion. Geophysics 2018, 83, E229–E244. [Google Scholar] [CrossRef]
- Zhong, J.; Song, J.; You, C. Threshold selection wavelet denoising method based on signal-to-noise ratio evaluation. J. Tsinghua Univ. Nat. Sci. Ed. 2014, 259–263. [Google Scholar] [CrossRef]


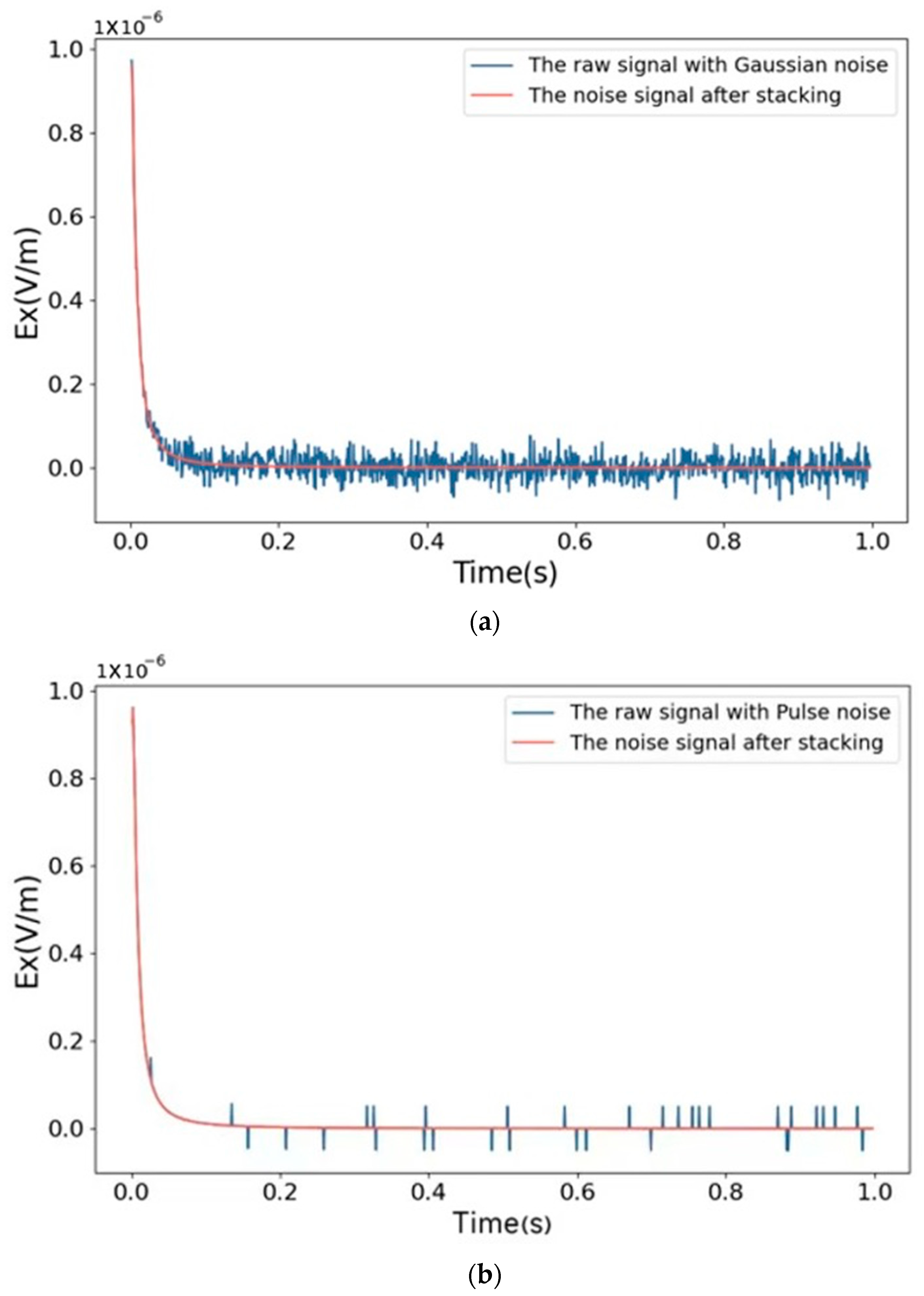


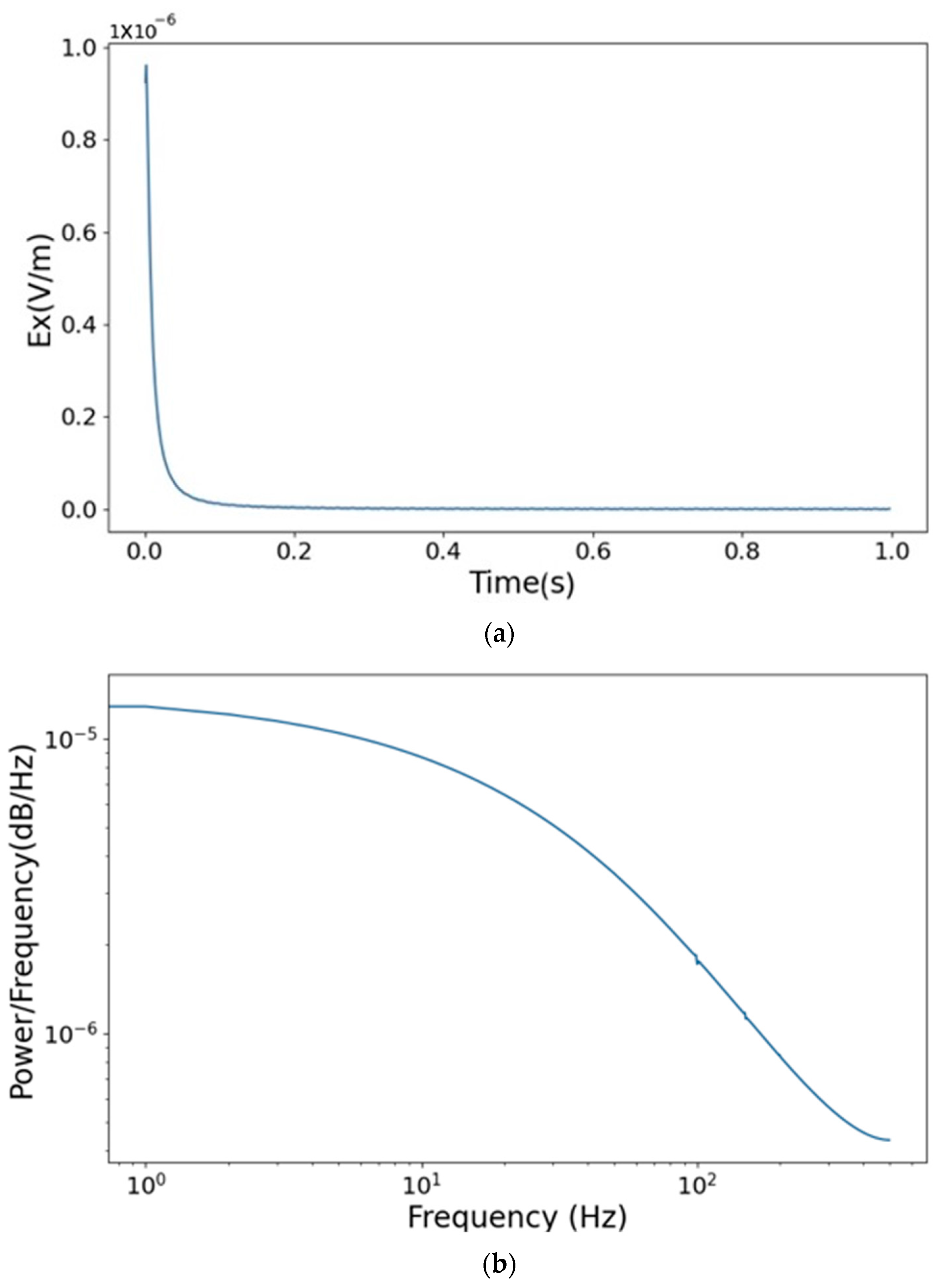
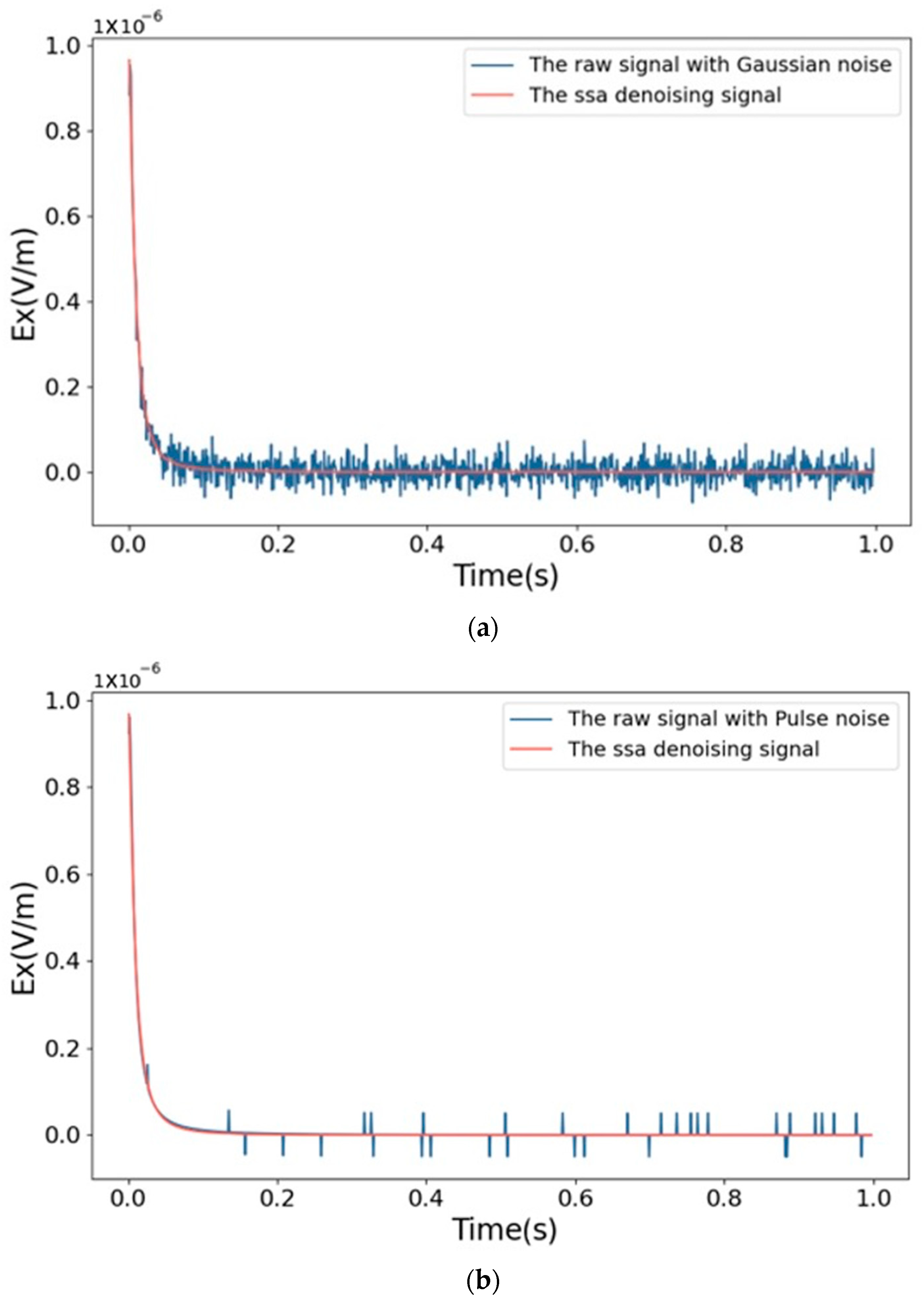
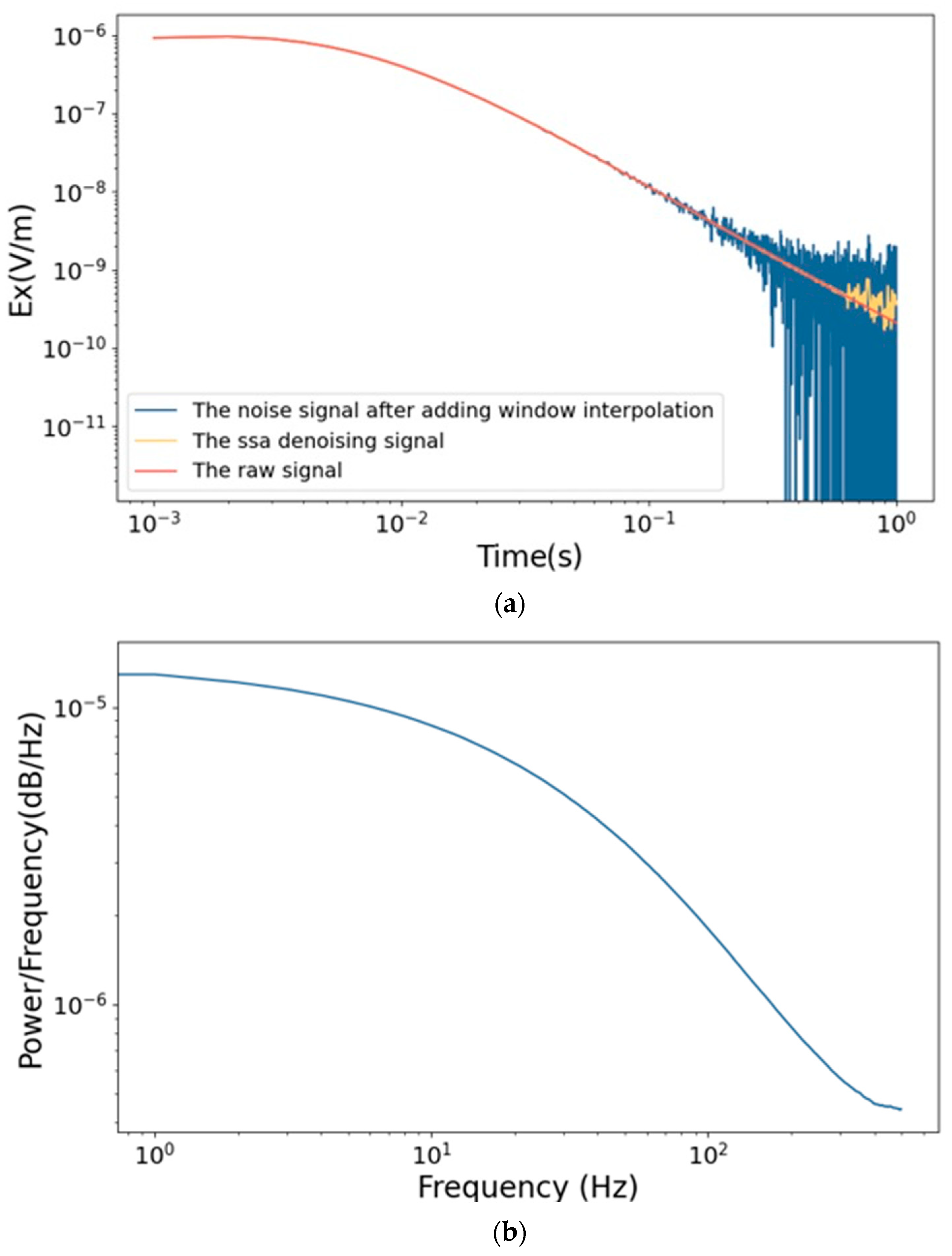



| Signal | RMSE | SNR |
|---|---|---|
| Simulated noisy signal (Gaussian) | 4.39 × 10−8 | 10 |
| Signal after stacking Denoising | 5.65 × 10−9 | 38.16 |
| Simulated noisy signal (Pulse) | 1.81 × 10−8 | 16.41 |
| Signal after stacking denoising | 4.84 × 10−10 | 44.05 |
| Simulated noisy signal (Frequency) | 1.16 × 10−8 | 14.36 |
| Signal after stacking denoising | 1.52 × 10−8 | 15.05 |
| Simulated noisy signal (three types of noise) | 2.98 × 10−08 | 8.29 |
| Signal after stacking denoising | 1.41 × 10−08 | 14.77 |
| Signal | RMSE | SNR |
|---|---|---|
| Simulated noisy signal (Gaussian) | 7.46 × 10−9 | 11.16 |
| SSA denoised signal (Gaussian) | 2.76 × 10−9 | 24.78 |
| Simulated noisy signal (Pulse) | 8.37 × 10−9 | 23.17 |
| SSA denoised signal (Pulse) | 1.26 × 10−9 | 35.64 |
| Signal | RNE |
|---|---|
| Signal a | 0.0283 |
| Signal b | 0.2261 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, C.; Xie, X.; Xu, Y.; Zhou, L.; Yan, L. Study on Post-Stack Signal Denoising for Long-Offset Transient Electromagnetic Data Based on Combined Windowed Interpolation and Singular Spectrum Analysis. Geosciences 2025, 15, 121. https://doi.org/10.3390/geosciences15040121
Lu C, Xie X, Xu Y, Zhou L, Yan L. Study on Post-Stack Signal Denoising for Long-Offset Transient Electromagnetic Data Based on Combined Windowed Interpolation and Singular Spectrum Analysis. Geosciences. 2025; 15(4):121. https://doi.org/10.3390/geosciences15040121
Chicago/Turabian StyleLu, Chuyang, Xingbing Xie, Yang Xu, Lei Zhou, and Liangjun Yan. 2025. "Study on Post-Stack Signal Denoising for Long-Offset Transient Electromagnetic Data Based on Combined Windowed Interpolation and Singular Spectrum Analysis" Geosciences 15, no. 4: 121. https://doi.org/10.3390/geosciences15040121
APA StyleLu, C., Xie, X., Xu, Y., Zhou, L., & Yan, L. (2025). Study on Post-Stack Signal Denoising for Long-Offset Transient Electromagnetic Data Based on Combined Windowed Interpolation and Singular Spectrum Analysis. Geosciences, 15(4), 121. https://doi.org/10.3390/geosciences15040121







