Next Article in Journal
Prediction of Sonic Well Logs Using Deep Neural Network: Application to Petroleum Reservoir Characterization in Mexico
Previous Article in Journal
Experimental Study on the Mechanical Response and Failure Behavior of High-Pressure Frozen Ice Under Axial Loading Conditions
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Geosciences
Volume 15
Issue 11
10.3390/geosciences15110423
geosciences-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Geological Modelling of Urban Environments Under Data Uncertainty

by
Charalampos Ntigkakis
,
Stephen Birkinshaw
* and
Ross Stirling
School of Engineering, Newcastle University, Newcastle upon Tyne NE1 7RU, UK
*
Author to whom correspondence should be addressed.
Geosciences 2025, 15(11), 423; https://doi.org/10.3390/geosciences15110423
Submission received: 27 July 2025 / Revised: 5 September 2025 / Accepted: 31 October 2025 / Published: 5 November 2025
Browse Figures
Versions Notes

Abstract

Geological models form the basis for scientific investigations of both the surface and subsurface of urban environments. Urban cover, however, usually prohibits the collection of new subsurface data. Therefore, models depend on existing subsurface datasets that are often of poor quality and have an uneven spatial and temporal distribution, introducing significant uncertainty. This research proposes a novel method to mitigate uncertainty caused by clusters of uncertain data points in kriging-based geological modelling. This method estimates orientations from clusters of uncertain data and randomly selects points for geological interpolation. Unlike other approaches, it relies on the spatial distribution of the data and translating geological information from points to geological orientations. This research also compares the proposed approach to locally changing the accuracy of the interpolator through data-informed local smoothing. Using the Ouseburn catchment, Newcastle upon Tyne, UK, as a case study, results indicate good correlation between both approaches and known conditions, as well as improved performance of the proposed methodology in model validation. Findings highlight a trade-off between model uncertainty and model precision when using highly uncertain datasets. As urban planning, water resources, and energy analyses rely on a robust geological interpretation, the modelling objective ultimately guides the best modelling approach.

1. Introduction

Geological modelling is generally referred to as the process of constructing a (typically three-dimensional) representation of the geological setting [1]. Three-dimensional geological models are a useful tool for visually conveying geological information [2] and geometrically representing the current understanding of the subsurface, as well as geological structures and features [3]. They often form the basis for future studies [4] and can be used in a wide range of applications. These might include serving as a data repository of existing subsurface information, which can then form a basis for future data gathering [5]. They can also be used in hydrogeological modelling to inform the conceptualisation phase and organise and interpret the relevant hydrogeological information [6,7]. Applications might also include other types of scientific investigations, geotechnical studies, mining operations, as well as policymaking [3].
Geological modelling methods can be deterministic or stochastic [8]. In terms of deterministic approaches, they can generally be separated into two categories: (i) explicit modelling, and (ii) implicit modelling. Explicit modelling, relies on an explicit definition of each model feature (e.g., stratigraphy, faults, etc.), through the definition of surfaces and their spatial arrangement [9,10]. In a sense, explicit modelling is a set of 2D interpretations (i.e., cross-sections) that are joined together in the 3D domain [10,11]. As such, it requires each surface to be directly defined [12], and the geometrical information of each surface to be located on the surface itself [13]. Implicit modelling relies on the definition of the geological interfaces, usually through the potential field method [14]. Geological interfaces are not constructed directly [10] but are defined as an isovalue of one or multiple geometric scalar fields. Implicit methods usually employ the kriging approach [15] for geological interpolation, which is a spatial interpolation method that can be described as a multiple linear regression extended to a spatial context [16]. 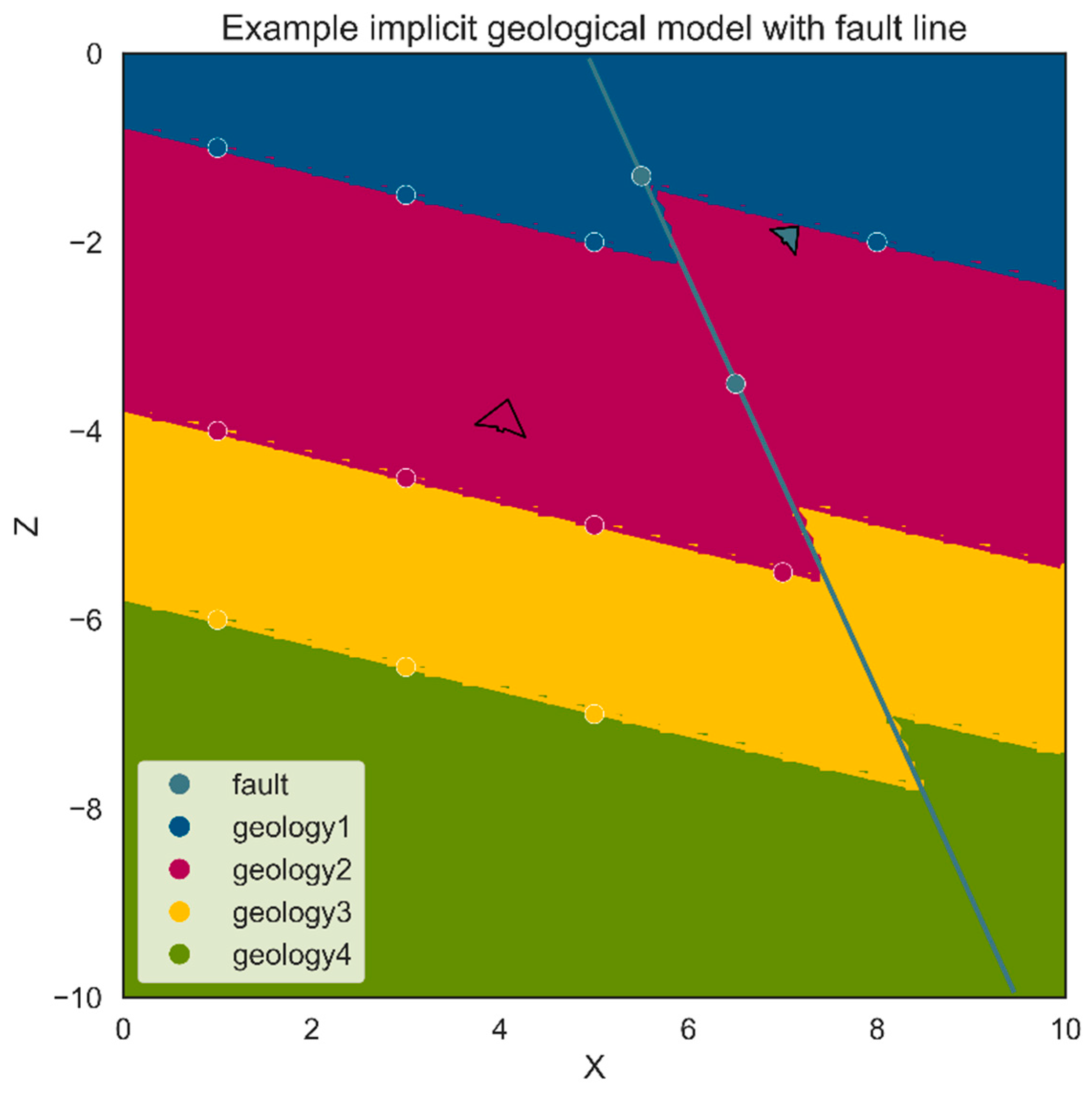This research focused on implicit methods that use the universal co-kriging approach [17]. Universal co-kriging is an evolution of kriging which allows multivariate cases to be considered, i.e., the combination of different types of input data. As such, each scalar field can be defined by simultaneously considering both contact points and orientations of the geological interfaces, which do not necessarily need to be part of the actual geological surface. Orientations can be obtained through dip and strike measurements or inferred from contact points. These orientations can then be used to define the orientation of the scalar field. Thus, implicit methods decouple the representation of geological features from the actual geometry of those features [13]. An example of that could be the representation of surfaces on one side of a fault, with information obtained for the surfaces on the other side, and the fault line itself. This example is graphically presented in Figure 1.
Geological models however, like any other model, are a simplification of reality and therefore contain uncertainties [3]. If a model was to capture all the complexity of the real-world, it would need to be as complex as the system it simulates [18]. Uncertainty is therefore an integral part of any geological investigation, and is caused by differences between the true geology and the perceived geological structure [19]. As such, robust geological modelling depends primarily on a good quality geological dataset [20,21,22], especially since the data configuration is known to have a big influence on kriging-based modelling approaches [23].
In the context of urban areas, geological models are an invaluable tool for subsurface investigations. Rapid urban development has put increasing pressure on the urban subsurface, leading to increasingly challenging environmental problems [24,25,26]. This has led researchers and urban planners to focus more on the urban subsurface space [27,28]. Urban groundwater flooding is an example of such an environmental challenge gaining more attention [29,30]. Groundwater flooding can cause significant economic and social disruptions, as well as pose risks to public health, due to the concentration of human activities within the built environment [31,32]. Furthermore, there is a growing interest in Blue-Green Infrastructure within urban areas for stormwater management. However, increased groundwater recharge because of such infrastructure may lead to excessive rising of the water table [33]. This can have significant consequences in areas of shallow groundwater, or areas prone to groundwater flooding [34]. As such, there is an increasing need for a robust understanding of the urban subsurface through geological modelling.
Data uncertainty within urban areas, however, has been recognised as a major source of model uncertainty. More specifically, one of the main contributing factors for data uncertainty within urban areas is data scarcity, especially in the context of underground and geological data [25]. Urban geological datasets can be limited in both their size and information they provide [28]. Furthermore, they have an uneven distribution both in the spatial and temporal contexts. Geological data collection tends to cluster around infrastructure projects, which have been constructed during different time periods. As such, geological data can contain different information and accuracy, as they were collected by different means, for different purposes, over different decades.
It should be noted however that this problem of data scarcity is not exclusively found in urban areas. However, urban modelling usually requires much finer model resolution and detail and therefore is more sensitive to data quality and configuration. Furthermore, considering that urban coverage generally prohibits the collection of new data or makes it economically unsustainable [35], these existing low-quality datasets are of growing importance. It is also important to highlight that urban development tends to alter the upper parts of the geological domain. Therefore, geological records of neighbouring locations may contradict each other, as they might represent different points in time. This phenomenon of measurements of the same quantity from nearby locations contradicting each other has been described as disinformation [36], and in the context of implicit methods may lead to the representation of unrealistic and (usually) circular modelling artefacts.
Several approaches have been developed to deal with data uncertainty, data scarcity, and the uncertainty due to clusters of data containing conflicting information. These methods rely on either locally or globally updating the interpolator to overcome the problems caused by data clustering. Examples include regularising and parameterising the geological structure and including expert knowledge as modelling objectives [37], dynamically updating the model with the addition of new data [38], probabilistically tuning model parameters [8], and deep learning algorithms [39,40,41,42,43]. However, these approaches may struggle to overcome the challenges presented by highly uncertain, spatially, and temporally variable datasets containing conflicting information, like those within urban areas.
Another recent advancement in this area is informed local smoothing [44], which applies a smoothing function to the interpolator. As such, the accuracy of the interpolator is locally reduced, allowing it to locally not fit to data points. Therefore, it can account for local uncertainties in the input dataset and variations caused by localised and dense data clusters. To the best of the authors’ knowledge, informed local smoothing has not been applied for geological modelling beyond a theoretical level, using a manufactured dataset.
Finally, this research proposes a novel approach which relies on utilising the ability of universal co-kriging to combine multiple types of input data (i.e., point data and orientations) for the definition of a scalar field. To that end, the information contained within data clusters is used to estimate orientations from the contact points of different geological formations. This involves a fixed-radius nearest neighbour search to group data points together and using the covariance matrix to estimate an orientation from each group. Following that, only one of the contact points from each group is then selected at random to be used for the interpolation, along with the estimated orientation. This follows the assumption that at least 3 contact points are required to estimate an orientation, and thus orientation estimations tend to be clustered where there is a cluster of contact points. These locations could influence both the contact points and the orientation estimations, potentially introducing bias into the final model. With the proposed approach, the geological information from all the points is included within the orientation estimation, but the potential bias is reduced by randomly selecting a single point from each group to be used as a contact point for the interpolation. Compared to the approaches discussed earlier, the proposed methodology relies simply on the spatial distribution of the input dataset and the ability to translate information into a different data format.
This research therefore aims to evaluate the feasibility of using the proposed orientation estimation and random point selection technique, as well as informed local smoothing [44], to overcome the challenges presented by urban geological datasets. To that end, it examines the case study of the Ouseburn catchment in the wider Newcastle upon Tyne (UK) area. The objectives of this research are therefore to: (i) Use an existing geological borehole dataset, along with GemPy (v2.3.1) [45] and the universal co-kriging algorithm to develop a superficial thickness model of the study area; (ii) Consider the uneven spatial and temporal distribution of borehole data and evaluate the use of informed local smoothing, as well as the novel orientation estimation and random point selection technique, to overcome the uncertainties introduced by data clustering; (iii) Assess the uncertainties in the resulting superficial thickness model through a Monte Carlo analysis; (iv) Validate the model results through the use of unutilized borehole data. Ultimately, the goal is to assess how the geological uncertainty affects the hydrogeological model results, which is the subject of future research.

2. Study Area and Data

2.1. Study Area

The Ouseburn catchment is a peri-urban catchment, located in the wider Newcastle upon Tyne area, in the North-East of England. The catchment covers an area of approximately 61.6 km2 and has gentle slopes. The upstream part of the catchment is the northwestern end, which is predominantly rural and is used for agriculture [46]. The catchment follows a smooth “urbanisation gradient”, i.e., it becomes progressively more urbanised downstream, towards the southern and southeastern parts. Figure 2 shows the boundaries of the Ouseburn catchment and the location of the Ouseburn River.

2.2. Bedrock Geology

The Ouseburn catchment is located on the northeastern corner of the Alston Fault Block, in the North-East of England. The Alston Block is bound by the Ninety Fathoms Fault to the north, the Butterknowle Fault to the south, the Pennine Fault to the west, while to the east it extends to the North Sea [47]. The Block is primarily comprised of rocks from the Carboniferous (359–299 MYA) [48].
The younger rocks within the Newcastle area are those of the Upper Carboniferous and more specifically, the Pennine Coal Measures of the Westphalian (313–303 MYA). The Pennine Coal Measures consist of a series of mudstones, sandstones, siltstones and shales, as well as coal seams and seatearths [49]. The Coal Measures are further divided into Lower, Middle, and Upper Coal Measures, whose bases are defined by significant marine bands [48]. However, within the study area, only the Lower and Middle Coal Measures are present (Figure 3). Coal seams within the study area, especially within the Middle Coal Measures, have been worked extensively. This primarily involved subsurface mining, and to a significantly lesser extent open cast mines which have since been filled [50]. As a result, there is an extensive network of old coal mines across the entire area, however, the location and extent of them are poorly documented.

2.3. Superficial Geology

Overlying the bedrock within the study area are the sediments from the Quaternary Period (Figure 4), which are linked to the last Ice Age. As a result, most of the visible landscape today has been shaped by the formation, movement, and retreat of glacial sheets [51], and the subsequent deposition of Quaternary superficial deposits. These Quaternary sediments are widespread across the whole area and cover most of the underlying carboniferous rock.
The superficial deposits consist primarily of boulder clay (glacial till), glacial and glaciofluvial sand and gravel, laminated clays and silts, as well as alluvium deposits. The most common of these deposits is glacial till, which covers most of the study area. It has a maximum thickness of 30 m and in most areas, it is the only drift deposit [49]. Sand and gravel deposits are consistent with the deposition having occurred in a subglacial setting and can be attributed to ephemeral streams and water pools under wasting or stagnant ice. Laminated clays and silts are sparser within the catchment. They are generally thought to have been deposited in glacial lakes and overlie the glacial till but can also be present within the sand and gravel deposits. Finally, alluvium deposits within the study area are attributed to fluvial activity and are considered to overlie the glacial till and laminated clay deposits.
Made ground occurs primarily within the urban areas and where mining and industrial activities took place. Composition of the made ground is poorly documented and varies greatly, but the most common components are concrete, bricks, ashes, colliery waste, domestic, industrial, and chemical refuse, urban rubble, as well as surface material redistributed during landscaping [49]. Urban waste has also been used as infill for quarries and buried valleys, the composition and extent of which is not well-documented. Made ground has not been widely mapped, especially in areas where it cannot be easily defined due to urban cover.

2.4. Available Data

The availability, resolution, and quality of appropriate data also influenced the strategy and rationale behind the development of the 3D superficial thickness model. These data include Digital Terrain Models (DTMs), historical geological borehole records, geological maps, as well as a national superficial thickness model. It should be noted that within the literature, the terms “digital elevation model (DEM)” and “digital terrain model (DTM)” can be used to describe models with different degrees of surface features removed. For the purposes of this research, both terms are used interchangeably and represent the digital surface model, with all surface objects removed.
The DTM used in this research was the LIDAR Composite Digital Terrain Model (DTM) with 1 m resolution [52]. This DTM was derived using a combination of the Environment Agency’s Time Stamp archive and National LIDAR Programme surveys. Due to restrictions in the computational capacity of both the software and hardware used for the 3D modelling, the DTM was resampled to match the model grid resolution (25 m). It was then used to constrain the ground surface elevation in the resulting superficial thickness model.
Borehole records used for the analysis were derived from the British Geological Survey’s (BGS) GeoIndex [53], which provides access to the National Geoscience Data Centre’s (NGDC) repository of onshore borehole, well, and shaft records. Within the model area, there are 7620 borehole records (Figure 5), which primarily originated from site investigations and historic mining activity. Site investigation boreholes are predominately shallow, with depths commonly less than 10 m. Boreholes related to historic mining are usually deeper and were mainly drilled to prove the presence of coal resources at depth.
The borehole locations are also not evenly distributed throughout the area. The main portion of the boreholes are located within the Newcastle city centre, as well as areas with concentrated historic coal mining activity. Elsewhere, borehole distribution is relatively sparse and largely clustered along main transport routes. Within the Ouseburn catchment specifically, most of the boreholes are along the A1 and A696 dual carriageways. This clustering, along with the complexity of the underlying geology, is one of the main sources of uncertainty.
The quality of the borehole records also varies greatly due to these records being collected from different site investigations spanning multiple decades. As a result, borehole records may contradict each other due to them representing different points in time. For the study area, this issue is common for borehole records within the heavily urbanized areas, as well as those around big infrastructure projects. Moreover, there are no digital records that can be directly used within the modelling software, and all the records are provided in the form of scanned physical documents. Furthermore, there is a mixture of formats available with some records being handwritten, and others being typed. This inconsistency can also be extended to the length units used within the records, with some of them using SI units, others using feet and inches, and others using decimal feet measurements. Finally, several records either have information missing (e.g., coordinates, ground surface, etc.) or use measurements without decimal places, indicating possible rounding of numbers during the investigation phase.
Digital geological maps for the model area are available from the BGS at 1:50,000 and 1:10,000 scales. 3D geological models are primarily created using information from geological maps, and thus rely on information from boreholes and outcrops to define the stratigraphic boundaries of the geological units [54]. As a result, the geological maps are used to inform and constrain the model to the ground surface, as well as to qualitatively validate it.
Finally, a national superficial thickness model has been developed by the BGS [55]. This model offers superficial thickness estimations at a 1:50,000 scale across Great Britain, at a rasterized format. However, these estimations do not have a resolution suitable for direct use within this research. As such, they have been used to qualitatively validate the superficial thickness model.

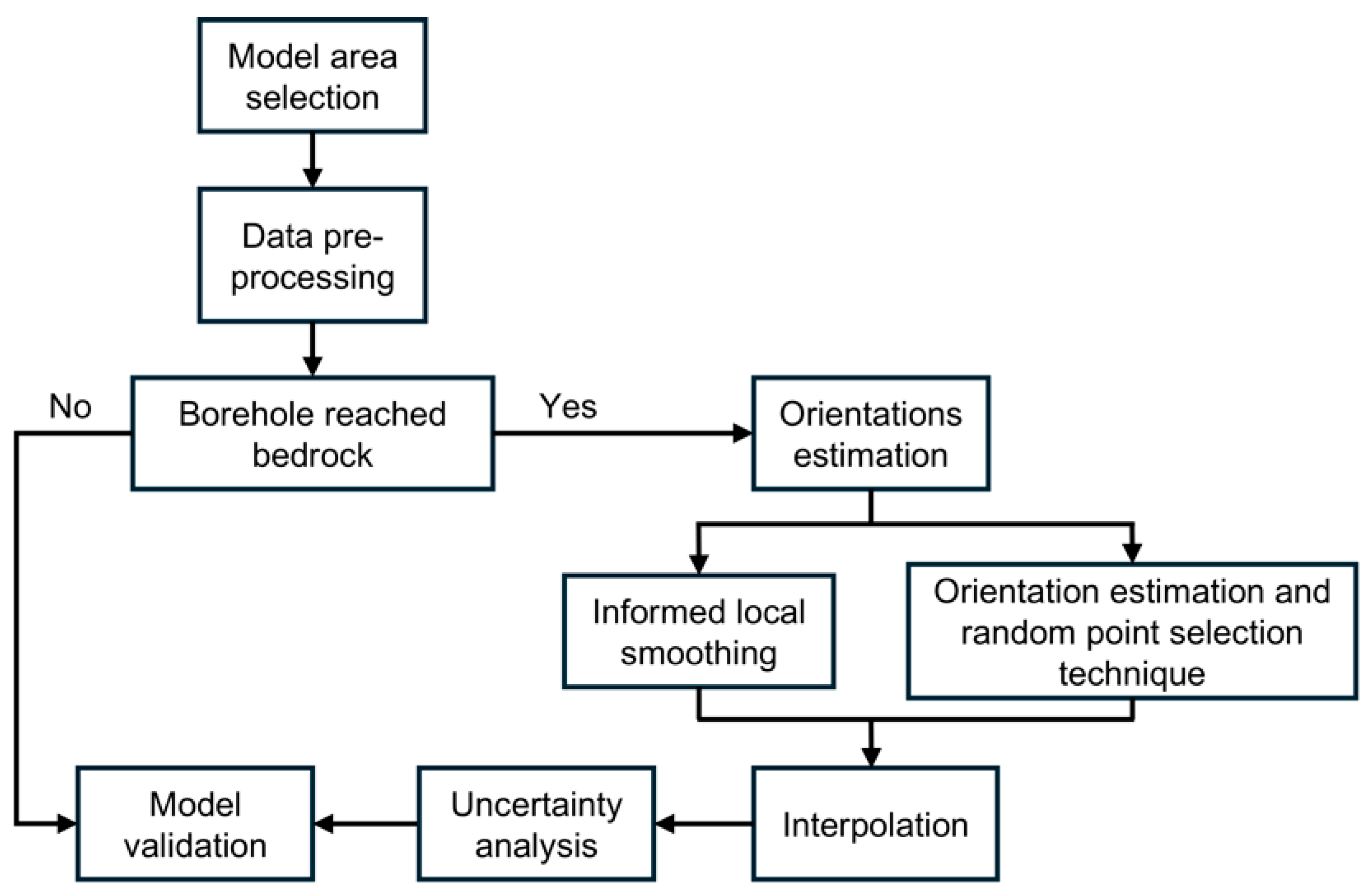
3. Methods

Figure 6 shows a graphical representation of the analysis presented within this section:

3.1. Model Area

The model area was defined so that it encompassed the Ouseburn catchment, as well as a buffer zone of 500 m beyond the catchment boundaries. This buffer zone was selected to avoid any potential boundary effects, as well as to capture geological information from the immediate area around the catchment. A rectangular model domain was chosen, defined in the OSGB36-Ordnance Survey National Grid (EPSG:27700) reference system by the points: (414950, 564500), (414950, 572900), (431000, 572900), and (431000, 564500). The selection of a rectangular modelling domain was because of a limitation of GemPy, which only allows for the creation of rectangular model domains. The results were then trimmed in the post-processing phase to only include the Ouseburn catchment.
GemPy uses a meshless interpolator and therefore the interpolated surfaces can be evaluated anywhere in space [45]. However, it uses a user-defined grid to perform the 3D visualization of the generated model. This grid is required, regardless of whether 3D visualization is one of the objectives. For this reason, a regular grid was defined with cell sizes of 25 m, as this was found to be an optimal trade-off between computational intensity, and detailed resolution.

3.2. Data Preprocessing

Due to the data quality issues discussed earlier, a set of queries was performed on the available borehole records to identify those that could be used for the development of the superficial thickness model. The depth of the available borehole records within the model area varies greatly, with the shallowest being less than 1 m and the deepest approximately 510 m. Given prior knowledge about the superficial thickness within the study area (see [55]) and the high volume of available records, only those deeper than 20 m were considered for this research as they were the ones with higher chances of penetrating the bedrock. Boreholes were initially selected to be within the boundaries of the Ouseburn catchment. Furthermore, several boreholes were selected outside the catchment boundaries to constrain the model along the edges and avoid any boundary effects. Finally, only boreholes drilled later than 1950 were considered, as these records presented the greatest chances of being typed instead of handwritten, and therefore greater chances of being able to be efficiently digitized.
Following these constraints, 507 boreholes were evaluated. These were manually examined and digitized to evaluate the depth and location of the top of the bedrock (rockhead). These were then converted to a format that could be input into GemPy. Following this process, 217 boreholes were rejected due to the records being either illegible or missing important information (i.e., coordinates, surface elevation, etc.), and 290 were accepted for further analysis. The locations of the accepted and rejected boreholes are presented in Figure 7. Out of the 290 accepted boreholes, only 210 were deep enough to penetrate the bedrock and were used for the superficial thickness model development. The rest were used for model validation.

3.3. Model Development

GemPy [45] is an open-source implicit geological modelling algorithm developed in Python (v3.10.16 used for this research). It constitutes a geomodelling suite ideal for advanced geomodelling investigations. GemPy can be adapted to suit a variety of applications using Python. More specifically, GemPy has been integrated with, among others, Bayesian inference frameworks [45,56], model topology analysis [57,58], offshore hydrogeological heterogeneity characterization analysis [59], gravity and magnetic fields analyses [5,45,60], as well as hydrogeological and hydrostratigraphical investigations [6,7].
GemPy uses the potential field method [7,14]. With the potential field method, geological surfaces can be interpolated away from the actual data locations. In principle, the aim of the method is to construct an interpolation function Z x 0 , where x 0 = ( x , y , z ) ∈ R 3 is any point in the 3D space, that describes a scalar (or potential) field [45]. Any geological surface, k , can then be described as Z x 0 = t k , where t k is some value of the scalar field, i.e., a surface of the scalar field where each of its points has the same value (isosurface). Equally, any point belonging to a geological formation between two successive surfaces k and l , is defined such as t k < Z x 0 < t l [7]. The slope of the scalar field will also follow the planar orientation of the geological volume for every point of the volume. The interpolation function Z ( x 0 ) is obtained using the universal co-kriging approach [17].
It is important to note that the interpolation method described above is meshless [60], and the value of the scalar field can be evaluated anywhere in space. In practice, as stated earlier, the objective of a geological model is to define the spatial distribution of geological formations and convey that information visually. Therefore, there is a need for the discretization of the three-dimensional domain, which GemPy performs using a grid of voxels. For the purposes of this research, however, the focus was the location of geological interfaces and to produce a rasterized output. The meshless interpolator thus allows for the evaluation of these interfaces anywhere in space, regardless of the grid size.
As discussed earlier, GemPy requires two types of data for the interpolation function: (i) point data, and (ii) orientations. Point data refer to the contact points between two geological formations, which can be used to define the geological interface. Orientations, on the other hand, refer to the orientation of that interface in the three-dimensional space and can either be measured directly or inferred from the contact points. Therefore, the information acquired from the borehole records represents the contact points between the bedrock and the superficial deposits. Direct orientation measurements were not available for the study area and were thus inferred from the point data. To that end, a fixed-radius nearest neighbour search was performed on all the point data. Orientations were estimated for the points where 2 or more nearest neighbours were identified, i.e., where there is a group of 3 or more points. Finally, the distance for the radius search was defined as multiples of the grid size (25 m). The radii evaluated were 2, 3, 4, and 5 times the grid size, i.e., 50 m, 75 m, 100 m, and 125 m, respectively. The different fixed-radius values produced similar results, and the analysis appeared to not be sensitive to the parameter value. Therefore, only the results for 50 m fixed-radius nearest neighbour search are presented within this research.
No information was available regarding the fault lines within the model domain. GemPy treats faults like any other surface and therefore requires point data and orientations to model them. The lack of these data meant that the fault lines could not be modelled within this research and were therefore omitted. This follows the assumption that since the objective was the development of a superficial thickness model and not a 3D structural geological model, and given the glacial history of the area, the interface between bedrock and superficial deposits was assumed to have been smoothed by the movement of the glacial sheets. Therefore, the omission of the fault lines would not have a significant influence on the resulting model.
Exporting the interpolation results in a rasterized format required the development of a custom Python function. This function adapted some functionality of GemGIS (v1.1.8) [61] to create visualization meshes and 3D depth maps of model surfaces by extracting the elevation values from the visualization mesh needed to create these depth maps. These elevation values were then exported as a raster output in the same spatial extent and grid resolution as the DTM.
Finally, the interpolated surface represented the elevation of the rockhead. This surface, however, was represented without considering the topography. To that end, the ground surface elevation was obtained from the DTM and then compared to the interpolated surface. The elevation of the rockhead was trimmed depending on the ground surface elevation, and the cells where the rockhead was estimated above the ground surface were set to NaN. The final rockhead elevation estimation was subtracted from the ground surface elevation to acquire an estimation of the surficial thickness.

3.4. Data Clustering

The point data used in the analysis are not evenly distributed throughout the model area and tend to form clusters. As a result, these cluster locations introduce bias into the model. This is especially true considering that 3 points are required to estimate an orientation, and thus orientation estimations tend to be clustered where there is a cluster of point data. These locations could therefore influence both the point data and the orientation data used for the interpolation. To mitigate this, two different approaches were evaluated for handling the uncertainty and potential bias introduced by the uneven spatial data distribution and data clustering: (i) orientation estimation and random point selection, and (ii) informed local smoothing [44].
The orientation estimation and random point selection technique aimed to assimilate all the information contained within the borehole records into the modelling framework while also mitigating any potential bias from the clustering effect. To that end, this method was applied to the nearest neighbour groups used for orientation estimations. More specifically, for every group of nearest neighbours calculated with 3 or more points, all the points were used for the orientation estimations and thus all the information from the data points was contained within the orientation estimation. However, only one of the points was chosen at random to be used as a contact point for the interpolation.
Informed local smoothing was applied to the locations where there were clusters of borehole records, as described in Von Harten et al. (2021) [44]. More specifically, the smoothing applied to those locations was informed by the data configuration, and a Kernel Density Estimation (KDE) was applied to inform the smoothing values. KDE is a non-parametric statistical method used to estimate the probability density functions of a set of random variables [62,63]. In the context of data used in geological modelling, it can provide a relative indicator of data density [44]. Furthermore, the modelling application described within this research was considered to not be of high complexity, as it only describes the formulation of a superficial thickness model. Therefore, as suggested by Von Harten et al. (2021) [44], the KDE was normalised and the resulting values were applied as localised smoothing within GemPy.

3.5. Uncertainty Analysis

An uncertainty analysis was also performed on the input data, as they were identified as a major source of uncertainty for the development of the superficial thickness model. The uncertainty analysis was performed using a Monte Carlo approach on the location of the contact points obtained from the borehole records. More specifically, the coordinates of the points in the three-dimensional space (X,Y,Z) were treated as a random variable, and the value of each coordinate was chosen at random from a range of ±1 m from the value recorded within the borehole logs. The selection of the range for the Monte Carlo analysis was influenced by the assumed rounding of recorded values within the borehole records, as well as the expected conversion errors when converting the recorded units to SI. This step was performed on every contact point, prior to that point being input into the modelling framework and the calculation of orientations. This process was repeated 1000 times, choosing a different subset of coordinate values for each point every time, resulting in an ensemble of 1000 different realisations of the superficial thickness model. Finally, the uncertainty analysis was repeated for both approaches for mitigating the clustering effect.

3.6. Model Validation

As discussed earlier, only the borehole records that penetrated the bedrock were used for the development of the superficial thickness model and the remaining were used for model validation. To that end, the simulated superficial thickness was compared to the maximum superficial thickness recorded in the boreholes that did not penetrate the bedrock, and a binary approach was adopted. For the locations where the simulated superficial thickness was higher than the maximum recorded within the borehole record, the model was considered validated. On the other hand, for the locations where the simulated superficial thickness was lower than the maximum thickness recorded within the borehole record, model validation was considered to have failed.

4. Results

Figure 8 shows the mean estimated superficial thickness within the catchment following the uncertainty analysis for the 50 m fixed-radius search using the orientation estimation and random point selection technique (Figure 8a) and informed local smoothing (Figure 8b). Both Figure 8a,b showed similar overall results, with higher estimated superficial thickness in the eastern parts of the catchment, just east of the A1 dual carriageway, as well as the northwestern part of the catchment near the Ouseburn River headwaters. Figure 8c shows the difference between the values in Figure 8a,b and was used as a comparison measure between the two. The figure shows large areas of the catchment with positive differences, which highlights that applying informed local smoothing results in consistently lower overall estimations of the superficial thickness. More specifically, the mean difference across the catchment area was 2.78 m, with a standard deviation of 9.84 m. For the southwestern part of the catchment specifically, the lower estimated superficial thickness from the application of informed local smoothing was also consistent with the superficial thickness map in Figure 4 and the areas of no superficial cover. Finally, the differences plot highlights that the areas in the eastern part of the catchment, for which the orientation estimation and random point selection technique resulted in higher estimated superficial thickness, appear to be controlled by two different clusters of points at the north and south edges of the catchment.
Figure 9 shows the standard deviation of estimated superficial thickness within the catchment, following the uncertainty analysis for the 50 m fixed-radius search using the orientation estimation and random point selection technique (Figure 9a) and informed local smoothing (Figure 9b). Both figures primarily showed low standard deviation where there were borehole records, and higher standard deviations where the borehole records were sparse. This showcases the effects of the uneven spatial distribution of input data to the overall modelling uncertainty. However, both figures showed high standard deviations in the southwestern part of the catchment, indicating a highly uncertain area that is consistent across both approaches. There was a big concentration of data points just east of that area, which possibly controls this uncertainty. Figure 9c shows the difference between the values in Figure 9a,b, and was again used as a comparison measure between the two methods. The figure showed a good correlation between the two methods, and the differences between the two methods had a mean value of 1.00 m and a standard deviation of 3.19 m. However, two locations in the northern part of the catchment, just north of the Ouseburn River, showed higher differences compared to the rest of the area. As such, the application of informed local smoothing resulted in significantly higher uncertainty at these locations. It is also important to highlight that these two locations were again adjacent to data clusters, indicating that the data points within the clusters contained highly conflicting information.
The model validation for the 50 m fixed-radius search used in the orientation estimations is presented in Figure 10. The validation for the models using the orientation estimation and random point selection technique (Figure 10a) consistently failed at the southeastern edge of the catchment (near the outlet), as well as at two locations along the A1 dual carriageway. It is worth highlighting that there are a lot of borehole records at those locations, and these records may contain conflicting information. Furthermore, these locations have also been heavily influenced by human activities. More specifically, the A1 is a big transportation infrastructure project, and the model failed validation at the locations of big intersections. As for the catchment outlet, that area is heavily urbanised and has been artificially altered to create Jesmond Dene–a recreation park. Therefore, these borehole records may contain information about the subsurface at different points in time, thus highlighting the uncertainty originating from the temporal variability of the input data.
Examining the results from the models using informed local smoothing (Figure 10b), they again consistently failed validation at the southeastern edge of the catchment near the catchment outlet. Furthermore, they failed validation at one of the two locations along the A1 dual carriageway. Informed local smoothing, by definition, makes the interpolator less accurate at the locations where smoothing is applied [44]. Therefore, it was able to better handle the conflicting information contained withing the records for that cluster of points. It is worth highlighting, however, that the models using informed local smoothing consistently failed validation at the southern part of the catchment, between the A1 and the catchment outlet. A possible explanation for this is the lower accuracy of the interpolator at the locations of data clusters and the spatial distribution of borehole records. More specifically, there were two locations with large clusters of data: along the A1 and the catchment outlet. As stated earlier, by definition, the interpolator was purposely made less accurate at the locations of data clusters through the application of informed local smoothing. However, there were not enough borehole records between those two locations to further inform and constrain the interpolation (see Figure 7), therefore resulting in a worse overall result.

5. Discussion

This study focused on overcoming the uncertainty originating from geological datasets being unevenly distributed, both spatially and temporally, and containing data with conflicting information—a common problem usually found within urban areas [25,28]. Firstly, this research proposes a novel approach for overcoming these challenges based on converting geological information into different data types. To that end, it used a fixed-radius nearest neighbour search to group geological borehole records and used the covariance matrix to estimate an orientation from each group. Then, one point from each group was selected at random to be used as a contact point for the interpolation, along with the estimated orientation. Secondly, this research assessed the suitability of applying data informed local smoothing [44] on a real-world application. To that end, we developed a case study for an urban catchment with a highly uncertain dataset and performed an uncertainty analysis, as well as model validation, to compare the suitability of the two approaches.
Informed local smoothing appeared to result in lower estimated superficial thickness (Figure 8). This is consistent with the way that informed local smoothing is applied to the dataset, as by definition, the accuracy of the interpolator is locally reduced depending on the uncertainty of the input dataset [44]. Therefore, due to the highly uncertain nature of the dataset used within this research, the smoothing applied to locations of dense and highly uncertain clusters was possibly too extreme, resulting in an overall reduced accuracy. This was also evident from the model validation results. More specifically, the models that employed informed local smoothing failed validation more frequently, especially around areas of dense data clusters, or directly adjacent to them.
It should be noted, however, that the informed local smoothing applied in this research was based on kernel density. This selection was made as this method is easy to apply with the normal techniques described in the kriging literature [64,65]. However, a limitation of this approach is that modelling artefacts were not eliminated from this analysis, as seen by the circular patterns in Figure 9b. This was expected, since the uncertainty analysis was performed on the input data by adjusting the recorded coordinates of the points within the borehole logs by ±1 m. As such, it is expected that there will be model formulations which include the extremes of this range for neighbouring data points and thus represent unrealistic scenarios. Furthermore, another limitation is that no optimisation was performed for the smoothing parameters, which is expected to create more robust solutions, especially if applied for an inversion problem [66]. Finally, as stated earlier, data-informed local smoothing has not previously been applied to another real-world model. As such, the suitability of the approach has only been evaluated for the case study presented within this research.
On the other hand, using the orientation estimation and random point selection technique resulted in higher estimated superficial thickness (Figure 8) and better model validation (Figure 10). As such, it is plausible that this approach can result in a better representation of the real geological setting. However, it should be noted that although model validation was better, there were still areas of the model domain that consistently failed validation. This was especially the case around areas with big clusters of highly uncertain data, showcasing that that model validation is spatially variable.
Furthermore, the orientation estimation and random point selection technique resulted in higher variability in the model results. This is evident from the standard deviation plots (Figure 9). As stated earlier, informed local smoothing purposely made the interpolator locally less accurate. As a result, when dealing with a highly uncertain dataset, the interpolator will be consistently less accurate at the locations of high uncertainty. This reduced accuracy will result in geological interpretations that are similar across different model formulations. Evaluating these results in isolation will show lower standard deviation and thus lower uncertainty. It is, however, important to evaluate whether these model formulations are also plausible through prior knowledge about the area being modelled.
Modelling in general is a compromise between realism, generality, and precision [67]. As discussed earlier, models are a simplification of a complex natural system. Therefore, defining the modelling purpose is crucial to determining the extent of the simplification and the amount of detail to be included, in order to achieve the model objectives. Selecting an appropriate modelling approach and a way to deal with model uncertainty is a therefore a trade-off between the different objectives of the model. From the two approaches examined within this research, the orientation estimation and random point selection technique resulted in higher uncertainty due to higher variability in the results, as evident from the high standard deviation in Figure 9. However, it also resulted in better results in terms of model validation, as shown in Figure 10. On the other hand, informed local smoothing resulted in less variable—and thus less uncertain—results (Figure 9), however, it failed model validation more frequently in certain parts of the model domain (Figure 10).
Normally, this uncertainty could be reduced by acquiring more data points, or several measurements of the same value [68]. For a highly uncertain dataset, however, overall model uncertainty may increase when more data points are considered, especially when data points conflict with each other [69]. As discussed earlier, urban subsurface datasets can be limited in the size, quality, and information they provide, as well as their spatial and temporal distribution. As such, these urban datasets can be highly uncertain. Moreover, further subsurface data collection may be inhibited by urban coverage and other infrastructure. Therefore, the only viable option is to perform the various subsurface investigations using these already existing and highly uncertain datasets. It is thus necessary to find an approach to mitigate that uncertainty, which is suitable for both the dataset and the modelling purpose. Further work is currently being carried out to assess how the uncertainty originating from the geological interpretation propagates to a hydrogeological study of the area.
It should be noted that the orientation estimation and random point selection technique has only been evaluated for the case study presented within this research. Furthermore, the presented technique has only been evaluated against data-informed local smoothing, which has not been previously applied beyond a theoretical level. Therefore, there is a need to investigate the suitability of the proposed approach for other applications, as well as evaluate its performance compared to other methods for mitigating data uncertainty.

6. Conclusions

This research investigated different approaches for geological modelling using a highly uncertain dataset. More specifically, it focused on the uncertainty originating from an uneven temporal and spatial distribution of data points, which may contain conflicting information. To that end, we developed a case study and performed an uncertainty analysis by proposing a novel approach for mitigating the uncertainty from clusters of uncertain data points. This approach was based on converting geological information into orientations and contact points used for implicit geological modelling. Furthermore, this research evaluated the suitability of applying data informed local smoothing for a real-world application, which to the best of the authors’ knowledge has not yet been applied beyond a theoretical level.
From the two approaches examined in this research, the orientation estimation and random point selection technique resulted in higher uncertainty but better model validation, compared to informed local smoothing. If the objective of an analysis is to create the most realistic representation of the subsurface, the orientation estimation and random point selection technique might be preferred due to its better results in terms of model validation. However, when looking at how the uncertainty in the geological representation propagates to further, downstream analyses that depend on the geological interpretation, data informed local smoothing might be better suited due to its lower uncertainty. When evaluating urban planning, flooding, or energy studies, a better understanding of the subsurface can result in improved design, engineering, and financial planning. This research therefore highlights that there is a trade-off between realism, simplicity, and precision when developing a model, guided by the modelling objective and the selected approach.
Recognising this trade-off is important when dealing with highly uncertain datasets, like those usually found within urban areas. As interest in urban subsurface infrastructure, water resources, and energy continues to grow, the investigation of the urban subsurface is becoming increasingly important, with modelling playing a central role in these efforts. As such, robust modelling will depend on finding ways to use the existing datasets and mitigating the uncertainty within them.

Key Takeaways

  • Urban geological datasets are usually highly uncertain, resulting in higher model uncertainty. Collection of new urban subsurface data is often prohibited due to urban cover. Therefore, there is a need for new approaches to mitigate the uncertainty within existing datasets.
  • To that end, this research presents a novel method for reducing geological modelling uncertainty caused by uneven and conflicting geological data by converting geological information into orientations and contact points for the geological interpolation.
  • This research also compares the results from the proposed methodology to data-informed local smoothing of the geological interpolator.
  • The proposed methodology resulted in better results in terms of model validation, but higher uncertainty compared to data-informed local smoothing.
  • This research highlights that there is a trade-off between model precision, realism, and simplicity, especially when working with highly uncertain datasets. This trade-off is guided by the model objective.

Author Contributions

Conceptualization, C.N., S.B., and R.S.; Methodology, C.N.; Software, C.N.; Validation, C.N., S.B., and R.S.; Formal Analysis, C.N.; Investigation, C.N.; Resources, S.B., and R.S.; Data Curation, C.N.; Writing—Original Draft Preparation, C.N.; Writing—Review and Editing, S.B., and R.S.; Supervision, S.B., and R.S.; Project Administration, R.S.; Funding Acquisition, R.S. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by Newcastle University and the Water Infrastructure and Resilience Centre for Doctoral Training (WIRe CDT) funded by the Engineering and Physical Sciences Research Council (EPSRC) under grant EP/S023666/1.

Data Availability Statement

The methodology uses the open-source software packages GemPy v2 (https://github.com/gempy-project/gempy_legacy last accessed on 26 July 2025) and GemGIS (https://github.com/cgre-aachen/gemgis last accessed on 26 July 2025). Additional material to support the methodology followed in this work can be found under https://github.com/hntig/ouseburn_geomodel (last accessed on 26 July 2025).

Acknowledgments

The Authors would like to thank Brian Thomas for his invaluable contributions to the initial stages of this research.

Conflicts of Interest

We declare no conflicts of interest.

References

  1. Wellmann, F.; Schaaf, A.; De La Varga, M.; Von Hagke, C. From Google Earth to 3D Geology Problem 2: Seeing Below the Surface of the Digital Earth. In Developments in Structural Geology and Tectonics; Elsevier: Amsterdam, The Netherlands, 2019; Volume 5, pp. 189–204. ISBN 978-0-12-814048-2. [Google Scholar]
  2. Campbell, D.; De Beer, J.; Mielby, S.; Van Campenhout, I.; Van Der Meulen, M.; Erikkson, I.; Ganerod, G.; Lawrence, D.; Bacic, M.; Donald, A.; et al. Transforming the Relationships Between Geoscientists and Urban Decision-Makers: European Cost Sub-Urban Action (TU1206). Procedia Eng. 2017, 209, 4–11. [Google Scholar] [CrossRef]
  3. Wellmann, F.; Caumon, G. 3-D Structural Geological Models: Concepts, Methods, and Uncertainties. Adv. Geophys. 2018, 59, 1–121. [Google Scholar] [CrossRef]
  4. Caumon, G.; Collon-Drouaillet, P.; Le Carlier de Veslud, C.; Viseur, S.; Sausse, J. Surface-Based 3D Modeling of Geological Structures. Math. Geosci. 2009, 41, 927–945. [Google Scholar] [CrossRef]
  5. Scott, S.W.; Covell, C.; Júlíusson, E.; Valfells, Á.; Newson, J.; Hrafnkelsson, B.; Pálsson, H.; Gudjónsdóttir, M. A Probabilistic Geologic Model of the Krafla Geothermal System Constrained by Gravimetric Data. Geotherm. Energy 2019, 7, 29. [Google Scholar] [CrossRef]
  6. Marquetto, L.; Jüstel, A.; Troian, G.C.; Reginato, P.A.R.; Simões, J.C. Developing a 3D Hydrostratigraphical Model of the Emerged Part of the Pelotas Basin along the Northern Coast of Rio Grande Do Sul State, Brazil. Environ. Earth Sci. 2024, 83, 329. [Google Scholar] [CrossRef]
  7. Haehnel, P.; Freund, H.; Greskowiak, J.; Massmann, G. Development of a Three-dimensional Hydrogeological Model for the Island of Norderney (Germany) Using GemPy. Geosci. Data J. 2024, 11, 267–283. [Google Scholar] [CrossRef]
  8. Yan, W.; Yang, C.; Shen, P.; Zhou, W.-H. Efficient Probabilistic Tunning of Large Geological Model (LGM) for Underground Digital Twin. Eng. Geol. 2025, 350, 107996. [Google Scholar] [CrossRef]
  9. Guo, J.; Wang, J.; Wu, L.; Liu, C.; Li, C.; Li, F.; Lin, M.; Jessell, M.W.; Li, P.; Dai, X.; et al. Explicit-Implicit-Integrated 3-D Geological Modelling Approach: A Case Study of the Xianyan Demolition Volcano (Fujian, China). Tectonophysics 2020, 795, 228648. [Google Scholar] [CrossRef]
  10. Cowan, J.; Beatson, R.; Ross, H.J.; Fright, W.R.; McLennan, T.J.; Evans, T.R.; Carr, J.C.; Lane, R.G.; Bright, D.V.; Gillman, A.J.; et al. Practical Implicit Geological Modelling. In Proceedings of the Fifth International Mining Geology Conference, Bendigo, Victoria, 17–19 November 2003; pp. 17–19. [Google Scholar]
  11. Kentwell, D.J. Destroying the Distinction Between Explicit and Implicit Geological Modelling. 2019. Available online: https://www.srk.com/en/publications/destroying-the-distinction-between-explicit-and-implicit-geological-modelling (accessed on 28 October 2025).
  12. Wei, X.; Yin, Z.; Bonner, W.; Caers, J. Knowledge-Driven Stochastic Modeling of Geological Geometry Features Conditioned on Drillholes and Outcrop Contacts. Comput. Geosci. 2025, 196, 105779. [Google Scholar] [CrossRef]
  13. Jessell, M.; Aillères, L.; Kemp, E.D.; Lindsay, M.; Wellmann, F.; Hillier, M.; Laurent, G.; Carmichael, T.; Martin, R. Next Generation Three-Dimensional Geologic Modeling and Inversion. In Building Exploration Capability for the 21st Century; Society of Economic Geologists: Littleton, CO, USA, 2014; ISBN 978-1-62949-142-4. [Google Scholar]
  14. Lajaunie, C.; Courrioux, G.; Manuel, L. Foliation Fields and 3D Cartography in Geology: Principles of a Method Based on Potential Interpolation. Math. Geol. 1997, 29, 571–584. [Google Scholar] [CrossRef]
  15. Matheron, G. Splines and Kriging: Their Formal Equivalence. In Down to Earth Statistics: Solutions Looking for Geological Problems; Syracuse University Geological Contributions: Syracuse, NY, USA, 1981; pp. 77–95. [Google Scholar]
  16. Wackernagel, H. Multivariate Geostatistics: An Introduction with Applications; Springer: Berlin/Heidelberg, Germany, 2003; Volume 3, ISBN 978-3-540-44142-7. [Google Scholar]
  17. Chilès, J.-P.; Delfiner, P. Geostatistics: Modeling Spatial Uncertainty; John Wiley & Sons: Hoboken, NJ, USA, 2009; ISBN 978-0-470-31783-9. [Google Scholar]
  18. Doherty, J.E.; Hunt, R.J. Approaches to Highly Parameterized Inversion-A Guide to Using PEST for Groundwater-Model Calibration; U.S. Geological Survey Scientific Investigations Report 2010–5169; US Geological Survey: Reston, VA, USA, 2010. [Google Scholar]
  19. Randle, C.H.; Bond, C.E.; Lark, R.M.; Monaghan, A.A. Uncertainty in Geological Interpretations: Effectiveness of Expert Elicitations. Geosphere 2019, 15, 108–118. [Google Scholar] [CrossRef]
  20. Lin, M.-L.; Lin, C.-H.; Li, C.-H.; Liu, C.-Y.; Hung, C.-H. 3D Modeling of the Ground Deformation along the Fault Rupture and Its Impact on Engineering Structures: Insights from the 1999 Chi-Chi Earthquake, Shigang District, Taiwan. Eng. Geol. 2021, 281, 105993. [Google Scholar] [CrossRef]
  21. Li, N.; Song, X.; Xiao, K.; Li, S.; Li, C.; Wang, K. Part II: A Demonstration of Integrating Multiple-Scale 3D Modelling into GIS-Based Prospectivity Analysis: A Case Study of the Huayuan-Malichang District, China. Ore Geol. Rev. 2018, 95, 292–305. [Google Scholar] [CrossRef]
  22. Price, S.J.; Terrington, R.L.; Busby, J.; Bricker, S.; Berry, T. 3D Ground-Use Optimisation for Sustainable Urban Development Planning: A Case-Study from Earls Court, London, UK. Tunn. Undergr. Space Technol. 2018, 81, 144–164. [Google Scholar] [CrossRef]
  23. Webster, R.; Oliver, M.A. Geostatistics for Environmental Scientists, 2nd ed.; Statistics in Practice; John Wiley & Sons: Chichester, UK, 2007; ISBN 978-0-470-02858-2. [Google Scholar]
  24. Attard, G.; Rossier, Y.; Eisenlohr, L. Urban Groundwater Age Modeling under Unconfined Condition—Impact of Underground Structures on Groundwater Age: Evidence of a Piston Effect. J. Hydrol. 2016, 535, 652–661. [Google Scholar] [CrossRef]
  25. Hou, W.; Yang, L.; Deng, D.; Ye, J.; Clarke, K.; Yang, Z.; Zhuang, W.; Liu, J.; Huang, J. Assessing Quality of Urban Underground Spaces by Coupling 3D Geological Models: The Case Study of Foshan City, South China. Comput. Geosci. 2016, 89, 1–11. [Google Scholar] [CrossRef]
  26. Doyle, M.R. From Hydro/Geology to the Streetscape: Evaluating Urban Underground Resource Potential. Tunn. Undergr. Space Technol. 2016, 55, 83–95. [Google Scholar] [CrossRef]
  27. Zhou, F.; Li, M.; Huang, C.; Liang, H.; Liu, Y.; Zhang, J.; Wang, B.; Hao, M. Lithology-Based 3D Modeling of Urban Geological Attributes and Their Engineering Application: A Case Study of Guang’an City, SW China. Front. Earth Sci. 2022, 10, 918285. [Google Scholar] [CrossRef]
  28. Zhu, J.; Zhou, X.; Zhang, L. Large-Scale Urban 3D Geological Modeling Based on Multi-Method Coupling Under Multi-Source Heterogeneous Data Conditions. Appl. Sci. 2024, 14, 12059. [Google Scholar] [CrossRef]
  29. Macdonald, D.; Dixon, A.; Newell, A.; Hallaways, A. Groundwater Flooding within an Urbanised Flood Plain. J. Flood Risk Manag. 2012, 5, 68–80. [Google Scholar] [CrossRef]
  30. Morris, S.E.; Cobby, D.; Zaidman, M.; Fisher, K. Modelling and Mapping Groundwater Flooding at the Ground Surface in Chalk Catchments. J. Flood Risk Manag. 2018, 11, S251–S268. [Google Scholar] [CrossRef]
  31. Aicha, O.; Abdessamad, G.; Hassane, J.O. Groundwater Flooding in Urban Areas: Occurrence Process, Potential Impacts and the Role Of Remote Sensing and GIS Techniques in Preventing It. In Proceedings of the 2020 IEEE International Conference of Moroccan Geomatics (Morgeo), Casablanca, Morocco, 11–13 May 2020; pp. 1–5. [Google Scholar]
  32. Allocca, V.; Di Napoli, M.; Coda, S.; Carotenuto, F.; Calcaterra, D.; Di Martire, D.; De Vita, P. A Novel Methodology for Groundwater Flooding Susceptibility Assessment through Machine Learning Techniques in a Mixed-Land Use Aquifer. Sci. Total Environ. 2021, 790, 148067. [Google Scholar] [CrossRef]
  33. Locatelli, L.; Mark, O.; Mikkelsen, P.S.; Arnbjerg-Nielsen, K.; Deletic, A.; Roldin, M.; Binning, P.J. Hydrologic Impact of Urbanization with Extensive Stormwater Infiltration. J. Hydrol. 2017, 544, 524–537. [Google Scholar] [CrossRef]
  34. Zhang, K.; Chui, T.F.M. A Review on Implementing Infiltration-Based Green Infrastructure in Shallow Groundwater Environments: Challenges, Approaches, and Progress. J. Hydrol. 2019, 579, 124089. [Google Scholar] [CrossRef]
  35. Yan, W.; Yi, S.; Huang, T.; Zou, J.; Zhou, W.-H.; Shen, P. Geophysics-Informed Stratigraphic Modeling Using Spatial Sequential Bayesian Updating Algorithm. J. Rock Mech. Geotech. Eng. 2025, 17, 4400–4412. [Google Scholar] [CrossRef]
  36. Beven, K. Facets of Uncertainty: Epistemic Uncertainty, Non-Stationarity, Likelihood, Hypothesis Testing, and Communication. Hydrol. Sci. J. 2016, 61, 1652–1665. [Google Scholar] [CrossRef]
  37. Lyu, M.; Ren, B.; Wu, B.; Tong, D.; Ge, S.; Han, S. A Parametric 3D Geological Modeling Method Considering Stratigraphic Interface Topology Optimization and Coding Expert Knowledge. Eng. Geol. 2021, 293, 106300. [Google Scholar] [CrossRef]
  38. Tian, Y.; Xiao, S.; Zhang, R.; Weng, Z.; Wu, X.; Wu, Y. Local Dynamic Update Methods for 3D Geological Body Structure Model and Voxel Model. Earth Sci. Inform. 2024, 17, 841–851. [Google Scholar] [CrossRef]
  39. Shi, C.; Wang, Y. Data-Driven Construction of Three-Dimensional Subsurface Geological Models from Limited Site-Specific Boreholes and Prior Geological Knowledge for Underground Digital Twin. Tunn. Undergr. Space Technol. 2022, 126, 104493. [Google Scholar] [CrossRef]
  40. He, Z.; Xu, X.; Peng, P.; Wang, L.; Tian, S. A Deep Learning-Driven Three-Dimensional Geological Modeling Method Using Sparse Borehole Sampling Data. Measurement 2025, 256, 118461. [Google Scholar] [CrossRef]
  41. Hang, Z.; Xue, T.; Chen, J.; Shi, Y.; Yin, Z.; Cui, Z.; Zhou, G. A 3D Geological Modeling Method Using the Transformer Model: A Solution for Sparse Borehole Data. Minerals 2025, 15, 301. [Google Scholar] [CrossRef]
  42. Guo, J.; Xu, X.; Wang, L.; Wang, X.; Wu, L.; Jessell, M.; Ogarko, V.; Liu, Z.; Zheng, Y. GeoPDNN 1.0: A Semi-Supervised Deep Learning Neural Network Using Pseudo-Labels for Three-Dimensional Shallow Strata Modelling and Uncertainty Analysis in Urban Areas from Borehole Data. Geosci. Model Dev. 2024, 17, 957–973. [Google Scholar] [CrossRef]
  43. Lyu, B.; Wang, Y.; Shi, C. Multi-Scale Generative Adversarial Networks (GAN) for Generation of Three-Dimensional Subsurface Geological Models from Limited Boreholes and Prior Geological Knowledge. Comput. Geotech. 2024, 170, 106336. [Google Scholar] [CrossRef]
  44. Von Harten, J.; De La Varga, M.; Hillier, M.; Wellmann, F. Informed Local Smoothing in 3D Implicit Geological Modeling. Minerals 2021, 11, 1281. [Google Scholar] [CrossRef]
  45. De La Varga, M.; Schaaf, A.; Wellmann, F. GemPy 1.0: Open-Source Stochastic Geological Modeling and Inversion. Geosci. Model Dev. 2019, 12, 1–32. [Google Scholar] [CrossRef]
  46. Birkinshaw, S.J.; Kilsby, C.; O’Donnell, G.; Quinn, P.; Adams, R.; Wilkinson, M.E. Stormwater Detention Ponds in Urban Catchments—Analysis and Validation of Performance of Ponds in the Ouseburn Catchment, Newcastle upon Tyne, UK. Water 2021, 13, 2521. [Google Scholar] [CrossRef]
  47. Critchley, M.F. Variscan Tectonics of the Alston Block, Northern England. Geol. Soc. Lond. Spec. Publ. 1984, 14, 139–146. [Google Scholar] [CrossRef]
  48. Waters, C.N. Carboniferous Geology of Northern England. Open Univ. Geol. Soc. J. 2009, 30, 5–16. [Google Scholar]
  49. Mills, D.A.C.; Holliday, D.W. Geology of the District Around Newcastle Upon Tyne, Gateshead and Consett: Memoir for 1:50,000 Geological Sheet 20 (England and Wales); British Geological Survey: Nottingham, UK, 1998; ISBN 978-0-11-884538-0. [Google Scholar]
  50. Waters, C.N.; Davies, S.J. Carboniferous: Extensional Basins, Advancing Deltas and Coal Swamps. In The Geology of England and Wales; Brenchley, P.J., Rawson, P.F., Eds.; The Geological Society of London: London, UK, 2006; pp. 173–223. ISBN 978-1-86239-388-2. [Google Scholar]
  51. Bradwell, T.; Stoker, M.S.; Golledge, N.R.; Wilson, C.K.; Merritt, J.W.; Long, D.; Everest, J.D.; Hestvik, O.B.; Stevenson, A.G.; Hubbard, A.L.; et al. The Northern Sector of the Last British Ice Sheet: Maximum Extent and Demise. Earth Sci. Rev. 2008, 88, 207–226. [Google Scholar] [CrossRef]
  52. Environment Agency. LIDAR Composite Digital Terrain Model (DTM)—1m; Environment Agency: Bristol, UK, 2023. [Google Scholar]
  53. British Geological Survey. BGS GeoIndex—Onshore; British Geological Survey: Nottingham, UK, 2024. [Google Scholar]
  54. Kearsey, T.I.; Whitbread, K.; Arkley, S.L.B.; Finlayson, A.; Monaghan, A.A.; Mclean, W.S.; Terrington, R.L.; Callaghan, E.A.; Millward, D.; Campbell, S.D.G. Creation and Delivery of a Complex 3D Geological Survey for the Glasgow Area and Its Application to Urban Geology. Earth Environ. Sci. Trans. R. Soc. Edinb. 2019, 2019, 123–140. [Google Scholar] [CrossRef]
  55. Lawley, R.; Garcia-Bajo, M. The National Superficial Deposit Thickness Model (SDTM V5): A User Guide; British Geological Survey: Nottingham, UK, 2010. [Google Scholar]
  56. De La Varga, M.; Wellmann, J.F. Structural Geologic Modeling as an Inference Problem: A Bayesian Perspective. Interpretation 2016, 4, SM15–SM30. [Google Scholar] [CrossRef]
  57. Brisson, S.; Wellmann, F.; Chudalla, N.; Von Harten, J.; Von Hagke, C. Estimating Uncertainties in 3-D Models of Complex Fold-and-Thrust Belts: A Case Study of the Eastern Alps Triangle Zone. Appl. Comput. Geosci. 2023, 18, 100115. [Google Scholar] [CrossRef]
  58. Schaaf, A.; De La Varga, M.; Wellmann, F.; Bond, C.E. Constraining Stochastic 3-D Structural Geological Models with Topology Information Using Approximate Bayesian Computation in GemPy 2.1. Geosci. Model Dev. 2021, 14, 3899–3913. [Google Scholar] [CrossRef]
  59. Thomas, A.T.; Von Harten, J.; Jusri, T.; Reiche, S.; Wellmann, F. An Integrated Modeling Scheme for Characterizing 3D Hydrogeological Heterogeneity of the New Jersey Shelf. Mar. Geophys. Res. 2022, 43, 11. [Google Scholar] [CrossRef]
  60. Güdük, N.; De La Varga, M.; Kaukolinna, J.; Wellmann, F. Model-Based Probabilistic Inversion Using Magnetic Data: A Case Study on the Kevitsa Deposit. Geosciences 2021, 11, 150. [Google Scholar] [CrossRef]
  61. Jüstel, A.; Correira, A.E.; Pischke, M.; de la Varga, M.; Wellmann, F. GemGIS—Spatial Data Processing for Geomodeling. J. Open Source Softw. 2022, 7, 3709. [Google Scholar] [CrossRef]
  62. Scott, D.W.; Sain, S.R. Multidimensional Density Estimation. In Handbook of Statistics; Elsevier: Amsterdam, The Netherlands, 2005; Volume 24, pp. 229–261. ISBN 978-0-444-51141-6. [Google Scholar]
  63. Silverman, B.W. Density Estimation for Statistics and Data Analysis, 1st ed.; Routledge: Oxfordshire, UK, 2018; ISBN 978-1-315-14091-9. [Google Scholar]
  64. Krivoruchko, P.; Gribov, A.; Ver Hoef, J.M. A New Method for Handling the Nugget Effect in Kriging. In Stochastic Modeling and Geostatistics; Coburn, T.C., Yarus, J.M., Chambers, R.L., Eds.; American Association of Petroleum Geologists: Tulsa, OK, USA, 2006; pp. 81–89. ISBN 978-0-89181-704-8. [Google Scholar]
  65. Christensen, W.F. Filtered Kriging for Spatial Data with Heterogeneous Measurement Error Variances. Biometrics 2011, 67, 947–957. [Google Scholar] [CrossRef]
  66. Tarantola, A. Inverse Problem Theory and Methods for Model Parameter Estimation; Other Titles in Applied Mathematics; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2005; ISBN 978-0-89871-572-9. [Google Scholar]
  67. Barnett, B.; Townley, L.; Post, V.; Evans, R.; Hunt, R.; Peeters, L.; Richardson, S.; Werner, A.; Knapton, A.; Boronkay, A. Australian Groundwater Modelling Guidelines; Australian National Water Commission: Canberra, Australia, 2012; ISBN 978-1-921853-91-3. [Google Scholar]
  68. Mann, J.C. Uncertainty in Geology. In Computers in Geology—25 Years of Progress; Oxford University Press, Inc.: Oxford, UK, 1993; pp. 241–254. [Google Scholar]
  69. Zimmermann, H.-J. An Application-Oriented View of Modeling Uncertainty. Eur. J. Oper. Res. 2000, 122, 190–198. [Google Scholar] [CrossRef]
Geosciences 15 00423 g001
Figure 1. Example of implicit geological model with a fault line. Points in the figure represent the contact points between geological formations and arrows represent the orientations. The geological surfaces on the right side of the fault line are represented with the orientation and contact points obtained from the left side of the fault line.
Figure 1. Example of implicit geological model with a fault line. Points in the figure represent the contact points between geological formations and arrows represent the orientations. The geological surfaces on the right side of the fault line are represented with the orientation and contact points obtained from the left side of the fault line.
Geosciences 15 00423 g001
Geosciences 15 00423 g002
Figure 2. Map showing the Ouseburn River and its tributaries, as well as the boundaries of the Ouseburn catchment (contains: Map data from OpenStreetMap; OS data © Crown copyright 2025; EA data © Crown copyright 2025).
Figure 2. Map showing the Ouseburn River and its tributaries, as well as the boundaries of the Ouseburn catchment (contains: Map data from OpenStreetMap; OS data © Crown copyright 2025; EA data © Crown copyright 2025).
Geosciences 15 00423 g002
Geosciences 15 00423 g003
Figure 3. Map of the bedrock within the study area (contains: EA data © Crown copyright 2025; BGS materials © UKRI 2025).
Figure 3. Map of the bedrock within the study area (contains: EA data © Crown copyright 2025; BGS materials © UKRI 2025).
Geosciences 15 00423 g003
Geosciences 15 00423 g004
Figure 4. Map of the superficial deposits within the study area. Gaps represent areas with no superficial cover (contains EA data © Crown copyright 2025; BGS materials © UKRI 2025).
Figure 4. Map of the superficial deposits within the study area. Gaps represent areas with no superficial cover (contains EA data © Crown copyright 2025; BGS materials © UKRI 2025).
Geosciences 15 00423 g004
Geosciences 15 00423 g005
Figure 5. Map showing the location of all of the geological borehole records held by BGS within the model area (contains map data from OpenStreetMap; OS data © Crown copyright 2025; EA data © Crown copyright 2025; BGS materials © UKRI 2025).
Figure 5. Map showing the location of all of the geological borehole records held by BGS within the model area (contains map data from OpenStreetMap; OS data © Crown copyright 2025; EA data © Crown copyright 2025; BGS materials © UKRI 2025).
Geosciences 15 00423 g005
Geosciences 15 00423 g006
Figure 6. Flowchart showing the steps of the analysis.
Figure 6. Flowchart showing the steps of the analysis.
Geosciences 15 00423 g006
Geosciences 15 00423 g007
Figure 7. Map showing the locations of geological borehole records held by BGS within the model area that were deeper than 20 m and were evaluated for the development of the superficial thickness model. The records were separated between those that were accepted (290 boreholes) and rejected (217 boreholes) for further analysis, depending on their quality and lack of important information (e.g., coordinates, ground surface elevation, etc.) (contains map data from OpenStreetMap; OS data © Crown copyright 2025; EA data © Crown copyright 2025; BGS materials © UKRI 2025).
Figure 7. Map showing the locations of geological borehole records held by BGS within the model area that were deeper than 20 m and were evaluated for the development of the superficial thickness model. The records were separated between those that were accepted (290 boreholes) and rejected (217 boreholes) for further analysis, depending on their quality and lack of important information (e.g., coordinates, ground surface elevation, etc.) (contains map data from OpenStreetMap; OS data © Crown copyright 2025; EA data © Crown copyright 2025; BGS materials © UKRI 2025).
Geosciences 15 00423 g007
Geosciences 15 00423 g008
Figure 8. Spatial plot of the mean estimated superficial thickness within the Ouseburn catchment for the uncertainty analysis with 1000 different model formulations, for the 50 m fixed-radius nearest neighbour search used in the orientation estimations. (a) Orientation estimation and random point selection. (b) Informed local smoothing. (c) Difference (a,b) (contains map data from OpenStreetMap; OS data © Crown copyright 2025; EA data © Crown copyright 2025; BGS materials © UKRI 2025).
Figure 8. Spatial plot of the mean estimated superficial thickness within the Ouseburn catchment for the uncertainty analysis with 1000 different model formulations, for the 50 m fixed-radius nearest neighbour search used in the orientation estimations. (a) Orientation estimation and random point selection. (b) Informed local smoothing. (c) Difference (a,b) (contains map data from OpenStreetMap; OS data © Crown copyright 2025; EA data © Crown copyright 2025; BGS materials © UKRI 2025).
Geosciences 15 00423 g008
Geosciences 15 00423 g009
Figure 9. Spatial plot of the standard deviation within the Ouseburn catchment for the uncertainty analysis with 1000 different model formulations, for the 50 m fixed-radius nearest neighbour search used in the orientation estimations. (a) Orientation estimation and random point selection. (b) Informed local smoothing. (c) Difference (a,b) (contains map data from OpenStreetMap; OS data © Crown copyright 2025; EA data © Crown copyright 2025; BGS materials © UKRI 2025).
Figure 9. Spatial plot of the standard deviation within the Ouseburn catchment for the uncertainty analysis with 1000 different model formulations, for the 50 m fixed-radius nearest neighbour search used in the orientation estimations. (a) Orientation estimation and random point selection. (b) Informed local smoothing. (c) Difference (a,b) (contains map data from OpenStreetMap; OS data © Crown copyright 2025; EA data © Crown copyright 2025; BGS materials © UKRI 2025).
Geosciences 15 00423 g009
Geosciences 15 00423 g010
Figure 10. Spatial plot showing the model validation results within the Ouseburn catchment for analysis with 1000 different model formulations, for the 50 m fixed-radius nearest neighbour search used in the orientation estimations. (a) Orientation estimation and random point selection. (b) Informed local smoothing. (contains map data from OpenStreetMap; OS data © Crown copyright 2025; EA data © Crown copyright 2025).
Figure 10. Spatial plot showing the model validation results within the Ouseburn catchment for analysis with 1000 different model formulations, for the 50 m fixed-radius nearest neighbour search used in the orientation estimations. (a) Orientation estimation and random point selection. (b) Informed local smoothing. (contains map data from OpenStreetMap; OS data © Crown copyright 2025; EA data © Crown copyright 2025).
Geosciences 15 00423 g010
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Ntigkakis, C.; Birkinshaw, S.; Stirling, R. Geological Modelling of Urban Environments Under Data Uncertainty. Geosciences 2025, 15, 423. https://doi.org/10.3390/geosciences15110423

AMA Style

Ntigkakis C, Birkinshaw S, Stirling R. Geological Modelling of Urban Environments Under Data Uncertainty. Geosciences. 2025; 15(11):423. https://doi.org/10.3390/geosciences15110423

Chicago/Turabian Style

Ntigkakis, Charalampos, Stephen Birkinshaw, and Ross Stirling. 2025. "Geological Modelling of Urban Environments Under Data Uncertainty" Geosciences 15, no. 11: 423. https://doi.org/10.3390/geosciences15110423

APA Style

Ntigkakis, C., Birkinshaw, S., & Stirling, R. (2025). Geological Modelling of Urban Environments Under Data Uncertainty. Geosciences, 15(11), 423. https://doi.org/10.3390/geosciences15110423

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop