Upwellings and Mantle Ponding Zones in the Lower Mantle Transition Zone (660–1000 km)
Abstract
1. Introduction
2. Full Waveform Seismic Imaging of Mantle Plumes
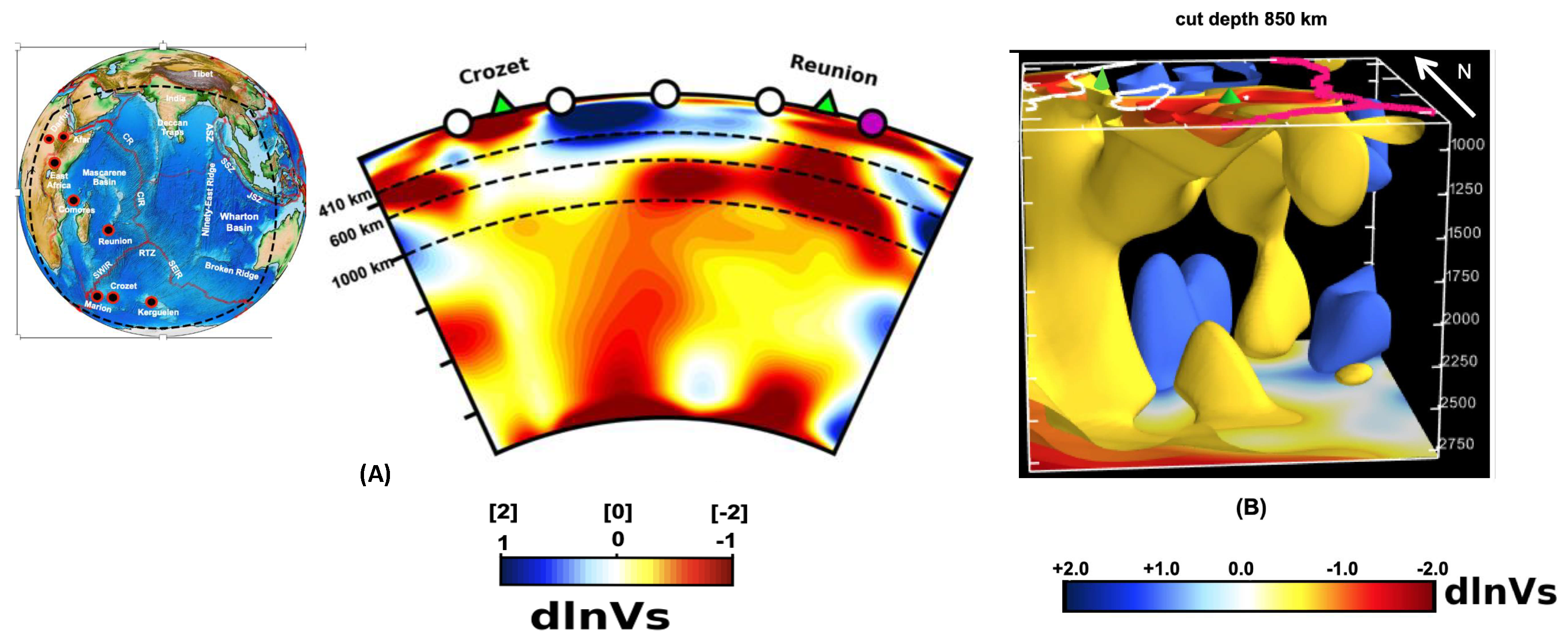
2.1. Seismic Tomographic Imaging of La Réunion Plume
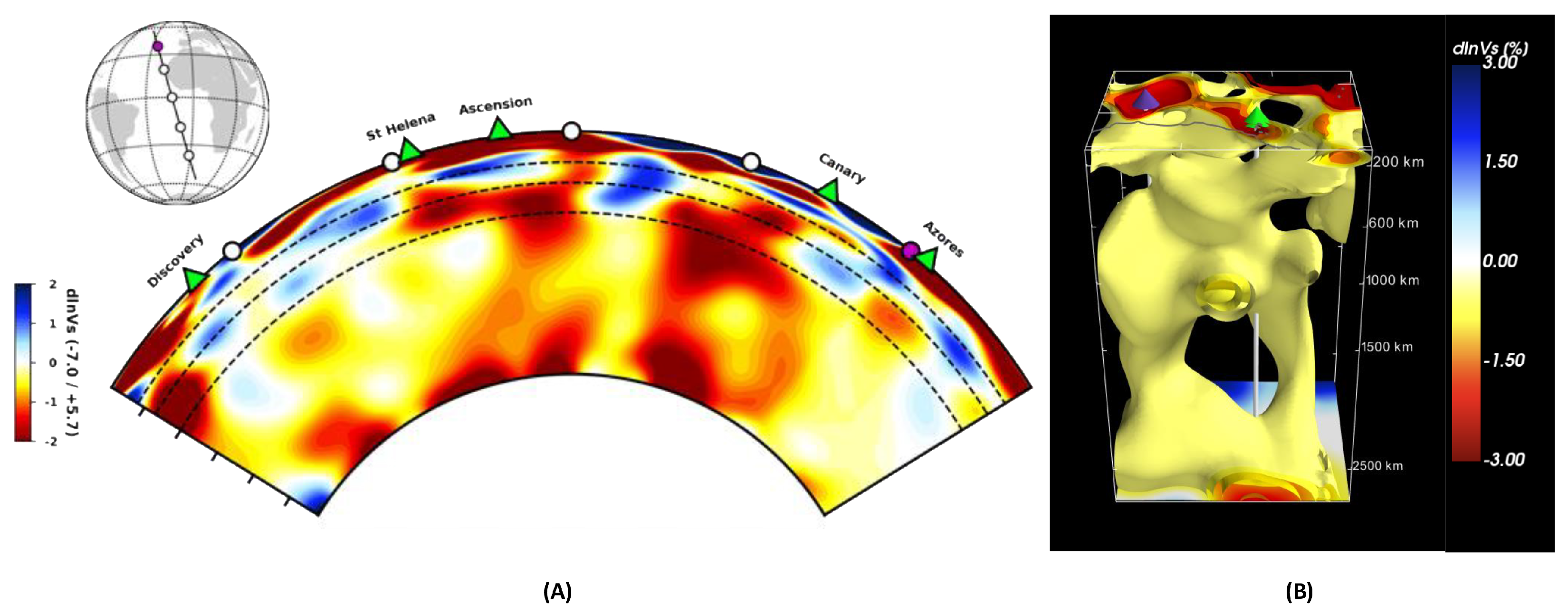
2.2. Full Waveform Tomography of the Southern and Central Atlantic Mantle
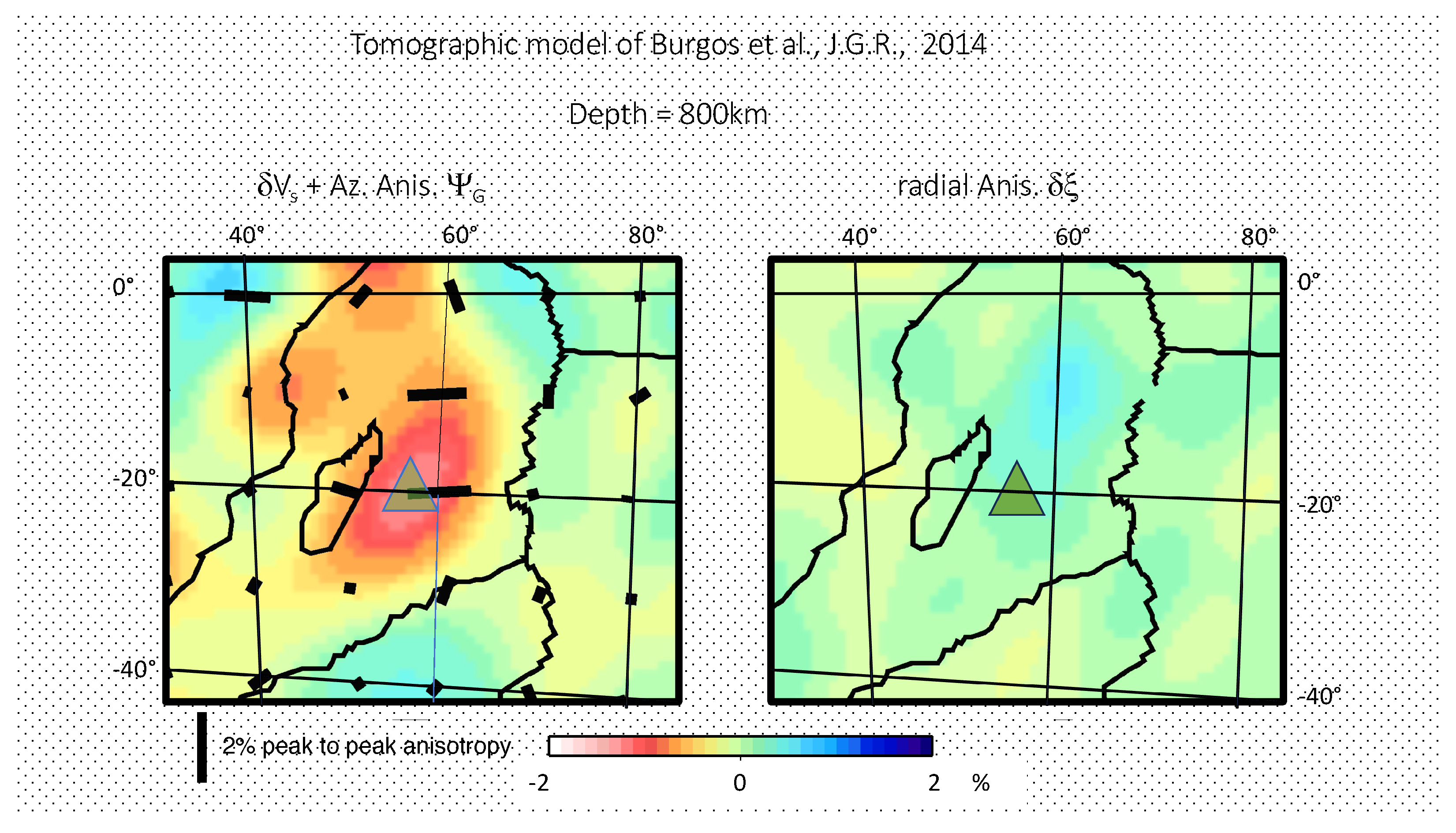
3. Seismic Anisotropy
4. Discussion
4.1. Discontinuities of 660 km and 1000 km
4.2. Mineral Physics and Anisotropy
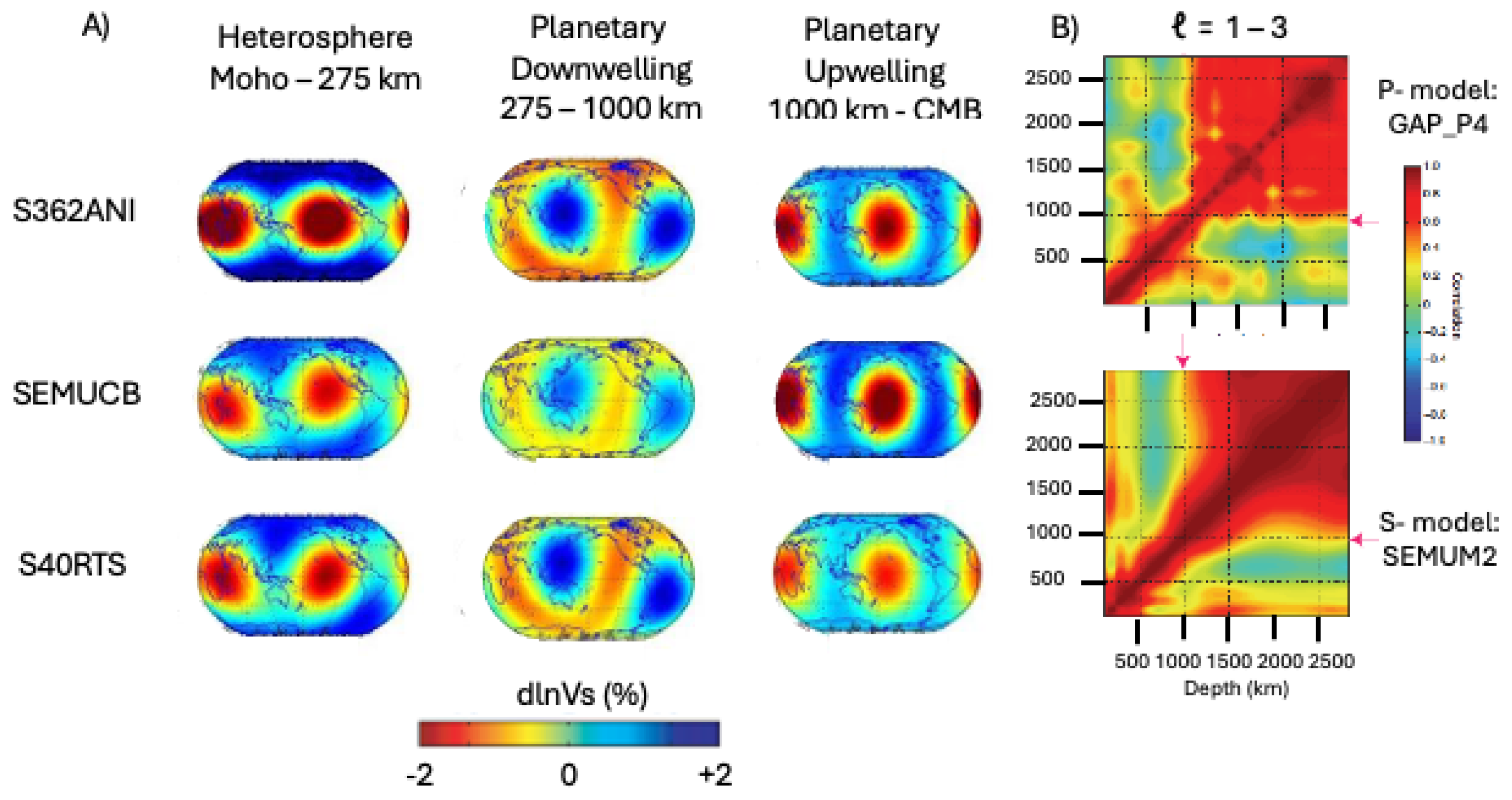
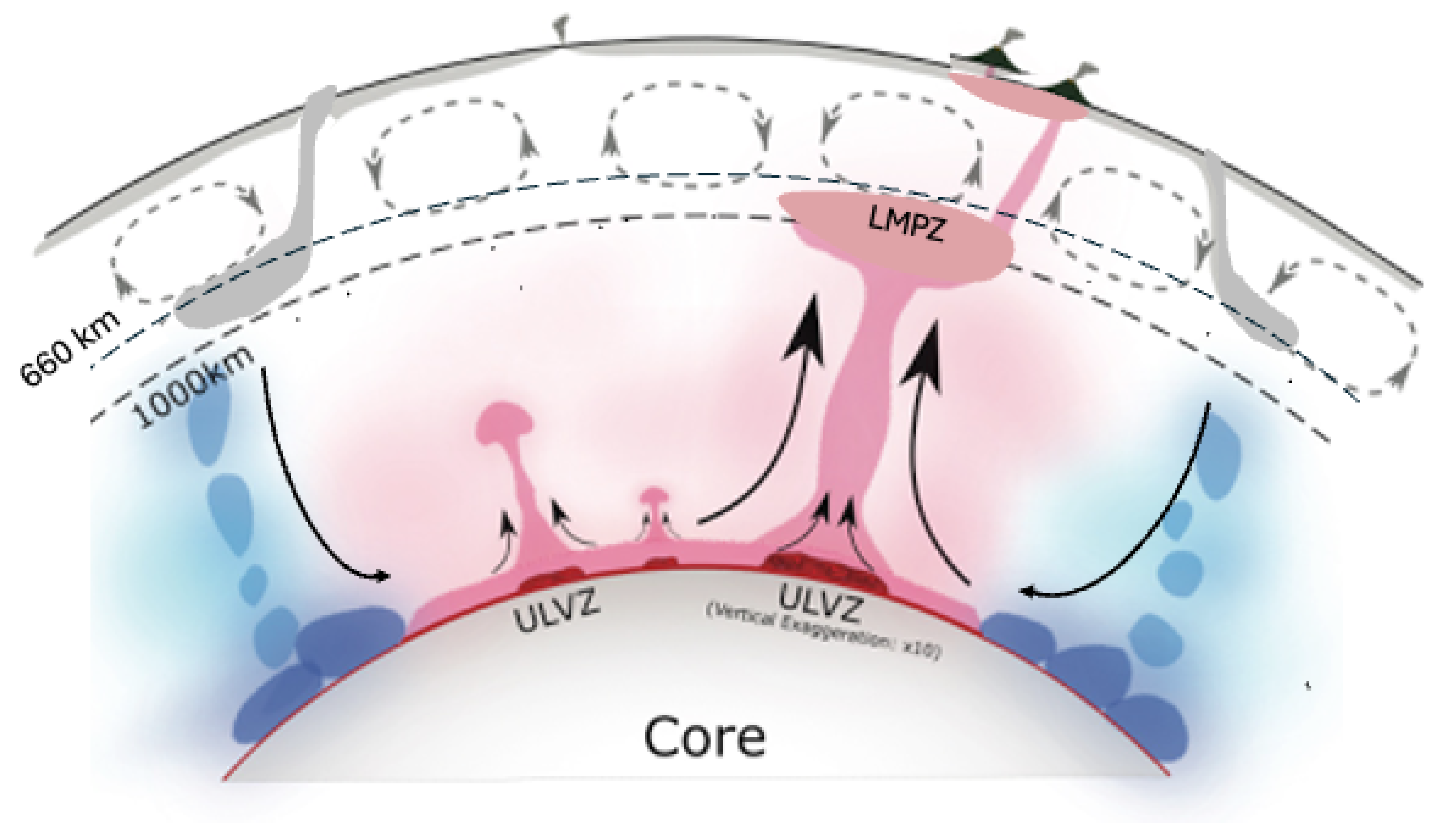
4.3. Geodynamic Consequences of LMPZ
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tuzo Wilson, J. Evidence from ocean islands suggesting movement in the earth. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Sci. 1965, 258, 145–167. [Google Scholar]
- Morgan, W.J. Convection plumes in the lower mantle. Nature 1971, 230, 42–43. [Google Scholar] [CrossRef]
- Richards, M.A.; Duncan, R.A.; Courtillot, V.E. Flood basalts and hot-spot tracks: Plume heads and tails. Science 1989, 246, 103–107. [Google Scholar] [CrossRef] [PubMed]
- Olsen, P.E. Giant lava flows, mass extinctions, and mantle plumes. Science 1999, 284, 604–605. [Google Scholar] [CrossRef]
- Courtillot, V.; Jaupart, C.; Manighetti, I.; Tapponnier, P.; Besse, J. On causal links between flood basalts and continental breakup. Earth Planet. Sci. Lett. 1999, 166, 177–195. [Google Scholar] [CrossRef]
- Whitehead, J.J.A.; Luther, D.S. Dynamics of laboratory diapir and plume models. J. Geophys. Res. 1975, 80, 705–717. [Google Scholar] [CrossRef]
- Griffiths, R. The differing effects of compositional and thermal buoyancies on the evolution of mantle diapirs. Phys. Earth Planet. Inter. 1986, 43, 261–273. [Google Scholar] [CrossRef]
- Foulger, G.R. Plates vs. Plumes: A Geological Controversy; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Montagner, J.P. Can seismology tell us anything about convection in the mantle? Rev. Geophys. 1994, 32, 115–137. [Google Scholar] [CrossRef]
- Courtillot, V.; Davaille, A.; Besse, J.; Stock, J. Three distinct types of hotspots in the Earth’s mantle. Earth Planet. Sci. Lett. 2003, 205, 295–308. [Google Scholar] [CrossRef]
- Steinberger, B.; Antretter, M. Conduit diameter and buoyant rising speed of mantle plumes: Implications for the motion of hot spots and shape of plume conduits. Geochem. Geophys. Geosyst. 2006, 7, Q11018. [Google Scholar] [CrossRef]
- Davaille, A. Simultaneous generation of hotspots and superswells by convection in a heterogeneous planetary mantle. Nature 1999, 402, 756–760. [Google Scholar] [CrossRef]
- Lin, S.C.; van Keken, P.E. Dynamics of thermochemical plumes: 2. Complexity of plume structures and its implications for mapping mantle plumes. Geochem. Geophys. Geosyst. 2006, 7, Q03003. [Google Scholar] [CrossRef]
- Davaille, A.; Carrez, P.; Cordier, P. Fat plumes may reflect the complex rheology of the lower mantle. Geophys. Res. Lett. 2018, 45, 1349–1354. [Google Scholar] [CrossRef] [PubMed]
- Vinnik, L.; Chevrot, S.; Montagner, J.P. Evidence for a stagnant plume in the transition zone? Geophys. Res. Lett. 1997, 24, 1007–1010. [Google Scholar] [CrossRef]
- Tsekhmistrenko, M.; Sigloch, K.; Hosseini, K.; Barruol, G. A tree of Indo-African mantle plumes imaged by seismic tomography. Nat. Geosci. 2021, 14, 612–619. [Google Scholar] [CrossRef]
- Nolet, G.; Karato, S.I.; Montelli, R. Plume fluxes from seismic tomography. Earth Planet. Sci. Lett. 2006, 248, 685–699. [Google Scholar] [CrossRef]
- Sleep, N.H. Lateral flow and ponding of starting plume material. J. Geophys. Res. Solid Earth 1997, 102, 10001–10012. [Google Scholar] [CrossRef]
- Frazer, W.D.; Korenaga, J. Dynamic topography and the nature of deep thick plumes. Earth Planet. Sci. Lett. 2022, 578, 117286. [Google Scholar] [CrossRef]
- Montelli, R.; Nolet, G.; Dahlen, F.; Masters, G.; Engdahl, E.R.; Hung, S.H. Finite-frequency tomography reveals a variety of plumes in the mantle. Science 2004, 303, 338–343. [Google Scholar] [CrossRef]
- Komatitsch, D.; Vilotte, J.P. The spectral element method: An efficient tool to simulate the seismic response of 2D and 3D geological structures. Bull. Seismol. Soc. Am. 1998, 88, 368–392. [Google Scholar] [CrossRef]
- Komatitsch, D.; Tromp, J. Introduction to the spectral element method for three-dimensional seismic wave propagation. Geophys. J. Int. 1999, 139, 806–822. [Google Scholar] [CrossRef]
- Li, X.D.; Romanowicz, B. Global mantle shear velocity model developed using nonlinear asymptotic coupling theory. J. Geophys. Res. Solid Earth 1996, 101, 22245–22272. [Google Scholar] [CrossRef]
- Ritsema, J.; Maguire, R.; Cobden, L.; Goes, S. Seismic imaging of deep mantle plumes. In Mantle Convection and Surface Expressions; Wiley Online Library: Hoboken, NJ, USA, 2021; pp. 353–369. [Google Scholar]
- Rickers, F.; Fichtner, A.; Trampert, J. The Iceland–Jan Mayen plume system and its impact on mantle dynamics in the North Atlantic region: Evidence from full-waveform inversion. Earth Planet. Sci. Lett. 2013, 367, 39–51. [Google Scholar] [CrossRef]
- French, S.; Romanowicz, B. Broad plumes rooted at the base of the Earth’s mantle beneath major hotspots. Nature 2015, 525, 95–99. [Google Scholar] [CrossRef]
- Wamba, M.; Montagner, J.P.; Romanowicz, B. Imaging deep-mantle plumbing beneath La Réunion and Comores hot spots: Vertical plume conduits and horizontal ponding zones. Sci. Adv. 2023, 9, eade3723. [Google Scholar] [CrossRef] [PubMed]
- Munch, F.D.; Romanowicz, B.; Mukhopadhyay, S.; Rudolph, M.L. Deep mantle plumes feeding periodic alignments of asthenospheric fingers beneath the central and southern Atlantic Ocean. Proc. Natl. Acad. Sci. USA 2024, 121, e2407543121. [Google Scholar] [CrossRef] [PubMed]
- Nelson, P.L.; Grand, S.P. Lower-mantle plume beneath the Yellowstone hotspot revealed by core waves. Nat. Geosci. 2018, 11, 280–284. [Google Scholar] [CrossRef]
- Davaille, A.; Romanowicz, B. Deflating the LLSVPs: Bundles of mantle thermochemical plumes rather than thick stagnant piles. Tectonics 2020, 39, e2020TC006265. [Google Scholar] [CrossRef]
- Fukao, Y.; Widiyantoro, S.; Obayashi, M. Stagnant slabs in the upper and lower mantle transition region. Rev. Geophys. 2001, 39, 291–323. [Google Scholar] [CrossRef]
- Fukao, Y.; Obayashi, M. Subducted slabs stagnant above, penetrating through, and trapped below the 660 km discontinuity. J. Geophys. Res. Solid Earth 2013, 118, 5920–5938. [Google Scholar] [CrossRef]
- Li, X.D.; Romanowicz, B. Comparison of global waveform inversions with and without considering cross-branch modal coupling. Geophys. J. Int. 1995, 121, 695–709. [Google Scholar] [CrossRef]
- Romanowicz, B. Global seismic tomography using time domain waveform inversion. Appl. Data Assim. Inverse Probl. Earth Sci. 2023, 5, 220. [Google Scholar]
- Cupillard, P.; Delavaud, E.; Burgos, G.; Festa, G.; Vilotte, J.P.; Capdeville, Y.; Montagner, J.P. RegSEM: A versatile code based on the spectral element method to compute seismic wave propagation at the regional scale. Geophys. J. Int. 2012, 188, 1203–1220. [Google Scholar] [CrossRef]
- French, S.; Romanowicz, B. Whole-mantle radially anisotropic shear velocity structure from spectral-element waveform tomography. Geophys. J. Int. 2014, 199, 1303–1327. [Google Scholar] [CrossRef]
- Wamba, M.; Montagner, J.P.; Romanowicz, B.; Barruol, G. Multi-mode waveform tomography of the Indian ocean upper and mid-mantle around the Réunion hotspot. J. Geophys. Res. Solid Earth 2021, 126, e2020JB021490. [Google Scholar] [CrossRef]
- Barruol, G.; Sigloch, K. Investigating La Réunion hot spot from crust to core. Eos Trans. Am. Geophys. Union 2013, 94, 205–207. [Google Scholar] [CrossRef]
- Stähler, S.C.; Sigloch, K.; Hosseini, K.; Crawford, W.C.; Barruol, G.; Schmidt-Aursch, M.C.; Tsekhmistrenko, M.; Scholz, J.R.; Mazzullo, A.; Deen, M. Performance report of the RHUM-RUM ocean bottom seismometer network around La Réunion, western Indian Ocean. Adv. Geosci. 2016, 41, 43–63. [Google Scholar] [CrossRef]
- Mazzullo, A.; Stutzmann, E.; Montagner, J.P.; Kiselev, S.; Maurya, S.; Barruol, G.; Sigloch, K. Anisotropic tomography around La Réunion island from Rayleigh waves. J. Geophys. Res. Solid Earth 2017, 122, 9132–9148. [Google Scholar] [CrossRef]
- Barruol, G.; Sigloch, K.; Scholz, J.R.; Mazzullo, A.; Stutzmann, E.; Montagner, J.P.; Kiselev, S.; Fontaine, F.R.; Michon, L.; Deplus, C.; et al. Large-scale flow of Indian Ocean asthenosphere driven by Réunion plume. Nat. Geosci. 2019, 12, 1043–1049. [Google Scholar] [CrossRef]
- Montagner, J.P. 3-dimensional structure of the Indian Ocean inferred from long period surface waves. Geophys. Res. Lett. 1986, 13, 315–318. [Google Scholar] [CrossRef]
- Debayle, E.; Lévêque, J. Upper mantle heterogeneities in the Indian Ocean from waveform inversion. Geophys. Res. Lett. 1997, 24, 245–248. [Google Scholar] [CrossRef]
- Montagner, J.P.; Kennett, B. How to reconcile body-wave and normal-mode reference Earth models. Geophys. J. Int. 1996, 125, 229–248. [Google Scholar] [CrossRef]
- Yuan, K.; Beghein, C. Seismic anisotropy changes across upper mantle phase transitions. Earth Planet. Sci. Lett. 2013, 374, 132–144. [Google Scholar] [CrossRef]
- Vinnik, L.; Romanowicz, B.; Le Stunff, Y.; Makeyeva, L. Seismic anisotropy in the D″-layer. Geophys. Res. Lett. 1995, 22, 1657–1660. [Google Scholar] [CrossRef]
- Maupin, V.; Garnero, E.J.; Lay, T.; Fouch, M.J. Azimuthal anisotropy in the D″-layer beneath the Caribbean. J. Geophys. Res. Solid Earth 2005, 110. [Google Scholar] [CrossRef]
- Meade, C.; Silver, P.G.; Kaneshima, S. Laboratory and seismological observations of lower mantle isotropy. Geophys. Res. Lett. 1995, 22, 1293–1296. [Google Scholar] [CrossRef]
- Nowacki, A.; Kendall, J.M.; Wookey, J.; Pemberton, A. Mid-mantle anisotropy in subduction zones and deep water transport. Geochem. Geophys. Geosyst. 2015, 16, 764–784. [Google Scholar] [CrossRef]
- Ferreira, A.M.; Faccenda, M.; Sturgeon, W.; Chang, S.J.; Schardong, L. Ubiquitous lower-mantle anisotropy beneath subduction zones. Nat. Geosci. 2019, 12, 301–306. [Google Scholar] [CrossRef]
- Montagner, J.P.; Burgos, G.; Capdeville, Y.; Beucler, E.; Mocquet, A. The mantle transition zone dynamics as revealed through seismic anisotropy. Tectonophysics 2021, 821, 229133. [Google Scholar] [CrossRef]
- Anderson, D.L. Elastic wave propagation in layered anisotropic media. J. Geophys. Res. 1961, 66, 2953–2963. [Google Scholar] [CrossRef]
- Love, A. A Treatise on the Mathematical Theory of Elasticity; Dover Publications: New York, NY, USA, 1927; p. 643. [Google Scholar]
- Aki, K.; Kaminuma, K. Crustal structure in Japan from the phase velocity of Rayleigh waves: Part 2. Rayleigh waves from the Aleutian shock of March 9, 1957. Bull. Earthq. Res. Inst. 1963, 41, 243–259. [Google Scholar]
- Beghein, C.; Resovsky, J.; Van Der Hilst, R.D. The signal of mantle anisotropy in the coupling of normal modes. Geophys. J. Int. 2008, 175, 1209–1234. [Google Scholar] [CrossRef]
- Kustowski, B.; Ekstrom, G.; Dziewonski, A.M. Anisotropic shear- wave velocity structure of the Earth’s mantle: A global model. J. Geophys. Res. Solid Earth 2008, 113, 2156–2202. [Google Scholar] [CrossRef]
- Moulik, P.; Ekstrom, G. An anisotropic shear velocity model of the Earth’s mantle using normal modes, body waves, surface waves and long-period waveforms. Geophys. J. Int. 2014, 199, 1713–1738. [Google Scholar] [CrossRef]
- Auer, L.; Boschi, L.; Becker, T.W.; Nissen-Meyer, T.; Giardini, D. Savani: A variable resolution whole-mantle model of anisotropic shear velocity variations based on multiple data sets. J. Geophys. Res. Solid Earth 2014, 119, 3006–3034. [Google Scholar] [CrossRef]
- Chang, S.J.; Ferreira, A.M.; Ritsema, J.; van Heijst, H.J.; Woodhouse, J.H. Joint inversion for global isotropic and radially anisotropic mantle structure including crustal thickness perturbations. J. Geophys. Res. Solid Earth 2015, 120, 4278–4300. [Google Scholar] [CrossRef]
- Montagner, J.P.; Nataf, H.C. A simple method for inverting the azimuthal anisotropy of surface waves. J. Geophys. Res. Solid Earth 1986, 91, 511–520. [Google Scholar] [CrossRef]
- Vinnik, L.; Montagner, J.P. Shear wave splitting in the mantle Ps phases. Geophys. Res. Lett. 1996, 23, 2449–2452. [Google Scholar] [CrossRef]
- Wookey, J.; Kendall, J.M.; Barruol, G. Mid-mantle deformation inferred from seismic anisotropy. Nature 2002, 415, 777–780. [Google Scholar] [CrossRef]
- Trampert, J.; van Heijst, H.J. Global azimuthal anisotropy in the transition zone. Science 2002, 296, 1297–1299. [Google Scholar] [CrossRef]
- Yuan, K.; Beghein, C. Three-dimensional variations in Love and Rayleigh wave azimuthal anisotropy for the upper 800 km of the mantle. J. Geophys. Res. Solid Earth 2014, 119, 3232–3255. [Google Scholar] [CrossRef]
- Debayle, E.; Dubuffet, F.; Durand, S. An automatically updated S-wave model of the upper mantle and the depth extent of azimuthal anisotropy. Geophys. Res. Lett. 2016, 43, 674–682. [Google Scholar]
- Schaeffer, A.; Lebedev, S. Global shear speed structure of the upper mantle and transition zone. Geophys. J. Int. 2013, 194, 417–449. [Google Scholar] [CrossRef]
- Huang, Q.; Schmerr, N.; Waszek, L.; Beghein, C. Constraints on seismic anisotropy in the mantle transition zone from long-period SS precursors. J. Geophys. Res. Solid Earth 2019, 124, 6779–6800. [Google Scholar] [CrossRef]
- Beucler, E.; Stutzmann, E.; Montagner, J.P. Surface wave higher-mode phase velocity measurements using a roller-coaster-type algorithm. Geophys. J. Int. 2003, 155, 289–307. [Google Scholar]
- Visser, K.; Trampert, J.; Kennett, B. Global anisotropic phase velocity maps for higher mode Love and Rayleigh waves. Geophys. J. Int. 2008, 172, 1016–1032. [Google Scholar] [CrossRef]
- Burgos, G.; Montagner, J.P.; Beucler, E.; Capdeville, Y.; Mocquet, A.; Drilleau, M. Oceanic lithosphere-asthenosphere boundary from surface wave dispersion data. J. Geophys. Res. Solid Earth 2014, 119, 1079–1093. [Google Scholar] [CrossRef]
- Burgos, G. Tomographie du Manteau Supérieur par Inversion des Ondes de Surface. Ph.D. Thesis, Institut de Physique du Globe de Paris (IPGP), Paris, France, 2013. [Google Scholar]
- Ringwood, A. Composition and Petrology of the Earth’s Mantle; McGraw-Hill: New York, NY, USA, 1975; Volume 618. [Google Scholar]
- Tschauner, O.; Ma, C.; Beckett, J.R.; Prescher, C.; Prakapenka, V.B.; Rossman, G.R. Discovery of bridgmanite, the most abundant mineral in Earth, in a shocked meteorite. Science 2014, 346, 1100–1102. [Google Scholar] [CrossRef]
- Dubrovinsky, L.; Dubrovinskaia, N.; Saxena, S.; Annersten, H.; Hålenius, E.; Harryson, H.; Tutti, F.; Rekhi, S.; Bihan, T.L. Stability of ferropericlase in the lower mantle. Science 2000, 289, 430–432. [Google Scholar] [CrossRef]
- Murakami, M.; Hirose, K.; Kawamura, K.; Sata, N.; Ohishi, Y. Post-perovskite phase transition in MgSiO3. Science 2004, 304, 855–858. [Google Scholar] [CrossRef]
- Grocholski, B.; Catalli, K.; Shim, S.H.; Prakapenka, V. Mineralogical effects on the detectability of the postperovskite boundary. Proc. Natl. Acad. Sci. USA 2012, 109, 2275–2279. [Google Scholar] [CrossRef] [PubMed]
- Bina, C.R.; Helffrich, G. Phase transition Clapeyron slopes and transition zone seismic discontinuity topography. J. Geophys. Res. Solid Earth 1994, 99, 15853–15860. [Google Scholar] [CrossRef]
- Kawakatsu, H.; Niu, F. Seismic evidence for a 920-km discontinuity in the mantle. Nature 1994, 371, 301–305. [Google Scholar] [CrossRef]
- Niu, F.; Kawakatsu, H. Depth variation of the mid-mantle seismic discontinuity. Geophys. Res. Lett. 1997, 24, 429–432. [Google Scholar] [CrossRef]
- Vinnik, L.; Niu, F.; Kawakatsu, H. Broadband converted phases from midmantle discontinuities. Earth Planets Space 1998, 50, 987–997. [Google Scholar] [CrossRef]
- Jenkins, J.; Deuss, A.; Cottaar, S. Converted phases from sharp 1000 km depth mid-mantle heterogeneity beneath Western Europe. Earth Planet. Sci. Lett. 2017, 459, 196–207. [Google Scholar] [CrossRef]
- Zhang, Z.; Irving, J.C.; Simons, F.J.; Alkhalifah, T. Seismic evidence for a 1000 km mantle discontinuity under the Pacific. Nat. Commun. 2023, 14, 1714. [Google Scholar] [CrossRef]
- Ballmer, M.D.; Schmerr, N.C.; Nakagawa, T.; Ritsema, J. Compositional mantle layering revealed by slab stagnation at ∼1000-km depth. Sci. Adv. 2015, 1, e1500815. [Google Scholar] [CrossRef]
- Wu, W.; Ni, S.; Irving, J.C. Inferring Earth’s discontinuous chemical layering from the 660-kilometer boundary topography. Science 2019, 363, 736–740. [Google Scholar] [CrossRef]
- Waszek, L.; Schmerr, N.C.; Ballmer, M.D. Global observations of reflectors in the mid-mantle with implications for mantle structure and dynamics. Nat. Commun. 2018, 9, 385. [Google Scholar] [CrossRef]
- Mitrovica, J.; Forte, A. A new inference of mantle viscosity based upon joint inversion of convection and glacial isostatic adjustment data. Earth Planet. Sci. Lett. 2004, 225, 177–189. [Google Scholar] [CrossRef]
- Rudolph, M.L.; Lekić, V.; Lithgow-Bertelloni, C. Viscosity jump in Earth’s mid-mantle. Science 2015, 350, 1349–1352. [Google Scholar] [CrossRef]
- Marquardt, H.; Miyagi, L. Slab stagnation in the shallow lower mantle linked to an increase in mantle viscosity. Nat. Geosci. 2015, 8, 311–314. [Google Scholar] [CrossRef]
- Shim, S.H.; Grocholski, B.; Ye, Y.; Alp, E.E.; Xu, S.; Morgan, D.; Meng, Y.; Prakapenka, V.B. Stability of ferrous-iron-rich bridgmanite under reducing midmantle conditions. Proc. Natl. Acad. Sci. USA 2017, 114, 6468–6473. [Google Scholar] [CrossRef]
- Deng, J.; Lee, K.K. Viscosity jump in the lower mantle inferred from melting curves of ferropericlase. Nat. Commun. 2017, 8, 1997. [Google Scholar] [CrossRef]
- Badro, J. Spin transitions in mantle minerals. Annu. Rev. Earth Planet. Sci. 2014, 42, 231–248. [Google Scholar] [CrossRef]
- Glišović, P.; Forte, A.M.; Ammann, M.W. Variations in grain size and viscosity based on vacancy diffusion in minerals, seismic tomography, and geodynamically inferred mantle rheology. Geophys. Res. Lett. 2015, 42, 6278–6286. [Google Scholar] [CrossRef]
- Fei, H.; Ballmer, M.D.; Faul, U.; Walte, N.; Cao, W.; Katsura, T. Variation in bridgmanite grain size accounts for the mid-mantle viscosity jump. Nature 2023, 620, 794–799. [Google Scholar] [CrossRef]
- Vacher, P.; Mocquet, A.; Sotin, C. Computation of seismic profiles from mineral physics: The importance of the non-olivine components for explaining the 660 km depth discontinuity. Phys. Earth Planet. Inter. 1998, 106, 275–298. [Google Scholar] [CrossRef]
- Anderson, D. New Theory of the Earth, 2nd ed.; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Mainprice, D. Seismic anisotropy of the deep Earth from a mineral and rock physics perspective. In Treatise of Geophysics; Elsevier: Amsterdam, The Netherlands, 2015; Volume 2. [Google Scholar]
- Shearer, P. Transition zone velocity gradients and the 520km discontinuity. J. Geophys. Res. 1996, 101, 3053–3066. [Google Scholar]
- Karato, S.I. Seismic anisotropy in the deep mantle, boundary layers and the geometry of mantle convection. In Geodynamics of Lithosphere & Earth’s Mantle: Seismic Anisotropy as a Record of the Past and Present Dynamic Processes; Birkhäuser: Basel, Switzerland, 1998; pp. 565–587. [Google Scholar]
- Van der Meijde, M.; Marone, F.; Giardini, D.; Van der Lee, S. Seismic evidence for water deep in Earth’s upper mantle. Science 2003, 300, 1556–1558. [Google Scholar] [CrossRef]
- Bercovici, D.; Karato, S.i. Whole-mantle convection and the transition-zone water filter. Nature 2003, 425, 39–44. [Google Scholar] [CrossRef]
- Huang, X.; Xu, Y.; Karato, S.i. Water content in the transition zone from electrical conductivity of wadsleyite and ringwoodite. Nature 2005, 434, 746–749. [Google Scholar] [CrossRef]
- Tommasi, A.; Mainprice, D.; Cordier, P.; Thoraval, C.; Couvy, H. Strain-induced seismic anisotropy of wadsleyite polycrystals and flow patterns in the mantle transition zone. J. Geophys. Res. Solid Earth 2004, 109, B12405-1. [Google Scholar] [CrossRef]
- Wu, W.; Nishihara, Y.; Tsujino, N. Crystallographic preferred orientation of phase D at high pressure and temperature: Implications for seismic anisotropy in the mid-mantle. J. Geophys. Res. Solid Earth 2024, 129, e2024JB029734. [Google Scholar] [CrossRef]
- Kattemalavadi, A.; Devoe, M.; Wenk, H.R. Deformation of Hydrous Phases Egg [AlSiO3(OH)], δ [AlO(OH)] and Stishovite [Si1-nH4nO2] Relevant to Anisotropy of the Earth’s Mantle. J. Geophys. Res. Solid Earth 2025, 130, e2025JB031362. [Google Scholar] [CrossRef]
- Gay, J.P.; Ledoux, E.E.; Krug, M.; Chantel, J.; Pakhomova, A.; Sanchez-Valle, C.; Speziale, S.; Merkel, S. Depth dependent deformation and anisotropy of pyrolite in the Earth’s lower mantle. Geophys. Res. Lett. 2024, 51, e2024GL109433. [Google Scholar] [CrossRef]
- Farnetani, C.; Samuel, H. Beyond the thermal plume paradigm. Geophys. Res. Lett. 2005, 32, L07311. [Google Scholar] [CrossRef]
- Durand, S.; Debayle, E.; Ricard, Y.; Zaroli, C.; Lambotte, S. Confirmation of a change in the global shear velocity pattern at around 1000 km depth. Geophys. J. Int. 2017, 211, 1628–1639. [Google Scholar] [CrossRef]
- Ritsema, J.; Deuss, A.; van Heijst, H.; Woodhouse, J.H. S40RTS: A degree-40 shear-velocity model for the mantle from new Rayleigh wave dispersion, teleseismic traveltime and normal-mode splitting function measurements. Geophys. J. Int. 2011, 184, 1223–1236. [Google Scholar] [CrossRef]
- Romanowicz, B.; Dziewonski, A. Tomographic Stratigraphy: A Possible New Framework for Mantle Dynamics. In Proceedings of the AGU Fall Meeting Abstracts; American Geophysical Union (AGU): Washington, DC, USA, 2015; Volume 2015, p. DI23A-08. [Google Scholar]
- French, S.; Lekic, V.; Romanowicz, B. Waveform tomography reveals channeled flow at the base of the oceanic asthenosphere. Science 2013, 342, 227–230. [Google Scholar] [CrossRef]
- Yuan, K.; Romanowicz, B. Seismic evidence for partial melting at the root of major hot spot plumes. Science 2017, 357, 393–397. [Google Scholar] [CrossRef] [PubMed]
- Dupré, B.; Allègre, C.J. Pb–Sr isotope variation in Indian Ocean basalts and mixing phenomena. Nature 1983, 303, 142–146. [Google Scholar] [CrossRef]
- Hart, S.R. A large-scale isotope anomaly in the Southern Hemisphere mantle. Nature 1984, 309, 753–757. [Google Scholar] [CrossRef]
- Castillo, P. The Dupal anomaly as a trace of the upwelling lower mantle. Nature 1988, 336, 667–670. [Google Scholar] [CrossRef]
- Schouten, T.L.; Gebraad, L.; Noe, S.; Gülcher, A.J.; Thrastarson, S.; van Herwaarden, D.P.; Fichtner, A. Full-waveform inversion reveals diverse origins of lower mantle positive wave speed anomalies. Sci. Rep. 2024, 14, 26708. [Google Scholar] [CrossRef]
- Coffin, M.F.; Eldholm, O. Large igneous provinces: Crustal structure, dimensions, and external consequences. Rev. Geophys. 1994, 32, 1–36. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Montagner, J.-P.; Romanowicz, B.; Wamba, M.; Burgos, G. Upwellings and Mantle Ponding Zones in the Lower Mantle Transition Zone (660–1000 km). Geosciences 2025, 15, 413. https://doi.org/10.3390/geosciences15110413
Montagner J-P, Romanowicz B, Wamba M, Burgos G. Upwellings and Mantle Ponding Zones in the Lower Mantle Transition Zone (660–1000 km). Geosciences. 2025; 15(11):413. https://doi.org/10.3390/geosciences15110413
Chicago/Turabian StyleMontagner, Jean-Paul, Barbara Romanowicz, Mathurin Wamba, and Gael Burgos. 2025. "Upwellings and Mantle Ponding Zones in the Lower Mantle Transition Zone (660–1000 km)" Geosciences 15, no. 11: 413. https://doi.org/10.3390/geosciences15110413
APA StyleMontagner, J.-P., Romanowicz, B., Wamba, M., & Burgos, G. (2025). Upwellings and Mantle Ponding Zones in the Lower Mantle Transition Zone (660–1000 km). Geosciences, 15(11), 413. https://doi.org/10.3390/geosciences15110413





