Micropolar Modeling of Shear Wave Dispersion in Marine Sediments and Deep Earth Materials: Deriving Scaling Laws
Abstract
1. Introduction

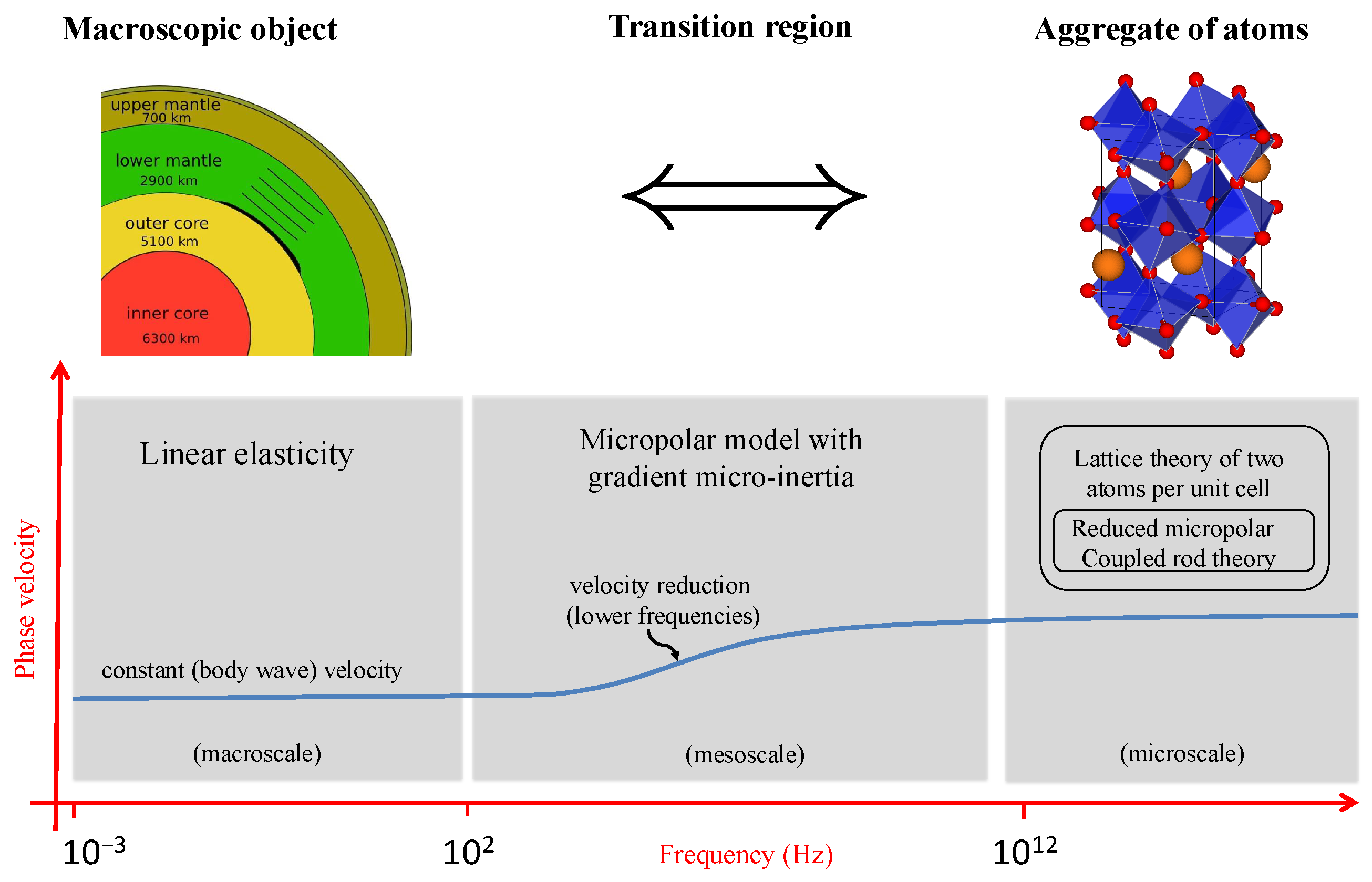
2. Theoretical Developments: Drawing Connections Between Micro, Macro and Mass-in-Mass Theories
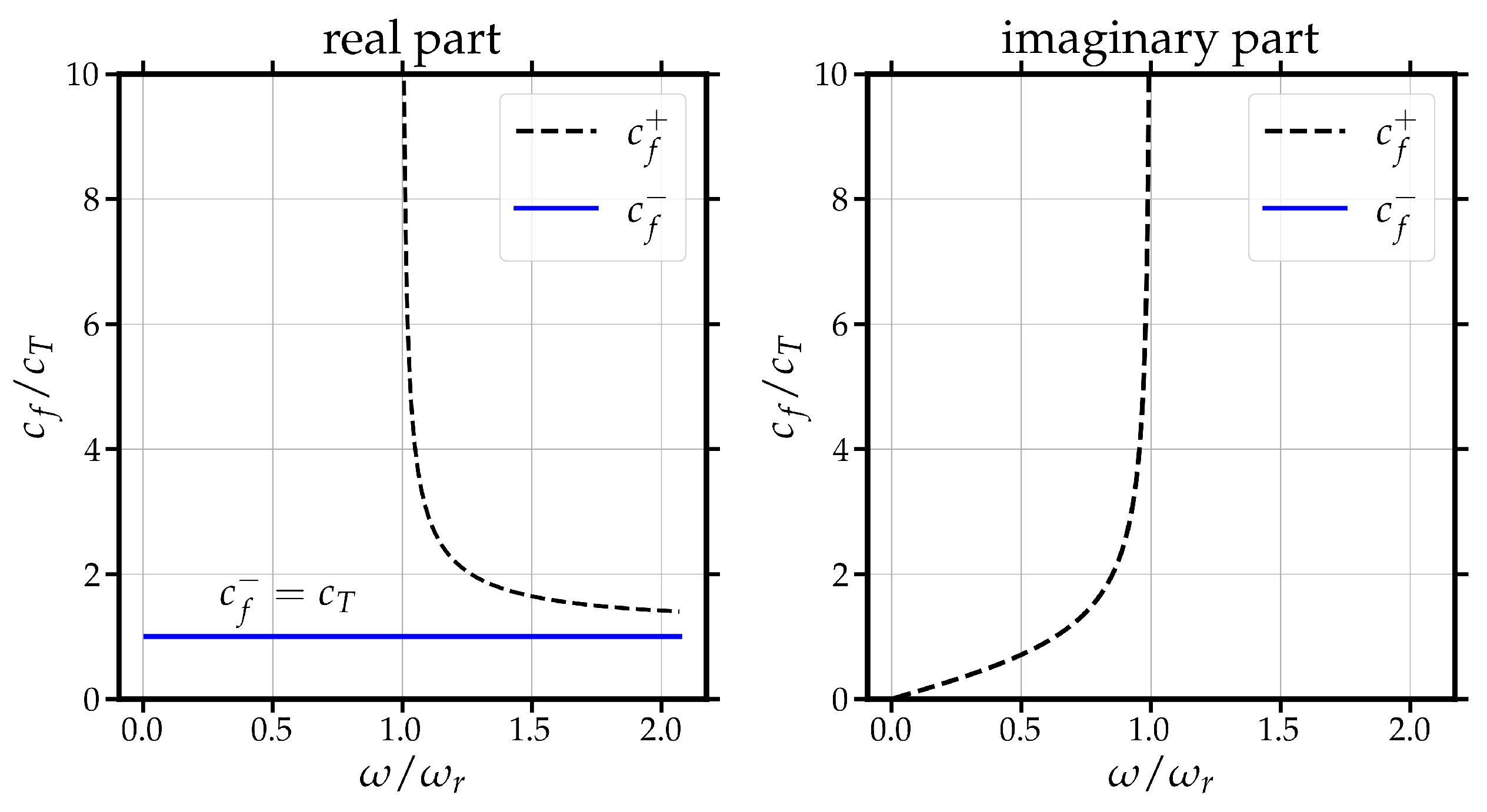
2.1. The General (Continuum) Equation
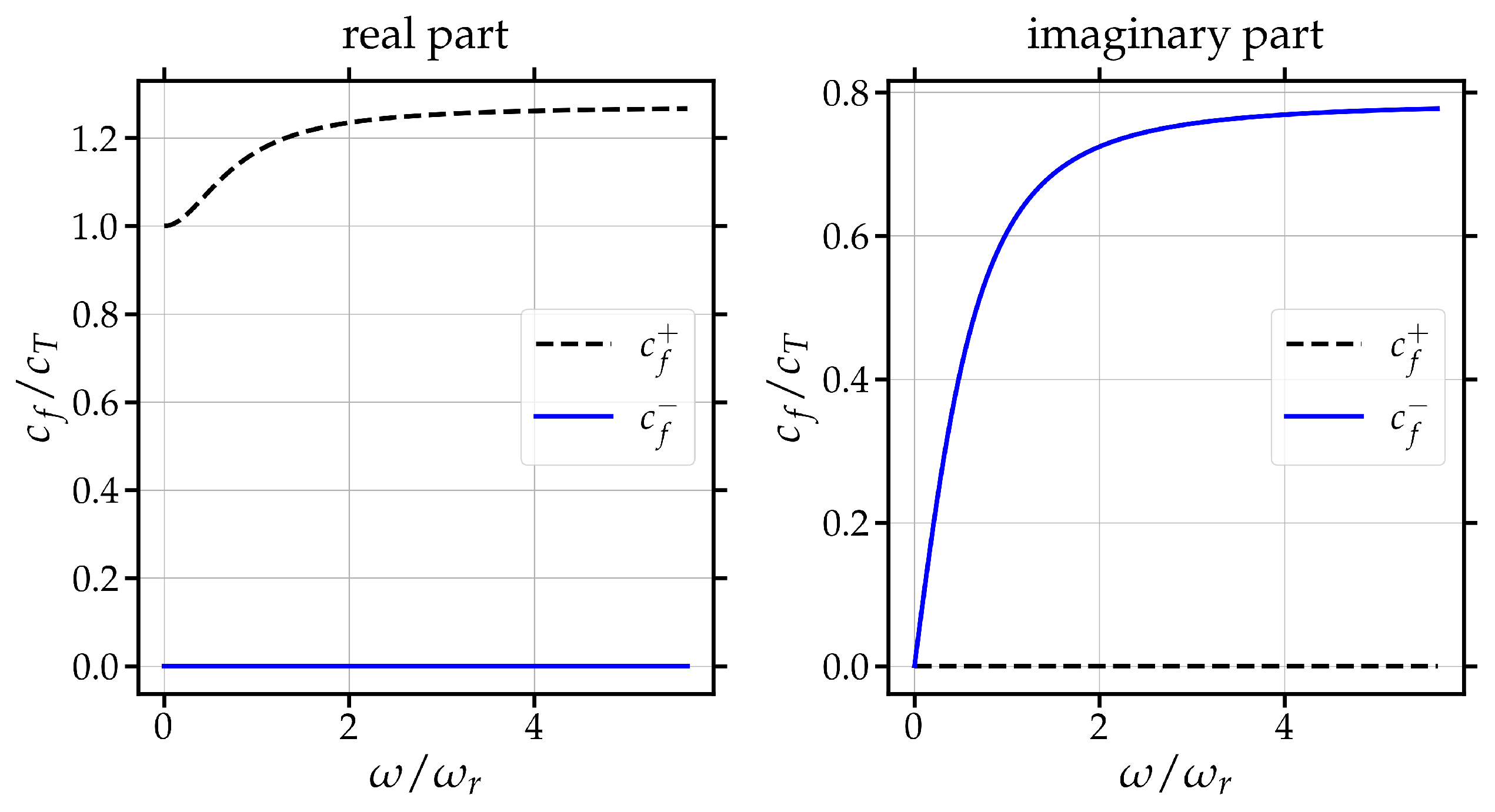
- ➙
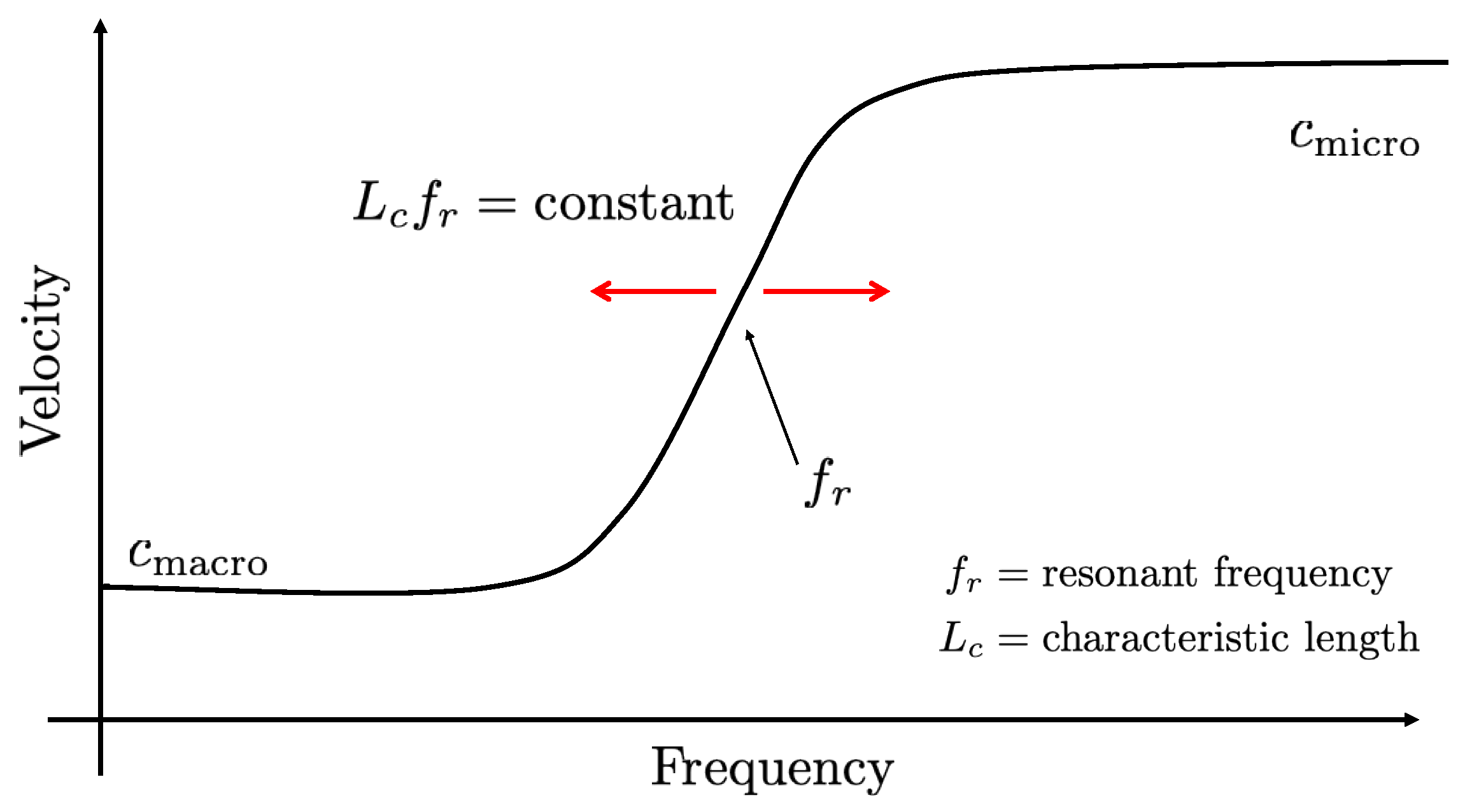
- is the limit of phase (and group) (rotatory) velocity at high frequencies.
- ➙
- is the limit of phase (and group) velocity at high frequencies.
- ➙
- is the resonant (cut-off) frequency (optic mode). No real signal propagates at that frequency.
- ➙
- is the limit of phase (and group) velocity at low frequencies.
2.2. The Macroscopic Description: Linear Continuum Mechanics
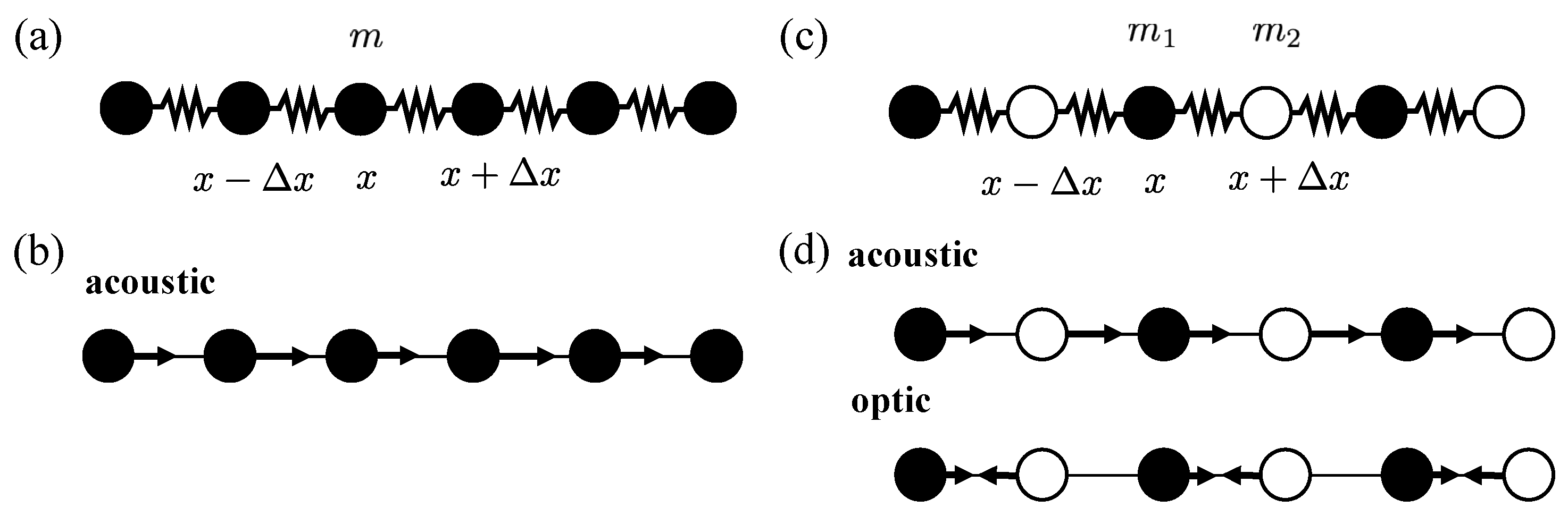
2.2.1. Linear Elasticity: Lattice Description
2.2.2. Linear Elasticity: Continuum Description
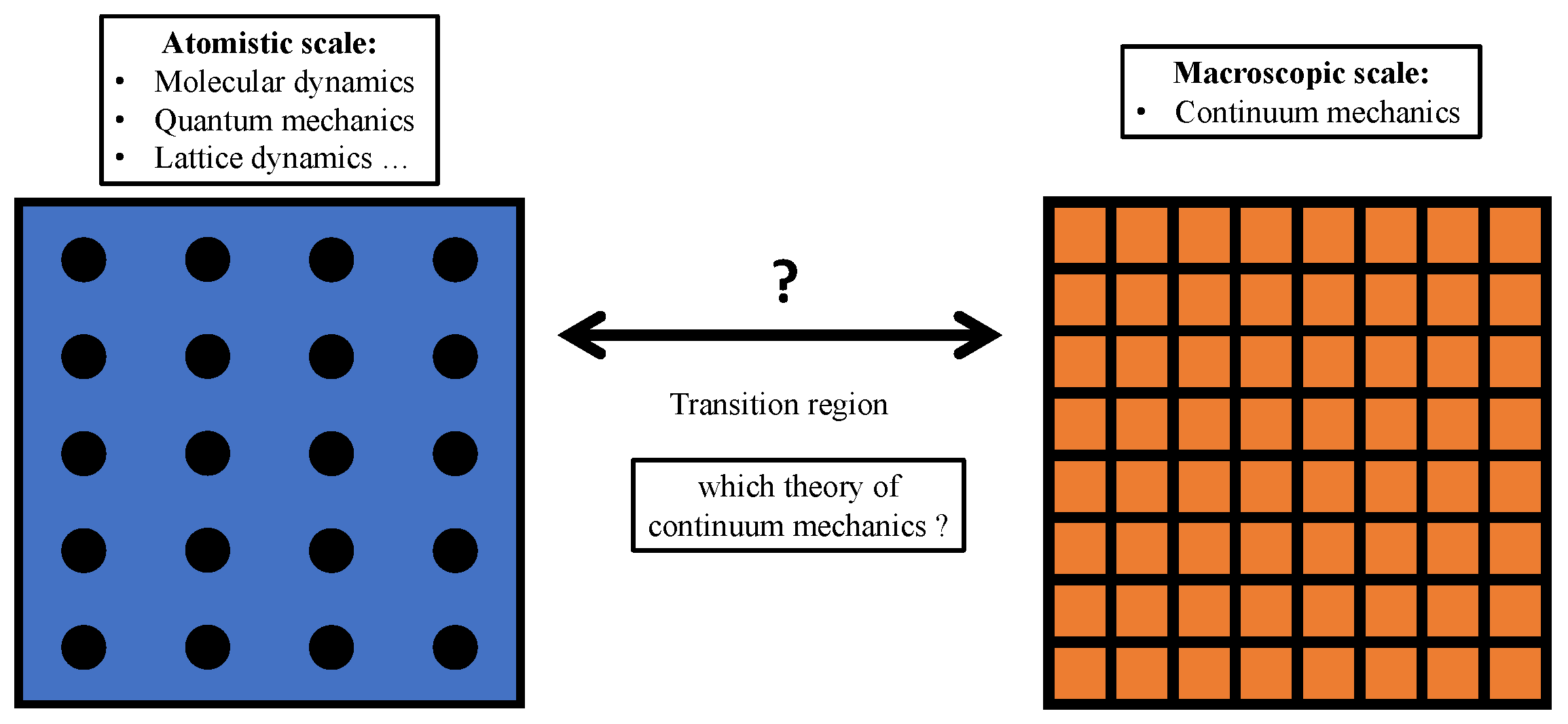
2.2.3. How Do We Pass from the Lattice to the Continuum Description?
2.3. The Microscopic Descriptions: Lattice and/or Continuum?
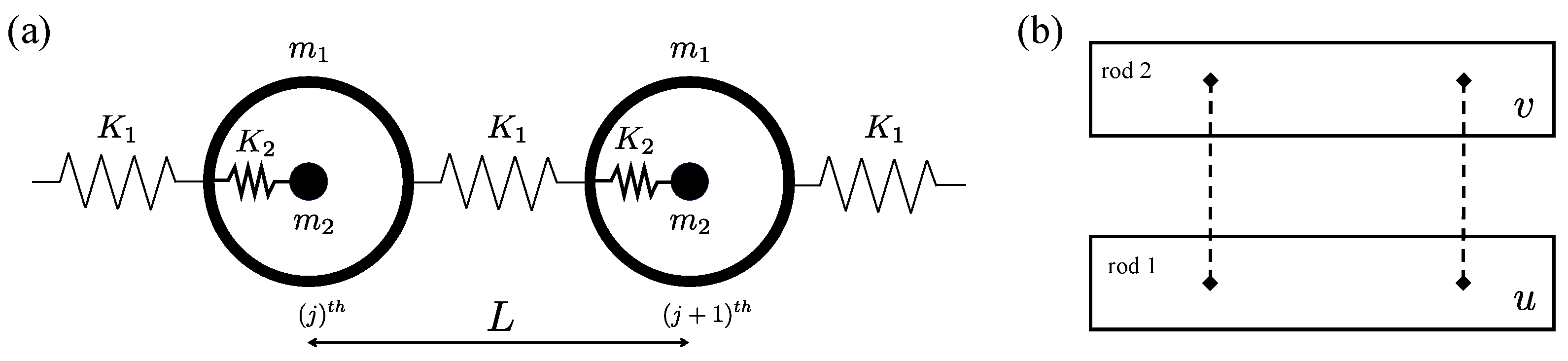
2.3.1. The Lattice Model of Two Atoms per Primitive Unit Cell
2.3.2. Micro-Continuum Field Theories
Micropolar Model
Reduced Micropolar Model
Microstretch Model
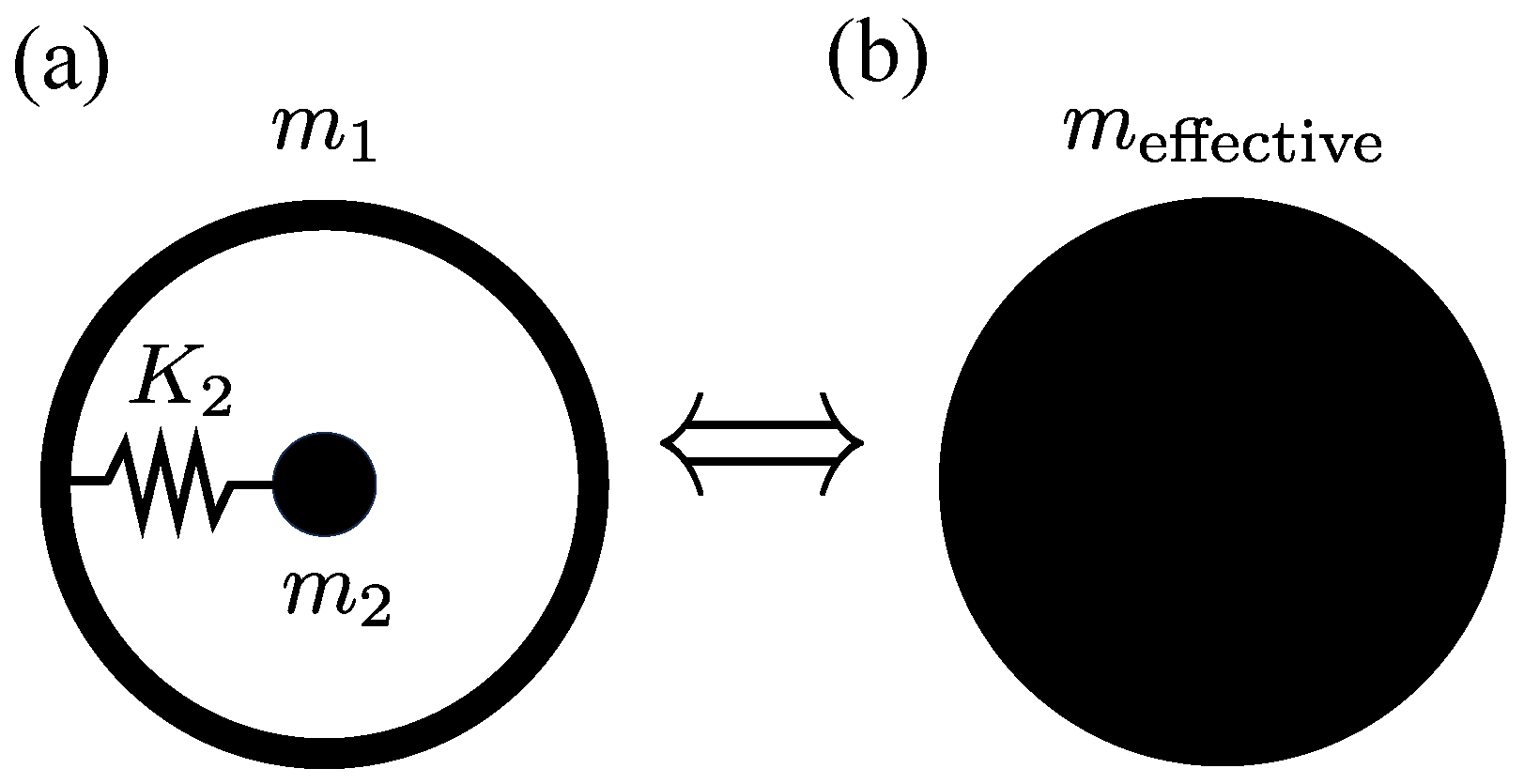
2.4. Mass-in-Mass Systems
2.4.1. Acoustic Metamaterials
2.4.2. Theory of Wave Propagation in a Coupled Rod
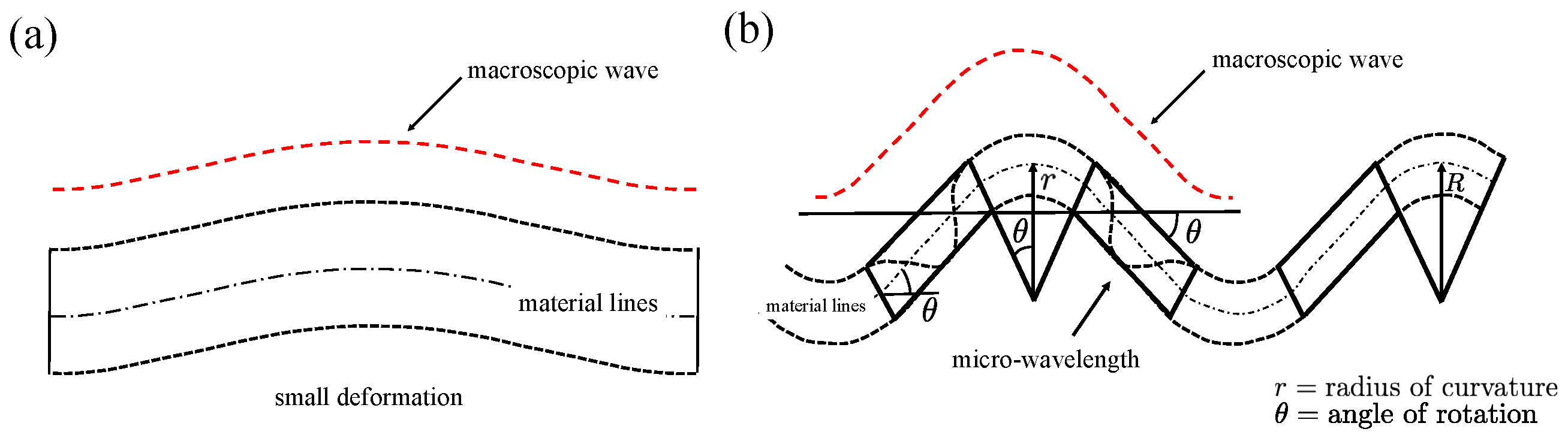
2.5. Micropolar Theory with Gradient Micro-Inertia
2.6. Summary of Theoretical Findings
3. Applications in Earth Sciences
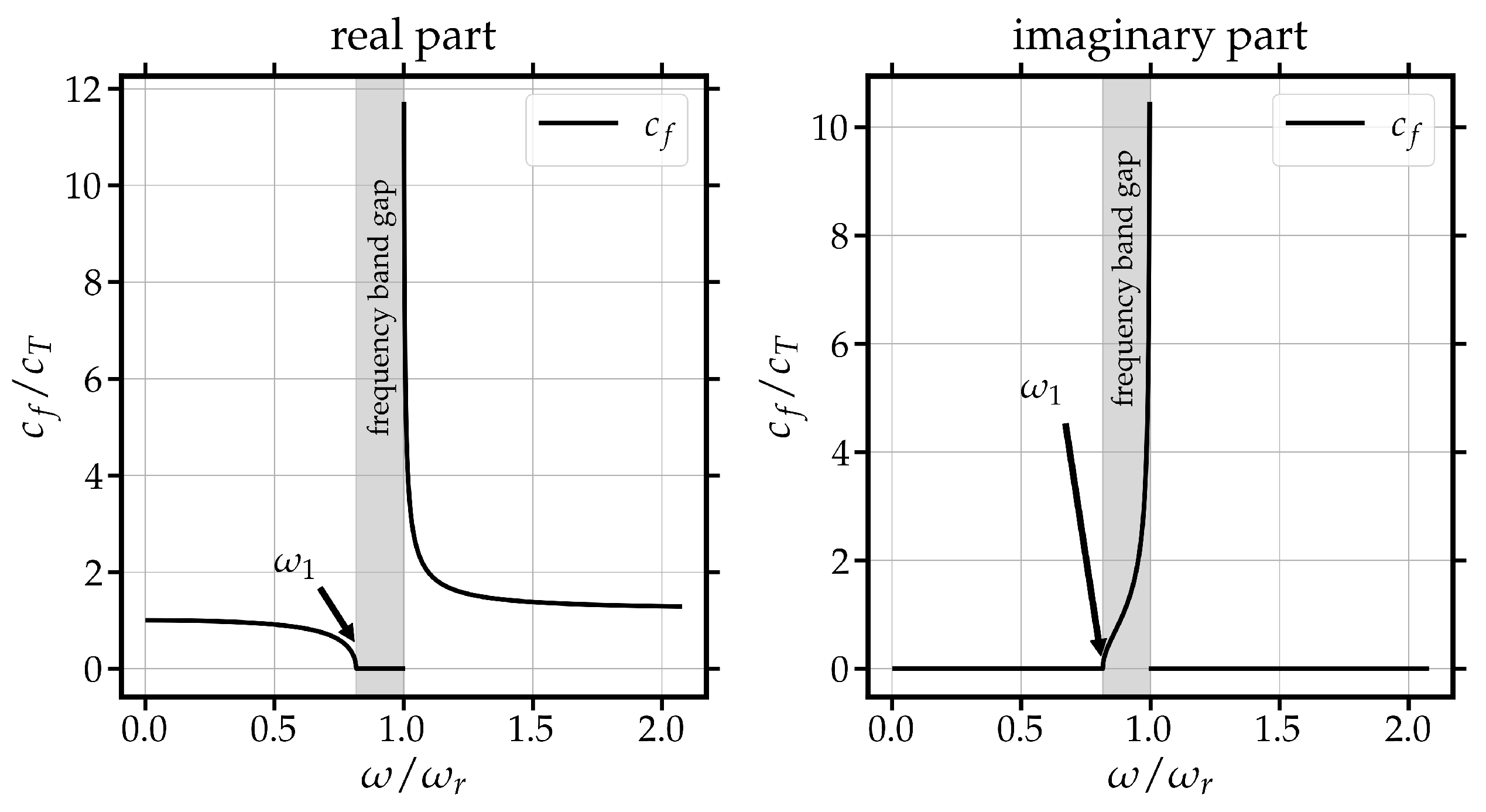
- Earth scientists observe only one mode of propagation. They cannot differentiate between acoustic and optic modes.
- No frequency band gaps have ever been observed in seismological data.
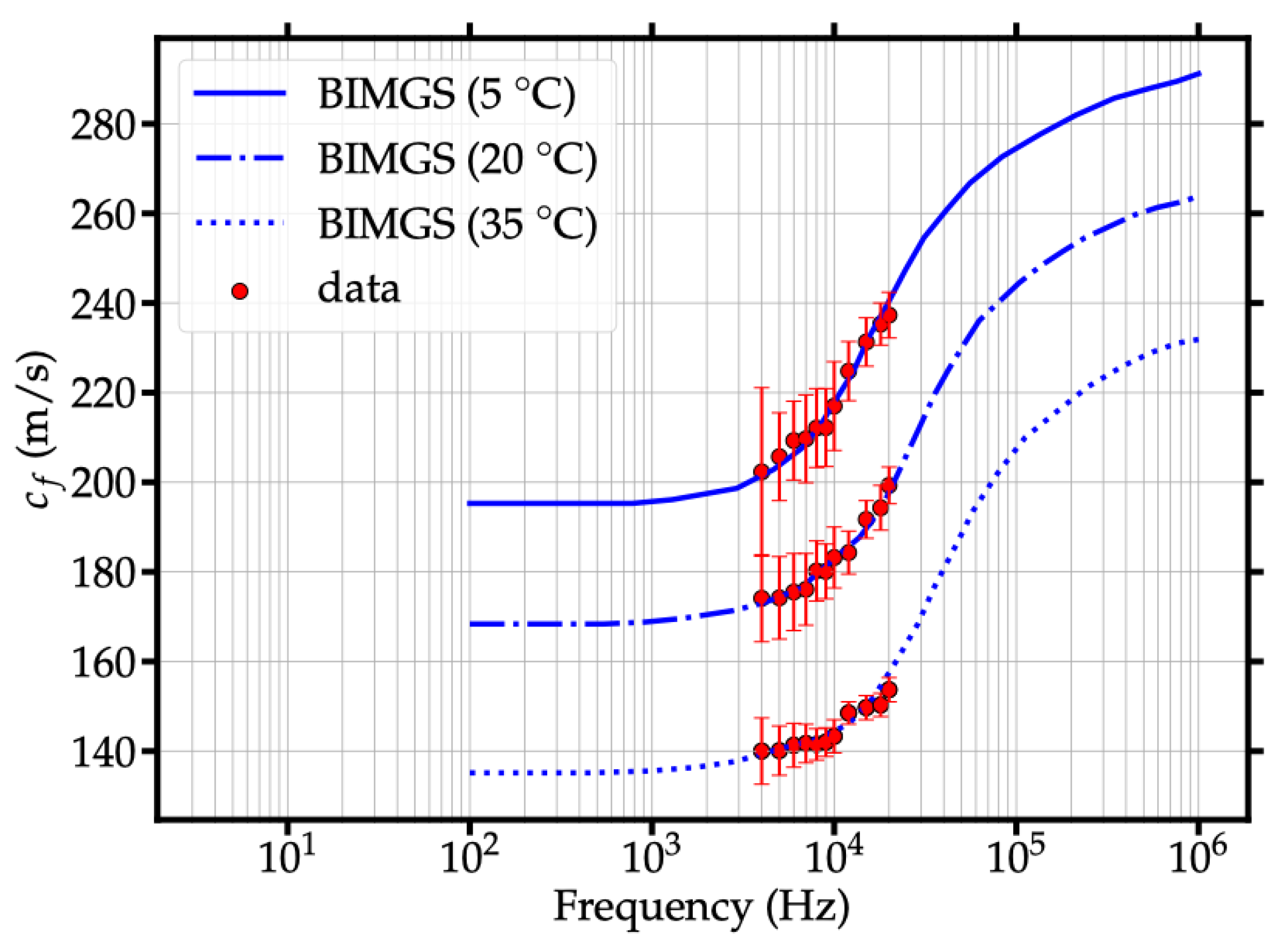
3.1. Accurate Modeling of Shear-Wave Speed Dispersion in Granular Marine Sediments Without Biot’s Theory
3.1.1. The Problem: Too Many Parameters
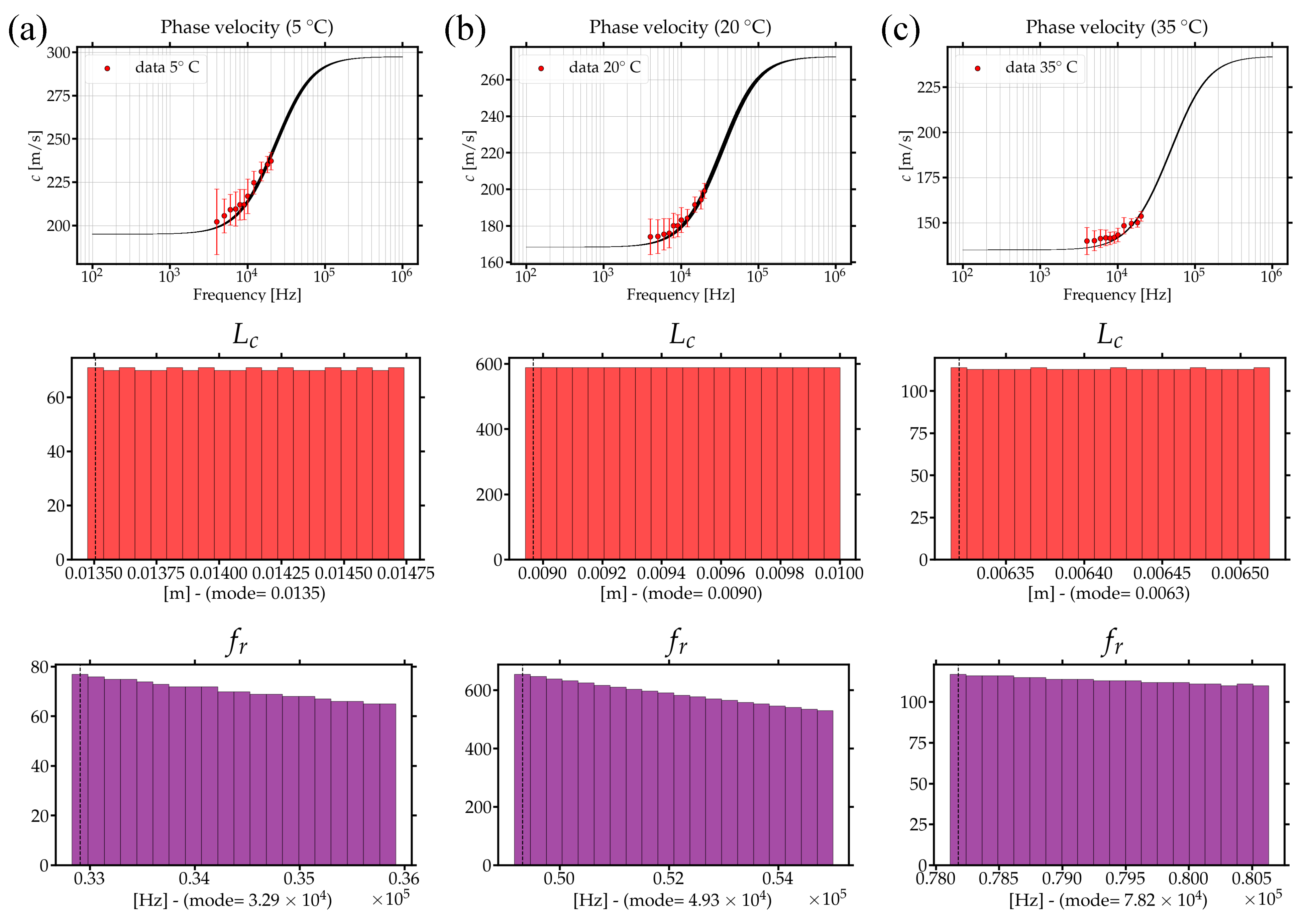
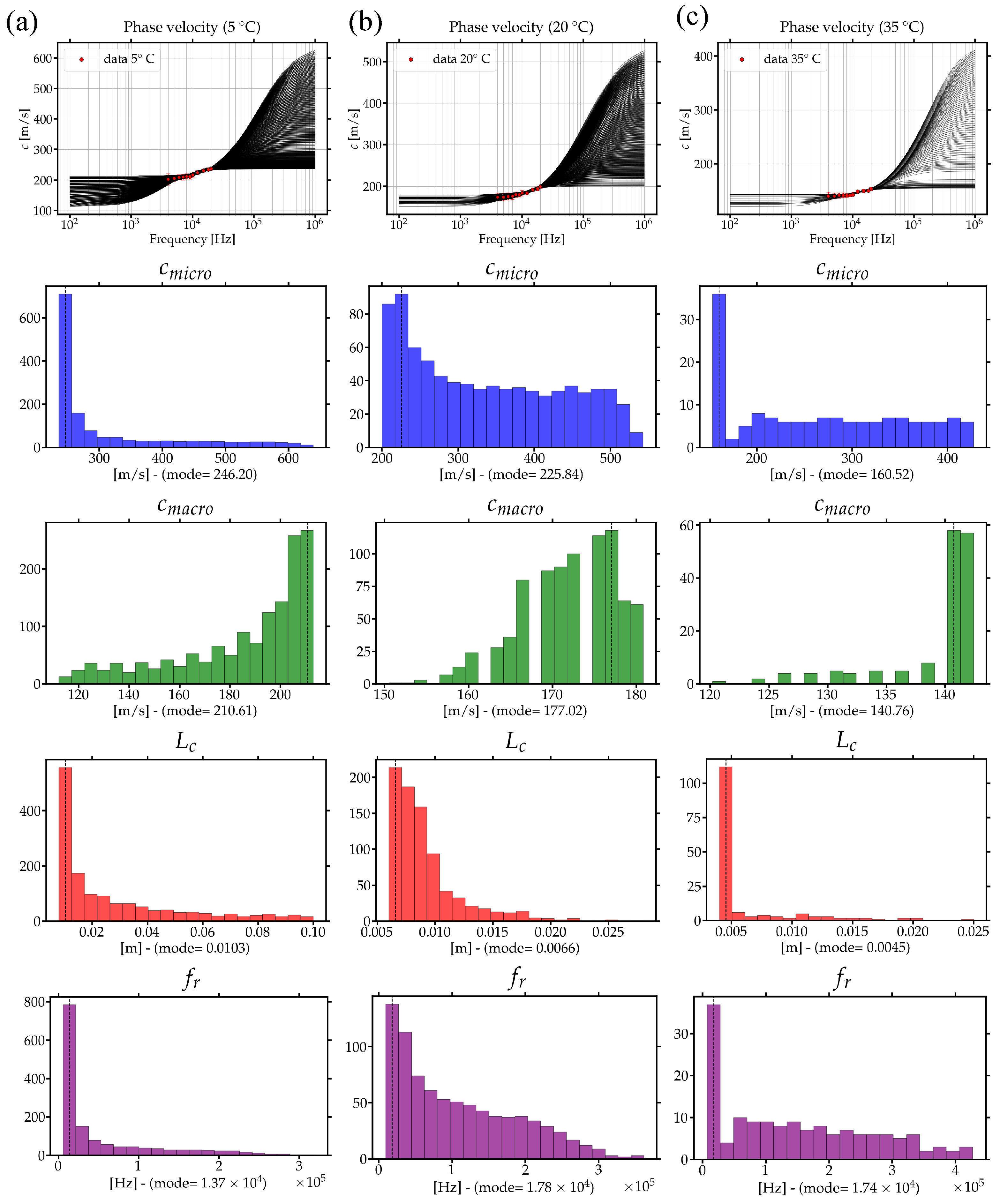
3.1.2. The Solution: Experimental Validation of the Micropolar Model with Gradient Micro-Inertia
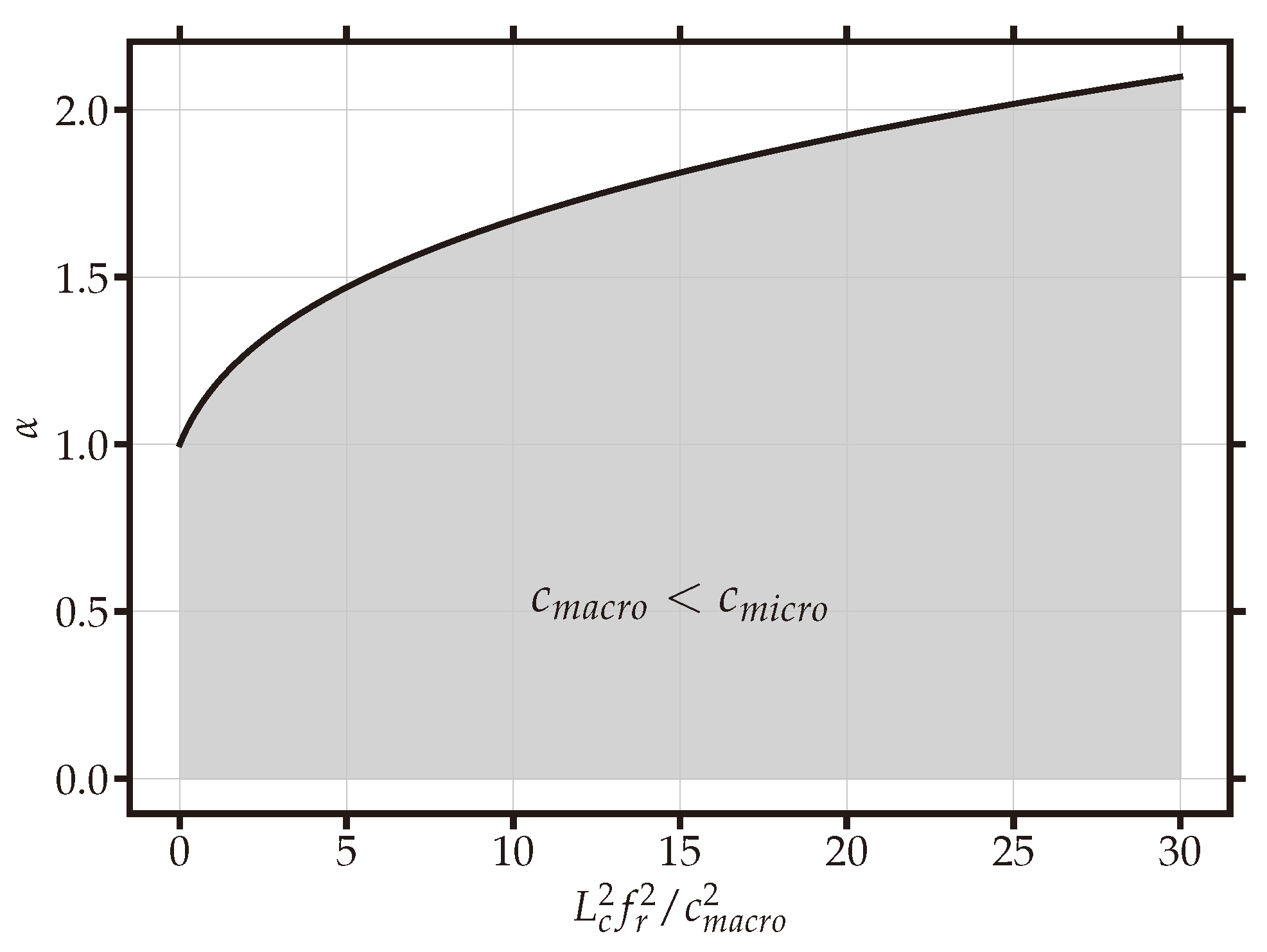
3.2. A Mechanical Link Between Micro- and Macoscales
3.2.1. The Presence of Bridgmanite in the Lower Mantle
Data
- Average length of the sides of the unit cell:
- The total volume of the bridgmanite unit cell reported by [9] is of . It is reasonable to assume the unit cell as a cube and take the side of the cube as the characteristic length, from which we can obtain
Results
4. Discussion and Conclusions
4.1. Different Theories: One Equation
4.2. Poroelastic Modeling Without Biot’s Theory: The Need for a Simpler Theory in Seismology
- The Meaning of the Resonant Frequency
- The Meaning of the Characteristic Length
4.3. From Micro- to Macroscales and Vice Versa
4.4. Body-Wave Velocity Dispersion Without Viscoelastic Effects
4.5. Bridgmanite in the Lower Mantle
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Explicit Calculations: The Lattice Model of Two Atoms per Primitive Unit Cell
References
- Bregman, N.; Bailey, R.; Chapman, C. Crosshole seismic tomography. Geophysics 1989, 54, 200–215. [Google Scholar]
- Chiao, L.Y.; Kuo, B.Y. Multiscale seismic tomography. Geophys. J. Int. 2001, 145, 517–527. [Google Scholar] [CrossRef]
- Tape, C.; Liu, Q.; Maggi, A.; Tromp, J. Seismic tomography of the southern California crust based on spectral-element and adjoint methods. Geophys. J. Int. 2010, 180, 433–462. [Google Scholar]
- Nolet, G. A Breviary of Seismic Tomography: Imaging the Interior of the Earth and Sun; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Rawlinson, N.; Pozgay, S.; Fishwick, S. Seismic tomography: A window into deep Earth. Phys. Earth Planet. Inter. 2010, 178, 101–135. [Google Scholar]
- French, S.W.; Romanowicz, B.A. Whole-mantle radially anisotropic shear velocity structure from spectral-element waveform tomography. Geophys. J. Int. 2014, 199, 1303–1327. [Google Scholar] [CrossRef]
- Lei, W.; Ruan, Y.; Bozdağ, E.; Peter, D.; Lefebvre, M.; Komatitsch, D.; Tromp, J.; Hill, J.; Podhorszki, N.; Pugmire, D. Global adjoint tomography–model GLAD-M25. Geophys. J. Int. 2020, 223, 1–21. [Google Scholar]
- Thrastarson, S.; van Herwaarden, D.P.; Noe, S.; Josef Schiller, C.; Fichtner, A. REVEAL: A global full-waveform inversion model. Bull. Seismol. Soc. Am. 2024, 114, 1392–1406. [Google Scholar]
- Oganov, A.R.; Ono, S. Theoretical and experimental evidence for a post-perovskite phase of MgSiO3 in Earth’s D′′ layer. Nature 2004, 430, 445–448. [Google Scholar]
- Kaminsky, F. Mineralogy of the lower mantle: A review of ‘super-deep’ mineral inclusions in diamond. Earth-Sci. Rev. 2012, 110, 127–147. [Google Scholar]
- Irifune, T.; Tsuchiya, T. Mineralogy of the Earth-Phase transitions and mineralogy of the lower mantle. Miner. Phys. 2007, 2, 33–62. [Google Scholar]
- Kesson, S.; Fitz Gerald, J.; Shelley, J. Mineralogy and dynamics of a pyrolite lower mantle. Nature 1998, 393, 252–255. [Google Scholar]
- Murakami, M.; Ohishi, Y.; Hirao, N.; Hirose, K. A perovskitic lower mantle inferred from high-pressure, high-temperature sound velocity data. Nature 2012, 485, 90–94. [Google Scholar] [PubMed]
- Passchier, C.W.; Trouw, R.A.J. Microtectonics; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Goetze, C.; Brace, W. The upper mantle laboratory observations of high-temperature rheology of rocks. Tectonophysics 1972, 13, 583–600. [Google Scholar]
- Wang, N.; Montagner, J.P.; Fichtner, A.; Capdeville, Y. Intrinsic versus extrinsic seismic anisotropy: The radial anisotropy in reference Earth models. Geophys. Res. Lett. 2013, 40, 4284–4288. [Google Scholar] [CrossRef]
- Capdeville, Y.; Zhao, M.; Cupillard, P. Fast Fourier homogenization for elastic wave propagation in complex media. Wave Motion 2015, 54, 170–186. [Google Scholar]
- Capdeville, Y.; Guillot, L.; Marigo, J.J. 2-D non-periodic homogenization to upscale elastic media for P–SV waves. Geophys. J. Int. 2010, 182, 903–922. [Google Scholar]
- Capdeville, Y.; Cupillard, P.; Singh, S. Chapter Six—An introduction to the two-scale homogenization method for seismology. In Machine Learning in Geosciences; Advances in Geophysics; Moseley, B., Krischer, L., Eds.; Elsevier: Amsterdam, The Netherlands, 2020; Volume 61, pp. 217–306. [Google Scholar]
- Hedjazian, N.; Capdeville, Y.; Bodin, T. Multiscale seismic imaging with inverse homogenization. Geophys. J. Int. 2021, 226, 676–691. [Google Scholar]
- Capdeville, Y. Homogenization of seismic point and extended sources. Geophys. J. Int. 2021, 226, 1390–1416. [Google Scholar]
- Cupillard, P.; Capdeville, Y. Non-periodic homogenization of 3-D elastic media for the seismic wave equation. Geophys. J. Int. 2018, 213, 983–1001. [Google Scholar]
- Mainprice, D.; Barruol, G.; Ismaïl, W.B. The seismic anisotropy of the Earth’s mantle: From single crystal to polycrystal. In Earth’s Deep Interior: Mineral Physics and Tomography from the Atomic to the Global Scale; American Geophysical Union: Washington, DC, USA, 2013; pp. 237–264. [Google Scholar]
- Nakata, N.; Beroza, G.C. Stochastic characterization of mesoscale seismic velocity heterogeneity in Long Beach, California. Geophys. J. Int. 2015, 203, 2049–2054. [Google Scholar]
- Yuen, D.A.; Cserepes, L.; Schroeder, B.A. Mesoscale structures in the transition zone: Dynamical consequences of boundary layer activities. Earth Planets Space 1998, 50, 1035–1045. [Google Scholar]
- Capolungo, L.; Spearot, D.; Cherkaoui, M.; McDowell, D.; Qu, J.; Jacob, K. Dislocation nucleation from bicrystal interfaces and grain boundary ledges: Relationship to nanocrystalline deformation. J. Mech. Phys. Solids 2007, 55, 2300–2327. [Google Scholar]
- McDowell, D.; Gall, K.; Horstemeyer, M.; Fan, J. Microstructure-based fatigue modeling of cast A356-T6 alloy. Eng. Fract. Mech. 2003, 70, 49–80. [Google Scholar]
- McDowell, D.; Dunne, F. Microstructure-sensitive computational modeling of fatigue crack formation. Int. J. Fatigue 2010, 32, 1521–1542. [Google Scholar]
- Tucker, G.J.; Tiwari, S.; Zimmerman, J.A.; McDowell, D.L. Investigating the deformation of nanocrystalline copper with microscale kinematic metrics and molecular dynamics. J. Mech. Phys. Solids 2012, 60, 471–486. [Google Scholar]
- Wernik, J.; Meguid, S.A. Coupling atomistics and continuum in solids: Status, prospects, and challenges. Int. J. Mech. Mater. Des. 2009, 5, 79. [Google Scholar]
- Rudd, R.E.; Broughton, J.Q. Concurrent coupling of length scales in solid state systems. Comput. Simul. Mater. At. Level 2000, 217, 251–291. [Google Scholar]
- Rudd, R.E.; Broughton, J.Q. Coarse-grained molecular dynamics and the atomic limit of finite elements. Phys. Rev. B 1998, 58, R5893. [Google Scholar]
- Tadmor, E.B.; Ortiz, M.; Phillips, R. Quasicontinuum analysis of defects in solids. Philos. Mag. A 1996, 73, 1529–1563. [Google Scholar]
- Eringen, C. Nonlocal Continuum Field Theories; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Abreu, R.; Durand, S. Understanding micropolar theory in the Earth sciences I: The eigenfrequency ωr. Pure Appl. Geophys. 2021, 179, 915–932. [Google Scholar]
- Slawinski, M. Waves and Rays in Elastic Continua; World Scientific Publishing Company: Singapore, 2010. [Google Scholar]
- Eringen, A.C.; Suhubi, E. Nonlinear theory of simple micro-elastic solids—I. Int. J. Eng. Sci. 1964, 2, 189–203. [Google Scholar]
- Whitham, G.B. Linear and Nonlinear Waves; John Wiley & Sons: Hoboken, NJ, USA, 1999. [Google Scholar]
- Kittel, C. Introduction to Solid State Physics, 8th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2005. [Google Scholar]
- Engel, E. Density Functional Theory; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Merzbacher, E. Quantum Mechanics; John Wiley & Sons: Hoboken, NJ, USA, 1998. [Google Scholar]
- Madeo, A.; Neff, P.; Ghiba, I.D.; Placidi, L.; Rosi, G. Wave propagation in relaxed micromorphic continua: Modeling metamaterials with frequency band-gaps. Contin. Mech. Thermodyn. 2015, 27, 551–570. [Google Scholar]
- Eringen, C.; Kafadar, C. Polar Field Theories, Continuum Physics; Academic Press: Cambridge, MA, USA, 1976; Volume IV, pp. 1–75. [Google Scholar]
- Eringen, C. Microcontinuum Field Theories I: Foundations and Solids; Springer: Berlin/Heidelberg, Germany, 1999. [Google Scholar]
- Grekova, E.; Kulesh, M.; Herman, G. Waves in linear elastic media with microrotations, Part 2: Isotropic reduced Cosserat model. Bull. Seismol. Soc. Am. 2009, 99, 1423–1428. [Google Scholar]
- Madeo, A. Generalized Continuum Mechanics and Engineering Applications; Elsevier: Amsterdam, The Netherlands, 2015. [Google Scholar]
- Chen, Y.; Lee, J.D.; Eskandarian, A. Atomistic viewpoint of the applicability of microcontinuum theories. Int. J. Solids Struct. 2004, 41, 2085–2097. [Google Scholar]
- Abreu, R.; Thomas, C.; Durand, S. Effect of observed micropolar motions on wave propagation in deep Earth minerals. Phys. Earth Planet. Inter. 2018, 276, 215–225. [Google Scholar] [CrossRef]
- Pouget, J.; Aşkar, A.; Maugin, G. Lattice model for elastic ferroelectric crystals: Continuum approximation. Phys. Rev. B 1986, 33, 6320. [Google Scholar]
- Askar, A. Molecular crystals and the polar theories of the continua. Experimental values of material coefficients for KNO3. Int. J. Eng. Sci. 1972, 10, 293–300. [Google Scholar]
- Askar, A. Lattice Dynamical Foundations of Continuum Theories: Elasticity, Piezoelectricity, Viscoelasticity, Plasticity; World Scientific: Singapore, 1986; Volume 2. [Google Scholar]
- Matsushima, T.; Saomoto, H.; Tsubokawa, Y.; Yamada, Y. Grain rotation versus continuum rotation during shear deformation of granular assembly. Soils Found. 2003, 43, 95–106. [Google Scholar]
- Twiss, R.J. An asymmetric micropolar moment tensor derived from a discrete-block model for a rotating granular substructure. Bull. Seismol. Soc. Am. 2009, 99, 1103–1131. [Google Scholar]
- Schwartz, L.M.; Johnson, D.L.; Feng, S. Vibrational modes in granular materials. Phys. Rev. Lett. 1984, 52, 831–834. [Google Scholar]
- Merkel, A.; Luding, S. Enhanced micropolar model for wave propagation in ordered granular materials. Int. J. Solids Struct. 2017, 106, 91–105. [Google Scholar] [CrossRef]
- Merkel, A.; Tournat, V.; Gusev, V. Experimental evidence of rotational elastic waves in granular phononic crystals. Phys. Rev. Lett. 2011, 107, 225502. [Google Scholar] [CrossRef] [PubMed]
- Madeo, A.; Barbagallo, G.; d’Agostino, M.V.; Placidi, L.; Neff, P. First evidence of non-locality in real band-gap metamaterials: Determining parameters in the relaxed micromorphic model. Proc. R. Soc. A Math. Phys. Eng. Sci. 2016, 472, 20160169. [Google Scholar] [CrossRef]
- Frenzel, T.; Kadic, M.; Wegener, M. Three-dimensional mechanical metamaterials with a twist. Science 2017, 358, 1072–1074. [Google Scholar] [CrossRef]
- Grekova, E.F.; Abreu, R. Isotropic Linear Viscoelastic Reduced Cosserat Medium: An Acoustic Metamaterial and a First Step to Model Geomedium. In New Achievements in Continuum Mechanics and Thermodynamics: A Tribute to Wolfgang H. Müller; Abali, B.E., Altenbach, H., dell’Isola, F., Eremeyev, V.A., Öchsner, A., Eds.; Springer International Publishing: Berlin/Heidelberg, Germany, 2019; pp. 165–185. [Google Scholar]
- Rizzi, G.; d’Agostino, M.V.; Voss, J.; Bernardini, D.; Neff, P.; Madeo, A. From frequency-dependent models to frequency-independent enriched continua for mechanical metamaterials. Eur. J. Mech.-A/Solids 2024, 106, 105269. [Google Scholar] [CrossRef]
- Demetriou, P.; Rizzi, G.; Madeo, A. Reduced relaxed micromorphic modeling of harmonically loaded metamaterial plates: Investigating boundary effects in finite-size structures. Arch. Appl. Mech. 2024, 94, 81–98. [Google Scholar] [CrossRef]
- Voss, J.; Rizzi, G.; Neff, P.; Madeo, A. Modeling a labyrinthine acoustic metamaterial through an inertia-augmented relaxed micromorphic approach. Math. Mech. Solids 2023, 28, 2177–2201. [Google Scholar] [CrossRef]
- Rizzi, G.; Neff, P.; Madeo, A. Metamaterial shields for inner protection and outer tuning through a relaxed micromorphic approach. Philos. Trans. R. Soc. A 2022, 380, 20210400. [Google Scholar] [CrossRef]
- Neff, P.; Eidel, B.; d’Agostino, M.V.; Madeo, A. Identification of scale-independent material parameters in the relaxed micromorphic model through model-adapted first order homogenization. J. Elast. 2020, 139, 269–298. [Google Scholar] [CrossRef]
- Rayleigh, J.W.S.B. The Theory of Sound; Macmillan: New York, NY, USA, 1896; Volume 2. [Google Scholar]
- Watts, A.B. Isostasy and Flexure of the Lithosphere; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Timoshenko, S.P. On the correction for shear of the differential equation for transverse vibrations of prismatic bars. London Edinburgh Dublin Philos. Mag. J. Sci. 1921, 41, 744–746. [Google Scholar] [CrossRef]
- Oldham, R.D. The constitution of the interior of the Earth, as revealed by earthquakes. Q. J. Geol. Soc. 1906, 62, 456–475. [Google Scholar]
- Aki, K.; Richards, P.G. Quantitative Seismology, 2nd ed.; University Science Books: Herndon, VA, USA, 2002. [Google Scholar]
- Dahlen, F.; Tromp, J. Theoretical Global Seismology; Princeton University Press: Princeton, NJ, USA, 1998. [Google Scholar]
- Thomas, J.W. Numerical Partial Differential Equations: Finite Difference Methods; Springer: Berlin/Heidelberg, Germany, 1995. [Google Scholar]
- Huang, H.; Sun, C.; Huang, G. On the negative effective mass density in acoustic metamaterials. Int. J. Eng. Sci. 2009, 47, 610–617. [Google Scholar] [CrossRef]
- Teisseyre, R.; Takeo, M.; Majewski, E. Earthquake Source Asymmetry, Structural Media and Rotation Effects; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Cosserat, E.; Cosserat, F. Théorie des Corps Déformables; A. Hermann et Fils; Delphenich, D., Translator; Librairie Scientifique: Paris, France, 2009; ISBN 978-27056-6920-1. [Google Scholar]
- Twiss, R.J.; Souter, B.J.; Unruh, J.R. The effect of block rotations on the global seismic moment tensor and the patterns of seismic P and T axes. J. Geophys. Res. Solid Earth 1993, 98, 645–674. [Google Scholar]
- Gade, M.; Raghukanth, S. Seismic response of reduced micropolar elastic half-space. J. Seismol. 2016, 20, 787–801. [Google Scholar]
- Unruh, J.R.; Twiss, R.J.; Hauksson, E. Seismogenic deformation field in the Mojave block and implications for tectonics of the eastern California shear zone. J. Geophys. Res. Solid Earth 1996, 101, 8335–8361. [Google Scholar] [CrossRef]
- Unruh, J.; Humphrey, J.; Barron, A. Transtensional model for the Sierra Nevada frontal fault system, eastern California. Geology 2003, 31, 327. [Google Scholar]
- Lewis, J.C.; Boozer, A.C.; López, A.; Montero, W. Collision versus sliver transport in the hanging wall at the Middle America subduction zone: Constraints from background seismicity in central Costa Rica. Geochem. Geophys. Geosyst. 2008, 9, Q07S06. [Google Scholar]
- Twiss, R.J.; Protzman, G.M.; Hurst, S.D. Theory of slickenline patterns based on the velocity gradient tensor and micro-rotation. Tectonophysics 1991, 186, 215–239. [Google Scholar]
- Lewis, J.C.; O’Hara, D.J.; Rau, R.J. Seismogenic strain across the transition from fore-arc slivering to collision in southern Taiwan. J. Geophys. Res. Solid Earth 2015, 120, 4539–4555. [Google Scholar] [CrossRef]
- Neff, P.; Jeong, J. A new paradigm: The linear isotropic Cosserat model with conformally invariant curvature energy. Z. Angew. Math. Mech. 2009, 89, 107–122. [Google Scholar]
- Neff, P.; Jeong, J.; Fischle, A. Stable identification of linear isotropic Cosserat parameters: Bounded stiffness in bending and torsion implies conformal invariance of curvature. Acta Mech. 2010, 211, 237–249. [Google Scholar]
- Neff, P.; Jeong, J.; Münch, I.; Ramézani, H. Linear Cosserat elasticity, conformal curvature and bounded stiffness. In Mechanics of Generalized Continua: One Hundred Years After the Cosserats; Maugin, G.A., Metrikine, A.V., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 55–63. [Google Scholar]
- Abreu, R.; Kamm, J.; Reiß, A.S. Micropolar modelling of rotational waves in seismology. Geophys. J. Int. 2017, 210, 1021–1046. [Google Scholar]
- Kulesh, M.; Grekova, E.; Shardakov, I. The problem of surface wave propagation in a reduced Cosserat medium. Acoust. Phys. 2009, 55, 218–226. [Google Scholar] [CrossRef]
- Grekova, E. Linear reduced Cosserat medium with spherical tensor of inertia, where rotations are not observed in experiment. Mech. Solids 2012, 47, 538–543. [Google Scholar]
- Grekova, E. Nonlinear isotropic elastic reduced Cosserat continuum as a possible model for geomedium and geomaterials. Spherical prestressed state in the semilinear material. J. Seismol. 2012, 16, 695–707. [Google Scholar]
- Grekova, E. Plane waves in the linear elastic reduced Cosserat medium with a finite axially symmetric coupling between volumetric and rotational strains. Math. Mech. Solids 2016, 21, 73–93. [Google Scholar]
- Erofeev, V.I.; Malkhanov, A.O. Macromechanical modelling of elastic and visco-elastic Cosserat continuum. J. Appl. Math. Mech. 2017, 97, 1072–1077. [Google Scholar]
- Liu, Y.f.; Huang, J.k.; Li, Y.g.; Shi, Z.f. Trees as large-scale natural metamaterials for low-frequency vibration reduction. Constr. Build. Mater. 2019, 199, 737–745. [Google Scholar]
- Muhammad; Lim, C.W. Natural seismic metamaterials: The role of tree branches in the birth of Rayleigh wave bandgap for ground born vibration attenuation. Trees 2021, 35, 1299–1315. [Google Scholar] [CrossRef]
- Frenzel, T.; Köpfler, J.; Jung, E.; Kadic, M.; Wegener, M. Ultrasound experiments on acoustical activity in chiral mechanical metamaterials. Nat. Commun. 2019, 10, 3384. [Google Scholar]
- Miniaci, M.; Krushynska, A.; Bosia, F.; Pugno, N.M. Large scale mechanical metamaterials as seismic shields. New J. Phys. 2016, 18, 083041. [Google Scholar] [CrossRef]
- Wu, W.; Hu, W.; Qian, G.; Liao, H.; Xu, X.; Berto, F. Mechanical design and multifunctional applications of chiral mechanical metamaterials: A review. Mater. Des. 2019, 180, 107950. [Google Scholar] [CrossRef]
- Chen, Y.; Frenzel, T.; Guenneau, S.; Kadic, M.; Wegener, M. Mapping acoustical activity in 3D chiral mechanical metamaterials onto micropolar continuum elasticity. J. Mech. Phys. Solids 2020, 137, 103877. [Google Scholar] [CrossRef]
- Liu, X.; Hu, G. Elastic metamaterials making use of chirality: A review. Stroj. Vestn.-J. Mech. Eng. 2016, 62, 403–418. [Google Scholar] [CrossRef]
- Brûlé, S.; Javelaud, E.; Enoch, S.; Guenneau, S. Experiments on seismic metamaterials: Molding surface waves. Phys. Rev. Lett. 2014, 112, 133901. [Google Scholar] [CrossRef]
- Brûlé, S.; Enoch, S.; Guenneau, S. Emergence of seismic metamaterials: Current state and future perspectives. Phys. Lett. A 2020, 384, 126034. [Google Scholar] [CrossRef]
- Porubov, A.; Grekova, E. On nonlinear modeling of an acoustic metamaterial. Mech. Res. Commun. 2020, 103, 103464. [Google Scholar] [CrossRef]
- Meng, J. Coupled Wave Propagation in a Rod with a Dynamic Absorber Layer. Master’s Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1991. [Google Scholar]
- Chen, J.S.; Wang, R.T. Wave propagation and power flow analysis of sandwich structures with internal absorbers. J. Vib. Acoust. 2014, 136, 041003. [Google Scholar] [CrossRef]
- Grekova, E.F. On one class of theoretically constructed isotropic single negative continuous acoustic metamaterials. In Proceedings of the International Conference Days on Diffraction 2014, St. Petersburg, Russia, 26–30 May 2014; IEEE: New York, NY, USA, 2014; pp. 101–106. [Google Scholar]
- Abreu, R.; Durand, S. Understanding micropolar theory in the Earth sciences II: The seismic moment tensor. Pure Appl. Geophys. 2021, 178, 4325–4343. [Google Scholar] [CrossRef]
- Stoll, R.D. Velocity dispersion in water-saturated granular sediment. J. Acoust. Soc. Am. 2002, 111, 785–793. [Google Scholar] [CrossRef]
- Williams, K.L.; Jackson, D.R.; Thorsos, E.I.; Tang, D.; Schock, S.G. Comparison of sound speed and attenuation measured in a sandy sediment to predictions based on the Biot theory of porous media. IEEE J. Ocean. Eng. 2002, 27, 413–428. [Google Scholar] [CrossRef]
- Ballard, M.S.; Lee, K. The acoustics of marine sediments. Acoust. Today 2017, 13, 11–18. [Google Scholar]
- Kimura, M. Grain-size dependence of shear wave speed dispersion and attenuation in granular marine sediments. J. Acoust. Soc. Am. 2014, 136, EL53–EL59. [Google Scholar]
- Turgut, A.; Yamamoto, T. In situ measurements of velocity dispersion and attenuation in New Jersey Shelf sediments. J. Acoust. Soc. Am. 2008, 124, EL122–EL127. [Google Scholar]
- Yu, P.F.; Jiang, J.M.; Geng, J.H.; Zhang, B.J. Shear wave velocity inversion of marine sediments using deep-water OBS Scholte-wave data. Appl. Geophys. 2024, 21, 13–30. [Google Scholar] [CrossRef]
- Kugler, S.; Bohlen, T.; Forbriger, T.; Bussat, S.; Klein, G. Scholte-wave tomography for shallow-water marine sediments. Geophys. J. Int. 2007, 168, 551–570. [Google Scholar]
- Biot, M.A. Theory of elastic waves in a fluid-saturated porous solid. I. Low frequency range. J. Acoust. Soc. Am. 1956, 28, 168–178. [Google Scholar]
- Biot, M. Theory of elastic waves in a fluid-saturated porous solid. II. Higher frequency range. J. Acoust. Soc. Am. 1956, 28, 179–191. [Google Scholar] [CrossRef]
- Stoll, R.D. Acoustic waves in ocean sediments. Geophysics 1977, 42, 715–725. [Google Scholar] [CrossRef]
- Chotiros, N.P.; Isakson, M.J. A broadband model of sandy ocean sediments: Biot–Stoll with contact squirt flow and shear drag. J. Acoust. Soc. Am. 2004, 116, 2011–2022. [Google Scholar] [CrossRef]
- Attenborough, K. Pore Shape and the Biot-Stoll Model for Saturated Sediments. In Ocean Seismo-Acoustics: Low-Frequency Underwater Acoustics; Akal, T., Berkson, J.M., Eds.; Springer: New York, NY, USA, 1986; pp. 435–444. [Google Scholar]
- Holland, C.W.; Brunson, B.A. The Biot–Stoll sediment model: An experimental assessment. J. Acoust. Soc. Am. 1988, 84, 1437–1443. [Google Scholar]
- Badiey, M.; Cheng, A.H.; Mu, Y. From geology to geoacoustics—Evaluation of Biot–Stoll sound speed and attenuation for shallow water acoustics. J. Acoust. Soc. Am. 1998, 103, 309–320. [Google Scholar]
- Shin, H.C.; Taherzadeh, S.; Attenborough, K.; Whalley, W.; Watts, C. Non-invasive characterization of pore-related and elastic properties of soils in linear Biot–Stoll theory using acoustic-to-seismic coupling. Eur. J. Soil Sci. 2013, 64, 308–323. [Google Scholar]
- Brunson, B.A. Shear Wave Attenuation in Unconsolidated Laboratory Sediments. Ph.D. Thesis, Oregon State University, Corvallis, OR, USA, 1984. [Google Scholar]
- Brunson, B.A. Shear wave attenuation in unconsolidated laboratory sediments. In Shear Waves in Marine Sediments; Springer: Berlin/Heidelberg, Germany, 1991; pp. 141–147. [Google Scholar]
- Kimura, M. Frame bulk modulus of porous granular marine sediments. J. Acoust. Soc. Am. 2006, 120, 699–710. [Google Scholar]
- Kimura, M. Experimental validation and applications of a modified gap stiffness model for granular marine sediments. J. Acoust. Soc. Am. 2008, 123, 2542–2552. [Google Scholar]
- Kimura, M. Shear wave speed dispersion and attenuation in granular marine sediments. J. Acoust. Soc. Am. 2013, 134, 144–155. [Google Scholar]
- Tschauner, O.; Ma, C.; Beckett, J.R.; Prescher, C.; Prakapenka, V.B.; Rossman, G.R. Discovery of bridgmanite, the most abundant mineral in Earth, in a shocked meteorite. Science 2014, 346, 1100–1102. [Google Scholar]
- Hemley, R.; Jackson, M.; Gordon, R. Theoretical study of the structure, lattice dynamics, and equations of state of perovskite-type MgSiO3 and CaSiO3. Phys. Chem. Miner. 1987, 14, 2–12. [Google Scholar]
- Karki, B.; Wentzcovitch, R.; De Gironcoli, S.; Baroni, S. Ab initio lattice dynamics of MgSiO3 perovskite at high pressure. Phys. Rev. B 2000, 62, 14750. [Google Scholar]
- Durben, D.J.; Wolf, G.H. High-temperature behavior of metastable MgSiO3 perovskite: A Raman spectroscopic study. Am. Mineral. 1992, 77, 890–893. [Google Scholar]
- Chopelas, A. Thermal expansivity of lower mantle phases MgO and MgSiO3 perovskite at high pressure derived from vibrational spectroscopy. Phys. Earth Planet. Inter. 1996, 98, 3–15. [Google Scholar] [CrossRef]
- Williams, Q.; Jeanloz, R.; McMillan, P. Vibrational spectrum of MgSiO3 perovskite: Zero-pressure Raman and mid-infrared spectra to 27 GPa. J. Geophys. Res. Solid Earth 1987, 92, 8116–8128. [Google Scholar] [CrossRef]
- Shim, S.H.; Kubo, A.; Duffy, T.S. Raman spectroscopy of perovskite and post-perovskite phases of MgGeO3 to 123 GPa. Earth Planet. Sci. Lett. 2007, 260, 166–178. [Google Scholar] [CrossRef]
- Pouget, J.; Aşkar, A.; Maugin, G. Lattice model for elastic ferroelectric crystals: Microscopic approach. Phys. Rev. B 1986, 33, 6304. [Google Scholar] [CrossRef]
- Dziewonski, A.M.; Anderson, D.L. Preliminary reference Earth model. Phys. Earth Planet. Inter. 1981, 25, 297–356. [Google Scholar] [CrossRef]
- Morelli, A.; Dziewonski, A.M. Body wave traveltimes and a spherically symmetric P-and S-wave velocity model. Geophys. J. Int. 1993, 112, 178–194. [Google Scholar] [CrossRef]
- Kennett, B.; Engdahl, E. Traveltimes for global earthquake location and phase identification. Geophys. J. Int. 1991, 105, 429–465. [Google Scholar] [CrossRef]
- Kennett, B.L.; Engdahl, E.; Buland, R. Constraints on seismic velocities in the Earth from traveltimes. Geophys. J. Int. 1995, 122, 108–124. [Google Scholar] [CrossRef]
- Weber, M.; Davis, J. Evidence of a laterally variable lower mantle structure from P-and S-waves. Geophys. J. Int. 1990, 102, 231–255. [Google Scholar] [CrossRef]
- Liu, H.P.; Anderson, D.L.; Kanamori, H. Velocity dispersion due to anelasticity; implications for seismology and mantle composition. Geophys. J. Int. 1976, 47, 41–58. [Google Scholar] [CrossRef]
- Kjartansson, E. Constant Q–wave propagation and attenuation. J. Geophys. Res. Solid Earth 1979, 84, 4737–4748. [Google Scholar]
- Romanowicz, B. Attenuation Tomography of the Earth’s Mantle: A Review of Current Status. In Q of the Earth: Global, Regional, and Laboratory Studies; Mitchell, B.J., Romanowicz, B., Eds.; Birkhäuser: Basel, Switzerland, 1999; pp. 257–272. [Google Scholar]
- Zhu, H.; Bozdağ, E.; Duffy, T.S.; Tromp, J. Seismic attenuation beneath Europe and the North Atlantic: Implications for water in the mantle. Earth Planet. Sci. Lett. 2013, 381, 1–11. [Google Scholar]
- Durand, S.; Matas, J.; Ford, S.; Ricard, Y.; Romanowicz, B.; Montagner, J.P. Insights from ScS–S measurements on deep mantle attenuation. Earth Planet. Sci. Lett. 2013, 374, 101–110. [Google Scholar] [CrossRef]
- Widmer, R.; Masters, G.; Gilbert, F. Spherically symmetric attenuation within the Earth from normal mode data. Geophys. J. Int. 1991, 104, 541. [Google Scholar]
- Bezada, M.J. Insights into the lithospheric architecture of Iberia and Morocco from teleseismic body-wave attenuation. Earth Planet. Sci. Lett. 2017, 478, 14–26. [Google Scholar] [CrossRef]
- Ford, S.R.; Garnero, E.J.; Thorne, M.S. Differential t* measurements via instantaneous frequency matching: Observations of lower mantle shear attenuation heterogeneity beneath western Central America. Geophys. J. Int. 2012, 189, 513–523. [Google Scholar]
- Garnero, E.J.; Thorne, M.S.; McNamara, A.; Rost, S. Fine-Scale Ultra-Low Velocity Zone Layering at the Core-Mantle Boundary and Superplumes. In Superplumes: Beyond Plate Tectonics; Yuen, D.A., Maruyama, S., Karato, S.I., Windley, B.F., Eds.; Springer: Dordrecht, The Netherlands, 2007; pp. 139–158. [Google Scholar]
- McNamara, A.K. A review of large low shear velocity provinces and ultra low velocity zones. Tectonophysics 2019, 760, 199–220. [Google Scholar]
- Romanowicz, B. Seismic tomography of the Earth’s mantle. Annu. Rev. Earth Planet. Sci. 1991, 19, 77–99. [Google Scholar] [CrossRef]
- Frost, D.A.; Rost, S. The P-wave boundary of the large-low shear velocity province beneath the Pacific. Earth Planet. Sci. Lett. 2014, 403, 380–392. [Google Scholar] [CrossRef]
- Torsvik, T.H.; Smethurst, M.A.; Burke, K.; Steinberger, B. Large igneous provinces generated from the margins of the large low-velocity provinces in the deep mantle. Geophys. J. Int. 2006, 167, 1447–1460. [Google Scholar]
- Burke, K.; Steinberger, B.; Torsvik, T.H.; Smethurst, M.A. Plume generation zones at the margins of large low shear velocity provinces on the core–mantle boundary. Earth Planet. Sci. Lett. 2008, 265, 49–60. [Google Scholar]
- Tanaka, S.; Suetsugu, D.; Shiobara, H.; Sugioka, H.; Kanazawa, T.; Fukao, Y.; Barruol, G.; Reymond, D. On the vertical extent of the large low shear velocity province beneath the South Pacific Superswell. Geophys. Res. Lett. 2009, 36, L07305. [Google Scholar]
- Steinberger, B.; Torsvik, T.H. A geodynamic model of plumes from the margins of Large Low Shear Velocity Provinces. Geochem. Geophys. Geosyst. 2012, 13, Q01W09. [Google Scholar]
- Ballmer, M.D.; Schumacher, L.; Lekic, V.; Thomas, C.; Ito, G. Compositional layering within the large low shear-wave velocity provinces in the lower mantle. Geochem. Geophys. Geosyst. 2016, 17, 5056–5077. [Google Scholar]
- Deschamps, F.; Cobden, L.; Tackley, P.J. The primitive nature of large low shear-wave velocity provinces. Earth Planet. Sci. Lett. 2012, 349, 198–208. [Google Scholar]
- Dziewonski, A.M.; Hager, B.H.; O’Connell, R.J. Large-scale heterogeneities in the lower mantle. J. Geophys. Res. 1977, 82, 239–255. [Google Scholar]
- Thorne, M.S.; Zhang, Y.; Ritsema, J. Evaluation of 1-D and 3-D seismic models of the Pacific lower mantle with S, SKS, and SKKS traveltimes and amplitudes. J. Geophys. Res. Solid Earth 2013, 118, 985–995. [Google Scholar]
- Williams, Q.; Garnero, E.J. Seismic evidence for partial melt at the base of Earth’s mantle. Science 1996, 273, 1528–1530. [Google Scholar]
- Ni, S.; Helmberger, D.V. Probing an ultra-low velocity zone at the core mantle boundary with P and S waves. Geophys. Res. Lett. 2001, 28, 2345–2348. [Google Scholar]
- Wen, L.; Helmberger, D.V. Ultra-low velocity zones near the core-mantle boundary from broadband PKP precursors. Science 1998, 279, 1701–1703. [Google Scholar]
- Kawai, K.; Geller, R.J. Waveform inversion for localized seismic structure and an application to D” structure beneath the Pacific. J. Geophys. Res. Solid Earth 2010, 115, B01305. [Google Scholar]
- Yao, J.; Wen, L. Seismic structure and ultra-low velocity zones at the base of the Earth’s mantle beneath Southeast Asia. Phys. Earth Planet. Inter. 2014, 233, 103–111. [Google Scholar]
- Thorne, M.S.; Garnero, E.J.; Jahnke, G.; Igel, H.; McNamara, A.K. Mega ultra low velocity zone and mantle flow. Earth Planet. Sci. Lett. 2013, 364, 59–67. [Google Scholar] [CrossRef]
- Zhang, Y.; Ritsema, J.; Thorne, M.S. Modeling the ratios of SKKS and SKS amplitudes with ultra-low velocity zones at the core-mantle boundary. Geophys. Res. Lett. 2009, 36, L19303. [Google Scholar] [CrossRef]
- Murakami, M.; Hirose, K.; Kawamura, K.; Sata, N.; Ohishi, Y. Post-perovskite phase transition in MgSiO3. Science 2004, 304, 855–858. [Google Scholar] [PubMed]
- Hirose, K.; Brodholt, J.; Lay, T.; Yuen, D. Post-Perovskite: The Last Mantle Phase Transition; John Wiley & Sons: Hoboken, NJ, USA, 2013; Volume 174. [Google Scholar]
- Shim, S.H. The postperovskite transition. Annu. Rev. Earth Planet. Sci. 2008, 36, 569–599. [Google Scholar]
- Tateno, S.; Hirose, K.; Sata, N.; Ohishi, Y. Determination of post-perovskite phase transition boundary up to 4400 K and implications for thermal structure in D″ layer. Earth Planet. Sci. Lett. 2009, 277, 130–136. [Google Scholar] [CrossRef]
- Tsuchiya, T.; Tsuchiya, J. Effect of impurity on the elasticity of perovskite and postperovskite: Velocity contrast across the postperovskite transition in (Mg, Fe, Al)(Si, Al) O3. Geophys. Res. Lett. 2006, 33. [Google Scholar]
- McDonough, W.F.; Sun, S.S. The composition of the Earth. Chem. Geol. 1995, 120, 223–253. [Google Scholar]
- Helffrich, G.R.; Wood, B.J. The Earth’s mantle. Nature 2001, 412, 501. [Google Scholar]
- Wicks, J.K.; Duffy, T.S. Crystal Structures of Minerals in the Lower Mantle. In Deep Earth; American Geophysical Union (AGU): Washington, DC, USA, 2016; Chapter 6; pp. 69–87. [Google Scholar]
- Frost, D.J.; Myhill, R. Chemistry of the Lower Mantle. In Deep Earth; American Geophysical Union (AGU): Washington, DC, USA, 2016; Chapter 18; pp. 225–240. [Google Scholar]
- Kawai, K.; Tsuchiya, T. Small shear modulus of cubic CaSiO3 perovskite. Geophys. Res. Lett. 2015, 42, 2718–2726. [Google Scholar] [CrossRef]


| Model | |||||
|---|---|---|---|---|---|
| Linear elasticity | ✗ | ✗ | ✗ | ✓ | ✓ |
| Diatomic | ✓ | ✗ | ✓ | ✓ | ✓ |
| Micropolar | ✓ | ✓ | ✓ | ✓ | ✓ |
| Reduced micropolar | ✓ | ✓ | ✗ | ✓ | ✓ |
| Microstretch | ✓ | ✓ | ✓ | ✓ | ✓ |
| Mass in mass | ✓ | ✓ | ✗ | ✓ | ✓ |
| Coupled rod | ✓ | ✓ | ✗ | ✓ | ✓ |
| Micropolar (gradient micro-inertia) | ✓ | ✓ | ✓ | ✓ | ✓ |
| Parameter | 5 °C | 20 °C | 35 °C | ||
|---|---|---|---|---|---|
| Grain | Diameter | d [mm] | 0.113 | 0.113 | 0.113 |
| Density | [kg/m3] | 2659 | 2659 | 2659 | |
| Bulk modulus | [Pa] | ||||
| Pore fluid | Density | [kg/m3] | 1000 | 998.2 | 994 |
| Bulk modulus | [Pa] | ||||
| Viscosity | [Pa s] | ||||
| Frame | Porosity | 0.368 | 0.368 | 0.368 | |
| Permeability | [m2] | ||||
| Pore size | [m] | ||||
| Structure factor | 1.86 | 1.86 | 1.86 | ||
| (Biot–Stoll) | Frame’s shear modulus | [Pa] | |||
| Shear log decrement | 0.12 | 0.12 | 0.12 | ||
| Reference frequency | [KHz] | 13.86 | 9.15 | 6.63 | |
| (BIMGS) | Hertz–Mindlin shear modulus | [Pa] | |||
| Maximum gap stiffness term of the frame’s shear modulus | [Pa] | ||||
| Aspect ratio | |||||
| Correction factor for attenuation | 0.17 | 0.14 | 0.20 | ||
| Relaxation frequency | [KHz] | 19.58 | 32.02 | 46.46 | |
| Calculated shear wave speed at | [m/s] | 195.1 | 168.3 | 135.0 | |
| Calculated shear wave speed at | [m/s] | 297.4 | 272.7 | 242.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abreu, R. Micropolar Modeling of Shear Wave Dispersion in Marine Sediments and Deep Earth Materials: Deriving Scaling Laws. Geosciences 2025, 15, 124. https://doi.org/10.3390/geosciences15040124
Abreu R. Micropolar Modeling of Shear Wave Dispersion in Marine Sediments and Deep Earth Materials: Deriving Scaling Laws. Geosciences. 2025; 15(4):124. https://doi.org/10.3390/geosciences15040124
Chicago/Turabian StyleAbreu, Rafael. 2025. "Micropolar Modeling of Shear Wave Dispersion in Marine Sediments and Deep Earth Materials: Deriving Scaling Laws" Geosciences 15, no. 4: 124. https://doi.org/10.3390/geosciences15040124
APA StyleAbreu, R. (2025). Micropolar Modeling of Shear Wave Dispersion in Marine Sediments and Deep Earth Materials: Deriving Scaling Laws. Geosciences, 15(4), 124. https://doi.org/10.3390/geosciences15040124