Abstract
Regional-scale swarms of subparallel linear topographic features, known as lineament domains, are a common feature of planetary surfaces. Lineament domains are superficial manifestations of the crustal stress field trajectory. Notably, one of the effects of active tectonics is seismicity. Italy is one of the most seismically active regions in the Mediterranean, with many destructive earthquakes that have occurred in past centuries. Here, we assess the seismic meaning of the main lineament domain in the tectonically active region of Central Italy. We describe the use of an automated analysis of satellite imagery coupled with spatial grid analysis to identify three lineament domains of the Central Apennines. Spatial and azimuthal comparisons of the main lineament domain (i.e., the Apennine Domain), with the known locations of earthquakes (moment magnitude of Mw > 5.5) that occurred during the past century, revealed the most seismically active tectonic areas and their spatial distributions. Further, we present a conceptual seismo-geodynamic model for the Central Apennines, which is characterized by regional arching and explains the presence of an extensional tectonic regime in the upper crustal layer of the active Apennines fold-and-thrust belt.
1. Introduction
Most planetary surfaces include linear features (called lineaments) that group into regional-scale subparallel populations, as revealed by synthetic scaled satellite images and digital representation of topography [1,2,3,4,5,6,7,8]. These populations, which appear in the image as straight subtle anisotropies related to organized linear texture, are known as lineament domains (sensu [5,9]), and persist over regions spanning hundreds to thousands of square kilometers. Lineament domains occur in areas characterized by both nearly flat surface landscapes [8,10,11] and morphologies with moderate to high topographic contrast [4,7,12,13,14]. Lineaments are among the most controversial geological features and an unequivocal definition is still missing in the literature. For this reason, they are often considered with skepticism, and ambiguity may even result in their interpretation. Lineaments analyzed in the present study do not correspond to surface faults or fractures; rather, they represent surface the geotexture (e.g., [9]). Lineament texture results from weathering and erosional etching of the subtle features produced by extension in the brittle upper crust sitting above deeper crustal layers that behave in a more ductile fashion [2,7,9,12,13]. In this way, lineaments represent the surface imprint of tectonic structures related to the structural architecture/crustal grain of the region. The structural grain of a region is often partly hidden by sedimentary covers (as well as by ice on other planetary surfaces). The dynamic adjustment through geologic times of such covers (including sediment compaction) record on their surface the bedrock architecture, whose smoothed signature is hardly discernible from classical field work. Satellite scale images are the best means to detect such tectonic textures.
Here, the term domain is intended to stress the importance of the azimuthal family rather than the individual lineament, which is commonly poorly visible by normal visual observations. Many scientists have erroneously tried to describe each lineament individually in terms of classical geological elements, such as fractures, faults, dykes, or crustal discontinuities (e.g., [15,16,17,18,19,20,21,22,23,24]). However, lineament domains are instead superficial manifestations of the crustal stress field trajectory—their mean azimuth is parallel to the maximum horizontal stress of the upper (rigid) crust of the region in which the domain occur [5,7,9,10,11,14,25]. Hence, lineament domains relate to surficial features under the tectonic control of deep crustal features.
Lineament domain investigations in various geodynamic environments have previously been performed to: (i) highlight the tectonic setting and regional stress field of a region [3,7,9,10,12,26,27,28]; (ii) better understand secondary permeability by identifying the directions of the most permeable faults and fractures in water/oil reservoirs [13,22,29,30]; (iii) to define the fracture pattern associated with main faults [9,31]; and (iv) to assess the volcano-tectonic setting and the fracture distribution in geothermal areas [23,31,32,33,34,35]. All of these studies have revealed a relationship between lineament domains and recent/active tectonics in the studied region and confirm that they are indicators of active stress fields. Notably, one of the effects of active tectonics is seismicity. However, the relationship between surface geology and seismicity is often complex (e.g., [36,37]) and the relationship between earthquakes and surface geology (i.e., faults) is described by linking the surface ruptures to the main shock. Notably, recent works based on the analysis of seismic reflection profiles (e.g., [38,39,40]) or potential field (e.g., gravimetric analysis, [24]) allowed to successfully fill this gap. Unfortunately, such data are not always available, and their acquisition is expensive and mostly performed for oil exploration purposes. This paper aims at providing clues on the seismic meaning of lineament domains in a notably known seismically active region such as Central Italy in order to develop a methodological approach to be potentially applied to other regions where available subsurface data are few or absent. The constant rectilinear attitude of lineament populations, which persists for tens of kilometers, suggests that lineaments may be understood as the intersection with the topography of virtual vertical planar surfaces striking parallel to maximum horizontal compression (sigma1 or sigma2) [5,7,9]. The integration of information related to the surface brittle deformation (attitude, typology, intensity, and spatial distribution) with the upper crustal stress field, as derived from lineament domain analysis, can be used to infer the geological setting at depth.
The pioneer work of [3] represents one of the first systematic attempts to examine the relationship between lineament domains and the seismotectonic setting of an active region. Based on morphological evidence of the San Andreas Fault, [41] stated: “Many lineaments are identical to seismotectonic lines and they, therefore, afford a means (to some extent) of determining in advance the lines of greatest danger from earthquake shocks.” However, these early works, performed using the shadow technique [3,5], whereby lineament populations are manually traced (e.g., [42,43]), often introduced operator bias. Modern methodologies for automatic lineament extraction from raster images, therefore, represent a significant step forward and provide the necessary objectivity and reliability for lineament domain analysis by reducing the operator bias [11,14,44,45]. To this end, in this study we present an original methodology for automatic lineament identification performed with our in-house software SID [45].
Italy is one of the most seismically active regions of the Mediterranean, where many destructive earthquakes have occurred in past centuries and thousands of small-to-moderate events are recorded every year [46]. The epicentral locations of the strongest earthquakes lie along a band that roughly follows the NW–SE trend of the Apennines (Figure 1), making this active tectonic setting an appropriate site to investigate the relationship between seismicity and the lineament domains of this region.
In this paper, we explore the relationship between the lineament domains outcropping in the Central Apennines and their seismotectonic setting. The results allow for the recognition of the most seismically active tectonic trends, the identification of their spatial distributions and the proposition of a geodynamic model for the area, which is characterized by regional arching and can explain the observed seismicity and tectonic settings.
2. Geological Setting
The present-day geological setting of the Central Apennines region is the result of the complex oblique collision between the Eurasian and African plates related to the closure of the Thetis Ocean during the Permian–Cenozoic [47,48,49,50,51,52]. The collision started during the Oligocene and was associated with the opening of several secondary rotational basins [53,54,55]. Evidence of the Oligocene collision is still present, both in eastern Sardinia [56,57] and along the western side of the Italian Peninsula [58]. This earlier chain was partially dissected and further deformed by the opening of the Tyrrhenian Basin, which started during the Lower Miocene (Langhian) and is still active today, with the development of young oceanic crust in its southern sector (e.g., Mt. Marsili, Mt. Vavilov, [59]). During the same time period, we refer to the collision between the relicts of the former fold-and-thrust belt with a portion of the sedimentary prism of the Adriatic microplate (commonly associated with the Africa plate), which had not yet been involved with the collision. This resulted in the rather asymmetric thrust chain of the Apennines, characterized by strong vergence toward the Adriatic microplate to the NE [60,61,62,63]. This later chain is formed by part of the previous collisional chain that slid off of the European crust from the Tyrrhenian Sea onto the Adriatic sedimentary prism, as proven by the Deep Sea Drilling Project (DSDP) drillings, which found a Hercynian basement (i.e., pre-collision) topped with Late Miocene and recent sediments [64].
The studied sector of the Central Apennines comprises two Meso-Cenozoic sedimentary domains, shaped by two phases of thrust tectonics and orogeny events [58]. This includes the Umbro-Marchigiana carbonate deep-water succession to the NW and the Latium-Abruzzi carbonate platform succession to the SE. Both developed during the Triassic-Miocene period and are topped by terrigenous sediments related to the final orogeny of the Apennine Chain [61,65,66].
As Africa and Eurasia continue to converge (associated with the E–W strike-slip component along the Mediterranean Sea [49,50]), the NW-trending Central Apennine belt is undergoing a NE–SW extension [67]. This is confirmed by the occurrence of normal faulting, strong earthquakes (moment magnitude Mw > 5.5), such as those reported in seismic catalogues (i.e., CMT catalogue, [68,69]; USGS/ANSS Comprehensive Catalog, [70]; Catalogo Parametrico dei Terremoti Italiani 2015, CPTI15 v2.0 from INGV, [46]). The epicenters of these earthquakes cluster within the belt located in the central, axial part of the chain (Figure 1).
Three main geodynamic provinces are present in the central sector of the Italian Peninsula [60,65,71,72]; from W to E, they are the Tyrrhenian Margin, the Apennine Fold Thrust Belt, and the Adriatic Foreland (Figure 1). The Tyrrhenian Margin Province relates to the E–W opening of the Tyrrhenian Basin since the late Tortonian and the SW margin of the Italian Peninsula, where a series of large volcanic centers have developed since the Quaternary [61]. This province is undergoing extensional tectonic activity due to N–S and subordered NW–SE normal and strike-slip faults [59,60,73,74]. The Apennine Fold Thrust Belt province is a Neogene fold-and-thrust belt characterized by approximate NE convergence and northeast migration of the collision, which is active today and at these latitudes offshore of the Adriatic [63,75,76,77]. The major thrust systems that developed in the Central Apennines during the Mio-Pliocene strike NW–SE and gradually become deep toward the southwest [60,65,66,73,78]. Associated with this main trend, N–S and E–W thrust systems also exist in the region [38,66,78].
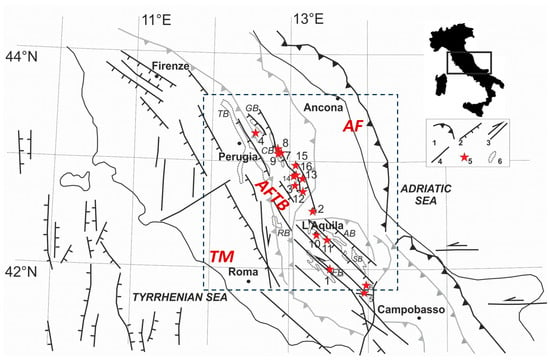
Figure 1.
Tectonic setting of Central Italy (modified after [73]) showing the main recent or active regional elements within the three identifiable geodynamic provinces: the Tyrrhenian Margin (TM), Apennine Fold Thrust Belt (AFTB), and Adriatic Foreland (AF). Legend: (1) main thrust fronts (grayed if no longer active); (2) normal faults; (3) strike-slip faults; (4) faults (generic); (5) epicenters of main earthquakes during the period 1915–2017 from the CMT catalogue [68,69], USGS/ANSS Comprehensive Catalog, [70], and Catalogo Parametrico dei Terremoti Italiani 2015 (CPTI15 from INGV, [46]), with the seismological parameters listed in Table 1; (6) intra-Apennine Plio-Quaternary basins. TB: Tiberino Basin; GB: Gubbio Basin; CB: Camerino Basin; RB: Rieti Basin; AQ: L’Aquila Basin; FB: Fucino Basin; SB: Sulmona Basin. The dashed black rectangle represents the main study area.

Table 1.
List of earthquakes included in the comparison of the Apennine Domain with the seismicity of the region. The seismological parameters were obtained from the CMT catalogue [68,69], USGS/ANSS Comprehensive Catalog, [70], and Catalogo Parametrico dei Terremoti Italiani 2015, CPTI15 v2.0 from INGV, [46]. The locations of the analyzed earthquakes are shown in Figure 1.
The latest tectonic episode in this portion of the Apennines is the development of several intra-Apennine depressions, which constitute Plio-Quaternary depocenters to form local continental basins [79]. These are superimposed upon the inactive compressional Neogene structures. The major Plio-Quaternary basins in the region include the Tiberino, Gubbio, Camerino, Rieti, L’Aquila, Fucino, and Sulmona basins (Figure 1). The more recent of these tectonic depressions cluster along a band of the Central Apennines that roughly corresponds to the locations of recent large earthquakes. These intra-Apennine basins are mainly confined by major NW–SE normal and strike-slip faults [80]. To the NE, the Adriatic Foreland geodynamic province is presently undergoing compressional deformation, characterized by the offshore presence of the NW–SE active frontal thrust systems of the Apennines, and involves deposits as recent as the Quaternary [61,66,67].
The geodynamic provinces in the Central Apennines differ in their crustal stress regimes and associated seismicity: ongoing extension of the western Tyrrhenian province, and compression of the Adriatic geodynamic province [67].
The 2016–2017 seismic sequence that struck Central Italy, which included nine earthquakes with Mw > 5 [24,38], developed along the axial zone ridge of the Apennines, where an active NE–SW extension was confirmed by both seismological and geodetic data at a rate of approximately 3 mm/year [81,82]. This active extensional belt elongates in the NW–SE direction and has hosted several important earthquakes during the past 40 years, such as the 1979 Norcia, 1980 Irpinia, 1997 Colfiorito, and 2009 L’Aquila earthquakes [46]. Normal faults trending from NW–SE to NNW–SSE were responsible for the main shocks of these earthquakes [38]. Recent works have highlighted the crosscutting relationship between the main seismogenetic faults [39] as well as the role played by subsurface geology, inherited compressional structures, fault geometry, and segmentation on the recent seismicity pattern of the study area [38,39,40].
3. Materials and Methods
Our analysis of lineament domains in the Central Apennines followed a three-step process, which included: (i) initial processing of a digital elevation model for the study region to enhance linear textures; (ii) automatic lineament detection using our in-house SID software (GeoQuTe Lab, Quantitative Geodynamics and Remote Sensing Lab at Roma Tre University [7,10,12,45,83]; and (iii) domain identification, using a Gaussian grid analysis of detected lineaments [84].
3.1. Image Data
Our automatic detection of lineament domains was conducted on data from the Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER) Global Digital Elevation Model (GDEM, [85]). The GDEM is generated from stereo image data from the ASTER sensor. This instrument has along-track stereoscopic capability using its near- infrared spectral band and nadir- and backward-viewing cameras. The GDEM is distributed in GeoTIFF format, with geographic latitude and longitude coordinates and a 1 arc-second grid of ~30 m at the latitude of the study area [86]. The study area was extrated performing a subset of the original GDEM from latitudes of 43.60904722° N to 41.81029444° N and longitudes of 11.89174722° E to 14.38292222° E for a total area of 160 km2. Geographic latitude/longitude were converted to the UMT (zone 32° N) coordinate system (i.e., WGS84 datum). The image was resampled via cubic convolution to obtain a spatial resolution of 250 m, which resulted in an image of 800 × 800 pixels. This resolution represents the best compromise between scale and resolution, provides a synoptic view of the study area while preserving the regionally sized signature of tectoncs, and thus allows us to represent the lineaments at the regional scale and avoid the spurious interpretation of local effects (such as anthropic features and local tectonic effects).
This resampled subset was further processed to enhance linear texture, using ENVI 4.8 software. First, a 3 × 3 low-pass kernel was applied to suppress morphological variations, with wavelength < 750 m, related to local-scale factors. Second, directional first-order derivatives were applied to produce a set of images with NE–SW, E–W, SE–NW and N–S directional filtering. This allowed us to reduce the bias associated with a single-directional first derivative, which tends to hide or slightly rotate lineaments that lie nearly parallel to the directional derivative [2]. Each image was then filtered by a Laplacian edge-enhancing filter [87] (3 × 3 kernel size) to emphasize the high spatial frequency related to the presence of linear textures. Subsequently, dynamic threshold filtering was performed to identify and select only significant pixels (i.e., pixels contributing to the image texture related to the presence of lineaments), to reduce the pixel number to ~10% of that of the original image. Finally, apparently significant but isolated pixels were removed by life filtering [7,8,10], which reduces random noise. The life filter compares each significant pixel (i.e., DN value higher than the threshold slice) with its surrounding pixels, and removes it if the number of significant surrounding pixels is below a given threshold (in the present analysis, four out of eight neighbors).
3.2. Automated Lineament Detection
Lineaments were automatically extracted from the prepared images using our in-house SID 195 software [45]. The parameters of the software were adjusted to describe the geometric characteristics of lineaments (e.g., minimum length, width, and sharpness) with a converging trial and error method [8]. This iteration is repeated until a statistically meaningful number of lineaments are detected for following polymodal Gaussian grid analysis, and robust azimuthal trends are identified (i.e., the results persist even with a slight variation in the SID parameters). The minimum length of detectable lineaments was 20 km, which corresponds to 80 pixels in the images. Lineaments were detected by the SID software using a dynamic pattern recognition process when the following conditions were met: (i) minimum pixel density of 2 pixels within a running interval of 3 pixels; (ii) a maximum of a 5-pixel interruption in the density stripes; (iii) a minimum meaningful pixel sequence length (i.e., lineament segment) of 7 pixels. All possible azimuthal directions were analyzed, with a resolution according to the image size (approximately 0.1°).
3.3. Domain Grouping/Identification via Polymodal Gaussian Grid Analysis
The extracted lineaments (mapped in Figure 2) were accumulated into a database and analyzed using the DAISY3.5.28 software [88] to identify the lineament domain through a polymodal Gaussian grid analysis according to methods presented in [5,84]. A significant number of lineaments cluster into domains: groups of lineaments with orientations about a given azimuth. Not all lineaments group into such domains, and a relatively small number are randomly distributed both spatially and azimuthally.
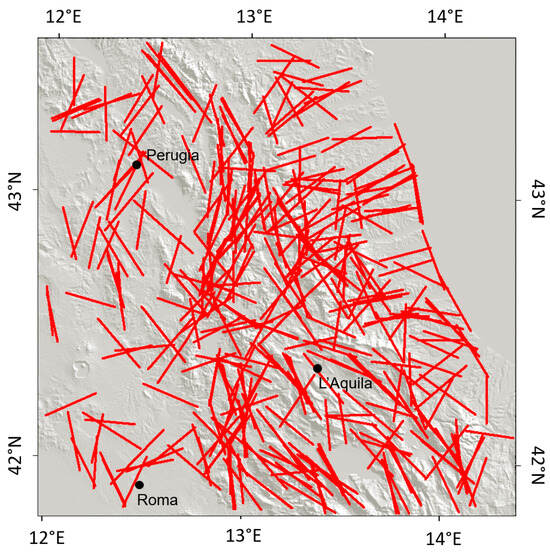
Figure 2.
Identified lineaments (red lines) over the N–S directional filtered DEM. Note the higher density areas correspond to the higher relief zone of the Apennines. This bias was eliminated in the analysis by using dynamic threshold processing (see main text).
Lineament domains were identified following an azimuthal and spatial analysis. In order to avoid complications due to the observed progressive rotation of the azimuth within lineament domains, the analyses were conducted in three stages: a local azimuthal frequency analyses, a spatial correlation analysis of lineament azimuths, and the eventual classification of lineaments using the results from step two. This process is illustrated in Figure 3, and described in detail below.
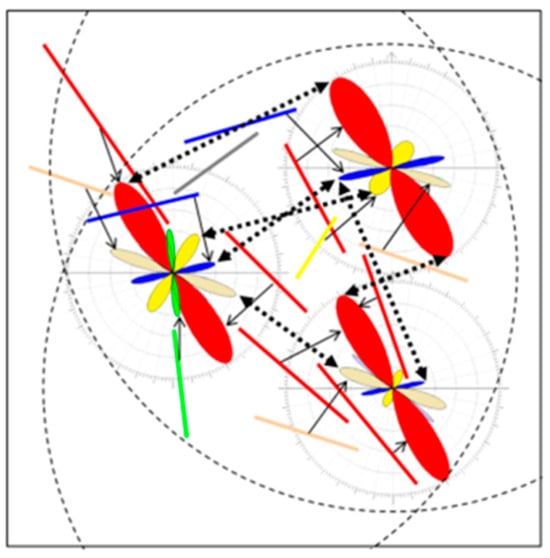
Figure 3.
Illustration of the lineament domain identification process. The lines represent individual example lineaments, and their colors refer to specific domain groups. Red, blue, and green correspond to major lineament domains, while yellow, beige, and violet represent minor domain groups. Step 1 (see Section 3.3.1): Three examples of azimuthal frequency analysis of lineaments from overlapping circular areas (dashed circles). The corresponding wind rose peak diagrams (i.e., polymodal Gaussian curves) are positioned over the circle centers. Step 2 (see Section 3.3.2): Group identification by azimuthal correlation between peaks from the frequency analysis of adjacent areas (thick, double-ended arrows). The difference in angle between peaks within a single group were limited to 5°. In this example, six groups were identified, three of which were recognized as potential domains. Step 3 (see Section 3.3.3): Association of lineaments with peak groups by their normalized minimum angle (expressed as a fraction of the standard deviation in the peak) with the peak in the closest circular area (thin arrows). The angle threshold was set to a maximum of ±1 sd, and angles greater than this threshold were unclassified (gray lines). A group was classified as a lineament domain when the number of associated peaks, representing their spatial distribution, and the number of corresponding lineaments exceeded 22 peaks and 10% of the total number of lineaments identified in the study area.
3.3.1. Azimuthal Analysis of Lineament Orientation
The first step was to identify the preferred orientation of lineaments, via a gridded azimuthal analysis of the lineaments extracted from circular areas within a square-centered net/hexagonal shape of circles, as illustrated in Figure 3. Each circle overlaps with six neighbors to provide connections among the analysis net. In the present study, 35 circular areas were selected, and the distance between circle centers was approximately 40 km, with a radius of 59.025 km, to provide proper overlaps.
Each analysis consisted of a polymodal Gaussian fit of the azimuthal frequency of the lineaments falling within each circular area. Polymodal analysis was performed using the methodology presented in previous studies [5,89,90]. The results include the statistical approximation for each independently and normally distributed system responsible for the found azimuthal distribution, which includes their azimuth mean, mode, and standard deviation (sd). Results are presented in Figure 4 where each analysis is represented by a wind rose of segments centered over the corresponding circles (each segment corresponding to a Gaussian peak). The identified azimuthal systems/Gaussian peaks are shown as segments oriented parallel to their mean azimuth, with a length proportional to the number of lineaments falling in the relative circle. Please note that their relatively estimated standard deviations are not represented.
3.3.2. Spatial Correlation between Azimuth Orientations and Identification of Potential Domains
In the second step, we compared the azimuthal data between each circular area and the neighboring six circles, and similar azimuthal systems/Gaussian peaks were correlated, as shown in Figure 3. To perform this grouping, we started with the most significant system/peak (that is, the system represented by the longest segment as shown in Figure 4) and multiplied its mode by the number of lineaments extracted. Azimuthal similarity is recognized by tolerating a slight peak rotation between adjacent analyses; in the present study, a maximum rotation of 5°/40 km was used as the threshold value. This grouping process was recursively repeated (forest-fire process, [91]) until no more peaks could be correlated. Each classified peak group represents a potential lineament domain, depending on the significance of its areal distribution (i.e., the number of associated peaks from the regular net). This process was then repeated among the residual, unclassified Gaussian peaks (always starting with the most significant) until all peaks were grouped. This resulted in the identification of 33 groups (including the single (not correlated) residual peaks), in which lineament domains were identified as groups that had a significant areal distribution, as expressed by the number of correlated peaks. By adopting a threshold of 22 associated peaks, in the analysis of the Central Apennines, three main lineament domains were identified. Relative peaks are presented as colored segments in Figure 4.
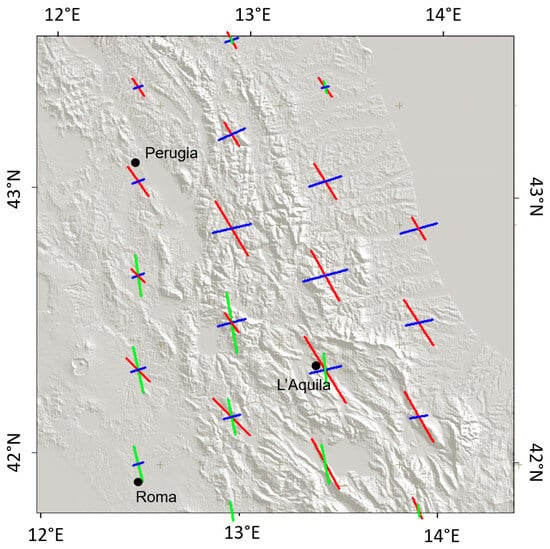
Figure 4.
Azimuthal frequency grid analysis of partially overlapping circles for the Apennine Domain (red), Adriatic Margin Domain (blue), and Tyrrhenian Margin Domain (green). Domain peaks (polymodal Gaussian fit analysis) are shown as segments parallel to their mean azimuths. The segment lengths are proportional to the number of associated lineaments. Note that due to the overlap between adjacent single circular analyses, the apparent regional distribution of each domain is exaggerated, as in the case of the last domain. Refer to following figures to visualize the Apennine Domain real distribution.
3.3.3. Domain Classification
In the third and final step, the lineaments were assigned to a domain group by comparing each lineament with the grouped/classified peak distribution (specifically, the peaks in the closest analysis according to their location in the circle center, Figure 3). Each lineament is associated with the domain belonging to the peak of least mean normalized angle with the lineament azimuth. The normalizing angle is obtained by dividing the azimuth difference (between the lineament and the relevant peak) by the standard deviation of the relevant peak. In addition, this final classification has a threshold that is consistent with the maximum allowable normalized angle—in the present study, this threshold was fixed to ±1 sd. As an example, for a peak with a mean azimuth of N32° and sd of 6.7°, a lineament falling within the corresponding area with an azimuth between N25.3° and N38.7° would have been associated with this domain, unless its normalized angle with a peak from another group is less. As expected, the association with peak groups leaves a number of unclassified lineaments. Furthermore, parts of the lineaments are associated with groups that do not satisfy the required areal distribution to represent lineament domains (e.g., 22 associated peaks). In the present study, 41.8% (165 out of 395) of lineaments are associated with the three identified domains, 44% (174 out of 395) are associated with smaller peak groups that do not reach the threshold for classification within a domain, and 14% (56 out of 395) remain unclassified.
The domains are finally presented as density plots obtained by the area counting process, with a given radius for the raster representation of the lineaments in each domain (Figure 5). The lineaments are traced on a raster image at a given resolution (307 m/px); then, a running counting circle through the image is used to compute lineament density (in m/km2). This parameter is computed for each circular running area by multiplying the number of pixels representing the lineaments by their dimension and dividing this result by the area of the counting circle.
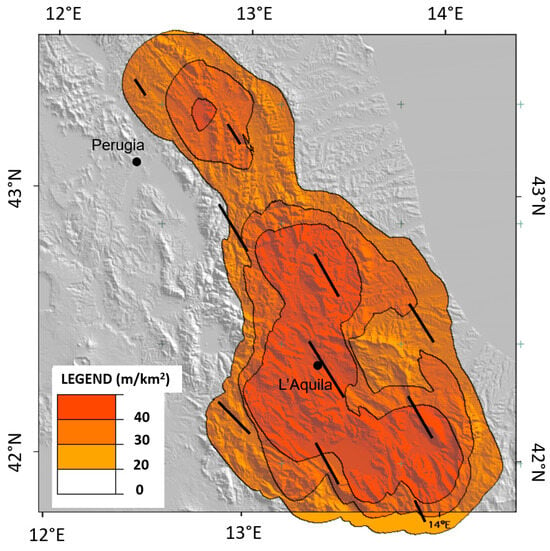
Figure 5.
Density distribution of the Apennine Domain. The black segments indicate the main lineament azimuth in the corresponding circular areas. The segments are reported only when the domain density is significant (>20 m/km).
4. Results
A total of 395 lineaments were detected in the investigated area (Figure 2), with a mean length of 24.963 km. Higher concentrations of lineaments were identified in the Central Apennines outcrops than in the relatively flat Tyrrhenian coastal area. The polynomial Gaussian grid analysis reveals the existence of three main lineament domains in the Central Apennines, defined by their azimuthal orientation and spatial distribution, trending on average N32° W, N72° E, and N11° W. The results of the azimuthal analyses of each lineament domain are presented in Figure 4 as segments (centered over the nodes of the hexagonal shape grid) oriented parallel to their mean azimuth. Each domain is represented by a different color and named according to the geodynamic domain on which they spatially cluster: the main Apennine Domain (red), the Adriatic Foreland Domain (blue), and the Tyrrhenian Margin Domain (green). Segment lengths are proportional to the number of lineaments in each circle. Relative azimuthal standard deviations are not represented. Other identified groups are characterized by populations of 288 lineaments and number of Gaussian peaks that are too small (<26 lineaments and <22 peaks) to represent lineament domains (not shown).
The N32° W domain is the largest of the three domains. It consists of 81 lineaments (21% of the total) and 28 associated Gaussian peaks, which indicates its significant spatial distribution. The lineament density plot of this domain (Figure 5) was obtained using a running counting circle, with a radius of 24.5 km (corresponding to 80 pixels). The area with a density higher than 20 m of lineaments per km2 exceeds 16,000 km2, and is located along a NW–SE band, which roughly corresponds to the axial ridge of the Central Apennine belt. This band is characterized by an across-strike width of approximately 100 km in the southern portion of the region, and halves in the northern part. The mean azimuths of the lineament domain are shown by the black segments in Figure 5, with segments limited to higher density zones (compared to Figure 3). For its azimuthal trend and areal distribution, we hereafter refer to this domain as the Apennine Domain.
The N72° E domain has about half as many lineaments as the Apennine Domain (43, representing 11% of the total), with a slightly shorter mean length of 23.485 km. A total of 27 Gaussian peaks is associated with this domain, which partly overlaps with the Apennine Domain but is slightly N and E. Figure 4 shows more scattered lineaments in this domain, which mainly cluster along the Adriatic Coast as a NNW–SSE trending belt, parallel to the Apennine thrust front. We named this domain the Adriatic Foreland Domain.
The N11° W lineament domain consists of 41 lineaments (10% of the total), with a mean length of 22.67 km. Despite a smaller number of Gaussian peaks being associated with this domain (Figure 4; 22 peaks), it is nonetheless classified as a lineament domain due to the spatial and numerical consistencies of its lineaments. It partly overlaps with the other two domains but mainly cluster with N–S direction along the boundary zone between the Apennines and Tyrrhenian coastal plain. The azimuthal direction and spatial distribution of lineaments from this domain recall the E–W extension that characterizes the Tyrrhenian Margin of the Apennines at this latitude. Therefore, we named this domain the Tyrrhenian Margin Domain. A minor contribution could be also related to the N–S and NNW–SSE tectonic structures belonging to the adjacent Apennine Fold Thrust Belt province.
The azimuthal trend and spatial distribution of the identified lineament domains correlate with known tectonic features of the three geodynamic provinces that interact within the study region. The Tyrrhenian Margin Province relates to the E–W opening of the Tyrrhenian Basin and is presently undergoing extensional tectonics along the main N–S normal and strike-slip faults. According to [5,7,10,28], the roughly N–S direction that characterizes the Tyrrhenian Margin Domain is compatible with the abovementioned E–W extension (Figure 1 and Figure 4). Similarly, the N72° E azimuthal trend of the Adriatic Foreland Domain parallels the compressive horizontal component that characterizes this area [67] due to ongoing active thrusting in the Adriatic Foreland that involves deposits as recent as Quaternary (model I in Figure 10 from [5]). Finally, the Apennine Fold Thrust Belt province is characterized by similarly oriented and spatially distributed seismicity as the Apennine Lineament Domain.
To further explore the seismotectonic meaning of the Apennine Domain, we compared the spatial and azimuths of this domain with the seismicity of the region. Here, we only consider the Apennine Domain. We mapped the epicenters of the strongest earthquakes (with moment magnitudes of Mw > 5.5) of the past ~100 years (Figure 6). Details of these earthquakes are presented in Table 1, along with their seismological parameters (magnitude; epicenter; focal mechanism nodal planes; and T, N, and P axis attitudes), obtained from the CMT catalogue [68,69], USGS/ANSS Comprehensive Catalog, [70], and Catalogo Parametrico dei Terremoti Italiani 2015, CPTI15 v2.0 from INGV, [46].
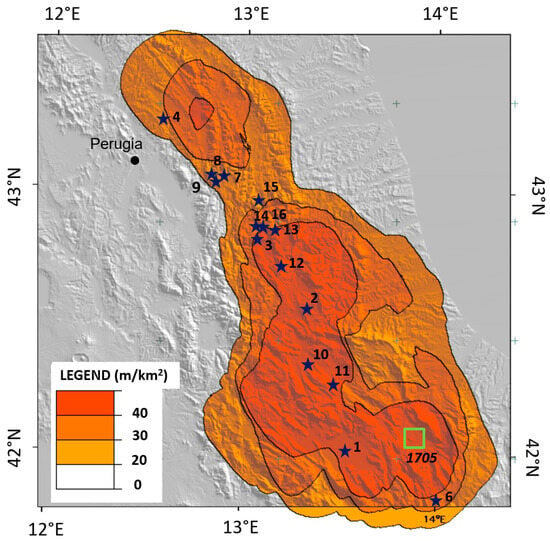
Figure 6.
Comparison between the spatial distribution of the Apennine Domain and the locations of strong earthquakes (with a moment magnitude of Mw > 5.5) in the region for the period 1915–2017. Earthquake data obtained from the CMT catalogue [68,69], USGS/ANSS Comprehensive Catalog, [70], and Catalogo Parametrico dei Terremoti Italiani 2015, CPTI15 v2.0 from INGV, [46]. The stars represent epicenters, and the numbers refer to the site numbers in Table 1, where the seismological parameters of each earthquake are listed. The green square is located over the Sulmona area, where a destructive earthquake occurred in 1706 with an estimated magnitude between 6.5 and 6.9 [46], which is different from the regional periodicity of large earthquakes (i.e., L’Aquila in 1461, 1703, and 2009). This area falls well within the Apennine Domain.
These 16 large earthquakes cluster along a NW–SE band corresponding to the Apennine Ridge and correlate with the Apennine Domain density, as shown in Figure 6. They are characteristically associated with local faults that share the same NW–SE direction [24,38,39,40,73,78,80] rather than the presence of major, unique regional faults (e.g., the San Andreas or Anatolian Faults). The distribution of the epicenters of these earthquakes and the area of highest lineament density in the Apennine Domain coincide along a well-defined band. This band is characterized by an extensional regime, as testified by focal mechanism solution, and geodetic and break-out data [67,82].
The correlation between the Apennine Domain and seismicity is strengthened by comparing the azimuths of this lineament domain with the null axes of the focal mechanisms. In extensional regimes, null axes correspond to the maximum horizontal compression and strike of the associated faults. The azimuthal frequency analysis of null axes (Figure 7) presents a mean direction of N36° W.
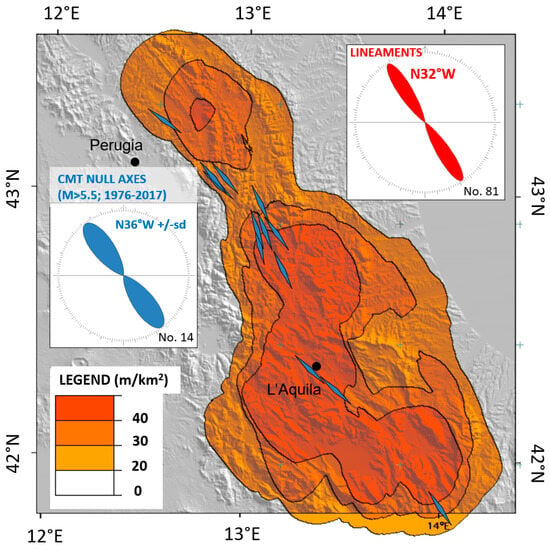
Figure 7.
Comparison between the average azimuths of the lineaments from the Apennine Domain and the azimuthal frequency wind rose diagram of the null axes of major earthquakes (moment magnitude of Mw > 5.5) during the period 1915–2017. The small angle difference (4°) is significantly less than their standard deviations, indicating a common cause.
The same analysis was performed for the lineaments of the Apennine Domain and provided a mean direction of N32° W.
Their near parallelism is testified by the small angular divergence of 4°, well within the sd of both distributions. Here, the angular divergence of 4° is well within the sd of both distributions, suggesting their strong correlation.
5. Discussion
The spatial correspondence between seismicity and the Apennine Domain allows us to present a geodynamical model (Figure 8) following the pioneering work by [3]. Crustal stresses operating in this sector of the chain that are responsible for the observed seismicity may influence the complexity of the phenomena that carve the landscape and leave typical signatures, as evidenced by the texture of the lineament domains.
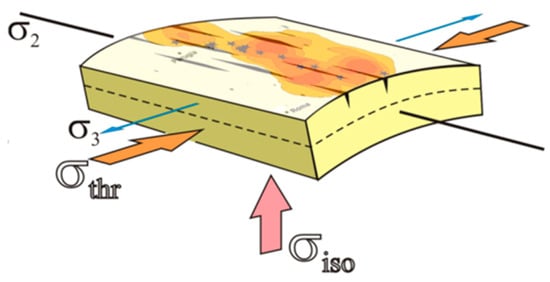
Figure 8.
A conceptual seismo-geodynamic model for the Central Apennines. Two “geodynamic engines” are active: NE–SW shortening produced by the Tyrrhenian Sea and the Adriatic front backstop responsible for the arching of the Apennines (σ thr) and the isostatic re-equilibrium (σ iso) related to differential erosion (i.e., related to the different uplift rate during arching). Both “engines” contribute to the development of a hinge in the crest zone of the arch, where resulting major curvature induces a NE–SW extension (σ 3) in the upper crustal layer. This geodynamic setting explains both the location of earthquakes along a narrow band and the corresponding interaction of crustal stress with the morphological carving phenomena, which produces the main Apennine Lineament Domain. Earthquake locations are shown with stars, and the lineaments are represented as “dry dyke swarm”, following the model proposed by [5]. Null axes, fault strikes, and lineaments from this domain always coincide with the arching axis. The iso-density of the spatial distribution of the Apennine Lineament Domain is also represented as in Figure 5.
The coupling of seismic activity and the presence of the Apennine Domain supports the preparation of the seismo-geodynamic model of the Central Apennines. The lineament domains confirm the presence of three geodynamic provinces in Central Italy. The Tyrrhenian Margin Province is further characterized by the presence of the Tyrrhenian Lineament Domain, with its main trend nearly parallel to the recent extensional faulting in the Tyrrhenian Sea (Figure 1 and Figure 4). Similarly, the Adriatic Foreland Province has been associated with the Adriatic Foreland Lineament Domain, which confirms, with its main parallel direction, the compressional regime related to the active Apennine thrust front. The Apennine Thrust Belt Province is characterized by similarly oriented and spatially distributed seismicity and the Apennine Lineament Domain.
The development of the Central Apennines/ Apennine Thrust Belt Province is driven by two concomitant processes, as shown in the conceptual model (Figure 8). First, a general NE–SW compression (σ thr) related to the Tyrrhenian Sea extension to the W, and a backstop provided by the Adriatic plate collision. This compression induces the shortening of the Apennine Thrust Belt Province, which is, in turn, accomplished by the regional arching of the Apennines. Second, the vertical stress (σ iso) induced by the isostatic re-equilibrium of the chain subjected to erosion during differential uplifting provides a vertical stress.
This is proportional to the uplift (maximum in the arching crest), which enhances the arching process and concentrates the arch curvature within the crest zone. In this way, the upper crustal zone (above the surface, indicated by the dashed line in Figure 8) is subject to an extension proportional to the arching curvature with a NE–SW extension (σ 3). The resulting brittle deformation that develops in the upper crustal layer will, therefore, be concentrated in the crest zone. This is confirmed by the presence of recent intra-Apennine depressions in the arch crest zone, by a seismic belt associated with a swarm of normal faults, and by the Apennine Lineament Domain.
Notably, the arch crest does not necessarily coincide with the chain axis or its divide due to the strong asymmetry of the Apennine fold-and-thrust belt, whose kinematics result from the combination of gravitational sliding from Tyrrhenian Basin uplifting and the collision of its front with the Adriatic plate.
This geodynamic model fully explains the presence of an extensional tectonic regime in the upper crustal layer of the active Apennines fold-and-thrust belt. The strike-slip component observed in several main shocks in the Apennines (e.g., [92]) might relate to inherited crustal weakness zones that were reactivated during the Africa-Eurasia plate convergence producing moderate to strong deep earthquakes specifically in the Adriatic side of southern Apennines [93]. In this way, the seismo-tectonic setting of the investigated region results from the contribution of first-order, geodynamic-scale, factors related to the ongoing convergence between Africa and Eurasia plate and of local-scale geologic setting that includes both possible inherited weakness zones and the NE–SW extension presently ongoing in the central sectors of the Apennine chain.
6. Conclusions
The presented geostatistical analysis of automatically detected lineaments allowed us to identify domains (sensu [5,9]) that relate to the geodynamic setting of Central Apennines. Our lineament domain analysis confirmed the existence of three geodynamic provinces in Central Italy.
Characterizing the precise relationship between surface geology (i.e., faults) and seismicity is often complex, especially when seismic reflection profiles or other geophysical data (such as potential fields) are not available.
Our results demonstrate that unconventional indicators of surface geology, such as lineament domains, can help to characterize deep tectonic processes as well as identify surface signatures of active and recent seismic activity. This offers a key/new tool for investigating the potential seismicity of a region.
We show a strong relationship between lineament domains and tectonic activity (notably associated with seismic events), which indicates a common origin/cause between lineament domains and earthquakes. In this way, the surface geotexture represents a key tool to unravel the potential seismicity of a region. In seismic and extensional tectonics, the azimuth of the main lineament domain and null axes from the focal mechanism are nearly parallel, which justifies a common cause.
In areas where seismicity is associated with lineament domains, they may be compared with the historical seismic record and known seismogenic faults observed at surface to support mapping of seismic hazards. This is particularly true where seismic gaps in the historical record are known (e.g., Sulmona area).
Lineament domain analysis is confirmed to be an effective tool to decipher geodynamic settings and can be used to investigate poorly characterized regions on Earth and other planetary bodies.
Author Contributions
Conceptualization, P.C. and F.S.; methodology, P.C. and F.S.; software, F.S.; validation, P.C., F.S. and D.M.; formal analysis, P.C.; investigation, P.C. and D.M.; resources, P.C.; data curation, P.C., F.S. and D.M.; writing—original draft preparation, P.C.; writing—review and editing, P.C., F.S. and D.M.; visualization, P.C. and D.M.; supervision, P.C.; project administration, P.C.; funding acquisition, P.C. and F.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was financially supported by Università degli Studi di Genova funding to Paola Cianfarra, (FRA, Fondi per Ricerca di Ateneo grant 100022-2022-PC-FRA_001) and by funding of the GeoQuTe Lab (responsible F. Salvini).
Data Availability Statement
Programs and data are available upon request to the Authors.
Acknowledgments
The authors thank the anonymous reviewers for their constructive comments that allowed to improve the original version of the paper and the editors for handling the manuscript. PC and FS acknowledge Matteo Maggi for the constructive and insightful discussions. PC dedicates this work to the loving memory of Anna Delia Mancini and Maria Rosa D’Amico. Daisy 3 and SID softwares are available as freeware to scientific institution and academics via email (francesco.salvini@uniroma3.it).
Conflicts of Interest
The authors declare no conflicts of interest.
Correction Statement
This article has been republished with a minor correction to the Funding statement. This change does not affect the scientific content of the article.
References
- Hobbs, W.H. Lineaments of the Atlantic Border region. Geol. Soc. Am. Bull. 1904, 15, 483–506. [Google Scholar] [CrossRef]
- Wise, D.U. Pseudo-radar topographic shadowing for detection of sub-continental sized fracture systems. In Proceedings of the Sixth International Symposium in Remote Sensing of Environment; University of Michigan: Ann Arbor, MI, USA, 1969; pp. 603–615. [Google Scholar]
- Funiciello, R.; Parotto, M.; Salvini, F.; Locardi, E.; Wise, D.U. Correlazione tra lineazioni rilevate con il metodo shadow e assetto tettonico dell’area vulcanica\Lazio. Boll. Di Geod. E Sci. Affin. 1977, 36, 451–470. [Google Scholar]
- Bodechtel, J.; Munzer, U. Satellite lineaments of the central Mediterranean region (Sicily/Calabria). In Alps, Apennines, Hellenides: Interunion Commission on Geodynamics Science Report 38; Cloos, H., Roeder, D., Schimdt, K., Eds.; Schweizerbart: Stuttgart, Germany, 1978; pp. 354–368. [Google Scholar]
- Wise, D.U.; Funiciello, R.; Parotto, M.; Salvini, F. Topographic lineament swarms: Clues to their origin from domain analysis of Italy. Geol. Soc. Am. Bull. 1985, 96, 952–967. [Google Scholar] [CrossRef]
- Patterson, G.W.; Head, J.W. Segmented lineaments on Europa: Implications for the formation of ridge complexes and bright bands. Icarus 2010, 205, 528–539. [Google Scholar] [CrossRef]
- Cianfarra, P.; Salvini, F. Lineament domain of regional strike-slip corridor: Insight from the Neogene transtensional De Geer transform fault in NW Spitsbergen. Pure Appl. Geophys. 2015, 172, 1185–1201. [Google Scholar] [CrossRef]
- Rossi, C.; Cianfarra, P.; Salvini, F.; Mitri, G.; Massé, M. Evidence of transpressional tectonics on the Uruk Sulcus region, Ganymede. Tectonophysics 2018, 749, 72–87. [Google Scholar] [CrossRef]
- Balbi, E.; Marini, F. Lineament Domain Analysis to Unravel Tectonic Settings on Planetary Surfaces: Insights from the Claritas Fossae (Mars). Geosciences 2024, 14, 79. [Google Scholar] [CrossRef]
- Cianfarra, P.; Salvini, F. Ice sheet surface lineaments as nonconventional indicators of East Antarctica bedrock tectonics. Geosphere 2014, 10, 1411–1418. [Google Scholar] [CrossRef]
- Rossi, C.; Cianfarra, P.; Salvini, F.; Bourgeois, O.; Tobie, G. Tectonics of Enceladus’ South Pole: Block rotation of the Tiger Stripes. J. Geophys. Res. Planets 2020, 125, e2020JE006471. [Google Scholar] [CrossRef]
- Mazzarini, F.; Salvini, F. Tectonic blocks in North Victoria Land (Antarctica): Geological and structural constraints by satellite lineament domain analysis. Terra Antarct. 1994, 1, 74–77. [Google Scholar]
- Lucianetti, G.; Cianfarra, P.; Mazza, R. Lineament domain analysis to infer groundwater flow paths: Clues from the Pale di San Martino fractured aquifer, Eastern Italian Alps. Geosphere 2017, 13, 1729–1746. [Google Scholar] [CrossRef]
- Pinheiro, M.R.; Cianfarra, P.; Villela, F.N.J.; Salvini, F. Tectonics of the Northeastern border of the Parana Basin (Southeastern Brazil) revealed by lineament domain analysis. J. South Am. Earth Sci. 2019, 94, 102231. [Google Scholar] [CrossRef]
- Campbell, J.B. Introduction to Remote Sensing; The Guilford Press: New York, NY, USA, 1987. [Google Scholar]
- Koch, M.; Mather, P.M. Lineament mapping for groundwater resource assessment: A comparison of digital Synthetic Aperture Radar (SAR) imagery and stereoscopic Large Format Camera (LFC) photographs in the Red Sea Hills, Sudan. Int. J. Remote Sens. 1997, 18, 1465–1482. [Google Scholar] [CrossRef]
- Haeberlin, Y.; Turberg, P.; Retiere, A.; Senegas, O.; Parriaux, A. Validation of Spot-5 satellite imagery for geological hazard iden-tification and risk assessment for landslides, mud and debris flows in Matagalpa, Nicaragua. Nat. Resour. Canada 2004, 35, 273–278. [Google Scholar]
- Gómez, H.; Kavzoglu, T. Assessment of shallow landslide susceptibility using artificial neural networks in Jabonosa River Basin, Venezuela. Eng. Geol. 2005, 78, 11–27. [Google Scholar] [CrossRef]
- Solomon, S.; Ghebreab, W. Lineament characterization and their tectonic significance using Landsat TM data and field studies in the central highlands of Eritrea. J. Afr. Earth Sci. 2006, 46, 371–378. [Google Scholar] [CrossRef]
- Morelli, M.; Piana, F. Comparison between remote sensed lineaments and geological structures in intensively uncultivated hills (Moanferrato and Langhe domains, NW Italy). Int. J. Remote Sens. 2006, 26, 1463–1475. [Google Scholar]
- Pal, S.K.; Majumdar, T.J.; Bhattacharya, A.K. Extraction of linear and anomalous features using ERS SAR data over Singhbhum Shear Zone, Jharkhand using fast Fourier transform. Int. J. Remote Sens. 2006, 27, 4513–4528. [Google Scholar] [CrossRef]
- Gaber, A.; Mohamed, A.K.; ElGalladi, A.; Abdelkareem, M.; Beshr, A.M.; Koch, M. Mapping the Groundwater Potentiality of West Qena Area, Egypt, Using Integrated Remote Sensing and Hydro-Geophysical Techniques. Remote Sens. 2020, 12, 1559. [Google Scholar] [CrossRef]
- Nappi, R.; Alessio, G.; Sessa, E.B. A case study comparing landscape metrics to geologic and seismic data from the Ischia Island (Southern Italy). Appl. Geomatics 2010, 2, 73–82. [Google Scholar] [CrossRef]
- Luiso, P.; Paoletti, V.; Nappi, R.; Gaudiosi, G.; Cella, F.; Fedi, M. Testing the value of a multi-scale gravimetric analysis in characterizing active fault 2 geometry at hypocentral depths: The 2016–2017 central Italy seismic sequence. Ann. Geophys. 2018, 61, 29. [Google Scholar] [CrossRef]
- Wise, D.U.; Funiciello, R.; Parotto, M.; Salvini, F. Domini di lineamenti e fratture in Italia. Pubbl. Dell’istituto Di Geol. E Paleontol. Dell’universita Degli Studi Di Roma 1979, 42, 1–53. [Google Scholar]
- Wise, D.U. Previously unreported fracture systems over vast areas of the Appalachians, U.S. Cordillera and Europe. Trans. AGU 1967, 48, 214. [Google Scholar]
- Salvini, F.; Ambrosetti, P.L.; Conti, A.M.; Carraro, F.; Funiciello, R.; Ghisetti, A.; Parotto, M.; Praturlon, A.; Vezzani, L. Tentativi di correlazione tra distribuzioni statistiche di lineamenti morfologici ed elementi di neotettonica. Contr. Prel. Carta Neotettonica d’Italia, 1979 pubbl. n. 51 P.F. Geodinamica, CNR. In Origem e Evolução de Bacias Sedimentares; Petrobras: Rio de Janeiro, Brazil, 1979. [Google Scholar]
- Cianfarra, P.; Salvini, F. Geodynamic constraints of the peri-Tyrrhenian orogen (Tyrrenian Sea-Apennines) from lineament swarm analysis. Rend. Line Della Soc. Geol. Ital. 2012, 21, 166. [Google Scholar]
- Mabee, S.B.; Hardcastle, K.C.; Wise, D.U. A Method of collecting and analyzing lineaments for regional-scale fractured-bedrock aquifer studies. Groundwater 1994, 32, 884–894. [Google Scholar] [CrossRef]
- Guo, G.; George, S.A.; Lindsey, R.P. Statistical analysis of surface lineaments and fractures for characterizing naturally fractured reservoirs. In Reservoir Characterization-Recent Advances, AAPG Memoir 71; Jordan, R.S.A.J., Ed.; American Association of Petroleum Geologists: Tulsa, OK, USA, 1999; Chapter 16; pp. 221–250. [Google Scholar]
- Pischiutta, M.; Anselmi, M.; Cianfarra, P.; Rovelli, A.; Salvini, F. Directional site effects in a non-volcanic gas emission area (Mefite d’Ansanto, southern Italy): Evidence of a local transfer fault transversal to large NW–SE extensional faults? Phys. Chem. Earth 2013, 63, 116–123. [Google Scholar] [CrossRef]
- Mazzarini, F.; D’Orazio, M. Spatial distribution of cones and satellite-detected lineaments in the Pali Aike Volcanic Field (south-ernmost Patagonia): Insight into the tectonic setting of a Neogene rift system. J. Volcanol. Geotherm. Res. 2003, 125, 291–305. [Google Scholar] [CrossRef]
- Norini, G.; Groppelli, G.; Capra, L.; De Beni, E. Morphological analysis of Nevado de Toluca volcano (Mexico): New insights into the structure and evolution of an andesitic to dacitic stratovolcano. Geomorphology 2004, 62, 47–61. [Google Scholar] [CrossRef]
- Pardo, N.; Macias, J.L.; Giordano, G.; Cianfarra, P.; Avellán, D.R.; Bellatreccia, F. The ∼1245 yr BP Asososca maar eruption: The youngest event along the Nejapa–Miraflores volcanic fault, Western Managua, Nicaragua. J. Volcanol. Geotherm. Res. 2009, 184, 292–312. [Google Scholar] [CrossRef]
- Giordano, G.; Pinton, A.; Cianfarra, P.; Baez, W.; Chiodi, A.; Viramonte, J.; Norini, G.; Groppelli, G. Structural control on geothermal circulation in the Cerro Tuzgle–Tocomar geothermal volcanic area (Puna plateau, Argentina). J. Volcanol. Geotherm. Res. 2013, 249, 77–94. [Google Scholar] [CrossRef]
- Carmignani, L.; Cello, G.; Cerrina Feroni, A.; Funiciello, R.; Kalin, O.; Meccheri, M.; Patacca, E.; Pertusati, P.; Plesi, G.; Salvini, F.; et al. Analisi del campo di fratturazione superficiale indotto dal terremoto Campano-Lucano del 23/11/19Rend. Soc. Geol. It. 1981, 4, 451–465. [Google Scholar]
- Villani, F.; Pucci, S.; Civico, R.; De Martini, P.M.; Cinti, F.R.; Pantosti, D. Surface faulting of the 30 October 2016 Mw 6.5 central Italy earthquake: Detailed analysis of a complex coseismic rupture. Tectonics 2018, 37, 3378–3410. [Google Scholar] [CrossRef]
- Porreca, M.; Minelli, G.; Ercoli, M.; Brobia, A.; Mancinelli, P.; Cruciani, F.; Giorgetti, C.; Carboni, F.; Mirabella, F.; Cavinato, G.; et al. Seismic Reflection Profiles and Subsurface Geology of the Area Interested by the 2016–2017 Earthquake Sequence (Central Italy). Tectonics 2018, 37, 1116–1137. [Google Scholar] [CrossRef]
- Barchi, M.R.; Carboni, F.; Michele, M.; Ercoli, M.; Giorgetti, C.; Porreca, M.; Azzaro, S.; Chiaraluce, L. The influence of subsurface geology on the distribution of earthquakes during the 2016–2017 Central Italy seismic sequence. Tectonophysics 2021, 807, 228797. [Google Scholar] [CrossRef]
- Barchi, M.R.; Carboni, F.; Michele, M.; Ercoli, M.; Giorgetti, C.; Porreca, M.; Azzaro, S.; Chiaraluce, L. The impact of structural complexity, fault segmentation, and reactivation on seismotectonics: Constraints from the upper crust of the 2016–2017 Central Italy seismic sequence area. Tectonophysics 2021, 810, 228861. [Google Scholar] [CrossRef]
- Dodge, R.E.; Hobbs, W.H. Earth features and their meaning. Bull. Am. Geogr. Soc. 1912, 44, 384. [Google Scholar] [CrossRef]
- Wise, D.U. Linesmanship and the practice of linear geo-art. GSA Bull. 1982, 93, 886. [Google Scholar] [CrossRef]
- Scheiber, T.; Fredin, O.; Viola, G.; Jarna, A.; Gasser, D.; Łapińska-Viola, R. Manual extraction of bedrock lineaments from high-resolution LiDAR data: Methodological bias and human perception. GFF 2015, 137, 362–372. [Google Scholar] [CrossRef]
- Ghirotto, A.; Armadillo, E.; Crispini, L.; Zunino, A.; Tontini, F.C.; Ferraccioli, F. The Sub-Ice Structure of Mt. Melbourne Volcanic Field (Northern Victoria Land, Antarctica) Uncovered by High-Resolution Aeromagnetic Data. Journal of Geophysical Research. Solid Earth 2023, 128, e2022JB025687. [Google Scholar] [CrossRef]
- Salvini, F. Slope-intercept-density plots—A new method for line detection in images. In Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS’85), Amherst, MA, USA, 7–9 October 1985; pp. 715–720. [Google Scholar]
- Rovida, A.; Locati, M.; Camassi, R.; Lolli, B.; Gasperini, P. (Eds.) CPTI15, The 2015 Version of the Parametric Catalogue of Italian; Earthquakes; Istituto Nazionale di Geofisica e Vulcanologia: Rome, Italy, 2016. [CrossRef]
- Jolivet, L.; Faccenna, C. Mediterranean extension and the Africa-Eurasia collision. Tectonics 2000, 19, 1095–1106. [Google Scholar] [CrossRef]
- Barchi, M.; Landuzzi, A.; Minelli, G.; Pialli, G. Outer northern Apennines. In Anatomy of an Orogen: The Apennines and Adjacent Mediterranean BasinsI; Springer: Dordrecht, The Netherlands, 2001; pp. 215–253. [Google Scholar]
- Catalano, S.; Monaco, C.; Tortorici, L.; Paltrinieri, W.; Steel, N. Neogene-Quaternary tectonic evolution of the southern Apennines. Tectonics 2004, 23, 1–9. [Google Scholar] [CrossRef]
- Faccenna, C.; Piromallo, C.; Crespo-Blanc, A.; Jolivet, L.; Rossetti, F. Lateral slab deformation and the origin of the western Mediterranean arcs. Tectonics 2004, 23, TC1012. [Google Scholar] [CrossRef]
- Royden, L.; Faccenna, C. Subduction Orogeny and the Late Cenozoic Evolution of the Mediterranean Arcs. Annu. Rev. Earth Planet. Sci. 2018, 46, 261–289. [Google Scholar] [CrossRef]
- Corradino, M.; Morelli, D.; Ceramicola, S.; Scarfì, L.; Barberi, G.; Monaco, C.; Pepe, F. Active tectonics in the Calabrian Arc: Insights from the Late Miocene to Recent structural evolution of the Squillace Basin (offshore eastern Calabria). Tectonophysics 2023, 851, 229772. [Google Scholar] [CrossRef]
- Alvarez, W. A former continuation of the Alps. Geol. Soc. Am. Bull. 1976, 87, 891–896. [Google Scholar]
- Alvarez, W. Tectonic evolution of the Corsica-Apennines-Alps region studied by the method of successive approximations. Tectonics 1991, 10, 936–947. [Google Scholar] [CrossRef]
- Advokaat, E.L.; van Hinsbergen, D.J.; Maffione, M.; Langereis, C.G.; Vissers, R.L.; Cherchi, A.; Schroeder, R.; Madani, H.; Columbu, S. Eocene rotation of Sardinia, and the paleogeography of the western Mediterranean region. Earth Planet. Sci. Lett. 2014, 401, 183–195. [Google Scholar] [CrossRef]
- Arragoni, S.; Maggi, M.; Cianfarra, P.; Salvini, F. The Cenozoic fold-and-thrust belt of Eastern Sardinia: Evidences from the integration of field data with numerically balanced geological cross section. Tectonics 2016, 35, 1404–1422. [Google Scholar] [CrossRef]
- Salvini, F.; Arragoni, S.; Cianfarra, P.; Maggi, M. Reply to Comments on “the Cenozoic Fold-and-Thrust Belt of Eastern Sardinia: Evidences from the Integration of Field Data With Numerically Balanced Geological Cross Section” by Arragoni et al. (2016). Tectonics 2017, 36, 2273–2278. [Google Scholar] [CrossRef]
- Arragoni, S.; Fernández, L.P.; Cuesta, A.; Maggi, M.; Cianfarra, P.; Salvini, F. Origin of exotic clasts in the Central-Southern Apennines: Clues to the Cenozoic fold-and-thrust collisional belt in the Central Mediterranean area. Geol. Mag. 2017, 155, 479–505. [Google Scholar] [CrossRef]
- Marani, M.P.; Gamberi, F. Structural framework of the Tyrrhenian Sea unveiled by seafloor morphology. Mem. Descr. Carta Geol. d’It. 2004, 44, 97–108. [Google Scholar]
- Favali, P.; Funiciello, R.; Mattietti, G.; Mele, G.; Salvini, F. An active margin across the Adriatic Sea (central Mediterranean Sea). Tectonophysics 1993, 219, 109–117. [Google Scholar] [CrossRef]
- Parotto, M.; Praturlon, A. The Southern Apennine Arc. In Geology of Italy; Special Volume of the Italian Geological Society for the IGC 32 Florence; Crescenti, U., D’Offizi, S., Merlino, S., Sacchi, L., Eds.; Società Geologica Italiana: Rome, Italy, 2004; pp. 33–58. [Google Scholar]
- Ghisetti, F.; Barchi, M.; Bally, A.W.; Moretti, I.; Vezzani, L. Conflicting balanced structural sections across the Central Apennines (Italy): Problems and implications. In Generation, Accumulation and Production of Europe’s Hydrocarbons; European Association of Petroleum Geoscientists, Special Publication; Spencer, A.M., Ed.; Springer: Berlin/Heidelberg, Germany, 1993; Volume 3, pp. 219–231. [Google Scholar]
- Barchi, M.R. The Neogene-Quaternary evolution of the Northern Apennines: Crustal structure, style of deformation and seismicity. J. Virtual Explor. 2010, 36, 11. [Google Scholar] [CrossRef]
- Sartori, R.; Torelli, L.; Zitellini, N.; Carrara, G.; Magaldi, M.; Mussoni, P. Crustal features along a W–E Tyrrhenian transect from Sardinia to Campania margins (Central Mediterranean). Tectonophysics 2004, 383, 171–192. [Google Scholar] [CrossRef]
- Parotto, M.; Salvini, F.; Tozzi, M. Geologia di superficie e geometrie profonde nell’Italia Centrale: Per un profilo di previsione CROP 11 da Civitavecchia a Vasto. Mem. Soc. Geol. It. 1996, 51, 63–70. [Google Scholar]
- Patacca, E.; Scandone, P.; DI Luzio, E.; Cavinato, G.; Parotto, M. Structural architecture of the central Apennines: Interpretation of the CROP 11 seismic profile from the Adriatic coast to the orographic divide. Tectonics 2008, 27, TC3006. [Google Scholar] [CrossRef]
- Montone, P.; Mariucci, M.T. The new release of the Italian contemporary stress map. Geophys. J. Int. 2016, 205, 1525–1531. [Google Scholar] [CrossRef]
- Dziewonski, A.M.; Chou, T.; Woodhouse, J.H. Determination of earthquake source parameters from waveform data for studies of global and regional seismicity. J. Geophys. Res. 1981, 86, 2825–2852. [Google Scholar] [CrossRef]
- Ekström, G.; Nettles, M.; Dziewoński, A. The global CMT project 2004–2010: Centroid-moment tensors for 13,017 earthquakes. Phys. Earth Planet. Inter. 2012, 200–201, 1–9. [Google Scholar] [CrossRef]
- USGS/ANSS Comprehensive Catalog. Available online: https://earthquake.usgs.gov/earthquakes/search/ (accessed on 29 April 2021).
- Salvini, F.; Cianfarra, P.; Maggi, M. Preliminary geodynamic section of central Italy between the 41° and 42°N parallels. Rend. Line Della Soc. Geol. Ital. 2012, 21 Pt 1, 183–184. [Google Scholar]
- Catalano, S.; Cianfarra, P.; Maggi, M.; Romagnoli, G.; Salvini, F.; Tortorici, G.; Tortorici, L. The architecture of the peri-Tyrrhenian collision belt from Central Apennines to Sicily and the dynamics of the central Mediterranean. Rend. Line Della Soc. Geol. Ital. 2013, 29, 27–30. [Google Scholar]
- Meletti, C.; Patacca, E.; Scandone, P. Construction of a Seismotectonic Model: The Case of Italy. Pure Appl. Geophys. 2000, 157, 11–35. [Google Scholar] [CrossRef]
- Morelli, D.; Locatelli, M.; Crispini, L.; Corradi, N.; Cianfarra, P.; Federico, L.; Brandolini, P. 3D Modelling of Late Quaternary coastal evolution between Albenga and Loano (Western Liguria, Italy). J. Maps 2023, 19, 2227211. [Google Scholar] [CrossRef]
- Bally, A.W.; Burbi, L.; Cooper, C.; Ghelardoni, R. Balanced sections and seismic reflection profiles across the central Apennines. Mem. Soc. Geol. Ital. 1986, 35, 257–310. [Google Scholar]
- Mostardini, F.; Merlini, S. Appennino centro-meridionale: Sezioni geologiche e proposta di modello strutturale. Mem. Soc. Geol. Ital. 1986, 35, 177–202. [Google Scholar]
- Faccenna, C.; Becker, T.W.; Miller, M.S.; Serpelloni, E.; Willett, S.D. Isostasy, dynamic topography, and the elevation of the Apennines of Italy. Earth Planet. Sci. Lett. 2014, 407, 163–174. [Google Scholar] [CrossRef]
- Galadini, F.; Meletti, C.; Vittori, E. Major active faults in Italy: Available surficial data. Neth. J. Geosci. 2001, 80, 273–296. [Google Scholar] [CrossRef]
- Cosentino, D.; Asti, R.; Nocentini, M.; Gliozzi, E.; Kotsakis, T.; Mattei, M.; Esu, D.; Spadi, M.; Tallini, M.; Cifelli, F.; et al. New insights into the onset and evolution of the central Apennine extensional intermontane basins based on the tectonically active L’Aquila Basin (central Italy). Bull. Geol. Soc. Am. 2017, 129, 1314–1336. [Google Scholar] [CrossRef]
- Galadini, F.; Galli, P. Active tectonics in the Central Apennines (Italy)—Input Data for Seismic Hazard Assesment. Nat. Hazards 2000, 22, 225–270. [Google Scholar] [CrossRef]
- Frepoli, A.; Amato, A. Contemporaneous extension and compression in the northern Apennines from earthquake fault-plane solutions. Geophys. J. Int. 1997, 129, 368–388. [Google Scholar] [CrossRef]
- D’Agostino, N.; Mantenuto, S.; D’Anastasio, E.; Giuliani, R.; Mattone, M.; Calcaterra, S.; Gambino, P.; Bonci, L. Evidence for localized active extension in the central Apennines (Italy) from global positioning system observations. Geology 2011, 39, 291–294. [Google Scholar] [CrossRef]
- Bricalli, L.L.; Mello, C.L. Padrões de lineamentos relacionados a litoestrutura e fraturamento neotectônico(estado do espírito santo, -se do brasil). Rev. Bras. Geomorfol. 2014, 14. [Google Scholar] [CrossRef]
- Rossi, C.; Cianfarra, P.; Salvini, F. Structural geology of Ganymede regional groove systems (60° N–60° S). J. Maps 2020, 16, 6–16. [Google Scholar] [CrossRef]
- USGS The Global Data Explorer. Available online: http://gdex.cr.usgs.gov/gdex/ (accessed on 1 September 2016).[Green Version]
- Tachikawa, T.; Hato, M.; Kaku, M.; Iwasaki, A. Characteristics of ASTER GDEM version 2. In Proceedings of the 2011 IEEE International Geoscience and Remote Sensing Symposium—Proceedings: Vancouver, British Columbia, Institute of Electrical and Electronic Engineers, Vancouver, BC, Canada, 24–29 July 2011; pp. 3657–3660. [Google Scholar] [CrossRef]
- Drury, S. Image Interpretation in Geology (Third Edition); Blackwell Science Inc.: Malden, MA, USA, 2001; 304p. [Google Scholar]
- Salvini, F.; Billi, A.; Wise, D.U. Strike-slip fault propagation cleavage in carbonate rocks: The Mattinata fault zone, southern Ap-ennines, Italy. J. Struct. Geol. 1999, 21, 1731–1749. [Google Scholar] [CrossRef]
- Cianfarra, P.; Salvini, F. Quantification of fracturing within fault damage zones affecting Late Proterozoic carbonates in Svalbard. Rendiconti Lincei-Sci. Fis. Nat. 2016, 27, 229–241. [Google Scholar] [CrossRef]
- Cianfarra, P.; Locatelli, M.; Capponi, G.; Crispini, L.; Rossi, C.; Salvini, F.; Federico, L. Multiple Reactivations of the Rennick Graben Fault System (Northern Victoria Land, Antarctica): New Evidence From Paleostress Analysis. Tectonics 2022, 41, e2021TC007124. [Google Scholar] [CrossRef]
- Turcotte, D.L.; Brown, S.R. Fractals and Chaos in Geology and Geophysics. Phys. Today 1993, 46, 68. [Google Scholar] [CrossRef]
- Ciaccio, M.G.; Di Stefano, R.; Improta, L.; Mariucci, M.T. BSI Working Group First-motion focal mechanism solutions for 2015–2019 M ≥ 4.0 Italian earthquakes. Front. Earth Sci. 2021, 9, 630116. [Google Scholar] [CrossRef]
- Di Bucci, D.; Burrato, P.; Vannoli, P.; Valensise, G. Tectonic evidence for the ongoing Africa-Eurasia convergence in central Mediterranean foreland areas: A journey among long-lived shear zones, large earthquakes, and elusive fault motions. J. Geophys. Res. 2010, 115, 1–17. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).