What Is the Effect of Seismic Swarms on Short-Term Seismic Hazard and Gutenberg-Richter b-Value Temporal Variation? Examples from Central Italy, October–November 2023
Abstract
1. Introduction
2. Materials and Methods
2.1. The Seismic Catalog
2.2. The Italian Operational Earthquake Forecasting System
2.3. The Gutenberg–Richter b-Value Estimation
3. Results and Discussion
3.1. OEF Probabilities
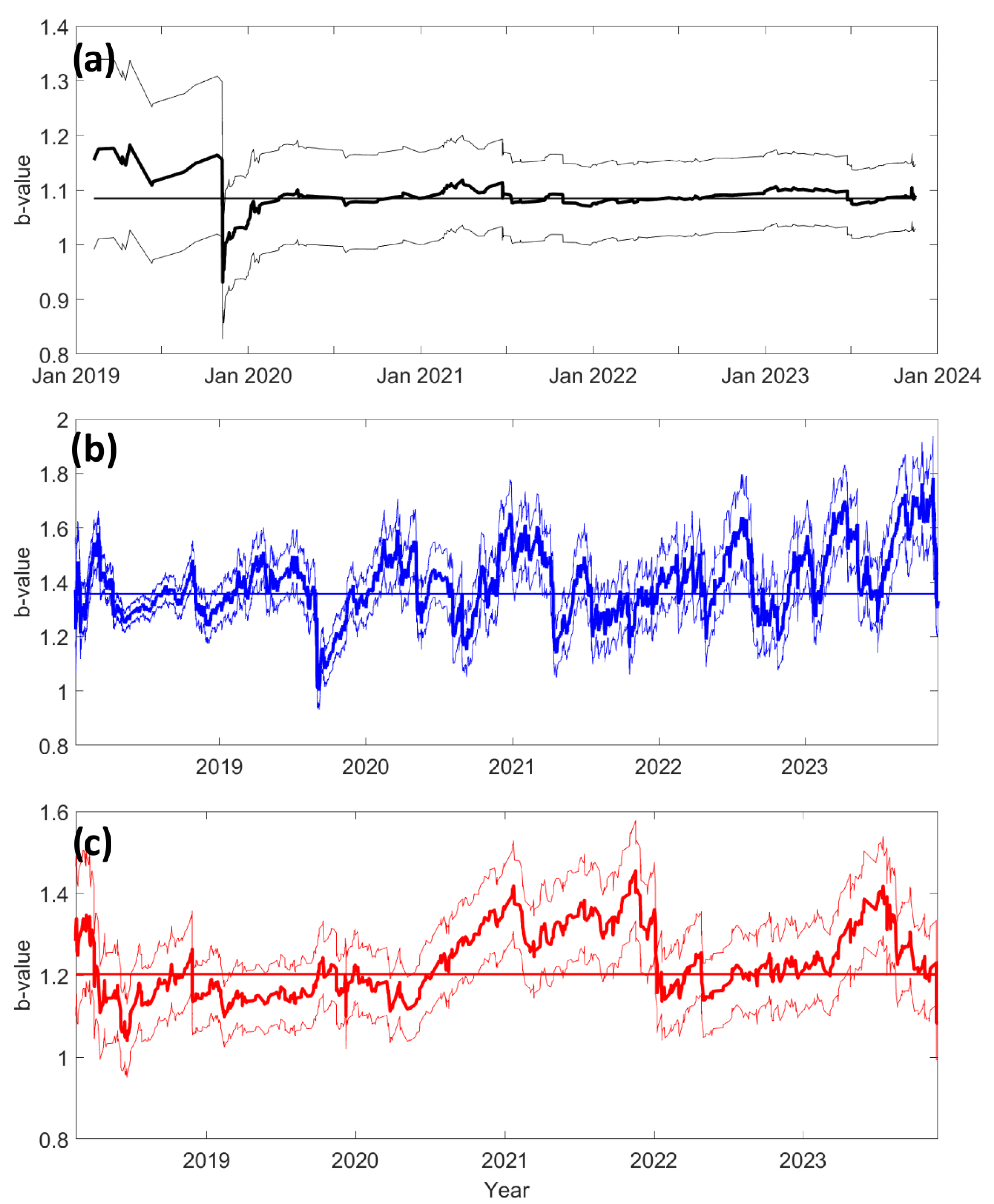
3.2. Temporal b-Value Variations
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Helmstetter, A.; Sornette, D. Foreshocks explained by cascades of triggered seismicity. J. Geophys. Res. Solid Earth 2003, 108. [Google Scholar] [CrossRef]
- Ogata, Y. Statisticals Models for Earthquake Occurrences and Residual Analysis for Point Processes. J. Amer. Statist. Assoc. 1988, 83, 9–27. [Google Scholar] [CrossRef]
- Ogata, Y. Space-time point-process models for earthquake occurrences. Ann. Inst. Stat. Math. 1998, 50, 379–402. [Google Scholar] [CrossRef]
- Jordan, T.H.; Marzocchi, W.; Michael, A.J.; Gerstenberger, M.C. Operational earthquake forecasting can enhance earthquake preparedness. Seismol. Res. Lett. 2014, 85, 955–959. [Google Scholar] [CrossRef]
- Marzocchi, W.; Lombardi, A.M.; Casarotti, E. The establishment of an operational earthquake forecasting system in Italy. Seismol. Res. Lett. 2014, 85, 961–969. [Google Scholar] [CrossRef]
- Christophersen, A.; Rhoades, D.A.; Gerstenberger, M.C.; Bannister, S.; Becker, J.; Potter, S.H.; McBride, S. Progress and challenges in operational earthquake forecasting in New Zealand. In Proceedings of the New Zealand Society for Earthquake Engineering Annual Technical Conference, Wellington, New Zealand, 26 April 2017. [Google Scholar]
- Field, E.H.; Milner, K.R.; Hardebeck, J.L.; Page, M.T.; van der Elst, N.; Jordan, T.H.; Michael, A.J.; Shaw, B.E.; Werner, M.J. A spatiotemporal clustering model for the third Uniform California Earthquake Rupture Forecast (UCERF3-ETAS): Toward an operational earthquake forecast. Bull. Seismol. Soc. Am. 2017, 107, 1049–1081. [Google Scholar] [CrossRef]
- Falcone, G.; Spassiani, I.; Ashkenazy, Y.; Shapira, A.; Hofstetter, R.; Havlin, S.; Marzocchi, W. An operational earthquake forecasting experiment for israel: Preliminary results. Front. Earth Sci. 2021, 9, 729282. [Google Scholar] [CrossRef]
- Chen, X.; Li, Y.; Chen, L. The characteristics of the b-value anomalies preceding the 2004 M w9. 0 Sumatra earthquake. Geomat. Nat. Hazards Risk 2022, 13, 390–399. [Google Scholar] [CrossRef]
- Gunti, S.; Roy, P.; Narendran, J.; Pudi, R.; Muralikrishnan, S.; Kumar, K.V.; Subrahmanyam, M.; Israel, Y.; Kumar, B.S. Assessment of geodetic strain and stress variations in Nepal due to 25 April 2015 Gorkha earthquake: Insights from the GNSS data analysis and b-value. Geod. Geodyn. 2022, 13, 288–300. [Google Scholar] [CrossRef]
- De Gori, P.; Lucente, F.P.; Lombardi, A.M.; Chiarabba, C.; Montuori, C. Heterogeneities along the 2009 L’Aquila normal fault inferred by the b-value distribution. Geophys. Res. Lett. 2012, 39, L15304. [Google Scholar] [CrossRef]
- Montuori, C.; Murru, M.; Falcone, G. Spatial variation of the value observed for the periods preceding and following the 24 August 2016. Amatrice earthquake ML 6.0) (Central Italy). Ann. Geophys. 2016, 59. [Google Scholar] [CrossRef]
- Henderson, J.; Main, I.; Pearce, R.; Takeya, M. Seismicity in North-Eastern Brazil: Fractal clustering and the evolution of the b value. Geophys. J. Int. 1994, 116, 217–226. [Google Scholar] [CrossRef]
- Gerstenberger, M.; Wiemer, S.; Giardini, D. A systematic test of the hypothesis that the b value varies with depth in California. Geophys. Res. Lett. 2001, 28, 57–60. [Google Scholar] [CrossRef]
- Amitrano, D. Brittle-ductile transition and associated seismicity: Experimental and numerical studies and relationship with the b-value. J. Geophys. Res. 2003, 108, 2044. [Google Scholar] [CrossRef]
- Scholz, C. On the stress dependence of the earthquake b-value, Geophys. Res. Lett. 2015, 42, 1399–1402. [Google Scholar] [CrossRef]
- Gulia, L.; Wiemer, S. Real-time discrimination of earthquake foreshocks and aftershocks. Nature 2019, 574, 193–199. [Google Scholar] [CrossRef]
- Nayak, K.; Romero-Andrade, R.; Sharma, G.; Zavala, J.L.C.; Urias, C.L.; Trejo Soto, M.E.; Aggarwal, S.P. A combined approach using b-value and ionospheric GPS-TEC for large earthquake precursor detection: A case study for the Colima earthquake of 7.7 Mw. Mexico. Acta Geod. Geophys. 2023, 58, 515–538. [Google Scholar] [CrossRef]
- Marzocchi, W.; Spassiani, I.; Stallone, A.; Taroni, M. How to be fooled searching for significant variations of the b-value. Geophys. J. Int. 2020, 220, 1845–1856. [Google Scholar] [CrossRef]
- Geffers, G.M.; Main, I.G.; Naylor, M. Biases in estimating b-values from small earthquake catalogues: How high are high b-values? Geophys. J. Int. 2022, 229, 1840–1855. [Google Scholar] [CrossRef]
- Spassiani, I.; Taroni, M.; Murru, M.; Falcone, G. Real time Gutenberg–Richter b-value estimation for an ongoing seismic sequence: An application to the 2022 marche offshore earthquake sequence (ML 5.7 central Italy). Geophys. J. Int. 2023, 234, 1326–1331. [Google Scholar] [CrossRef]
- Lombardi, A.M. Anomalies and transient variations of b-value in Italy during the major earthquake sequences: What truth is there to this? Geophys. J. Int. 2023, 232, 1545–1555. [Google Scholar] [CrossRef]
- Hu, F.; Zidek, J.V. The weighted likelihood. Can. J. Stat. 2002, 30, 347–371. [Google Scholar] [CrossRef]
- Taroni, M.; Vocalelli, G.; De Polis, A. Gutenberg–Richter B-value time series forecasting: A weighted likelihood approach. Forecasting 2021, 3, 561–569. [Google Scholar] [CrossRef]
- Aki, K. Maximum likelihood estimate of b in the formula log N = a-bM and its confidence limits. Bull. Earthq. Res. Inst. Tokyo Univ. 1965, 43, 237–239. [Google Scholar]
- Rovida, A.; Locati, M.; Camassi, R.; Lolli, B.; Gasperini, P. The Italian earthquake catalogue CPTI15. Bull. Earthq. Eng. 2020, 18, 2953–2984. [Google Scholar] [CrossRef]
- Gutenberg, B.; Richter, C.F. Frequency of earthquakes in California. Bull. Seismol. Soc. Am. 1944, 34, 185–188. [Google Scholar] [CrossRef]
- Lilliefors, H.W. On the Kolmogorov-Smirnov test for the exponential distribution with mean unknown. J. Am. Stat. Assoc. 1969, 64, 387–389. [Google Scholar] [CrossRef]
- Herrmann, M.; Marzocchi, W. Inconsistencies and lurking pitfalls in the magnitude–frequency distribution of high-resolution earthquake catalogs. Seismol. Res. Lett. 2021, 92, 909–922. [Google Scholar] [CrossRef]
- Wyss, M.; Schorlemmer, D.; Wiemer, S. Mapping asperities by minima of local recurrence time: San Jacinto-Elsinore fault zones. J. Geophys. Res. Solid Earth 2000, 105, 7829–7844. [Google Scholar] [CrossRef]
- Wiemer, S.; Wyss, M. Minimum magnitude of completeness in earthquake catalogs: Examples from Alaska, the western United States, and Japan. Bull. Seismol. Soc. Am. 2000, 90, 859–869. [Google Scholar] [CrossRef]
- Wiemer, S. A software package to analyze seismicity: ZMAP. Seismol. Res. Lett. 2001, 72, 373–382. [Google Scholar] [CrossRef]
- Massey, F.J., Jr. The Kolmogorov-Smirnov test for goodness of fit. J. Am. Stat. Assoc. 1951, 46, 68–78. [Google Scholar] [CrossRef]
- Schorlemmer, D.; Werner, M.J.; Marzocchi, W.; Jordan, T.H.; Ogata, Y.; Jackson, D.D.; Mak, S.; Rhoades, D.A.; Gerstenberger, M.C.; Hirata, N.; et al. The collaboratory for the study of earthquake predictability: Achievements and priorities. Seismol. Res. Lett. 2018, 89, 1305–1313. [Google Scholar] [CrossRef]
- Lombardi, A.M.; Marzocchi, W. The ETAS model for daily forecasting of Italian seismicity in the CSEP experiment. Ann. Geophys. 2010, 53, 155–164. [Google Scholar]
- Falcone, G.; Console, R.; Murru, M. Short-term and long-term earthquake occurrence models for Italy: ETES, ERS and LTST. Ann. Geophys. 2010, 53, 41–50. [Google Scholar]
- Woessner, J.; Christophersen, A.; Zechar, J.D.; Monelli, D. Building self-consistent, short-term earthquake probability (STEP) models: Improved strategies and calibration procedures. Ann. Geophys. 2010, 53, 141–154. [Google Scholar]
- Omori, F. On aftershocks of earthquakes. J. Coll. Sci. Imp. Univ. Tokyo 1894, 7, 111–200. [Google Scholar]
- Utsu, T. Magnitude of earthquakes and occurrence of their aftershocks. Zisin 1957, 10, 6–23. [Google Scholar] [CrossRef]
- Reasenberg, P.A.; Jones, L.M. Earthquake hazard after a mainshock in California. Science 1989, 243, 1173–1176. [Google Scholar] [CrossRef]
- Taroni, M.; Marzocchi, W.; Schorlemmer, D.; Werner, M.J.; Wiemer, S.; Zechar, J.D.; Heiniger, L.; Euchner, F. Prospective CSEP evaluation of 1-day, 3-month, and 5-yr earthquake forecasts for Italy. Seismol. Res. Lett. 2018, 89, 1251–1261. [Google Scholar] [CrossRef]
- Spassiani, I.; Falcone, G.; Murru, M.; Marzocchi, W. Operational Earthquake Forecasting in Italy: Validation after 10 years of operativity. Geophys. J. Int. 2023, 234, 2501–2518. [Google Scholar] [CrossRef]
- Marzocchi, W.; Sandri, L. A review and new insights on the estimation of the b-value and its uncertainty. Ann. Geophys. 2003, 46. [Google Scholar]
- Utsu, T. A statistical significance test of the difference in b-value between two earthquake groups. J. Phys. Earth 1966, 14, 37–40. [Google Scholar] [CrossRef]
- Utsu, T. A method for determining the value of b in a formula log n = a = bM showing the magnitude frequency relation for earthquakes. Geophys. Bull. Hokkaido Univ. 1965, 13, 99–103. [Google Scholar]
- Zhuang, J.; Ogata, Y.; Wang, T. Data completeness of the Kumamoto earthquake sequence in the JMA catalog and its influence on the estimation of the ETAS parameters. Earth Planets Space 2017, 69, 36. [Google Scholar] [CrossRef]
- Chiaraluce, L.; Chiarabba, C.; De Gori, P.; Di Stefano, R.; Improta, L.; Piccinini, D.; Schlagenhauf, A.; Traversa, P.; Valoroso, L.; Voisin, C. The 2009 L’Aquila (Central Italy) Seismic Sequence. Boll. Geofis. Teor. Appl. 2011, 52. [Google Scholar]
- Gentili, S.; Di Giovambattista, R. Forecasting strong aftershocks in earthquake clusters from northeastern Italy and western Slovenia. Phys. Earth Planet. Inter. 2020, 303, 106483. [Google Scholar] [CrossRef]
- Rundle, J.B.; Donnellan, A. Nowcasting earthquakes in Southern California with machine learning: Bursts, swarms, and aftershocks may be related to levels of regional tectonic stress. Earth Space Sci. 2020, 7, e2020EA001097. [Google Scholar] [CrossRef]

| Background (Last 5 yrs) | Maximum Probability Since October 2023 | Area Probability on 27 November 2023 | ||
|---|---|---|---|---|
| Sora | MMI VI+ | 0.003 | 0.004 (on 16 October) | 3.04 × 10−3 |
| MMI VII+ | 4 × 10−4 | 6 × 10−4 (on 16 October) | 4.55 × 10−4 | |
| MMI VIII+ | 8 × 10−5 | 1 × 10−4 (on 16 October and 11 November) | 9.8 × 10−5 | |
| ML 4+ | 0.002 | 0.003 (on 16 October, 11 and 25 November) | 2.26 × 10−3 | |
| ML 5.5+ | 6 × 10−5 | 9 × 10−5 (on 11 and 25 November) | 6.92 × 10−5 | |
| Monte Cavallo | MMI VI+ | 0.01 | 0.01 (stable in the period) | 1.1 × 10−2 |
| MMI VII+ | 0.001 | 0.002 (stable in the period) | 1.61 × 10−3 | |
| MMI VIII+ | 3 × 10−4 | 4 × 10−4 (stable in the period) | 3.68 × 10−4 | |
| ML 4+ | 0.009 | 0.01 (stable in the period) | 1 × 10−2 | |
| ML 5.5+ | 3 × 10−4 | 3 × 10−4 (stable in the period) | 3 × 10−4 | |
| Lucoli, AQ | MMI VI+ | 0.006 | 0.02 (on 22 November) | 9.45 × 10−3 |
| MMI VII+ | 9 × 10−4 | 0.004 (on 22 November) | 1.37 × 10−3 | |
| MMI VIII+ | 2 × 10−4 | 8 × 10−4 (on 22 November) | 3.13 × 10−4 | |
| ML 4+ | 0.006 | 0.02 (on 22 November) | 8.79 × 10−3 | |
| ML 5.5+ | 2 × 10−4 | 7 × 10−4 (on 22 November) | 2.76 × 10−4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Spassiani, I.; Taroni, M. What Is the Effect of Seismic Swarms on Short-Term Seismic Hazard and Gutenberg-Richter b-Value Temporal Variation? Examples from Central Italy, October–November 2023. Geosciences 2024, 14, 49. https://doi.org/10.3390/geosciences14020049
Spassiani I, Taroni M. What Is the Effect of Seismic Swarms on Short-Term Seismic Hazard and Gutenberg-Richter b-Value Temporal Variation? Examples from Central Italy, October–November 2023. Geosciences. 2024; 14(2):49. https://doi.org/10.3390/geosciences14020049
Chicago/Turabian StyleSpassiani, Ilaria, and Matteo Taroni. 2024. "What Is the Effect of Seismic Swarms on Short-Term Seismic Hazard and Gutenberg-Richter b-Value Temporal Variation? Examples from Central Italy, October–November 2023" Geosciences 14, no. 2: 49. https://doi.org/10.3390/geosciences14020049
APA StyleSpassiani, I., & Taroni, M. (2024). What Is the Effect of Seismic Swarms on Short-Term Seismic Hazard and Gutenberg-Richter b-Value Temporal Variation? Examples from Central Italy, October–November 2023. Geosciences, 14(2), 49. https://doi.org/10.3390/geosciences14020049








