Influence of Sampling Methods on the Accuracy of Machine Learning Predictions Used for Strain-Dependent Slope Stability
Abstract
1. Introduction
2. Enhanced Strain-Dependent Slope Stability Using Machine Learning
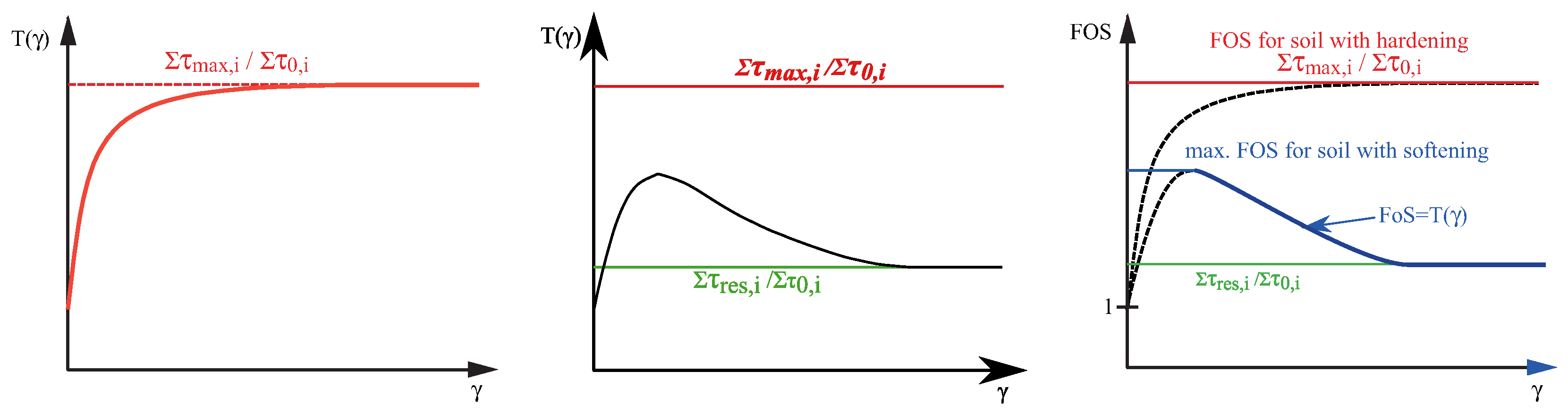
2.1. Strain-Dependent Slope Stability (SDSS)
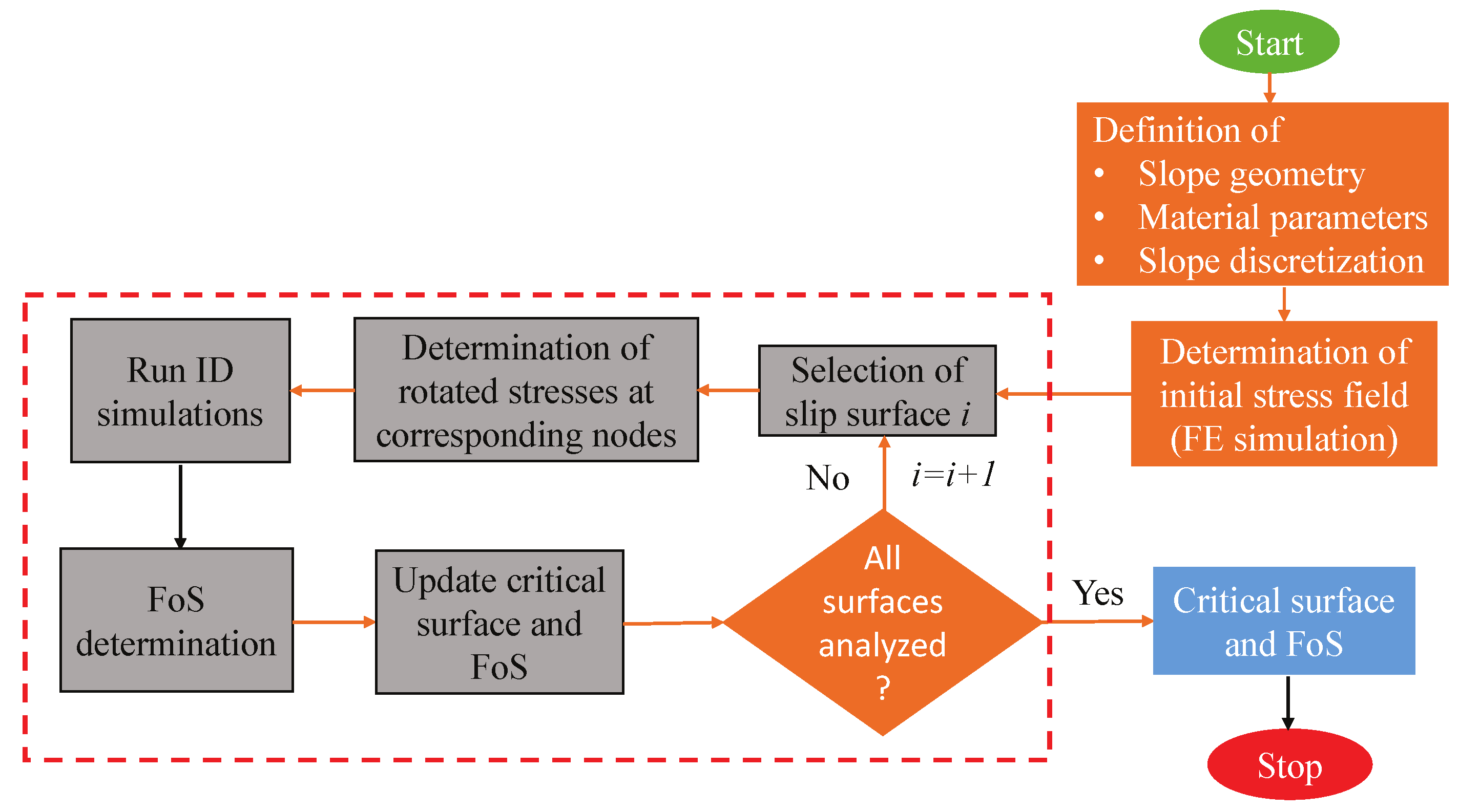
2.2. Implementation of SDSS
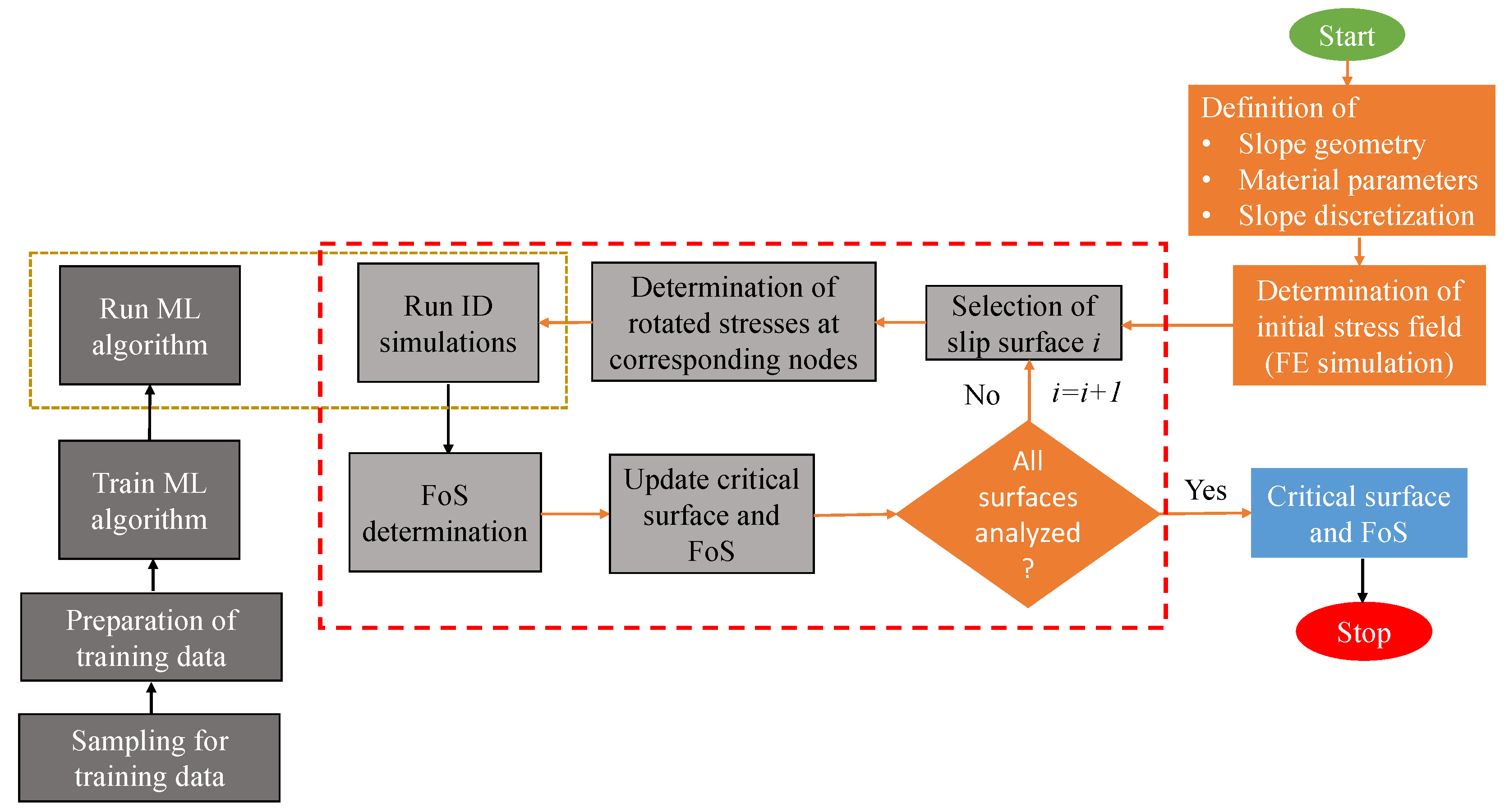
2.3. Application of Machine Learning in SDSS
3. Sampling
3.1. Motivation
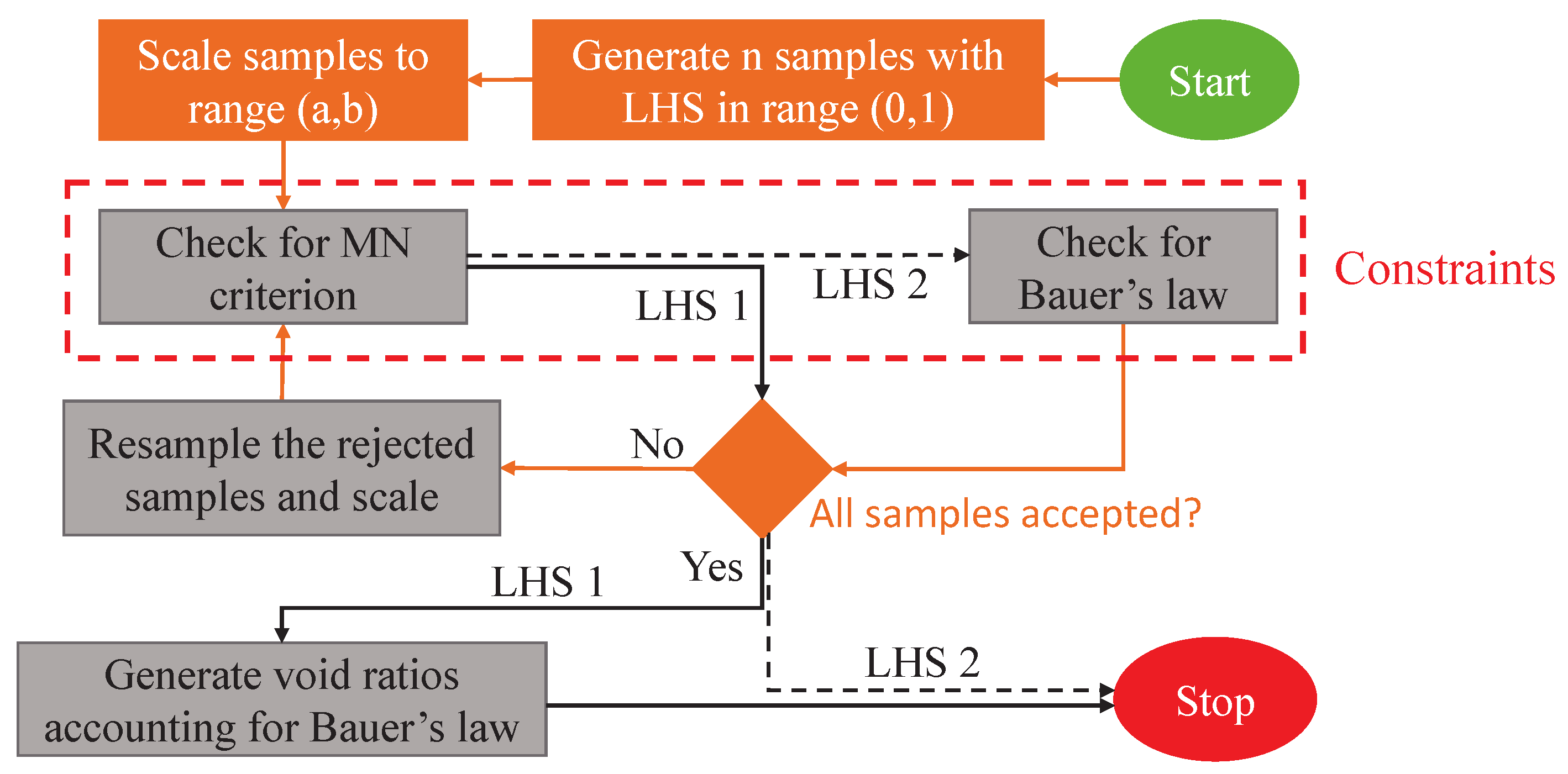
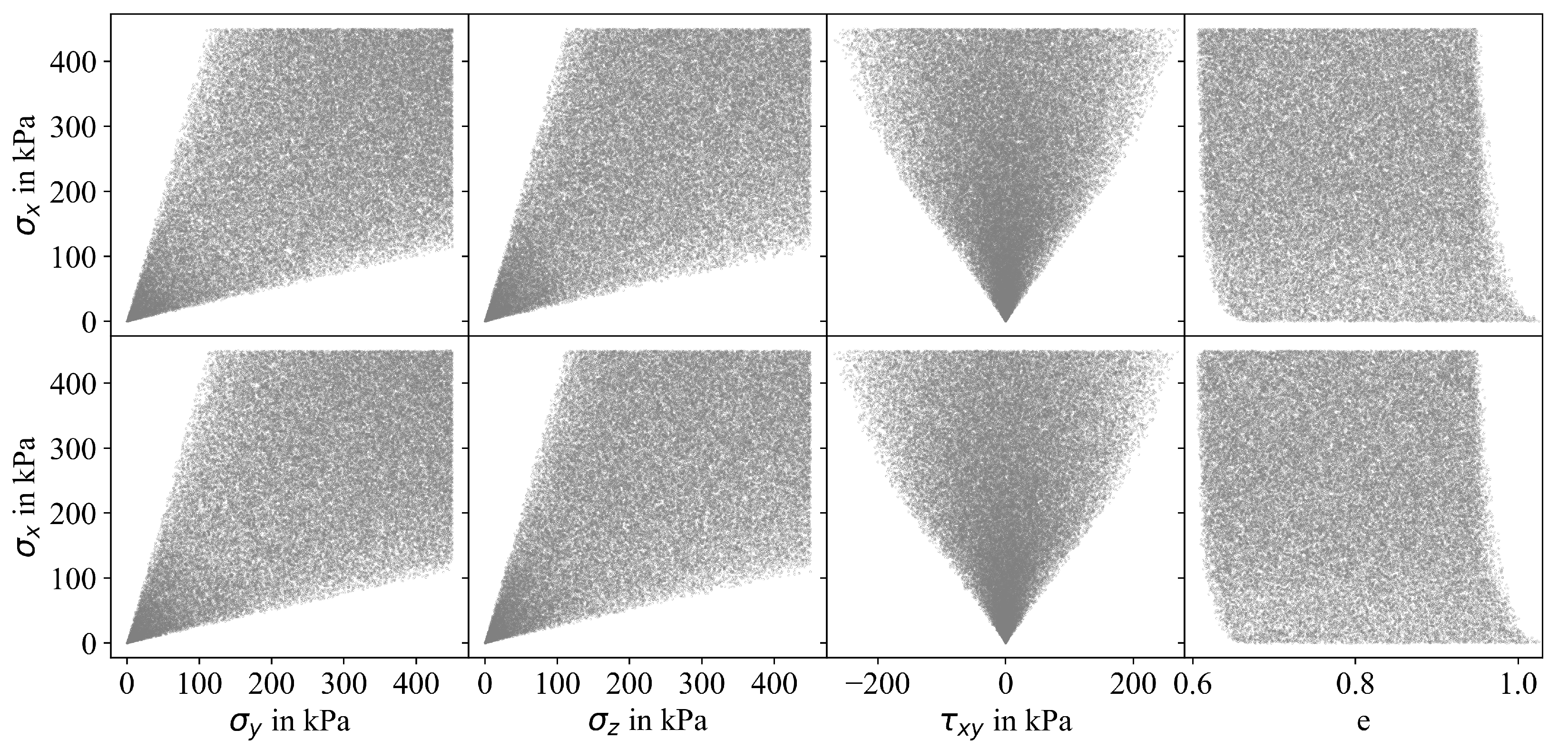
3.2. Modified Sampling Approaches
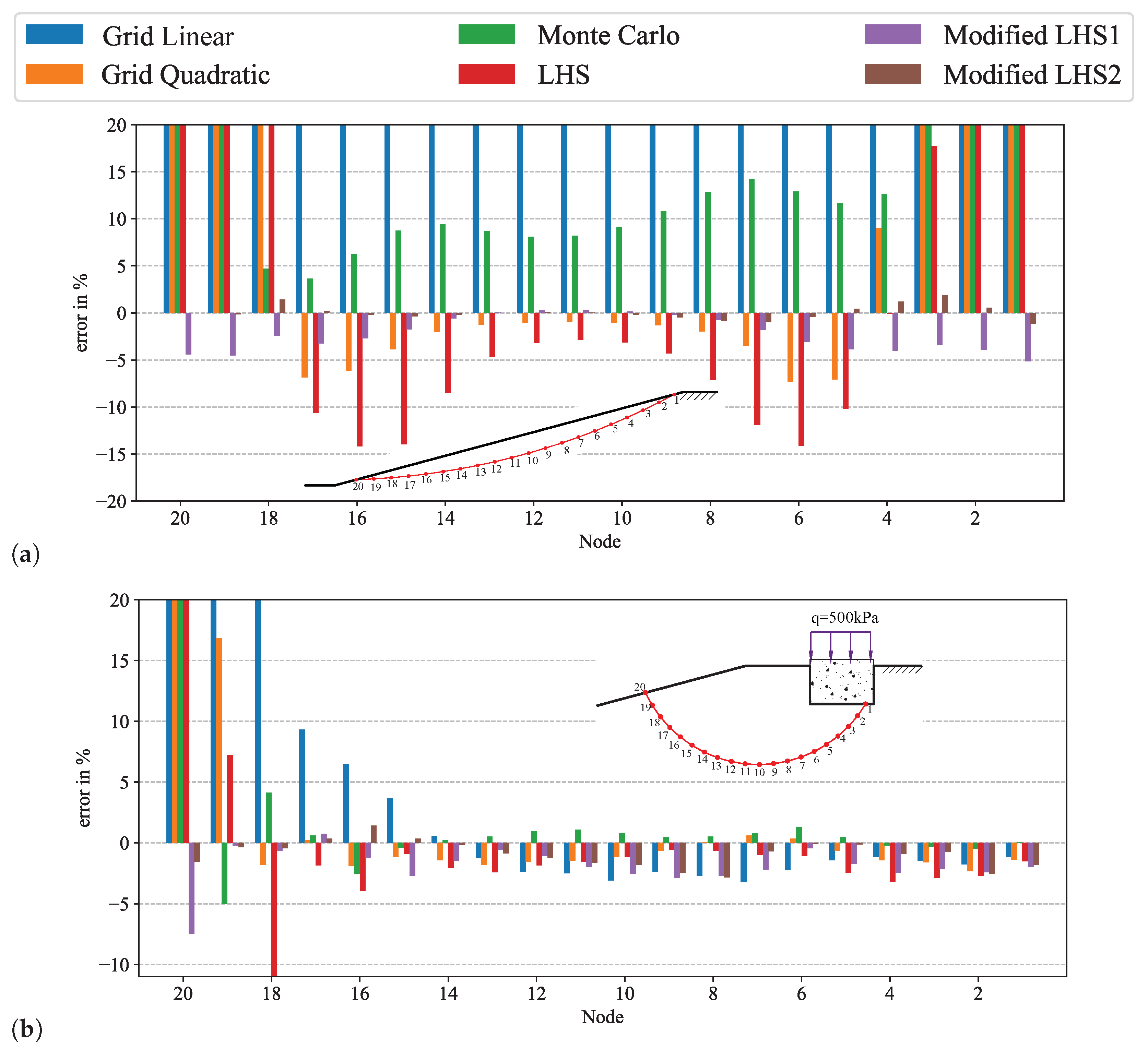
3.3. Influence of Sampling Approach on Accuracy of MLP Prediction
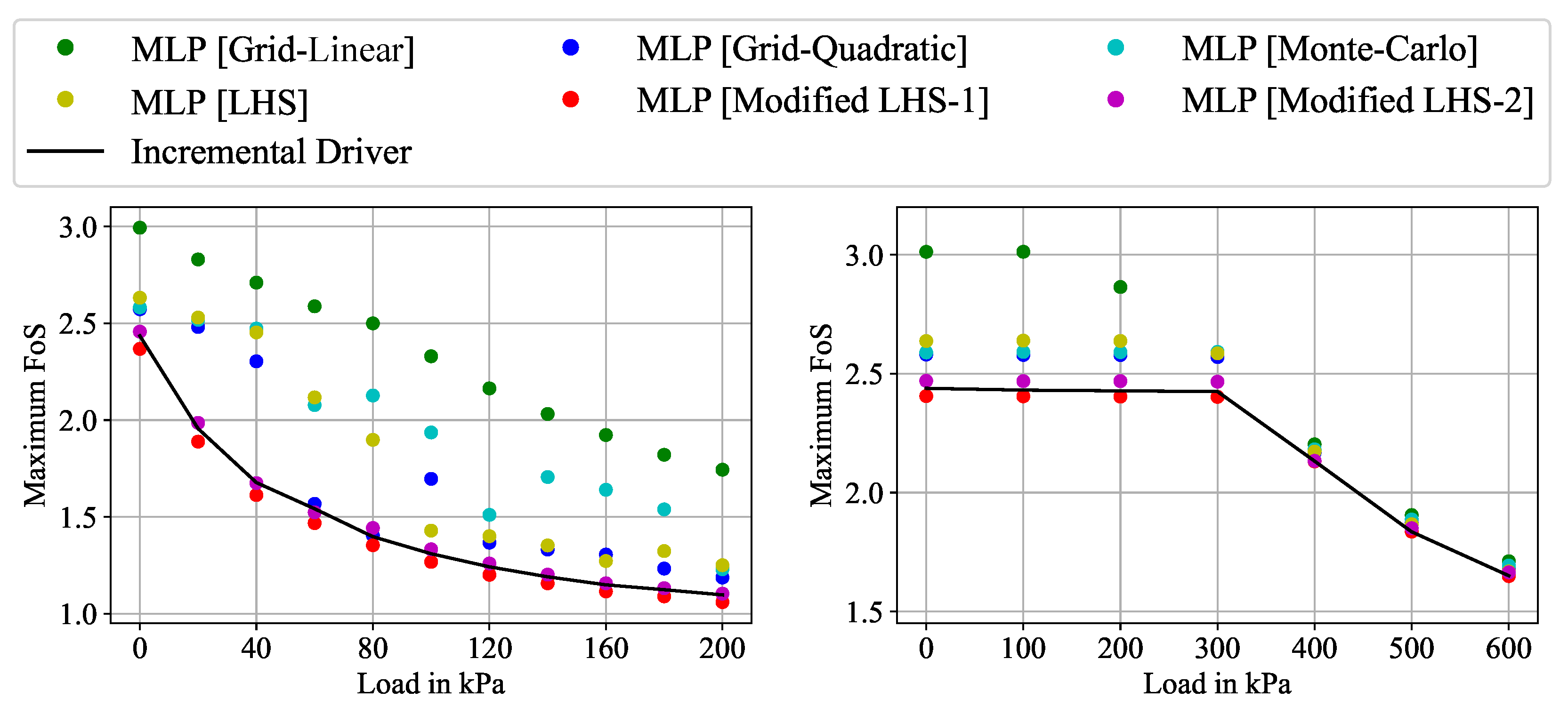
4. Influence of Sampling on the FoS for Slopes Subjected to Different Loading
4.1. Methodology
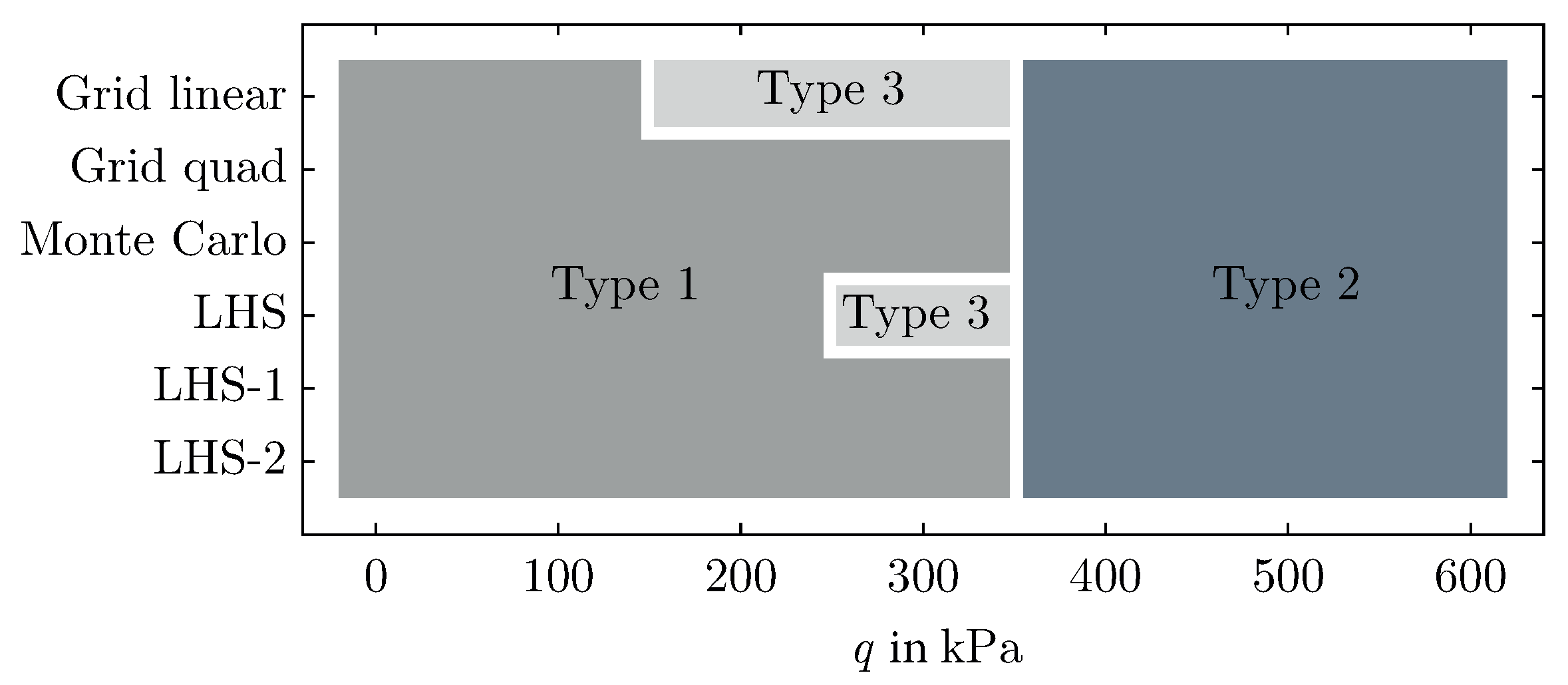
4.2. Results and Discussion
5. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ANN | Artificial neural network |
| DSS | Direct simple shear |
| FoS | Factor of safety |
| ID | Incremental Driver |
| IGS | Intergranular strain |
| KNN | K-nearest neighbors |
| LHS | Latin hypercube sampling |
| ML | Machine learning |
| MLP | Multilayer perceptron |
| RBF | Radial basis functions |
| RF | Random forest |
| SDSS | Strain-dependent slope stability |
| SVM | Suppor vector machines |
References
- Shi, J.; Ortigao, J.A.R.; Bai, J. Modular Neural Networks for Predicting Settlements during Tunneling. J. Geotech. Geoenviron. Eng. 1998, 124, 389–395. [Google Scholar] [CrossRef]
- Kim, C.; Bae, G.; Hong, S.; Park, C.; Moon, H.; Shin, H. Neural network based prediction of ground surface settlements due to tunnelling. Comput. Geotech. 2001, 28, 517–547. [Google Scholar] [CrossRef]
- Zhao, C.; Schmüdderich, C.; Barciaga, T.; Röchter, L. Response of building to shallow tunnel excavation in different types of soil. Comput. Geotech. 2019, 115, 103165. [Google Scholar] [CrossRef]
- Goh, A.C. Nonlinear modelling in geotechnical engineering using neural networks. Trans. Inst. Eng. Aust. Civ. Eng. 1994, 36, 293–297. [Google Scholar]
- Goh, A.T. Back-propagation neural networks for modeling complex systems. Artif. Intell. Eng. 1995, 9, 143–151. [Google Scholar] [CrossRef]
- Goh, A.T. Pile driving records reanalyzed using neural networks. J. Geotech. Eng. 1996, 122, 492–495. [Google Scholar] [CrossRef]
- Rahman, M.; Wang, J.; Deng, W.; Carter, J. A neural network model for the uplift capacity of suction caissons. Comput. Geotech. 2001, 28, 269–287. [Google Scholar] [CrossRef]
- Schmüdderich, C.; Shahrabi, M.M.; Taiebat, M.; Lavasan, A.A. Strategies for numerical simulation of cast-in-place piles under axial loading. Comput. Geotech. 2020, 125, 103656. [Google Scholar] [CrossRef]
- Sivakugan, N.; Eckersley, J.; Li, H. Settlement predictions using neural networks. Aust. Civ. Eng. Trans. 1998, 40, 49–52. [Google Scholar]
- Ni, S.H.; Lu, P.; Juang, C. A fuzzy neural network approach to evaluation of slope failure potential. Comput.-Aided Civ. Infrastruct. Eng. 1996, 11, 59–66. [Google Scholar] [CrossRef]
- Sakellariou, M.; Ferentinou, M. A study of slope stability prediction using neural networks. Geotech. Geol. Eng. 2005, 23, 419–445. [Google Scholar] [CrossRef]
- Ferentinou, M.; Sakellariou, M. Computational intelligence tools for the prediction of slope performance. Comput. Geotech. 2007, 34, 362–384. [Google Scholar] [CrossRef]
- Najjar, Y.M.; Ali, H.E. CPT-based liquefaction potential assessment: A neuronet approach. In Proceedings of the Geotechnical Earthquake Engineering and Soil Dynamics III. ASCE, Seattle, WA, USA, 3–6 August 1998; pp. 542–553. [Google Scholar]
- Tsai, C.C.; Hashash, Y.M. A novel framework integrating downhole array data and site response analysis to extract dynamic soil behavior. Soil Dyn. Earthq. Eng. 2008, 28, 181–197. [Google Scholar] [CrossRef]
- Tsai, C.C.; Hashash, Y.M. Learning of Dynamic Soil Behavior from Downhole Arrays. J. Geotech. Geoenviron. Eng. 2009, 135, 745–757. [Google Scholar] [CrossRef]
- Hashash, Y.; Marulanda, C.; Ghaboussi, J.; Jung, S. Systematic update of a deep excavation model using field performance data. Comput. Geotech. 2003, 30, 477–488. [Google Scholar] [CrossRef]
- Groholski, D.R.; Hashash, Y.M. Development of an inverse analysis framework for extracting dynamic soil behavior and pore pressure response from downhole array measurements. Int. J. Numer. Anal. Methods Geomech. 2013, 37, 1867–1890. [Google Scholar] [CrossRef]
- Groholski, D.R.; Hashash, Y.M.; Matasovic, N. Learning of pore pressure response and dynamic soil behavior from downhole array measurements. Soil Dyn. Earthq. Eng. 2014, 61, 40–56. [Google Scholar] [CrossRef]
- Ma, J.; Xia, D.; Wang, Y.; Niu, X.; Jiang, S.; Liu, Z.; Guo, H. A comprehensive comparison among metaheuristics (MHs) for geohazard modeling using machine learning: Insights from a case study of landslide displacement prediction. Eng. Appl. Artif. Intell. 2022, 114, 105150. [Google Scholar] [CrossRef]
- Zhang, W.; Gu, X.; Hong, L.; Han, L.; Wang, L. Comprehensive review of machine learning in geotechnical reliability analysis: Algorithms, applications and further challenges. Appl. Soft Comput. 2023, 136, 110066. [Google Scholar] [CrossRef]
- Goh, A. Empirical design in geotechnics using neural networks. Geotechnique 1995, 45, 709–714. [Google Scholar] [CrossRef]
- Lee, I.M.; Lee, J.H. Prediction of pile bearing capacity using artificial neural networks. Comput. Geotech. 1996, 18, 189–200. [Google Scholar] [CrossRef]
- Meyerhof, G.G. Shallow foundations. J. Soil Mech. Found. Div. 1965, 91, 21–31. [Google Scholar] [CrossRef]
- Terzaghi, K.; Peck, R.B.; Mesri, G. Soil Mechanics in Engineering Practice; John Wiley & Sons: Hoboken, NJ, USA, 1996. [Google Scholar]
- Schmertmann, J.H. Static cone to compute static settlement over sand. J. Soil Mech. Found. Div. 1970, 96, 1011–1043. [Google Scholar] [CrossRef]
- Shahin, M.A.; Jaksa, M.B.; Maier, H.R. Predicting the Settlement of Shallow Foundations on Cohesionless Soils Using Back-Propagation Neural Networks; Department of Civil and Environmental Engineering, University of Adelaide: Adelaide, Australia, 2000. [Google Scholar]
- Schmertmann, J.H.; Hartman, J.P.; Brown, P.R. Improved strain influence factor diagrams. J. Geotech. Eng. Div. 1978, 104, 1131–1135. [Google Scholar] [CrossRef]
- Schultze, E.; Sherif, G. Prediction of settlements from evaluated settlement observations for sand. In Proceedings of the Eighth International Conference on Soil Mechanics and Foundation Engineering, Moscow, Russia, 6–11 August 1973; Volume 1, pp. 225–230. [Google Scholar]
- Puri, N.; Prasad, H.D.; Jain, A. Prediction of geotechnical parameters using machine learning techniques. Procedia Comput. Sci. 2018, 125, 509–517. [Google Scholar] [CrossRef]
- Wei, W.; Li, X.; Liu, J.; Zhou, Y.; Li, L.; Zhou, J. Performance evaluation of hybrid WOA-SVR and HHO-SVR models with various kernels to predict factor of safety for circular failure slope. Appl. Sci. 2021, 11, 1922. [Google Scholar] [CrossRef]
- Nanehkaran, Y.A.; Pusatli, T.; Chengyong, J.; Chen, J.; Cemiloglu, A.; Azarafza, M.; Derakhshani, R. Application of Machine Learning Techniques for the Estimation of the Safety Factor in Slope Stability Analysis. Water 2022, 14, 3743. [Google Scholar] [CrossRef]
- Nanehkaran, Y.A.; Licai, Z.; Chengyong, J.; Chen, J.; Anwar, S.; Azarafza, M.; Derakhshani, R. Comparative analysis for slope stability by using machine learning methods. Appl. Sci. 2023, 13, 1555. [Google Scholar] [CrossRef]
- Schmüdderich, C.; Machaček, J.; Prada-Sarmiento, L.F.; Staubach, P.; Wichtmann, T. Strain-dependent slope stability for earthquake loading. Comput. Geotech. 2022, 152, 105048. [Google Scholar] [CrossRef]
- Nitzsche, K.; Herle, I. Strain-dependent slope stability. Acta Geotech. 2020, 15, 3111–3119. [Google Scholar] [CrossRef]
- Niemunis, A. Incremental Driver User’s Manual. 2014. Available online: https://soilmodels.com/idriver/ (accessed on 21 December 2023).
- Von Wolffersdorff, P.A. A hypoplastic relation for granular materials with a predefined limit state surface. Mech. Cohesive-Frict. Mater. Int. J. Exp. Model. Comput. Mater. Struct. 1996, 1, 251–271. [Google Scholar] [CrossRef]
- Taiebat, M.; Dafalias, Y.F. SANISAND: Simple anisotropic sand plasticity model. Int. J. Numer. Anal. Methods Geomech. 2008, 32, 915–948. [Google Scholar] [CrossRef]
- Niemunis, A.; Grandas-Tavera, C.; Prada-Sarmiento, L. Anisotropic visco-hypoplasticity. Acta Geotech. 2009, 4, 293–314. [Google Scholar] [CrossRef]
- Tafili, M.; Triantafyllidis, T. AVISA: Anisotropic visco-ISA model and its performance at cyclic loading. Acta Geotech. 2020, 15, 2395–2413. [Google Scholar] [CrossRef]
- Kenneth, S.R.; Storn, R.M. Differential evolution-a simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference On Neural Networks, Perth, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Zbigniew, M. Genetic algorithms+ data structures= evolution programs. Comput. Stat. 1996, 372–373. [Google Scholar]
- Niemunis, A. Extended Hypoplastic Models for Soils; Institut für Grundbau und Bodenmechanik Vienna: Vienna, Austria, 2003; Volume 34. [Google Scholar]
- Smith, P.J.; Shafi, M.; Gao, H. Quick simulation: A review of importance sampling techniques in communications systems. IEEE J. Sel. Areas Commun. 1997, 15, 597–613. [Google Scholar] [CrossRef]
- Singh, A.S.; Masuku, M.B. Sampling techniques & determination of sample size in applied statistics research: An overview. Int. J. Econ. Commer. Manag. 2014, 2, 1–22. [Google Scholar]
- ElRafey, A.; Wojtusiak, J. Recent advances in scaling-down sampling methods in machine learning. Wiley Interdiscip. Rev. Comput. Stat. 2017, 9, e1414. [Google Scholar] [CrossRef]
- Metropolis, N.; Ulam, S. The Monte Carlo method. J. Am. Stat. Assoc. 1949, 44, 335–341. [Google Scholar] [CrossRef] [PubMed]
- McKay, M.D.; Beckman, R.J.; Conover, W.J. A comparison of three methods for selecting values of input variables in the analysis of output from a computer code. Technometrics 2000, 42, 55–61. [Google Scholar] [CrossRef]
- Bauer, E. Calibration of a comprehensive hypoplastic model for granular materials. Soils Found. 1996, 36, 13–26. [Google Scholar] [CrossRef]
- Matsuoka, H.; Nakai, T. Stress-deformation and strength characteristics of soil under three different principal stresses. Jpn. Soc. Civ. Eng. 1974, 1974, 59–70. [Google Scholar] [CrossRef] [PubMed]
- Machaček, J. Contributions to the Numerical Modelling of Saturated and Unsaturated Soils. Ph.D. Thesis, Institute of Soil Mechanics and Rock Mechanics, Karlsruhe Institute of Technology, Karlsruhe, Germany, 2020. [Google Scholar]
- Machaček, J.; Staubach, P.; Tafili, M.; Zachert, H.; Wichtmann, T. Investigation of three sophisticated constitutive soil models: From numerical formulations to element tests and the analysis of vibratory pile driving tests. Comput. Geotech. 2021, 138, 104276. [Google Scholar] [CrossRef]
- Staubach, P.; Kimmig, I.; Machaček, J.; Wichtmann, T.; Triantafyllidis, T. Deep vibratory compaction simulated using a high-cycle accumulation model. Soil Dyn. Earthq. Eng. 2023, 166, 107763. [Google Scholar] [CrossRef]
- Staubach, P. Contributions to the Numerical Modelling of Pile Installation Processes and High-Cyclic Loading of Soils. Ph.D. Thesis, Chair of Soil Mechanics, Foundation Engineering and Environmental Geotechnics, Ruhr University Bochum, Bochum, Germany, 2022. [Google Scholar]
- Schmüdderich, C.; Lavasan, A.A.; Tschuchnigg, F.; Wichtmann, T. Bearing capacity of a strip footing placed next to an existing footing on frictional soil. Soils Found. 2020, 60, 229–238. [Google Scholar] [CrossRef]
- Schmüdderich, C.; Lavasan, A.A.; Tschuchnigg, F.; Wichtmann, T. Behavior of nonidentical differently loaded interfering rough footings. J. Geotech. Geoenviron. Eng. 2020, 146, 04020041. [Google Scholar] [CrossRef]






| Overall | ||||
|---|---|---|---|---|
| Grid sampling with linear spacing | 0.000 | 0.313 | 0.858 | 0.773 |
| Grid sampling with quadratic spacing | 0.000 | 0.750 | 0.934 | 0.887 |
| Monte Carlo sampling | 0.011 | 0.642 | 0.938 | 0.879 |
| Latin hypercube sampling | 0.003 | 0.603 | 0.878 | 0.823 |
| Modified Latin hypercube sampling-1 | 0.328 | 0.856 | 0.936 | 0.913 |
| Modified Latin hypercube sampling-2 | 0.769 | 0.823 | 0.917 | 0.907 |
| in ° | hs in MPa | n | |||||
|---|---|---|---|---|---|---|---|
| 33.1 | 4000 | 0.27 | 0.677 | 1.054 | 1.212 | 0.14 | 2.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shakya, S.; Schmüdderich, C.; Machaček, J.; Prada-Sarmiento, L.F.; Wichtmann, T. Influence of Sampling Methods on the Accuracy of Machine Learning Predictions Used for Strain-Dependent Slope Stability. Geosciences 2024, 14, 44. https://doi.org/10.3390/geosciences14020044
Shakya S, Schmüdderich C, Machaček J, Prada-Sarmiento LF, Wichtmann T. Influence of Sampling Methods on the Accuracy of Machine Learning Predictions Used for Strain-Dependent Slope Stability. Geosciences. 2024; 14(2):44. https://doi.org/10.3390/geosciences14020044
Chicago/Turabian StyleShakya, Sudan, Christoph Schmüdderich, Jan Machaček, Luis Felipe Prada-Sarmiento, and Torsten Wichtmann. 2024. "Influence of Sampling Methods on the Accuracy of Machine Learning Predictions Used for Strain-Dependent Slope Stability" Geosciences 14, no. 2: 44. https://doi.org/10.3390/geosciences14020044
APA StyleShakya, S., Schmüdderich, C., Machaček, J., Prada-Sarmiento, L. F., & Wichtmann, T. (2024). Influence of Sampling Methods on the Accuracy of Machine Learning Predictions Used for Strain-Dependent Slope Stability. Geosciences, 14(2), 44. https://doi.org/10.3390/geosciences14020044







