Landslide Hazard and Rainfall Threshold Assessment: Incorporating Shallow and Deep-Seated Failure Mechanisms with Physics-Based Models
Abstract
1. Introduction
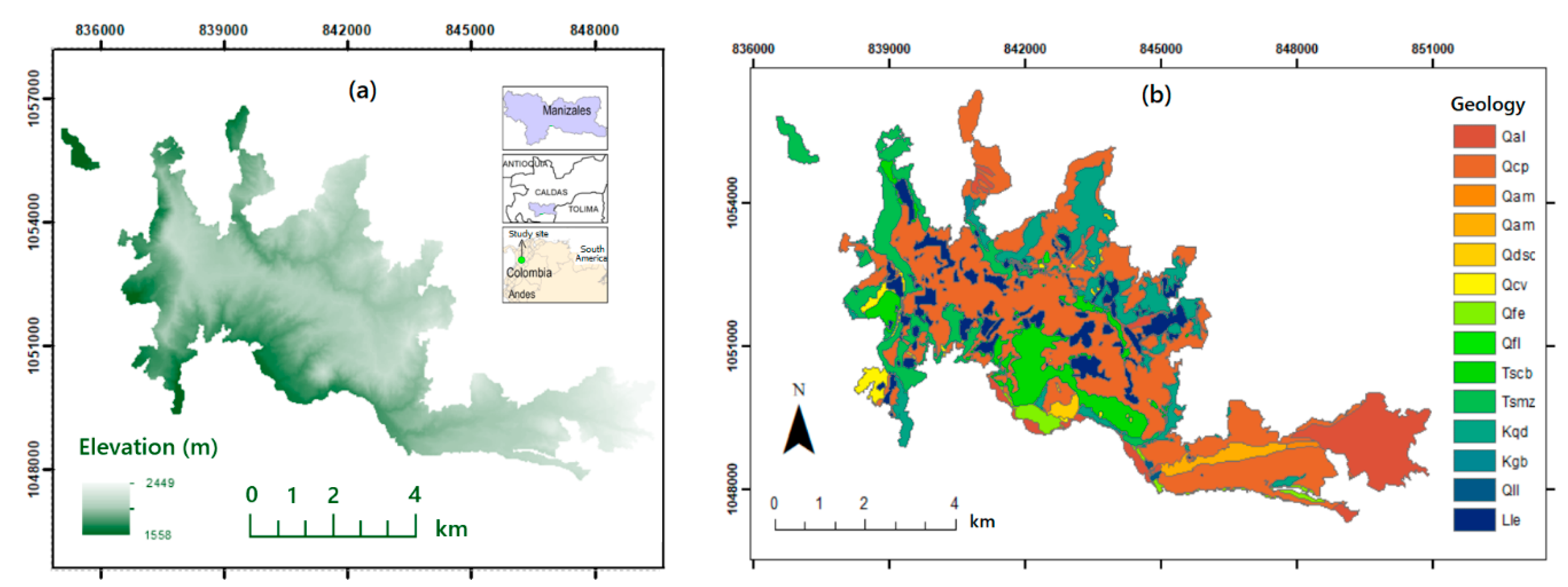
2. Case Study
3. Methods
3.1. TRIGRS
3.2. Scoops3D
3.3. FOSM
3.4. Physics-Based Rainfall Thresholds for Landslides
- They are relatively conservative, given that they are intended for the entire urban area of Manizales, but they aim to optimize a balance between accuracy and false alarms, which is valuable for an early warning system.
- Stability simulations are conducted considering antecedent rainfall conditions and an assumed initial groundwater level scenario prior to rainfall simulations.
- Approximately 596 rainfall events were simulated, encompassing a range of intensities and durations. Table 1 presents the simulated rainfall durations (10 durations in total). For events with durations between 1 and 6 h, the time step size is 1 h (1 h, 2 h, 3 h, …, 6 h). For events with durations from 6 to 14 h, the time step size is 2 h (6 h, 8 h, 10 h, …, 14 h). Table 2 details the simulated mean intensities for each duration (55 intensities). Similarly, the simulated rainfall events varied in intensity from 3 to 45 mm/h with a step size of 1 mm/h (3 mm/h, 4 mm/h, 5 mm/h, …, 45 mm/h), and from 45 to 100 mm/h with a step size of 5 mm/h (45 mm/h, 50 mm/h, 55 mm/h, …, 100 mm/h).
4. Results
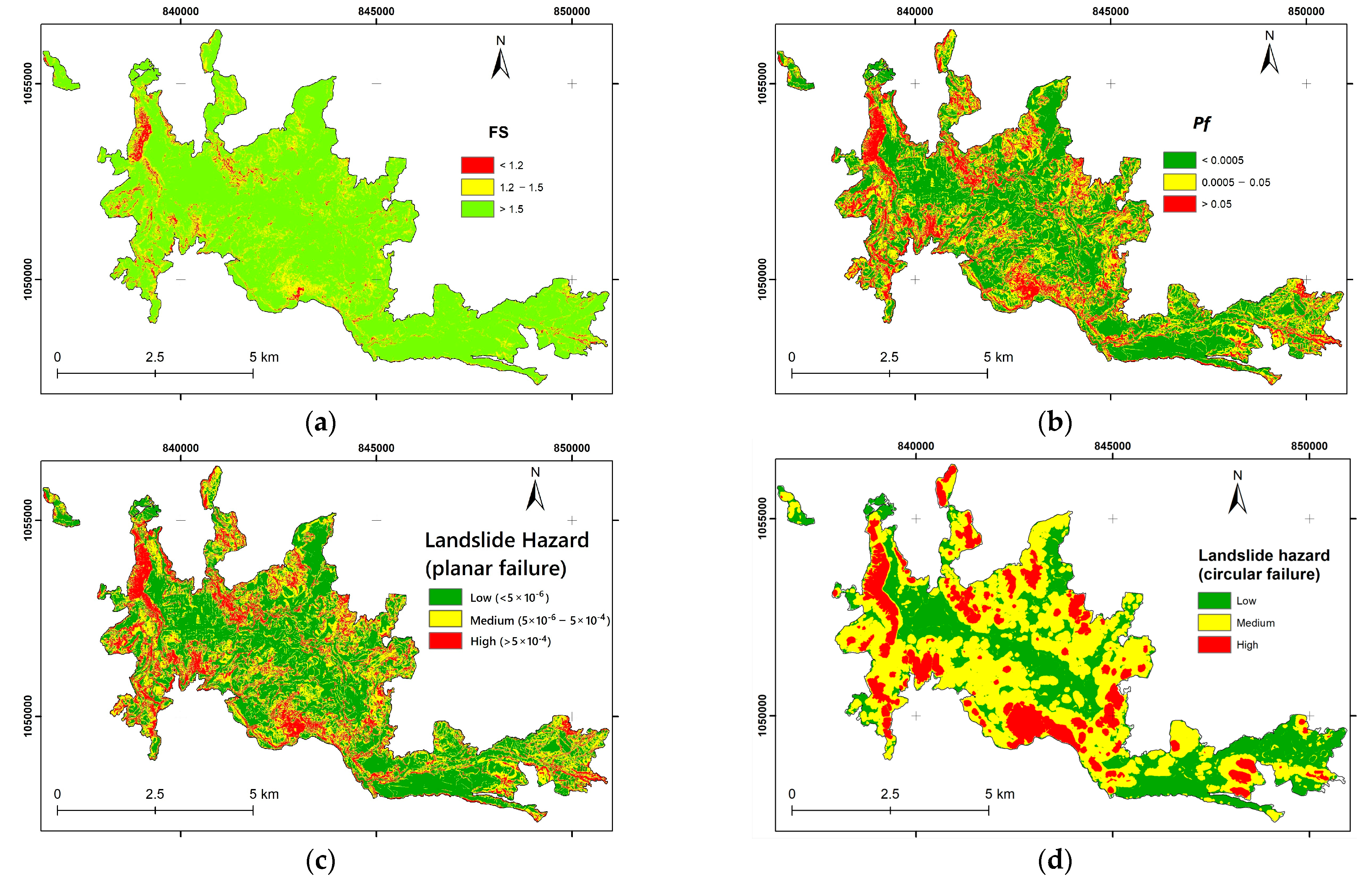
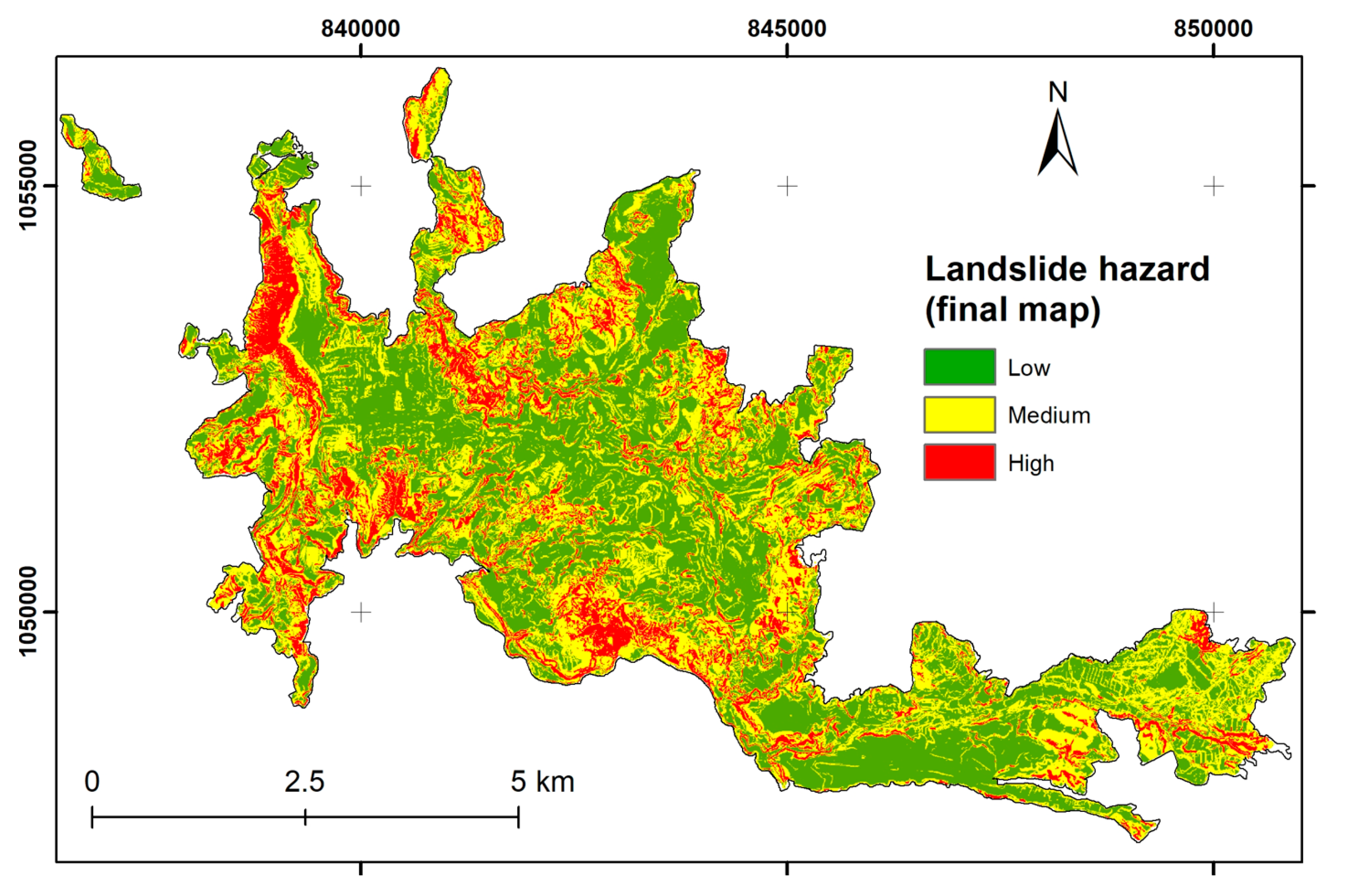
4.1. Landslide Hazard
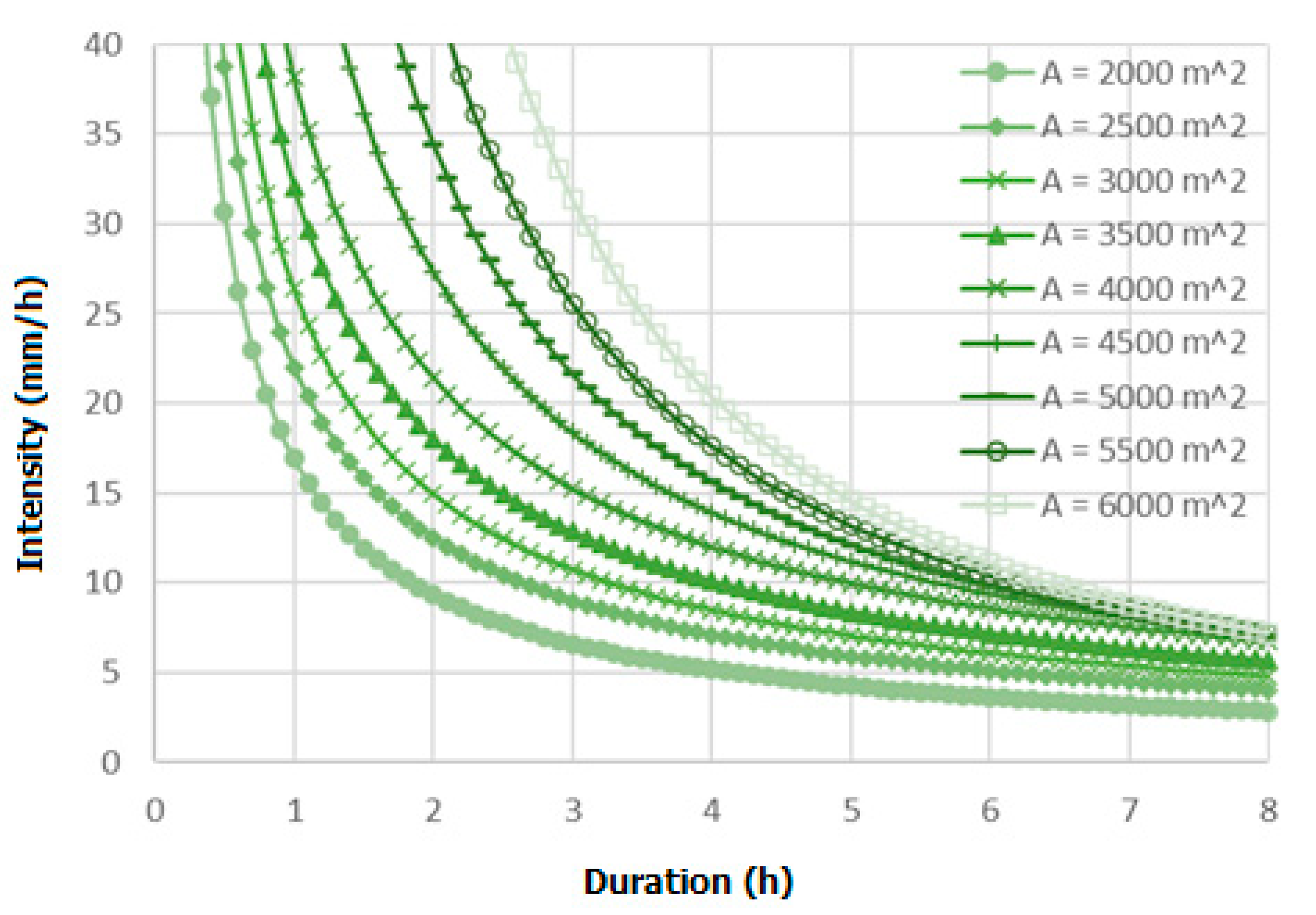
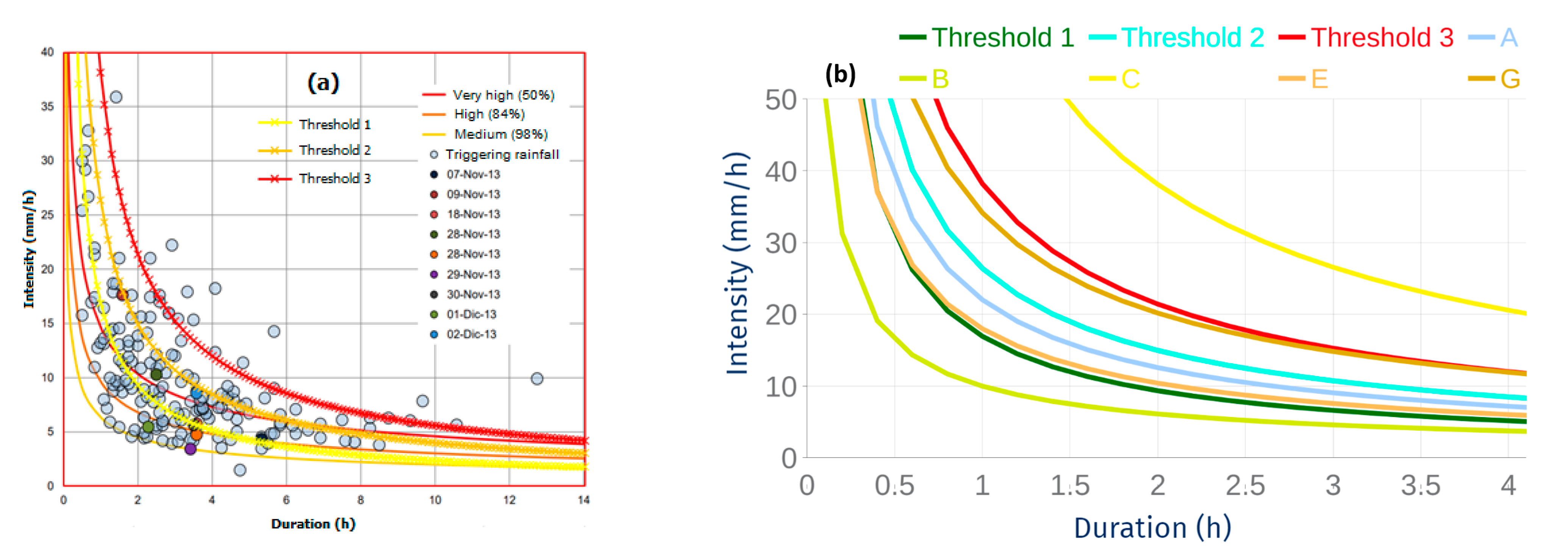
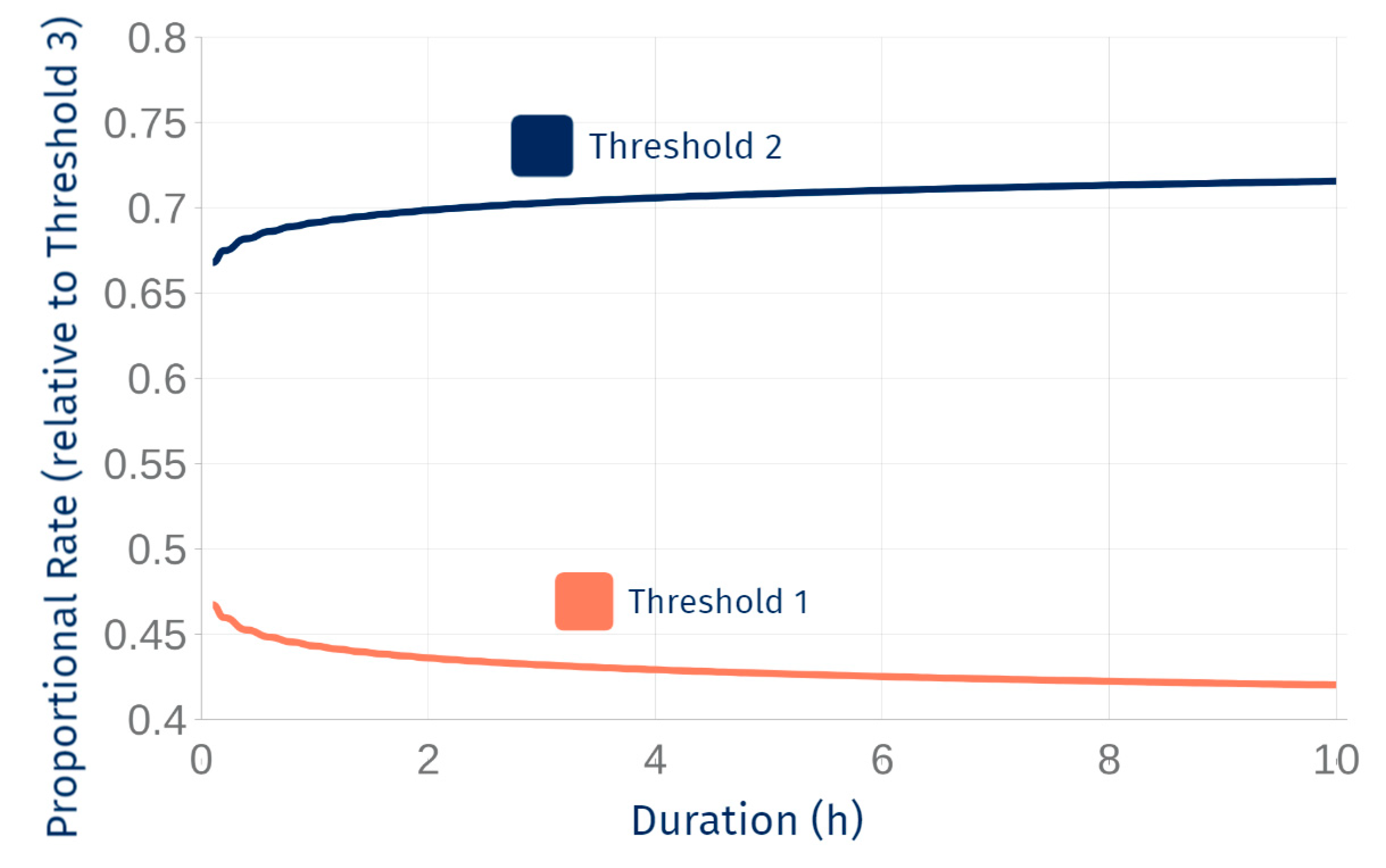
4.2. Rainfall Thresholds
5. Discussion
6. Conclusions
- Three rainfall intensity-duration thresholds for shallow landslides in the urban areas of Manizales were developed using the physics-based TRIGRS model, based on 596 simulations under various rainfall scenarios. These thresholds were compared to recorded rainfall events that triggered mass movements, ensuring a reliable foundation for their establishment.
- The TRIGRS model for planar failures and the Scoops3D model for circular failures effectively assessed and zoned hazards associated with both shallow and deep-seated landslides. The probabilistic First-Order Second-Moment (FOSM) method was identified as a straightforward approach for regional zonation analysis, integrating seamlessly with the TRIGRS model.
- Power-law equations were introduced to simplify the advisory levels for rainfall thresholds, proposed for implementation in the Manizales Early Warning System (EWS), thereby enhancing computational efficiency.
- The findings provide valuable insights for improving early warning systems and hazard mitigation strategies, contributing to more effective disaster management practices in landslide-prone regions.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Froude, M.J.; Petley, D.N. Global fatal landslide occurrence from 2004 to 2016. Nat. Hazards Earth Syst. Sci. 2018, 18, 2161–2181. [Google Scholar] [CrossRef]
- Gariano, S.L.; Guzzetti, F. Landslides in a changing climate. Earth Sci. Rev. 2016, 162, 227–252. [Google Scholar] [CrossRef]
- Aristizábal, E.; Sánchez, O. Spatial and temporal patterns and the socioeconomic impacts of landslides in the tropical and mountainous Colombian Andes. Disasters 2020, 44, 596–618. [Google Scholar] [CrossRef]
- Garcia-Delgado, H.; Petley, D.N.; Bermúdez, M.A.; Sepúlveda, S.A. Fatal landslides in Colombia (from historical times to 2020) and their socio-economic impacts. Landslides 2022, 19, 1689–1716. [Google Scholar] [CrossRef]
- Grima, N.; Edwards, D.; Edwards, F.; Petley, D.; Fisher, B. Landslides in the Andes: Forests can provide cost-effective landslide regulation services. Sci. Total Environ. 2020, 745, 141128. [Google Scholar] [CrossRef]
- Henao-Céspedes, V.; Garcés-Gómez, Y.A.; Olaya, M.N.M. Landslide early warning systems: A perspective from the internet of things. Int. J. Electr. Comput. Eng. 2023, 13, 2214–2222. [Google Scholar] [CrossRef]
- Zambrano-Nájera, J.; Luna, C.C.; Upegui, J.J.V. Performance assessment of indicators of a multi-hazards early warning system in an urban mountain region. Int. J. Disaster Risk Reduct. 2024, 112, 104767. [Google Scholar] [CrossRef]
- Pereira, S.; Santos, P.; Zêzere, J.; Tavares, A.; Garcia, R.; Oliveira, S. A landslide risk index for municipal land use planning in Portugal. Sci. Total Environ. 2020, 735, 139463. [Google Scholar] [CrossRef]
- Das, S.; Pandit, K.; Sarkar, S.; Kanungo, D.P. Stability and Hazard Assessment of the Progressive Zero Landslide in the Kalimpong Region of Darjeeling Himalaya, India. Geotech. Geol. Eng. 2024, 42, 1693–1709. [Google Scholar] [CrossRef]
- Oguz, E.A.; Depina, I.; Myhre, B.; Devoli, G.; Rustad, H.; Thakur, V. IoT-based hydrological monitoring of water-induced landslides: A case study in central Norway. Bull. Eng. Geol. Environ. 2022, 81, 217. [Google Scholar] [CrossRef]
- Panchal, S.; Shrivastava, A.K. Landslide hazard assessment using analytic hierarchy process (AHP): A case study of National Highway 5 in India. Ain Shams Eng. J. 2022, 13, 101626. [Google Scholar] [CrossRef]
- Sannino, G.; Bordoni, M.; Bittelli, M.; Meisina, C.; Tomei, F.; Valentino, R. Deterministic Physically Based Distributed Models for Rainfall-Induced Shallow Landslides. Geosciences 2024, 14, 255. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, R.; Dou, J.; Hou, S.; Xiang, Z.; Wang, H.; Yang, P.; Liu, X. Advancing reservoir landslide stability assessment via TS-InSAR and airborne LiDAR observations in the Daping landslide group, Three Gorges Reservoir Area, China. Landslides 2024, 1–20. [Google Scholar] [CrossRef]
- Devoli, G.; Tiranti, D.; Cremonini, R.; Sund, M.; Boje, S. Comparison of landslide forecasting services in Piedmont (Italy) and Norway, illustrated by events in late spring 2013. Nat. Hazards Earth Syst. Sci. 2018, 18, 1351–1372. [Google Scholar] [CrossRef]
- Park, J.Y.; Lee, S.R.; Lee, D.H.; Kim, Y.T.; Lee, J.S. A regional-scale landslide early warning methodology applying statistical and physically based approaches in sequence. Eng. Geol. 2019, 260, 105193. [Google Scholar] [CrossRef]
- Piciullo, L.; Abraham, M.T.; Drøsdal, I.N.; Paulsen, E.S. An operational IoT-based slope stability forecast using a digital twin. Environ. Model. Softw. 2024, 183, 106228. [Google Scholar] [CrossRef]
- Cui, H.; Medina, V.; Hürlimann, M.; Ji, J. Fast physically-based probabilistic modelling of rainfall-induced shallow landslide susceptibility at the regional scale considering geotechnical uncertainties and different hydrological conditions. Comput. Geotech. 2024, 172, 106400. [Google Scholar] [CrossRef]
- Gupta, K.; Satyam, N.; Gupta, V. Probabilistic physical modelling and prediction of regional seismic landslide hazard in Uttarakhand state (India). Landslides 2023, 20, 901–912. [Google Scholar] [CrossRef]
- Montrasio, L.; Valentino, R. A model for triggering mechanisms of shallow landslides. Nat. Hazards Earth Syst. Sci. 2008, 8, 1149–1159. [Google Scholar] [CrossRef]
- Marin, R.J.; Mattos, J. Physically-based landslide susceptibility analysis using Monte Carlo simulation in a tropical mountain basin. Georisk Assess. Manag. Risk Eng. Syst. Geohazards 2020, 14, 192–205. [Google Scholar] [CrossRef]
- Zeng, T.; Gong, Q.; Wu, L.; Zhu, Y.; Yin, K.; Peduto, D. Double-index rainfall warning and probabilistic physically based model for fast-moving landslide hazard analysis in subtropical-typhoon area. Landslides 2024, 21, 753–773. [Google Scholar] [CrossRef]
- Alvioli, M.; Melillo, M.; Guzzetti, F.; Rossi, M.; Palazzi, E.; von Hardenberg, J.; Brunetti, M.T.; Peruccacci, S. Implications of climate change on landslide hazard in Central Italy. Sci. Total Environ. 2018, 630, 1528–1543. [Google Scholar] [CrossRef] [PubMed]
- Papa, M.N.; Medina, V.; Ciervo, F.; Bateman, A. Derivation of critical rainfall thresholds for shallow landslides as a tool for debris flow early warning systems. Hydrol. Earth Syst. Sci. 2013, 17, 4095–4107. [Google Scholar] [CrossRef]
- Sannino, G.; Tomei, F.; Bittelli, M.; Bordoni, M.; Meisina, C.; Valentino, R. Implementation of a slope stability method in the CRITERIA-1D agro-hydrological modeling scheme. Landslides 2024, 1–20. [Google Scholar] [CrossRef]
- Bordoni, M.; Vivaldi, V.; Giarola, A.; Valentino, R.; Bittelli, M.; Meisina, C. Comparison between mechanical and hydrological reinforcement effects of cultivated plants on shallow slope stability. Sci. Total Environ. 2024, 912, 168999. [Google Scholar] [CrossRef]
- Guzzetti, F.; Gariano, S.L.; Peruccacci, S.; Brunetti, M.T.; Marchesini, I.; Rossi, M.; Melillo, M. Geographical landslide early warning systems. Earth-Sci. Rev. 2020, 200, 102973. [Google Scholar] [CrossRef]
- Marin, R.J.; Marin-Sanchez, J.C. LandScient_EWS: Real-Time Monitoring of Rainfall Thresholds for Landslide Early Warning-A Case Study in the Colombian Andes. J. Eng. Geol. 2024, 34, 173–191. [Google Scholar] [CrossRef]
- Guzzetti, F.; Peruccacci, S.; Rossi, M.; Stark, C.P. The rainfall intensity–duration control of shallow landslides and debris flows: An update. Landslides 2008, 5, 3–17. [Google Scholar] [CrossRef]
- Intrieri, E.; Carlà, T.; Gigli, G. Forecasting the time of failure of landslides at slope-scale: A literature review. Earth-Sci. Rev. 2019, 193, 333–349. [Google Scholar] [CrossRef]
- Monsieurs, E.; Dewitte, O.; Demoulin, A. A susceptibility-based rainfall threshold approach for landslide occurrence. Nat. Hazards Earth Syst. Sci. 2019, 19, 775–789. [Google Scholar] [CrossRef]
- Palau, R.M.; Berenguer, M.; Hürlimann, M.; Sempere-Torres, D. Implementation of hydrometeorological thresholds for regional landslide warning in Catalonia (NE Spain). Landslides 2023, 20, 2039–2054. [Google Scholar] [CrossRef]
- Segoni, S.; Piciullo, L.; Gariano, S.L. A review of the recent literature on rainfall thresholds for landslide occurrence. Landslides 2018, 15, 1483–1501. [Google Scholar] [CrossRef]
- Alvioli, M.; Loche, M.; Jacobs, L.; Grohmann, C.H.; Abraham, M.T.; Gupta, K.; Satyam, N.; Scaringi, G.; Bornaetxea, T.; Rossi, M.; et al. A benchmark dataset and workflow for landslide susceptibility zonation. Earth-Sci. Rev. 2024, 258, 104927. [Google Scholar] [CrossRef]
- Marin, R.J. Physically based and distributed rainfall intensity and duration thresholds for shallow landslides. Landslides 2020, 17, 2907–2917. [Google Scholar] [CrossRef]
- Londoño Grajales, F.J. Sostenibilidad Ambiental y Resistencia al Cortante Tangencial en Suelos Derivados de Cenizas Volcánicas y rocas Metamórficas de Zonas de ladera de la Ciudad de Manizales-Caldas. Master’s Thesis, Universidad Nacional de Colombia, Bogotá, Colombia, 2020. [Google Scholar]
- Bernal, G.A.; Salgado-Gálvez, M.A.; Zuloaga, D.; Tristancho, J.; González, D.; Cardona, O.-D. Integration of Probabilistic and Multi-Hazard Risk Assessment Within Urban Development Planning and Emergency Preparedness and Response: Application to Manizales, Colombia. Int. J. Disaster Risk Sci. 2017, 8, 270–283. [Google Scholar] [CrossRef]
- Correa, O.; García, F.; Bernal, G.; Cardona, O.D.; Rodriguez, C. Early warning system for rainfall-triggered landslides based on real-time probabilistic hazard assessment. Nat. Hazards 2020, 100, 345–361. [Google Scholar] [CrossRef]
- Carreño, M.L.; Cardona, O.-D.; Barbat, A.H.; Suarez, D.C.; Perez, M.d.P.; Narvaez, L. Holistic Disaster Risk Evaluation for the Urban Risk Management Plan of Manizales, Colombia. Int. J. Disaster Risk Sci. 2017, 8, 258–269. [Google Scholar] [CrossRef][Green Version]
- Baum, R.L.; Savage, W.Z.; Godt, J.W. TRIGRS: A Fortran Program for Transient Rainfall Infiltration and Grid-Based Regional Slope-Stability Analysis, Version 2.0; US Geological Survey: Reston, VA, USA, 2008; p. 75. [Google Scholar]
- Iverson, R.M. Landslide triggering by rain infiltration. Water Resour. Res. 2000, 36, 1897–1910. [Google Scholar] [CrossRef]
- Taylor, D.W. Fundamentals of Soil Mechanics. Soil Sci. 1948, 66, 161. [Google Scholar] [CrossRef]
- Reid, M.E.; Christian, S.B.; Brien, D.L.; Henderson, S.T. Scoops3D: Software to Analyze 3D Slope Stability throughout a Digital landscape; Book 14, Chapter A1; US Geological Survey: Reston, VA, USA, 2015; 218p. [Google Scholar] [CrossRef]
- Hungr, O. An extension of Bishop’s simplified method of slope stability analysis to three dimensions. Geotechnique 1987, 37, 113–117. [Google Scholar] [CrossRef]
- Baecher, G.B.; Christian, J.T. Reliability and Statistics in Geotechnical Engineering; John Wiley and Sons Ltd.: Chichester, UK, 2003; ISBN 978-0-470-87125-6. [Google Scholar]
- Marin, R.J.; Velásquez, M.F.; García, E.F.; Alvioli, M.; Aristizábal, E. Assessing two methods of defining rainfall intensity and duration thresholds for shallow landslides in data-scarce catchments of the Colombian Andean Mountains. Catena 2021, 206, 105563. [Google Scholar] [CrossRef]
- Marin, R.J.; Velásquez, M.F. Influence of hydraulic properties on physically modelling slope stability and the definition of rainfall thresholds for shallow landslides. Geomorphology 2020, 351, 106976. [Google Scholar] [CrossRef]
- Rosi, A.; Segoni, S.; Canavesi, V.; Monni, A.; Gallucci, A.; Casagli, N. Definition of 3D rainfall thresholds to increase operative landslide early warning system performances. Landslides 2021, 18, 1045–1057. [Google Scholar] [CrossRef]
- Marin, R.J.; Long, M. 2D and 3D numerical modelling for preliminary assessment of long-term deterioration in Irish glacial till geotechnical slopes. Georisk Assess. Manag. Risk Eng. Syst. Geohazards 2024, 1–27. [Google Scholar] [CrossRef]
- Shou, K.-J.; Chen, J. On the rainfall induced deep-seated and shallow landslide hazard in Taiwan. Eng. Geol. 2021, 288, 106156. [Google Scholar] [CrossRef]
- Marin, R.J.; García, E.F.; Aristizábal, E. Assessing the effectiveness of TRIGRS for predicting unstable areas in a tropical mountain basin (Colombian Andes). Geotech. Geol. Eng. 2021, 39, 2329–2346. [Google Scholar] [CrossRef]
- Vandromme, R.; Thiery, Y.; Bernardie, S.; Sedan, O. ALICE (Assessment of Landslides Induced by Climatic Events): A single tool to integrate shallow and deep landslides for susceptibility and hazard assessment. Geomorphology 2020, 367, 107307. [Google Scholar] [CrossRef]
- Crescenzo, L.; Peranić, J.; Arbanas, Ž.; Calvello, M. An approach to calibrate the unsaturated hydraulic properties of a soil through numerical modelling of a small-scale slope model exposed to rainfall. Acta Geotech. 2024, 19, 4437–4456. [Google Scholar] [CrossRef]
- Dini, B.; Manconi, A.; Loew, S. Investigation of slope instabilities in NW Bhutan as derived from systematic DInSAR analyses. Eng. Geol. 2019, 259, 105111. [Google Scholar] [CrossRef]
- Innocenti, A.; Pazzi, V.; Borselli, L.; Nocentini, M.; Lombardi, L.; Gigli, G.; Fanti, R. Reconstruction of the evolution phases of a landslide by using multi-layer back-analysis methods. Landslides 2023, 20, 189–207. [Google Scholar] [CrossRef]
- Mavrouli, O.; Núñez-Andrés, M.A.; Buill, F.; Lantada, N.; Corominas, J. Correlation between rockfall frequency and overhang geometrical attributes. Landslides 2024, 21, 1971–1985. [Google Scholar] [CrossRef]
- Loche, M.; Scaringi, G. Temperature and shear-rate effects in two pure clays: Possible implications for clay landslides. Results Eng. 2023, 20, 101647. [Google Scholar] [CrossRef]
- Tayyebi, S.M.; Pastor, M.; Hernandez, A.; Gao, L.; Stickle, M.M.; Yifru, A.L.; Thakur, V. Two-Phase Two-Layer Depth-Integrated SPH-FD Model: Application to Lahars and Debris Flows. Land 2022, 11, 1629. [Google Scholar] [CrossRef]
- Marin, R.J.; Long, M. Deterioration models for geotechnical slopes: A systematic review on the long-term behaviour of earthwork assets. Struct. Infrastruct. Eng. 2024, 1–17. [Google Scholar] [CrossRef]
| Time Step Size (Hours) | Range of Duration (Hours) |
|---|---|
| 1 | 1–6 |
| 2 | 6–14 |
| Mean Intensity Step Size (Intensity, mm/h) | Range of Intensity (mm/h) |
|---|---|
| 1 | 3–45 |
| 5 | 45–100 |
| Critical Area (A) | Threshold Equation |
|---|---|
| A = 2000 m2 | I = 16.904D−0.858 |
| A = 2500 m2 | I = 22.01D−0.817 |
| A = 3000 m2 | I = 26.379D−0.82 |
| A = 3500 m2 | I = 32.105D−0.834 |
| A = 4000 m2 | I = 38.174D−0.835 |
| A = 4500 m2 | I = 53.623D−0.974 |
| A = 5000 m2 | I = 75.924D−1.141 |
| A = 5500 m2 | I = 106.42D−1.298 |
| A = 6000 m2 | I = 163.91D−1.504 |
| Critical Area | Threshold Equation |
|---|---|
| A = 2000 m2, Threshold 1 | I = 16.904D−0.858 |
| A = 3000 m2, Threshold 2 | I = 26.379D−0.82 |
| A = 4000 m2, Threshold 3 | I = 38.174D−0.835 |
| Threshold | Equation |
|---|---|
| Medium Threshold (IDEA-Manizales) | I = 6.3204D−0.487 |
| High Threshold (IDEA-Manizales) | I = 9.462D−0.481 |
| Very High Threshold (IDEA-Manizales) | I = 14.372D−0.485 |
| Threshold A (Emilia Romagna, Italy) | I = 22.0D−0.81 |
| Threshold B (Emilia Romagna, Italy) | I = 9.96D−0.71 |
| Threshold C (Emilia Romagna, Italy) | I = 70.57D−0.89 |
| Threshold E (Emilia Romagna, Italy) | I = 17.96D−0.79 |
| Threshold G (Emilia Romagna, Italy) | I = 34.12D−0.76 |
| Threshold (Critical Intensity) | Equation | Range (Duration) | α | β | Ic (1 h) | Ic (2 h) | Ic (3 h) |
|---|---|---|---|---|---|---|---|
| Threshold 1 (Ic1) | I = 16.904D−0.858 | 0–10 h | 16.90 | −0.86 | 16.90 | 9.33 | 6.59 |
| Threshold 2 (Ic2) | I = 26.379D−0.82 | 0–10 h | 26.38 | −0.82 | 26.38 | 14.94 | 10.72 |
| Threshold 3 (Ic3) | I = 38.174D−0.835 | 0–10 h | 38.17 | −0.84 | 38.17 | 21.4 | 15.25 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marin, R.J.; Marín-Sánchez, J.C.; Mira, J.E.; García, E.F.; Zhao, B.; Zambrano, J. Landslide Hazard and Rainfall Threshold Assessment: Incorporating Shallow and Deep-Seated Failure Mechanisms with Physics-Based Models. Geosciences 2024, 14, 280. https://doi.org/10.3390/geosciences14100280
Marin RJ, Marín-Sánchez JC, Mira JE, García EF, Zhao B, Zambrano J. Landslide Hazard and Rainfall Threshold Assessment: Incorporating Shallow and Deep-Seated Failure Mechanisms with Physics-Based Models. Geosciences. 2024; 14(10):280. https://doi.org/10.3390/geosciences14100280
Chicago/Turabian StyleMarin, Roberto J., Julián Camilo Marín-Sánchez, Johan Estiben Mira, Edwin F. García, Binru Zhao, and Jeannette Zambrano. 2024. "Landslide Hazard and Rainfall Threshold Assessment: Incorporating Shallow and Deep-Seated Failure Mechanisms with Physics-Based Models" Geosciences 14, no. 10: 280. https://doi.org/10.3390/geosciences14100280
APA StyleMarin, R. J., Marín-Sánchez, J. C., Mira, J. E., García, E. F., Zhao, B., & Zambrano, J. (2024). Landslide Hazard and Rainfall Threshold Assessment: Incorporating Shallow and Deep-Seated Failure Mechanisms with Physics-Based Models. Geosciences, 14(10), 280. https://doi.org/10.3390/geosciences14100280







