Abstract
In geotechnical engineering, dynamic soil models are used to predict soil behavior under different loading conditions. This is crucial for many dynamic geotechnical problems related to earthquakes, train loading and machine foundation design. Researchers agree that under dry or drained conditions, cohesionless soils increase in stiffness with each loading cycle. Soil models that simulate the dynamic behaviors of soils are often coupled with the Masing criteria. Such models neglect the impact of stiffening during cyclic loading, leading to an underestimation in the shear modulus (G). This study investigates the stiffening behavior by conducting laboratory tests on three types of Danube sands using the Resonant Column-Torsional Simple Shear device (RC-TOSS). The increase in the dynamic shear modulus with an increasing number of cycles is substantial, especially for samples with low density. Sometimes, the dynamic shear modulus doubles when loaded at high stress levels for more than 50 cycles. A new model is introduced to simulate the stiffening behavior of dry sand when subjected to cyclic torsional loading. Modifications are proposed for the Ramberg–Osgood and Hardin–Drnevich models and for the Masing criteria to overcome the limitations that accompany these models due to the influence of stiffening caused by repetitive loading being ignored. This model can be implemented in finite element and finite difference software to solve dynamic geotechnical problems.
1. Introduction
Modeling the dynamic behavior of soil has become essential to address numerous geotechnical issues. Whether it is a cyclic loading problem (e.g., machine foundations and loading of train [1]) or a more complicated irregular loading, such as earthquake site response analysis [2,3], the advancements in computer technology and faster processing speeds have facilitated the use of numerical modeling (e.g., finite element and finite difference methods [4]) for quicker and more efficient calibration of models. The use of semi-static and equivalent linear methods has many limitations related to the assumptions made to simplify the problem. For instance, the equivalent linear method performed in a site response analysis assumes that the shear modulus and damping ratio are constant throughout the analysis. This assumption causes an underestimation or overestimation in the response depending on the soil type and earthquake record [5,6]. To overcome this limitation, nonlinear response analysis methods have been developed, which emphasize the need for nonlinear soil models that can simulate the shear stress–strain behavior accurately.
Vucetic (1994) [7] defined two types of shear strain thresholds during cyclic loading. Below the linear strain threshold (), the soil exhibits an elastic behavior. This limit is reached when the secant shear modulus to the small strain shear modulus (G/Gmax) equals 0.99. After exceeding this limit, the soil behavior becomes slightly elastoplastic (still elastic but nonlinear), and the permanent microstructural change is insignificant until the strains reach the second threshold, which is defined as the volumetric strain threshold (), after which the microstructure is altered irreversibly, and the soil stiffness changes permanently. The studies presented in [8,9,10] show that is associated with a G/Gmax range of 0.6 to 0.85.
When applying torsional cyclic loading to soil, the first loading curve in the shear stress–strain plot is termed the backbone curve. The stiffness of the soil represented by the shear modulus degrades with the increasing strain. When cyclically loading soil, the nonlinearity and stiffness recovering among load reversals generate hysteresis loops in the shear stress–strain space. The secant shear modulus, which represents the “average” shear stiffness of the soil, is determined by the slope of the line that connects the endpoints of the hysteresis loop (Figure 1).
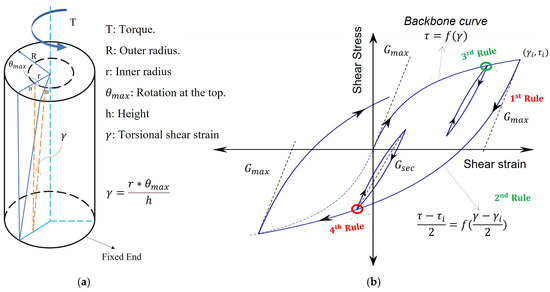
Figure 1.
Concept for torsional strain in a fixed-free hollow cylinder specimen. (a) Diagram of the concept. (b) Hysteresis loop and Masing criteria.
The nonlinear monotonic shear stress–strain curve of soils (backbone curve) can be simulated with a simple equation (e.g., Ramberg–Osgood (RO) and Hardin–Drnevich (HD) models). Nevertheless, cyclic and irregular load histories applied to soils increase the complexity of the problem, and additional principles are required to simulate the generated hysteresis loops. Therefore, soil models are often coupled with the Masing criteria. The first two rules were introduced by Masing (1926) [11] to describe the behavior of brass subjected to repeated, symmetric cyclic loading. Jennings added two more rules to study the earthquake response of a yielding structure represented by a single-degree-of-freedom system [12]. These four rules are acknowledged together in the literature as the extended Masing criteria [13,14,15,16,17,18,19] as follows:
- (1)
- The shear modulus in unloading/reloading is equal to the initial tangent modulus for the initial loading curve.
- (2)
- The unloading and reloading curves duplicate the initial curve, except its scale increases by a factor of two in both directions. The variables τ and γ in the formula become and (Figure 1b).
- (3)
- The unloading and reloading curves should follow the backbone curve in the case that the previous maximum shear strain is exceeded.
- (4)
- If the current loading or unloading curve intersects a previous one, it should follow the intersected curve.
The number of loading cycles seems to have a considerable impact on the soil stiffness beyond the cyclic volumetric strain threshold. Cyclic loading tests performed on dry or drained sand cause an increase in the shear modulus with the increasing number of cycles, which is referred to as “cyclic hardening in stiffness”. Complex mechanisms contribute to this phenomenon. However, they can be divided into three categories: fabric reorientation, particle relocation and contact area growth [20]. As shearing forces twist the specimen, particles reorient themselves, gaining and losing contact points with other particles. This is known as a change in fabric. The particles are reoriented to form a new, different fabric without a considerable change in the void ratio. Particle relocation occurs when individual particles move into a former void location. The new location will usually create different contact points between grains as well. This incident causes an increase in the stiffness with a small reduction in the void ratio. The three mechanisms occur simultaneously and can be viewed as successive stages in an ongoing process.
There is a lack of consensus among studies regarding the magnitude of this effect, with varying perspectives on whether it is minor or substantial. Silver and Seed (1971) [21] reported that the rise in stiffness is higher for the first 10 cycles and then becomes relatively low. For Sherif and Ishibashi (1976) [22], after 25 cycles, the shear modulus increased by up to 28% and then became almost constant. Ray (1984) [20] reported the highest increase in the shear modulus, which was around 5% per logarithmic cycle of loading. Ray and Woods (1988) [16] presented similar outcomes based on their Resonant Column-Torsional Simple Shear (RC-TOSS) tests, where the increase reached up to 120% of the initial value at a given strain level. In this study, the effect of the cyclic loading on the stiffness was found to be significant and had a great effect on the accuracy of the soil models.
Ahmad and Ray (2021) [19] showed the ability of the RO and HD modes to simulate the shear stress–strain curves when the sample was subjected to irregular loading. However, the results presented in that study originated from irregular tests conducted after 100 cycles of loading. As a result, the effect of the number of cycles does not show in the shear stress–strain curves because the stiffening effect is marginal after around 75 cycles. This explains the excellent fit between soil models and lab testing curves when using the Masing criteria. However, when applying an irregular loading history on soil without preconditioning cycles (not cyclically loaded before), the Masing criteria predict behavior much less accurately. There would be a significant deviation from the laboratory test results if they were subjected to more cycles. This study addresses the limitations of the soil models in simulating the shear stress–strain curves while accounting for the stiffening behavior caused by cyclic loading. Modifications to the Ramberg–Osgood and Hardin–Drnevich models and the Masing criteria are introduced.
2. Testing Program
The device used in this study is the combined Resonant Column-Torsional Simple Shear Device (RC-TOSS). It was first designed and built by Prof. Richard Ray at the University of Michigan in the 1980s based on ideas gathered from early designs from [23,24,25,26], and it included a few new developed features. The device’s design process, transducers, signal conditioning, data acquisition, and test control are presented in his dissertation [20] and are shown in Figure 2.

Figure 2.
RC-TOSS testing device.
The RC-TOSS equipment uses a fixed-free configuration. A rigid, massive steel plate anchors the device’s base, holding a measurement post and drive coil supports. The device applies torsion to the top of a hollow cylindrical specimen with an inner diameter (Di) of 4.0 cm, an outer diameter (Do) of 6.0 cm, and a length of 14 cm. The torsion is applied using a set of two permanent magnets and four electric coils. A porous, sintered bronze ring provides a rough surface for contact between the device and specimen, allowing for saturation and pore water movement. The top assembly moves freely where the specimen connects to the drive head through a retainer, plug and ring. Two permanent neodymium magnets, attached to the drive head, pass freely through four drive coils. Inner and outer neoprene membranes cover the specimen, allowing for external pressure or internal vacuum confinement. Vacuum confinement provides a more convenient means to apply isotropic stress but limits the maximum magnitude to about 97 kPa. External pressure using a confining chamber can increase the stress levels to about 300 kPa.
The RC test requires displacement measurements with very high accuracy at a very low amplitude ( = 10−4%), which is provided by an accelerometer mounted on the drive head and connected to a multimeter and oscilloscope, providing dynamic amplitude and frequency data. Two proximitors mounted on the measurement post measure the rotational displacement for the TOSS test.
For this research, three specimens of coarse soils were chosen. These samples originated from an area close to the Danube River in Hungary, specifically near Paks, and were taken from depths ranging between 5 and 15 m using a hollow-stem auger sampler. The soils were fluvial sediments of the river with a wide variation of in situ densities. Samples A and B contained a very low percentage of fines, while Sample C retained a 21.11% content of fines with low plasticity. The properties of the tested samples are detailed in Table 1, and the particle size distribution curves are demonstrated in Figure 3. The samples exhibited a complex grain structure with heterogeneous grain shapes varying between sub-angular and rounded shapes.

Table 1.
Properties of the tested soils.
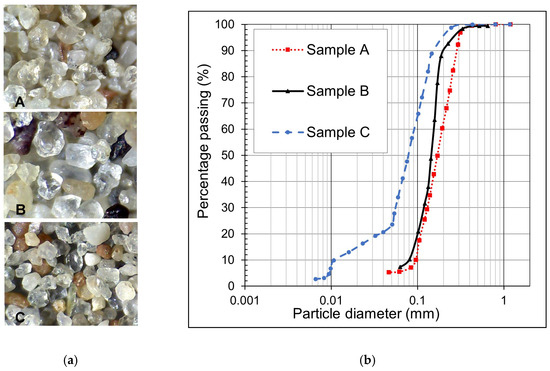
Figure 3.
Particle shape and size distribution of the tested samples. (a) Particle shape of the samples. (b) Particle size distribution of the samples.
The preparation method depended on the required initial density of the soil. The dry pluviation method created a dense specimen. Dry soil, poured slowly from a controlled height, fell and collided with the soil below, generating a dense condition. The height of the fall controlled the specimen’s density. A hollow cylinder specimen required a 50 cm cone to direct the falling soil outward into the space between the inner and outer molds. An outer tube, matching the specimen’s outer diameter, also directed the soil. For the tested soils in this study, the dry pluviation method achieved samples with relative densities that ranged between 0.72 and 0.80.
On the other hand, to prepare samples in a loose state, a method to produce the maximum void ratio of the soil was employed; this was the dry filling–tamping method, where a glass funnel with a 14 cm spout deposited the dry soil into the mold. To create a bulking effect on a uniform loose specimen, preparation started with the spout touching the base ring, and then the spout was carefully raised constantly and moved around to touch the surface of the soil gently. A slightly denser condition was accomplished by softly tapping the mold 10–15 times.
Two variations of TOSS tests allowed for the investigation of the impact of the number of cycles on the dynamic properties. Table 2 shows the testing program. In tests #1-#3-#5-#7-#9-#11, the backbone curve developed by loading the sample for only one cycle at progressively higher stress levels (5-10-15-20-25-30-35-40-45-50 kPa), and the equivalent shear modulus was found for each cycle (Figure 4a). A second identical specimen was constructed with the same void ratio and confining stress for tests #2-#4-#6-#8-#10-#12. However, in this case, the sample was subjected to 100 cycles of loading at every stress level. The duplicates revealed any effects of the number of cycles on specimen behavior (Figure 4b). More tests were conducted (#13 and #14) to determine the effect of the strain level on the stiffening behavior by loading the soil cyclically at the same peak-to-peak stress level but at different offsets.

Table 2.
Testing program.
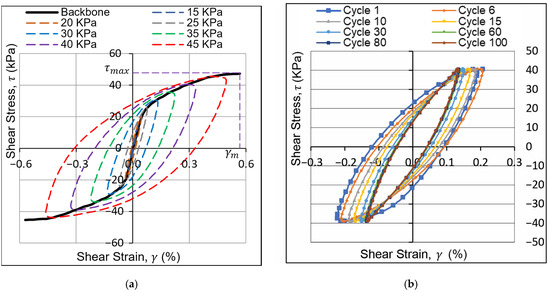
Figure 4.
Demonstration of the types of conducted tests (results for Sample B, loose state). (a) Backbone curve test; (b) 100 TOSS cycles at 40 kPa shear stress.
3. Original Soil Models
3.1. Ramberg–Osgood Model
The model introduced by Ramberg and Osgood (1943) [27] includes three parameters that describe the stress–strain behavior of carbon steel and aluminum alloy sheets. The form used today is different from the original paper. The model that is used for soil in geotechnical earthquake engineering was presented by Streeter, Wylie and Richart (1974) [28] and has since gained considerable prominence, and it has been extensively applied in numerous subsequent research endeavors (e.g., [16,29,30]). The formula for the shear stress–strain relation is
where and are the shear strain and shear stress, respectively. Gmax is the maximum shear modulus at very small strains. is the maximum shear strength, which is a function of the confining stress, the angle of friction, and cohesion obtained from the triaxial test. α, C and R, are constants used to fit the curve with the test data.
The original Masing criteria were later integrated to the Ramberg–Osgood model to simulate two-way loading. The equation for two-way loading is
where and are the shear stress and the shear strain at the turning point, respectively.
3.2. Modified Hardin–Drnevich Model
A hyperbolic equation was proposed by Hardin and Drnevich [31] as a relationship between the shear stress and the shear strain. Darendeli [32] modified the equation by adding a curvature coefficient. This provided higher accuracy and the ability to fit TOSS test data, as demonstrated in [19]. The final form used in this study has only two curve-fitting constants, and m, as shown in the following equation:
The formula that describes two-way loading, using the second Masing criteria, is presented as follows:
4. Results of the RC-TOSS Tests
The small strain shear modulus Gmax and the secant shear modulus up to a strain amplitude of 0.1% were obtained from the RC test by measuring the natural frequency of the specimen. The shear modulus from the cyclic TOSS test was calculated for each of the cycles at every tested shear stress level (Figure 5a). The normalized relationship between G/Gmax and is shown in Figure 5b, with the RO model curve that fits all samples. The change in the shear modulus with the increasing number of cycles was examined and is shown in Figure 6a.
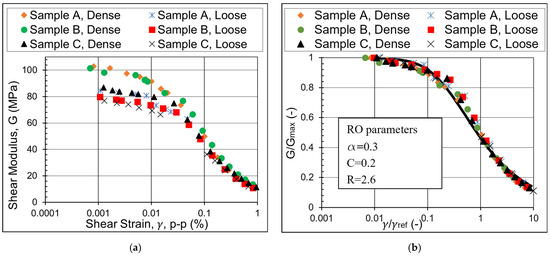
Figure 5.
Shear modulus degradation curves from RC-TOSS tests (a) for all tested samples and (b) samples standardized with RO fit.
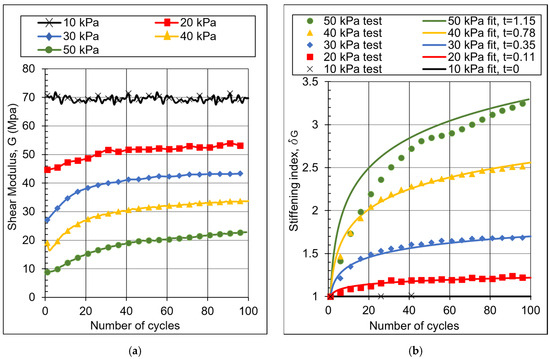
Figure 6.
Effect of number of cycles in Sample A (loose). (a) Shear modulus. (b) Stiffening index.
Therefore, the stiffening index , at a given stress level, is calculated as the ratio of the measured strain of the N-th cycle divided by the peak strain of the first cycle obtained from the initial backbone curve at that stress level. The increase in with the increasing number of cycles for Sample A in a loose state appears in Figure 6b. The stiffening behavior increases with the increasing stress or strain amplitude after exceeding the volumetric shear strain threshold (here, at a stress level of 20 KPa). The soil stiffening index () represents the ratio of secant modulus at cycle N to cycle 1 at the same stress level.
In Equation (5), (t) is the slope of the ( − 1)-log(N) plot and represents a stiffening parameter. Practically, t describes the slope of the relationship:
The deviation of the fit from the measured values at a high stress level (50 kPa in Figure 6b) is attributed to the high number of cycles applied at lower stress levels. However, the test can still show when the increase in stiffness levels off, and Equation (5) gives a good estimate of the stiffness.
At low strain levels (below ) where no stiffening is experienced by the soil due to the cyclic loading, the stiffening index will take the constant value ( = 1) and the stiffening parameter (t = 0). As the stress or strain amplitude increases, the stiffening rate also increases, leading to a rise in the value of t. Since the tests are stress-controlled with gradually increasing stress levels of cyclic loading, loose samples will reach higher strain amplitudes than dense samples at the same stress level due to their lower initial stiffness. Therefore, the stiffening parameter (t) is always higher for loose samples at a prescribed stress level, as shown in Figure 7a.
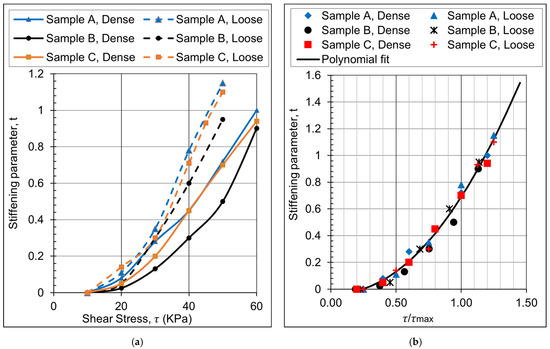
Figure 7.
Stiffening index increase with the increasing number of cycles for Sample A (loose). (a) Non-normalized shear stress–t curves. (b) Normalized shear stress–t curves for all samples.
The stiffening parameter (t) is normalized by plotting the parameter with the normalized shear stress (τ/τmax), as demonstrated in Figure 7b. This relationship produced a good fit for all tested samples with a coefficient of determination (R2) of 0.988, as follows:
Equations (6) and (7) can estimate the dynamic shear modulus of dry Danube sand after any number of cycles and at any shear stress level during a torsional simple shear test.
5. Limitations of the Soil Models and Extended Masing Criteria
When ignoring the impact of the stiffening behavior, the second Masing rule may be correct. However, applying cyclic loading causes a significant change in the size of the hysteresis loops. Some previous researchers suggested changing the scale (2) in the soil models (R-O or H-D) to fit with the test results [33,34,35,36]. Although this technique provided an improved estimate to the problem, it did not match the test outcomes in this investigation when employing the soil models, especially after a high number of cycles. Therefore, a new method should be employed to find the model parameters that would best fit the cyclic TOSS test results.
Simulating the stiffening behavior of cyclically loaded samples leads to further complications in the Masing criteria. We can apply the third rule to the maximum shear stress instead of strain in our stress-controlled tests. However, due to increased stiffness, the TOSS test results showed a considerable drift from the backbone curve during cyclic loading. In Figure 8, after 100 cycles of 40 kPa, the shear stress was increased to 50 kPa. If the third Masing criterion was followed, and after exceeding 40 kPa (point a), the curve would take path A. However, this does not concur with the test results. A proposed solution to this problem is discussed in the next section.
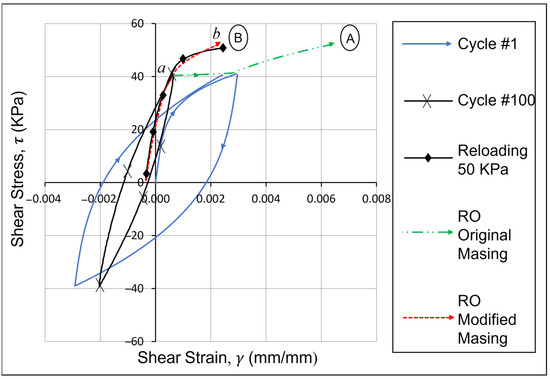
Figure 8.
Third Masing rule limitation.
The irregular behavior of the sample was studied in tests #13 and #14 with the effect of stress offset on the stiffness at the same peak-to-peak shear stress amplitude. The fourth Masing rule applies when neglecting the effect of the stiffening behavior [19]. Stiffening, due to cyclic loading, will cause the current shear stress–strain curve to intersect previous curves under different conditions, as shown in Figure 9. In this test, (a) the sample was loaded for five cycles at a shear stress of 45 kPa. Then, (b) it was loaded for 30 cycles between 40 kPa and −20 kPa (~30 kPa single amplitude), which caused more stiffening in the sample. Finally, (c) when the sample was unloaded to −40 kPa, the turning point that should be used after intersecting with the curve in the fifth cycle could not be identified due to the stiffening caused by the 30 cycles that followed that fifth cycle. Thus, it would be very difficult to introduce a model that can replace the fourth Masing criterion to predict the shear stress–shear strain curve of dry sand subjected to irregular loading patterns due to stiffening behavior.
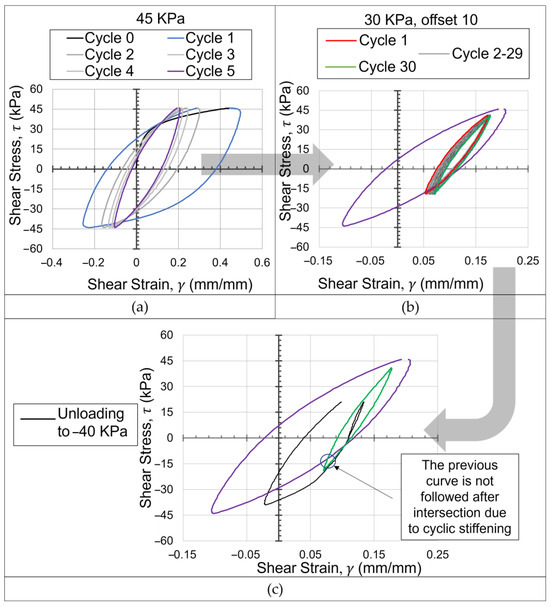
Figure 9.
Fourth Masing rule limitation. (a) Loading for 5 cycles at shear stress 45 Kpa. (b) Loading for 30 cycles between 40 KPa and −20 KPa (~30 KPa single amplitude). (c) Loading to 20 KPa then unloading to −40 KPa.
6. Proposed Soil Models
After determining the Gmax and values for each of the tested samples, the curve-fitting constants in the soil models that fit the TOSS test data were determined. The least square method was used by employing the Solver in Excel to minimize the sum of squared errors between the predicted and measured values of the backbone curve. VBA codes were developed to use the same technique to find the curve-fitting constants for each of the loops in the cyclic TOSS test to simulate stiffening behavior.
The RO model can fit to the backbone curves very well with the chosen curve-fitting constants shown in Table 3 with a coefficient of determination (R2) of > 0.99 for all tested samples, as shown in Figure 10. It is evident that identical curve-fitting constants can be utilized for the same soil specimen under different conditions by changing and Gmax depending on the state of the sample (angle of friction, confining stress and void ratio). The Gmax value can be determined based on the RC measurements or correlations that estimate its value from the void ratio and mean effective stress. Most relevant to this study is the correlation found in [17] after measuring the Gmax of the Danube sand over a wide range of densities and confinement stresses.

Table 3.
Backbone curve-fitting constants for the RO model.
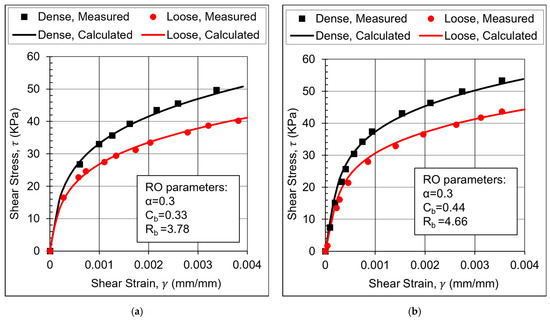
Figure 10.
Backbone curve comparison between TOSS test and Ramberg–Osgood model. (a) Sample A, (b) Sample B.
6.1. Modifications to the Ramberg–Osgood Model
It was found that the curve-fitting constants obtained for the backbone curve should be modified for the unloading–reloading curves for a better fit. While the value of α remained constant throughout the analysis, R and C were reduced for the unloading–reloading curves to better fit the reduced curvature observed for such curves, as demonstrated in Figure 11a.
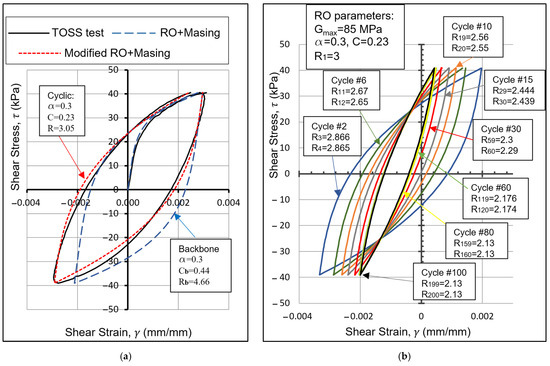
Figure 11.
Modifications to the RO model (a) for second Masing criterion limitations. (b) Modeling of the stiffening behavior.
It was apparent that the sample became stiffer with every half-cycle (unloading/reloading curve). The number of half-cycles in the test denoted by n is equal to the number of load reversals (turning points). By decreasing R after every load reversal during cyclic tests and keeping constant values of α and C in the two-way RO equation, the stiffening behavior of the sample was captured with a better fit of the data compared to when changing the scale factor (2 in the second Masing criterion). When applying the RO model with constant curve-fitting parameters for simulating the cyclic loading, the loops will always return to the same point on the shear stress–shear strain curve. However, by slightly decreasing the value of R after each half-cycle, the loops will start drifting from the first cycle following the stiffening behavior.
The VBA codes implemented the least squares method in Excel to find the optimum value of R that best fits the RO model to the lab curves for each half-cycle in the shear stress–strain plot, as shown in Figure 11b. For each stress level, we can consider a parameter δR that represents the ratio of the curvature coefficient (R) of the n-th half-cycle to the curvature coefficient of the first half-cycle (R1) at the same stress level.
The values of R1 increased with the increasing stress level after exceeding the volumetric shear strain threshold (). By conducting stress-controlled tests, we determined the relationship between the shear stress and curvature coefficient for each sample’s first unloading curve (R1). The relationship has a power form of R1 = a′ ∗ τb′, as shown in Table 4. Moreover, the relationship between R1 and the shear strains can be found at any point based on the known backbone curve from the RO model (Equation (1)). This relationship depends on the soil type and void ratio, which can be obtained separately for each test using a regression analysis.

Table 4.
Two-way modified RO model parameters for cyclic loading.
In Equation (8), b is the slope of the log-log(n) plot. Practically, b describes the negative slope of the relationship as follows:
For Samples A and B with very low percentages of fines, the curvature degradation parameter (b) is constant throughout the test. On the other hand, for Sample C with a content of fines of around 20%, the value of b followed the changes in the cyclic loading stress level, as shown in Figure 12a.
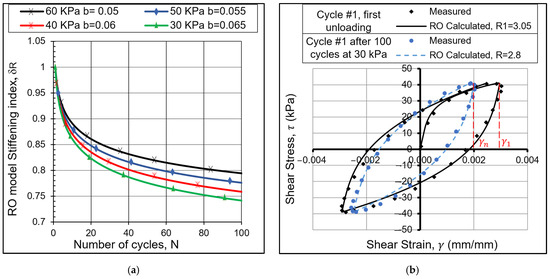
Figure 12.
Modifications to the RO model due to the stiffening behavior. (a) Change in RO model stiffening index with the number of cycles at each stress level for Sample C (dense). (b) Effect of previous cyclic loading in RO model (Sample B, loose).
Below the shear strain volumetric threshold (), = 1, the stiffening behavior is insignificant and b = 0 up to that point. Even though the value of b varies with the shear stress for Sample C, it does not substantially affect the stiffening behavior. Setting b = average constant throughout the test would still yield a good approximation to the problem.
To solve the problem with the third Masing criterion, demonstrated in Figure 8, a modification to the two-way RO equation is presented. In Equation (2), is replaced by R1, and R is reduced to (R/1.3). The “turning point” () is considered as the point where the previous maximum shear stress is exceeded (point a in Figure 8). The curve (ab) will follow this modified equation:
where is a parameter that decreases with the increasing maximum reached shear stress in the test. The relationship between and the maximum reached shear stress can be calculated by isolating from Equation (10) and setting (,) as the last measured point on the backbone curve before leveling off (point (,) in Figure 4a). The curve will aim to reach this point when the turning point is still on the backbone curve. Then, is calculated for each point on the backbone curve, presented as ( in the following equation:
By using Equation (11) after exceeding the shear stress of 40 kPa in the example given in Figure 8, the curve will follow path B. The new path closely agrees with the testing data. The dependency on the number of loops previously applied will be reflected on the curve by the curvature parameter (R) decrease in the equation. cannot have negative values. Moreover, whenever the shear stress exceeds while modeling using this method, will keep a constant positive value that is close to 0.
The stiffness of the cyclically loaded sample at any stress amplitude is affected by the previous cyclic loading at a lower stress level as long as it is above the volumetric threshold. As shown in Figure 12b, the stiffness at a stress level of 40 kPa increased by 55% compared to the backbone curve due to the previous 100 cycles applied at 30 kPa for a loose sample. Previous cycling also decreased the curvature parameter (R) from 3.05 to 2.8. It is challenging to study the effect of the number of previously applied cycles at lower stress levels on the stiffness because of the long time and high effort required for sample preparation and testing using the RC-TOSS device. However, there is a method to find the curvature parameter R in the RO equation based on an equivalent number of half-cycles (neq). The equivalent number of half-cycles (load reversals) depends on the peak strain amplitude when the unloading starts at a higher stress level than the previous cycle ( in Figure 12b). This method allows for the prediction of the shear stress–strain curve, and hence, the stiffness of the sample.
After obtaining R1 and b at each stress level for a sample, we can calculate the peak strain amplitude of each cycle from 1 to 100. By considering the strain amplitude on the backbone curve as the peak strain of the first half-cycle (), we can find a parameter δγ that represents the ratio of peak strain amplitude (γ) of the n-th half-cycle to the peak strain amplitude of the first half-cycle () at the same stress level:
The parameter (k) is the slope of the log-log(n) plot that represents the change in the peak strain amplitude with the number of load reversals. K increases with the increasing stress level, as shown in Table 4. Note that k keeps a constant maximum value when the stress level exceeds .
After any sequence of cyclic loading, and when exceeding the previously reached maximum shear stress, the strain amplitude will result from Equation (10) before the start of the next unloading phase (curve ab in Figure 8). From the strain where the unloading begins, an equivalent number of load reversals at that stress level can be calculated from the following equation:
For instance, in a loose Sample A, 100 cycles at a stress level of 30 kPa were equivalent to 42 cycles at a stress level of 40 kPa. The equivalent number of load reversals (half-cycles) in that case is = 84. The curvature parameter Rn that corresponds to the calculated equivalent number of load reversals at that stress level is calculated as follows:
Subsequently, the cyclic loading will be restarted with , and the curvature coefficient will continue to diminish with the rising number of load reversals.
6.2. Modifications to the Hardin–Drnevich Model
The modified Hardin–Drnevich equation contains only two curve-fitting constants (), making it more straightforward than the Ramberg–Osgood model to simulate the behavior, especially since these parameters can be considered constant regardless of the shear strain amplitude with reasonable accuracy.
Similar to the RO model, and due to the problem discussed and shown in Figure 11a, the parameter for the backbone curve can be higher than for the unloading–reloading curves. In order to simulate the stiffening behavior, increases with the increasing number of half-cycles (n), while m remains constant throughout the analysis.
The modified HD model calculates the stresses based on the given strain history; therefore, to study the stiffening behavior, this model is more conveniently calibrated using a strain-controlled test. However, since our device is only capable of conducting stress-controlled tests and we found that the HD model’s parameters can be considered independent of the strain/stress amplitude (unlike the RO model), we can find the rate of increase in using a stress-controlled test by adjusting for each half-cycle to match the TOSS test results based on the measured shear strains.
For each stress level, we can consider a parameter that represents the ratio of the parameter () of the n-th half-cycle to the curvature coefficient of the first half-cycle () at the same stress level.
where f is the slope of the log-log(n) plot. Practically, f describes the slope of the relationship:
The Hardin–Drnevich curve-fitting constants and the calculated stiffening parameter f for all the samples are shown in Table 5. The cyclic strain-controlled test results based on the HD model, considering the stiffening behavior using the parameters for Soil A in a dense state, appear in Figure 13a.

Table 5.
Backbone and two-way modified HD model parameters for cyclic loading.
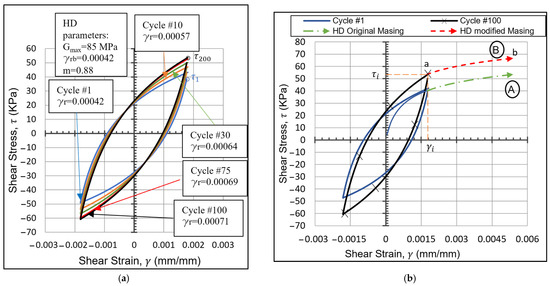
Figure 13.
Modifications to the HD model due to the stiffening behavior. (a) HD model stiffening behavior for a strain-controlled test. (b) Modification to the third extended Masing criterion in HD model.
The same limitation to the third Masing criterion in the RO model described in the previous section applies to the HD model, and a different equation is necessary when exceeding the previously reached maximum shear strain, as shown in Figure 13b. The curve cannot follow the backbone curve (path A) due to stiffening behavior and higher stress levels at the same strain amplitude; instead, it should follow path B.
Figure 13b shows a cyclic strain-controlled test. After exceeding the maximum previously reached strain amplitude, the curve (ab) can follow the same two-way HD equation (Equation (4)) by introducing a factor ( that reduces Gmax while considering the turning point () to be the point where the previous maximum shear strain is exceeded (point a). Therefore, the curve in path B follows Equation (17).
where can be calculated for any strain amplitude from the backbone curve as follows:
where (,) is the last measured point on the backbone curve before leveling off (point (,) in Figure 4a), which is the point that the curve will aim to reach when the turning point is still on the backbone curve. This parameter can be found from the previously calibrated curve-fitting constants, and no extra curve-fitting or calibrations are needed.
The same method proposed for the RO model can be exploited to find the curvature parameter in the HD equation based on an equivalent number of half-cycles that depends on the maximum stress amplitude after any previously applied cyclic loading.
After obtaining and f for each strain level in a specimen, we can find the peak stress amplitude for each loop from 1 to 100 ( to in Figure 13a). By considering the stress amplitude on the backbone curve as the peak stress of the first half-cycle , we can find a parameter that represents the ratio of peak stress amplitude of the n-th half-cycle () to the peak stress amplitude of the first half-cycle () at the same strain level:
The parameter (s) is the slope of the log-log(n) plot that represents the change in the peak stress amplitude with the number of half-cycles. s increases with the increasing strain level, as shown in Table 5. Note that s keeps a constant maximum value when the stress level exceeds .
After any sequence of cyclic loading, and when the previously maximum shear strain is exceeded, the shear stresses will be calculated from Equation (17) (curve ab in Figure 13b) before the start of the next unloading phase. From the calculated stress at the turning point (b), an equivalent number of load reversals at that strain level can be calculated from the following equation:
The curvature parameter corresponding to the calculated equivalent number of load reversals at that strain level is as follows:
7. Conclusions
In this research, the RC-TOSS device is used to test three types of dry sand and examine the stiffening behavior of the samples when subjected to cyclic and irregular loading patterns. The substantial effect of the stiffening behavior on the dynamic properties is presented in two equations, (5) and (6), that can be used to estimate the dynamic shear modulus ( of dry Danube sand after N number of cycles at any shear stress ().
The limitations of the soil models coupled with the Masing criteria commonly used in practice are discussed. Such limitations are a result of neglecting the impact of the cyclic loading on the stiffness of the soil, which is reflected in the shear stress–strain curves. A new method is presented as modifications to the RO and HD models to provide the ability of such models to predict the stiffening behavior.
The RO model is modified by considering different curve-fitting constants (C and R) for the unloading–reloading curves. C and R are lower than the constants of the backbone curve (Cb and Rb). For a better fit with the tested data, R increases with the increasing shear stress level and decreases with the increasing number of cycles to simulate the stiffening behavior. A stiffening parameter (b) is introduced to the model, which represents the slope of the log()-log(n) plot, where is the ratio between the parameter R at the n-th loop (Rn) and the first loop (R1). A method has been introduced to surpass the limitation of the third Masing criteria by continuing the shear stress–strain curve based on the point where the previous maximum shear stress was exceeded. A parameter (k) was introduced to the model to find the change in the parameter (R) due to any previous cyclic loading based on an equivalent number of cycles.
Even though we cannot precisely predict the behavior of soils under irregular (earthquake) loading patterns, we can approximate the loading history as a series of cyclic loadings that gradually increase in intensity until they reach a maximum stress level and then decrease in intensity until they reach zero. This would be similar to the TOSS tests performed in this research. By approximating the stiffening behavior in this way, we can apply the proposed model and modify the Masing criteria to account for stiffening effects when the soil is subjected to intense irregular loading patterns.
Author Contributions
Conceptualization, M.A. and R.R.; methodology, M.A. and R.R.; software, R.R.; investigation, M.A.; resources, R.R.; writing—original draft preparation, M.A.; writing—review and editing, R.R.; visualization, M.A.; supervision, R.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Tempus Foundation and the Stipendium Hungaricum Scholarship, grant number 192800.
Data Availability Statement
The data presented in this study are available upon request from the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Alsirawan, R.; Koch, E. Dynamic Analysis of Geosynthetic-Reinforced Pile-Supported Embankment for a High-Speed Rail. Acta Polytech. Hung. 2023, 21. [Google Scholar] [CrossRef]
- Zhao, K.; Wang, Q.; Zhuang, H.; Li, Z.; Chen, G. A fully coupled flow deformation model for seismic site response analyses of liquefiable marine sediments. Ocean Eng. 2022, 251, 111144. [Google Scholar] [CrossRef]
- Yang, H.-C.; Chou, H.-C.; Hsu, S.-Y.; Chang, W.-K. The influence of boundary conditions on nonlinear time domain site response analysis using LS-DYNA. Comput. Geotech. 2023, 159, 105477. [Google Scholar] [CrossRef]
- Wang, Y.; Liang, J.; Ba, Z. Weak nonlinear seismic response of 3D sedimentary basin using a new masing soil nonlinear model. Soil Dyn. Earthq. Eng. 2023, 171, 107982. [Google Scholar] [CrossRef]
- Ozsarac, V.; Monteiro, R.; Askan, A.; Calvi, G.M. Impact of local site effects on seismic risk assessment of reinforced concrete bridges. Soil Dyn. Earthq. Eng. 2023, 164, 107624. [Google Scholar] [CrossRef]
- Civelekler, E.; Afacan, K.B.; Okur, D.V. Effect of site specific soil characteristics on the nonlinear ground response analysis and comparison of the results with equivalent linear analysis. J. Appl. Geophys. 2024, 220, 105250. [Google Scholar] [CrossRef]
- Vucetic, M.; Vucetic, A.M.M.; Member, A.A. Cyclic threshold shear strains in soils. J. Geotech. Eng. 1994, 120, 2208–2228. [Google Scholar] [CrossRef]
- Anderson, B.A. Deformation Characteristics of Soft, High-Plastic Clays under Dynamic Loading Conditions; Chalmers University of Technology: Gothenburg, Sweden, 1979. [Google Scholar]
- Ladd, R.S. Geotechnical Laboratory Testing Program for Study and Evaluation of Liquefaction Ground Failure Using Stress and Strain Approaches: Heber Road Site, October 15, 1979 Imperial Valley Earthquake; Woodward-Clyde Consultants, Eastern Region: Wayne, NJ, USA, 1982; Volume I–III. [Google Scholar]
- Georgiannou, V.N.; Rampello, S.; Silvestri, F. Static and Dynamic Measurements of Undrained Stiffness of Natural Overconsolidated Clays. In Proceedings of the l0th European Conference on Soil Mechanics and Foundation Engineering, Florence, Italy, 26–30 May 1991; Volume 1, pp. 91–95. [Google Scholar]
- Masing, G. Internal stresses and hardening in brass. In Proceedings of the Second International Congress of Applied Mechanics, Zurich, Switzerland, 12–17 September 1926; pp. 332–335. (In German). [Google Scholar]
- Jennings, P. Earthquake Response of a Yielding Structures. J. Geotech. Eng. Div. 1965, 91, 41–68. [Google Scholar] [CrossRef]
- Constantopoulos, I.V.; Roesset, J.M.; Christian, J.T. A Comparison of Linear and Exact Nonlinear Analyses of Soil Amplification. In Proceedings of the 5th WCEE, Rome, Italy, 25–29 June 1973. [Google Scholar]
- Finn, W.D.L.; Lee, K.W.; Martin, G. An Effective Stress Model for · Liquefaction. J. Geotech-Nical Eng. Div. 1977, 103, 517–533. [Google Scholar] [CrossRef]
- Pyke, R.M. Nonlinear soil models for irregular cyclic loadings. J. Geotech. Eng. Div. 1979, 105, 715–726. [Google Scholar] [CrossRef]
- Ray, R.P.; Woods, R.D.; Ray, A.M.R.P.; Member, A.A. Modulus and damping due to uniform and variable cyclic loading. J. Geotech. Eng. 1988, 114, 861–876. [Google Scholar] [CrossRef]
- Szilvágyi, Z. Dynamic Soil Properties of Danube Sands. Ph.D. Dissertation, Széchenyi István University, Győr, Hungary, 2017. [Google Scholar]
- Valera, J.E.; Berger, E.; Kim, H.-S.; Reaugh, J.E.; Golden, R.D.; Hofmann, R. Study of Nonlinear Effects on One-Dimensional Earthquake Response; Report No. NP-865; Electric Power Research Institute: Palo Alto, CA, USA, 1978. [Google Scholar]
- Ahmad, M.; Ray, R. Comparison between Ramberg-Osgood and Hardin-Drnevich soil models in Midas GTS NX. Pollack Period. 2021, 16, 52–57. [Google Scholar] [CrossRef]
- Ray, R.P. Changes in Shear Modulus and Damping in Cohesionless Soils Due to Repeated Loading. Ph.D. Dissertation, University of Michigan, Washtenaw County, MI, USA, 1984; p. 417. [Google Scholar]
- Silver, M.L.; Seed, H.B. Volume changes in sands during cyclic loading. J. Soil Mech. Found. Div. 1971, 97, 1171–1182. [Google Scholar] [CrossRef]
- Sherif, M.A.; Ishibashi, I. Dynamic shear modulus for dry sands. J. Geotech. Eng. Div. 1976, 102, 1171–1184. [Google Scholar] [CrossRef]
- Hall, J.R.; Richart, F.E. Dissipation of Elastic Wave Energy in Granular Soils. J. Soil Mech. Found. Div. 1963, 89, 27–56. [Google Scholar] [CrossRef]
- Hardin, B.O.; Music, J. Apparatus for Vibration of Soil Specimens during the Triaxial Test, Instruments and Apparatus for Soil and Rock Mechanics; American Society for Testing and Materials: West Conshohocken, PA, USA, 1965. [Google Scholar]
- Drnevich, V.P. Effect of Strain History on the Dynamic Properties of Sand. Ph.D. Dissertation, University of Michigan, Washtenaw County, MI, USA, 1967. [Google Scholar]
- Isenhower, W.M. Torsional Simple Shear/Resonant Column Properties of San Francisco Bay Mud. Master’s Thesis, University of Texas at Austin, Austin, TX, USA, 1979. [Google Scholar]
- Ramberg, W.; Osgood, W.R. Description of Stress Strain Curves by Three Parameters; Technical Note No. 902; National Advisory Committee for Aeronautics: Washington, DC, USA, 1943. [Google Scholar]
- Streeter, V.L.; Wylie, E.B.; Richart, F.E. Soil Motion Computations by Characteristics Method. J. Geotech. Eng. Div. 1974, 100, 247–263. [Google Scholar] [CrossRef]
- Benz, T. Small Strain Stiffness of Soils and Its Numerical Consequences. Ph.D. Dissertation, Universität Stuttgart Institut für Geotechnik, Stuttgart, Germany, 2006; p. 209. [Google Scholar]
- Szilvagyi, Z.; Ray, R.P. Verification of the Ramberg-Osgood Material Model in Midas GTS NX with the Modeling of Torsional Simple Shear Tests. Period. Polytech. Civ. Eng. 2018, 62, 629–635. [Google Scholar] [CrossRef]
- Hardin, B.O.; Drnevich, V.P. Shear modulus and damping in soils: Design equations and curves. J. Soil Mech. Found. Div. 1972, 98, 667–692. [Google Scholar] [CrossRef]
- Darendeli, B. Development of a New Family of Normalized Modulus Reduction and Material Damping Curves. Ph.D. Dissertation, University of Texas at Austin, Austin, TX, USA, 2001; pp. 1–362. [Google Scholar]
- Idriss, I.M.; Dobry, R.; Singh, R.D. Nonlinear behavior of soft clays during cyclic loading. J. Geotech. Eng. Div. 1978, 104, 1427–1447. [Google Scholar] [CrossRef]
- Lin, M.L.; Chen, J.Y. Degradation Behavior of Normally Consolidated Clay under Cyclic Loading Condition; University of Missouri: St. Louis, MO, USA, 1991. [Google Scholar]
- Presti, D.C.F.L.; Cavallaro, A.; Maugeri, M.; Pallara, O.; Ionescu, F. Modelling of Hardening and Degradation Behavior of Clays and Sands During Cyclic Loading. In Proceedings of the 12th Word Conference on Earthquake Engineering, Paper n°. 1849/5/A, Auckland, New Zealand, 30 January–4 February 2000; ISBN 0-9582154-1-3. [Google Scholar]
- Lo Presti, D.C.; Lai, C.G.; Puci, I. ONDA: Computer Code for Nonlinear Seismic Response Analyses of Soil Deposits. J. Geotech. Geoenviron. Eng. 2006, 132, 223–236. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).