Effect of Vehicle Cyclic Loading on the Failure of Canal Embankment on Soft Clay Deposit
Abstract
1. Introduction
2. Previous Studies Related to Embankment Failure on Bangkok Soft Clay Due to Vehicle Loading
2.1. Geotechnical Characteristics of Bangkok Soft Clay
2.2. Shear Strength Characteristics of Bangkok Soft Clay
2.3. Conventional and Dynamic Triaxial Approaches
2.3.1. Consolidated Undrained (CU) Triaxial Test
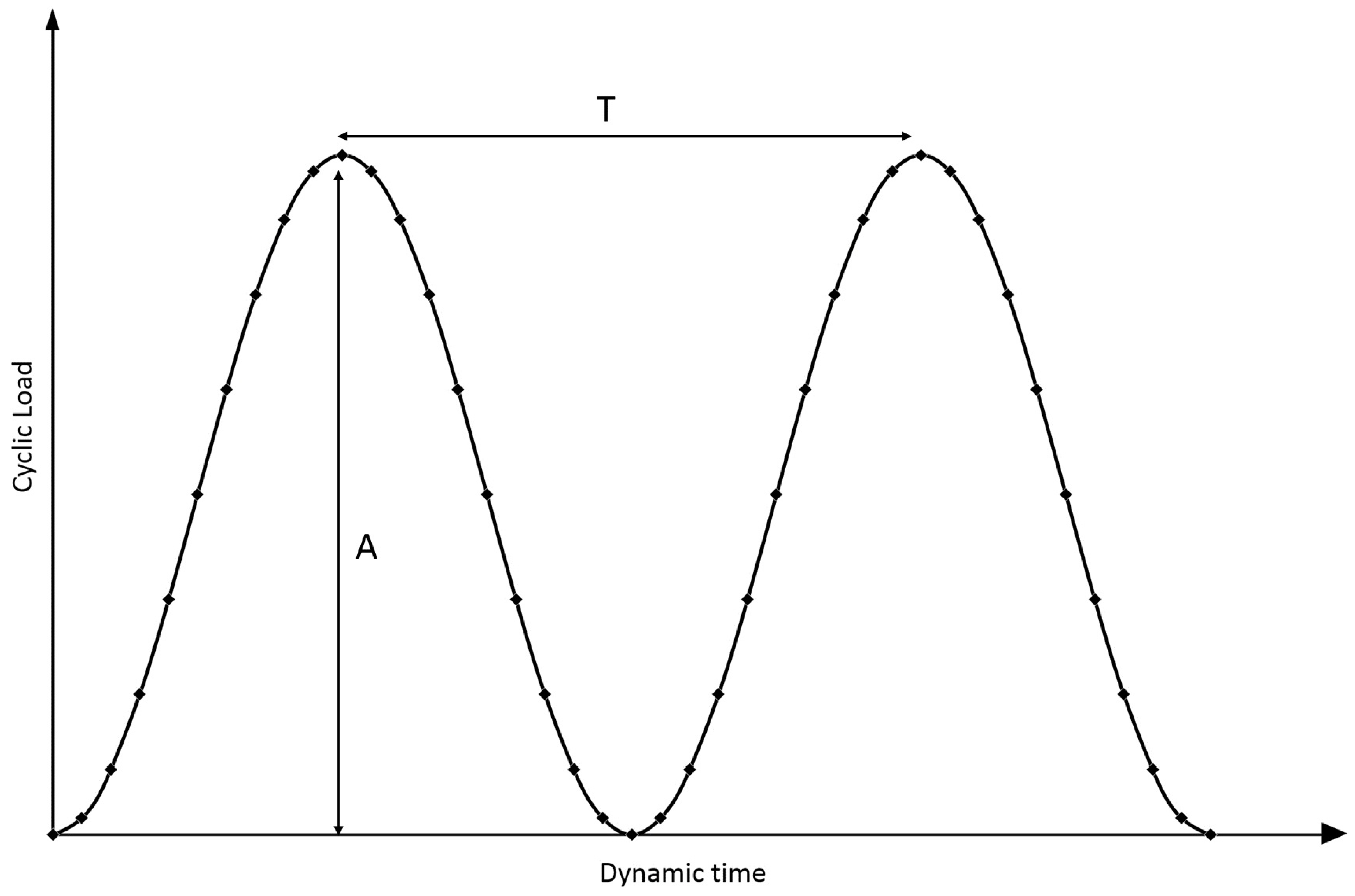
2.3.2. Dynamic Undrained (DU) Triaxial Test
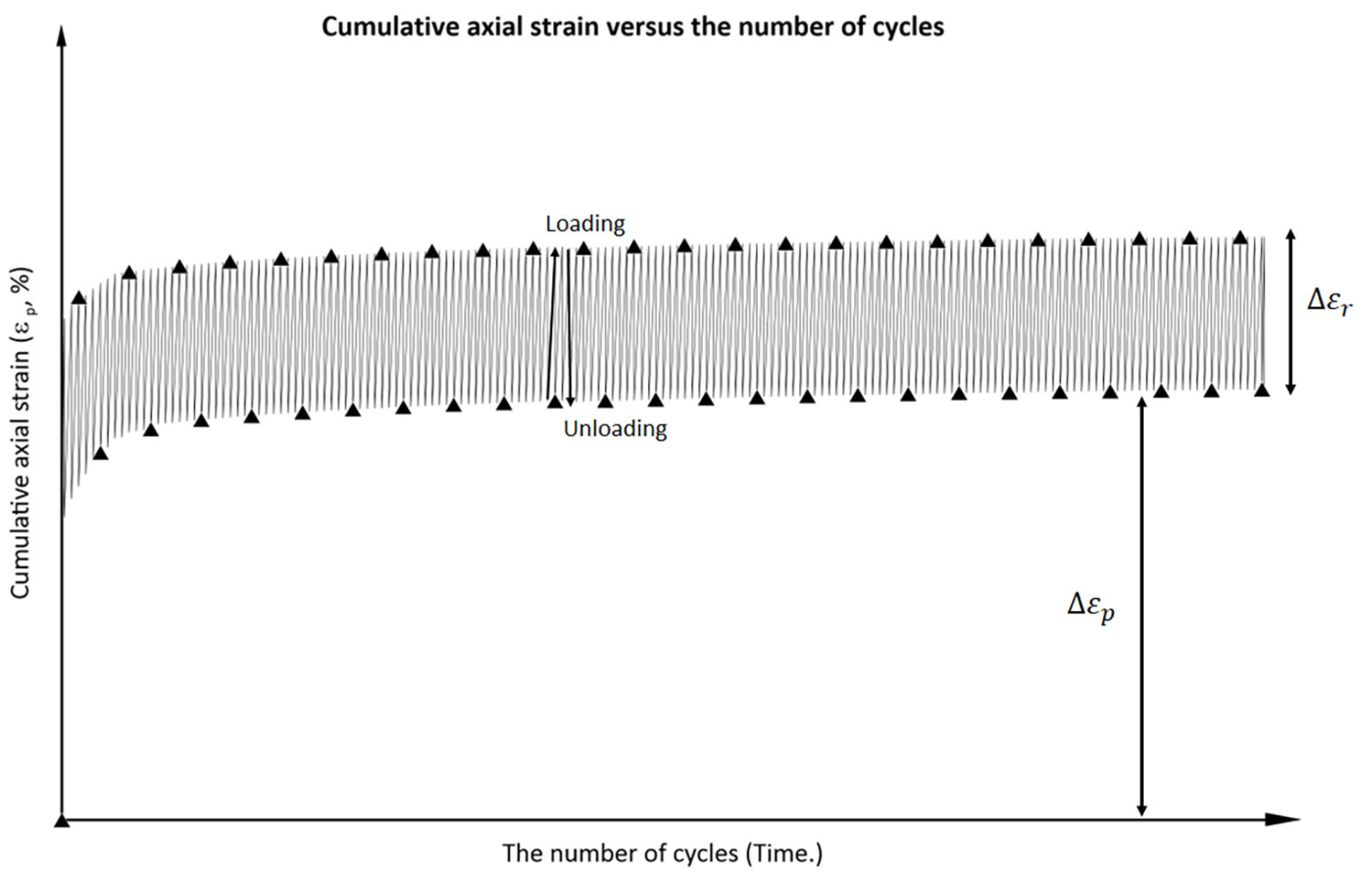
2.4. Previous Study for Embankment Failure Due to Vehicle Loading
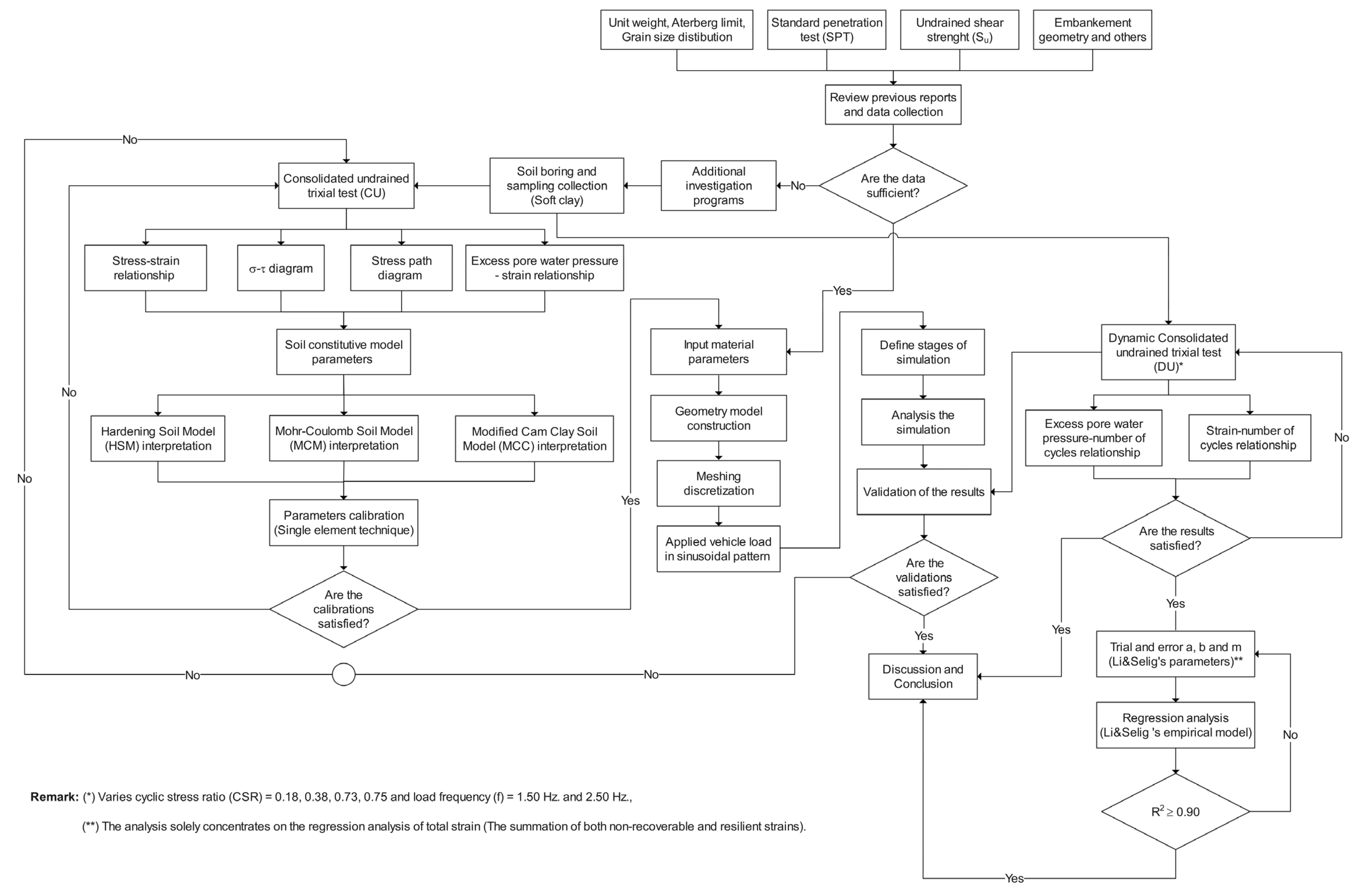
3. Methodology Used in This Study
4. Analyses of Traffic Loading on the Canal Embankment Failure
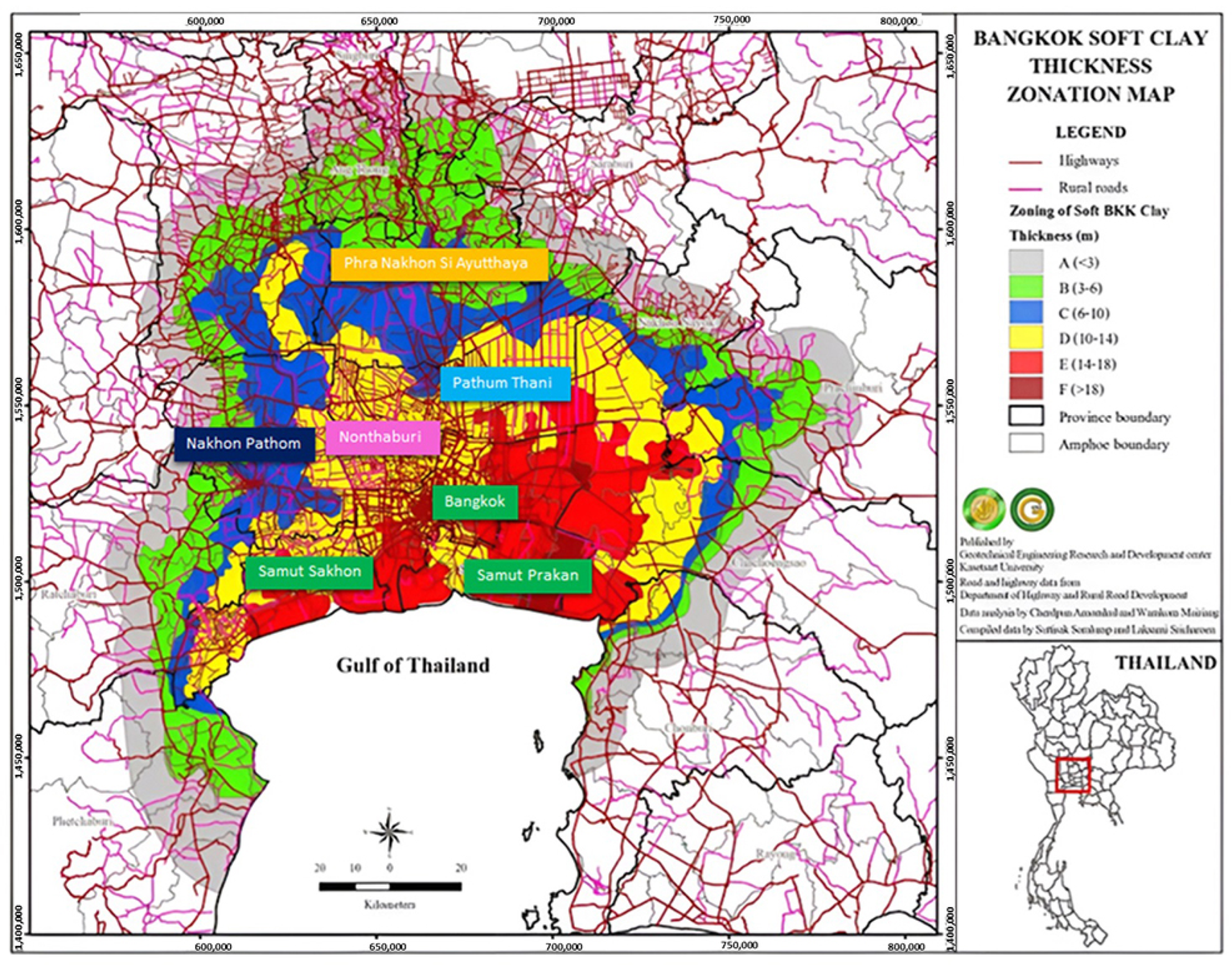
4.1. Site Information and Field Data Collection
4.2. Laboratory Testing
4.2.1. Conventional Consolidated Undrained (CU) Triaxial Tests
4.2.2. Dynamic Consolidated Undrained Triaxial (DU) Tests
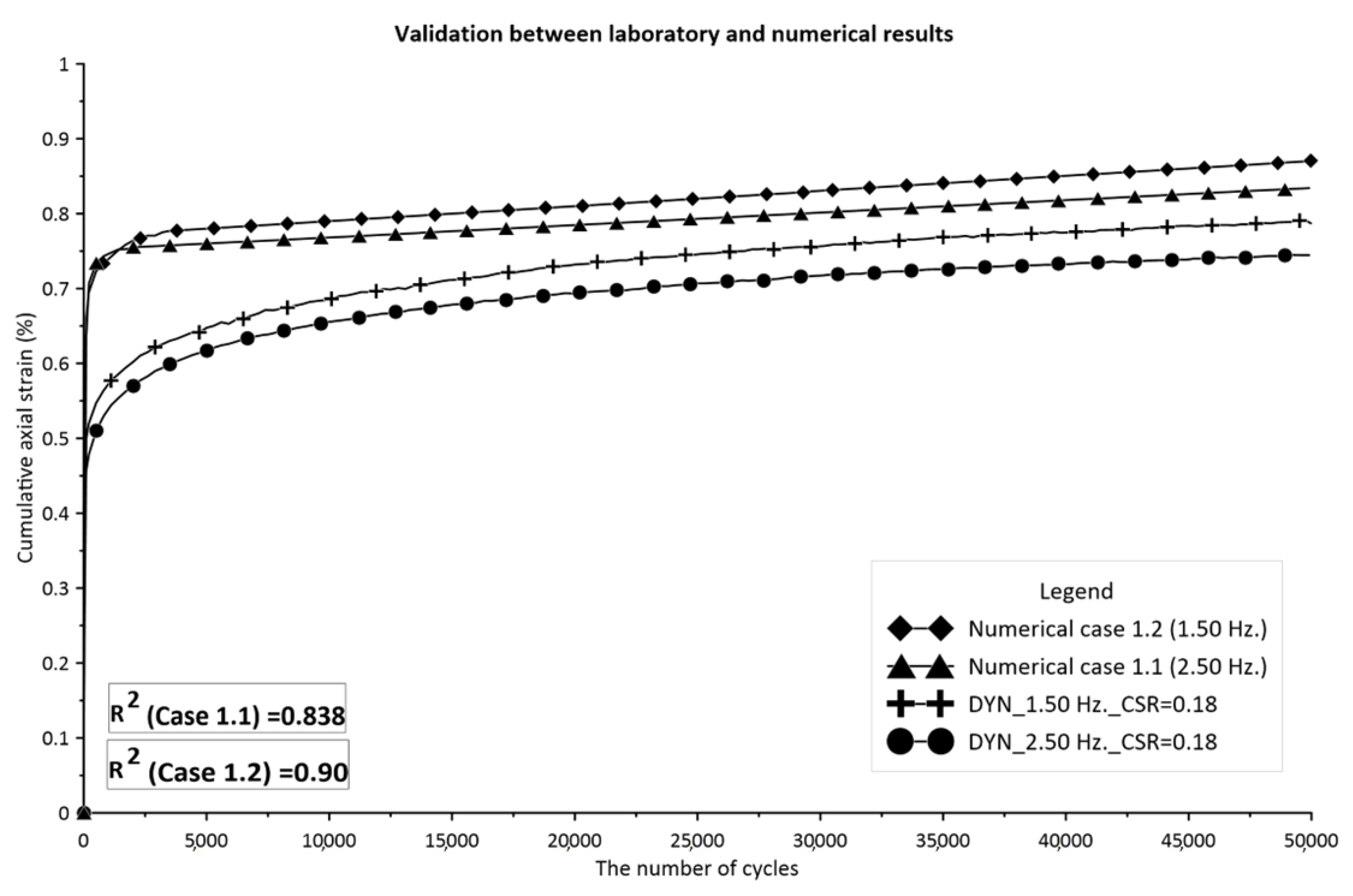
4.2.3. Validation of Cyclic Triaxial Results with the Li and Selig Empirical Model
4.3. Finite Element Numerical Analysis
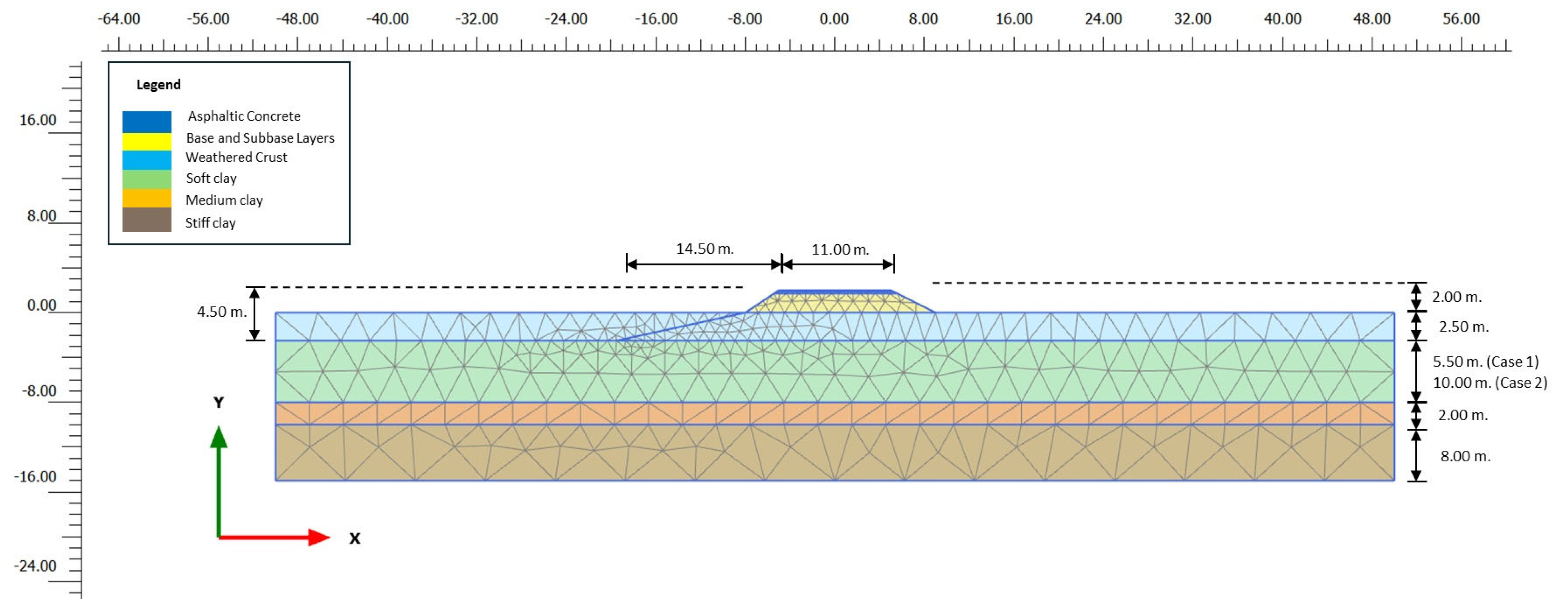
4.3.1. Model Description
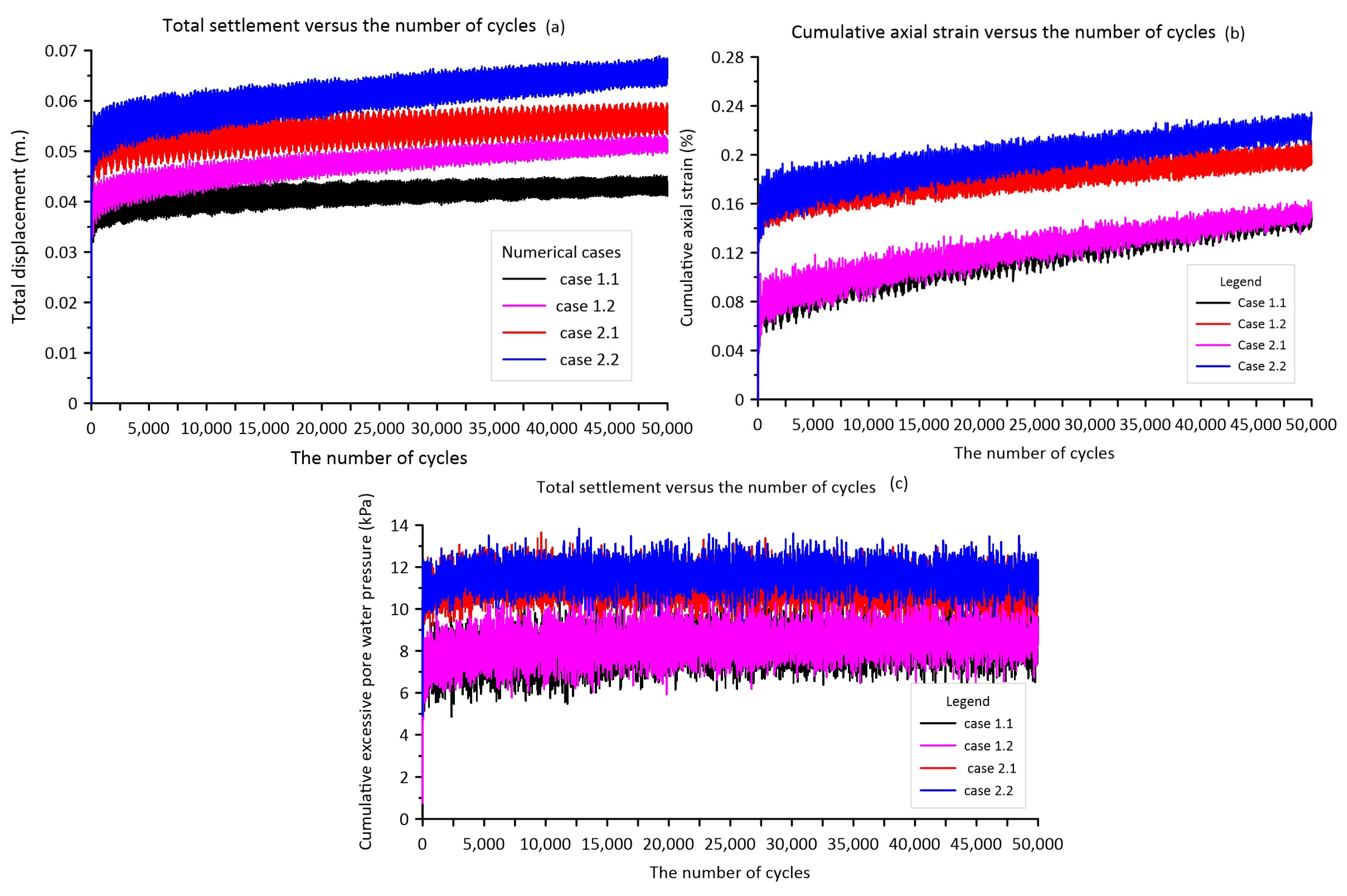
4.3.2. Results of 2-D Cyclic Loading Simulation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bergado, D.T.; Patron, B.C.; Youyongwatana, W.; Chai, J.-C. Yudhbir Reliability-Based Analysis of Embankment on Soft Bangkok Clay. Struct. Saf. 1994, 13, 247–266. [Google Scholar]
- Chaiyaput, S.; Suksawat, T.; Ayawanna, J. Evaluation of the Road Failure Using Resistivity and Screw Driving Sounding Testing Techniques: A Case Study in Ang Thong Province, Thailand. Eng. Fail. Anal. 2021, 121, 105171. [Google Scholar] [CrossRef]
- Nanthannanthan, N. Investigation on Road Failure along the Khlong Song Irrigation Canal, Khlong Song, Pathumthani. Master’s Thesis, Asain Insititute of Technology, Pathum Thani, Thailand, 1998. [Google Scholar]
- Nanthananthan, N.; Dissanayake, D.M.D.O.K.; Phien-Wej, N.; Zou, D.H.S. A Case Study of Road Failure along an Irrigation Canal in Bangkok Plain. Annu. Trans. IESL 2005, 1–9. [Google Scholar]
- Wilson, N.E.; Greenwood, J.R. Pore Pressures and Strains After Repeated Loading of Saturated Clay. Can. Geotech. J. 1974, 11, 269–277. [Google Scholar] [CrossRef]
- Kongpanickul, S. Threshold Stress and Plastic Settlement for High Speed Railway Foundation on Bangkok Soft Clay under Cyclic Loading. Master’s Thesis, Asain Insititute of Technology, Pathum Thani, Thailand, 2019. [Google Scholar]
- Loh, B.H. Behaviour of Railway Track Subgrade under Cyclic Loading. Ph.D. Thesis, Curtin University, Bentley, Australia, 2011. [Google Scholar]
- Li, D.; Selig, E.T. Cumulative Plastic Deformation for Fine-Grained Subgrade Soils. J. Geotech. Engrg. 1996, 122, 1006–1013. [Google Scholar] [CrossRef]
- Likitlersuang, S.; Pholkainuwatra, P.; Chompoorat, T.; Keawsawasvong, S. Numerical modelling of railway embankments for high-speed train constructed on soft soil. J. Geo-Eng. 2018, 13, 149–159. [Google Scholar]
- Wijeyakulasuriya, V.; Balasubramaniam, A.S. A Constitutive Model for Soft Bangkok Clay. In Proceedings of the ICGE Colombo-2015, Sri Lankan Geotechnical Society (SLGS), Colombo, Sri Lanka, 10 August 2015; pp. 1–5. [Google Scholar]
- Cox, J.B. Shear Strength Characteristics of the Recent Marine Clays in South East Asia. JSE Asian Soc. Soil Eng. 1970, 1, 1–27. [Google Scholar]
- Sinsakul, S. Evidence of Quarternary Sea Level Changes in the Coastal Areas of Thailand: A Review. J. Southeast Asian Earth Sci. 1992, 7, 23–37. [Google Scholar] [CrossRef]
- Horpibulsuk, S.; Shibuya, S.; Fuenkajorn, K.; Katkan, W. Assessment of Engineering Properties of Bangkok Clay. Can. Geotech. J. 2007, 44, 173–187. [Google Scholar] [CrossRef]
- Amornkul, C. Engineering Subsoil Database of Lower Central Plain, Thailand. Master’s Thesis, Kasetsart University, Bangkok, Thailand, 2010. [Google Scholar]
- Moh, Z.C.; Nelson, J.D.; Brand, E.W. Strength and Deformation Behavior of Bangkok Clay. In Proceedings of the Seventh International Conference of Soil Mechanics and Foundation Engineering, Mexico City, Mexico, 25–29 August 1969; Volume 1, pp. 287–296. [Google Scholar]
- Balasubramaniam, A.S.; Chaudry, A.R. Deformation and Strength Characteristics of Soft Bangkok Clay. J. Geotech. Engrg. Div. 1978, 104, 1153–1167. [Google Scholar] [CrossRef]
- Matasovic, N.; Vucetic, M. A Pore Pressure Model for Cyclic Straining of Clay. Soils Found. 1992, 32, 156–173. [Google Scholar] [CrossRef] [PubMed]
- Lefebvre, G.; LeBoeuf, D.; Demers, B. Stability Threshold for Cyclic Loading of Saturated Clay. Can. Geotech. J. 1989, 26, 122–131. [Google Scholar] [CrossRef]
- Guo, L.; Wang, J.; Cai, Y.; Liu, H.; Gao, Y.; Sun, H. Undrained Deformation Behavior of Saturated Soft Clay under Long-Term Cyclic Loading. Soil Dyn. Earthq. Eng. 2013, 50, 28–37. [Google Scholar] [CrossRef]
- Guo, L.; Cai, Y.; Jardine, R.J.; Yang, Z.; Wang, J. Undrained Behaviour of Intact Soft Clay under Cyclic Paths That Match Vehicle Loading Conditions. Can. Geotech. J. 2018, 55, 90–106. [Google Scholar] [CrossRef]
- Kongpanickul, S.; Mudden, F.; Chao, K.C.; Saowiang, K. Evaluation of threshold stress for high-speed railway foundation on Bangkok soft clay under cyclic loading. In Proceedings of the 20th International Conference on Soil Mechanics and Geotechnical Engineering, Sydney, Australia, 1–5 May 2022; pp. 1–6. [Google Scholar]
- Indraratna, B.; Singh, M.; Nguyen, T.T.; Leroueil, S.; Abeywickrama, A.; Kelly, R.; Neville, T. Laboratory Study on Subgrade Fluidization under Undrained Cyclic Triaxial Loading. Can. Geotech. J. 2020, 57, 1767–1779. [Google Scholar] [CrossRef]
- Head, K.H. Manual of Soil Laboratory Testing. 3: Effective Stress Tests, 2nd ed.; Pentech Pr: London, UK, 1998; ISBN 978-0-471-97795-7. [Google Scholar]
- Lade, P. Triaxial Testing of Soils; John Wiley & Sons Inc: Hoboken, NJ, USA, 2016; ISBN 978-1-119-10659-3. [Google Scholar]
- D18 Committee. Test Method for Consolidated Undrained Triaxial Compression Test for Cohesive Soils; ASTM International: West Conshohocken, PA, USA, 2020. [Google Scholar]
- Skempton, A.W. The Pore-Pressure Coefficients A and B. Géotechnique 1954, 4, 143–147. [Google Scholar] [CrossRef]
- Bjerrum, L. Problems of Soil Mechanics and Construction on Soft Clays and Structurally Unstable Soils (Collapsible, Expansive and Others). In Proceedings of the Eighth International Conference of Soil Mechanics and Foundation Engineering, Moscow, Russia, 6–11 August 1973; Volume 3, pp. 111–159. [Google Scholar]
- Ladd, C.C.; Foott, R. New Design Procedure for Stability of Soft Clays. J. Geotech. Engrg. Div. 1974, 100, 763–786. [Google Scholar] [CrossRef]
- Seah, T.; Lai, K. Strength and Deformation Behavior of Soft Bangkok Clay. Geotech. Test. J. 2003, 26, 421–431. [Google Scholar] [CrossRef]
- Burton, G.J.; Airey, D.W. Strain Rate Calculation in Consolidated Undrained Triaxial Testing and Implications on Design Strengths. In Proceedings of the 11th Australia—New Zealand Conference on Geomechanics, Melbourne, Australia, 15–18 July 2012; pp. 1063–1068. [Google Scholar]
- Holtz, R.D.; Kovacs, W.D.; Sheahan, T.C. An Introduction to Geotechnical Engineering, 2nd ed.; Pearson: Upper Saddle River, NJ, USA, 2011; ISBN 978-0-13-249634-6. [Google Scholar]
- Das, B.M. Advanced Soil Mechanic, 5th ed.; CRC Press/Taylor & Francis Group: Boca Raton, FL, USA, 2019; ISBN 978-0-8153-7913-3. [Google Scholar]
- Ree, S. Part three: Dynamic Triaxial Testing, GDS. Available online: https://www.gdsinstruments.com/information/white-paper-introduction-to-triaxial-testing (accessed on 10 January 2022).
- Owende, P.M.O.; Hartman, A.M.; Ward, S.M.; Gilchrist, M.D.; O’Mahony, M.J. Minimizing Distress on Flexible Pavements Using Variable Tire Pressure. J. Transp. Eng. 2001, 127, 254–262. [Google Scholar] [CrossRef]
- Lu, Z.; Fang, R.; Yao, H.; Hu, Z.; Liu, J. Evaluation and Analysis of the Traffic Load–Induced Settlement of Roads on Soft Subsoils with Low Embankments. Int. J. Geomech. 2018, 18, 04018043. [Google Scholar] [CrossRef]
- Liu, J.; Xiao, J. Experimental Study on the Stability of Railroad Silt Subgrade with Increasing Train Speed. J. Geotech. Geoenviron. Eng. 2010, 136, 833–841. [Google Scholar] [CrossRef]
- Al-Qadi, I.L.; Elseifi, M.A.; Yoo, P.J.; Dessouky, S.H.; Gibson, N.; Harman, T.; D’Angelo, J.; Petros, K. Accuracy of Current Complex Modulus Selection Procedure from Vehicular Load Pulse: NCHRP Project 1-37A Mechanistic-Empirical Pavement Design Guide. Transp. Res. Rec. 2008, 2087, 81–90. [Google Scholar] [CrossRef]
- Yang, Q.; Ren, Y.; Niu, J.; Cheng, K.; Hu, Y.; Wang, Y. Characteristics of Soft Marine Clay under Cyclic Loading: A Review. Bull Eng. Geol. Environ. 2018, 77, 1027–1046. [Google Scholar] [CrossRef]
- Sævarsdóttir, Þ. Performance Modelling of Flexible Pavements Tested in a Heavy Vehicle Simulator. Ph.D. Thesis, University of Iceland, Reykjavik, Iceland, 2014. [Google Scholar]
- Abusharar, S.W.; Han, J. Two-Dimensional Deep-Seated Slope Stability Analysis of Embankments over Stone Column-Improved Soft Clay. Eng. Geol. 2011, 120, 103–110. [Google Scholar] [CrossRef]
- Huang, Y.H. Slope Stability Analysis by the Limit Equilibrium Method; ASCE Press: Reston, VA, USA, 2014; ISBN 978-0-7844-1288-6. [Google Scholar]
- Selig, E.T.; Waters, J.M. Track Geotechnology and Substructure Management; Thomas Telford Publishing: London, UK, 1994; ISBN 978-0-7277-4982-6. [Google Scholar]
- Eberhardt, E. Geological Engineering Practice I–Rock Engineering (Lecture 10: Deformation Analysis and Elasto-Plastic Yield); Geological Engineering, University of British Columbia: Vancouver, BC, Canada, 2017; Available online: https://www.eoas.ubc.ca/courses/eosc433/lecture-material/eosc433-downloads (accessed on 23 December 2021).
- Ezzat, M. Numerical Analysis in Geotechnical Engineering (Theory and Application, Lecture 5). Available online: https://www.academia.edu/37895341/Lecture_Notes_Numerical_Analysis_In_Geotechnical_Engineering_Theory_and_Application_Part_2_, (accessed on 16 December 2021).
- Potts, D.M.; Zdravković, L. Finite Element Analysis in Geotechnical Engineering. Application; Thomas Telford: London, UK, 2001; ISBN 978-0-7277-2783-1. [Google Scholar]
- PLAXIS Material Models CONNECT Edition V20.02, Bentley Communities. Available online: https://communities.bentley.com/cfs-file/__key/communityserver-wikis-components-files/00-00-00-05-58/0118.PLAXIS3DCE_2D00_V20.02_2D00_3_2D00_Material_2D00_Models.pdf (accessed on 15 October 2020).
- Obrzud, R.F.; Truty, A. The Hardening Soil Model–A Practical Guidebook; Zace Services Ltd.: Lausanne, Switzerland, 2018; pp. 1–127. [Google Scholar]
- Surarak, C.; Likitlersuang, S.; Wanatowski, D.; Balasubramaniam, A.; Oh, E.; Guan, H. Stiffness and Strength Parameters for Hardening Soil Model of Soft and Stiff Bangkok Clays. Soils Found. 2012, 52, 682–697. [Google Scholar] [CrossRef]
- Jamsawang, P. Full Scale Tests on Stiffened Deep Cement Mixing (SDCM) Pile Including 3D Finite Element Simulation. Ph.D. Thesis, Asain Insititute of Technology, Khlong Nueng, Thailand, 2009. [Google Scholar]
- Bergado, D.T. (Ed.) Soft Ground Improvement: In Lowland and Other Environments; ASCE Press: New York, NY, USA, 1996; ISBN 978-0-7844-0151-4. [Google Scholar]
- Viggiani, G. Geotechnical Aspects of Underground Construction in Soft Ground, Proceedings of the 7th International Symposium on Geotechnical Aspects of Underground Construction in Soft Ground, Roma, Italy, 17–19 May 2011; Viggiani, G., Ed.; CRC Press: Boca Raton, FL, USA, 2012; ISBN 978-0-415-68367-8. [Google Scholar]
- Likitlersuang, S.; Surarak, C.; Balasubramaniam, A.; Oh, E.; Syeung Ryull, K.; Wanatowski, D. Duncan-Chang-Parameters for Hyperbolic Stress Strain Behaviour of Soft Bangkok Clay. In Proceedings of the 18th International Conference on Soil Mechanics and Geotechnical Engineering (ICSMGE’13), Paris, France, 2–6 September 2013. [Google Scholar]
- Jongpradist, P.; Detkhong, T.; Youwei, S. Numerical Simulations of Geotechnical Works in Bangkok Subsoil Using Advanced Soil Models Available in Plaxis and through User-Defined Model-GeoStudio|PLAXIS Wiki-GeoStudio|PLAXIS-Bentley Communities. Available online: https://bentleysystems.service-now.com/community?id=kb_article&sys_id=4556a7781bf18a90f3fc5287624bcba1 (accessed on 23 February 2024).
- Saowiang, K. Sea-Level Related Engineering Geology and Intrinsic Compression Behaviour of Bangkok Clays. GEOMATE 2019, 17, 144–153. [Google Scholar] [CrossRef]
- Mulungye, R.M.; Owende, P.M.O.; Mellon, K. Finite Element Modelling of Flexible Pavements on Soft Soil Subgrades. Mater. Des. 2007, 28, 739–756. [Google Scholar] [CrossRef]
- Leonardi, G.; Palamara, R.; Calvarano, L.S. Numerical Analysis of Flexible Pavement Reinforced with Geogrids. In Airfield and Highway Pavements 2017; ASCE: Reston, VA, USA, 2017; pp. 416–427. [Google Scholar]
- Karatağ, H.; Firat, S.; Işik, N.S. Evaluation of Flexible Highway Embankment Under Repetitive Wheel Loading Using Finite Element Analysis. In Proceedings of the 3rd International Sustainable Buildings Symposium (ISBS 2017); Firat, S., Kinuthia, J., Abu-Tair, A., Eds.; Lecture Notes in Civil Engineering; Springer International Publishing: Cham, Switzerland, 2018; Volume 6, pp. 705–716. ISBN 978-3-319-63708-2. [Google Scholar]

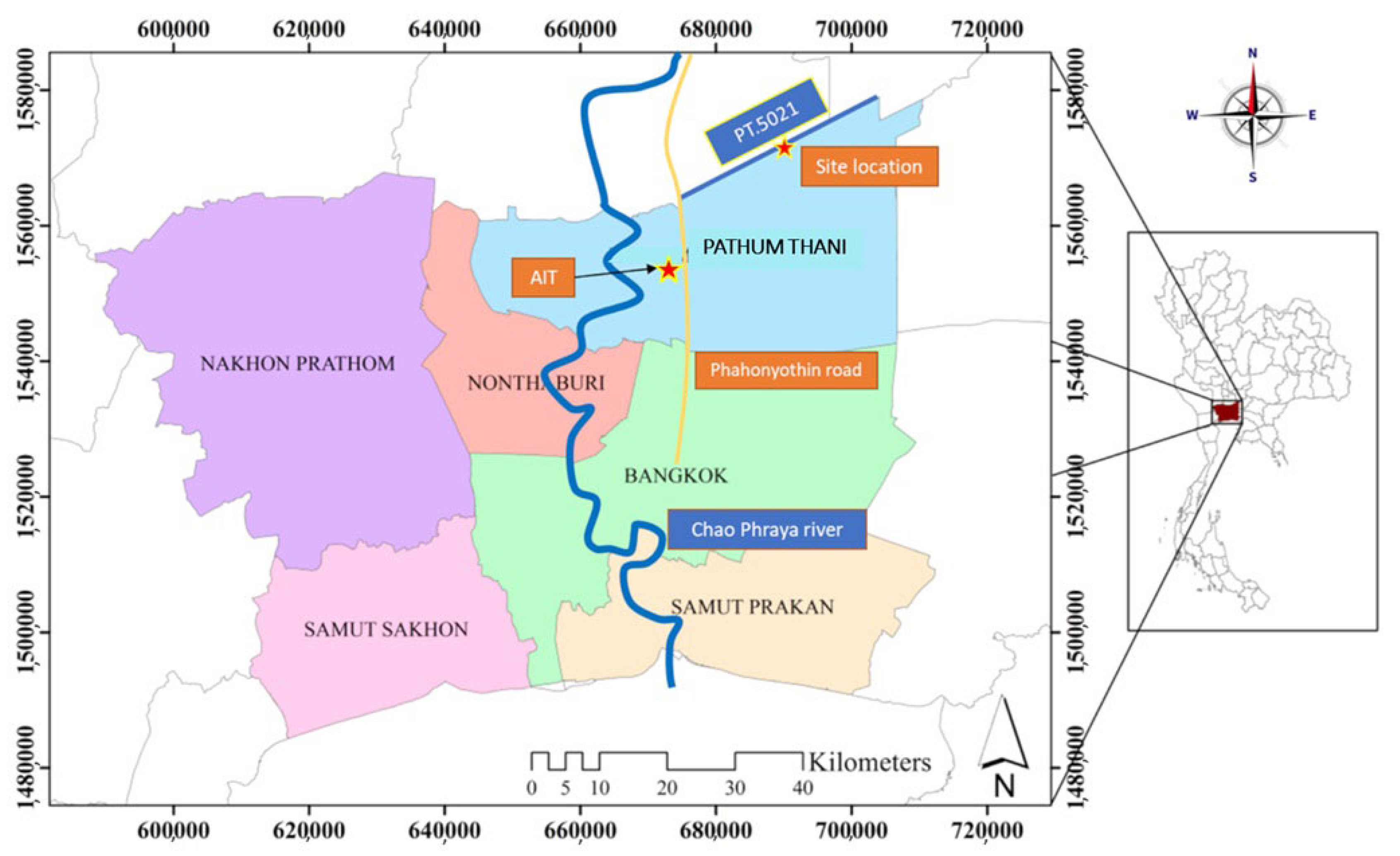
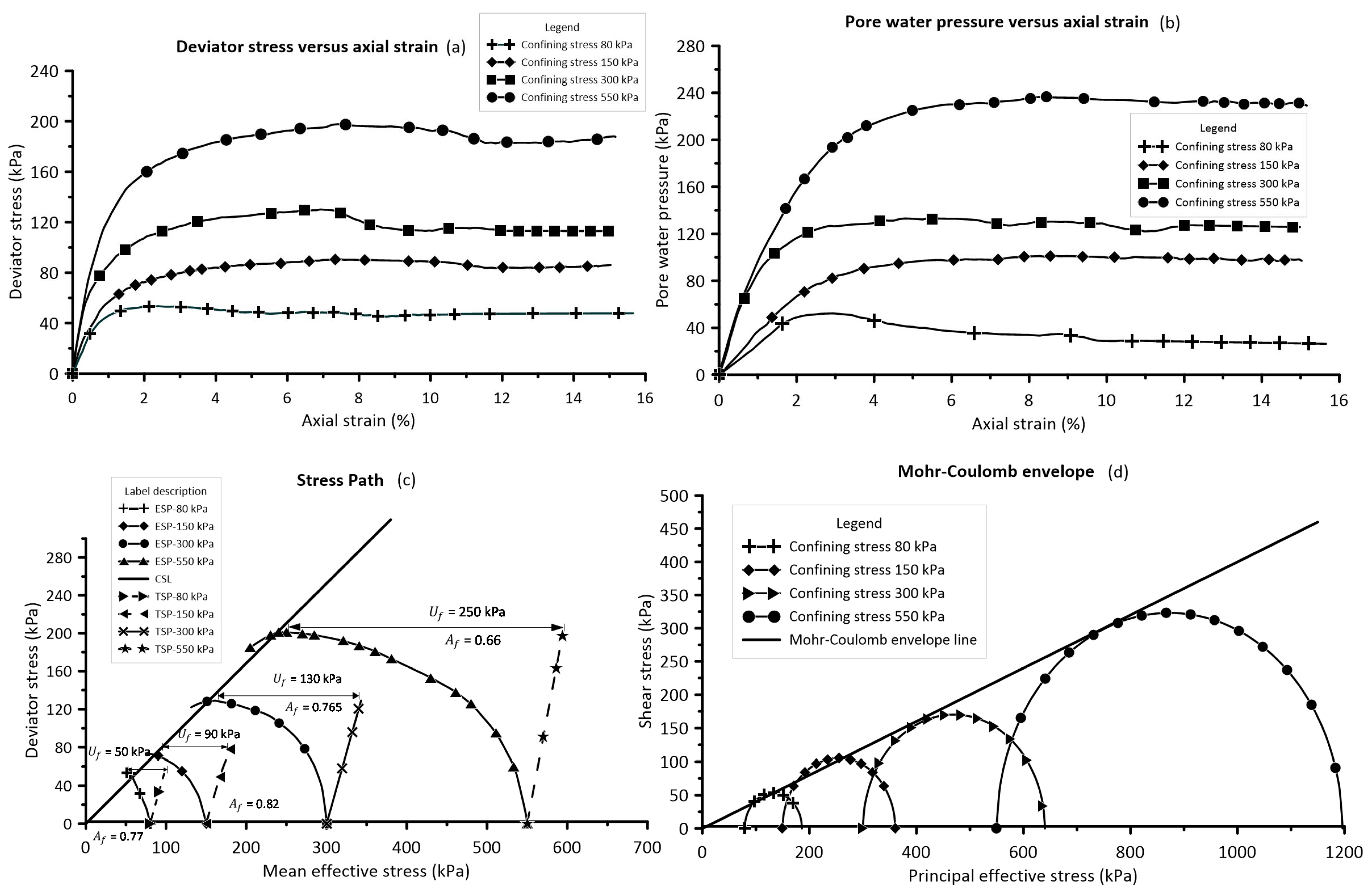
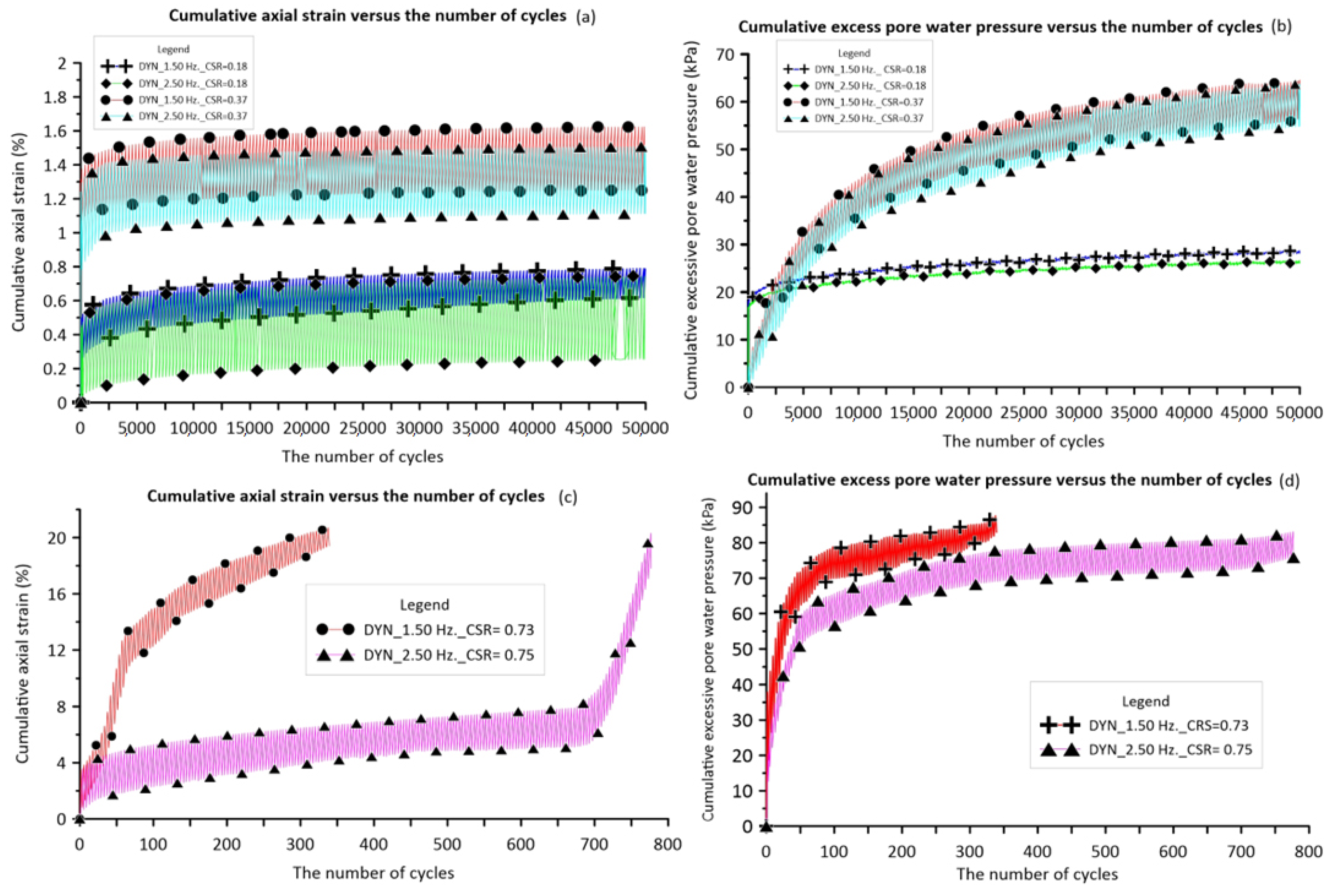
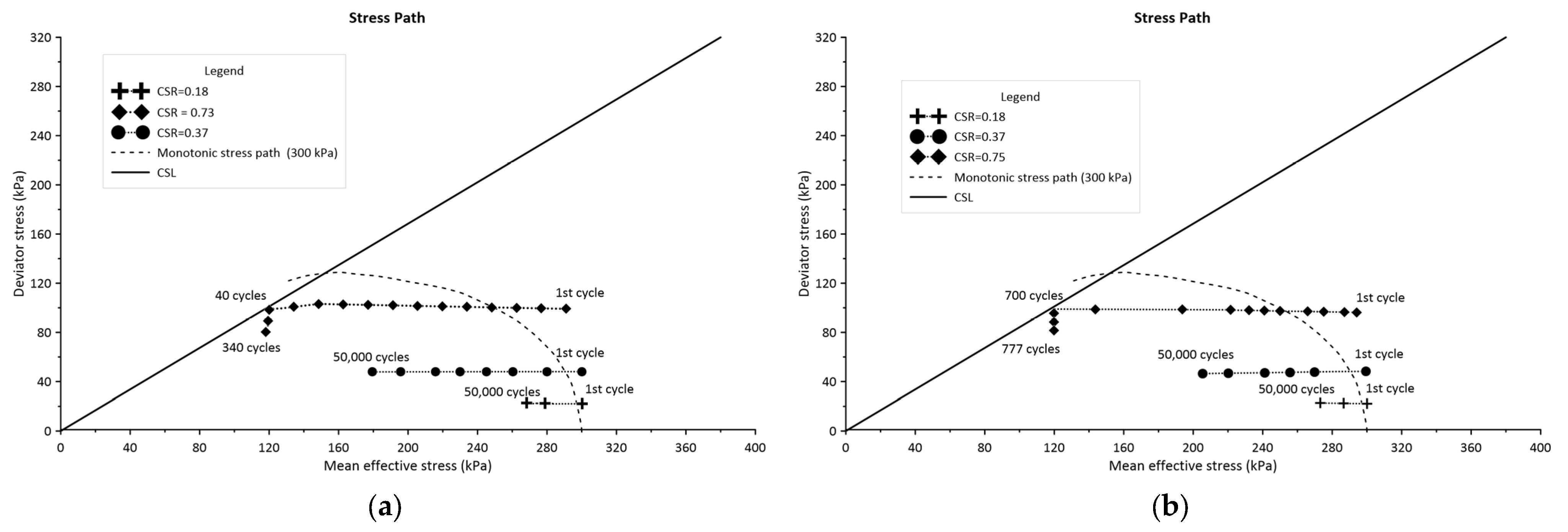



| Soil Type | Series | Test No. | Depth (m) | (kPa) | (kPa) | Targeted OCR | |
|---|---|---|---|---|---|---|---|
| Soft clay | CIU-I | CIU-1 | 5.50 | 80 | 50.50 | 1.58 | 1 |
| CIU-2 | 5.50 | 150 | 50.50 | 2.97 | 1 | ||
| CIU-3 | 5.25 | 300 | 50.50 | 6.15 | 1 | ||
| CIU-4 | 5.25 | 550 | 50.50 | 11.28 | 1 |
| Order | Lists of Parameters | Interpreted Results | Literature Results | Reference |
|---|---|---|---|---|
| 1 | Initial stiffness () | 9000–13,333 (kPa) | 7690–11,300 | Viggiani, 2012 [51] |
| Surarak et al., 2012 [48] | ||||
| 2 | 50% deviatoric stress stiffness () | 10,000–15,000 (kPa) | 4831–10,000 (kPa) | Jongpadit et al., 2010 Surarak et al., 2012 Likitlersuang et al., 2013 Viggiani, 2012 [48,51,52,53] |
| 3 | Frictional angle () | Moh et al., 1969 [15] | ||
| 4 | Cohesion () | 0 (kPa) | 0–17.50 (kPa) | Moh et al., 1969 [15] |
| Order | Description | (kPa) | Load Frequency (Hz.) | The Number of Cycles | |
|---|---|---|---|---|---|
| 1 | Threshold stress | 300 | 0.73–0.75 | 1.50 and 2.50 | - |
| 2 | Simulated vehicle loading | 300 | 0.38 | 50,000 | |
| 3 | 300 | 0.18 | 50,000 |
| Order | CSR | Frequency (Hz.) | a | b | m | Equation | |
|---|---|---|---|---|---|---|---|
| 1 | 0.18 | 1.50 | 2.50 | 0.11 | 1.348 | () | 0.970 |
| 2 | 0.18 | 2.50 | 2.57 | 0.11 | 1.385 | () | 0.981 |
| 3 | 0.37 | 1.50 | 6.40 | 0.042 | 1.820 | () | 0.957 |
| 4 | 0.37 | 2.50 | 6.30 | 0.039 | 1.840 | () | 0.950 |
| Case No. | Frequency (Hz.) | Thickness of Soft Clay (m.) | The Number of Cycles |
|---|---|---|---|
| 1.1 | 2.50 | 5.50 | 50,000 |
| 1.2 | 1.50 | 5.50 | |
| 2.1 | 2.50 | 10.00 | |
| 2.2 | 1.50 | 10.00 |
| Materials | Soil Model | Behavior | MCC. | HSM. and MCM. | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| M | (kPa) | (kPa) | (kPa) | m | (kPa) | (kPa) | (Deg) | |||||
| Asphaltic concrete | LEM | Drain | - | - | - | - | - | - | - | - | - | |
| Granular material | MCM. | Drain | - | - | - | - | - | - | - | 400,000 | 80 | 39 |
| Soft clay | MCC, HSM | Undrain | 0.36 | 0.049 | 0.84 | 7900 | 7100 | 20,800 | 1 | - | 0.05 | 20.25 |
| Weather crust | MCM | - | - | - | - | - | - | - | 15,000 | 40 | 20 | |
| Medium clay | MCM. | - | - | - | - | - | - | - | 12,000 | 10 | 25 | |
| Stiff clay | MCM | - | - | - | - | - | - | - | 20,000 | 10 | 26 | |
| Order | Case No. | FS before Traffic Loading Simulation | FS after Traffic Loading Simulation |
|---|---|---|---|
| 1 | Case 1.1 | 1.655 | 1.284 |
| 2 | Case 1.2 | 1.655 | 1.331 |
| 3 | Case 2.1 | 1.623 | 1.281 |
| 4 | Case 2.2 | 1.623 | 1.308 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chao, K.C.; Kongsung, T.; Saowiang, K. Effect of Vehicle Cyclic Loading on the Failure of Canal Embankment on Soft Clay Deposit. Geosciences 2024, 14, 163. https://doi.org/10.3390/geosciences14060163
Chao KC, Kongsung T, Saowiang K. Effect of Vehicle Cyclic Loading on the Failure of Canal Embankment on Soft Clay Deposit. Geosciences. 2024; 14(6):163. https://doi.org/10.3390/geosciences14060163
Chicago/Turabian StyleChao, Kuo Chieh, Tanawoot Kongsung, and Krit Saowiang. 2024. "Effect of Vehicle Cyclic Loading on the Failure of Canal Embankment on Soft Clay Deposit" Geosciences 14, no. 6: 163. https://doi.org/10.3390/geosciences14060163
APA StyleChao, K. C., Kongsung, T., & Saowiang, K. (2024). Effect of Vehicle Cyclic Loading on the Failure of Canal Embankment on Soft Clay Deposit. Geosciences, 14(6), 163. https://doi.org/10.3390/geosciences14060163









