Physical- and Social-Based Rain Gauges—A Case Study on Urban Flood Detection
Abstract
1. Introduction
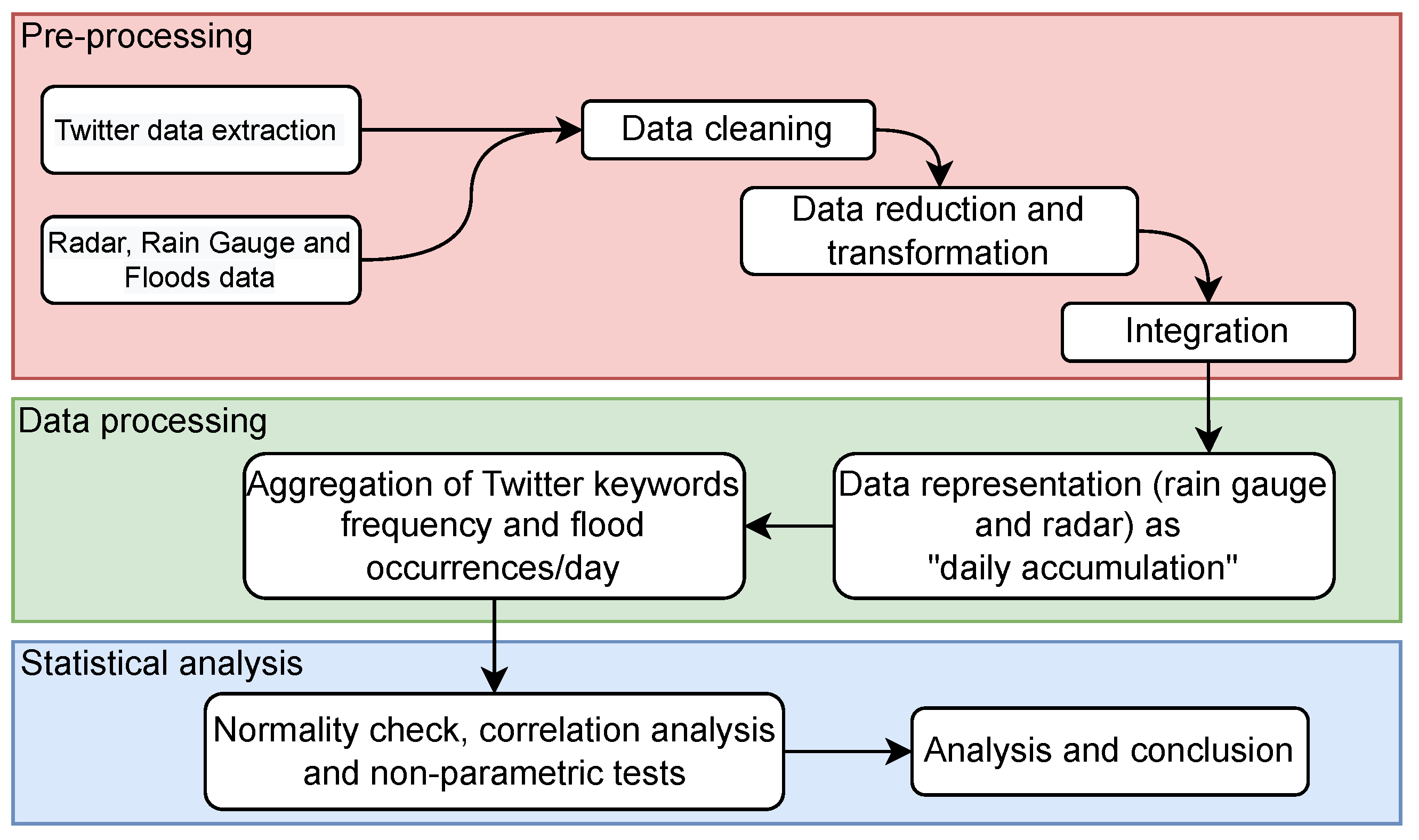
2. Material and Methods
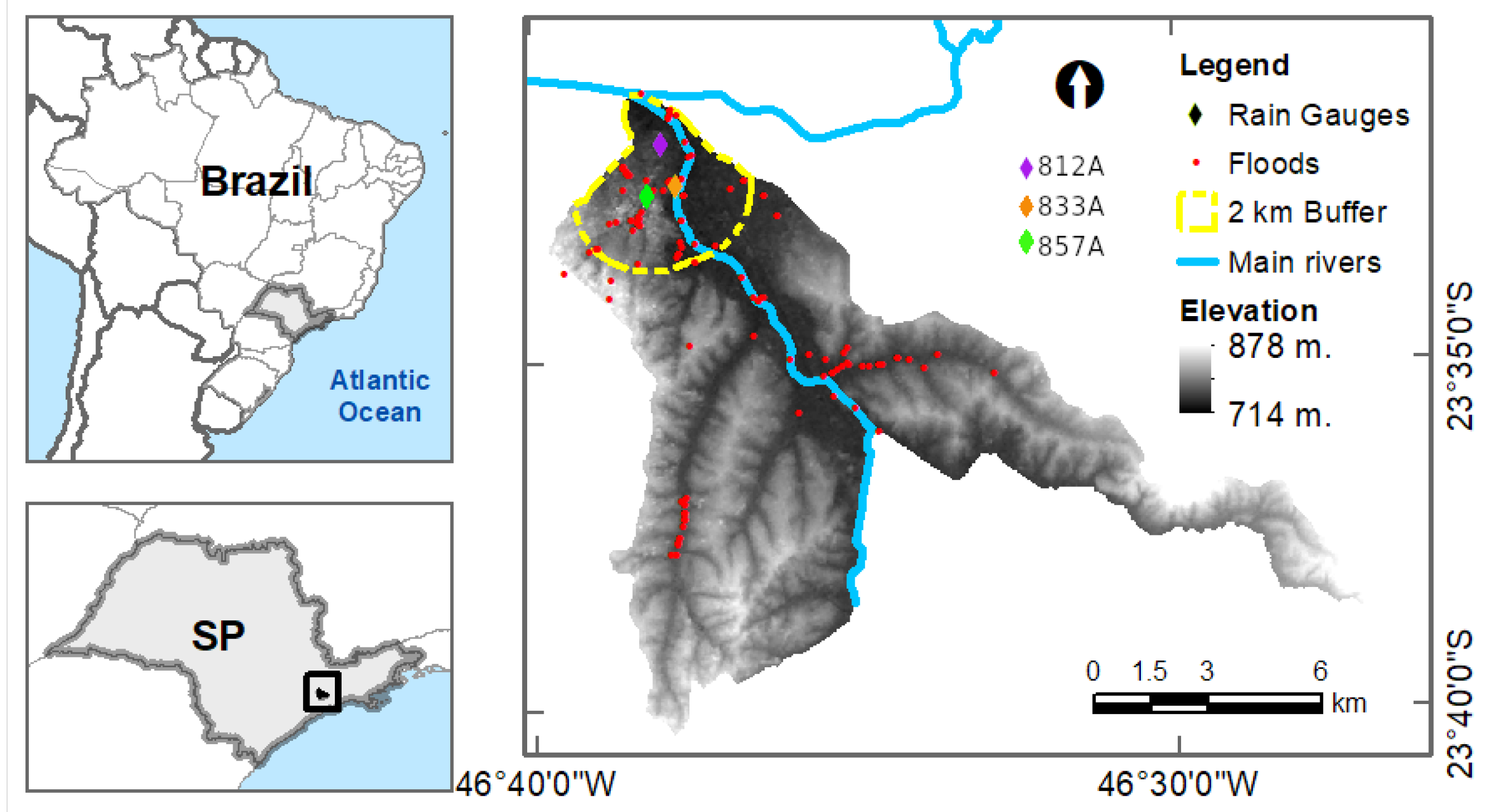
2.1. Study Area: The (Mega) City of São Paulo
2.2. Traditional/Physical and Social Data
2.3. Statistical Tests
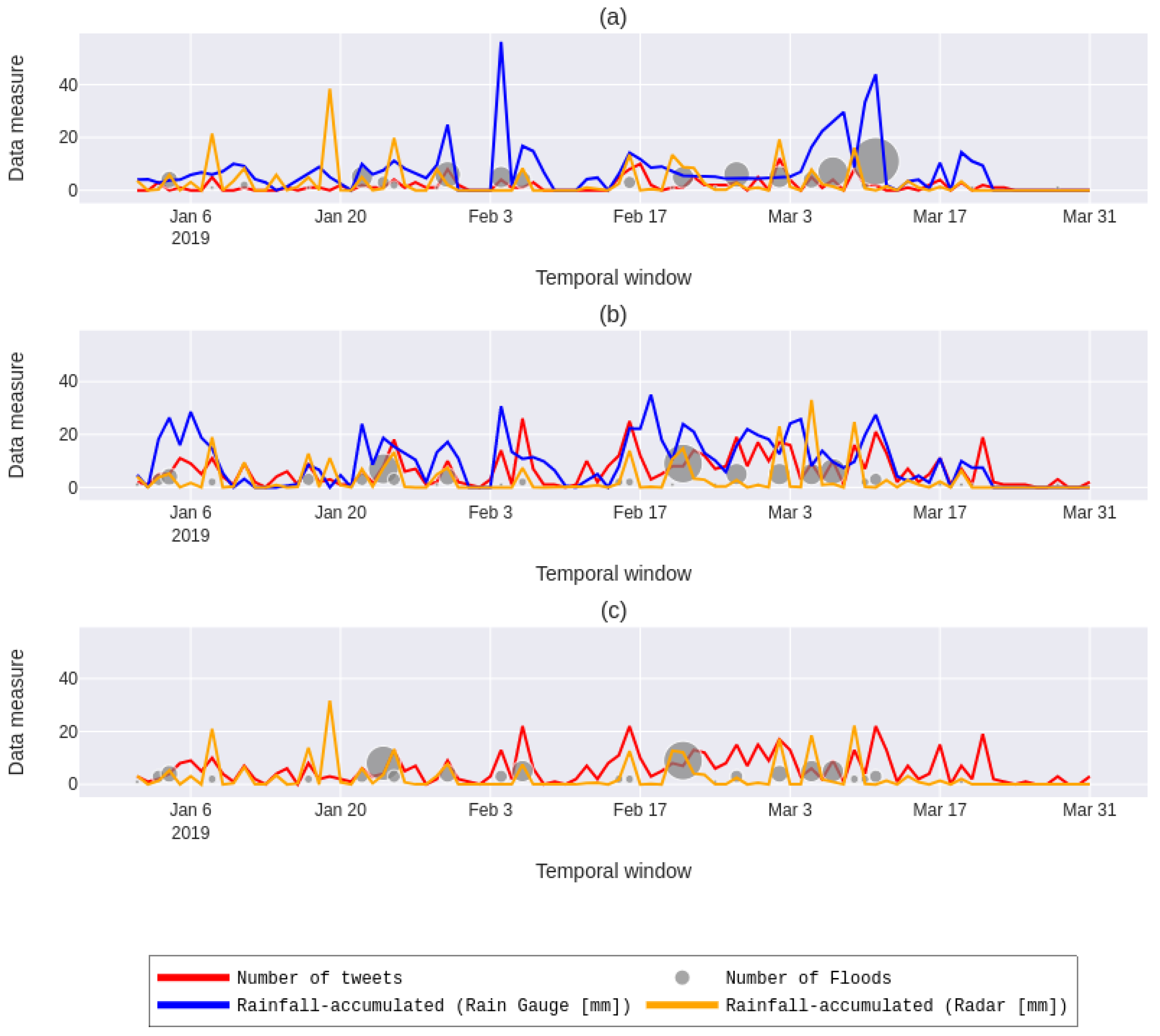
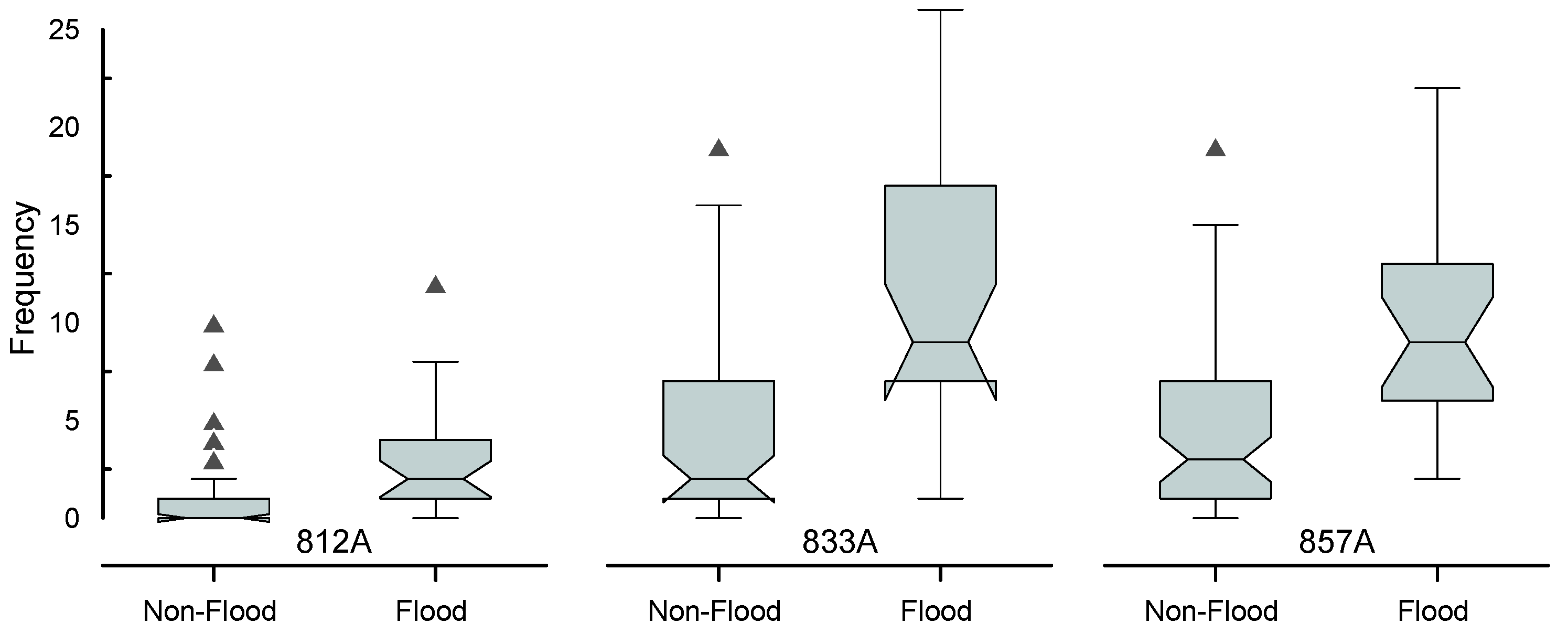
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sachs, J.; Kroll, C.; Lafortune, G.; Fuller, G.; Woelm, F. Sustainable Development Report 2022; Cambridge University Press: Cambridge, UK, 2022. [Google Scholar] [CrossRef]
- United Nations Office for Disaster Risk Reduction (UNISDR). Sendai Framework for Disaster Risk Reduction 2015–2030; United Nations: Geneva, Switzerland, 2015. [Google Scholar]
- Monsoons, A.V.; Cherchi, A.; Turner, A. (Eds.) Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2021; pp. 2193–2204. [Google Scholar] [CrossRef]
- Powell, J.H.; Mustafee, N.; Chen, A.; Hammond, M. System-focused risk identification and assessment for disaster preparedness: Dynamic threat analysis. Eur. J. Oper. Res. 2016, 254, 550–564. [Google Scholar] [CrossRef]
- Khankeh, H.R.; Hosseini, S.H.; Farrokhi, M.; Hosseini, M.A.; Amanat, N. Early warning system models and components in emergency and disaster: A systematic literature review protocol. Syst. Rev. 2019, 8, 315. [Google Scholar] [CrossRef] [PubMed]
- Sullivan, H.T.; Häkkinen, M.T. Disaster preparedness for vulnerable populations: Determining effective strategies for communicating risk, warning, and response. In Proceedings of the Mc Grann Conference Rutgers, New Brunswick, NJ, USA, 21–22 April 2006. [Google Scholar]
- Cools, J.; Innocenti, D.; O’Brien, S. Lessons from flood early warning systems. Environ. Sci. Policy 2016, 58, 117–122. [Google Scholar] [CrossRef]
- Sufri, S.; Dwirahmadi, F.; Phung, D.; Rutherford, S. A systematic review of community engagement (CE) in disaster early warning systems (EWSs). Prog. Disaster Sci. 2020, 5, 100058. [Google Scholar] [CrossRef]
- Horita, F.E.; de Albuquerque, J.P.; Degrossi, L.C.; Mendiondo, E.M.; Ueyama, J. Development of a spatial decision support system for flood risk management in Brazil that combines volunteered geographic information with wireless sensor networks. Comput. Geosci. 2015, 80, 84–94. [Google Scholar] [CrossRef]
- Albuquerque, J.P.; Herfort, B.; Brenning, A.; Zipf, A. A geographic approach for combining social media and authoritative data towards identifying useful information for disaster management. Int. J. Geogr. Inf. Sci. 2015, 29, 667–689. [Google Scholar] [CrossRef]
- Andrade, S.C.; Porto de Albuquerque, J.; Restrepo-Estrada, C.; Westerholt, R.; Rodriguez, C.A.M.; Mendiondo, E.M.; Delbem, A.C.B. The effect of intra-urban mobility flows on the spatial heterogeneity of social media activity: Investigating the response to rainfall events. Int. J. Geogr. Inf. Sci. 2021, 36, 1140–1165. [Google Scholar] [CrossRef]
- Goodchild, M.F. Citizens as sensors: The world of volunteered geography. GeoJournal 2007, 69, 211–221. [Google Scholar] [CrossRef]
- Tully, D.; Rhalibi, A.E.; Carter, C.; Sudirman, S. Hybrid 3D Rendering of Large Map Data for Crisis Management. ISPRS Int. J. Geo-Inf. 2015, 4, 1033–1054. [Google Scholar] [CrossRef]
- Brovelli, M.A.; Minghini, M.; Molinari, M.; Mooney, P. Towards an Automated Comparison of OpenStreetMap with Authoritative Road Datasets. Trans. GIS 2017, 21, 191–206. [Google Scholar] [CrossRef]
- Fonte, C.C.; Martinho, N. Assessing the applicability of OpenStreetMap data to assist the validation of land use/land cover maps. Int. J. Geogr. Inf. Sci. 2017, 31, 2382–2400. [Google Scholar] [CrossRef]
- Lanfranchi, V.; Wrigley, S.N.; Ireson, N.; Wehn, U.; Ciravegna, F. Citizens’ observatories for situation awareness in flooding. In Proceedings of the ISCRAM 2014 Conference Proceedings—11th International Conference on Information Systems for Crisis Response and Management, University Park, PA, USA, 18–21 May 2014; The Pennsylvania State University: University Park, PA, USA, 2014; pp. 145–154. [Google Scholar]
- Degrossi, L.C.; Abe, B.B.; de Albuquerque, J.A.P.; de Mattos Fortes, R.P. Enhancing Usability of a Citizen Observatory Based on User-Centered Design. In Proceedings of the 8th International Conference on Software Development and Technologies for Enhancing Accessibility and Fighting Info-Exclusion, DSAI 2018, New York, NY, USA, 20–22 June 2018; pp. 294–301. [Google Scholar] [CrossRef]
- Yu, M.; Yang, C.; Li, Y. Big data in natural disaster management: A review. Geosciences 2018, 8, 165. [Google Scholar] [CrossRef]
- Huang, Q.; Xiao, Y. Geographic situational awareness: Mining tweets for disaster preparedness, emergency response, impact, and recovery. ISPRS Int. J.-Geo-Inf. 2015, 4, 1549–1568. [Google Scholar] [CrossRef]
- Pereira Filho, A.J.; dos Santos, C.C. Modeling a densely urbanized watershed with an artificial neural network, weather radar and telemetric data. J. Hydrol. 2006, 317, 31–48. [Google Scholar] [CrossRef]
- Schneider, R.M.; Aureliano, L.; Minkel, C.W.; São, P. Encyclopedia Britannica. 2022. Available online: https://www.britannica.com/place/Sao-Paulo-Brazil (accessed on 23 September 2022).
- IBGE. Fundação Instituto Brasileiro de Geografia e Estatística—Panorama of Brazilian Municipalities. 2022. Available online: https://cidades.ibge.gov.br/brasil/sp/sao-paulo/panorama (accessed on 18 September 2022).
- Dickson, E.; Baker, J.L.; Hoornweg, D.; Tiwari, A. Urban Risk Assessments: An Approach for Understanding Disaster and Climate Risk in Cities; World Bank Publications: Washington, DC, USA, 2012. [Google Scholar] [CrossRef]
- Litzinger, P.; Navratil, G.; Sivertun, Å.; Knorr, D. Using weather information to improve route planning. In Bridging the Geographic Information Sciences; Springer: Berlin/Heidelberg, Germany, 2012; pp. 199–214. [Google Scholar]
- CET. Traffic Engineering Company. 2022. Available online: http://www.cetsp.com.br (accessed on 1 September 2022).
- Vale, R.C.C. Quanto Custa a Imobilidade Urbana em São Paulo? Instituto Escolhas POLICY: São Paulo, Brazil, 2020; Available online: https://www.escolhas.org/wp-content/uploads/2020/04/PB_03_Ricardo-Campante_Quanto-custa-a-imobilidade-urbana-em-SP.pdf (accessed on 2 September 2022).
- CGE. São Paulo’s Emergency Management Center—Flood Records in São Paulo, Brazil, in 2019; CGE: São Paulo, Brazil, 2022; Available online: https://www.cgesp.org/v3/alagamentos.jsp (accessed on 24 July 2022).
- Tomás, L.R.; Soares, G.G.; Jorge, A.A.S.; Mendes, J.F.; Freitas, V.L.S.; Santos, L.B.L. Flood risk map from hydrological and mobility data: A case study in São Paulo (Brazil). Trans. GIS 2022, 26, 2341–2365. [Google Scholar] [CrossRef]
- Chacon-Hurtado, J.C.; Alfonso, L.; Solomatine, D.P. Rainfall and streamflow sensor network design: A review of applications, classification, and a proposed framework. Hydrol. Earth Syst. Sci. 2017, 21, 3071–3091. [Google Scholar] [CrossRef]
- Shapiro, S.S.; Wilk, M.B. An analysis of variance test for normality (complete samples). Biometrika 1965, 52, 591–611. [Google Scholar] [CrossRef]
- Anderson, T.W.; Darling, D.A. Asymptotic Theory of Certain “Goodness of Fit” Criteria Based on Stochastic Processes. Ann. Math. Stat. 1952, 23, 193–212. [Google Scholar] [CrossRef]
- Razali, N.M.; Wah, Y.B. Power comparisons of shapiro-wilk, kolmogorov-smirnov, lilliefors and anderson-darling tests. J. Stat. Model. Anal. 2011, 2, 21–33. [Google Scholar]
- Pearson, E.S.; Hartley, H.O. Biometrika Tables for Statisticians. Inc. Stat. 1960, 10, 52–53. [Google Scholar] [CrossRef]
- Stephens, M.A. Goodness of Fit for the Extreme Value Distribution. Biometrika 1977, 64, 583–588. [Google Scholar] [CrossRef]
- Akoglu, H. User’s guide to correlation coefficients. Turk. J. Emerg. Med. 2018, 18, 91–93. [Google Scholar] [CrossRef] [PubMed]
- McKnight, P.E.; Najab, J. Mann-Whitney U Test. Corsini Encycl. Psychol. 2010. [Google Scholar] [CrossRef]
- Zar, J.H. Spearman rank correlation. Encycl. Biostat. 2005, 7. [Google Scholar] [CrossRef]
- Zar, J.H. Significance testing of the Spearman rank correlation coefficient. J. Am. Stat. Assoc. 1972, 67, 578–580. [Google Scholar] [CrossRef]
- Eplett, W.J.R. The Small Sample Distribution of a Mann-Whitney Type Statistic for Circular Data. Ann. Stat. 1979, 7, 446–453. [Google Scholar] [CrossRef]
| R-812A | R-833A | R-857A | RG-812A | RG-833A | ||
|---|---|---|---|---|---|---|
| Statistic | 14.552 | 14.885 | 15.72 | 7.553 | 2.561 | |
| Statistic | 0.541 | 0.567 | 0.558 | 0.688 | 0.903 | |
| p-value | 0.0 | 0.0 | 0.0 | 0.0 | 5.8 |
| 812A | 833A | 857A | |
|---|---|---|---|
| Tweets and floods | |||
| Tweets and radar | ) | () | ) |
| Tweets and rain gauge | — | ||
| Floods and radar | ) | ) | |
| Floods and rain gauge | — | ||
| Radar and rain gauge | — |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hossaki, V.Y.; Seron, W.F.M.S.; Negri, R.G.; Londe, L.R.; Tomás, L.R.; Bacelar, R.B.; Andrade, S.C.; Santos, L.B.L. Physical- and Social-Based Rain Gauges—A Case Study on Urban Flood Detection. Geosciences 2023, 13, 111. https://doi.org/10.3390/geosciences13040111
Hossaki VY, Seron WFMS, Negri RG, Londe LR, Tomás LR, Bacelar RB, Andrade SC, Santos LBL. Physical- and Social-Based Rain Gauges—A Case Study on Urban Flood Detection. Geosciences. 2023; 13(4):111. https://doi.org/10.3390/geosciences13040111
Chicago/Turabian StyleHossaki, Vitor Y., Wilson F. M. S. Seron, Rogério G. Negri, Luciana R. Londe, Lívia R. Tomás, Roberta B. Bacelar, Sidgley C. Andrade, and Leonardo B. L. Santos. 2023. "Physical- and Social-Based Rain Gauges—A Case Study on Urban Flood Detection" Geosciences 13, no. 4: 111. https://doi.org/10.3390/geosciences13040111
APA StyleHossaki, V. Y., Seron, W. F. M. S., Negri, R. G., Londe, L. R., Tomás, L. R., Bacelar, R. B., Andrade, S. C., & Santos, L. B. L. (2023). Physical- and Social-Based Rain Gauges—A Case Study on Urban Flood Detection. Geosciences, 13(4), 111. https://doi.org/10.3390/geosciences13040111








