Maximum Likelihood Instead of Least Squares in Fracture Analysis by Means of a Simple Excel Sheet with VBA Macro
Abstract
:1. Introduction
2. Recalls about Maximum Likelihood Estimation in Linear Regression
3. Methods
3.1. Linear Regression by Means of Maximum Likelihood Estimation

3.2. Different Response to Data Truncation of the Proposed MLE and LSM, in Linear Regression
3.3. The Excel Sheet and VBA Program
- -
- Sub Maximize() and Sub Minimize_LS(): analyze a data set by maximizing or minimizing an object function, which is Log likelihood for the former and residual standard deviation for the latter.
- -
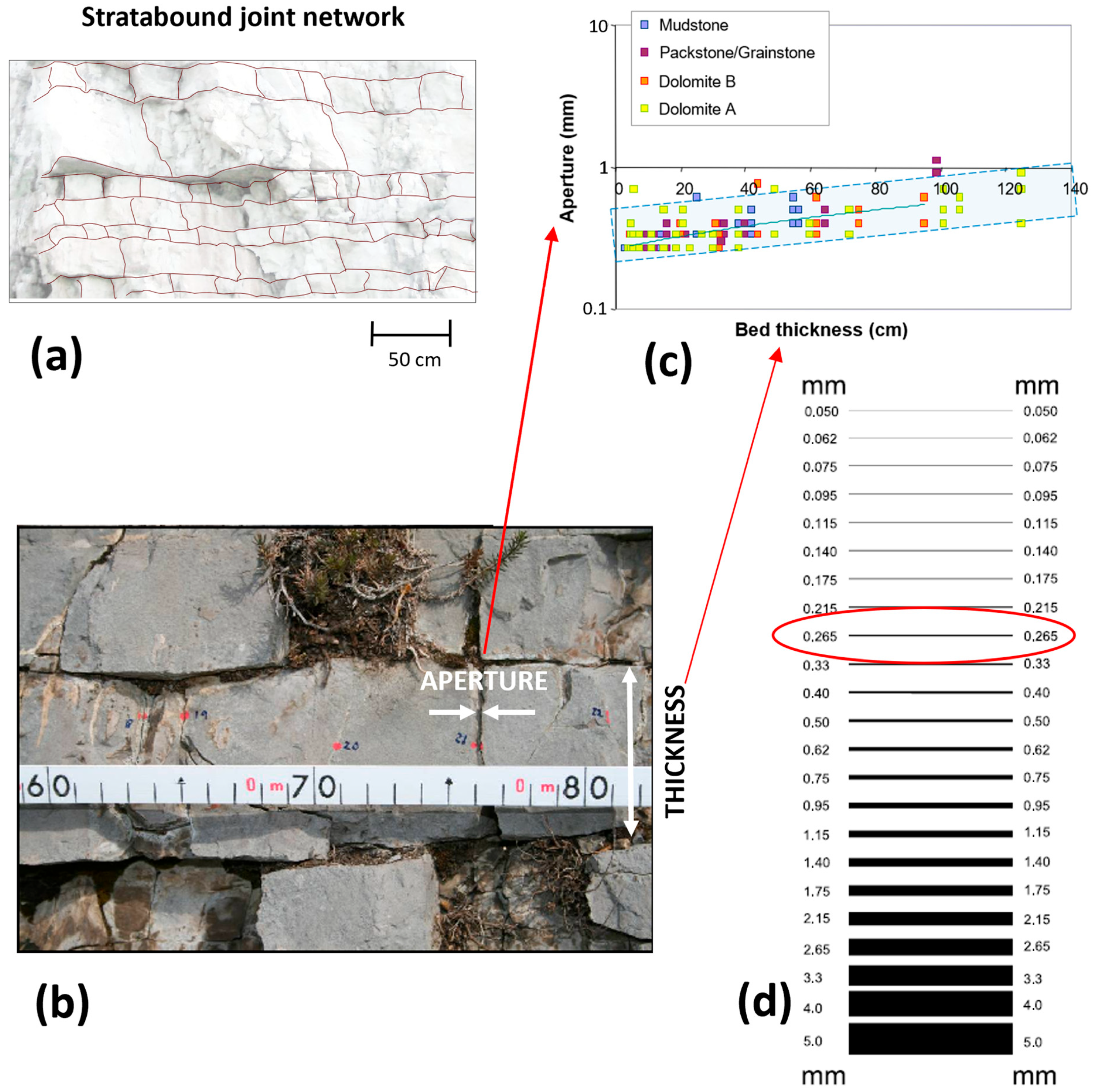
- Sub Simul_Apert_Data(): based on thickness field data (#7 in Figure 2) and assigned (true) values of the parameters m, n and d (#2 in Figure 2), it produces a data set, composed of 35 paired values, by (i) resampling thickness data and (ii) producing a random aperture value for each thickness value (Section 3.3). Then, it identifies which class, and related limits, belongs to (#6).
- -
- Sub Simul_100(): for each triplet of true values m, n and d, it produces 100 simulated data sets and analyzes each one by means of Sub Maximize(), in sheet MLE, and Sub Minimize_LS(), in sheet LSM. Then, it saves the estimated values in columns S, T and U.
- -
- Sub Monte_Carlo(): varies the n true value in the range 0.05–4.75 mm, and for each value produces simulations by calling Sub Simul_100(), then saves the related results (#11) in sheet Results (Figure 3).
3.4. Validation by Means of Monte Carlo Simulation
- Produce a data set, constituted by paired values (aperture, thickness), using the known parameters (m,n,d),
- Simulate data truncation, including all joints belonging to the aperture class of 0.265 mm or lesser, in the 0.265 mm class,
- Analyze by means of MLE,
- Analyze by means of LS,
- Compare known parameter values with estimates by MLE and LS,
- Go back to step #1.
4. Use of the Spreadsheet for Analysis of Field Data
5. Results Discussion
6. Concluding Remarks
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Odling, N.E.; Gillespie, P.; Bourgine, B.; Castaing, C.; Chiles, J.P.; Christensen, N.P.; Fillion, E.; Genter, A.; Olsen, C.; Thrane, L.; et al. Variations in fracture system geometry and their implications for fluid flow in fractured hydrocarbon reservoirs. Pet. Geosci. 1999, 5, 373–384. [Google Scholar] [CrossRef]
- Hooker, J.N.; Laubach, S.E.; Marrett, R. Fracture-aperture size—Frequency, spatial distribution, and growth processes in strata-bounded and non-strata-bounded fractures, Cambrian Mesón Group, NW Argentina. J. Struct. Geol. 2013, 54, 54–71. [Google Scholar] [CrossRef]
- Guerriero, V.; Dati, F.; Giorgioni, M.; Iannace, A.; Mazzoli, S.; Vitale, S. The role of stratabound fractures for fluid migration pathways and storage in well-bedded carbonates. Ital. J. Geosci. 2015, 134, 383–395. [Google Scholar] [CrossRef]
- Guerriero, V.; Mazzoli, S.; Iannace, A.; Vitale, S.; Carravetta, A.; Strauss, C. A permeability model for naturally fractured carbonate reservoirs. Mar. Pet. Geol. 2013, 40, 115–134. [Google Scholar] [CrossRef]
- Camacho Velazquez, R.; Fuentes-Cruz, G.; Vasquez-Cruz, M.A. Decline curve analysis of fractured reservoirs with fractal geometry. SPE Reserv. Eval. Eng. 2008, 11, 606–619. [Google Scholar] [CrossRef]
- Ortega, O.J.; Marrett, R.A.; Laubach, S.E. Scale-independent approach to fracture intensity and average spacing measurement. AAPG Bull. 2006, 90, 193–208. [Google Scholar] [CrossRef]
- Massonnat, G.; Viszkok, J. Hierarchical organization of flow network in fractured carbonate reservoirs: Identification and characterization of key parameters. In Proceedings of the SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 29 September–2 October 2002. [Google Scholar] [CrossRef]
- Ozkan, E.; Brown, M.; Raghavan, R.; Kazemi, H. Comparison of Fractured Horizontal-Well Performance in Conventional and Unconventional Reservoirs. In Proceedings of the SPE Western Regional Meeting, San Jose, CA, USA, 24–26 March 2009. [Google Scholar]
- Yan, B.; Wang, Y.; Killough, J.E. Beyond dual-porosity modeling for the simulation of complex flow mechanisms in shale reservoirs. Comput. Geosci. 2016, 20, 69–91. [Google Scholar] [CrossRef]
- Spagnuolo, A.M.; Wright, S. Analysis of a multiple-porosity model for single-phase flow through naturally fractured porous media. J. Appl. Math. 2003, 2003, 327–364. [Google Scholar] [CrossRef]
- Kim, J.; Sonnenthal, E.L.; Rutqvist, J. Formulation and sequential numerical algorithms of coupled fluid/heat flow and geomechanics for multiple porosity materials. Int. J. Numer. Methods Eng. 2012, 92, 425–456. [Google Scholar] [CrossRef]
- Dreier, J.; Ozkan, E.; Kazemi, H. New Analytical Pressure-Transient Models to Detect and Characterize Reservoirs with Multiple Fracture Systems. In Proceedings of the SPE International Petroleum Conference in Mexico, Puebla, Mexico, 8–9 November 2004. [Google Scholar]
- Al-Ahmadi, H.A.; Wattenbarger, R.A. Triple-porosity Models: One Further Step Towards Capturing Fractured Reservoirs Heterogeneity. In Proceedings of the SPE/DGS Saudi Arabia Section Technical Symposium and Exhibition, Al-Khobar, Saudi Arabia, 15–18 May 2011. [Google Scholar]
- Liu, C.-Q. Exact solution for the compressible flow equations through a medium with triple-porosity. Appl. Math. Mech. 1981, 2, 457–462. [Google Scholar]
- Guerriero, V. 1923–2023: One Century since Formulation of the Effective Stress Principle, the Consolidation Theory and Fluid–Porous-Solid Interaction Models. Geotechnics 2022, 2, 961–988. [Google Scholar] [CrossRef]
- Huang, Q.; Angelier, J. Fracture spacing and its relation to bed thickness. Geol. Mag. 1989, 126, 355–362. [Google Scholar] [CrossRef]
- Narr, W.; Suppe, J. Joint spacing in sedimentary rocks. J. Struct. Geol. 1991, 13, 1037–1048. [Google Scholar] [CrossRef]
- Mandal, N.; Deb, S.K.; Khan, D. Evidence for a nonlinear relationship between fracture spacing and layer thickness. J. Struct. Geol. 1994, 16, 1275–1281. [Google Scholar] [CrossRef]
- Narr, W. Estimating average fracture spacing in subsurface rock. AAPG Bull. 1996, 80, 1565–1586. [Google Scholar] [CrossRef]
- Pascal, C.; Angelier, J.; Cacas, M.-C.; Hancock, P.L. Distribution of joints: Probabilistic modeling and case study near Cardiff (Wales, U.K.). J. Struct. Geol. 1997, 19, 1273–1284. [Google Scholar] [CrossRef]
- Wu, H.; Pollard, D.D. An experimental study of the relationship between joint spacing and layer thickness. J. Struct. Geol. 1995, 17, 887–905. [Google Scholar] [CrossRef]
- Bai, T.; Pollard, D.D. Fracture spacing in layered rocks: A new explanation based on the stress transition. J. Struct. Geol. 2000, 22, 43–57. [Google Scholar] [CrossRef]
- Guerriero, V.; Mazzoli, S. Theory of Effective Stress in Soil and Rock and Implications for Fracturing Processes: A Review. Geosciences 2021, 11, 119. [Google Scholar] [CrossRef]
- Marrett, R.; Ortega, O.J.; Kelsey, C.M. Extent of power-law scaling for natural fractures in rock. Geology 1999, 27, 799–802. [Google Scholar] [CrossRef]
- Gale, J.F.W.; Laubach, S.E.; Marrett, R.A.; Olson, J.E.; Holder, J.; Reed, R.M. Predicting and characterizing fractures in dolostone reservoirs: Using the link between diagenesis and fracturing. Geol. Soc. Lond. Spec. Publ. 2004, 235, 177–192. [Google Scholar] [CrossRef]
- Ortega, O.J.; Gale, J.F.; Marrett, R.A. Quantifying diagenetic and stratigraphic controls on fracture intensity in platform carbonates: An example from the Sierra Madre Oriental, northeast Mexico. J. Struct. Geol. 2010, 32, 1943–1959. [Google Scholar] [CrossRef]
- Hooker, J.N.; Gale, J.F.W.; Gomez, L.A.; Laubach, S.E.; Marrett, R.; Reed, R.M. Aperture-size scaling variations in a low-strain opening-mode fracture set, Cozzette Sandstone, Colorado. J. Struct. Geol. 2009, 31, 707–718. [Google Scholar] [CrossRef]
- Hooker, J.N.; Gomez, L.A.; Laubach, S.E.; Gale, J.F.W.; Marrett, R. Effects of diagenesis (cement precipitation) during fracture opening on fracture aperture-size scaling in carbonate rocks. In Advances in Carbonate Exploration and Reservoir Analysis: Geological Society; Garland, J., Laubach, S., Neilson, J., Whidden, K.J., Eds.; Special Publication: London, UK, 2012; Volume 370, pp. 187–206. [Google Scholar]
- Hooker, J.N.; Laubach, S.E.; Marrett, R. A universal power-law scaling exponent for fracture apertures in sandstone. Geol. Soc. Am. Bull. 2014, 126, 1340–1362. [Google Scholar] [CrossRef]
- Guerriero, V.; Iannace, A.; Mazzoli, S.; Parente, M.; Vitale, S.; Giorgioni, M. Quantifying uncertainties in multi-scale studies of fractured reservoir analogues: Implemented statistical analysis of scan line data from carbonate rocks. J. Struct. Geol. 2010, 32, 1271–1278. [Google Scholar] [CrossRef]
- Guerriero, V.; Vitale, S.; Ciarcia, S.; Mazzoli, S. Improved statistical multi-scale analysis of fractured reservoir analogues. Tectonophysics 2011, 504, 14–24. [Google Scholar] [CrossRef]
- Rizzo, R.E.; Healy, D.; De Siena, L. Benefits of maximum likelihood estimators for fracture attribute analysis: Implications for permeability and up-scaling. J. Struct. Geol. 2017, 95, 17–31. [Google Scholar] [CrossRef]
- Giorgioni, M.; Iannace, A.; D’Amore, M.; Dati, F.; Galluccio, L.; Guerriero, V.; Mazzoli, S.; Parente, M.; Strauss, C.; Vitale, S. Impact of early dolomitization on multi-scale petrophysical heterogeneities and fracture intensity of low-porosity platform carbonates (Albian-Cenomanian, southern Apennines, Italy). Mar. Pet. Geol. 2016, 73, 462–478. [Google Scholar] [CrossRef]
- Iannace, A.; Galluccio, L.; Guerriero, V.; Mazzoli, S.; Parente, M.; Vitale, S. Dolomites within the Mesozoic carbonates of Southern Apennines (Italy): Genetic models and reservoir implications. Rend. Online Soc. Geol. Ital. 2008, 2, 109–114. [Google Scholar]
- Vitale, S.; Dati, F.; Mazzoli, S.; Ciarcia, S.; Guerriero, V.; Iannace, A. Modes and timing of fracture network development in poly-deformed carbonate reservoir analogues, Mt. Chianello, southern Italy. J. Struct. Geol. 2012, 34, 223–235. [Google Scholar] [CrossRef]
- Dekking, F.M.; Kraaikamp, C.; Lopuhaa, H.P.; Meester, L.E. A Modern Introduction to Probability and Statistics: Understanding Why and How; Springer: London, UK, 2005. [Google Scholar]
- Myung, I.J. Tutorial on maximum likelihood estimation. J. Math. Psychol. 2003, 47, 90–100. [Google Scholar] [CrossRef]
- Da Silva, S.L.E.F.; dos Santos Lima, G.Z.; Volpe, E.V.; de Araújo, J.M.; Corso, G. Robust approaches for inverse problems based on Tsallis and Kaniadakis generalised statistics. Eur. Phys. J. Plus 2021, 136, 518. [Google Scholar] [CrossRef]
- Chambers, J.; Cleveland, W.; Kleiner, B.; Tukey, P. Graphical Methods for Data Analysis; Chapter 6; Wadsworth: Belmont, CA, USA, 1983. [Google Scholar]
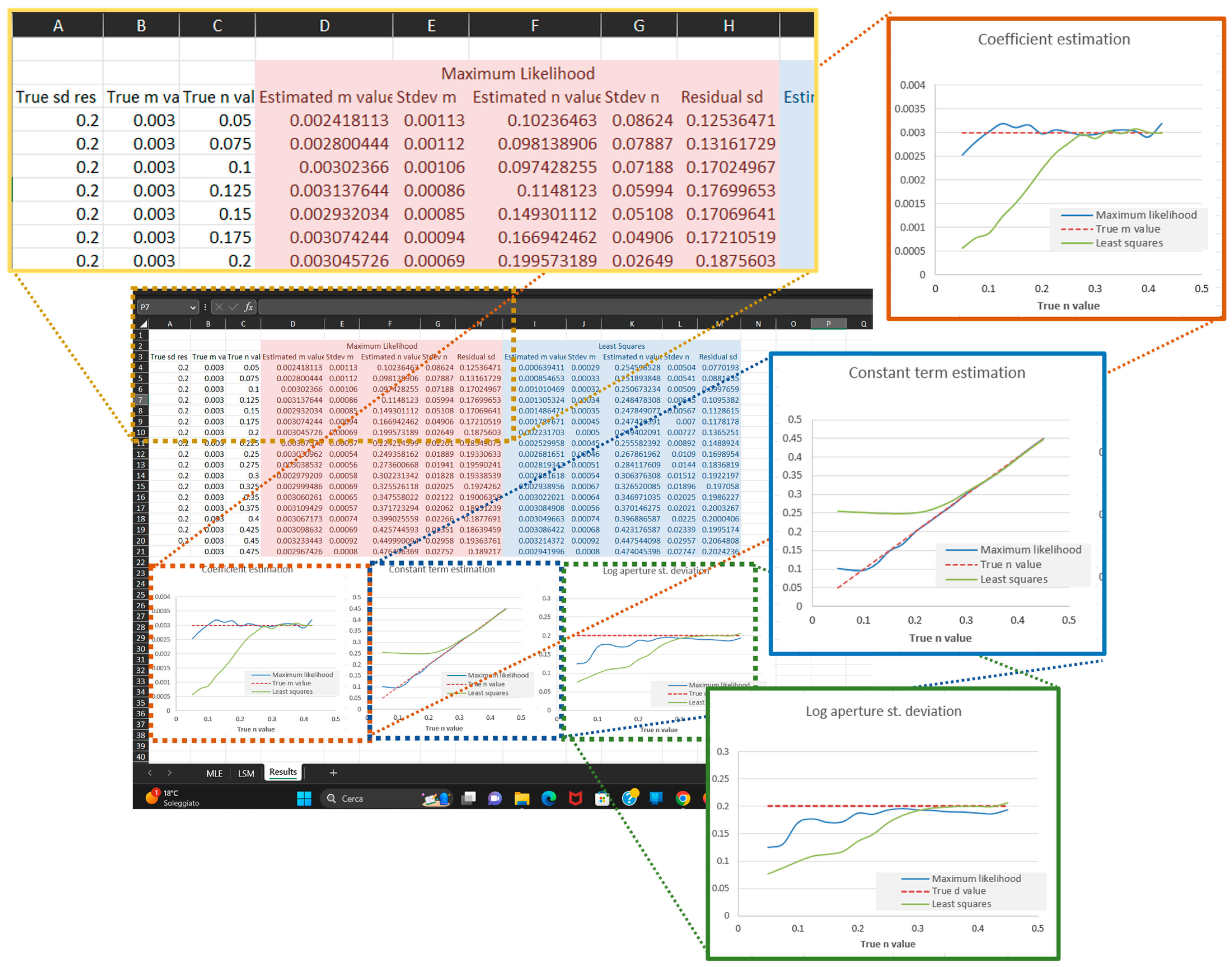
| Method: Maximum Likelihood Estimation True m = 0.003, True Residual std dev = 0.2, Sample Number = 35 | ||||||
|---|---|---|---|---|---|---|
| True n Value | Estimated m | Std dev. m | Estimated n | Std dev. n | Estimated Residual std dev. | Std dev. Residual std dev. |
| 0.05 | 0.0024 | 0.00113 | 0.102 | 0.086 | 0.125 | 0.105 |
| 0.075 | 0.0028 | 0.00112 | 0.098 | 0.079 | 0.132 | 0.089 |
| 0.1 | 0.0030 | 0.00106 | 0.097 | 0.072 | 0.170 | 0.088 |
| 0.125 | 0.0031 | 0.00086 | 0.115 | 0.060 | 0.177 | 0.085 |
| 0.15 | 0.0029 | 0.00085 | 0.149 | 0.051 | 0.171 | 0.071 |
| 0.175 | 0.0031 | 0.00094 | 0.167 | 0.049 | 0.172 | 0.053 |
| 0.2 | 0.0030 | 0.00069 | 0.200 | 0.026 | 0.188 | 0.052 |
| 0.225 | 0.0031 | 0.00057 | 0.224 | 0.022 | 0.185 | 0.047 |
| 0.25 | 0.0030 | 0.00054 | 0.249 | 0.019 | 0.193 | 0.043 |
| 0.275 | 0.0030 | 0.00056 | 0.274 | 0.019 | 0.196 | 0.039 |
| 0.3 | 0.0030 | 0.00058 | 0.302 | 0.018 | 0.193 | 0.035 |
| 0.325 | 0.0030 | 0.00069 | 0.326 | 0.020 | 0.192 | 0.034 |
| 0.35 | 0.0031 | 0.00065 | 0.348 | 0.021 | 0.190 | 0.033 |
| 0.375 | 0.0031 | 0.00057 | 0.372 | 0.021 | 0.190 | 0.032 |
| 0.4 | 0.0031 | 0.00074 | 0.399 | 0.023 | 0.188 | 0.031 |
| 0.425 | 0.0031 | 0.00069 | 0.426 | 0.024 | 0.186 | 0.030 |
| 0.45 | 0.0032 | 0.00092 | 0.450 | 0.030 | 0.194 | 0.029 |
| 0.475 | 0.0030 | 0.00080 | 0.476 | 0.028 | 0.189 | 0.027 |
| 0.05 | 0.0024 | 0.00113 | 0.102 | 0.086 | 0.125 | 0.105 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guerriero, V. Maximum Likelihood Instead of Least Squares in Fracture Analysis by Means of a Simple Excel Sheet with VBA Macro. Geosciences 2023, 13, 379. https://doi.org/10.3390/geosciences13120379
Guerriero V. Maximum Likelihood Instead of Least Squares in Fracture Analysis by Means of a Simple Excel Sheet with VBA Macro. Geosciences. 2023; 13(12):379. https://doi.org/10.3390/geosciences13120379
Chicago/Turabian StyleGuerriero, Vincenzo. 2023. "Maximum Likelihood Instead of Least Squares in Fracture Analysis by Means of a Simple Excel Sheet with VBA Macro" Geosciences 13, no. 12: 379. https://doi.org/10.3390/geosciences13120379
APA StyleGuerriero, V. (2023). Maximum Likelihood Instead of Least Squares in Fracture Analysis by Means of a Simple Excel Sheet with VBA Macro. Geosciences, 13(12), 379. https://doi.org/10.3390/geosciences13120379







