Abstract
Probabilistic models for long-term estimations and deep learning models for short-term predictions have been evaluated and analyzed for ocean wave parameters. Estimation of design and operational wave parameters for long-term return periods is essential for various coastal and ocean engineering applications. Three probability distributions, namely generalized extreme value distribution (EV), generalized Pareto distribution (PD), and Weibull distribution (WD), have been considered in this work. The design wave parameter considered is the maximal wave height for a specified return period, and the operational wave parameters are the mean maximal wave height and the highest occurring maximal wave height. For precise location-based estimation, wave heights are considered from a nested wave model, which has been configured to have a 10 km spatial resolution. As per availability, buoy-observed data are utilized for validation purposes at the Agatti, Digha, Gopalpur, and Ratnagiri stations along the Indian coasts. At the stations mentioned above, the long short-term memory (LSTM)-based deep learning model is applied to provide short-term predictions with higher accuracy. The probabilistic approach for long-term estimation and the deep learning model for short-term prediction can be used in combination to forecast wave statistics along the coasts, reducing hazards.
1. Introduction
Design and operational wave statistics, which have wide availability and higher accuracy, are essential for coastal management and marine operations. Coastal and naval engineering studies need reliable wave data for the construction and design of coastal and offshore structures. Spectral ocean wave models like WAVEWATCH III [1,2,3,4,5] have been extensively used for forecasting ocean wave parameters but have limitations for long-term predictions. Probabilistic predictive models can be used to estimate long-term wave parameters, and verification of such models against observed buoy data is a pre-requisite. In this work, probabilistic models have been discussed to predict wave statistics, such as the significant wave height parameter for a long period, like 100 years. The estimated wave heights are validated against available buoy-observed data along the Indian coasts. As early as 1952, Reference [6] stated that wave heights follow Rayleigh distribution. While Reference [7] provided the joint distribution of individual wave heights and periods for a narrow band spectrum, Reference [8] discussed the same for wave records with wide band spectra. For better accuracy, Reference [9] conducted seasonal analysis of extreme events using a Poisson process to model the storm occurrence and a generalized Pareto distribution to model the extreme values above some given threshold value. Reference [10] combined the Gumbel, Frechet, and Weibull distributions to formulate the generalized extreme value distribution. He mentioned that in the presence of hourly or daily data, threshold models like the generalized Pareto distribution are more useful. Reference [11] generated the modified Weibull distribution to estimate extreme wave heights and design wave height parameters for given return periods and showed that the new distribution gives better results than the Weibull distribution. They conducted experiments with different ranges of cyclonic wave heights and established the modified Weibull distribution to effectively model the daily maximum wave heights along the Indian coasts. Reference [12] studied buoy-measured wave height data along the Portuguese coast and fitted the data with Rayleigh and Weibull distributions. Reference [13] evaluated non-stationary extreme value models by critically analyzing different model parameterizations and inference schemes. Reference [14] proposed a superior model based on the fractal properties of ocean waves for estimating wave heights for larger return periods. Reference [15] recommended the Monte Carlo method for estimating the return periods of wave and crest heights. In another study to analyze the nature of the time series, daily, monthly, and annual maximum wave height data were estimated for a 50-year return period, using generalized extreme value and generalized Pareto distributions [16]. The Peak Over Threshold method and generalized Pareto distribution were used to estimate sea and swell wave heights seasonally for Sri Lanka [17]. They concluded that although return levels of the sea waves are higher than the swell waves, both need to be considered for coastal construction and design purposes. Reference [18] generated return period maps of wave heights for 100 years for the Bay of Bengal region using the Peak Over Threshold method and generalized Pareto distribution. Return value maps were generated for the Bay of Bengal region for 10, 15, 25, 50, and 100 years, and finally, the error map between the computed and actual values showed a maximum error of 2 m. The study involves coarse-resolution data averaged over the region, and thus, estimation involving extreme events was not performed. There are several studies [19,20,21,22,23,24] describing the stochastic ocean parameters using joint probability distributions, indicating the role of the probabilistic approach in future ocean and marine research.
In this paper, three different probability distributions have been compared and utilized to estimate the return value of wave heights and calculate operational wave parameters like the mean maximal wave height and the highest occurring maximal wave height using the analyzed expressions. Probabilistic models are discussed for the design and operational wave statistics using the EV, PD, and WD, and a comparison is conducted to test the accuracy of the model performances. To train the predictive models, wave data are generated from a high-resolution ocean nested model configured for the Indian Ocean. To validate the outputs, observed buoy data at Agatti, Digha, Gopalpur, and Ratnagiri stations have been utilized. The probabilistic approach estimated wave statistics for return values of 5, 10, 25, 50, and 100 years with efficiency. Further, for short-term predictions, like a few days or hours, deep learning models have been applied, which have shown promising results in various studies [25,26,27,28,29]. Machine learning approaches have been utilized to improve spatial and temporal ocean and marine studies [30,31,32,33,34].
Reference [35] reviewed how machine learning developed in geoscience over the last 70 years. The author explored the shift from neural networks to machine learning, which includes both shallow and deep networks. He discussed the applications and developments of shallow and deep models in various branches of earth science. Reference [36] performed short-term predictions (3 days) of wave parameters using neural network methods for 1 to 12 multistep ahead-time steps. Reference [37] performed similar studies for short-term predictions (3 days) of wave parameters for cyclonic events for 1 to 12 multistep ahead-time steps using deep network architectures with better accuracies. Another study [38] discussed present and future trends of deep learning models in geophysics. They reviewed the difficulties faced while applying deep models in fields like space science and atmospheric science and showed future directions, like unsupervised learning and transfer learning. Reference [39] introduced deep learning network models in environmental remote sensing. They reviewed applications, challenges, and future scopes of deep models in ocean color, solar radiation, vegetation, hydrology, surface temperature (land and air), and many more fields. Optimized deep learning models were proposed with better accuracy compared to physics-based and statistical models for short-term forecasting of ocean wave energy at different locations [40]. Spatiotemporal sea surface temperature patterns were predicted for the next 7 days using deep learning models after mode decompositions in the South China Sea [41]. Although the new data-driven process gives enhanced forecasts of spatiotemporal fields, during extreme events, the error increases. Location-specific predictions of sea surface temperatures in the Indian Ocean were compared using shallow and deep models for 30-year time-series data [42]. The long short-term memory (LSTM)-based deep network architecture demonstrated a 60% lessor error compared to the shallow feedforward model. The successful application and performance of LSTM-based deep networks can be seen in various branches of science and technology [43,44,45,46,47].
From the various studies discussed above, the enhanced performance of deep learning models for short-term predictions of ocean and other geophysical parameters is obvious. In this study, the six-hourly significant wave height (SWH) parameter at the Agatti, Digha, Gopalpur, and Ratnagiri stations along the Indian coasts have been predicted using LSTM-based deep learning model for 1 to 4 delays corresponding to 06, 12, 18, and 24 h, respectively. Thus, the probabilistic approach for design and operational wave estimations for 100 years and the deep learning network model for short predictions (24 h) are assessed for locations along the Indian Ocean coasts.
2. Materials and Methods
The WAVEWATCH III model is configured globally with a 1 × 1-degree spatial resolution and nested for the Indian Ocean domain (65° E to 90° E and 25° N to 5° N), having a 0.5 × 0.5-degree spatial resolution and further nested for the Bay of Bengal (75° E to 90° E and 25° N to 5° N) and Arabian Sea (65° E to 75° E and 25° N to 5° N) regions with a 0.1 × 0.1-degree or 10 km spatial resolution. For all the domains, input wind is obtained from ECMWF at a 0.25-degree spatial resolution and 06 hourly temporal resolution (ERA-Interim winds). In this work, model integrations from 2001 to 2016 are considered. For precise location-based estimation, wave heights are considered from the model having a 10 km spatial resolution. The stations Agatti, Digha, Gopalpur, and Ratnagiri are chosen for validation purposes, as per the availability of buoy observed data. For significant wave height (SWH) data, the period 2001–2006 is chosen as the training period. The probability distributions used to generate the estimation models in this work to obtain maximum wave return values include the generalized extreme value distribution (EV), the generalized Pareto distribution (PD), and the Weibull distribution (WD). For the above three probability distributions, the expressions for the maximal wave height for the specified return period, mean maximal wave height, and highest occurring maximal wave heights have been estimated and then compared. In the next section, the estimation of these expressions is discussed. For the EV model, monthly maximum values are considered. For the PD model, a value near the mean is chosen as the threshold value. For the WD model, all the six-hourly data are obtained and fitted after replacing the 0.00 value with 0.01 since WD fit numbers are greater than zero only.
2.1. Generalized Extreme Value Distribution
The cumulative distribution function of generalized extreme value distribution [10] for a given random variable X is given as
In the above expression, µ, σ, and ξ signify the position, scale, and shape parameters in the given range—∞ < µ < ∞, σ > 0, and—∞ < ξ < ∞.
Let us consider n wave heights given by X1, X2 … Xn. The probability of the maximal wave height not exceeding X is given by . Let us denote the nex .
Thus, =
Analysis of the return period
Let X be any arbitrary random variable denoting maximal wave heights, and the distribution function of X is given by F (X).
Let us consider N maximal wave heights given by X1, X2 … XN. The probability of the largest maximal wave height not exceeding XL is given by
and
The maximal wave height that can be anticipated for a prescribed period of return Tp is described by
or .
The maximal wave height that can be estimated for a prescribed period of return T is given by
2.2. Generalized Pareto Distribution
Let X be a given random variable. The cumulative distribution function for the generalized Pareto distribution is given as
In the above expression µ, σ, and ξ represent the location, scale, and shape parameters. Also,—∞ < µ < ∞, σ > 0, and—∞ < ξ < ∞.
Let X1, X2 … Xn be a set of n wave heights. The probability for the maximal wave height not exceeding X is given by .
Let us denote the next .
Thus,
Analysis of the return period
By applying the same procedure for calculating the return period, the maximum wave height that can be anticipated for a prescribed return period T is given by
2.3. Weibull Distribution
Let X be a given random variable. The distribution function for the Weibull distribution [11] is given as
In the above expression, ‘a’ is the scale parameter, and ‘b’ is the shape parameter.
Also, X > 0, a > 0, and b > 0.
Let X1, X2 … Xn be a set of n wave heights. The probability of the maximal wave height not exceeding X is given by
Analysis of the return period
Applying the same procedure for calculating the return period, the maximal wave height anticipated for a prescribed return period T is given by
Mean Maximal Wave height (Xmax)
The following expression gives the probability density function of Weibull distribution for maximal wave height distribution: .
The mean maximal wave height is given as
Highest occurring maximal wave height (Xmode)
The highest occurring maximal wave height is the mode of the function G(X). The parameter is estimated by solving the equation .
Thus, .
Four locations are chosen—Digha and Gopalpur along the east coast and Ratnagiri and Agatti along the west coast—for estimating wave return values using the expressions discussed. Both coasts are sensitive to cyclonic conditions [48], and the chosen stations have witnessed several extreme conditions in the past decades. For the probabilistic models using the distributions, namely EV, PD, and WD, the period 2001–2006 is chosen as the training period. The experiments are conducted for each of the above four locations, the distributions are fitted, and the scale, location, and shape parameters are calculated for the training period. The largest wave height that will be encountered for different return periods is estimated for 5, 10, 25, 50, and 100 years and compared with the configured ocean model (WAVEWATCH III) values and buoy-estimated values.
For accurate short-term predictions, the LSTM-based deep learning model is applied to the six-hourly model-generated and buoy-observed SWH time-series data at the Agatti, Digha, Gopalpur, and Ratnagiri stations. To minimize the error, different epochs and hidden units are tested and then fixed, and the initial learning rate and the drop learn rate are specified in the network. For predictions related to short-term horizons, different delays are applied from 1 to 4, corresponding to 06, 12, 18, and 24 h, respectively. To train the model, 80% of the data is used, and the remaining 20% is the testing set. The model performances are evaluated in terms of the root mean square error (RMSE). Expressions related to the input, output, and hidden layers of the LSTM deep model architecture can be obtained in detail from [49,50].
3. Results and Discussions
The multi-nested WAVEWATCH III model or WW3 model has been globally simulated from 2001 to 2016, and SWH values for return periods till 100 years are estimated using different probabilistic models in this work. Data obtained for the period 2001–2006 have been deliberated as training period data. As per buoy data availability for 2016, locations Digha and Gopalpur along the east coast are chosen, and Agatti and Ratnagiri along the west coast are chosen. The model-computed SWH values from 2001 to 2006 at the above stations depicted precise annual periodicity. Digha, being very near the coast with shallow depth, recorded low wave heights, whereas Agatti and Ratnagiri, along the west coast, measured wave heights more than 4 m.
Figure 1, Figure 2, Figure 3 and Figure 4 provide a comparison between the model-computed and buoy-observed SWH values for 2016 at Digha, Gopalpur, Agatti, and Ratnagiri, respectively. The SWH values for Digha, which is very near the coast, are underestimated by the model compared to buoy observations. For Gopalpur, the model mostly overestimated. Similar trends are observed for Ratnagiri. For Agatti, which is again very near the coast, the model underestimates the SWH values. The stations being very near the coast, the model with 25 km wind as input could not generate accurate outputs. The mean square error calculated between the model-computed and buoy-observed values at Digha, Gopalpur, Agatti, and Ratnagiri for 2016 is 0.24, 0.33, 0.62, and 0.83 m, respectively.
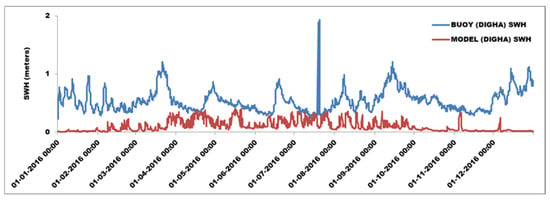
Figure 1.
Comparison of WW3 model-computed and buoy-observed SWH for DIGHA for 2016.
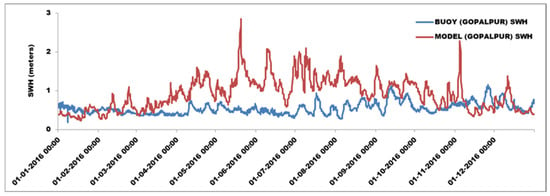
Figure 2.
Comparison of WW3 model-computed and buoy-observed SWH for GOPALPUR for 2016.
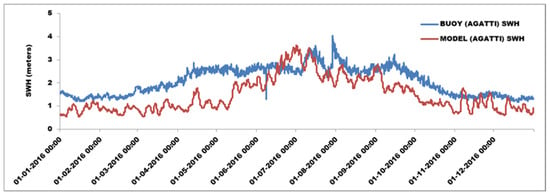
Figure 3.
Comparison WW3 model-computed and buoy-observed SWH for AGATTI for 2016.
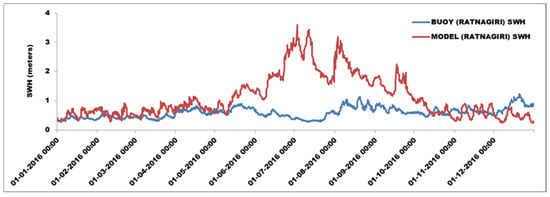
Figure 4.
Comparison of WW3 model-computed and buoy-observed SWH for RATNAGIRI for 2016.
The mean square error suggests that the model-computed and buoy-observed SWH values are not in good agreement for 2016 along the east coast (Digha and Gopalpur) and along the west coast (Agatti and Ratnagiri), and thus, the probabilistic predictive models come to importance. Six years of model wave data at the given four locations are fitted with different probability distributions. Considering the monthly maximums, EV overestimated highly for negative shape parameters, while for the positive ones, there are constant values. Estimations given by the PD model are the closest, except for Digha, which had a sudden peak that is modeled better by WD.
After training the probabilistic models using model data from 2001–2006, maximal wave heights are predicted for different return periods. The distributions are fitted, and the scale, location, and shape parameters are calculated for the training period. Table 1 gives the log-likelihood values for Digha. The fitting is considered good for a larger likelihood value. The likelihood function is given by , where . The sample observations have a probability function , where θ is the parameter.

Table 1.
Likelihood values for Digha (training set data 2001–2006).
Table 2 provides the shape, scale, and location parameter values. Table 3 gives the buoy-observed, WW3-computed, and probabilistic model-predicted maximal wave heights for different periods of return. It is observed from Table 3 that the performance of WD is the best for sudden peak values. Otherwise, PD estimates well, while EV gives excessively high values. Thus, the entire six-hourly data set used for the WD is more effective in comparison to the monthly maximums used in EV and above the threshold values used in PD. Table 4 computes the mean maximal wave height and the highest occurring maximal wave height using the WD model. The values are in agreement with the model-computed ones.

Table 2.
Parameters calculated for Digha (training set data 2001–2006).

Table 3.
Maximal wave heights for Digha.

Table 4.
Mean maximal wave height and highest occurring maximal wave height for Digha.
Table 5, Table 6, Table 7 and Table 8 give similar estimations for Gopalpur along the east coast. Further estimations are given in Table 9, Table 10, Table 11 and Table 12 for Agatti and Table 13, Table 14, Table 15 and Table 16 for Ratnagiri. As far as fitting is concerned, PD fitted best for Gopalpur, Agatti, and Ratnagiri, although for Digha, WD gave better predictions. For Gopalpur, PD and WD performed similarly in predicting maximal wave heights, while the PD model performed better for Agatti and Ratnagiri stations. For the operational wave parameters, WD performed with reasonable accuracy. Using WW3 computed model data and probabilistic models, estimations of return wave height values for 100 years for locations along the Indian coasts are performed with reasonable accuracy. The temporal scale varies widely for the buoy-observed data and the probabilistic model-predicted ones, and thus, a one-to-one comparison failed in this case.

Table 5.
Likelihood values for Gopalpur (training set data 2001–2006).

Table 6.
Parameters calculated for Gopalpur (training set data 2001–2006).

Table 7.
Maximal wave heights for Gopalpur.

Table 8.
Mean maximal wave height and highest occurring maximal wave height for Gopalpur.

Table 9.
Likelihood values for Agatti (training set data 2001–2006).

Table 10.
Parameters calculated for Agatti (training set data 2001–2006).

Table 11.
Maximal wave heights for Agatti.

Table 12.
Mean maximal wave height and highest occurring maximal wave height for Agatti.

Table 13.
Likelihood values for Ratnagiri (training set data 2001–2006).

Table 14.
Parameters calculated for Ratnagiri (training set data 2001–2006).

Table 15.
Maximal wave heights for Ratnagiri.

Table 16.
Mean maximal wave height and highest occurring maximal wave height for Ratnagiri.
For short-term predictions, the time series of SWH data for 2016 is considered at the four aforementioned stations. In separate experiments, both the datasets from model simulations and buoy observations are trained and tested. The LSTM-based deep learning model is trained with an 80% dataset for lead times from 1 to 4. Table 17 and Table 18 provide the RMSE values for the training and testing datasets from model simulations, and Table 19 and Table 20 provide the same from buoy observations. As the forecast horizon increases, the error also increases. For Digha, there is a spike in the buoy-observed SWH values, and thus, the errors are higher for the forecasts using the buoy dataset compared to the model dataset. Considering all the deep model runs, the maximum error is approximately 0.2 m for a 24 h forecast.

Table 17.
RMSE values for LSTM training set (model) with different lead times.

Table 18.
RMSE values for LSTM testing set (model) with different lead times.

Table 19.
RMSE values for LSTM training set (buoy) with different lead times.

Table 20.
RMSE values for LSTM testing set (buoy) with different lead times.
4. Conclusions
This study combined the assessment of the design and operational wave parameters for both long-term (100 years) and short-term (24 h) durations along the Indian coasts. The evaluation conducted and outcomes attained will help in the long- and short-term wave statistics prediction for locations, which may aid as a fast escort to recognizing the most vulnerable seaside areas. The stations, Digha and Gopalpur along the east coast and Agatti and Ratnagiri along the west coast, were chosen as per buoy data availability and witnessed several extreme events in the past decades. For most of the cases, PD fitted better, followed by WD for particular extreme events. It is observed that Digha and WD estimated the design and operational wave parameters most effectively in the case of a sudden peak value. For the other stations, PD performed better, followed by WD. Each distribution had its own benefits and inadequacies. The probabilistic models, along with WW3 model data used for training purposes, performed satisfactorily for long-term wave height return value estimation. Considering short-term predictions using less data and fewer computations, the LSTM-based deep model predicted SWH values for different lead times with high accuracy for all four stations. In the future, similar vulnerable locations along the coast may be subjected to such probabilistic and deep models to reduce hazards.
Author Contributions
Conceptualization, M.S. (Mourani Sinha), M.B. and S.A.B.; methodology, M.S. (Mourani Sinha), M.B. and M.S. (M. Seemanth); software, M.S. (Mourani Sinha) and M.S. (M. Seemanth); validation, M.S. (Mourani Sinha), M.B., and S.A.B.; formal analysis, M.S. (Mourani Sinha), M.B. and M.S. (M. Seemanth); investigation, M.S. (Mourani Sinha), M.B. and S.A.B.; resources, M.S. (Mourani Sinha), M.B. and M.S. (M. Seemanth); data curation, M.S. (Mourani Sinha) and M.S. (M. Seemanth); writing—original draft preparation, M.S. (Mourani Sinha) and M.B.; writing—review and editing M.S. (Mourani Sinha), M.B. and S.A.B.; visualization, M.S. (Mourani Sinha); supervision, S.A.B.; project administration, M.S. (Mourani Sinha) and S.A.B.; funding acquisition, M.S. (Mourani Sinha), S.A.B. and M.S. (M. Seemanth). All authors have read and agreed to the published version of the manuscript.
Funding
Part of this research (SAMUDRA project) was funded by the Space Application Centre (SAC) of the Indian Space Research Organization (ISRO), grant number EPSA/SAMUDRA/WP/12/2017.
Data Availability Statement
Data used in this study are available from the corresponding author on reasonable requests.
Acknowledgments
The authors are thankful to the Environmental Modeling Center, Marine Modeling and Analysis Branch, for the NOAA WAVEWATCH III model version 5.16, the ECMWF for the ERA-Interim wind fields, and the National Institute of Ocean Technology India for the buoy data.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Tolman, H.L. A third-generation model for wind waves on slowly varying, unsteady, and inhomogeneous depths and currents. J. Phys. Oceanogr. 1991, 21, 782–797. [Google Scholar] [CrossRef]
- Tolman, H.L. Alleviating the Garden Sprinkler Effect in wind wave models. Ocean Model. 2002, 4, 269–289. [Google Scholar] [CrossRef]
- Tolman, H.L. A mosaic approach to wind wave modeling. Ocean Model. 2007, 25, 35–47. [Google Scholar] [CrossRef]
- Abdolali, A.; Roland, A.; Van der Westhuysen, A.; Meixner, J.; Chawla, A.; Hesser, T.J.; Smith, J.M.; Sikiric, M.D. Large-scale hurricane modeling using domain decomposition parallelization and implicit scheme implemented in WAVEWATCH III wave model. Coast. Eng. 2020, 157, 103656. [Google Scholar] [CrossRef]
- Abdolali, A.; van der Westhuysen, A.; Ma, Z.; Mehra, A.; Roland, A.; Moghimi, S. Evaluating the accuracy and uncertainty of atmospheric and wave model hindcasts during severe events using model ensembles. Ocean Dyn. 2021, 71, 217–235. [Google Scholar] [CrossRef]
- Longuet-Higgins, M.S. On the statistical distribution of the height of sea waves. J. Mar. Res. 1952, 11, 245–266. Available online: https://images.peabody.yale.edu/publications/jmr/jmr11-03-01.pdf (accessed on 10 November 2023).
- Longuet-Higgins, M.S. On the joint distribution of the periods and amplitudes of sea waves. J. Geophys. Res. 1975, 80, 2688–2694. [Google Scholar] [CrossRef]
- Chakrabarti, S.K.; Cooley, R.P. Statistical distribution of periods and heights of ocean waves. J. Geophys. Res. 1977, 82, 1363–1368. [Google Scholar] [CrossRef]
- Morton, I.D.; Bowers, J.; Mould, G. Estimating return period wave heights and wind speeds using a seasonal point process model. Coast. Eng. 1997, 31, 305–326. [Google Scholar] [CrossRef]
- Coles, S. An Introduction to Statistical Modeling of Extreme Values; Springer Series in Statistics; Springer: London, UK, 2001. [Google Scholar]
- Muraleedharan, G.; Rao, A.D.; Kurup, P.G.; Nair, N.U.; Sinha, M. Modified Weibull distribution for maximum and significant wave height simulation and prediction. Coast. Eng. 2007, 54, 630–638. [Google Scholar] [CrossRef]
- Guedes Soares, C.; Carvalho, A.N. Probability Distributions of Wave Heights and Periods in Measured Combined Sea-States from the Portuguese Coast. J. Offshore Mech. Arct. Eng. 2003, 125, 198–204. [Google Scholar] [CrossRef]
- Jones, M.; Randell, D.; Ewans, K.; Jonathan, P. Statistics of extreme ocean environments: Non-stationary inference for directionality and other covariate effects. Ocean Eng. 2016, 119, 30–46. [Google Scholar] [CrossRef]
- Wang, L.; Xu, X.; Liu, G.; Chen, B.; Chen, Z. A new method to estimate wave height of specified return period. Chin. J. Oceanol. Limnol. 2017, 35, 1002–1009. [Google Scholar] [CrossRef]
- Mackay, E.; Johanning, L. Long-term distributions of individual wave and crest heights. Ocean Eng. 2018, 165, 164–183. [Google Scholar] [CrossRef]
- Naseef, T.M.; Kumar, V.S.; Joseph, J.; Jena, B.K. Uncertainties of the 50-year wave height estimation using generalized extreme value and generalized Pareto distributions in the Indian Shelf seas. Nat. Hazards 2019, 97, 1231–1251. [Google Scholar] [CrossRef]
- Thevasiyani, T.; Perera, K. Statistical analysis of extreme ocean waves in Galle, Sri Lanka. Weather Clim. Extrem. 2014, 5–6, 40–47. [Google Scholar] [CrossRef]
- Roy, S.; Sinha, M.; Pradhan, T. Generation of 100-year-return value maps of maximum significant wave heights with automated threshold value estimation. Spat. Inf. Res. 2020, 28, 335–344. [Google Scholar] [CrossRef]
- Wang, Y. Prediction of height and period joint distributions for stochastic ocean waves. China Ocean Eng. 2017, 31, 291–298. [Google Scholar] [CrossRef]
- Antão, E.; Soares, C.G. Approximation of the joint probability density of wave steepness and height with a bivariate gamma distribution. Ocean Eng. 2016, 126, 402–410. [Google Scholar] [CrossRef]
- Mazas, F.; Hamm, L. An event-based approach for extreme joint probabilities of waves and sea levels. Coast. Eng. 2017, 122, 44–59. [Google Scholar] [CrossRef]
- Huang, W.; Dong, S. Probability distribution of wave periods in combined sea states with finite mixture models. Appl. Ocean Res. 2019, 92, 101938. [Google Scholar] [CrossRef]
- Huang, W.; Dong, S. Joint distribution of significant wave height and zero-up-crossing wave period using mixture copula method. Ocean Eng. 2020, 219, 108305. [Google Scholar] [CrossRef]
- Zhao, M.; Deng, X.; Wang, J. Description of the Joint Probability of Significant Wave Height and Mean Wave Period. J. Mar. Sci. Eng. 2022, 10, 1971. [Google Scholar] [CrossRef]
- Polson, N.G.; Sokolov, V.O. Deep learning for short-term traffic flow prediction. Transp. Res. Part C Emerg. Technol. 2017, 79, 1–17. [Google Scholar] [CrossRef]
- Romascanu, A.; Ker, H.; Sieber, R.; Greenidge, S.; Lumley, S.; Bush, D.; Morgan, S.; Zhao, R.; Brunila, M. Using deep learning and social network analysis to understand and manage extreme flooding. J. Contingencies Crisis Manag. 2020, 28, 251–261. [Google Scholar] [CrossRef]
- Cheng, S.; Jin, Y.; Harrison, S.P.; Prentice, I.C.; Guo, Y.; Arcucci, R. Parameter Flexible Wildfire Prediction Using Machine Learning Techniques: Forward and Inverse Modelling. Remote Sens. 2021, 14, 3228. [Google Scholar] [CrossRef]
- Wang, Y.; Qin, L.; Wang, Q.; Chen, Y.; Yang, Q.; Xing, L.; Ba, S. A novel deep learning carbon price short-term prediction model with dual-stage attention mechanism. Appl. Energy 2023, 347, 121380. [Google Scholar] [CrossRef]
- Xu, P.; Zhang, M.; Chen, Z.; Wang, B.; Cheng, C.; Liu, R. A Deep Learning Framework for Day Ahead Wind Power Short-Term Prediction. Appl. Sci. 2022, 13, 4042. [Google Scholar] [CrossRef]
- Foster, D.; Gagne, D.J.; Whitt, D.B. Probabilistic Machine Learning Estimation of Ocean Mixed Layer Depth From Dense Satellite and Sparse In Situ Observations. J. Adv. Model. Earth Syst. 2021, 13, e2021MS002474. [Google Scholar] [CrossRef]
- Panda, J.P. Machine learning for naval architecture, ocean and marine engineering. J. Mar. Sci. Technol. 2023, 28, 1–26. [Google Scholar] [CrossRef]
- Lou, R.; Lv, Z.; Dang, S.; Su, T.; Li, X. Application of machine learning in ocean data. Multimed. Syst. 2023, 29, 1815–1824. [Google Scholar] [CrossRef]
- Chen, J.; Pillai, A.C.; Johanning, L.; Ashton, I. Using machine learning to derive spatial wave data: A case study for a marine energy site. Environ. Model. Softw. 2021, 142, 105066. [Google Scholar] [CrossRef]
- James, S.C.; Zhang, Y.; O’Donncha, F. A machine learning framework to forecast wave conditions. Coast. Eng. 2018, 137, 1–10. [Google Scholar] [CrossRef]
- Dramsch, J.S. 70 years of machine learning in geoscience in review. Adv. Geophys. 2019, 61, 1–55. [Google Scholar] [CrossRef]
- Bhattacharya, M.; Sinha, M. Basin scale wind-wave prediction using empirical orthogonal function analysis and neural network models. Results Geophys. Sci. 2021, 8, 100032. [Google Scholar] [CrossRef]
- Biswas, S.; Sinha, M. Assessment and Prediction of a Cyclonic Event: A Deep Learning Model. In Proceedings of the 7th International Conference on Advances in Computing and Data Sciences (ICACDS 2023), Kumool, India, 22–23 April 2023; Singh, M., Tyagi, V., Gupta, P., Flusser, J., Ören, T., Eds.; Springer: Cham, Switzerland, 2023; Volume 1848. [Google Scholar] [CrossRef]
- Yu, S.; Ma, J. Deep Learning for Geophysics: Current and Future Trends. Rev. Geophys. 2021, 59, e2021RG000742. [Google Scholar] [CrossRef]
- Yuan, Q.; Shen, H.; Li, T.; Li, Z.; Li, S.; Jiang, Y.; Zhang, L. Deep learning in environmental remote sensing: Achievements and challenges. Remote Sens. Environ. 2020, 241, 111716. [Google Scholar] [CrossRef]
- Bento, P.; Pombo, J.; Mendes, R.; Calado, M.; Mariano, S. Ocean wave energy forecasting using optimised deep learning neural networks. Ocean Eng. 2020, 219, 108372. [Google Scholar] [CrossRef]
- Xu, S.; Dai, D.; Cui, X.; Yin, X.; Jiang, S.; Pan, H.; Wang, G. A deep learning approach to predict sea surface temperature based on multiple modes. Ocean Model. 2023, 181, 102158. [Google Scholar] [CrossRef]
- Biswas, S.; Sinha, M. Assessment of Shallow and Deep Learning Models for Prediction of Sea Surface Temperature. In Proceedings of the 7th Annual International Conference on Information System and Artificial Intelligence (ISAI 2022), Chengdu, China, 24–26 October 2022; Sk, A.A., Turki, T., Ghosh, T.K., Joardar, S., Barman, S., Eds.; Springer: Cham, Switzerland, 2022; Volume 1695. [Google Scholar] [CrossRef]
- Rather, A.M. LSTM-based Deep Learning Model for Stock Prediction and Predictive Optimization Model. EURO J. Decis. Process. 2020, 9, 100001. [Google Scholar] [CrossRef]
- Saka, K.; Kakuzaki, T.; Metsugi, S.; Kashiwagi, D.; Yoshida, K.; Wada, M.; Tsunoda, H.; Teramoto, R. Antibody design using LSTM based deep generative model from phage display library for affinity maturation. Sci. Rep. 2021, 11, 1–13. [Google Scholar] [CrossRef]
- Bakhshi Ostadkalayeh, F.; Moradi, S.; Asadi, A.; Moghaddam Nia, A.; Taheri, S. Performance Improvement of LSTM-based Deep Learning Model for Streamflow Forecasting Using Kalman Filtering. Water Resour. Manag. 2023, 37, 3111–3127. [Google Scholar] [CrossRef]
- Yang, H. LSTM-Based Deep Model for Investment Portfolio Assessment and Analysis. Appl. Bionics Biomech. 2022, 2022, 1852138. [Google Scholar] [CrossRef]
- Crivellari, A.; Beinat, E. LSTM-Based Deep Learning Model for Predicting Individual Mobility Traces of Short-Term Foreign Tourists. Sustainability 2019, 12, 349. [Google Scholar] [CrossRef]
- Sinha, M.; Jha, S.; Kumar, A. A Comparison of Wave Spectra during Pre-Monsoon and Post-Monsoon Tropical Cyclones under an Intense Positive IOD Year 2019. Climate 2023, 11, 44. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. Available online: https://www.bioinf.jku.at/publications/older/2604.pdf (accessed on 10 November 2023). [CrossRef]
- Biswas, S.; Sinha, M. Performances of deep learning models for Indian Ocean wind speed prediction. Model. Earth Syst. Environ. 2021, 7, 809–831. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).