Thermal Conductivity Variations in Frozen Hydrate-Bearing Sand upon Heating and Dissociation of Pore Gas Hydrate

Abstract

High-latitude permafrost, including hydrate-bearing frozen ground, changes its properties in response to natural climate change and to impacts from petroleum production. Of special interest is the behavior of thermal conductivity, one of the key parameters that control the thermal processes in permafrost containing gas hydrate accumulations. Thermal conductivity variations under pressure and temperature changes were studied in the laboratory through physical modeling using sand sampled from gas-bearing permafrost of the Yamal Peninsula (northern West Siberia, Russia). When gas pressure drops to below equilibrium at a constant negative temperature (about −6 °C), the thermal conductivity of the samples first becomes a few percent to 10% lower as a result of cracking and then increases as pore gas hydrate dissociates and converts to water and then to ice. The range of thermal conductivity variations has several controls: pore gas pressure, hydrate saturation, rate of hydrate dissociation, and amount of additionally formed pore ice. In general, hydrate dissociation can cause up to 20% thermal conductivity decrease in frozen hydrate-bearing sand. As the samples are heated to positive temperatures, their thermal conductivity decreases by a magnitude depending on residual contents of pore gas hydrate and ice: the decrease reaches ~30% at 20–40% hydrate saturation. The thermal conductivity decrease in hydrate-free saline frozen sand is proportional to the salinity and can become ~40% lower at a salinity of 0.14%. The behavior of thermal conductivity in frozen hydrate-bearing sediments under a pressure drop below the equilibrium and a temperature increase to above 0 °C is explained in a model of pore space changes based on the experimental results.

1. Introduction

Natural gas in the hydrate (clathrate) form is an important alternative source of energy [1,2] and is being studied in this respect in many countries worldwide [3,4,5,6,7,8,9,10]. Natural gas hydrates (mainly methane) are accumulated in marine sediments and in permafrost [11]. The amount of methane sequestered in permafrost-related gas hydrates reaches ~3.7 × 10¹³ [12]. The behavior of gas hydrates as a component of permafrost causes considerable influence on its properties, including its thermal conductivity. Specifically, the thermal conductivity of intrapermafrost hydrate-bearing horizons can be expected to depend on the relative percentages of pore hydrate and ice, unlike the unfrozen subpermafrost gas hydrate deposits. The reason is that gas hydrates and liquid water have similar values of thermal conductivity, around 0.6 W/(m·K) [13,14,15,16], but that value is almost four times lower than in ice, where it reaches 2.2 W/(m·K) [17]. Therefore, the theoretical knowledge and experimental evidence about thermal properties of hydrate-bearing sediments [3,18] are indispensable for creating efficient technologies for methane hydrate production and CO₂ sequestration, as well as for the modeling of permafrost and gas hydrate responses to climate change.

In Russia, the thermal properties of hydrate-bearing sediments have been studied since the late 1970s–early 1980s. The first results demonstrated that the thermal conductivity of frozen sand was much lower in the presence of pore gas hydrate [19]. Later measurements of hydrate-free Ottawa frozen quartz sand [20] showed an 80% higher thermal conductivity than in similar hydrate-bearing samples. In 2005, thermal conductivity was measured in core samples from the Mallik 5L-38 gas hydrate production research well (Mackenzie Delta, Canada) by a cylindrical probe in a pressure cell under equilibrium conditions [21]. The measurements revealed a 20–25% thermal conductivity difference between frozen and unfrozen samples, higher in the former. The results allowed an inference that the thermal conductivity of hydrate-bearing sediments may be largely controlled by relationships in the ‘gas hydrate–ice’ and ‘gas hydrate–liquid water’ systems in the pores [21]. On the other hand, further experiments proved that the relative percentages of pore hydrate and water cause almost no influence on the thermal conductivity of sand at positive temperatures [22].

There is a wealth of evidence on the sensitivity of thermal conductivity in fine-grained hydrate-bearing sediments to hydrate contents and various soil parameters [23]. The issue was investigated in samples saturated with gas hydrate in the laboratory [14,19,20,22,24,25,26,27,28,29,30,31,32,33,34] and in natural core samples from gas hydrate reservoirs [21,35,36,37,38,39]. However, most of the work focused on marine and subpermafrost hydrate-bearing sediments at positive temperatures, which were considered to be rich reservoirs favorable for hydrate production, while intrapermafrost ice- and hydrate-bearing reservoirs received much less attention. The thermal conductivity of frozen hydrate-bearing soils during accumulation and dissociation of gas hydrates was the subject of few studies, only [40,41,42,43]. The first experimental data on a decrease in the thermal conductivity of frozen sandy soil during hydrate formation under negative temperature conditions were shown in the work [41]. Moreover, further thermal conductivity decreases, up to 30–40%, were revealed in experiments with freezing–thawing cycles at above-equilibrium gas pressures, which induced additional hydrate formation [42]. The thermal conductivity difference between frozen hydrate-bearing and hydrate-free sediments was explained by self-preservation of pore methane hydrate [43]. The self-preservation mechanism decelerates or almost completely stops the dissociation of gas hydrates triggered by a pressure drop below the triple-phase equilibrium in the ‘gas—hydrate—ice’ system, due to the formation of an ice coat on gas hydrate particles at <0 °C temperatures. Experiments at 0.1 MPa and temperatures below 0 °C [43] investigated the sensitivity of thermal conductivity in frozen sediments with self-preserved pore gas hydrate to particle size distribution (sand, silt, and clay samples), type of hydrate-forming gas (CH₄ or CO₂), and the microstructure of rocks.

Nevertheless, the thermal properties of frozen hydrate-bearing sediments remain insufficiently studied, though the respective knowledge has been in high demand for predicting the responses of permafrost to global climate change and for development of the Arctic oil and gas fields [44,45,46,47,48]. Of special value in this respect is evidence from physical modeling that simulates the behavior of thermal parameters in frozen hydrate-bearing samples subjected to warming (to positive temperatures) and pressure drop (to below equilibrium).

2. Materials and Methods

The thermal conductivity of frozen hydrate-bearing sand was studied in a test pressure cell (Figure 1) with a system of gas supply and automatic pressure and temperature recording (Figure 2), which was placed into a 0.25 m³ climatic cell with set temperature conditions. The temperature and pressure in the pressure cell were monitored by an ADC connected to a PC. The thermal conductivity of frozen hydrate-free and hydrate-bearing sediments was measured by a METER Group Inc. (NE Hopkins, USA) KD-2 dual-needle probe, with needles 30 mm long and 1.3 mm in diameter (sensor SH-1). The heat impact from the probe caused no more than 0.5 °C additional heating of the samples. The theoretical background for the use of the dual-needle probe for measuring the thermal properties was provided earlier [49]. An earlier modification of the KD-2 instrument (Decagon, NE Hopkins, Pullman, WA, USA) was used successfully in experiments with frozen, unfrozen, and hydrate-bearing samples [43]. The thermal conductivity of frozen samples was measured at an accuracy no worse than ±5%.

The measurements were applied to natural sand sampled from depths of 37–47 m at the South Tambey gas condensate field in the Yamal Peninsula (northern West Siberia). Drilling operations in this area revealed numerous gas emissions, which is implicit evidence for the presence of relict gas hydrates that may be self-preserved in shallow permafrost [50]. The samples mainly consisted of quartz, with particle sizes ~95.6% sand (0.25–0.1 mm), ~3.7% silt (0.05–0.001 mm), and <0.7% clay (<0.001 mm). The salinity was no more than 0.05%.

The air-dry soil samples were prepared with a specified initial moisture content and density. To attain the designed water content, the dry soil samples, with initial parameters as listed in

Table 1. Main initial parameters of frozen sand samples.

Run	Moisture Content, %	Dry Density, g/cm3	Porosity, u.f.	${\mathit{S}}_{\mathit{i}}$, %
1	16	1.64	0.37	78
2	16	1.65	0.37	78
3	14	1.68	0.35	73
4	16	1.69	0.35	85

, were mixed with distilled water and then left 30 min for stabilization. The wet soil was compacted layer by layer into cylindrical plastic containers, 90 mm in height and 60–70 mm in diameter.

The samples had a moisture content of 14 to 16%, a dry density of 1.64 to 1.69 g/cm³, a porosity of ~35 to 37%, and an ice saturation ($S_i$) of 73 to 85% (Table 1). They were not saline in runs 1 to 3 but saline in run 4 (NaCl, salinity 0.14%).

For laboratory hydrate saturation, the samples with the wanted moisture content were placed into the pressure cell, which was then sealed, vacuumed, cooled down (−6 to −8 °C), and filled with hydrate-forming gas (CH₄). The hydrate saturation lasted several days at conditions of above-equilibrium pressure required for pore hydrate formation (6–8 MPa) and a temperature first maintained at a constant negative level and then varied cyclically between −6 to −8 °C and +2 °C (Figure 2). Then the frozen hydrate-saturated samples were exposed to nonequilibrium conditions by decreasing the pressure in the cell to 0.1 MPa (in runs 1, 3, and 4) and to 1.5 MPa in run 2, while the temperature was a constant negative (about −6 °C). Then, the pressure cell with the frozen hydrate-bearing samples was heated slowly to +3 °C at 0.1 °C per hour. Thermal conductivity and hydrate content were monitored at each step of the procedure. The laboratory hydrate saturation provided 44 to 58% conversion of pore ice to hydrate (hydrate coefficient, $K_h$), which filled 47–60% of pore volume (hydrate saturation, $S_h$).

3. Results

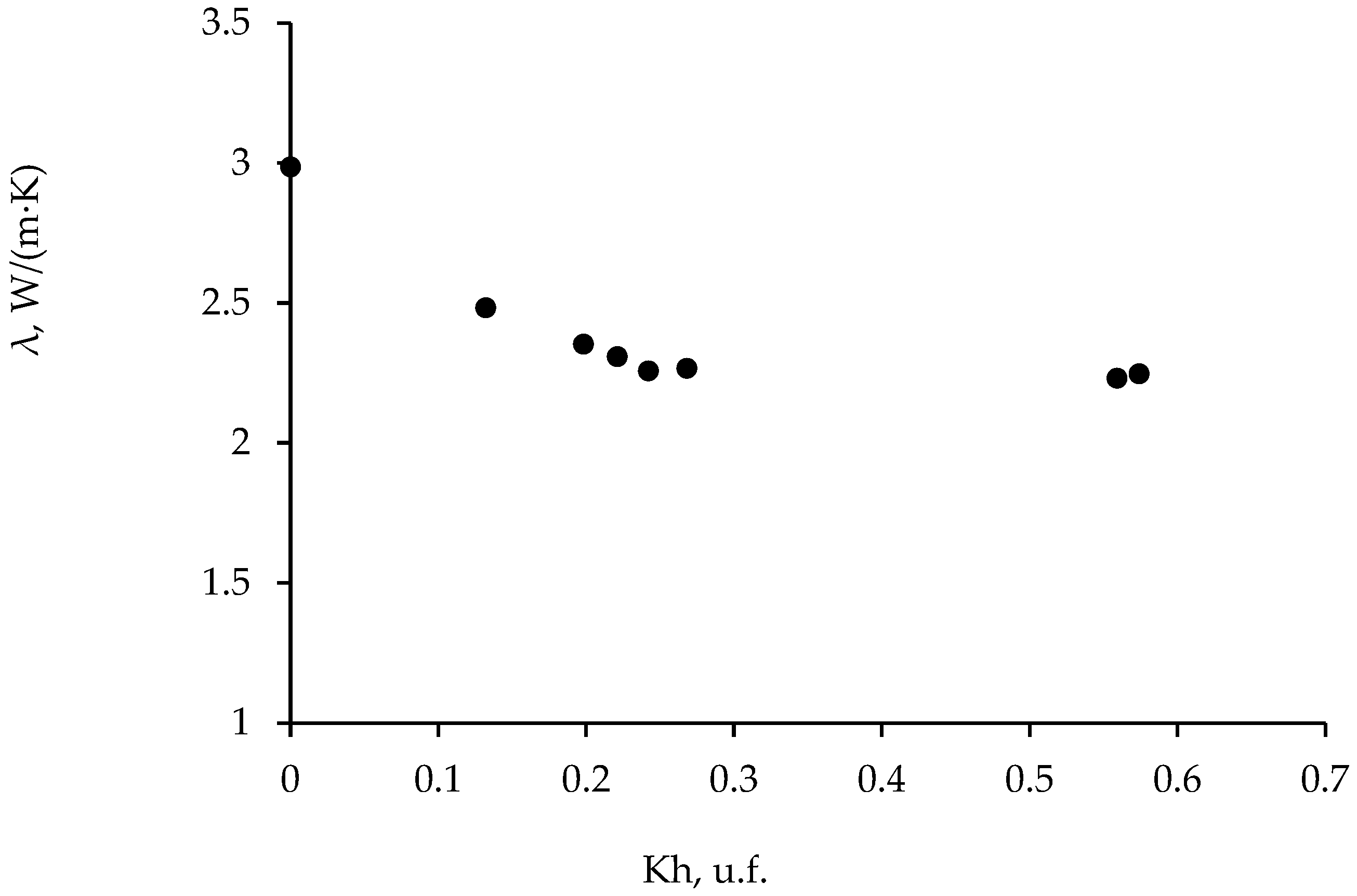
3.1. Thermal Conductivity of Frozen Sand: Effect of Gas Hydrate Component

The performed modeling confirms that the thermal conductivity of frozen sand is lower in the presence of pore gas hydrate in the soil system, while more thermally conductive pore ice has lower percentages. The behavior of thermal conductivity depends on the fraction of pore ice converted to hydrate (hydrate coefficient, $K_h$), as shown in Figure 3.

The thermal conductivity of sand with 78% ice saturation (run 1) was 2.98 W/m·K prior to saturation with gas hydrate and reduced to 2.25 W/m·K when 57% of pore ice converted to hydrate. The decrease was the most rapid in the beginning of the run: it reached 20% (out of the total 25%) as $K_h$ rose to 0.2 and was slow upon further increase in the hydrate coefficient (Figure 3). The same behavior was observed in other runs as well, with thermal conductivity decreasing for 25–30% upon hydrate saturation of the sand samples, as 45–50% of pore ice converted to hydrate.

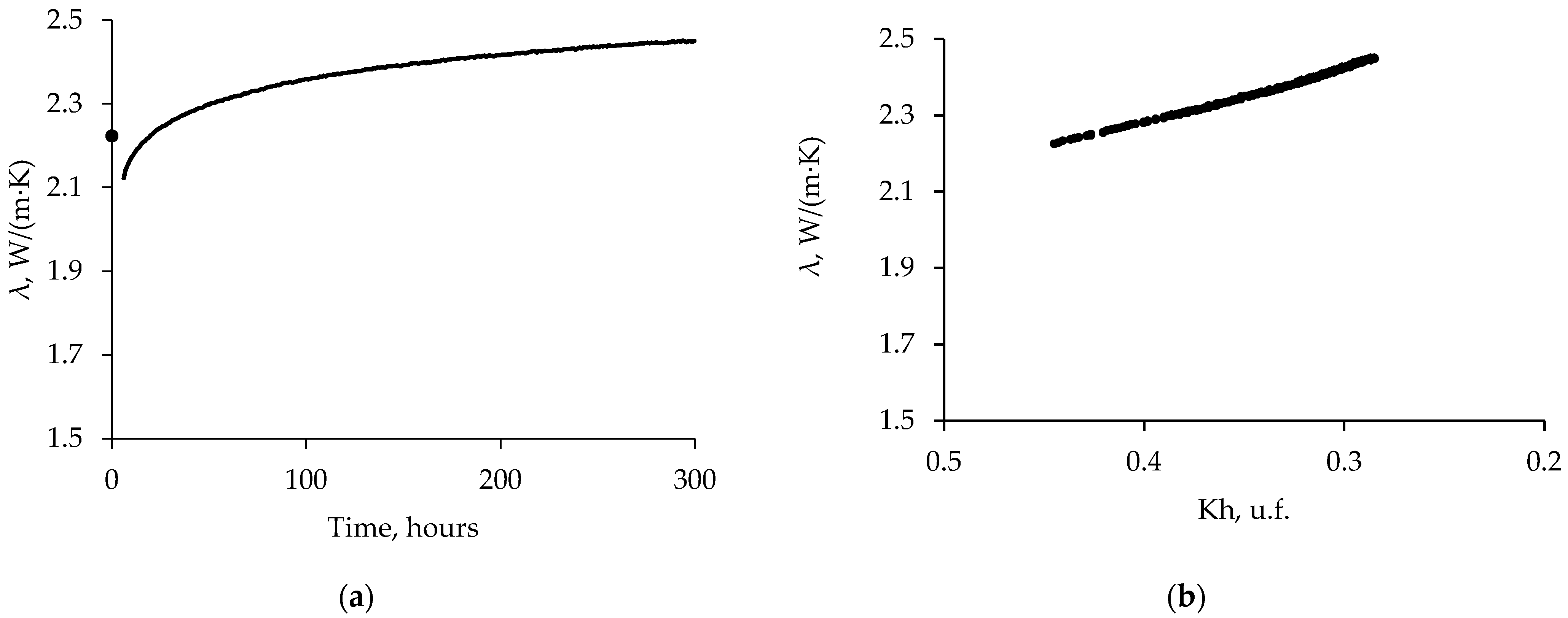
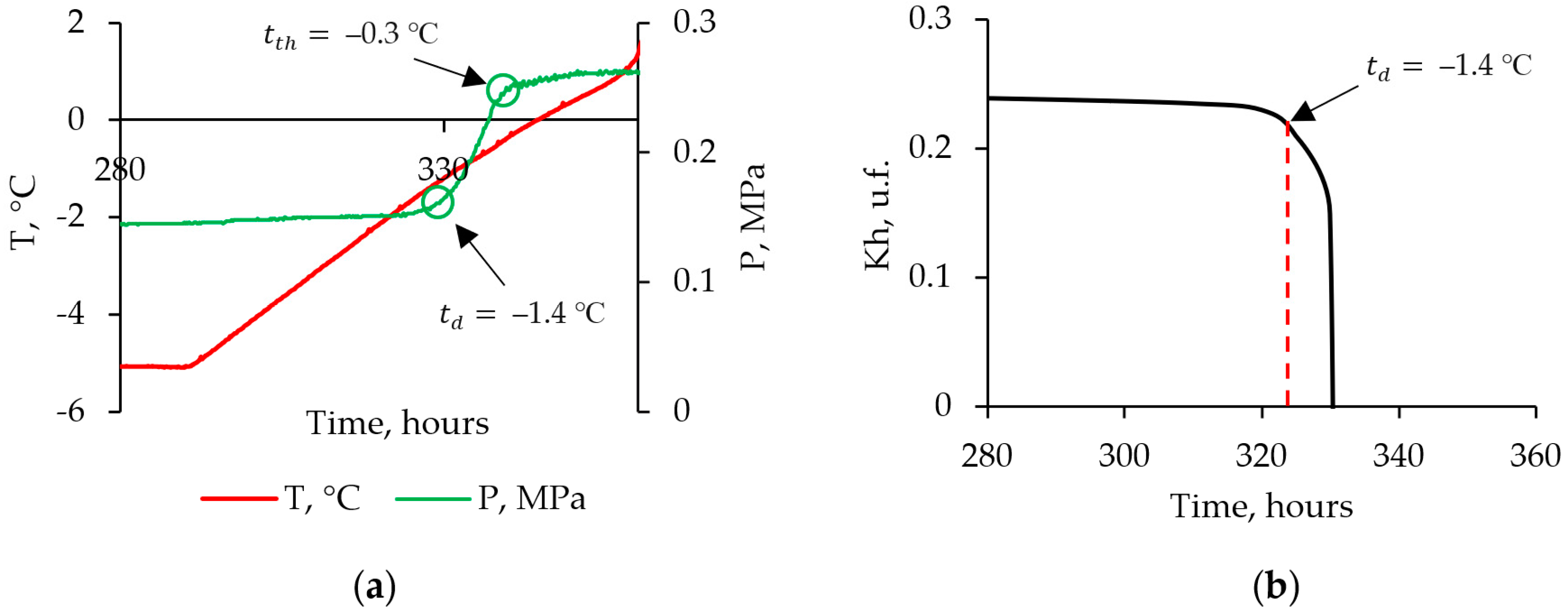
3.2. Thermal Conductivity of Frozen Sand: Effect of Pressure Drop to Below Equilibrium

The samples, which were saturated with methane hydrate and frozen, were then exposed to a pressure decrease to the below-equilibrium level at a constant temperature of −6 °C. As a result (

Table 2. Hydrate saturation of frozen samples before and after pressure drop.

Run	Hydrate Saturation
	Equilibrium Pressure		Below-Equilibrium Pressure
	${\mathit{S}}_{\mathit{h}}$, %	${\mathit{K}}_{\mathit{h}}$, u.f	${\mathit{S}}_{\mathit{h} \mathit{f}\mathit{i}\mathit{n}}$, %	${\mathit{K}}_{\mathit{h} \mathit{f}\mathit{i}\mathit{n}}$, u.f	${\mathit{K}}_{\mathit{s}\mathit{p}}$, u.f	${\mathsf{\tau }}_{\mathit{d}\mathit{i}\mathit{s}}$, Hours
1	58	0.57	32	0.31	53	300
2	48	0.46	40	0.39	84	175
3	46	0.48	21	0.21	44	140
4	50	0.44	0	0	0	50

$S_h$—hydrate saturation; $K_h$—hydrate coefficient; $S_{h fin}$—final hydrate saturation; $K_{h fin}$—final hydrate coefficient; $K_{sp}$—self-preservation coefficient; ${\mathsf{\tau }}_{dis}$—time of dissociation.

), the pore gas hydrate dissociated completely in run 4 (saline sand) but incompletely in runs 1, 2, and 3 (nonsaline sand) due to self-preservation.

The samples of runs 1–3 still contained 21 to 40% of pore hydrate ($K_h$ = 0.21–0.39) in the end of the dissociation process, while all methane hydrate dissociated in 6 h after the pressure drop in run 4. The self-preservation coefficient ($K_{sp}$), which is a ratio of hydrate saturation at the end of the run to the initial value, was the highest in run 2 but lower in runs 1 and 3: 84%, 44%, and 53%, respectively. The preservation of pore hydrate in run 2 was high because the dissociation stopped as the gas pressure at −5.5 °C reached the equilibrium value 2.1 MPa.

The thermal conductivity variations depending on hydrate coefficient, upon pressure drop, can be illustrated by the results of run 1 (Figure 4).

The pressure drops in run 1 caused ~10% thermal conductivity increase (from 2.25 to 2.45 W/m·K) as the supercooled liquid phase that formed during the hydrate dissociation froze up and healed cracks (Figure 4a). The ice component thereby increased while the hydrate component decreased correspondingly (Figure 4b).

In other runs, the thermal conductivity also increased during hydrate dissociation (Figure 5).

The pressure drops to below the equilibrium first led to a thermal conductivity decrease as a result of microstructure changes (including cracking) in the frozen hydrate-bearing samples, which then increased gradually (Figure 5). The magnitude of the initial decrease apparently depended on pressure, salinity, and hydrate saturation: it was 5%, 9%, 1%, and ~10% in runs 1, 2, 3, and 4, respectively.

In run 1, thermal conductivity became 10% higher upon hydrate dissociation: from 2.25 to 2.45 W/m·K. However, it remained almost the same in run 2 (2.60 W/m·K), as the dissociation was incomplete and did not exceed 16% when the equilibrium pressure decreased to 1.5 MPa at −6 °C and then increased. In run 3, on the contrary, thermal conductivity changed from 2.1 to 2.5 W/m·K, as the ice and hydrate saturation values were lower (~56% of pore hydrate converted to ice in run 3 and no more than 47% in run 1), and hydrate dissociation was more rapid than in the case of run 1. The thermal conductivity increase in run 4 (saline sample) was more than 10%, from 2.3 to 2.56 W/m·K, for ~22 h. The reason was that the self-preservation effect in that sample was weakly pronounced, and pore gas hydrate dissociated rapidly. After that point, the thermal conductivity value remained at about the 2.56 W/m·K level (Figure 5).

The revealed pore hydrate dissociation patterns in frozen sand samples show that the dissociation rate and self-preservation of gas hydrate in frozen-ground systems depend on their nonequilibrium pressure and salinity.

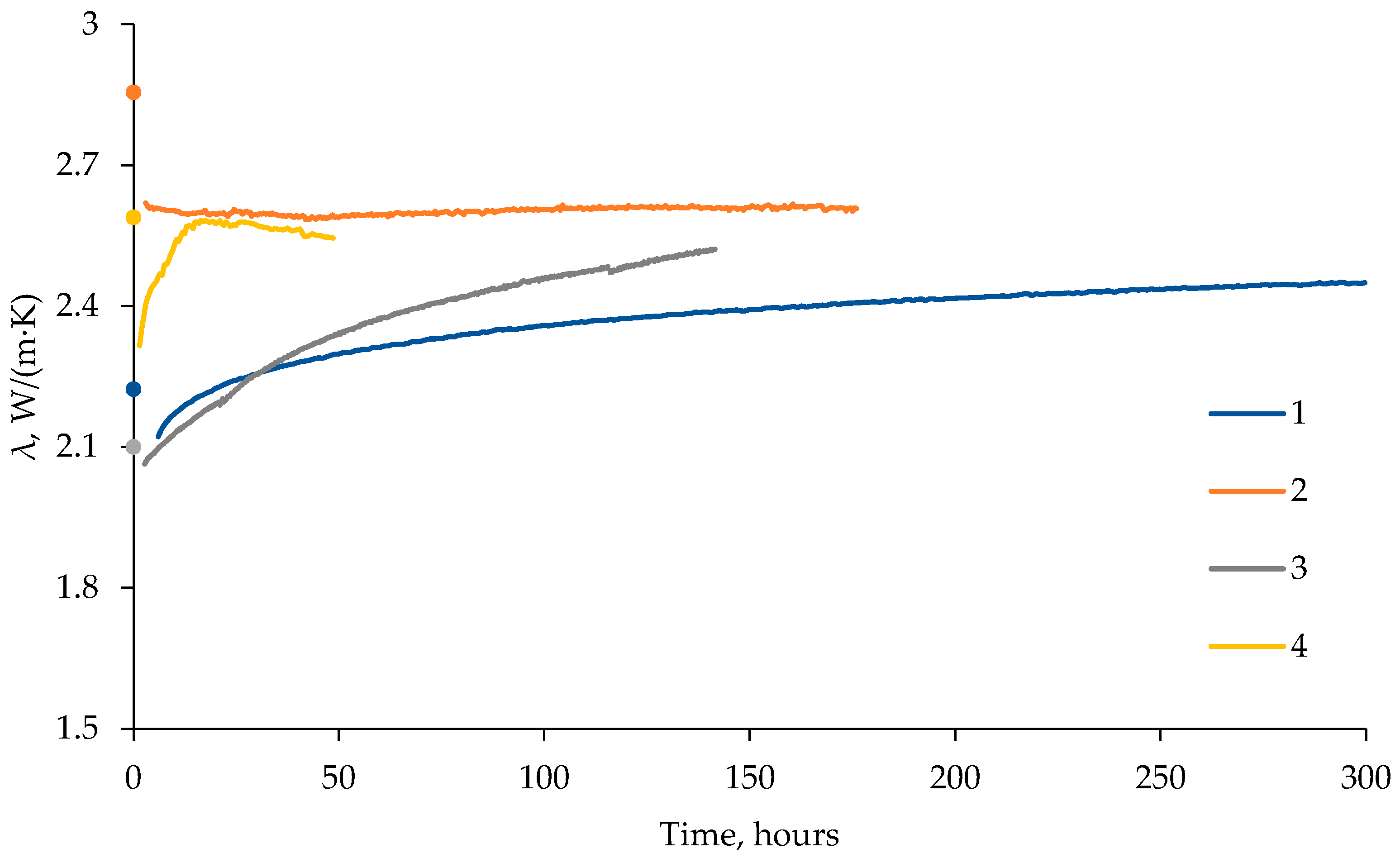
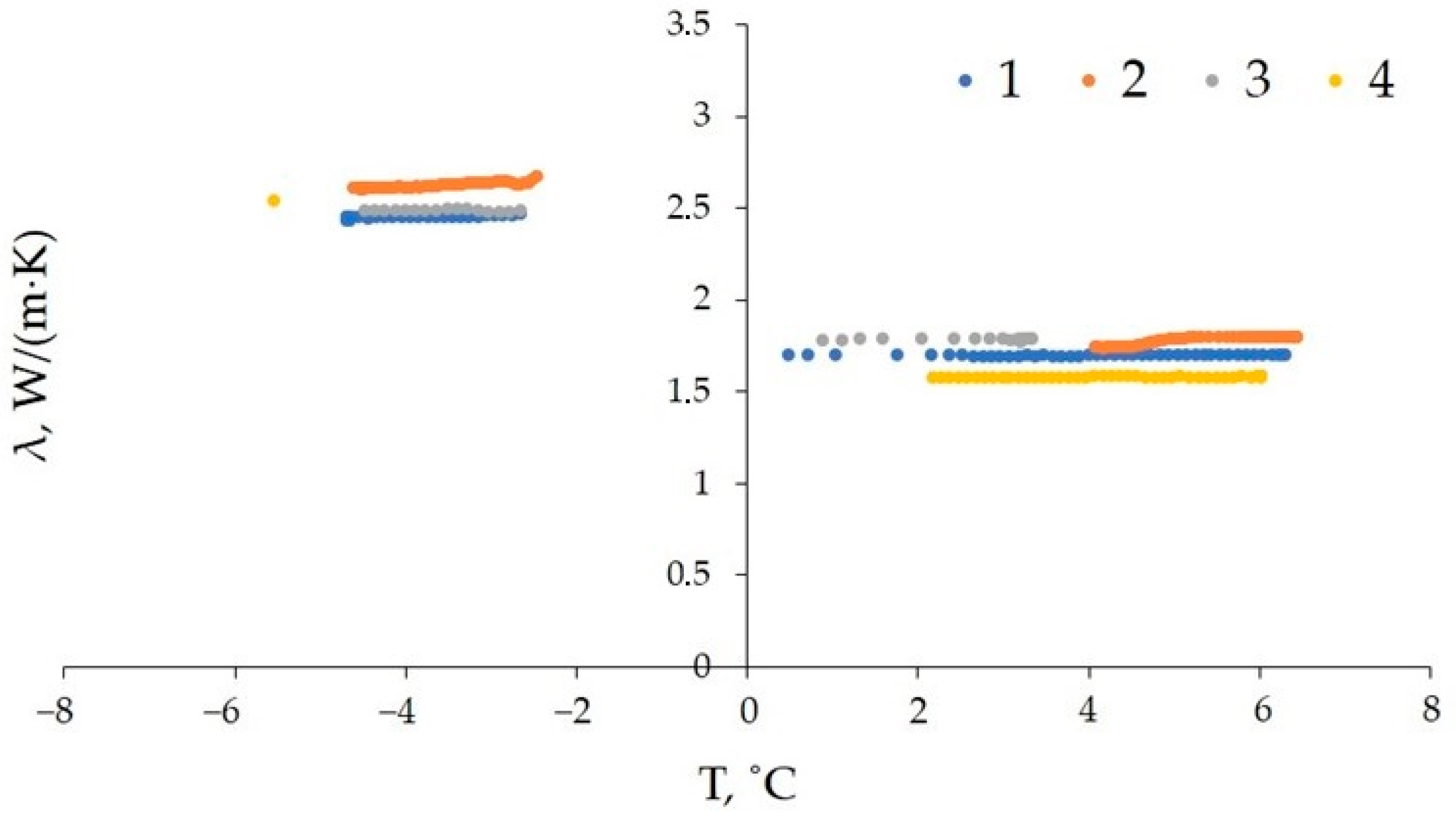
3.3. Thermal Conductivity of Frozen Sand: Effect of Temperature Increase

At the next step of the experimental procedure, the frozen hydrate-bearing sand samples were heated to +3 °C at 0.1 °C/h, at different pressure levels, whereby the hydrate coefficient changed with time (Figure 6a,b, run 1).

The temperature increase in the cell pressure with the samples was accompanied by an increase in the gas pressure (as gas expanded upon heating), dissociation of pore gas hydrate detectable from rapid pressure increase, and thawing of pore ice. Calculations for time-dependent contents of pore hydrates showed that dissociation occurs at a certain critical temperature ($t_d$) controlled by pressure and soil composition. In run 1, it was −1.4 °C, after which the pore ice melted upon further heating. The ice melting temperature was −0.3 °C, according to experiments on the freezing of pore moisture under methane pressure in the sampled soil (Figure 6).

Pore hydrate in the sand sample of run 2 dissociated at a higher temperature (about −0.4 °C), as the gas pressure reached the equilibrium value (2.1 MPa) at −5.5 °C. The temperature of the hydrate dissociation onset approached that of pore ice melting. Heating of the sample in run 3 led to pore hydrate dissociation at −1.2 °C, at a gas pressure higher than in run 1 (~0.4 MPa). Upon further heating, pore ice melted at −0.3 °C.

The measurements of thermal conductivity in frozen hydrate-bearing samples exposed to heating revealed two temperature ranges where it remained almost invariable after pressure decrease: from −5 °C to −2.5 °C and +0.5 to +6 °C. However, the thermal conductivity values measured between −2.5 °C and +0.5 °C were unreliable because of phase transitions (Figure 6). The thermal conductivity of sample 1 was 2.45 W/m·K in the −5 °C to − 2.5 °C range and about 1.7 W/m·K between +0.5 and +4 °C. In runs 2 and 3, the values were 2.6 and 2.5 W/m·K in the −4.5 °C to −2.6 °C interval, respectively. At positive temperatures, they were ~1.8 W/m·K from +4 to +6 °C in run 2 and about 1.8 W/m·K in the +0.8 to +3 °C interval in run 3 (Figure 7).

The saline sample (run 4) had a thermal conductivity of ~2.5 W/m·K at −5.5 °C after the pore hydrate dissociated. As the temperature increased, thermal conductivity could be measured only within the +2 to +6 °C interval (1.6 W/m·K) and was unreliable in the large interval of phase transitions.

In general, heating of frozen hydrate-bearing samples led to a 28–32% decrease in thermal conductivity on account of pore ice melting and dissociation of residual pore hydrate; the decrease even approached 40% in run 4, in the absence of gas hydrate.

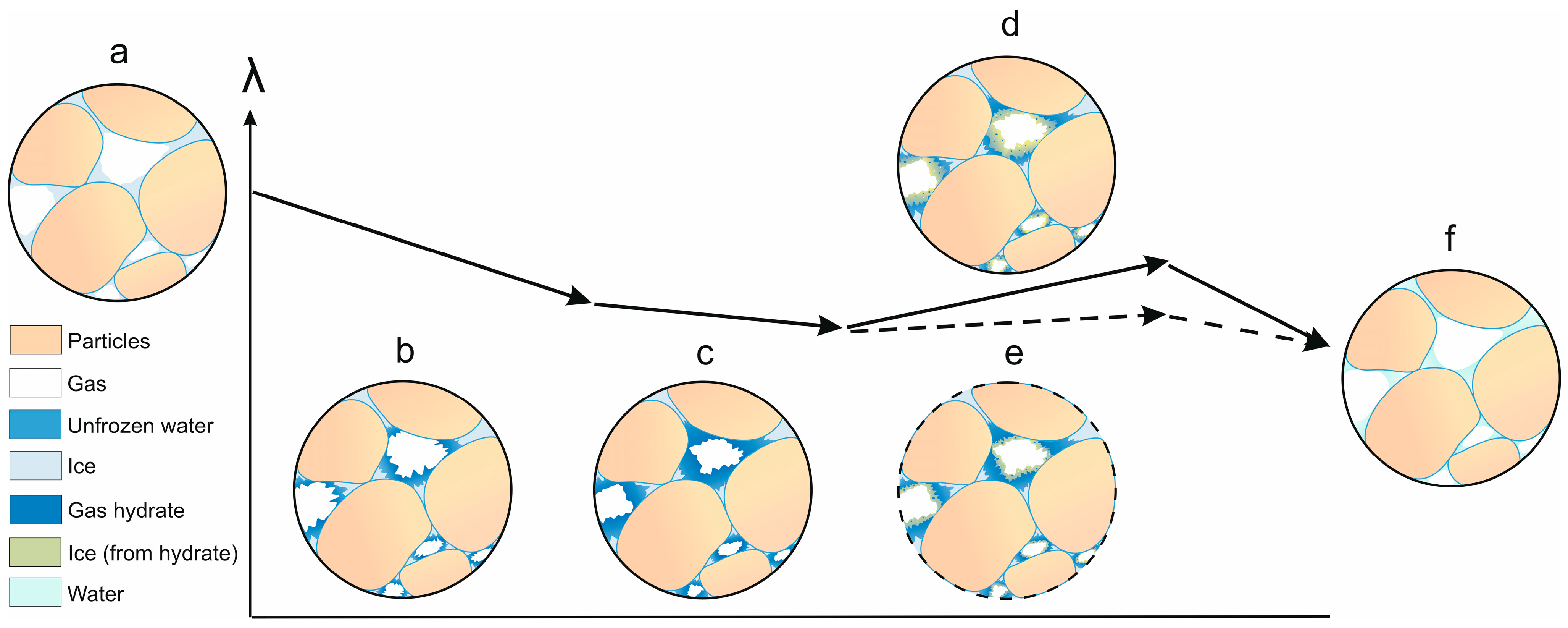
4. Discussion

The experimental results made the basis for a physical model that explains the observed thermal conductivity patterns in frozen hydrate-bearing sand exposed to pressure decrease to below the equilibrium and subsequent heating to positive temperatures. The model simulates qualitative changes of thermal conductivity in the context of the main processes in the pore space of the soil system (Figure 8).

At the initial stage, the pore space of sand is partly filled with ice (Figure 8a). As the sample is saturated with a hydrate-forming gas, the gas pressure increases to an above-equilibrium level, and some portion of pore ice converts to hydrate (Figure 8b). Gas hydrate formation starts from the ice surface and propagates along cracks and grain defects inward to the pore ice. The process decays with time according to the kinetics of hydrate formation as the penetration of the hydrate-forming gas to the ice–hydrate transition front progressively slows down [51,52]. The conversion of pore ice to hydrate decreases the thermal conductivity of frozen ground as the ice percentage reduces (Figure 8b). The same trend was observed in our earlier studies [42].

Freezing–thawing cycles to below and above 0 °C, at an above-equilibrium gas pressure, induce more active pore hydrate formation in frozen sand, while the pore ice not yet converted to hydrate melts and more hydrate can form. The additional hydrate formation is facilitated by the appearance of new gas–water contacts in the pore space. The resulting presence of components with low thermal conductivity makes the frozen hydrate-bearing sand generally less thermally conductive (Figure 8c).

At the next step, the pressure of hydrate-forming gas decreases to 0.1 MPa, and the pore gas hydrate dissociates into supercooled water and gas. Non-equilibrium supercooled water freezes up on the surface of hydrate particles, and the ice coat precludes further hydrate dissociation, whereby thermal conductivity increases (Figure 8d).

Later on, at a minor decrease in gas pressure relative to the equilibrium in the frozen hydrate-bearing soil system, subsequent rapid pressure increases till the equilibrium due to the dissociation of pore gas hydrate leads to partial surface hydrate dissociation. As a result, thermal conductivity remains almost invariable (Figure 8e).

Further heating of the hydrate-bearing samples leads to complete dissociation of pore gas hydrate and thawing, while thermal conductivity decreases (Figure 8f).

5. Conclusions

The reported laboratory experiments with frozen hydrate-bearing sandy soils exposed to decreasing pressure and increasing temperature revealed several trends in the behavior of thermal conductivity:

(1)

Thermal conductivity increased (up to 20%) during dissociation of pore gas hydrate in frozen hydrate-bearing sand samples as gas pressure dropped below the equilibrium, as the relative percentages of low- and high-conductive components (methane hydrate and ice, respectively) shifted toward the latter. However, thermal conductivity first became a few percent to 10% lower, due to cracking, before increasing as the dissociated gas hydrate converted into ice (via liquid water).

(2)

Heating of hydrate-bearing sand containing 20–40% of residual pore hydrate to positive temperatures led to a 30% decrease in its thermal conductivity. The magnitude of thermal conductivity decreases in saline sand free from residual pore hydrate correlated with salinity (it was 40% at a salinity of ~0.14%).

The experimental results made the basis for a model that explained the observed thermal conductivity trends in terms of pore space changes in the frozen hydrate-bearing sediments associated with hydrate formation, decompression, and heating.