Naïve and Semi-Naïve Bayesian Classification of Landslide Susceptibility Applied to the Kulekhani River Basin in Nepal as a Test Case
Abstract
:1. Introduction
2. Materials and Methods
2.1. Methods
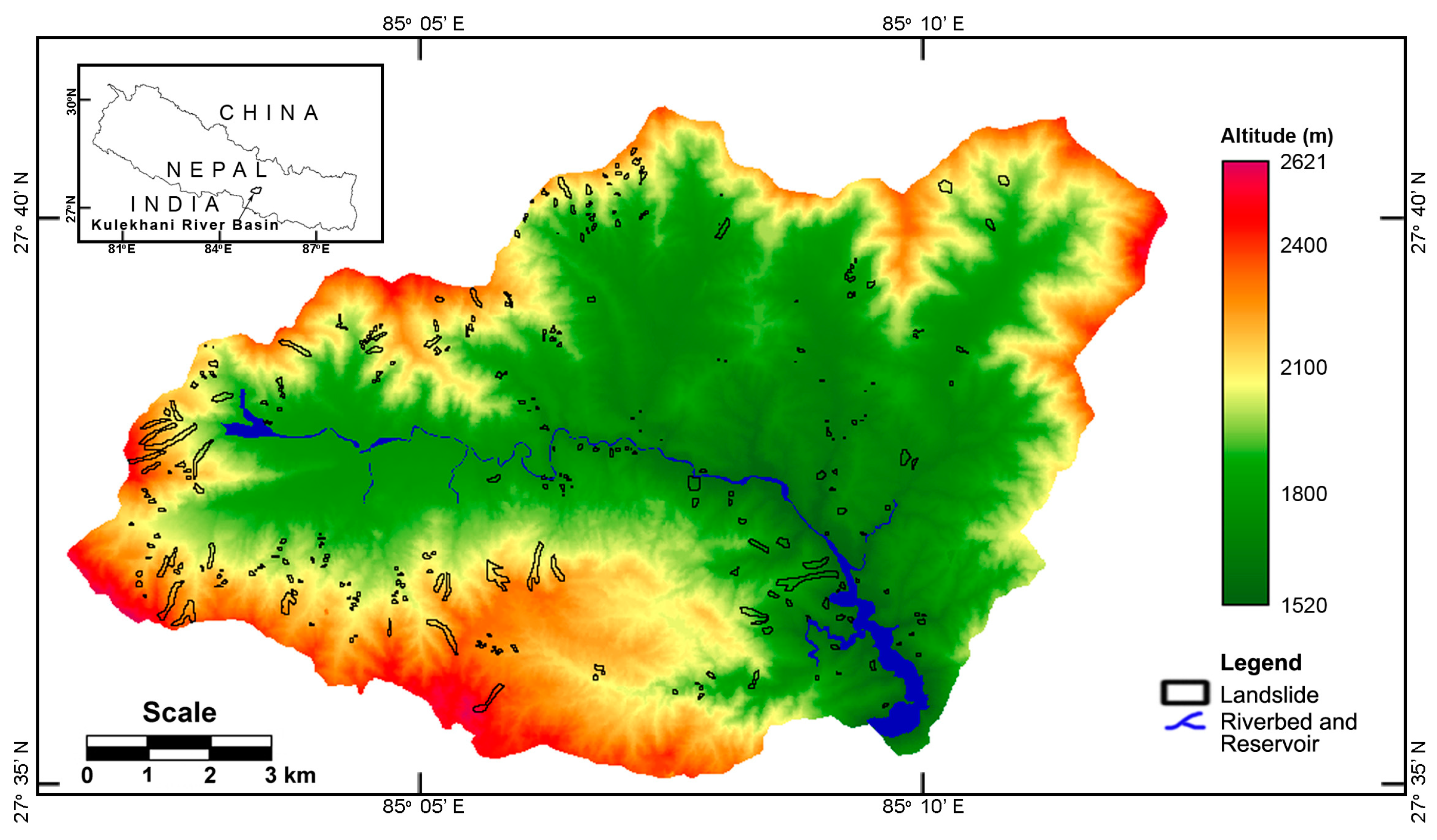
2.2. Test Case
3. Results
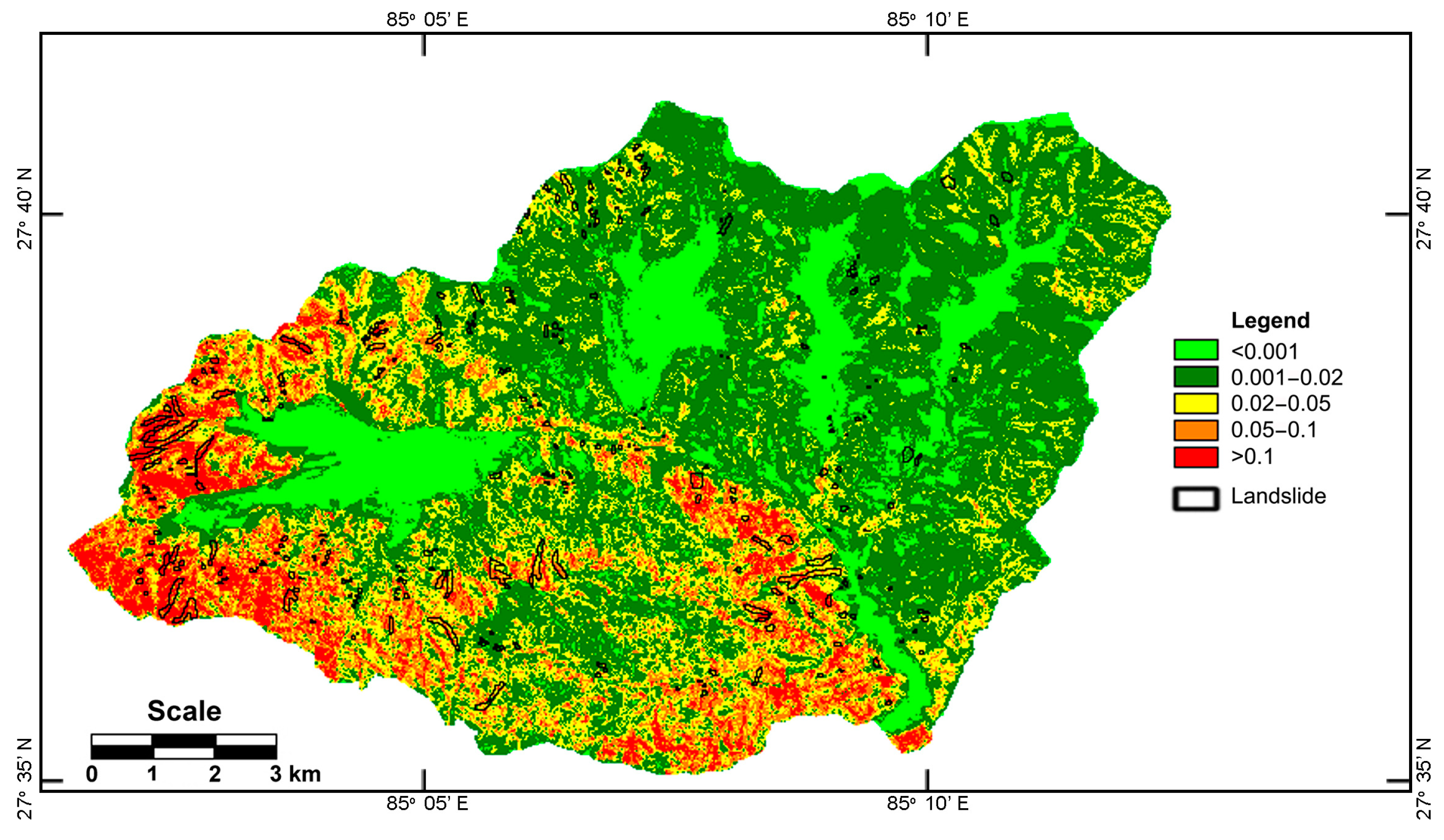
3.1. Naïve Bayes Model
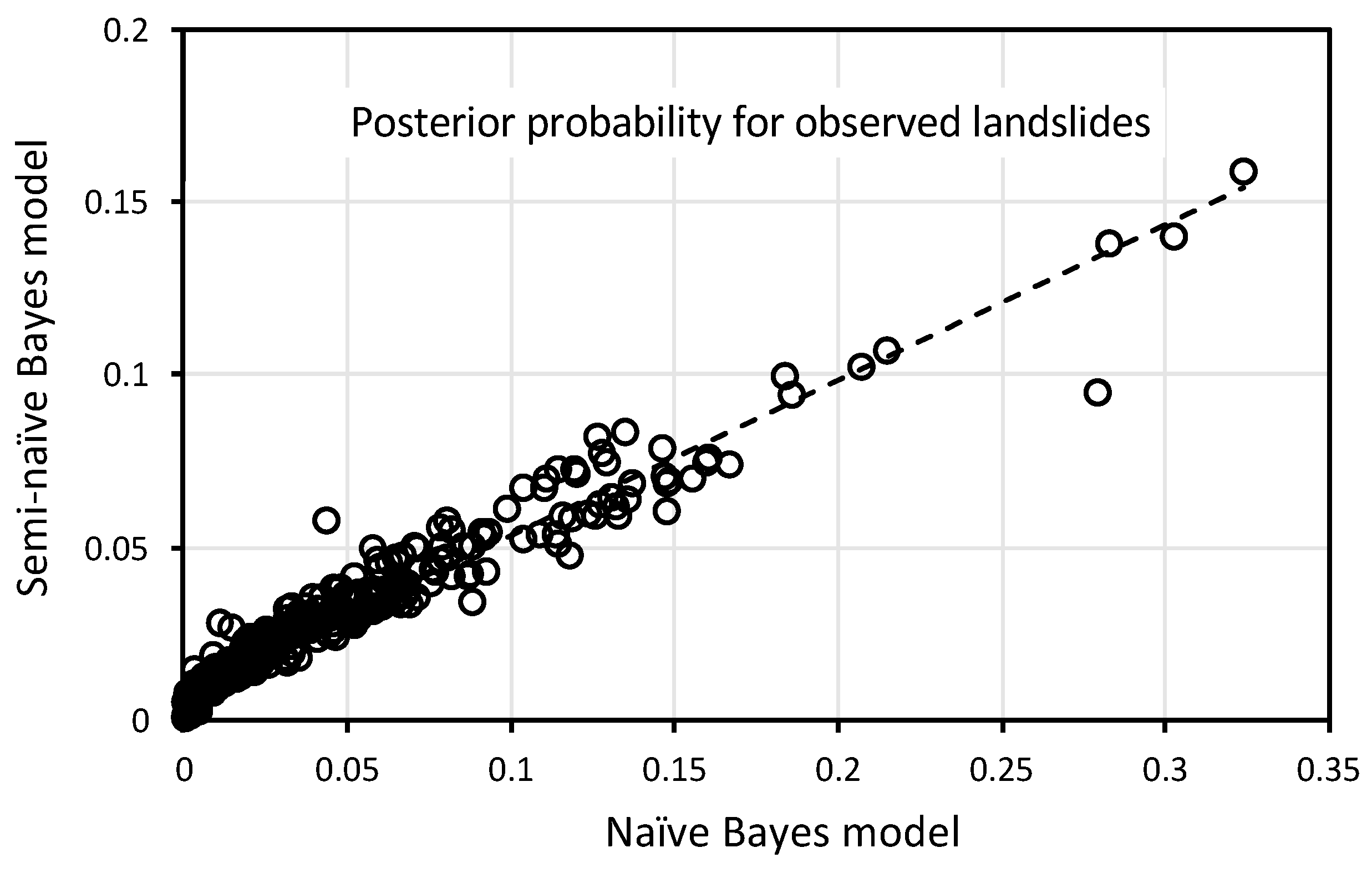
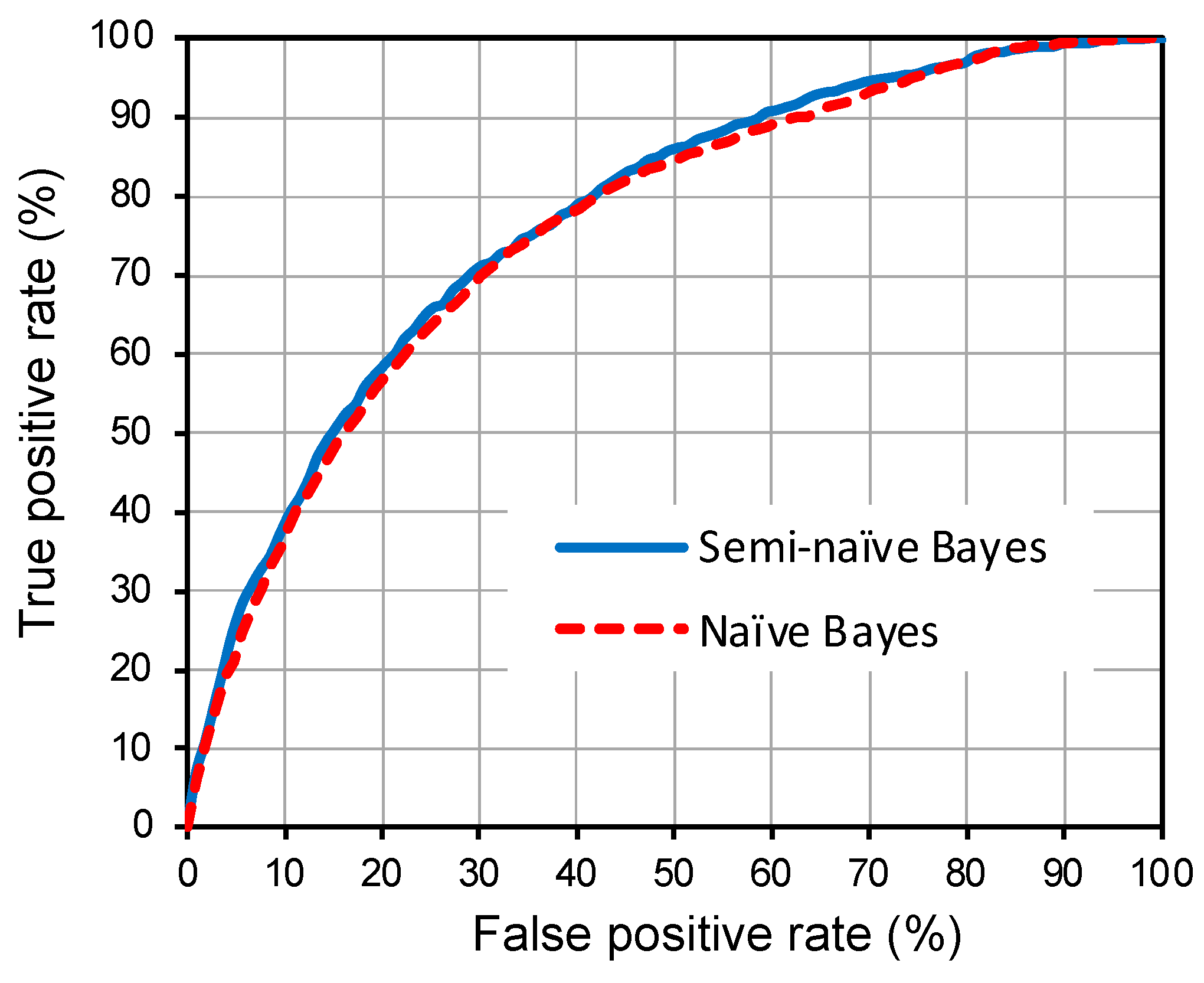
3.2. Semi-Naïve Bayes Model
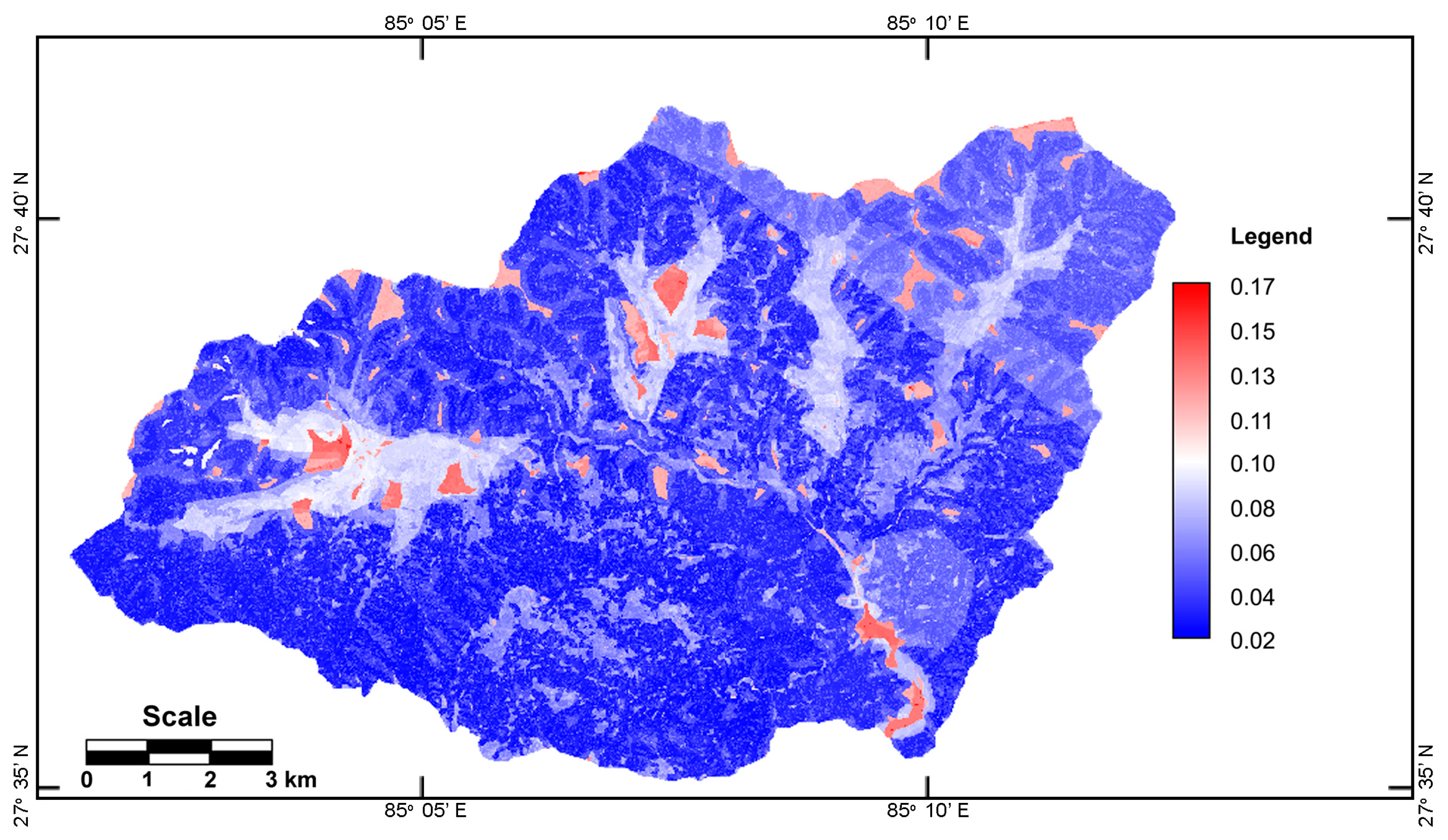
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wickramasinghe, I.; Kalutarage, H. Naive Bayes: Applications, variations and vulnerabilities: A review of literature with code snippets for implementation. Soft. Comput. 2021, 25, 2277–2293. [Google Scholar] [CrossRef]
- Zaidi, N.A.; Cerquides, J.; Carman, M.J.; Webb, G.I. Alleviating naive Bayes attribute independence assumption by attribute weighting. J. Mach. Learn. Res. 2013, 14, 1947–1988. [Google Scholar]
- Guzzetti, F.; Reichenbach, P.; Cardinali, M.; Galli, M.; Ardizzone, F. Probabilistic landslide hazard assessment at the basin scale. Geomorphology 2005, 72, 272–299. [Google Scholar] [CrossRef]
- Wu, W.; Sidle, R.C. A distributed slope stability model for steep forested basins. Water Resour. Res. 1995, 31, 2097–2110. [Google Scholar] [CrossRef]
- Dai, F.C.; Lee, C.F.; Xu, Z.W. Assessment of landslide susceptibility on the natural terrain of Lantau Island, Hong Kong. Env. Geol. 2001, 40, 381–391. [Google Scholar] [CrossRef]
- Dahal, R.K.; Hasegawa, S.; Nonomura, A.; Yamanaka, M.; Dhakal, S.; Paudyal, P. Predictive modeling of rainfall-induced landslide hazard in the Lesser Himalaya of Nepal based on weights-of-evidence. Geomorphology 2008, 102, 496–510. [Google Scholar] [CrossRef]
- Huabin, W.; Gangjun, L.; Gonghui, W. GIS-based landslide hazard assessment: An overview. Prog. Phys. Geog. 2005, 29, 548–567. [Google Scholar] [CrossRef]
- Van Westen, C. Statistical Landslide Hazard Analysis ILWIS 21 for Windows Application Guide; ITC Publication: Enschede, The Netherlands, 1997; pp. 73–84. [Google Scholar]
- Lee, S.; Choi, J.; Min, K. Landslide susceptibility analysis and verification using the Bayesian probability model. Env. Geol. 2002, 43, 120–131. [Google Scholar] [CrossRef]
- Lee, S. Current and future status of GIS-based landslide susceptibility mapping: A literature review. Korean J. Remote Sens. 2019, 35, 179–193. [Google Scholar] [CrossRef]
- Reichenbach, P.; Rossi, M.; Malamud, B.D.; Mihir, M.; Guzzetti, F. A review of statistically-based landslide susceptibility models. Earth Sci. Rev. 2018, 180, 60–91. [Google Scholar] [CrossRef]
- Rossi, M.; Guzzetti, F.; Reichenbach, P.; Mondini, A.C.; Peruccacci, S. Optimal landslide susceptibility zonation based on multiple forecasts. Geomorphology 2010, 114, 129–142. [Google Scholar] [CrossRef]
- Bonham-Carter, G.F.; Agterberg, F.P.; Wright, D.F. Weights of evidence modeling: A new approach to mapping mineral potential. In Statistical Applications in the Earth Sciences; Agterberg, F.P., Bonham-Carter, G.F., Eds.; GSC-89-9; Geological Survey: Ottawa, ON, Canada, 1989; pp. 171–183. [Google Scholar]
- Bonham-Carter, G.F. Geographic Information Systems for Geoscientists; Pergamon: Oxford, UK, 1994; 398p. [Google Scholar]
- Zhang, D.; Agterberg, F. Modified weights-of-evidence modeling with example of missing geochemical data. Complexity 2018, 2018, 7945960. [Google Scholar] [CrossRef]
- Van Westen, C.J.; Rengers, N.; Soeters, R. Use of geomorphological information in indirect landslide susceptibility assessment. Nat. Hazards 2003, 30, 399–419. [Google Scholar] [CrossRef]
- Neuhäuser, B.; Terhorst, B. Landslide susceptibility assessment using “weights-of-evidence” applied to a study area at the Jurassic escarpment (SW-Germany). Geomorphology 2007, 86, 12–24. [Google Scholar] [CrossRef]
- Regmi, N.R.; Giardino, J.R.; Vitek, J.D. Modeling susceptibility to landslides using the weight of evidence approach: Western Colorado, USA. Geomorphology 2010, 115, 172–187. [Google Scholar] [CrossRef]
- Cervi, F.; Berti, M.; Borgatti, L.; Ronchetti, F.; Manenti, F.; Corsini, A. Comparing predictive capability of statistical and deterministic methods for landslide susceptibility mapping: A case study in the northern Apennines (Reggio Emilia Province, Italy). Landslides 2010, 7, 433–444. [Google Scholar] [CrossRef]
- Chen, X.; Chen, H.; You, Y.; Chen, X.; Liu, J. Weights-of-evidence method based on GIS for assessing susceptibility to debris flows in Kangding County, Sichuan Province, China. Environ. Earth Sci. 2016, 75, 70. [Google Scholar] [CrossRef]
- Rahman, M.S.; Ahmed, B.; Di, L. Landslide initiation and runout susceptibility modeling in the context of hill cutting and rapid urbanization: A combined approach of weights of evidence and spatial multi-criteria. J. Mt. Sci. 2017, 14, 1919–1937. [Google Scholar] [CrossRef]
- Polykretis, C.; Chalkias, C. Comparison and evaluation of landslide susceptibility maps obtained from weight of evidence, logistic regression, and artificial neural network models. Nat. Hazards 2018, 93, 249–274. [Google Scholar] [CrossRef]
- Jaafari, A. LiDAR-supported prediction of slope failures using an integrated ensemble weights- of-evidence and analytical hierarchy process. Environ. Earth Sci. 2018, 77, 42. [Google Scholar] [CrossRef]
- Agterberg, F.P.; Cheng, Q. Conditional independence test for Weights-of-Evidence modelling. Nat. Resour. Res. 2002, 11, 249–255. [Google Scholar] [CrossRef]
- Deng, M. A conditional dependence adjusted weights of evidence model. Nat. Resour. Res. 2009, 18, 249–258. [Google Scholar] [CrossRef]
- Schaeben, H. A mathematical view of weights-of-evidence, conditional independence, and logistic regression in terms of markov random fields. Math. Geosci. 2014, 46, 691–709. [Google Scholar] [CrossRef]
- Agterberg, F. A modified weights-of-evidence method for regional mineral resource estimation. Nat. Resour. Res. 2011, 20, 95–101. [Google Scholar] [CrossRef]
- Siddiqi, N. Credit Risk Scorecards; John Wiley and Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Larsen, K. Data Exploration with Weight of Evidence and Information Value in R. 2015. Available online: https://multithreaded.stitchfix.com/blog/2015/08/13/weight-of-evidence/ (accessed on 10 August 2023).
- Zhang, D.; Agterberg, F.; Cheng, Q.; Zuo, R. A comparison of modified fuzzy weights of evidence, fuzzy weights of evidence, and logistic regression for mapping mineral prospectivity. Math. Geosci. 2014, 46, 869–885. [Google Scholar] [CrossRef]
- Stöcklin, J.; Bhattarai, K.D. Geology of Kathmandu area and central Mahabharat Range, Nepal Himalaya. In HMG/UNDP Mineral Exploration Project, Technical Report; Department of Mines and Geology: Kathmandu, Nepal, 1977; 86p. [Google Scholar]
- Stöcklin, J. Geology of Nepal and its regional frame. J. Geol. Soc. 1980, 137, 1–34. [Google Scholar] [CrossRef]
- Regmi, M. Geology of Khulekhani Watershed in Central Nepal with Special Reference to Landslides and Weathering. Master’s Thesis, Tribhuvan University, Kirtipur, Kathmandu, Nepal, 2002. [Google Scholar]
- Dhital, M.R. Geology of the Nepal Himalaya; Springer: New York, NY, USA, 2015; 498p. [Google Scholar]
- Dhital, M.R.; Khanal, N.; Thapa, K.B. The Role of Extreme Weather Events, Mass Movements, and Land Use Changes in Increasing Natural Hazards; International Centre for Integrated Mountain Development: Kathmandu, Nepal, 1993; 108p. [Google Scholar]
- Dhakal, A.S.; Amada, T.; Aniya, M. Landslide hazard mapping and the application of GIS in the Kulekhani watershed, Nepal. Mt. Res. Dev. 1999, 19, 3–16. [Google Scholar] [CrossRef]
- Dhakal, A.S.; Amada, T.; Aniya, M. Landslide hazard mapping and its evaluation using GIS: An investigation of sampling schemes for a grid-cell based quantitative method. Photogramm. Eng. Remote Sens. 2000, 66, 981–989. [Google Scholar]
- Dhital, M.R. Causes and consequences of the 1993 debris flows and landslides in the Kulekhani watershed, central Nepal. In Debris-Flow Hazards Mitigation: Mechanics, Prediction, and Assessment; Rickenmann, D., Chen, C.L., Eds.; Millpress: Rotterdam, The Netherlands, 2003; pp. 931–942. [Google Scholar]
- Dhar, M.S.; Dhital, M.R. Application of Morishita Spread Index in the study of landslides from the Kulekhani watershed, central Nepal. J. Nepal Geol. Soc. 2004, 30, 123–126. [Google Scholar] [CrossRef]
- Kayastha, P.; Dhital, M.R.; De Smedt, F. Evaluation and comparison of GIS based landslide susceptibility mapping procedures in Kulekhani watershed, Nepal. J. Geol. Soc. India 2013, 81, 219–231. [Google Scholar] [CrossRef]
- Larsen, K. Information: Data Exploration with Information Theory (Weight-of-Evidence and Information Value). Available online: https://CRAN.R-project.org/package=Information (accessed on 12 August 2023).
- Lee, S.; Min, K. Statistical analysis of landslide susceptibility at Yongin, Korea. Env. Geol. 2001, 40, 1095–1113. [Google Scholar] [CrossRef]
- R Core Team. Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria. 2017; Available online: http://www.R-project.org/ (accessed on 15 November 2021).


| IV | Predictive Power |
|---|---|
| < 0.02 | Unpredictive |
| 0.02–0.1 | Weak |
| 0.1–0.3 | Medium |
| > 0.3 | Strong |
| Factor and Class | ||||
|---|---|---|---|---|
| Slope aspect | ||||
| N | 0.131 | 0.116 | 0.121 | 0.002 |
| NE | 0.228 | 0.149 | 0.427 | 0.034 |
| E | 0.168 | 0.127 | 0.279 | 0.011 |
| SE | 0.140 | 0.136 | 0.026 | 0.000 |
| S | 0.093 | 0.119 | –0.242 | 0.006 |
| SW | 0.074 | 0.122 | –0.502 | 0.024 |
| W | 0.051 | 0.107 | –0.743 | 0.042 |
| NW | 0.114 | 0.120 | –0.051 | 0.000 |
| Flat | 0.000 | 0.003 | –2.165 | 0.006 |
| Slope angle | ||||
| <5° | 0.020 | 0.081 | –1.408 | 0.087 |
| 5–15° | 0.097 | 0.193 | –0.685 | 0.066 |
| 15–25° | 0.221 | 0.236 | –0.063 | 0.001 |
| 25–35° | 0.296 | 0.229 | 0.260 | 0.018 |
| 35–45° | 0.255 | 0.182 | 0.335 | 0.024 |
| >45° | 0.110 | 0.079 | 0.335 | 0.010 |
| Slope shape | ||||
| Convex | 0.439 | 0.397 | 0.100 | 0.004 |
| Straight | 0.138 | 0.207 | –0.410 | 0.029 |
| Concave | 0.423 | 0.395 | 0.068 | 0.002 |
| Relative relief | ||||
| <25 m/ha | 0.049 | 0.206 | –1.447 | 0.228 |
| 25–50 m/ha | 0.381 | 0.425 | –0.110 | 0.005 |
| 50–100 m/ha | 0.566 | 0.362 | 0.448 | 0.092 |
| >100 m/ha | 0.005 | 0.007 | –0.457 | 0.001 |
| Drainage distance | ||||
| <25 m | 0.681 | 0.489 | 0.331 | 0.064 |
| 25–50 m | 0.232 | 0.275 | –0.170 | 0.007 |
| 50–100 m | 0.085 | 0.197 | –0.837 | 0.093 |
| >100 m | 0.002 | 0.039 | –3.130 | 0.117 |
| Geology | ||||
| Chitlang Formation | 0.025 | 0.085 | –1.244 | 0.075 |
| Chandragiri Limestone | 0.009 | 0.050 | –1.780 | 0.075 |
| Sopyang Formation | 0.009 | 0.015 | –0.578 | 0.004 |
| Tistung Formation | 0.148 | 0.227 | –0.428 | 0.034 |
| Markhu Formation | 0.130 | 0.119 | 0.088 | 0.001 |
| Kulikhani Formation | 0.282 | 0.103 | 1.003 | 0.179 |
| Chisapani Quartzite | 0.007 | 0.006 | 0.165 | 0.000 |
| Palung Granite | 0.379 | 0.289 | 0.270 | 0.024 |
| Quarternary deposits | 0.013 | 0.104 | –2.116 | 0.194 |
| Land use | ||||
| Built-up area | 0.000 | 0.000 | 0.000 | 0.000 |
| Agriculture | 0.372 | 0.494 | –0.284 | 0.035 |
| Forest | 0.514 | 0.412 | 0.221 | 0.023 |
| Nursery | 0.000 | 0.002 | 0.000 | 0.000 |
| Grassland | 0.002 | 0.001 | 0.980 | 0.001 |
| Bush | 0.093 | 0.074 | 0.223 | 0.004 |
| Riverbed | 0.003 | 0.005 | –0.626 | 0.001 |
| Barren land | 0.016 | 0.002 | 2.278 | 0.033 |
| Reservoir | 0.000 | 0.010 | 0.000 | 0.000 |
| Annual rainfall | ||||
| <1500 mm/y | 0.010 | 0.026 | –0.962 | 0.016 |
| 1500–1750 mm/y | 0.599 | 0.732 | –0.200 | 0.027 |
| >1750 mm/y | 0.390 | 0.242 | 0.480 | 0.071 |
| Factor | IV | Predictive Strength |
|---|---|---|
| Geology | 0.587 | very strong |
| Relative relief | 0.326 | strong |
| Drainage distance | 0.281 | medium |
| Slope angle | 0.205 | medium |
| Slope aspect | 0.125 | medium |
| Annual rainfall | 0.114 | medium |
| Land use | 0.097 | weak |
| Slope shape | 0.035 | weak |
| Factor | Coefficient | Estimate | Std. Error | z-Value | Pr (>|z|) |
|---|---|---|---|---|---|
| (Intercept) | –3.976 | 0.015 | –256.8 | <10–16 | |
| Slope aspect | 0.536 | 0.041 | 12.9 | <10–16 | |
| Slope angle | 0.185 | 0.043 | 4.3 | 1.8 × 10–5 | |
| Slope shape | 0.017 | 0.079 | 0.2 | 0.83 | |
| Relative relief | 0.694 | 0.038 | 18.2 | <10–16 | |
| Drainage distance | 0.875 | 0.035 | 24.9 | <10–16 | |
| Geology | 0.817 | 0.022 | 36.4 | <10–16 | |
| Land use | 0.481 | 0.040 | 11.9 | <10–16 | |
| Annual rainfall | 0.719 | 0.040 | 18.1 | <10–16 |
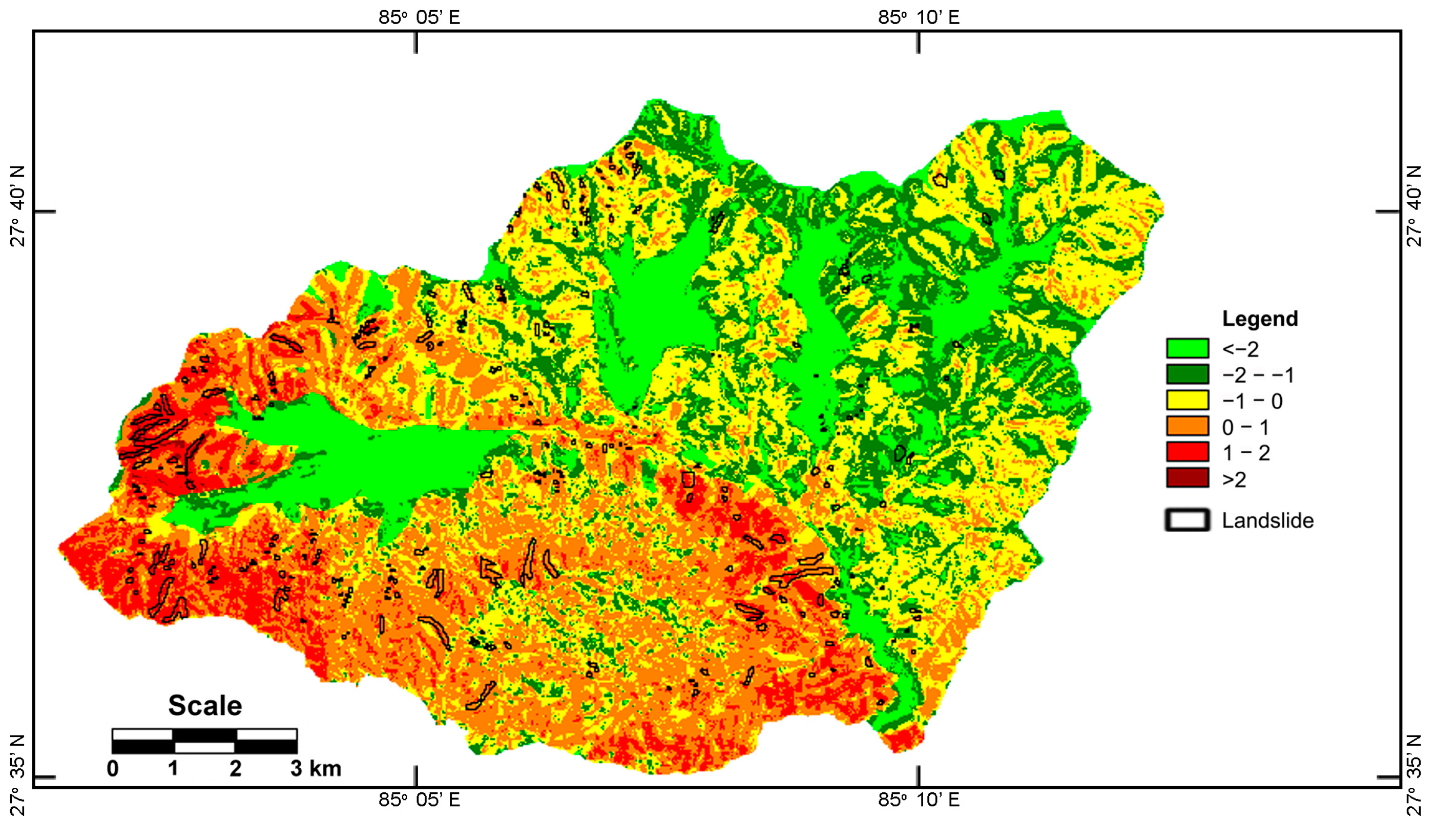
| Category | LSI-Value | Area (%) | Landslides (%) | Ratio |
|---|---|---|---|---|
| 1 | <−2 | 15.6 | 1.6 | 0.1 |
| 2 | −2––1 | 17.3 | 6.1 | 0.4 |
| 3 | −1–0 | 30.3 | 16.2 | 0.5 |
| 4 | 0–1 | 28.1 | 42.5 | 1.5 |
| 5 | 1–2 | 8.5 | 30.6 | 3.6 |
| 6 | >2 | 0.2 | 3.0 | 13.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
De Smedt, F.; Kayastha, P.; Dhital, M.R. Naïve and Semi-Naïve Bayesian Classification of Landslide Susceptibility Applied to the Kulekhani River Basin in Nepal as a Test Case. Geosciences 2023, 13, 306. https://doi.org/10.3390/geosciences13100306
De Smedt F, Kayastha P, Dhital MR. Naïve and Semi-Naïve Bayesian Classification of Landslide Susceptibility Applied to the Kulekhani River Basin in Nepal as a Test Case. Geosciences. 2023; 13(10):306. https://doi.org/10.3390/geosciences13100306
Chicago/Turabian StyleDe Smedt, Florimond, Prabin Kayastha, and Megh Raj Dhital. 2023. "Naïve and Semi-Naïve Bayesian Classification of Landslide Susceptibility Applied to the Kulekhani River Basin in Nepal as a Test Case" Geosciences 13, no. 10: 306. https://doi.org/10.3390/geosciences13100306
APA StyleDe Smedt, F., Kayastha, P., & Dhital, M. R. (2023). Naïve and Semi-Naïve Bayesian Classification of Landslide Susceptibility Applied to the Kulekhani River Basin in Nepal as a Test Case. Geosciences, 13(10), 306. https://doi.org/10.3390/geosciences13100306










