Abstract
Multi-parameter observations, powerful for the study of lithosphere–atmosphere–ionosphere coupling (LAIC), have been performed for a recent Tokyo earthquake (EQ) with a moderate magnitude (M = 5.9) and rather larger depth (~70 km) on 7 October 2021, in the hope of predicting the next Kanto (Tokyo) huge EQ, such as the 1923 Great Kanto EQ (with a magnitude greater than 7). Various possible precursors have been searched during the two-month period of 1 September to 31 October 2021, based on different kinds of data sets: (i) ULF (ultra-low frequency) magnetic data from Kakioka, Japan, (ii) ULF/ELF (extremely low frequency) magnetic field data from the Chubu University network, (iii) meteorological data (temperature and humidity) from the Japan Meteorological Agency (JMA), (iv) AGW (atmospheric gravity wave) ERA5 data provided by the European Centre for Medium-Range Weather Forecast (ECMWF), (v) subionospheric VLF/LF (very low frequency/low frequency) data from Russia and Japan, (vi) ionosonde Japanese data, and (vii) GIM (global ionosphere map) TEC (total electron content) data. After extensive analyses of all of the above data, we have found that there are a few obvious precursors: (i) ULF/ELF electromagnetic radiation in the atmosphere, and (ii) lower ionospheric perturbations (with two independent tools from the ULF depression and subionospheric VLF anomaly) which took place just two days before the EQ. Further, ULF/ELF atmospheric electromagnetic radiation has been observed from approximately one week before the EQ until a few days after the EQ, which seems to be approximately synchronous in time to the anomalous variation in meteorological parameters (a combination of temperature and humidity, atmospheric chemical potential). On the other hand, there have been no clear anomalies detected in the stratospheric AGW activity, and in the NmF2 and TEC data for the upper F region ionosphere. So, it seems that the lithospheric origin is not strong enough to perturb the upper F region. Finally, we discuss the possible hypothesis for the LAIC process, and we can conclude that the AGW hypothesis might be ruled out, but other possible channels such as the chemical channel (radon emanation) and the associated effects might be in operation, at least, for this Tokyo EQ.
Keywords:
earthquake (EQ) precursors; multi-parameter observation; ULF lithospheric radiation; meteorological anomaly; ULF/ELF atmospheric radiation; AGW stratospheric activity; ULF depression; VLF subionospheric propagation; lithosphere–atmosphere–ionosphere coupling (LAIC); the 2021 October Tokyo EQ 1. Introduction
In seismically active regions of the globe, earthquake (EQ) prediction (especially short-term) is of essential importance in saving human lives and economical loss, and many scientists have been challenging this difficult task for the last few decades [1]. In 1923, the Japanese people encountered a destructive historical EQ called the Great Kanto EQ in the Tokyo area [2], where it is known from seismological studies that there are over 10 active fault regions in the Kanto (Tokyo) district as a likely candidate for the next Kanto EQ. Therefore, those living in the Tokyo district are very much afraid of a forthcoming huge EQ (with magnitude (M) class 7) in one of those fault zones in the near future. In this district, there happened to be a moderate (M~6) EQ in one of those EQ-prone fault regions, i.e., the Tokyo Bay Chiba region, on 7 October 2021. Even though this magnitude is modest, compared with the expected M~7, it is very worthwhile to study the presence (or absence) of any electromagnetic precursors as a likely precursor to the next Kanto EQ, which will be the purpose of this paper.
Related to the general EQ prediction studies, there has been enormous progress in the field of the seismo-electromagnetic field, and the experimental evidence demonstrates that various electromagnetic phenomena appear not only in the lithosphere, but also in the atmosphere and ionosphere, mainly before an EQ as precursors [3,4,5,6,7,8,9,10,11,12]. Some of them are due to electromagnetic radiation in a wide frequency range (from DC/ULF/ELF/VLF (ultra-low frequency/extremely low frequency/very low frequency) to HF (high frequency), and others are the appreciable perturbations taking place on the Earth’s surface (e.g., as surface latent heat flux), in the lower and upper atmosphere, and within the whole ionosphere (bottom lower ionosphere and upper F region). The most recent trend in seismo-electromagnetics, suggested by Ouzounov et al. (Eds) (2018) [6], is the simultaneous collection of different physical parameters for any particular EQ, and there have been several papers published in this research direction e.g., [12,13,14].
Unfortunately, nearly all papers published so far were focused on very large EQs with a magnitude greater than 7 (such as the 1923 Great Kanto EQ), for example, the 1999 Chi-Chi EQ, the 2004 Sumatra EQ, the 2008 Wenchuan EQ, the 2011 Tohoku EQ, the 2015 Nepal EQ, and so on [1,5,6,12]. For example, our latest paper [14] has dealt with two huge (M~7) EQs in the Tohoku, offshore in 2021, and they have found numerous precursors in different regions of the LAIC process. So, this paper will deal with a much smaller magnitude EQ to study the response of different physical parameters to such a small EQ, as compared with huge EQ cases. We will, of course, follow such multi-parameter observations, with targets of ground-based ULF lithospheric radiation, near-surface meteorological parameters, ULF/ELF atmospheric radiation, AGW (atmospheric gravity wave) data (for the study of AGW activity in the stratosphere), ULF depression (for lower ionospheric perturbation), subionospheric VLF/LF sub-ionospheric propagation data (for the study of lower ionospheric perturbation), TEC (total electron content) data, and ionospheric sounding data (both for the study of ionospheric anomalies) in Japan. These multi-parameter observations are known to be very powerful for the investigation of general seismogenic phenomena and the elucidation of the corresponding lithosphere–atmosphere–ionosphere coupling (LAIC) process [3,4,5,6,7,8,9,15,16,17], and the advance in this direction is expected to be essential for the realization of short-term EQ prediction.
The hypotheses for this LAIC have been proposed [3,4,5], such as electrostatic channel of the generation of electric fields in the atmosphere [15,16,17], chemical channel by the emanation of radon and different gases [18,19], acoustic channel (i.e., generation of AGWs, acoustic waves) [4,20,21,22,23,24], and others. Using the observed results of many physical parameters for this Tokyo EQ, in the final section of this paper we will discuss the possible LAIC channel for this particular modest EQ.
The construction of the present paper is as follows: Section 2 is the EQ information. Section 3 deals with the observational results of multi-parameter seismogenic phenomena. Section 3.1 deals with ULF lithospheric radiation, Section 3.2 with meteorological anomalies, Section 3.3 with ULF/ELF atmospheric electromagnetic radiation, Section 3.4 with AGW activity in the stratosphere, Section 3.5 with ULF depression for the monitoring of the lower ionosphere, Section 3.6 with the subionospheric VLF/LF propagation anomaly for the lower ionospheric perturbation, Section 3.7 with the TEC result, and finally, Section 3.8 deals with the ionosonde result. Then, Section 4 will deal with summary and discussion, and Section 5 is the conclusion on the LAIC process.
2. EQ Data
The EQ of our interest happened on 7 October at 22 h 41 m JST (or October 7, 13 h 41 m UT), and its EQ epicenter is located at the geographic coordinates of (35°35.4′ N, 140° 06.2′ E), as shown by a red circle in Figure 1 (together with EQs with a magnitude (M) greater than 5.8). The magnitude (M) is 5.9, according to the Japan Meteorological Agency (JMA), but its depth is rather large at ~70 km. This EQ is characterized by the fact that an extremely wide area of Kanto Tokyo district was characterized by a seismicity (I) of over 4, probably due to the larger depth.
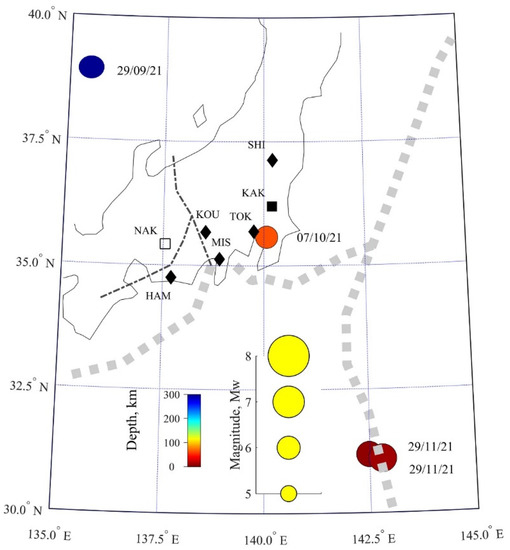
Figure 1.
Map illustrating the positions of magnetic observatories (black box of Kakioka (KAK) and white box (Nakatsugawa, NAK)), together with weather stations of SHI, TOK, MIS, KOU, and HAM (in rhombus). A red circle is the epicenter of our EQ, together with EQs with M > 5.8, which occurred from 1 August to 31 November 2021.
Next, we discuss the EQ preparation zone with the formula (R (in km) = 100.43M [25]), which implies that R = 344 km for this EQ M = 5.9. This range is expected to be perturbed during the EQ preparation phase.
3. Observational Results
3.1. ULF Magnetic Field Observations
Ground-based ULF magnetic field data can be used for the old seismogenic topic of ULF radiation from the lithosphere [3,4,5,6,7], and many workers are still engaged in this topic all over the world [4,5]. In addition, because we treat the same ULF data for ULF depression indicative of the lower ionospheric perturbation [4,5,7], we will be presenting here only its analysis method, but the analysis results will be discussed later in Section 3.5.
3.1.1. Data
This section deals with ULF electromagnetic phenomena (lithospheric radiation) related to this EQ. First, we use the ULF magnetic field data observed at the Kakioka (KAK) Observatory (geographic coordinates: (36.23° N, 140.18° E)) belonging to JMA during the period of 1 September to 30 October 2021. This station is indicated by KAK in Figure 1, and at KAK they measure the three magnetic field components with a sampling frequency of 1 Hz (see the details in [14]).
3.1.2. ULF Data Analysis and Results
Figure 2 illustrates the analysis results of the Kakioka ULF data. The top panel indicates the temporal evolutions of magnetic (Kp) and seismic activity (KLS) defined by the following relationship:
where M is EQ magnitude, and R is the distance between the EQ epicenter and the observing station (km) [4]. In Figure 2, the occurrence time of our target EQ is indicated by a vertical dotted red line. First of all, we have to mention that the geomagnetic activity during the three weeks before the EQ is generally rather quiet, as seen from the Kp index variation. The second and third panels refer to the temporal evolutions of the horizontal and vertical magnetic field components (Fh and Fz, in arbitrary unit) at the frequency of f = 0.01–0.02 Hz, where the artificial noise was at the minimum. The fourth panel refers to the polarization of Pz/h (see [25,26]). These plots refer to the subject of radiation from the lithosphere.
KLS = 100.75M/10(R + 100)
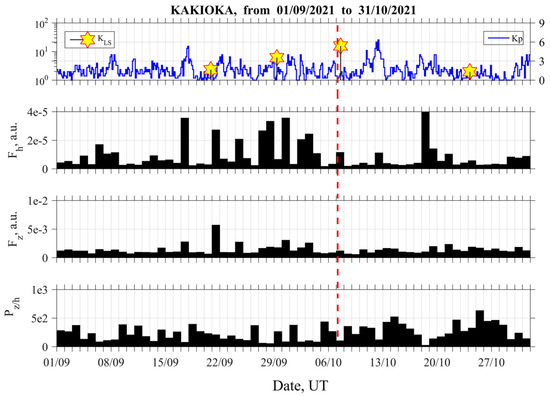
Figure 2.
Different characteristics of ULF magnetic field recorded in Kakioka (KAK). Top panel refers to the magnetic (Kp) and local seismic activity (KLS). A vertical dotted red line is the occurrence time of our EQ. The second and third panels refer to Fh and Fz, and the fourth panel indicates the polarization (Pz/h), as characterized by the ratio of Fz to Fh.
Let us discuss the observational results of lithospheric ULF radiation. Figure 2 indicates that the horizontal magnetic field component (Fh) exhibits temporal variations which are likely to be closely synchronous with that of the geomagnetic activity (Kp). In addition, nearly the same tendency was observed, even for the vertical component (Fz). Consequently, it is very difficult to identify any seismogenic lithospheric radiation. However, Hayakawa et al. (1996) [26] have suggested a possible use of polarization (Pz/h) to distinguish a seismogenic effect from other noises, which would be useful to find out the seismogenic radiation as an increase in Pz/h [26,27]. We can notice a small increase in Pz/h two days before the EQ, but it is not significant enough to conclude that this peak might be seismogenic.
Using the same ULF data, we can study the depression of the horizontal magnetic field component, and the corresponding relative depression, which will be the topic of Section 3.5, as an indicator of lower ionospheric perturbation. Though details of Dep and ΔDep are given in [14], we have to repeat the essential expressions again. Dep is the inverse of the horizontal magnetic field component (1/Fh2) and ΔDep is a measure of relative depression. The value of absolute depression Deph in the horizontal component H of ULF magnetic field variations is calculated as
where in the denominator we have the squared output signal Fh observed by the sensor in the frequency band of ΔF = 0.01–0.02 Hz, averaged over the local night interval ΔT = 01–05 JST(LT). As a measure of relative depression for the i-th date ΔDephi, we adopt the following value:
Here Dephi, is the depression for the i-th date. N is the filter parameter equal to the number of preceding days for averaging, and, in the present study, N = 7 is taken to reduce the effect of one to a few days of changes in the variations of the magnetic field. Processing parameters (ΔF, ΔT and N) are determined experimentally from the properties of local interference and depression. The results will be presented in Section 3.5.
3.2. Meteorological Phenomena
Despite the promising prospects for predicting EQs based on electromagnetic phenomena [3,4,5,6,7,8], they are difficult to implement in regions with a high population density and saturation with energy facilities such as Tokyo, due to the high level of electromagnetic interference. This is why it is important to look for any other types of simple phenomena associated with seismicity, even though they would be less sensitive to electromagnetic tools. Here, we attempted to detect meteorological anomalies caused by possible radon emanation related to this Tokyo EQ. It is now generally accepted that the ionization of air by radon causes an increase in its temperature (T) and a simultaneous decrease in humidity (Hum) [18,19]. In the case under consideration, we assume a high probability of radon release at places located close to the Earth’s crust faults [28,29,30] in the Honshu Island. Pulinets et al. (2006) [18] considered the physical nature of this phenomenon in sufficient detail. Examples of changes in temperature and humidity before powerful EQs are presented here, and the conditions necessary for the occurrence of the phenomenon are analyzed. Several works have indicated a possibility of using this phenomenon to predict EQs [3], and we have also described a similar phenomenon observed around the 2011 Tohoku EQ [31].
The possibility of using meteorological phenomena to predict EQs depends on the degree of statistical connection between their characteristics and the parameters of seismic events. To do this, we need to know the characteristics of meteorological variations associated with seismicity as accurately as possible. The accuracy of estimating the characteristics of meteorological phenomena depends on the ratio of their magnitude to the magnitude of the interference, where the interference plays daily and seasonal roles in the variations of meteorological parameters that are not related to seismic effects. In this work, we try to isolate seismic-related variations by subtracting the moving average of the original data. Previously, it was found that the characteristics most sensitive to air ionization are the ratio of temperature-to-humidity (T/Hum) and the value of atmospheric chemical potential (ACP) [3,18,19].
3.2.1. Data and Processing
We obtained seismic data from the USGS EQ catalog (https://earthquake.usgs.gov/earthquakes/search/ accessed on 15 December 2021). We took daily data of the maximum temperature and minimum humidity for five weather stations located in the vicinity of Tokyo from the JMA catalog (https://www.data.jma.go.jp/obd/stats/etrn/ accessed on 15 December 2021). These stations are Tokyo (TOK, 35.69° N, 139.75° E), Kofu (KOU, 35.67° N, 138.55° E), Mishima (MIS, 35.13° N, 138.90° E), Hamamatsu (HAM, 34.75° N, 137.71° E), and Shirakawa (SHI, 37.13° N, 140.215° E). They are shown as black diamonds on the map of the central portion of Honshu Island, as demonstrated in Figure 3. Here, colored circles also indicate the positions of EQ epicenters that occurred from July to December 2021. Their dates are marked next to them. The color of the circles depends on the depth of the hypocenters in accordance with the color bar located at the top right. Their size depends on the EQ magnitude. This relationship is shown in the lower right panel with yellow circles. EQ parameters are also shown in Table 1. The first row is the date of the EQ, and the second and third rows indicate their coordinates (latitude and longitude). The third and fifth rows are EQ magnitude and depth. DIST (in km) is the distance of the EQ epicenter from Tokyo as a reference. The thick gray dotted lines depict the location of deep-sea trenches, and the thin black dashed-dotted lines display the positions of faults in the Earth’s crust. These trenches and faults are located at the boundaries of tectonic plates, causing a high seismic activity in the region.
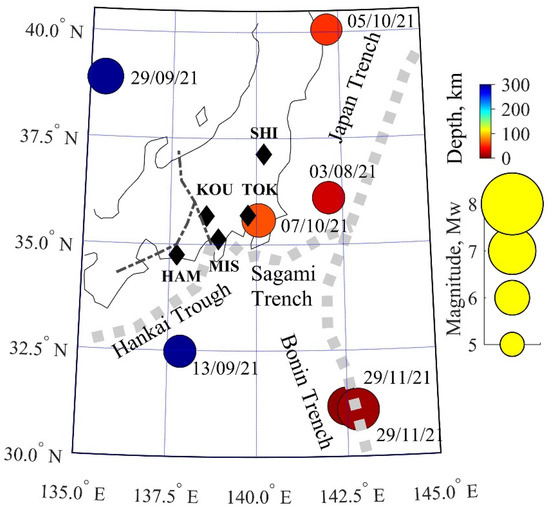
Figure 3.
Map of JMA weather stations (SHI, TOK, MIS, KOU, HAM), together with deep-sea trenches, crust faults, and EQs with magnitude >5.7 that occurred during July–December 2021. This shows the epicenter of our EQ that occurred on 7 October, as well as the TOK weather station located within Tokyo.

Table 1.
The parameters of the EQs shown on the map in Figure 3.
Here we try to find anomalies in the air temperature and humidity, supposedly caused by air ionization by radon released during the preparation of EQs and sometime after it. It is believed that this effect should be detected as an increase in air temperature and a decrease in its humidity [18]. It has been shown that the ratio of temperature-to-humidity T/Hum is the most sensitive air characteristic to this phenomenon. On the other hand, the so-called atmospheric chemical potential ACP is the latent heat of water molecules that can be released due to reaction of condensation caused by ionization [18]. ACP is expressed in terms of air temperature and humidity, and has the dimension of eV:
where T is air temperature in °C, and Hum is air humidity in %.
ACP = 5.8 × 10−10 × (20 T + 5436) × log (100/Hum)
We used the maximum daily temperature T and minimum daily humidity Hum to look at their maximum ratio. We compare these characteristics with EQs, the impact of which is estimated by the coefficient of local seismicity KLS.
Figure 4 illustrates the appearance of original data and its combined characteristics at Mishima from July to the end of 2021. The top panel shows the temporal evolution of seismicity KLS for Tokyo. The evolution of the maximum daily air temperature T and minimum daily humidity Hum is shown on the 2nd and 3rd panels. The evolution of T/Hum and ACP is displayed on the bottom two panels.
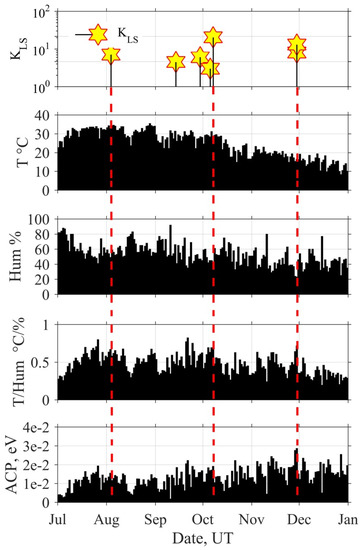
Figure 4.
The top panel displays the evolution of seismicity KLS for Tokyo; Mishima station. 2nd and 3rd panels show the evolution of maximum daily air temperature and minimum daily humidity, and the corresponding evolutions of T/Hum and ACP are depicted on bottom two panels.
Following on from this figure, the comparison of weather characteristics with seismicity does not confirm their relation at the first glance. The main reason is that their parameters mainly depend on powerful atmospheric processes that are not related to seismicity.
Previous experience has shown that meteorological phenomena caused by seismicity are rather “short-lived” with their duration being several days. At the same time, ordinary meteorological processes, in addition to daily fluctuations, are subject to seasonal fluctuations and can change noticeably during the month, as can be seen from Figure 4. So, to improve the detection of “short-term” events, we proposed to subtract 30-day moving averages of T/Hum and ACP. As a result, we obtained their variations Δ(T/Hum) and Δ(ACP). Below are Expressions (5) and (6) for their calculations:
Here (T/Hum)i and ACPi are the ratio of the maximum daily air temperature to its minimum daily humidity and ACP value for i-th date. N is the averaging interval equal to the number of preceding days for averaging, and here we take N = 30.
Figure 5 shows an example of such calculations for the ratio of T/Hum at the Mishima station data for 6 months. Here, the evolution of seismicity is depicted in the top panel. In the next panel, the gray bars refer to the temporal evolution of the ratio T/Hum, and the black dotted line shows its 30-day moving average. The bottom panel illustrates the result of this procedure as the ratio variation δ(T/Hum). In the future, we will be interested only in their positive values δ(T/Hum)pos and δACPpos, which correspond to the process of air ionization.
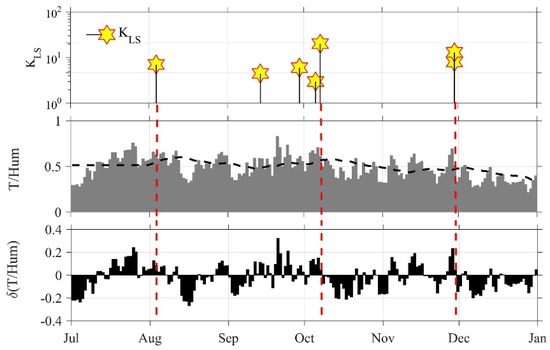
Figure 5.
An example of the procedure for removing the trend and obtaining ratio variations Δ(T/Hum) at Mishima station. The top panel shows the evolution of seismicity. The evolution of T/Hum and its moving average is shown in the second panel. The bottom panel shows the result of the procedure. The unit of T/Hum is °C/%.
To calculate the moving average of the combined characteristics according to Expressions (5) and (6), a copy of their first N values was added to the beginning of the data array. This caused distortions in the moving average at the begining interval of length N. However, for large common intervals or continuous data analysis, this is not essential.
3.2.2. Analysis Results
Figure 6 demonstrates positive variations of the ratio of temperature-to-humidity δ(T/Hum)pos at five meteorological stations and evolution of the local seismicity calculated for Tokyo on the top panel. Our Tokyo EQ has the largest value of KLS ~30. The next five panels display the temporal evolutions of δ(T/Hum)pos at the following stations of Shirakawa, Tokyo, Kofu, Mishima, and Hamamatsu. A noticeable correlation with seismicity is observed at the Mishima (MIS) and Kofu (KOU) stations, where the maxima before the Tokyo EQ appear most confidently and exceed all other peaks over the interval of August–November 2021.
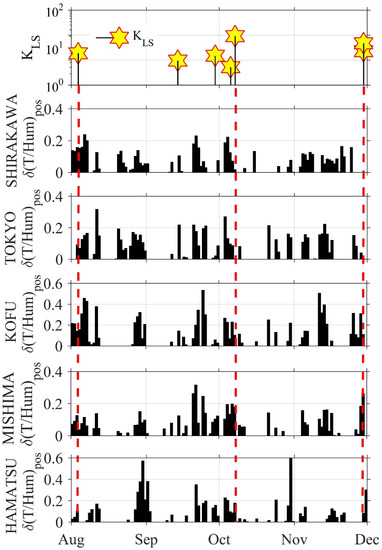
Figure 6.
The evolution of the local seismicity (for Tokyo) and variations of the ratio of temperature-to-humidity at five meteorological stations. A best correlation with seismicity is observed at the Mishima (MIS) and Kofu (KOU) stations, where peaks have a lead time of 2–3 weeks) before the Tokyo EQ exceeds all other ones. The unit of T/Hum is °C/%.
Figure 7 demonstrates such a connection of combined air characteristics at Mishima station with local seismicity calculated for Tokyo during July–December 2021. As before, the temporal evolution of seismicity is shown on the top panel. The behavior of variations of the ratio, δ(T/Hum)pos, and atmospheric chemical potential, δACPpos, are shown in the next two panels. An increase in the number of peaks and their amplitude before the main EQs is clearly visible in all three EQ cases.
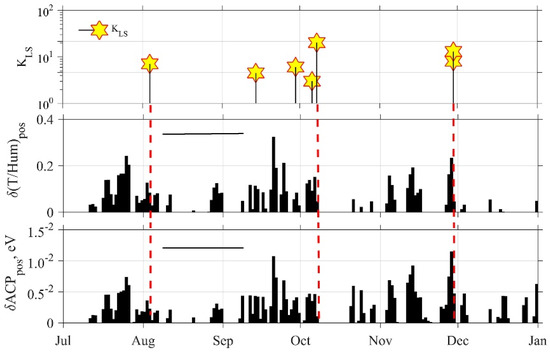
Figure 7.
Relationship of combined air characteristics with local seismicity at Mishima. Top panel shows the temporal evolution of KLS (for Tokyo) seismic activity, and next two panels demonstrate the behavior of combined air characteristic variations. An increase in the number of peaks and their amplitude before EQs is observed as a possible anomaly period indicated by horizontal bars in the second and third panels. The unit of T/Hum is °C/%.
The evolutions of δ(T/Hum)pos for all five stations during the period of August–November are summarized in Figure 6. This figure confirms the assumption that the most reliable effect should be observed near the active faults in the Earth’s crust. This can be seen at the two stations of Kofu and Mishima, where those stations are located close to the active fault regions (see Figure 3), leading to the possible emanation of radon and related gases. Here the maximum peak before the Tokyo EQ exceeds all other peaks for the August–November 2021 interval. However, other factors affect the success of detection of seismo-related meteorological phenomena. For example, the climate of large cities can mask natural phenomena in the atmosphere, such as those associated with meteorological effects (https://www.britannica.com/science/urban-climate accessed on 15 November, 2021). Perhaps that is why they are weakly manifested at the Tokyo Meteorological Station (TOK).
We increased the data analysis interval to six months to understand what is happening near seismic events located at the edges of the interval shown in Figure 6. The result observed at the Mishima station is shown in Figure 7. It can be seen that, in addition to the seismic activity observed in the vicinity of the Tokyo EQ, two more events are observed at the edges of the considered interval. One of them occurred on August 3 with a magnitude M = 5.8 at a distance of 217 km from Tokyo, and, on November 29, two EQs with magnitudes of 6.3 and 6.6 occurred almost simultaneously at a distance of 562 and 584 km. They are also shown on the map in Figure 3. The next two panels reflect the evolution of the variations of combined air characteristics, where a sequence of peaks are visible near all three intervals of seismic activity, both in terms of the temperature–humidity ratio and the chemical potential of the atmosphere. These peaks are observed during 1–1.5 months before EQs and a few days after them, as a possible meteorological anomaly.
It should be noted that these properties differ from those of similar phenomena published by previous authors. As a rule, there are short-term peaks in temperature or humidity within one to three days. It is possible that these authors find only the maximum values, since they did not look at the variations in the parameters, but at their absolute values against the background of their diurnal variation. At the same time, we observed meteorological anomalies in the area of the Tohoku EQ for several years [31], which is in better agreement with the results of this work.
3.3. ULF/ELF Electromagnetic Radiation
ULF/ELF atmospheric ULF/ELF electromagnetic radiation (as impulsive noises) is known to be a regular EQ precursor with high probability gain [32,33,34] and is currently used for the prospective EQ prediction in Kamchatka [35]. Nevertheless, this phenomenon is not so popular, even in the scientific society, so we try to repeat analysis methods here.
3.3.1. Data
We used the data from observations by the ULF/ELF network of the Chubu University induction magnetometers at three stations, but here we utilize the data recorded only at one of the three stations of Nakatsugawa (NAK) (35.42° N, 137.55° E) (a white box in Figure 1) during the interval from 1 September to 15 October 2021. In NAK, we measure three magnetic field components with the sampling frequency of 100 Hz (see the details of the equipment in [14,36]).
3.3.2. Analysis and Results
Figure 8 displays an example of daily dynamic ULF/ELF spectra observed on 1 October 2021 in NAK. Impulse noises of artificial origin are clearly visible in this dynamic spectrum. The low interference level is observed at the beginning of the day and especially from 3 to 5 o’clock local time (LT) (or UT = 18~20 h). Therefore, this is the best interval suitable for detecting any seismogenic signals, but this period is very short, so that there is a high probability of missing seismogenic effects.
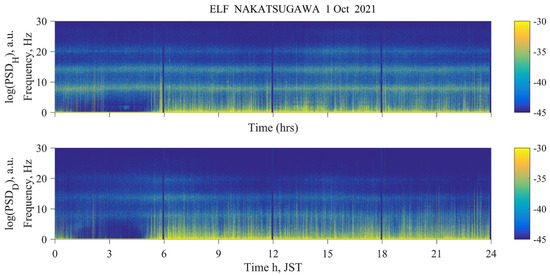
Figure 8.
Dynamic spectra of ULF/ELF magnetic field (H and D) components observed on 1 October 2021 at NAK. Minimum level of interference is in the LT interval from 3 h to 5 h in the morning.
Here, Figure 9a shows the temporal evolution of seismic (KLS) and geomagnetic (Kp) activity (top panel), the spectra of the ULF/ELF field components (second panel), polarization (third panel), and its dispersion (fourth panel) for the intervals of the local nighttime hours of LT = 3–5 h, as observed from 1 September, while Figure 9b is the same as Figure 9a, but for full days. It is found from both figures that significant anomalies are not visible in the vicinity of the EQ. This kind of simple spectral analysis cannot yield any definite seismogenic signature.
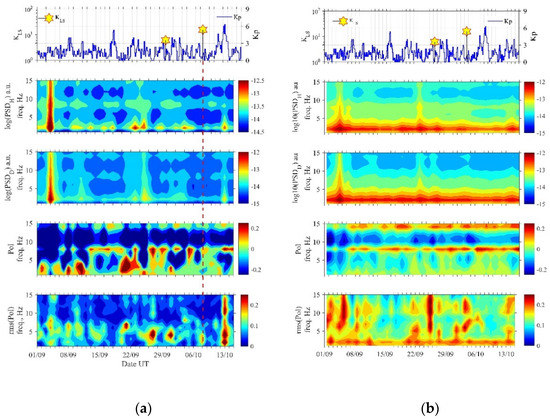
Figure 9.
(a) Temporal evolution of magnetic (Kp) and seismic activity (KLS) (top panel), spectra (horizontal H and D magnetic fields) (second and third panels), polarization (fourth panel) and its dispersion (bottom panel). Time interval is local nighttime (LT = 3–5 h). (b) The same as (a), but for full days.
So, we move on to a more sophisticated analysis for these ULF/ELF atmospheric radio emissions as impulsive noises. As is already described in detail in [32,33,34,35,36], we have to use a new parameter ∆S in order to detect seismo-atmospheric ULF/ELF radiation, which is given as follows:
A success in the application of this parameter ΔSew is partly because a majority of nearby EQs take place east of our Kamchatka station [33,35]. In order to detect radiation from all directions, we added a similar characteristic ΔSns for orthogonal direction.
The numerator contains the ratio of two horizontal spectral components Phh (NS component of magnetic field) (corresponding to Ph in the ULF analysis) and Pdd (EW component) (Pd in the ULF analysis). The denominator is the root mean square (rms) of the deviation of the signal ellipticity. The expression of β is given by the following equation:
Here Im means imaginary part. Because Schekotov et al. [32,33] have compared different parameters and have found an enhancement in the spectral ratio of Phh/Pdd and a reduction in the polarization ellipticity before an EQ, the parameter introduced by Equations (7) and (8) is proved to be most sensitive and reproducible to seismic shock [36,37,38,39,40]. The ellipticity or the ratio of minor axis to major axis is defined by tan β. The sense of polarization is characterized by the sign of β; when β > 0, the polarization is right-hand (RH), and β < 0 means the left-hand (LH) polarization. The linear polarization is expressed by β = 0 [37].
The field component power spectral densities, Phh, Pdd and their cross-power spectral densities Phd, Pdh were calculated by using Fourier transforms with a frequency resolution of about 0.1 Hz. Spectral components in a frequency range from 0.1 to 30 Hz were taken into account in this paper. They were averaged over one-Hz intervals such as 0.1–1, 1.1–2,…, 29.1–30 Hz, so that we have 30 spectral densities.
Based on the above analyses, Figure 10a,b shows the temporal evolutions of seismic (KLS) and geomagnetic (Kp) activity (top panel), and the spectra of combined ULF/ELF field characteristics ΔSew and ΔSns for the morning (LT = 3–5 h) and full-day intervals (second and third panels), respectively, observed during the period from 1 September to 15 October 2021. In particular, Figure 10b shows a significant increase in ∆Sns at the frequencies of 2–6 Hz in the vicinity of the EQ date (or about one week before and about one week after the EQ). Then, the three round panels in the bottom of Figure 10 illustrate the azimuth distributions averaged over 15 days in the frequency range of 3–5 Hz. The details of direction finding are given in [32,33,37]. Both figures (the rightmost figures in bottom panels) show the same azimuthal distributions, and it is found that the main lobe of the azimuthal distribution in the last full-day interval is directed towards the EQ epicenter, which gives us evidence that this ULF/ELF radiation must be originated near the EQ epicenter. Finally, we can conclude that this ULF/ELF atmospheric radiation is a likely EQ precursor.
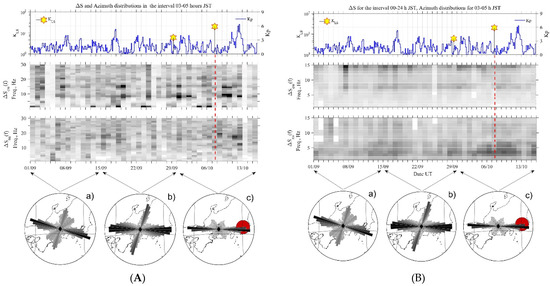
Figure 10.
Temporal evolutions of seismic (KLS) and geomagnetic (Kp) activity (top panel), the spectra of ΔSew and ΔSns for LT = 3–5 h (A) and full-day intervals (B) observed from 1 September to 15 October 2021 (second and third panels). The three round panels ((a),(c)) in the bottom depict the azimuth distributions averaged over 15 days in the 3–5 Hz frequency band.
3.4. Stratospheric and Lower Mesospheric AGW Activity
AGW activity in the stratosphere, possibly triggered by EQs, has been studied in our recent papers for the 2011 Tohoku EQ and the 2016 Kumamoto EQ [23,24], in which ERA5 reanalysis data have been used to investigate the vertical (altitudinal) perturbations of temperature vertical (height) profiles for the study of AGW activities.
3.4.1. Analysis Method
ERA5 is a reanalysis dataset produced by the European Centre for Medium-Range Weather Forecasts (ECMWF), providing numerous atmospheric, land, and oceanic variables. Many kinds of observations including satellites, radiosondes, radars, and air-based and ground-based in-situ measurements, are assimilated into ECMWF’s meteorological forecast model [38]. ERA5 provides hourly temperature profiles covering the globe with a ~31 km horizontal resolution from January 1950 to the present. ERA5 data are available from near-surface to 0.01 hPa (~80 km altitude) with 137 model levels in the vertical direction. However, we only focus on the stratosphere (around 15–50 km altitude) in this paper because evident anomalies on AGW activity have been found in the stratosphere in our previous EQs [23,24]. On the other hand, ERA5 provides global temperature profiles, and so, not only the data at our EQ epicenter, but also in the neighborhood of Japan are taken to investigate AGW activity in this paper. The particular region being taken is longitude from 110° E to 160° E and latitude from 20° N to 60° N.
Here, we have to describe the potential energy Ep, as a representative of AGW activity in the stratosphere ([23,24] and references therein).
where g is the gravitational acceleration, N is the Brunt–Vaisala frequency that can be derived from atmospheric temperature T, and T′ is the fluctuation in temperature with respect to the background temperature . Both T and Ep are functions of latitude, longitude, altitude, and time. AGW activity is presumed to be triggered around the ground surface or lower atmosphere and further propagates into the upper atmosphere in the vertical direction. For evaluating AGW activity at the EQ epicenter, the vertical temperature profile there at a specific time is retrieved from ERA5, and a 2–10 km band-stop filter is used to filter out the wave components from T to establish . T′ is the difference between T and , i.e., T′ = T − . The variance term (T′/)2, acting as the moving average of Ep, is calculated within a 2-km layer. A vertical profile of Ep is evaluated. The same procedure is repeated numerous times until all the Ep values in the region of 110–160° E and 20–60° N are evaluated.
3.4.2. Observational Results
The AGW potential energy (Ep) over the EQ epicenter [plus/minus 1.5° both in latitude and longitude around the epicenter] was enhanced at three different altitudes before the EQ, as seen in Figure 11: (1) At 20 km on 28–30 September. This one seems to be the influence of a typhoon (No. 2116) in the south of Japan, as shown in Figure 12. The Ep map of Figure 13 shows that the most active region was located around the typhoon; (2) At 35 km on 29 September–4 October. AGW activity at this altitude was high in the Northwest Pacific. Besides the typhoon mentioned above, some mesoscale systems also existed, including a cold-core low pressure in the upper troposphere in the Northwest Pacific. AGWs caused by these systems propagated from the ocean to the Kanto area during this period (see Figure 14); (3) Around 44 km on 27 September–1 October. This enhancement seems to be related to warming around the stratopause. The Ep value not only enhanced over the Kanto area but also the whole Northeast Asia and Northwest Pacific, as seen in Figure 15. Although we do not know the cause of this warming, this should be a large-scale phenomenon but not a local effect. Overall, we come to the conclusion that the enhancements at the three different altitudes and periods do not seem to be a pre-EQ effect.
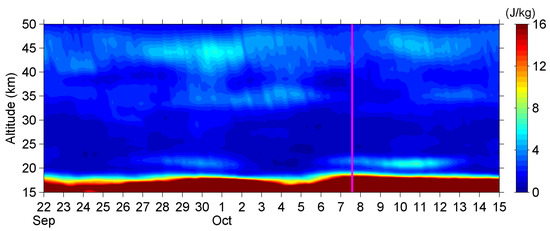
Figure 11.
Time–altitude intensity of AGW potential energy (Ep) over the EQ epicenter for the 2021 EQ. The magenta line indicates the occurrence of the EQ.
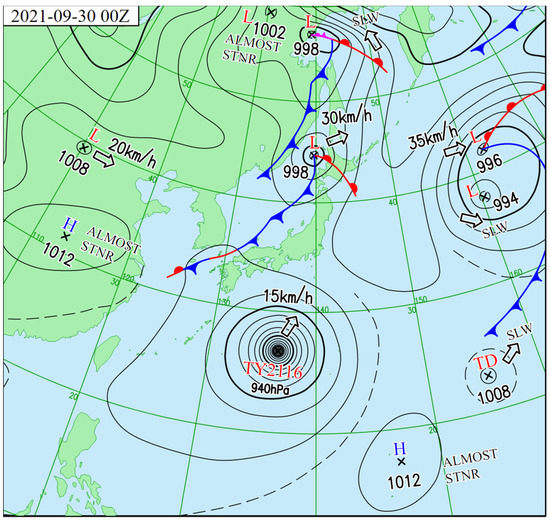
Figure 12.
The normal weather map on 30 September. H is high pressure, L low pressure, TD tropical depression and TY is typhoon. Also, SLW means slowly, and STNR means stationary.
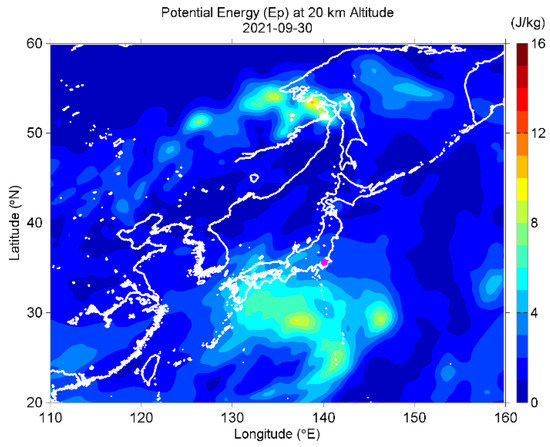
Figure 13.
The Ep map at 20 km altitude on 30 September.
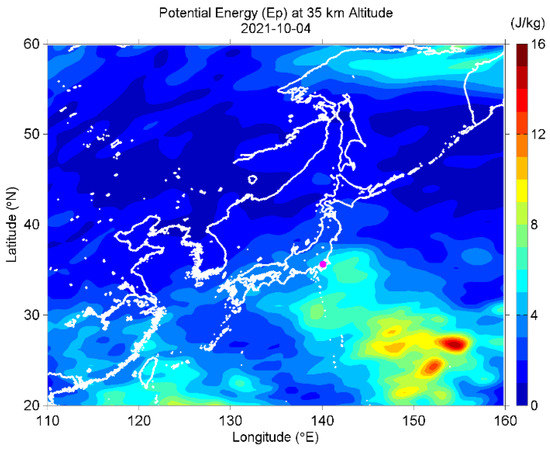
Figure 14.
The Ep map at 35 km altitude on 4 October.
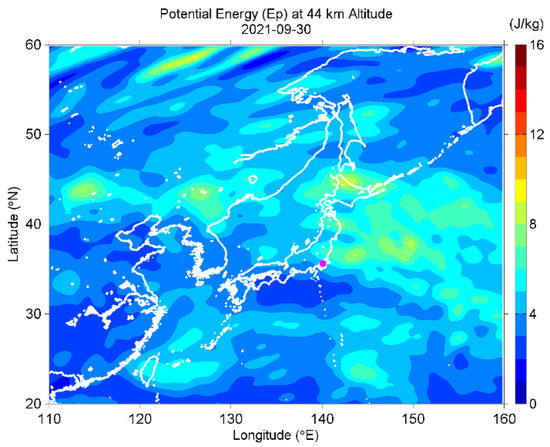
Figure 15.
The Ep map at 44 km altitude on 30 September.
3.5. ULF Depression (Lower Ionospheric Perturbation)
The lower ionospheric perturbation can be firstly investigated with the use of ULF depression [39,40,41,42], which is regarded as a perturbation in the lower ionosphere. Unfortunately this phenomenon is not so popular, even in the scientific society, but we want to emphasize the importance of this phenomenon as an EQ precursor [34].
3.5.1. Analysis Method
In Section 3.1, we have already presented the analysis method of ULF depression.
3.5.2. Analysis Results
Figure 16 presents the results of the ULF depression. It is found from this figure that the most important quantity of δDep is extremely well enhanced (of the order of five) two days before the EQ, and we can clearly conclude that this U LF depression is a well-established signature of EQ precursor, even for our Tokyo EQ with a moderate magnitude. This ULF depression is the effect of the depletion of irregular magnetic pulsations generated in the magnetosphere, which is due to the enhanced absorption in the lower ionosphere or generation of lower ionospheric turbulence [14,34,38].
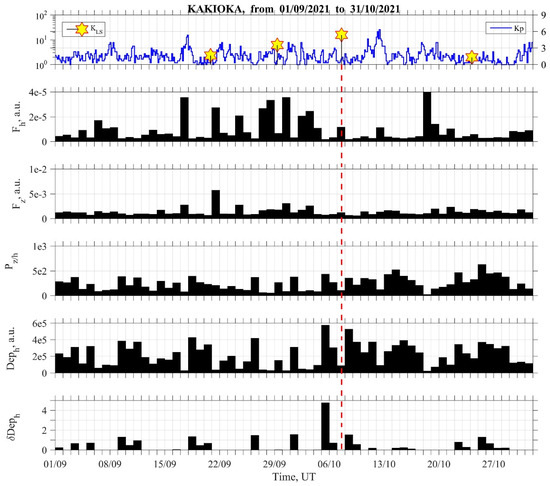
Figure 16.
Bottom two panels refer to the characteristics of ULF depression (depression Deph and relative depression δDeph). Top panel refers to the magnetic (Kp) and local seismic activity (KLS). A vertical dotted red line is the occurrence time of our EQ. For the sake of comparison, we have reproduced the results of the lithospheric ULF radiation (Figure 2); the second and third panels refer to Fh and Fz, and the fourth panel to polarization Pz/h.
3.6. VLF/LF Subionospheric Propagation Measurements
The second method for monitoring the lower ionosphere is the use of subionospheric VLF/LF propagation. As already described by Hayakawa et al. (2021) [14], the lower ionosphere can be effectively monitored by subionospheric VLF/LF propagation, in which signals from VLF/LF transmitters propagate in the Earth–ionosphere waveguide. So, any space weather perturbations, such as the effects of geomagnetic storms, can be detected as a perturbation in VLF/LF data [43,44], and Hayakawa et al. (1996) [45] found convincing evidence of ionospheric perturbations prior to the 1995 Kobe EQ. Since then, a lot of attention has been paid to the use of subionospheric VLF/LF signals for seismo-ionospheric disturbance studies [46,47,48,49,50,51,52,53].
3.6.1. Observational Results in Kamchatka
Russian colleagues [49,50] have established an observing station at Petropavlovsk (PTK), Kamchatka, Russia (53.09° N, 158.55° E), where the electric field of subionospheric VLF/LF signals in the frequency range from 10 kHz to 50 kHz is detected by a VLF/LF receiver and the associated software, and both the amplitude and phase of transmitter signals are measured. The target transmitters treated in this paper are (1) JJY (Fukushima. f = 40 kHz), and (2) JJI (Miyazaki in Kyushu, f = 22.2 kHz). Though the results are not shown as graphs, we have found no clear anomalies for the two transmitters of JJY and JJI. The EQ epicenter is located far south of the wave sensitive zone of the JJY-PTK propagation path, so that it is easy to understand that we do not expect any propagation anomaly. Nearly the same results are obtained for the JJI transmitter.
3.6.2. Observational Results in Japan
We have tried to find any propagation anomaly from the Japanese VLF data. The observing station is located in Chofu, Tokyo (35.656·°N, 139.544° E), where nearly the same VLF system is used with the Softpal digital system [54]. The EQ epicenter is very close to the VLF station of Chofu (the distance is only 40 km). We observed a few transmitter signals at this Chofu station, but we showed significant results only from the Australian VLF transmitter of NWC (19.8 kHz) (21.816° S, 114.165° E), as seen in Figure 17. Unfortunately, the observation was not in operation until 4 days before the EQ, but the VLF data from 3 days before the EQ onwards are available. So, it is useful for us to compare this VLF result with the conspicuous ULF depression anomaly two days before the EQ, as already described before in Section 3.5. Figure 17 illustrates the sequential plots of the amplitude diurnal variations observed at Chofu from −3 days to +7 days of the EQ (minus means before the EQ, while plus means after the EQ). There is no VLF plot for +2 days, because no observation was made on this day. The abscissa of each plot is UT from UT = 0 h to 24 h. One of the most fundamental analysis methods is the so-called terminator time analysis [45], paying attention to the times of amplitude minima around sunset and sunrise as the effect of modal interference. For example, let us look at the amplitude minima around sunset; there are two amplitude minima around sunset indicated by SS1 and SS2 on the plot of −1 day, and we notice those minima on all days have only good quality data. First of all, we can notice that the time of SS1 does not change significantly during the whole days before and after the EQ. On the other hand, we observe an obvious shift in the second terminator time of SS2, only two days before the EQ (−2 days). That is, the second terminator SS2 is found to be split into minima, both with a remarkable shift in time. In the same way, the morning terminator times (not indicated by SR1 and SR2) are detected clearly around the times of sunset, but a close inspection shows that both minima do not exhibit any change, remaining unchanged during the whole period. In addition, we observe that SS2 showed a small shift even after the EQ (+1 day). Finally, we can conclude that a significant shift in the evening terminator time, which means that the length of day as seen by VLF signal is extremely elongated on −2 days (two days before the EQ), suggesting that the lower ionosphere is severely perturbed on this day, seen as the lowering of the ionosphere by a few kilometers. Detailed study on the lower ionospheric perturbation, together with the phase information is highly necessary in the future.
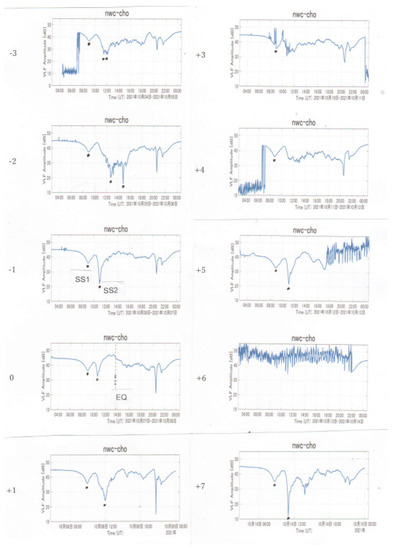
Figure 17.
Sequential plots of the amplitude diurnal variations during the period from −3 days to +7 days of the EQ. Time goes from left top to bottom, then from right top to bottom. The abscissa is UT from 0 h to 24 h. Sunset terminator times as indicated by dots are SS1 and SS2. The EQ time is indicated by a vertical line of EQ in the plot of day 0.
3.7. TEC (Total Electron Contents) Measurements
The upper ionosphere, i.e., F region of the ionosphere has already been identified to be very sensitive to pre-EQ activity, because there has been a lot of evidence accumulated on seismogenic effects in TEC and ionosonde data since the publication of [55,56,57].
3.7.1. Analysis Method
In the last two decades, scientists tried to use GPS/GNSS (global navigation satellite system) signals to derive TEC, which is highly correlated with the electron density in the F region. With the dense network of GPS/GNSS receivers around the globe nowadays, it is possible to obtain a global view of TEC, and these TEC data are reliable and easy to obtain from a public dataset. In this study, we use TEC data from the GIM (global ionosphere map) produced by CODE (Center for Orbit Determination in Europe). CODE GIM is constructed from GNSS signals observed by receivers around the world (see detailed information on this dataset in [57]). Its spatial resolution is 5 degrees in longitude and 2.5 degrees in latitude, and its temporal resolution is one hour.
3.7.2. Observational Results
Figure 18a shows the time series of TEC retrieved from CODE GIM (black curve) with the relevant past 30-day mean value of TEC (gray) around the EQ. The red/blue bars at the bottom of Figure 18a refer to the deviation of TEC from the mean value; however, only the deviations that exceed ±1.5σ (σ is the standard deviation, defined as positive/negative anomalies) are plotted here. Most positive anomalies are found during high F10.7 index (Figure 18b) or negative Dst index periods, and most negative anomalies are found during low F10.7 index periods. This tendency could be clearer if the threshold of the TEC anomaly was set to ±1σ, but almost every hour during the period shown in Figure 18 will become anomalous, so ±1.5σ was selected here.
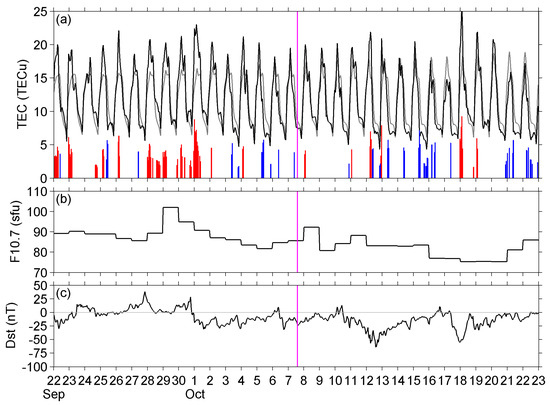
Figure 18.
(a) TEC, (b) Solar radio flux at 10.7 cm (F10.7), and (c) Dst index. The red/blue bars in (a) refer to positive/negative deviations exceeding ±1.5σ. A vertical pink line indicates the EQ time.
The global plots of positive anomalies (for example, the plots on the two most anomalous days of 28 September and 1 October, shown in Figure 19 and Figure 20) indicate that the positive anomalies should be a global effect. On the other hand, negative anomalies (3 and 5 October in Figure 21 and Figure 22) were mainly distributed at high latitudes in the northern hemisphere and around Japan before the EQ. However, similar anomalies also existed around Japan during the negative anomalous periods in mid-October (considered to be caused by lower solar activity). It seems these negative anomalies around Japan should be a local effect due to solar-terrestrial conditions or just some artificial errors of the dataset, but not a precursor to the 2021 Tokyo EQ.
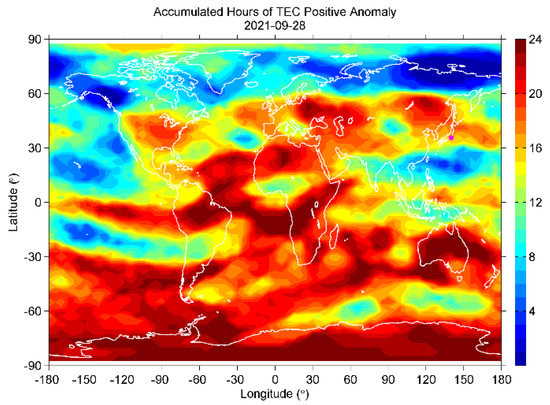
Figure 19.
The accumulated hours (max = 24) of TEC positive anomaly on 28 September.
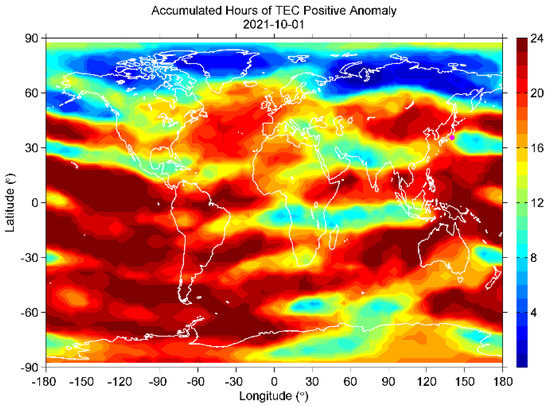
Figure 20.
Same as in Figure 19, but for 1 October.
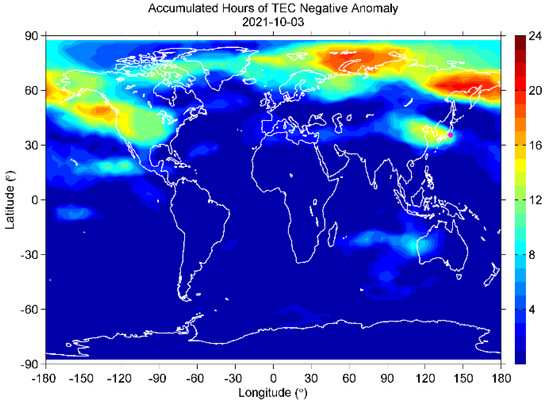
Figure 21.
Same as in Figure 19, but for negative anomaly on 3 October.
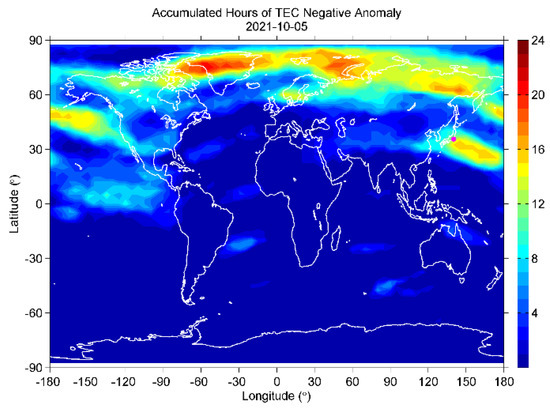
Figure 22.
Same as in Figure 21, but for 5 October.
3.8. NmF2 Ionosonde Measurements
3.8.1. Data
In this section, the manually scaled version of the ionospheric parameters with a 1-h resolution was used with Japanese ionosonde data (Kokubunji (35.71° N, 139.49° E) and others). The foF2 value was converted to NmF2 because the latter is more reasonable during the calculation of the 30-day mean value. The analysis method is the same as that used for TEC.
3.8.2. Analysis Results
Figure 23 shows the NmF2 observed at Kokubunji in Tokyo for the 2021 EQ, in the same form as in Figure 18. Certainly, the NmF2 variations are somewhat different from the TEC variations in Figure 18. However, they have almost the same tendency and polarity. NmF2 positively deviated during periods of high solar radio flux or geomagnetic storms. The occurrence of a positive anomaly decreased during the days around the EQ, but it should be considered as a solar-terrestrial effect. Figure 24 illustrates the corresponding NmF2 observed at the other two stations of Sarobetsu (in Hokkaido) (45.16° N, 141.75° E) and Yamagawa (in Kagoshima) (31.20° N, 130.62° E). The data at Okinawa are available, but not included here because Okinawa is close to the EIA (equatorial ionospheric anomaly) region, so it is not suitable for our study. NmF2 anomalies at Sarobetsu and Yamagawa had similar properties as at Kokubunji, indicating the anomalies at Kokubunji should be a wide-area effect, but not a local effect.
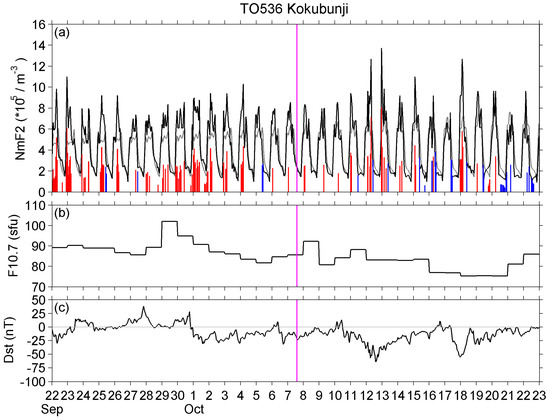
Figure 23.
Same as in Figure 18, but panel (a) showing the NmF2 at Kokubunji. A vertical pink line indicates the EQ time. (b) Solar activity (F10.7) and (c) geomagnetic activity Dst index.
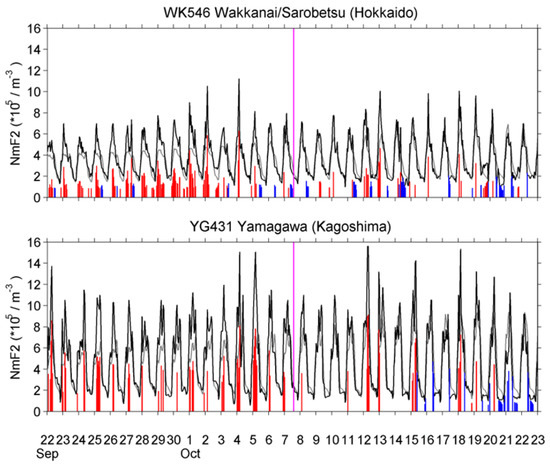
Figure 24.
The corresponding NmF2 at Sarobetsu in Hokkaido (top panel) and Yamagawa in Kyushu (bottom panel). A vertical pink line indicates the EQ occurrence time.
4. Summary and Discussion
Starting from the lowest region of the lithosphere as the origin of the LAIC process, to the upper region of the ionosphere, we will summarize candidates for possible pre-seismic phenomena during the preparatory phase of the moderate Tokyo EQ of our interest. Table 2 shows the summary of EQ precursors (anomalies and trends) for this Tokyo EQ.

Table 2.
Summary of anomalies and trends.
- Lithospheric effects: Prior to large EQs, we understand that the electromagnetic radiation in the ULF range appears before large EQs, such as the 1988 Spitak EQ [58], the 1989 Loma Prieta EQ [59,60], and the 1993 Guam EQs [61], probably due to the generation of electric currents during the pre-seismic activity (or build-up of stresses) in the lithospheric tectonics, even though the mechanism is poorly understood, e.g., [4,5,62,63,64]. When those ULF emissions are observed, the lithosphere is found to be in critical state [65,66,67,68,69]. However, the ULF data at Kakioka (Figure 2) has suggested that we could not detect any clear evidence of ULF lithospheric radiation for this EQ. The first possibility of this absence is that the epicentral distance of KAK is close to the reception threshold for this EQ magnitude [70]. The second possibility is that the long-term analysis by Han [71] has indicated that the probability gain for this ULF radiation is not large enough.
- Owing to the criticality in the lithosphere, we can expect significant deformation within the lithosphere and the Earth’s surface; that is, formation of cracks in the lithosphere, emanation of radon and different gases, surface deformation etc. [3,4,5,6,7,8]. Actually, Kamiyama et al. [72] have found clear short-term surface deformation before the 2011 Tohoku EQ with GPS data, in close association with various electromagnetic precursors. In addition, similar surface deformation has been detected before the 2016 Kumamoto EQ [73]. Unfortunately, even though extensive works have been performed on the GPS surface deformation [74,75], we do not attempt to use the GPS data for this Tokyo EQ. Instead, we have analyzed the anomalies of meteorological parameters at different sites in Japan, and we have found that the ratio of temperature-to-humidity and ACP exhibited anomalous variations approximately one week before the EQ and a few days after the EQ (Figure 6 and Figure 7). In particular, the meteorological stations in close vicinity to active fault regions are found to be very sensitive to the pre-EQ activity, based on our improved analysis over the previous ones. It is needless to say that the meteorological parameters are known to be closely related to the surface latent heat flux variations [1,2,3,4,5,6,7,8,9,10,11,12,76,77].
- The most significant precursor was observed in the atmosphere from the analysis of ULF/ELF electromagnetic radiation with the use of our new signal methodology (Figure 10). As already summarized in our recent review [34], we have found that this atmospheric ULF/ELF radiation is an excellent regular precursor with high probability gain, which was also confirmed in this paper. We have found a significant increase in ∆Sns at the frequencies of 2–6 Hz in the vicinity of the EQ date (or approximately one week before and one week after the EQ), which seems to be synchronous in time with the previous meteorological anomaly. In addition, our direction finding indicated that the main lobe of the azimuthal distribution in the last full-day interval is directed just towards the EQ epicenter. Recently, some other scientists presented additional evidence on this kind of ULF/ELF radiation before the EQs [78,79]. So, we can conclude that this ULF/ELF atmospheric radiation (as impulsive noises) is generated as a clear EQ precursor. However, the generation mechanism is not well understood, but is closely related to the subsurface disturbances such as radon emanation and its associated disturbances [34,80].
- What about the perturbation in the stratosphere? Even though we have extensively investigated this AGW activity in the stratosphere, it is very unfortunate that no clear AGW activity related to the EQ is observed. Nearly all AGW activities observed in this paper are found to be attributed to active meteorological disturbances. Although we have already found clear signatures of these AGW stratospheric activities for the great EQs such as the 2011 Tohoku EQ [24] and the 2016 Kumamoto EQ [23], Kundu et al. [81] have supplied additional evidence of seismogenic AGW activity for huge EQs.
- What about any seismogenic disturbance in the lowest ionosphere during the last phase of EQ preparation? It is definite that the lower ionosphere for this EQ is perturbed before the EQ with two independent methods. The first is the conspicuous presence of ULF depression two days before the EQ (Figure 16). This ULF depression is considered to be due to the perturbation in the lower ionosphere [34,35,36,37], which is regarded as the seismogenic generation of ULF turbulence or increased absorption when passing through the lower ionosphere of down-going magnetospheric ULF irregular pulsations. The observation site of KAK is located within the EQ preparation zone [25]. The second piece of evidence is provided by conventional VLF subionospheric observation near the EQ center (Chofu) of a long-distance VLF transmitter (NWC), which indicated the clear anomaly on the same day of two days before the EQ (Figure 17). Of course, we need extensive further analysis on which kind of lower ionospheric perturbation is generated two days before the EQ and how it is generated.
- Finally, we summarize what is happening in the upper ionosphere, such as the F region of the ionosphere [82,83]. Our extensive analyses both on the TEC and ionosonde observational data have indicated that no clear anomalies are detected during the last phase of EQ preparation, unlike the situation in the lower ionosphere. So, it seems that the initial lithospheric origin of the LAIC process is not strong enough to reach the upper F region of the ionosphere.
5. Conclusions
Based on the summary of observational facts in the previous summary, we will try to discuss the possible channel for the LAIC process, which is the most common and fundamental process that explains the transfer of energy from the lowest region of the lithosphere to the upper ionosphere. For large EQs such as the 2011 Tohoku EQ and the 2016 Kumamoto EQ, the most important distinction of the present Tokyo EQ is its modest magnitude of M = 5.9 and a rather larger depth of 75 km. As is summarized in Table 2, we have detected significant EQ precursors. The most remarkable ones are (i) ULF depression, (ii) VLF subionospheric perturbations, (iii) ULF/ELF electromagnetic radiation, and (iv) meteorological parameters. First, it is important to note that first three physical phenomena are very regular precursors, even for a modest magnitude EQ such as our Tokyo EQ. Additionally we have found newcomers in terms of meteorological parameters (temperature/humidity ratio and ACP) with extensive improvement in analysis methods. On the other hand, stratospheric AGW activity and perturbations in the upper ionosphere (F region) have not been detected clearly. Finally, the major three channels of the LAIC process are as follows: (i) the electrostatic channel (generation of electric fields in the atmosphere) [15,16]; (ii) the chemical channel such as radon emanation and its associated effects [18,19]; and (iii) the acoustic channel, in which acoustic waves and/or AGWs are generated near the Earth’s surface, propagating upwards and leading to the generation of lower ionospheric perturbation [4,20,21,22,23,24]. The most important signature in favor of (iii), the AGW channel, is the presence of stratospheric AGW activity, which is always accompanied by VLF/LF lower ionospheric perturbations for huge EQs [23,24,73]; however, our observational results indicate no evidence of AGW activity in the stratosphere. Therefore, we suggest that we might rule out the third AGW channel (as has been recently evidenced for huge EQs) for this modest EQ; however, other possible channels, such as a chemical channel with, for example, the emanation of radon and associated gases and the related effects, might have been in operation, at least, for this EQ.
Author Contributions
Conceptualization, M.H.; methodology and analysis, J.I., A.S., S.-S.Y., M.S. and Y.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Informed Consent Statement
Not applicable.
Data Availability Statement
The 1-second ULF magnetic field data at Kakioka is available from https://www.kakioka-jma.go.jp/obsdata/metadata/en/orders/new/2960 (accessed on November 15, 2021), and the source of Kp and Dst index data is the World Data Center for Geomagnetism, Kyoto (https://wdc.kugi.kyoto-u.ac.jp/kp/index/html)(accessed on 15 December 2021). Then ERA5 temperature data is produced by the European Centre for Medium-Range Weather Forecasts (ECMWF) within the Copernicus Climate Change Service (C3S), and the data can be downloaded from https://cds.climate.copernicus.eu/ (accessed on 15 December 2021). Ionosonde data is available at https://wdc.nict.go.jp/IONO/HP2009/ISDJ/index-E.html (accessed on 15 December 2021). Finally, CODE GIM is a product of the Center for Orbit Determination in Europe (CODE) and is available at http://ftp.aiub.ch/CODE/ (accessed on 15 November 2021).
Acknowledgments
The authors thank the colleagues of UEC for their useful discussions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hayakawa, M. Earthquake Prediction Studies in Japan. In Pre-Earthquake Processes: A Multidisciplinary Approach to Earthquake Prediction Studies; Ouzounov, D., Pulinets, S., Hattori, K., Taylor, P., Eds.; AGU Monograph 234; Wiley: Hoboken, NJ, USA, 2018; pp. 7–18. [Google Scholar]
- Wikipedia. 1923 Great Kantō Earthquake. Available online: https://:en.wikipedia.org/wiki1923_kanto_earthquake (accessed on 15 December 2021).
- Pulinets, S.A.; Boyarchuk, K. Ionospheric Precursors of Earthquakes; Springer: Berlin, Germany, 2004; 315p. [Google Scholar]
- Molchanov, O.A.; Hayakawa, M. Seismo Electromagnetics and Related Phenomena: History and Latest Results; Terrapub: Tokyo, Japan, 2008; 189p. [Google Scholar]
- Hayakawa, M. Earthquake Prediction with Radio Techniques; John Wiley and Sons: Singapore, 2015; 294p. [Google Scholar]
- Ouzounov, D.; Pulinets, S.; Hattori, K.; Taylor, P. (Eds.) Pre-Earthquake Processes: A Multidisciplinary Approach to Earthquake Prediction Studies; AGU Geophysical Monograph 234; Wiley: Hoboken, NJ, USA, 2018; 365p. [Google Scholar]
- Hayakawa, M. (Ed.) Earthquake Prediction Studies: Seismo Electromagnetics; Terrapub: Tokyo, Japan, 2013; 168p. [Google Scholar]
- Pulinets, S.A.; Ouzounov, D. The Probability of Earthquake Prediction: Learning from Nature; IOP (Institute of Physics) Publishing: Bristol, UK, 2018; 168p. [Google Scholar]
- Parrot, M. Anomalous Seismic Phenomena: View from space. In Electromagnetic Phenomena Associated with Earthquakes; Hayakawa, M., Ed.; Transworld Research Network: Trivandrum, India, 2009; pp. 205–233. [Google Scholar]
- Tronin, A.A.; Hayakawa, M.; Molchanov, O.A. Thermal IR satellite data application for earthquake research in Japan and China. J. Geodyn. 2002, 33, 519–534. [Google Scholar] [CrossRef]
- Tramutoli, V.; Cuomo, V.; Filizzola, C.; Pergola, N.; Pietrapertosa, C. Assesing the potential of thermal infrared satellite surveys for monitoring seismically active areas: The case of Kocaeli (Izmit) earthquake, August 07, 1999. Remote Sens. Environ. 2005, 96, 409–426. [Google Scholar] [CrossRef]
- Ouzounov, D.; Pulinets, S.; Davidenko, D.; Rozhnoi, A.; Solovieva, M.; Fedun, V.; Dwivedi, B.N.; Rybin, A.; Kafatos, M.; Taylor, P. Transient effects in atmosphere and ionosphere preceding the 2015 M7.8 and M7.3 Gorkha-Nepal earthquakes. Front. Earth Sci. 2021, 9, 757358. [Google Scholar] [CrossRef]
- Sasmal, S.; Chowdhury, S.; Kundu, S.; Politis, D.Z.; Potirakis, S.M.; Balasis, G.; Hayakawa, M.; Chakrabarti, S.K. Pre-seismic irregularities during the 2020 Samos (Greece) earthquake (M = 6.9) as investigated from multi-parameter approach by ground and space-based techniques. Atmosphere 2021, 12, 1059. [Google Scholar] [CrossRef]
- Hayakawa, M.; Izutsu, J.; Schekotov, A.; Yang, S.S.; Solovieva, M.; Budilova, E. Lithosphere-atmosphere-lithosphere coupling effects based on multiparameter precursor observations for February–March 2021 earthquakes (M~7) in the offshore of Tohoku area of Japan. Geosciences 2021, 11, 481. [Google Scholar] [CrossRef]
- Freund, F.T. Earthquake forewarning—A multidisciplinary challenge from the ground up to space. Acta Geophys. 2013, 61, 775–807. [Google Scholar] [CrossRef]
- Sorokin, V.M.; Chmyrev, V.M.; Hayakawa, M. A review on electrodynamic influence of atmospheric processes to the ionosphere. Open J. Earthq. Res. 2020, 9, 113–141. [Google Scholar] [CrossRef]
- Sorokin, V.V.; Chmyrev, V.; Hayakawa, M. Electrodynamic Coupling of Lithosphere-Atmosphere-Ionosphere of the Earth; NOVA Science Pub. Inc.: New York, NY, USA, 2015; 355p. [Google Scholar]
- Pulinets, S.A.; Ouzounov, D.; Karelin, A.V.; Boyarchuk, K.A.; Pokhmelnykh, L.A. The physical nature of thermal anomalies observed before strong earthquakes. Phys. Chem. Earth 2006, 31, 143–153. [Google Scholar] [CrossRef]
- Pulinets, S.; Ouzounov, D. Lithosphere-atmosphere-ionosphere coupling (LAIC) model—A unified concept for earthquake precursors validation. J. Asian Earth Sci. 2011, 41, 371–382. [Google Scholar] [CrossRef]
- Hayakawa, M.; Kasahara, Y.; Nakamura, T.; Hobara, Y.; Rozhnoi, A.; Solovieva, M.; Molchanov, O.A.; Korepanov, K. Atmospheric gravity waves as a possible candidate for seismo-ionospheric perturbations. J. Atmos. Electr. 2011, 31, 129–140. [Google Scholar] [CrossRef]
- Korepanov, V.; Hayakawa, M.; Yampolski, Y.; Lizunov, G. AGW as a seismo-ionospheric coupling responsible agent. Phys. Chem. Earth 2009, 34, 485–495. [Google Scholar] [CrossRef]
- Lizunov, G.; Skorokhod, T.; Hayakawa, M.; Korepanov, V. Formation of ionospheric precursors of earthquakes—Probable mechanism and its substantiation. Open J. Earthq. Res. 2020, 9, 142. [Google Scholar] [CrossRef]
- Yang, S.S.; Asano, T.; Hayakawa, M. Abnormal gravity wave activity in the stratosphere prior to the 2016 Kumamoto earthquakes. J. Geophys. Res. Space Phys. 2019, 124, 1410–1425. [Google Scholar] [CrossRef]
- Yang, S.S.; Hayakawa, M. Gravity wave activity in the stratosphere before the 2011 Tohoku earthquake as the mechanism of lithosphere-atmosphere-ionosphere coupling. Entropy 2020, 22, 110. [Google Scholar] [CrossRef] [PubMed]
- Dobrovolsky, I.R.; Zubrov, S.I.; Myachkin, V.I. Estimation of the size of earthquake preparation zone. Pure Appl. Geophys. 1979, 117, 1025–1044. [Google Scholar] [CrossRef]
- Hayakawa, M.; Kawate, R.; Molchanov, O.A.; Yumoto, K. Results of ultra-low-frequency magnetic field measurements during the Guam earthquake of 8 August 1993. Geophys. Res. Lett. 1996, 23, 241–244. [Google Scholar] [CrossRef]
- Currie, J.L.; Waters, C.L. On the use of geomagnetic indices and ULF waves for earthquake precursor signatures. J. Geophys. Res. Space Phys. 2014, 119, 992–1003. [Google Scholar] [CrossRef]
- Guiliani, G.G.; Giuliani, R.; Totani, G.; Eusani, G.; Totani, F. Radon Observations by Gamma Detectors “PM4 and PM2” during the Seismi Period (January–April 2009) in A’Aquila Basin; AGU Fall meeting, U14A-03; American Geophysical Union: Washington, DC, USA, 2009. [Google Scholar]
- Kuntoro, Y.; Setiwan, H.L.; Wijayanti, T.; Haerundin, N. The Correlation between Radon Emission Concentration and Subsurface Geological Condition; IOP Conference Series: Earth and Environmental Science; IOP Publishing Ltd.: Bristol, UK, 2018; Volume 132. [Google Scholar] [CrossRef]
- Fu, C.C.; Wang, P.K.; Lee, L.C.; Lin, C.H.; Chang, W.Y.; Giuliani, G.; Ouzounov, D. Temporal variation of gamma ray as a possible precursor of earthquake in the longitudinal valley of eastern Taiwan. J. Asian Earth Sci. 2015, 114, 362–372. [Google Scholar] [CrossRef]
- Schekotov, A.; Hayakawa, M. Seismo-meteo-electromagnetic phenomena observed during a 5-year interval around the 2011 Tohoku earthquake. Phys. Chem. Earth 2015, 85, 167–173. [Google Scholar] [CrossRef]
- Schekotov, A.Y.; Molchanov, O.A.; Hayakawa, M.; Fedorov, E.N.; Chebrov, V.N.; Sinitsin, V.I.; Gordeev, E.F.; Belyaev, G.G.; Yagova, N.V. ULF/ELF magnetic field variation from atmosphere by seismicity. Radio Sci. 2007, 42, RS6S90. [Google Scholar] [CrossRef]
- Schekotov, A.; Fedorov, E.; Molchanov, O.A.; Hayakawa, M. Low frequency electromagnetic precursors as a prospect for earthquake prediction. In Earthquake Prediction Studies: Seismo Electromagnetics; Hayakawa, M., Ed.; Terrapub: Tokyo, Japan, 2013; pp. 81–99. [Google Scholar]
- Hayakawa, M.; Schekotov, A.; Izutsu, J.; Nickolaenko, A.P. Seismogenic effects in ULF/ELF/VLF electromagnetic waves. Int. J. Electron. Appl. Res. 2019, 6, 1–86. [Google Scholar] [CrossRef]
- Schekotov, A.; Chebrov, D.; Hayakawa, M.; Belyaev, G.; Berseneva, N. Short-term earthquake prediction at Kamchatka using low-frequency magnetic field. Nat. Hazards 2020, 100, 735–755. [Google Scholar] [CrossRef]
- Ohta, K.; Izutsu, J.; Schekotov, A.; Hayakawa, M. The ULF/ELF electromagnetic radiation before the 11 March 2011 Japanese earthquake. Radio Sci. 2013, 48, 589–596. [Google Scholar] [CrossRef]
- Fowler, R.A.; Kotick, B.J.; Elliot, R.D. Polarization analysis of natural and artificially induced geomagnetic micropulsations. J. Geophys. Res. 1967, 72, 2871–2875. [Google Scholar] [CrossRef]
- Herbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horanyi, A.; Munoz-Sabataer, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Molchanov, O.A.; Schekotov, A.Y.; Fedorov, E.N.; Belyaev, G.G.; Gordeev, E.E. Preseismic ULF electromagnetic effect from observation at Kamchatka. Nat. Hazards Earth Syst. Sci. 2003, 3, 203–209. [Google Scholar] [CrossRef]
- Molchanov, O.A.; Schekotov, A.Y.; Fedorov, E.; Belyaev, G.G.; Gordeev, E.E. Preseismic ULF electromagnetic effect and possible interpretation. Ann. Geophys. 2004, 47, 119–131. [Google Scholar]
- Schekotov, A.; Molchanov, O.; Hattori, K.; Fedorov, E.; Gladyshev, V.A.; Belyaev, G.G.; Chebrov, V.; Sinitsin, V.; Gordeev, E.; Hayakawa, M. Seismo-ionospheric depression of the ULF geomagnetic fluctuations at Kamchatka and Japan. Phys. Chem. Earth 2006, 31, 313–318. [Google Scholar] [CrossRef]
- Hayakawa, M.; Schekotov, A.; Fedorov, E.; Hobara, Y. On the ultra-low-frequency magnetic field depression for three huge oceanic earthquakes in Japan and in the Kurile islands. Earth Sci. Res. 2013, 2, 33. [Google Scholar] [CrossRef][Green Version]
- Kikuchi, T.; Evans, D.S. Quantitative study of substorm-associated VLF phase anomalies and precipitating energetic electrons on November 13, 1979. J. Geophys. Res. Space Phys. 1983, 88, 871–880. [Google Scholar] [CrossRef]
- Peter, W.B.; Chevalier, M.W.; Inan, U.S. Perturbations of midlatitude subionospheric VLF signals associated with lower ionospheric disturbances during major geomagnetic storms. J. Geophys. Res. Space Phys. 2006, 111, A3. [Google Scholar] [CrossRef]
- Hayakawa, M.; Molchanov, O.A.; Ondoh, T.; Kawai, E. The precursory signature effect of the Kobe earthquake on VLF subionospheric signals. J. Commun. Res. Lab. 1996, 43, 169–180. [Google Scholar]
- Hayakawa, M.; Kasahara, Y.; Nakamura, T.; Muto, F.; Horie, T.; Maekawa, S.; Hobara, Y.; Rozhnoi, A.A.; Solovieva, M.; Molchanov, O.A. A statistical study on the correlation between lower ionospheric perturbations as seen by subionospheric VLF/LF propagation and earthquakes. J. Geophys. Res. 2010, 115, A09305. [Google Scholar] [CrossRef]
- Molchanov, O.A.; Hayakawa, M. Subionospheric VLF signal perturbations possibly related to earthquakes. J. Geophys. Res. 1998, 103, 17489–17504. [Google Scholar] [CrossRef]
- Biagi, P.F.; Ermini, A. Geochemical and VLF-LF radio precursors of strong earthquakes. In Earthquake Prediction Studies: Seismo Electromagnetics; Hayakawa, M., Ed.; Terrapub: Tokyo, Japan, 2013; pp. 153–168. [Google Scholar]
- Rozhnoi, A.; Solovieva, M.; Molchanov, O.A.; Hayakawa, M. Middle latitude LF (40 kHz) phase variations associated with earthquakes for quiet and disturbed geomagnetic conditions. Phys. Chem. Earth 2004, 29, 589–598. [Google Scholar] [CrossRef]
- Rozhnoi, A.; Solovieva, M.; Hayakawa, M. VLF/LF signals method for searching for electromagnetic earthquake precursors. In Earthquake Prediction Studies: Seismo Electromagnetics; Hayakawa, M., Ed.; Terrapub: Tokyo, Japan, 2013; pp. 31–48. ISBN 978-4-88704-163-9. [Google Scholar]
- Maekawa, S.; Horie, T.; Yamauchi, T.; Sawaya, T.; Ishikawa, M.; Hayakawa, M.; Sasaki, H. A statistical study on the effect of earthquakes on the ionosphere, as based on the subionospheric LF of propagation data in Japan. Ann. Geophys. 2006, 24, 2219–2225. [Google Scholar] [CrossRef]
- Ray, S.; Chakrabarti, S.K.; Mondal, S.M.; Sasmal, S. Ionospheric anomaly due to seismic activities III: Correlation between nighttime VLF amplitude fluctuations and effective magnitudes in Indian sub-continent. Nat. Hazards Earth Syst. Sci. 2011, 11, 2699–2704. [Google Scholar] [CrossRef][Green Version]
- Hayakawa, M.; Asano, T.; Rozhnoi, A.; Solovieva, M. Very-low and low-frequency sounding of ionospheric perturbations and possible association with earthquakes. In Pre-Earthquake Processes: A Multidisciplinary Approach to Earthquake Prediction Studies; Ouzounov, D., Pulinets, S., Hattori, K., Taylor, P., Eds.; AGU monograph; Wiley: Hoboken, NJ, USA, 2018; pp. 277–304. [Google Scholar]
- Pal, S.; Hobara, Y.; Chakrabarti, S.K.; Schnor, P.W. Effects of the major sudden stratospheric warming events of 2009 on the subionospheric very low frequency/low frequency radio signals. J. Geophys. Res. Space Phys. 2017, 122, 7555–7566. [Google Scholar] [CrossRef]
- Liu, J.Y.; Chen, Y.I.; Chuo, Y.J.; Chen, C.S. A statistical investigation of pre-earthquake ionospheric anomaly. J. Geophys. Res. 2006, 111, A05304. [Google Scholar] [CrossRef]
- Le, H.; Liu, J.Y.; Liu, L. A statistical analysis of ionospheric anomalies before 736 M 6.0+ earthquakes during 2002–2010. J. Geophys. Res. Space Phys. 2011, 116, A02303. [Google Scholar] [CrossRef]
- Schaer, S. Mapping and Predicting the Earth’s Ionosphere Using the Global Positioning System. Ph.D. Thesis, Astronomical Institute, University of Berne, Berne, Switzerland, 1999. [Google Scholar]
- Kopytenko, Y.A.; Matiashvily, T.G.; Voronov, P.M.; Kopytenko, E.A.; Molchanov, O.A. Detection of ULF emissions connected with the Spitak earthquake and its aftershock activity based on geomagnetic pulsations data at Dusheti and Vardziya observatories. Phys. Earth Planet. Inter. 1990, 77, 85–95. [Google Scholar] [CrossRef]
- Molchanov, O.A.; Kopytenko, Y.A.; Voronov, P.M.; Kopytenko, E.A.; Matiashvily, T.G.; Fraser-Smith, A.C.; Bernardi, A. Results of ULF magnetic field measurements near the epicenters of the Spitac (Ms = 6.9) and Loma Prieta (Ms = 7.1) earthquakes: Comparative analysis. Geophys. Res. Lett. 1992, 19, 1495–1498. [Google Scholar] [CrossRef]
- Fraser-Smith, A.C.; Bernardi, A.; McGill, P.R.; Ladd, M.E.; Helliwell, R.A.; Villard, O.G., Jr. Low-frequency magnetic field measurements near the epicenter of the Ms 7.1 Loma Prieta earthquake. J. Geophys. Res. 1990, 17, 1465–1468. [Google Scholar]
- Hayakawa, M.; Kawate, R.; Molchanov, O.A. Ultra-low-frequency signatures of the Guam earthquake of 8 August 1993 and its implications. J. Atmos. Electr. 1996, 16, 193–198. [Google Scholar]
- Mizutani, H.; Ishido, T.; Yokokura, T.; Ohnishi, S. Electrokinetic phenomena associated with earthquakes. Geophys. Res. Lett. 1976, 3, 365–368. [Google Scholar] [CrossRef]
- Molchanov, M.; Hayakawa, M. Generation of ULF electromagnetic emissions by microfracturing. Geophys. Res. Lett. 1995, 22, 3091–3094. [Google Scholar] [CrossRef]
- Tzanis, A.; Vallianatos, F. A physical model of electric earthquake precursors due to crack propagation and the motion of charged edge dislocations. In Seismo Electromagnetics: Lithosphere-Atmosphere-Ionosphere Coupling; Hayakawa, M., Molchanov, O.A., Eds.; Terrapub: Tokyo, Japan, 2002; pp. 117–130. [Google Scholar]
- Eftaxias, K.; Potirakis, S.M.; Contoyiannis, Y. Four-stage model of earthquake generation in terms of fracture-induced electromagnetic emission: A review. In Complexity of Seismic Time Series; Chelidze, T., Vallianatos, F., Teleska, L., Eds.; Elsevier: Amsterdam, The Netherlands, 2018; pp. 437–502. [Google Scholar]
- Varotsos, P.; Sarlis, N.; Skordas, E.S. Phenomena preceding major earthquakes interconnected through physical model. Ann. Geophys. 2019, 37, 315–324. [Google Scholar] [CrossRef]
- Potirakis, S.M.; Contoyiannis, Y.; Koulouras, G.; Nomicos, C. Recent field observations indicating an earth system in critical condition before the occurrence of a significant earthquake. IEEE Geosci. Remote Sens. Lett. 2015, 12, 631–635. [Google Scholar] [CrossRef]
- Potirakis, S.M.; Schekotov, A.; Asano, T.; Hayakawa, M. Natural time analysis on the ultra-low frequency magnetic field variations prior to the 2016 Kumamoto (Japan) earthquakes. J. Asian Earth Sci. 2018, 154, 419–427. [Google Scholar] [CrossRef]
- Potirakis, S.M.; Contoyiannis, Y.; Schekotov, A.; Eftaxias, K.; Hayakawa, M. Evidence of critical dynamics in various electromagnetic precursors. Eur. Phys. J. Spec. Top. 2021, 230, 151–177. [Google Scholar] [CrossRef]
- Hattori, K. ULF geomagnetic changes associated with large earthquakes. Terr. Atmos. Ocean. Sci. 2004, 15, 329–360. [Google Scholar] [CrossRef]
- Han, P.; Hattori, K.; Hirokawa, M.; Zhuang, J.; Chen, C.H.; Febriani, F.; Yamaguchi, H.; Yoshino, C.; Liu, J.Y.; Yoshida, S. Statistical analysis of ULF seismomagnetic phenomena at Kakioka, Japan, during 2001–2010. J. Geophys. Res. Space Phys. 2014, 119, 4998–5011. [Google Scholar] [CrossRef]
- Kamiyama, M.; Sugito, M.; Kuse, M.; Schekotov, A.; Hayakawa, M. On the precursors to the 2011 Tohoku earthquake: Crustal movements and electromagnetic signatures. Geomat. Nat. Hazards Risk 2014, 7, 471–492. [Google Scholar] [CrossRef]
- Yang, S.S.; Potirakis, S.M.; Sasmal, S.; Hayakawa, M. Natural time analysis of Global Navigation Satellite System surface deformation: The case of the 2016 Kumamoto earthquakes. Entropy 2020, 22, 674. [Google Scholar] [CrossRef]
- Bedford, J.R.; Moreno, M.; Deng, Z.; Oncken, O.; Schurr, B.; John, T.; Baez, T.C.; Bevis, M. Months-long thousand-kilometre-scale wobbling before great subduction earthquakes. Nature 2020, 580, 628–639. [Google Scholar] [CrossRef]
- Chen, C.H.; Lin, L.C.; Yeh, T.K.; Wen, S.; Yu, H.; Yu, C.; Gao, Y.; Han, P.; Sun, Y.Y.; Liu, J.Y.; et al. Determination of epicenters before earthquakes utilizing far seismic and GNSS data: Insights from ground vibrations. Remote Sens. 2020, 12, 3252. [Google Scholar] [CrossRef]
- Cervone, G.; Maekawa, S.; Singh, R.P.; Hayakawa, M.; Katafos, M.; Shvets, A. Surface heat flux and nighttime LF anomalies prior to the Mw = 8.3 Tokai-oki earthquake. Nat. Hazards Earth Syst. Sci. 2006, 6, 109–114. [Google Scholar] [CrossRef]
- Gosh, S.; Chowdhury, S.; Kundu, S.; Sasmal, S.; Politis, D.; Potirakis, S.; Hayakawa, M.; Chakraborti, S.; Chakrabarti, S.K. Unusual surface latent heat flux variations and their critical dynamics revealed before strong earthquakes. Entropy 2022, 24, 23. [Google Scholar] [CrossRef]
- Fidani, C.; Orsini, M.; Iezzi, G.; Vicentini, N.; Stoppa, F. Electric and magnetic recordings by Cieti CIEN station during the intense 2016–2017 seismic swarms in Central Italy. Front. Earth Sci. 2020, 8, 536332. [Google Scholar] [CrossRef]
- Straser, V.; Cataldi, G.; Cataldi, D. SELF and VLF electromagnetic signal variations that preceded the Central Italy earthquake on August 24, 2016. New Concepts Glob. Tecton. J. 2016, 4, 473–477. [Google Scholar]
- Schekotov, A.; Hayakawa, M.; Potirakis, S.M. Does air ionization by radon cause low-frequency earthquake precursor? Nat. Hazards 2021, 106, 701–714. [Google Scholar] [CrossRef]
- Kundu, S.; Chowdhury, S.; Gosh, S.; Sasmal, S.; Politis, D.; Potirakis, S.M.; Yang, S.S.; Chakrabarti, S.K.; Hayakawa, M. Seismogenic anomalies in Atmospheric Gravity Waves observed by SABER/TIMED satellite during large earthquakes. J. Sens. 2022, 2022, 3201104. [Google Scholar] [CrossRef]
- Picozza, P.; Conti, L.; Sotgiu, A. Looking for earthquake precursors from space. Front. Earth Sci. 2021, 9, 578. [Google Scholar] [CrossRef]
- Conti, L.; Picozza, P.; Sotgiu, A. A critical review of ground-based observations of earthquake precursors. Front. Earth Sci. 2021, 9, 676766. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).