In-Situ Evolution of Calcite Twinning during Uniaxial Compression of Carrara Marble at Room Temperature
Abstract
:1. Introduction
2. Materials and Preparation Protocol
2.1. Sample Preparation
2.2. Kinematic Markers and DIC Principles
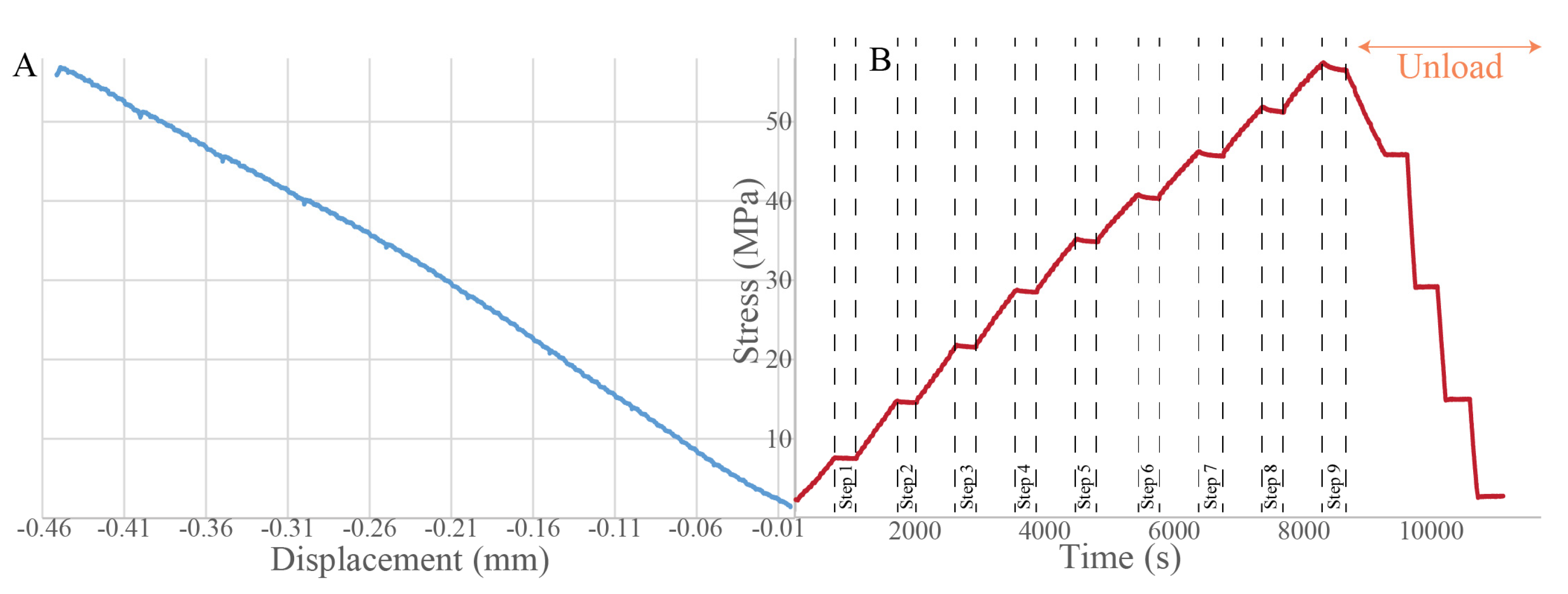
2.3. In-Situ SEM Deformation
3. Results
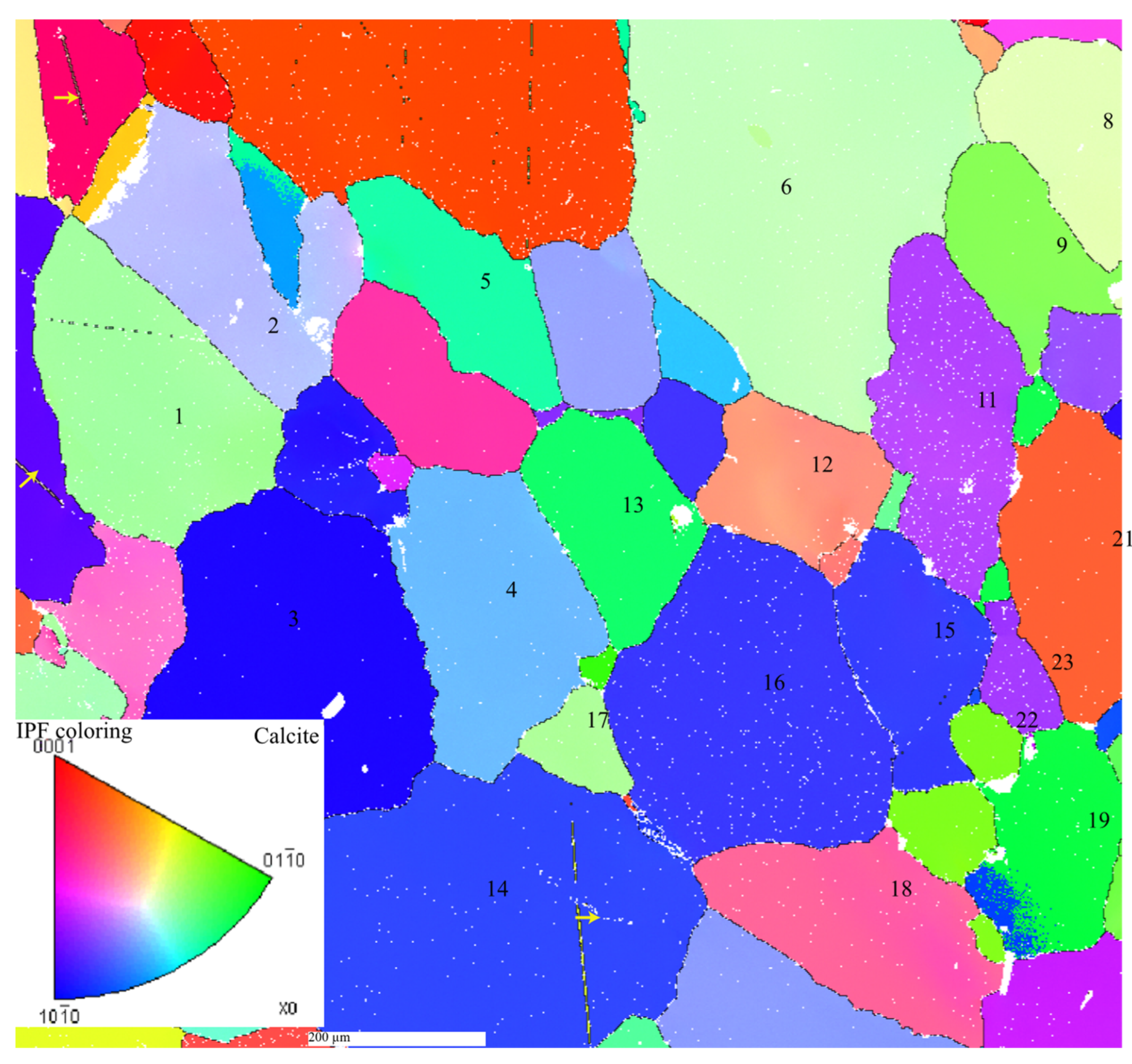
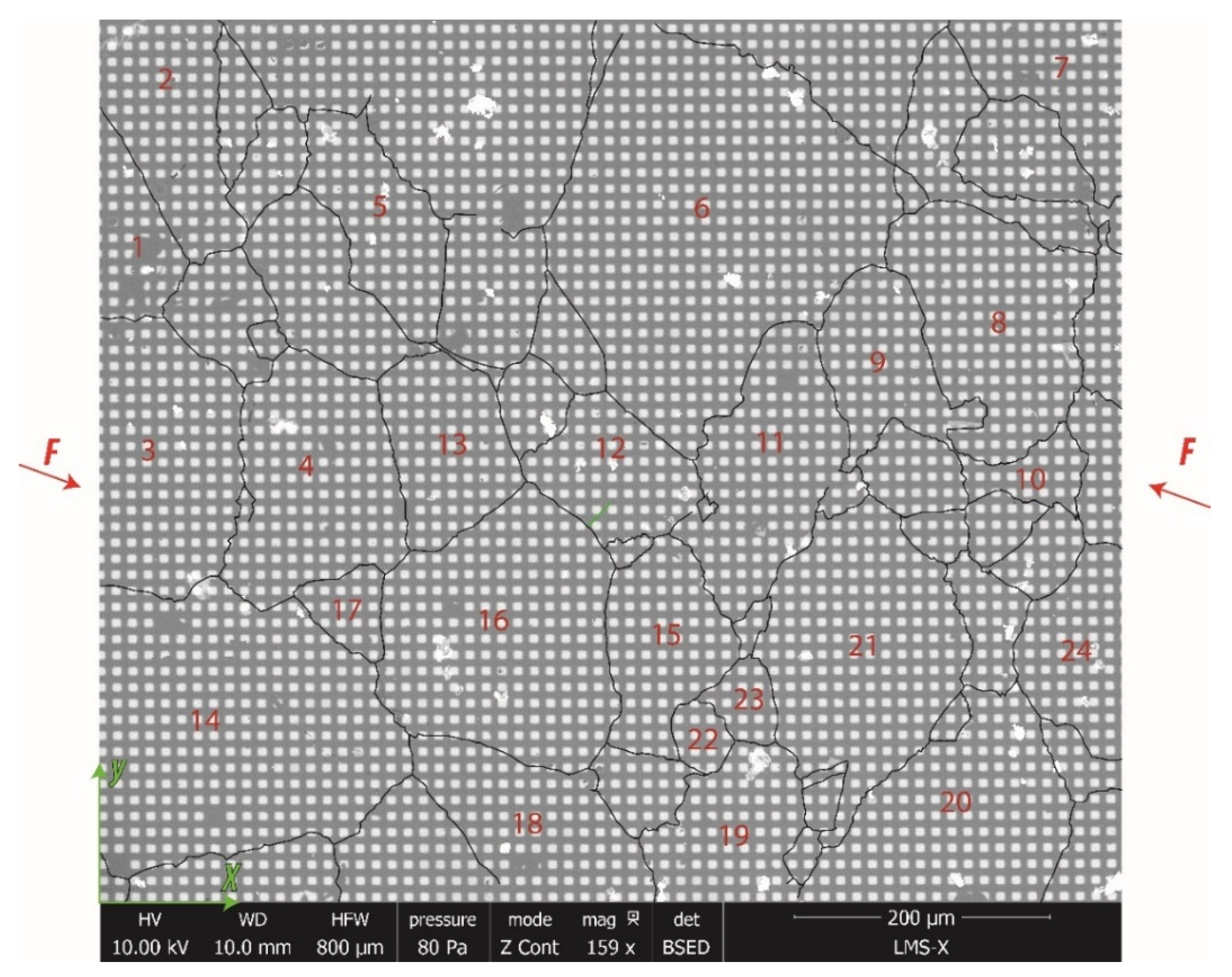
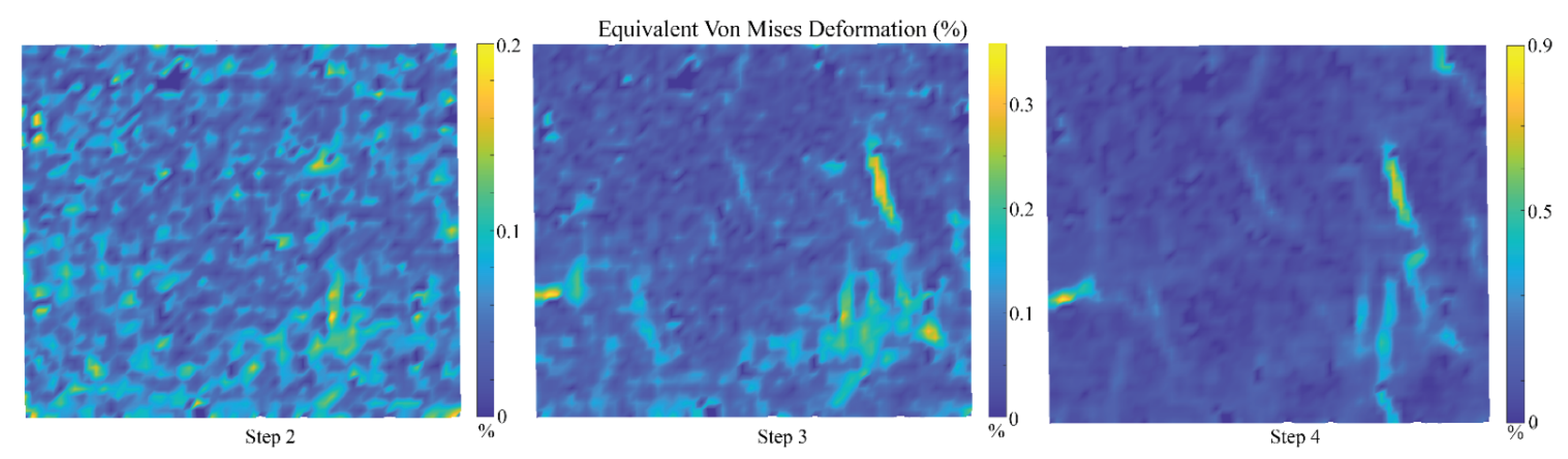
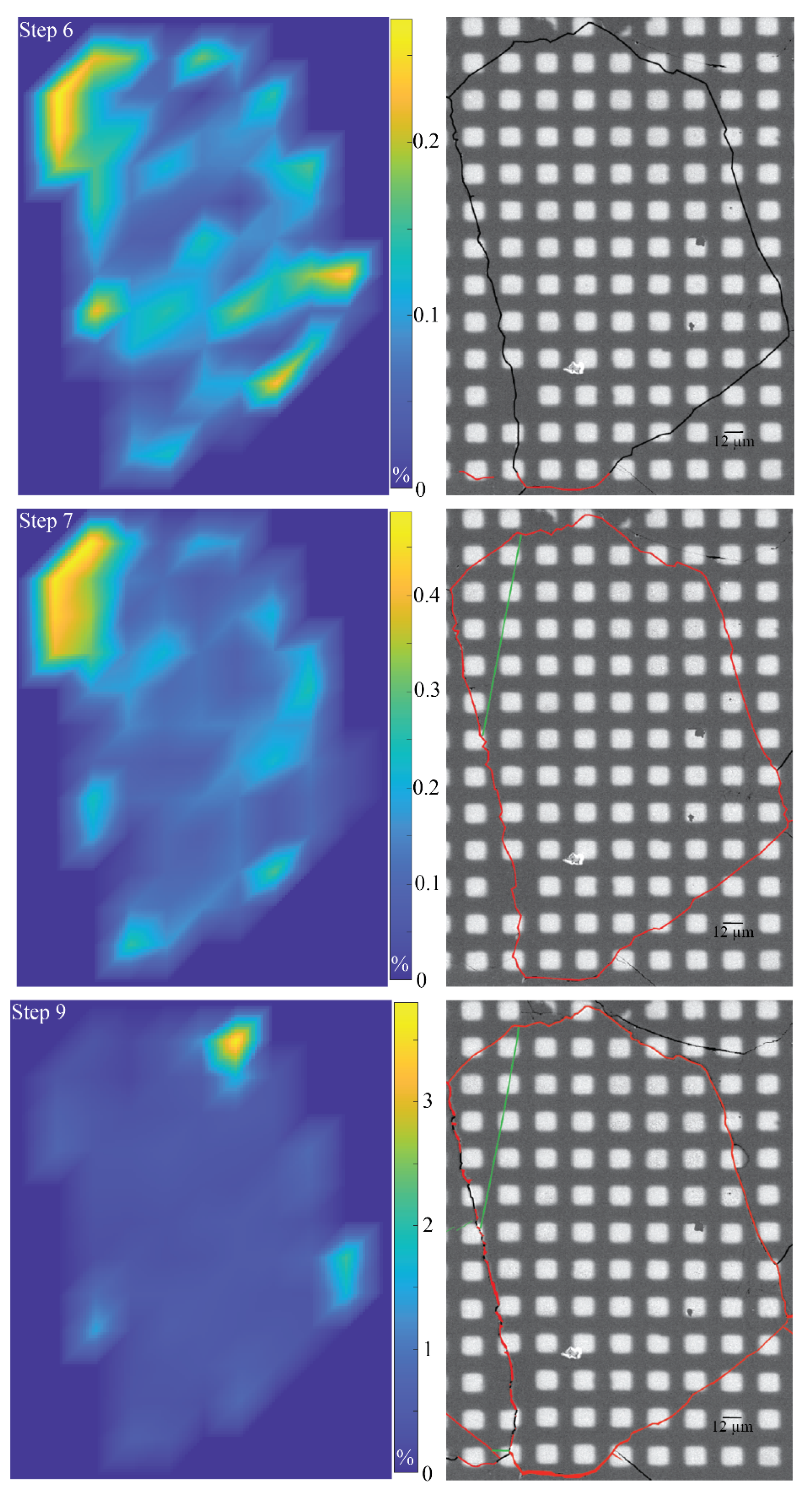
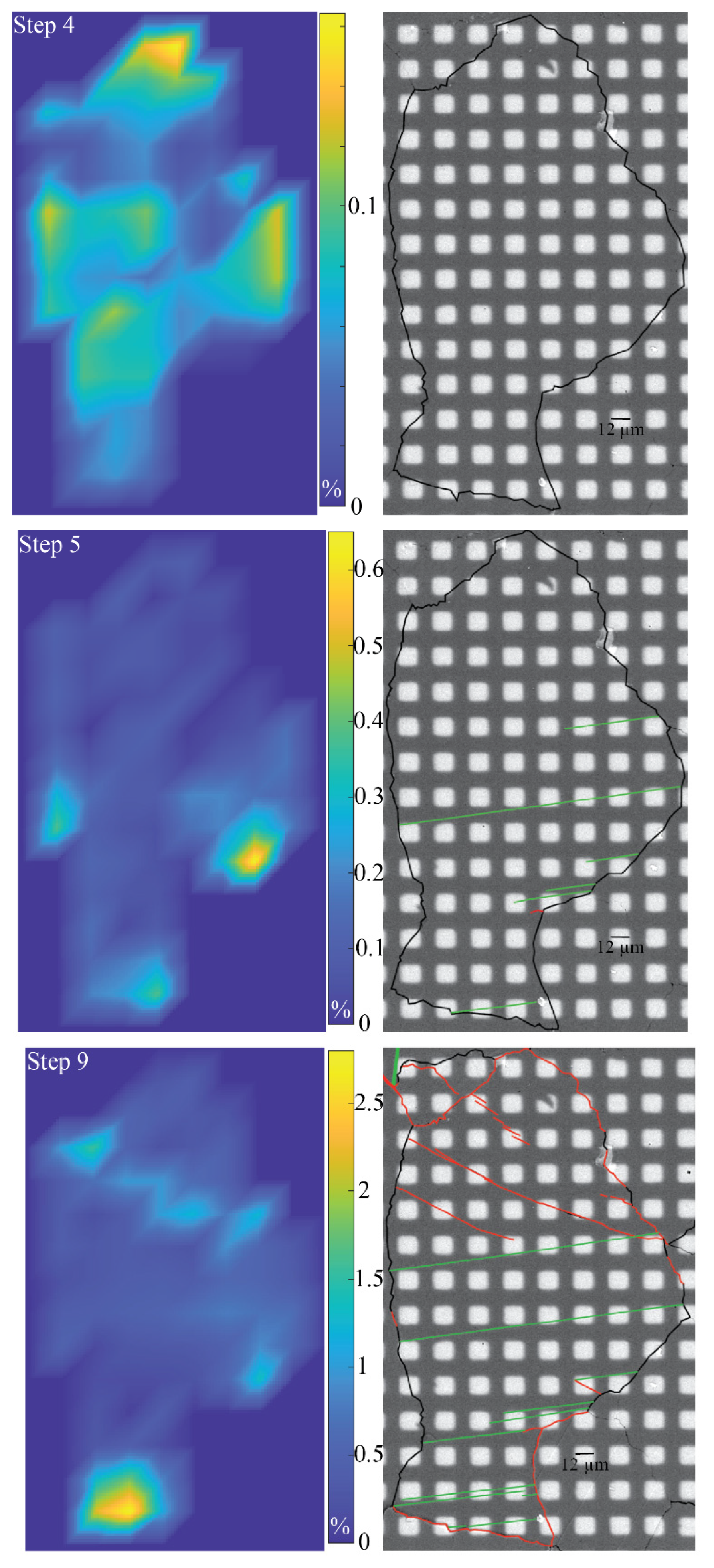
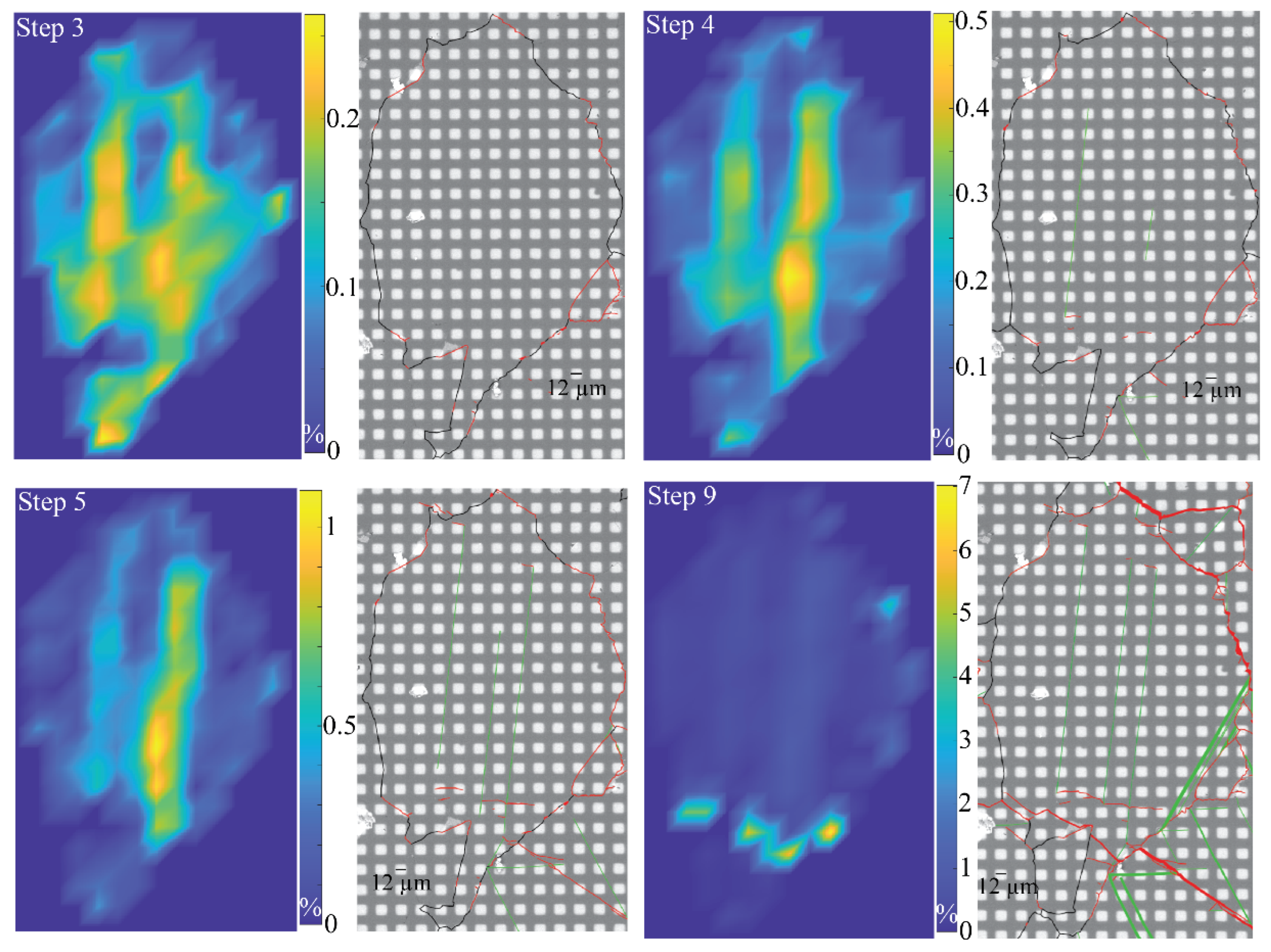
3.1. Overall Surface Observation
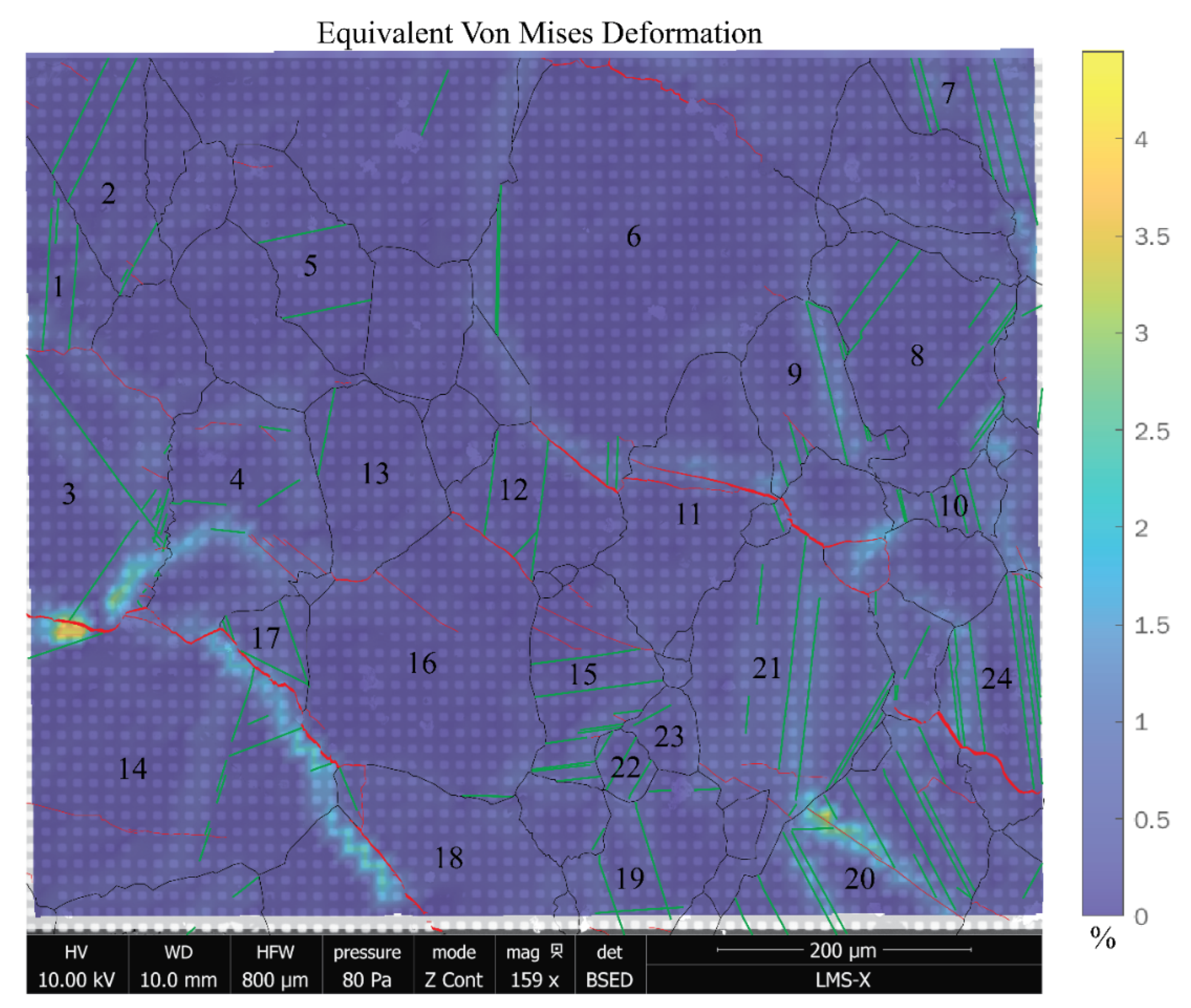
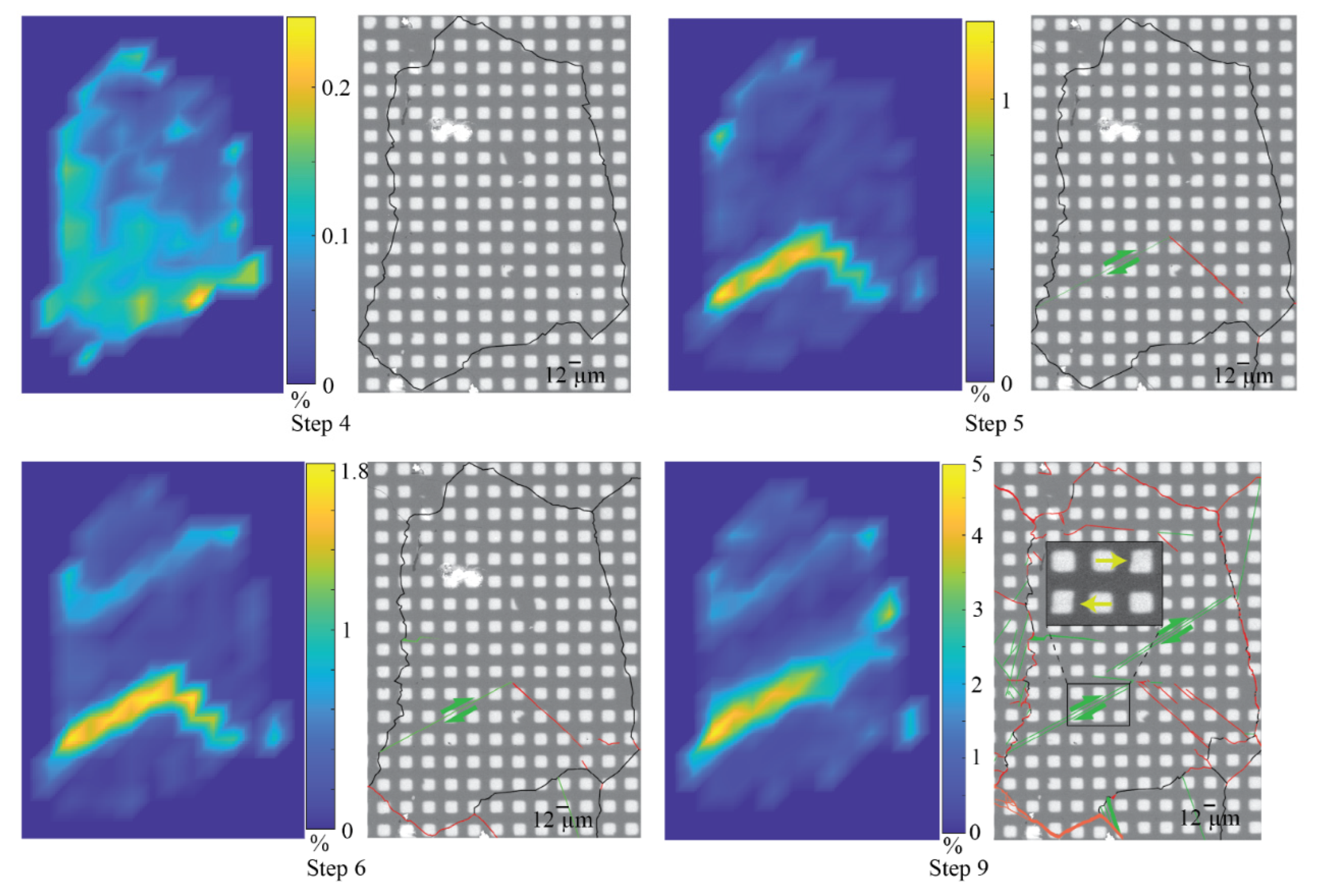
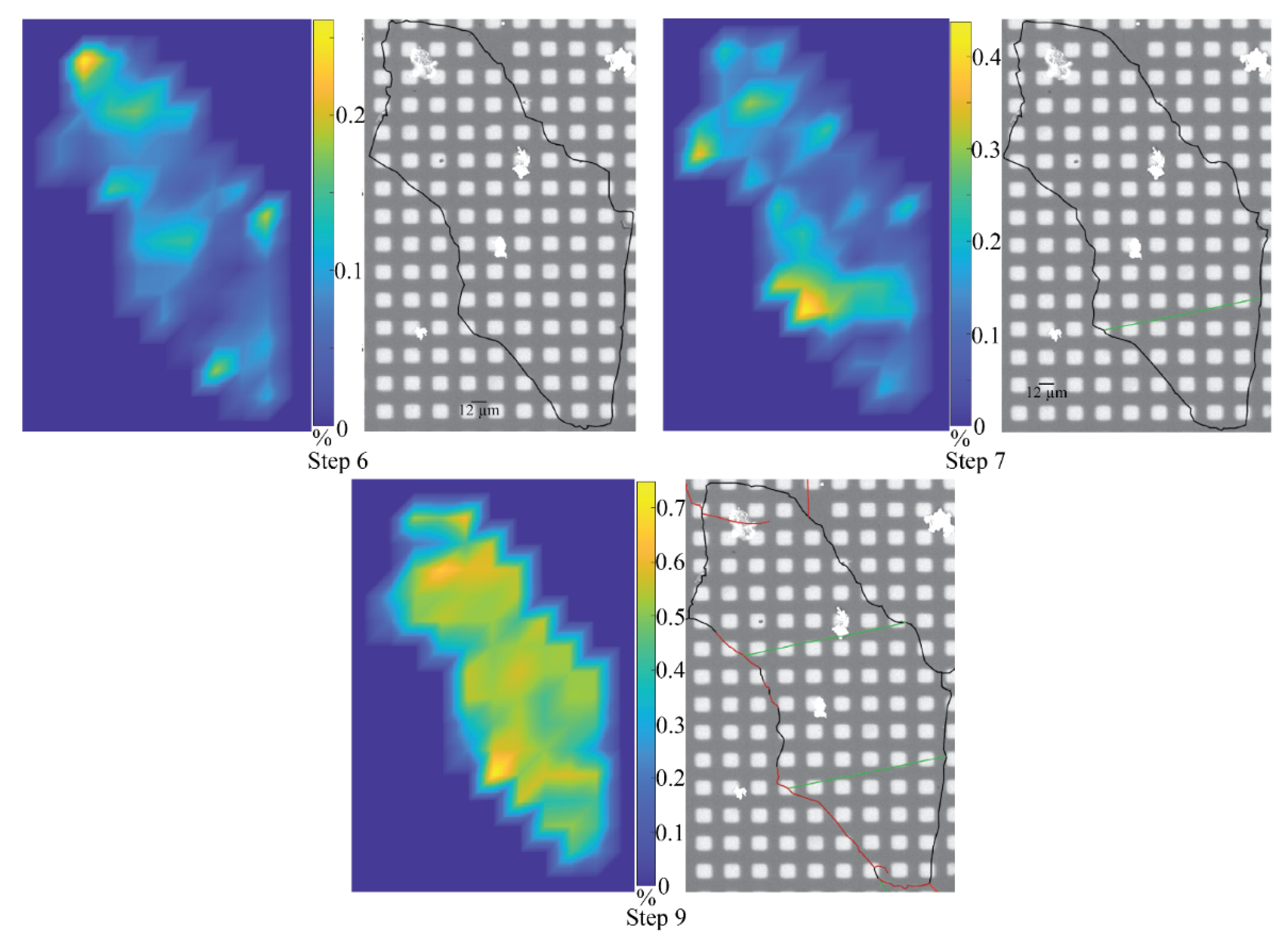
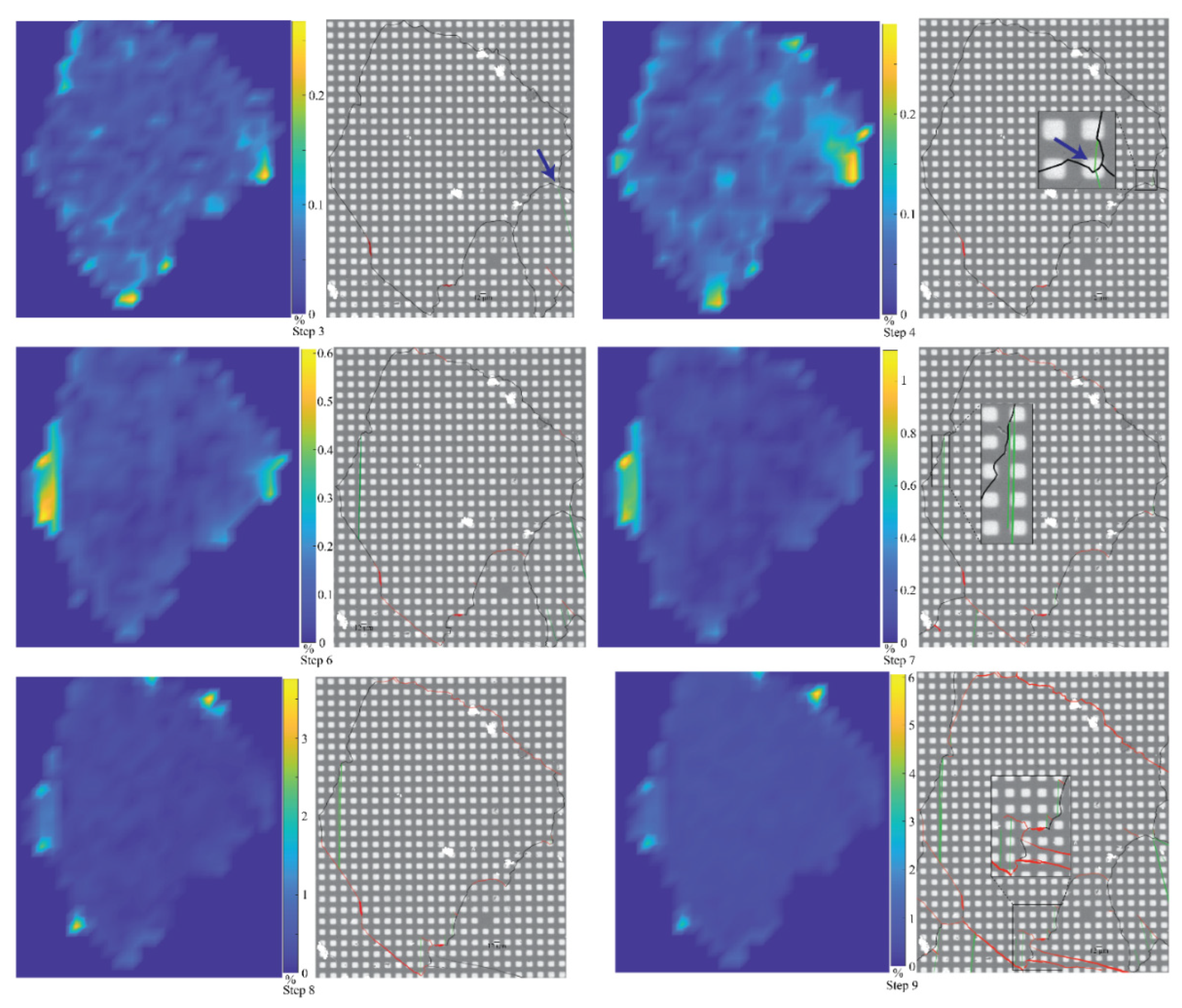
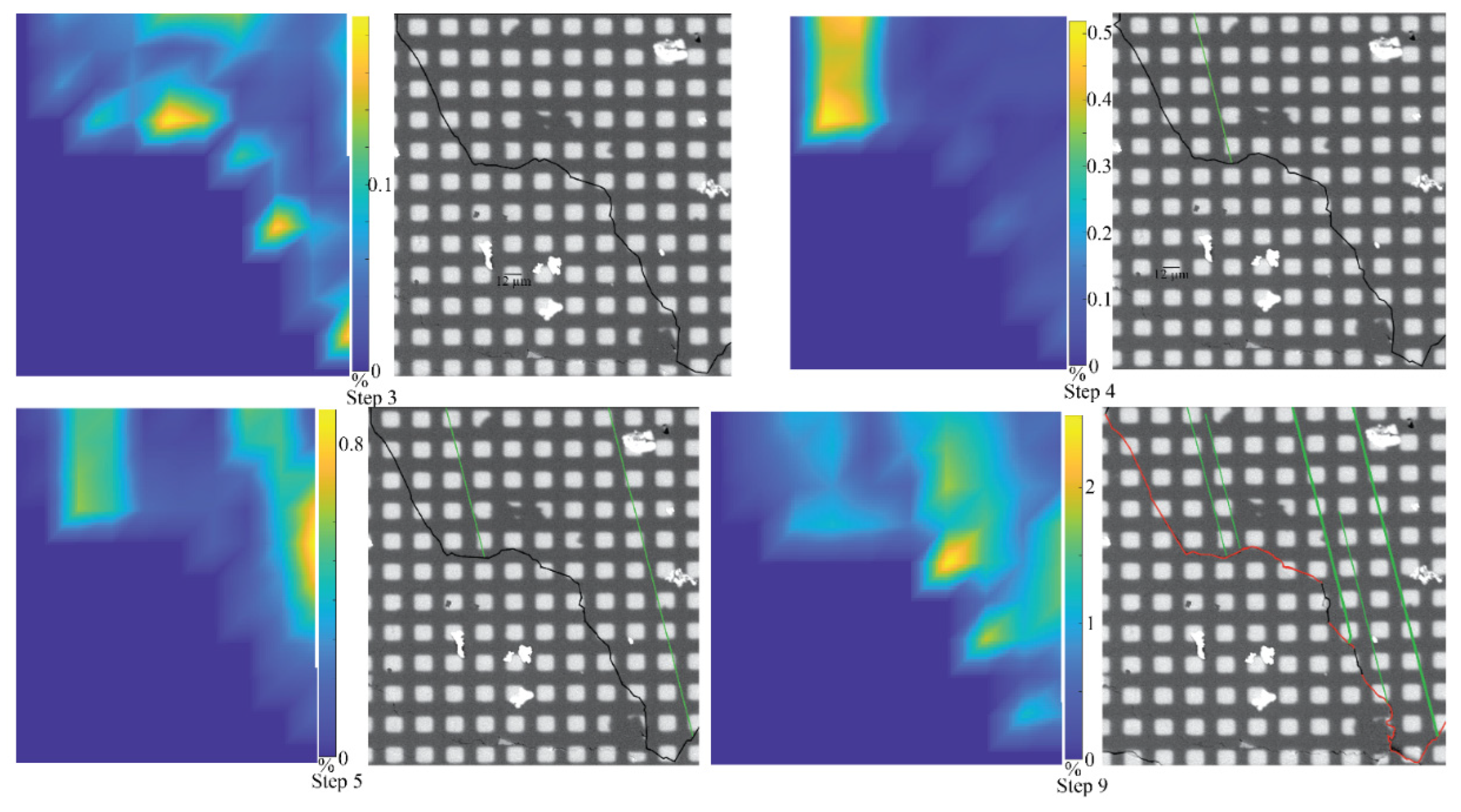
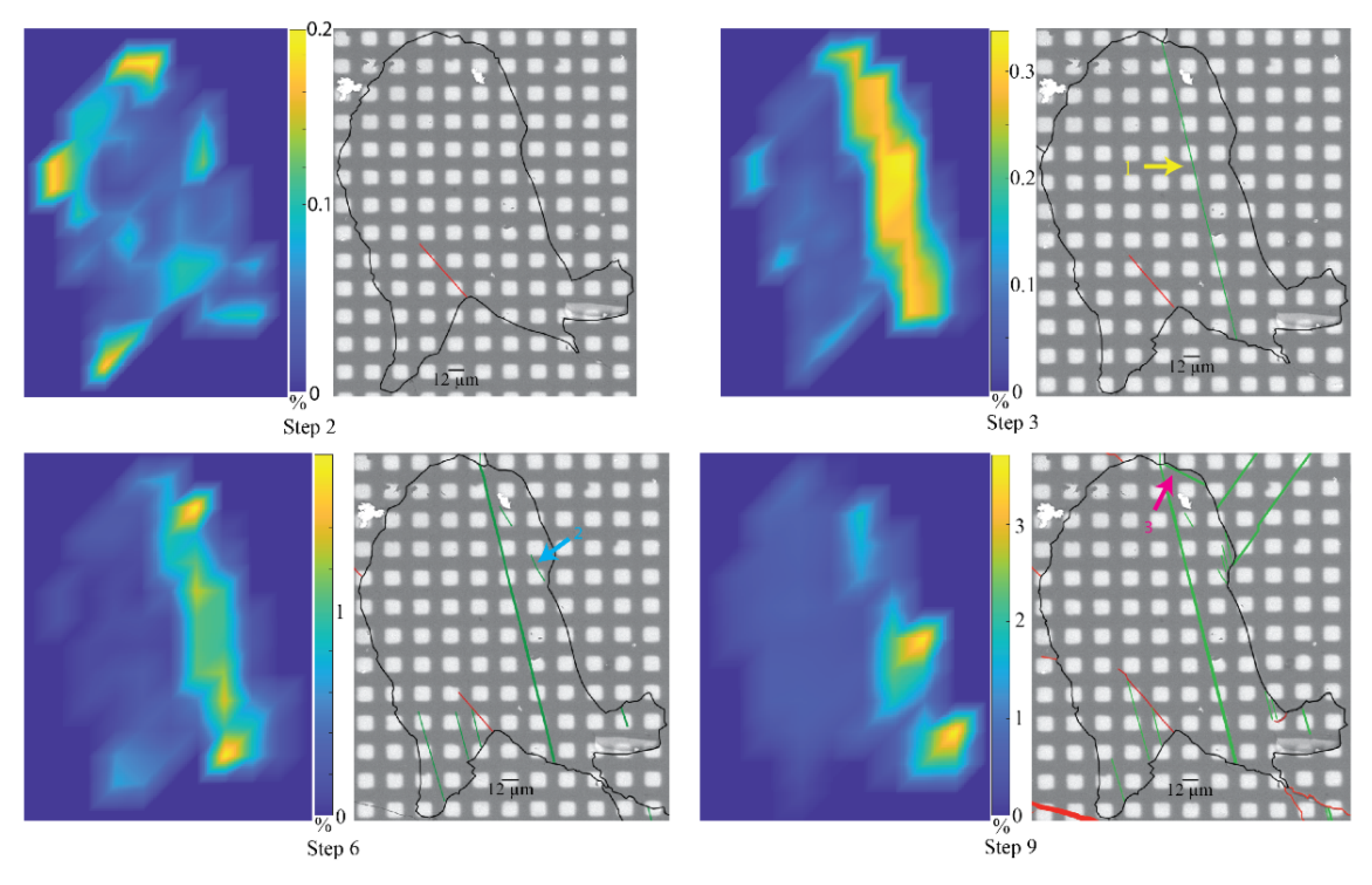
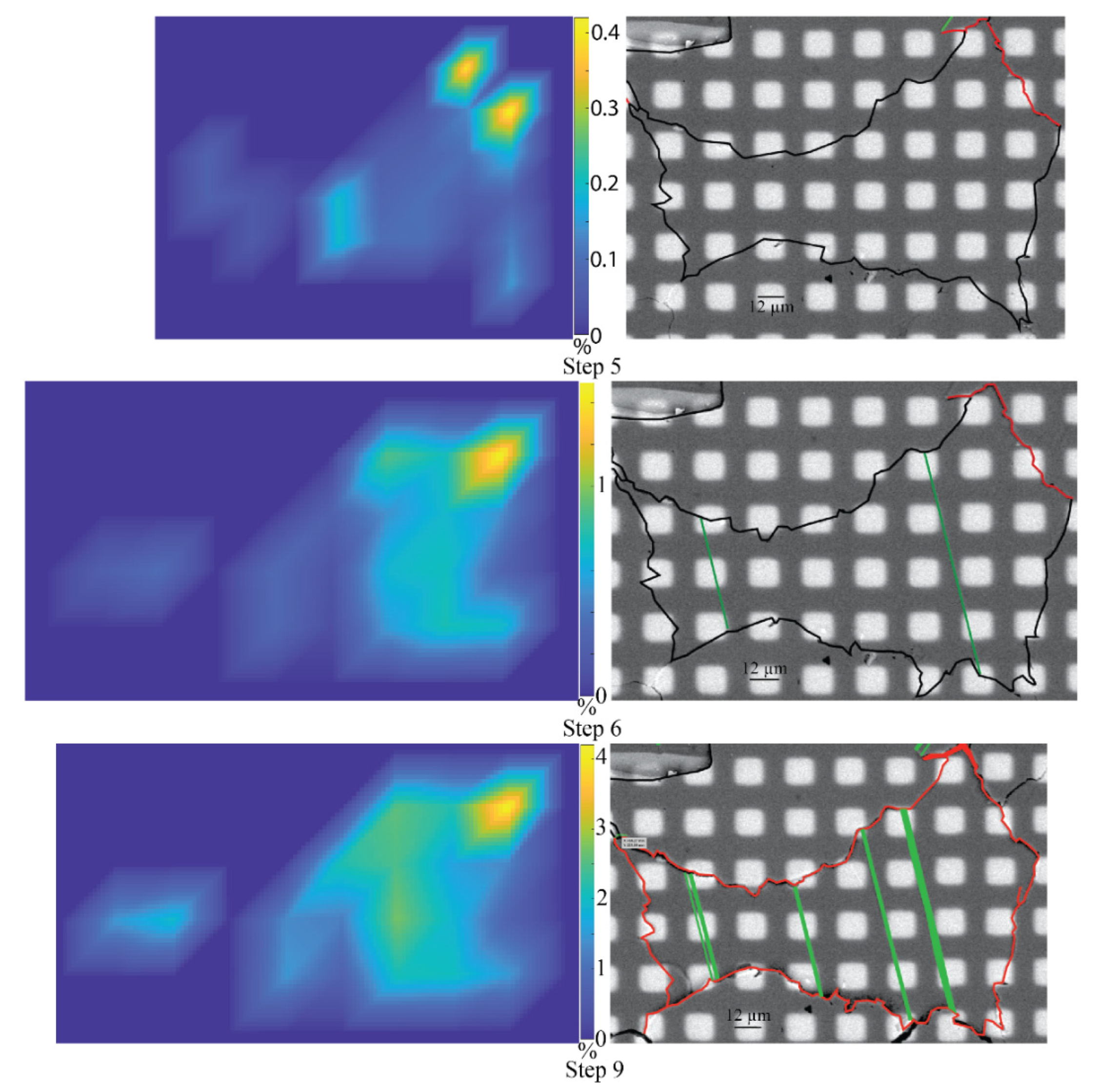
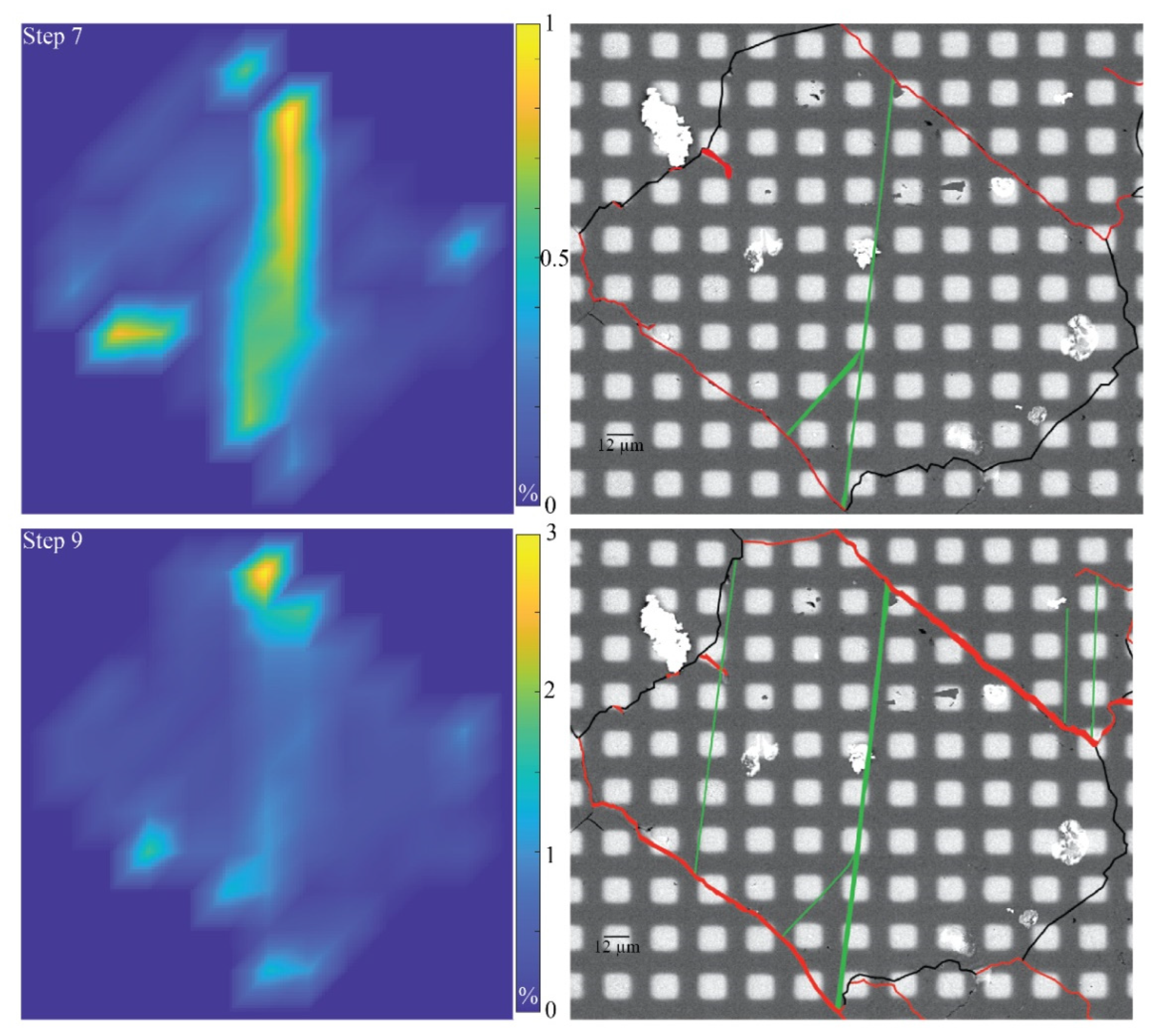
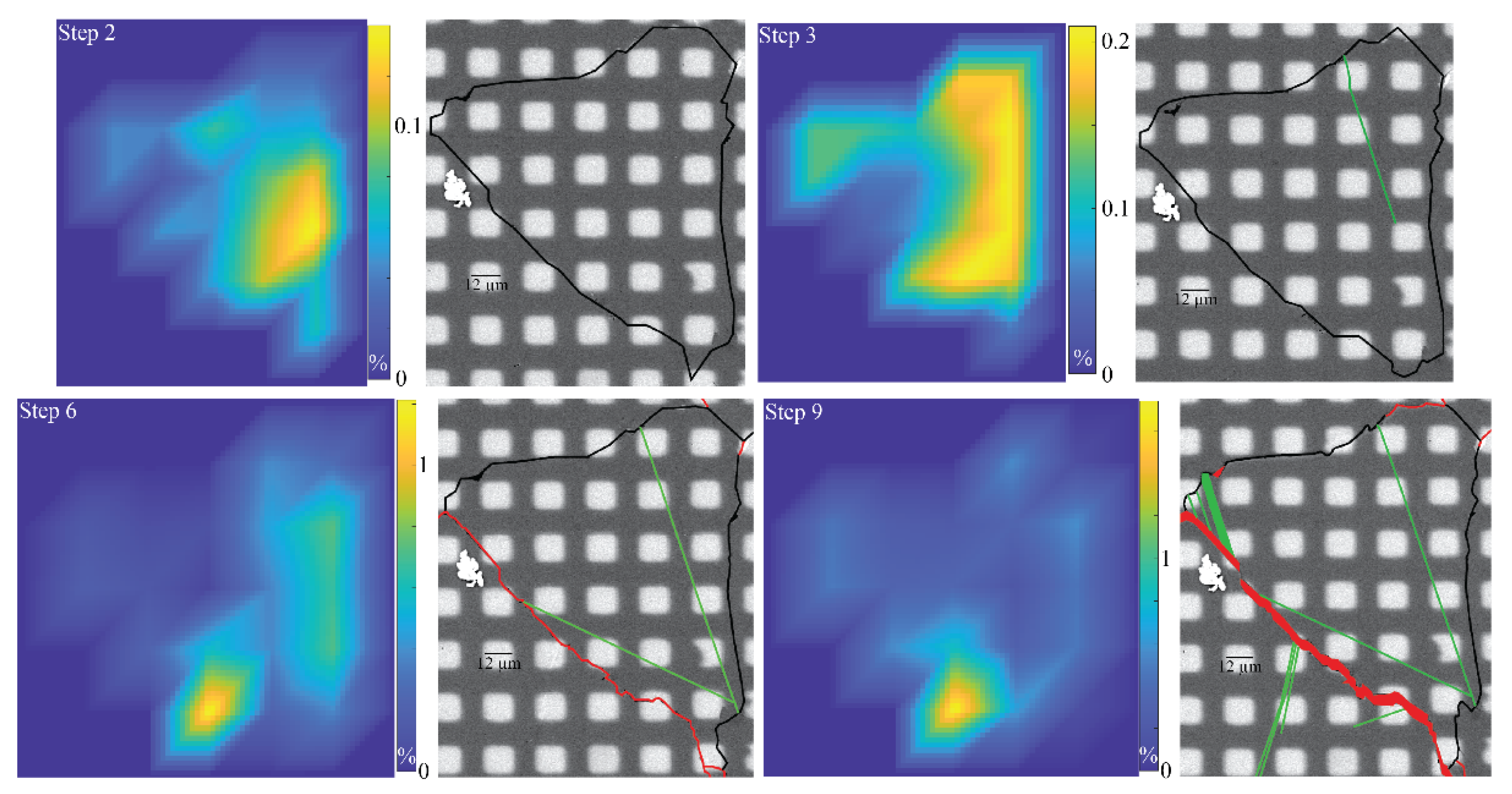
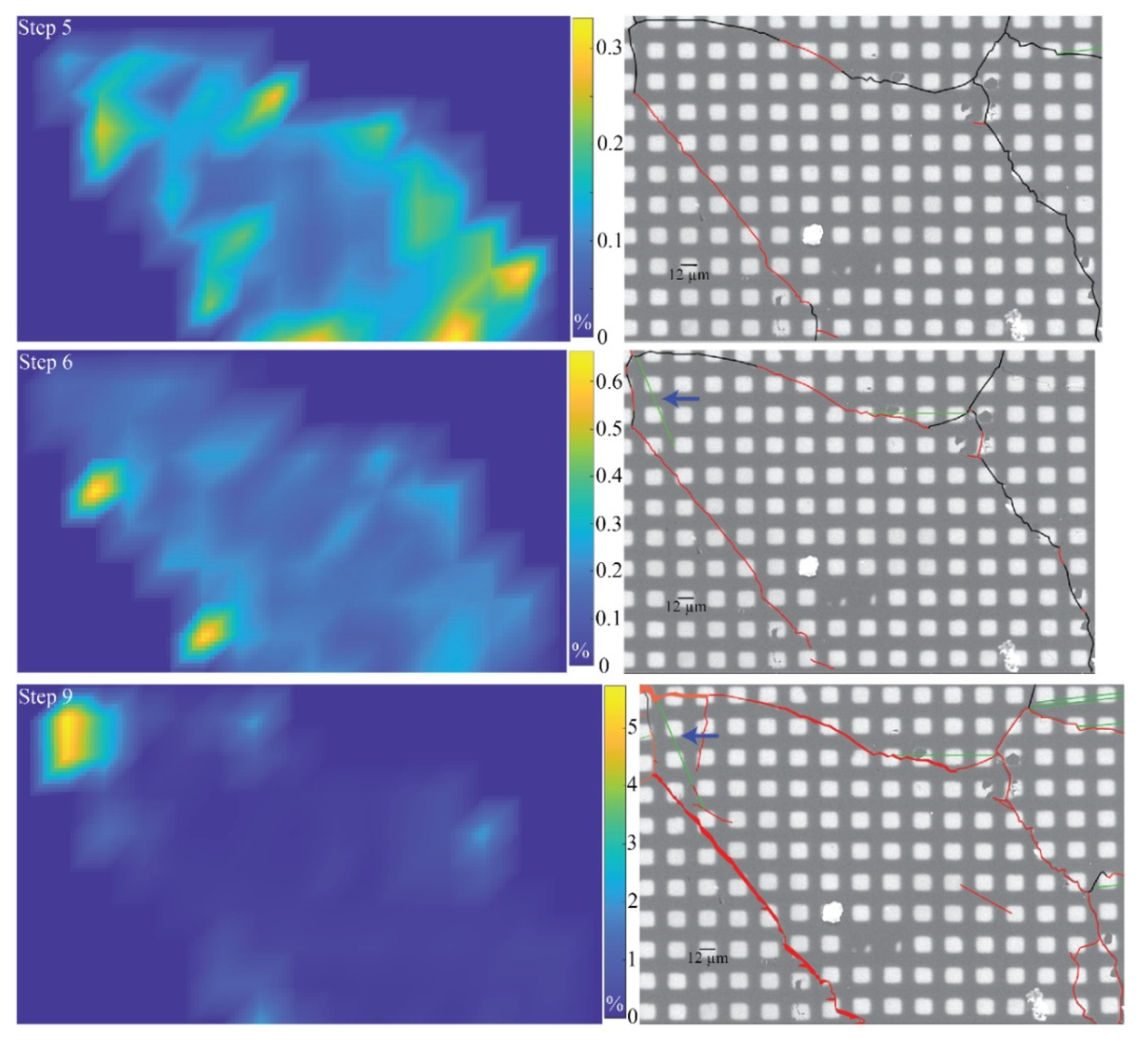
3.2. Observation of Individual Grains
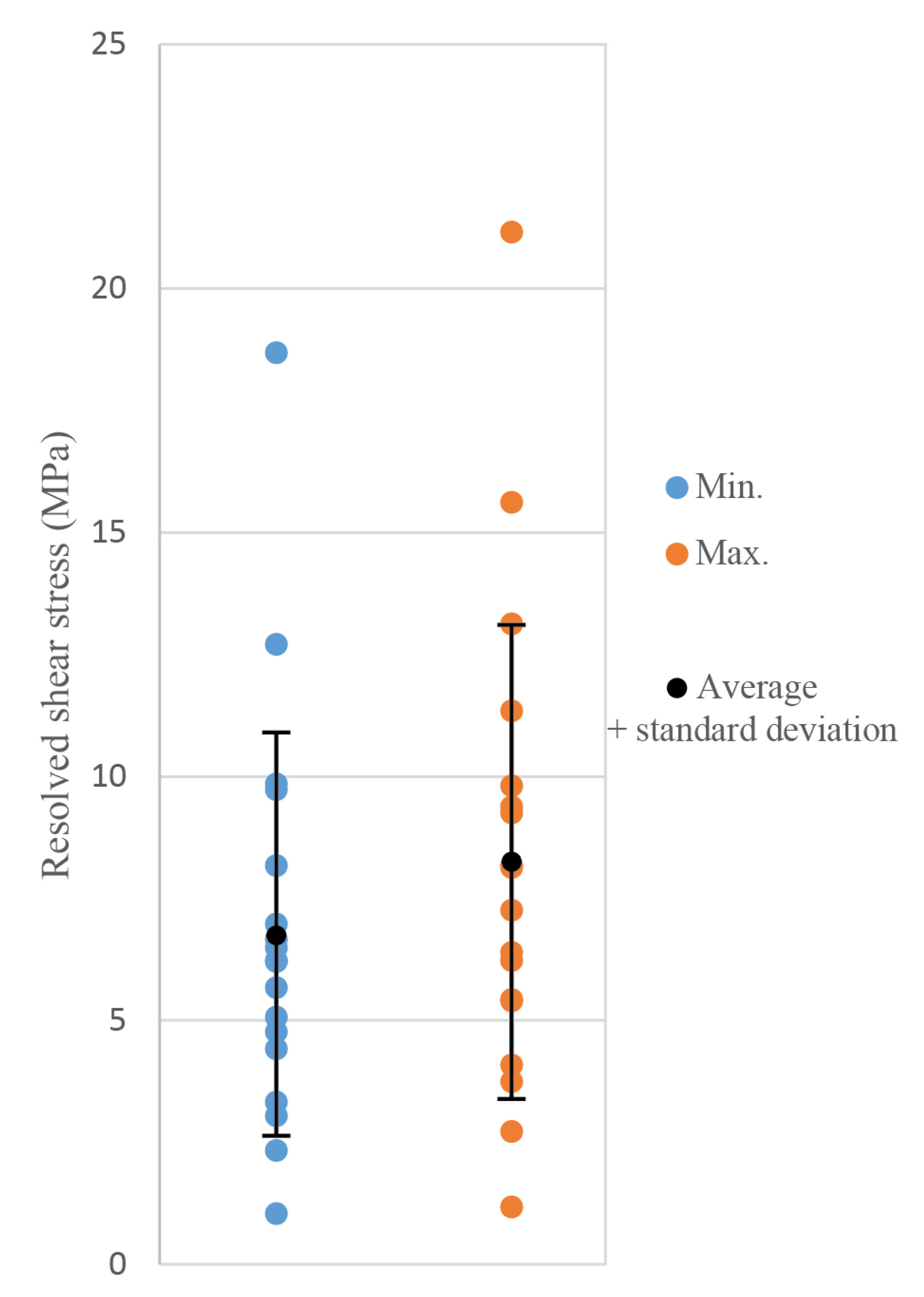
3.3. CSIT-2 Inversion
4. Discussion
4.1. Crystal Deformation
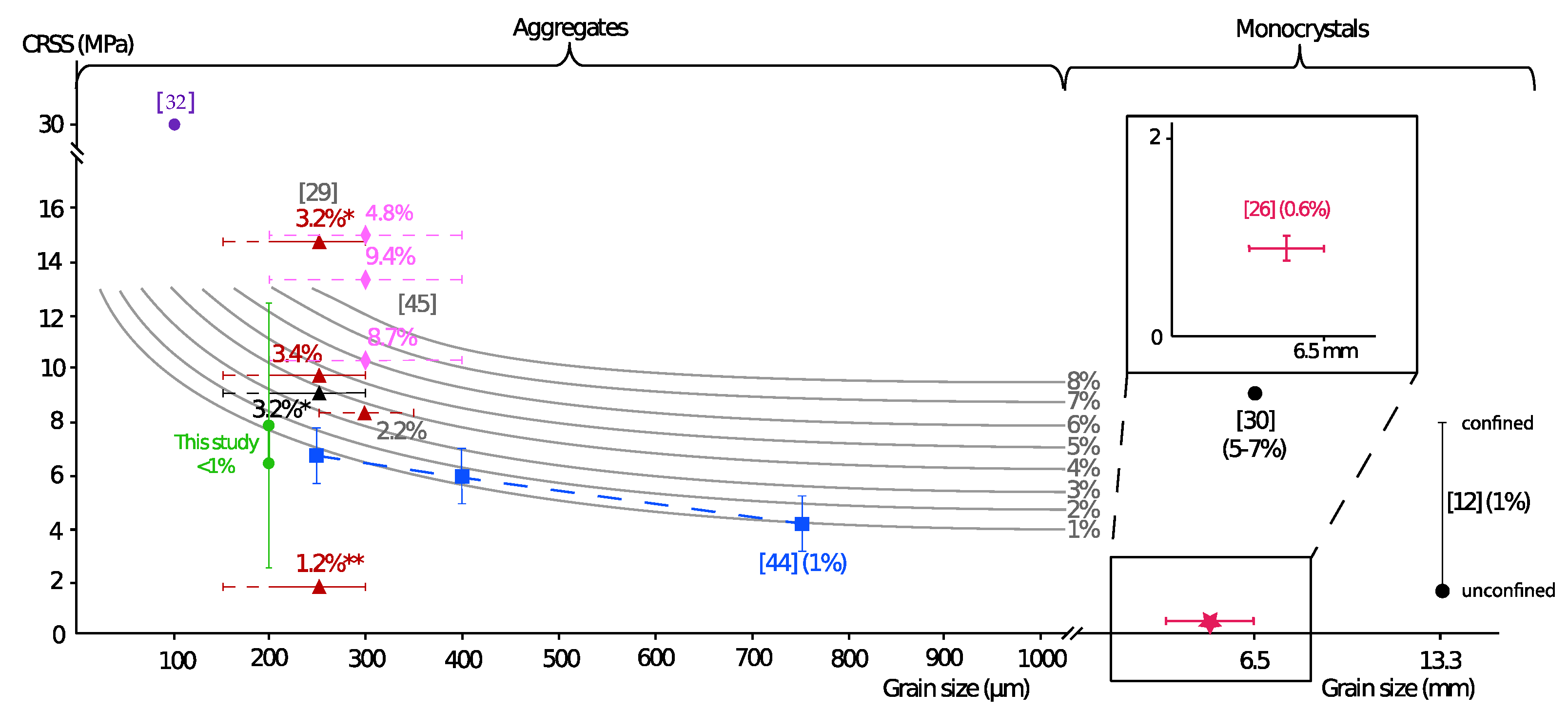
4.2. Inversion and Critical Resolved Shear Stress
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Abdallah, Y.; Sulem, J.; Bornert, M.; Ghabezloo, S.; Stefanou, I. Compaction banding in high-prosity carbonate rocks: 1. Experimental Observations. J. Geophys. Res. Solid Earth 2021, 126, e2020JB020538. [Google Scholar] [CrossRef]
- Dautriat, J.; Bornert, M.; Gland, N.; Dimanov, A.; Rphanel, J. Localized deformation induced by heterogeneities in porous carbonate analysed by multi-scale digital image correlation. Tectonophysics 2011, 503, 100–116. [Google Scholar] [CrossRef]
- Cilona, A.; Faulkner, D.; Tondi, E.; Agosta, F.; Mancini, L.; Rustichelli, A.; Baud, P.; Vinciguerra, S. The effects of rock heterogeneity on compaction localization in porous carbonates. J. Struct. Geol. 2014, 67, 75–93. [Google Scholar] [CrossRef]
- Baud, B.; Schubnel, A.; Wong, T.-F. Dilatancy, compaction, and failure mode in Solnhofen limestone. J. Geophys. Res. Solid Earth 2000, 105, 19289–19303. [Google Scholar] [CrossRef]
- Nicolas, A.; Fortin, J.; Regnet, B.; Verberne, A.; Plümper, O.; Dimanov, A. Brittle and semibrittle creep of Tavel limestone deformed at room temperature. J. Geophys. Res. Solid Earth 2017, 122, 4436–4459. [Google Scholar] [CrossRef]
- Kaga, H.; Gilman, J. Twinning and detwinning in calcite. J. Appl. Phys. 1969, 40, 3196–3207. [Google Scholar] [CrossRef]
- Barber, D.; Wenk, H. Deformation twinning in calcite, dolomite, and other rhomboedral carbonates. Phys. Chem. Miner. 1979, 5, 141–165. [Google Scholar] [CrossRef]
- Borg, I.; Turner, F. Deformation of Yule marble: Part VI—Identify and significance of deformation lamellae and parting in calcite grains. Bull. Geol. Soc. Am. 1953, 64, 1343–1352. [Google Scholar] [CrossRef]
- Bowden, F.; Cooper, R. Velocity of twin propagation in crystals. Nature 1962, 195, 1091–1092. [Google Scholar] [CrossRef]
- De Bresser, J. Steady state dislocation densities in experimentally deformed calcite materials: Single crystals versus polycrystals. J. Geophys. Res. 1996, 101, 22189–22201. [Google Scholar] [CrossRef]
- De Bresser, J. Intracrystalline Deformation of Calcite. Ph.D. Thesis, University Utrecht, Utrecht, The Netherlands, 1991. [Google Scholar]
- Turner, F. Nature and dynamic interpretation of deformation lamellae in calcite of three marbles. Am. J. Sci. 1953, 251, 276–298. [Google Scholar] [CrossRef]
- Parlangeau, C.; Lacombe, O.; Schueller, S.; Daniel, J. Inversion of calcite data for paleostress orientations and magnitudes: A new technique tested and calibrated on numerically-generated and natural data. Tectonophysics 2018, 722, 462–485. [Google Scholar] [CrossRef] [Green Version]
- Groshong, R. Experimental test of least-squares strain calculations using twinned calcite. Geol. Soc. Am. Bull. 1974, 85, 1855–1864. [Google Scholar] [CrossRef]
- Rez, J. TwinCalc: A multitool for calcite twinning based stress analysis. Appl. Comput. Geosci. 2020, 5, 100020. [Google Scholar] [CrossRef]
- Etchecopar, A. Etude des Etats de Contraintes en Tectonique Cassante et Simulation de Deformations Plastiques (Approche Mathematique). Ph.D. Thesis, Université Sciences et Techniques du Languedoc, Montpellier, France, 1984; 270p. [Google Scholar]
- Yamaji, A. Generalized Hough transform for the stress inversion of calcite twin data. J. Struct. Geol. 2015, 80, 2–15. [Google Scholar] [CrossRef] [Green Version]
- Shan, Y.; Zheng, J.; Liang, X. Inversion of polyphase calcite twin data for deviatoric stress tensors: 1. Anovel numerical approach. J. Struct. Geol. 2019, 128, 103873. [Google Scholar] [CrossRef]
- Lacombe, O.; Amrouch, K.; Mouthereau, F.; Dissez, L. Calcite twinning constraints on late Neogene stress patterns and deformation mechanisms in the active Zagros collision belt. Geology 2007, 35, 263–266. [Google Scholar] [CrossRef]
- Amrouch, K.; Lacombe, O.; Bellahsen, N.; Daniel, J.M.; Callot, J.P. Stress and strain patterns, kinematics and deformation mechanisms in a basement-cored anticline: Sheep Mountain Anticline, Wyoming. Tectonics 2010, 29, TC1005. [Google Scholar] [CrossRef] [Green Version]
- Beaudoin, N.; Koehn, D.; Lacombe, O.; Lecouty, A.; Billi, A.; Aharonov, A.; Parlangeau, C. Fingerprinting stress: Stylolite and calcite twinning paleopiezometry revealing the complexity of progressive stress patterns during foldings—The case of the Monte Nero anticline in the Apennines, Italy. Tectonics 2016, 35, 1687–1712. [Google Scholar] [CrossRef] [Green Version]
- Beaudoin, N.; Lacombe, O. Recent and future trends in paleopiezometry in the diagenetic domain: Insights into the tectonic paleostress and burial depth history of fold-and-thrust belts and sedimentary basins. J. Struct. Geol. 2018, 114, 357–365. [Google Scholar] [CrossRef]
- Lacombe, O.; Parlangeau, C.; Beaudoin, N.; Amrouch, K. Calcite twins: Formation, measurement and use as stress-strain indicators. A review of progress over the last decade. Geosciences 2021, 11, 445. [Google Scholar] [CrossRef]
- Burkhard, M. Calcite twins, their geometry, appearance and significance as stress-strain markers and indicators of tectonic regime: A review. J. Struct. Geol. 1993, 15, 351–368. [Google Scholar] [CrossRef] [Green Version]
- Olsson, W. Grain size dependence of yield stress in marble. J. Geophys. Res. 1974, 79, 4859–4862. [Google Scholar] [CrossRef]
- Parlangeau, C.; Dimanov, A.; Lacombe, O.; Hallais, S.; Daniel, J.M. Uniaxial compression of calcite crystals at room temperature: Insights into twinning activation and development. Solid Earth 2019, 10, 307–316. [Google Scholar] [CrossRef] [Green Version]
- Newman, J. The influence of grain size and grain size distribution on methods for estimating paleostresses from twinning in carbonates. J. Struct. Geol. 1994, 16, 1589–1601. [Google Scholar] [CrossRef]
- Rowe, K.; Rutter, E. Paleostress estimation using calcite twinning: Experimental calibration and application to nature. J. Struct. Geol. 1990, 12, 1–17. [Google Scholar] [CrossRef]
- Lacombe, O.; Laurent, P. Determination of deviatoric stress tensors based on inversion of calcite twin data from experimentally deformed monophase samples: Preliminary results. Tectonophysics 1996, 255, 189–202. [Google Scholar] [CrossRef]
- De Bresser, J.H.P.; Spiers, C.J. Strength characteristics of the r, f, and c slip systems in calcite. Tectonophysics 1997, 272, 1–23. [Google Scholar] [CrossRef]
- Ferrill, D.A. Critical re-evaluation of differential stress estimates from calcite twins in coarse-grained limestone. Tectonophysics 1998, 285, 77–86. [Google Scholar] [CrossRef]
- Covey-Crump, S.J.; Schofield, P.F.; Oliver, E.C. Using neutron diffraction to examine the onset of mechanical twinning in calcite rocks. J. Struct. Geol. 2017, 100, 77–97. [Google Scholar] [CrossRef] [Green Version]
- Tullis, T. The use of mechanical twinning in minerals as a measure of shear stress magnitudes. J. Geophys. Res. 1980, 85, 6263. [Google Scholar] [CrossRef]
- Ferrill, D.A.; Morris, A.P.; Evans, M.A.; Burkhard, M.; Groshong, R.H.; Onasch, C.M. Calcite twin morphology: A low temperature deformation geothermometer. J. Struct. Geol. 2004, 26, 1521–1529. [Google Scholar] [CrossRef] [Green Version]
- Ferrill, D.A. Calcite twin widths and intensities as metamorphis indicators in natural low-temperature deformation of limestone. J. Struct. Geol. 1991, 13, 667–675. [Google Scholar] [CrossRef]
- Bourcier, M.; Bornert, M.; Dimanov, A.; Héripré, E.; Raphanel, J.L. Multiscale experimental investigation of crystal plasticity and grain boundary sliding in synthetic halite using digital image correlation. J. Geophys. Res. Solid Earth 2013, 118, 511–526. [Google Scholar] [CrossRef] [Green Version]
- Quintanilla-Terminel, A.; Zimmerman, M.; Evans, B.; Kohlstedt, D. Microscale and nanoscale strain mapping techniques applied to creep of rocks. Solid Earth 2017, 8, 751–765. [Google Scholar] [CrossRef]
- Luzin, V.; Nikolayev, D.; Siegesmund, S. Temperature induced internal stress in Carrara marble. Mater. Sci. Forum 2014, 777, 148–154. [Google Scholar] [CrossRef]
- Frederich, J.; Evans, B.; Wong, T.-F. Micromechanics of the brittle to plastic transition in Carrara marble. J. Geophys. Res. 1989, 94, 4129–4145. [Google Scholar] [CrossRef]
- Renner, J.; Rummel, F. The effect of experimental and microstructural parameters on the transition from brittle to cataclastic flow of carbonate. Tectonophysics 1996, 258, 151–169. [Google Scholar] [CrossRef]
- Amrouch, K. Apport de L’analyse Microstructurale à la Comprehension des Mécanismes de Plissement: Exemples de Structures Plissées aux USA (Wyoming) et en Iran (Zagros). Ph.D. Thesis, Pierre and Marie Curie University, Paris, France, 2010. [Google Scholar]
- Robertson, E. Experimental study of the strength of rocks. Geol. Soc. Am. Bull. 1955, 66, 1275–1314. [Google Scholar] [CrossRef]
- Tal, Y.; Brian, E.; Mok, U. Direct observations of damage during unconfined brittle failure of Carrara marble. J. Geophys. Res. Solid Earth 2016, 121, 1584–1609. [Google Scholar] [CrossRef] [Green Version]
- Rocher, M.; Cushing, M.; Lemeille, F.; Lozac’h, Y.; Angelier, J. Intraplate paleostresses reconstructed with calcite twinning and faulting: Improved method and application to the eastern Paris Basin (Lorraine, France). Tectonophysics 2004, 387, 1–21. [Google Scholar] [CrossRef]
- Laurent, P.; Kern, H.; Lacombe, O. Determination of deviatoric stress tensors based on inversion of calcite twin data from experimentally deformed monophase samples. Part II. Axial and triaxial stress experiments. Tectonophysics 2000, 327, 131–148. [Google Scholar] [CrossRef]









| Schmid Factor (Tensor from the Inversion) | ||||
|---|---|---|---|---|
| Crystal | E1 | E2 | E3 | nb Activation |
| 1 | 0.454 | −0.249 | −0.062 | 1 |
| 2 | −0.35 | −0.099 | −0.089 | 1 |
| 4 | −0.45 | 0.119 | 0.283 | 2 |
| 5 | −0.044 | −0.047 | 0.466 | 1 |
| 6 | 0.469 | −0.275 | −0.079 | 1 |
| 8 | 0.181 | −0.171 | −0.316 | 1 |
| 9 | 0.467 | 0.181 | 0.125 | 3 |
| 11 | −0.191 | 0.127 | 0.047 | 0 |
| 12 | −0.299 | 0.204 | −0.118 | 2 |
| 13 | 0.026 | −0.124 | −0.175 | 1 |
| 15 | −0.399 | 0.158 | 0.146 | 1 |
| 16 | 0.17 | −0.032 | 0.266 | 1 |
| 17 | 0.447 | 0.193 | 0.203 | 2 |
| 18 | 0.287 | 0.068 | −0.179 | 1 |
| 21 | 0.109 | −0.243 | −0.283 | 2 |
| 22 | 0.238 | −0.106 | −0.232 | 1 |
| 23 | −0.16 | 0.119 | 0.058 | 1 |
| Total | 22 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Parlangeau, C.; Dimanov, A.; Hallais, S. In-Situ Evolution of Calcite Twinning during Uniaxial Compression of Carrara Marble at Room Temperature. Geosciences 2022, 12, 233. https://doi.org/10.3390/geosciences12060233
Parlangeau C, Dimanov A, Hallais S. In-Situ Evolution of Calcite Twinning during Uniaxial Compression of Carrara Marble at Room Temperature. Geosciences. 2022; 12(6):233. https://doi.org/10.3390/geosciences12060233
Chicago/Turabian StyleParlangeau, Camille, Alexandre Dimanov, and Simon Hallais. 2022. "In-Situ Evolution of Calcite Twinning during Uniaxial Compression of Carrara Marble at Room Temperature" Geosciences 12, no. 6: 233. https://doi.org/10.3390/geosciences12060233
APA StyleParlangeau, C., Dimanov, A., & Hallais, S. (2022). In-Situ Evolution of Calcite Twinning during Uniaxial Compression of Carrara Marble at Room Temperature. Geosciences, 12(6), 233. https://doi.org/10.3390/geosciences12060233






