Abstract
Rock avalanches and landslides lead to gravitational flow into their runout areas, which poses increasing danger to settlement areas and infrastructure in the Alpine region as a result of climate change. In recent years, a significant increase in extreme events has been registered in the Alps due to climate change. These changes in the threat to settlement areas in the Alpine region have resulted in the need for the construction of sustainable protective structures. Many structures are rigid, but others are now also increasingly flexible, e.g., net and dam structures, which are mainly earth dams with geogrids. In this study, empirical model experiments and numerical simulations were carried out to estimate the flow depth, the deposition forms and the effects on protective structures. Numerical programs usually require unknown input parameters and long computation times for a realistic simulation of the process. This study shows the results of model tests with different granular materials. Furthermore, different design approaches of different authors are presented. Finally, a design model based on the model tests of the University of Innsbruck for rigid barriers, nets and dams due to rock avalanches is presented.
1. Introduction
Rock avalanches and granular flows in steep terrain attain high velocities and consequently cause large impacts on protective structures. The total impact is a function of the size, thickness, velocity, geological and geotechnical properties of the mass movement, the subsurface properties and the stiffness of the structure. In general, the estimation of the total quasi-static equivalent impact on the structure is performed by summing up a static part under the consideration of a pressure coefficient and a dynamic part, which is formed from the velocity, flow height, impact area and an empirical coefficient. In many approaches, the temporal course of the action is not taken into account, and thus the fact that the maximum static action and the maximum dynamic action do not load the structure at the same time should be accounted for. However, for the design and verification of protective structures (rigid concrete structures, protection embankments or flexible structures), the duration and the development over time of the action are important. On the other hand, in this context, it is necessary to discuss which safety level is to be selected for the design event (partial safety factors) and for which actions the ultimate limit state and the serviceability limit state are to be fulfilled. For an economic construction method, the question also arises as to what damage is just acceptable to such protective structures.
2. Aims of this work
There are a number of empirical approaches to estimating the impacts on protective structures for the debris flow process. However, the fundamentals for impacts from the processes of landslides and rock avalanches have not yet been investigated to such an extent that they have been taken into account in regulations in order for them to provide a sufficient basis for a design. In order to estimate the course of the process, the flow depth and the impacts on rigid and flexible protective structures as well as on embankments for “dry” granular flow processes, extensive model experiments and back calculations were carried out in this work using the ROCKY ® software from ESSS. The aim of the investigations was to provide empirical formulas based on the quasi-static method for the different types of structures based on geotechnical theories, such as the development of earth pressure, which in Austria is known as “creep pressure theory”. In the first phase of our investigation, the results of [1] were repeated and evaluated. In the next step, the results were extended with additional test material and various protective structures. The comparison of the different model experiments and the numerical simulations with the help of the discrete element method (DEM) from the literature showed a large scattering of the results depending on the grain sizes and grain shapes, the internal dynamic friction angles, the roughness of the flume and the inclination of the barrier on the channel. Relatively large differences in the maximum impact force were noticeable at inclinations of the flume of more than 45° [2]. A significant influence on the magnitude of the maximum impact force is the dead zone created in front of the protective structure, on which the subsequent, still undisturbed granular flow impinges [3]. The dependence of the impact on the shape of the dead zone is discussed in this paper. Of crucial importance is the force dependence on time and the maximum total impact force determined from it. Therefore, the results of the model experiments for this work were compared with the maximum impact forces of the model experiments from the literature [1,2,4,5,6,7,8,9], and the findings from numerical simulations and the empirical approximation formula were compared.
3. Model Experiments with Dry Granular Flow
3.1. Flume Apparatus of the University of Innsbruck
Extensive investigations have already been carried out with the flume apparatus of [1], which were published by [10]. It was possible to observe the dry granular flow and to measure the impact on different types of structures. The flume consists of a reservoir, an automatic gate and an inclined plane up to the barriers. Figure 1 shows the flume, the rigid barrier, the flexible barrier and the protection embankment. The lateral acrylic walls allow for the visual inspection of the process and enable a two-dimensional image of the flow along the flume to be taken. In the reservoir, the material was placed in an uncompacted state before the experiment. The gate can be opened in less than 0.15 s.
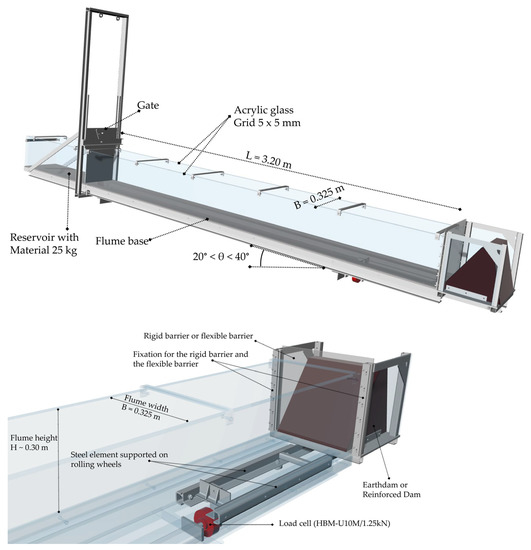
Figure 1.
Flume apparatus of the University of Innsbruck.
A fundamental issue in conducting model experiments is the scaling of test results. Dimensional analysis makes it possible to relate model experiments to the prototype. In fluid mechanics, a distinction is made between geometric, dynamic and kinematic similarity. Geometric similarity is found when all geometric dimensions are reduced by the same scale factor λ. The Froude number sets the inertial force of the mass under investigation in relation to the force of gravity. For an open channel, the Froude number results from the velocity the gravitation g and the characteristic flow depth [11].
If Froude’s model law is applied, the individual scale factors (e.g., velocity or force ) can be determined as a function of the geometric scaling factor (λ). The scale factors for the velocity and the force ( therefore equal
The resulting scaling factors with respect to the investigation of impacts on protective structures can be taken from Table 1. If scale factors are used to interpret the model results, the individual parameters (e.g., velocity or flow depth) must be checked for plausibility. Parameters of the real prototype can be determined from observations or back calculations. According to [12,13,14], velocities of approximately 30–40 m/s are realistic values for rock avalanches and granular flows. In addition, the maximum grain size in the model experiments should represent the grain size range for cobbles or boulders (cobbles < 200 mm < boulder).

Table 1.
Scales of the model experiments depending on physical quantities (grain diameter d, duration t, velocity v, density , Froude number Fr, peak total force Fpeak).
On the north face of Piz Cengalo in Switzerland, a landslide with an estimated volume of about 3.1 million m3 occurred in August 2017 [12]. During the mass flow, the individual blocks and stones (granodiorite) collided and fragmented. The subsequent contact of the rock mass on the underlying glacier (Vadrec dal Cengal) resulted in water absorption by the rock avalanche. This is reported to have increased the velocity of the mass movement from about 55 m/s to 75 m/s. The quantities compiled from the documented observations are summarized in Table 2. A comparison between the parameters of the model experiment of the University of Innsbruck and the observations or the back calculations results in a possible scaling factor between λ = 30 and λ = 50 (Table 1).

Table 2.
Parameters from the back calculation of the Punta Thurwieser and Piz Cengalo events.
In order to investigate the influence of grain size, grain roughness and grain size distribution, four different materials were selected for the model experiments. These consisted of sand with a grain size of 0.5/1.0 mm, a mixture of sand and gravel (grain size 0.5/1.0 mm and 4.0/8.0 mm) and steel and glass spheres with a diameter of 2 mm. Due to the high density of steel, the low “grain roughness” of the smooth steel spheres and the resulting high velocities, an upper bound of the impacts can be determined. The friction angles φdyn between particles and between the particle and the flume (φb), as well as the densities (ρ), can be taken from Table 3. The determination of the friction angle φdyn and φb was determined following Hungr (2008). The dynamic internal friction angle of the material between the individual particles (φdyn) was determined with tilt tests, with sliding of the bulk material caused by continuously increasing the inclination of the plane. In addition, shear tests were also carried out for the natural sand material and the mixture. The maximum slope angle along the flume was defined to determine the friction angle between the material and the sliding plane. A reservoir was filled with model soil, and then the inclination of the plane was gradually increased until the maximum possible angle was reached. All model tests were carried out with 25 kg of each test material. A total of 185 laboratory experiments with different materials and barriers were carried out (Table 4).

Table 3.
Material parameters according to [1] and the University of Innsbruck.

Table 4.
Number of laboratory experiments at the University of Innsbruck.
The flow was recorded by video (three cameras with 1020 × 720 px, 100 fps). The impact force on the barriers was measured with a load cell (type Hottinger Brüel & Kajer (HBM, Vienna, Austria)—U10 Force Transducer/1.25 kN, 4800 Hz). Two high-performance laser distance sensors (type, Baumer, Frauenfeld, Switzerland, OM70-L0600 2400 HZ) were used to determine the flow height ℎf. By placing the two lasers at a distance of approximately 27.5 cm, the velocity of the granular mass was also able to be determined from runtime measurements. In addition, the velocity was determined with the help of a line grid at a distance of 5 × 5 mm and the video recordings. The evaluation of the geometric quantities and the forces from the laboratory experiments, as well as the determination of the dimensionless Froude number Fr, can be taken from Table 5.

Table 5.
Summary of the mean values of all test results with the flume apparatus of the University of Innsbruck for the test series on a rigid barrier.
3.2. Experiments with Rigid Barrier
The rigid barrier consisted of an 8 mm-thick steel plate (Figure 2). A total of 91 laboratory experiments with different materials and inclinations θ were carried out with the rigid barrier.
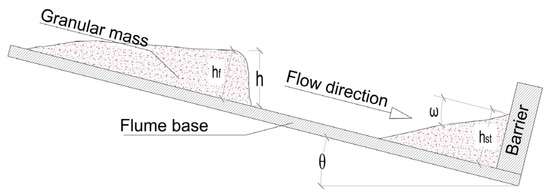
Figure 2.
Definitions of mass movement during the flow movement and in the final state, flow depth h and hf, height of discharge hst and angle of discharge ω.
A total of 185 experiments were available for the interpretation of the mean values of the flow properties. The characteristics of the granular flow included the mean velocity v immediately before hitting the barrier, the mean of the flow height hf and the mean Froude number Fr. Table 5 shows the mean values of all laboratory experiment results depending on the material and the inclination of the flume θ. The impact forces Fpeak and Fstat on the rigid barrier resulted from the 91 laboratory experiments that were carried out.
3.3. Experiments with Flexible Barriers—Nets
For the experiments with flexible barriers, three different stiffnesses were used for the nets. By choosing a very stiff, flexible barrier, a very elastic, flexible barrier and a barrier that lies between them in terms of stiffness, the influence of the stiffness of the barrier on the actions was able to be investigated. For the stiffest flexible barrier, a grid made of glass fibers with a mesh size of 1.5 × 1.5 mm was chosen. The other two barriers used were cotton fabrics with different stiffnesses. Figure 3 shows the tensile tests used to determine the extensional stiffness for the three meshes. To investigate the effects on flexible barriers, a total of 62 laboratory experiments were carried out with the mixture and glass spheres. The glass spheres had a density similar to soil with an almost perfect surface. This made it possible to better describe the influence of the interaction between the individual particles.
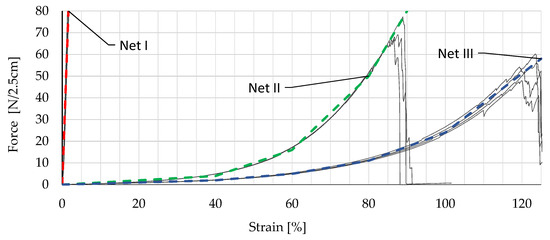
Figure 3.
Tensile tests from a 2.5 cm-wide strip of the flexible material of Net I, Net II and Net III; colored lines are the mean values of the tensile test results.
3.4. Experiments with Protection Embankment
To investigate the effects of rock avalanches on a protection embankment, two different types of embankments—embankments with and without geotextiles—were investigated in the experiments. The embankments without geotextiles were designed with an inclination to the flume on the impact side of approximately 3:2, and with a crown width of 6 cm and a height of 30 cm. The embankments with geotextiles were designed as geogrid-reinforced embankments with a slope on the action side of 70°, a crest width of 6 cm and a height of 30 cm (Figure 4). The spacing of the model geogrids [15] was 2 cm. A total of 35 laboratory experiments were carried out to investigate the effects on the embankment.
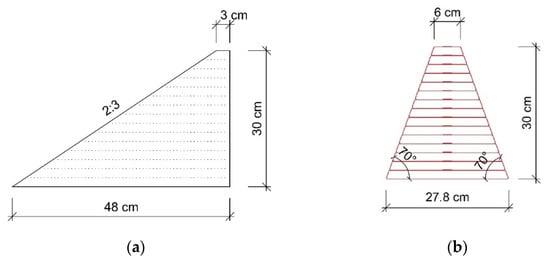
Figure 4.
Geometry of the two types of embankments: (a) earth dam without geotextiles, inclination 2:3 on the impact side; (b) reinforced dam with geotextiles, inclination 70° on the impact side.
4. Interpretation of the Laboratory Experiments
4.1. Kinematics of the Granular Flow on Rigid Barriers
The flow process can be divided into three phases (Figure 5). During phase 1, there is an acceleration of the dry granular flow. The maximum impact force Fpeak on the rigid barrier is reached in phase 2. In the last phase, phase 3, there is a reduction in the residual value Fstat. In phase 1, the dry granulate reaches velocities of up to 7 m/s, depending on the inclination of the flume θ and the material. In this work, a rigid, fixed structure with a steel plate as a barrier was used. In [4], it was reported that, already with a displacement in the rigid barrier of 3%, a reduction in the resultant force of 40% was measured.
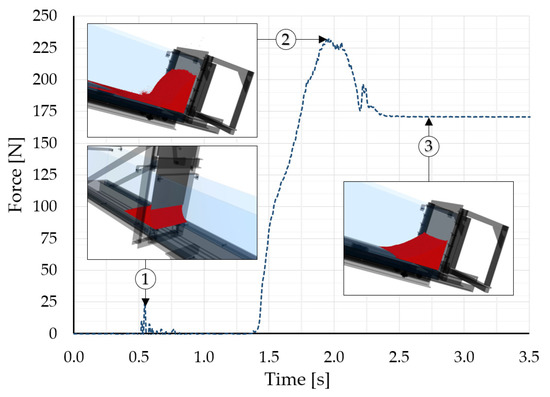
Figure 5.
Example of a force–time history for phases 1 to 3 of the experimental procedure.
The analysis of the 185 laboratory experiments of the dry granulate revealed that both the velocity and the flow height hf increased with the increasing inclination of the flume θ. The plot of the Froude number Fr in relation to the inclination of the flume θ shows an analogous behavior. These observations apply irrespective of the density and grain shape of all materials used.
Figure 6a–d show the impact force–time history on the rigid barrier for phases 1 to 3 for the various materials (sand, mixture, glass and steel spheres) at different inclinations of the flume θ. The major differences between the steel spheres and the natural material (sand and mixture) are striking. While only a very slight dissipation of energy occurred in phase 2 with the steel spheres, this effect was clearly recognizable with the natural material. At time t = 0, the energy was only formed by the potential energy EPOT, and the shares of the kinetic EKIN and total dissipative energy ETDE were zero. With the start of the flow process, the kinetic energy EKIN increased disproportionately with a simultaneous drop in the potential energy EPOT until the granular flow hit the barrier in phase 2. The following phase, phase 3, was characterized by a rapid decrease in the kinematic energy EKIN to zero and a more or less constant fraction of the potential EPOT and total dissipative energy ETDE. This relationship E = EPOT + EKIN + ETDE and the differences depending on the stiffness of the barriers were described in detail in [8,16]. For the natural material sand and the mixture, there were small differences between the static (phase 3) and dynamic (phase 2) impacts on the rigid barrier (Figure 6a,b). In contrast, the ratios of the peak impact force Fpeak in phase 2 to the static force Fstat in phase 3 were between 1.1 and 3.0 for the steel spheres and between 1.0 and 1.7 for the glass spheres (Figure 7a). This can be explained by the fact that there was a significantly lower share of the total dissipative energy ETDE. For the sand and mixture materials, the ratio Fpeak/Fstat ranged between 1.0 and 1.15 (Figure 7b). Transferred to the soil mechanical properties, these results mean that, in the case of dry rock avalanches from a quarry area with a low rock strength and greater potential for fragmentation, the impact forces are lower, and an estimate of these can also follow from static considerations. A large slope in the impact force–time diagram is an indication of higher velocities and, correspondingly, greater maximum impact forces Fpeak. A lower internal friction angle of the material also caused a higher load in phase 2 compared to phase 3. For materials with a lower density and non-spherical particles, the occurring forces were considerably lower. The glass spheres had a similar density to the sand and the mixture, but the impact of the sand and the mixture was significantly lower, and a low pronounced maximum impact force Fpeak occurred. In contrast, a very high maximum impact force Fpeak occurred with the steel spheres, which corresponded to up to three times the static force Fstat (Figure 7a).
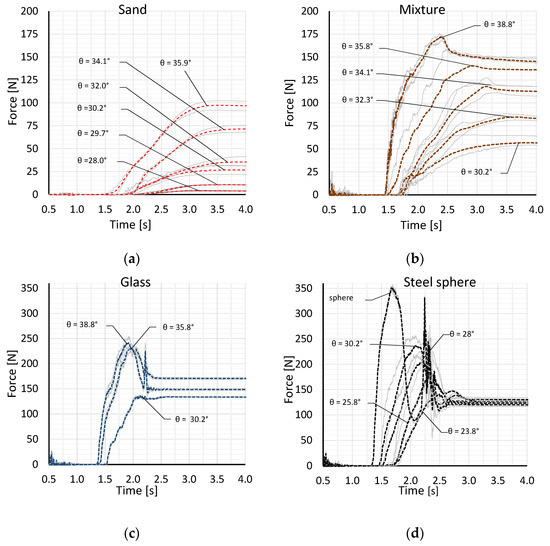
Figure 6.
Impacts depending on the inclination of the flume base for the materials (a) sand, (b) mixture, (c) glass and (d) steel spheres on a rigid barrier.
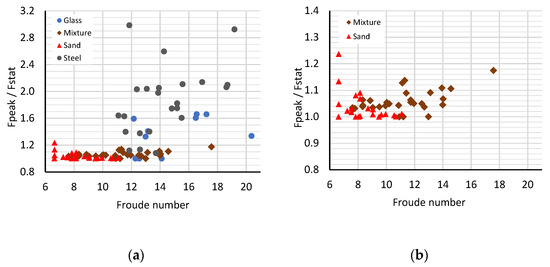
Figure 7.
Fpeak/Fstat ratio for different Froude numbers for impacts on a rigid barrier: (a) for all materials, and (b) for the natural material sand and the mixture.
Figure 7a,b show the Fpeak/Fstat ratios as a function of the Froude number Fr. For the sand and the mixture, the ratios were between 1.0 and 1.15. It should be noted that the Froude numbers from the model experiments, which were approximately 5–13, agree relatively well with those of the rock avalanches from the documented natural events, which were approximately 3 to 15 (Table 2). In phase 3, the magnitude of the static force Fstat was determined by the deposition geometry (height and inclination) of the material at the barrier and the basal friction angle φb between the flume and the material. The static impact force Fstat effect of the steel spheres with φroll = 0° was thus exclusively due to the deposition geometry, since no force component tangential to the flume reduced the force effect on the barrier.
An interesting observation was made when comparing the impact force effect of corroded steel spheres with smooth steel spheres. The use of rough steel spheres led to a lower maximum impact force Fpeak but, at the same time, a higher static force Fstat (Figure 8). This can be explained, on the one hand, by there being a higher total dissipative energy ETDE in phase 2 and, on the other, by there being a larger deposit body in phase 3. This finding makes clear the sensitivity of the effects caused by the surface roughness and the shape of the particle or grain. The influence of surface roughness on rheological parameters was studied in [17].
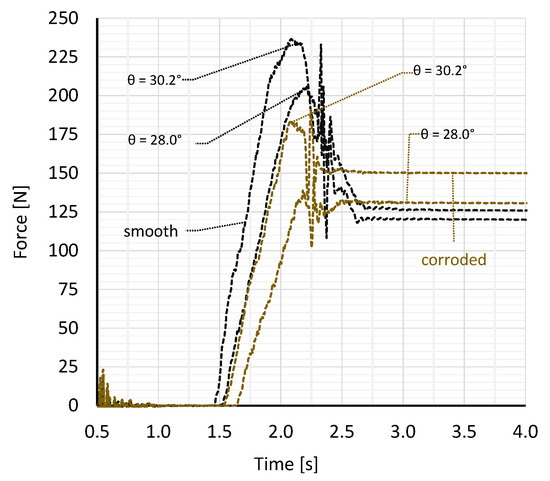
Figure 8.
Comparison of the impact force–time history of the corroded and the smooth steel spheres for the inclinations of the flume base of 28° and 30.2°.
As also described in [18], the smooth surface of the particles led to fast and thin rock avalanches. In contrast, particles with a rough surface resulted in relatively slower and thicker rock avalanches.
During phase 3, a thin jet of steel spheres rode up the face of the barrier (so-called “run-up”) and then fell down [1]. A small amount of sand flowed upwards along the rigid barrier, and a sand wedge (dead zone) was created between the barrier and the transport level. The following material flowed continuously over the dead zone (so-called “pile-up”). This resulted in a significant attenuation (deflection) in the impact force from the subsequent granular flow. The dead zone was significantly higher than it was with steel spheres. The mixture rode up immediately after impact. The gravel grains reached higher velocities than the sand particles, the mixture segregated and the gravel grains moved turbulently. Increasingly, a wedge (dead zone) built up between the barrier and the transport level. The following material flowed over this wedge. In the final state, segregation was clearly visible in the mixture. The large particles (gravel) tended to be at the top, and the smaller particles (sand) tended to be at the bottom. The sand particles migrated downwards, partly due to the larger gaps between the gravel grains (sieve effect). On the basis of the video recordings, it can be seen that the effect of segregation already developed during phase 1 along the transport plane. Transferred to nature, this finding would mean that in the presence of blocks with a higher compressive strength in phase 3, a “run-up” effect is to be expected and thus a higher freeboard for the barrier must be provided. In contrast, if the particles are more intensively fragmented in the flow process, a larger catchment ditch is necessary. The authors of [5] proposed that, for a rigid barrier, a dead zone can attenuate the dynamic impact of the subsequent granular flow on the barrier by redirecting the flow.
The phenomena “run-up” and “pile-up” can be illustrated most clearly for the sand and steel spheres. While the steel spheres rode up vertically on the barrier (“run-up”), a continuous “pile-up” of the already dead zone in front of the barrier was observed with the sand. Figure 9 illustrates that the phenomenon depends on the material and the inclination of the flume. In the case of sand, an overflow “pile-up” was observed at an inclination of 28°, and the “run-up” effect was observed from an inclination of 35.9°. Transferred to nature, this finding could mean that for slopes with an inclination close to the friction angle of the rock avalanche, the “pile-up” phenomenon occurs, and for higher inclinations, the “run-up” phenomenon occurs. For the first case (pile-up), a longer catchment ditch and thus a greater distance between the barrier and the beginning of the runout area are required. For the second case (run-up), higher protective structures would be required to ensure a sufficient freeboard. Accordingly, a realistic assessment of the internal shear strength of the particles of rock avalanches is of decisive importance for the choice and location of the protective structure.

Figure 9.
Phenomena of “pile-up” for inclination θ = 28.0° (above) and “run-up” for inclination θ = 35.9° (below). The figures were taken from a preliminary test with a slightly adapted test design.
During the impact of the rock avalanche (dry granulate) on the rigid barriers, the deformation of the barrier and the dissipation of energy led to effects that reduced the maximum impact forces. The authors of [4] have already described these effects in their work.
4.2. Test Results with Flexible Barriers
The flexible barriers (Figure 10) behaved similarly to the rigid barriers in the model experiments. For all three investigated barriers with different net stiffnesses, an increase in the maximum impact force with the increasing inclination angle θ of the flume was observed. It is remarkable that, for the flexible barriers, there was almost no change in the static force Fstat due to a change in the inclination of the flume of 38.8° (Figure 11a,b). As the stiffness of the nets decreased, the maximum impact force Fpeak increased, while the static impact force Fstat remained constant. The reason for the greater maximum impact force with the soft nets can be explained by the filling process, which consisted of the filling height hstat and the expansion f of the nets (Figure 10). This phenomenon has already been observed by [1].
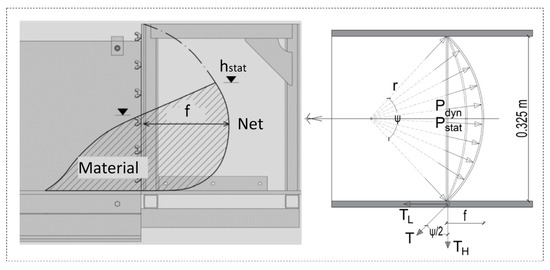
Figure 10.
Deposition of the material in the flexible barrier: tangential rope force (T), horizontal component (TH) and normal impact forces (TL) of the rope.
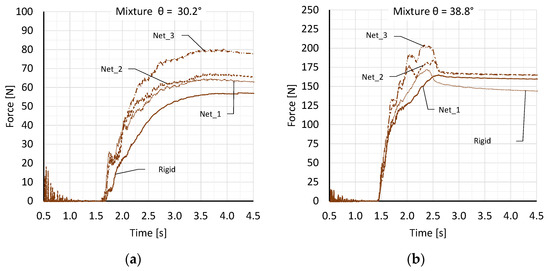
Figure 11.
Force–time history for flexible barriers, mixture and inclinations of the flume base (θ) of (a) 30.2° and (b) 38.8°.
Figure 11a,b compare the forces of the different flexible and rigid barriers for the respective inclinations of the flume θ. The effects of increasing elasticity on the impact force can be clearly seen in the diagrams. For the flexible barriers, forces of at least the same magnitude of, but predominantly even greater than, those for the rigid barriers were measured. Especially at the inclinations of 30.2° and 38.8°, the maximum impact force Fpeak of the nets was much higher than the maximum impact force Fpeak of the rigid barrier. At the inclination of θ = 35.8°, similar force procedures were measured for all investigated barriers. Here, the procedures of the different barriers overlapped for the most part. It can be read from the diagrams that the maximum impact force Fpeak increased as a function of the stiffness of the flexible barrier. At first sight, the results are untypical for flexible barriers, since according to theory, the deflection and elongation of the barrier type should result in a force reduction compared to the rigid barrier. When the first particles hit the rigid barrier, there was a damping effect in the dead zone for the following material. This effect could not be observed with the flexible barriers. In addition, the flexible barrier was able to interact with much more material than the rigid barrier during dynamic impact. During the experiments, it was observed that, with the increased flexibility, the first grains of the material decisively deflected and stretched the mesh. The remaining, subsequent material was then subsequently channeled into the deflected net, and an increased maximum impact force Fpeak was observed.
Comparable results were observed in the laboratory experiments by [1]. They also did not observe any significant differences in the measured forces for the rigid and flexible barriers. The authors of [1] concluded that barriers with too much flexibility lead to a higher measured impact force. It was further stated that a limited amount of flexibility should be ideal for barriers, with a barrier that is too rigid again negating the benefits of the flexible barrier. The authors concluded from their experiments that flexible barriers under the effect of a mass movement are conceptually different from flexible barriers under the effect of a rockfall, as in the latter, the increase in the impulse duration results in a reduction in the total load.
In [19], a non-linear finite element model was used for the back analysis of laboratory experiments carried out with a centrifuge. Among other things, the effect of the barrier stiffness on the forces occurring with the flexible barrier was determined. In order to be able to compare the results with different stiffnesses, variations in the rope stiffness were included in the numerical model. In the model considered (Figure 10), the tangential rope force T was decomposed into a component normal to the barrier TI and a horizontal component TH. The sum of the two components normal to the barrier was the total measured force. The normal impact force TI was relatively insensitive to the barrier stiffness. The impact force varied by only 20% within the entire stiffness range by a factor of 80. The normal force T in the ropes was very sensitive with regard to the stiffness of the barrier, and this was only due to geometric effects. A lower barrier stiffness facilitated larger barrier deflection and a larger deflection angle. The cable force was reduced accordingly, even though the impact force remained constant. The authors of [20] also pointed to the structural problems with erosion and scour in flexible nets. For flexible barriers, [21] showed that the dynamic coefficient for rock avalanches with a grain diameter between 15 and 30 mm was α = 2.0, and for debris flows α = 0.5. The lower value for debris flows is justified by the flow through the flexible protective net.
4.3. Test Results with Protective Dams
Figure 12 shows the force–time histories for the earth dams and geogrid-reinforced dam for the different materials. Analogous to the rigid barrier, the steel and glass spheres reached the highest impact force Fpeak. The peak impact forces Fpeak were also achieved here by the steel spheres. If the test results for the individual dam types are compared at an inclination of 30.2°, it can be seen that a consistently higher peak impact force Fpeak was obtained for the earth dam type, irrespective of the material used. The same material was used for both types of embankments. A transverse distribution through the geogrid-reinforced elements in the dam can be neglected due to the small width of the laboratory experiments (32.5 cm) and the measurement of the force as a total impact. The geogrid-reinforced embankment can be made much steeper on the impact side (Figure 4). A steeper slope encouraged the faster formation of a dead zone. Further impulsive effects of the material were thus reduced. In Figure 12, it can be seen that the geogrid-reinforced embankments for the mixture and the glass spheres were subjected to less action.
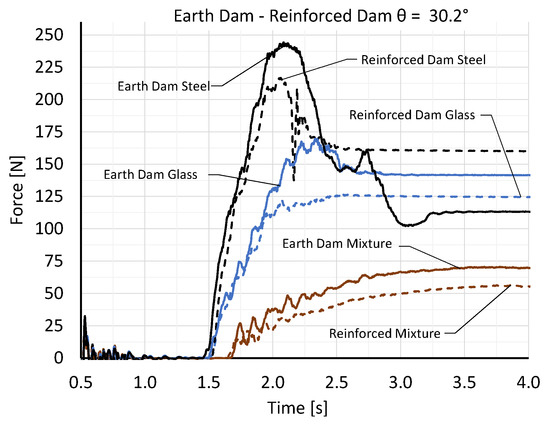
Figure 12.
Force–time history comparison between an earth dam and a geogrid-reinforced dam for an inclination of the flume base of θ = 30.2°.
4.4. Comparison of Impacts for Rigid Barriers, Flexible Structures and Embankments
For the mixture, the Fpeak/Fstat ratio for rigid barriers reached 1.15, and for flexible barriers, a value of up to 1.30 was reached. For dams, however, the ratio of Fpeak/Fstat, 1.06, was significantly lower (Figure 13a). It can be seen from the results that the variation was independent of the Froude number. The results show the advantage of embankments. The test results confirm the behavior of flexible structures compared to rigid barriers, as already described by [1,19]. No lower Fpeak values for flexible barriers than for rigid barriers were observed. On the contrary, predominantly larger maximum impact forces were mostly found for the flexible nets. The embankments can be assessed as a favorable protective structure when considering the static and dynamic impacts.
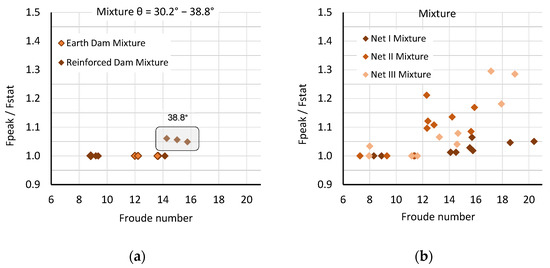
Figure 13.
Fpeak/Fstat as a function of the barrier and the Froude number for (a) Dam and (b) Nets. Test results in the frame in Figure 13 (a) for the inclination of 38.8°.
4.5. Comparison of the Laboratory Experiments with the DEM Simulation
For this work, simulations were carried out using the DEM software ROCKY® from ESSS to verify the experimental results. In the DEM calculation, each individual particle was modeled as an independent unit. In addition, the relationships between the particles and the particles and the flume can be defined. The geometry was able to be read with an inclination of the flume of 0° (horizontal). For the computer simulations, a so-called inlet was defined for the particles. In order to be able to guarantee a realistic simulation, this inlet of the particles was placed half a meter above the flume of the reservoir. This inlet filled the reservoir with 25 kg of material within the first second of the simulation. After all particles were created, the gate was opened and the material started to flow. For the steel spheres, sphere particles with a diameter of 2 mm were defined. These had a mass of 25 kg and a steel density of 7850 kg/m3, which resulted in approximately 760,000 particles. It was observed that the elastic modulus of the material had only a very small, negligible influence on the results, but a very large influence on the necessary calculation time. For the calibration, a parameter study was carried out with the following parameters:
- -
- Coefficient of friction particle–particle: sand = 0.61; mixture = 0.66.
- -
- Coefficient of friction particle–flume: sand = 0.50; mixture = 0.48.
- -
- Rolling friction coefficient: sand = 0.52; mixture = 0.45.
- -
- Restitution factor particle–particle: sand = 0.35; mixture = 0.15.
- -
- Restitution factor particle–flume: sand = 0.55; mixture = 0.55.
These parameters were varied for the respective material until a result was achieved that was in accordance with the laboratory experiments in the simulation. Figure 14 shows the simulation results in comparison to the measured forces of the mixture at a slope of 35.8°. The results of the simulation reflect the observed run-up process. For the description of the interaction between the particles or between the particles and the flume, the normal force interaction was considered in the numerical DEM simulation using a linear spring dashpot model, and the tangential force was considered by means of a linear spring model with Coulomb limit. In the simulation, the friction coefficient between the particles for the material was chosen to be between 0.61 (sand) and 0.66 (mixture). The coefficients of friction between the particles and the model were assumed to be 0.50 (sand) and 0.48 (mixture). The restitution factor between the particles was 0.35 for the sand and 0.15 for the mixture. The restitution factor between the particles and the flume was 0.55 for both the sand and the mixture. For the sand and the mixture, the rolling resistance factor was considered to be 0.52 and 0.45, respectively. For modeling the almost perfectly round particles (e.g., steel spheres), the rolling resistance factor was assumed to be 0.
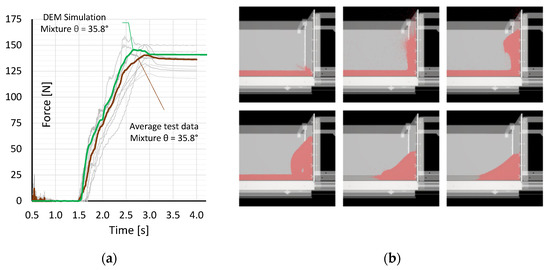
Figure 14.
(a) Force–time history comparison of model test data with the results of the DEM simulation; (b) images from the DEM simulation showing the impact in 6 steps.
5. Comparison of the Effects of Debris Flows and Rock Avalanches with Different Design Approaches for Rigid Structures
The original notation in the following equations was taken directly from the publications of the indicated authors. Definitions of these parameters, if not given, can be taken from the respective publications.
5.1. Comparison of the Laboratory Experiments of this Work with the Design Approaches According to Ng et al. for Debris Flows
For the laboratory experiments in the centrifuge, the maximum impact forces Fpeak on the rigid and flexible barriers were investigated using the approach of [5]. For this purpose, the water–solid mixture was varied with a solid content of 0 to 50%. The results of the dynamic impact Fpeak were then used to determine the dynamic coefficient . To determine the dynamic coefficient , Equation (3) was used:
* sin(β) is determined as a function of the measurement of the flow height, where is the flow depth, w the width of the barrier and is the angle between the barrier and the flume. The results, according to [22], enable the determination of the distribution of the dynamic coefficients over the normalized barrier height H/hf (height of barrier/flow depth). The lowest dynamic coefficient results were found for the material with 0% solid content. The largest dynamic coefficients were achieved by the material with 50% solid content. In Figure 15, the dynamic coefficients from the various publications and the laboratory experiments from this work are compared.
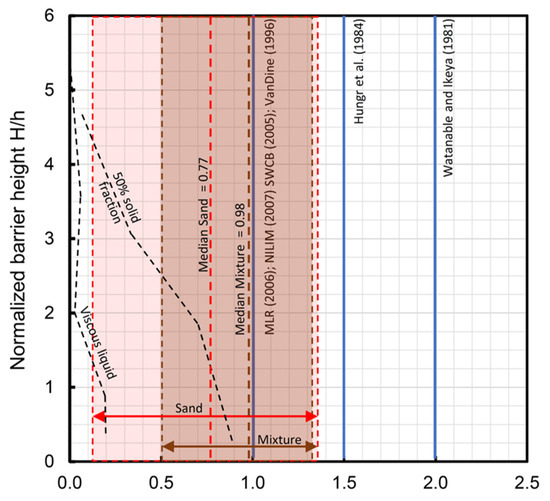
Figure 15.
Dynamic coefficient according to [22] with the addition of the experimental results of this work.
5.2. Comparison of the Laboratory Experiments of this Work with the Hydrodynamic Approaches for Debris Flows
For impacts on rigid structures from debris flow processes, various approaches are presented in the literature, some of which are contradictory. A common approach for estimating the impact from a debris flow, based on the momentum theorem, can be taken from [23], according to which the sum of the static force FSt and dynamic force FDyn (Equation (4)) is to be used to determine the total impact. For the dynamic impact in Equation (6), the dynamic coefficient α was set to be equal to 1.0. The measured maximum impact force from the laboratory experiments Fpeak for this work was subsequently compared with the dynamic impact Fpeak calculated using Equations (6) and (7), and the impact coefficient α was determined. For the smooth steel spheres, the impact coefficient α was four times higher than that for the natural grains. The impact coefficient α of the glass spheres was still twice as high as that of the sand and the mixture. The decrease in the impact coefficient α due to the rough surface of the corroded steel spheres is striking, with the impact coefficient α lying between 0.78 and 1.11. The largest differences between [23]’s approach for debris flows and the laboratory experiment results occurred in the case of sand, for which the impacts based on the approach according to [23] were up to approximately eight times higher. For the mixture, the calculated results with Equation (7) were approximately two times higher than the measured results. Transferred to nature, this finding would mean that impacts on rigid structures from rock avalanches estimated on the basis of the impulse theorem with an impact coefficient α = 1.0 for debris flow-like processes are on the safe side. Consequently, water in the debris flow or rock avalanches leads to significantly higher impacts.
with
5.3. Comparison of the Test Results of this Work with the Design Approaches According to Ho et al. for Debris Flows
According to the design approaches of [24], for debris flows, the pressure is composed of a dynamic pressure component and a static pressure component . The maximum pressure is given by
where is the dynamic coefficient, is the density and v is the velocity. For a rigid barrier, a dynamic coefficient = 2.5 is recommended. The static pressure is obtained from
with the lateral pressure coefficient denoted by K, the acceleration due to gravity denoted by g and hf denoting the dumping height at the end of the process. The recommended value for K is given as 1. If the calculated dynamic impacts are compared with the results of the laboratory experiments with the inclined flume, it can be seen that the calculated maximum impact forces Fd with = 2.5 clearly overestimated the maximum impact forces F peak measured. In contrast, however, the static forces Fstatic with K = 1 and Formula (9) were underestimated compared with the laboratory experiments (Figure 16).
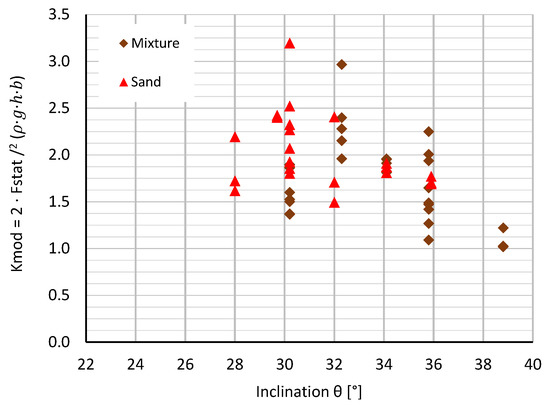
Figure 16.
Back-calculated creep pressure coefficients Kmod for the sand and mixture test materials on the rigid barrier based on Equation (16).
5.4. Design Approach According to Ashwood and Hungr for Rock Avalanches
The maximum impact forces according to [1] differ by a constant factor of 0.5 compared to the approach for debris flows (Equation (10)).
5.5. Newly Proposed Impact Model for Barriers According to Choi et al. for Dry Granular Flow
The authors of [25] proposed that, for a rigid barrier solved by [26], the relationship between the hydrodynamic force (Equation (12)) and the hydrostatic force (Equation (13)) can be expressed as follows:
where Fr is the incoming Froude number (much larger than unity), ξ is the function of the Froude number or, according to Equation (3) in [25], the jump height ratio of hst and hf (Equation (14)), α is the dynamic pressure coefficient and is the channel inclination.
According to [25], when Fr >> 1, it can be calculated from Equation (14) that 2 Fr2/ξ2 = 1, and therefore
Figure 17 shows the interpretation of Equation (15). The authors of [25] conducted a series of flume experiments with dry granular flows and a rigid barrier. The findings from this study were that the dead zone can attenuate the dynamic impact of the subsequent flow on the barrier [5] and the dynamic pressure coefficient in a range from 0.2 to 0.5.
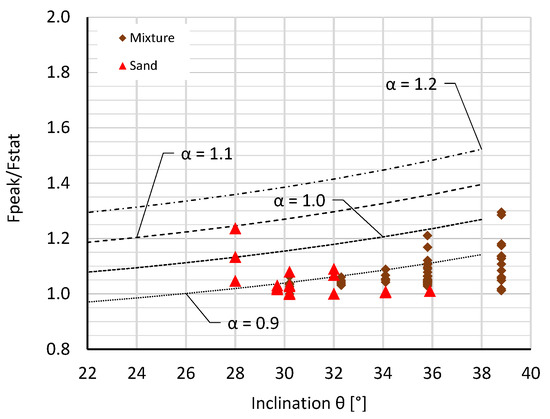
Figure 17.
Relation of Fpeak/Fstat as a function of the dynamic pressure coefficient and the inclination of the flume base (θ). For a constant factor α, a higher inclination angle (θ) results in a higher ratio of Fpeak/Fstat.
6. Comparison of the Effects of Debris Flows and Rock Avalanches with Quasi-Static Design Approaches for Rigid Structures
6.1. General Aspects
Despite the extensive research by the authors, no sufficiently documented events of rockfalls, landslides or mass movements with subsequent rock avalanches in the runout area and their effects on protective structures could be found. In most cases, a sufficient description of the process of rock avalanches that allows for accurate conclusions about the effects on protective structures is not available. The maximum impact forces Fpeak on the rigid barrier measured in the model experiments also represent the maximum possible impact of the debris flow on a barrier. Protective barriers reduce the maximum impact forces Fpeak while increasing the impact duration. With flexible barriers, however, an increase in the maximum impact forces must be assumed. Froude numbers with a maximum of 16 were determined in the laboratory experiments for this work for the sand and the mixture. In nature, Froude numbers with a maximum of 15 were back-calculated for the rock avalanches for comparison.
6.2. Impact Model for Barriers with the Approach of “Creep Pressure”
In order to determine the static action on rigid supporting structures caused by slowly moving mass movements, the theory of creep pressure, according to [27], can be used. The aim of the investigations was to provide empirical formulae for the different types of barriers based on geotechnical theories, such as the development of earth pressure, which in Austria is known as “creep pressure theory”. Since, in the laboratory experiments, the inclination of the flume was usually greater than the angle of the bed friction, creep pressure theory cannot be transferred directly. The authors’ extension of the theory for the laboratory experiments includes making a distinction between the angle of the bottom friction φb and the friction angle φi of the soil as well as the determination of the static force Fstat due to the creep pressure. The geotechnical model with consideration of the bottom friction angle φb with the aid of the force vectors is shown in Figure 18. The creep pressure coefficient Kmod back-calculated from the laboratory experiments using Equation (16) for the rigid barrier reached values between 1.0 and 3.2 (Figure 17).
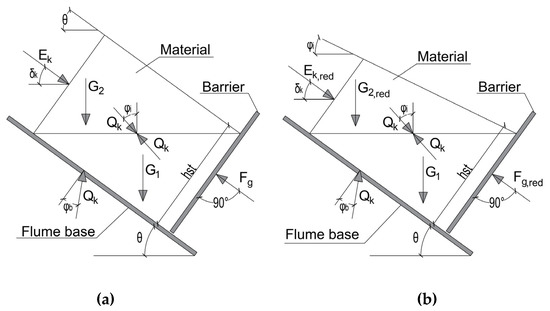
Figure 18.
Force vectors for the determination of the creep pressure Kg using the partial sliding bodies and taking into account the angle of the bottom friction: (a) surface inclination equal to , and (b) surface inclination equal to .
If the creep pressure coefficients Kg are calculated on the basis of creep pressure theory, taking into account the angle of friction at the bottom and the maximum inclination of the surface at the level of the friction angle of the material, the earth pressure coefficient Kg can be determined. From Figure 18a, the static force Fg and the creep pressure coefficient Kg due to the creep pressure can be calculated with Equations (17)–(21). Kg is the creep pressure coefficient, hst is the height at the barrier, θ is the inclination of the flume, ρ is the density, g is the acceleration due to gravity and b is the width of the barrier.
For inclinations of the transport plane θ > φi, a slope inclination with the internal friction angle φi was established at the surface of the deposit shape (Figure 18b). This geometric shape of the surface led to a reduction in the weight force G2 and thus to a reduction in the static force Fstat. Thus, the weight force G2,red was given by Equation (18). By taking the weight G2,red into account in Equations (19) and (20), the reduced earth pressure coefficient according to creep theory Kg,red can be determined using Equation (21). The comparison of the reduced earth pressure coefficient according to creep theory Kg,red and the existing earth pressure coefficient Kmod is shown in Figure 19. It can be seen that the back-calculated earth pressure coefficients Kmod differed by a factor of 0.39 to 1.44 from the theoretically determined earth pressure coefficient The comparison in Figure 19 shows, on the one hand, that the Froude number hardly influenced the Kmod/Kg,red ratio and, on the other hand, that the static force can be determined on the basis of creep theory, according to Figure 18.
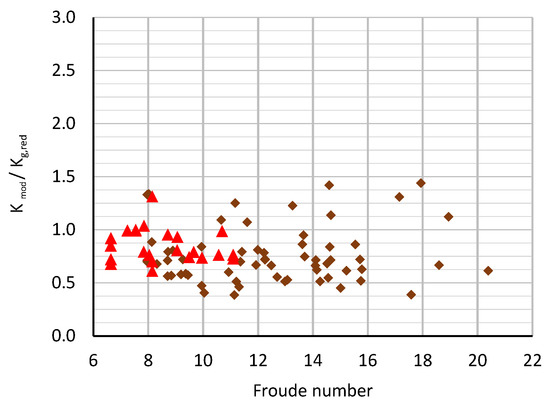
Figure 19.
Earth pressure coefficients Kmod/Kg,red for the mixture and the sand depending on the Froude number.
6.3. Proposal for the Estimation of the Peak Impact Force based on the Quasi-Static Models
Based on creep pressure theory and the model in Figure 18b, the static force Fstat can be determined using Equation (22). Provided that the Fpeak/Fstat ratio is known as a function of the material, and that its geological–geotechnical properties (dynamic internal friction angle, basal friction angle, density, grain size distribution and fragmentation properties of the rock avalanche) as well as the inclination of the flume, flow height, flow velocity and thus the Froude number are all known, the hydrodynamic force Fpeak can be estimated in a certain range using Equation (23). Based on the investigations of this work, the following procedure would be appropriate.
For the sand and the mixture, a maximum impact force Fpeak in the range of 1.06 to 1.3 Fstat was measured. An estimate of the hydrodynamic impact Fpeak can thus be made on the basis of creep pressure theory and the Fpeak/Fstat ratio.
Determination of the static force Fstat:
where:
- Fg,red = static force obtained from creep pressure theory;
- ζs = static coefficient independent of the structure type (rigid, flexible, embankment);
- ζs = 1.0 to 1.5.
Determination of the dynamic action:
where:
- ζd = dynamic coefficient depending on the type of structure;
- ζd = 1.0 to 1.06 for the embankment;
- ζd = 1.0 to 1.15 for the rigid barrier;
- ζd = 1.0 to 1.30 for the flexible barrier.
7. Summary for Rigid Barriers
In the laboratory experiments according to [1], which enable investigations of “rock avalanches”, the granular flow was accelerated along the flume in phase 1 and then hit a rigid barrier in phase 2. For this work, 185 laboratory experiments with rigid barriers, flexible barriers and embankments were carried out. In the laboratory experiments, laterally restricted rock avalanches were investigated. This restriction leads to less favorable forces on the protective structures than in the case of laterally unrestricted rockfall avalanches. In the laboratory tests, laminar flow behavior without any turbulent behavior was observed. These properties of rock avalanches can also be found in [28].
The material used and the inclination of the flume had a significant influence on the impact on the barrier. In addition to the inclination, the velocity of the granular flow was also strongly dependent on the material used, the grain shape and the grain roughness. The model experiments with steel spheres showed a maximum impact force that was up to twice as high as the static impact. This effect could not be observed for the sand, mixture and glass spheres. For the mixture and the sand, the maximum impact force was at most 15% higher than the static impact. With the model experiments, it could be demonstrated that the damping of the dynamic impact was also essentially dependent on the material used.
A disadvantage of determining the maximum impact force is the complexity of obtaining the dynamic coefficients. The comparison of “Fluid Impact Models” published by [29] revealed that, for example, [30,31,32] recommend different coefficients as dynamic factors. Based on the equations of the conservation of momentum, impact coefficients α between 0.7 and 12 are recommended. According to [33], an impact coefficient α of 2.0 is recommended.
The authors of [5] also concluded that the dynamics of debris flows depend on the interaction of the solids and the viscous fluid. Using the Froude number alone for the application of a design concept is inconsistent. There needs to be a consideration of changes in pore water pressures for the impact of debris flows on protective structures to be determined ([34,35,36,37]). Many guidelines for the estimation of impacts from debris flows do not consider the interaction of solids and fluids. Even for impacts from rock avalanches on protective structures, the Froude number should not be used as a basis. Rather, the geological–geotechnical boundary conditions, such as the block size distribution, shear strength and compressive strength of the solid bodies, and the tendency toward fragmentation, are important ([38]). According to [5], an increase in the impact coefficient α occurs in debris flows with increasing solid content up to 50%. In the investigations of this paper with dry materials, lower impact coefficients α were determined than for debris flows.
Evidence obtained from laboratory experiments and real events can then yield design concepts such as the one developed by [15] for rockfall embankments. The aim is to subsequently validate the tests carried out with various numerical modeling programs [39,40]. One possibility could be to estimate the impact on the protective structures using the Fpeak/Fstat ratio. Table 6 provides a summary of the various literature references.

Table 6.
Summary of the various literature references.
8. Conclusions
This paper dealt with different approaches to determining the effects of rock avalanches on protective structures. The results from model experiments with dry material are mostly used to determine equations and approaches that are easy to handle in practice. In this paper, the model experiment of the University of Innsbruck was presented first, followed by the results as a force–time effect. The aim of this paper was to compare the results with selected approaches from different authors. Design approaches for rock avalanches calculated using the impulse theorem to determine the maximum impact force on rigid barriers lead, based on the investigations of this thesis, to an overestimation of the maximum impact force and to an underestimation of the static force.
In order to estimate the static force Fstat on barriers, creep pressure theory can be applied. Based on the results from the model experiments, the resulting force from creep pressure theory can be increased by a factor of 1.0 to 1.5 to obtain the static force Fstat. The subsequent multiplication with a coefficient to 1.3 depending on the type of structure determines the maximum force Fpeak. The available results of the model experiments with rigid barriers reveal that the maximum impact Fpeak for granular mass flow corresponded to a maximum of 1.15 times the static impact Fstat. This conclusion is confirmed by considering the maximum impact force and static force for the results for φdyn = in the various literature references.
In conclusion, the first step should be the estimation of the static force as a function of the protective structure, the geometry of the protective structure and the material of the rock avalanche. In addition, the rock avalanche should be evaluated from a geological and geotechnical point of view. The dynamic internal friction angle, the basal friction angle, the density, the grain size distribution and the fragmentation properties of the rock avalanche are essential. For rock avalanches, the use of the Froude number to estimate the “Fpeak/Fstat” ratio is difficult. In Figure 7a, for rigid barriers, it is shown that the Fpeak/Fstat ratio increased with increases in the Froude number. This behavior was not observed for dams (Figure 13a). Moreover, for rigid barriers and nets, it can be observed that for a given Froude number, several ratios of “Fpeak/Fstat” were obtained.
However, further large-scale model experiments with granular flows are definitely required to better determine the Fpeak/Fstat relationship as a function of scale. In this context, proposals for the design of protective embankments against rockfalls have already been prepared and included in the Austrian standard concept for protective structures against natural hazards.
The experiments demonstrated the dependence of the flow velocity, the flow height and the static and dynamic effects on protective structures on the particle shape and roughness. The results of the laboratory experiments also demonstrate significant differences for the Fpeak/Fstat ratio and thus the necessity of considering the geological–geotechnical parameters for the design of protective structures. Particles with a smooth surface lead to fast and thin rock avalanches. In contrast, particles with a rough surface lead to relatively slower and thicker rock avalanches. Too much flexibility in the protective structure leads to an increase in mass and thus to an increase in static force; therefore, an embankment with an “adjusted” stiffness is an appropriate structure.
In our work, the three-dimensional numerical model was used to simulate the granular flow to the protective structure. The motion sequence was calculated with the discrete element method (DEM) and the software ROCKY® from ESSS. For the choice of parameters, it is of particular importance that the experience of geotechnical engineers and geologists in connection with subsoil exploration is applied. Then, parameter studies with numerical calculations (DEM) can provide a useful alternative for estimating the impacts on protective structures, the flow velocity and the flow depth. In this work, ROCKY® was used to simulate the course of the impact of the material on the barrier and the maximum impact force Fpeak and static force Fstat on the protective structure for different materials.
Further research will involve an extension to landslide runout for large-scale simulations. The aim is to model the velocity of rock avalanches and the associated erosion as well as the influence of fragmentation with the help of suitable field investigations. For this purpose, back calculations with various past rock avalanches in Tyrol/Austria and the associated rheological and geotechnical parameters are currently being carried out.
Author Contributions
Conceptualization, R.H. and S.B.; methodology, R.H. and S.B.; software, S.B.; validation, R.H. and S.B.; formal analysis, R.H.; investigation, R.H.; resources, R.H.; data curation, R.H. and S.B; writing—original draft preparation, R.H. and S.B; writing—review and editing, R.H. and S.B; visualization, R.H. and S.B; supervision, R.H. and S.B; project administration, R.H.; funding acquisition, R.H. and S.B. All authors have read and agreed to the published version of the manuscript.
Funding
Open access funding is provided by the Vice Rectorate for Research of the University of Innsbruck.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Acknowledgments
The computational results (DEM simulation) presented here were achieved (in part) using the LEO HPC infrastructure of the University of Innsbruck. The authors would like to thank the anonymous reviewers who thoroughly reviewed the manuscript; their critical comments and valuable suggestions were very helpful in preparing this paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ashwood, W.; Hungr, O. Estimating total resisting force in flexible barrier impacted by a granular avalanche using physical and numerical modeling. Can. Geotech. J. 2016, 53, 1700–1717. [Google Scholar] [CrossRef]
- Moriguchi, S.; Borja, R.I.; Yashima, A.; Sawada, K. Estimating the impact force generated by granular flow on a rigid obstruction. Acta Geotech. 2009, 4, 57–71. [Google Scholar] [CrossRef]
- Albaba, A.; Lambert, S.; Faug, T. Dry granular avalanche impact force on a rigid wall: Analytic shock solution versus discrete element simulations. Phys. Rev. E 2018, 97, 052903. [Google Scholar] [CrossRef] [PubMed]
- Ng, C.W.W.; Wang, C.; Choi, C.E.; de Silva, W.A.R.K.; Poudyal, S. Effects of barrier deformability on load reduction and energy dissipation of granular flow impact. Comput. Geotech. 2020, 121, 103445. [Google Scholar] [CrossRef]
- Ng, C.W.W.; Song, D.; Choi, C.E.; Liu, L.H.D.; Kwan, J.S.H.; Koo, R.C.H.; Pun, W.K. Impact mechanisms of granular and viscous flows on rigid and flexible barriers. Can. Geotech. J. 2017, 54, 188–206. [Google Scholar] [CrossRef]
- Song, D.; Chen, X.; Zhou, G.G.; Lu, X.; Cheng, G.; Chen, Q. Impact dynamics of debris flow against rigid obstacle in laboratory experiments. Eng. Geol. 2021, 291, 106211. [Google Scholar] [CrossRef]
- Gao, L.; Zhang, L.M.; Chen, H.X. Wo-dimensional simulation of debris flow impact pressures on buildings. Eng. Geol. 2017, 226, 236–244. [Google Scholar] [CrossRef]
- Ng, C.; Choi, C.; Liu, H.; Wang, C.; Kwan, J. Impact mechanisms of debris flow on barriers: Modelling, analysis and design. In Proceedings of the Scg-XIII International Symposium on Landslides, Cartagena, Colombia, 22–26 February 2021. [Google Scholar]
- Shu, H.; Ma, J.; Qi, S.; Chen, P.; Guo, Z.; Zhang, P. Experimental results of the impact pressure of debris flows in loess regions. Nat. Hazards 2020, 103, 3329–3356. [Google Scholar] [CrossRef]
- Berger, S.; Hofmann, R.; Wimmer, L. Einwirkungen auf starre Barrieren durch fließähnliche gravitative Massenbewegungen. Geotechnik 2021, 44, 77–91. [Google Scholar] [CrossRef]
- Strobl, T.; Zunic, F. Hydraulic Engineering—Current Basics—New Developments; Springer: Munich, Germany, 2006. [Google Scholar]
- Margreth, S.; Bartelt, P.; Bühler, Y.; Christen, M.; Graf, C.; Schweizer, J. Expert Report G2017.20 Modelling of the Cengalo Landslide with Different Framework Conditions, Bondo, GR; WSL Institute for Snow and Avalanche Research SLF: Davos, Switzerland, 2017. [Google Scholar]
- Sosio, R.; Crosta, G.B.; Hungr, O. Complete dynamic modeling calibration for the Thurwieser rock avalanche (Italian Central Alps). Eng. Geol. 2008, 100, 11–26. [Google Scholar] [CrossRef]
- PLANAT. PLANAT National Platform Natural Hazards Federal Office for the Environment FOEN. 2020. Landslide and Rockfall—Origin of Rockfall and Rockslide [Online]. Available online: http://www.planat.ch/de/wissen/rutschung-und-felssturz/steinschlag-felssturz/entstehung-s-f/ (accessed on 6 August 2020).
- Hofmann, R.; Vollmert, L. Rockfall embankments: Construction and Design. Geomech. Tunn. 2020, 13, 21–31. [Google Scholar] [CrossRef]
- Song, D.R.; Zhou, G.G.; Choi, C.E.; Zheng, Y. Debris flow impact on flexible barrier: Effects of debris-barrier stiffness and flow aspect ratio. J. Mt. Sci. 2019, 16, 1629–1645. [Google Scholar] [CrossRef]
- Tapia, F.; Pouliquen, O.; Guazzelli, E. Influence of surface roughness on the rheology of immersed and dry frictional spheres. Phys. Rev. Fluids 2019, 4, 104302. [Google Scholar] [CrossRef] [Green Version]
- Baselt, I.; de Oliveira, G.Q.; Fischer, J.T.; Pudasaini, S.P. Evolution of stony debris flows in laboratory experiments. Geomorphology 2021, 372, 107431. [Google Scholar] [CrossRef]
- Song, D.; Zhou, G.G.; Xu, M.; Choi, C.E.; Li, S.; Zheng, Y. Quantitative analysis of debris-flow flexible barrier capacity from momentum and energy perspectives. Eng. Geol. 2019, 251, 81–92. [Google Scholar] [CrossRef]
- Wendeler, C.; Salzmann, H.; Feiger, N. Flexible Debris Flow Barriers and Their Ability Proof; Second JTC1 Workshop: Hong Kong, 2018; pp. 167–170. [Google Scholar]
- Tan, D.Y.; Yin, J.H.; Feng, W.Q.; Qin, J.Q.; Zhu, Z.H. Influence of Debris Penetration on Impact Loading for Flexible Barrier Design; Second JTC1 Workshop: Hong Kong, 2018; pp. 155–158. [Google Scholar]
- Ng, C.W.; Choi, C.E.; Song, D.; Calvello, M.; Kwan, J.S.H.; Wang, G. Interaction of debris flow with rigid and flexible barriers: Centrifuge and numerical simulations. In Proceedings of the TC1 Workshop on Advances in Landslide Understanding, Barcelona, Spain, 24–26 May 2017. [Google Scholar]
- Hübl, J.; Suda, J.; Proske, D.; Kaitna, R.; Scheidl, C. Debris flow impact estimation. In Proceedings of the 11th International Symposium on Water Management and Hydraulic Engineering, Ohrid, Macedonia, 1–5 September 2009; University od Ss Cyril and Methodius, Faculty of Civil Engineering: Skopje, Macedonia, 2009. [Google Scholar]
- Ho, K.; Koo, R.; Kwan, J. Advances in debris flow risk mitigation practice in Hong Kong, Second JTC1 Workshop. In Triggering and Propagation of Rapid Flow-Like Landslides; Joint Technical Committee on Natural Slopes and Landslides: Hong Kong, 2018. [Google Scholar]
- Choi, C.E.; Ng, C.W.W.; Liu, H.; Wang, Y. Interaction between dry granular flow and rigid barrier with basal clearance: Analytical and physical modelling. Can. Geotech. J. 2020, 57, 236–245. [Google Scholar] [CrossRef]
- Zanuttigh, B.; Lamberti, A. Experimental analysis of the impact of dry avalanches on structures and implication for debris flows. J. Hydraul. Res. 2006, 44, 522–534. [Google Scholar] [CrossRef]
- Haefeli, P. Zur Erd- und Kriechdruck-Theorie. Schweiz. Bauztg. 1944, 124, 256–260, Erratum in Schweiz. Bauztg. 1944, 124, 267–271. [Google Scholar]
- Strom, A.; Li, L.; Lan, H. Role of Confinement on Spreading of Flow-Like Dry Rock Avalanches; Second JTC1 Workshop: Hong Kong, 2018; pp. 151–154. [Google Scholar]
- Huang, H.P.; Yang, K.C.; Lai, S.W. Impact Force of Debris Flow on Filter Dam. In Momentum; National Taiwan University: Taiwan, 2007; Volume 9, p. 03218. [Google Scholar]
- Scotton, P.; Deganutti, A.M. Phreatic line and dynamic impact in laboratory debris flow experiments. In Debris-Flow Hazards Mitigation: Mechanics, Prediction, and Assessment; ASCE: Reston, VA, USA, 1997; pp. 777–786. [Google Scholar]
- Daido, A. Impact force of mud-debris flows on structures. In Proceedings of the Congress-International Association for Hydraulic Research, Local Organizing Committee of The XXV Congress, Tokyo, Japan, 30 August–3 September 1993; Volume 3, p. 211. [Google Scholar]
- Armanini, A.; Scotton, P. On the dynamic impact of a debris flow on structures. In Proceedings of the Congress-International Association for Hydraulic Research, Local Organizing Committee of The XXV Congress, Tokyo, Japan, 30 August–3 September 1993; Volume 3, p. 203. [Google Scholar]
- Volkwein, A. Design of flexible debris flow barriers. In WSL Berichte, 18; Swiss Federal Institute for Forest, Snow and Landscape Research WSL: Birmensdorf, Switzerland, 2014. [Google Scholar]
- Ng, C.W.W.; Song, D.; Choi, C.E.; Koo, R.C.H.; Kwan, J.S.H. A novel flexible barrier for landslide impact in centrifuge. Géotechnique Lett. 2016, 6, 221–225. [Google Scholar] [CrossRef]
- Choi, C.E.; Au-Yeung, S.C.H.; Ng, C.W.W.; Song, D. Flume investigation of landslide granular debris and water runup mechanisms. Géotechnique Lett. 2015, 5, 28–32. [Google Scholar] [CrossRef]
- Song, D.; Ng, C.W.W.; Choi, C.E.; Zhou, G.G.; Kwan, J.S.; Koo, R.C.H. Influence of debris flow solid fraction on rigid barrier impact. Can. Geotech. J. 2017, 54, 1421–1434. [Google Scholar] [CrossRef] [Green Version]
- Hofmann, R.; Kolymbas, D. Wasserdruck auf Konsolidierungssperren. In Bauingenieur BD.95; VDI Fachmedien: Düsseldorf, Germany, 2020; Volume 2020. [Google Scholar]
- Ng, C.W.W.; Choi, C.E.; Cheung, D.K.H.; Cui, Y. Effects of dynamic fragmentation on the impact force exerted on rigid barrier: Centrifuge modelling. Can. Geotech. J. 2019, 56, 1215–1224. [Google Scholar] [CrossRef]
- Li, X.; Zhao, J.; Soga, K. A new physically based impact model for debris flow. Géotechnique 2021, 71, 674–685. [Google Scholar] [CrossRef]
- Hungr, O. Simplified models of spreading flow of dry granular material. Can. Geotech. J. 2008, 45, 1156–1168. [Google Scholar] [CrossRef]
- Ng, C.W.W.; Majeed, U.; Choi, C.E.; de Silva, W.A.R.K. New impact equation using barrier Froude number for the design of dual rigid barriers against debris flows. Landslides 2021, 18, 2309–2321. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).