Suitability of Screened Monitoring Wells for Temperature Measurements Regarding Large-Scale Geothermal Collector Systems
Abstract
1. Introduction
1.1. Importance of Monitoring Groundwater Temperature
1.2. Vertical Flows in MWs due to Convection
- = thermal Rayleigh number
- = gravitational acceleration [m/s2]
- = thermal expansion coefficient [1/K]
- = radius of water column [m]
- = kinematic viscosity [m2/s]
- = thermal diffusivity [m2/s]
- = thermal gradient [K/m]
1.3. Aims of This Study
2. Materials and Methods
2.1. Study Site and Hydrogeological Conditions
2.2. GWT and Electrical Conductivity Measurements
- ΔTi = calculated temperature difference at the depth i [K]
- T(MW)i = measured temperature in MW at the depth i [°C]
- T(TMS)i = linearly interpolated temperature in TMS at the depth i [°C]
- i = depth [m b. g. l.]
- z = depth [m b. gw. l.]
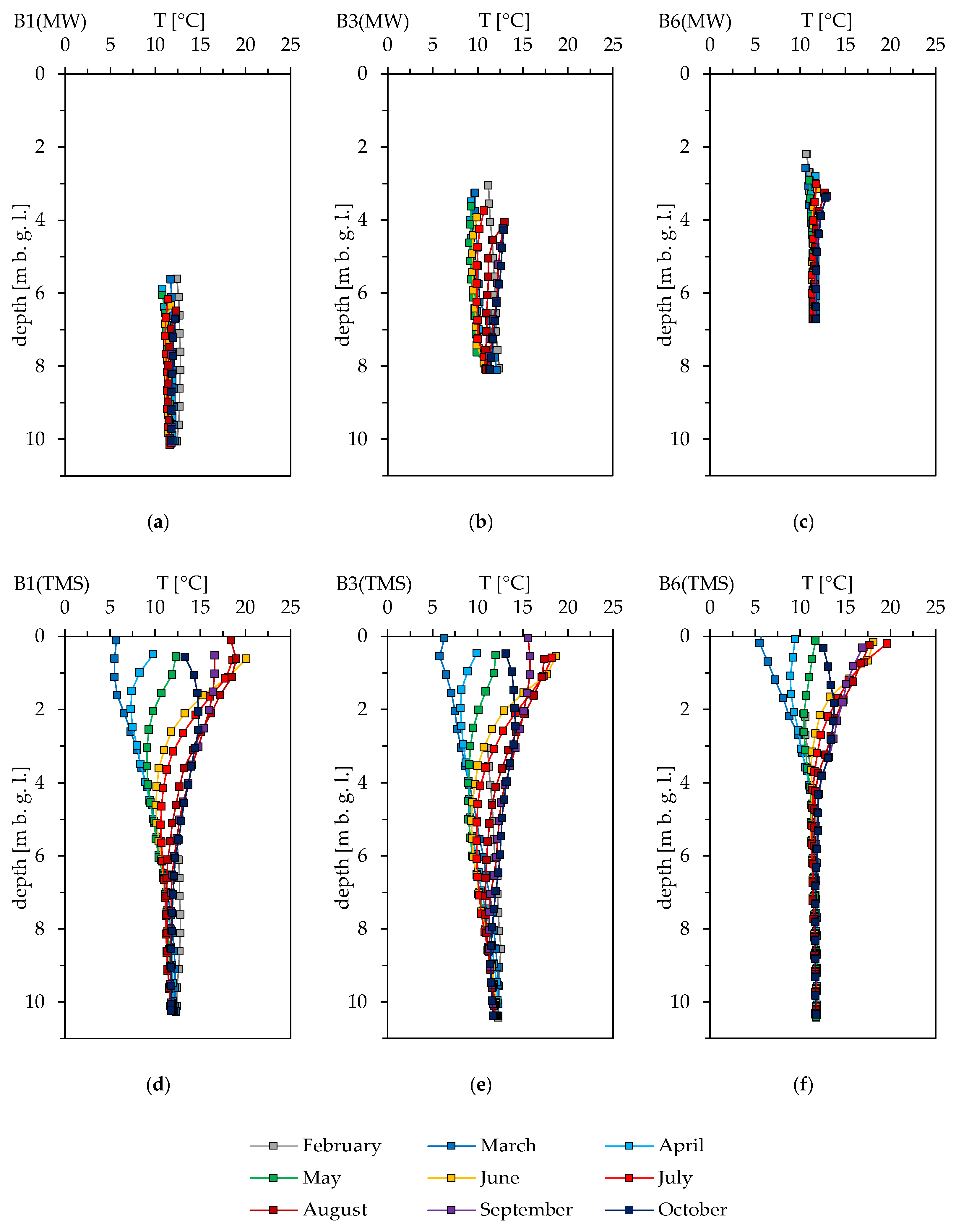
3. Results
3.1. Temperatures and Differences between MWs and TMSs
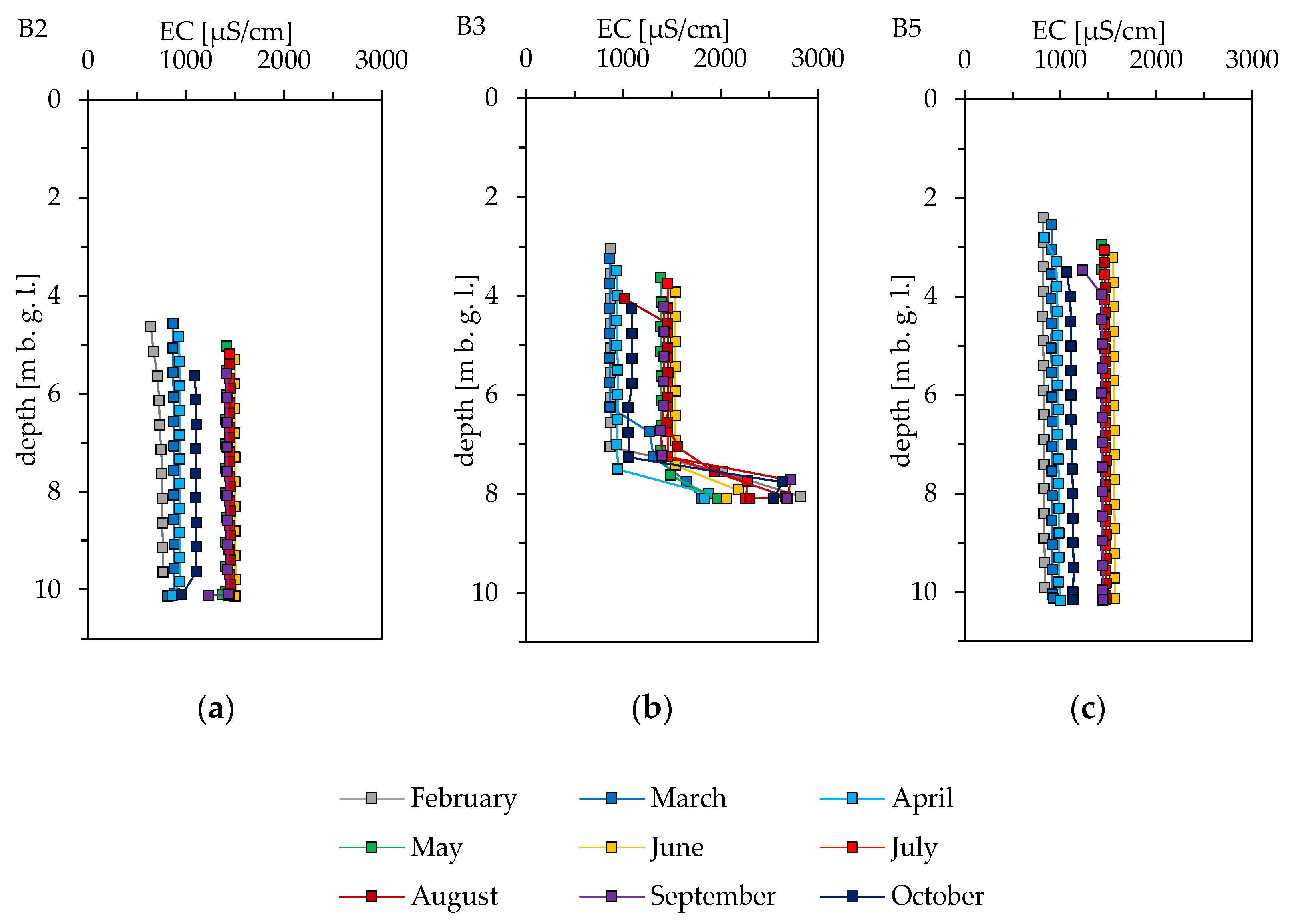
3.2. Electrical Conductivities in MWs
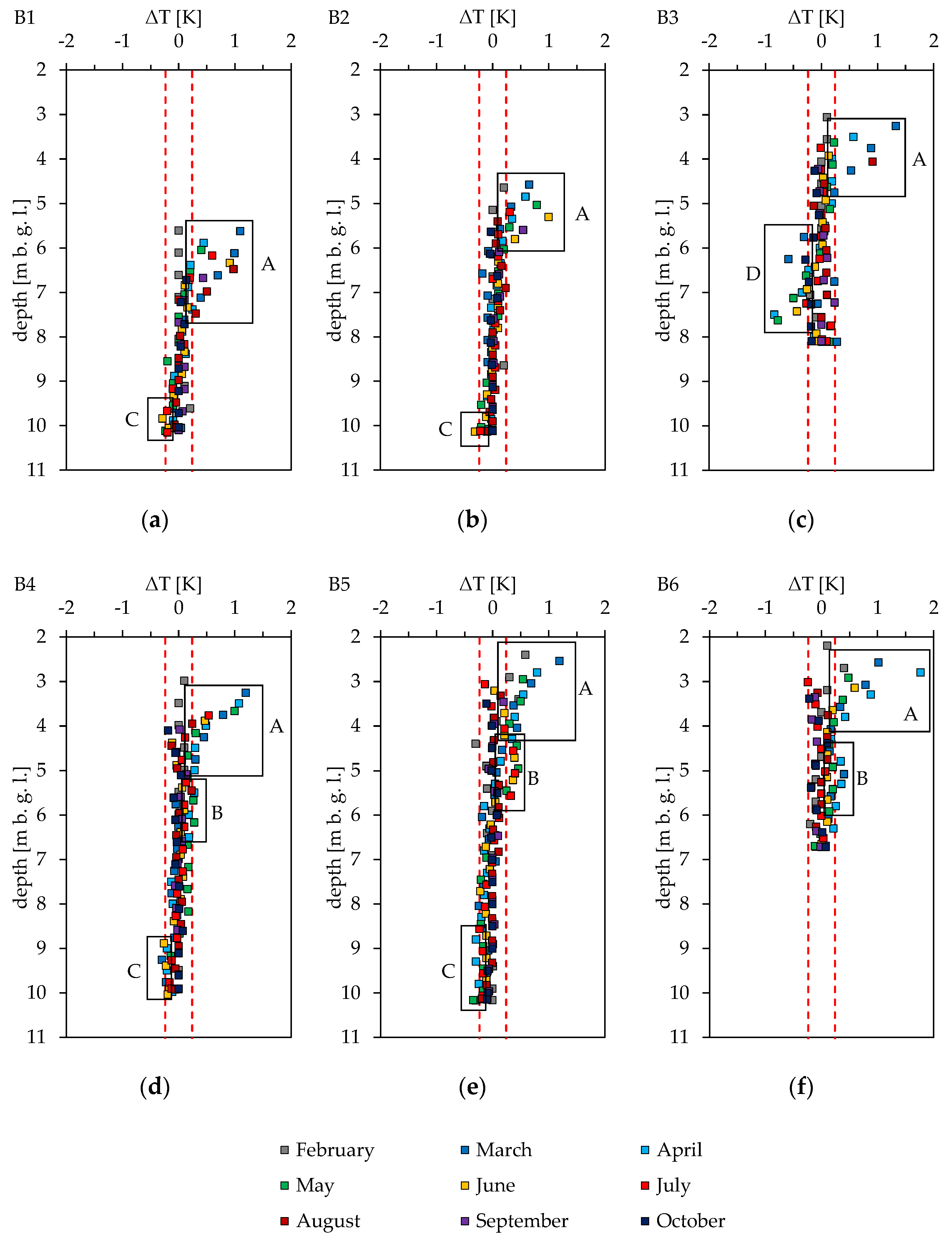
3.3. Comparison of Temperature Deviations and Thermal Gradients
4. Discussion
4.1. Deviations of GWT from the Ambient Subsurface Temperature in MWs
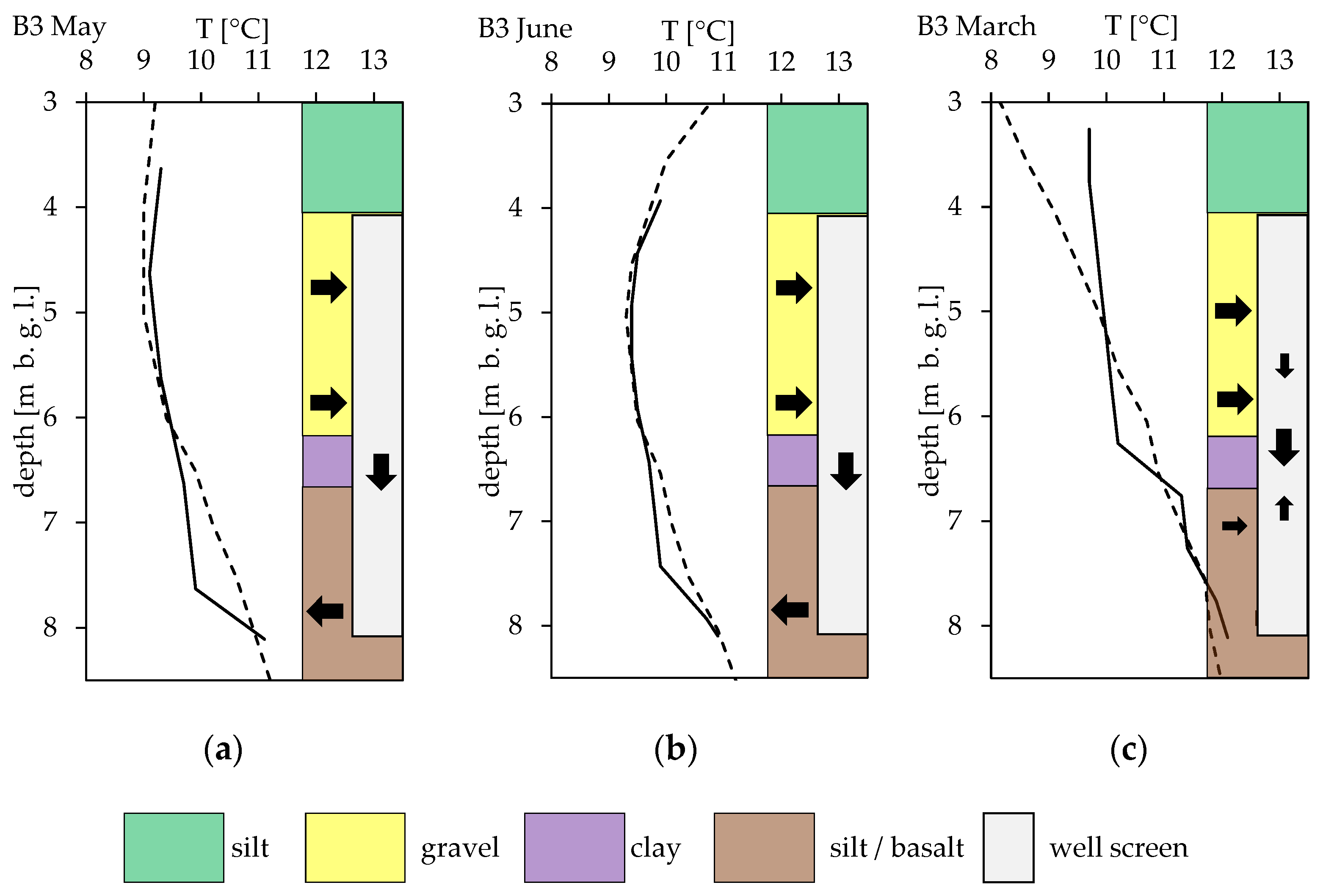
4.2. Impact of Forced Convection on GWT Measurements
4.3. Impact of Thermal Convection on GWT Measurements
4.4. Recommended Monitoring Concept for LSCs
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Farouki, O.T. Thermal Properties of Soils; Cold Regions Research and Engineering Lab Hanover NH: Hanover, NH, USA, 1981. [Google Scholar]
- Bertermann, D.; Klug, H.; Morper-Busch, L.; Bialas, C. Modelling vSGPs (very shallow geothermal potentials) in selected CSAs (case study areas). Energy 2014, 71, 226–244. [Google Scholar] [CrossRef]
- Bertermann, D.; Schwarz, H. Laboratory device to analyse the impact of soil properties on electrical and thermal conductivity. Int. Agrophys. 2017, 31, 157–166. [Google Scholar] [CrossRef]
- Di Sipio, E.; Bertermann, D. Factors Influencing the Thermal Efficiency of Horizontal Ground Heat Exchangers. Energies 2017, 10, 1897. [Google Scholar] [CrossRef]
- Di Sipio, E.; Bertermann, D. Thermal properties variations in unconsolidated material for very shallow geothermal application (ITER project). Int. Agrophys. 2018, 32, 149–164. [Google Scholar] [CrossRef]
- Schwarz, H.; Bertermann, D. Mediate relation between electrical and thermal conductivity of soil. Géoméch. Geophys. Geo-Energy Geo-Resour. 2020, 6, 50. [Google Scholar] [CrossRef]
- Xu, X.; Zhang, W.; Fan, C.; Li, G. Effects of temperature, dry density and water content on the thermal conductivity of Genhe silty clay. Results Phys. 2020, 16, 102830. [Google Scholar] [CrossRef]
- Alexander, M.D.; MacQuarrie, K.T.B. The measurement of groundwater temperature in shallow piezometers and standpipes. Can. Geotech. J. 2005, 42, 1377–1390. [Google Scholar] [CrossRef]
- Huber, H.; Arslan, U.; Sass, I. Zum Einfluss der Filtergeschwindigkeit des Grundwassers auf die effektive Wärmeleitfähigkeit. Grundwasser 2014, 19, 173–179. [Google Scholar] [CrossRef]
- Taylor, C.A.; Stefan, H.G. Shallow groundwater temperature response to climate change and urbanization. J. Hydrol. 2009, 375, 601–612. [Google Scholar] [CrossRef]
- Benz, S.A.; Bayer, P.; Winkler, G.; Blum, P. Recent trends of groundwater temperatures in Austria. Hydrol. Earth Syst. Sci. 2018, 22, 3143–3154. [Google Scholar] [CrossRef]
- Gunawardhana, L.N.; Kazama, S. Climate change impacts on groundwater temperature change in the Sendai plain, Japan. Hydrol. Process. 2011, 25, 2665–2678. [Google Scholar] [CrossRef]
- Hemmerle, H.; Bayer, P. Climate Change Yields Groundwater Warming in Bavaria, Germany. Front. Earth Sci. 2020, 8, 575894. [Google Scholar] [CrossRef]
- Menberg, K.; Bayer, P.; Zosseder, K.; Rumohr, S.; Blum, P. Subsurface urban heat islands in German cities. Sci. Total Environ. 2013, 442, 123–133. [Google Scholar] [CrossRef] [PubMed]
- Schweighofer, J.A.V.; Wehrl, M.; Baumgärtel, S.; Rohn, J. Detecting Groundwater Temperature Shifts of a Subsurface Urban Heat Island in SE Germany. Water 2021, 13, 1417. [Google Scholar] [CrossRef]
- Tissen, C.; Benz, S.A.; Menberg, K.; Bayer, P.; Blum, P. Groundwater temperature anomalies in central Europe. Environ. Res. Lett. 2019, 14, 104012. [Google Scholar] [CrossRef]
- Zhu, K.; Bayer, P.; Grathwohl, P.; Blum, P. Groundwater temperature evolution in the subsurface urban heat island of Cologne, Germany. Hydrol. Process. 2015, 29, 965–978. [Google Scholar] [CrossRef]
- Vienken, T.; Händel, F.; Epting, J.; Dietrich, P.; Liedl, R.; Huggenberger, P. Energiewende braucht Wärmewende–Chancen und Limitierungen der intensiven thermischen Nutzung des oberflächennahen Untergrundes in urbanen Gebieten vor dem Hintergrund der aktuellen Energiedebatte in Deutschland. Grundwasser 2016, 21, 69–73. [Google Scholar] [CrossRef]
- Hähnlein, S.; Molina-Giraldo, N.; Blum, P.; Bayer, P.; Grathwohl, P. Ausbreitung von Kältefahnen im Grundwasser bei Erdwärmesonden. Grundwasser 2010, 15, 123–133. [Google Scholar] [CrossRef]
- Steiner, C.; Heimlich, K.; Hilberg, S. Vergleichende Temperaturfahnenprognose anhand zweier industriell genutzter Grundwasserwärmepumpen: FEFLOW vs. ÖWAV-Modell. Grundwasser 2016, 21, 173–185. [Google Scholar] [CrossRef]
- Vienken, T.; Kreck, M.; Dietrich, P. Monitoring the impact of intensive shallow geothermal energy use on groundwater temperatures in a residential neighborhood. Geotherm. Energy 2019, 7, 8. [Google Scholar] [CrossRef]
- Fuji, H.; Tsuya, S.; Harada, R.; Kosukegawa, H. Field Test of Horizontal Ground Heat Exchangers Installed Using Horizontal Directional Drilling Technology. In Proceedings of the 44th Workshop on Geothermal Reservoir Engineering, Stanford, CA, USA, 11–13 February 2019. [Google Scholar]
- Fuji, H.; Yamasaki, S.; Maehara, T. Numerical modeling of slinky-coil horizontal ground heat exchangers considering snow coverage effects. In Proceedings of the Thirty-Eighth Workshop on Geothermal Reservoir Engineering, Stanford, CA, USA, 11–13 February 2013. [Google Scholar]
- Ramming, K. Bewertung und Optimierung Oberflächennaher Erdwärmekollektoren für Verschiedene Lastfälle. Ph.D. Thesis, Technische Universität Dresden, Dresden, Germany, 2007. [Google Scholar]
- Sangi, R.; Müller, D. Dynamic modelling and simulation of a slinky-coil horizontal ground heat exchanger using Modelica. J. Build. Eng. 2018, 16, 159–168. [Google Scholar] [CrossRef]
- Selamat, S.; Miyara, A.; Kariya, K. Analysis of Short Time Period of Operation of Horizontal Ground Heat Exchangers. Resources 2015, 4, 507–523. [Google Scholar] [CrossRef]
- Wu, Y.; Gan, G.; Verhoef, A.; Vidale, P.L.; Gonzalez, R.G. Experimental measurement and numerical simulation of horizontal-coupled slinky ground source heat exchangers. Appl. Therm. Eng. 2010, 30, 2574–2583. [Google Scholar] [CrossRef]
- Zeh, R.; Ohlsen, B.; Philipp, D.; Bertermann, D.; Kotz, T.; Jocic, N.; Stockinger, V. Large-Scale Geothermal Collector Systems for 5th Generation District Heating and Cooling Networks. Sustainability 2021, 13, 6035. [Google Scholar] [CrossRef]
- Arning, E.; Kölling, M.; Schulz, H.D.; Panteleit, B.; Reichling, J. Einfluss oberflächennaher Wärmegewinnung auf geochemische Prozesse im Grundwasserleiter. Grundwasser 2006, 11, 27–39. [Google Scholar] [CrossRef]
- Bonte, M.; van Breukelen, B.M.; Stuyfzand, P.J. Temperature-induced impacts on groundwater quality and arsenic mobility in anoxic aquifer sediments used for both drinking water and shallow geothermal energy production. Water Res. 2013, 47, 5088–5100. [Google Scholar] [CrossRef]
- Brielmann, H.; Lueders, T.; Schreglmann, K.; Ferraro, F.; Avramov, M.; Hammerl, V.; Blum, P.; Bayer, P.; Griebler, C. Oberflächennahe Geothermie und ihre potenziellen Auswirkungen auf Grundwasserökosysteme. Grundwasser 2011, 16, 77–91. [Google Scholar] [CrossRef]
- Griebler, C.; Brielmann, H.; Haberer, C.; Kaschuba, S.; Kellermann, C.; Stumpp, C.; Hegler, F.; Kuntz, D.; Walker-Hertkorn, S.; Lueders, T. Potential impacts of geothermal energy use and storage of heat on groundwater quality, biodiversity, and ecosystem processes. Environ. Earth Sci. 2016, 75, 1391. [Google Scholar] [CrossRef]
- VDI. VDI 4640 Part 1. Thermal Use of the Underground Fundamentals, Approvals, Environmental Aspects; Beuth Verlag GmbH: Berlin, Germany, 2010. [Google Scholar]
- Hähnlein, S.; Bayer, P.; Ferguson, G.; Blum, P. Sustainability and policy for the thermal use of shallow geothermal energy. Energy Policy 2013, 59, 914–925. [Google Scholar] [CrossRef]
- Börner, F.; Berthold, S. Vertical flows in groundwater monitoring wells. In Groundwater Geophysics; Kirsch, R., Ed.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 367–389. [Google Scholar]
- Church, P.E.; Granato, G.E. Bias in Ground-Water Data Caused by Well-Bore Flow in Long-Screen Wells. Groundwater 1996, 34, 262–273. [Google Scholar] [CrossRef]
- Elçi, A.; Flach, G.; Molz, F. Detrimental Effects of Natural Vertical Head Gradients on Chemical and Water Level Measurements in Observation Wells: Identification and Control. J. Hydrol. 2003, 281, 70–81. [Google Scholar] [CrossRef]
- Berthold, S.; Börner, F. Detection of free vertical convection and double-diffusion in groundwater monitoring wells with geophysical borehole measurements. Environ. Geol. 2008, 54, 1547–1566. [Google Scholar] [CrossRef]
- Diment, W.H. Thermal Regime of a Large Diameter Borehole: Instability Of The Water Column And Comparison Of Air- And Water-filled Conditions. Geophysics 1967, 32, 720–726. [Google Scholar] [CrossRef]
- Krige, L.J. Borehole temperatures in the Transvaal and Orange Free State. Proc. R. Soc. Lond. 1939, 173, 450–474. [Google Scholar] [CrossRef][Green Version]
- Sammel, E.A. Convective flow and its effect on temperature logging in small-diameter wells. Geophysics 1968, 33, 1004–1012. [Google Scholar] [CrossRef]
- Rayleigh, L. LIX. On convection currents in a horizontal layer of fluid, when the higher temperature is on the under side. Lond. Edinb. Philos. Mag. J. Sci. 1916, 32, 529–546. [Google Scholar] [CrossRef]
- Gershuni, G.Z.; Zhukhovitskii, E.M. Convective Stability of Incompressible Fluids; Keter Publishing House Jerusalem Ltd.: Jerusalem, Israel, 1976. [Google Scholar]
- Berthold, S.; Resagk, C. Investigation of thermal convection in water columns using particle image velocimetry. Exp. Fluids 2012, 52, 1465–1474. [Google Scholar] [CrossRef]
- Eppelbaum, L.; Kutasov, i. Estimation of the effect of thermal convection and casing on the temperature regime of boreholes: A review. J. Geophys. Eng. 2011, 8, R1–R10. [Google Scholar] [CrossRef]
- Kümmerle, E. Geologische Karte von Hessen 1:25,000 5618 Friedberg; Hessisches Landesamt Für Bodenforschung: Wiesbaden, Germany, 1976. [Google Scholar]
- Hölting, B.; Coldewey, W.G. Hydrogeology, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2019; p. 357. [Google Scholar]
- Kümmerle, E. Erläuterungen zur Geologischen Karte von Hessen 1:25,000: Blatt Nr. 5618 Friedberg; Hessisches Landesamt für Bodenforschung: Wiesbaden, Germany, 1976; p. 247. [Google Scholar]
- Kurylyk, B.; Macquarrie, K.; Caissie, D.; McKenzie, J. Shallow groundwater thermal sensitivity to climate change and land cover disturbances: Derivation of analytical expressions and implications for stream temperature modeling. Hydrol. Earth Syst. Sci. 2015, 19, 2469–2489. [Google Scholar] [CrossRef]
- Schäffer, R.; Sass, I. Ausbreitung und Vermischung geogener, kohlendioxidführender Thermalsole in oberflächennahem Grundwasser, Bad Nauheim. Grundwasser 2016, 21, 305–319. [Google Scholar] [CrossRef]
- Chen, W.; Bense, V. Using transient temperature–depth profiles to assess vertical groundwater flow across semi-confining layers in the Chianan coastal plain aquifer system, southern Taiwan. Hydrogeol. J. 2019, 27, 2155–2166. [Google Scholar] [CrossRef]
- Constantz, J.; Tyler, S.W.; Kwicklis, E. Temperature-Profile Methods for Estimating Percolation Rates in Arid Environments. Vadose Zone J. 2003, 2, 12–24. [Google Scholar] [CrossRef]
- Taniguchi, M. Estimated Recharge Rates from Groundwater Temperatures In The Nara Basin, Japan. Appl. Hydrogeol. 1994, 2, 7–14. [Google Scholar] [CrossRef]
- Taniguchi, M.; Turner, J.V.; Smith, A.J. Evaluations of groundwater discharge rates from subsurface temperature in Cockburn Sound, Western Australia. Biogeochemistry 2003, 66, 111–124. [Google Scholar] [CrossRef]
- Doussan, C.; Toma, A.; Poitevin, G.; Ledoux, E.; Detay, M. Coupled use of thermal and hydraulic head data to characterize river-groundwater exchanges. J. Hydrol. 1994, 153, 215–229. [Google Scholar] [CrossRef]
- Hunt, R.J.; Krabbenhoft, D.P.; Anderson, M.P. Groundwater inflow measurements in wetland systems. Water Resour. Res. 1996, 32, 495–507. [Google Scholar] [CrossRef]
- Land, L.A.; Paull, C.K. Thermal gradients as a tool for estimating groundwater advective rates in a coastal estuary: White Oak River, North Carolina, USA. J. Hydrol. 2001, 248, 198–215. [Google Scholar] [CrossRef]





| Diameter of MW [mm] | 5 °C | 10 °C | 15 °C | 20 °C | 25 °C | 30 °C |
|---|---|---|---|---|---|---|
| 25 | 11.02 | 1.26 | 0.64 | 0.42 | 0.31 | 0.24 |
| 50 | 0.69 | 0.08 | 0.04 | 0.03 | 0.02 | 0.01 |
| 80 | 0.11 | 0.01 | 0.01 | <0.01 | <0.01 | <0.01 |
| 100 | 0.0 | <0.01 | <0.01 | <0,01 | <0.01 | <0.01 |
| 125 | 0.02 | <0.01 | <0.01 | <0,01 | <0.01 | <0.01 |
| Borehole | Elevation [m a. s. l.] | Depth MW [m b. g. l] | Depth TMS [m b. g. l.] | Well Screen [m b. g. l] | Loam [m b. g. l.] | Gravel [m b. g. l.] | Permeable Basalt [m b. g. l.] |
|---|---|---|---|---|---|---|---|
| B1 | 142.5 | 10.1 | 10.4 | 6.1–10.1 | 0.8–6.4 | 6.4–8.5 | 10.0–10.5 |
| B2 | 141.3 | 10.0 | 10.3 | 6.0–10.0 | 0.8–4.6 | 4.6–7.3 | - |
| B3 | 139.9 | 8.1 | 10.4 | 4.1–8.1 | 0.8–4.1 | 4.1–6.2 | 6.7–10.5 |
| B4 | 139.5 | 10.0 | 10.3 | 5.0–10.0 | 1.3–3.5 | 3.5–7.8 | - |
| B5 | 139.2 | 10.1 | 10.3 | 5.1–10.1 | 0.8–3.3 | 3.3–5.8 | 6.9–10.4 |
| B6 | 138.7 | 6.0 | 10.3 | 4.0–6.0 | 0.3–3.1 | 3.1–5.5 | 8.1–10.5 |
| z | B1 | B2 | B3 | B4 | B5 | B6 | Total | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| r | Gt | r | Gt | r | Gt | r | Gt | r | Gt | r | Gt | r | Gt | |
| 0.0 | 0.0 | - | 0.2 | - | 0.9 | 0.3 | 0.5 | 0.2 | 0.6 | 0.2 | 0.7 | 0.4 | 0.5 | 0.3 |
| 0.5 | 0.6 | 0.3 | 0.5 | 0.3 | 1.0 | 0.4 | 0.8 | 0.3 | 0.7 | 0.3 | 0.8 | 0.2 | 0.7 | 0.3 |
| 1.0 | 0.7 | 0.3 | 0.6 | 0.3 | 0.9 | 0.5 | 0.9 | 0.5 | 0.9 | 0.4 | 0.3 | - | 0.7 | 0.4 |
| 1.5 | 0.7 | 0.3 | −0.2 | - | 0.9 | 0.8 | 0.8 | 0.5 | 0.5 | 0.5 | 0.3 | - | 0.7 | 0.4 |
| Benefit of Specific Well Casing | MW | PM | TMS | MW/TMS |
|---|---|---|---|---|
| groundwater level | + | + | − | + |
| temperature in unsaturated zone | − | − | + | + |
| continuous temperatures with data logger | + | −/+ | + | + |
| minimised natural convection | − | + | + | + |
| no forced convection | − | −/+ | + | + |
| pumping tests or other hydraulic tests | + | − | − | + |
| groundwater sampling | + | − | − | + |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bertermann, D.; Rammler, M. Suitability of Screened Monitoring Wells for Temperature Measurements Regarding Large-Scale Geothermal Collector Systems. Geosciences 2022, 12, 162. https://doi.org/10.3390/geosciences12040162
Bertermann D, Rammler M. Suitability of Screened Monitoring Wells for Temperature Measurements Regarding Large-Scale Geothermal Collector Systems. Geosciences. 2022; 12(4):162. https://doi.org/10.3390/geosciences12040162
Chicago/Turabian StyleBertermann, David, and Mario Rammler. 2022. "Suitability of Screened Monitoring Wells for Temperature Measurements Regarding Large-Scale Geothermal Collector Systems" Geosciences 12, no. 4: 162. https://doi.org/10.3390/geosciences12040162
APA StyleBertermann, D., & Rammler, M. (2022). Suitability of Screened Monitoring Wells for Temperature Measurements Regarding Large-Scale Geothermal Collector Systems. Geosciences, 12(4), 162. https://doi.org/10.3390/geosciences12040162







