Analysis of HVSR Data Using a Modified Centroid-Based Algorithm for Near-Surface Geological Reconstruction
Abstract
1. Introduction
2. Materials and Methods
3. Results
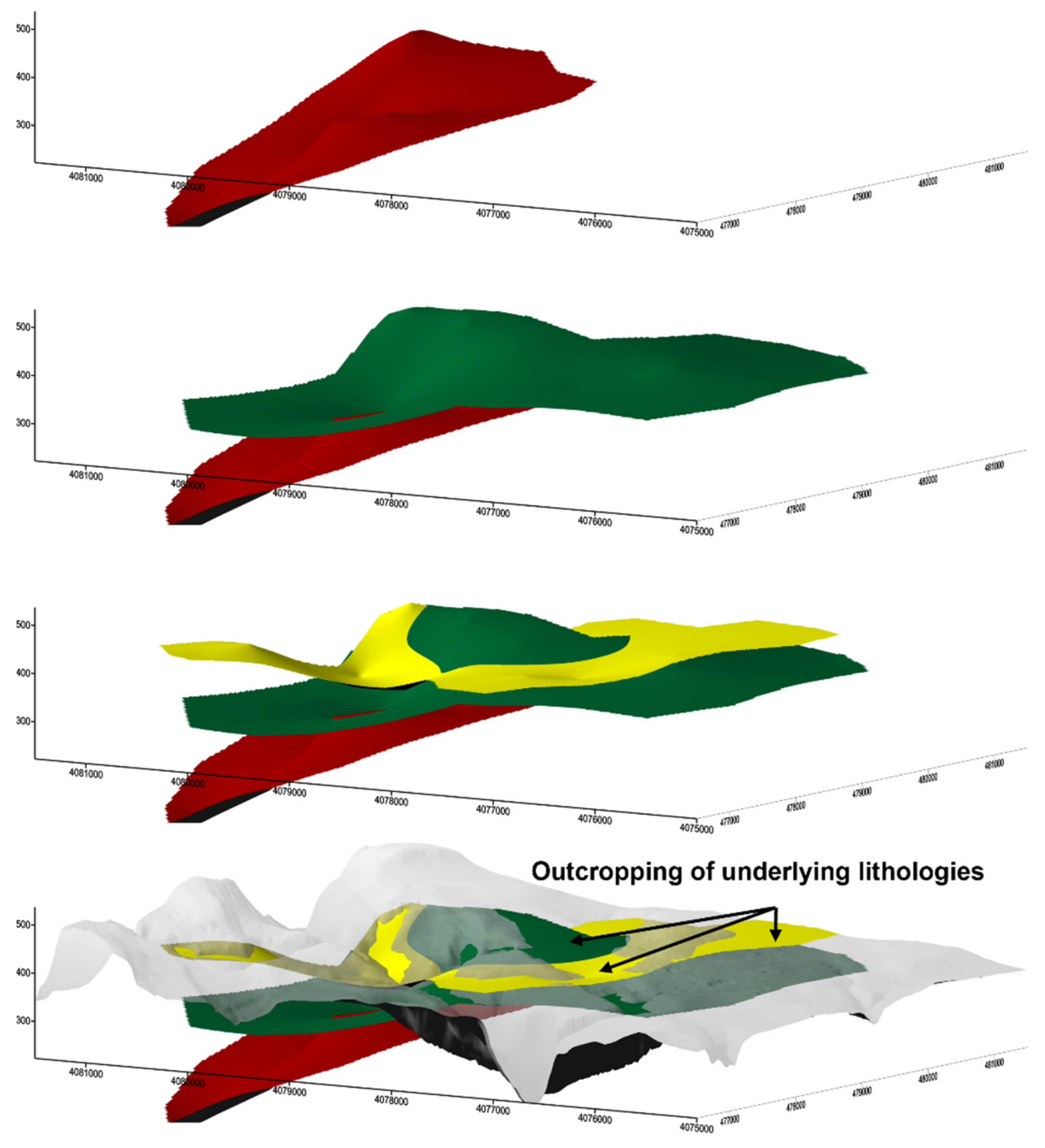
3.1. Geological Outlines
3.2. Application of the HVSR Technique to Microtremor Measurements
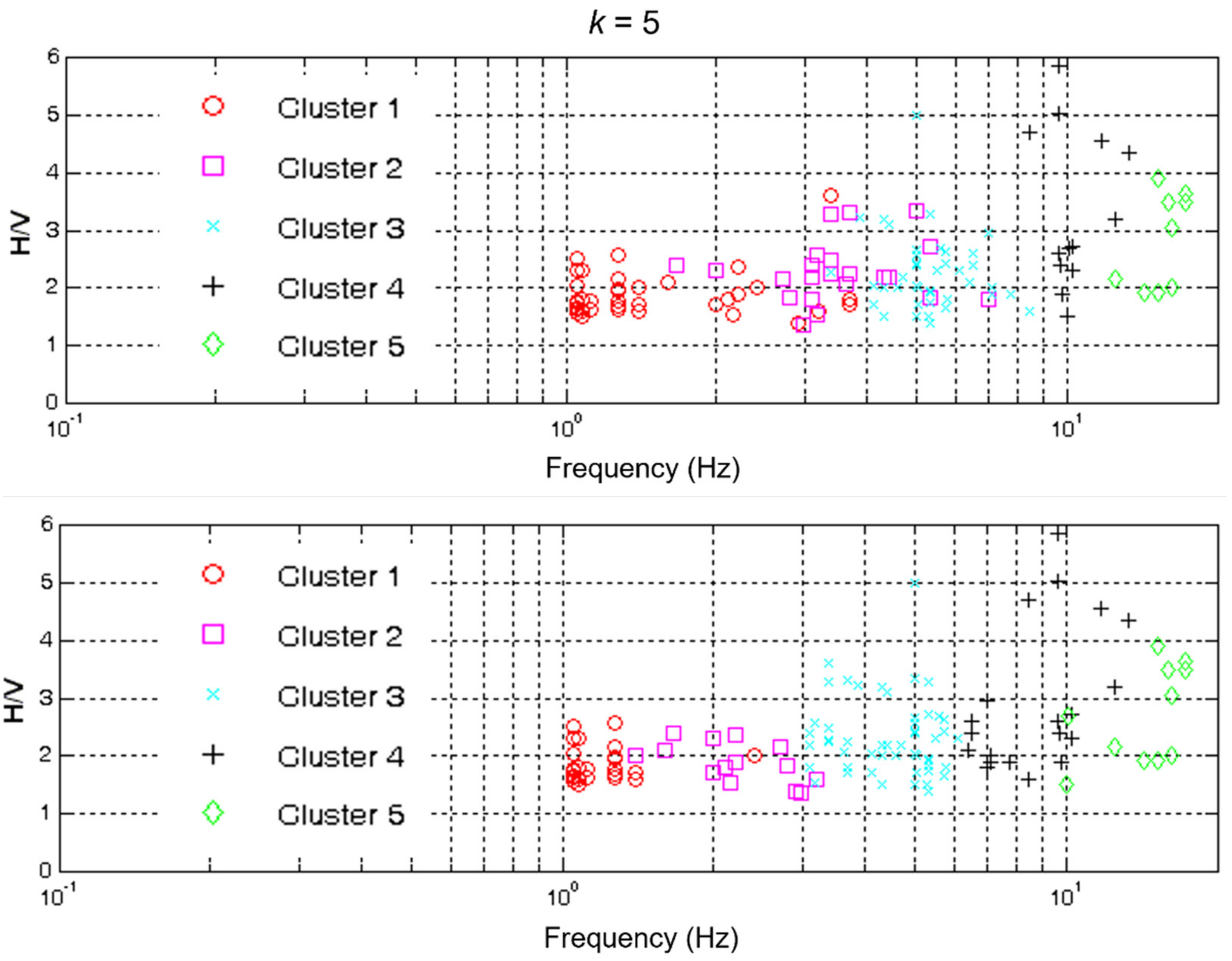
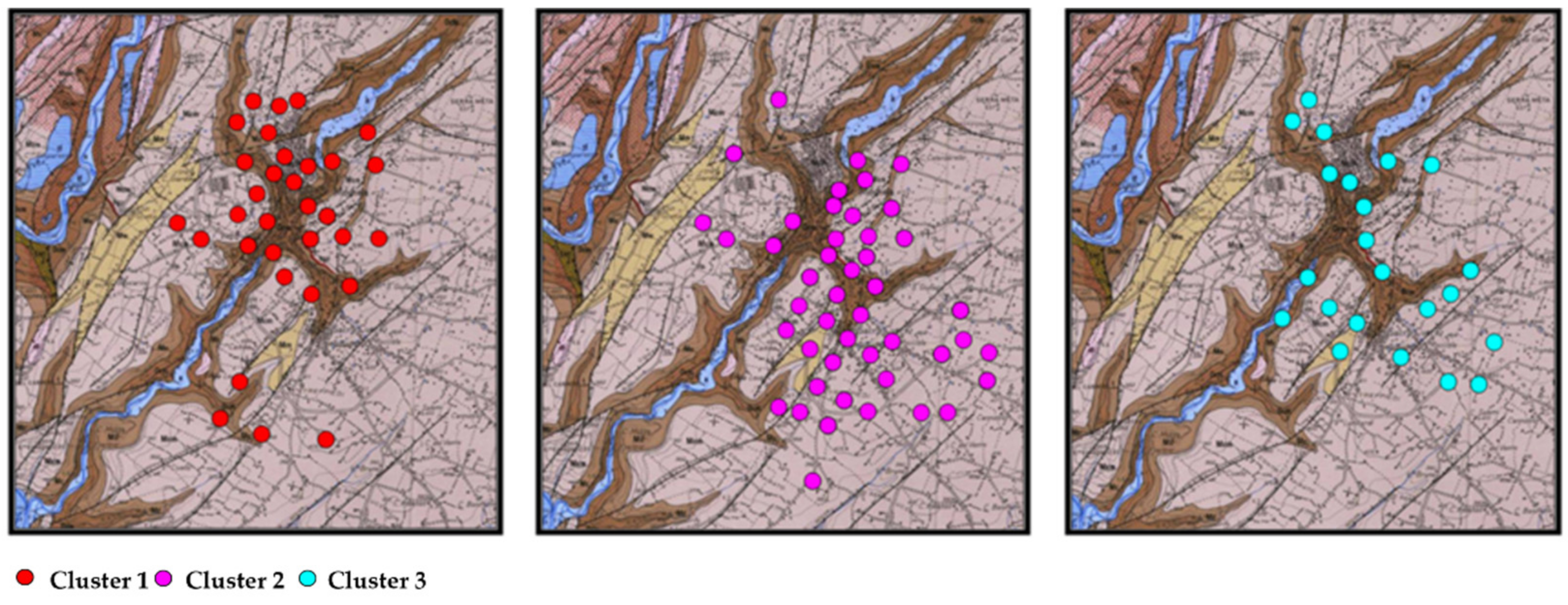
3.3. Cluster Analysis of the H/V Peaks
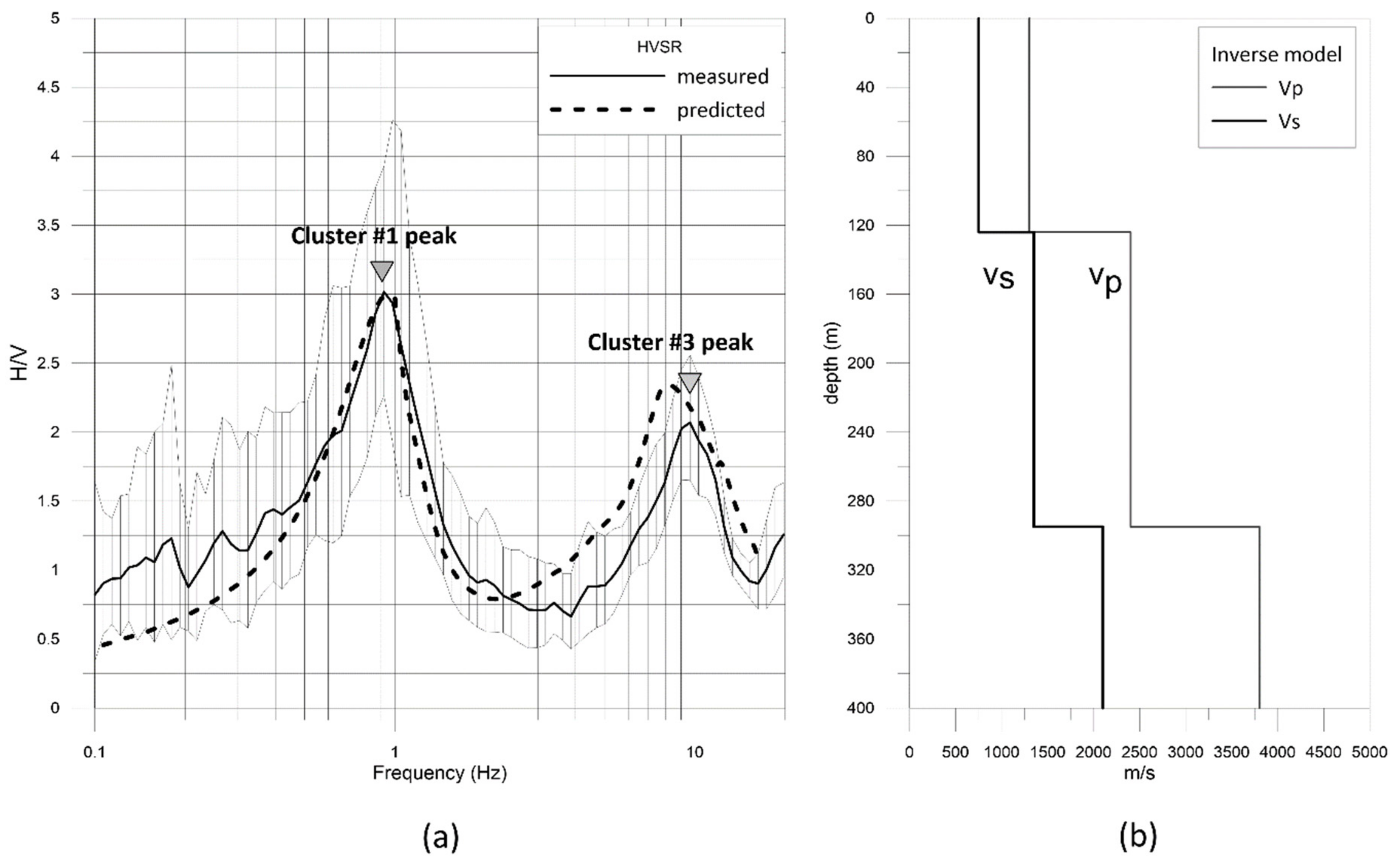
3.4. Seismo-Stratigraphic Modeling
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Nakamura, Y. Method for dynamic characteristics estimation of subsurface using microtremor on the ground surface. Q. Rep. RTRI Railw. Tech. Res. Inst. 1989, 30, 25–33. [Google Scholar]
- Nakamura, Y. Clear Identification of Fundamental Idea of Nakamura’s Technique and its Applications. In Proceedings of the 12th World Conference on Earthquake Engineering, Auckland, New Zealand, 30 January–4 February 2000; p. 2656. [Google Scholar]
- Nakamura, Y. What Is the Nakamura Method? Seismol. Res. Lett. 2019, 90, 1437–1443. [Google Scholar] [CrossRef]
- Lachet, C.; Bard, P.Y. Numerical and theoretical investigations on the possibilities and limitations of Nakamura’s technique. J. Phys. Earth 1994, 42, 377–397. [Google Scholar] [CrossRef]
- Kudo, K. Practical estimates of site response. State-of-art report. In Proceedings of the 5th International Conference on Seismic Zonation, Nice, France, 17–19 October 1995. [Google Scholar]
- Bard, P.Y. Microtremor measurements: A tool for site effect estimation? In Proceedings of the 2nd International Symposium on the Effects of Surface Geology on Seismic Motion, Yokohama, Japan, 1–3 December 1998; pp. 1251–1279. [Google Scholar]
- Mucciarelli, M.; Gallipoli, M.R.; Arcieri, M. The stability of the horizontal-to-vertical spectral ratio of triggered noise and earthquake recordings. Bull. Seismol. Soc. Am. 2003, 93, 1407–1412. [Google Scholar] [CrossRef]
- Bonnefoy-Claudet, S.; Cotton, F.; Bard, P.-Y. The nature of noise wavefield and its applications for site effects studies. A literature review. Earth Sci. Rev. 2006, 79, 205–227. [Google Scholar] [CrossRef]
- Ibs-von Seht, M.; Wohlenberg, J. Microtremor measurements used to map thickness of soft sediments. Bull. Seismol. Soc. Am. 1999, 89, 250–259. [Google Scholar] [CrossRef]
- Bignardi, S.; Yezzi, A.J.; Fiussello, S.; Comelli, A. OpenHVSR—Processing toolkit: Enhanced HVSR processing of distributed microtremor measurements and spatial variation of their informative content. Comput. Geosci. 2018, 120, 10–20. [Google Scholar] [CrossRef]
- D’Alessandro, A.; Luzio, D.; Martorana, R.; Capizzi, P. Selection of time windows in the Horizontal to Vertical Noise Spectral Ratio by means of cluster analysis. Bull. Seismol. Soc. Am. 2016, 106, 560–574. [Google Scholar] [CrossRef]
- Rodriguez, V.H.S.; Midorikawa, S. Applicability of the H/V spectral ratio of microtremors in assessing site effects on seismic motion. Earthq. Eng. Struct. Dyn. 2002, 31, 261–279. [Google Scholar] [CrossRef]
- Martorana, R.; Capizzi, P.; Avellone, G.; Siragusa, R.; D’Alessandro, A.; Luzio, D. Assessment of a geological model by surface wave analyses. J. Geophys. Eng. 2017, 14, 159–172. [Google Scholar] [CrossRef]
- Martorana, R.; Agate, M.; Capizzi, P.; Cavera, F.; D’Alessandro, A. Seismo-stratigraphic model of “La Bandita” area (Palermo Plain, Sicily) through HVSR inversion constrained by stratigraphic data. Ital. J. Geosci. 2018, 137, 73–86. [Google Scholar] [CrossRef]
- Fäh, D.; Kind, F.; Giardini, D. Inversion of local S wave velocity structures from average H/V ratios, and their use for the estimation of site-effects. J. Seismol. 2003, 7, 449–467. [Google Scholar] [CrossRef]
- Picotti, S.; Francese, R.; Giorgi, M.; Pettenati, F.; Carcione, J.M. Estimation of glaciers thicknesses and basal properties using the horizontal-to-vertical component spectral ratio (HVSR) technique from passive seismic data. J. Glaciol. 2017, 63, 229–248. [Google Scholar] [CrossRef]
- Martorana, R.; Capizzi, P.; D’Alessandro, A.; Luzio, D.; Di Stefano, P.; Renda, P.; Zarcone, G. Contribution of HVSR measures for seismic microzonation studies. Ann. Geophys. 2018, 61, SE225. [Google Scholar] [CrossRef]
- Konno, K.; Ohmachi, T. Ground-motion characteristics estimated from spectral ratio between horizontal and vertical components of microtremor. Bull. Seismol. Soc. Am. 1998, 88, 228–241. [Google Scholar] [CrossRef]
- Parolai, S.; Bindi, D.; Augliera, P. Application of the Generalized Inversion Technique (GIT) to a microzonation study: Numerical simulations and comparison with different site-estimation techniques. Bull. Seismol. Soc. Am. 2000, 90, 286–297. [Google Scholar] [CrossRef]
- Fäh, D.; Kind, F.; Giardini, D. A theoretical investigation of average H/V ratios. Geophys. J. Int. 2001, 145, 535–549. [Google Scholar] [CrossRef]
- Bignardi, S. The uncertainty of estimating the thickness of soft sediments with the HVSR method: A computational point of view on weak lateral variations. J. Appl. Geophy. 2017, 145, 28–38. [Google Scholar] [CrossRef]
- Scherbaum, F.; Hinzen, K.-G.; Ohrnberger, M. Determination of shallow shear-wave velocity profiles in Cologne, Germany area using ambient vibrations. Geophys. J. Int. 2003, 152, 597–612. [Google Scholar] [CrossRef]
- Arai, H.; Tokimatsu, K. S-wave velocity profiling by inversion of microtremor H/V spectrum. Bull. Seismol. Soc. Am. 2004, 94, 53–63. [Google Scholar] [CrossRef]
- Parolai, S.; Picozzi, M.; Richwalski, S.M.; Milkereit, C. Joint inversion of phase velocity dispersion and H/V ratio curves from seismic noise recordings using a genetic algorithm, considering higher modes. Geophys. Res. Lett. 2005, 32, L01303. [Google Scholar] [CrossRef]
- Parolai, S.; Richwalski, S.M.; Milkereit, C.; Fäh, D. S-wave velocity profiles for earthquake engineering purposes for the Cologne Area (Germany). Bull. Earthq. Eng. 2006, 4, 65–94. [Google Scholar] [CrossRef]
- Picozzi, M.; Parolai, S.; Richwalski, S.M. Joint inversion of H/V ratios and dispersion curves from seismic noise: Estimating the S-wave velocity of bedrock. Geophys. Res. Lett. 2005, 32, L11308. [Google Scholar] [CrossRef]
- Imposa, S.; Grassi, S.; De Guidi, G.; Battaglia, F.; Lanaia, G.; Scudero, S. 3D subsoil model of the San Biagio ‘Salinelle’ mud volcanoes (Belpasso, SICILY) derived from geophysical surveys. Surv. Geophys. 2016, 37, 1117–1138. [Google Scholar] [CrossRef]
- Imposa, S.; Grassi, S.; Fazio, F.; Rannisi, G.; Cino, P. Geophysical surveys to study a landslide body (north-eastern Sicily). Nat. Hazards 2017, 86, 327–343. [Google Scholar] [CrossRef]
- Zor, E.; Özalaybey, S.; Karaaslan, A.; Tapirdamaz, M.C.; Özalaybey, S.Ç.; Tarancioglu, A.; Erkan, B. Shear wave velocity structure of the Izmit Bay area (Turkey) estimated from active-passive array surface wave and single-station microtremor methods. Geophys. J. Int. 2010, 182, 1603–1618. [Google Scholar] [CrossRef]
- Capizzi, P.; Martorana, R. Integration of constrained electrical and seismic tomographies to study the landslide affecting the Cathedral of Agrigento. J. Geophys. Eng. 2014, 11, 045009. [Google Scholar] [CrossRef]
- Castellaro, S. The complementarity of H/V and dispersion curves. Geophysics 2016, 81, T323–T338. [Google Scholar] [CrossRef]
- Panzera, F.; Sicali, S.; Lombardo, G.; Imposa, S.; Gresta, S.; D’Amico, S. A microtremor survey to define the subsoil structure in a mud volcanoes area: The case study of Salinelle (Mt. Etna, Italy). Environ. Earth Sci. 2016, 75, 1140. [Google Scholar] [CrossRef]
- Capizzi, P.; Martorana, R.; Stassi, G.; D’Alessandro, A.; Luzio, D. Centroid-based cluster analysis of HVSR data for seismic microzonation. In Proceedings of the Near Surface Geoscience 2014—20th European Meeting of Environmental and Engineering Geophysics, Athens, Greece, 14–18 September 2014. [Google Scholar] [CrossRef]
- Hartigan, J.A. Clustering Algorithms; Wiley: New York, NY, USA, 1975. [Google Scholar]
- Adelfio, G.; Chiodi, M.; D’Alessandro, A.; Luzio, D.; D’Anna, G.; Mangano, G. Simultaneous seismic wave clustering and registration. Comput. Geosci. 2012, 44, 60–69. [Google Scholar] [CrossRef]
- D’Alessandro, A.; Mangano, G.; D’Anna, G.; Luzio, D. Waveforms clustering and single-station location of microearthquake multiplets recorded in the northern Sicilian offshore region. Geophys. J. Int. 2013, 194, 1789–1809. [Google Scholar] [CrossRef][Green Version]
- Gan, G.; Ma, C.; Wu, J. Data Clustering: Theory, Algorithms, and Applications; Cambridge University Press: Cambridge, UK, 2007; p. 184. ISBN 9780898716238. [Google Scholar]
- Everitt, B.S.; Landau, S.; Leese, M.; Stahl, D. Cluster Analysis, 5th ed.; Wiley Series in Probability and Statistics; John Wiley & Sons, Ltd.: London, UK, 2011; p. 332, ISBN-10 0470749911, ISBN-13 978-0470749913. [Google Scholar]
- Rand, W.M. Objective criteria for the evaluation of clustering methods. J. Am. Stat. Assoc. 1971, 66, 846–850. [Google Scholar] [CrossRef]
- Everitt, B.S. Unresolved problems in cluster analysis. Biometrics 1979, 35, 169–181. [Google Scholar] [CrossRef]
- Ohsumi, N. Evaluation procedure of agglomerative hierarchical clustering methods by fuzzy relations. In Data Analysis and Informatics: Proceedings of the II International Symposium on Data Analysis and Informatics, Versailles, France, 17–19 October 1979; Tomassone, R., Pagès, J.P., Lebart, L., Diday, E., Eds.; North Holland Publishing Company: Amsterdam, The Netherlands, 1980. [Google Scholar]
- Silvestri, L.; Hill, I.R. Some problems of the taxometric approach. In Phenetic and Phylogenetic Classification; Heywood, V.H., Mc Neil, J., Eds.; Systematic Association: London, UK, 1964. [Google Scholar]
- McQueen, J. Some methods for classification and analysis of multivariate observations. In Proceedings of the 5-th Berkeley Symposium on Mathematical Statistics and Probability, Volume 1: Statistics, Los Angeles, CA, USA, 21 June–18 July 1965; 27 December 1965–7 January 1966; Le Cam, L.M., Neyman, J., Eds.; The Regents of the University of California: Los Angeles, CA, USA, 1967; pp. 281–297. [Google Scholar]
- Grasso, M.; Reuther, C.D. The western margin of the Hyblean Plateau: A neotectonic transform system on the S.E. Sicilian foreland. Ann. Tecton. 1988, 2, 107–120. [Google Scholar]
- Grasso, M.; Lickorish, W.H.; Diliberto, S.E.; Geremia, F.; Maniscalco, R.; Maugeri, S.; Pappalardo, G.; Rapisarda, F.; Scamarda, G. Carta Geologica Della Struttura a Pieghe di Licata (Sicilia Centro-Meridionale). Scala 1:50.000; Tipografia SELCA: Florence, Italy, 1997. [Google Scholar]
- SESAME Project. Guidelines for the Implementation of the H/V Spectral Ratio Technique on Ambient Vibrations. Measurements, Processing and Interpretation, SESAME European Research Project WP12—Deliverable D23.12, December 2004. Available online: http://sesame.geopsy.org/Papers/HV_User_Guidelines.pdf (accessed on 27 February 2022).
- Park, C.B.; Miller, R.D.; Xia, J. Multichannel analysis of surface waves. Geophysics 1999, 64, 800–808. [Google Scholar] [CrossRef]
- Wathelet, M.; Jongmans, D.; Ohrnberger, M. Surface-wave inversion using a direct search algorithm and its application to ambient vibration measurements. Near Surf. Geophys. 2004, 2, 211–221. [Google Scholar] [CrossRef]




| Weight Set # | Location Weight a | Frequency Weight b | Amplitude Weight c | Lithology Weight d |
|---|---|---|---|---|
1  | 0.6 | 0.2 | 0.15 | 0.05 |
2  | 0.55 | 0.25 | 0.15 | 0.05 |
3  | 0.5 | 0.3 | 0.15 | 0.05 |
4  | 0.45 | 0.35 | 0.15 | 0.05 |
5  | 0.4 | 0.4 | 0.15 | 0.05 |
6  | 0.35 | 0.45 | 0.15 | 0.05 |
7  | 0.3 | 0.5 | 0.15 | 0.05 |
8  | 0.25 | 0.55 | 0.15 | 0.05 |
9  | 0.2 | 0.6 | 0.15 | 0.05 |
| C1 | C2 | C3 | C4 | C5 | C6 | C7 | |
|---|---|---|---|---|---|---|---|
| k = 2 | 1.05 Hz | 17.35 Hz | |||||
| k = 3 | 1.05 Hz | 4.27 Hz | 17.35 Hz | ||||
| k = 4 | 1.05 Hz | 2.67 Hz | 6.81 Hz | 17.35 Hz | |||
| k = 5 | 1.05 Hz | 2.12 Hz | 4.27 Hz | 8.60 Hz | 17.35 Hz | ||
| k = 6 | 1.05 Hz | 1.84 Hz | 3.22 Hz | 5.65 Hz | 9.90 Hz | 17.35 Hz | |
| k = 7 | 1.05 Hz | 1.67 Hz | 2.67 Hz | 4.27 Hz | 6.81 Hz | 10.87 Hz | 17.35 Hz |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Capizzi, P.; Martorana, R. Analysis of HVSR Data Using a Modified Centroid-Based Algorithm for Near-Surface Geological Reconstruction. Geosciences 2022, 12, 147. https://doi.org/10.3390/geosciences12040147
Capizzi P, Martorana R. Analysis of HVSR Data Using a Modified Centroid-Based Algorithm for Near-Surface Geological Reconstruction. Geosciences. 2022; 12(4):147. https://doi.org/10.3390/geosciences12040147
Chicago/Turabian StyleCapizzi, Patrizia, and Raffaele Martorana. 2022. "Analysis of HVSR Data Using a Modified Centroid-Based Algorithm for Near-Surface Geological Reconstruction" Geosciences 12, no. 4: 147. https://doi.org/10.3390/geosciences12040147
APA StyleCapizzi, P., & Martorana, R. (2022). Analysis of HVSR Data Using a Modified Centroid-Based Algorithm for Near-Surface Geological Reconstruction. Geosciences, 12(4), 147. https://doi.org/10.3390/geosciences12040147







