Comparison between Calculation and Measurement of Total Sediment Load: Application to Streams of NE Greece

Abstract

Sediment transport and stream discharge are two of the natural procedures which affect the hydromorphological profile of a watercourse. Measurements of water discharge, bed load transport rate and suspended sediment concentration were conducted in Kosynthos River and Kimmeria Torrent –two intermittent streams– in north-eastern Greece. The total sediment concentration was calculated, in both streams, by means of various nonlinear regression equations and by means of the formulas of Yang, after calibrating the coefficients of the formulas. In the computations according to the Yang formulas, two different states were examined regarding the incipient motion: one considering and one disregarding the critical conditions. The results obtained from Yang’s multiple regression-derived equations had a better fit compared to the original equations and were acceptable in both cases. Ultimately, two counterparts of Yang’s stream sediment transport formulas were constructed and made available to the readership. The comparison between the calculated and measured total sediment concentrations was achieved by means of several statistical criteria. The results indicate that the modified formulas of Yang can be successfully used for the determination of the total sediment concentration in Kosynthos River and Kimmeria Torrent.

1. Introduction

One of the long-lasting problems hydraulic engineers are faced with is understanding and modeling the processes that govern sediment transport in streams. The difficulty in solving this problem lies in the complexity of the physical processes that describe it [1] and the variety of the types of the existing watercourses. On the other hand, sediment monitoring stations are very sparse, and hence the bulk of streams worldwide remains ungauged. In addition, the estimation of sediment discharge by conventional measurement methods is expensive and labor intensive, and therefore, alternative, less expensive approaches to predict their background processes are desirable [2,3].

Langbein and Iseri [4] introduced a classification of rivers as “perennial”, “intermittent” and “ephemeral”, based on their relation to time and seasonality. Perennial rivers have a continuous flow throughout the year, intermittent or seasonal rivers flow at specific wet seasons of the year when there are sufficient water resources, while the flow of ephemeral streams emanates only from surface runoff or snowmelt. Williamson et al. [5] took this one step further by developing a standardized protocol based not only on field-based procedures, but also on regionally calibrated hydrologic models, to classify ephemeral, intermittent, and perennial streams in the area of Kentucky, USA. Sefton et al. [6] created heat maps using spatial analysis in order to classify the hydrological state of headwaters of the Thames River basin in the UK.

Greece has big rivers (e.g., Evros, Nestos, and Strymonas) which drain the southern part of the Balkan Peninsula and convey large volumes of water and sediment. Situated, however, in the Mediterranean semi-arid climate zone, Greece is teeming with ephemeral streams in all regions of the country. There is a variety of watercourses which are characterized by the instability of flow conditions and hydrological fluctuations.

The scientific interest focuses on studying the sediment transport processes and monitoring, modeling and predicting the sediment loads. Apart from theory and modeling, sediment research has been focusing on creating sediment transport databases, either by conducting field measurements or by gathering data from the literature [7,8], in order to quantify the sediment transport of different types of streams. In this direction, the Section of Hydraulic Engineering, Civil Engineering Department, Democritus University of Thrace, has been conducting measurements of the bed load transport rate and suspended sediment concentration at the basin outlet of all three different types of rivers of north-eastern Greece, such as Nestos River (perennial), Kosynthos River, Kimmeria Torrent (intermittent) and a few ephemeral streams.

There is a great variety of sediment transport formulas which can be applied to watercourses, depending on the type of the stream, the hydraulic conditions and the available measurements. Apart from the well-known equations for sediment transport [9,10,11,12,13,14], there is a large number of formulas developed based on various natural rivers or laboratory flumes which can be applied in similar case studies [15].

The data-based calibrated formulas result from applying different types of regression depending on the type of the original formula. In that way, counterparts of established stream sediment formulas are constructed by minimizing the sum of square errors, using linear or nonlinear regression equations, or even by using fuzzy regression equations [8]. Regression analysis has been extensively employed in the literature to either derive sediment transport/concentration equations as a function of hydraulic or hydrometeorological parameters or to adjust existing well-known sediment transport models to environments with specific features different from the ones they were created for. Based on measured sediment data from the Yellow River, Wu et al. [16] modified Yang’s (1996) model [17] by means of regression analysis, resulting in an equation form similar to Yang’s (1979) model [18]. Baniya et al. [19] derived a nonlinear regression equation for annual suspended sediment yield as a function of flow discharge for Kali Gandaki River in Nepal. Ulke et al. [20] satisfactorily generated daily suspended sediment load data for a missing record period in Gediz River in Turkey by means of multiple linear and nonlinear regressions using the discharge and precipitation of the target day and one day prior to the target day as predictors.

Nonlinear regression equations between bed load transport rate and stream flow rate, as well as between suspended load transport rate and stream flow rate have been established for the outlets of Nestos River basin [21], Kosynthos River basin [22,23] and Kimmeria Torrent basin [23]. Based on the available data for each basin, various polynomial, exponential and hyperbolic regression curves were derived in order to estimate bed load, suspended load and total load transport rates. Metallinos and Hrissanthou [23] used nonlinear regression equations to determine the sediment transport of a stream as a function of hydrologic parameters, such as stream discharge, rainfall depth and rainfall intensity.

Avgeris et al. [24] applied Yang’s formulas, a hydraulic approach to the problem of sediment transport, in which the leading parameter is the unit stream power. In the present study, Yang’s formulas are also used, as they are best implemented in this type of available datum. The objective of this study is to redetermine the arithmetic coefficients of the total sediment transport rate formulas of Yang based on field data of Kosynthos River and Kimmeria Torrent, using multiple regressions, and thus create modified equations that will provide substantially more accurate calculations of sediment concentration in these streams. This research also aspires to highlight the significance of customizing and adapting well-established sediment formulas to the specific morphological and flow conditions of rivers and streams. This could effectively tackle the problem of sediment data scarcity.

The results emerging from sediment transport formulas usually differ drastically from each other and from the measured data. Consequently, none of the published sediment transport formulas has gained universal acceptance for confidently predicting sediment transport rates, especially in natural rivers [25].

2. Description of the Study Area

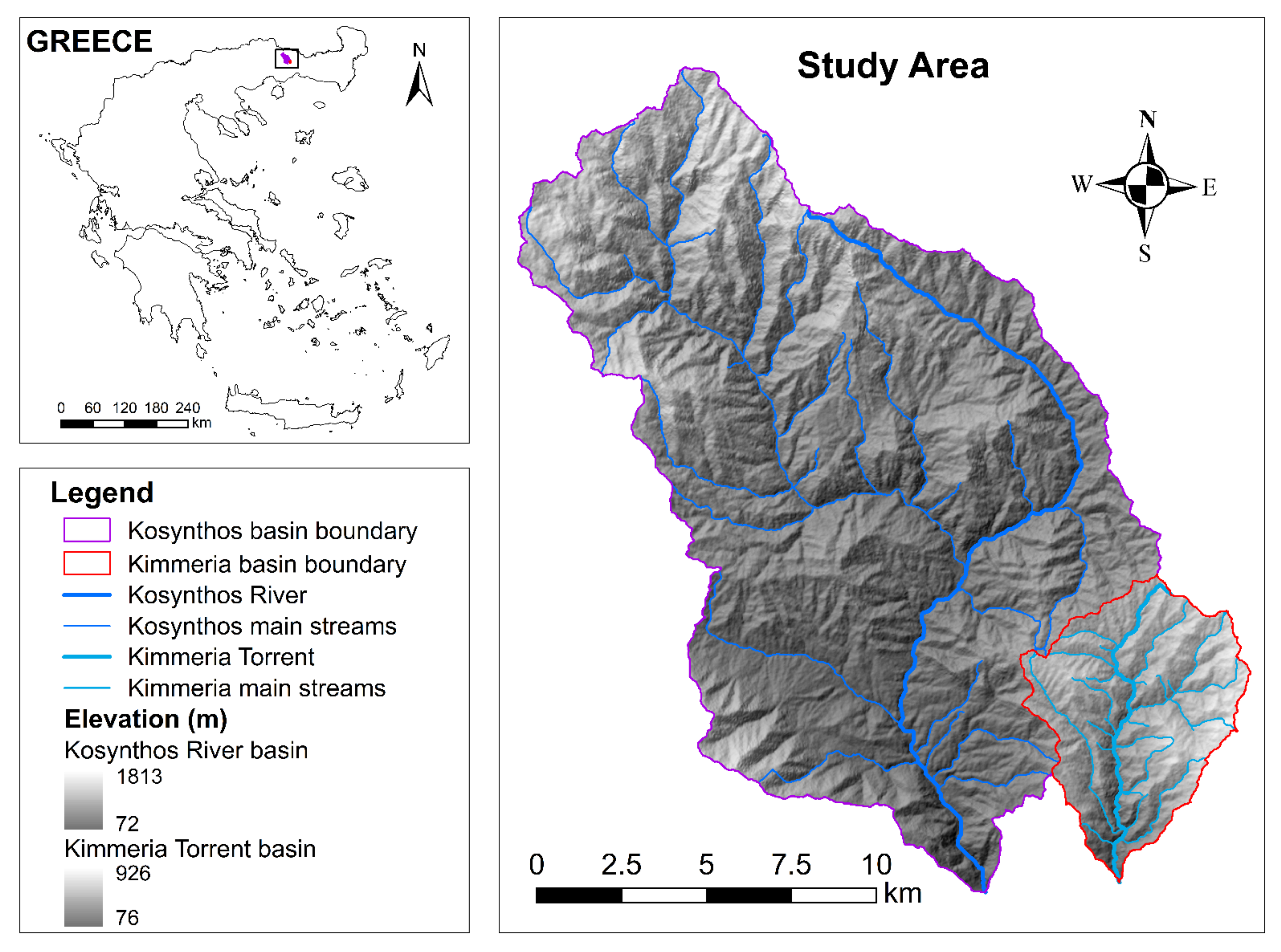
Kosynthos River and Kimmeria Torrent are located in north-eastern Greece (Figure 1), and present similar characteristics regarding their seasonality and physiography. Both basins of the watercourses are considered mainly as rural with a significant coverage of bushy areas, while the mean slope of the main watercourses does not exceed 6%. The average annual temperature is 14 °C and approximately 750 mm of precipitation falls every year. The climate of the study area is characterized as semi-arid, bordering a temperate Mediterranean climate.

The mountainous part of Kosynthos River basin (Figure 1) covers a total area of 237 km² with elevation ranging from 72 m to 1813 m a.s.l. Kosynthos River flows in a south-eastern course, passing through the city of Xanthi, and its basin outlet is considered at the first Kosynthos’ bridge (inside the city of Xanthi). The length of the main stream that runs the basin is approximately 30.3 km and the mean cross-section width of the stream is 14 m. According to the available measured data, Kosynthos River has an average stream discharge of 1.38 m³ s⁻¹, a mean sediment transport rate of 0.0166 kg s⁻¹ m⁻¹ and a median particle diameter of 0.0009 m.

The mountainous part of Kimmeria Torrent basin (Figure 1) extends to an area of 35 km² and has an altitude ranging from 76 m to 926 m a.s.l. Kimmeria Torrent runs a course of 11.6 km over the basin’s surface and flows through the village of Kimmeria which lies in the northeast and is a short distance from the city of Xanthi. The basin outlet is located downstream of Kimmeria bridge, and the mean width of the cross-section is 7 m. According to the measurements, Kimmeria Torrent has an average stream discharge of 0.74 m³ s⁻¹, a mean sediment transport rate of 0.0767 kg s⁻¹ m⁻¹ and a median particle diameter of 0.0011 m. It must be noted that the measurements in Kosynthos River and Kimmeria Torrent were conducted on different dates under different flow conditions and are not comparable. The sediment transport rate refers to the total sediment (i.e., bed load and suspended load), while the median particle diameter refers to the bed material which can transition to suspension. Though the median diameter is similar, it can easily be observed that two times lower mean stream discharge, in Kimmeria Torrent, can lead to approximately seven times higher mean sediment discharge compared to Kosynthos River. This can easily be explained by the appreciably smaller geometry of Kimmeria Torrent, which leads to higher flow velocities, even when the discharge is considerably lower.

The end part of the natural basins of Kosynthos River and Kimmeria Torrent is a lowland plain. Kosynthos River flows out to Vistonis Lake, while Kimmeria Torrent is a tributary to Kosynthos River. Figure 1 depicts only the mountainous part of both basins, and the outlets were considered at Kosynthos bridge and Kimmeria bridge, where the measurements were conducted.

3. Data and Methods

A total of 84 datasets of measured stream flow rate, flow depth, bed load transport rate, suspended load transport rate, median particle diameter, and cross-sectional geometry were used. The sum of the measured bed load and suspended load transport rates provides the measured total load transport rate, from which the total sediment concentration can be estimated.

Apart from the measurements, the total sediment concentration was calculated by means of five different ways:

• Three combinations of hydrologic nonlinear regression relationships, based on the paper of Metallinos and Hrissanthou [23], are established and used to predict the total sediment transport load, on the basis of two different sets of field measurements in Kosynthos River and Kimmeria Torrent.
• Yang’s (1973) [11] formula for total sediment concentration.
• Yang’s (1973) [11] formula for total sediment concentration with calibrated coefficients by means of multiple regression based on the field measurements.
• Yang’s (1979) [18] formula for total sediment concentration, without critical conditions for incipient motion.
• Yang’s (1979) [18] formula for total sediment concentration, without critical conditions for incipient motion, with calibrated coefficients by means of multiple regression based on the field measurements.

The efficiency of the methods was evaluated by comparison between calculated and site-measured total sediment concentration.

A crucial stage for stream sediment transport modeling is choosing the proper model among the plethora of total sediment load formulas (e.g., [14,26]). In most cases, the results of these formulas not only differ, but the calculated sediment loads are often of different order of magnitude. This is largely attributed to the empirical or semi-empirical nature of these formulas (and the way they have been derived), which throws their global applicability into question. As stated by Yang et al. [27], the results of sediment transport formulas often differ from each other, as well as from measured data, and some parameters are more effective than others for the estimation of total sediment load.

To evaluate the selection of the right model, we first tested the model of Engelund and Hansen [14], which is also a very well-known formula for total sediment load. The application to both the under-study streams was far from satisfactory resulting in NSE (Nash–Sutcliffe efficiency) values much smaller than the acceptable limits.

The reason for choosing the Yang sediment transport formulas is primarily because they have proven to be efficient in streams similar to the ones of our study. Among some such examples is the application of Yang’s formulas to the main streams of Forggensee Reservoir basin in Austria, Germany [28], to the main streams of Kastoria Lake basin in Greece [29], to the main streams of Kompsatos River basin in Thrace, Greece [30], to the main streams of Yermasoyia Reservoir basin in Cyprus [31], and to the main streams of Nestos River basin in Bulgaria and Greece [32].

3.1. Procedure of Stream Flow Rate and Sediment Transport Rate Measurements

The stream flow rate measurements were conducted by measuring the average flow velocity using a Valeport open-channel flow meter at the outlet of the basins. Each cross-section was divided into sub-sections, the mean velocity was measured at 40% of the flow depth from the bed and then multiplied by the wetted area of the sub-section, resulting in the stream flow rate. The stream discharge of the whole cross-section is the aggregation of the stream discharges of the sub-sections.

The suspended sediment concentration was determined by obtaining a sample of water from the center of the cross-section and subsequently infiltrating it through retention paper filters. The retained mass of the suspended sediment was dried out and divided by the water volume of the sample to define the concentration of the suspended sediment [33].

The bed load transport rate measurements were conducted using a Helley-Smith sampler. The bed load transport rate resulted by dividing the trapped bed load dry mass by the trap width and the duration of the measurement. The median particle diameter of the bed material was determined by means of sieve analysis.

3.2. Calculation of Total Sediment Concentration

3.2.1. Hydrologic Nonlinear Regression Relationships

In a previous study [23], hydrologic nonlinear regression relationships between the sediment transport rate and hydrologic variables were established for Kosynthos River and Kimmeria Torrent. In this paper, a similar attempt has been made, using a larger amount of data, and resulted in the correlation of the following variables for both basins:

• Suspended load transport rate (g s⁻¹) versus stream discharge (m³ s⁻¹).
• Suspended load transport rate (g s⁻¹) versus daily rainfall depth (mm).
• Suspended load transport rate (g s⁻¹) versus rainfall intensity (mm h⁻¹).
• Bed load transport rate (kg s⁻¹ m⁻¹) versus stream discharge (m³ s⁻¹).

Table 1. Hydrologic nonlinear regression relationships for Kosynthos River basin.

Suspended Load Transport Rate versus Stream Discharge	Suspended Load Transport Rate versus Rainfall Depth	Suspended Load Transport Rate versus Rainfall Intensity	Bed Load Transport Rate versus Stream Discharge
y = 2.0491 exp (1.5402 x)	y = 0.1992 x2 − 19.806 x + 513.65	y = −345.2 x2 + 1463.4 x + 36.294	y = −0.0035 x5 + 0.0337 x4 − 0.1202 x3 + 0.1896 x2 − 0.1284 x + 0.0361

illustrates the derived equations for Kosynthos River basin and

Table 2. Hydrologic nonlinear regression relationships for Kimmeria Torrent basin.

Suspended Load Transport Rate versus Stream Discharge	Suspended Load Transport Rate versus Rainfall Depth	Suspended Load Transport Rate versus Rainfall Intensity	Bed Load Transport Rate versus Stream Discharge
y = −702.2 x5 + 4542.9 x4 − 9727.5 x3 + 7997.2 x2 − 1995.5 x + 119.22	y = −0.0029 x4 + 0.2278 x3 − 5.5178 x2 + 45.77 x + 20.374	y = 0.0419 x3 − 3.1046 x2 + 64.056 x − 16.953	y = −0.0273 x4 + 0.1494 x3 − 0.2596 x2 + 0.2018 x + 0.0079

the relationships for Kimmeria Torrent basin.

In the present study, 84 sets of measured data were applied to the relationships in Table 1 and Table 2. The comparison is made on the basis of total calculated and measured sediment concentrations and, for this reason, three combinations of the relationships are created:

• Suspended and bed load transport rate versus stream discharge (Combination 1).
• Suspended load transport rate versus daily rainfall depth, and bed load transport rate versus stream discharge (Combination 2).
• Suspended load transport rate versus rainfall intensity, and bed load transport rate versus stream discharge (Combination 3).

By transforming the units of the above-mentioned relationships, we were able to calculate, firstly, the total load transport rate in kg m⁻¹ s⁻¹ for all three combinations, and secondly, the total sediment concentration (ppm by weight).

3.2.2. Yang (1973)

In 1973, Yang derived a formula for the total sediment transport in rivers and streams by applying a multiple regression analysis for 463 sets of data in laboratory flumes [11]:

$${\mathrm{logc}}_{\mathrm{F}}=5.435-0.286\log \frac{{\mathrm{wD}}_{50}}{\mathrm{v}}-0.457\log \frac{{\mathrm{u}}_{\ast }}{\mathrm{w}}+\left(1.799-0.409\log \frac{{\mathrm{wD}}_{50}}{\mathrm{v}}-0.314\log \frac{{\mathrm{u}}_{\ast }}{\mathrm{w}}\right)\log \left(\frac{\mathrm{us}}{\mathrm{w}}-\frac{{\mathrm{u}}_{\mathrm{cr}}\mathrm{s}}{\mathrm{w}}\right)$$

(1)

where c_F is the total sediment concentration (ppm by weight); w is the terminal fall velocity of the sediment particles (m s⁻¹); D₅₀ is the median particle diameter (m); ν is the kinematic viscosity of water (m² s⁻¹); s is the energy slope; u is the mean flow velocity (m s⁻¹); u_cr is the critical mean flow velocity (m s⁻¹); and u_* is the shear velocity (m s⁻¹). The product us is characterized as unit stream power.

3.2.3. Yang (1979)

In 1979, Yang concluded that the critical unit stream power term in Equation (1) can be neglected without causing much error when the measured sediment concentration is greater than 20 ppm. The simplified unit stream power equation was derived as:

$${\mathrm{logc}}_{\mathrm{F}}=5.165-0.153\log \frac{{\mathrm{wD}}_{50}}{\mathrm{v}}-0.297\log \frac{{\mathrm{u}}_{\ast }}{\mathrm{w}}+\left(1.780-0.360\log \frac{{\mathrm{wD}}_{50}}{\mathrm{v}}-0.480\log \frac{{\mathrm{u}}_{\ast }}{\mathrm{w}}\right)\log \left(\frac{\mathrm{us}}{\mathrm{w}}\right)$$

(2)

The latter Yang formula was developed based on 1259 sets of laboratory and field data.

4. Results

4.1. Modification of Yang’s Equations on the Basis of Kosynthos River and Kimmeria Torrent Data

In order to redetermine the coefficients of Equation (1), a multiple regression analysis was applied [24]. The logarithmic total sediment concentration, logc_F, was set as the dependent variable and the following auxiliary variables x₁, x₂, x₃, x₄ and x₅ were set as the independent variables:

$$\begin{gathered} {\mathrm{x}}_1=\log \left({\mathrm{wD}}_{50}/\mathrm{v}\right) \\ {\mathrm{x}}_2=\log \left({\mathrm{u}}_{\ast }/\mathrm{w}\right) \\ {\mathrm{x}}_3=\log \left(\mathrm{us}/\mathrm{w}-{\mathrm{u}}_{\mathrm{cr}}s/\mathrm{w}\right) \\ {\mathrm{x}}_4=\log \left(\frac{\mathrm{us}}{\mathrm{w}}-\frac{{\mathrm{u}}_{\mathrm{cr}}s}{\mathrm{w}}\right)\log \left({\mathrm{wD}}_{50}/\mathrm{v}\right) \\ {\mathrm{x}}_5=\log \left(\frac{\mathrm{us}}{\mathrm{w}}-\frac{{\mathrm{u}}_{\mathrm{cr}}s}{\mathrm{w}}\right)\log \left({\mathrm{u}}_{\ast }/\mathrm{w}\right) \end{gathered}$$

(3)

Then, Yang’s formula can be written as a multiple linear regression equation:

$${\mathrm{logc}}_{\mathrm{F}}=5.435-0.286 {\mathrm{x}}_1-0.457 {\mathrm{x}}_2+1.799 {\mathrm{x}}_3-0.409 {\mathrm{x}}_4-0.314 {\mathrm{x}}_5$$

(4)

Similarly, if the following auxiliary variables x^′₁, x^′₂, x^′₃, x^′₄ and x^′₅ are considered:

$$\begin{gathered} {{\mathrm{x}}^{\prime }}_1=\log \left({\mathrm{wD}}_{50}/\mathrm{v}\right) \\ {{\mathrm{x}}^{\prime }}_2=\log \left({\mathrm{u}}_{\ast }/\mathrm{w}\right) \\ {{\mathrm{x}}^{\prime }}_3=\log \left(\mathrm{us}/\mathrm{w}\right) \\ {{\mathrm{x}}^{\prime }}_4=\log \left(\mathrm{us}/\mathrm{w}\right)\log \left({\mathrm{wD}}_{50}/\mathsf{\nu }\right) \\ {{\mathrm{x}}^{\prime }}_5=\log \left(\mathrm{us}/\mathrm{w}\right)\log \left({\mathrm{u}}_{\ast }/\mathrm{w}\right) \end{gathered}$$

(5)

Equation (2) can be written as a multiple linear regression equation:

$${\mathrm{logc}}_{\mathrm{F}}=5.165-0.153 {{\mathrm{x}}^{\prime }}_1-0.297 {{\mathrm{x}}^{\prime }}_2+1.780 {{\mathrm{x}}^{\prime }}_3-0.360 {{\mathrm{x}}^{\prime }}_4-0.480 {{\mathrm{x}}^{\prime }}_5$$

(6)

On the basis of Kosynthos River data, the arithmetic coefficients of the original formulas of Yang, Equations (1) and (2), are modified, respectively, as follows:

$${\mathrm{logc}}_{\mathrm{F}}=3.960-0.984\log \frac{{\mathrm{wD}}_{50}}{\mathrm{v}}-0.706\log \frac{{\mathrm{u}}_{\ast }}{\mathrm{w}}-\left(0.471-0.224\log \frac{{\mathrm{wD}}_{50}}{\mathrm{v}}-1.292\log \frac{{\mathrm{u}}_{\ast }}{\mathrm{w}}\right)\log \left(\frac{\mathrm{us}}{\mathrm{w}}-\frac{{\mathrm{u}}_{\mathrm{cr}}\mathrm{s}}{\mathrm{w}}\right)$$

(7)

$${\mathrm{logc}}_{\mathrm{F}}=3.394-0.595\log \frac{{\mathrm{wD}}_{50}}{\mathrm{v}}-0.100\log \frac{{\mathrm{u}}_{\ast }}{\mathrm{w}}-\left(0.953-0.517\log \frac{{\mathrm{wD}}_{50}}{\mathrm{v}}-1.955\log \frac{{\mathrm{u}}_{\ast }}{\mathrm{w}}\right)\log \left(\frac{\mathrm{us}}{\mathrm{w}}\right)$$

(8)

The corresponding modified formulas of Yang for the Kimmeria Torrent data can be seen in Equations (9) and (10):

$${\mathrm{logc}}_{\mathrm{F}}=0.892+1.064\log \frac{{\mathrm{wD}}_{50}}{\mathrm{v}}+3.004\log \frac{{\mathrm{u}}_{\ast }}{\mathrm{w}}-\left(0.436-0.297\log \frac{{\mathrm{wD}}_{50}}{\mathrm{v}}-1.287\log \frac{{\mathrm{u}}_{\ast }}{\mathrm{w}}\right)\log \left(\frac{\mathrm{us}}{\mathrm{w}}-\frac{{\mathrm{u}}_{\mathrm{cr}}\mathrm{s}}{\mathrm{w}}\right)$$

(9)

$${\mathrm{logc}}_{\mathrm{F}}=0.179+1.551\log \frac{{\mathrm{wD}}_{50}}{\mathrm{v}}+3.830\log \frac{{\mathrm{u}}_{\ast }}{\mathrm{w}}-\left(1.042-0.693\log \frac{{\mathrm{wD}}_{50}}{\mathrm{v}}-2.096\log \frac{{\mathrm{u}}_{\ast }}{\mathrm{w}}\right)\log \left(\frac{\mathrm{us}}{\mathrm{w}}\right)$$

(10)

In concrete terms, the new arithmetic coefficients of Equations (7)–(10) were determined by means of the conventional least squares regression. Regarding Equations (9) and (10), without the critical condition, it should be noted that the measured total sediment concentrations in Kosynthos River and Kimmeria Torrent do not exceed the threshold of 20 ppm set by Yang [18].

The measured stream flow rate (m³ s⁻¹), the measured total sediment concentration (ppm), as well as the calculated total sediment concentration (ppm), by means of all equations, for Kosynthos River and Kimmeria Torrent, are provided in

Table 3. Measured stream flow rate and total sediment concentration—calculated total sediment concentration in Kosynthos River.

No	Stream Flow Rate (m3 s−1)	Total Load cF (Meas.) (ppm)	Total Load cF (Calc.) Original Yang 1973 (ppm)	Total Load cF (Calc.) Calibrated Yang 1973 (ppm)	Total Load cF (Calc.) Original Yang 1979 (ppm)	Total Load cF (Calc.) Calibrated Yang 1979 (ppm)	Combination 1 (ppm)	Combination 2 (ppm)	Combination 3 (ppm)
1	0.43	335.8140	606.9675	291.9432	687.3276	319.9174	26.6573	1212.0674	101.9372
2	0.43	390.6977	1577.2966	366.1491	1792.6057	364.9354	26.6573	1212.0674	1416.9012
3	2.79	98.4946	2903.1226	113.6817	2701.8774	120.7814	51.6607	181.8078	511.0045
4	2.74	135.7664	3866.5061	148.8852	4008.2888	150.1945	48.7144	185.3100	528.6445
5	0.99	275.9596	3165.5488	255.5665	3468.8142	244.6086	16.8067	526.1865	1165.6607
6	3.20	150.9688	6520.0077	398.9830	6706.9759	372.4731	84.5233	112.0747	366.1508
7	2.68	280.0746	1177.9012	164.5355	960.8742	183.7974	45.4383	176.6227	549.8305
8	2.24	420.9375	5503.9324	568.6986	4801.4911	560.8989	28.7733	190.4951	706.3331
9	2.89	794.5329	10030.6309	632.1469	9075.8942	584.5008	58.1812	138.9315	475.7453
10	3.46	772.3121	21039.6846	872.2630	18227.9591	771.0490	115.5053	68.1192	272.8705
11	2.44	681.5574	5997.4014	571.9428	5190.2282	562.8918	34.8892	202.9815	634.8973
12	1.65	421.5152	5269.8290	727.9598	4484.3783	713.9938	20.2844	294.6348	920.3635
13	0.72	35.7064	1246.2457	124.1635	1443.8983	125.2208	16.1946	670.5773	--
14	1.61	823.4988	340.1047	131.9498	503.6457	135.5321	20.0374	243.5369	--
15	0.26	228.9318	213.4221	208.4815	419.7129	215.5683	62.2784	1708.4376	--
16	0.68	95.4235	999.9242	120.0870	1152.2387	123.6992	16.4721	651.5061	--
17	0.64	58.7231	668.6828	115.4120	766.5622	122.2408	16.9567	508.9825	--
18	2.56	36.4975	509.6009	16.2327	755.3064	16.7229	39.7811	100.4242	--
19	1.13	111.5372	460.2337	67.6208	598.9375	66.6613	17.5593	--	--
20	0.88	150.8719	869.0922	84.0420	949.9506	87.4506	16.2695	305.7240	--
21	1.16	57.4119	808.8774	86.4070	889.4492	90.2433	17.7220	232.6690	--
22	1.39	56.1637	643.7348	60.8842	776.0480	62.9939	18.8769	193.8200	--
23	1.97	118.1591	1004.9264	56.7567	1120.4445	57.3948	23.5287	--	--
24	3.05	114.5769	1113.3538	28.8865	1412.1443	27.3677	70.8410	161.8150	--
25	2.44	61.9491	1061.4399	52.0406	1254.2076	51.4907	34.8856	201.3962	--
26	1.44	59.0078	285.8463	30.2175	594.0616	29.5393	19.1150	--	--
27	1.85	24.3287	495.7374	23.6265	712.3381	24.2399	22.0287	274.8598	--
28	0.98	59.7626	91.3430	71.4738	467.5021	60.6577	16.7392	--	--
29	1.39	31.8719	159.4453	28.9519	563.8075	27.9248	18.8573	242.0712	--
30	0.37	65.2952	790.4330	183.4181	1090.1627	172.6388	33.8823	--	--
31	0.90	10.2722	357.2231	40.2602	628.5402	42.0112	16.3661	518.1544	--
32	0.54	81.8351	490.8300	154.0273	568.0208	160.1939	19.5752	694.3618	--
33	1.07	485.6047	1019.9564	138.4587	881.7582	151.8081	17.2189	352.5406	--
34	1.26	32.0713	850.4692	92.6831	807.8663	98.5171	18.2447	413.7905	--
35	1.20	565.9081	749.2211	83.9788	747.1782	88.0473	17.9531	433.7064	--
36	1.31	40.1614	1337.2851	126.8143	1425.4967	130.9070	18.4919	326.1858	--
37	0.25	1490.9644	1310.4288	591.2591	1359.5938	587.7304	68.4937	1956.7439	--
38	0.32	1359.4902	1081.9123	383.2361	1237.4700	374.9873	44.8738	1411.5200	--
39	0.22	1080.8928	1007.7275	494.1553	1131.6184	491.9484	83.1688	1181.9161	--
40	0.16	1411.7143	1004.9021	844.4405	1051.0541	866.7638	144.3981	1701.1444	--
41	0.76	545.1180	234.9519	144.7907	477.6216	114.5575	16.0824	298.0294	--
42	1.45	13.6481	830.0665	42.2166	849.9139	43.3873	19.1634	359.4885	--
43	1.76	10.4712	647.9586	36.2533	732.0247	36.1116	21.1315	--	--
44	1.24	60.4020	653.8342	51.8893	738.7671	53.3864	18.1535	419.9050	--
45	1.58	38.1351	590.9242	47.3734	703.7601	48.3790	19.8699	--	--
46	0.84	25.2489	329.4808	67.3573	540.2682	68.4105	16.1539	618.8063	--
47	0.96	33.0981	209.6013	61.6282	484.6377	62.7791	16.6548	--	--
48	0.87	32.8566	491.6201	82.1484	606.0382	83.5098	16.2625	595.0111	--
49	1.06	31.0041	416.1793	72.9338	573.9715	71.2795	17.1916	--	--
50	0.68	24.8344	387.1575	75.2133	559.6605	74.8298	16.4996	766.7018	--
51	0.64	42.8419	365.9389	105.2314	526.9587	104.7744	17.0008	--	--
52	0.61	52.3821	483.4832	118.9038	622.3600	125.8161	17.5492	--	--
53	1.13	111.5372	460.2337	67.6208	598.9375	66.6613	17.5593	--	--
54	2.56	36.4975	509.6009	16.2327	755.3064	16.7229	39.7811	--	--
55	1.97	118.1591	1004.9264	56.7567	1120.4445	57.3948	23.5287	--	--
56	3.05	114.5769	1113.3538	28.8865	1412.1443	27.3677	70.8410	--	--
57	1.44	59.0078	285.8463	30.2175	594.0616	29.5393	19.1150	--	--
58	1.85	24.3287	495.7374	23.6265	712.3381	24.2399	22.0287	--	--
59	0.98	59.7626	45.7595	75.3405	461.7282	59.3784	16.7392	--	--
60	1.39	31.8719	52.0816	27.4987	520.7066	28.6008	18.8573	--	--
61	0.37	65.2952	143.6963	113.7347	416.0687	122.9017	33.8823	--	--
62	0.90	10.2722	357.2231	40.2602	628.5402	42.0112	16.3661	--	--

and

Table 4. Measured stream flow rate and total sediment concentration—calculated total sediment concentration in Kimmeria Torrent.

No	Stream Flow Rate (m3 s−1)	Total Load cF (Meas.) (ppm)	Total Load cF (Calc.) Original Yang 1973 (ppm)	Total Load cF (Calc.) Calibrated Yang 1973 (ppm)	Total Load cF (Calc.) Original Yang 1979 (ppm)	Total Load cF (Calc.) Calibrated Yang 1979 (ppm)	Combination 1 (ppm)	Combination 2 (ppm)	Combination 3 (ppm)
1	0.67	607.1642	2416.3347	425.7431	2332.9124	437.1424	497.2385	287.3469	373.0340
2	3.05	312.8525	3243.5092	1043.5132	4303.9802	1019.5731	100.8742	54.4245	101.2946
3	0.66	402.4242	3754.7200	492.4234	3780.0516	492.0866	498.4780	308.6660	314.5621
4	0.92	405.3804	2594.0813	450.9815	2257.3528	473.6653	369.3545	231.2532	471.6457
5	0.81	473.3827	5664.9279	1083.5447	6759.7054	1045.1551	444.0038	--	--
6	0.04	1102.5000	437.2637	302.4060	538.7160	331.3937	1678.7662	3326.5581	3573.8288
7	1.26	222.1270	3732.0542	521.4311	3515.1297	538.1428	113.3945	171.5556	--
8	0.81	762.1235	7001.7301	421.6593	5931.9290	431.5201	444.0038	256.5022	--
9	0.15	461.9125	241.4923	394.7844	383.2360	404.8596	14.5879	761.0303	--
10	0.38	197.0604	580.8441	504.2258	595.0125	496.8450	332.5521	197.2796	--
11	0.14	408.7243	73.5463	434.0411	299.9628	417.4983	26.6895	1597.8254	--
12	0.30	809.3880	455.8342	557.4092	486.9880	530.7350	203.7949	637.7894	--
13	0.20	745.6392	327.0242	584.0636	403.9684	535.9286	38.7167	298.9349	--
14	0.43	256.3497	1569.7231	580.1319	1025.0548	594.1154	392.0229	406.7581	--
15	1.16	426.9984	258.1951	443.0588	678.1001	547.6003	180.3820	263.4147	--
16	0.30	1390.9597	334.9787	575.1409	616.0164	576.0628	210.1573	588.4338	--
17	0.31	700.2786	545.3716	560.6055	719.2123	539.1392	224.6357	562.0170	--
18	0.50	4801.3057	973.3962	693.2609	953.2653	629.2469	458.0387	607.0277	--
19	1.89	574.0803	1949.6213	697.7435	1709.0208	697.7430	212.5039	148.6929	--
20	0.06	4884.2681	310.5068	560.9651	565.1381	551.6226	765.8154	1339.4157	--
21	1.07	576.9531	1299.8879	574.2564	1136.9432	567.0584	252.9423	316.5356	--
22	1.23	1400.4858	1219.0957	708.2767	987.9857	660.2543	129.9650	--	--

, respectively. The double dashes displayed at the aforementioned tables indicate the absence of measured values at the specific type of relationship.

4.2. Comparison between Calculated and Measured Total Sediment Concentration

The comparison between the calculated and measured total sediment concentration is made on the basis of the following statistical criteria [34].

4.2.1. Mean Relative Error (MRE) (%)

$$\mathrm{MRE}=\frac{1}{\mathrm{n}}{{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{n}}\frac{\left({\mathrm{y}}_{\mathrm{i}}-{\widehat{\mathrm{y}}}_{\mathrm{i}}\right)}{{\mathrm{y}}_{\mathrm{i}}}100$$

(11)

The Mean Relative Error (MRE) provides the relative size of the error. It is an index of how good an approximation between the predicted and measured value is, in relation to the magnitude of the physical quantity’s value.

4.2.2. Nash–Sutcliffe Efficiency (NSE)

$$\mathrm{NSE}=1-\frac{{{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{n}}{\left({\mathrm{y}}_{\mathrm{i}}-{\widehat{\mathrm{y}}}_{\mathrm{i}}\right)}^2}{{{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{n}}{\left({\mathrm{y}}_{\mathrm{i}}-\overline{\mathrm{y}}\right)}^2}$$

(12)

where $\overline{\mathrm{y}}$ is the average value of ${\mathrm{y}}_{\mathrm{i}}$.

NSE [35] indicates how well the plot of measured versus calculated data fits the line of agreement (1:1 line). Nash–Sutcliffe efficiency ranges from −∞ to 1, with 1 being the optimal value.

4.2.3. Linear Correlation Coefficient r

$$\mathrm{r}=\frac{{{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{n}}({\mathrm{y}}_{\mathrm{i}}-\overline{\mathrm{y}})\left({\widehat{\mathrm{y}}}_{\mathrm{i}}-\overline{\widehat{\mathrm{y}}}\right)}{\sqrt{{{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{n}}{\left({\mathrm{y}}_{\mathrm{i}}-\overline{\mathrm{y}}\right)}^2}\sqrt{{{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{n}}{\left({\widehat{\mathrm{y}}}_{\mathrm{i}}-\overline{\widehat{\mathrm{y}}}\right)}^2}}$$

(13)

where $\overline{\widehat{\mathrm{y}}}$ is the average value of ${\widehat{\mathrm{y}}}_{\mathrm{i}}$.

The coefficient r expresses the degree of mutual linear dependence between the variables ${\mathrm{y}}_{\mathrm{i}}$ and ${\widehat{\mathrm{y}}}_{\mathrm{i}}$, and ranges among the values −1 and +1. The values r = ±1 represent the ideal occasion, when the marks representing the pairs of values ${\mathrm{y}}_{\mathrm{i}}$ and ${\widehat{\mathrm{y}}}_{\mathrm{i}}$, depicted on an orthogonal coordinate system, lie on the regression line, with a positive or negative slope, respectively.

4.2.4. Determination Coefficient R²

The determination coefficient R² yields the percentage of change of the calculated values, which can be explained by the linear relationship between calculated and measured values. It ranges between 0 and 1. A value of 0 states that there is no correlation, whereas a value of 1 indicates that the variance of the calculated values equals the variance of the measured values [34].

4.2.5. Discrepancy Ratio

The discrepancy ratio represents the percentage of the calculated total sediment concentration values, lying between pre-determined margins of the corresponding measured total sediment concentration values. These margins vary depending on the type of the watercourse and the reliability of the results. As far as the present study is concerned, the discrepancy ratio represents the percentage of the calculated total sediment concentration values that lie between the quadruple and the one quarter of the corresponding measured total sediment concentration values.

The total sediment concentration was calculated by means of the three combined equations and by means of both the original and the modified Yang formulas. The values of the above-mentioned statistical criteria are displayed in

Table 5. Statistical criteria of combined equations, Yang’s original and calibrated formulas for Kosynthos River.

	Number of Paired Values	MRE (%)	NSE	r	R2	Discrepancy Ratio
Original 1973	62	−1226.540	−83.404	0.317	0.101	0.226
Calibrated 1973	62	−37.293	0.521	0.766	0.587	0.968
Original 1979	62	−1577.191	−66.701	0.306	0.094	0.177
Calibrated 1979	62	−38.302	0.522	0.776	0.602	0.887
Combination 1	62	56.865	−0.270	0.598	0.357	0.613
Combination 2	41	−598.067	−0.349	0.543	0.295	0.561
Combination 3	12	−128.081	−3.796	−0.088	0.008	0.833

and

Table 6. Statistical criteria of combined equations, Yang’s original and calibrated formulas for Kimmeria Torrent.

	Number of Paired Values	MRE (%)	NSE	r	R2	Discrepancy Ratio
Original 1973	22	−298.247	−3.248	−0.244	0.059	0.500
Calibrated 1973	22	−14.884	−0.114	0.069	0.005	0.909
Original 1979	22	−307.673	−3.247	−0.239	0.057	0.636
Calibrated 1979	22	−15.268	−0.132	0.006	0.000	0.909
Combination 1	22	43.135	−0.180	0.298	0.089	0.682
Combination 2	20	7.524	−0.112	0.057	0.003	0.900
Combination 3	5	−22.497	−14.312	0.954	0.910	1.000

.

The first combination of the equations, in which both the bed and suspended load are expressed as a function of the stream discharge, has a better fit to the available data measurements, in comparison to the other two combinations, based on the number of the paired values along with the values of R² and discrepancy ratio.

The values of the Nash–Sutcliffe Efficiency, on the basis of the calibrated formulas, can be considered fairly satisfactory, as they are optimized and tend to the ideal value of 1 for Kosynthos River. Additionally, the degree of linear dependence between calculated and measured total sediment concentration, expressed by the linear correlation coefficient r, is acceptable for the case study of Kosynthos River.

The results of the discrepancy ratio are illustrated in Figure 2, Figure 3, Figure 4, Figure 5, Figure 6 and Figure 7. Figure 2 and Figure 5 illustrate the discrepancy ratio between measured and calculated values of total sediment concentration by means of the combined equations. The plots of Figure 3a, Figure 4a, Figure 6a and Figure 7a represent the discrepancy ratio between measured and calculated values of total sediment concentration by means of the original formulas, whilst the plots of Figure 3b, Figure 4b, Figure 6b and Figure 7b represent the discrepancy ratio with the calibrated formulas. It should be noted that both coordinate axes in all plots are in logarithmic scale.

5. Discussion

In this paper, 84 sets of measurements were available: 62 field measurement data for Kosynthos River, for the period between 2005 and 2015, and 22 field measurement data for Kimmeria Torrent, for the period 2004–2015.

Table 5 illustrates that the first combination was applied to all sets of measured data, the second one used 41 sets and the third combination was implemented to 12 sets of measured data for Kosynthos River. For Kimmeria Torrent (Table 6), the first combination was carried out for all available data, the second combination was applied to 20 data sets and the third combination to five sets of measured data. The variation in the number of datasets that were used lies in the fact that no rainfall measurements were available for all the sediment transport measurements.

The discrepancy ratio plot between measured and calculated values of total sediment concentration by means of the combined equations and the fact that all the data sets were used prove that the first combination of the equations, in which suspended and bed load transport rates are expressed as a function of the stream discharge, has a better fit to the available data measurements of Kosynthos River. However, by examining the discrepancy ratio along with the R² for the case study of Kimmeria Torrent, no safe conclusion could be established regarding the application of the combined equations to the available data. Overall, Figure 2 and Figure 5 show that all three combinations have better application in the case of Kosynthos River in comparison to Kimmeria Torrent. The reason for that is that more data sets were available for Kosynthos basin than Kimmeria basin.

Though the data for Kimmeria Torrent is limited, and the correlation is not satisfactory, the results are substantially improved by means of the calibrated Yang formulas. Given the intermittent and very low flow of Kimmeria Torrent, and the complex nature of the stream sediment transport processes, the estimation of total sediment load is a challenging task. The obtained results indicate the difficulty of modeling the total sediment load in intermittent streams and underline the need for further research. The main objective of the present study is to point out the need of calibrating/adjusting existing formulas to the specific conditions of the streams they are applied.

Regarding Yang’s formulas, their coefficients are redefined based on all available field measurements and the statistical criteria of both calibrated Yang’s formulas are improved in comparison to those of Yang’s original formulas. Specifically, the MRE displays a notable decrease, whilst the NSE, especially for Kosynthos River, is significantly improved. The linear correlation coefficient r and the determination coefficient R² tend to the optimal values. Overall, the results can be considered satisfactory for the case of Kosynthos River, while for Kimmeria Torrent more data should be taken into account.

A similar project, regarding Nestos River [24], produced satisfactory results and proved that Yang’s formulas could be modified for a perennial river. In this study, 111 pairs of measured stream flow rate and measured total load transport rate in Nestos River were used and total sediment concentrations were calculated by means of Yang’s formulas, both original and calibrated. This enabled the comparison between calculated and site-measured total sediment concentrations. The statistical criteria of that study, shown in

Table 7. Statistical criteria of Yang’s formulas (1973)—original and calibrated—for Nestos River.

	Number of Paired Values	MRE (%)	NSE	r	R2	Discrepancy Ratio
Original	111	−11,649.317	−20.474	0.416	0.173	0.315
Calibrated	111	−240.746	0.480	0.695	0.483	0.838

and

Table 8. Statistical criteria of Yang’s formulas (1979)—original and calibrated—for Nestos River.

	Number of Paired Values	MRE (%)	NSE	r	R2	Discrepancy Ratio
Original	111	−16,196.804	−35.110	0.491	0.241	0.243
Calibrated	111	−218.745	0.492	0.716	0.513	0.820

, indicate that the original Yang’s formulas do not describe the sediment transport rate of Nestos River as well as those of Kosynthos River. However, after the calibration of their coefficients using multiple linear regression, both Yang’s formulas were improved.

Although Nestos River differs from Kosynthos River in many parameters, such as water discharge, sediment transport rate and median particle diameter, Yang’s formulas can be successfully calibrated for both perennial and intermittent rivers.

This work demonstrates an efficient way for adjusting well-known sediment transport formulas, the global application of which could be questionable for the specific conditions of rivers and streams. It is, however, noted that the application of Equations (7) and (8) should be bounded in Kosynthos River and Equations (9) and (10) in Kimmeria Torrent.

6. Conclusions

There is a variety of equations and relationships that can be applied and developed in order to calculate the sediment transport rate, depending on the type of the stream and the available measurements.

In this study, three combinations of nonlinear regression equations were created based on the derived relationships between bed load transport rate and stream discharge, suspended load transport rate and rainfall depth, suspended load transport rate and rainfall intensity, and suspended load transport rate and stream discharge. On the basis of the above nonlinear regression equations, the total load transport rate was calculated indirectly as a function of stream discharge, rainfall depth and rainfall intensity. These relationships can be characterized as “hydrologic”. The comparison results between calculated and measured total load transport rates for Kosynthos River basin and Kimmeria Torrent basin (north-eastern Greece) are relatively satisfactory.

The suspended load transport rate was expressed mathematically as a function of rainfall characteristics and stream discharge, namely hydrologic variables, by means of regression equations, because the suspended material in a stream originates mainly from soil erosion products, due to rainfall and runoff, of the corresponding basin.

Total load transport rate was also calculated as a function of “hydraulic” variables, e.g., flow velocity, critical flow velocity, grain diameter, settling velocity, by means of Yang formulas for Kosynthos River and Kimmeria Torrent. Yang’s formulas constitute multiple nonlinear regression equations that were linearized in the present study.

The original 1973 Yang’s formula is based on the assumption of a critical situation, while, in the original 1979 Yang’s formula, a critical situation is not considered. The original 1973 Yang’s formula has a better fit to Kosynthos River than the original 1979 Yang’s formula. Regarding Kimmeria Torrent, the original 1979 Yang’s formula outperforms the original 1973 Yang’s formula, based on the available data. However, the “hydrologic” regression equations, especially the first combination, provide more satisfactory results than both original equations.

The arithmetic coefficients of the independent variables in the original Yang’s formulas were calibrated on the basis of the available “hydraulic” data for Kosynthos River and Kimmeria Torrent. Both calibrated Yang’s formulas provide more satisfactory results than the corresponding original formulas for both Kosynthos River and Kimmeria Torrent. The calibrated 1973 Yang’s formula outperforms the calibrated 1979 Yang’s formula for both Kosynthos River and Kimmeria Torrent.

Comparing the resulting modified equations for the intermittent Kosynthos River and Kimmeria Torrent and the perennial Nestos River, the more satisfactory values of the statistical criteria were achieved in the case study of Kosynthos River.

Both Yang’s formulas can be successfully calibrated for the intermittent watercourses of the present case studies, Kosynthos River and Kimmeria Torrent, provided that there are sufficient data available. This calls for further investigation, as the methods presented in this study could effectively remedy the lack of sediment data.

A natural follow-up of this study would be the application of regression analysis for determining the relationships between various, hydraulic and hydrologic, variables of ephemeral rivers, as well as the calibration of established sediment transport formulas. Along with the aforementioned study, Yang’s formulas could be applied and calibrated based on the available data measurements of ephemeral rivers.