Updated Understanding of the Thompson River Valley Landslides Kinematics Using Satellite InSAR
Abstract
:1. Introduction
1.1. Landslide Remote Sensing and Satellite InSAR
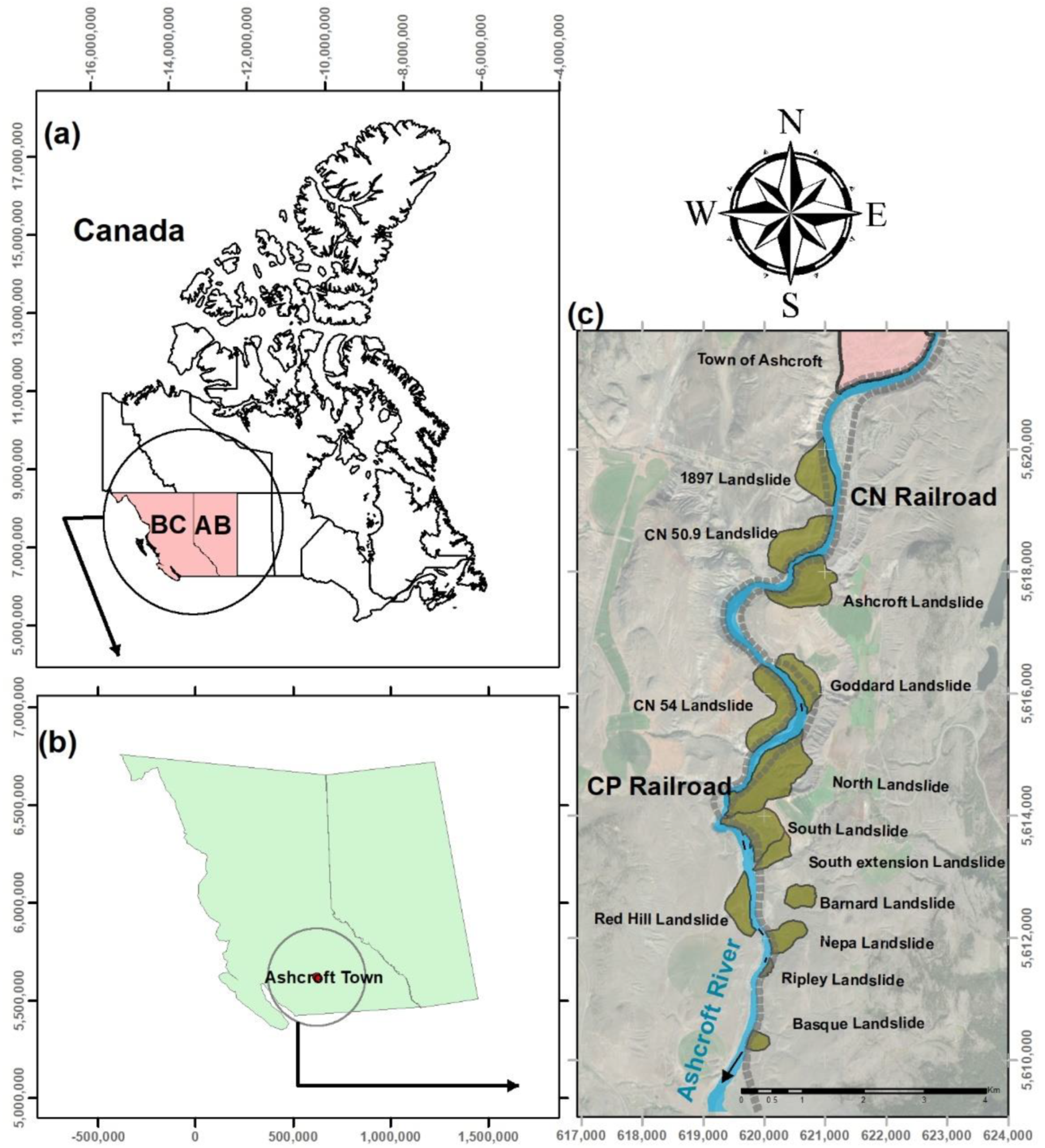
1.2. The Thompson River Valley Landslides South of Ashcroft
2. Materials and Methods
2.1. Satellite InSAR Displacement Data
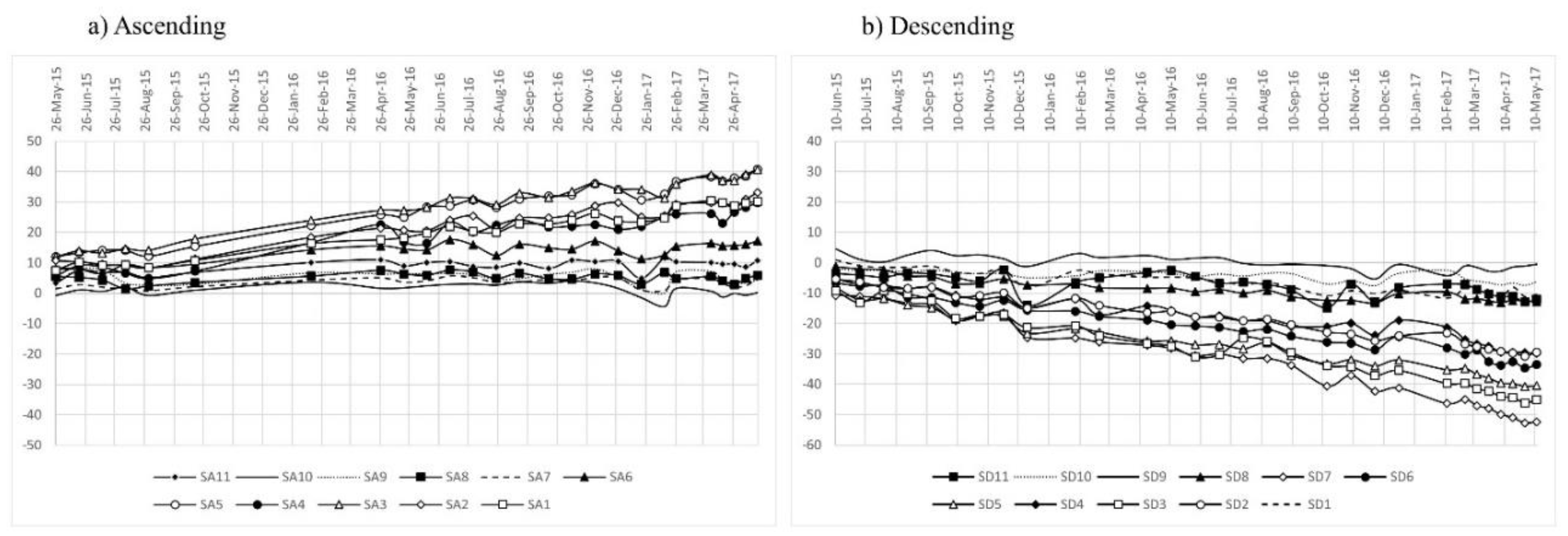
2.2. Surface Ground Displacement Calculations Based on InSAR LOS Displacements
3. Results
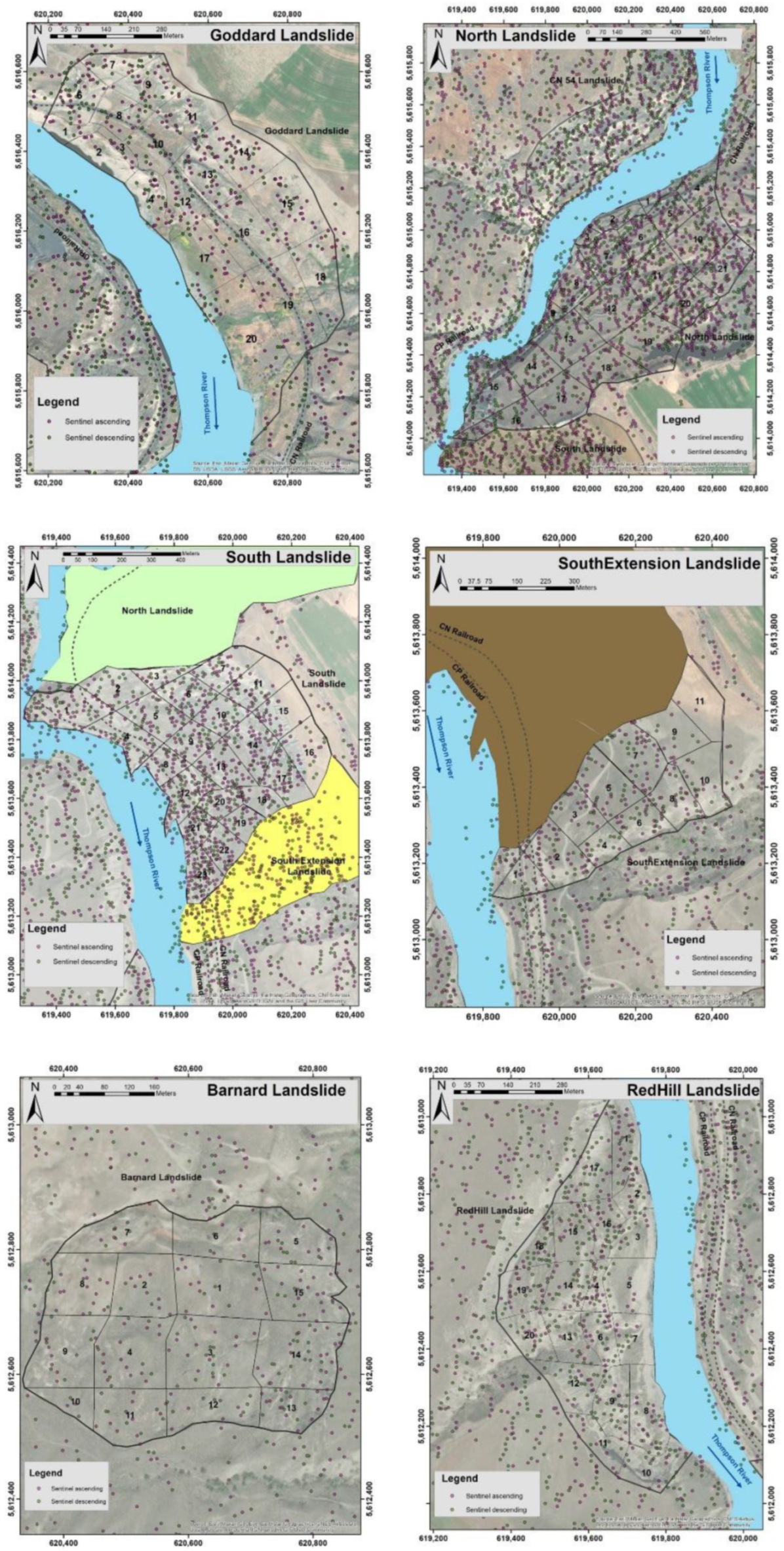
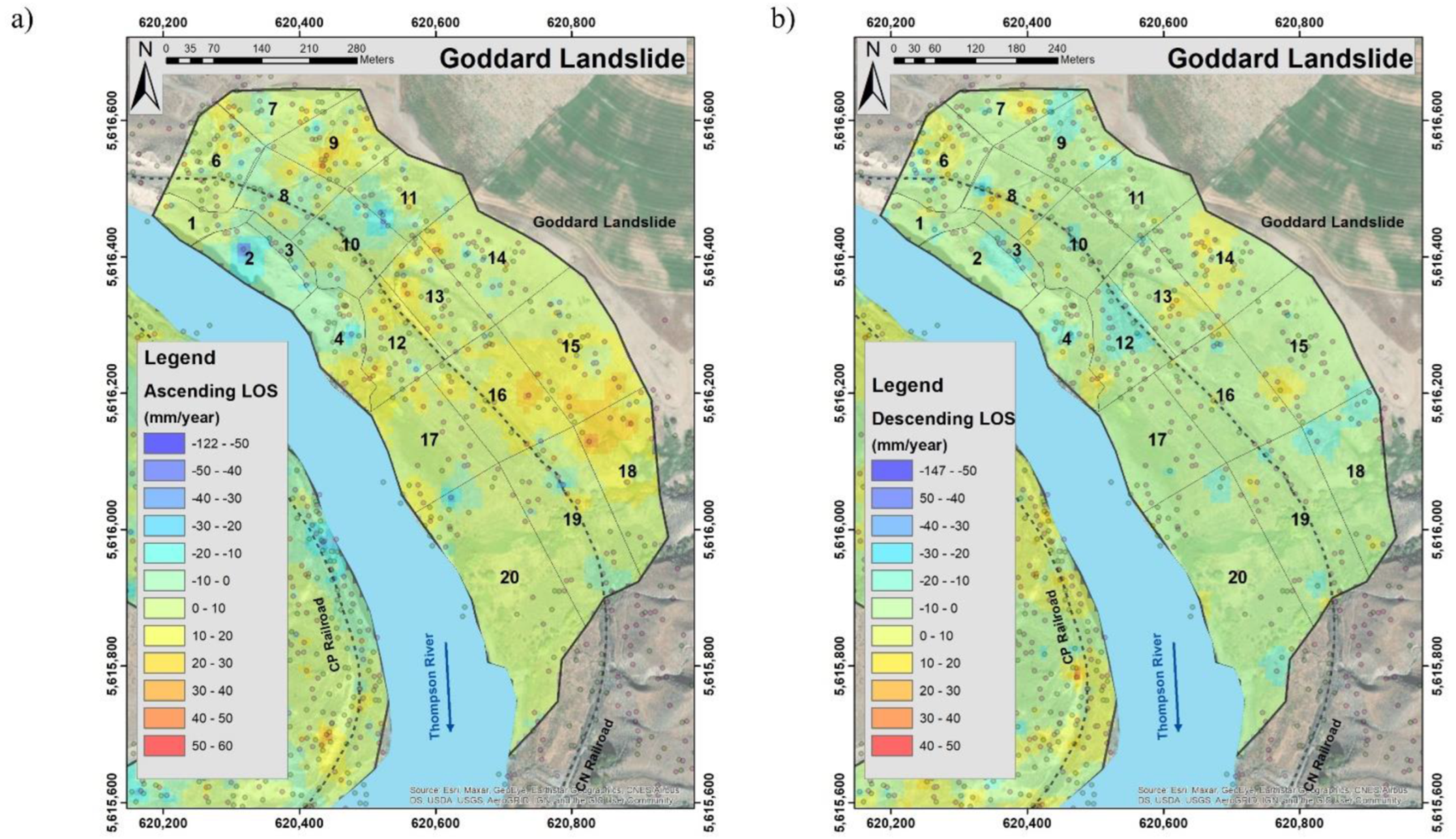
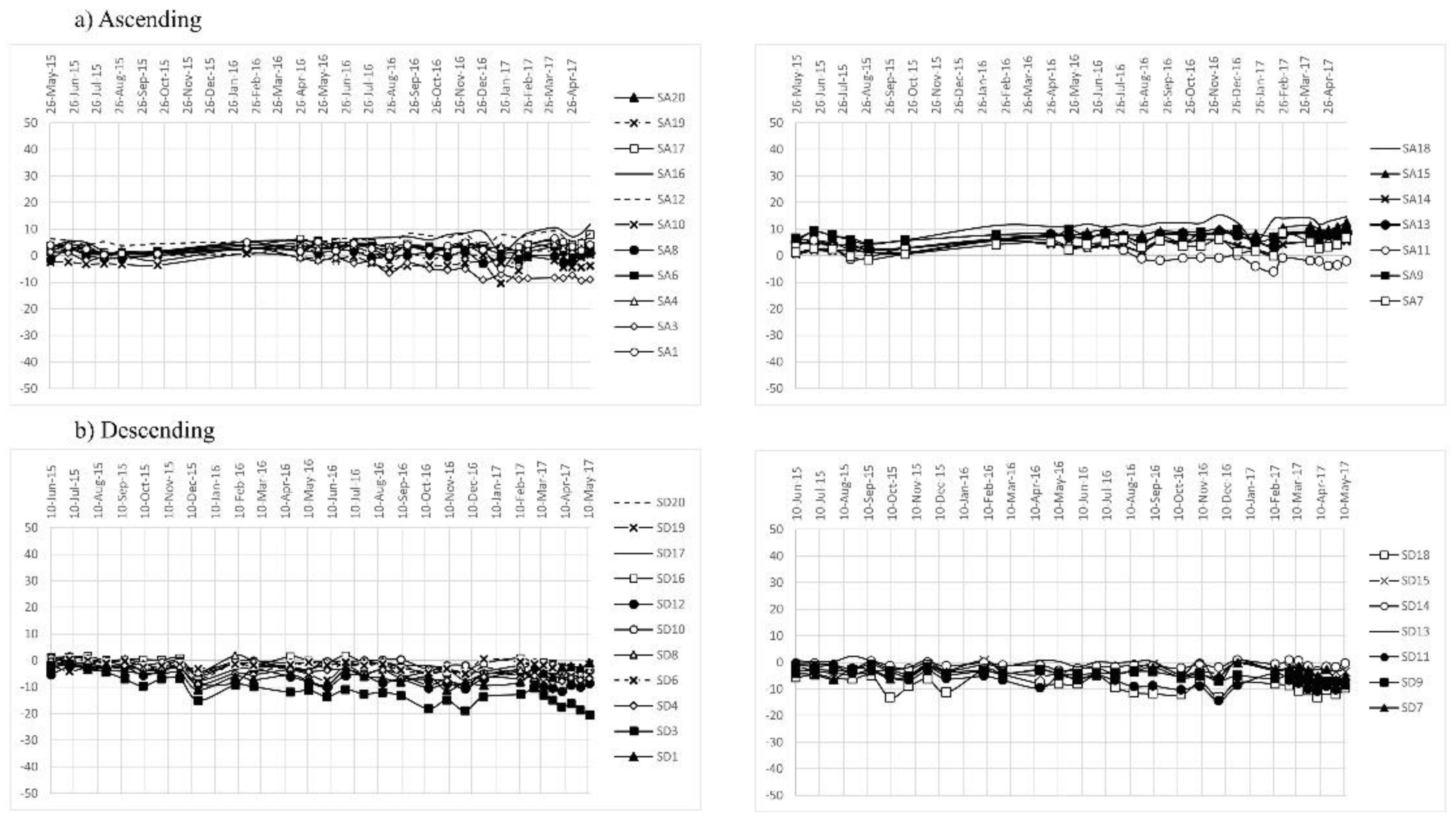
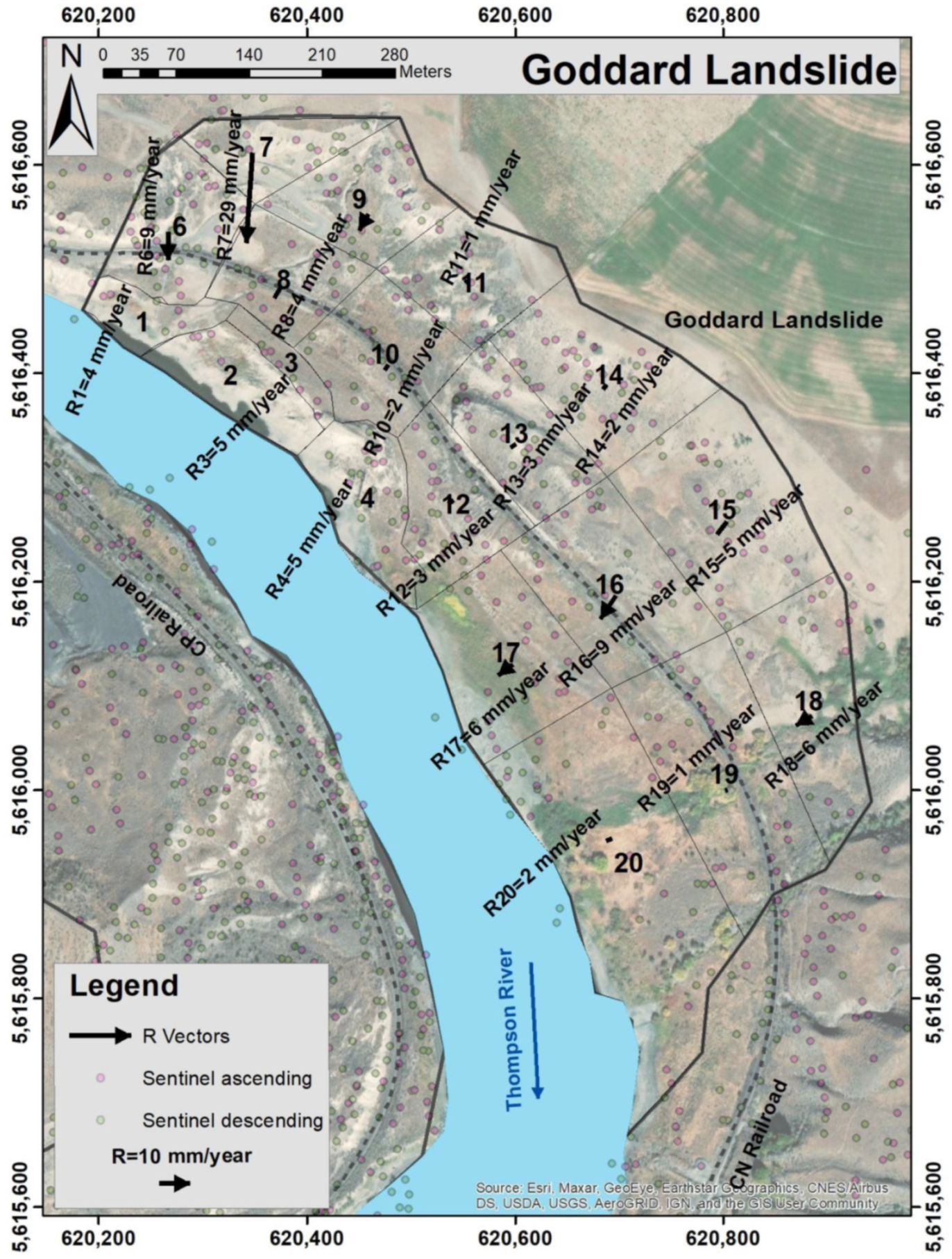
3.1. Goddard Landslide
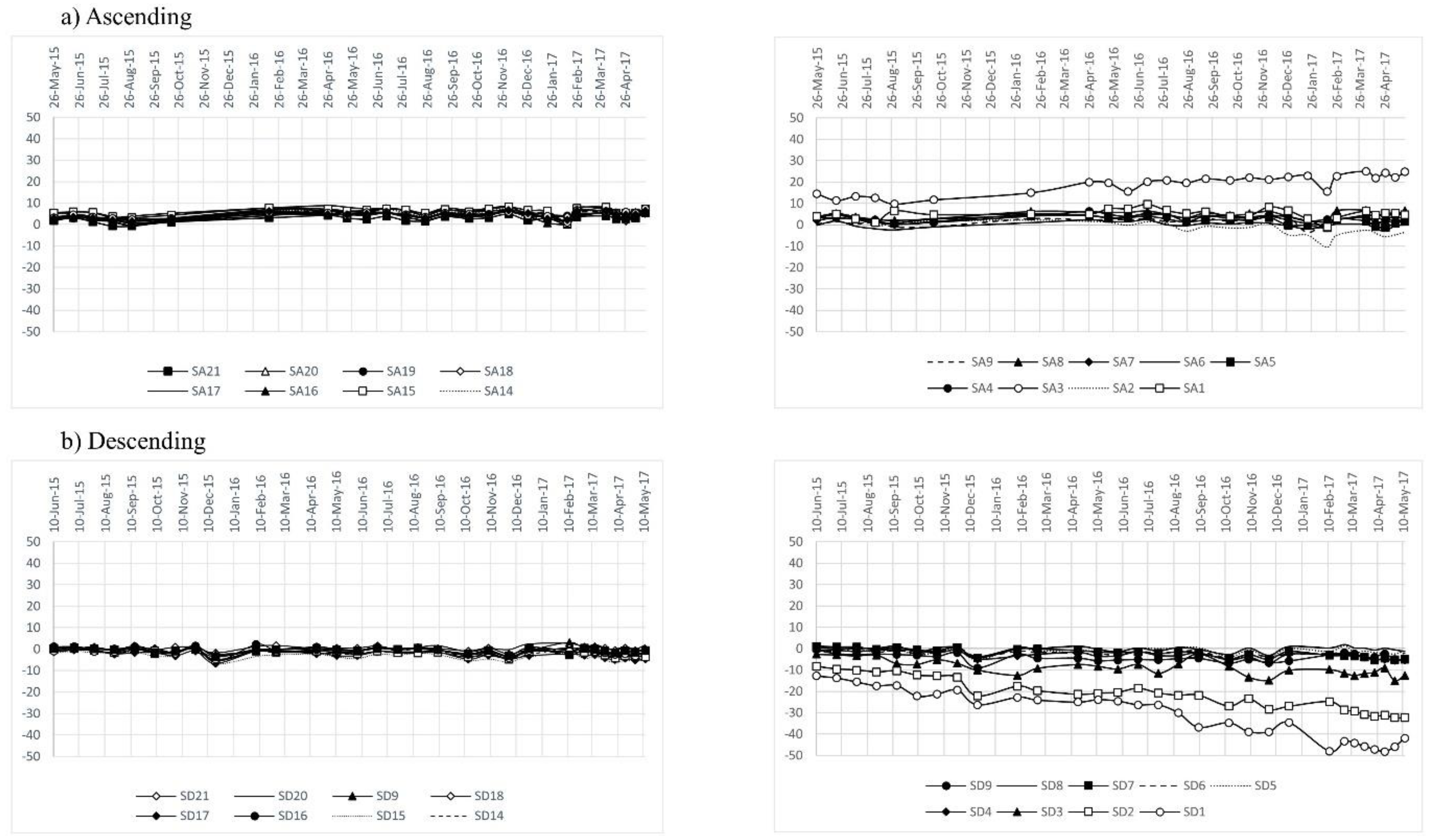
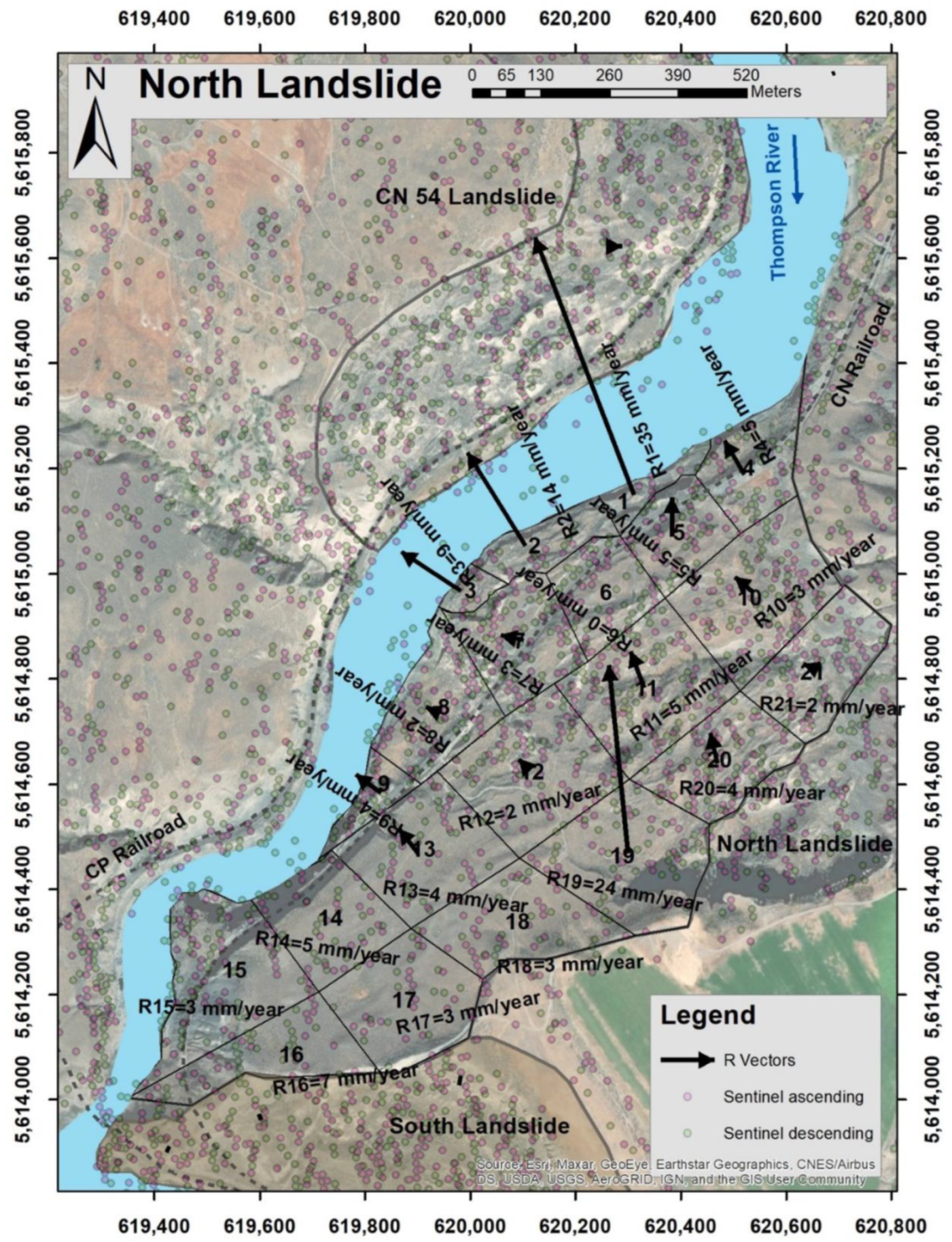
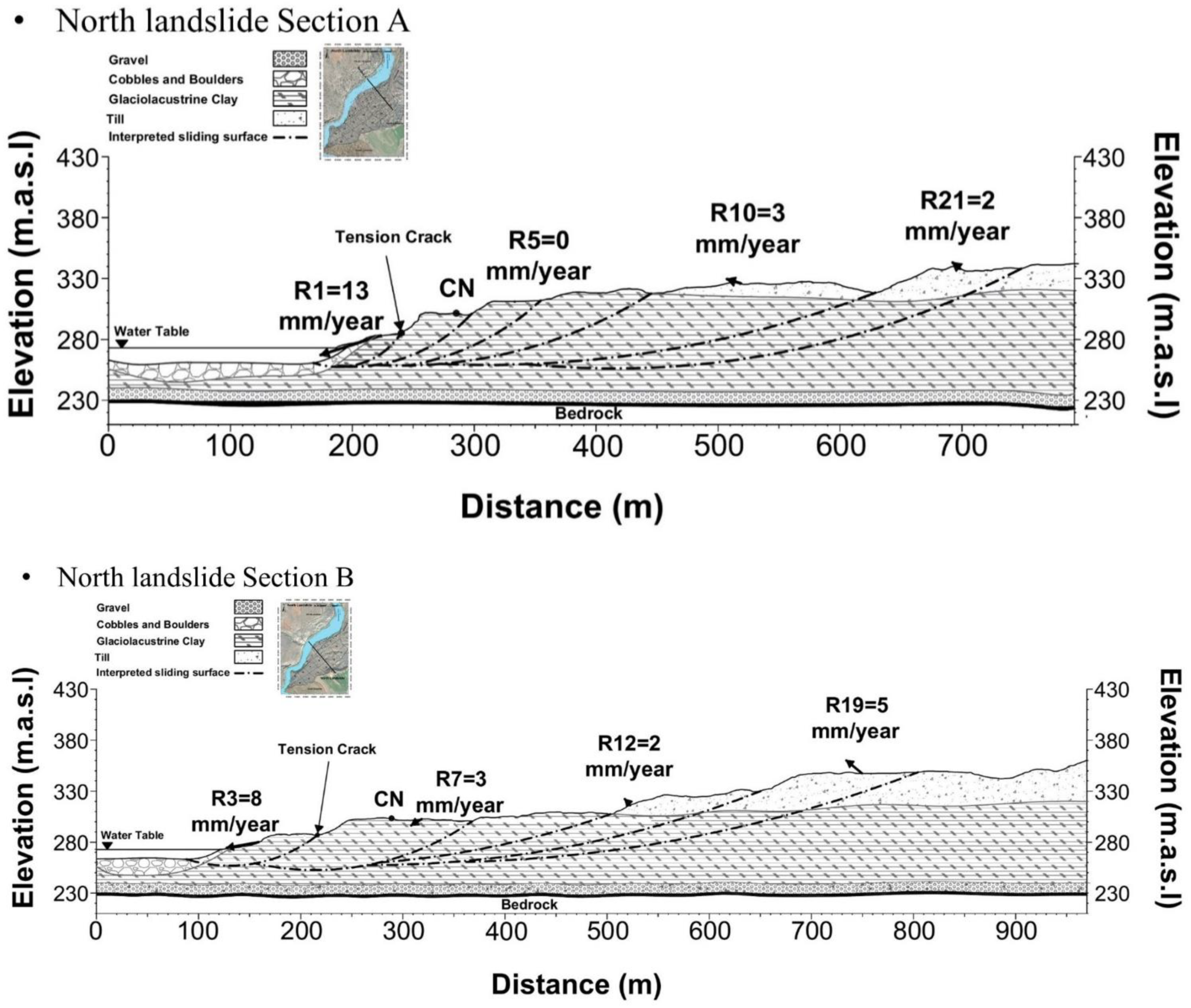
3.2. North Landslide
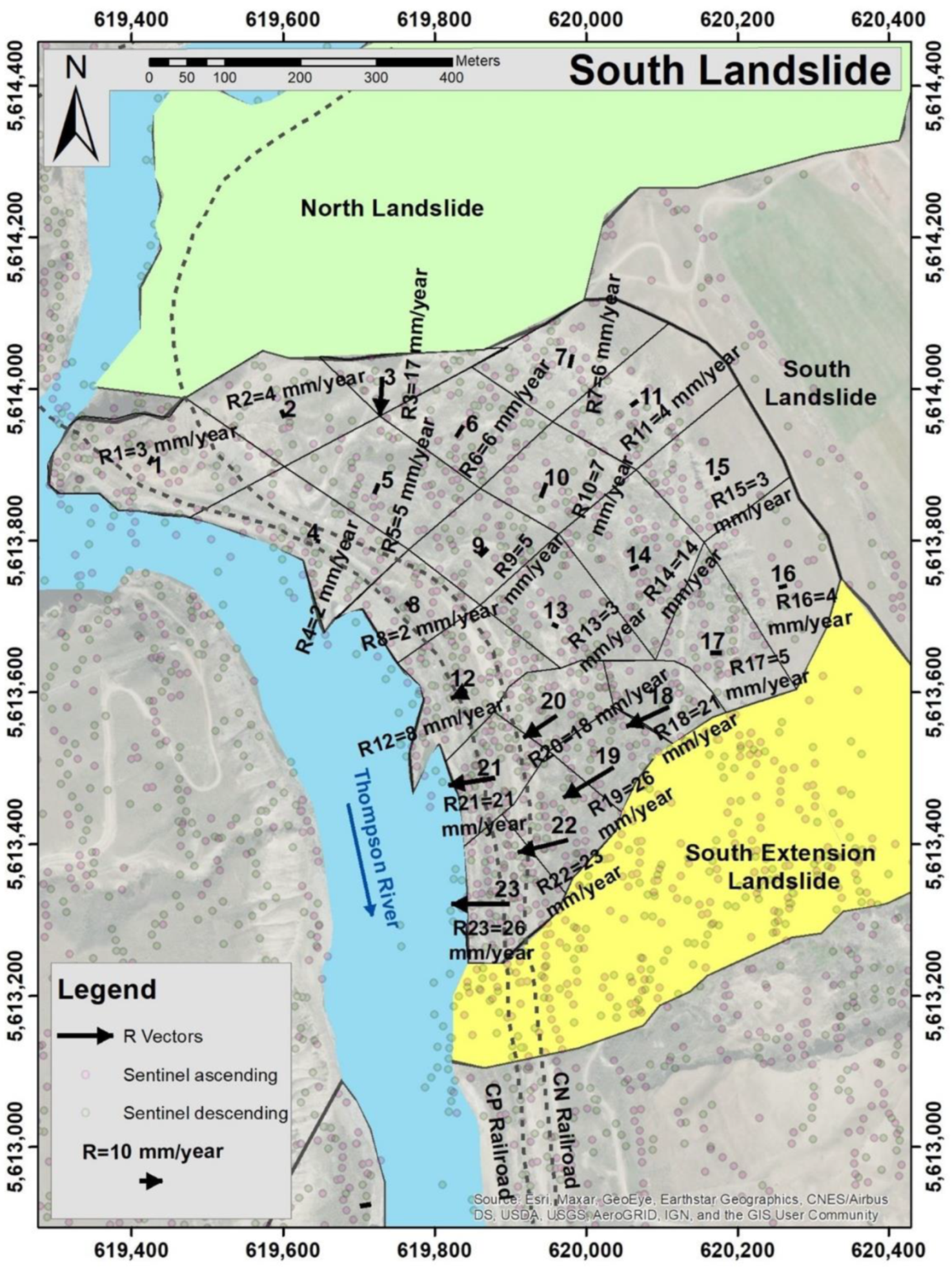
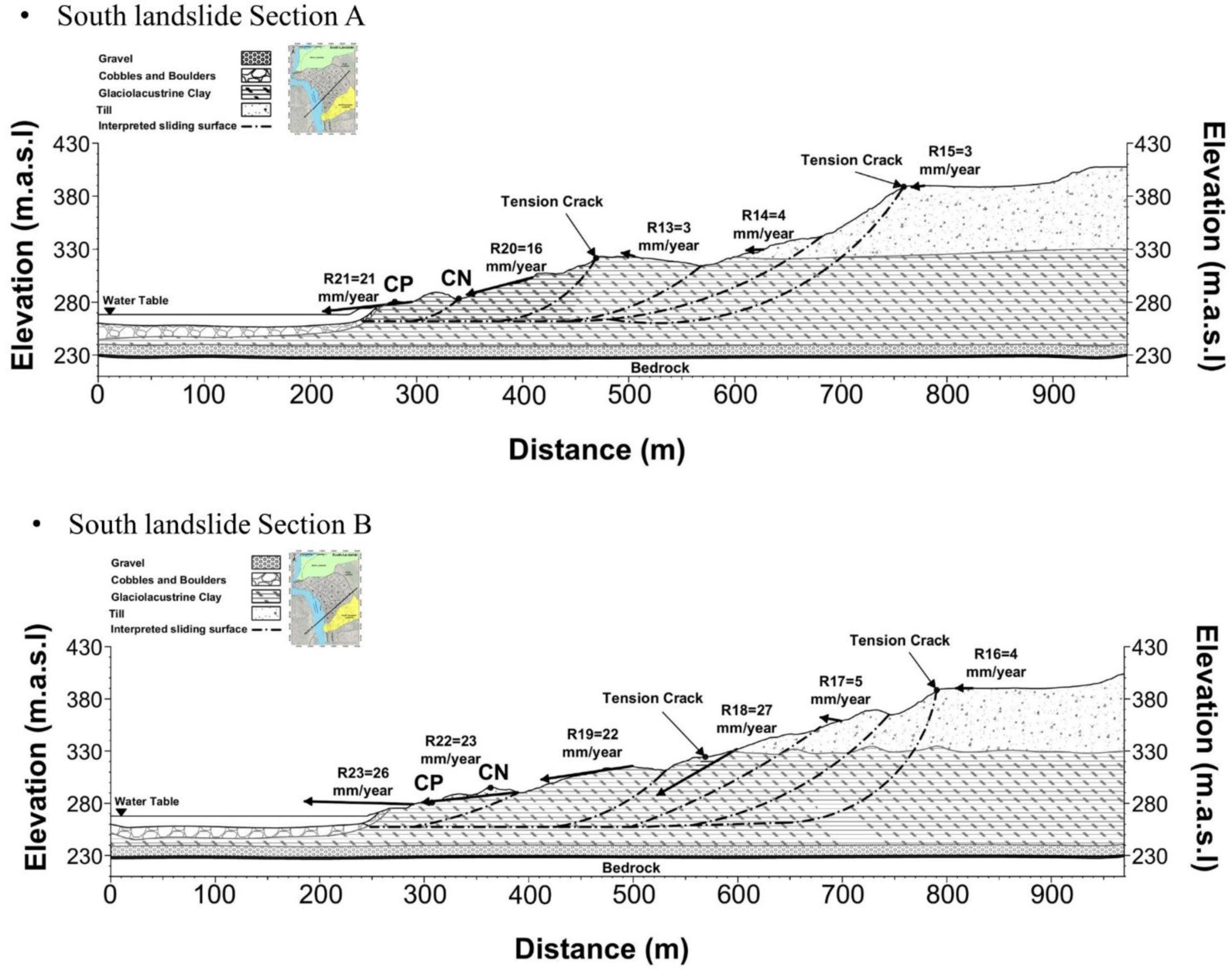
3.3. South Landslide
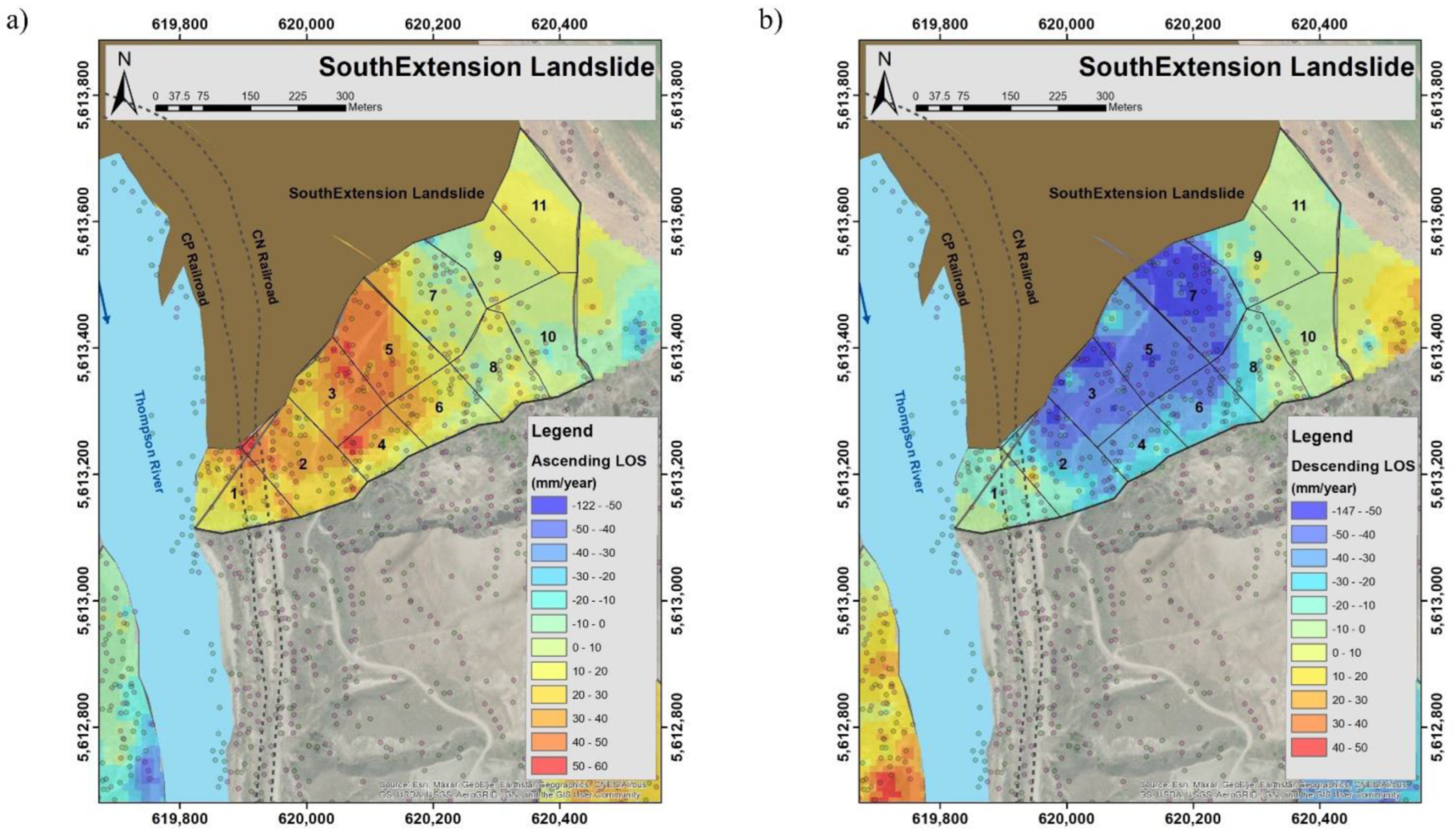
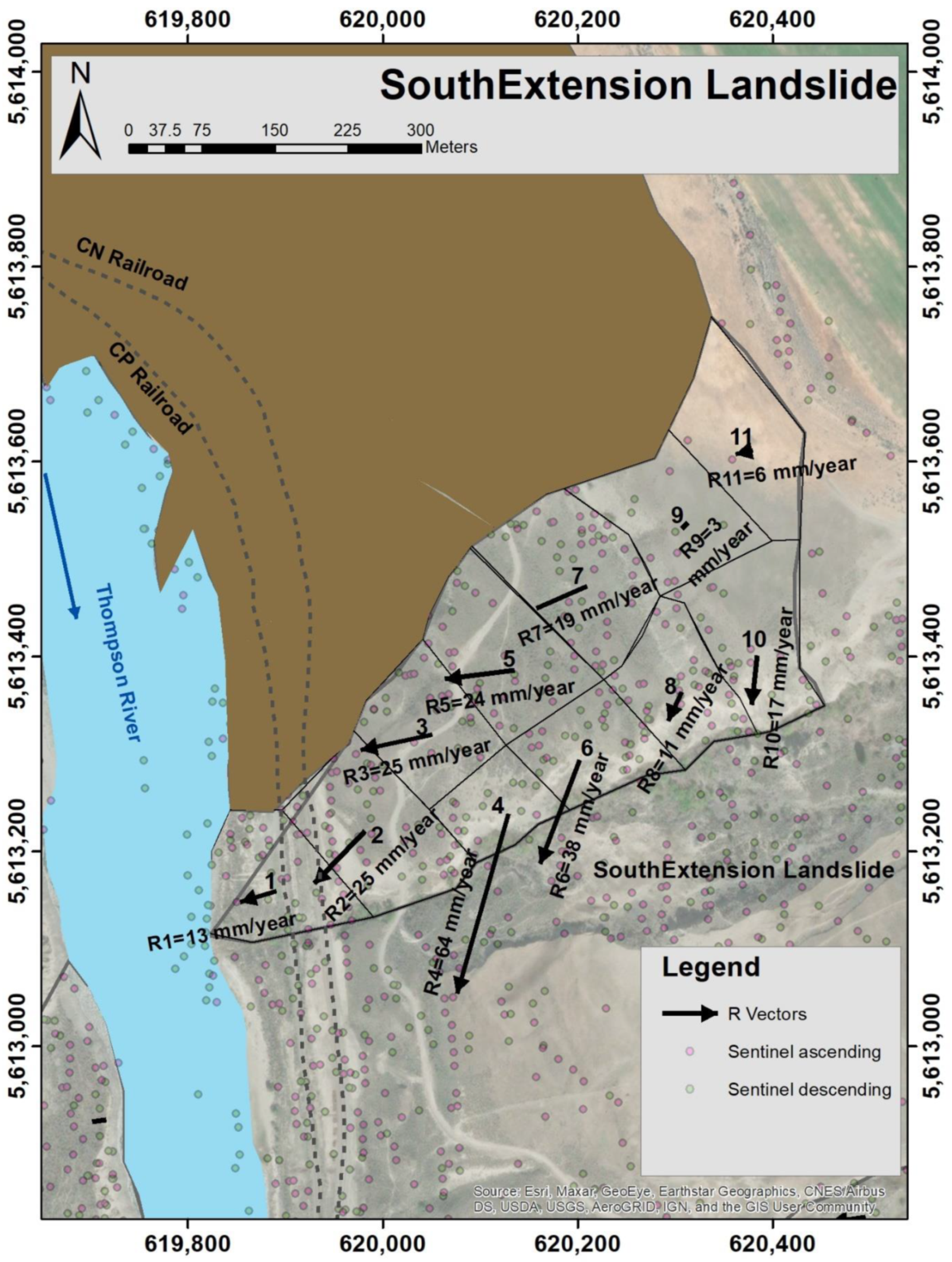
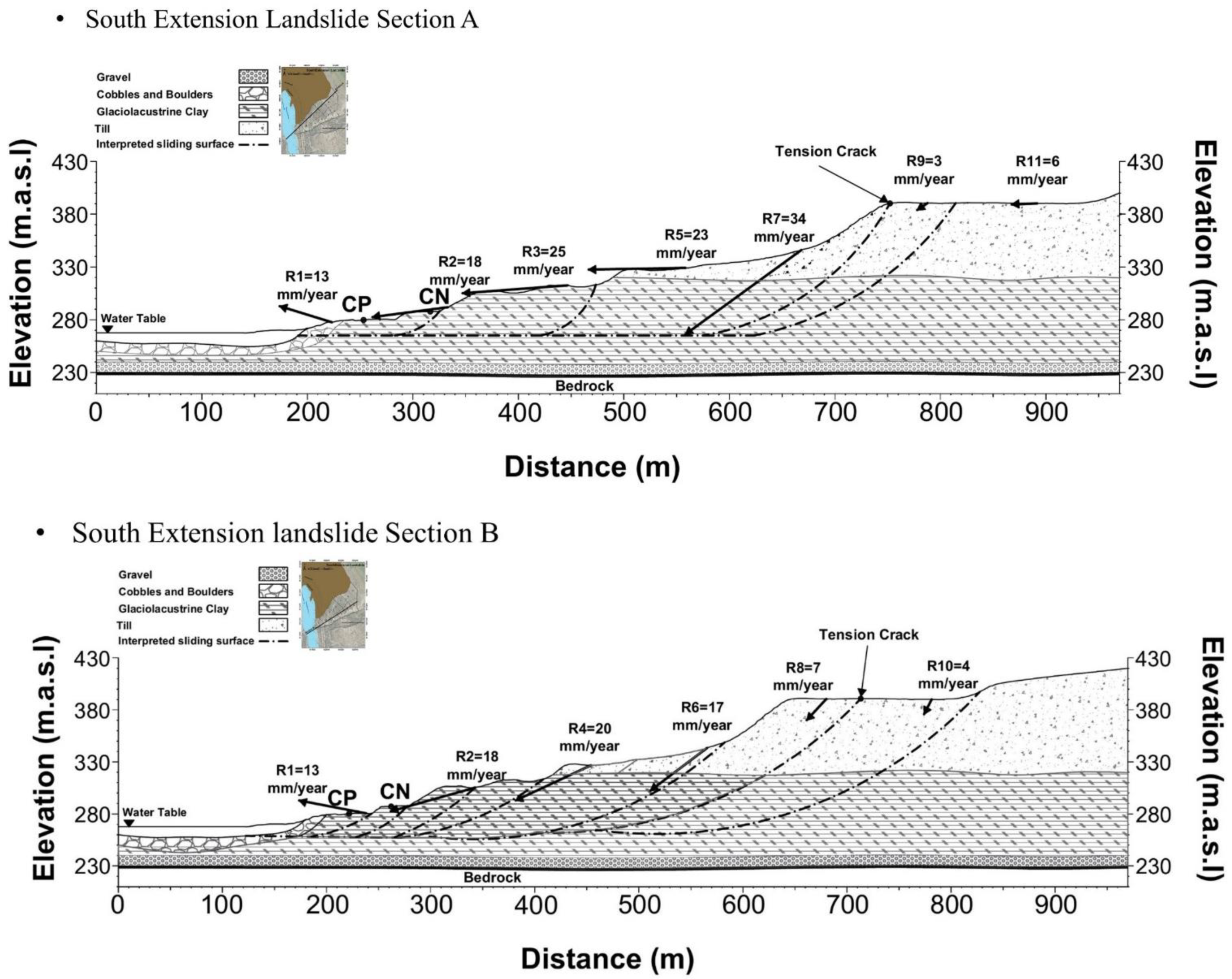
3.4. South Extension Landslide
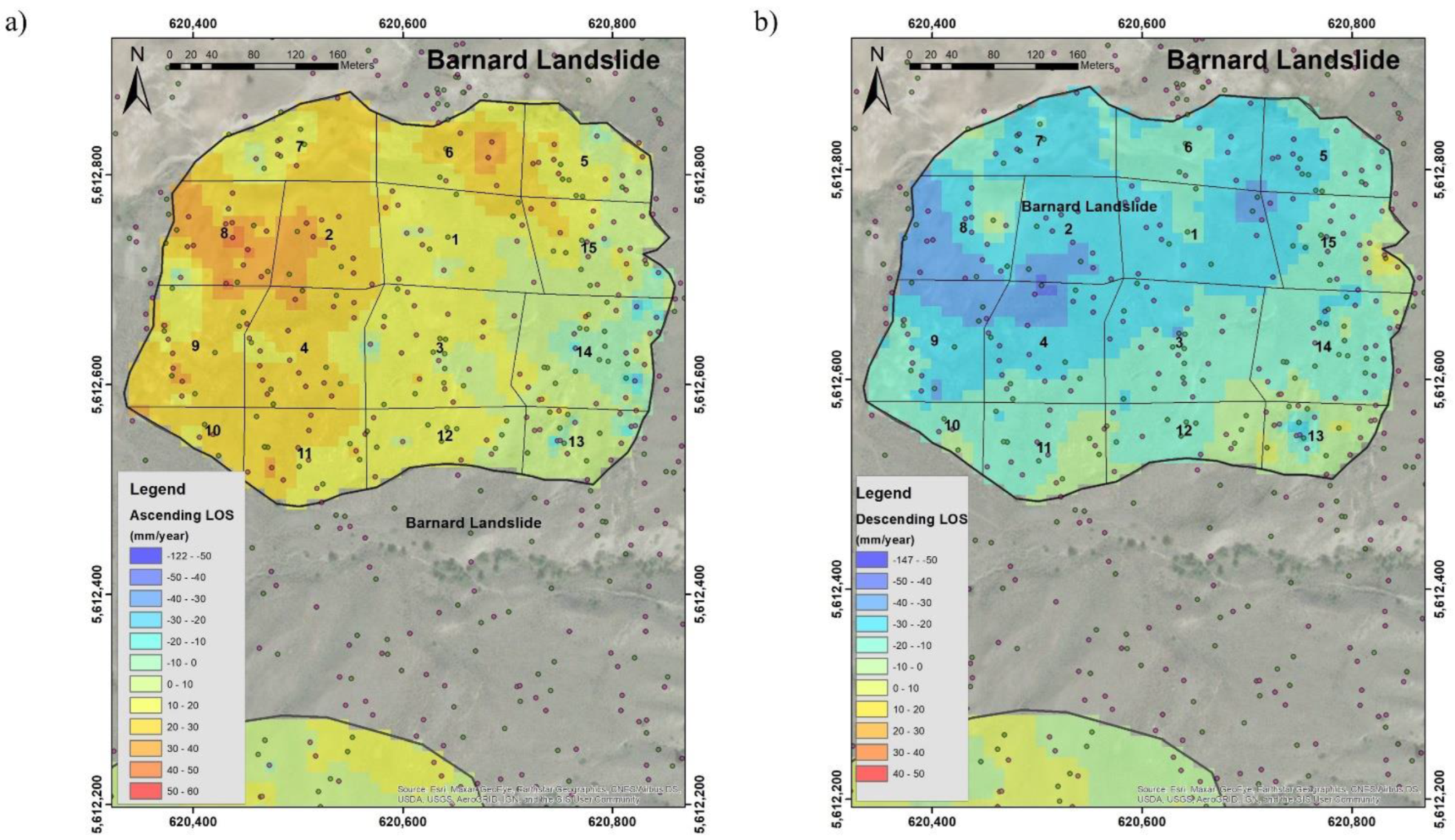
3.5. Barnard Landslide
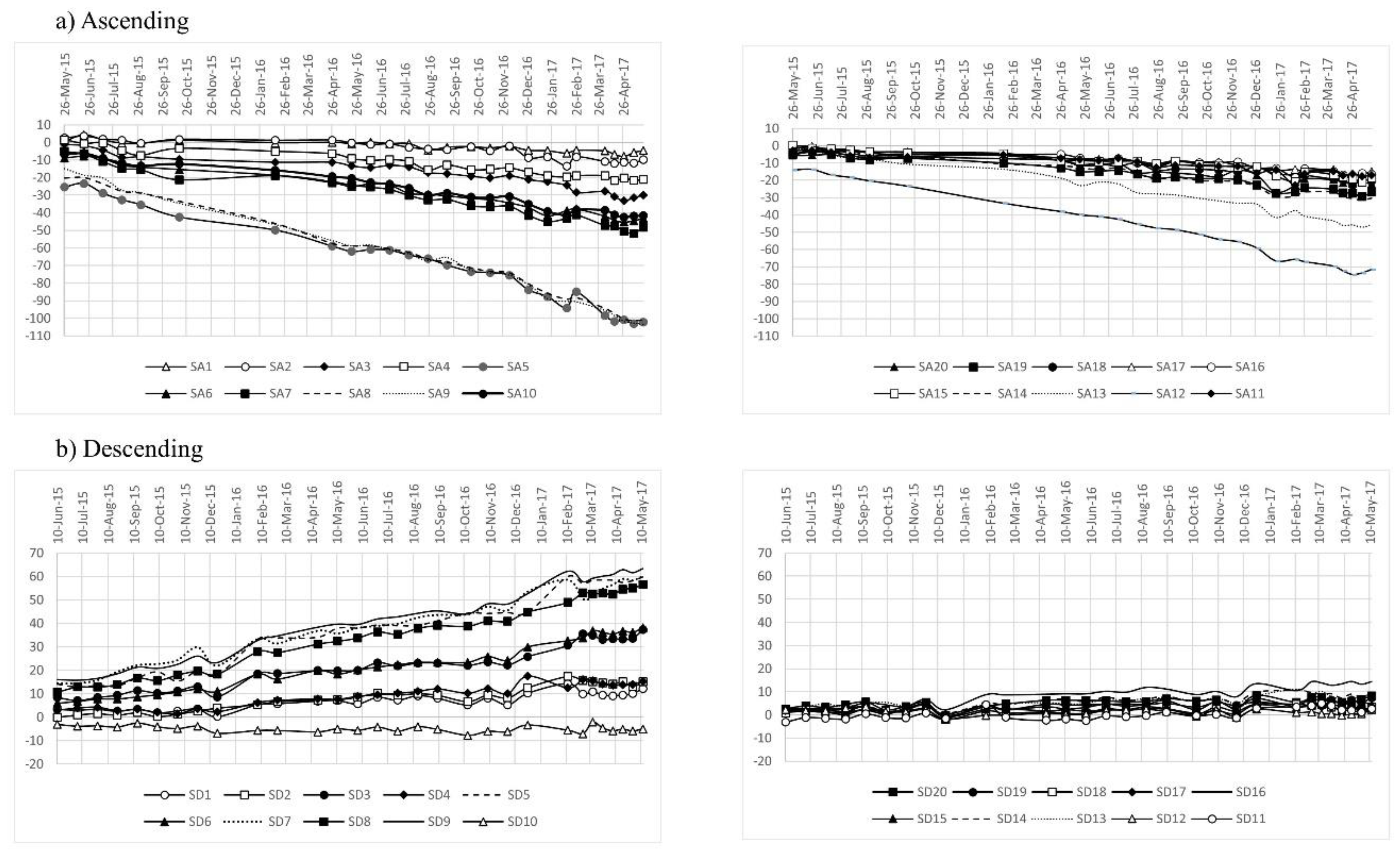
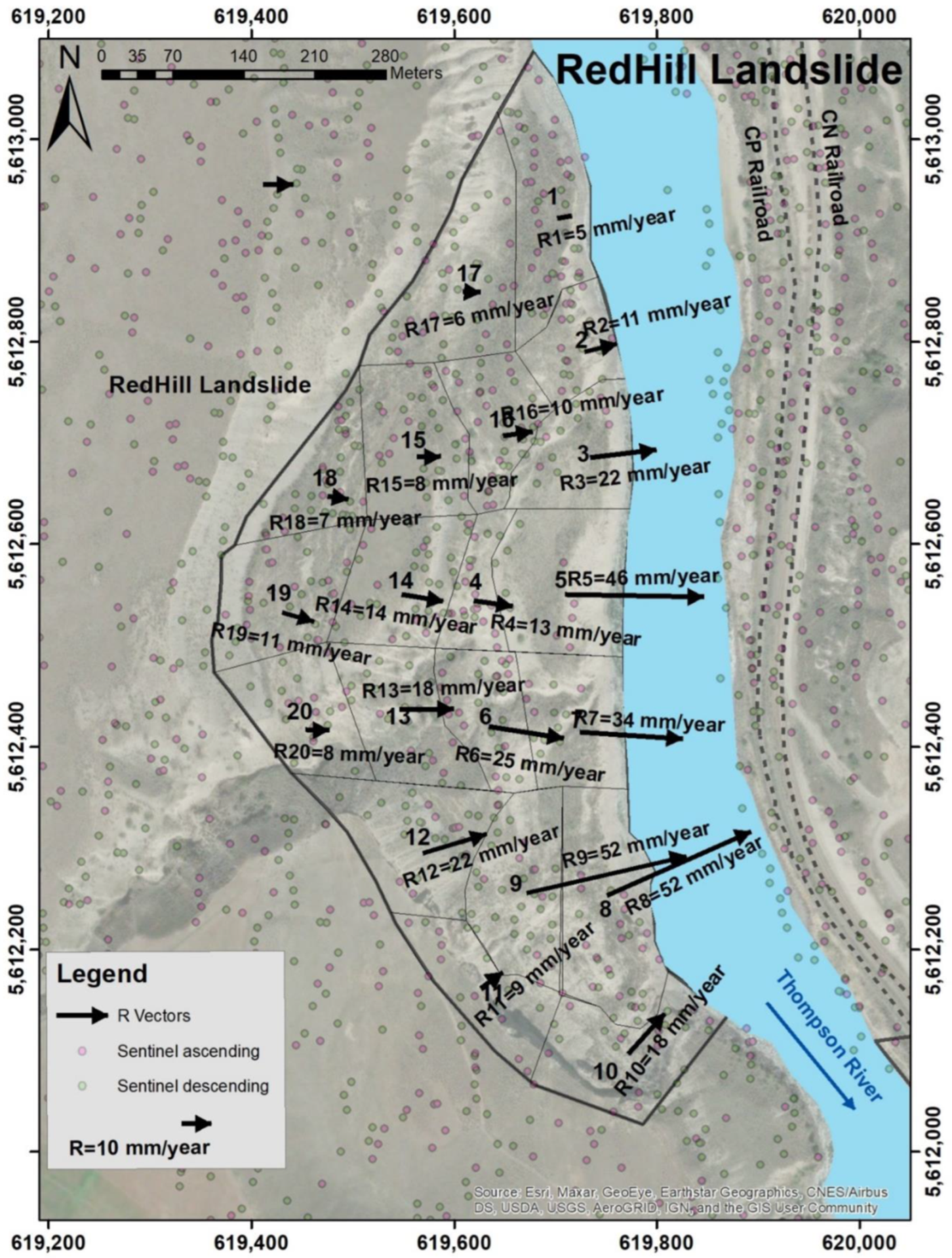
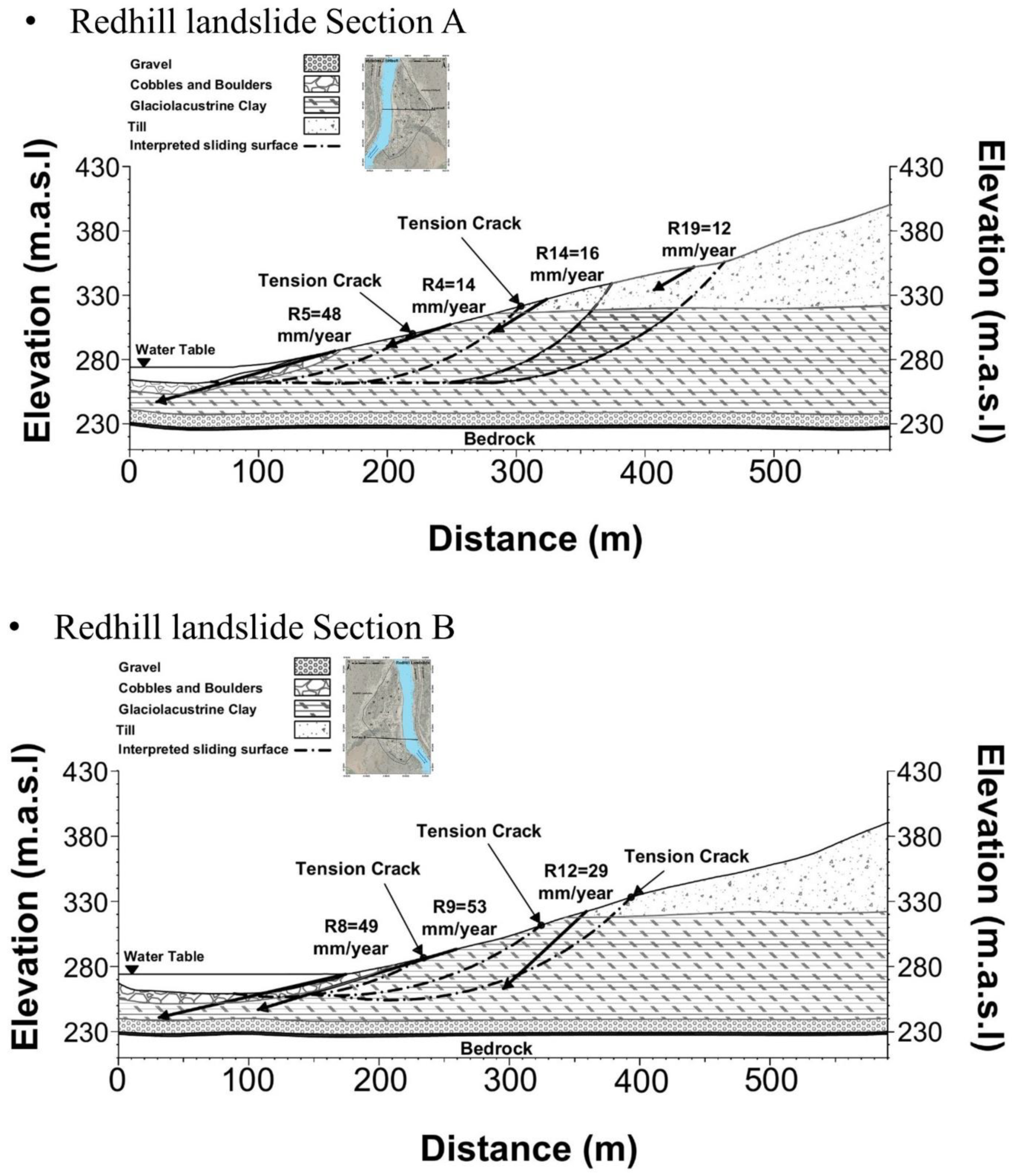
3.6. Redhill Landslide
4. Summary and Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Charrière, M.; Humair, F.; Froese, C.; Jaboyedoff, M.; Pedrazzini, A.; Longchamp, C. From the source area to the deposit: Collapse, fragmentation, and propagation of the Frank Slide. GSA Bull. 2016, 128, 332–351. [Google Scholar] [CrossRef]
- Cruden, D.M.; Martin, C.D. Before the Frank Slide. Can. Geotech. J. 2007, 44, 765–780. [Google Scholar] [CrossRef]
- Mei, S.; Poncos, V.; Froese, C. Mapping millimetre-scale ground deformation over the underground coal mines in the Frank Slide area, Alberta, Canada, using spaceborne InSAR technology. Can. J. Remote Sens. 2008, 34, 113–134. [Google Scholar] [CrossRef]
- Vallee, M. Falling in Place: Geoscience, Disaster, and Cultural Heritage at the Frank Slide, Canada’s Deadliest Rockslide. Space Cult. 2019, 22, 66–76. [Google Scholar] [CrossRef]
- Choe, B.-H.; Blais-Stevens, A.; Samsonov, S.; Dudley, J. Sentinel-1 and RADARSAT Constellation Mission InSAR Assessment of Slope Movements in the Southern Interior of British Columbia, Canada. Remote Sens. 2021, 13, 3999. [Google Scholar] [CrossRef]
- Huntley, D.; Bobrowsky, P.; Hendry, M.; Macciotta, R.; Elwood, D.; Sattler, K.; Best, M.; Chambers, J.; Meldrum, P. Application of multi-dimensional electrical resistivity tomography datasets to investigate a very slow-moving landslide near Ashcroft, British Columbia, Canada. Landslides 2019, 16, 1033–1042. [Google Scholar] [CrossRef]
- Journault, J.; Macciotta, R.; Hendry, M.T.; Charbonneau, F.; Huntley, D.; Bobrowsky, P.T. Measuring displacements of the Thompson River valley landslides, south of Ashcroft, BC, Canada, using satellite InSAR. Landslides 2018, 15, 621–636. [Google Scholar] [CrossRef]
- Macciotta, R.; Hendry, M.; Martin, C.D. Developing an early warning system for a very slow landslide based on displacement monitoring. Nat. Hazards 2016, 81, 887–907. [Google Scholar] [CrossRef]
- Rodriguez, J.; Deane, E.; Hendry, M.; Macciotta, R.; Evans, T.; Gräpel, C.; Skirrow, R. Practical evaluation of single-frequency dGNSS for monitoring slow-moving landslides. Landslides 2021, 18, 3671–3684. [Google Scholar]
- Macciotta, R.; Hendry, M. Remote Sensing Applications for Landslide Monitoring and Investigation in Western Canada. Remote Sens. 2021, 13, 366. [Google Scholar] [CrossRef]
- Lan, H.; Zhao, X.; Macciotta, R.; Peng, J.; Li, L.; Wu, Y.; Zhu, Y.; Liu, X.; Zhang, N.; Liu, S.; et al. The cyclic expansion and contraction characteristics of a loess slope and implications for slope stability. Sci. Rep. 2021, 11, 2250. [Google Scholar] [CrossRef] [PubMed]
- Woods, A.; Macciotta, R.; Hendry, M.; Stewart, T.; Marsh, J. Updated understanding of the deformation characteristics of the Checkerboard Creek rock slope through GB-InSAR monitoring. Eng. Geol. 2020, 281, 105974. [Google Scholar] [CrossRef]
- Macciotta, R.; Gräpel, C.; Skirrow, R. Fragmented Rockfall Volume Distribution from Photogrammetry-Based Structural Mapping and Discrete Fracture Networks. Appl. Sci. 2020, 10, 6977. [Google Scholar] [CrossRef]
- Deane, E.; Macciotta, R.; Hendry, M.; Gräpel, C.; Skirrow, R. Leveraging historical aerial photographs and digital photogrammetry techniques for landslide investigation—A practical perspective. Landslides 2020, 17, 1989–1996. [Google Scholar] [CrossRef]
- Huntley, D.; Rotheram-Clarke, D.; Cocking, R.; Joseph, J.; Bobrowsky, P. Understanding plateau and prairie landslides: Annual report on landslide research in the Thompson River valley, British Columbia, and the Assiniboine River valley, Manitoba-Saskatchewan 2020–2021. Geol. Surv. Can. 2021, 8838, 3–73. [Google Scholar]
- Huntley, D.; Rotheram-Clarke, D.; Pon, A.; Tomaszewicz, A.; Leighton, J.; Cocking, R.; Joseph, J. Benchmarked RADARSAT-2, SENTINEL-1 and RADARSAT Constellation Mission Change-Detection Monitoring at North Slide, Thompson River Valley, British Columbia: Ensuring a Landslide-Resilient National Railway Network. Can. J. Remote Sens. 2021, 47, 635–656. [Google Scholar] [CrossRef]
- Hendry, M.T.; Macciotta, R.; Martin, C.D.; Reich, B. Effect of Thompson River elevation on velocity and instability of Ripley Slide. Can. Geotech. J. 2015, 52, 257–267. [Google Scholar] [CrossRef]
- Huntley, D.; Bobrowsky, P.; Hendry, M.; Macciotta, R.; Best, M. Multi-technique Geophysical Investigation of a Very Slow-moving Landslide near Ashcroft, British Columbia, Canada. J. Environ. Eng. Geophys. 2019, 24, 87–110. [Google Scholar] [CrossRef]
- Eshraghian, A.; Martin, D.; Cruden, D. Complex Earth Slides in the Thompson River Valley, Ashcroft, British Columbia. Environ. Eng. 2007, 13, 161–181. [Google Scholar] [CrossRef]
- Huntley, D.; Holmes, J.; Bobrowsky, P.; Chambers, J.; Meldrum, P.; Wilkinson, P.; Donohue, S.; Elwood, D.; Sattler, K.; Hendry, M.; et al. Hydrogeological and geophysical properties of the very slow-moving Ripley Landslide, Thompson River valley, British Columbia. Can. J. Earth Sci. 2020, 57, 1371–1391. [Google Scholar] [CrossRef]
- Sattler, K.; Elwood, D.; Hendry, M.T.; Huntley, D.; Holmes, J.; Wilkinson, P.B.; Chambers, J.; Donohue, S.; Meldrum, P.I.; Macciotta, R.; et al. Quantifying the contribution of matric suction on changes in stability and displacement rate of a translational landslide in glaciolacustrine clay. Landslides 2021, 18, 1675–1689. [Google Scholar] [CrossRef]
- Schafer, M. Kinematics and Controlling Mechanics of the Slow Moving Ripley Landslide. Master’s Thesis, University of Alberta, Edmonton, AB, Canada, 2016. [Google Scholar]
- Xu, D.; Hu, X.-Y.; Shan, C.-L.; Li, R.-H. Landslide monitoring in southwestern China via time-lapse electrical resistivity tomography. Appl. Geophys. 2016, 13, 1–12. [Google Scholar] [CrossRef]
- Rodriguez, J.; Macciotta, R.; Hendry, M.T.; Roustaei, M.; Gräpel, C.; Skirrow, R. UAVs for monitoring, investigation, and mitigation design of a rock slope with multiple failure mechanisms—A case study. Landslides 2020, 17, 2027–2040. [Google Scholar] [CrossRef]
- Abe, T.; Iwahana, G.; Efremov, P.V.; Desyatkin, A.R.; Kawamura, T.; Fedorov, A.; Zhegusov, Y.; Yanagiya, K.; Tadono, T. Surface displacement revealed by L-band InSAR analysis in the Mayya area, Central Yakutia, underlain by continuous permafrost. Earth Planets Space 2020, 72, 138. [Google Scholar] [CrossRef]
- Herrera, G.; Gutierrez, F.; Garcia-Davalilo, J.C.; Guerrero, J.; Notti, D.; Galve, J.P.; Fernandez-Merodo, J.A.; Cooksley, G. Mul-ti-sensor advanced DInSAR monitoring of very slow landslides: The Tena Valley case study (Central Spanish Pyrenees). Remote Sens. Environ. 2012, 381–387, 08037. [Google Scholar]
- Colesanti, C.; Wasowski, J. Investigating landslides with space-borne Synthetic Aperture Radar (SAR) interferometry. Eng. Geol. 2006, 88, 173–199. [Google Scholar] [CrossRef]
- Vadivel, S.K.P.; Kim, D.J.; Kim, Y.C. Time-series InSAR Analysis and post-processing Using ISCE-StaMPS package for Meas-uring Bridge Displacements. Korean. J. Remote Sens. 2020, 36, 527–534. [Google Scholar]
- Motagh, M.; Shamshiri, R.; Haghighi, M.H.; Wetzel, H.-U.; Akbari, B.; Nahavandchi, H.; Roessner, S.; Arabi, S. Quantifying groundwater exploitation induced subsidence in the Rafsanjan plain, southeastern Iran, using InSAR time-series and in situ measurements. Eng. Geol. 2017, 218, 134–151. [Google Scholar] [CrossRef]
- Hooper, A.; Bekaert, D.; Spaans, K.; Arıkan, M. Recent advances in SAR interferometry time series analysis for measuring crustal deformation. Tectonophysics 2012, 514–517, 1–13. [Google Scholar] [CrossRef]
- Chen, B.; Li, Z.; Zhang, C.; Ding, M.; Zhu, W.; Zhang, S.; Han, B.; Du, J.; Cao, Y.; Zhang, C.; et al. Wide Area Detection and Distribution Characteristics of Landslides along Sichuan Expressways. Remote Sens. 2022, 14, 3431. [Google Scholar] [CrossRef]
- Liu, Y.; Yao, X.; Gu, Z.; Zhou, Z.; Liu, X.; Chen, X.; Wei, S. Study of the Automatic Recognition of Landslides by Using InSAR Images and the Improved Mask R-CNN Model in the Eastern Tibet Plateau. Remote Sens. 2022, 14, 3362. [Google Scholar] [CrossRef]
- Mastro, P.; Masiello, G.; Serio, C.; Pepe, A. Change Detection Techniques with Synthetic Aperture Radar Images Experimens with Random Forests and Sentinel-1 Observations. Remote Sens. 2022, 14, 3323. [Google Scholar] [CrossRef]
- Abdel-Hamid, A.; Dubovyk, O.; Greve, K. The potential of sentinel-1 InSAR coherence for grasslands monitoring in Eastern Cape, South Africa. Int. J. Appl. Earth Obs. Geoinf. ITC J. 2021, 98, 102306. [Google Scholar] [CrossRef]
- Dumka, K.R.; SuriBabu, D.; Malik, K.; Prajapati, S.; Narain, P. PS-InSAR derived deformation study in the Kachchh, Western India. Appl. Comput. Geosci. 2020, 8, 100041. [Google Scholar] [CrossRef]
- Castellazzi, P.; Schmid, W. Interpreting C-band InSAR ground deformation data for large-scale groundwater management in Australia. J. Hydrol. Reg. Stud. 2021, 34, 100774. [Google Scholar] [CrossRef]
- Solari, L.; Del Soldato, M.; Raspini, F.; Barra, A.; Bianchini, S.; Confuorto, P.; Casagli, N.; Crosetto, M. Review of Satellite Interferometry for Landslide Detection in Italy. Remote Sens. 2020, 12, 1351. [Google Scholar] [CrossRef]
- Zhai, C.; Lu, Z. Remote Sensing of Landslides (A review). Remote Sens. 2018, 10, 279. [Google Scholar] [CrossRef]
- Lu, Z.; Kim, J. A Framework for Studying Hydrology-Driven Landslide Hazards in Northwestern US Using Satellite InSAR, Precipitation and Soil Moisture Observations: Early Results and Future Directions. GeoHazards 2021, 2, 17–40. [Google Scholar] [CrossRef]
- Mancini, F.; Grassi, F.; Cenni, N. A Workflow Based on SNAP–StaMPS Open-Source Tools and GNSS Data for PSI-Based Ground Deformation Using Dual-Orbit Sentinel-1 Data: Accuracy Assessment with Error Propagation Analysis. Remote Sens. 2021, 13, 753. [Google Scholar] [CrossRef]
- Porter, M.J.; Savigny, K.W.; Keegan, T.R.; Bunce, C.M.; MacKay, C. Controls on stability of the Thompson River landslides. In Proceedings of the 55th Canadian Geotechnical Conference, Niagara Falls, ON, Canada, 20–23 October 2002. [Google Scholar]
- Clague, J.J.; Evans, S.G. Geologic Framework of Large Historic Landslides in Thompson River Valley, British Columbia. Environ. Eng. Geosci. 2003, 9, 201–212. [Google Scholar] [CrossRef]
- Huntley, D.H.; Bobrowsky, P.T. Surficial geology and monitoring of the Ripley Slide, near Ashcroft, British Columbia, Canada. Geol. Surv. Can. Open File 2014, 7531, 21. [Google Scholar] [CrossRef]
- Stark, T.D.; Eid, H.T. Drained Residual Strength of Cohesive Soils. J. Geotech. Eng. 1994, 120, 856–871. [Google Scholar] [CrossRef]
- Ferretti, A.; Fumagalli, A.; Novali, F.; Prati, C.; Rocca, F.; Rucci, A. A new algorithm for processing interferometric data-stacks: SqueeSAR. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3460–3470. [Google Scholar] [CrossRef]
- TRE ALTAMIRA Group. Ground Deformation InSAR Analysis over the Thompson Canyon, British Columbia Technical Details; TRE ALTAMIRA Group: Vancouver, BC, Canada, 2018. [Google Scholar]
- Soltanieh, A.; Macciotta, R. Updated understanding of the Ripley landslide kinematics using satellite InSAR. Geosciences 2022, 12, 298. [Google Scholar] [CrossRef]
- ArcGIS, ArcMAP; Version 10.7.1; ESRI: Redlands, CA, USA, 2019.
- Eshraghian, A. Hazard Analysis of Reactivated Earth Slides in the Thompson River Valley, Ashcroft, British Columbia. Ph.D. Thesis, University of Alberta, Edmonton, AB, Canada, 2007. [Google Scholar]
- Hungr, O.; Leroueil, S.; Picarelli, L. The Varnes classification of landslide types, an update. Landslides 2014, 11, 167–194. [Google Scholar] [CrossRef]
- Cruden, D.M.; Varnes, D.J. Landslides: Investigation and Mitigation. Chapter 3—Landslides Types and Processes. In Transportation Research Board Special Report 247; Transportation Research Board: Washington, DC, USA, 1996. [Google Scholar]
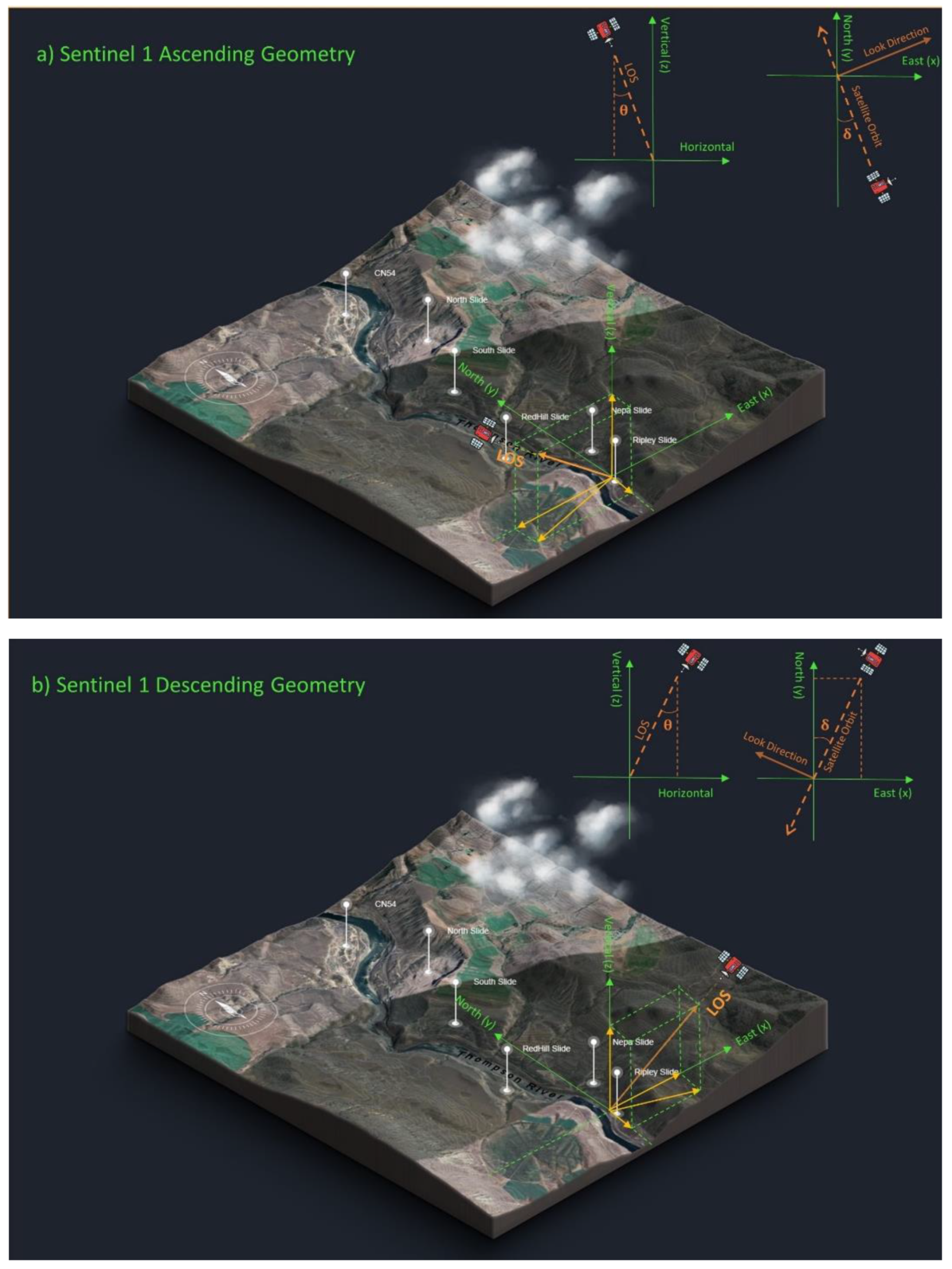





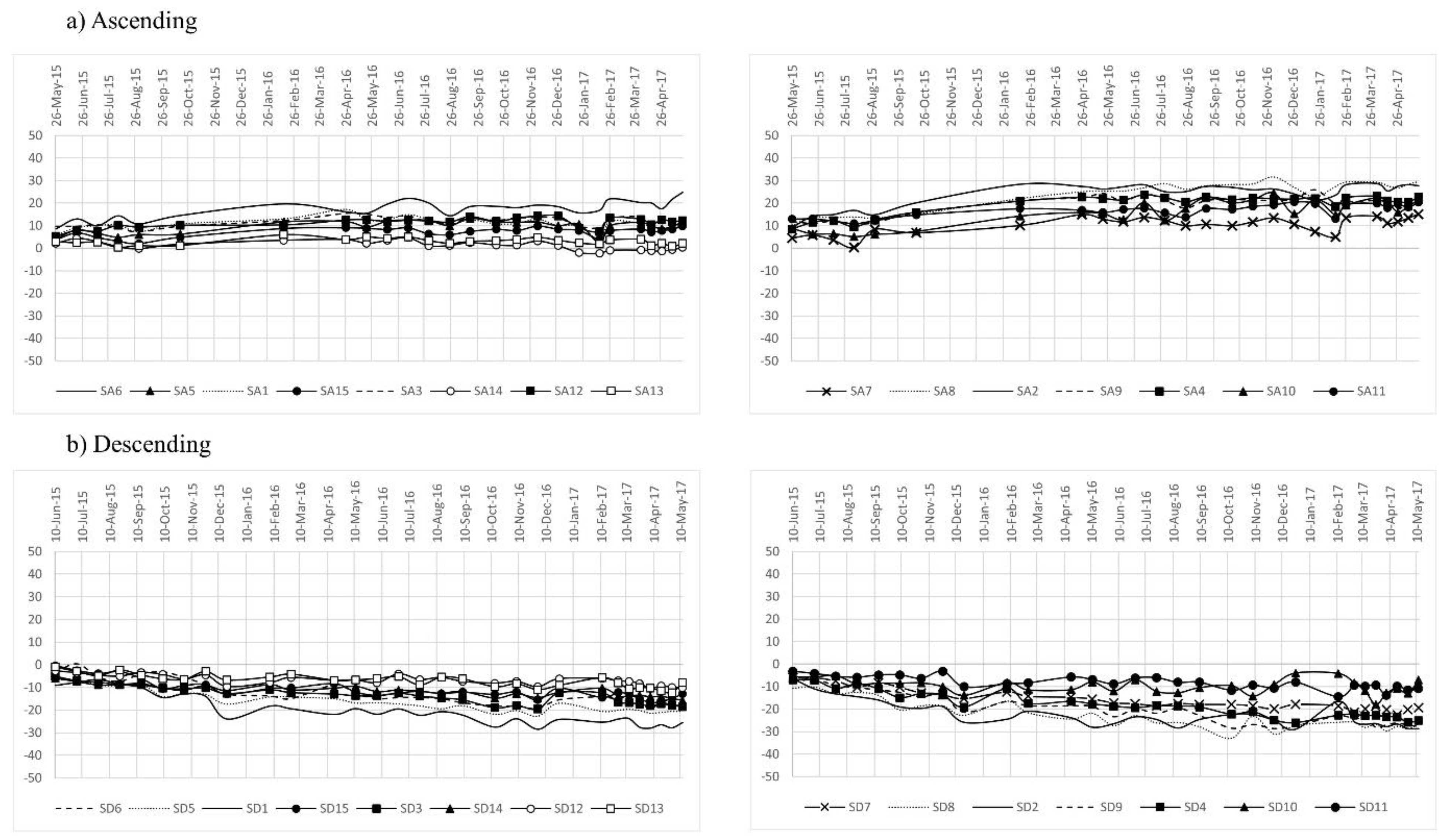
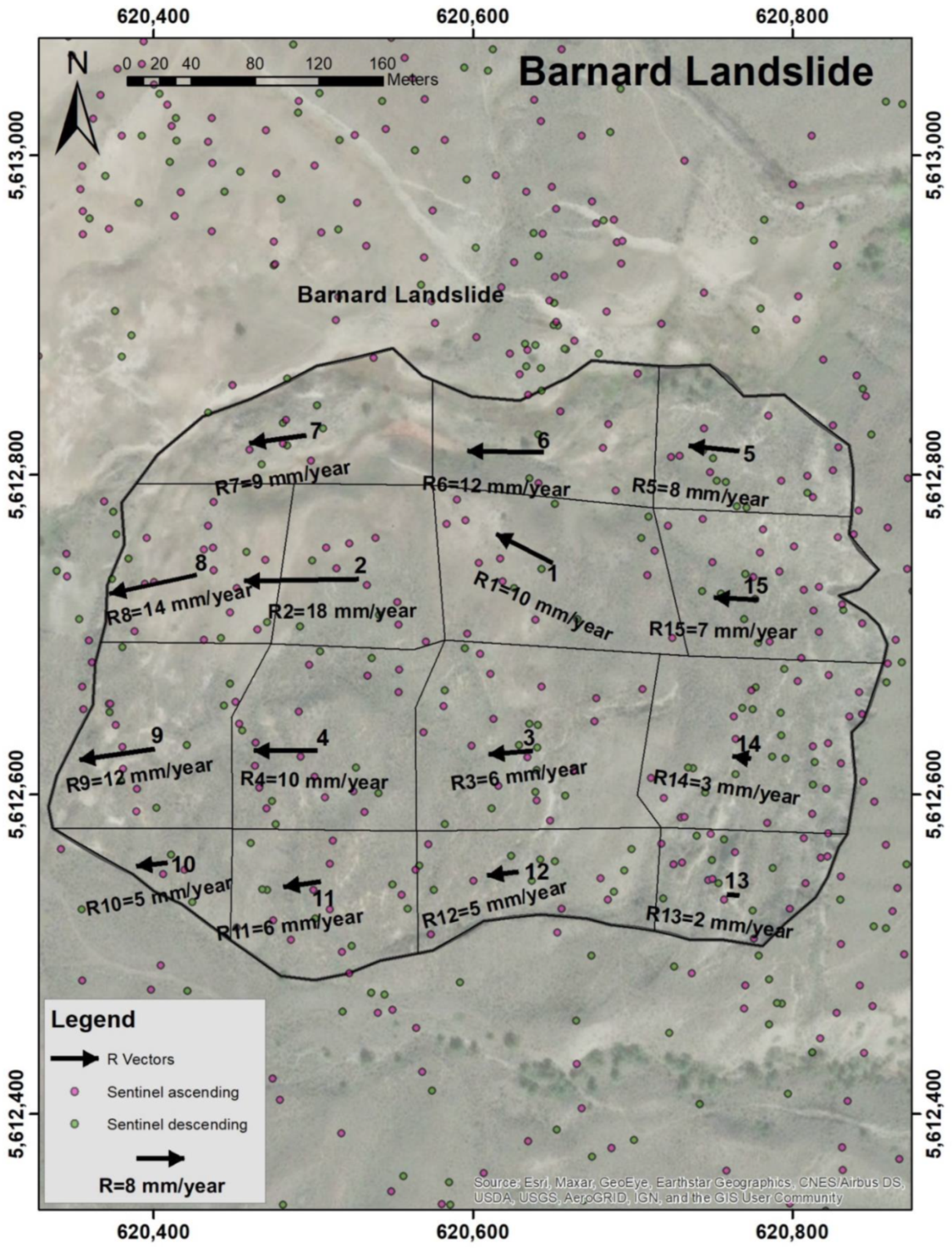
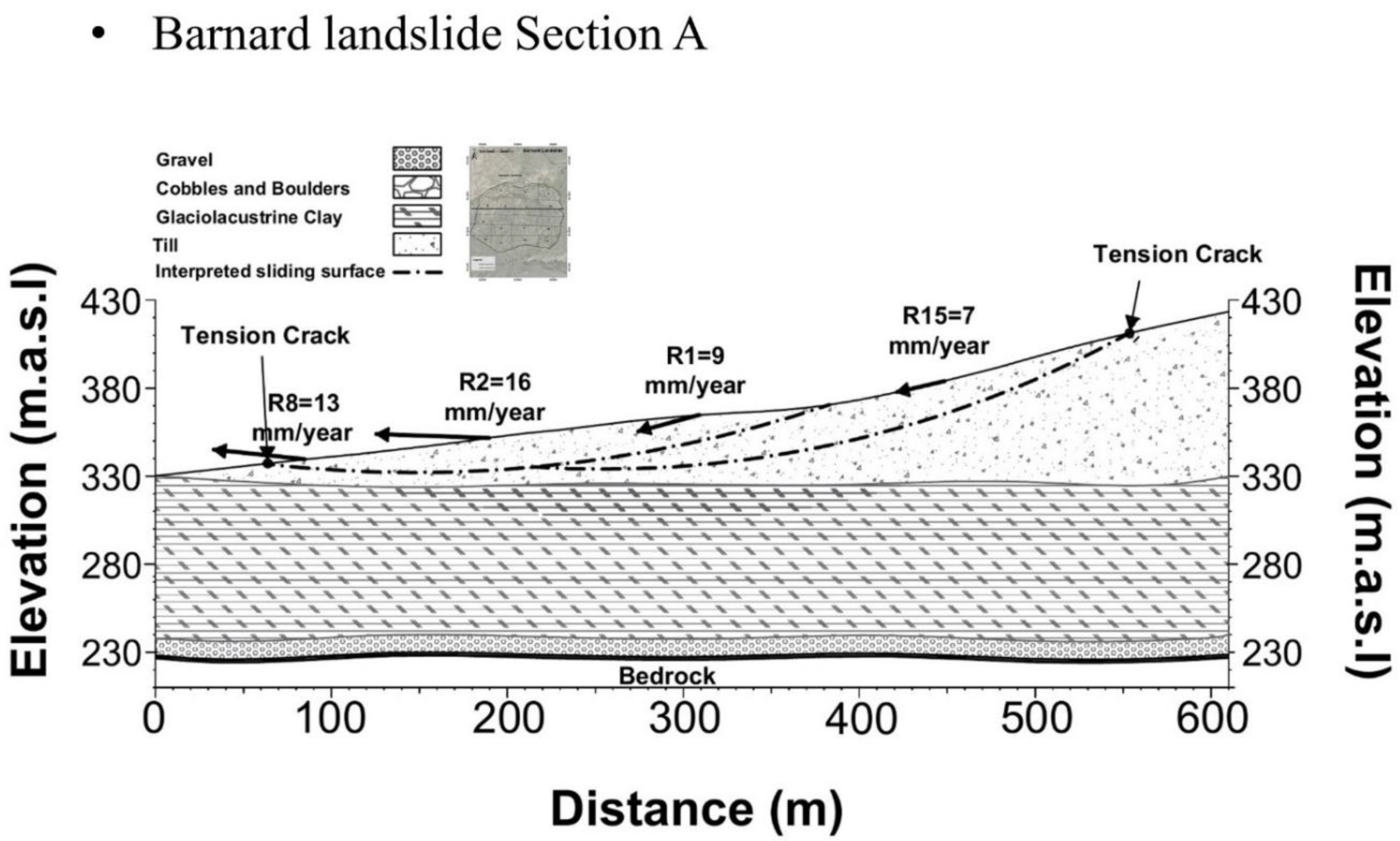
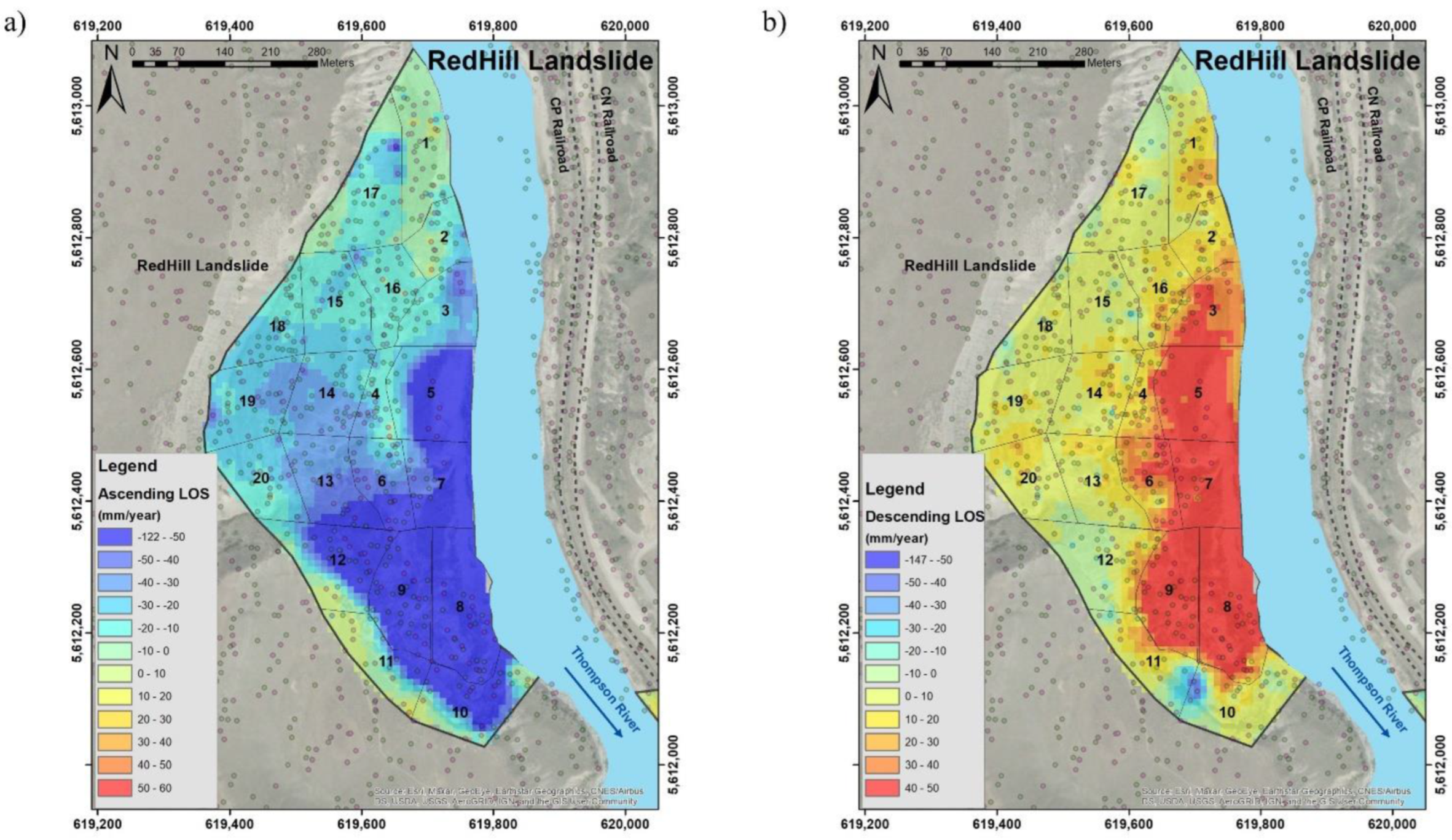
| Satellite | Orbit Geometry | Track | Sensor Mode | Symbol | Angle (degree) |
|---|---|---|---|---|---|
| Sentinel | Ascending | 64 | IW | θ δ | 38.66 11.33 |
| Sentinel | Descending | 115 | IW | θ δ | 44.29 7.79 |
| Radar Data Information | ||
|---|---|---|
| Satellite | Sentinel 1 | Sentinel 1 |
| Acquisition Geometry | Ascending | Descending |
| Period Covered by Imagery | 3 November 2014 to 17 March 2018 | 6 November 2014 to 1 April 2018 |
| No. of Processed Images | 51 | 59 |
| Coordinate System | WGS 1984 | WGS 1984 |
| Area of Interest | 869.2 | 869.2 |
| Number of PS + DS | 194,083 (112,343 PS, 81,740 DS) | 178,396 (89,510 PS, 88,886 DS) |
| Sensor Mode | IW | IW |
| Image Resolution | 20 m × 5 m | 20 m × 5 m |
| Area | Recorded Date | Total Magnitude (mm/year) | Horizontal Magnitude (mm/year) | X Direction Component (mm/year) | Y Direction Component (mm/year) | Z Direction Component (mm/year) | Azimuth Angle (degree) | Angle with Horizontal Plane (degree) |
|---|---|---|---|---|---|---|---|---|
| R1 | May 2015 to May 2017 | 4 | 4 | −2 | −3 | −2 | 208 | 27 |
| R2 | May 2015 to May 2017 | Insufficient data | ||||||
| R3 | May 2015 to May 2017 | 11 | 5 | −4 | −4 | −10 | 222 | 62 |
| R4 | May 2015 to May 2017 | 6 | 5 | −3 | −4 | −2 | 213 | 27 |
| R6 | May 2015 to May 2017 | 9 | 9 | 0 | −9 | −2 | 182 | 11 |
| R7 | May 2015 to May 2017 | 29 | 29 | −2 | −29 | −3 | 184 | 5 |
| R8 | May 2015 to May 2017 | 4 | 4 | −2 | −4 | −1 | 210 | 8 |
| R9 | May 2015 to May 2017 | 6 | 6 | −3 | −5 | −1 | 210 | 13 |
| R10 | May 2015 to May 2017 | 3 | 2 | −1 | −2 | −2 | 212 | 42 |
| R11 | May 2015 to May 2017 | 4 | 1 | 0 | 0 | −4 | 223 | 82 |
| R12 | May 2015 to May 2017 | 3 | 3 | −2 | −2 | −1 | 226 | 13 |
| R13 | May 2015 to May 2017 | 3 | 3 | −2 | −2 | 0 | 234 | 2 |
| R14 | May 2015 to May 2017 | 2 | 2 | −1 | −2 | 1 | 217 | 25 |
| R15 | May 2015 to May 2017 | 5 | 5 | −3 | −4 | 1 | 217 | 11 |
| R16 | May 2015 to May 2017 | 9 | 9 | −5 | −7 | 1 | 213 | 4 |
| R17 | May 2015 to May 2017 | 6 | 6 | −4 | −3 | 0 | 233 | 0 |
| R18 | May 2015 to May 2017 | 6 | 6 | −5 | −3 | 2 | 239 | 16 |
| R19 | May 2015 to May 2017 | 2 | 1 | −1 | 0 | −2 | 246 | 65 |
| R20 | May 2015 to May 2017 | 3 | 2 | −2 | −1 | −1 | 250 | 21 |
| Area | Recorded Date | Total Magnitude (mm/year) | Horizontal Magnitude (mm/year) | X Direction Component (mm/year) | Y Direction Component (mm/year) | Z Direction Component (mm/year) | Azimuth Angle (degree) | Angle with Horizontal Plane (degree) |
|---|---|---|---|---|---|---|---|---|
| R1 | May 2015 to May 2017 | 35 | 35 | −12 | 32 | −4 | 339 | 7 |
| R2 | May 2015 to May 2017 | 16 | 14 | −8 | 12 | −8 | 328 | 28 |
| R3 | May 2015 to May 2017 | 9 | 9 | −8 | 5 | 1 | 303 | 8 |
| R4 | May 2015 to May 2017 | 5 | 5 | −2 | 4 | 0 | 330 | 3 |
| R5 | May 2015 to May 2017 | 5 | 5 | 0 | 5 | 0 | 0 | 3 |
| R6 | May 2015 to May 2017 | 0 | 0 | 0 | 0 | 0 | − | − |
| R7 | May 2015 to May 2017 | 3 | 3 | −3 | 1 | −2 | 282 | 30 |
| R8 | May 2015 to May 2017 | 2 | 2 | −2 | 1 | 1 | 295 | 18 |
| R9 | May 2015 to May 2017 | 4 | 4 | −3 | 1 | −2 | 282 | 3 |
| R10 | May 2015 to May 2017 | 4 | 3 | −3 | 2 | 0 | 306 | 3 |
| R11 | May 2015 to May 2017 | 5 | 5 | −2 | 4 | 2 | 339 | 18 |
| R12 | May 2015 to May 2017 | 3 | 2 | −1 | 2 | 2 | 318 | 39 |
| R13 | May 2015 to May 2017 | 4 | 4 | −2 | 3 | 0 | 322 | 2 |
| R14 | May 2015 to May 2017 | 5 | 5 | −3 | 5 | 0 | 327 | 1 |
| R15 | May 2015 to May 2017 | 3 | 3 | −2 | 2 | 0 | 307 | 4 |
| R16 | May 2015 to May 2017 | 7 | 7 | −2 | 7 | 0 | 344 | 3 |
| R17 | May 2015 to May 2017 | 3 | 3 | −2 | 2 | 0 | 311 | 4 |
| R18 | May 2015 to May 2017 | 3 | 3 | −2 | 2 | 1 | 318 | 12 |
| R19 | May 2015 to May 2017 | 24 | 24 | −2 | 23 | 4 | 354 | 9 |
| R20 | May 2015 to May 2017 | 4 | 4 | −1 | 3 | 2 | 346 | 29 |
| R21 | May 2015 to May 2017 | 2 | 2 | −2 | 1 | 1 | 292 | 38 |
| Area | Recorded Date | Total Magnitude (mm/year) | Horizontal Magnitude (mm/year) | X Direction Component (mm/year) | Y Direction Component (mm/year) | Z Direction Component (mm/year) | Azimuth Angle (degree) | Angle with Horizontal Plane (degree) |
|---|---|---|---|---|---|---|---|---|
| R1 | May 2015 to May 2017 | 3 | 3 | −1 | −3 | 0 | 207 | 1 |
| R2 | May 2015 to May 2017 | 4 | 4 | −2 | 4 | 0 | 157 | 4 |
| R3 | May 2015 to May 2017 | 17 | 17 | −1 | −17 | −3 | 184 | 10 |
| R4 | May 2015 to May 2017 | 2 | 2 | −1 | −2 | 0 | 196 | 6 |
| R5 | May 2015 to May 2017 | 5 | 5 | −2 | −5 | 1 | 200 | 7 |
| R6 | May 2015 to May 2017 | 6 | 6 | −3 | −5 | 1 | 211 | 8 |
| R7 | May 2015 to May 2017 | 6 | 6 | −1 | −6 | −3 | 192 | 26 |
| R8 | May 2015 to May 2017 | 3 | 2 | −1 | −2 | 3 | 222 | 49 |
| R9 | May 2015 to May 2017 | 5 | 5 | −3 | −5 | −1 | 210 | 11 |
| R10 | May 2015 to May 2017 | 7 | 7 | −2 | −7 | 1 | 199 | 8 |
| R11 | May 2015 to May 2017 | 4 | 4 | −3 | −2 | 0 | 232 | 0 |
| R12 | May 2015 to May 2017 | 8 | 8 | −7 | −4 | 0 | 243 | 2 |
| R13 | May 2015 to May 2017 | 3 | 3 | −3 | 1 | 1 | 295 | 13 |
| R14 | May 2015 to May 2017 | 4 | 4 | −4 | −2 | 0 | 247 | 2 |
| R15 | May 2015 to May 2017 | 3 | 3 | −3 | −1 | 0 | 258 | 7 |
| R16 | May 2015 to May 2017 | 4 | 4 | −4 | −1 | 1 | 270 | 11 |
| R17 | May 2015 to May 2017 | 5 | 5 | −5 | 0 | 1 | 270 | 11 |
| R18 | May 2015 to May 2017 | 24 | 21 | −19 | −9 | −11 | 245 | 27 |
| R19 | May 2015 to May 2017 | 26 | 26 | −22 | −13 | −1 | 239 | 3 |
| R20 | May 2015 to May 2017 | 19 | 18 | −15 | −10 | −4 | 236 | 12 |
| R21 | May 2015 to May 2017 | 21 | 21 | −21 | −3 | −2 | 261 | 10 |
| R22 | May 2015 to May 2017 | 23 | 23 | −22 | −6 | −4 | 256 | 10 |
| R23 | May 2015 to May 2017 | 26 | 26 | −26 | 0 | 1 | 270 | 1 |
| Area | Recorded Date | Total Magnitude (mm/year) | Horizontal Magnitude (mm/year) | X Direction Component (mm/year) | Y Direction Component (mm/year) | Z Direction Component (mm/year) | Azimuth Angle (degree) | Angle with Horizontal Plane (degree) |
|---|---|---|---|---|---|---|---|---|
| R1 | May 2015 to May 2017 | 14 | 13 | −13 | −4 | 4 | 253 | 16 |
| R2 | May 2015 to May 2017 | 25 | 25 | −18 | −18 | −2 | 224 | 5 |
| R3 | May 2015 to May 2017 | 25 | 25 | −25 | −5 | −2 | 258 | 4 |
| R4 | May 2015 to May 2017 | 65 | 64 | −18 | −62 | −8 | 196 | 7 |
| R5 | May 2015 to May 2017 | 24 | 24 | −23 | −3 | 0 | 263 | 1 |
| R6 | May 2015 to May 2017 | 39 | 38 | −14 | −35 | −10 | 201 | 15 |
| R7 | May 2015 to May 2017 | 23 | 19 | −18 | −8 | −13 | 246 | 34 |
| R8 | May 2015 to May 2017 | 12 | 11 | −5 | −10 | −5 | 205 | 24 |
| R9 | May 2015 to May 2017 | 4 | 3 | −2 | −2 | −2 | 225 | 26 |
| R10 | May 2015 to May 2017 | 18 | 17 | −2 | −17 | −4 | 186 | 12 |
| R11 | May 2015 to May 2017 | 6 | 6 | −6 | −1 | 0 | 257 | 2 |
| Area | Recorded Date | Total Magnitude (mm/year) | Horizontal Magnitude (mm/year) | X Direction Component (mm/year) | Y Direction Component (mm/year) | Z Direction Component (mm/year) | Azimuth Angle (degree) | Angle with Horizontal Plane (degree) |
|---|---|---|---|---|---|---|---|---|
| R1 | May 2015 to May 2017 | 10 | 10 | −9 | 4 | −3 | 297 | 15 |
| R2 | May 2015 to May 2017 | 18 | 18 | −16 | 8 | 1 | 297 | 2 |
| R3 | May 2015 to May 2017 | 7 | 6 | −6 | 0 | −3 | 266 | 29 |
| R4 | May 2015 to May 2017 | 10 | 10 | −10 | 0 | −1 | 270 | 3 |
| R5 | May 2015 to May 2017 | 8 | 8 | −8 | 1 | −2 | 276 | 10 |
| R6 | May 2015 to May 2017 | 12 | 12 | −12 | 0 | 1 | 271 | 6 |
| R7 | May 2015 to May 2017 | 9 | 9 | −9 | −1 | −1 | 262 | 4 |
| R8 | May 2015 to May 2017 | 14 | 14 | −13 | −3 | 1 | 258 | 6 |
| R9 | May 2015 to May 2017 | 12 | 12 | −12 | −2 | −3 | 262 | 14 |
| R10 | May 2015 to May 2017 | 7 | 5 | −5 | −1 | 4 | 264 | 37 |
| R11 | May 2015 to May 2017 | 6 | 6 | −6 | −1 | 0 | 262 | 1 |
| R12 | May 2015 to May 2017 | 5 | 5 | −5 | −1 | 0 | 263 | 0 |
| R13 | May 2015 to May 2017 | 3 | 2 | −2 | 0 | −2 | 275 | 44 |
| R14 | May 2015 to May 2017 | 5 | 3 | −3 | 0 | −4 | 278 | 48 |
| R15 | May 2015 to May 2017 | 7 | 7 | −7 | 0 | −2 | 273 | 13 |
| Area | Recorded Date | Total Magnitude (mm/year) | Horizontal Magnitude (mm/year) | X Direction Component (mm/year) | Y Direction Component (mm/year) | Z Direction Component (mm/year) | Azimuth Angle (degree) | Angle with Horizontal Plane (degree) |
|---|---|---|---|---|---|---|---|---|
| R1 | May 2015 to May 2017 | 6 | 5 | 5 | 1 | 1 | 81 | 11 |
| R2 | May 2015 to May 2017 | 11 | 11 | 10 | 3 | 1 | 75 | 4 |
| R3 | May 2015 to May 2017 | 22 | 22 | 22 | 3 | −1 | 83 | 2 |
| R4 | May 2015 to May 2017 | 14 | 13 | 13 | −2 | −4 | 98 | 18 |
| R5 | May 2015 to May 2017 | 48 | 46 | 46 | −1 | −13 | 91 | 16 |
| R6 | May 2015 to May 2017 | 25 | 25 | 25 | 0 | −2 | 89 | 4 |
| R7 | May 2015 to May 2017 | 34 | 34 | 34 | −2 | −1 | 94 | 2 |
| R8 | May 2015 to May 2017 | 53 | 52 | 48 | 21 | −11 | 66 | 12 |
| R9 | May 2015 to May 2017 | 54 | 52 | 51 | 12 | −15 | 77 | 16 |
| R10 | May 2015 to May 2017 | 21 | 18 | 12 | 13 | −11 | 42 | 32 |
| R11 | May 2015 to May 2017 | 9 | 9 | 7 | 5 | −2 | 54 | 14 |
| R12 | May 2015 to May 2017 | 29 | 22 | 21 | 6 | −19 | 73 | 41 |
| R13 | May 2015 to May 2017 | 23 | 18 | 18 | 0 | −14 | 89 | 37 |
| R14 | May 2015 to May 2017 | 16 | 14 | 13 | −2 | −8 | 99 | 31 |
| R15 | May 2015 to May 2017 | 10 | 8 | 8 | 0 | −6 | 89 | 37 |
| R16 | May 2015 to May 2017 | 11 | 10 | 10 | 1 | −2 | 82 | 9 |
| R17 | May 2015 to May 2017 | 8 | 6 | 6 | 0 | −5 | 93 | 40 |
| R18 | May 2015 to May 2017 | 8 | 7 | 7 | −1 | −5 | 99 | 36 |
| R19 | May 2015 to May 2017 | 13 | 11 | 11 | −3 | −6 | 106 | 29 |
| R20 | May 2015 to May 2017 | 9 | 8 | 8 | 0 | −4 | 91 | 64 |
| Landslide | Monitoring Timeline | Maximum Velocity (mm/year) | Minimum Velocity (mm/year) | Velocity Classification | Type of Landslide’s Kinematic |
|---|---|---|---|---|---|
| Goddard | May2015 to May 2017 | 2 | 29 | Very Slow | Retrogressive rotational |
| North | May2015 to May 2017 | 2 | 35 | Very Slow | Rotational on the toe |
| South | May2015 to May 2017 | 2 | 26 | Very Slow | transitional |
| South Extension | May2015 to May 2017 | 3 | 64 | Very Slow | Transitional on the toe + Retrogressive rotational |
| Barnard | May2015 to May 2017 | 2 | 18 | Very Slow | Rotational retrogressive |
| Redhill | May2015 to May 2017 | 8 | 56 | Very Slow | Retrogressive rotational |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Soltanieh, A.; Macciotta, R. Updated Understanding of the Thompson River Valley Landslides Kinematics Using Satellite InSAR. Geosciences 2022, 12, 359. https://doi.org/10.3390/geosciences12100359
Soltanieh A, Macciotta R. Updated Understanding of the Thompson River Valley Landslides Kinematics Using Satellite InSAR. Geosciences. 2022; 12(10):359. https://doi.org/10.3390/geosciences12100359
Chicago/Turabian StyleSoltanieh, Amir, and Renato Macciotta. 2022. "Updated Understanding of the Thompson River Valley Landslides Kinematics Using Satellite InSAR" Geosciences 12, no. 10: 359. https://doi.org/10.3390/geosciences12100359
APA StyleSoltanieh, A., & Macciotta, R. (2022). Updated Understanding of the Thompson River Valley Landslides Kinematics Using Satellite InSAR. Geosciences, 12(10), 359. https://doi.org/10.3390/geosciences12100359








