3D Numerical Prediction of Thermal Weakening of Granite under Tension
Abstract
:1. Introduction
2. Numerical Methods
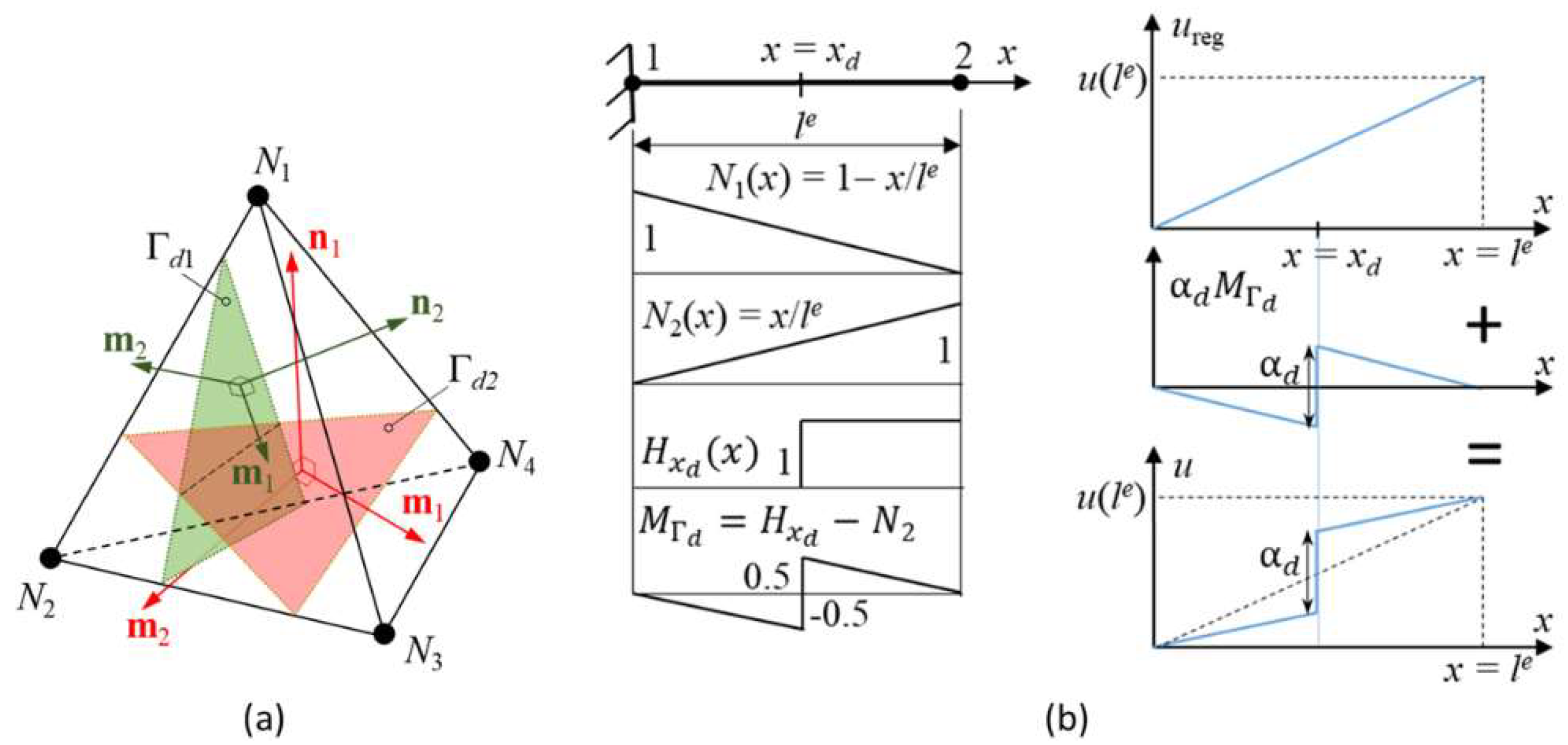
2.1. Failure Model for Rock
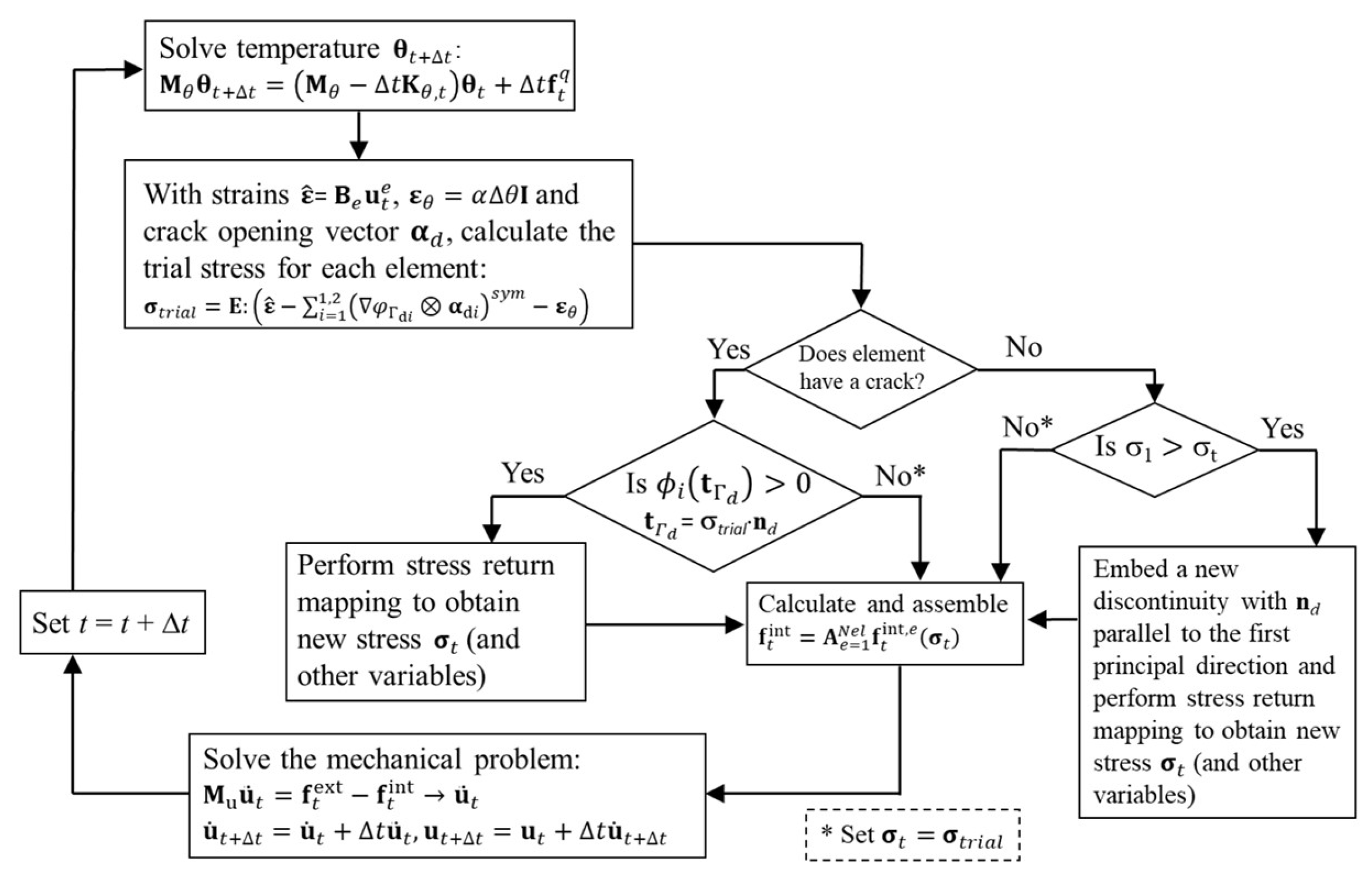
2.2. Staggered Explicit Scheme for Solving Global Thermo-Mechanical Problem
3. Numerical Examples
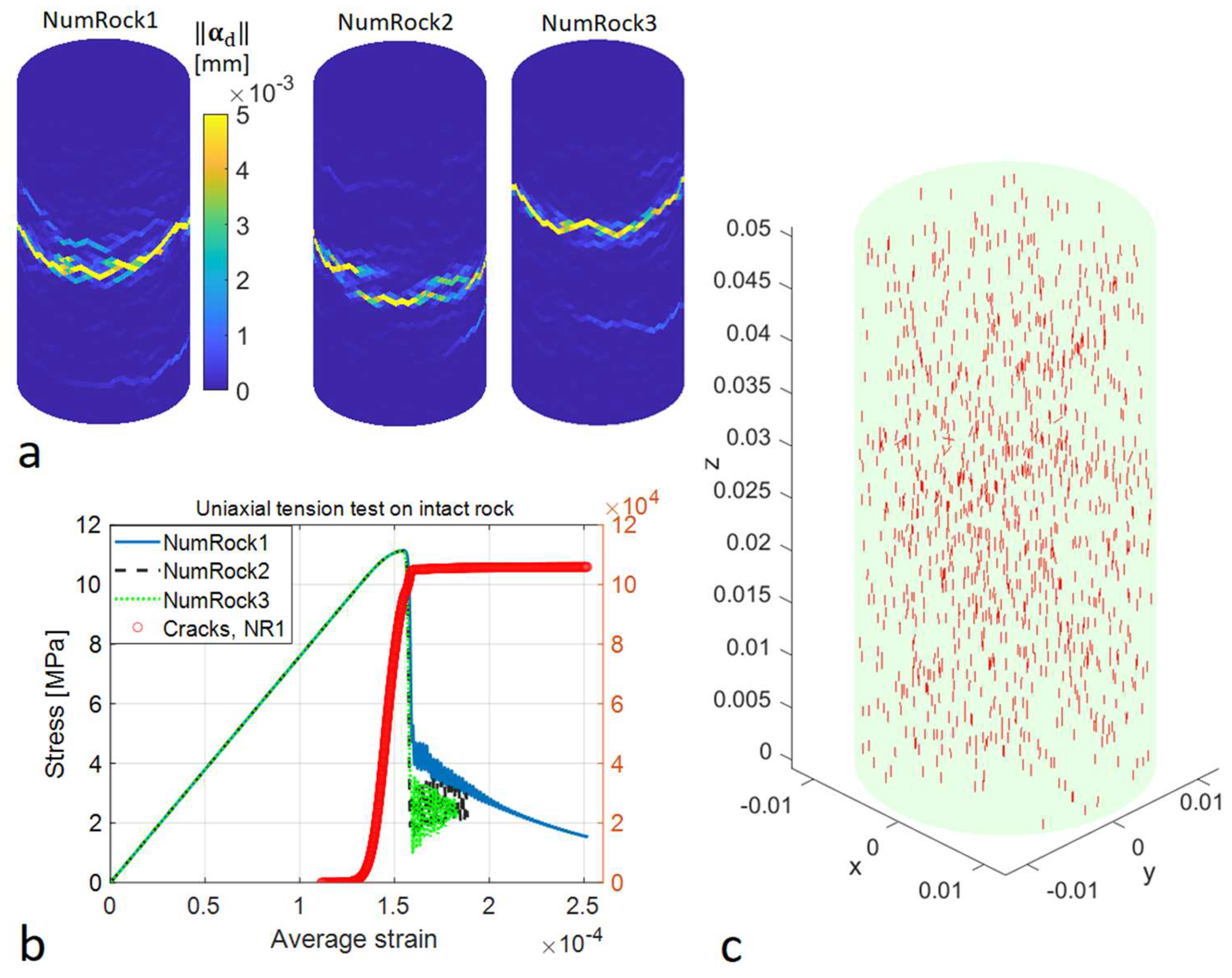
3.1. Numerical Rock Description
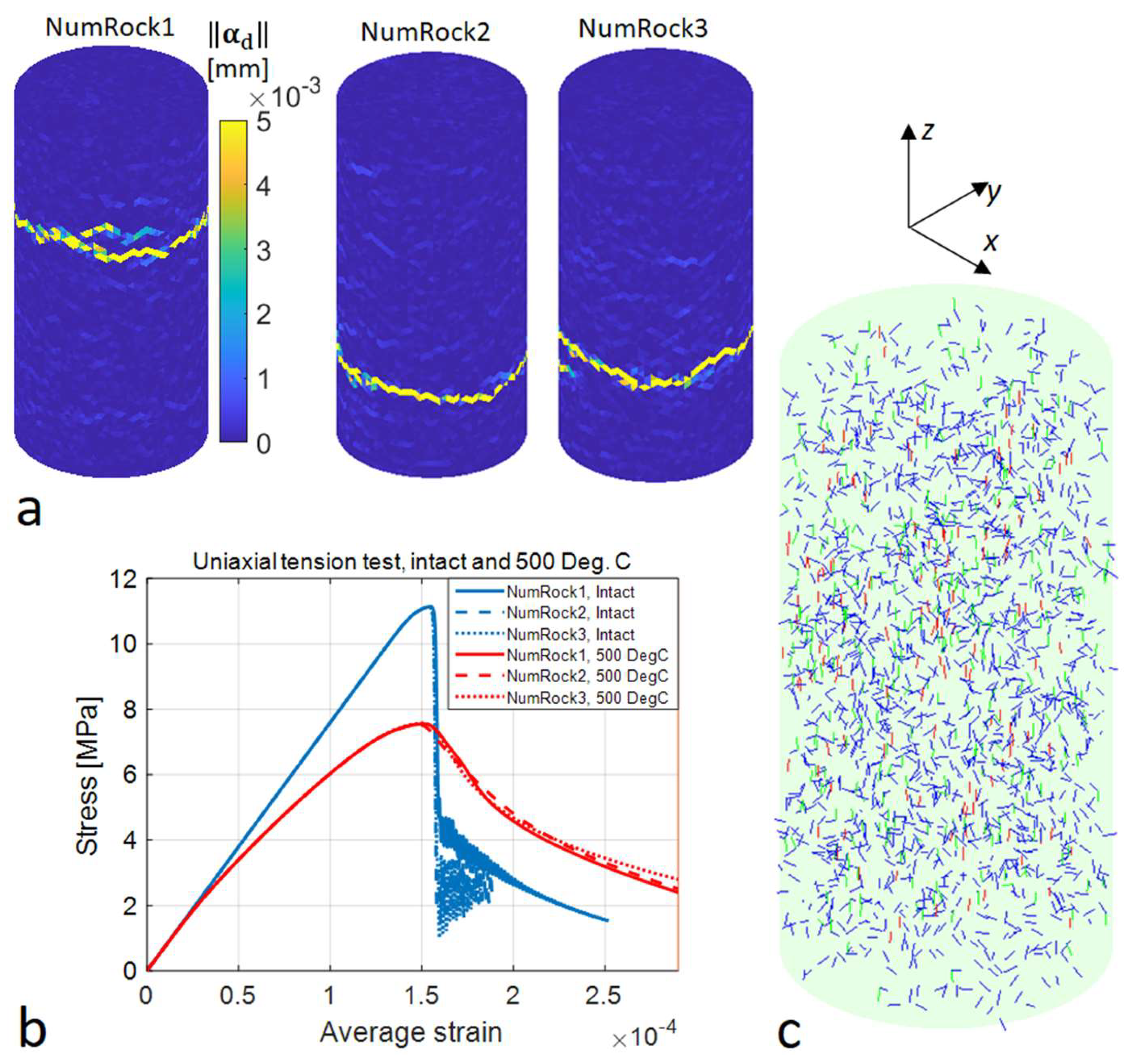
3.2. Numerical Rock Heat Treatment
3.3. Numerical Tension Tests on Intact and Heat Treated Rock
4. Discussion
5. Conclusions
- An explicit staggered scheme is an effective method to solve the nonlinear coupled problem of thermal cracking due to uniform temperature fields. The present method, based on the embedded discontinuity finite elements to model rock fracture, is computationally fast and has physically meaningful model parameters.
- The non-inertial nature of the slow heating of a rock sample to a homogeneous temperature field enables using drastic mass scaling for the mechanical part of the coupled problem. The mass scaling increases the critical time step of the explicit time stepping for the mechanical part of the governing initial/boundary value problem.
- In terms of modelling, the major factor influencing the thermo-mechanical behavior of granitic rocks seems to be the deviant behavior of Quartz mineral. More specifically, the thermal cracking induced reduction of the tensile strength of granite can be correctly predicted by accounting for the heterogeneity of the mechanical properties (stiffness and tensile strength) and the temperature dependence of Quartz thermal expansion.
- This method, as it does not use any experimental data on the temperature dependence of the tensile strength as a model input, replicates the experimental weakening effect in a non-circular way. The practical benefit of the method is thus a fast and reliable 3D prediction of the tensile strength of granite rock at elevated temperatures with a small set of measurable parameters of a Quartz bearing rock.
Funding
Data Availability Statement
Conflicts of Interest
References
- Kumari, W.G.P.; Ranjith, P.G.; Perera, M.S.A.; Shao, S.; Chen, B.K.; Lashin, A.; Arifi, N.A.; Rathnaweera, T.D. Mechanical behaviour of Australian Strathbogie granite under in-situ stress and temperature conditions: An application to geothermal energy extraction. Geothermics 2017, 65, 44–59. [Google Scholar] [CrossRef]
- Heuze, F.E. Geotechnical Modeling of High-Level Nuclear Waste Disposal by Rock Melting (No. UCRL-53183); Lawrence Livermore National Lab.: Livermore, CA, USA, 1981. [Google Scholar]
- Kant, M.A.; Rossi, E.; Madonna, C.; Höser, D.; von Rohr, P.R. A theory on thermal spalling of rocks with a focus on thermal spallation drilling. J. Geophys. Res. Solid Earth 2017, 122, 1805–1815. [Google Scholar] [CrossRef]
- Carpenter, M.A.; Salje, E.K.H.; Graeme-Barber, A.; Wruck, B.; Dove, M.T.; Knight, K.S. Calibration of excess thermodynamic properties and elastic constant variations associated with the α-β phase transition in quartz. Am. Mineral. 1998, 83, 2–22. [Google Scholar] [CrossRef] [Green Version]
- Gautam, P.K.; Verma, A.K.; Jha, M.K.; Sharma, P.; Singh, T.N. Effect of high temperature on physical and mechanical properties of Jalore granite. J. Appl. Geophys. 2018, 159, 460–474. [Google Scholar] [CrossRef]
- Heuze, F. High temperature mechanical, physical and thermal properties of granitic rocks—A review. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1983, 20, 3–10. [Google Scholar] [CrossRef]
- Toifl, M.; Hartlieb, P.; Meisels, R.; Antretter, T.; Kuchar, F. Numerical study of the influence of irradiation parameters on the microwave-induced stresses in granite. Miner. Eng. 2017, 103–104, 78–92. [Google Scholar] [CrossRef]
- Yang, S.Q.; Ranjith, P.G.; Jing, H.W.; Tian, W.L.; Ju, Y. An experimental investigation on thermal damage and failure mechanical behavior of granite after exposure to different high temperature treatments. Geothermics 2017, 65, 180–197. [Google Scholar] [CrossRef]
- Yin, T.; Shu, R.; Li, X.; Wang, P.; Liu, X. Comparison of mechanical properties in high temperature and thermal treatment granite. Trans. Nonferrous Met. Soc. China 2016, 26, 1926–1937. [Google Scholar] [CrossRef]
- Vázquez, P.; Shushakova, V.; Gómez-Heras, M. Influence of mineralogy on granite decay induced by temperature increase: Experimental observations and stress simulation. Eng. Geol. 2015, 189, 58–67. [Google Scholar] [CrossRef]
- Wang, F.; Konietzky, H. Thermo-Mechanical Properties of Granite at Elevated Temperatures. and Numerical Simulation of Thermal Cracking. Rock Mech. Rock Eng. 2019, 52, 3737–3755. [Google Scholar] [CrossRef]
- Wang, F.; Konietzky, H.; Frühwirt, T.; Li, L.; Dai, Y. The Influence of Temperature and High-Speed Heating on Tensile Strength of Granite and the Application of Digital Image Correlation on Tensile Failure Processes. Rock Mech. Rock Eng. 2020, 53, 1935–1952. [Google Scholar] [CrossRef]
- Griffiths, L.; Heap, M.J.; Baud, P.; Schmittbuhl, J. Quantification of microcrack characteristics and implications for stiffness and strength of granite. Int. J. Rock. Mech. Min. Sci. 2017, 100, 138–150. [Google Scholar] [CrossRef]
- Zhao, Z.; Xu, H.; Wang, J.; Zhao, X.; Cai, M.; Yang, Q. Auxetic behavior of Beishan granite after thermal treatment: A microcracking perspective. Eng. Fract. Mech. 2020, 231, 107017. [Google Scholar] [CrossRef]
- Pressacco, M.; Saksala, T. Numerical modelling of thermal shock assisted rock fracture. Int. J. Numer. Anal. Methods Geomech. 2020, 44, 40–68. [Google Scholar] [CrossRef]
- Raude, S.; Laigle, F.; Giot, R.; Fernandes, R. A unified thermoplastic/viscoplastic constitutive model for geomaterials. Acta Geotech. 2016, 11, 849–869. [Google Scholar] [CrossRef]
- Saksala, T. Numerical modelling of adiabatic heat generation during rock fracture under dynamic loading. Numer. Anal. Methods Geomech. 2019, 43, 1770–1783. [Google Scholar] [CrossRef]
- Jing, L.; Hudson, J.A. Numerical methods in rock mechanics. Int. J. Rock Mech. Min. Sci. 2002, 39, 409–427. [Google Scholar] [CrossRef]
- Nikolić, M.; Roje-Bonacci, T.; Ibrahimbegović, A. Overview of the numerical methods for the modelling of rock mechanics problems. Teh. Vjesn./Tech. Gaz. 2016, 23, 627–637. [Google Scholar]
- Hamdi, P.; Stead, D.; Elmo, D. Characterizing the influence of stress-induced microcracks on the laboratory strength and fracture development in brittle rocks using a finite-discrete element method-micro discrete fracture network FDEM-μDFN approach. J. Rock Mech. Geotech. 2015, 7, 609–625. [Google Scholar] [CrossRef] [Green Version]
- Simo, J.C.; Oliver, J.; Armero, F. An analysis of strong discontinuities induced by strain-softening in rate-independent inelastic solids. Comput. Mech. 1993, 12, 277–296. [Google Scholar] [CrossRef]
- Belytschko, T.; Black, T. Elastic crack growth in finite elements with minimal remeshing. Int. J. Numer. Methods Eng. 1999, 45, 601–620. [Google Scholar] [CrossRef]
- Mosler, J. On advanced solution strategies to overcome locking effects in strong discontinuity approaches. Int. J. Numer. Meth. Eng. 2005, 63, 1313–1341. [Google Scholar] [CrossRef]
- Saksala, T. Numerical modelling of temperature effect on tensile strength of granitic rock. Appl. Sci. 2021, 11, 4407. [Google Scholar] [CrossRef]
- Saksala, T.; Brancherie, D.; Harari, I.; Ibrahimbegovic, A. Combined continuum damage-embedded discontinuity model for explicit dynamic fracture analyses of quasi-brittle materials. Int. J. Numer. Methods Eng. 2015, 101, 230–250. [Google Scholar] [CrossRef]
- Ottosen, N.S.; Ristinmaa, M. The Mechanics of Constitutive Modeling; Elsevier: Amsterdam, The Netherlands, 2005. [Google Scholar]
- Saksala, T.; Ibrahimbegovic, A. Thermal shock weakening of granite rock under dynamic loading: 3D numerical modelling based on embedded discontinuity finite elements. Int. J. Numer. Anal. Methods Geomech. 2020, 44, 1788–1811. [Google Scholar] [CrossRef]
- Zhao, D.; Zhang, S.; Wang, M. Microcrack Growth Properties of Granite under Ultrasonic High-Frequency Excitation. Adv. Civ. Eng. 2019, 2019, 3069029. [Google Scholar] [CrossRef]
- Mahabadi, O.K. Investigating the Influence of Micro-Scale Heterogeneity and Microstructure on the Failure and Mechanical Behaviour of Geomaterials. PhD Thesis, University of Toronto, Toronto, ON, Canada, 2012. [Google Scholar]
- Zhang, Q.B.; Zhao, J. A Review of Dynamic Experimental Techniques and Mechanical Behaviour of Rock Materials. Rock Mech. Rock. Eng. 2014, 47, 1411–1478. [Google Scholar] [CrossRef] [Green Version]




| Property/Mineral | Quartz | Feldspars | Biotite |
|---|---|---|---|
| Young’s modulus E [GPa] | 90 | 70 | 40 |
| Poisson’s ratio ν | 0.1 | 0.3 | 0.2 |
| Tensile strength σt0 [MPa] | 14 | 11 | 7 |
| Mode I fracture energy GIc [J/m2] | 40 | 40 | 28 |
| Density ρ [kg/m3] | 2650 | 2650 | 2650 |
| Thermal expansion coeff. α0 [1/K] | |||
| Specific heat capacity c [J/kgK] | 820 | 820 | 820 |
| Thermal conductivity k [W/mK] | 2.6 | 2.6 | 2.6 |
| Fraction [%] | 33 | 60 | 7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saksala, T. 3D Numerical Prediction of Thermal Weakening of Granite under Tension. Geosciences 2022, 12, 10. https://doi.org/10.3390/geosciences12010010
Saksala T. 3D Numerical Prediction of Thermal Weakening of Granite under Tension. Geosciences. 2022; 12(1):10. https://doi.org/10.3390/geosciences12010010
Chicago/Turabian StyleSaksala, Timo. 2022. "3D Numerical Prediction of Thermal Weakening of Granite under Tension" Geosciences 12, no. 1: 10. https://doi.org/10.3390/geosciences12010010
APA StyleSaksala, T. (2022). 3D Numerical Prediction of Thermal Weakening of Granite under Tension. Geosciences, 12(1), 10. https://doi.org/10.3390/geosciences12010010





