Unique Path Method of the Pinch-Out Profile Based on Unified Stratigraphic Sequence
Abstract
1. Introduction
2. Content and Method of Research
2.1. Theory of the Unique Path Method of Pinch-Out Profile Based on a Unified Stratigraphic Sequence
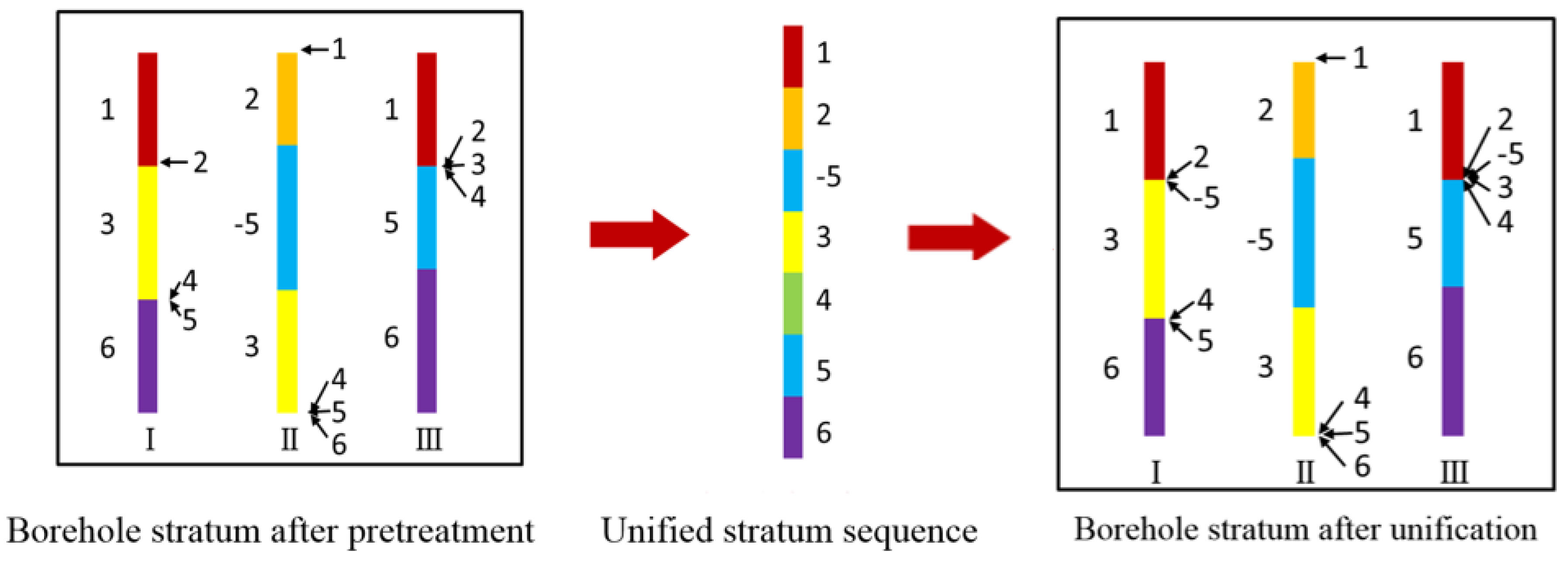
2.2. Unique Path Method of Pinch-Out Profile Based on a Unified Stratigraphic Sequence
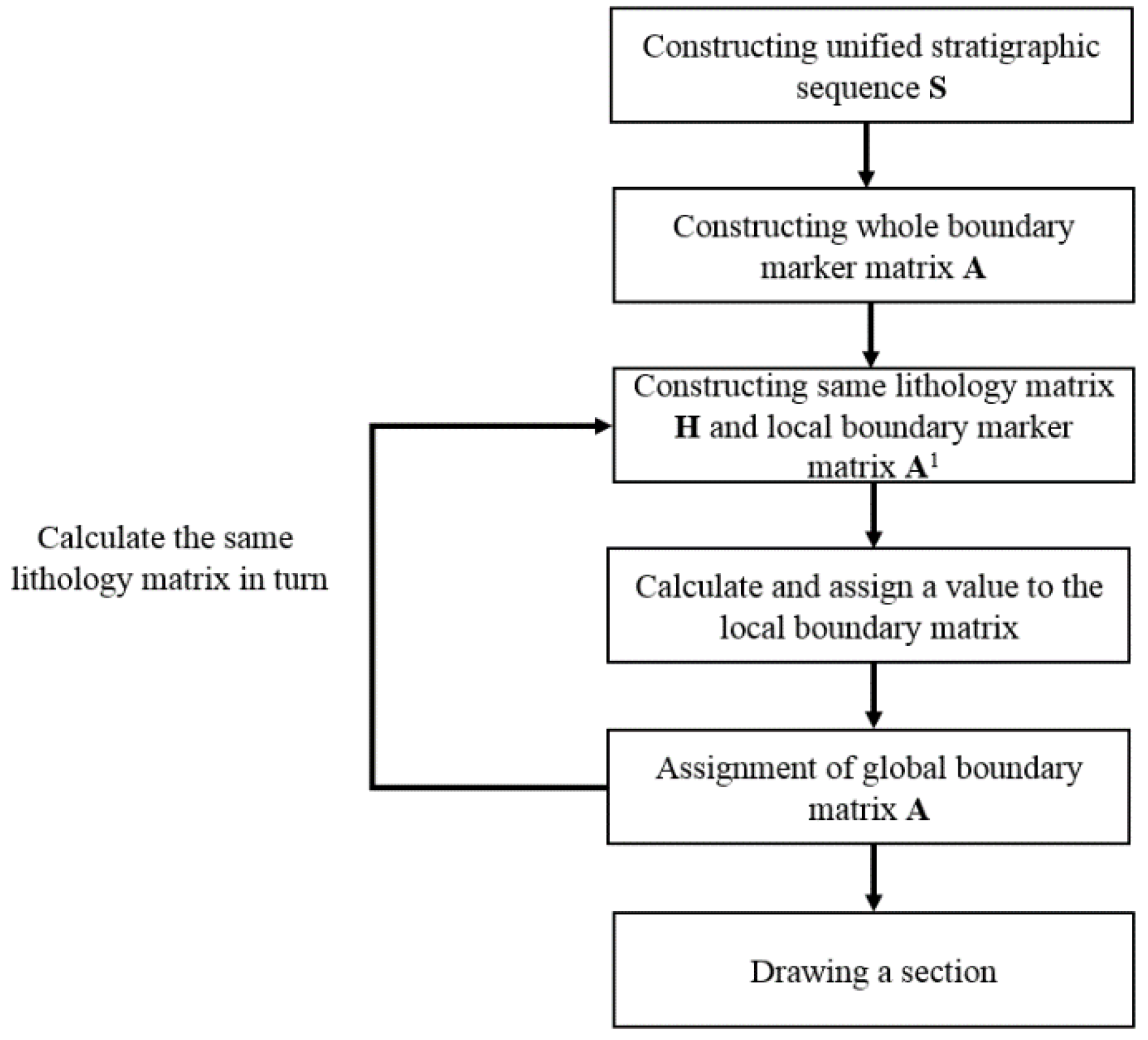
2.3. Procedure of the Unique Path Method for Pinch-Out Profiles Based on a Unified Stratigraphic Sequence
- Convert the data into a specific format and account for missing data and errors within the data;
- Integrate the drilling data with depth data and stratigraphic data;
- Integrate the sequences from all boreholes to establish a unified stratum sequence S according to Equation (1);
- Set the default values of marker matrix A for establishing whether the overall stratum boundary exists to 1;
- Establish two-dimensional homogenous lithologic boundaries matrix H by turn according to the unified stratigraphic sequence S and E;
- Generate boundary matrix H(m, n) for each row in matrix E, and then generate upper boundary matrix B(m−3, n) and lower boundary matrix C(m−3, n) from boundary matrix H(m, n). Perform stratum boundary contact detection to obtain multiple local boundary marker matrixes A1;
- Assign and correct the values within overall boundary marker matrix A based on all local boundary marker matrix A1 by repeating steps 5–6;
- According to the matrix A and E, the Bessel curve representing each boundary of strata can be drawn and the strata between the curves can be filled with different customized basic patterns using the common library (canvas library in JavaScript).
3. Application to a Case and Discussion of Results
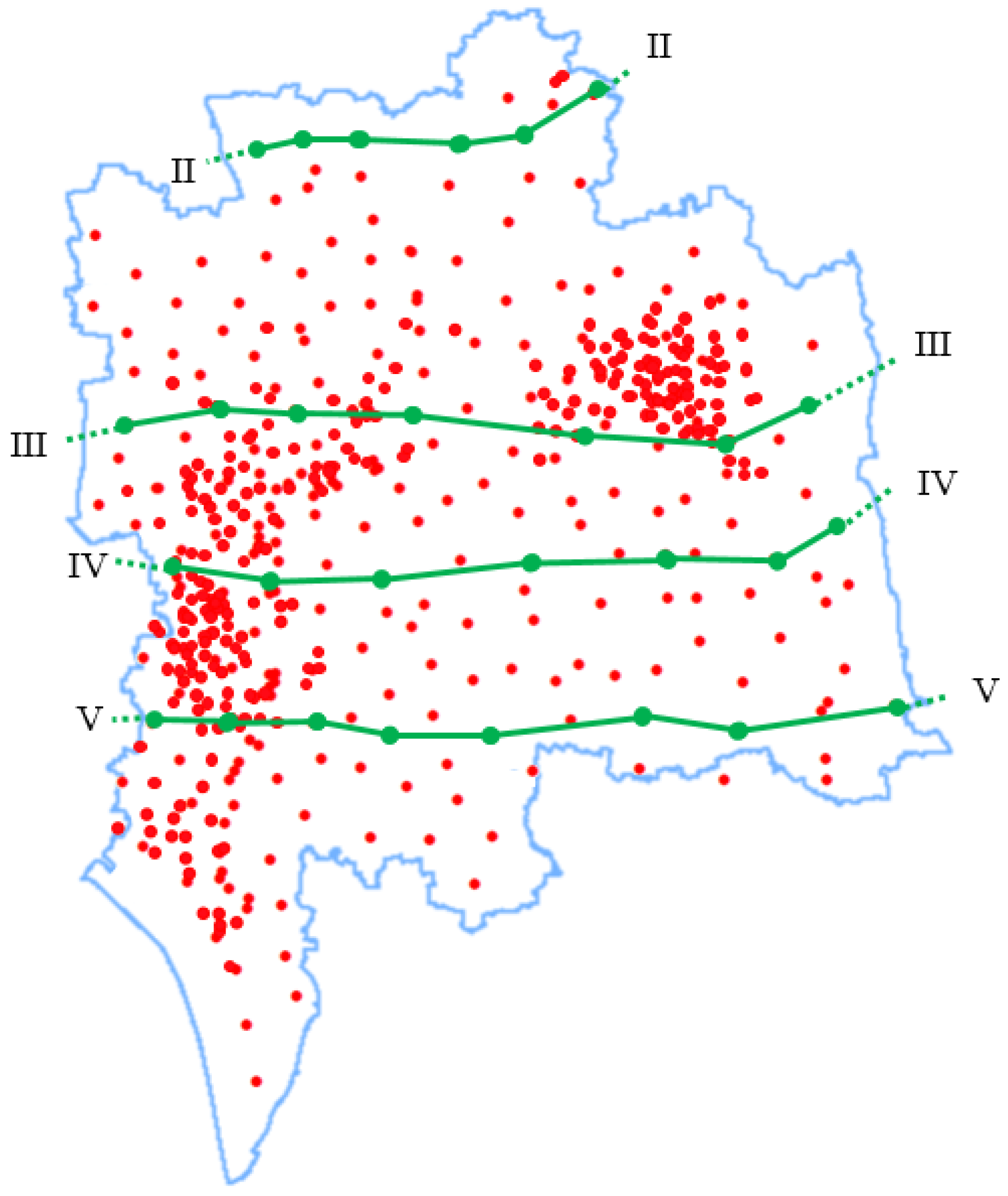
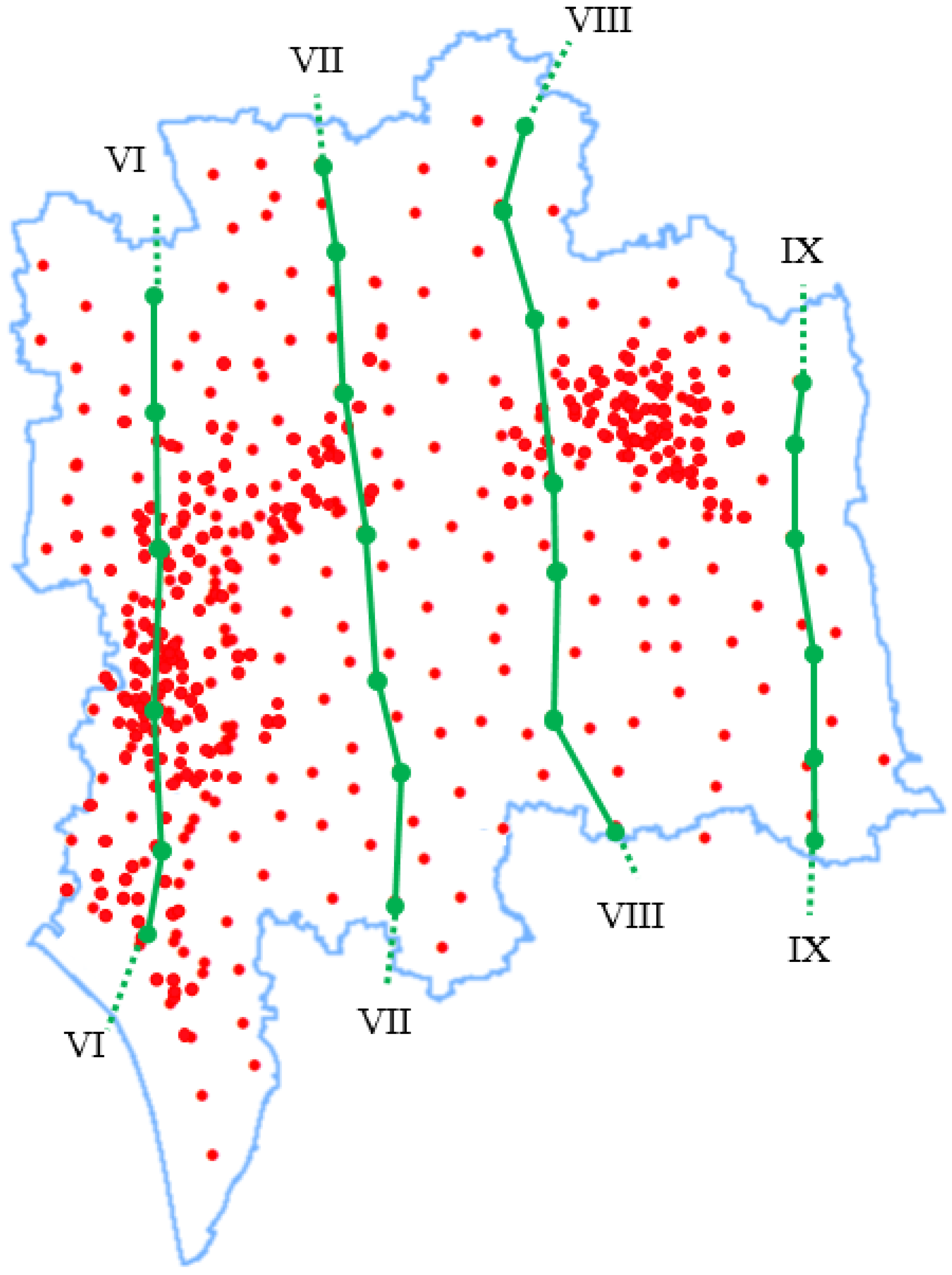
3.1. Geographical and Geological Overview
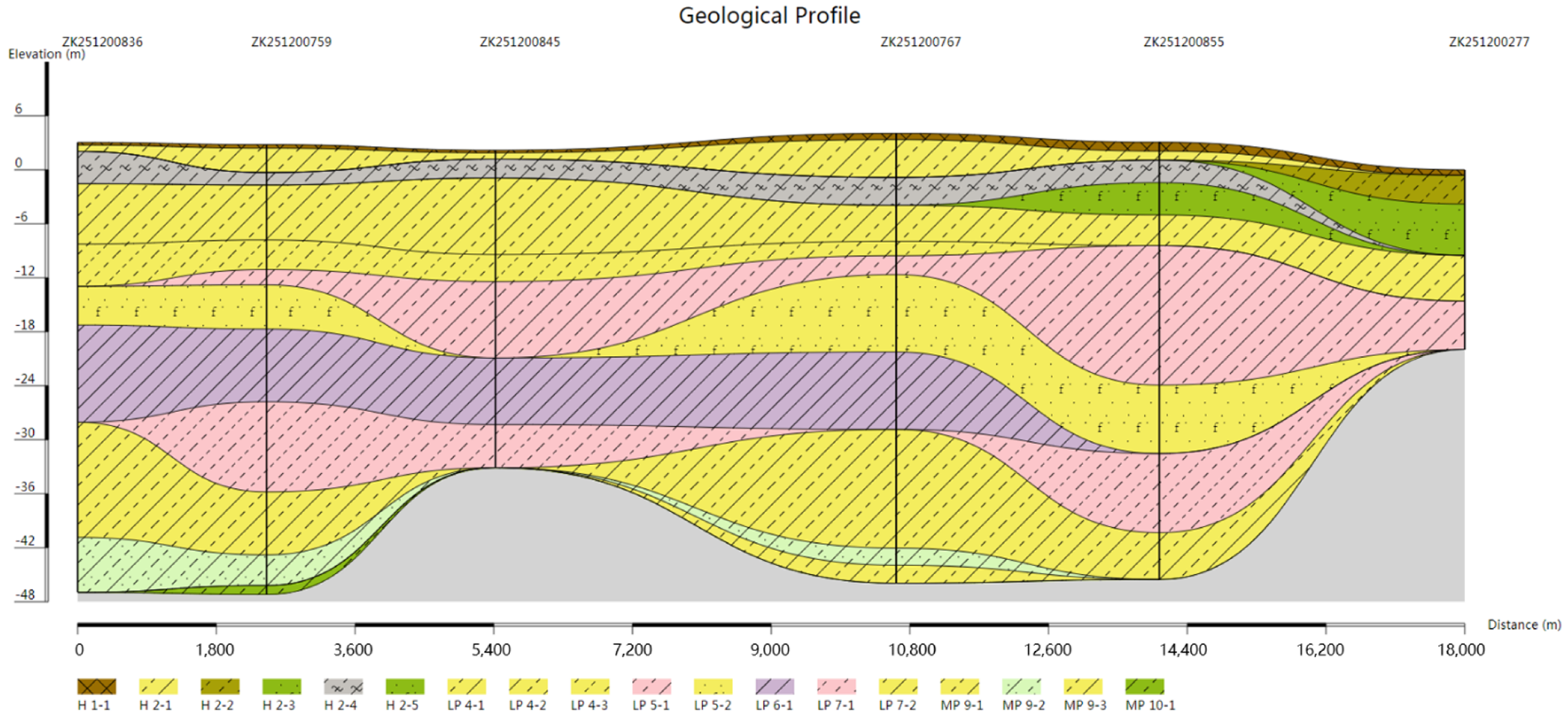
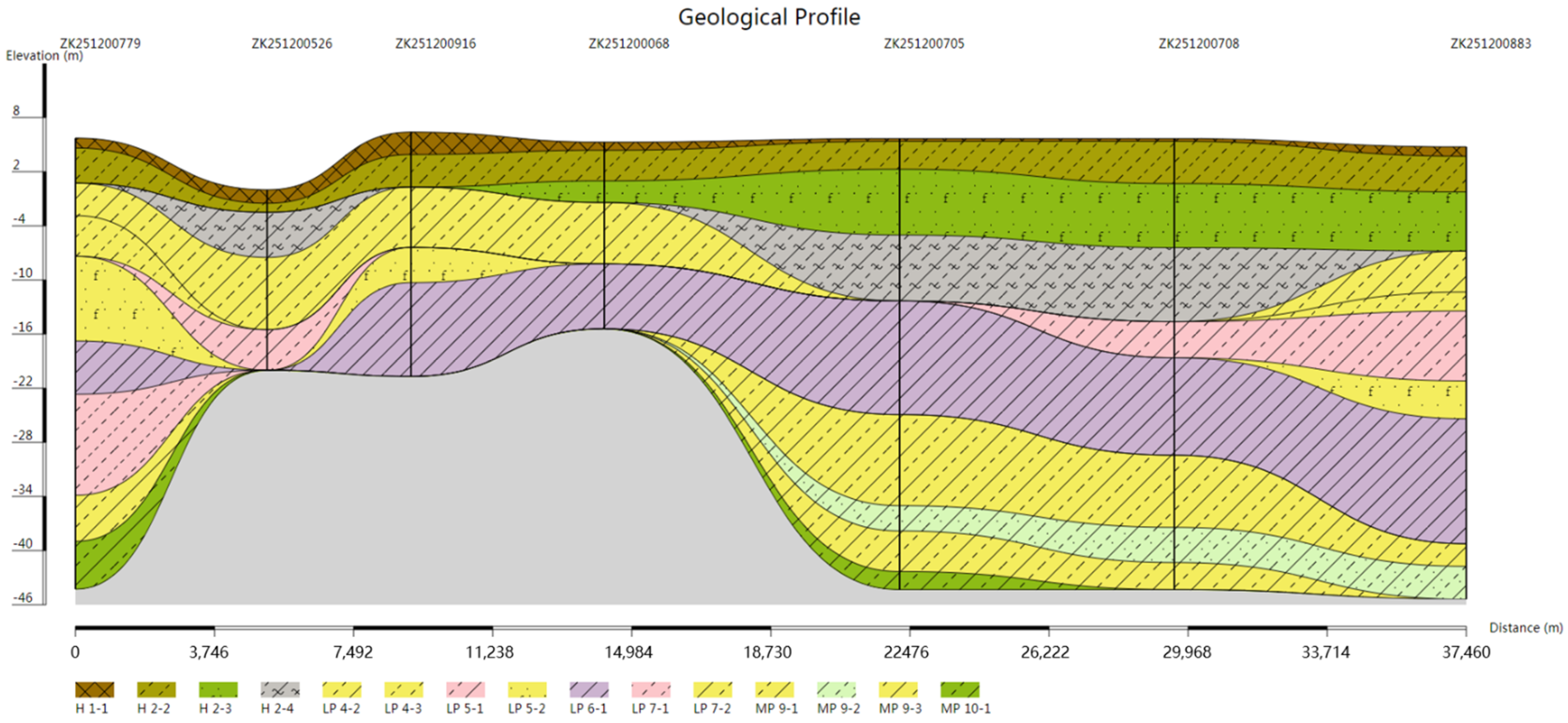
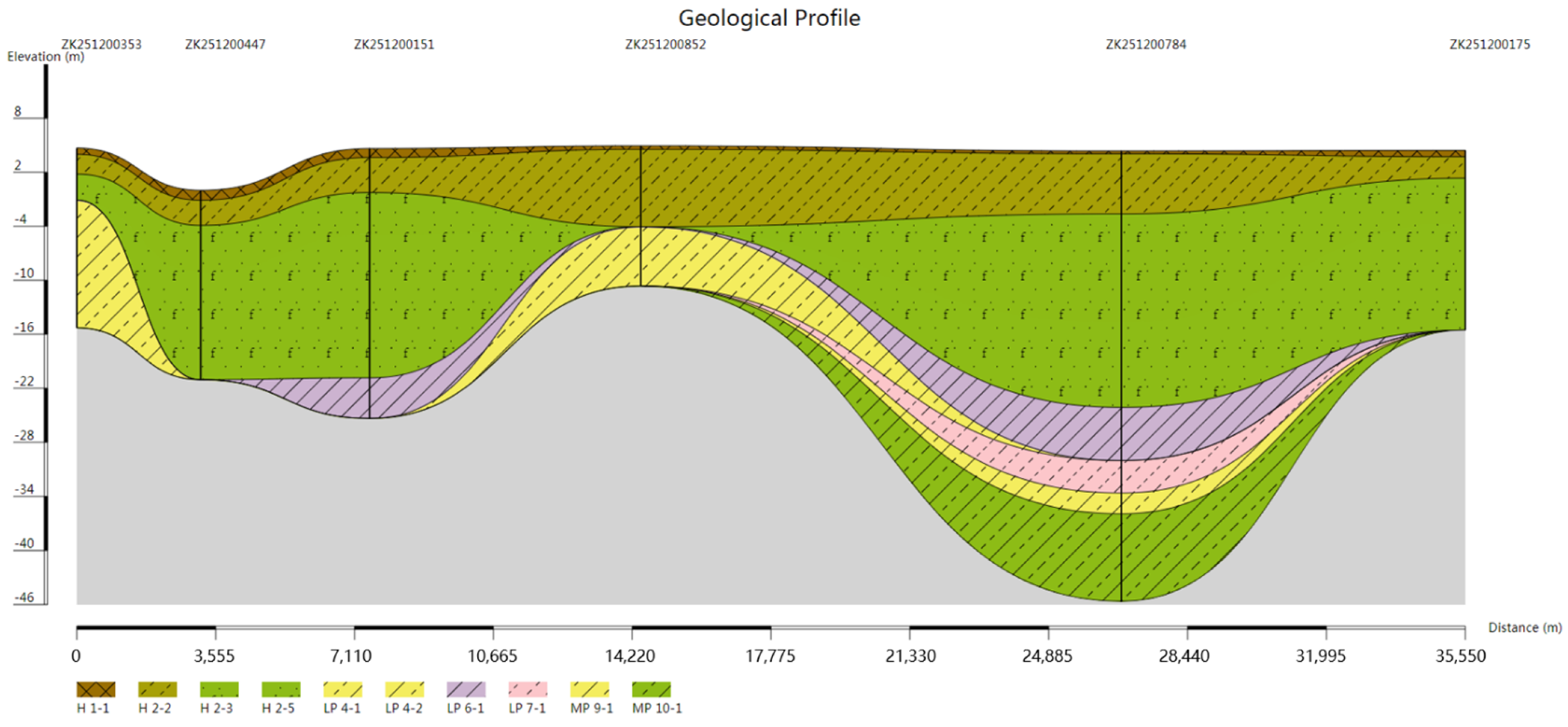
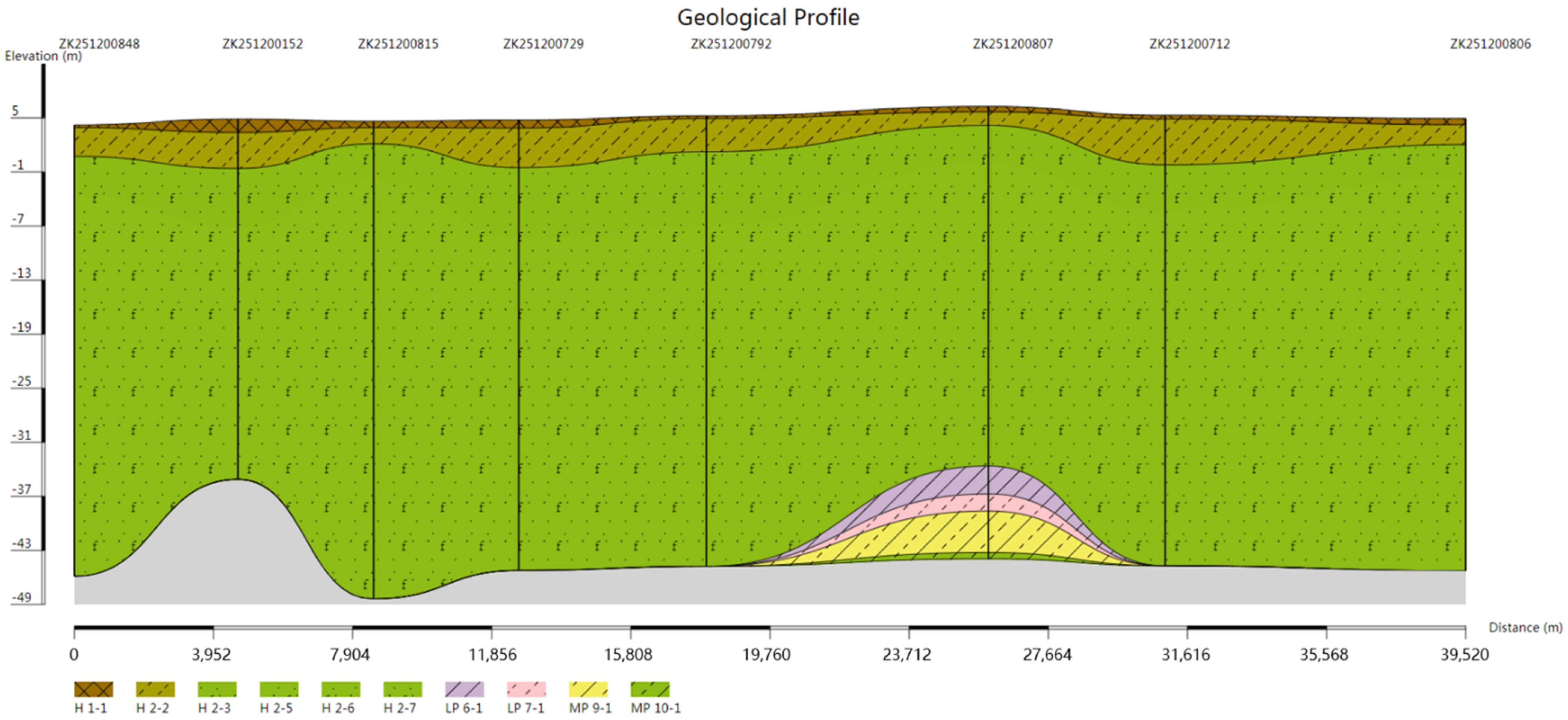
3.2. Drawing of Pinch-Out Profiles Using the Unique Path Method on a Unified Stratigraphic Sequence
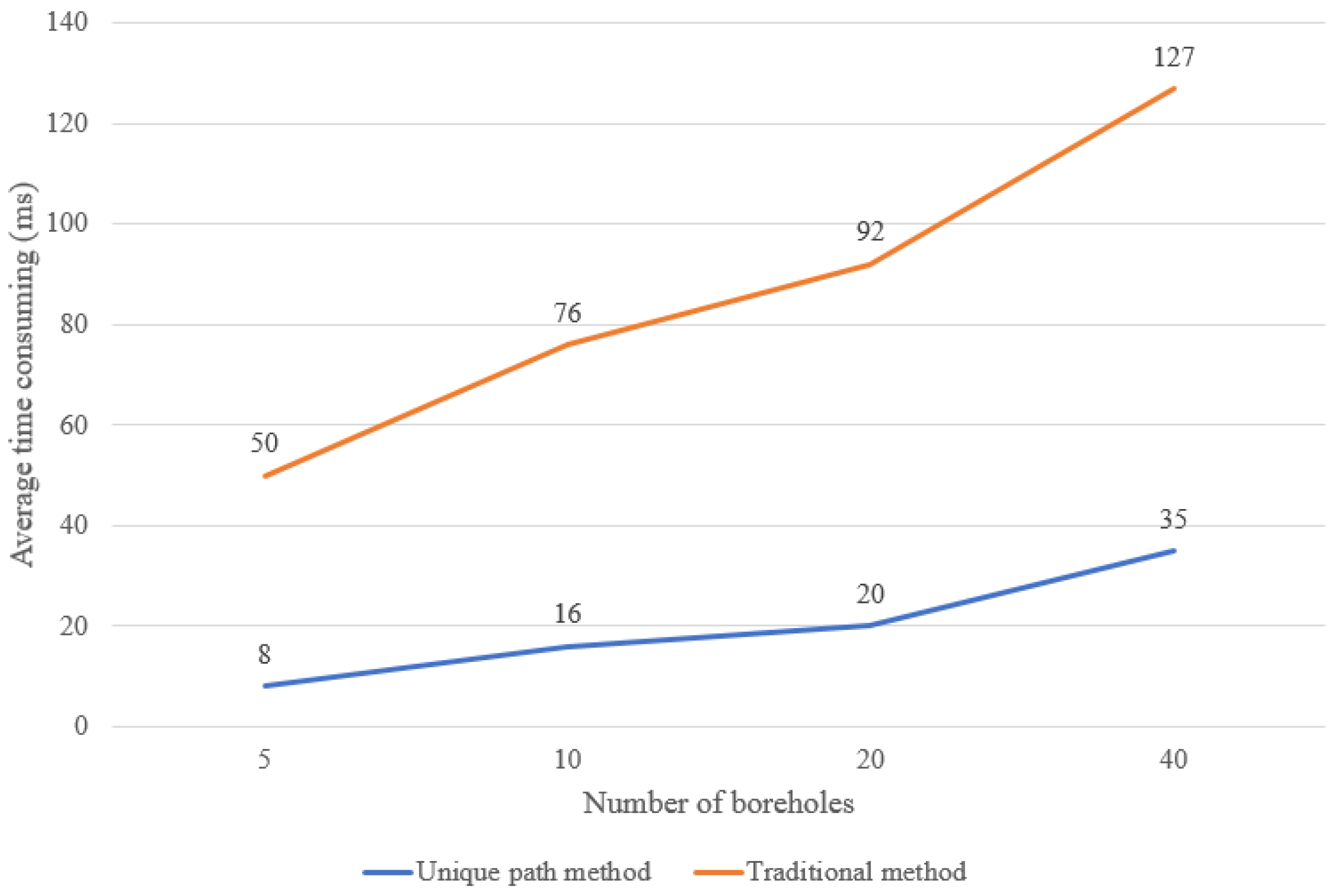
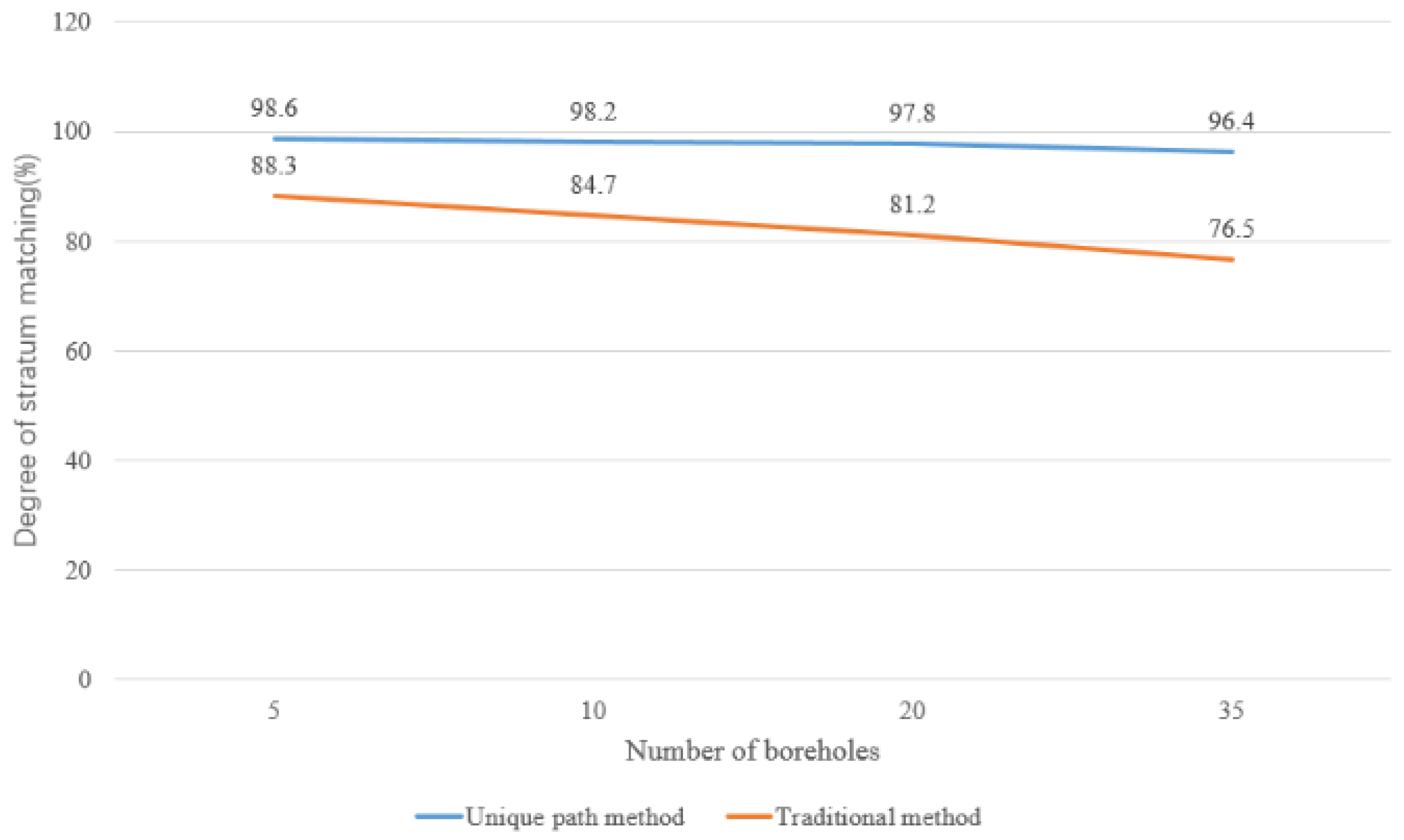
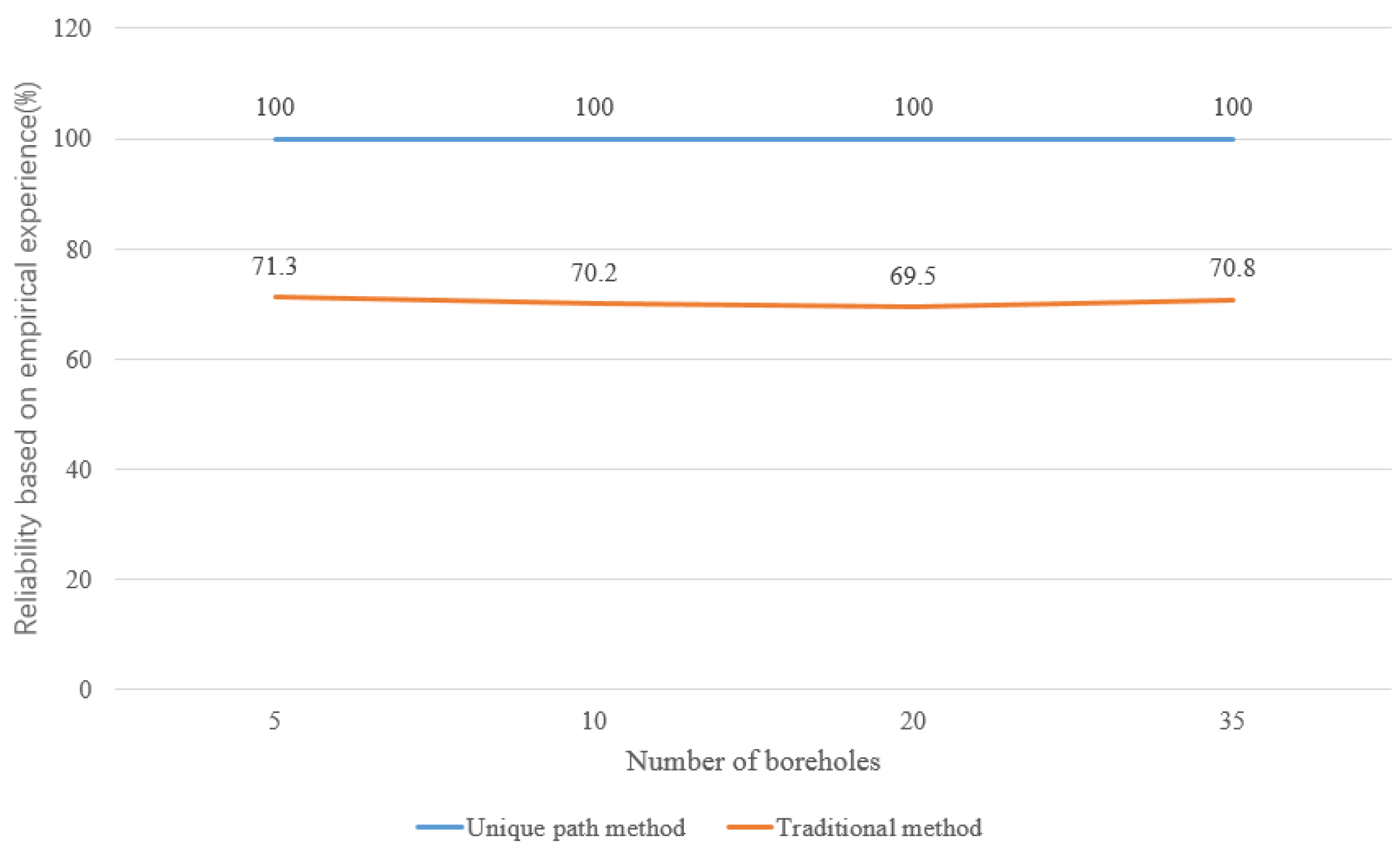
3.3. Comparison and Analysis
4. Conclusions
- Traditional geological profile drawing methods are complex because of too many branches and little consideration of pinch-outs. Aiming at this problem, this paper proposes a unique path method based on a unified stratigraphic sequence to draw pinch-out profiles based on the principle that pinch-out manifest in cartography as explicit or implicit boundaries. This method can accurately draw the cusp if the data pattern meets the requirements of pinch-out in the method no matter what depositional environment is. The influence of other depositional conditions on the sequence was considered in the unified stratigraphic sequence method. This method avoids the problem in which the traditional method produces an excessive number of branch paths, reduces the complexity of drawing pinch-out in geological profiles, and achieves high-speed and accurate rendering, which can meet the requirements of modern geological profile drawing standards;
- The method was successfully applied to an example in the interaction between marine and continental deposition. A comparison of the results with the profiles drawn by experts and traditional methods demonstrates that the unique path method can accurately draw pinch-outs. The unique path method based on a unified stratigraphic sequence greatly improves the rendering speed without reducing the accuracy. Using this method proposed in this paper, a geological map containing pinch-outs was drawn for an engineering project, and the geological situation of the area was discussed according to geological profiles of the area, thereby showing that the unique path method is highly reliable in the actual operation process;
- The method is shown to be relatively reliable, as it uses a relatively simple way to plot pinch-out in four discontinuous distributions, and the technique can be extended to the drawing of inverted strata. This method achieves high-speed rendering without reducing the accuracy, and thus, can better meet the requirements of modern geological profile drawing standards than existing methods. This method has the potential to be applied to urban geological and oil and gas drilling platforms due to its good performance in large and complex geological area, but it needs to be evaluated whether it can really adapt to different geological environments.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Seidler, L.; Steel, R. Pinch-out style and position of tidally influenced strata in a regressive–transgressive wave-dominated deltaic sandbody, Twentymile Sandstone, Mesaverde Group, NW Colorado. Sedimentology 2001, 48, 399–414. [Google Scholar] [CrossRef]
- Graciansky, P.C.D. Sequence stratigraphy on the Northwest European margin. Mar. Petrol. Geol. 1996, 13, 974. [Google Scholar] [CrossRef]
- Al-Rahim, A.M. Locating of promising stratigraphic traps of pinch-out type in Iraq—New sense. Arab. J. Geosci. 2013, 6, 1381–1393. [Google Scholar] [CrossRef]
- Gardner, R.L.; Piazolo, S.; Daczko, N.R. Pinch and swell structures: Evidence for strain localisation by brittle—Viscous behaviour in the middle crust. Solid Earth 2015, 6, 1045–1061. [Google Scholar] [CrossRef]
- Santolaria, P.; Vendeville, B.C.; Graveleau, F.; Soto, R.; Casas-Sainz, A. Double evaporitic décollements: Influence of pinch-out overlapping in experimental thrust wedges. J. Struct. Geol. 2015, 76, 35–51. [Google Scholar] [CrossRef]
- Basilone, L. Mesozoic tectono-sedimentary evolution of the Trapanese South-ern Tethyan margin (NW Sicily) integrating facies and stratigraphic analysis with sub-sidence history. Ital. J. Geosci. 2020, 139, 54–75. [Google Scholar] [CrossRef]
- Basilone, L.; Lena, G.; Gasparo-Morticelli, M. Synsedimentary-tectonic, soft-sediment deformation and volcanism in the rifted Tethyan margin from the Upper Triassic–Middle Jurassic deep-water carbonates in Central Sicily. Sediment. Geol. 2014, 308, 63–79. [Google Scholar] [CrossRef]
- Carminati, E.; Santantonio, M. Control of differential compaction on the geometry of sediments onlapping paleoescarpments: Insights from field geology (Central Apennines, Italy) and numerical modeling. Geology 2005, 33, 353–356. [Google Scholar] [CrossRef]
- Cipriani, A.; Zuccari, C.; Innamorati, G.; Marino, M.C.; Petti, F.M. Mass-transport deposits from the Toarcian of the Umbria-Marche-Sabina Basin (Central Italy). Ital. J. Geosci. 2020, 139, 9–29. [Google Scholar] [CrossRef]
- Cipriani, A.; Bottini, C. Early Cretaceous tectonic rejuvenation of an Early Jurassic margin in the Central Apennines: The “Mt. Cosce Breccia”. Sediment. Geol. 2019, 387, 57–74. [Google Scholar] [CrossRef]
- Cipriani, A.; Bottini, C. Unconformities, neptunian dykes and mass-transport deposits as an evidence for Early Cretaceous syn-sedimentary tectonics: New insights from the Central Apennines. Ital. J. Geosci. 2019, 138, 333–354. [Google Scholar] [CrossRef]
- Cipriani, A.; Fabbi, S.; Lathuilière, B.; Santantonio, M. A reef coral in the con-densed Maiolica facies on the Mt. Nerone pelagic carbonate platform (Marche Apennines): The enigma of ancient pelagic deposits. Sediment. Geol. 2019, 385, 45–60. [Google Scholar] [CrossRef]
- Santantonio, M. Facies associations and evolution of pelagic carbonate plat-form/basin systems: Examples from the Italian Jurassic. Sedimentology 1993, 40, 1039–1067. [Google Scholar] [CrossRef]
- Assis, C.A.M.; Ceia, M.A.R.; Misságia, R.M.; Lupinacci, W.M. Mapping fluid distribution in a pinch-out reservoir model: A physical modeling study. J. Appl. Geophys. 2014, 109, 313–322. [Google Scholar] [CrossRef]
- Tao, S.; Yuan, X.; Hou, L.; Zhang, G.; Gao, C. Formation and distribution of large lithologic-stratigraphic oil & gas fields (provinces). J. Nat. Gas Geosci. 2018, 3, 51–65. [Google Scholar]
- Gilles, L.; Serge, B.; Hugues, F. Seaward pinching out and internal stratigraphy of the Gironde incised valley on the shelf (Bay of Biscay). Mar. Geol. 2001, 175, 183–197. [Google Scholar]
- Olsen, T.R.; Steel, R.J. Shoreface Pinch-Out Style on the Front of the Brent delta in the Easterly Tampen Spur Area; Norwegian Petroleum Society Special Publications: Stavanger, Norway, 1995; Volume 5, pp. 273–289. [Google Scholar]
- Peters, M.; Berger, A.; Herwegh, M.; Regenauer-Lieb, K. Strain localization in ductile rocks: A comparison of natural and simulated pinch-and-swell structures. Tectonophysics 2016, 680, 140–154. [Google Scholar] [CrossRef]
- Cipriani, A.; Caratelli, M.; Santantonio, M. Geological mapping reveals the role of Early Jurassic palaeogeography in the distribution of shallow water-derived calci-turbidites: New insights from the Central and Northern Apennines. Basin Res. 2020, 32, 1485–1509. [Google Scholar] [CrossRef]
- Chen, J.H.; Zhou, Z.Y.; Chen, G.; Gu, D.S. Automatic formation method of prospecting line profile map based on drill hole database. J. Cent. South Univ. Technol. (Nat. Sci.) 2005, 3, 486–490. [Google Scholar]
- Stawikowski, W. Structural Geology, 2nd ed.; Geologos: Poznan, Poland, 2017; p. 23. [Google Scholar]
- Levoy, M. Display of surfaces from volume data. IEEE Comput. Graph. 1988, 8, 29–37. [Google Scholar] [CrossRef]
- Jia, R.; Liu, B.; Fu, X.; Gong, L.; Liu, Z. Transformation Mechanism of a Fault and Its Associated Microstructures in Low-Porosity Rocks: A Case Study of the Tanan Depression in the Hailar-Tamtsag Basin. J. Mar. Sci. Eng. 2019, 7, 286. [Google Scholar] [CrossRef]
- Zhu, X.G. Geometry of Ore Body; China University of Mining and Technology Press: Xuzhou, China, 1987. [Google Scholar]
- Kimberley, M.M. Cross Sections and Volume Measurement of Stratigraphic Units. Microcomput. Appl. Geol. 1990, 161–169. [Google Scholar] [CrossRef]
- Wu, L. Topological relations embodied in a generalized tri-prism (GTP) model for a 3D geoscience modeling system. Comput. Geosci. 2004, 30, 405–418. [Google Scholar] [CrossRef]
- Ichoku, C.; Chorowicz, J.; Parrot, J.F. Computerized construction of geological cross sections from digital maps. Comput. Geosci. 1994, 20, 1321–1327. [Google Scholar] [CrossRef]
- Zhou, C.Y.; Du, Z.C.; Ouyang, J.W.; Zhang, Z.L.; Liu, Z. A 3D geological model and cutting algorithm based on a vertically projected triangulated network. Comput. Geosci. 2020, 143, 104562. [Google Scholar] [CrossRef]
- Mallet, J.L. {GOCAD}: A Computer-Aided Design Program for Geological Applications; Springer: Berlin, Germany, 1992. [Google Scholar]
- Zhou, C.Y.; Ouyang, J.W.; Ming, W.H.; Zhang, G.; Liu, Z. A Stratigraphic Prediction Method Based on Machine Learning. Appl. Sci. 2019, 9, 3553. [Google Scholar] [CrossRef]
- Xu, T.; Li, F.; Wu, Z.; Wu, C.; Gao, E.; Zhou, B.; Zhang, Z.; Xu, G. A successive three-point perturbation method for fast ray tracing in complex 2D and 3D geological models. Tectonophysics 2014, 627, 72–81. [Google Scholar] [CrossRef]
- Salvo, C.D.; Mancini, M.; Cavinato, G.P.; Moscatelli, M.; Simionato, M.; Stigliano, F.; Rea, R.; Rodi, A. A 3D Geological Model as a Base for the Development of a Conceptual Groundwater Scheme in the Area of the Colosseum (Rome, Italy). Geosciences 2020, 10, 266. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, Z.L.; Zhou, C.Y.; Ming, W.H.; Du, Z.C. An Adaptive Inverse-Distance Weighting Interpolation Method Considering Spatial Differentiation in 3D Geological Modeling. Geosciences 2021, 11, 51. [Google Scholar] [CrossRef]
- Chen, H.Q. Decision thinking for the northern demarcation line of Yangtzi River Delta. J. Zhejiang North Univ. (Nat. Sci.) 2004, 27, 76–79. [Google Scholar]
- Yang, L. The research and implementation on automaticmapping system of geological plane/section map. Cent. South Univ. 2013, 80. [Google Scholar] [CrossRef]




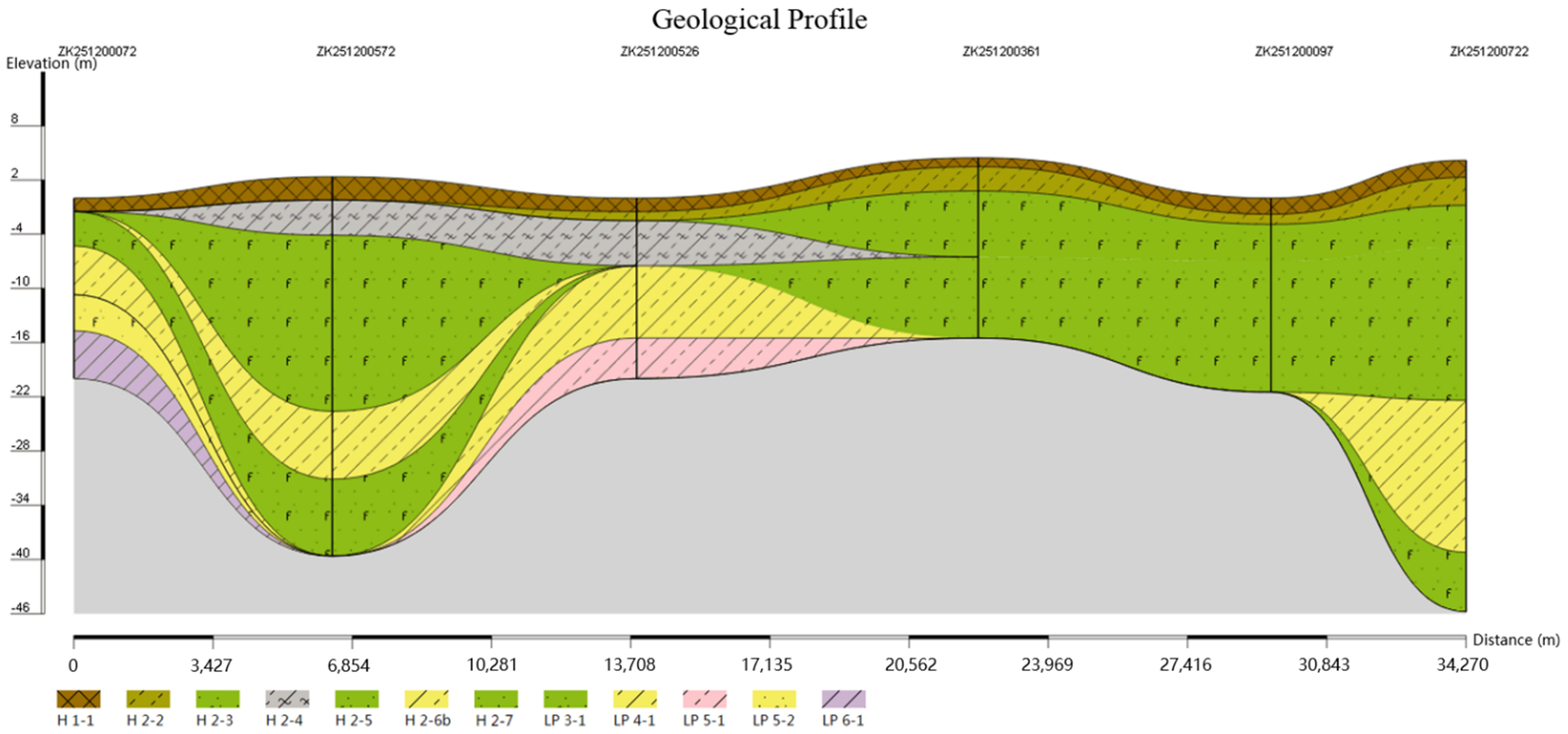
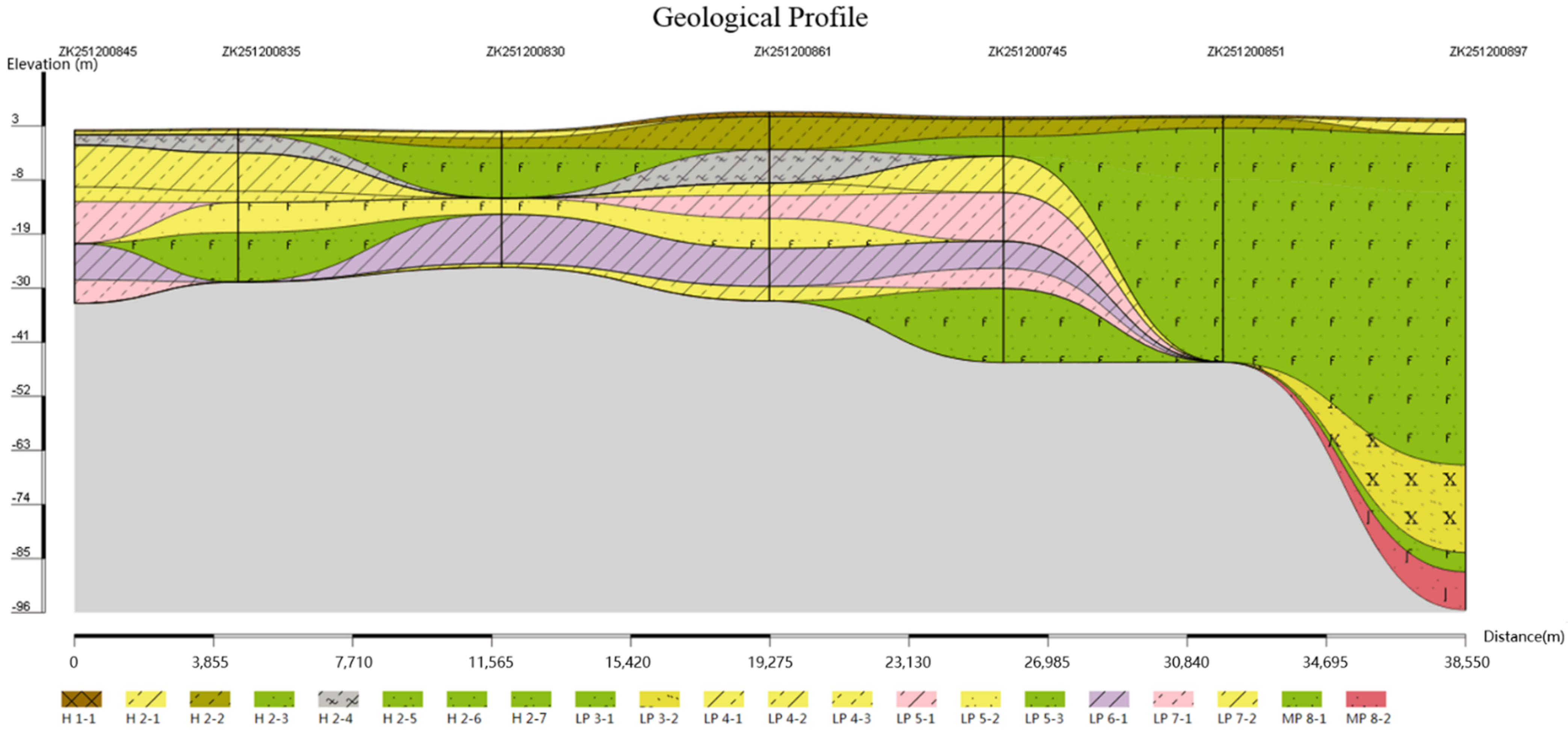

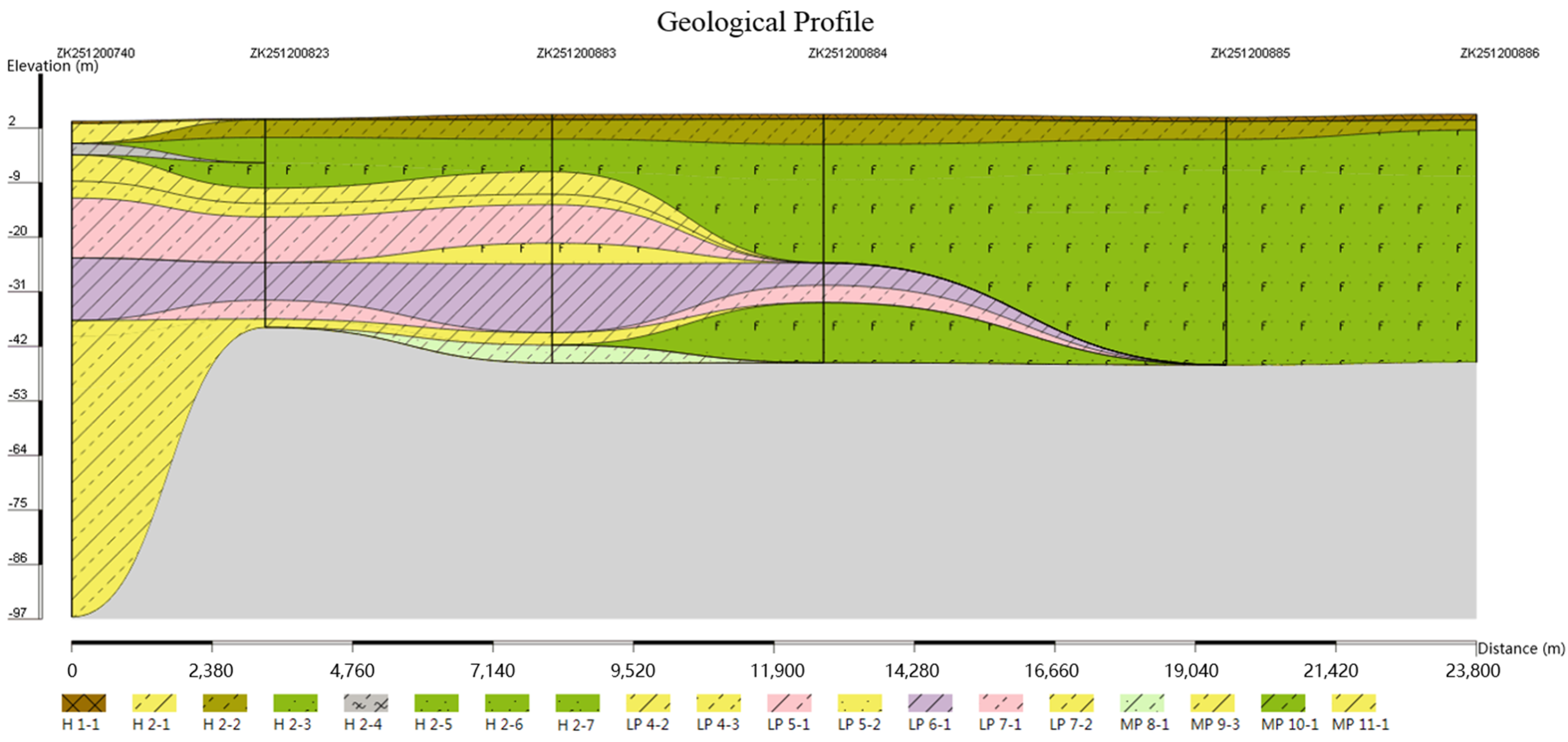
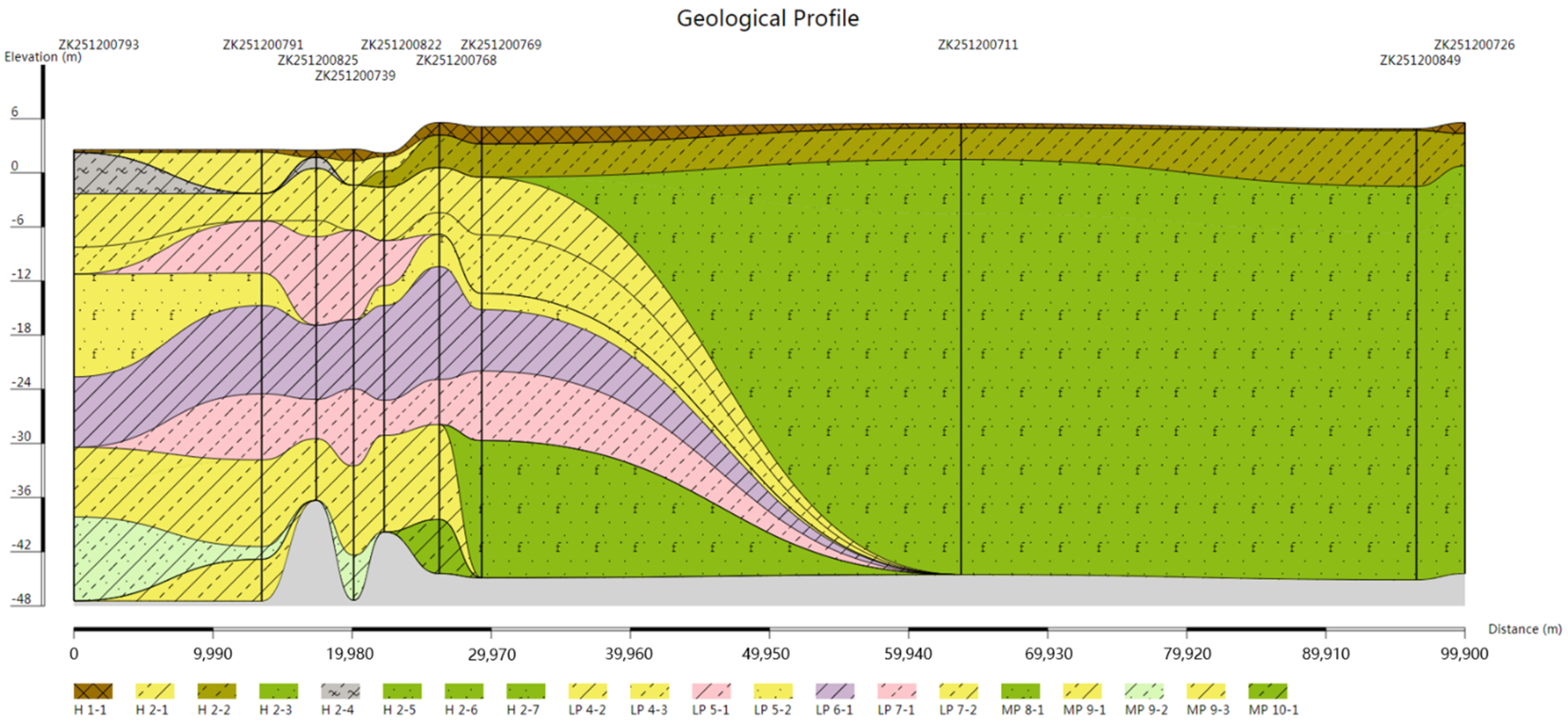
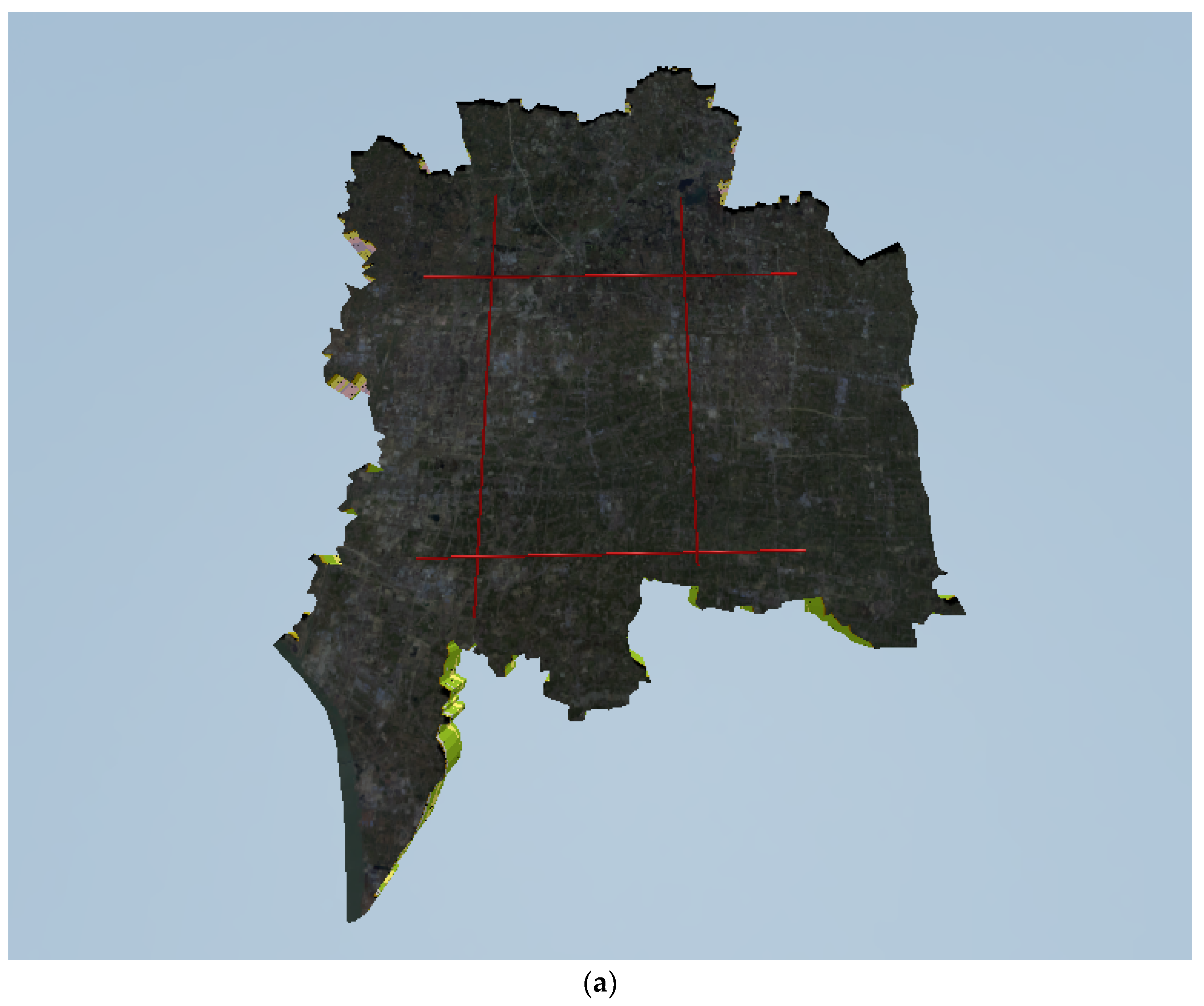
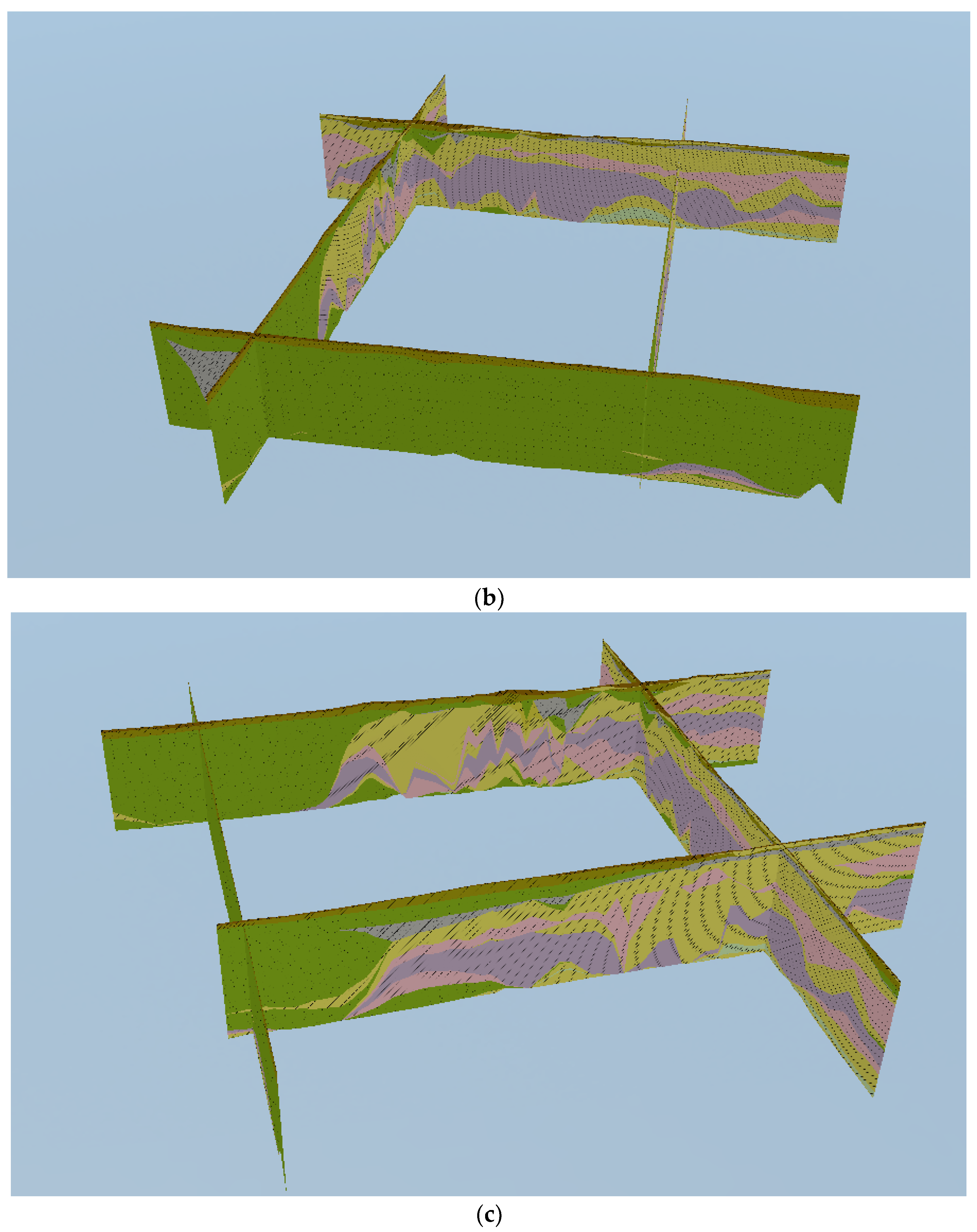

| Formation | Group | Period | Series | Age from Now (Ma) |
|---|---|---|---|---|
| Sanduo formation | Cenozoic | Lower Tertiary | Eocene series | 38.0–50.5 |
| Funing formation | Cenozoic | Lower Tertiary | Paleocene | 54.9–65.0 |
| Taizhou formation | Mesozoic | Cretaceous | Upper | 65.0–83.0 |
| Pukou formation | Mesozoic | Cretaceous | Upper | 83.0–97.5 |
| Longwangshan formation | Mesozoic | Jurassic | Upper | 125.3–136.0 |
| Age | Layer Number | Sublayer | Layer Name | Buried Depth (Average Value) (m) | Layer Thickness (Average Value) (m) | Distribution |
|---|---|---|---|---|---|---|
| Holocene | 1 | 1-1 | earth filling | — | 0.20–4.10 (0.80) | universal distribution |
| 2 | 2-1 | silty clay | 0.20–4.10 (0.66) | 0.40–4.60 (1.75) | northern region | |
| 2-2 | silt | 0.40–4.90 (0.93) | 0.80–13.70 (3.74) | whole area | ||
| 2-3 | siltstone | 0.80–11.0 (4.25) | 1.60–13.10 (6.18) | whole area | ||
| 2-4 | muddy silty clay | 0.30–15.40 (3.75) | 0.9–22.8 (4.43) | local region | ||
| 2-5 | siltstone | 3.4–19.00 (9.94) | 0.9–21.1 (13.46) | Yangtze River floodplain | ||
| 2-6 | siltstone | 17.40–29.40 (24.14) | 6.30–22.80 (14.90) | Yangtze River floodplain | ||
| 2-6b | silty clay | 13.50–37.40 (24.98) | 4.40–25.00 (13.63) | Yangtze River floodplain | ||
| 2-7 | siltstone | 30.80–46.10 (40.09) | 4.00–19.20 (10.40) | Yangtze River floodplain | ||
| Late Pleistocene | 3 | 3-1 | siltstone (fine sand) | 33.10–56.90 (48.44) | 3.10–18.09 (13.01) | Yangtze River floodplain |
| 3-2 | fine sand (medium and coarse sand) | 59.19–70.33 (65.74) | 13.24–29.90 (20.49) | Yangtze River floodplain | ||
| 4 | 4-1 | silty clay | 2.40–14.50 (5.53) | 1.00–4.23 (2.21) | Lixiahe Plain | |
| 4-2 | silty clay | 2.50–22.30 (7.02) | 1.30–9.00 (5.40) | Lixiahe Plain | ||
| 4-3 | silty clay mixed with silt | 4.00–26.50 (11.40) | 0.80–6.90 (2.99) | Lixiahe Plain | ||
| 5 | 5-1 | silt, siltstone | 7.40–28.30 (14.40) | 0.90–21.45 (8.16) | Lixiahe Plain | |
| 5-2 | silty clay | 10.50–28.60 (15.82) | 1.40–14.60 (5.95) | Lixiahe Plain | ||
| 5-3 | siltstone | 21.10–30.00 (26.32) | 2.20–13.60 (8.46) | Lixiahe Plain | ||
| 6 | 6-1 | cay, silty clay | 14.20–39.90 (23.18) | 1.70–16.80 (8.61) | Lixiahe Plain | |
| 7 | 7-1 | silt, siltstone | 23.60–43.00 (31.25) | 0.20–14.05 (5.62) | Lixiahe Plain | |
| 7-2 | silty clay | 27.00–44.00 (33.22) | 0.80–10.30 (4.36) | Lixiahe Plain | ||
| Middle Pleistocene | 8 | 8-1 | siltstone, fine sand | 30.40–93.07 (44.91) | 4.75–29.00 (12.16) | Yangtze River floodplain |
| 8-2 | gravel sand (gravel layer) | 40.10–97.70 (68.50) | 2.30–33.00 (14.56) | Yangtze River floodplain | ||
| 9 | 9-1 | silty clay | 31.30–44.90 (37.10) | 1.50–13.60 (6.57) | Lixiahe Plain | |
| 9-2 | silty clay with silt | 37.40–50.40 (42.91) | 0.90–9.70 (4.29) | Lixiahe Plain | ||
| 9-3 | silty clay | 40.00–50.80 (45.19) | 1.22–16.20 (5.34) | Lixiahe Plain | ||
| 10 | 10-1 | siltstone | 40.30–61.31 (48.55) | 0.60–9.89 (3.72) | Lixiahe Plain | |
| 11 | 11-1 | silty clay | 49.20–62.99 (56.19) | 1.51–14.70 (6.66) | Lixiahe Plain | |
| 11-2 | siltstone | 59.70–66.30 (62.40) | 1.23–6.26 (3.42) | Lixiahe Plain | ||
| 11-3 | silty clay, clay | 54.20–71.00 (64.45) | 2.85–13.84 (7.76) | Lixiahe Plain | ||
| 11-4 | silty clay with silt | 76.60 | 6.80 | Lixiahe Plain | ||
| 12 | 12-1 | siltstone, (fine, medium) sand | 64.37–78.20 (71.31) | 1.53–33.77 (12.54) | Lixiahe Plain | |
| 13 | 13-1 | silty clay | 67.40–79.83 (73.61) | 2.50–8.10 (5.63) | Lixiahe Plain | |
| 13-2 | clay, silty clay | 75.50–86.13 (80.82) | 13.87–20.50 (17.19) | Lixiahe Plain | ||
| Early Pleistocene | 14 | 14-1 | siltstone | 79.02–83.40 (81.21) | 6.60–18.12 (17.36) | whole area |
| 14-2 | silty clay, clay | 72.50–97.14 (82.34) | 2.86–23.60 (11.17) | whole area | ||
| 14-3 | siltstone, fine sand | 86.27–98.20 (91.49) | 1.80–13.73 (8.18) | whole area | ||
| 14-4 | silty clay | 98 | 2.0 | whole area |
| Borehole ID | Longitude | Latitude | Layer Number | Top Elevation | Bottom Elevation |
|---|---|---|---|---|---|
| 1 | — | — | 2-1 | 3.05 | 6.45 |
| 2 | — | — | 3-2 | 6.45 | 13.2 |
| … | … | … | … | … | … |
| 3 | — | — | 1-1 | 3 | 8 |
| 4 | — | — | 1-1 | 3 | 8 |
| … | … | … | … | … | … |
| Number of boreholes | 5 | 10 | 20 | 40 |
| Average time of the unique path method (ms) | 8 | 16 | 20 | 35 |
| Average time of the traditional method (ms) | 50 | 76 | 92 | 127 |
| Unique Path Method | Traditional Method | |
|---|---|---|
| Degree of stratum matching between boreholes | 98.39% | 85.71% |
| Reliability based on empirical experience | 100% | 69.23% |
| Average computation time per 100 boreholes/ms | 127 | 570 |
| Adaptive types of stratigraphic distributions | 5 | 3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Luo, J.; Wang, X.; Ming, W.; Zhou, C. Unique Path Method of the Pinch-Out Profile Based on Unified Stratigraphic Sequence. Geosciences 2021, 11, 251. https://doi.org/10.3390/geosciences11060251
Liu Z, Luo J, Wang X, Ming W, Zhou C. Unique Path Method of the Pinch-Out Profile Based on Unified Stratigraphic Sequence. Geosciences. 2021; 11(6):251. https://doi.org/10.3390/geosciences11060251
Chicago/Turabian StyleLiu, Zhen, Jin Luo, Xiangdong Wang, Weihua Ming, and Cuiying Zhou. 2021. "Unique Path Method of the Pinch-Out Profile Based on Unified Stratigraphic Sequence" Geosciences 11, no. 6: 251. https://doi.org/10.3390/geosciences11060251
APA StyleLiu, Z., Luo, J., Wang, X., Ming, W., & Zhou, C. (2021). Unique Path Method of the Pinch-Out Profile Based on Unified Stratigraphic Sequence. Geosciences, 11(6), 251. https://doi.org/10.3390/geosciences11060251






