On the Poroelastic Biot Coefficient for a Granitic Rock
Abstract
1. Introduction
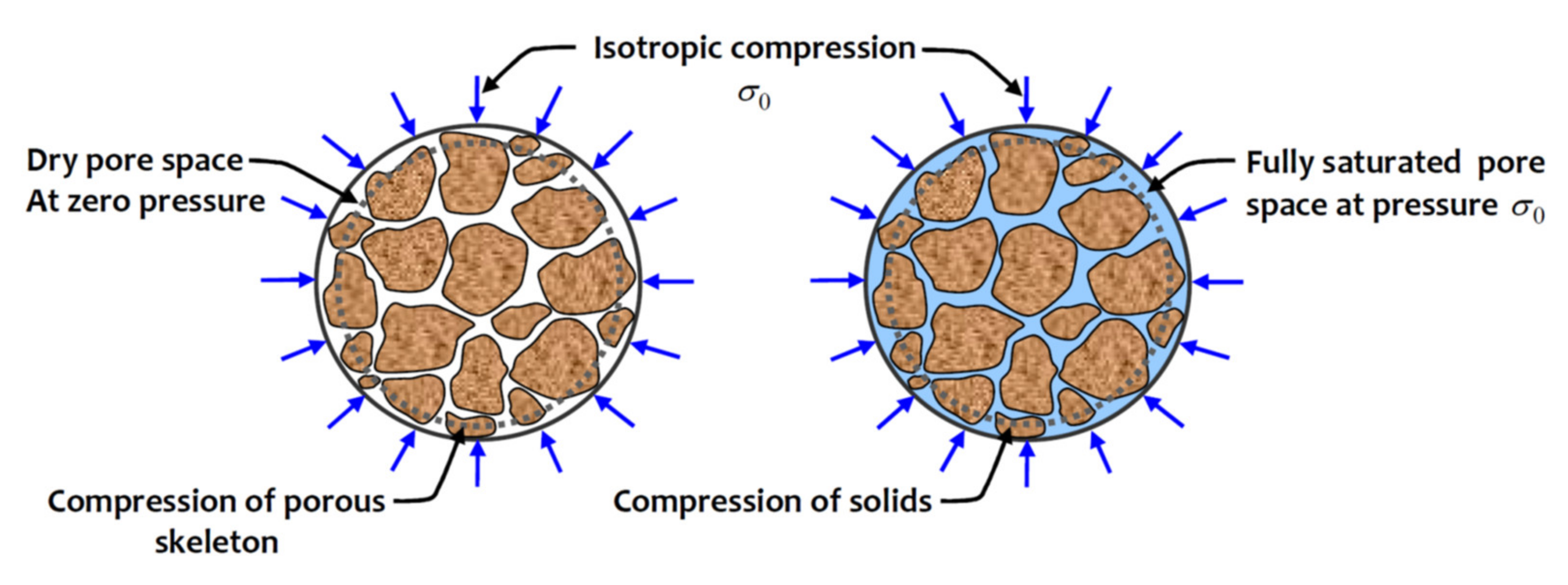
2. The Biot Coefficient
3. Estimation of the Skeletal Compressibility of the Lac du Bonnet Granite
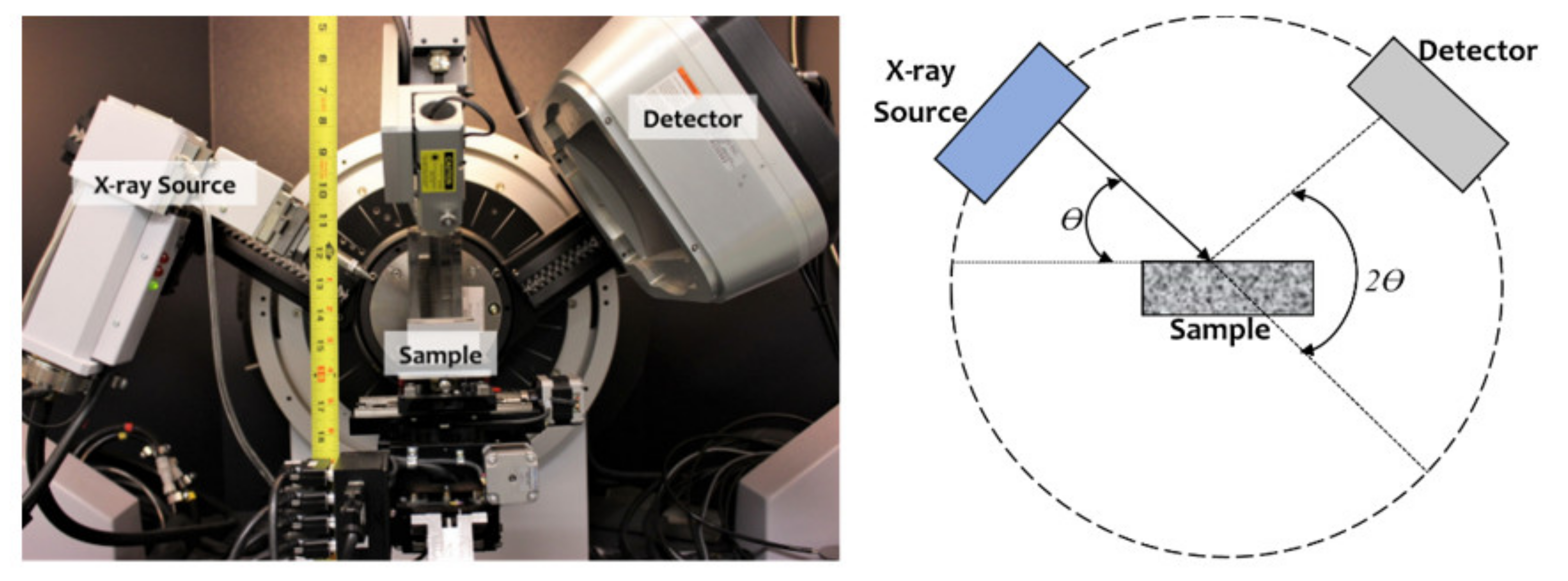
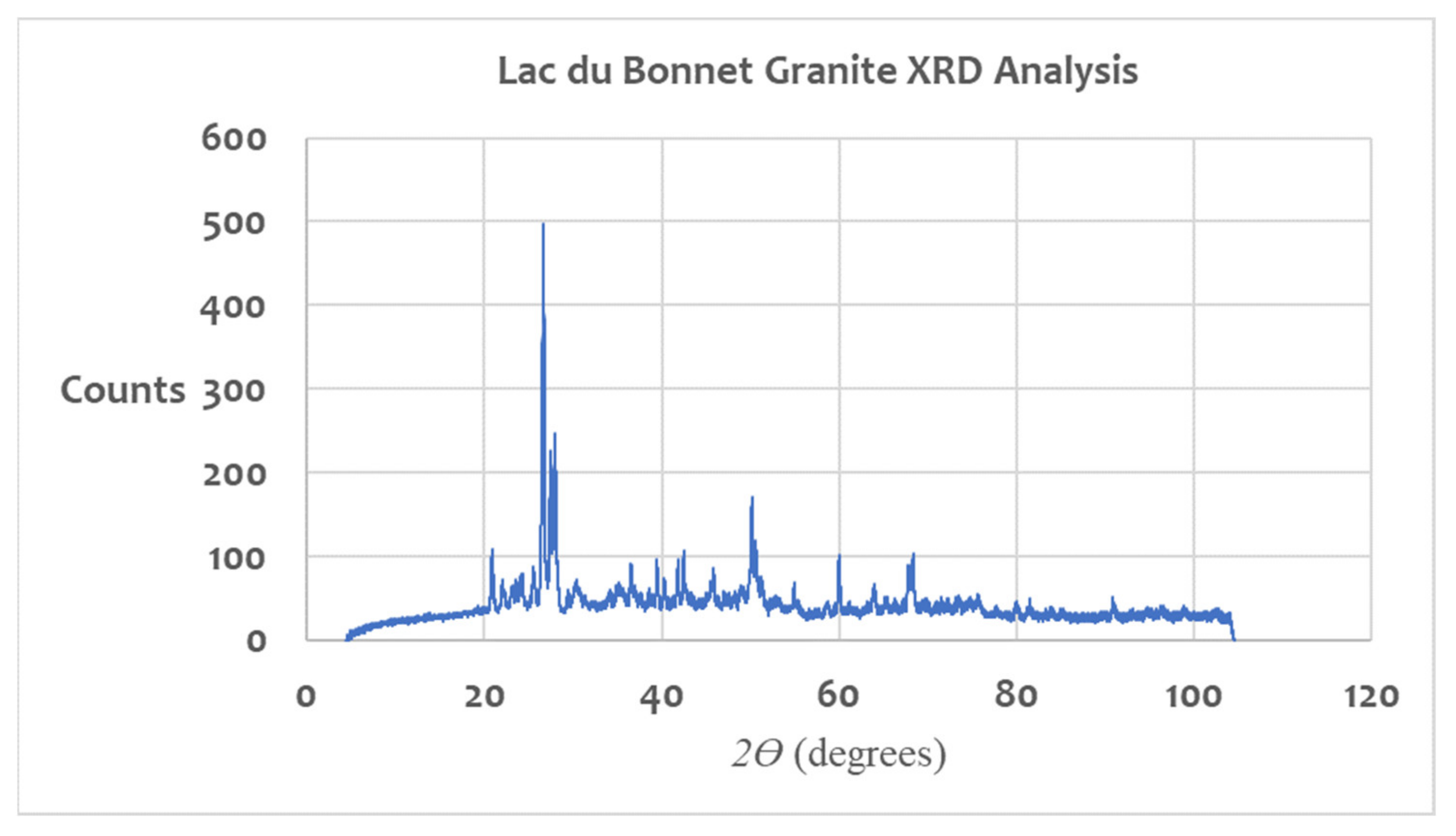
4. Estimation of the Mineralogical Composition of the Lac du Bonnet Granite
5. The Compressibility of the Solid Material Composing the Lac du Bonnet Granite
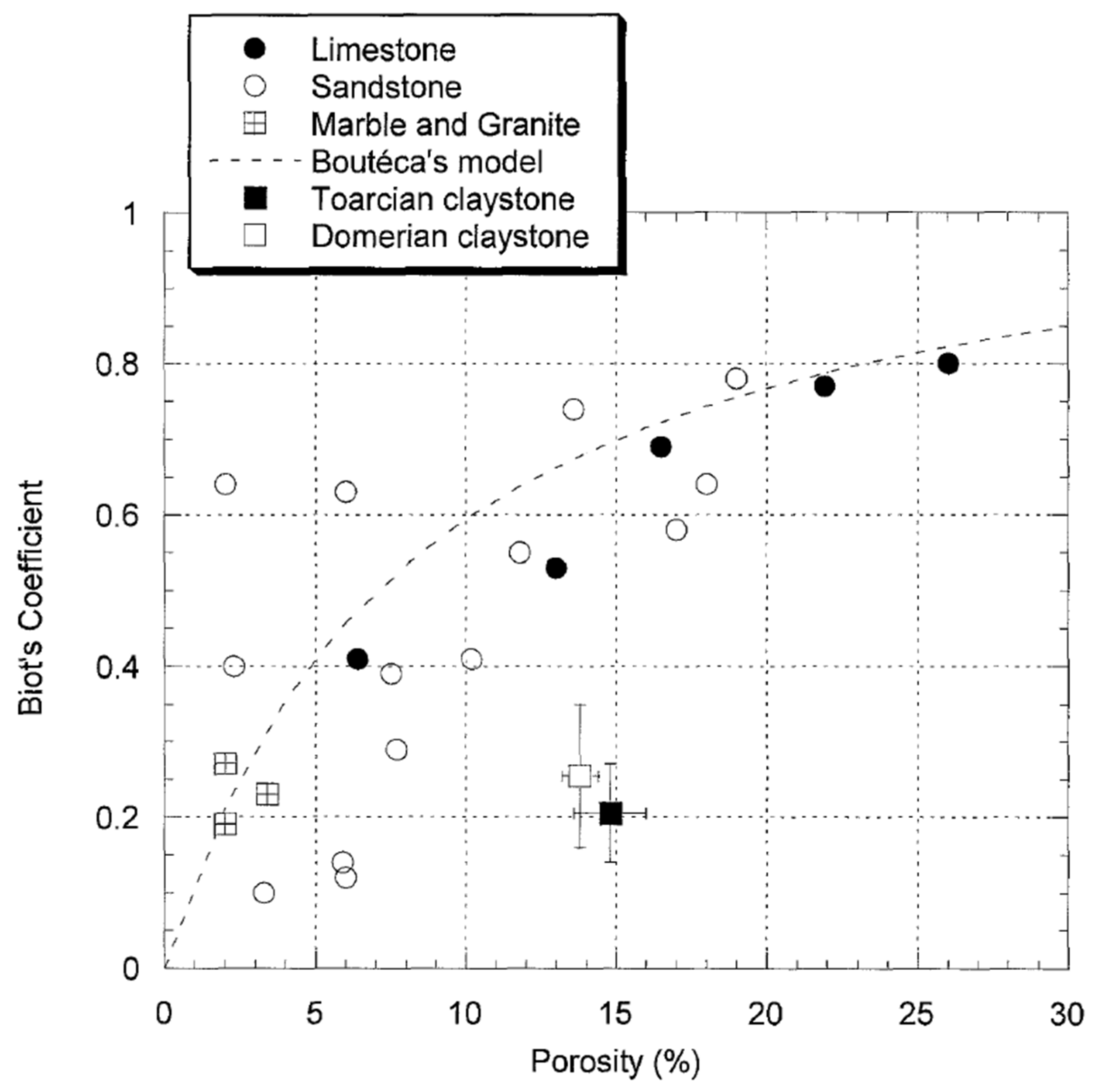
6. Estimates of the Biot Coefficient for the Lac du Bonnet Granite
7. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Laughton, A.S.; Roberts, L.E.J.; Wilkinson, D.; Gray, D.A. The Disposal of Long-lived and Highly Radioactive Wastes. In Proceedings of the Royal Society Discussion Meeting, London, UK, 30 May 1985; Royal Society: London, UK, 1986. [Google Scholar]
- Testa, S.M. Geological Aspects of Hazardous Waste Management; CRC Press: Boca Raton, FL, USA, 1994. [Google Scholar]
- Miller, W.; Alexander, R.; Chapman, N.; McKinley, J.C.; Smellie, J.A.T. Geological Disposal of Radioactive Wastes and Natural Analogues; Waste Management Series; Pergamon Press: Amsterdam, The Netherlands, 2000; Volume 2. [Google Scholar]
- IAEA. Scientific and Technical Basis for Geologic Disposal of Radioactive Waste; Technical Reports Series No. 413; International Atomic Energy Agency: Vienna, Austria, 2000. [Google Scholar]
- NIREX. A Review of the Deep Borehole Disposal Concept for Radioactive Waste; Report No. N/108; Nirex Limited: Didcot, UK, 2004. [Google Scholar]
- Stephansson, O.; Hudson, J.; Jing, L. (Eds.) Coupled Thermo-Hydro-Mechanical-Chemical Processes in Geo-Systems: Fundamentals, Modelling, Experiments and Applications; Elsevier Geo-Engineering Book Series; Elsevier: Amsterdam, The Netherlands, 2004. [Google Scholar]
- Alonso, E.; Alcoverro, J.; Coste, F.; Malinsky, L.; Merrien-Soukatchoff, V.; Kadiri, I.; Nowak, T.; Shao, H.; Nguyen, T.; Selvadurai, A.; et al. The FEBEX benchmark test: Case definition and comparison of modelling approaches. Int. J. Rock Mech. Min. Sci. 2005, 42, 611–638. [Google Scholar] [CrossRef]
- Selvadurai, A.P.S.; Suvorov, A.P.; Selvadurai, P.A. Thermo-hydro-mechanical processes in fractured rock formations during a glacial advance. Geosci. Model Dev. 2015, 8, 2167–2185. [Google Scholar] [CrossRef]
- Selvadurai, A.P.S.; Blain-Coallier, A.; Selvadurai, P.A. Estimates for effective permeability of intact granite obtained from the eastern and western flanks of the Canadian Shield. Minerals 2020, 10, 667. [Google Scholar] [CrossRef]
- Yardley, B.W.D.; Ewing, R.C.; Whittleston, R.A. (Eds.) Deep-mined geological disposal of radioactive waste. Elements 2016, 12, 233–274. [Google Scholar] [CrossRef]
- Selvadurai, A.P.S.; Suvorov, A.P. Thermo-Poroelasticity and Geomechanics; Cambridge University Press: Cambridge, UK, 2016. [Google Scholar]
- Faybishenko, B.; Birkholzer, J.; Sassani, D.; Swift, P. (Eds.) International Approaches for Deep Geological Disposal of Nuclear Waste: Geological Challenges in Radioactive Waste Isolation. In Fifth Worldwide Review; LBNL-1006984; Lawrence Berkeley National Laboratory, Sandia National Laboratories: Albuquerque, NM, USA, 2016. [Google Scholar]
- Nguyen, T.S. Progressive damage of a Canadian granite in laboratory compression tests and underground excavations. Minerals 2021, 11, 10. [Google Scholar] [CrossRef]
- NWMO. People, Science, Indigenous Knowledge. Moving Towards Partnership. In Annual Report of the Nuclear Waste Management Organization; NWMO: Toronto, ON, Canada, 2017; pp. 1–104. [Google Scholar]
- NWMO. Ontario Power Generation’s Deep Geologic Repository for Low and Intermediate Level Waste, Post-Closure Safety Assessment, NWMO DGR-TR-2011-25; NWMO: Toronto, ON, Canada, 2011. [Google Scholar]
- NWMO. Ontario Power Generation’s Deep Geologic Repository for Low and Intermediate Level Waste, Geosynthesis, NWMO DGR-TR-2011-11; NWMO: Toronto, ON, Canada, 2011. [Google Scholar]
- NWMO. NWMO’s Program for Research and Development for Long-Term Management of Used Nuclear Fuel; NWMO TR-2019-18; Nuclear Waste Management Organization: Toronto, ON, Canada, 2019. [Google Scholar]
- OPG 2016. Ontario Power Generation’s Deep Geologic Repository for Low and Intermediate Level Waste: DGR: Protecting Lake Huron: Ontario Power Generation. Available online: www.opg.com/dgr (accessed on 12 May 2020).
- Selvadurai, A.P.S. Geomechanical Characterization of the Cobourg Limestone; Nuclear Waste Management Organization Technical Report NWMO-TR-2017-7; NWMO: Toronto, ON, Canada, 2017. [Google Scholar]
- Boulton, J. (Ed.) Management of Radioactive Wastes: The Canadian Disposal Program; Atomic Energy of Canada Limited Report AECL-6314; Whiteshell Laboratories: Pinawa, MB, Canada, 1978. [Google Scholar]
- Simmons, G.R.; Baumgartner, P. The Disposal of Canada’s Nuclear Fuel Waste: Engineering for a Disposal Facility; AECL Res Rep AECL-10715, COG-93-5; Whiteshell Laboratories: Pinawa, MB, Canada, 1994. [Google Scholar]
- Johnson, L.H.; LeNeveau, D.M.; Shoesmith, D.W.; Oscarson, D.W.; Gray, M.N.; Lemire, R.J.; Garisto, C. The Disposal of Canada’s Nuclear Fuel Waste: The Vault Model for Post-Closure Assessment; AECL Research Report AECL-1071; Whiteshell Laboratories: Pinawa, MB, Canada, 1994. [Google Scholar]
- Stevenson, D.R.; Kozak, E.T.; Davison, C.C.; Gascoyne, M.; Broadfoot, R.A. Hydrogeologic Characteristics of Domains of Sparsely Fractured Rock in the Granitic Lac du Bonnet Batholith; AECL-11558, COG-96-117; Atomic Energy of Canada Limited: Chalk River, ON, Canada; Whiteshell Laboratories: Pinawa, MB, Canada, 1996. [Google Scholar]
- Chandler, N.A. Twenty-five years of underground research at Canada’s URL. In Proceedings of the Waste Management Conference, Tucson, AZ, USA, 23–27 February 2003; pp. 1–15. [Google Scholar]
- Biot, M.A. General theory of three-dimensional consolidation. J. Appl. Phys. 1941, 12, 155–164. [Google Scholar] [CrossRef]
- Kumpel, H.-J. Poroelasticity: Parameters reviewed. Geophys. J. Int. 1991, 105, 783–799. [Google Scholar] [CrossRef]
- Cheng, A.H.-D. Poroelasticity; Springer: Berlin, Germany, 2016. [Google Scholar]
- Selvadurai, A.; Nguyen, T. Computational modelling of isothermal consolidation of fractured porous media. Comput. Geotech. 1995, 17, 39–73. [Google Scholar] [CrossRef]
- Selvadurai, A.P.S. (Ed.) Mechanics of Poroelastic Media; Kluwer Academic Publ.: Dordrecht, The Netherlands, 1996. [Google Scholar]
- Selvadurai, A.P.S. Stationary damage modelling of poroelastic contact. Int. J. Solids Struct. 2004, 41, 2043–2064. [Google Scholar] [CrossRef]
- Selvadurai, A.P.S. The Analytical Method in Geomechanics. Appl. Mech. Rev. 2007, 60, 87–106. [Google Scholar] [CrossRef]
- Selvadurai, A.P.S. A Multi-Phasic Perspective of the Intact Permeability of the Heterogeneous Argillaceous Cobourg Limestone. Sci. Rep. 2019, 9, 17388. [Google Scholar] [CrossRef]
- Selvadurai, A.P.S. The Biot coefficient for a low permeability heterogeneous limestone. Contin. Mech. Thermodyn. 2019, 31, 939–953. [Google Scholar] [CrossRef]
- Selvadurai, A. Irreversibility of soil skeletal deformations: The pedagogical limitations of Terzaghi’s celebrated model for soil consolidation. Comput. Geotech. 2021, 135, 104137. [Google Scholar] [CrossRef]
- Khalili, N.; Selvadurai, A.P.S. A fully coupled Thermo-Hydro-Mechanical for a medium with double porosity. Geophys. Res. Lett. 2003, 30. [Google Scholar] [CrossRef]
- Selvadurai, A.P.S.; Shirazi, A. Mandel-Cryer effects in fluid inclusions in damage susceptible poroelastic media. Comp. Geotech. 2004, 37, 285–300. [Google Scholar] [CrossRef]
- Nguyen, T.; Selvadurai, A.P.S.; Armand, G. Modelling the FEBEX THM experiment using a state surface approach. Int. J. Rock Mech. Min. Sci. 2005, 42, 639–651. [Google Scholar] [CrossRef]
- Selvadurai, A.P.S.; Suvorov, A.P. Boundary heating of poroelastic and poro-elastoplastic spheres. Proc. Roy. Soc. Math. Phys. Sci. Ser. A 2012. [Google Scholar] [CrossRef]
- Selvadurai, A.P.S.; Suvorov, A.P. Thermo-poromechanics of a fluid-filled cavity in a fluid-saturated geomaterial. Proc. R. Soc. A Math. Phys. Eng. Sci. 2014, 470, 20130634. [Google Scholar] [CrossRef]
- Najari, M.; Selvadurai, A.P.S. Thermo-hydro-mechanical response of granite to temperature changes. Environ. Earth Sci. 2014, 72, 189–198. [Google Scholar] [CrossRef]
- Nur, A.; Byerlee, J. An exact effective stress law for elastic deformation of rock with fluids. J. Geophys. Res. 1971, 76, 6414–6419. [Google Scholar] [CrossRef]
- Selvadurai, A.P.S.; Głowacki, A. Evolution of permeability hysteresis of Indiana Limestone during isotropic compression. Ground Water 2008, 46, 113–119. [Google Scholar] [CrossRef]
- Selvadurai, A.P.S.; Selvadurai, P.A.; Nejati, M. A multi-phasic approach for estimating the Biot coefficient for Grimsel granite. Solid Earth 2019, 10, 2001–2014. [Google Scholar] [CrossRef]
- Kasani, H.A.; Selvadurai, A.P.S. A review of techniques for measuring Biot’s effective stress coefficient for rocks: Recent advances and scientific issues. Geomech. Energy Environ. 2021. under review. [Google Scholar]
- Pariseau, W.G. Poroelastic-plastic consolidation-analytical solution. Int. J. Numer. Anal. Methods Geomech. 1999, 23, 577–594. [Google Scholar] [CrossRef]
- Suvorov, A.; Selvadurai, A. The Biot coefficient for an elasto-plastic material. Int. J. Eng. Sci. 2019, 145, 103166. [Google Scholar] [CrossRef]
- Selvadurai, A.P.S.; Suvorov, A.P. The influence of the pore shape on the bulk modulus and the Biot coefficient of fluid-saturated porous rocks. Sci. Rep. 2020, 10, 18959. [Google Scholar] [CrossRef] [PubMed]
- Voigt, W. Lehrbuch der Kristallphysik; Teubner: Leipzig, Germany, 1928. [Google Scholar]
- Reuss, A. Berechnung der Flieβgrenze von Mischkristallen auf Grund der Plastizitätsbedingung für Einkristalle. J. Appl. Math. Mech. 1929, 9, 49–58. [Google Scholar]
- Hill, R. The elastic behaviour of a crystalline aggregate. Proc. Phys. Soc. 1952, 65, 349–354. [Google Scholar] [CrossRef]
- Hill, R. Self-consistent mechanics of composite materials. J. Mech. Phys. Solids 1965, 13, 213–222. [Google Scholar] [CrossRef]
- Hashin, Z. The elastic moduli of heterogeneous materials. J. Appl. Mech. 1962, 29, 143–150. [Google Scholar] [CrossRef]
- Hashin, Z.; Shtrikman, S.A. Variational approach to the theory of elastic behaviour of multiphase materials. J. Mech. Phys. Solids 1963, 11, 127–140. [Google Scholar] [CrossRef]
- Beran, M.J. Statistical Continuum Theories; Wiley Interscience: New York, NY, USA, 1968. [Google Scholar]
- Brace, W.F. Some new measurements of linear compressibility of rocks. J. Geophys. Res. 1965, 70, 391–398. [Google Scholar] [CrossRef]
- Christensen, R.M. Mechanics of Composite Materials; Wiley: New York, NY, USA, 1979. [Google Scholar]
- Milton, G.W. The Theory of Composites; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Mavko, G.; Mukerji, T.; Dvorkin, J. The Rock Physics Handbook, Tools for Seismic Analysis of Porous Media; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Markov, K.; Preziosi, L. (Eds.) Heterogeneous Media. Micromechanics Modeling Methods and Simulations; Birkhauser: Boston, MA, USA, 2000. [Google Scholar]
- Selvadurai, A.P.S.; Letendre, A.; Hekimi, B. Axial flow hydraulic pulse testing of an argillaceous limestone. Environ. Earth Sci. 2011, 64, 2047–2058. [Google Scholar] [CrossRef]
- Walpole, L.J. On bounds for the overall elastic moduli of inhomogeneous systems. J. Mech. Phys. Solids 1966, 14, 151–162. [Google Scholar] [CrossRef]
- Hale, D.K. The mechanical properties of composite materials. J. Mat. Sci. 1976, 11, 2105–2141. [Google Scholar] [CrossRef]
- Thomsen, L. Elasticity of polycrystals and rocks. J. Geophys. Res. 1972, 77, 315–327. [Google Scholar] [CrossRef]
- Kröner, E. Elastic moduli of perfectly disordered composite materials. J. Mech. Phys. Solids 1967, 15, 319–329. [Google Scholar] [CrossRef]
- Selvadurai, A.P.S.; Glowacki, A. Stress-induced permeability alterations in an argillaceous limestone. Rock Mech. Rock Eng. 2017, 50, 1079–1096. [Google Scholar] [CrossRef]
- TCNA. The Testing Council of North America; Report No TCNA 232-10; Product Testing Services: Anderson, SC, USA, 2010. [Google Scholar]
- Martin, C.D.; Chandler, N.A. Progressive failure of Lac du Bonnet granite. Int. J. Rock Mech. Min. Sci. 1994, 31, 643–659. [Google Scholar] [CrossRef]
- Martin, C.D.; Stimpson, B. Effect of sample disturbance on laboratory properties of Lac du Bonnet granite. Can. Geotech. J. 1994, 31, 692–702. [Google Scholar] [CrossRef]
- Jackson, R.; Lau, J.S.O.; Annor, A. Mechanical, thermo-mechanical and joint properties of rock samples from the site of the AECL’s Underground Research Laboratory, Lac du Bonnet, Manitoba. In Proceedings of the 42nd Canadian Geotechnical Conference, Winnipeg, MB, Canada, 22–25 October 1989; pp. 41–49. [Google Scholar]
- Stone, D.; Kamineni, D.C.; Brown, A.; Everitt, R.A. Comparison of fracture styles in two granite bodies of the Superior Province. Can. J. Earth Sci. 1989, 26, 387–403. [Google Scholar] [CrossRef]
- Carter, B.J.; Duncan, E.S.; Lajtai, E.Z. Fitting strength criteria to intact rock. Geotech. Geol. Eng. 1991, 9, 73–81. [Google Scholar] [CrossRef]
- Read, R.S.; Martin, C.D. Technical Summary of AECL’s Mine-by Experiment. Phase 1: Excavation Response; AECL-11311, COG-95-171; Whiteshell Laboratories: Pinawa, MB, Canada, 1996. [Google Scholar]
- Tammemagi, H.Y.; Kerford, P.S.; Requeima, J.C.; Temple, C.A.A. Geological Reconnaissance Study of the Lac du Bonnet Batholith; AECL-6439; Whiteshell Nuclear Research Establishment: Pinawa, MB, Canada, 1980. [Google Scholar]
- Chernis, P.J.; Robertson, P.B. Thermal Cracking in Lac du Bonnet Granite During Slow Heating to 205 °C; AECL-10937, COG-93-358; Whiteshell Nuclear Research Establishment: Pinawa, MB, Canada, 1993. [Google Scholar]
- Duevel, B.; Haimson, B. Mechanical characterization of pink lac du Bonnet granite: Evidence of non-linearity and anisotropy. Int. J. Rock Mech. Min. Sci. 1997, 34, 3–4. [Google Scholar] [CrossRef]
- Eberhardt, E.; Stimpson, B.; Stead, D. Effect of grain size on the initiation and propagation thresholds of stress-induced brittle fractures. Rock Mech. Rock Eng. 1999, 32, 81–99. [Google Scholar] [CrossRef]
- Lukkarila, M.J. Report on Cold Spring Granite; Cemstone Engineering Services: Mendota Heights, MN, USA, 2004. [Google Scholar]
- Rietveld, H.M. A profile refinement method for nuclear and magnetic structures. J. Appl. Cryst. 1969, 2, 65–71. [Google Scholar] [CrossRef]
- Waber, H.N.; Mäder, U.K.; Koroleva, M.; de Haller, A. Testing Methods for the Characterization of Saline Pore Water in an Ordovician Limestone (Cobourg Formation, St Mary’s Quarry, Ontario) Feasibility Study; Technical Report TR 07-01; Rock-Water Interaction (RWI) Institute of Geological Sciences, University of Bern: Bern, Switzerland, 2007. [Google Scholar]
- Selvadurai, A.P.S.; Rezaei Niya, S.M. The effective thermal conductivity of an intact heterogeneous limestone. Rock Mech. Geotech. Eng. 2020, 12, 682–692. [Google Scholar] [CrossRef]
- Diffrac-Suite. User Manual; Bruker, A.X.S. GmbH: Karlsruhe, Germany, 2011. [Google Scholar]
- Alexandrov, K.S.; Rhyzova, T.V.; Beliko, B.P. The elastic properties of pyroxenes. Sov. Phys. Crystallogr. 1964, 8, 589–591. [Google Scholar]
- Anderson, O.L.; Nafe, J.E. The bulk modulus –volume relationship for oxide compounds and related geophysical problems. J. Geophys. Res. 1965, 70, 3951–3963. [Google Scholar] [CrossRef]
- Carmichael, R.S. Practical Handbook of Physical Properties of Rocks and Minerals; CRC Press: Boca Raton, FL, USA, 1990. [Google Scholar]
- Wenning, Q.C.; Madonna, C.; de Haller, A.; Burg, J.-P. Permeability and seismic velocity anisotropy across a ductile-brittle fault zone in crystalline rock. Solid Earth 2018, 9, 683–698. [Google Scholar] [CrossRef]
- Ramakrishnan, N.; Arunachalam, V.S. Effective elastic moduli of porous ceramic materials. J. Am. Ceramic. Soc. 1993, 76, 2745–2752. [Google Scholar] [CrossRef]
- Lau, J.S.O.; Chandler, N.A. Innovative laboratory testing. Int. J. Rock Mech. Min. Sci. 2004, 41, 1427–1445. [Google Scholar] [CrossRef]
- Rutqvist, J.; Borgesson, L.; Chijimatsu, M.; Hernelind, J.; Jing, L.; Kobayashi, A.; Nguyen, T.S. Modeling of Damage, Permeability Changes and Pressure Responses during Excavation of TSX Tunnel in Granite Rock at URL, Canada. 2009. Available online: https://escholarship.org/uc/item/8f12b5cf (accessed on 1 June 2020).
- Chan, T.; Stanchell, F.W. DECOVALEX THMC TASK E-Implications of Glaciation and Coupled Thermohydromechanical Processes on Shield Flow System Evolution and Performance Assessment; NWMO TR-2008003; Nuclear Waste Management Organization: Toronto, ON, Canada, 2008. [Google Scholar]
- Cosenza, P.; Ghoryechi, M.; de Marsily, G.; Vasseur, G.; Violette, S. Theoretical prediction of poroelastic properties of argillaceous rocks from in situ specific storage coefficient. Water Res. Res. 2002, 38. [Google Scholar] [CrossRef]
- Rice, J.R.; Cleary, M.P. Some basic stress diffusion solutions for fluid-saturated elastic porous media with compressible constituents. Rev. Geophys. Space Phys. 1976, 14, 227–241. [Google Scholar] [CrossRef]
- Cheng, A.-H.D.; Detournay, E. Fundamentals of poroelasticity, Chapter 5 in Comprehensive Rock Engineering: Principles, Practice and Projects. In Analysis and Design Method; Fairhurst, C., Ed.; Pergamon Press: Oxford, UK, 1993; Volume II, pp. 113–171. [Google Scholar]
- Bouteca, M.; Sarda, J.-P. Elements of thermo-poroelasticity. In Mechanics of Porous Media; Charlez, P.A., Ed.; Balkema: Rotterdam, The Netherlands, 1995; pp. 21–30. [Google Scholar]
- Charlez, P. Rocks Mechanics. In Petroleum Applications; Technip: Paris, France, 1997; Volume II. [Google Scholar]
- Fabre, D.; Gustkiewicz, J. Poroelastic properties of limestones and sandstones under hydrostatic conditions. Int. J. Rock Mech. Min. Sci. 1997, 34, 127–134. [Google Scholar] [CrossRef]
- Berryman, J.G. Effective stress for transport properties of inhomogeneous porous rock. J. Geophys. Res. 1992, 97, 17409–17424. [Google Scholar] [CrossRef]
- Wang, H.F. Quasi-static poroelastic parameters in rock and their geophysical applications. Pure Appl. Geophys. 1993, 141, 269–286. [Google Scholar] [CrossRef]
- Souley, M.; Lopez, P.; Boulon, M.J.; Thoraval, A. Experimental hydromechanical characterization and numerical modelling of a fractured and porous sandstone. Rock Mech. Rock Eng. 2015, 48, 1143–1161. [Google Scholar] [CrossRef]
- Hu, C.; Agostini, F.; Skoczylas, F.; Jeannin, L.; Potier, L. Poromechanical properties of a sandstone under different stress states. Rock Mech. Rock Eng. 2018, 51, 3699–3717. [Google Scholar] [CrossRef]
- Chen, Y.; Selvadurai, A.P.S.; Liang, W. Computational modelling of groundwater inflow during a longwall coal mining advance: A Case study from the Shanxi Province China. Rock Mech. Rock Eng. 2019, 52, 917–934. [Google Scholar] [CrossRef]
- Selvadurai, A.P.S.; Zhang, D.; Kang, Y. Permeability evolution in natural fractures and their potential influence on loss of productivity in ultra-deep gas reservoirs of the Tarim Basin, China. J. Nat. Gas Sci. Eng. 2018, 58, 162–177. [Google Scholar] [CrossRef]
- Braun, P.; Ghabezloo, S.; Delage, P.; Sulem, J.; Conil, N. Determination of multiple thermo-hydro-mechanical rock properties in a single transient experiment: Application to shales. Rock Mech. Rock Eng. 2019, 52, 2030–2038. [Google Scholar] [CrossRef]
- Chen, R.; Xia, K. Determination of Dynamic Fracture Properties of Rocks Using Semi-Circular Bend Technique; Sanchidrian, J., Ed.; Taylor and Francis Group: London, UK, 2010; pp. 51–57. [Google Scholar]
- Wang, H.F. Theory of Linear Poroelasticity with Applications to Geomechanics and Hydrogeology; Princeton University Press: Princeton, NJ, USA, 2000. [Google Scholar]
- Zimmerman, R.W.; Somerton, W.H.; King, M.S. Compressibility of porous rocks. J. Geophys. Res. 1986, 91, 12765–12777. [Google Scholar] [CrossRef]
- Zimmerman, R.W. Coupling in poroelasticity and thermoelasticity. Int. J. Rock Mech. Min. Sci. 2000, 17, 79–87. [Google Scholar] [CrossRef]
- Schmitt, D.R.; Zoback, M.D. Poroelastic effects in the determination of the maximum horizontal principal stress in hydraulic fracturing tests-A proposed breakdown equation employing a modified effective stress relation for tensile fracture. Int. J. Rock Mech. Min. Sci. 1989, 26, 499–506. [Google Scholar] [CrossRef]
- Duan, Z.; Skoczylas, F. Experimental study of the permeability and poromechanical properties of thermally damaged granite. Eur. J. Environ. Civ. Eng. 2019, 25. [Google Scholar] [CrossRef]
- Tan, X.; Konietzky, H. Numerical study of Biot’s coefficient evolution during failure process for Aue granite using an empirical equation based on GMR Method. Rock Mech. Rock Eng. 2017, 50, 1683–1689. [Google Scholar] [CrossRef]
- Coyner, K.B. Effects of Stress, Pore Pressure, and Pore Fluids on Bulk Strain, Velocity, and Permeability of Rocks. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1984. [Google Scholar]
- Selvadurai, A.P.S.; Selvadurai, P.A. Surface permeability tests: Experiments and modelling for estimating effective permeability. Proc. Roy. Soc. Math. Phys. Sci. Ser. A 2010, 466, 2819–2846. [Google Scholar] [CrossRef]



| Testing Facility | Sample Dimensions | Young’s Modulus | Poisson’s Ratio |
|---|---|---|---|
|
MTS Rock Testing Machine | 100 mm diameter 200 mm long | 70.8 GPa to 72.2 GPa | 0.21 to 0.23 |
|
MTS Rock Testing Machine | 150 mm diameter 300 mm long | 70.4 GPa | N/A |
|
HCLC Uniaxial Testing Machine | 150 mm diameter 300 mm long | 72.0 GPa | 0.213 |
| Reference | Young’s Modulus | Poisson’s Ratio |
|---|---|---|
| Jackson et al. [69] | 68.0 GPa | 0.24 |
| Stone et al. [70] | 66.7 GPa | 0.27 |
| Carter et al. [71] | 70.0 GPa | 0.21 |
| Read and Martin [72] | (65.0 ± 5) GPa | (0.25 ± 0.05) |
| Martin and Stimpson [68] | 68.0 GPa | 0.26 |
| Reference | Quartz (%) | Feldspar (%) | Mica, etc. (%) |
|---|---|---|---|
| MIAM | 38.4 | 60.2 | 1.4 |
| Tammemagi et al. [73] | 30.0 | 65.0 | 5.0 |
| Chernis & Robertson [74] | 30.6 | 64.8 | 4.6 |
| Duevel & Haimson [75] | 30.0 | 60.0 | 10.0 |
| Eberhardt et al. [76] | 30.0 | 65.0 | 5.0 |
| Lukkarila [77] | 34.0 | 56.0 | 10.0 |
| Mineral | Specific Gravity | (%) | (GPa) | (GPa) |
|---|---|---|---|---|
| Quartz | 2.72 | 38.4 | 38 | 45 |
| Feldspar | 2.60 | 60.2 | 76 | 26 |
| Mica, etc | 2.70 | 1.4 | 61 | 41 |
| Reference | Rock Designation | Porosity | Biot Coefficient |
|---|---|---|---|
| Brace [55] | Stone Mountain | 0.003 | 0.027 to 0.86 |
| Schmitt and Zoback [107] | Kent Cliffs cryst. rock | 0.0015 | 0.24 to 0.68 |
| Berryman [96] | Barre granite | 0.007 | 0.75 |
| Berryman [96] | Westerly granite | 0.008 | 0.55 |
| Berryman [96] | Chelmsford granite | 0.011 | 0.85 |
| Selvadurai & Nguyen [28] | Canadian Shield | 0.005 | 0.60 |
| Cosenza et al. [90] | Tennessee marble | 0.02 | 0.19 |
| Cosenza et al. [90] | Charcoal granite | 0.02 | 0.27 |
| Cosenza et al. [90] | Westerly granite | 0.01 | 0.47 |
| Chan and Stanchell [89] | Lac du Bonnet granite | 0.002 | 0.73 |
| Najari and Selvadurai [40] | Stanstead granite | 0.007 | 0.44 |
| Duan and Skoczylas [108] | Beishan granite | 0.0005 | 0.70 to 0.90 |
| Tan and Konietzky [109] | Aue granite | 0.0158 to 0.023 | 0.35 to 0.41 |
| Selvadurai et al. [43] | Grimsel granite | 0.0048 | 0.48 to 0.71 |
| Lau and Chandler [87] | Lac du Bonnet granite | 0.002 | 0.73 |
| Current Study | Stanstead granite | 0.0077 | 0.44 |
| Current Study | Lac du Bonnet granite | 0.0026 | 0.30 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Selvadurai, A.P.S. On the Poroelastic Biot Coefficient for a Granitic Rock. Geosciences 2021, 11, 219. https://doi.org/10.3390/geosciences11050219
Selvadurai APS. On the Poroelastic Biot Coefficient for a Granitic Rock. Geosciences. 2021; 11(5):219. https://doi.org/10.3390/geosciences11050219
Chicago/Turabian StyleSelvadurai, A. P. S. 2021. "On the Poroelastic Biot Coefficient for a Granitic Rock" Geosciences 11, no. 5: 219. https://doi.org/10.3390/geosciences11050219
APA StyleSelvadurai, A. P. S. (2021). On the Poroelastic Biot Coefficient for a Granitic Rock. Geosciences, 11(5), 219. https://doi.org/10.3390/geosciences11050219






