Stiffness and Strength of Stabilized Organic Soils—Part II/II: Parametric Analysis and Modeling with Machine Learning
Abstract
1. Introduction
2. Background
3. Modeling
3.1. Experimental Database
3.2. Artificial Neural Networks
3.2.1. Radial Basis Functions
3.2.2. Multilayer Perceptron
3.2.3. Multiple Linear Regression (MLR)
4. Analysis and Results
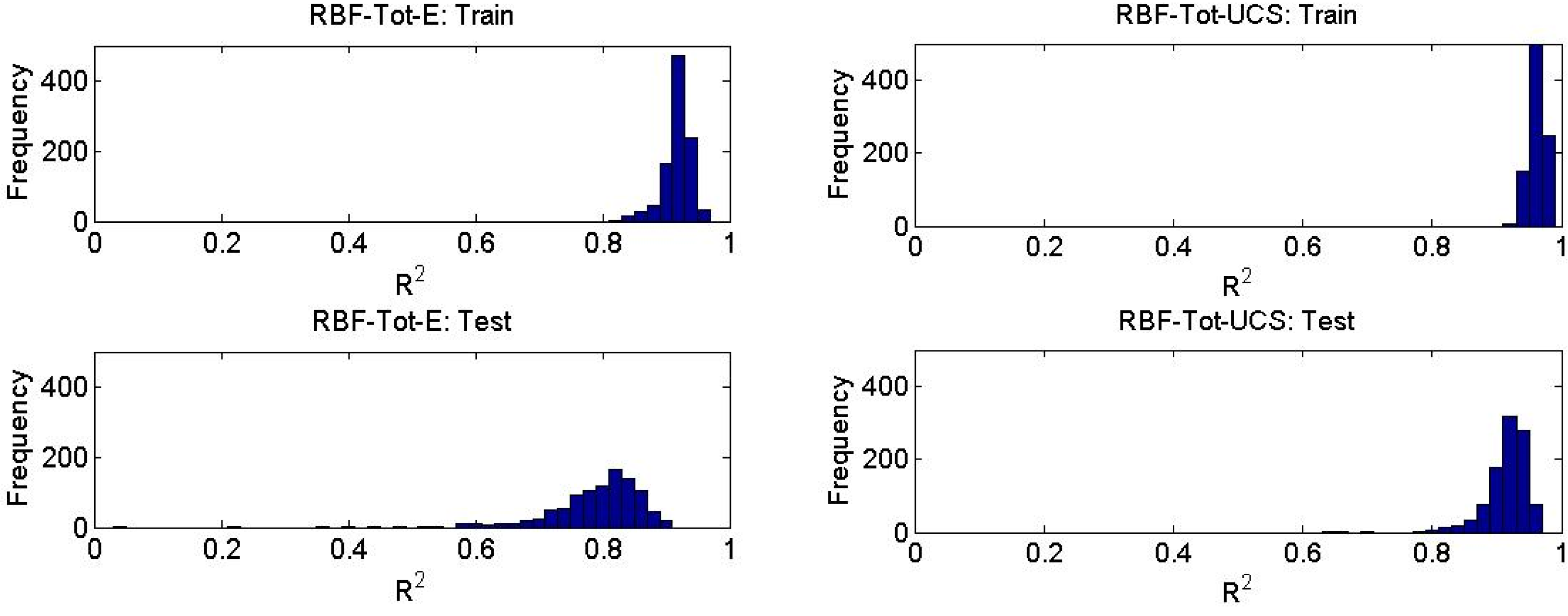
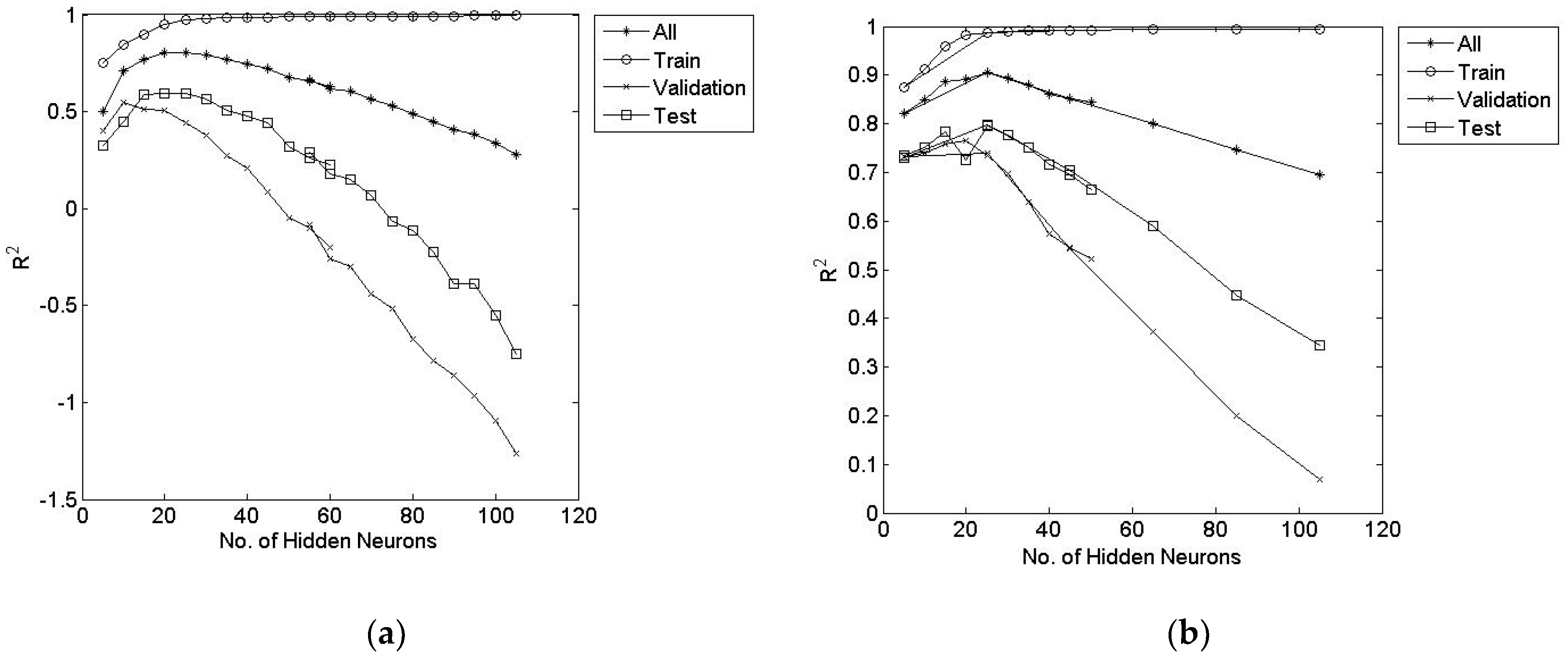
4.1. RBF Network Analysis
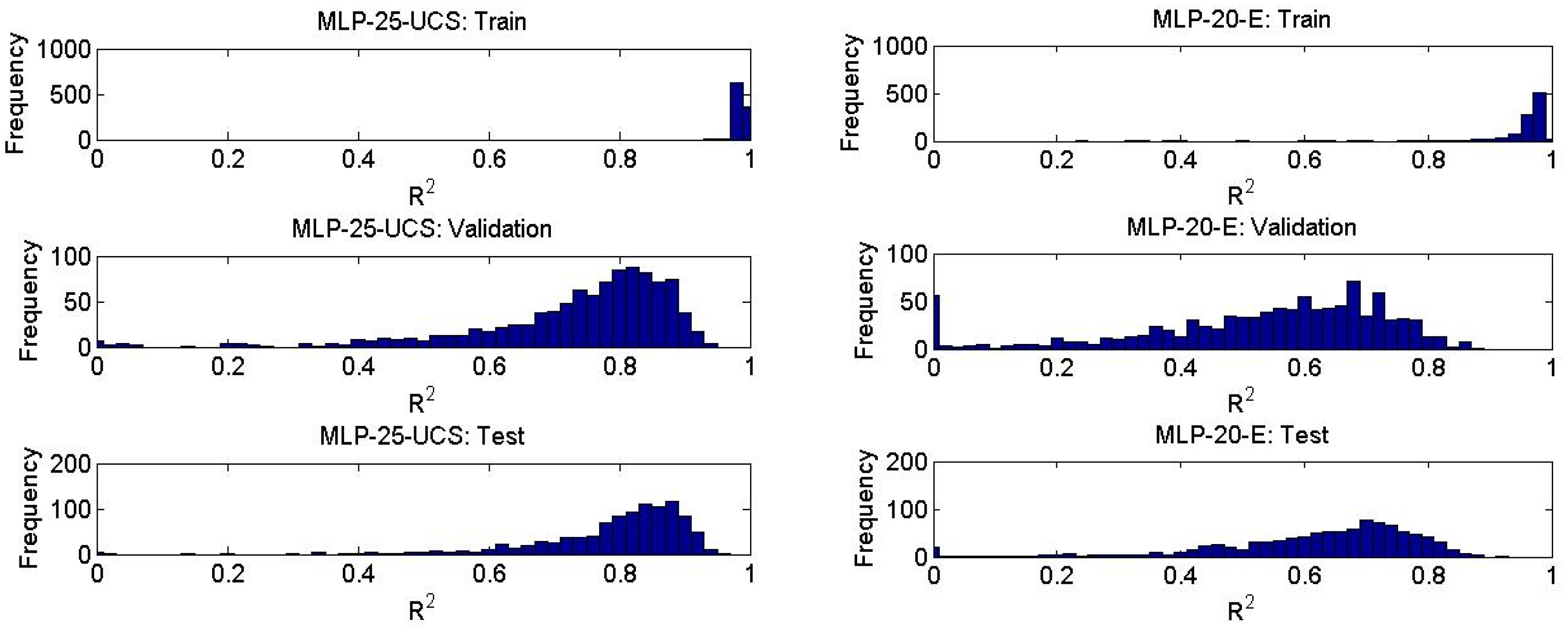
4.2. MLP Network Analysis
4.3. Stepwise Parameter Selection for ANNs
4.4. Linear Regression Analysis
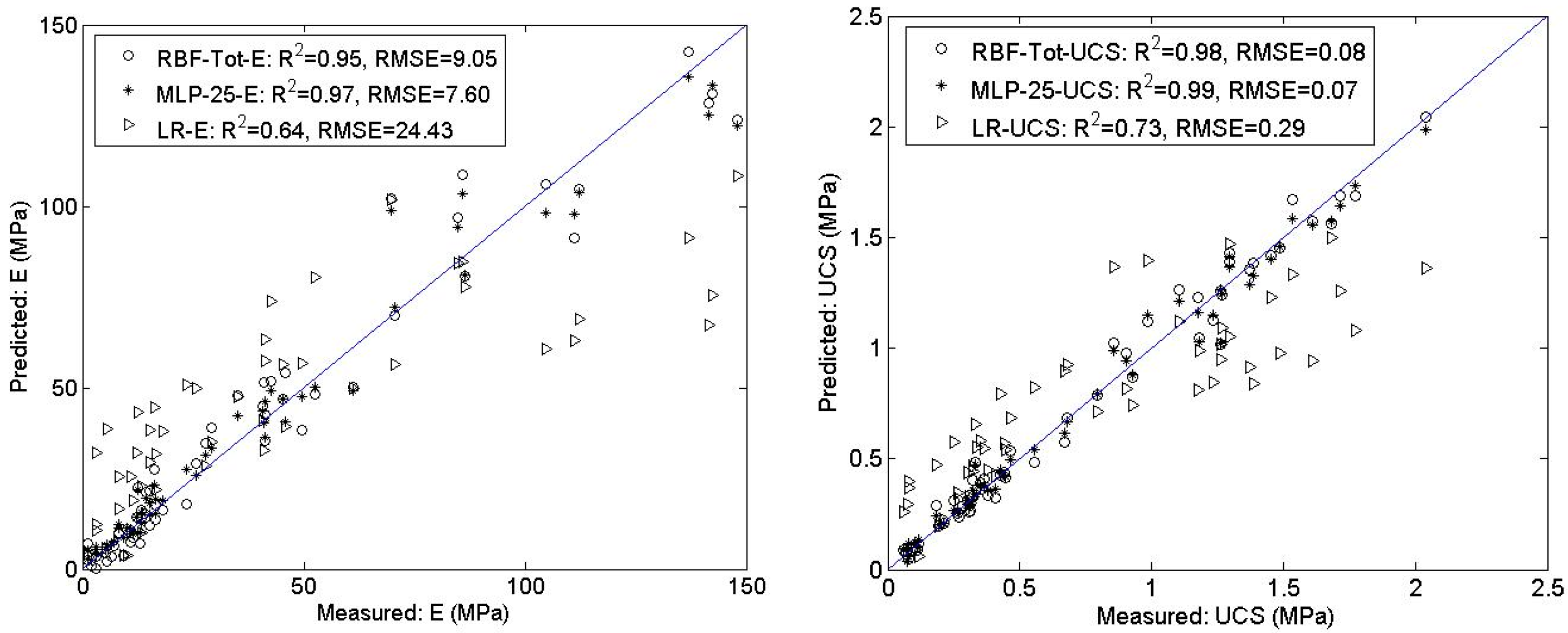
4.5. Model Comparison
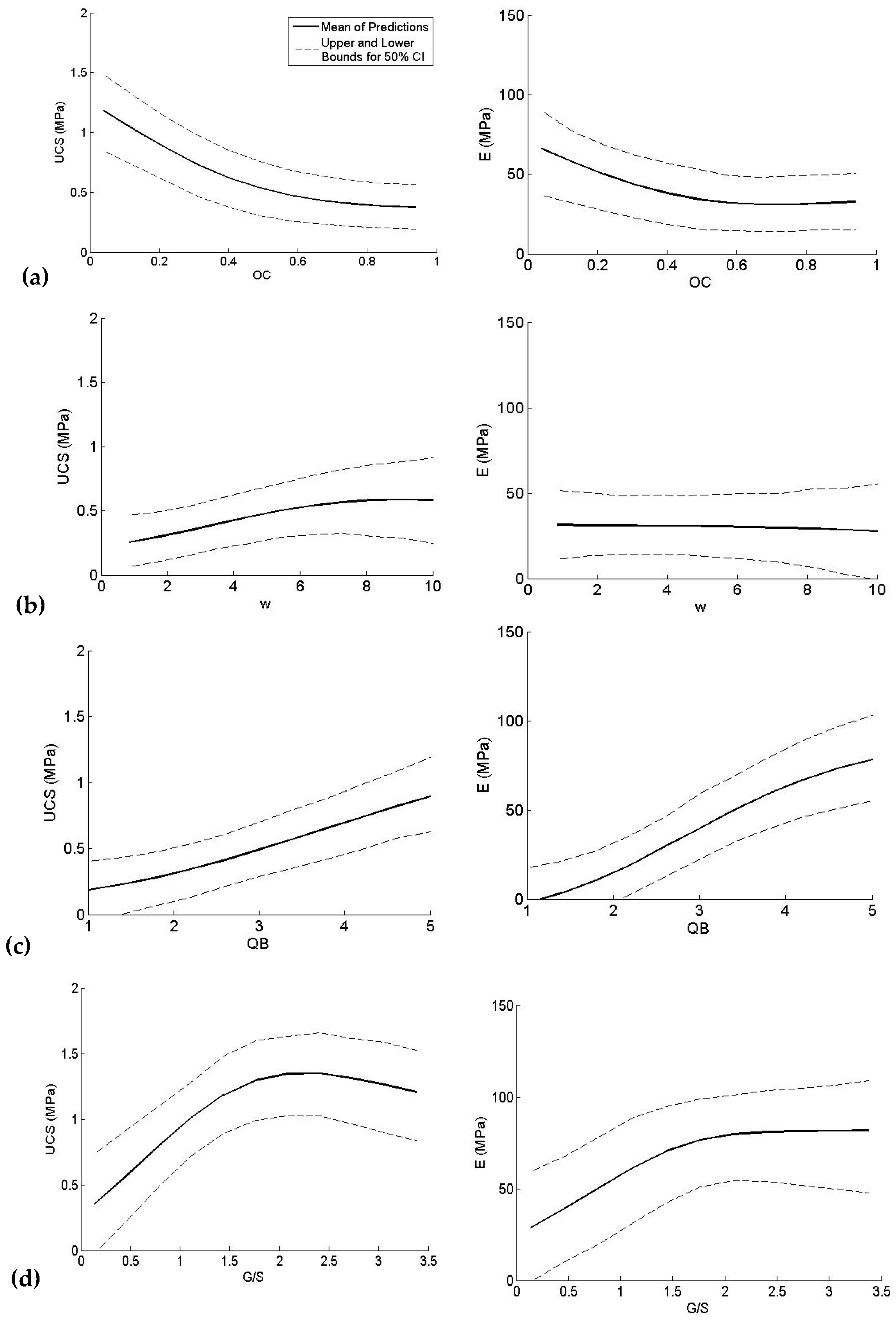
4.6. Sensitivity Analysis
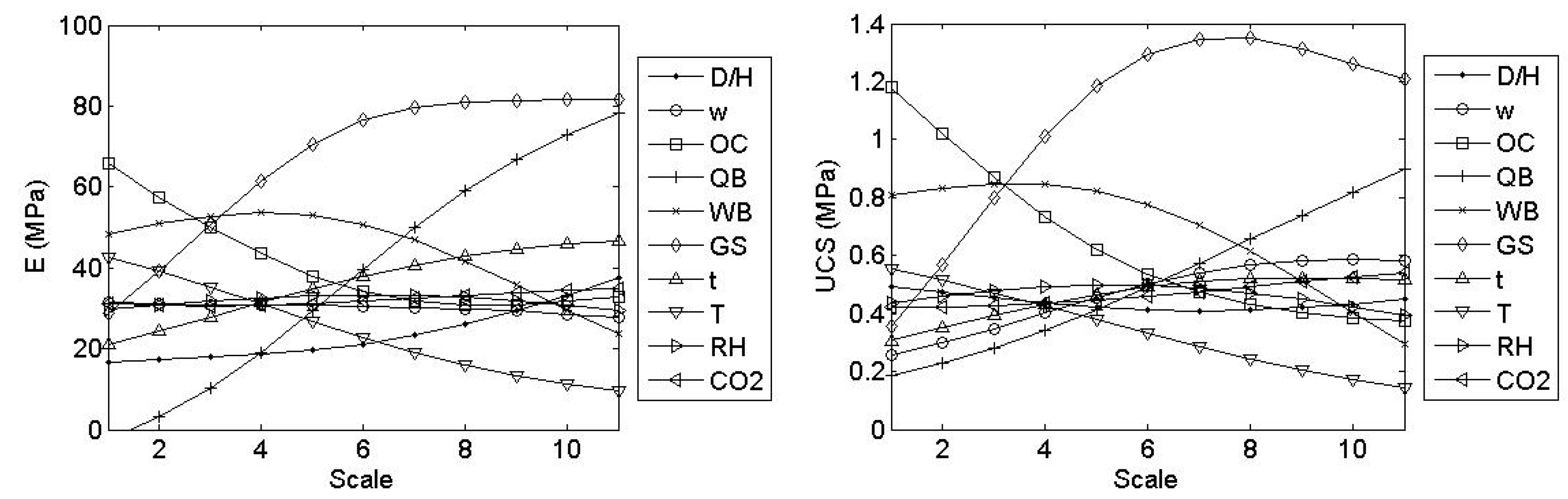
- UCS shows a slight increase with w, reaching maximum at a range between 800% to 1000%, opposing the generally expected trend. Such a trend has occurred primarily in the field when the initial water content is very low, also when adding large quantities of dry binders that prevent proper mixing and hydration [81].
- Increasing G/S increases both E and UCS up to a certain value. In this analysis, the optimum range for G/S is between 2 and 2.5.
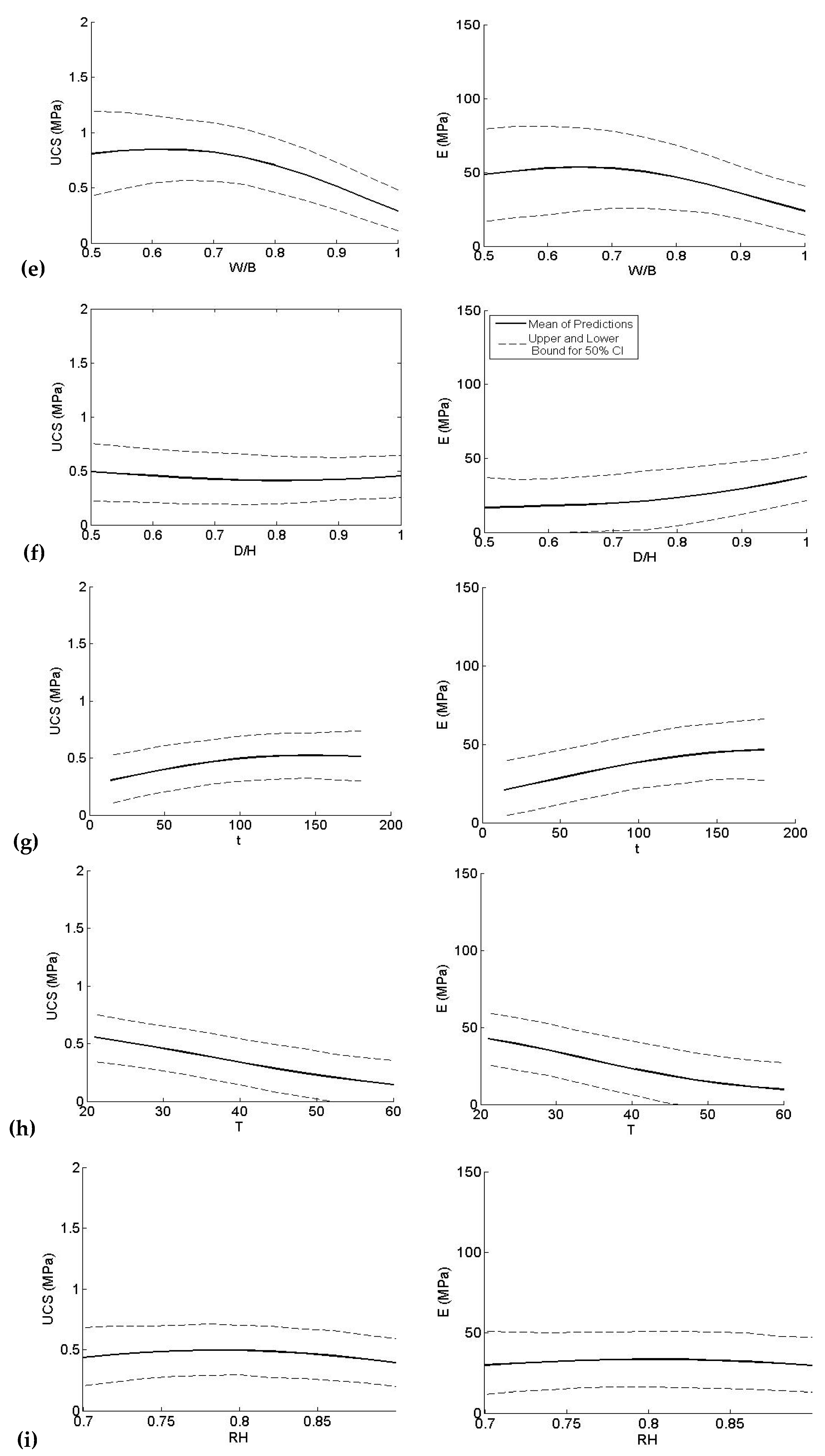
- The optimum range for W/B is between 0.6 to 0.7, and larger values of W/B cause a considerable decrease in E and UCS.
- D/H does not show a significant impact on UCS; however, E shows to increase with D/H slightly.
- Age of the specimen is positively correlated with E and UCS. E and UCS rapidly increase during the first 90 days (a time when much of the hydration process developed). After that, the rate of increase decays.
- Both E and UCS decay with an increase in curing temperature (T), opposing the behavior of common stabilized mineral soils, where the temperature increases the strength and stiffness. The negative effect of temperature on the stiffness and strength of organic soils is related to several factors, such as gradual loss of the initial evaporable water in the mix, dehydration during chemical reactions, and porosity changes [20].
- RH = 0.8 is shown to be the optimum value for both E and UCS, although the overall trend suggests that relative humidity is not a significant parameter.
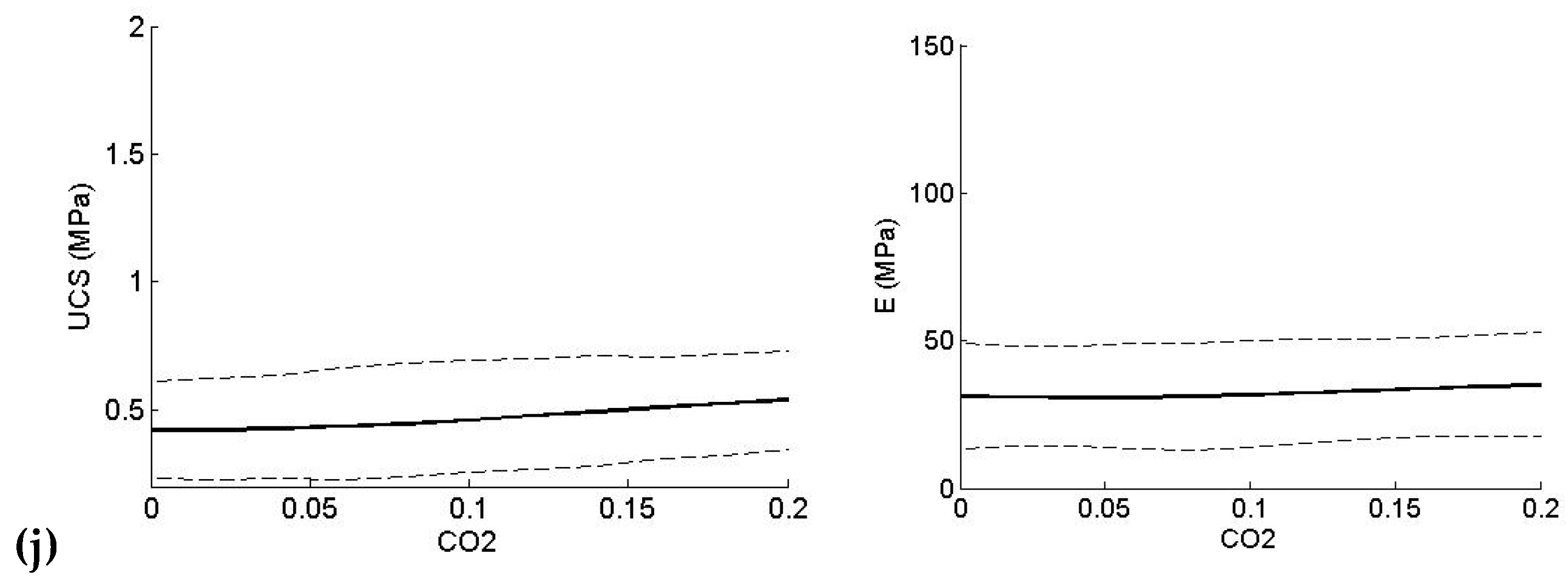
- CO2 shows a minimal effect on E and UCS, with a slight developing trend observed for UCS.
5. Conclusions
- Part I and II of this study together provide comprehensive details and descriptions of both experimental and computational investigations. Unlike most of the other studies, the experiments were designed to generate a well-populated database suitable for application of ML. This is essential for developing robust, reliable predictive models on any experimental database. Full access to the database and descriptive statistics are provided in Part I.
- The mechanical behavior of stabilized organic soils has not been comprehensively addressed by other studies. In this study, using a hybrid experimental and ML approach, the stiffness and strength as the two critical engineering design parameters were investigated, and the impacts of the relevant factors on the stiffness and strength of stabilized organic soils were evaluated.
- This study investigated various types of soils (low and high plasticity clays) and binders (both cement and non-cement based).
- Using a novel ML approach, the most influential parameters (control variables) were identified, the trends of strength and stiffness variation with these parameters (with 50% CI) were developed, and the optimum ranges were identified, allowing for an optimal mixture design.
- The two most prominent ANN algorithms were successfully applied to predict the stiffness and strength, and the full details of the architecture development and training methods were provided. Comparing their performance with other ML methods recently applied in other studies showed that these ANN algorithms are still highly competent.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Edil, T.N.; Den Haan, E.J. Settlement of Peats and Organic Soils Settlement; ASCE Geotechnical Special Publication: Boston, MA, USA, 1994; Volume 4, pp. 1543–1572. [Google Scholar]
- Kruse, G.; Haan, E.D. Characterisation and Engineering Properties of Dutch Peats Characterisation and Engineering Properties of Natural Soils; Taylor & Francis: Abingdon, UK, 2006. [Google Scholar]
- Hampton, M.B.; Edil, B. Strength gain of organic ground with cement-type binders. In Soil Improvement for Big Digs, Proceedings of the Geo-Congress ’98, Boston, MA, USA, 18–21 October 1998; ASCE Geotechnical Special Publication: New York, NY, USA, 1998. [Google Scholar]
- Hayashi, H.; Nishimoto, S. Strength characteristics of stabilized peat using different types of binders. In Proceedings of the International Conference on Deep Mixing Best Practice and Recent Advances, Stockholm, Sweden, 23–25 May 2005; Deep Stabilization Research Centre: Stockholm, Sweden, 2005; Volume 1.1, pp. 55–62. [Google Scholar]
- Jelisic, N.; Leppanen, M. Mass stabilisation of organic soils and soft clay. In Proceedings of the Grouting and Ground Treatment: Proceedings of the Third International Conference, New Orleans, LA, USA, 10–12 February 2003; ASCE: Reston, VA, USA, 2003; pp. 552–561. [Google Scholar]
- Lambrechts, J.R.; Ganse, M.A.; Layhee, C.A. Soil Mixing to Stabilize organic Clay for I-95 Widening. In Proceedings of the third International Conference in Grouting and Ground Treatment, New Orleans, LA, USA, 10–12 February 2003; ASCE: New Oreans, LA, USA, 2003; pp. 575–585. [Google Scholar]
- Chew, S.H.; Kamruzzaman, A.H.M.; Lee, F.H. Physicochemical and engineering behavior of cement treated clays. J. Geotech. Geoenviron. Eng. 2004, 130, 7696–7706. [Google Scholar] [CrossRef]
- Consoli, N.C.; Cruz, R.C.; Floss, M.F.; Festugato, L. Parameters controlling tensile and compressive strength of artificially cemented sand. J. Geotech. Geoenviron. Eng. 2010, 136, 759–763. [Google Scholar] [CrossRef]
- Consoli, N.C.; da Fonseca, A.V.; Cruz, R.C.; Heineck, K.S. Fundamental parameters for the stiffness and strength control of artificially cemented sand. J. Geotech. Geoenviron. Eng. 2009, 135, 1347–1353. [Google Scholar] [CrossRef]
- Consoli, N.C.; Foppa, D.; Festugato, L.; Heineck, K.S. Key parameters for strength control of artificially cemented soils. J. Geotech. Geoenviron. Eng. 2007, 133, 197–205. [Google Scholar] [CrossRef]
- Kitazume, M. Technical session 2a: Ground improvement. In Proceedings of the 16th International Conference on Soil Mechanics and Geotechnical Engineering, Osaka, Japan, 12–16 September 2005; Milpress: Rotterdam, The Netherlands, 2005; Volume 1–5, pp. 3011–3020. [Google Scholar]
- Porbaha, A. Design aspects and properties of treated ground. In Proceedings of the Deep Mixing Workshop, Geo-Trans, Los Angeles, CA, USA, 27–31 July 2004. [Google Scholar]
- Schnaid, F.; Prietto, P.D.M.; Consoli, N.C. Characterization of cemented sand in triaxial compression. J. Geotech. Geoenviron. Eng. 2001, 127, 857–868. [Google Scholar] [CrossRef]
- Grubb, D.G.; Chrysochoou, M.; Smith, C.J.; Malasavage, N.E. Stabilized dredged material. I: Parametric study. J. Geotech. Geoenviron. Eng. 2010, 136, 1011–1024. [Google Scholar] [CrossRef]
- Grubb, D.G.; Malasavage, N.E.; Smith, C.J.; Chrysochoou, M. Stabilized dredged material. II: Geomechanical behavior. J. Geotech. Geoenviron. Eng. 2010, 136, 1025–1036. [Google Scholar] [CrossRef]
- Huttunen, E.; Kujala, K. On the stabilization of organic soils. In Proceedings of the Second International Conference on Ground Improvement Geosystems, Tokyo, Japan, 14–17 May 1996; Balkema: Rotterdam, The Netherlands, 1996; pp. 411–414. [Google Scholar]
- Tremblay, H.; Duchesne, J.; Locat, J.; Leroueil, S. Influence of the nature of organic compounds on fine soil stabilization with cement. Can. Geotech. J. 2002, 39, 535–546. [Google Scholar] [CrossRef]
- MMcGinn, A.J.; O’Rourke, T.D. Performance of Deep Mixing Methods at Fort Point Channel; Cornell University: Ithaca, NY, USA, 2003. [Google Scholar]
- Hernandez-Martinez, F.G.; Al-Tabbaa, A.; Medina-Cetina, Z.; Yousefpour, N. Stiffness and Strength of Stabilized Organic Soils—Part I/II: Experimental Database and Statistical Description for Machine Learning Modeling. Application of Artificial Intelligence and Machine Learning in Geotechnical Engineering. Geosciences 2021. [Google Scholar]
- Hernandez-Martinez, F.G. Ground Improvement of Organic Soils Using Wet Deep Soil Mixing. Ph.D. Thesis, University of Cambridge, Cambridge, UK, 2006. [Google Scholar]
- Yousefpour, N.; Fallah, S. Applications of Machine Learning in Geotechnics. In Proceedings of the Civil Engineering Research in Ireland Conference, Dublin, Ireland, 29–30 August 2018. [Google Scholar]
- Goh, A.T.C. Nonlinear modelling in geotechnical engineering using neural networks. Aust. Civ. Eng. Trans. CE 1994, 36, 293–297. [Google Scholar]
- Goh, A.T.C. Empirical design in geotechnics using neural networks. Empir. Des. Geotech. Neural Netw. 1995, 45, 709–714. [Google Scholar] [CrossRef]
- Goh, A.T.C. Pile driving records reanalyzed using neural networks. J. Geotech. Geoenviron. Eng. 1996, 122, 492. [Google Scholar] [CrossRef]
- Chow, Y.K.; Chan, W.T.; Liu, L.F.; Lee, S.L. Prediction of pile capacity from stress-wave measurements: A neural network approach. Int. J. Numer. Anal. Meth. Geomech. 1995, 19, 107–126. [Google Scholar] [CrossRef]
- Lee, I.-M.; Lee, J.-H. Prediction of pile bearing capacity using artificial neural networks. Comput. Geotech. 1996, 18, 189–200. [Google Scholar] [CrossRef]
- Goh, A.T.C.; Kulhawy, F.H.; Chua, C.G. Bayesian neural network analysis of undrained Side resistance of drilled shafts. J. Geotech. Geoenviron. Eng. 2005, 131, 84–93. [Google Scholar] [CrossRef]
- Pal, M.; Deswal, S. Modeling pile capacity using support vector machines and generalized regression neural network. J. Geotech. Geoenviron. Eng. 2008, 134, 1021–1024. [Google Scholar] [CrossRef]
- Zhang, W.; Goh, A.T.C. Multivariate adaptive regression splines and neural network models for prediction of pile drivability. Geosci. Front. 2016, 7, 45–52. [Google Scholar] [CrossRef]
- Shahin, M.A. State-of-the-art review of some artificial intelligence applications in pile foundations. Geosci. Front. 2016, 7, 33–44. [Google Scholar] [CrossRef]
- Ellis, G.W.; Yao, C.; Zhao, R.; Penumadu, D. Stress-strain modeling of sands using artificial neural networks. J. Geotech. Geoenviron. Eng. 1995, 121, 429–435. [Google Scholar] [CrossRef]
- Ghaboussi, J.; Sidarta, D.E. New nested adaptive neural networks (NANN) for constitutive modeling. Comput. Geotech. 1998, 22, 29–52. [Google Scholar] [CrossRef]
- Penumadu, D.; Jean-Lou, C. Geomaterial modeling using artificial neural networks. In Artificial Neural Networks for Civil Engineers: Fundamentals and Applications; ASCE: Reston, VA, USA, 1997; pp. 160–184. [Google Scholar]
- Penumadu, D.; Zhao, R. Triaxial compression behavior of sand and gravel using artificial neural networks (ANN). Comput. Geotech. 1999, 24, 207–230. [Google Scholar] [CrossRef]
- Das, S.K.; Basudhar, P. Prediction of residual friction angle of clay artificial neural network. Eng. Geol. 2008, 100, 142–145. [Google Scholar] [CrossRef]
- Obrzud, R.F.; Vulliet, L.; Truty, A. A combined neural network/gradient-based approach for the identification of constitutive model parameters using self-boring pressuremeter tests. Int. J. Numer. Anal. Meth. Geomech. 2009, 33, 817–849. [Google Scholar] [CrossRef]
- Khan, S.Z.; Suman, S.; Pavani, M.; Das, S.K. Prediction of the residual strength of clay using functional networks. Geosci. Front. 2016, 7, 67–74. [Google Scholar] [CrossRef]
- Rizzo, D.M.; Lillys, T.P.; Dougherty, D.E. Comparisons of site characterization methods using mixed data. In Uncertainty in the Geologic Environment: From Theory to Practice; Geotechnical Special Publication; ASCE: Reston, VA, USA, 1996; Volume 58, pp. 157–179. [Google Scholar]
- Tsiaousi, D.; Travasarou, T.; Drosos, V.; Ugalde, J.; Chacko, J. Machine Learning Applications for Site Characterization Based on CPT Data. In Geotechnical Earthquake Engineering and Soil Dynamics V: Slope Stability and Landslides, Laboratory Testing, and In Situ Testing; ASCE: Reston, VA, USA, 2018; pp. 461–472. [Google Scholar]
- Goh, A.T.; Kulhawy, F.H. Reliability assessment of serviceability performance of braced retaining walls using a neural network approach. Int. J. Numer. Anal. Meth. Geomech. 2005, 29, 627–642. [Google Scholar] [CrossRef]
- Sivakugan, N.; Eckersley, J.D.; Li, H. Settlement predictions using neural networks. Aust. Civ. Eng. Trans. CE 1998, 40, 49–52. [Google Scholar]
- Shahin, M.A.; Jaksa, M.B.; Maier, H.R. Predicting the Settlement of Shallow Foundations on Cohesionless Soils Using Back-Propagation Neural Networks; Research Report No. R 167; The University of Adelaide: Aldelaide, Australia, 2000. [Google Scholar]
- Yousefpour, N.; Medina-Cetina, Z.; Briaud, J.-L. Evaluation of Unknown Foundations of Bridges Subjected to Scour: Physically Driven Artificial Neural Network Approach. Transp. Res. Rec. 2014, 2433, 27–38. [Google Scholar] [CrossRef]
- Ni, S.H.; Lu, P.C.; Juang, C.H. A Fuzzy Neural Network Approach to Evaluation of Slope Failure Potential. Comput. Civ. Infrastruct. Eng. 1996, 11, 59–66. [Google Scholar] [CrossRef]
- Chok, Y.; Jaksa, M.; Kaggwa, W.; Griffiths, D.; Fenton, G. Neural network prediction of the reliability of heterogeneous cohesive slopes. Int. J. Numer. Anal. Methods Géoméch. 2016, 40, 1556–1569. [Google Scholar] [CrossRef]
- Shi, J.; Ortigao, J.A.R.; Bai, J. Modular neural networks for predicting settlements during tunneling. J. Geotech. Geoenviron. Eng. 1998, 124, 389–395. [Google Scholar] [CrossRef]
- Morgenroth, J.; Khan, U.T.; Perras, M.A. An Overview of Opportunities for Machine Learning Methods in Underground Rock Engineering Design. Geosciences 2019, 9, 504. [Google Scholar] [CrossRef]
- Goh, A.T.C. Seismic Liquefaction Potential Assessed by Neural Networks. J. Geotech. Eng. 1994, 120, 1467–1480. [Google Scholar] [CrossRef]
- Juang, C.H.; Chen, C.J. CPT-Based Liquefaction Evaluation Using Artificial Neural Networks. Comput. Civ. Infrastruct. Eng. 1999, 14, 221–229. [Google Scholar] [CrossRef]
- Najjar, Y.M.; Ali, H.E. CPT-based liquefaction potential assessment: A neuronet approach. In Geotechnical Earthquake Engineering and Soil Dynamics III; Geotechnical Special Publication; ASCE: Reston, VA, USA, 1998; Volume 1, pp. 542–553. [Google Scholar]
- Samui, P.; Sitharam, T.G. Machine learning modelling for predicting soil liquefaction susceptibility. Nat. Hazards Earth Syst. Sci. 2011, 11, 1–9. [Google Scholar] [CrossRef]
- Young-Su, K.; Byung-Tak, K. Use of artificial neural networks in the prediction of liquefaction resistance of sands. J. Geotech. Geoenviron. Eng. 2006, 132, 1502–1504. [Google Scholar] [CrossRef]
- Najjar, Y.M.; Basheer, I.A. Utilizing computational neural networks for evaluating the permeability of compacted clay liners. J. Geotech. Geoenviron. Eng. 1996, 14, 193–212. [Google Scholar]
- Basheer, I.A.; Najjar, Y.M. A neural-network for soil compaction. In Proceedings of the 5th International Symposium on Numerical Models in Geomechanics, Davos, Switzerland, 6–8 September 1995; Pande, G.N., Pietruszczak, S., Eds.; Balkema: Roterdam, The Netherlands, 1995; pp. 435–440. [Google Scholar]
- Najjar, Y.M.; Basheer, I.A.; Naouss, W.A. On the identification of compaction characteristics by neuronets. Comput. Geotech. 1996, 18, 167–187. [Google Scholar] [CrossRef]
- Yudong, C. Soil classification by neural network. Adv. Eng. Softw. 1995, 22, 95–97. [Google Scholar]
- Bhattacharya, B.; Solomatine, D.P. Machine learning in soil classification. Neural Netw. 2006, 19, 186–195. [Google Scholar] [CrossRef]
- Tinoco, J.; Alberto, A.; da Venda, P.; Correia, A.G.; Lemos, L. A novel approach based on soft computing techniques for unconfined compression strength prediction of soil cement mixtures. Neural Comput. Appl. 2020, 32, 8985–8991. [Google Scholar] [CrossRef]
- Molaabasi, H.; Saberian, M.; Kordnaeij, A.; Omer, J.; Li, J.; Kharazmi, P. Predicting the stress-strain behaviour of zeolite-cemented sand based on the unconfined compression test using GMDH type neural network. J. Adhes. Sci. Technol. 2019, 33, 1–18. [Google Scholar] [CrossRef]
- Suman, S.; Mahamaya, M.; Das, S.K. Prediction of Maximum Dry Density and Unconfined Compressive Strength of Cement Stabilised Soil Using Artificial Intelligence Techniques. Int. J. Geosynth. Ground Eng. 2016, 2, 11. [Google Scholar] [CrossRef]
- Wang, O.; Al-Tabbaa, A. Preliminary model development for predicting strength and stiffness of cement-stabilized soils using artificial neural networks. In Computing in Civil Engineering, Proceedings of the 2013 ASCE International Workshop on Computing in Civil Engineering, Los Angeles, CA, USA, 23–25 June 2013; ASCE: Reston, VA, USA, 2013; pp. 299–306. [Google Scholar]
- Shrestha, R.; Al-Tabbaa, A. Introduction to the development of an information management system for soil mix technology using artificial neural networks. In Proceedings of the Geo-Frontiers 2011, Dallas, TX, USA, 13–16 March 2011; ASCE: Reston, VA, USA, 2011; pp. 816–825, ISSN 0895-0563. [Google Scholar]
- Stegemann, J.A.; Buenfeld, N.R. Prediction of unconfined compressive strength of cement paste with pure metal compound additions. Cem. Concr. Res. 2002, 32, 903–913. [Google Scholar] [CrossRef]
- Stegemann, J.A.; Buenfeld, N.R. Prediction of unconfined compressive strength of cement paste containing industrial wastes. Waste Manag. 2003, 23, 321–332. [Google Scholar] [CrossRef]
- Stegemann, J.A.; Buenfeld, N.R. Mining of existing data for cement-solidified wastes using neural networks. J. Environ. Eng. 2004, 130, 508–515. [Google Scholar] [CrossRef]
- Narendra, B.S.; Sivapullaiah, P.V.; Suresh, S.; Omkar, S.N. Prediction of unconfined compressive strength of soft grounds using computational intelligence techniques: A comparative study. Comput. Geotech. 2006, 33, 196–208. [Google Scholar] [CrossRef]
- Das, S.; Samui, P.; Sabat, A. Application of artificial intelligence to maximum dry density and unconfined compressive strength of cement stabilized soil. J. Geotech. Geoenviron. Eng. 2011, 29, 329–342. [Google Scholar] [CrossRef]
- Mozumder, R.A.; Laskar, A.I. Prediction of unconfined compressive strength of geopolymer stabilized clayey soil using Artificial Neural Network. Comput. Geotech. 2015, 69, 291–300. [Google Scholar] [CrossRef]
- McCulloch, W.; Pitts, W. A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biol. 1943, 5, 115–133. [Google Scholar] [CrossRef]
- Bishop, C.M. Neural Networks for Pattern Recognition; Oxford University Press: Oxford, UK, 1995. [Google Scholar]
- Haykin, S. Neural Networks: A Comprehensive Foundation; Prentice Hall International, Inc.: Hoboken, NJ, USA, 1999. [Google Scholar]
- Picard, R.; Cook, R.D. Cross-validation of regression model. J. Am. Stat. Asoc. 1984, 79, 575–583. [Google Scholar] [CrossRef]
- Seber, G.A.F.; Lee, A.J. Linear Regression Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- MATLAB. Neural Network Toolbox Release 2009b (2009a); The MathWorks, Inc.: Natick, MA, USA, 2009. [Google Scholar]
- Hornik, K.; Stinchcombe, M.; White, H. Multilayer feedforward networks are universal approximators. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
- Trenn, S. Multilayer Perceptrons: Approximation Order and Necessary Number of Hidden Units. IEEE Trans. Neural Netw. 2008, 19, 836–844. [Google Scholar] [CrossRef]
- Gevrey, M.; Dimopoulos, L.; Lek, S. Review and comparison of methods to study the contribution of variables in artificial neural network models. Ecol. Model. 2003, 160, 249–264. [Google Scholar] [CrossRef]
- Kitazume, M.; Terashi, M. The Deep Mixing Method; CRC Press, Taylor & Francis: Leiden, The Netherlands, 2013. [Google Scholar]
- Lek, S.; Delacoste, M.; Baran, P.; Dimopoulos, I.; Lauga, J.; Aulagnier, S. Application of neural networks to modelling nonlinear relationships in ecology. Ecol. Model. 1996, 90, 39–52. [Google Scholar] [CrossRef]
- Santagata, M.; Bobet, A.; Johnston, C.T.; Hwang, J. One-dimensional compression behavior of a soil with high organic matter content. J. Geotech. Geoenviron. Eng. 2008, 134, 1–13. [Google Scholar] [CrossRef]
- Åhnberg, H. Strength of Stabilised Soils: A Laboratory Study on Clays and Organic Soils Stabilised with Different Types of Binder; Report No. 16. Swedish Deep Stabilization Research Center: Linköping, Sweden, 2006. [Google Scholar]
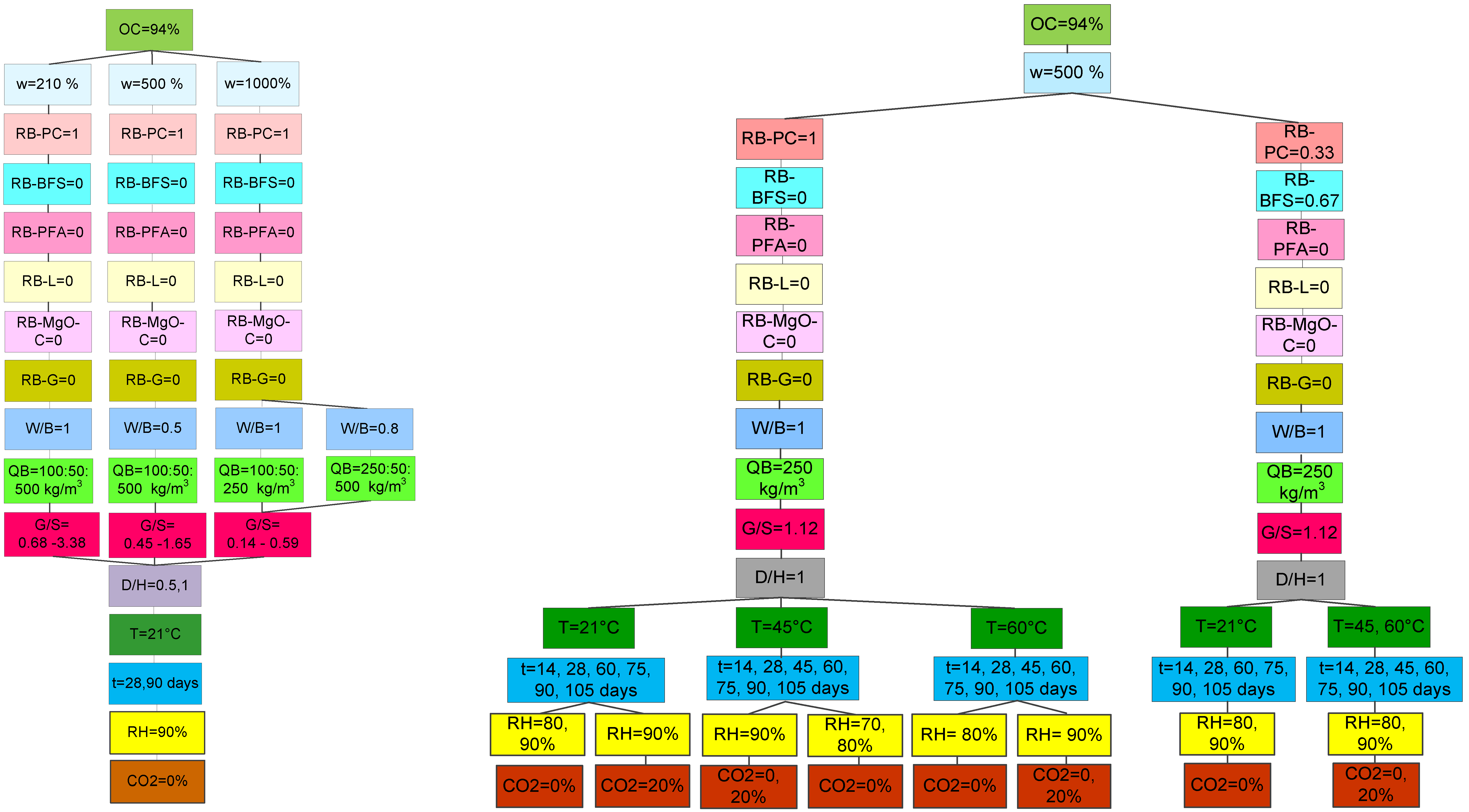

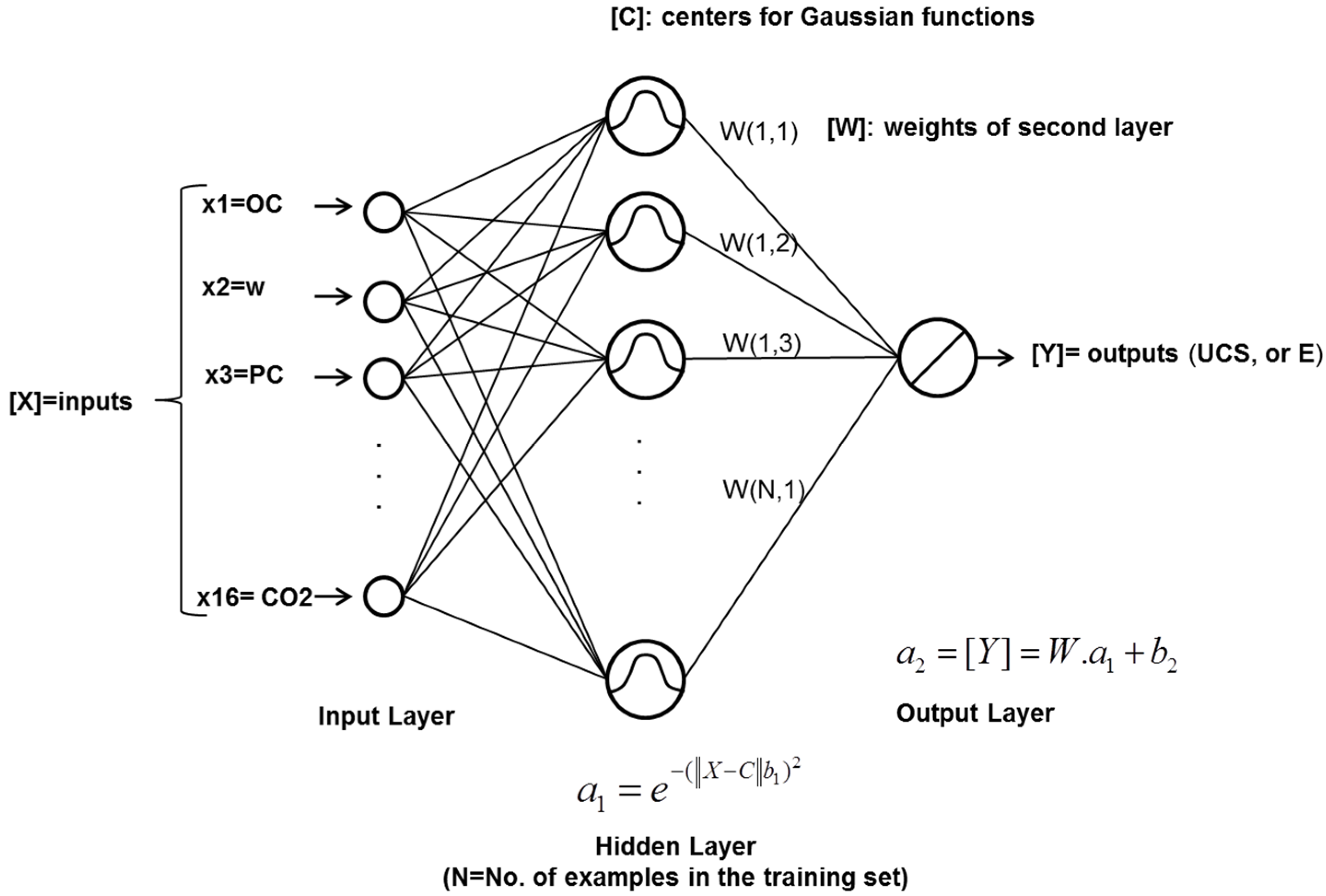
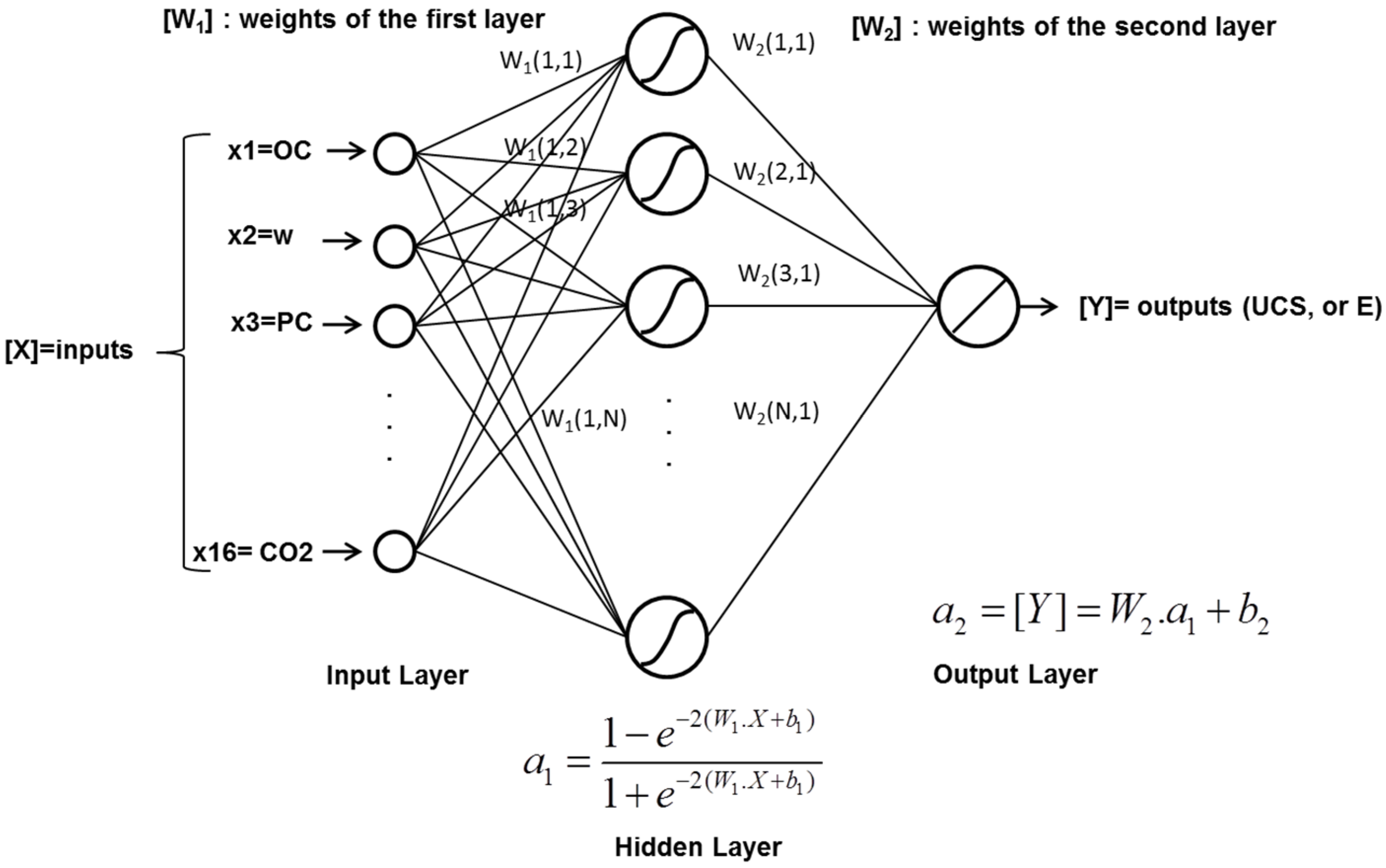
| Organic Soil | Density (kg/m3) | OC (%) | w (%) |
|---|---|---|---|
| Irish Moss Peat (Pt) | 294 | 94 | 210 |
| 446 | 500 | ||
| 1014 | 1000 | ||
| Medium Organic Clay (OH-1) | 1219 | 30 | 180 |
| Low Organic Clay (OH-2) | 1471 | 4 | 85 |
| Binders | Binder Mixtures | Ratio |
|---|---|---|
| Portland Cement (PC) | PC | |
| Blast Furnace Slag (BFS) | PC + BFS | 1:2 |
| Pulverized Fuel Ash (PFA) | PC + PFA | 1:1 |
| Lime (L) | PC + PFA + L | 3:6:1 |
| Magnesium Oxide Cement (MgO-C) | PC + PFA + MgO-C | 2:6:2 |
| Gypsum (G) | L + G + BFS | 1:1:1 |
| No. | Variables | Range of Variation | Mean | Standard Deviation |
|---|---|---|---|---|
| Control Variables (Input Parameters) | ||||
| 1 | Organic Content of Soil (OC) | 4 (OH-2), 30 (OH-1), 94 (Pt) (%) | 69.2 (%) | 33.2 (%) |
| 2 | Water Content of Soil (w) | 85, 180, 210, 500, 1000 (%) | 400.2 (%) | 258.6 (%) |
| 3 | Ratio of Binder for Portland Cement (RB-PC) | 0, 0.2, 0.3, 0.33, 0.5, 1 | 0.749 | 0.339 |
| 4 | Ratio of Binder for Blast Furnace Slag (RB-BFS) | 0, 0.33, 0.67 | 0.180 | 0.292 |
| 5 | Ratio of Binder for Pulverized Fuel Ash (RB-PFA) | 0, 0.5, 0.6 | 0.045 | 0.154 |
| 6 | Ratio of Binder for Lime (RB-L) | 0, 0.1, 0.33 | 0.012 | 0.056 |
| 7 | Ratio of Binder for Magnesium Oxide (RB-MgO-C) | 0, 0.2 | 0.005 | 0.032 |
| 8 | Ratio of Binder for Gypsum (RB-G) | 0, 0.33 | 0.009 | 0.054 |
| 9 | Quantity of Binder (QB) | 100–500 (kg/m3) | 265.9 (kg/m3) | 76.6 (kg/m3) |
| 10 | Grout to Soil Ratio (G/S) | 0.14–3.38 | 0.856 | 0.568 |
| 11 | Water to Binder ratio (W/B) | 0.5, 0.8, 1 | 0.937 | 0.157 |
| 12 | Specimen Diameter/Height (D/H) | 0.5, 1 | 0.920 | 0.183 |
| 13 | Time (t) | 14–180 (days) | 61 (days) | 36 (days) |
| 14 | Temperature (T) | 21, 45, 60 (°C) | 32.9 (°C) | 15.7 (°C) |
| 15 | Relative Humidity (RH) | 70, 80, 90 (%) | 87.6 (%) | 4.9 (%) |
| 16 | Carbonation (CO2) | 0, 20 (%) | 2.9 (%) | 7.1 (%) |
| Response Variables (Target Parameters) | ||||
| Unconfined Tangent Modulus (E) | 0.83–214.62 (MPa) | 34.03 (MPa) | 31.44 (MPa) | |
| Unconfined Compression Strength (UCS) | 0.04–2.09 (MPa) | 0.50 (MPa) | 0.40 (MPa) | |
| Model | All | Training | Test | |||
|---|---|---|---|---|---|---|
| R2ave | RMSEave | R2ave | RMSEave | R2ave | RMSEave | |
| RBF-Tot-E | 0.89 | 2.78 | 0.92 | 0.03 | 0.77 | 13.77 |
| RBF-Tot-UCS | 0.95 | 0.09 | 0.96 | 0.08 | 0.92 | 0.11 |
| Model | All | Training | Validation | Test | ||||
|---|---|---|---|---|---|---|---|---|
| R2ave | RMSEave | R2ave | RMSEave | R2ave | RMSEave | R2ave | RMSEave | |
| MLP-20-E | 0.81 | 13.58 | 0.95 | 6.15 | 0.50 | 20.74 | 0.61 | 18.47 |
| MLP-25-UCS | 0.90 | 0.12 | 0.99 | 0.04 | 0.73 | 0.20 | 0.80 | 0.17 |
| RBF-E | RBF-UCS | |||||
|---|---|---|---|---|---|---|
| Order of Addition/Elimination | FSS | BSE | Ranking/Sequence of Addition | FSS | BSE | Ranking/Sequence of Addition |
| 1 | Binder Type | w | Binder Type | G/S | W/B | G/S |
| 2 | G/S | OC | G/S | Binder Type | Binder Type | |
| 3 | t | QB | t | t | t | |
| 4 | D/H | W/B | D/H | T | T | |
| 5 | T | T | RH | RH | ||
| 6 | RH | RH | CO2 | CO2 | ||
| 7 | CO2 | CO2 | D/H | D/H | ||
| 8 | w | w | ||||
| 9 | OC | OC | ||||
| 10 | QB | QB | ||||
| 11 | W/B | W/B | ||||
| MLP-E | MLP-UCS | |||||
|---|---|---|---|---|---|---|
| Order of Addition/Elimination | FSS | BSE | Ranking/Sequence of Addition | FSS | BSE | Ranking/Sequence of Addition |
| 1 | Binder Type | W/B | Binder Type | G/S | QB | G/S |
| 2 | G/S | G/S | Binder Type | Binder Type | ||
| 3 | t | t | t | t | ||
| 4 | D/H | D/H | T | T | ||
| 5 | T | T | RH | RH | ||
| 6 | RH | RH | CO2 | CO2 | ||
| 7 | CO2 | CO2 | W/B | W/B | ||
| 8 | QB | QB | D/H | D/H | ||
| 9 | w | QB | QB | |||
| 10 | OC | OC | OC | |||
| 11 | W/B | w | ||||
| OC | w | PC | BFS | PFA | L | MgO-C | G | QB | G/S | W/B | D/H | t | T | RH | CO2 | E | UCS | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| OC | 1.00 | 0.69 | 0.32 | −0.17 | −0.23 | −0.16 | −0.13 | −0.13 | 0.16 | 0.61 | −0.30 | −0.33 | −0.07 | −0.16 | 0.11 | −0.09 | 0.08 | 0.19 |
| w | 1.00 | 0.26 | −0.17 | −0.16 | −0.12 | −0.09 | −0.09 | 0.14 | 0.00 | −0.81 | −0.29 | −0.05 | −0.17 | 0.11 | −0.10 | −0.19 | −0.09 | |
| PC | 1.00 | −0.79 | −0.37 | −0.42 | −0.27 | −0.36 | 0.15 | 0.18 | −0.30 | −0.32 | −0.07 | −0.13 | −0.01 | −0.02 | 0.18 | 0.30 | ||
| BFS | 1.00 | −0.18 | 0.05 | −0.10 | 0.08 | −0.13 | −0.11 | 0.25 | 0.27 | 0.00 | 0.33 | −0.11 | 0.12 | −0.07 | −0.14 | |||
| PFA | 1.00 | 0.13 | 0.60 | −0.05 | −0.06 | −0.12 | 0.12 | 0.13 | 0.10 | −0.22 | 0.14 | −0.12 | −0.16 | −0.27 | ||||
| L | 1.00 | −0.03 | 0.95 | −0.04 | −0.08 | 0.08 | 0.09 | 0.07 | −0.16 | 0.10 | −0.09 | −0.13 | −0.15 | |||||
| MgO−C | 1.00 | −0.03 | −0.03 | −0.07 | 0.07 | 0.07 | 0.05 | −0.13 | 0.08 | −0.07 | −0.08 | −0.16 | ||||||
| G | 1.00 | −0.03 | −0.07 | 0.07 | 0.07 | 0.05 | −0.13 | 0.08 | −0.07 | −0.10 | −0.11 | |||||||
| QB | 1.00 | 0.46 | −0.28 | −0.19 | −0.01 | −0.16 | 0.10 | −0.09 | 0.40 | 0.59 | ||||||||
| G/S | 1.00 | 0.22 | −0.20 | −0.05 | −0.12 | 0.08 | −0.07 | 0.45 | 0.56 | |||||||||
| W/B | 1.00 | 0.37 | 0.02 | 0.30 | −0.20 | 0.17 | 0.16 | 0.02 | ||||||||||
| D/H | 1.00 | 0.02 | 0.33 | −0.21 | 0.18 | 0.11 | −0.21 | |||||||||||
| t | 1.00 | −0.03 | 0.02 | −0.01 | 0.09 | 0.11 | ||||||||||||
| T | 1.00 | −0.31 | 0.35 | −0.21 | −0.29 | |||||||||||||
| RH | 1.00 | 0.20 | −0.02 | 0.05 | ||||||||||||||
| CO2 | 1.00 | −0.08 | −0.09 |
| Model | R2ave | RMSEave | ||||
|---|---|---|---|---|---|---|
| All | Training | Test | All | Training | Test | |
| LR-E | 0.49 | 0.51 | 0.42 | 22.33 | 22.04 | 23.48 |
| LR-UCS | 0.66 | 0.67 | 0.62 | 0.23 | 0.23 | 0.25 |
| Ranking | Parameter | Max. E Variation (MPa) | Parameter | Max. UCS Variation (MPa) |
|---|---|---|---|---|
| 1 | QB | 80.59 | G/S | 0.99 |
| 2 | G/S | 53.07 | OC | 0.81 |
| 3 | OC | 34.97 | QB | 0.71 |
| 4 | T | 32.91 | W/B | 0.55 |
| 5 | W/B | 29.93 | T | 0.41 |
| 6 | t | 25.61 | w | 0.33 |
| 7 | D/H | 20.88 | t | 0.22 |
| 8 | CO2 | 4.25 | CO2 | 0.12 |
| 9 | RH | 3.94 | RH | 0.10 |
| 10 | w | 3.74 | D/H | 0.08 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yousefpour, N.; Medina-Cetina, Z.; Hernandez-Martinez, F.G.; Al-Tabbaa, A. Stiffness and Strength of Stabilized Organic Soils—Part II/II: Parametric Analysis and Modeling with Machine Learning. Geosciences 2021, 11, 218. https://doi.org/10.3390/geosciences11050218
Yousefpour N, Medina-Cetina Z, Hernandez-Martinez FG, Al-Tabbaa A. Stiffness and Strength of Stabilized Organic Soils—Part II/II: Parametric Analysis and Modeling with Machine Learning. Geosciences. 2021; 11(5):218. https://doi.org/10.3390/geosciences11050218
Chicago/Turabian StyleYousefpour, Negin, Zenon Medina-Cetina, Francisco G. Hernandez-Martinez, and Abir Al-Tabbaa. 2021. "Stiffness and Strength of Stabilized Organic Soils—Part II/II: Parametric Analysis and Modeling with Machine Learning" Geosciences 11, no. 5: 218. https://doi.org/10.3390/geosciences11050218
APA StyleYousefpour, N., Medina-Cetina, Z., Hernandez-Martinez, F. G., & Al-Tabbaa, A. (2021). Stiffness and Strength of Stabilized Organic Soils—Part II/II: Parametric Analysis and Modeling with Machine Learning. Geosciences, 11(5), 218. https://doi.org/10.3390/geosciences11050218








