The Use of Polyurethane Injection as a Geotechnical Seismic Isolation Method in Large-Scale Applications: A Numerical Study
Abstract
1. Introduction
2. Soil Improvement Using Polyurethane
2.1. Master Builders Solutions’ Technologies for Soil Improvement through Grouting
3. Dynamic Characterisation of Polyurethane by Means of Laboratory Tests
3.1. Sample Preparation
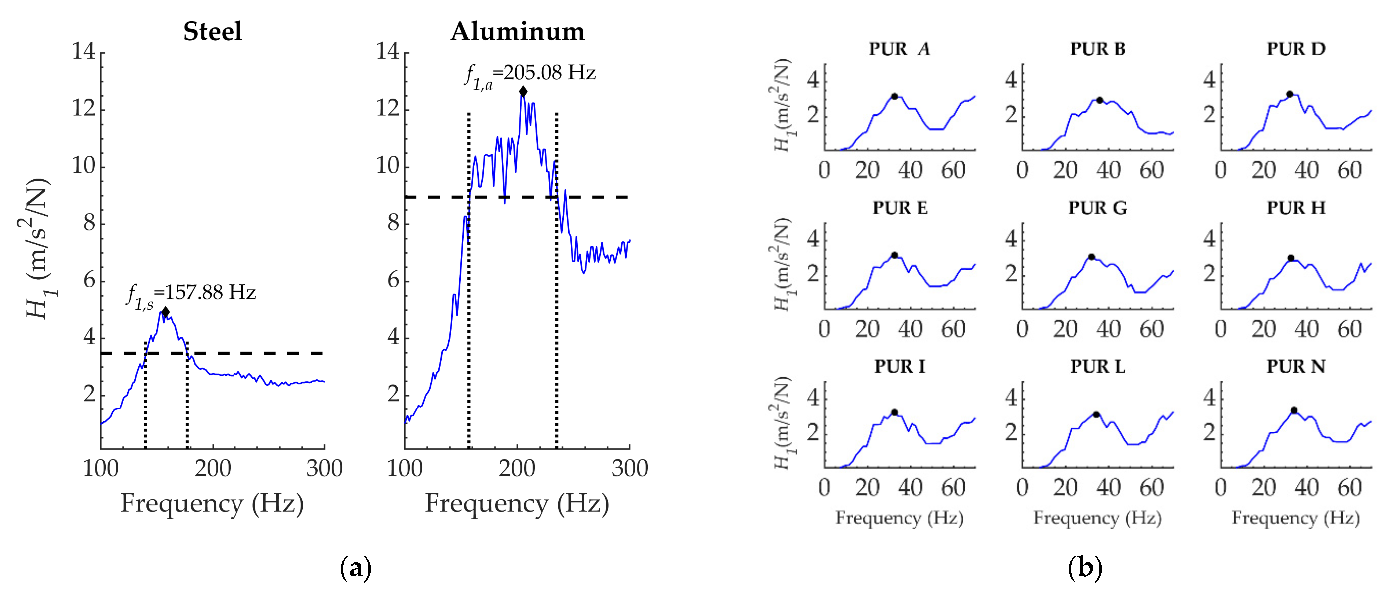
3.2. Impact Tests
4. The Finite Element Numerical Model
- Loose sand (LS), with DR = 15–35%
- Medium sand (MS), with DR = 35–65%
- Medium-dense sand (MDS), with DR = 65–85%
- Dense sand (DS), with DR = 85–100%
4.1. Model Description
4.2. The Pressure-Dependent Multi-Yield Model (PDMY)
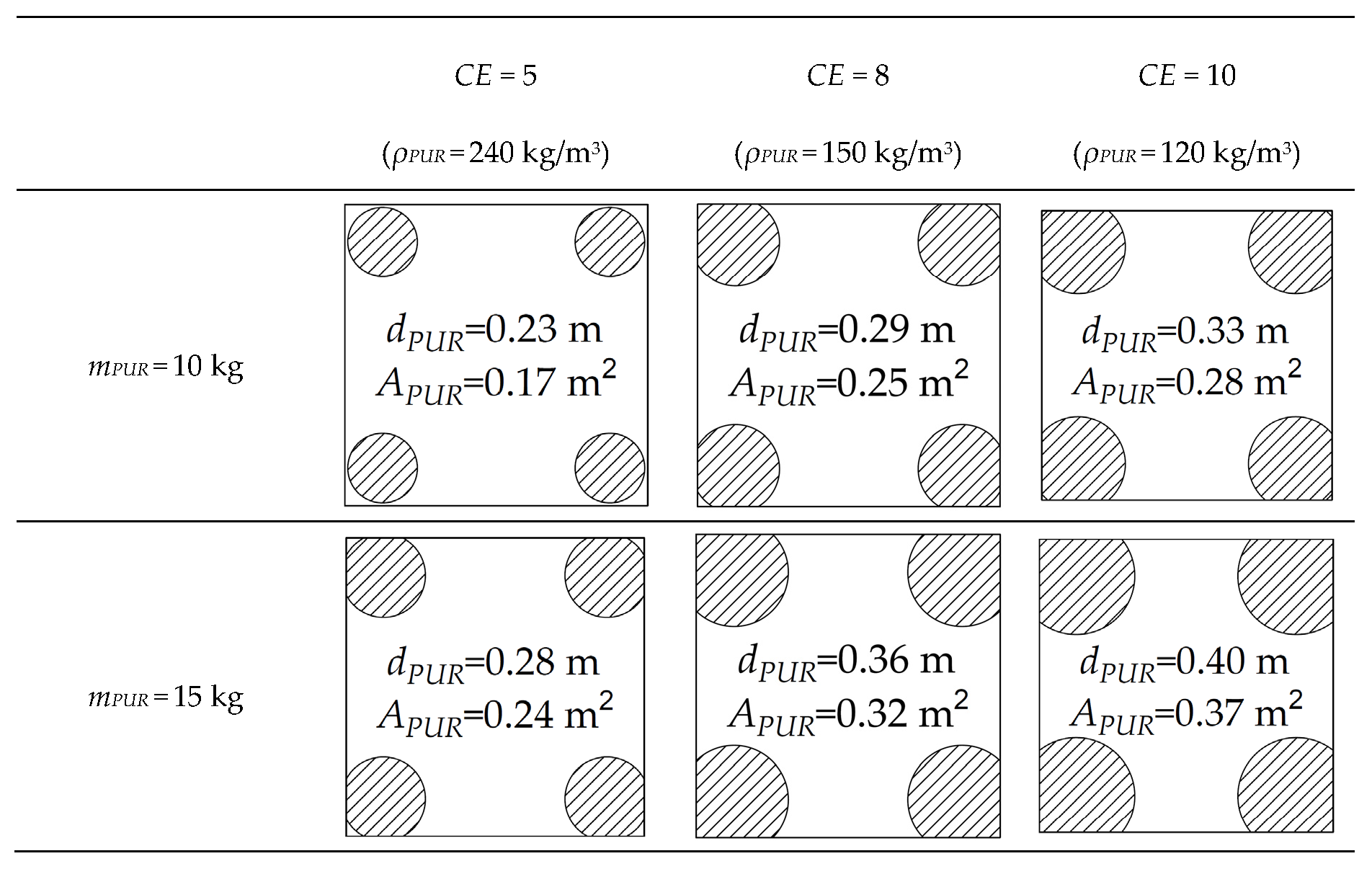
4.3. Calibration of the PDMY Constitutive Model for the Sand–Polyurethane Composite Material
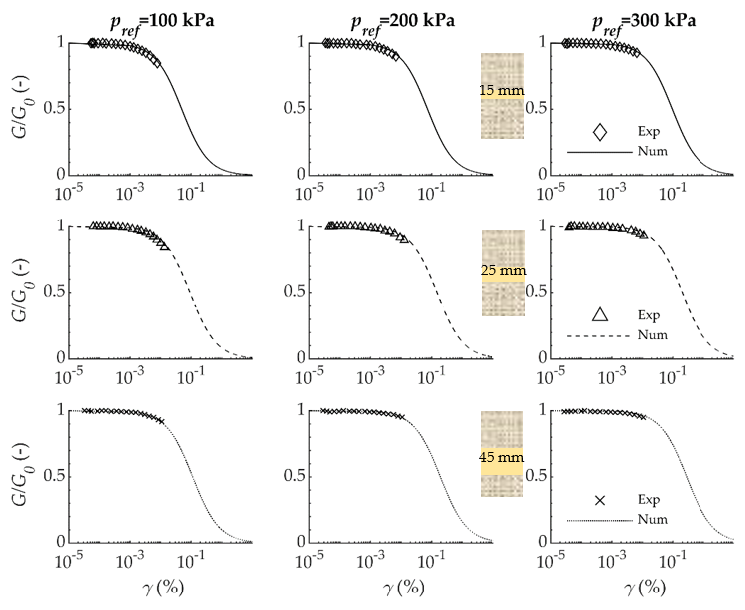
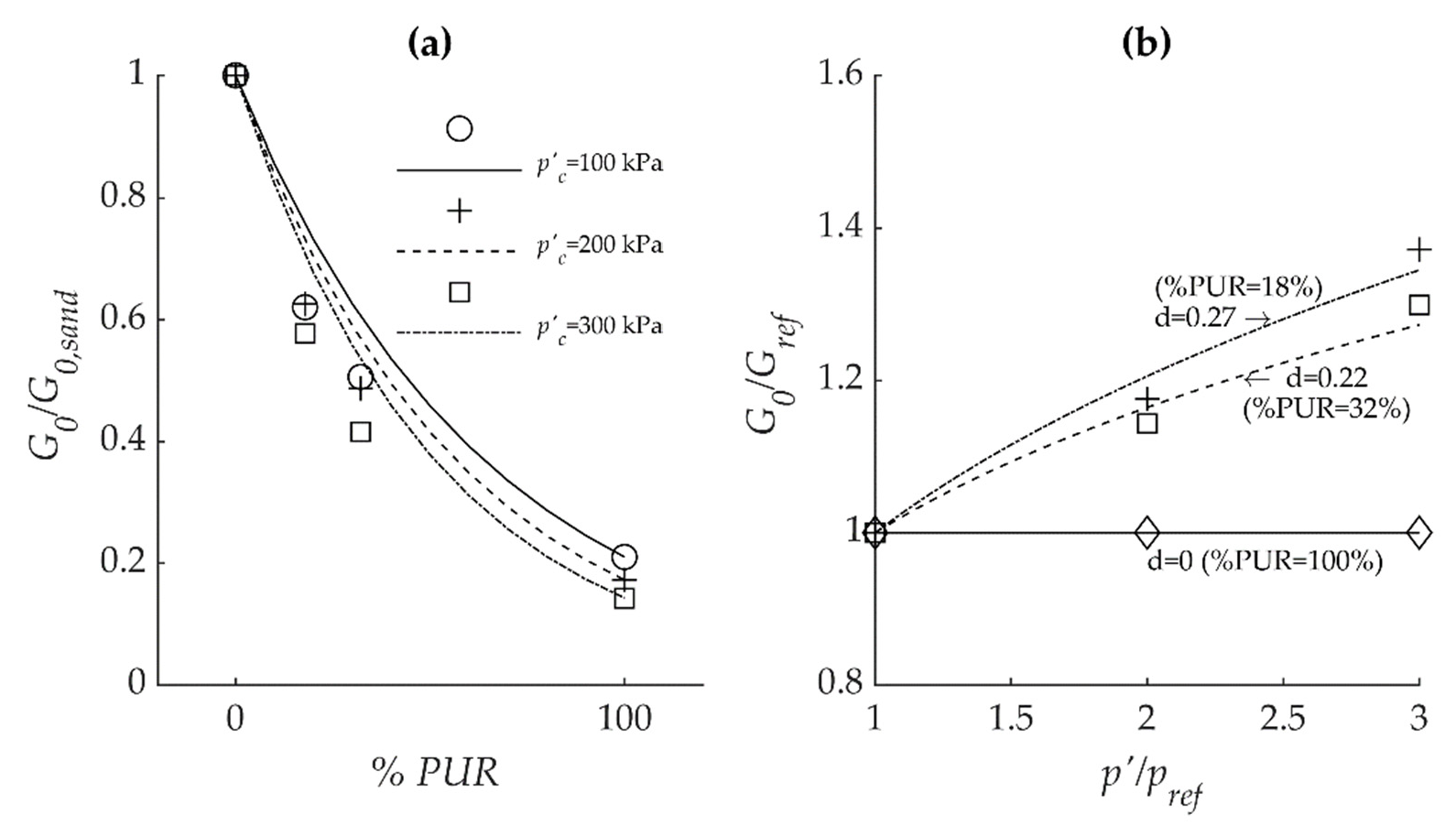
5. Results
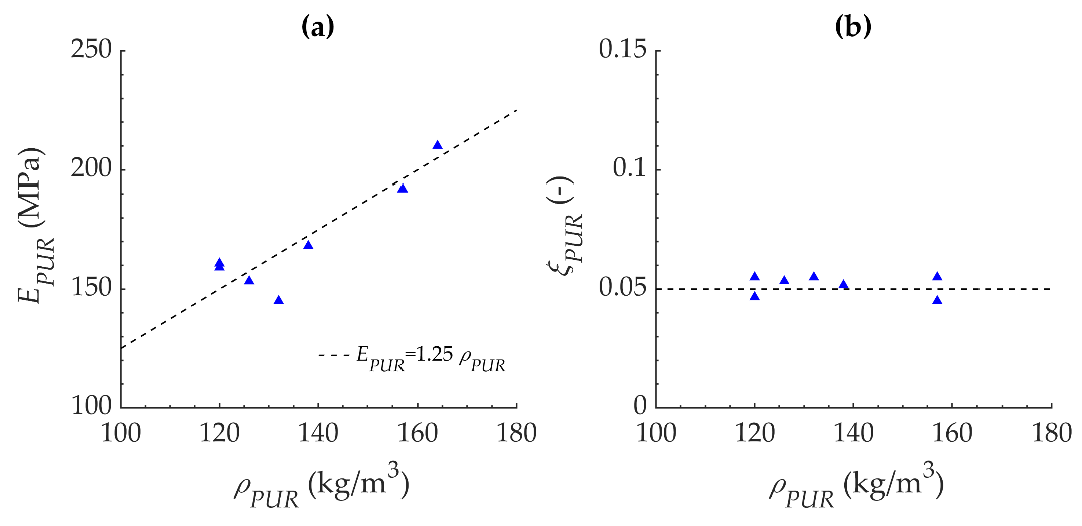
5.1. Elastic Modulus and Damping Coefficient for Polyurethane MP355 at Different Densities, Evaluated through Impact Tests
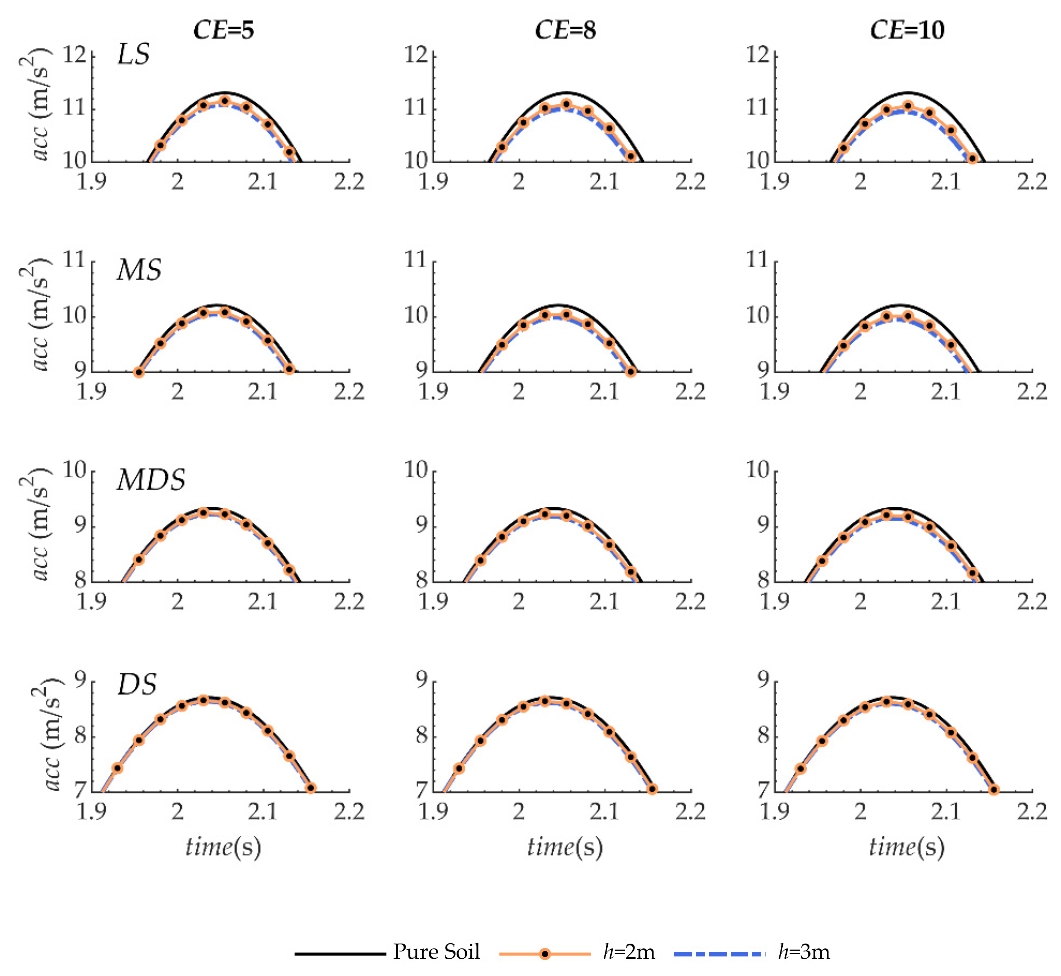
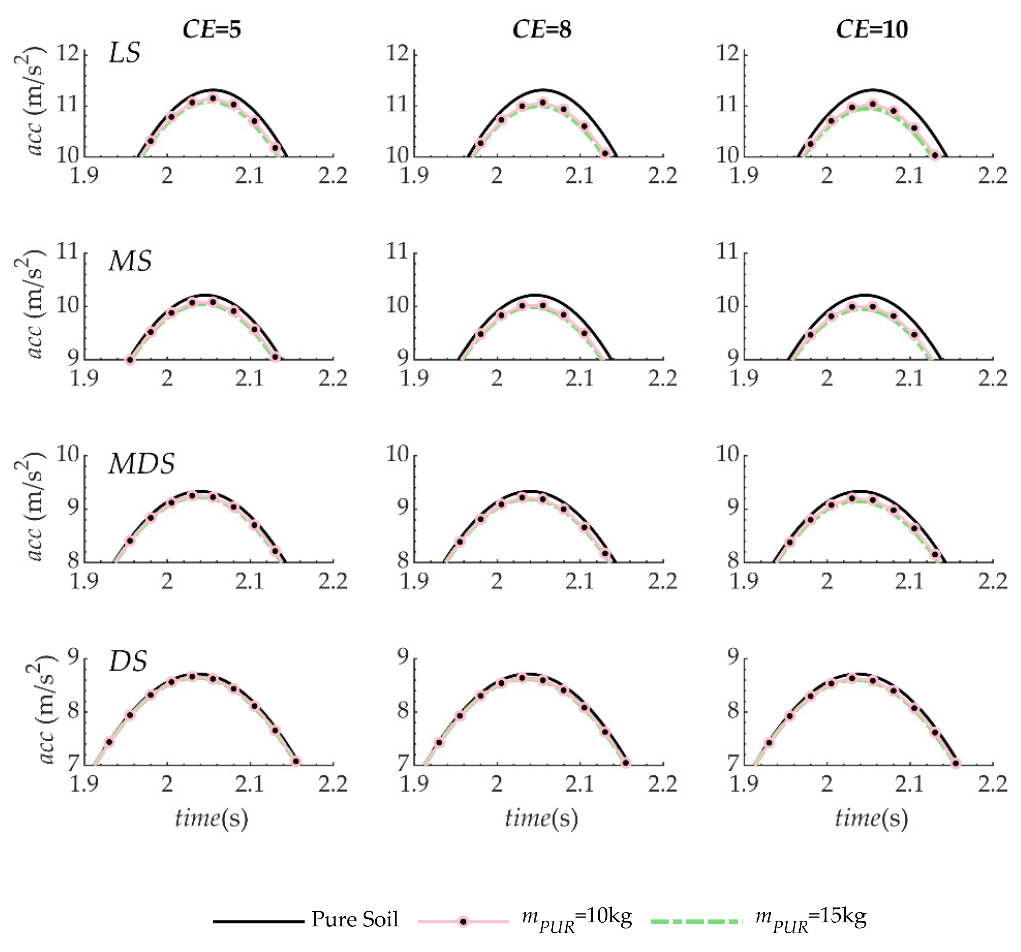
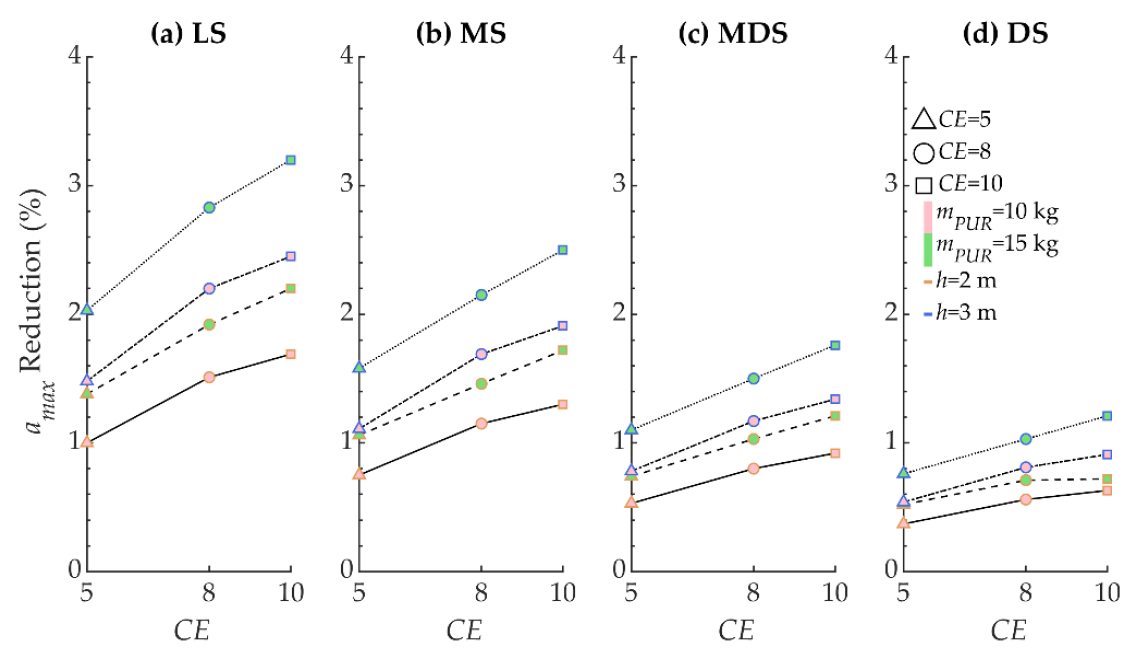
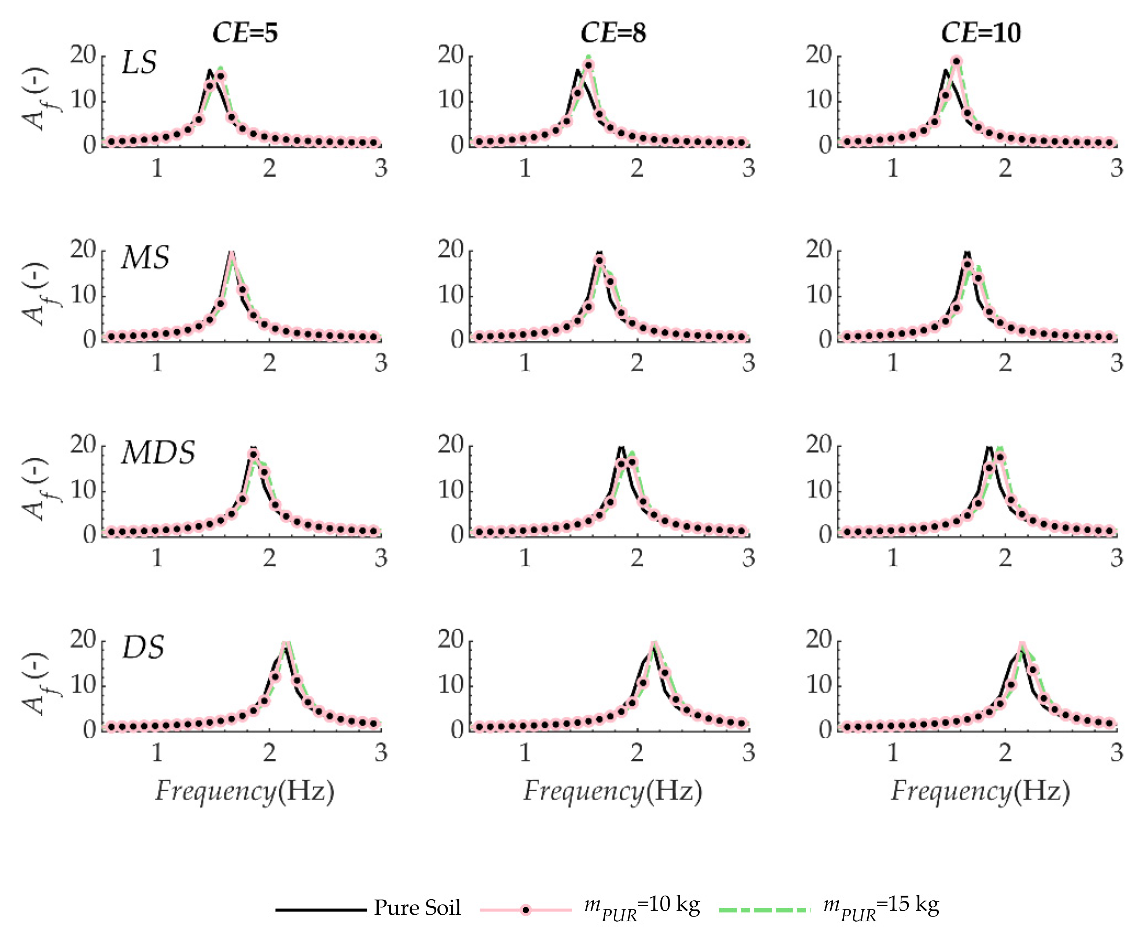
5.2. Seismic Response of Composite Material
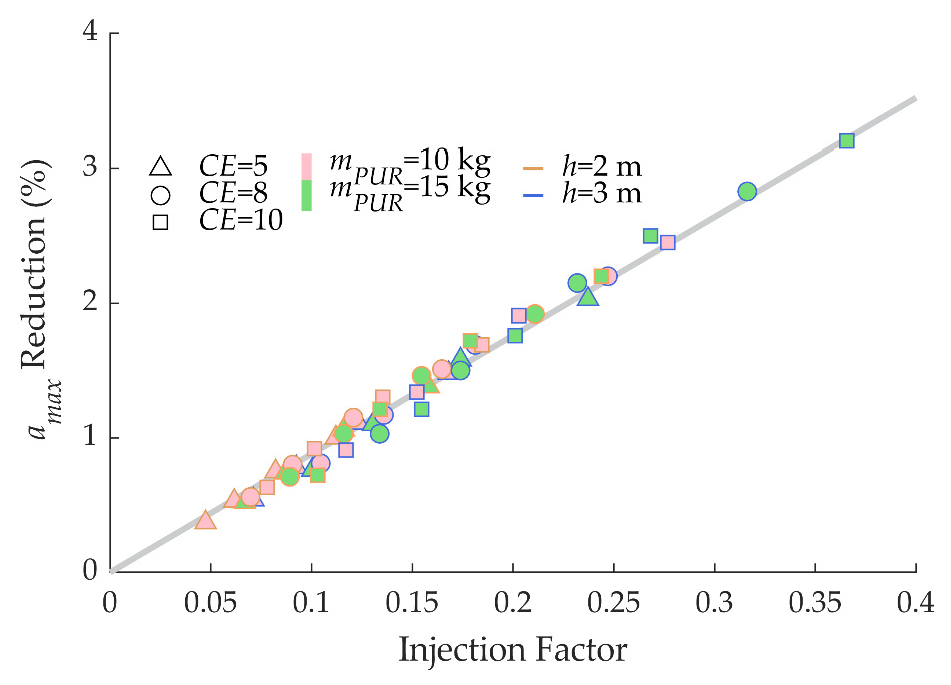
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Furtado, A.; Vila-Pouca, N.; Varum, H.; Arêde, A. Study of the Seismic Response on the Infill Masonry Walls of a 15-Storey Reinforced Concrete Structure in Nepal. Buildings 2019, 9, 39. [Google Scholar] [CrossRef]
- Gautam, D.; Rodrigues, H. Impacts and Insights of Gorkha Earthquake in Nepal; Elsevier: Amsterdam, The Netherlands, 2018. [Google Scholar]
- Anelli, A.; Santa-Cruz, S.; Vona, M.; Tarque, N.; Laterza, M. A proactive and resilient seismic risk mitigation strategy for existing school buildings. Struct. Infrastruct. Eng. 2019, 15, 137–151. [Google Scholar] [CrossRef]
- Han, Z.; Lu, X.; Hörhager, E.I.; Yan, J. The effects of trust in government on earthquake survivors’ risk perception and preparedness in China. Nat. Hazards 2017, 86, 437–452. [Google Scholar] [CrossRef]
- Jones, S.; Oven, K.J.; Wisner, B. A comparison of the governance landscape of earthquake risk reduction in Nepal and the Indian State of Bihar. Int. J. Disaster Risk Reduct. 2016, 15, 29–42. [Google Scholar] [CrossRef]
- Castelli, F.; Lentini, V.; Grasso, S. Recent developments for the seismic risk assessment. Bull. Earthq. Eng. 2017, 15, 5093–5117. [Google Scholar] [CrossRef]
- Fardis, M.N.; Panagiotakos, T.B. Seismic Design And Response Of Bare And Masonry-Infilled Reinforced Concrete Buildings. Part Ii: Infilled Structures. J. Earthq. Eng. 1997, 1, 475–503. [Google Scholar] [CrossRef]
- Barbagallo, F.; Bosco, M.; Marino, E.M.; Rossi, P.P.; Stramondo, P.R. A multi-performance design method for seismic upgrading of existing RC frames by BRBs. Earthq. Eng. Struct. Dyn. 2017, 46, 1099–1119. [Google Scholar] [CrossRef]
- Barbagallo, F.; Bosco, M.; Marino, E.M.; Rossi, P.P. Seismic retrofitting of braced frame buildings by RC rocking walls and viscous dampers. Earthq. Eng. Struct. Dyn. 2018, 47, 2682–2707. [Google Scholar] [CrossRef]
- Pantò, B.; Rossi, P.P. A new macromodel for the assessment of the seismic response of infilled RC frames. Earthq. Eng. Struct. Dyn. 2019, 48, 792–817. [Google Scholar] [CrossRef]
- Barbagallo, F.; Bosco, M.; Marino, E.M.; Rossi, P.P. Variable vs. invariable elastic response spectrum shapes: Impact on the mean annual frequency of exceedance of limit states. Eng. Struct. 2020, 214, 110620. [Google Scholar] [CrossRef]
- Romis, F.; Caprili, S.; Salvatore, W.; Ferreira, T.M.; Lourenço, P.B. An Improved Seismic Vulnerability Assessment Approach for Historical Urban Centres: The Case Study of Campi Alto di Norcia, Italy. Appl. Sci. 2021, 11, 849. [Google Scholar] [CrossRef]
- Ghasemi, S.; Nezamabadi, M.F.; Moghadam, A.S.; Hosseini, M. Optimization of relative-span ratio in rocking steel braced dual-frames. Bull. Earthq. Eng. 2021, 19, 805–829. [Google Scholar] [CrossRef]
- Rodrigues, H.; Arêde, A.; Furtado, A.; Rocha, P. Seismic Rehabilitation of RC Columns Under Biaxial Loading: An Experimental Characterization. Structures 2015, 3, 43–56. [Google Scholar] [CrossRef]
- Furtado, A.; Rodrigues, H.; Varum, H.; Arêde, A. Mainshock-aftershock damage assessment of infilled RC structures. Eng. Struct. 2018, 175, 645–660. [Google Scholar] [CrossRef]
- Hermanns, L.; Fraile, A.; Alarcón, E.; Álvarez, R. Performance of buildings with masonry infill walls during the 2011 Lorca earthquake. Bull. Earthq. Eng. 2014, 12, 1977–1997. [Google Scholar] [CrossRef]
- Tsang, H.-H. Seismic isolation by rubber–soil mixtures for developing countries. Earthq. Eng. Struct. Dyn. 2008, 37, 283–303. [Google Scholar] [CrossRef]
- Tsang, H.-H.; Lo, S.H.; Xu, X.; Neaz Sheikh, M. Seismic isolation for low-to-medium-rise buildings using granulated rubber-soil mixtures: Numerical study. Earthq. Eng. Struct. Dyn. 2012, 41, 2009–2024. [Google Scholar] [CrossRef]
- Abate, G.; Gatto, M.; Massimino, M.R.; Pitilakis, D. Large scale soil-foundation-structure model in greece: Dynamic tests vs fem simulation. In Proceedings of the 6th International Conference on Computational Methods in Structural Dynamics and Earthquake Engineering (COMPDYN 2017), Rhodes Island, Greece, 15–17 June 2017; pp. 1347–1359. [Google Scholar] [CrossRef]
- Pitilakis, K.; Karapetrou, S.; Tsagdi, K. Numerical investigation of the seismic response of RC buildings on soil replaced with rubber–sand mixtures. Soil Dyn. Earthq. Eng. 2015, 79, 237–252. [Google Scholar] [CrossRef]
- Argyroudis, S.; Palaiochorinou, A.; Mitoulis, S.; Pitilakis, D. Use of rubberised backfills for improving the seismic response of integral abutment bridges. Bull. Earthq. Eng. 2016, 14, 3573–3590. [Google Scholar] [CrossRef]
- Tsiavos, A.; Alexander, N.A.; Diambra, A.; Ibraim, E.; Vardanega, P.J.; Gonzalez-Buelga, A.; Sextos, A. A sand-rubber deformable granular layer as a low-cost seismic isolation strategy in developing countries: Experimental investigation. Soil Dyn. Earthq. Eng. 2019, 125, 105731. [Google Scholar] [CrossRef]
- Tsang, H.; Tran, D.; Hung, W.; Pitilakis, K.; Gad, E.F. Performance of geotechnical seismic isolation system using rubber-soil mixtures in centrifuge testing. Earthq. Eng. Struct. Dyn. 2020, 50, 1271–1289. [Google Scholar] [CrossRef]
- Forcellini, D. Assessment of Geotechnical Seismic Isolation (GSI) as a Mitigation Technique for Seismic Hazard Events. Geosciences 2020, 10, 222. [Google Scholar] [CrossRef]
- Bathurst, R.J.; Zarnani, S.; Gaskin, A. Shaking table testing of geofoam seismic buffers. Soil Dyn. Earthq. Eng. 2007, 27, 324–332. [Google Scholar] [CrossRef]
- Azinović, B.; Koren, D.; Kilar, V. The seismic response of low-energy buildings founded on a thermal insulation layer—A parametric study. Eng. Struct. 2014, 81, 398–411. [Google Scholar] [CrossRef]
- Karatzia, X.A.; Mylonakis, G.E. Geotechnical seismic isolation using EPS geofoam around piles. In Proceedings of the 6th International Conference on Computational Methods in Structural Dynamics and Earthquake Engineering (COMPDYN 2017), Rhodes Island, Greece, 15–17 June 2017; pp. 1042–1057. [Google Scholar] [CrossRef]
- Yegian, M.K.; Kadakal, U. Foundation isolation for seismic protection using a smooth synthetic liner. J. Geotech. Geoenviron. Eng. 2004, 130, 1121–1130. [Google Scholar] [CrossRef]
- Yegian, M.K.; Catan, M. Soil Isolation for Seismic Protection Using a Smooth Synthetic Liner. J. Geotech. Geoenviron. Eng. 2004, 130, 1131–1139. [Google Scholar] [CrossRef]
- Banović, I.; Radnić, J.; Grgić, N. Geotechnical Seismic Isolation System Based on Sliding Mechanism Using Stone Pebble Layer: Shake-Table Experiments. Shock Vib. 2019, 2019, 1–26. [Google Scholar] [CrossRef]
- Cavallaro, A.; Castelli, F.; Ferraro, A.; Grasso, S.; Lentini, V. Site response analysis for the seismic improvement of a historical and monumental building: The case study of Augusta Hangar. Bull. Eng. Geol. Environ. 2018, 77, 1217–1248. [Google Scholar] [CrossRef]
- Saint-Michel, F.; Chazeau, L.; Cavaillé, J.-Y.; Chabert, E. Mechanical properties of high density polyurethane foams: I. Effect of the density. Compos. Sci. Technol. 2006, 66, 2700–2708. [Google Scholar] [CrossRef]
- Montrasio, L.; Gatto, M.P.A. Experimental Analyses on Cellular Polymers for Geotechnical Applications. Procedia Eng. 2016, 158, 272–277. [Google Scholar] [CrossRef]
- Montrasio, L.; Gatto, M.P.A. Experimental analyses on cellular polymers in different forms for geotechnical applications. In Proceedings of the ICSMGE 2017—19th International Conference on Soil Mechanics and Geotechnical Engineering, Seoul, Korea, 17–27 September 2017; pp. 1063–1066. [Google Scholar]
- Gatto, M.P.A.; Montrasio, L.; Tsinaris, A.; Pitilakis, D.; Anastasiadis, A. The dynamic behaviour of polyurethane foams in geotechnical conditions. In Proceedings of the 7th International Conference on Earthquake Geotechnical Engineering, Rome, Italy, 17–20 June 2019; pp. 2566–2573. [Google Scholar]
- Gatto, M.P.A.; Montrasio, L.; Berardengo, M.; Vanali, M. Experimental Analysis of the Effects of a Polyurethane Foam on Geotechnical Seismic Isolation. J. Earthq. Eng. 2020, 1–22. [Google Scholar] [CrossRef]
- Mazzoni, S.; McKenna, F.; Scott, M.H.; Fenves, G.L. OpenSees Command Language Manual; Pacific Earthquake Engineering Research (PEER) Center: Berkeley, CA, USA, 2006. [Google Scholar]
- Coll, A.; Ribó, R.; Pasenau, M.; Escolano, E.; Perez, J.S.; Melendo, A.; Monros, A.; Gárate, J. GiD v.14 Reference Manual. 2018. Available online: www.gidhome.com (accessed on 25 May 2020).
- Papanikolaou, V.K.; Kartalis-Kaounis, T.; Protopapadakis, V.K.; Papadopoulos, T. GiD+OpenSees Interface: An Integrated Finite Element Analysis Platform; Lab of R/C and Masonry Structures, Aristotle University of Thessaloniki: Thessaloniki, Greece, 2017. [Google Scholar]
- Castelli, F.; Cavallaro, A.; Ferraro, A.; Grasso, S.; Lentini, V.; Massimino, M.R. Static and dynamic properties of soils in Catania (Italy). Ann. Geophys. 2018, 61, SE221. [Google Scholar] [CrossRef]
- Ciancimino, A.; Lanzo, G.; Alleanza, G.A.; Amoroso, S.; Bardotti, R.; Biondi, G.; Cascone, E.; Castelli, F.; Di Giulio, A.; D’onofrio, A.; et al. Dynamic characterization of fine-grained soils in Central Italy by laboratory testing. Bull. Earth. Eng. 2020, 18, 5503–5531. [Google Scholar] [CrossRef]
- Master Builders Solutions. Available online: https://www.master-builders-solutions.com/it-it (accessed on 15 January 2021).
- MasterRoc MP 355—Master Builders Solutions. Available online: https://assets.master-builders-solutions.com/it-it/tds-masterroc-mp355-it.pdf (accessed on 15 January 2021).
- Brandt, A.; Berardengo, M.; Manzoni, S.; Cigada, A. Scaling of mode shapes from operational modal analysis using harmonic forces. J. Sound Vib. 2017, 407, 128–143. [Google Scholar] [CrossRef]
- Brandt, A.; Berardengo, M.; Manzoni, S.; Vanali, M.; Cigada, A. Global scaling of operational modal analysis modes with the OMAH method. Mech. Syst. Signal Process. 2019, 117, 52–64. [Google Scholar] [CrossRef]
- Lysmer, J.; Kuhlemeyer, R.L. Finite Dynamic Model for Infinite Media. J. Eng. Mech. Div. 1969, 95, 859–877. [Google Scholar] [CrossRef]
- Joyner, W.B.; Chen, A.T.F. Calculation of nonlinear ground response in earthquakes. Bull. Seismol. Soc. Am. 1975, 65(5), 1315–1336. [Google Scholar]
- Ricker, N. Transient Waves in Visco-Elastic Media; Elsevier Science: Amsterdam, The Netherlands, 1977. [Google Scholar]
- Loli, M.; Knappett, J.A.; Anastasopoulos, I.; Brown, M.J. Use of Ricker motions as an alternative to pushover testing. Int. J. Phys. Model. Geotech. 2015, 15, 44–55. [Google Scholar] [CrossRef]
- LeVeque, R.J. Finite Difference Methods for Ordinary and Partial Differential Equations—Steady-State and Time-Dependent Problems; SIAM: Philadelphia, PA, USA, 2007. [Google Scholar]
- Chopra, A.K. Dynamics of Structures: Theory and Applications to Earthquake Engineering; Prentice Hall: Upper Saddle River, NJ, USA, 2011. [Google Scholar]
- Kramer, S.L. Geotechnical Earthquake Engineering; Prentice Hall: Upper Saddle River, NJ, USA, 1996. [Google Scholar]
- Parra, E. Numerical Modeling of Liquefaction and Lateral Ground Deformation Including Cyclic Mobility and Dilation Response in Soil Systems; Rensselaer Polytechnic Institute: Troy, NY, USA, 1996. [Google Scholar]
- Yang, Z.; Elgamal, A.; Parra, E. Computational Model for Cyclic Mobility and Associated Shear Deformation. J. Geotech. Geoenviron.Eng. 2003, 129, 1119–1127. [Google Scholar] [CrossRef]
- Elgamal, A.; Yang, Z.; Parra, E.; Ragheb, A. Modeling of cyclic mobility in saturated cohesionless soils. Int. J. Plast. 2003, 19, 883–905. [Google Scholar] [CrossRef]
- Dafalias, Y.F.; Manzari, M.T. Simple Plasticity Sand Model Accounting for Fabric Change Effects. J. Eng. Mech. ASCE 2004, 130. [Google Scholar] [CrossRef]
- Patel, P.S.; Shepherd, D.E.; Hukins, D.W. Compressive properties of commercially available polyurethane foams as mechanical models for osteoporotic human cancellous bone. BMC Musculoskelet. Disord. 2008, 9, 137. [Google Scholar] [CrossRef] [PubMed]
- Qiu, D.; He, Y.; Yu, Z. Investigation on compression mechanical properties of rigid polyurethane foam treated under random vibration condition: An experimental and numerical simulation study. Materials 2019, 12, 3385. [Google Scholar] [CrossRef] [PubMed]
- Horak, Z.; Dvorak, K.; Zarybnicka, L.; Vojackova, H.; Dvorakova, J.; Vilimek, M. Experimental measurements of mechanical properties of pur foam used for testing medical devices and instruments depending on temperature, density and strain rate. Materials 2020, 13, 4560. [Google Scholar] [CrossRef]
- Brotons, V.; Tomás, R.; Ivorra, S.; Grediaga, A.; Martínez, J.M.; Benavente, D.; Heras, M.G. Improved correlation between the static and dynamic elastic modulus of different types of rocks. Mater. Struct. 2015, 49, 3021–3037. [Google Scholar] [CrossRef]

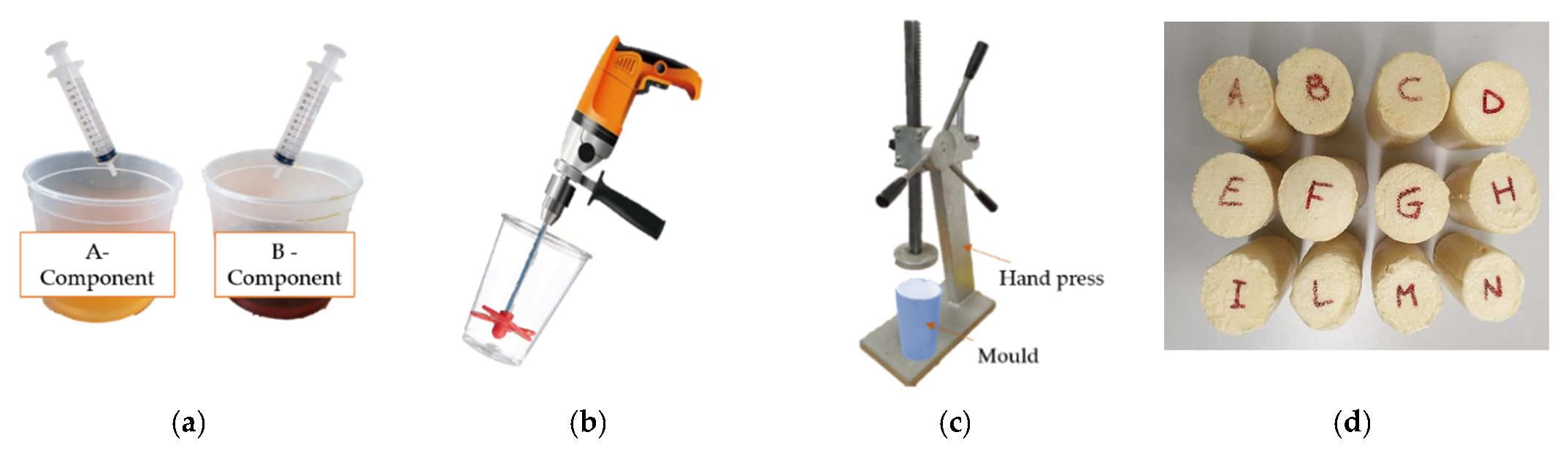
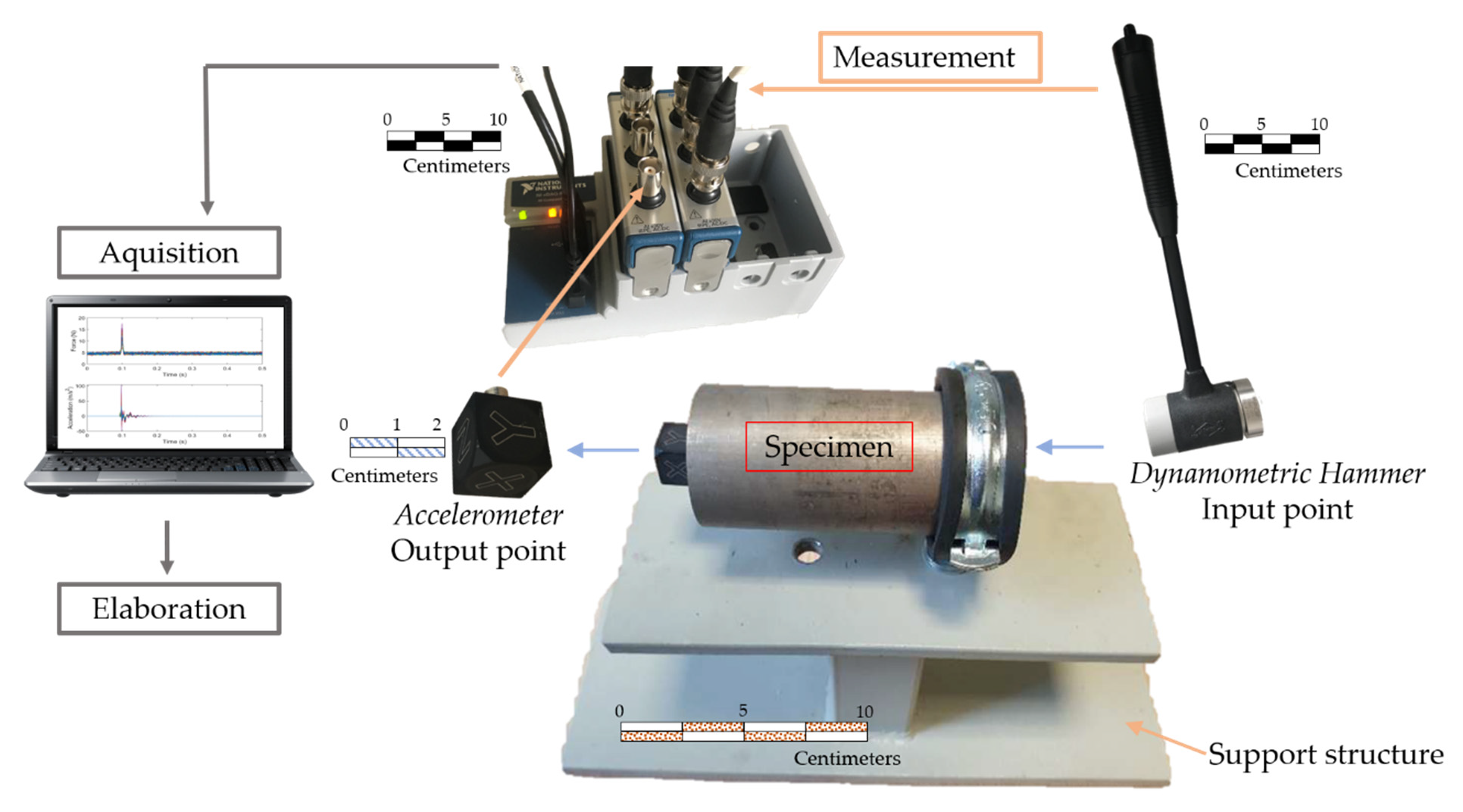
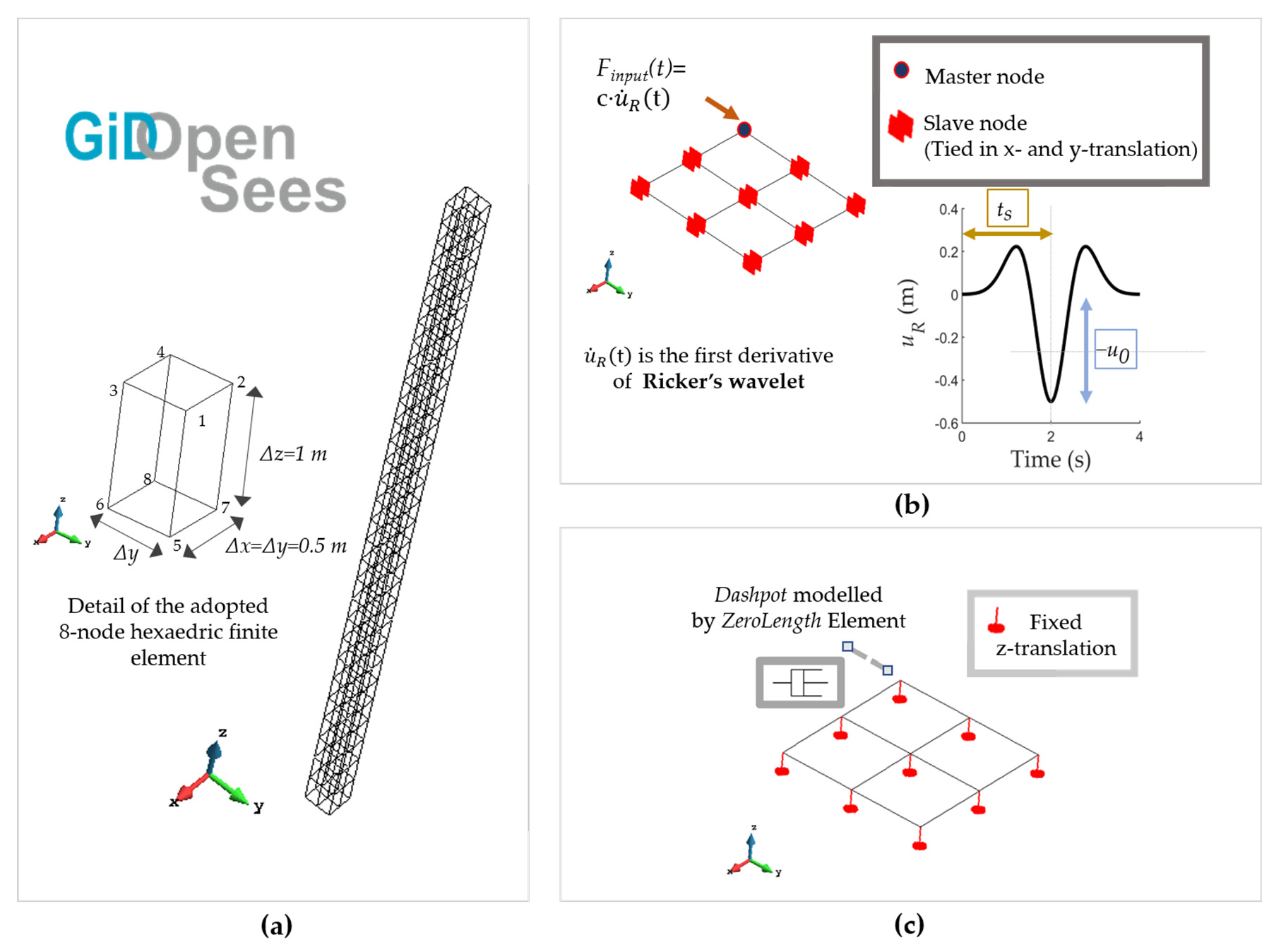
| Specimen | Initial CE | Mass, mA + B (g) | Vi (mL) | Final CE | Density, ρPUR (kg/m3) |
|---|---|---|---|---|---|
| A | 6 | 25 | 22 | 7.16 | 157 |
| B | 6 | 26 | 23 | 6.88 | 164 |
| C | 6 | 24 | 21 | 7.45 | 151 |
| D | 6 | 25 | 22 | 7.16 | 157 |
| E | 8 | 21 | 19 | 8.52 | 132 |
| F | 8 | 19 | 17 | 9.41 | 120 |
| G | 8 | 22 | 20 | 8.13 | 138 |
| H | 8 | 22 | 20 | 8.13 | 138 |
| I | 9 | 20 | 18 | 8.94 | 126 |
| L | 9 | 19 | 17 | 9.41 | 120 |
| M | 9 | 18 | 16 | 9.94 | 113 |
| N | 9 | 19 | 17 | 9.41 | 120 |
| Cohesionless Material | ||||
|---|---|---|---|---|
| LS | MS | MDS | DS | |
| Ρ (t/m3) | 1.7 | 1.9 | 2 | 2.1 |
| Gref (MPa) | 55 | 75 | 100 | 130 |
| Bref (MPa) | 150 | 200 | 300 | 390 |
| (°) | 29 | 33 | 37 | 40 |
| CE = 5 | CE = 8 | CE = 10 | ||||
|---|---|---|---|---|---|---|
| mPUR = 10 kg | mPUR = 15 kg | mPUR = 10 kg | mPUR = 15 kg | mPUR = 10 kg | mPUR = 15 kg | |
| LS | 62 | 65 | 58 | 59 | 55 | 55 |
| MS | 80 | 82 | 73 | 73 | 69 | 67 |
| MDS | 101 | 102 | 91 | 88 | 84 | 80 |
| DS | 126 | 125 | 111 | 106 | 102 | 94 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gatto, M.P.A.; Lentini, V.; Castelli, F.; Montrasio, L.; Grassi, D. The Use of Polyurethane Injection as a Geotechnical Seismic Isolation Method in Large-Scale Applications: A Numerical Study. Geosciences 2021, 11, 201. https://doi.org/10.3390/geosciences11050201
Gatto MPA, Lentini V, Castelli F, Montrasio L, Grassi D. The Use of Polyurethane Injection as a Geotechnical Seismic Isolation Method in Large-Scale Applications: A Numerical Study. Geosciences. 2021; 11(5):201. https://doi.org/10.3390/geosciences11050201
Chicago/Turabian StyleGatto, Michele Placido Antonio, Valentina Lentini, Francesco Castelli, Lorella Montrasio, and Davide Grassi. 2021. "The Use of Polyurethane Injection as a Geotechnical Seismic Isolation Method in Large-Scale Applications: A Numerical Study" Geosciences 11, no. 5: 201. https://doi.org/10.3390/geosciences11050201
APA StyleGatto, M. P. A., Lentini, V., Castelli, F., Montrasio, L., & Grassi, D. (2021). The Use of Polyurethane Injection as a Geotechnical Seismic Isolation Method in Large-Scale Applications: A Numerical Study. Geosciences, 11(5), 201. https://doi.org/10.3390/geosciences11050201






