Abstract
There is an increasing need for quantitative rockfall hazard and risk assessment that requires a precise definition of the terms and concepts used for this particular type of landslide. This paper suggests using terms that appear to be the most logic and explicit as possible and describes methods to derive some of the main hazards and risk descriptors. The terms and concepts presented concern the rockfall process (failure, propagation, fragmentation, modelling) and the hazard and risk descriptors, distinguishing the cases of localized and diffuse hazards. For a localized hazard, the failure probability of the considered rock compartment in a given period of time has to be assessed, and the probability for a given element at risk to be impacted with a given energy must be derived combining the failure probability, the reach probability, and the exposure of the element. For a diffuse hazard that is characterized by a failure frequency, the number of rockfalls reaching the element at risk per unit of time and with a given energy (passage frequency) can be derived. This frequency is relevant for risk assessment when the element at risk can be damaged several times. If it is not replaced, the probability that it is impacted by at least one rockfall is more relevant.
1. Introduction
There is an increasing need for quantitative rockfall hazard and risk assessment that requires a precise definition of the terms and concepts used for this particular type of landslide. A definition of terms used for landslide susceptibility, hazard, and risk zoning and a framework for landslide risk management was given by [1] in the guidelines for landslide susceptibility, hazard, and risk zoning for land use planning on behalf of the JTC-1 Joint Technical Committee on Landslides and Engineered Slopes (joint ISSMGE, ISRM and IAEG Technical Committee), but the definitions and concepts need to be detailed and completed for practical use in quantitative rockfall hazard and risk assessment. No international specific guidelines exist for rockfall hazard and risk, but states of the art were presented by [2,3,4,5]. The objectives of this paper are to suggest terms that appear to be most logic and explicit as possible, and to describe methods to derive some of the main hazard and risk descriptors.
2. The Rockfall Process
The most widely used classification system of landslides is the one derived from the Varnes classification [6], which was slightly modified by [7] and more recently by [8]. Excluding slope deformation, five types of rock movements are described by [8]: rock fall; rock topple; rock slide; rock spread; and rock avalanche. A rock fall is defined as the “detachment, fall, rolling, and bouncing of rock fragments. It may occur singly or in clusters, but there is little dynamic interaction between the most mobile moving fragments, which interact mainly with the substrate (path). Fragment deformation is unimportant, although fragments can break during impacts”. A rock avalanche is defined as an “extremely rapid, massive, flow-like motion of fragmented rock from a large rock slide or rock fall”. As there is a continuous transition between rock falls and rock avalanches by a progressive increase of volume, both have been included in the scope of this article. However, for the sake of simplicity, we will use the term “rock fall” to name both. Figure 1 shows an example of rockfall.

Figure 1.
Rockfall with a volume bigger than 1000 m3 occurred in 2008 in Saint-Paul de Varces (French Subalpine Ranges). Note steep talus slope and large boulder runouts. Photo S. Gominet (IRMa).
Ref. [9] divided flow-like movements (where particles interact with each other and travel as deforming mass) into dry granular flows and granular flows with special mobilization phenomena, which have usually a bigger size, but it is difficult to establish a fixed boundary. Their excessive mobility could be the result, for instance, of undrained loading.
Note that the two nouns of “rock fall” are separated according to the general principle of the Varnes classification (the first noun describes the material and the second describes the type of movement), but the term “rockfall” is often used by engineers [10]. Thus, we will use “rockfall” within the rest of this article. The term “fragmental rockfall” may be used to name a rockfall strico sensu.
2.1. Failure
The detachment can be defined as a movement that results in a complete loss of contact of a rock compartment with the surface by which it was in contact with the cliff. The detachment (or release) results from a failure process by which the rock compartment begins to move. This failure usually occurs by a sliding or a toppling mechanism, but tensile, bending, and buckling failures may also play a role. According to the principle of the Varnes classification, a composite term can be used to describe both the failure mechanism and the transport process (examples: rock topple–rock fall, rockslide–rock fall, rockslide–rock avalanche). The mechanical analysis of slide and topple was described, for example, by [11,12]. The term “rock compartment” is preferred to “rock mass”, which refers to a larger rock volume in rock engineering. Most failures are controlled by the discontinuities of the rock mass, but non-structurally-controlled failures can occur when the rock mass strength is exceeded, and result in the movement of a rock compartment that slides on the rest of the rock mass.
When a rock compartment is prone to fall, it can be qualified as potentially unstable. When it slowly moves before the detachment of the rock compartment, it can be qualified as unstable and called an instability. After a rockfall, the surface by which the fallen rock compartment was in contact with the cliff (and which is often well visible), is called the scar or the source area or the release area of the rockfall. The deposited material is called the deposit or debris. When the deposit forms a continuous layer, it is known as talus. Its slope is usually lower than 40°.
2.2. Fragmentation
Usually, a potentially unstable rock compartment is initially made of a number of blocks, which are delineated by cohesionless discontinuities, but it can include cohesive or non-persistent discontinuities with rock bridges. The sizes of these blocks are characterized by the in situ block size distribution (IBSD) that was introduced by [13]. Note that the non-persistence of the discontinuities and the existence of rock bridges can lead to an underestimation of the size of the initial blocks.
When falling, an initial block can break into several smaller blocks during the impacts on the substrate or with other blocks. The final distribution of the fragments is called the rockfall block size distribution (RBSD). Ref. [14] proposed a terminology to describe the fragmentation processes occurring during a rockfall. The fragmentation of a rock compartment results from the disaggregation that occurs during the failure process (Figure 2) and the breakage (dynamic fragmentation) that occurs during the impacts of the rock fragments between each other or on the substrate. The fragmentation of a potentially unstable rock compartment should be considered in the hazard analysis [15].
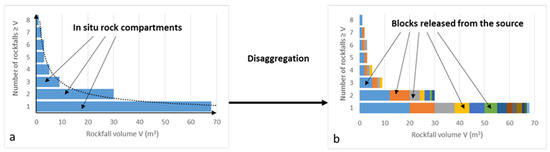
Figure 2.
The in situ rock compartments (a) disaggregate into individual blocks (b).
2.3. Rockfall Modelling
Fragmental rockfalls may be analyzed by simulating the propagation of one single block that interacts only with the substrate (single block methods, [16]) or by including a fragmentation law [17,18]. Rock mass falls can be analyzed by modelling each rock fragment (multi-block methods, including discrete element methods [19]) or as a granular flow remaining in a fairly continuous contact with the flow bed [9]. The methods that model explicitly the rock fragments may or not model the breakage. They also may or not model the interaction with the vegetation [3]. The simplest methods allow a lot of simulations to be run in a probabilistic approach.
A simplified energetic approach can also be used with the concept of reach angle that express the energy loss during the propagation. The energy line represents the energy (divided by the weight) of a rock mass as a function of the horizontal displacement along the rockfall path. Theoretically, it starts from the gravity center of the rock mass before its detachment. The energy consists of potential energy and kinetic energy. The energy line decreases along the rockfall path due to the energy that is lost when the rock fragments rebound, roll, or slide on the ground. Thus, its inclination reflects the energy loss per unit of horizontal displacement. When a rock mass reaches the intersection of the energy line with the topography, the energy consists only of its potential energy and then it stops.
For sliding, it can be shown that the energy line is inclined at an angle equal to the dynamic friction angle of the interface between the rock and the ground [20]. For bouncing or rolling, its inclination cannot be related to a simple mechanical parameter. The reach angle was assessed empirically. For practical reasons, the empirical reach angle or Fahrböschung of a rockfall [21] has been defined from the highest point of the rockfall scar to the stopping point of the longest run-out boulder [22]. It should thus be called maximal reach angle. Authors in [22] suggest an alternative angle, the shadow angle, which is defined from the apex of the talus slope to the outer margin of the rockfall shadow. The rockfall shadow is the area downslope of the talus slope, which is covered discontinuously by scattered large boulders that have rolled or bounced beyond the base of the talus. This alternative approach supposes a profile such that most of the kinetic energy is absorbed during the first impact on the talus slope. The effect of rockfall activity is integrated over time by considering the longest boulder run-out in a given rockfall shadow. Note that the reach angle and the shadow angle as defined originally are related respectively to a rockfall event and a rockfall area and represent a minimum of the angles that can be measured for individual boulders. The statistical analysis of the individual boulder reach (or shadow) angles allows a probabilistic analysis of the propagation [23].
3. Rockfall Hazard
The definition of hazard given by [1] is “A condition with the potential for causing an undesirable consequence. The description of landslide hazard should include the location, volume (or area), classification and velocity of the potential landslides and any resultant detached material, and the probability of their occurrence within a given period of time.” Note that this definition of the hazard is larger than the previous definition [24], as the probability is no more identified to the hazard but is only a component.
For rockfalls, the condition with the potential for causing an undesirable consequence is the passage of rock material, and the parameters that directly determine the consequence are the volume, the trajectory, and the velocity of the rock fragments. They depend on the location and geometry of the prone to fall rock compartments and on the characteristics of the propagation zone. The description of rockfall hazard at a given location should ideally include the probabilities (or the frequencies) of a rock fragment reaching this location within a given period of time and with a minimum volume, velocity or energy, and height. Different periods of time and other parameters can be considered. When an element at risk is on the top of a cliff, the condition is just the release of a rock compartment that supports the element at risk. When the time frame is not taken into account explicitly, the rockfall hazard is not fully described and the analysis is called a susceptibility analysis [1]. Comprehensive hazard and susceptibility analyses can be qualitative or quantitative.
According to the type of study, two approaches can be taken: a localized hazard approach, where the prone to fall (or potentially unstable) rock compartments are localized and described, and a diffuse (or global) approach, where it is assumed that a rock compartment may fall from any point of a homogenous source area. According to the approach taken, the way to obtain the probability of a rock fragment reaching a location within a given period of time and the concepts used are different.
3.1. Frequency and Probability
Following [25,26], one may assume that in a homogenous area where a lot of independent rock compartments are at different evolutionary stages, the occurrence of rockfalls is stationary at a yearly scale and is described by a Poisson law. Note that at a daily scale, the dates of the rockfalls are not independent because several rockfalls can be triggered by the same meteorological episode. The probability that N rockfalls occur (failure probability) during a reference period of length t, on a cliff where the failure frequency is λ, is as follows:
and the probability that one or more rockfall occurs is as follows:
If λt is small, this probability can be approximated by λt. The same formulae can be applied to the rockfall passage probability, where λ is the rockfall passage frequency. Unlike for rockfall events, the Poisson law cannot be applied to the passage of rock fragments at a yearly scale, because they fall in clusters.
3.2. Localized Hazard
For a prone to fall rock fragment to pass through a point within a given period of time (event C), it must be released from the source area (event A) and propagate (or travel) from the source to the point considered (event B). Thus, the probability of event C is the probability of event A multiplied by the probability of event B, given that event A has occurred [27,28,29]:
Different expressions have been used to name these probabilities (or the frequencies). For PA, the expression failure probability [15], onset probability [3,29], rockfall probability [2], and release probability have been used. For PB, the expressions propagation probability [15,30,31], transit or impact probability [29], reach probability [32], and travel probability [33] have been used. For PC, the expressions impact probability [22,34], passage probability [29], reach probability [35], occurrence probability [3], and rockfall probability [36] have been used. As passing through a point for a rock compartment needs to be released (or fail) and to propagate down to (or reach) this point, we suggest using the following expressions: failure probability or release probability for event A; propagation probability or reach probability for event B; and passage probability for event C. Note that the expressions probability of occurrence and onset probability are too general, because the occurrence or onset may refer to different events (failure, passage, impact).
In the context of a risk analysis, the authors in [35] used the expression of impact probability to describe the probability of an element at risk to be impacted by a rockfall. This probability is different from the passage probability if the element at risk is mobile, as its exposure is included.
According to the expressions suggested to name the different probabilities, Equation (3) can be rewritten as follows:
where Pp is the passage probability, Pf is the failure probability, and Pr is the reach probability.
In the present state of knowledge, no validated mechanical approach is able to quantitatively determine the failure probability of a potentially unstable rock compartment in a given period of time, and it is usually assessed by expert judgement. An example of quantitative assessment by expert judgement is given by [37]. When localized hazards belong to a homogenous area where the overall failure frequency has been estimated, the failure probabilities estimated by expert judgement can be constrained by the overall frequency [38,39]. For monitored unstable compartments, the analysis of accelerating creep sometimes allows the time of failure to be predicted. Different prediction methods and case studies were described for large rockslides by [40,41,42,43].
The reach probability of a rock fragment or a whole rock compartment can be determined using the reach angle or simulating its trajectory (possibly simulating fragmentation and interactions). It is the proportion of simulations that reaches the considered point, cell, or line [44]. An in situ rock compartment is made up of blocks with an in situ block size distribution (IBSD) that determines the volumes of the blocks to be launched (or the number of blocks for different volume classes). A deterministic simulation of a rockfall can give the number of blocks that reach each cell of the slope, their volume, energy and passing height. In a probabilistic analysis, several rockfalls are simulated, allowing one to assess the probability for a cell of the slope to be reached by at least one block or any number of blocks, possibly for different classes of volume, energy, or passing height (for example, see [45]).
When the interaction between blocks is negligible, single block methods (one block launched per simulation) can be used (possibly with fragmentation). Probabilistic methods give the probability Pri that at least one fragment reaches a point, given that a single block i has been released. The probability Pr that at least one fragment reaches a point, given that the whole compartment has fallen is as follows:
where N is the number of fragments making up the fallen compartment. If the probabilities Pri of the blocks are small, Pr can be approximated by the following:
If in addition the rock fragments have the same propagation probability, Pri, Pr can be approximated by [15] the following:
When there are N independent prone to fall rock compartments, each of them having a passage probability Ppi, the passage probability Pp is given by the following:
3.3. Diffuse Hazard
An element at risk exposed to a diffuse hazard may be impacted periodically by a rockfall. That is why a diffuse hazard is usually assessed by a passage temporal frequency that is obtained from a rockfall inventory (or data base) covering a known period. This inventory may identify rockfall events having occurred in a given area or rock fragments deposited in an area of interest. As the frequency is strongly dependent on the volume, an inventory should include the volume of each event or fragment. Note that the concept of temporal frequency is not suitable to describe a localized hazard, because the release of a given rock compartment occurs once only. However, in some cases, a big localized compartment that has a given failure probability can be viewed also as a homogenous area where falls of smaller blocks represent a diffuse hazard.
3.3.1. Frequency
Temporal frequency is the number of occurrences per unit of time. It can be divided by an area (cliff area for example) or a length (cliff length or road length for example), giving a spatial–temporal frequency. When the qualifiers “temporal” and “spatial–temporal” are not used, confusion is possible with the term “frequency” used in the statistical sense, which does not refer to time.
Different temporal (or spatial–temporal) frequencies can be used:
- -
- Failure frequency or rockfall release frequency: the number of rock compartments that detach from a given source area, per unit of time (and per unit of area for the spatial–temporal frequency). The spatial–temporal release frequency allows to compare the activity of different cliff areas [46,47].
- -
- Fragment release frequency: the number of rock fragments that detach from a given source area, per unit of time (and per unit of area for the spatial–temporal frequency). Ref. [34] proposed a method to derive the fragment release frequency from the failure frequency.
- -
- Event passage frequency: the number of rock fall events that pass through a given location, per unit of time (and per unit of length for the spatial–temporal frequency). In other words, it is the number of rock fall events, at least one fragment of which passes through the given location. The spatial–temporal passage frequency allows one to derive the passage frequency at any location according to its width, measured perpendicularly to the movement direction [22].
- -
- Fragment passage frequency: the number of rock fragments that pass through a given area or location, per unit of time (and per unit of length for the spatial–temporal frequency).
- -
- Fragment deposit or landing frequency [22,33]: the number of rock fragments that stop in a given area, per unit of time (and per unit of area for the spatial–temporal frequency).
Remark: The fragment passage frequency is higher than the event passage frequency, particularly when breakage occurs [44]. Which one of these frequencies is the most relevant depends on the type of consequence that is considered. As pointed out by [48], the passage frequency can be obtained either directly from an inventory of the rockfall events or fragments having reached the considered area during an observation period, or indirectly by combining a release frequency analysis and a propagation analysis.
3.3.2. Rockfall Event Inventory
The volume of a rockfall event can be assessed by measuring the deposited fragments after the event or by comparing digital models of the cliff before and after the event (topographical inventory). An example of topographical inventory using diachronic terrestrial laser scanning is given in Figure 3. Ref. [49] showed that the event volumes may change depending on the observation window. A single scar identified between two measurements can be the result of not a single event but multiple successive smaller events. This implies that a rockfall event must be defined by a time interval.

Figure 3.
Detection of rockfalls with diachronic terrestrial laser scanning. Up: 3D view of the cliff. Red and green points are detected rockfalls. Red perimeters are smooth surfaces without rockfalls. Down: Photo of the cliff [46].
Different definitions of a rockfall event can be proposed. From a mechanical point of view, it can be defined as the fall, rolling, and bouncing of rock fragments resulting from the detachment and the fragmentation of the same rock compartment, or resulting from the same triggering factor. From a practical point of view, it can be defined as the fall, rolling, and bouncing of rock fragments whose times of occurrence cannot be distinguished according to the detection method. In the case of continuous monitoring (seismic or topographic) or when there are witnesses, the time interval of an event can be defined to the second or the minute. In cases of discontinuous monitoring, the precision is the measuring interval, which ensues that distinct events (from a mechanical point of view) may be mixed in a unique event.
The larger their volume is, the more seldom the events are. To assess the spatial–temporal frequency of the biggest rockfall events, one must consider a long period of time and a large area. Ref. [50] analyzed rock avalanches bigger than 20 million m3 that occurred in different regions during the post-glacial period and calculated spatial–temporal frequencies. One of the oldest known terrestrial rockfalls on Earth was dated to 1.2 billion years [51], but it is difficult to assess rockfall frequency for periods older than the post-glacial period.
3.3.3. Rockfall Fragment Inventory
A rock fragment inventory allows one to assess the fragment landing frequency. The authors in [22] assessed this frequency by counting boulders in strip-like areas along the contour lines and then derived the boulder passage frequency by integrating the landing frequency over an influence area. Ref. [52] suggested counting boulders in homogenous strip-like areas along the reach or shadow angle contours rather than elevation contours, defining the reach angle from the cliff crest. A rock fragment inventory can help to define a design volume. A rock fragment survey allows one to measure the volume of the fragments, but the time during which the fragment falls have occurred may be unknown. Inversely, the observation of damages on trees [53,54,55] allows one to date the impacts, but there is large uncertainty of the block volumes.
3.3.4. Volume–Frequency Relation
As the frequency is strongly dependent on the volume (and of the energy for the passage frequency), the volume (or energy)–frequency relation is usually analyzed by showing the cumulative (or non-cumulative) frequency as a function of the minimal volume considered (or of the volume interval). The relation between the energy and the passage frequency (or the return period) can be called the hazard curve [56]. Ref. [29] considered also the fly height, introducing a rockfall hazard vector, the components of which are the passage frequency, the maximum velocity, and the maximum fly height.
The relation between the volume and the rockfall (or fragment) release frequency is often fitted by a mathematical law, most often a power law (for example, [57,58]). Examples of rockfall volume–frequency relations are given in Figure 4. The extrapolation of this law allows one to estimate the frequency for volumes outside the range of the observed volumes, but in the domain of validity of the law. The question arises of the maximal possible volume of a rockfall event (or a rock fragment) to be considered in the hazard assessment, which is usually higher than the maximal observed volume. This was discussed by [59].
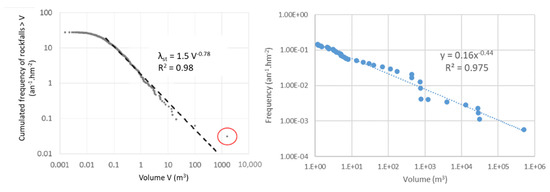
Figure 4.
Examples of rockfall volume–release frequency relations. Left: bedded Sequanian limestone (topographical inventory). Right: massive Urgonian limestone (topographical inventory under 1000 m3, historical inventory over 1000 m3). The spatial–temporal frequency of rockfalls bigger than 1 m3 is at about 10 times smaller in massive limestone than in bedded limestone. However, the frequency of rockfalls bigger than 1000 m3 is higher in massive limestone.
3.3.5. Derivation of the Passage Frequency from the Release Frequency through Propagation Analysis
In the case of a diffuse hazard, a rockfall of unknown volume can start from any point of a homogenous release area. The spatial–temporal rockfall release frequency depends on the rockfall volume, and the observed or modelled volume–frequency relation determines the volumes of the compartments that must be released from each source cell of the digital cliff model to simulate the rockfalls occurring in a given fictive period (simulated period), assuming a constant release frequency (Figure 2a). This period should be long enough for a sufficient number of rockfalls to be simulated in each source cell for each volume class. In practice, as the periods needed for different volume classes are different (periods needed for big rockfalls are longer), the passage frequencies are often determined separately for different volume classes and then are summed to obtain the total passage frequency. The choice of the class limit values falls within the expert judgement. For a given rockfall volume class having a failure frequency per cell λfc, the length Ts of the simulated period is the number of rockfalls simulated per source cell Nsc divided by λfc.
For a rockfall volume class, an in situ rock compartment is made up of blocks with an in situ block size distribution (IBSD) that determines the number of blocks to be launched for this volume class to simulate one rockfall event (Figure 2b). For a given rockfall volume class, the simulations can give different parameters for each cell of the slope.
The total number of blocks passing through the cell (Nbc) divided by the length of the simulated period (Ts) gives the fragment passage frequency per cell.
Note that the passages of a fragment are not independent events, as a unique rockfall event often produces many fragments. The number of simulations with Nbc ≥ 1 (Nsc1) divided by the length of the simulated period (Ts) gives the event passage frequency per cell.
The proportion Nsc1/Nsc is the probability of propagation in a cell, given that a rockfall start from each source cell. Note that the frequencies per cell depend on the cell size and must be divided by the cell width to derive a usable spatial–temporal passage frequency.
Considering an event release frequency λf for a given source area comprising Nc cells, Ts can be written as follows:
In this case, the fragment and event passage frequencies can be written as follows:
where Nb is the number of blocks passing through a line of interest, and Ns1 is the number of simulations with Nb ≥ 1. These passage frequencies can also be determined considering a minimal value of the fragment volume or energy or a minimal value of the energy of all blocks passing through the cell. The maximum kinetic energy or the maximum passing height of each block passing through a cell can be calculated, and their distribution functions can be displayed.
Figure 5 shows a simple illustration of the method. The source area is divided into two cells (Nc = 2). The failure frequency per cell (λfc) is one event per year. Two simulations are carried out for the two cells (Nsc = 2), simulating a 2-year period (Ts = 2 years). Each rockfall event produces three blocks. Another presentation of diffuse rockfall hazard assessment is given in this Special Issue by [60].
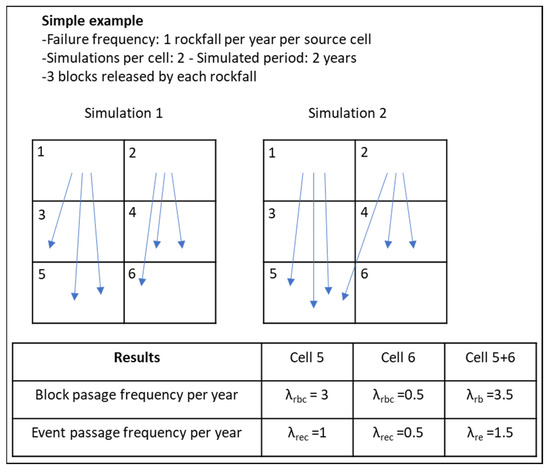
Figure 5.
Simulation of 2 years of rockfalls from 2 source cells and annual frequencies obtained.
4. Rockfall Risk
The definition of risk given by [1] is: “A measure of the probability and severity of an adverse effect to health, property or the environment. Risk is often estimated by the product of probability of a phenomenon of a given magnitude times the consequences. However, a more general interpretation of risk involves a comparison of the probability and consequences in a non-product form. For Quantitative Risk Assessment the use of the landslide intensity is recommended.” In addition to the product of probability times the consequences, the risk can be described by the annual probability of different levels of loss [1,61].
In the case of rockfalls, the risk is often analyzed considering different volumes and energies, which have different probabilities (or frequencies). A method for rockfall quantitative risk assessment is described by [2]. The main concepts are recalled below.
Different types of risk can be considered [1].
- Individual risk to life (or individual human risk): “The annual probability that a particular life will be lost”.
- Societal risk to life (or societal human risk): “The risk of multiple fatalities or injuries in society as a whole”, which can be expressed as the annual number of deaths.
- Non-human societal risk concerns “financial, environmental, and other losses”. The elements at risk can be “buildings and engineering works, economic activities, public services utilities, infrastructure and environmental features in the area potentially affected by landslides”.
4.1. Localized Hazard
4.1.1. Trivial Case of a Unique Block without Fragmentation
The risk for a given element at risk at a given location can be expressed as follows:
Pp is the passage probability for the period of interest of a location whose width is the width of the element at risk plus the width of a rock fragment if a lumped mass model is used for rockfall modelling.
Pt is the temporal probability of the element at risk. This probability is 1 for a static element at risk. For a moving element at risk (person or vehicle), it is the proportion of the time when it is in the considered location. For a vehicle moving perpendicularly to the trajectory of the block, the exposure is [57,62]
Lm is the length of the vehicle, Vm is its velocity, Wb is the width of the block, and Fv is the passage frequency of the vehicle considered. If the societal risk is considered, Fv is the traffic (number of vehicles per time unit).
V is the vulnerability or lethality of the element at risk or its degree of loss (a number between 0 and 1). It depends mainly of the energy of the block. The relation between the energy and the vulnerability can be called the vulnerability curve 35.
C is the value of the element at risk.
4.1.2. Case of a Rock Compartment with Fragmentation
In this case, the element at risk can be impacted by several blocks with different energies. The more relevant passage probability to consider is the probability that the total energy of the blocks reaching the considered location belongs to an energy class. The risks corresponding to different energies can be added because the corresponding events are exclusive for a unique rock compartment. The total risk is
Pp(Ej) is the probability that the total energy of the blocks passing through the considered location belongs to the interval (Ej,Ej+1), and V(Ej) is the vulnerability of the element at risk for this energy interval.
4.1.3. Case of Several Rock Compartments
In this case, the element at risk may be damaged several times, and the relevant risk depends on whether it is soon replaced or repaired when damage occurs (its value remains constant) or it is not repaired (its value has decreased) or it is removed. If the rockfall events are independent of each other and if the element at risk is replaced or repaired when a damage occurs, the damages can accumulate, and the risks corresponding to the different compartments can be added [24]. This ensues that the risk can be higher than the value of the element at risk.
However, if only the first damage is considered (the element at risk is removed or abandoned), the risks corresponding to the different compartments cannot be added (otherwise the total risk could be higher than the value of the element at risk). In this case, the passage probability for each class of energy (and corresponding vulnerability and damage) can be determined. For the energy class j, it is
N is the number of potential rockfalls, Ppij is the probability that the compartment i reaches the considered location with an energy of class j, and Pt is the temporal probability of the element at risk at the considered location. The risks corresponding to the different classes of energy cannot be added as in Equation (16), because the corresponding events are not exclusive (a compartment can produce an energy of class j and another one can produce an energy of a different class). The total risk is
When the passage probabilities or the temporal probabilities are sufficiently low (less than 0.01 according to [63]), the risks corresponding to different compartments or to different energy classes can be added, simplifying Equations (18) and (19). The case of non-independent events was discussed by [24].
4.2. Diffuse Hazard
Two approaches can be used according to the risk management policy. When the element at risk is replaced or repaired after being damaged, the event passage frequency should be considered to estimate the annualized loss (for example, when a road remains open after a car has been hit or when a protective structure is repaired). When the element at risk is not replaced or repaired, the probability that it is impacted by at least one rockfall should be considered (for example, when an impacted house is not rebuilt). Note that if the annual frequency is small, it is close to the annual probability. In what follows, we will consider the event passage frequency. The passage frequency can be determined either for a location whose width is the width of the element at risk [35] plus the width of a rock fragment if a lumped mass model is used for rockfall modelling, or for a wider area of interest [62,64]. In this case, the hazard is homogenized, and the more critical locations may not be detected.
In the first case, the annual risk (or annualized loss) for a given element at risk in the considered location is
λp is the passage frequency of the events for which the total energy of all the blocks reaching the considered location belongs to the interval (Ej, Ej+1). Alternatively, volume intervals can also be considered. Pt is the temporal probability of the element at risk to be in the considered location (Equation (17)). V(Ej) is the vulnerability of the element at risk for this energy interval.
In the second case, the temporal probability for a vehicle is
where Wa is the width of the area of interest. As the passage frequency refers to an area of interest that is much wider than the element at risk, the probability that a rockfall reaching this area impacts the element at risk must be introduced [59]. Refs. [57,59] named this probability the spatial probability (of an event reaching the element at risk given that it occurs in the area of interest). It can be expressed as
We is the width of an event in the area of interest. Note that [59] neglected the length of the element at risk. For a vehicle crossing the whole area of interest, the risk is then
The product PtPs can be called the temporal spatial probability or the exposure.
Ref. [44] pointed out that the rockfall front may be continuous or consist of scattered blocks. In the latter case, the width of an event must be replaced by the sum of the widths of the scattered blocks. An example of calculation of human risk for a 195 m long trail section exposed to a diffuse rockfall hazard is given in Table 1.

Table 1.
Example of calculation of human risk for a 195 m long trail section exposed to a diffuse rockfall hazard (modified from [44]).
5. Conclusions
Many concepts and descriptors can be used for a quantitative characterization of rockfall hazard and risk according to the context of the study (level of detail, data available, nature of the element at risk, purpose of the analysis, risk management). In this paper, various concepts and descriptors are precisely defined, and methods for quantitative hazard and risk assessment are suggested.
For localized hazards, a theoretical approach for quantitative hazard and risk assessment is described, even though the assessment of the failure probability must be based on expert judgement.
For a diffuse hazard, quantitative hazard and risk assessment is usually based on a rockfall inventory that gives a failure frequency, which is then combined with a propagation analysis to derive the temporal frequency for a given location to be reached or for a given element at risk to be impacted.
The relevant method to assess the risk depends on whether the element at risk is soon replaced or repaired when a damage occurs (its value remains constant) or it is not repaired (its value has decreased) or it is removed.
As many concepts and descriptors can be used for quantitative rockfall hazard and risk analyses, the authors recommend that those be precisely defined in future articles or reports.
Using modern surveying techniques should enhance the description of the rock wall structure, the identification of potential failures, and the assessment of rockfall frequency.
A better description of the rock wall structure should favor a more realistic modelling of the failure process and should allow for a better assessment of the maximal possible rockfall volume and of the in situ block size distribution. Progress is also needed in fragmentation modelling.
Funding
This research received no external funding
Acknowledgments
We are grateful for the financial support by the French research project C2ROP.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Fell, R.; Corominas, J.; Bonnard, C.; Cascini, L.; Leroi, E.; Savage, W.Z. Guidelines for landslide susceptibility, hazard and risk zoning for land use planning. Eng. Geol. 2008, 102, 85–98. [Google Scholar] [CrossRef]
- Corominas, J.; Mavrouli, O. Rockfall quantitative risk assessment. In Rockfall Engineering; Lambert, S., Nicot, F., Eds.; ISTE: London, UK, 2011; pp. 255–301. [Google Scholar]
- Volkwein, A.; Schellenberg, K.; Labiouse, V.; Agliardi, F.; Berger, F.; Bourrier, F.; Dorren, L.K.A.; Gerber, W.; Jaboyedoff, M. Rockfall characterisation and structural protection—A review. Nat. Hazards Earth Syst. Sci. 2011, 11, 2617–2651. [Google Scholar] [CrossRef]
- Crosta, G.B.; Agliardi, F.; Frattini, P.; Lari, S. Key Issues in Rock Fall Modeling, Hazard and Risk Assessment for Rockfall Protection. In Engineering Geology for Society and Territory—Volume 2; Lollino, G., Giordan, D., Crosta, G.B., Corominas, J., Azzam, R., Wasowski, J., Sciarra, N., Eds.; Springer International Publishing: Berlin/Heidelberg, Germany, 2015; pp. 43–58. [Google Scholar]
- Scavia, C.; Barbero, M.; Castelli, M.; Marchelli, M.; Peila, D.; Torsello, G.; Vallero, G. Evaluating Rockfall Risk: Some Critical Aspects. Geosciences 2020, 10, 98. [Google Scholar] [CrossRef]
- Varnes, D.J. Slope movement types and processes. In Special Report 176: Landslides: Analysis and Control; Schuster, R.L., Krizek, R.J., Eds.; TRB, National Research Council: Washington, DC, USA, 1978; pp. 11–33. [Google Scholar]
- Cruden, D.M.; Varnes, D.J. Landslide types and processes. In Landslides, Investigation and Mitigation; Turner, A.K., Schuster, R.L., Eds.; Transport Research Board, National Research Council: Washington, DC, USA, 1996. [Google Scholar]
- Hungr, O.; Leroueil, S.; Picarelli, L. The Varnes classification of landslide types, an update. Landslides 2014, 11, 167–194. [Google Scholar] [CrossRef]
- Bourrier, F.; Dorren, L.; Hungr, O. The use of ballistic trajectory and granular flow models in predicting rockfall propagation. Earth Surf. Process. Landf. 2013, 38, 435–440. [Google Scholar] [CrossRef]
- Turner, A.K.; Jayaprakash, G.P. Introduction. In Rockfall Characterization and Control; Turner, A.K., Schuster, R.L., Eds.; Transportation Research Board, National Academy of Sciences: Washington, DC, USA, 2012; pp. 3–20. [Google Scholar]
- Hoek, E.; Bray, J.W. Rock Slope Engineering; The Institution of Mining and Metallurgy: London, UK, 1981. [Google Scholar]
- Wyllie, D.C. Rock Slope Engineering, Civil Applications; CRC Press: Boca Raton, FL, USA, 2017; p. 568. [Google Scholar]
- Lu, P.; Latham, J.P. Developments in the Assessment of In-situ Block Size Distributions of Rock Masses. Rock Mech. Rock Eng. 1999, 32, 29–49. [Google Scholar] [CrossRef]
- Ruiz-Carulla, R.; Corominas, J.; Mavrouli, O. Comparison of block size distribution in rockfalls. In Landslides and Engineered Slopes. Experience, Theory and Practice; Associazione Geotecnica Italiana: Naples, Italy, 2016. [Google Scholar]
- Jaboyedoff, M.; Dudt, J.P.; Labiouse, V. An attempt to refine rockfall hazard zoning based on the kinetic energy, frequency and fragmentation degree. Nat. Hazards Earth Syst. Sci. 2005, 5, 621–632. [Google Scholar] [CrossRef]
- Dorren, L.K.A. A review of rockfall mechanics and modelling approaches. Prog. Phys. Geogr. Earth Environ. 2003, 27, 69–87. [Google Scholar] [CrossRef]
- Wang, Y.; Tonon, F. Discrete Element Modeling of Rock Fragmentation upon Impact in Rock Fall Analysis. Rock Mech. Rock Eng. 2011, 44, 23–35. [Google Scholar] [CrossRef]
- Matas, G.; Lantada, N.; Corominas, J.; Gili, J.A.; Ruiz-Carulla, R.; Prades, A. RockGIS: A GIS-based model for the analysis of fragmentation in rockfalls. Landslides 2017, 14, 1565–1578. [Google Scholar] [CrossRef]
- Richefeu, V.; Villard, P. Modeling Gravity Hazards from Rockfalls to Landslides; ISTE Press Ltd.: London, UK, 2016. [Google Scholar]
- Scheidegger, A.E. On the prediction of the reach and velocity of catastrophic landslides. Rock Mech. 1973, 5, 231–236. [Google Scholar] [CrossRef]
- Heim, A. Bergsturz und Menschenleben; Fretz und Wasmuth Verlag: Zürich, Switzerland, 1932; p. 218. [Google Scholar]
- Evans, S.G.; Hungr, O. The assessment of rockfall hazard at the base of talus slopes. Can. Geotech. J. 1993, 30, 620–636. [Google Scholar] [CrossRef]
- Hantz, D.; Rossetti, J.-P.; Servant, F.; D’Amato, J. Etude de la distribution des blocs dans un éboulement pour l’évaluation de l’aléa. In Rock Slope Stability 2014; Comité français de Mécanique des Roches: Marrakesh, Morocco, 2014. [Google Scholar]
- Fell, R.; Ho, K.; Lacasse, S.; Leroi, E. A Framework for Landslide Risk Assessment and Management. In Landslide Risk Management; Hungr, O., Fell, R., Couture, R., Eberhardt, E., Eds.; Taylor and Francis: Vancouver, BC, Canada, 2005; pp. 3–26. [Google Scholar]
- Durville, J.-L. Quelques remarques sur l’emploi des probabilités dans le domaine des risques naturels: Cas des mouvements de terrain. Bull. Des Lab. Ponts Chaussées 2004, 249, 3–17. [Google Scholar]
- Rat, M. Optimisation de la gestion de la route du littoral à la Réunion vis-à-vis du risque de chutes de blocs. Bull. Des Lab. Ponts Chaussées 2006, 263–264, 43–52. [Google Scholar]
- Leroueil, S.; Locat, J. Slope movements—Geotechnical characterization, risk assessment and mitigation. In Geotechnical Hazards; Maric, B., Lisac, L., Szavits-Nossan, A., Eds.; Balkema: Rotterdam, The Netherlands, 1998; pp. 95–106. [Google Scholar]
- Jaboyedoff, M.; Baillidard, F.; Hantz, D.; Heidenreich, B.; Mazzoccola, D. Terminologie. In Prévention des Mouvements de VERSANTS et des Instabilités de Falaises; Carere, K., Ratto, S., Zanolini, F., Eds.; Programme Interreg IIc: Aosta, Italy, 2001; pp. 48–57. [Google Scholar]
- Crosta, G.B.; Agliardi, F. A methodology for physically based rockfall hazard assessment. Nat. Hazards Earth Syst. Sci. 2003, 3, 407–422. [Google Scholar] [CrossRef]
- Corominas, J.; van Westen, C.; Frattini, P.; Cascini, L.; Malet, J.P.; Fotopoulou, S.; Catani, F.; Van Den Eeckhaut, M.; Mavrouli, O.; Agliardi, F.; et al. Recommendations for the quantitative analysis of landslide risk. Bull. Eng. Geol. Environ. 2014, 73, 209–263. [Google Scholar] [CrossRef]
- Moos, C.; Fehlmann, M.; Trappmann, D.; Stoffel, M.; Dorren, L. Integrating the mitigating effect of forests into quantitative rockfall risk analysis—Two case studies in Switzerland. Int. J. Disaster Risk Reduct. 2018, 32, 55–74. [Google Scholar] [CrossRef]
- Farvacque, M.; Lopez-Saez, J.; Corona, C.; Toe, D.; Bourrier, F.; Eckert, N. How is rockfall risk impacted by land-use and land-cover changes? Insights from the French Alps. Glob. Planet. Chang. 2019, 174, 138–152. [Google Scholar] [CrossRef]
- van Veen, M.; Hutchinson, D.J.; Bonneau, D.A.; Sala, Z.; Ondercin, M.; Lato, M. Combining temporal 3-D remote sensing data with spatial rockfall simulations for improved understanding of hazardous slopes within rail corridors. Nat. Hazards Earth Syst. Sci. 2018, 18, 2295–2308. [Google Scholar] [CrossRef]
- Hantz, D.; Rossetti, J.-P.; Valette, D.; Bourrier, F. Quantitative rockfall hazard assessment at the Mont Saint-Eynard (French Alps). In Proceedings of the 6th Interdisciplinary Workshop on Rockfall Protection, Barcelona, Spain, 22–24 May 2017. [Google Scholar]
- Agliardi, F.; Crosta, G.B.; Frattini, P. Integrating rockfall risk assessment and countermeasure design by 3D modelling techniques. Nat. Hazards Earth Syst. Sci. 2009, 9, 1059–1073. [Google Scholar] [CrossRef]
- Macciotta, R.; Hendry, M.; Cruden, D.M.; Blais-Stevens, A.; Edwards, T. Quantifying rock fall probabilities and their temporal distribution associated with weather seasonality. Landslides 2017, 14, 2025–2039. [Google Scholar] [CrossRef]
- Macciotta, R.; Martin, C.D.; Morgenstern, N.R.; Cruden, D.M. Development and application of a quantitative risk assessment to a very slow moving rock slope and potential sudden acceleration. Landslides 2016, 13, 765–785. [Google Scholar] [CrossRef]
- Hantz, D.; Vengeon, J.M.; Dussauge-Peisser, C. An historical, geomechanical and probabilistic approach to rock-fall hazard assessment. Nat. Hazards Earth Syst. Sci. 2003, 3, 693–701. [Google Scholar] [CrossRef]
- Wang, X.; Frattini, P.; Crosta, G.B.; Zhang, L.; Agliardi, F.; Lari, S.; Yang, Z. Uncertainty assessment in quantitative rockfall risk assessment. Landslides 2014, 11, 711–722. [Google Scholar] [CrossRef]
- Federico, A.; Popescu, M.; Murianni, A. Temporal prediction of landslide occurrence: A possibility or a challenge? Ital. J. Eng. Geol. Environ. 2015, 1, 41–60. [Google Scholar]
- Bozzano, F.; Mazzanti, P.; Esposito, C.; Moretto, S.; Rocca, A. Potential of satellite InSAR monitoring for landslide Failure Forecasting. In Landslides and Engineered Slopes. Experience, Theory and Practice; Aversa, A.E., Ed.; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Carlà, T.; Farina, P.; Intrieri, E.; Botsialas, K.; Casagli, N. On the monitoring and early-warning of brittle slope failures in hard rock masses: Examples from an open-pit mine. Eng. Geol. 2017, 228, 71–81. [Google Scholar] [CrossRef]
- Scoppettuolo, M.R.; Cascini, L.; Babilio, E. Typical displacement behaviours of slope movements. Landslides 2020, 17, 1105–1116. [Google Scholar] [CrossRef]
- Corominas, J.; Matas, G.; Ruiz-Carulla, R. Quantitative analysis of risk from fragmental rockfalls. Landslides 2019, 16, 5–21. [Google Scholar] [CrossRef]
- Agliardi, F.; Crosta, G.B. High resolution three-dimensional numerical modelling of rockfalls. Int. J. Rock Mech. Min. Sci. 2003, 40, 455–471. [Google Scholar] [CrossRef]
- Guerin, A.; D’amato, J.; Hantz, D.; Rossetti, J.-P.; Jaboyedoff, M. Investigating rockfall frequency using Terrestrial Laser Scanner. In Proceedings of the Vertical Geology Conference 2014, Lausanne, Switzerland, 6–7 February 2014; University of Lausanne, Switzerland: Lausanne, Switzerland, 2014. [Google Scholar]
- D’Amato, J.; Guerin, A.; Hantz, D.; Rossetti, J.P.; Baillet, L.; Mariscal, A.; Jaboyedoff, M. Influence of Geological and Meteorological Factors on the Frequency of Rockfalls. In Proceedings of the ISRM Regional Symposium—EUROCK 2015, Salzburg, Austria, 7–10 October 2010; International Society for Rock Mechanics and Rock Engineering: Salzburg, Austria, 2015; p. 6. [Google Scholar]
- Roberds, W. Estimating temporal and spatial variability and vulnerability. In Landslide Risk Management; Hungr, O., Fell, R., Couture, R., Eberhardt, E., Eds.; Taylor and Francis: London, UK, 2005; pp. 129–158. [Google Scholar]
- Williams, J.G.; Rosser, N.J.; Hardy, R.J.; Brain, M.J. The Importance of Monitoring Interval for Rockfall Magnitude-Frequency Estimation. J. Geophys. Res. Earth Surf. 2019, 124, 2841–2853. [Google Scholar] [CrossRef]
- Hungr, O.; Evans, S.G. The Occurrence and Classification of Massive Rock Slope Failure. Felsbau 2004, 22, 16–23. [Google Scholar]
- Killingback, Z.; Holdsworth, R.E.; Walker, R.J.; Nielsen, S.; Dempsey, E.; Hardman, K. A bigger splat: The catastrophic geology of a 1.2-b.y.-old terrestrial megaclast, northwest Scotland. Geology 2021, 49, 180–184. [Google Scholar] [CrossRef]
- Hantz, D.; Colas, B. Caractérisation de L’aléa Éboulement Rocheux-Etat de L’art; CEREMA: Bron, France, 2020; p. 64. [Google Scholar]
- Stoffel, M.; Corona, C. Dendroecological Dating of Geomorphic Disturbance in Trees. Tree Ring Res. 2014, 70, 3–20. [Google Scholar] [CrossRef]
- Trappmann, D.; Stoffel, M. Counting scars on tree stems to assess rockfall hazards: A low effort approach, but how reliable? Geomorphology 2013, 180–181, 180–186. [Google Scholar] [CrossRef]
- Trappmann, D.; Stoffel, M. Visual dating of rockfall scars in Larix decidua trees. Geomorphology 2015, 245, 62–72. [Google Scholar] [CrossRef]
- Abbruzzese, J.M.; Labiouse, V. New Cadanav methodology for quantitative rock fall hazard assessment and zoning at the local scale. Landslides 2014, 11, 551–564. [Google Scholar] [CrossRef]
- Hungr, O.; Evans, S.; Hazzard, J. Magnitude and frequency of rock falls and rock slides along the main transportation corridors of southwestern British Columbia. Can. Geotech. J. 1999, 36, 224–238. [Google Scholar] [CrossRef]
- Dussauge-Peisser, C.; Helmstetter, A.; Grasso, J.R.; Hantz, D.; Desvarreux, P.; Jeannin, M.; Giraud, A. Probabilistic approach to rock fall hazard assessment: Potential of historical data analysis. Nat. Hazards Earth Syst. Sci. 2002, 2, 15–26. [Google Scholar] [CrossRef]
- Mavrouli, O.; Corominas, J. Evaluation of Maximum Rockfall Dimensions Based on Probabilistic Assessment of the Penetration of the Sliding Planes into the Slope. Rock Mech. Rock Eng. 2020, 53, 2301–2312. [Google Scholar] [CrossRef]
- Abbruzzese, J.M.; Labiouse, V. New Cadanav Methodology for Rock Fall Hazard Zoning Based on 3D Trajectory Modelling. Geosciences 2020, 10, 434. [Google Scholar] [CrossRef]
- Farvacque, M.; Eckert, N.; Bourrier, F.; Corona, C.; Lopez-Saez, J.; Toe, D. Quantile-based individual risk measures for rockfall-prone areas. Int. J. Disaster Risk Reduct. 2020, 53, 101932. [Google Scholar] [CrossRef]
- Nicolet, P.; Jaboyedoff, M.; Cloutier, C.; Crosta, G.B.; Lévy, S. Brief communication: On direct impact probability of landslides on vehicles. Nat. Hazards Earth Syst. Sci. 2016, 16, 995–1004. [Google Scholar] [CrossRef]
- Leroi, E.; Bonnard, C.; Fell, R.; McInnes, R. Risk assessment and management. In Landslide Risk Management; Hungr, O., Fell, R., Couture, R., Eberhardt, E., Eds.; Taylor and Francis: London, UK, 2005; pp. 159–198. [Google Scholar]
- Bründl, M.; Romang, H.E.; Bischof, N.; Rheinberger, C.M. The risk concept and its application in natural hazard risk management in Switzerland. Nat. Hazards Earth Syst. Sci. 2009, 9, 801–813. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).