Introducing Uncertainty in Risk Calculation along Roads Using a Simple Stochastic Approach
Abstract
1. Introduction
2. Model Data
3. Introducing Uncertainty into Risk Calculation
4. Results
5. Discussion and Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wieczorek, G.F.; Nishenko, S.P.; Varnes, D.J. Analysis of rock falls in the Yosemite Valley, California. In Proceedings of the 35th US Symposium on Rock Mechanics (USRMS), Reno, NV, USA, 5–7 June 1995; pp. 85–89. [Google Scholar]
- Hovius, N.; Allen, P.A.; Stark, C.P. Sediment flux from a mountain belt derived by landslide mapping. Geology 1997, 25, 231–234. [Google Scholar] [CrossRef]
- Dussauge, C.; Grasso, J.-R.; Helmstetter, A. Statistical analysis of rockfall volume distributions: Implications for rockfall dynamics. J. Geophys. Res. Solid Earth 2003, 108. [Google Scholar] [CrossRef]
- Hantz, D. Quantitative assessment of diffuse rock fall hazard along a cliff foot. Nat. Hazards Earth Syst. Sci. 2011, 11, 1303–1309. [Google Scholar] [CrossRef]
- Hungr, O.; Evans, S.G.; Hazzard, J. Magnitude and frequency of rock falls and rock slides along the main transportation corridors of southwestern British Columbia. Can. Geotech. J. 1999, 36, 224–238. [Google Scholar] [CrossRef]
- Hoek, E. Practical Rock Engineering. Available online: https://www.rocscience.com/learning/hoeks-corner/course-notes-books (accessed on 16 March 2021).
- Corominas, J.; van Westen, C.; Frattini, P.; Cascini, L.; Malet, J.P.; Fotopoulou, S.; Catani, F.; Van Den Eeckhaut, M.; Mavrouli, O.; Agliardi, F.; et al. Recommendations for the quantitative analysis of landslide risk. Bull. Eng. Geol. Environ. 2014, 73, 209–263. [Google Scholar] [CrossRef]
- Wyllie, D.C. Rock Slope Engineering: Civil Applications, 5th ed.; CRC Press: Boca Raton, FL, USA; London, UK; New York, NY, USA, 2018; p. 568. [Google Scholar]
- Dai, F.C.; Lee, C.F.; Ngai, Y.Y. Landslide risk assessment and management: An overview. Eng. Geol. 2002, 64, 65–87. [Google Scholar] [CrossRef]
- Nadim, F. Tools and Strategies for Dealing with Uncertainty in Geotechnics. In Probabilistic Methods in Geotechnical Engineering; Griffiths, D.V., Fenton, G.A., Eds.; Springer: Vienna, Austria, 2007; pp. 71–95. [Google Scholar]
- Wang, X.; Frattini, P.; Crosta, G.B.; Zhang, L.; Agliardi, F.; Lari, S.; Yang, Z. Uncertainty assessment in quantitative rockfall risk assessment. Landslides 2014, 11, 711–722. [Google Scholar] [CrossRef]
- Crosta, G.B.; Agliardi, F.; Frattini, P.; Lari, S. Key Issues in Rock Fall Modeling, Hazard and Risk Assessment for Rockfall Protection. In Engineering Geology for Society and Territory; Springer: Cham, Switzerland, 2015; Volume 2, pp. 43–58. [Google Scholar]
- Macciotta, R.; Martin, C.D.; Morgenstern, N.R.; Cruden, D.M. Quantitative risk assessment of slope hazards along a section of railway in the Canadian Cordillera—A methodology considering the uncertainty in the results. Landslides 2016, 13, 115–127. [Google Scholar] [CrossRef]
- Mitchell-Wallace, K.; Jones, M.; Hillier, J.; Foote, M. Natural Catastrophe Risk Management and Modelling—A Practitioner’s Guide; Wiley-Blackwell: Hoboken, NJ, USA, 2017; 536p. [Google Scholar]
- Nicolet, P.; Foresti, L.; Caspar, O.; Jaboyedoff, M. Shallow landslide’s stochastic risk modelling based on the precipitation event of August 2005 in Switzerland: Results and implications. Nat. Hazards Earth Syst. Sci. 2013, 13, 3169–3184. [Google Scholar] [CrossRef]
- Farvacque, M.; Eckert, N.; Bourrier, F.; Corona, C.; Lopez-Saez, J.; Toe, D. Quantile-based individual risk measures for rockfall-prone areas. Int. J. Disaster Risk Reduct. 2020, 53, 101932. [Google Scholar] [CrossRef]
- Haimes, Y.Y. Risk Modeling, Assessment, and Management, 4th ed.; Wiley: Hoboken, NJ, USA, 2015; 720p. [Google Scholar]
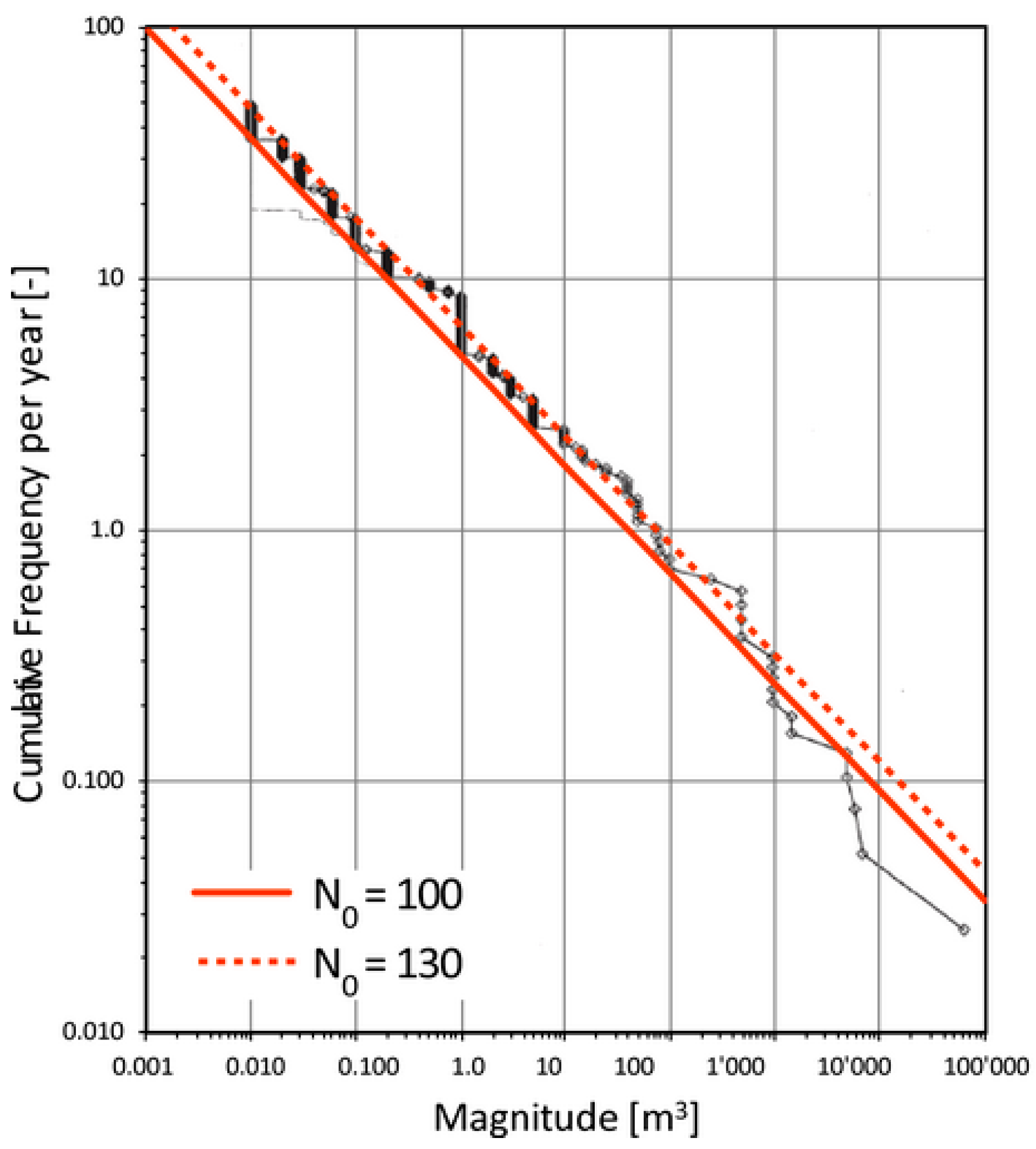
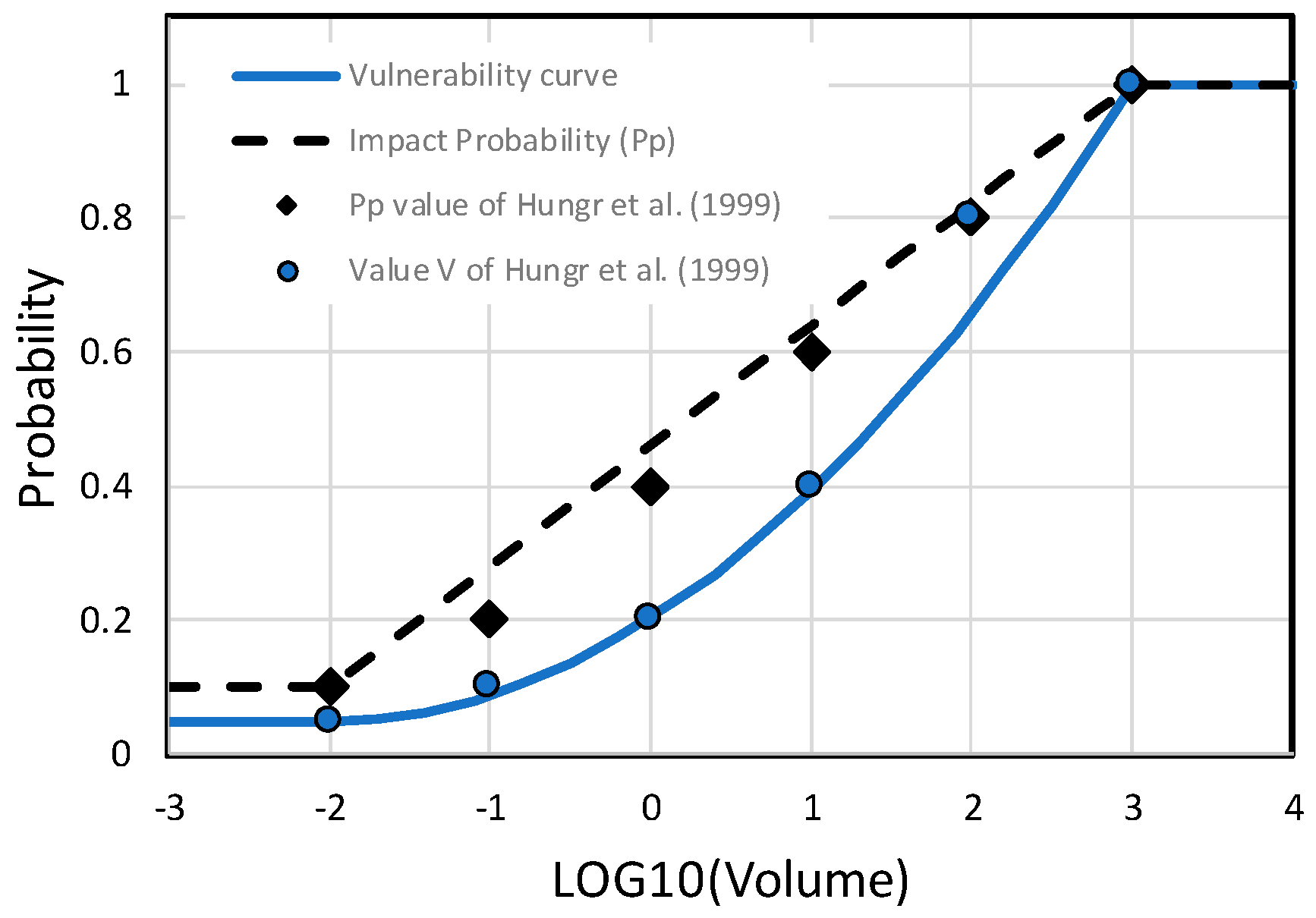
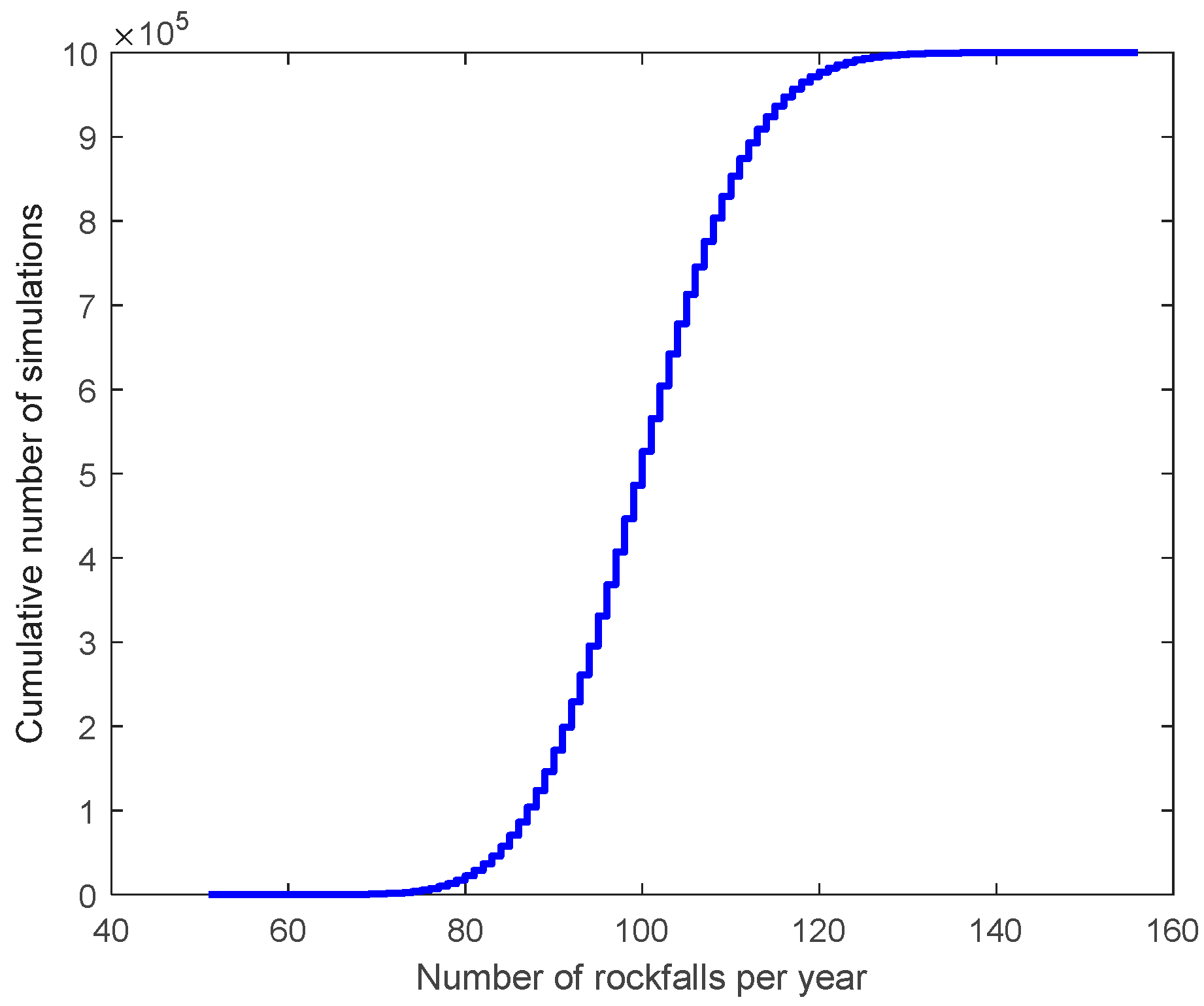
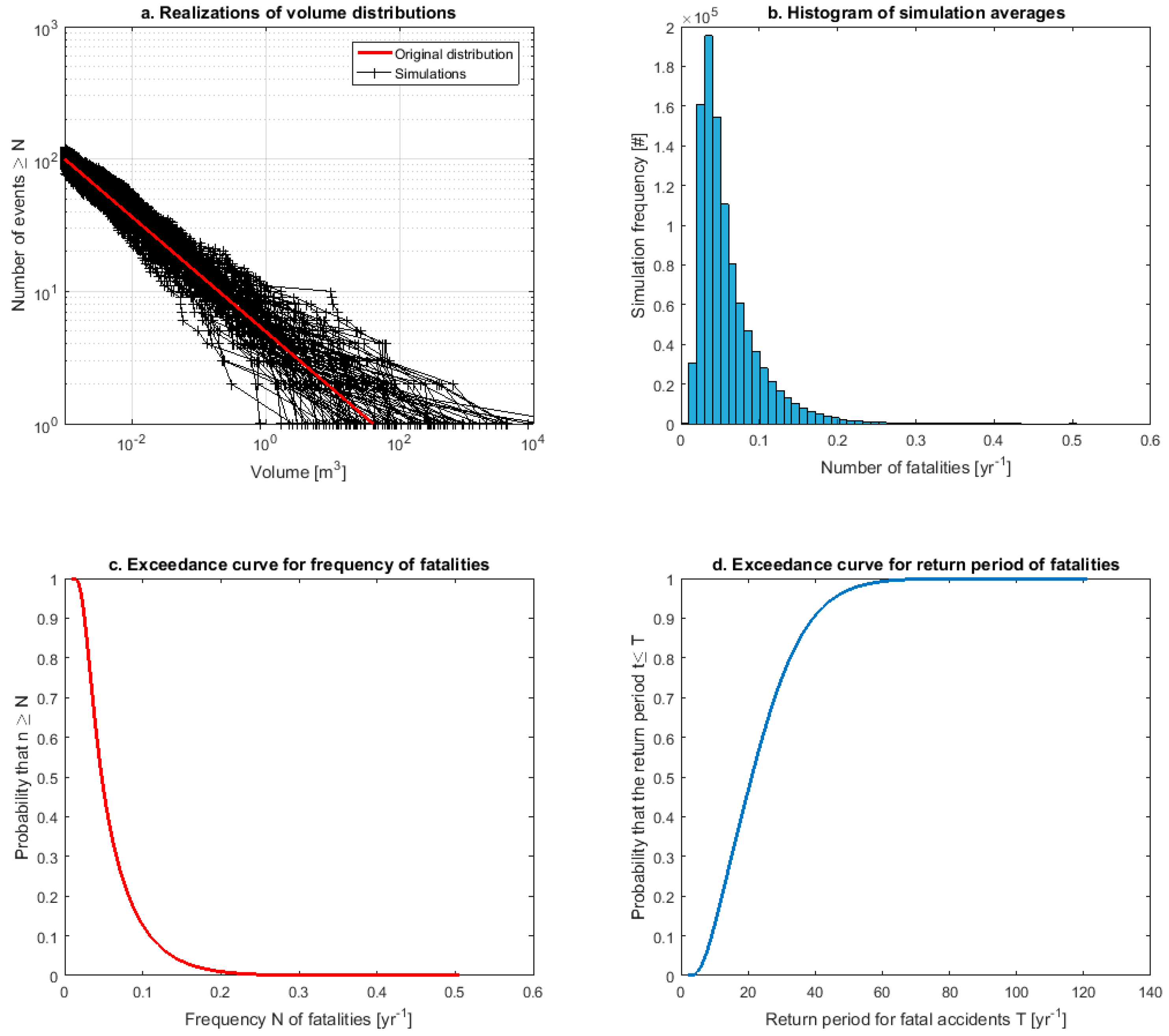
| Volume | 4.99 × Vol−0.434 | λr × fr | D~Vol(1/3) | Exp | Pp | V | H × Pp × Exp × V | 1/R |
|---|---|---|---|---|---|---|---|---|
| (m3) | (#/yr) | (#/yr) | (m) | (-) | (-) | (-) | (-) | (yr) |
| 0.001 | 100.000 | |||||||
| 0.010 | 36.813 | 63.187 | 0.2 | 0.0146 | 0.1 | 0.05 | 0.005 | 217.0 |
| 0.100 | 13.552 | 23.261 | 0.5 | 0.0154 | 0.2 | 0.1 | 0.007 | 139.9 |
| 1.0 | 4.989 | 8.563 | 1 | 0.0167 | 0.4 | 0.2 | 0.011 | 87.6 |
| 10 | 1.837 | 3.152 | 2 | 0.0193 | 0.6 | 0.5 | 0.018 | 54.9 |
| 100 | 0.676 | 1.160 | 5 | 0.0271 | 0.8 | 0.8 | 0.020 | 49.7 |
| 1000 | 0.249 | 0.427 | 10 | 0.0401 | 1.0 | 1.0 | 0.017 | 58.4 |
| 10,000 | 0.092 | 0.157 | 30 | 0.0922 | 1.0 | 1.0 | 0.014 | 69.0 |
| >10,000 | 0.092 | 50 | 0.1443 | 1.0 | 1.0 | 0.013 | 75.7 | |
| Total | 0.106 | 9.4 |
| Variables | Units (Remarks) | Minimum | Maximum |
|---|---|---|---|
| Debris width D | m | D/2 | 3D/2 |
| Vehicle speed vv | km/h | 57.5 | 102.5 |
| Number of vehicles Nv | Vehicles/day | 4500 | 5500 |
| Probability of impact or propagation at the vehicle location Pp | (-) (Integrated in the calculation; one order of magnitude of volume variability) | log10(V(d)) − 0.5 | log10(V(d)) + 0.5 |
| Vulnerability V(lethality) | idem | idem | idem |
| Thresholds | Frequency | Return Period T [Year] | |||
|---|---|---|---|---|---|
| Case | A | A | B | C | D |
| (events/year) | 1 occ. N0 = 100 | 1 occ. N0 = 130 | 1–2 occ. N0 = 100 | 1–2 occ. N0 = 130 | |
| Average | 0.059 | 16.8 | 13.0 | 11.2 | 8.6 |
| Minimum (max. T) | 0.010 | 103.3 | 80.9 | 75.4 | 48.6 |
| 97.50% | 0.020 | 51.2 | 35.4 | 34.8 | 24.1 |
| 95% | 0.022 | 45.6 | 31.8 | 31.0 | 21.6 |
| Median | 0.047 | 21.1 | 15.5 | 14.2 | 10.5 |
| 5% | 0.137 | 7.3 | 6.0 | 4.8 | 3.9 |
| 2.5 | 0.165 | 6.1 | 5.1 | 3.9 | 3.3 |
| Maximum (Min. T) | 0.603 | 1.7 | 1.6 | 1.2 | 1.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jaboyedoff, M.; Choanji, T.; Derron, M.-H.; Fei, L.; Gutierrez, A.; Loiotine, L.; Noel, F.; Sun, C.; Wyser, E.; Wolff, C. Introducing Uncertainty in Risk Calculation along Roads Using a Simple Stochastic Approach. Geosciences 2021, 11, 143. https://doi.org/10.3390/geosciences11030143
Jaboyedoff M, Choanji T, Derron M-H, Fei L, Gutierrez A, Loiotine L, Noel F, Sun C, Wyser E, Wolff C. Introducing Uncertainty in Risk Calculation along Roads Using a Simple Stochastic Approach. Geosciences. 2021; 11(3):143. https://doi.org/10.3390/geosciences11030143
Chicago/Turabian StyleJaboyedoff, Michel, Tiggi Choanji, Marc-Henri Derron, Li Fei, Amalia Gutierrez, Lidia Loiotine, François Noel, Chunwei Sun, Emmanuel Wyser, and Charlotte Wolff. 2021. "Introducing Uncertainty in Risk Calculation along Roads Using a Simple Stochastic Approach" Geosciences 11, no. 3: 143. https://doi.org/10.3390/geosciences11030143
APA StyleJaboyedoff, M., Choanji, T., Derron, M.-H., Fei, L., Gutierrez, A., Loiotine, L., Noel, F., Sun, C., Wyser, E., & Wolff, C. (2021). Introducing Uncertainty in Risk Calculation along Roads Using a Simple Stochastic Approach. Geosciences, 11(3), 143. https://doi.org/10.3390/geosciences11030143








