Theory of Effective Stress in Soil and Rock and Implications for Fracturing Processes: A Review

Abstract

The effective stress principle (ESP) plays a basic role in geology and engineering problems as it is involved in fundamental issues concerning strain and failure of rock and soil, as well as of other porous materials such as concrete, metal powders, biological tissues, etc. Although since its introduction in the 1920s the main ESP aspects have been unravelled and theoretically derived, these do not appear to have been always entirely perceived by many in the science community dealing with ESP-related topics but having little familiarity with the complex theories of porous media and poroelasticity. The purpose of this review is to provide a guidance for the reader who needs an updated overview of the different theoretical and experimental approaches to the ESP and related topics over the past century, with particular reference to geological fracturing processes. We begin by illustrating, after some introductive historical remarks, the basic theory underlying the ESP, based on theory of elasticity methods. Then the different ESP-related theories and experimental results, as well as main interpretations of rock jointing and fracturing phenomena, are discussed. Two main classical works are then revisited, and a rigorous ESP proof is derived. Such a proof is aimed at geologists, engineers and geophysicists to become more familiar with theories of porous media and poroelasticity, being based on the classical theory of elasticity. The final part of this review illustrates some still open issues about faulting and hydraulic fracturing in rocks.

1. Introduction

The effective stress principle (ESP), introduced by Terzaghi during the 1920s [1,2], is involved in fundamental issues concerning strain and failure of rock and soil, as well as of other porous materials such as concrete, metal powders, biological tissues, etc., as it allows one to predict the mechanical behaviour of saturated porous media. Based on his experimental data, Terzaghi stated that only a fraction of the total stress (σ) exceeding the pore-water pressure (p), which he called effective stress (σ’), is responsible for soil and rock strain and/or failure. On the other hand, at the same effective stress conditions, pore-water pressure (or neutral stress) magnitude has practically no influence on their stress–strain and/or failure behaviour.

The formulation proposed by Terzaghi [1,2] for the effective stress (ES) in one-dimensional form was:

σ’ = σ − p,

(1)

where σ’ denotes the effective stress, σ the total stress and p the pore water pressure or neutral stress. In terms of stress tensor components, the equivalent form is the following:

σ’_ij = σ_ij − δ_ij p,

where δij denotes the Kronecker delta. Here and in the following, the usual convention used by geologists of a positive sign for compressive stresses is adopted.

Such principle was introduced in the 1920s as an experimental law and the underlying theory was developed within less than one century. Since its experimental assessment, the effect of pore water pressure on rock strength and stress–strain behaviour, as well as the ESP, appeared controversial and has been object of long-standing debates (e.g., [3,4,5]); details about a heated debate between these authors has been reported by de Boer [6].

The understanding of ESP concept has been then rendered complicated as different formulations for ES have been proposed by various authors.

Fillunger [5], on theoretical grounds, derived the following ES law:

σ’ = σ − n p,

(2)

where n denotes rock or soil porosity (i.e., the ratio pore volume/rock volume).

Skempton [7] in a memorable work analysed, besides Terzaghi’s formulation Equation (1), also the following expressions for the ES by carrying out an extensive review of available formulations and experimental data in literature, in order to make clearer the theory:

σ’ = σ − (1 − a_c) p,

(3)

σ’ = σ − (1 − a_c tan ψ/tan φ’) p (for soil shear strength),

(4)

σ’ = σ − (1 − C_s/C) p (for volume change),

(5)

where a_c denotes the contact area ratio (i.e., the area of contact between the particles, per unit gross area of the material), φ the angle of shearing resistance, ψ the angle of intrinsic friction [7] and C_s and C the compressibility of the constituent material (i.e., nonporous, nonfractured rock/clast) and of rock or soil aggregate, respectively. We point out here as Skempton [7] opened its paper with the following sentence: “… it is of philosophical interest to examine the fundamental principles of effective stress, since it would seem improbable that an expression of the form (σ’ = σ − u), is strictly true…”.

In 1971 Nur and Byerlee [8] have provided a theoretical derivation of the Eq. 5, corroborated by experimental data and valid for stress–strain behaviour of rocks, in the following equivalent form:

σ’ = σ − (1 − K/K_s) p (for rock volume change),

where K and K_s are the bulk moduli of porous rock and solid rock (i.e., the inverse of C_s and C), respectively. Although their proof was rigorous, the authors pointed out several limits of their model, mainly related to the assumption of elastic linear behaviour of porous rock.

Suklje [9] theoretically derived the following form for ES:

σ’ = σ − (1 − (1 − n) (C_s/C)) p (for rock volume change),

(6)

which differs from Skempton’s as well as Nur and Byerlee’s formulation (Equation (5)) by the term (1 − n), i.e., the solid volume fraction.

Although it was recognised as some of these ES laws was in disagreement with experimental evidence (namely those given by Equations (2), (3) and (6), as explained in Section 3.1 and Section 4.1), various concerns remained about the scope of validity of the different ES formulations according to different basic assumptions.

The extensive work carried out by Biot along some decades [10,11,12,13,14,15,16,17] has widely developed the theory of Poroelasticity so providing relevant answers about the effect of pore pressure on rock and soil behaviour. Furthermore, already in the 1970s Auriault and Sanchez-Palencia [18,19,20] provided a theoretical treatise about saturated porous media that also explains the ESP.

Nevertheless, during the 1990s such principle appeared as still controversial. For instance, Oka [21] pointed out that: “…The question of why the effective stress is meaningful, however, still remains unanswered…”. De Buhan and Dormieux [22] referred to ESP as ‘Terzaghi’s postulate’ and tried to clarify several theoretical aspects of ESP validity. Bluhm and De Boer [23] stated that: “… Although the phenomenon of effective stresses was known for a long time, the theoretical foundation has remained unsatisfactory until now…”.

In the following two decades the study of porous media aroused growing interest, not only in the geological or geotechnical engineering disciplines but also in the field of porous materials of various nature such as metal powders, foams, composite materials and biological tissues (e.g., [24,25,26,27]). Consequently, the entire theoretical infrastructure has experienced a large development giving rise to the formation of practically autonomous scientific branches such as Theory of Porous Media, thanks to the extensive theoretical work carried out by Ehlers, De Boer, Coussy and their coauthors, [23,24,25,26,27,28,29,30] and Poroelasticity [31,32,33,34,35,36,37,38]. These theories represent an essential tool in the study of porous media in science and engineering and have also unravelled and clarified several aspects of the ESP, nevertheless, these are now so specialised that they may be accessible by few people in the scientific community, whereas many engineers, geologists and geophysicists, who often deal with themes involving the ESP (e.g., role of pore pressure in earthquakes, jointing and hydraulic fracturing of rocks, etc.), may not be familiar with them and might misinterpret some of their results.

Additionally, with reference to geological processes of brittle strain, such as faulting and jointing, the role of pore pressure is still debated. Several works point out the relevant role of pore pressure variations in earthquake triggering and coseismic slip evolution [39,40,41,42,43] as well as of other weakening mechanism, such as flash heating and frictional weakening (e.g., [44,45,46]). Although the numerous competing physical phenomena concurring in slip escalation are well established [43,47,48,49,50,51,52,53], quantifying the role of thermal pore overpressure among them is still a challenging task (Section 3.6 and Section 5). Similarly, within the framework of tensional joint network development, the role of pore pressure has been on the focus of a long-standing debate and it remains still unclear to date (Section 3.6 and Section 5).

A further issue is represented by the substantially different behaviour of soils and rocks. The question is why different models for such bodies—an aggregate of solids in contact for the former and a multiconnected solid including voids for the latter—lead to the same ESP formulations. This topic is addressed in Section 4.4.

Main aim of this review is to provide an overview of different proposed formulations for ESP as well as unravelling the underlying theory on the basis of the classical Theory of Elasticity, in order to clarify to the reader its fundamental role in geological processes and geotechnical engineering applications.

2. Basic Theory

2.1. Definition of ES

The ESP allows one to predict the mechanical behaviour of a porous medium, subjected to a tension state σij and a pore pressure p, on the basis of experimental data involving only dry samples. In other words, the usefulness of an appropriate ESP formulation consists in allowing to assess the behaviour of a porous body for whatever pore pressure value on the basis of experiments carried out at zero pore pressure.

An exhaustive definition for ES has been provided by Lade and De Boer [54] which define the ES as the stress, depending on the applied tension σ_ij and pore pressure p, which controls the strain or strength behaviour of soil and rock (or a generic porous body) for whatever pore pressure value or, in other terms, the stress which applied over a dry porous body (i.e., at p = 0) provides the same strain or strength behaviour which is observed at p ≠ 0.

All proposed formulations in literature for the ES, such as e.g., Equations (1)–(6), are in the following form:

σ’_ij = σ_ij − δ_ij η p,

(7)

or, in one dimensional form:

σ’ = σ − η p,

where η is a coefficient which generally can depend from the applied stress and pore pressure, as well as from other porous medium associated parameters (e.g., porosity, intrinsic and aggregate compressibility, etc.). It should be noted that, in spite of many available definitions in literature, Equation (7) does not establish a general linear dependence between ES and the variables (σ_ij, p), as the term η may be in general a nonlinear function of such variables. As an example, in the term (1 − C_s/C) of Equation (5), the porous rock or soil compressibility C is a (empirical or theoretical) nonlinear function of the difference (σ − p) so as proved experimentally by Nur and Byerlee [8] and theoretically by Zimmerman et al. [33,55].

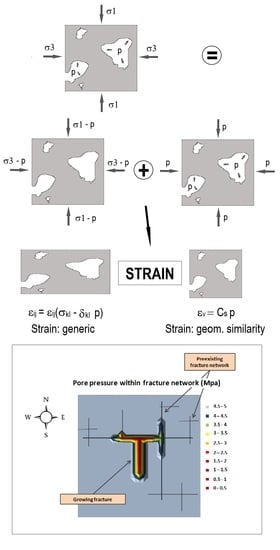
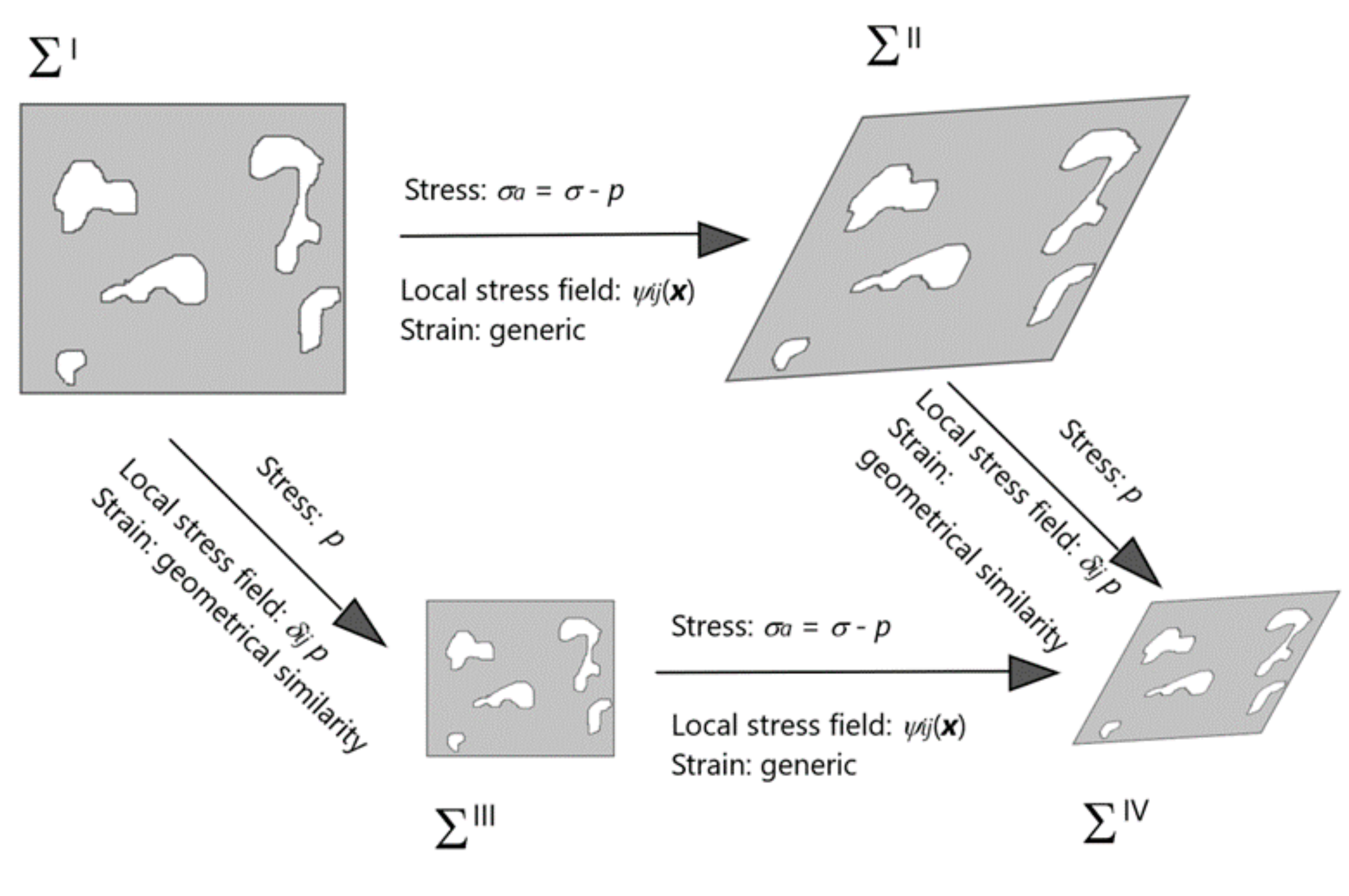
2.2. A First Simple Theoretical Proof of the ESP

In order to investigate the stress field features within the porous medium, we will carry out our analysis at a smaller scale than pores and/or clasts. Namely we consider here a control volume of porous medium, including many pores and voids. The elastic problem within such control volume will involve elementary volumes smaller than pores and/or clasts (Figure 1).

Here, σij denotes the stress tensor acting on a cubic control porous volume, whereas the stress acting on the elementary volume smaller than pores is denoted by ψ_ij. Therefore, σ_ij should be viewed as boundary condition for the elastic problem having as unknown the stress field ψ_ij. The boundary of the considered continuum is a surface Σ, composed by the external boundary surface Σ1 and the pore surface Σ2 (Figure 1). We will consider at the moment a single elastic body including interconnected voids (pores and fractures) fully filled by liquid under uniform pressure, which simulates rock or concrete behaviour, whereas the behaviour of granular media, i.e., constituted by many elastic bodies in contact, will be discussed in Section 4.4.

A basic here adopted assumption consists in considering the porous medium as constituted by a linear elastic, homogeneous and isotropic material. It should be noted that, despite such assumption, the porous aggregate can be nonlinear elastic (e.g., rock) or inelastic (e.g., soil, which are discussed later), anisotropic according to pore and fracture orientation, heterogeneous according to void spatial distribution (i.e.,as a consequence of spatially variable porosity). The appropriateness of such assumption has been discussed in detail by Zimmerman et al. [32,33,34,56]. We can conclude that, although such assumption reduces the general validity of such model, this latter covers with a good approximation avery wide variety of real cases and has the advantage of a relatively simple theoretical treatment.

The stress distribution inside a linear elastic body in absence of body forces is governed by the following linear elliptic differential system (e.g., [57]):

(1 + v) ∇²ψ_ij + ∂²ψ_kk/∂x_i∂x_j = 0,

(8)

where v is the Poisson ratio and ∇² is the Laplace operator and the Einstein convention about repeated indexes is adopted (e.g., ψ_kk = ψ₁ + ψ₂ + ψ₃ ).

The boundary conditions are defined by the external stress acting over the (strained) boundary surface ∑, i.e., over the outer surface ∑1 and pore surface ∑2:

ψ_ijn_j = t_i,

(9)

where n_j denotes the local boundary surface normal vector and t_i denotes the tension acting on the boundary at a point. Namely, the control volume is subjected to a stress σ_ij acting over ∑1 and a pressure p acting on ∑2. The pore pressure is assumed here to be uniform within the control volume.

The equation system 8 provides the basic relations of the Theory of Elasticity and is derived by combining local equilibrium equations with the compatibility conditions between infinitesimal strain components, as well as the elastic equations [57]. Its derivation is briefly illustrated in Appendix A1.

Now, in order to study the local stress field features, we proceed according to two commonly employed steps: (i) decomposition of the acting force system in an equivalent one and (ii) use of superposition principle.

(i)

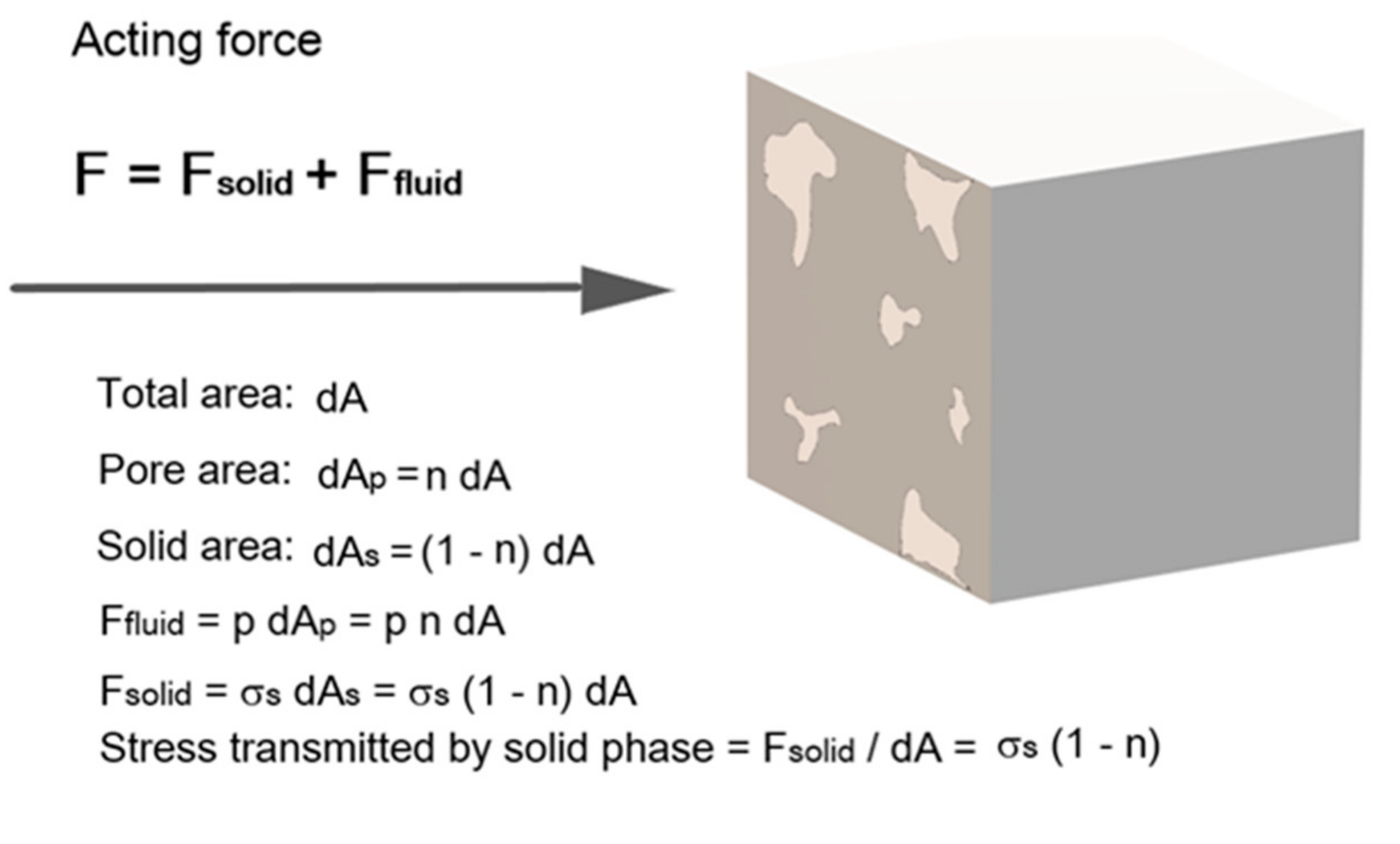
the stress σ_ij acting on the outer surface, can be decomposed as follows:

σ_ij = (σ_ij−δ_ijp) + δ_ijp,

(10)

This is only a simple algebraic operation which is always allowed in mechanics (with no generality loss); analogous decompositions are widely adopted in Continuum Mechanics and Theory of Elasticity (e.g., [57], in many theoretical proofs along the whole textbook)in order to decompose the boundary conditions in more simple systems whose associate solutions are already known or easily manageable.

(ii)

the superposition principle needs to be justified as it does not have general validity, in particular for the above described nonlinear elastic model. We provide a rigorous proof of its applicability in Section 4.2.

The stress field associated to the second term on the right side of Equation (10), (δ_ijp), which is now applied over ∑1 and ∑2, i.e., the whole boundary surface, is a well-known solution consisting of a uniform isotropic pressure equal to p(e.g., [57]) for whatever boundary or pore surface shape, whereas the stress at a point associated to the first term (σ_ij−δ_ijp) is a generic tensor ψ0_ij = ψ0_ij(σ_ij−δ_ijp). We point out as we are not interested in calculating the solution ψ_ij for each point but at achieving information about its features, namely at comparing the local stress and strain fields in a porous medium subjected to a pore pressure with those into an identical one in dry condition.

The solution of Equation (8), associated to the boundary stress of Equation (10) is given, by the superposition principle, by the sum of ψ0_ij and p:

ψ_ij = ψ0_ij (σ_kl−δ_klp) + δ_ijp,

(11)

This is not an ES law, but rather a description of the local stress field at a smaller scale than pores. Equation (11) plays a key role in the model developed in this study, as it allows one to evaluate relevant properties of local stresses within the material and can clarify several significant aspects of the ESP. The stress (and strain) field within the material constituting the porous body includes:

(i)

a term (δ_ijp) which is only responsible for a small volume reduction, according to the intrinsic bulk modulus of the solid Ks, with no shape—and pore shape—change,

(ii)

a term ψ0_ij, depending on (σ_kl−δ_klp), which produces the often more evident strainat both microscopic and macroscopic scales, in terms of aggregate volume and shape change as well as pore surface shape transformation. It should be noted that this stress and strain depend uniquely on Terzaghi’s ES (σ_kl−δ_kl p). This provides a first explanation of the ESP for stress–strain behaviour of rock. Two identical porous bodies, one subjected to pore pressure and one in dry condition but showing the same difference (σ_ij−δ_ij p), exhibit macroscopic strain which differ only by a small volume change associated to p.

The Nur–Byerlee–Skempton formulation for the ES (Equation (5)) takes into account such small difference by introducing a further corrective term in the ES expression, given by (1 − Cs/C), which is often slightly less than unity, being Cs << C in usual geotechnical application. Nevertheless, it should be noted that such a term might be substantially different from unity at depth of some kilometres in the Earth’s crust. For this reason, such ES expression may be more suitable than Terzaghi’s ES when dealing with stress–strain behaviour of rocks. On the basis of Equation (11) also this formulation can be derived (Section 4.1).

With reference to rock strength behaviour, tensional, as well as shear, fracture growth is mainly affected by forces acting in areas of high stress concentration, such as fracture tips. In these areas, in most of cases, pore pressure is negligible with respect to the maximum acting stress, denoted by ψ0_Max (Section 4), i.e.,

ψ0_Max>>p,

(12)

this implies that Equation (11) becomes:

ψ_Max ≈ ψ0_Max (σ_kl−δ_klp),

(13)

Details about effect of pore pressure on rock strength are discussed in Section 4.3. As rock inelastic behaviour is mainly controlled by concentrated stress ψ_Max, which is fully dependent on Terzaghi’s ES, this latter law well describes all these phenomena so as broadly experimentally observed (e.g., [7,55,56] and many others).

Section 4.4 shows that the above-illustrated reasoning about ESP in rock can also be extended to soils and granular media, which unlike rocks always exhibit an inelastic behaviour. The analysis of ESP for visco-plastic as well as visco-elastic strain according to several rheological models ([56], Chapter 9), despite its relevance in geological processes, is well beyond the scope of this paper. Indeed, deformation processes acting over geological time scales are likely associated to inelasticity also in rock. Here we limit ourselves by pointing out how several problems of rock visco-elasticity can be modelled considering relaxation phenomena such as variation of the initial shape (i.e., under no imposed external stress) and thus reconciling the problem of internal stress distribution between fluid and solid phases (i.e., ESP) to an elastic one with a changed geometry of the boundary surface. From this viewpoint, the above illustrated model may be still conceptually valid, although for their complexity visco-elastic problems need to be carefully dealt with and may be the object of future research.

2.3. Nonlinear Elastic Behaviour of Rock and Main Issues in Proving the ESP by Means of Theory of Elasticity

Rocks ordinarily exhibit nonlinear elastic behaviour although the constituent material may often display linear elasticity over a wide range of stress values. As clarified by many authors [8,31,32,33,34,36,55,58,59,60,61,62,63,64], rock macroscopic strain is mainly controlled by local strain of elongated pores and/or fractures and pore collapse phenomena. In case of nonlinear elastic behaviour, the use of the superposition principle is generally not allowed and the derivation of Equation (11) is not a trivial result. To better understand this concept, consider the following simple example involving a cubic specimen made up of a nonlinear elastic material. Let ε_a be the volume strain due to a confining isotropic pressure σ_a and ε_b due to σ_b. If we imagine to apply before σ_a and successively σ_b, the resulting strain ε_v is different from the sum of single strains (ε_a + ε_b) as, after application of σ_a, the specimen compressibility has changed and therefore the strain due to σ_b is different from that which was observed by application of σ_b over the unloaded specimen. However, in Section 4 we show that, for the special above described case (Section 2.2) such principle is still valid.

2.4. Conventional and Substantial Aspects of the ESP

The conventionality of ESP can be explained by means of a simple example involving an unjacketed test on rock. Let us imagine to carry on an unjacketed test, such as those described by Skempton [7], Nur and Byerlee [8] as well as Cheng ([38], Section 1.2.4), in which a rock sample is subjected to a pore pressure p, which is equal to the confining pressure Pc. In such a condition this sample is transformed in a geometrically similar smaller one. According to the above given definition, the ES is the stress which, applied on the dry sample, provides the same here observed volume strain, i.e., for which (C P’_c = C_sp), where P’_c denotes the confining ES. This latter stress can also be calculated by means of Equation (5), as (P’_c= p − (1 − C_s/C) p = (C_s/C) p). It should be noted that, although the sample in dry condition undergoing such stress exhibits the same volume change observed in the unjacketed test, these two strain processes are geometrically and mechanically substantially different. The unjacketed test produces a cubic volume strain with no pore shape change, whereas the dry sample shows volume strain involving relevant pore geometry change, pore collapse etc.

The substantial aspect of ESP is related to the fact that a fraction of the local stress given by (δ_klp) (i.e., related to neutral stress) has the only effect of producing an often unimportant cubic volume strain of porous medium, whereas the most relevant part of strain is attributable to the term ψ0_ij (σ_kl−δ_klp) of the local stress, which is fully dependent on Terzaghi’s ES. This latter contribution to strain is the most relevant for several reasons: (i) it is often the most evident or abundant, (ii) the pore/fracture shape changes which are related to ψ0_ij affect substantially the main mechanical and hydraulic rock features, such as compressibility and other elastic moduli [31,32,33,34,36,56,58,59,60,61,62,63,64], rock strength, permeability, etc.

Robin [65] discussed an analogous relationship to that provided by Equation (11) (although expressed in nonlocal terms and restricted to the case of isotropic confining pressure), highlighting that different ES laws can be defined according to the parameters to be investigated. He also pointed out that a widespread definition of ES, compatible with that proposed in Section 2.1, may be misleading, whereas the simpler Terzaghi formulation is more closely linked to the deformation state of the porous medium. Based on Robin’s studies, Hampton and Boitnott [66] emphasise how the term "effective pressure" has the misleading connotation of "equivalent pressure" and comment as follows: "... As such, the terms ’effective pressure’ and ’effective stress’ are misnomers that should be avoided without specific reference to a particular property… ".

Therefore, we can conclude that the ES definition is substantially conventional and related to the problem being treated. Among various ES formulations, Terzaghi’s seems particularly appropriate, for its simplicity and as it describes a stress system that is directly related to the internal geometry of pores and to the mechanical characteristics of the porous medium.

3. Development of Theories Involving ESP

3.1. Fillunger’s Approach

Fillunger [5,67] was the first to study, according to an organic theory, the effect of the pore pressure on strength and deformability of porous media such as soil, rock and concrete as well as the precursor of the modern Theory of Porous media [6,29,68]. He provided for the ES the formulation of Equation (2), which appears in disagreement with the experimental evidence. It should be taken into account that the study of porous media was an absolute novelty as at that time they were approximated with continuous systems. Therefore, the concept of ES was not aimed at predicting the behaviour of porous media on the basis of laboratory tests according to the definition given in Section 2.1. In the Fillunger model the ES was intended as stress, loading the solid skeleton, to be utilised within differential equilibrium and balance equations [5,6].

Under the hypothesis of isotropic pore distribution, it can be proved as rock porosity n is equal to surface porosity, i.e., to the ratio (void area/total area) evaluated on an ideal elementary surface within a porous medium (e.g., [69]). Therefore, denoting by P_c the total confining stress and by dA the area of such elementary surface, the net acting force across this latter, given by (P_cdA), is balanced by a force offered by the liquid phase on the pore surface, equal to (pndA), to which a force offered by the solid is added, equal to (σ_s (1 − n) dA), where σs denotes the stress acting on the solid phase (Figure 2).

We point out that the ratio between this latter force and the whole elementary surface area dA (i.e., area of solid and pores) is given by ((1 − n) σ_s), which can be interpreted as the stress effectively acting on the solid skeleton. Therefore, it results:

P_C dA = p n dA + σ_s (1 − n) dA,

from which:

(1 − n) σ_s = P_C− n p.,

(14)

This expression is identical to Equation (2) if the term at the first member is interpreted as ES. The problem of disagreement of such expression with experimental data can be imputed to an erroneous interpretation by the reader of the concept of ES, intended in the modern sense as the stress that applied to a dry sample gives the same observed response (Section 2.1). The expression is instead correct if the quantity at the first member is interpreted as the stress effectively acting on the solid through an elementary surface, in local equilibrium equations.

The stress effectively acting on the solid through an elementary surface is substantially different from the ES as defined in Section 2.1. This latter is referred to as the effect of the acting stresses on rock or soil, in terms of strain or strength behaviour, which depends on the stresses effectively acting on the outer surface of a control volume, i.e., Σ1, as well as that acting on the pore surface Σ2, whereas the former depends only on stress applied over Σ1.

Therefore, Fillunger was right, as his definition of ES was different from that given in Section 2.1, not being aimed at the experimental comparison of the mechanical behaviour of samples under different pore pressure conditions but at providing an appropriate variable for his mathematical model.

3.2. Terzaghi’s Work

Terzaghi’s work has provided the basis to soil and rock mechanics and, more generally, to geotechnical engineering [70]. Terzaghi was more oriented to an experimental approach than Fillunger and his definition of ESP is compatible with that given in Section 2.1, being aimed at predicting the behaviour of saturated soils and rocks on the basis of experimental tests. Terzaghi had also encountered the problem of the disagreement of the ESP provided by Equation (2) with the experimental data and, on the basis of the experimental evidence, finally proposed the well-known formulation given by Equation (1) [2]. As at that time the theory of soil and rock mechanics was in its infancy, it was not easy to interpret the subtle difference between stress effectively transmitted by the solid skeleton of a porous medium and ES as defined in Section 2.1.

Fillunger and other scientists in the 1910s had found experimental evidence of the role of ESP on soil behaviour, nevertheless according to Skempton [71], which commented as follows, only Terzaghi has gasped the extent of this fundamental law:“… This result is similarly a direct consequence of the principle of effective stress. Nevertheless it is clear that the physical meaning of these tests was in no way understood, and it required the genius of Terzaghi to clarify and enunciate this basic law of the mechanical properties of porous materials…”.

Along his prolific scientific career, Terzaghi carried out an extensive experimental and theoretical work by developing the one-dimensional consolidation and settlement theory, the design of earth, rock and concrete dams on all kinds of foundations, several methods of soil laboratory test and pore pressure measurement, as well as most of the methods of modern engineering geology, rock and soil mechanics and in general of geotechnical engineering [72]. Terzaghi’s ESP remains, today, the major reference in the above-mentioned subjects.

3.3. From Biot’s to Zimmerman’sWorks and the Modern Poroelasticity

After the works of Fillunger and Terzaghi, Heinrich followed the direction of the former whereas Biot of the latter. Heinrich’s work [73,74] was forgotten for decades and the theory of mixtures has been reused in the 1970s [6,75]. Biot, at the beginning of his career followed Terzaghi’s direction, giving the basis to the modern Poroelasticity. Biot fully developed the three-dimensional soil consolidation theory [10,76], extending the one-dimensional model previously developed by Terzaghi [1,4] to more general hypotheses and introducing the set of basic equations of poroelasticity. In this work Biot explained, according to a rational and rigorous theory, various aspects about the role of fluids on porous media strain and of ESP. Afterwards, Biot and Willis [17] provided the formulation of the ES according to Equation (5), under hypothesis of linear elasticity of the porous medium. In the same year Geertsma [77] rederived Biot’sporoelasticity equations, using a different set of variables and he too proved Equation (5) for the ES, according to the hypothesis of linear elastic behaviour. Biot then extended the consolidation theory to the case of anisotropic behaviour [11] and later to the case of nonlinear elasticity [15] using second order approximations of the elastic stress–strain relations. Furthermore, he has discussed in detail the general solutions of the poroelastic and consolidation model [12]. This model has also been adapted in order to study the behaviour of saturated porous media in dynamic and seismic conditions [13,78,79,80]. Porous media strain was then analysed from the thermodynamic point of view under very general hypotheses [16].

Skempton [7] experimentally verified some formulations of the ES, establishing that Equation (5) is the most appropriate, between various proposed formulations, at describing of the strain of granular media under high pressures, while Nur and Byerlee [8] theoretically derived this formulation for stress–strain rock behaviour. Details on these two works are illustrated below; here we limit ourselves to saying that, as highlighted by Nur and Byerlee, the main limitation of their proof lies in the fact that it assumes rock linear elastic behaviour. Garg and Nur [55] have provided a proof of Equation (5) based on the mixture theory, corroborating the conclusions obtained by Nur and Byerlee and extending their validity to the case of nonlinear elastic behaviour of rock. Namely, they established that Equation (5) correctly describes the stress–strain behaviour of rock, while Terzaghi’s ES (Equation (1)) adequately describes their strength behaviour.

The nonlinear elastic behaviour of rocks, i.e., characterised by compressibility and toughness depending onstress, has been explained by Walsh [58,59,60], who pointed out that it is mainly controlled by the modification in the geometry of more elongated pores. This concept was subsequently further clarified by Walsh and Grosenbaugh [61], as well as by Zimmerman [31,32,33,34,62] and more recently by other authors (e.g., [36,64]).

Zimmerman [33], analogously to Geertsma [77], approached the poroelastic problem in terms of more physically identifiable variables such as volume of porous body and of pores, confining and pore pressures (denoted by V_b, V_p, P_c, and P_p, respectively), providing relevant conclusions about stress–strain behaviour of nonlinear elastic saturated porous media as well as the ESP, rigorously corroborating the validity of Equation (5) for stress–strain ES, in which he proved that rock compressibility depends only from Terzaghi’s ES(σ − p). Zimmerman’s paper provides a relevant extension of Nur and Byerlee’s [8] work, as it overcomes its main limitations related to the assumption of rock linear elasticity and of rock compressibility dependence on Terzaghi’s ES and represents a main reference about these topics.

Since the 1990s, the theory of Poroelasticity has undergone significant developments, also making use of the results of the Homogenisation criteria and of the modern Theory of Porous Media, unravelling different aspects of porous media behaviour such as constitutive equations, micromechanics, variational energy formulations, poroelastodynamics, poroviscoelasticity, porothermoelasticity, and porochemoelasticity, as thoroughly illustrated by Cheng [38].

3.4. Homogenisation Theory

The homogenisation approach assumes periodic pore geometry and then extends the achieved results about the behaviour of a template elementary porous volume (control volume) to an aggregate made up of identical elementary volumes. Within this latter volume, solid and fluid phases occupy different spaces, i.e., variables such as density, stress/pressure field etc. are defined within the pore or solid space for fluid and solid, respectively. In such spaces the governing partial differential equations are defined. These are elasticity or other rheological models for solid and Navier–Stokes for fluid. Such equations, together with boundary conditions, are therefore simplified by considering perturbations of appropriate parameters and so analysing the first or second order related terms. As explained by Cheng [38], the homogenisation approach makes extensive use of mathematics and different mathematical treatments may lead to different and sometimes even inconsistent results; therefore, these results always need to be experimentally validated. Furthermore, we point out that, due to the complexity of these theories, some of the results might be misinterpreted.

The homogenisation theory has allowed an in-depth analysis of several aspects of porous media behaviour. A theoretical analysis of the ESP by means of this approach was carried out by Auriault and Sanchez-Palencia [18] and, for the case of inelastic behaviour, by De Buhan and Dormieux [22]. Such approach was used in order to build up micromechanical models for porous media behaviour [81,82,83,84] as well as for theoretical approaches to Darcy law [84,85,86], poroelastodynamic models [19,20,87,88], and porochemoelasticity(e.g., [89]).

3.5. Theory of Mixtures and the Modern Theory of Porous Media

The modern Theory of Porous Media (TPM) is based on the mixture theory combined with the volume fraction concept [68,90]. Unlike the homogenisation approach, in such models solid and liquid phases are considered as overlying continua within a porous control volume, whose associated characters are weighted by a volume fraction; as an example, the reduced fluid density, here denoted by ρ^f, consists of an averaged value over the control volume, equal to ρ^f = n ρ_f, where ρ_f denotes the real fluid density and n the porosity. Analogously, the solid reduced density is ρ^s = n^sρ_s, where n^s is the solid fraction, i.e., (1 −n) and ρ_s the real solid density. Therefore, solid and fluid phases are substituted by “smeared” continua that can be treated by methods of continuum mechanics ([24,30,90] Chapter 5).

About this model, Cheng [38] points out as follows: “This approach is largely mathematical, and the material coefficients generally do not possess physical meaning until a comparison is made with a theory that is in use, such as a phenomenological theory”; therefore, due to the abstractness of such theory, its results need to be carefully dealt with in order to avoid some misinterpretations. An example is given by the above discussed mixture theory based Fillunger’s ES formulation (Section 3.1) in which the stress effectively acting on the solid should not be confused with the ES as defined in Section 2.1. Another relevant example is given by Suklje’s [9] ES formulation. This latter might be defined as the stress producing strain involving the only solid phase (skeleton and solid particles; Section 4.1), which also in this case, should not be confused with the ES as defined in Section 2.1.

After its involvement by Fillunger, the mixture theory had been poorly adopted in porous media studies until the 1970s [6]. At that time Morland [91] used the mixture theory combined with volume fraction in order to build up the Theory of Interacting Continua, within the framework of porous media analysis. Based on such approach, Garg and Nur [55] have critically re-examined the theoretical and experimental bases of several ES laws.

In the last decades the TPM has allowed the analysis of porous media behaviour under general hypotheses in several areas of science and engineering, going from geotechnics to biomechanics (e.g., [24,25,26,27]). According to TPM approach, Bluhm and De Boer [23] have reviewed the underlying theory to the ESP, proving some of the previously proposed ES formulations. Didwania and De Boer [92] have provided a very interesting theoretical treatment of the ESP under general hypotheses.

The mixture theory has provided fundamental tools aimed at unravelling several aspects of macro- and micro-scale stress and strain field features, within saturated and unsaturated porous media [24,92,93,94,95], as well as at providing theoretical proofs of some ES laws [23,55]. Furthermore, according to such theory, variational energy formulations have been developed [24,91,96,97,98], as well as elastodynamic models for porous media [94,99,100], Porochemoelasticity [101,102,103], and mechanics of microporous media (e.g., [104]).

3.6. Effect of Pore Pressure on Rock Fracturing

Pore pressure plays significant roles in geological fracturing phenomena observable at different scales such as faulting, from the kilometre to the regional scale, and formation of tensional joints, at the metre to crystal scale. In the former case, the coseismic increase in pressure due to developed slip-related high temperatures can markedly affect the slip evolution; in the latter case pore pressure is considered as essential in order to justify fracturing phenomena, as it appears unlikely that in earth crust, in presence of lithostatic load, traction can develop in terms of total stresses (e.g., [105]).

3.6.1. Earthquake and Coseismic Overpressurisation

During an earthquake, at the fault plane high temperatures develop which cause an increase in pore pressure associated to vaporisation (e.g., [39,40,41,42,43,106,107]). This increase, in the coseismic phase, can notably affect slip evolution and speed, moreover, in the post-seismic phase it can control the aftershock phenomenon [108], as pore pressure increase slowly propagates into the surrounding rock.

From the viewpoint of Coulomb’s strength theory, an increase in fluid pressure reduces the normal stress acting on the fault plane that holds it in place, moreover fluids can exert a lubricating effect (e.g., [107] and references therein). It should be taken into account that coseismicoverpressurisation is a practically instantaneous phenomenon if compared with the fluid flow time resulting in low permeability fault core rocks and, therefore, such increase in pressure, denoted by Δp, occurs in a thin layer in correspondence of the fault plane, where in coseismic conditions, in the surrounding rock the pore pressure remains at the preseismic values, denoted by p₀. As fluid pressure acting on the fault plane walls, equal to (p₀ + Δp), is not counterbalanced by the pore pressure acting in the surrounding rock, equal to p₀, then the tangential stress offered at the fault plane is reduced to a greater extent than that which would be considered in terms of ordinary effective stress. For these reasons thermal overpressurisation may enhance the faulting process instability, as it provides a positive feedback between slip and strength at the fault plane as fault slip increases pore pressure and this latter reduces friction forces at the fault plane, thereby enhancing slip.

In post-seismic stage the pressure gradient between fault plane and neighbouring rock causes a fluid flow which increases pore pressure in the surrounding fracture networks and so it may trigger new faulting processes by reactivating neighbouring faults, giving rise to aftershocks. Analogously, also manmade pore pressure increase, by means of fluid injection in Earth’s crust, may induce seismicity (e.g., [52,109,110] and references therein).

3.6.2. Hydraulic Jointing

For a long time, formation of tensile fractures in rock has been considered a poorly explained phenomenon as stresses in the Earth’s crust are compressive, with the exception of particular cases involving very shallow rocks. Hubbert and Willis [111] clarified as fractures are produced when tensile ES (Equation (1)), rather than total stress, exceeds rock tensional strength. Subsequently Secor [112] explained how pore pressure in Earth crust can cause hydraulic fracturing without depth limits. Based on strain energy balance methods and following the Griffith crack growth model, Secor [113] illustrated an hydraulic fracturing model consisting of an elastic solid including random oriented elliptical flaws, hydraulically connected by a permeable matrix, filled by fluid under homogeneous pore pressure. According to Secor’s model if from an opportunely oriented flaw enucleates a fracture, a pressure drop occurs within this latter a cause of increase in void volume. Such process stage evolves at about sound speed and, so, fracture extension rapidly stops, being the final internal pore pressure lower than that in the surrounding rock. The produced pressure gradient, between the interior of growing fracture and surrounding pores, results in a fluid flow towards the fissure itself. When the pore pressure reaches a suitable value, the crack further extends. Therefore, according to this model, fracture extension is an intermittent process.

Fyfe et al. [105,114] questioned Secor’s model as it did not take into accountthat fluid pressure inside a growing fracture is counterbalanced by the pore pressure in the neighbouring rock. According to them, this fracturing mechanism is possible if the ES in the neighbouring rock is used in the formulation of Equation (5),in this way the fluid pressure into the growing fracture would be (albeit slightly) higher than decrease in total stress, given by ((1 − C_s/C) p), in the surrounding rock. This model is illustrated in detail by Engelder and Lacazette [115], in which mixed boundary conditions are defined in terms of both applied stress and displacements. Namely, the authors considered a condition of uniaxial strain for a control volume of rock, undergoing a vertical total stress σ1, a homogeneous pore pressure p and constrained in lateral expansion (note as this latter condition is expressed in terms of displacements rather than stresses). Therefore, lateral total stress is an increasing function of σ1 and p. It can be proved as, under such boundary conditions, tensional fracturing is possible only if ES, acting over the boundary of a control volume including the considered growing joint, is calculated according to Equation (5), rather than Equation (1) [114]. The illustrated model is interesting as it justifies occurrence of tensional joints also when horizontal extension is constrained, e.g., in areas characterised by no extensional tectonics, nevertheless, the reached conclusions should not be misinterpreted, deducing that fracturing is generally controlled by Skempton–Nur–Byerlee ES (Equation (5)) rather than Terzaghi’s ES (Eq. 1), as the validity of the former ES formulation is strictly related to the imposed boundary conditions. In fact, fracture growth is mainly controlled by local stresses at the fracture tip, for which Equations (12) and (13) hold.

Within the framework of geological fracturing processes, we should take into account, besides uniaxial strain, also other likely kinds of boundary conditions. Two common cases in nature are related to (i) pore pressure increase by natural or manmade (e.g., fluid injection) causes and (ii) tectonic-related total horizontal stress decrease.

In the case (i) it should be taken into account as pore pressure may show a strongly heterogeneous spatial distribution as illustrated by Figure 3 [116], with exception for cases of extremely slow fluid pressure increase; within the more permeable joint networks, fluid pressure increase is more rapid than in the less permeable ones in which in turn it is faster than that into the nonfractured porous host rock [116].

Therefore, for those fractures which are influenced by such increase, the internal fluid pressure is not counterbalanced by pore pressure in the surrounding rock, so enhancing fracture extension. In such condition, for sufficient pore pressure increase, fracture extension proceeds according to Secor’s model. The process of fracture extension is also described in detail in other interesting papers [117,118,119]. It should be noted that, in case of strongly heterogeneous pore pressure, the concept of effective stress appears ambiguous. Indeed, in this case fluid pressure assumes different values also within a small control porous fractured volume and it may be not clear whether both the pressures to be subtracted from the total stress is the increased pressure, inside a fracture, or that present in the surrounding porous rock. Finally, we point out that such fracture growth model can be applied only to the case of pre-existing joints/cracks already connected to the fracture network, whereas it is not applicable to isolated cracks/flaws (i.e., to nucleation of new fractures), with exception for cases of extremely slow pore pressure increase.

In the case (ii) of tectonic extension, the horizontal stress σ3 slowly decreases and the least effective stress (σ3’ = σ3 − p), may become tensional and eventually exceed the rock strength.

An opportunely oriented flaw, crack or fracture can extend if the stress at tips, namely the local stress at crystal lattice scale, is such that to produce detachment between adjacent crystals or two portions of the same crystal. At such scale of observation, notably stress concentrations occur and local stress, described by Equation (11), complies with Equations (12) and (13) (Section 4.3), therefore crystal detachment, as well as fracture extension, is controlled by Terzaghi’s ES. In such conditions, fracture extension proceeds according to Secor’smodel [113,117,118,119]. Analogous process is followed in case of very slow fluid pressure increase, as in such case pore pressure gradients are moderate and, therefore, pressure distribution is substantially homogeneous within rock.

It should be noted that in both above illustrated cases, fracture extension is always accompanied by pore pressure drop and, therefore, the trend of such pressure is always heterogeneous. This also applies in the above described case (ii), although the pore pressure is initially homogeneous. This makes the theoretical approach to jointing mechanisms problematic, because the definition of ES is not univocal; the condition of heterogeneous pore pressure should be carefully dealt with, as the derivation of Equation (11) requires a homogeneous distribution of these pressures.

3.6.3. Joint Spacing and Sequential Joint Filling

Pore pressure can also affect spacing between consecutive joints belonging to the same set. This parameter is of fundamental importance for fractured rock characterisation and modelling, as it strongly influences their hydraulic and mechanical properties. Within the framework of study of joint sequential filling processes (i.e., joint network developing in bedded rocks) different models have been proposed in order to explain the temporal evolution of joint networks and namely the observed distributions of spacing values between consecutive joints [120,121,122,123,124,125,126,127], nevertheless, they appear in agreement with field data only in some cases, whereas in others they appear incompatible with such data. Hobbs [120] provided a first model explaining the mechanism which produces tensile fractures showing spacing proportional to the mechanical layer thickness. Later, Ladeira and Price [121] explained the possible role of pore pressure in controlling spacing between joints in thick mechanical layers. Narr and Suppe [122] have improved Hobbs model by introducing the effect of flaws with random spatial distribution, which explains statistical variability of joint spacing around an average value. Furthermore, on the basis of this model, they have introduced the concept of joint saturation, i.e., a condition in which a fracture network is considered ’mature’ and a further bed extension tends to produce further extension of existing joint, rather than formation of new ones. Pollard and Segall [128] as well as Gross [123] explained and quantified the effect of stress shadow in the surroundings of a growing fracture, in hindering nucleation of new fractures in their vicinity, being fracture walls free from tensile stress. Therefore, stress gradually varies from zero, at the growing fracture walls, to the remote stress, far from such joint. The concept of stress shadow, as well as that of joint saturation, were then deepened by Bai and Pollard [124,125,126,127] by means of the stress transition model. Based on numerical simulations involving dry rock and a rigorous theoretical treatment based on the theory of elasticity, they quantitatively explained the effect of stress shadow and the concept of joint saturation that occurs when a critical value of the spacing to thickness ratio is reached. However, the same authors highlight how this model is not applicable in several cases in which the observed value of such ratio is well below the critical one [125,126], stating as such cases need to be explained by means of different models, possibly involving the effect of pore pressure. The above described models consider dry rock and can be adapted to the case in which pore pressure is present, only in the case in which the latter is homogeneous (Section 3.6.2 and Section 5.2). This represents an important limitation for such models as joint extension may be associated with heterogeneous pore pressure in pregrowth conditions in several cases and it always is during such growth. These criticalities of joint sequential filling models are discussed in Section 5.2.

4. Revisitation of Two Main Works and a Theoretical Proof of ESP

4.1. Skempton and Nur and ByerleeProof of ESP

Skempton [7] has carried out an extensive review of available formulations, given by Equations (1)–(5), and experimental data in literature, in order to (i) reject some of these expressions, (ii) clarify what expression was appropriate according to several work hypotheses, such as stress–strain or strength behaviour, saturated or nonsaturated media, rock/concrete or soil behaviour, etc. At that time the common opinion was that the effective stress was the intergranular stress acting between particles and/or clasts; this led to a formulation of ES given by Equation (3). Based on experimental data about oedometer tests on lead shot, whose results are summarised in

Table 1. Experimental data from oedometric test on lead shots. The test was carried out in steps; for each of them, an increment of total confining pressure was applied together with a known increment of pore pressure. Then, once the sample strain was measured, the pore pressure was reduced to zero. Modified from Skempton (1960).

Total Confining Stress (kg/cm2)	Pore Pressure (kg/cm2)	Contact Area Ratio ac	Biotcoeff. (1 − Cs/C)	InterganularStress Equation (3)	Terzaghi Equation (1)	SkemptonBiot Equation (5)	Experimental
256	0
		0.35	0.995	170	128	129	129
512	128
		0.6	0.99	50	128	127	127
512	0
		0.8	0.98	460	256	261	268
1024	256
		0.9	0.95	20	256	243	244
1024	0

, Skempton has proved that Equation (3) is invalid, whereas Equation (5) is appropriate for soil volume strain under high pressure.

Indeed, lead shot under high pressure experienced considerable plastic strain and so the contact area ratio a_c varied significantly during the various compression steps, also approaching the unit value, differently than soils for which a_c is always negligible with respect to the unity. Therefore, if the ES were described by Equation (3), in such experiments it should have significantly diverged from Terzaghi’s one. Instead, experimental data exhibited significant disagreement with Equation (3), whereas these were in excellent agreement with Equation (5) and displayed only small deviations from Terzaghi’s ES formulation, given by Equation (1) (Table 1).

In the framework of rock strength behaviour, he established that the use of Equations (1) and (4) provide differences which are comparable with experimental uncertainties, so concluding that Terzaghi’s expression (Equation (1)) can accurately describe the strength behaviour of soil, concrete and rock, as well as the stress–strain behaviour of soil under ordinary stress conditions in geotechnical applications.

Although the experiment on lead shot illustrated by [7] was perfectly adequate in order to define the role of contact area ratio variations on ES, the maximum reached stress is of the order of 100 MPa. It should be noted that, in case of higher stress values (e.g., of several hundreds of MPa) acting on soil or rock, the coefficient (1 − C_s/C) attains values below unit and may also approach zero.

In both works by Skempton [7] and Nur and Byerlee [8] the basic equation, referred to unjacketed tests where σ denotes a confining isotropic stress, from which Equation (5) is derived, is the following:

ΔV = ΔV₀ + ΔV_p,

(15)

where ΔV denotes the volume change of a control volume containing many pores (Section 2), ΔV₀ due to the difference between confining stress and pore pressure, (σ − p) and ΔV_p due to pore pressure.

Analogous relation can be achieved in terms of volume strain, by dividing by the initial volume, denoted by V.

ε_v = ΔV₀/V + ΔV_p/V = ε₀ + ε_p,

where ε_v, ε₀ and ε_p assume the same meaning of the above illustrated volume changes in terms of volume strain. This relation is based on the superposition principle. This latter has been assumed by Skempton [7], based on experimental evidence and by Nur and Byerlee [8] as necessary, although not justified, in order to carry on their theoretical proof. As the effective stress can be defined as the stress which applied over a dry sample provides the same observed volume strain (Section 2.1), therefore,ε_v can be substituted by (C σ’). Hence, substituting ε₀ and ε_p, in the latter equation, by (C(σ −p)) and (C_sp), respectively, it becomes:

C σ’ = C (σ - p) + Cs p,

(16)

which, after simple manipulations provides the Equation (5). It should be noted as Equations (15) and consequently (16) can be easily achieved starting from Equation (11), taking into account that the validity of superposition principle locally, i.e., for all elementary volumes, implies its validity at the control volume scale, as well as at the whole porous body scale.

It should be noted as the Suklje [9] ES expression (Equation (6)) can be achieved in an analogous way, where the second term on the right side of Equation (15) is substituted by the volume change of only grains, here denoted by ΔV_s.

ΔV = ΔV₀ + ΔV_s,

This may be interpreted as volume change of the only solid phase.

Taking into account that the initial volume of the solid fraction is equal to ((1 − n) V), the second contribution is equal to ((1 − n) V ε_p) = ((1 − n) V C_sp).

Hence:

ΔV = V C (σ − p) + (1 − n) V C_s p,

Then, dividing all terms by V, we get the following equation:

ε_v = C (σ − p) + (1 − n) C_sp,

(17)

where ε_v now denotes the strain involving the only solid phase (skeleton and solid particles). The Equation (17) differs from Equation (16) only by the term (1 − n) at the right side. If we put ε_v= C σ’, after simple manipulations the Equation (17) provides the Equation (6). It should be noted that the effective stress here defined should be intended as the stress producing strain involving the only solid phase and it should not be confused with the effective stress as defined in Section 2.1.

The above illustrated was the line of reasoning followed by Skempton, Nur and Byerlee, which led to an experimentally validated ES formulation (Equation (5)); this, nevertheless, appears in contrast with the inapplicability of the superposition principle in the case of nonlinear elastic rock behaviour and, even more so, with the inelastic behaviour of soils. This contrast is even more evident in the case of lead shot experiments, for which an inelastic behaviour is observed due to the spatial pellet rearrangement combined with phenomena of crystal plasticity involving individual lead spheres. In the next section we deal with the theoretical problem of superposition principle in the case of nonlinear elastic behaviour of rocks, referring to the following sections the case study of soils and lead shot.

The superposition principle is not generally applicable to the case of nonlinear elastic media (Section 2.3). For these reasons, the proof of applicability of the superposition principle assumes a key role in the theoretical treatment of ESP, as it allows us to validate Equation (11), from which (i) follows all the considerations drawn in Section 2 about stress–strain and strength behaviour of rocks and (ii) Equation (15) is derived, which provides the basis for the above illustrated Skempton–Nur–Byerlee proofs.

We rigorously prove below that, under the hypotheses introduced in Section 2.2, the superposition principle can be applied also to the case of nonlinear elastic porous solids.

4.2. Proof of Applicability of the Superposition Principle

The superposition principle requires that the elastic problem under consideration complies with two fundamental requirements: (i) linearity of governing equations and (ii) that there is no significant variation in geometry of the boundary surface (e.g., [57]). In our model the first requirement is guaranteed by the linear elasticity of the material constituting the porous medium, whereas the second is not a cause of variation in pore surface shape, whose non-negligibility is proven by the often observed considerable change in the elastic parameters of the aggregate (we recall that linear elasticity of the constituent material does not imply the linearity for the porous aggregate which is mainly controlled by pore shape geometry; Section 2.2, Section 2.3 and Section 3.3). It is pointed out that the solutions of the system of Equation (8) must fulfil the boundary conditions of Equation (9) on the deformed surface. To better understand this concept, consider the following example. Imagine subjecting a control volume, with an undeformed boundary surface Σ^I, to a stress σ_a, then subsequently unloading the sample and applying a second stress σ_b. Let Σ^IIdenote the deformed surface after application of σ_a and by Σ^III that obtained after application of σ_b. Let ψa(x) denote the stress field associated toσ_a and byψb(x) that associated toσ_b. Note that ψa(x) fulfils the boundary conditions of Equation (9) on the surface Σ^II and, correspondingly, ψb(x) on the surface Σ^III. If we now imagine submitting the control volume to the stress (σ_a + σ_b), the boundary surface becomes Σ^IV, which in general is different from Σ^II and Σ^III and, therefore, results:

ψ_ij(σ_a + σ_b) ≠ ψa_ij(σ_a) + ψb_ij(σ_b),

(18)

as neither ψa(x) nor ψb(x) generally fulfil the boundary conditions on the surface Σ^IV.

Therefore, the superposition principle is not valid in the considered case.

We will now prove that the superposition principle can also be applied in the case of nonlinear elasticity of the porous medium (as defined in Section 2.2), in the special case in which one of the two stress systems consists of a uniform hydrostatic pressure, applied to the whole boundary, i.e., on the external and pore surfaces.

Preliminarily, we provide the following proof that is achieved by applying well-known principles of similarity:

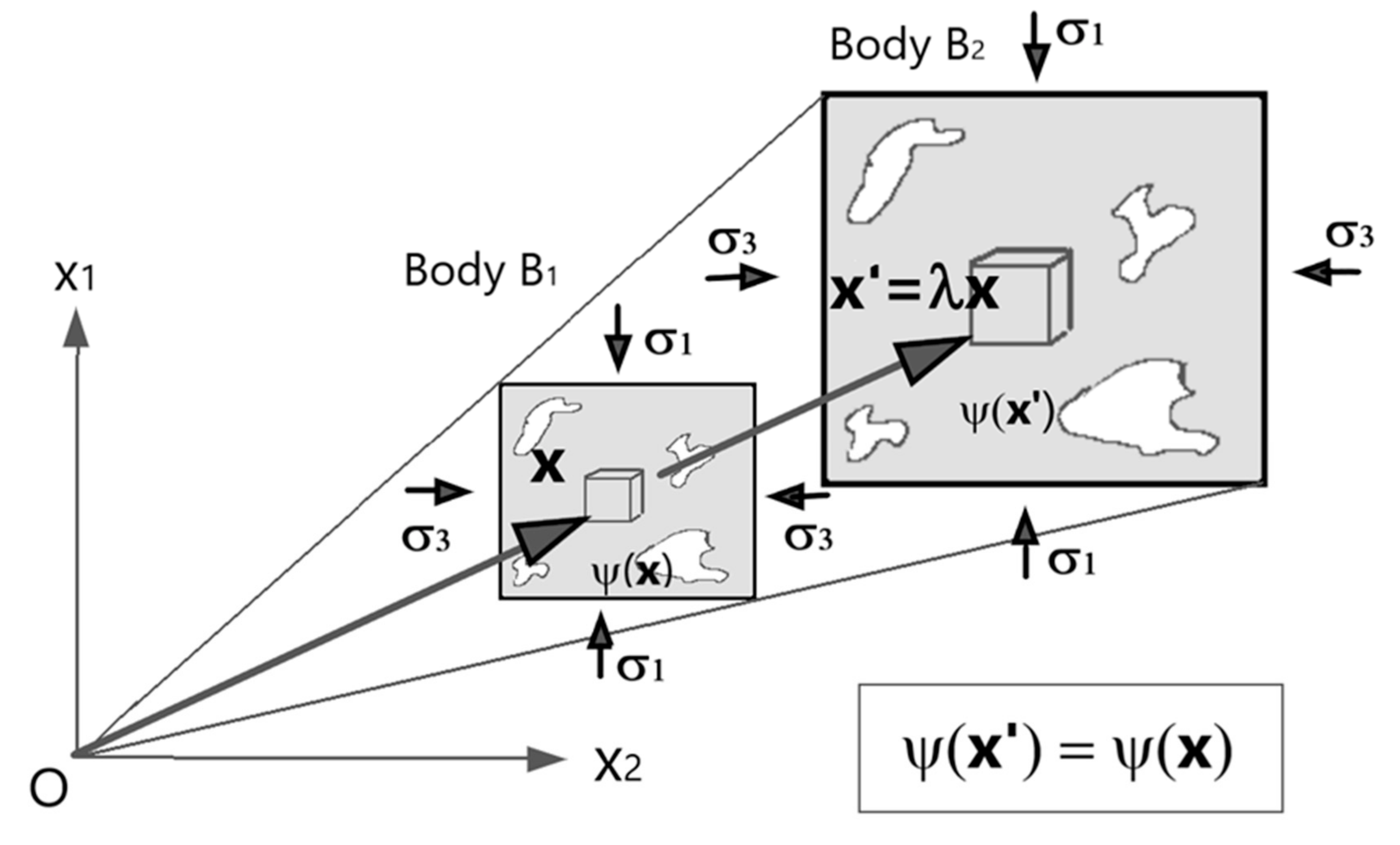
• Proof 1—the system of Equation (8) provides solutions that depend only on boundary surface shape and not on size.

Let us consider two geometrically similar bodies indicated with B1 and B2, i.e., such that B2 can be obtained from B1 by setting x’ = λx (Figure 4).

Let us imagine submitting them to the same system of stresses, so that the boundary conditions are the same for B1 and B2. Let us now consider system (8). Dividing both sides by λ² and taking into account that (∂²/∂x’_i²) = 1/λ² (∂/∂x_i²), we obtain the system:

(1+ν) ∇’²ψ_ij + ∂2ψ_kk/∂x’_i∂x’_j = 0,

(19)

where∇’² denotes (1/λ²∇²), which is formally identical to the system (8).

The application of the equation system (19) to the body B2 provides the identical solution obtained by use of the system (8) for the body B1. We can therefore conclude that, denoted by ψ(x) the solution relating to the considered boundary conditions, it results ψB1(x) = ψB2(x’) for each x belonging to B1.

• Proof 2—the superposition principle can be applied, even in the case of nonlinear elasticity of the porous medium, in the special case in which one of the two stress systems consists of a uniform hydrostatic pressure, applied to the whole boundary surface.

Let us now consider the same described above example of porous control volume submitted to the stress (σa + σb), in which the load σb is replaced by a uniform pressure p acting on the whole boundary, i.e., outer and pore surface, whose related solution is ψp(x): ψp_ij = δ_ijp. Use the same notation as above for the deformed surfaces (Figure 5).

In this case, as the pressure p produces a strain consisting of a geometric similarity, it follows that the surface Σ^IV is geometrically similar to Σ^II, i.e., the one that would be obtained for p = 0. Therefore, the solution ψ_a(x) fulfils the boundary conditions (9) also over Σ^IV. Taking into account that the solution ψp_ij= δ_ijp, fulfils the boundary condition relating to a uniform pressure for whatever boundary shape, then it results:

ψ_ij(σ_aij + δ_ijp) = ψa_ij(σ_aij) + δ_ijp,

(20)

as both terms on the right side fulfil the boundary conditions on Σ^IV.

By replacing σ_aij by the stress exceeding the pore pressure (σ_ij–δ_ijp), i.e., Terzaghi’s ES, we achieve the Equation (11), which is therefore valid together with all consequent above drawn considerations about ESP (Section 2).

4.3. ESP for Rock Strength

Based on field observations and theoretical considerations, many authors agree that fractures in rock start at cavities and microcracks ([105,112,113,125,126,128,129] and references therein, [130,131] and many others). Whilst shear fracturing dependence on Terzaghi’s ES can somewhat easily be explained by a reduction of the normal stress over the slip plane (e.g., [56,132]), tensile jointing is still controversial. Anyway, tensional, as well as shear, fracture growth is mainly affected by tensions acting in areas of high stress concentration, such as fracture tips. Namely, no matter if mode I, II or III fractures are considered, in the context of brittle strain the local stress needs to be sufficient to produce detachment between adjacent crystals or between two portions of the same crystal, associated to bond breaking at the crystal lattice scale. According to the leading models of mode I crack growth of Griffith [57,133,134,135], of Barenblatt (e.g., [136]) as well as of Nonlocal Continuum Field Theory [137,138], such phenomenon is characterised by stresses at the fracture tips (microscale stress) greater than remote stress (macroscale stress) of several orders of magnitude. For the kind of glass used in his experiments, Griffith found a theoretical tensional strength of ca. 11 GPa (1.6 × 10⁶ psi in his original paper). Theoretical tensile strength of common crystals, such as quartz or calcite, are of the same order of magnitude of that of Griffith’s glass (ca 10 GPa), whereas tensile rock strength commonly falls in the range 1–5 Mpa. Let us now consider a porous rock control volume, filled by fluid and under a total stress in the range 0–130 MPa (pertinent to depth in Earth crust within about 5 km). In order to achieve a tensional ES of the order of tensile strength, pore pressure ranges between the order of magnitude of tensile strength, at shallow depths, and that of total stress, at large depths. In all these cases pore pressure, which can attain maximum values of 0.13 Gpa, is negligible with respect to crystal lattice scale local stresses at crack/fracture tips, which are of the same order of magnitude of theoretical strength, i.e., about 10 GPa. Therefore, Equations (12) and (13) are always verified in Earth crust within 5 km depth and, with a good approximation also at a greater depth (e.g., 10 km).This is also valid for crystal plasticity, as also in correspondence of dislocations there are considerable stress concentrations which are responsible for various phenomena of dislocation creep, sliding etc., as evidenced by Burgers [139] and references therein, as well as later theoretically discussed by Eringen ([137,138,140], Section 6). A rigorous proof of this argument, related to both cases of crack growth and crystal plasticity, may be achieved, starting from our results, through criteria of the Nonlocal Continuum Field Theory, by setting Equation (11) as remote stress in order to calculate the stress field at crystal lattice scale ([137,138,140], Sections 6.10–6.15), nevertheless its formal development goes beyond the purposes of this work.

As rock brittle as well as ductile inelastic behaviour is mainly controlled by concentrated stresses according to Equation (13), which are fully dependent on Terzaghi’s ES, this explains why rock strength is substantially controlled by this latter ES.

4.4. Extending the Achieved Theoretical Results about Rocks to Granular Materials

The extension to soils and granular media of the above-illustrated model is not a trivial conclusion, as soils, unlike rocks, always exhibit inelastic behaviour. It is indeed pointed out how the differentiation between stress–strain and strength for soils is purely conventional, the strain process always being irreversible. Furthermore, as observed by Lade and de Boer [54], in nature a variety of porous media exists with intermediate characteristics, such as e.g., pyroclastites, weakly cemented sediments etc., for which rock and soil represent two extreme situations of a continuum of possible cases. Therefore, strictly speaking, the behaviour of these media should be studied according to the plasticity theory. Nevertheless, taking into account that clasts and crystals which constitute the porous aggregate show linear elastic behaviour, the Theory of Elasticity can provide some useful answers about local stress distribution within granular media.

Soil inelastic strain is a consequence of reciprocal displacements of the component clasts, which depend on their elastic strain both in terms of small variation in shape and of variation of forces on the contact areas. Let consider two identical granular bodies, whereby identical here we mean that one is an unrealistic replica of the other, i.e., that they have identical corresponding particles with identical spatial arrangement; if for two even different combinations of boundary stress systems the solutions of the elastic equilibrium equations provide identical results for each corresponding clast at a certain time, then the subsequent particle rearrangements will be the same and the entire (inelastic) strain history will have the same course. Furthermore, in theory of elasticity, when we consider the stress acting on an ideal surface inside a body, no matter whether the body part on one side of such surface is replaced by the stress exerted by it or if the two body parts on this surface are simply at contact or welded. When considering a system of bodies in contact with each other, such as e.g., clasts in a soil, if the system is in equilibrium (i.e., the particles do not move reciprocally) it can be considered as a single porous elastic body. When the applied forces on the boundary are such that cause mutual displacements between particles (i.e., if the local tangential force exceeds the local friction on contact between two particles, producing a sliding) then the system will reorganise itself, reaching a new spatial arrangement. On this new configuration it will be possible hypothetically to reapply the equations of elasticity as if the set of particles were a single body. These considerations do not allow one to calculate local stresses within inelastic soils but are sufficient to conclude that Equation (11) is applicable also within soil constituting particles.

In soils, as well as in granular media of various nature such as e.g., metal powders, the reciprocal displacement between grains (i.e., the macroscopic strain of aggregate) can occur (i) in the absence of significant grain deformations, as in the case of soils under load conditions in usual geotechnical applications, (ii) accompanied by grain fracturing (e.g., experiment on gypsum sand under high pressure by Lade and de Boer, 1996 [54]) and/or (iii) by means of a marked plastic strain of grains (e.g., experiment on lead shots under high pressure by Skempton [7]).

(i)

It is legitimate to assume that there is high stress concentration on the contact areas and that, therefore, in Equation (11) the pressure p is negligible with respect to the local stress between particles, being this latter of the same order of magnitude of the ratio between external stress σ and contact area ratio ac, as defined in Section 1. It follows that local stresses at particle contacts comply with Equations (12) and (13) and therefore they depend, with excellent approximation, uniquely on Terzaghi’s ES.

(ii)

Analogously to the case of rock fracturing, marked stress concentrations occur at fracture tips and, therefore, also particle brittle strain is controlled by Terzaghi’s ES.

(iii)

This strain mechanism is common for metal powders and also explains lead shot behaviour, which was discussed by Skempton [7]. In this case it can be assumed that there is no significant interaction between crystal plasticity phenomena and local hydrostatic pressure and namely that (a) pressure variations do not significantly hinder/favour phenomena such as dislocation sliding and (b) that following or simultaneously with dislocation gliding, the material always reacts to local hydrostatic pressure in the same way, i.e. according to elastic behaviour. The hypothesis of point (a) is guaranteed as metals exhibit negligible frictional behaviour showing intrinsic friction angle values near to zero (e.g., [7]); furthermore, near dislocations relevant stress concentration occur and therefore local stress complies with Equations (12) and (13).The hypothesis (b) is clearly an approximation as local plasticisation can lead to local anisotropies and heterogeneity within single clasts, due to dislocation propagation/extension/formation. However, it appears reasonable and in agreement with the experimental evidence in which nonporous crystalline aggregates, which do not show significant iso-orientations of crystals, show macroscopic linear elastic isotropic response at hydrostatic pressures, although local deviatoric stresses may occur at the interface between neighbouring crystals. Anyway, the assumption that the rock behaves elastically in hydrostatic compression and that viscoelastic effects occur only in shear is commonly adopted (e.g., [56], Chapter 9).

As particle aggregate strain is mainly controlled by concentrated stresses at the contact areas or at fracture tips within clasts or even in correspondence of crystal lattice dislocations, for which Equations (12) and (13) are valid, it follows that also granular media strain is mainly affected by Terzaghi’s ES. Analogously to the case of rocks, two identical loaded soil specimens, one subjected to pore pressure and one in dry condition but registering the same difference (σ_ij−δ_ijp), exhibit macroscopic strain which differ only by a small volume change associated to p. Therefore, also for granular media under high pressure the ES formulation according to Equation (5) may be suitable in order to take into account such small volume strain difference, whereas all transformations involving pore surface shape change, including strength behaviour, are governed by Terzaghi’s ES.

4.5. Validity Limits of the Illustrated Proof

The main restricting assumption in the here proposed proof of ESP is related to the hypothesis of linear elastic, homogeneous, isotropic constituting material. Rocks are constituted by crystals which commonly exhibit linear elastic behaviour for a wide range of stress values. Therefore, the linear elasticity of crystals is usually guaranteed in many geological processes, although this does not ensure linear elastic behaviour of the aggregate, a cause of change in shape of pores and/or fractures, pore collapse [8,31,55,58,59,61].

Many rocks are constituted by randomly oriented anisotropic crystals and as a consequence an elementary volume including many crystals, but no voids such as pores or fractures, shows isotropic features as well as with a good approximation linear elastic behaviour. Nevertheless, the hypothesis of elementary volume smaller than pores and/or clasts in some cases may be in contrast with that of elementary volume including many crystals, so leading considering volumes containing one or few crystals. In this instance the mentioned assumption implies an approximation that leads to neglecting local deviatoric stresses associated to local anisotropies and/or heterogeneities; so, in these cases, the validity of this model with the related approximation needs to be confirmed experimentally.

In some cases, rocks show preferentially oriented crystals (e.g., metamorphic rocks), so exhibiting an overall anisotropic aggregate behaviour or they show marked heterogeneities of the constituent material (i.e., not only associated to heterogeneous pore/fracture spatial distribution). In these cases, the above-mentioned assumption is strongly approximated or even invalid and, consequently, the derived model may fail. In such cases a more sophisticated theory, such as the Theory of Porous Media or Poroelasticity, may be needed in order to rigorously deal with the concept of effective stress.

Finally, as we are here mainly interested in the role of pore pressure at shallow crustal depths (i.e., up to 10 km) dominated by geological processes of brittle strain, in this paper we didnot consider the cases of: (i) unsaturated rocks, (ii) finite strain poroelasticity, and (iii) pressure exceeding the order of magnitude of some hundreds of MPa. The case of unsaturated soil and rock was not taken into account as it is pertinent to very shallow depths; nevertheless, given its relevance in soil and rock mechanics, interested readers are addressed to relevant papers [141,142,143]. Poroelasticity at finite strain wasnot considered here as brittle strain phenomena (i.e., fracturing) occur before rock reaches large strain. However, recent interesting developments about this topic can be found in the literature [144,145,146].

5. Open Issues about Rock Fracturing and Perspective of Future Research

5.1. Rock Faulting and Earthquakes

The role of coseismic thermal overpressurisation is still unclear; if it is known that it is among the competing phenomena in fault slip evolution [43,47,48,49,50,51,52,53], it is not clear what its weight is and how it varies at different depths in the Earth crust.

The coseismic increase in fluid pressure depends on tendency of fluid to increase its volume as a cause of phase transition when temperature increases and from elastic moduli of confining rock. The greater the rock stiffness, the smaller the increase in volume between fault walls and therefore the greater the increase in fluid pressure. At low effective pressure values (e.g., below 20–30 MPa) rock compressibility may be greater of one or two orders of magnitude than that observed at higher pressure (e.g., [7,8]). Therefore, for low ES values, e.g., at limited depths in the Earth crust, the co-eismic overpressure may be less relevant. On the other hand, according to overburden stress and geothermal gradient, water tendency in volume increase in case of phase transition resulting from increase in temperature may be less relevant at high depth. By way of example, at a depth of 10 km, temperature may be above 300 °C; when water temperature approaches the critical one (374 °C), the difference between volume of liquid phase and vapor phase is progressively reduced, until it disappears at the critical temperature. Under these conditions, any water phase transition may produce a minor increase in fluid pressure, compared to what occurs in more superficial rocks.

This phenomenon could contribute, together with well-known rheological behaviour criteria of rock materials at different pressure and temperature conditions, tohindering earthquake triggering at limited depth (less than 2–3 km) as well as at depths greater than 10 km (first brittle-ductile transition zone). It should be noted how this circumstance is in agreement with the statistical distribution of earthquakes in the upper crust observed by Marone and Scholz [147], in which the frequency is very limited at depths of less than 3 km and greater than 10 km. This aspect of earthquake thermal overpressuring is still scarcely studied and might be object of future research.

On the other hand, the effect of fluid overpressure in enhancing faulting process instability still appears controversial and still needs confirmation. In recent a work Scuderi and Collettini [107], based on experiments simulating induced seismicity, have pointed out how, according to the model illustrated by Scholz [148], fluid overpressure should stabilise fault slip, favouring stable aseismic slip rather than dynamic earthquake triggering. With reference to this issue Scuderi and Collettini [107] commented as follows: “This apparent contradiction of the role of fluid pressure in fault stability poses a serious problem in our understanding of earthquake physics with numerous implications, including a better assessment of the risk of human induced earthquakes”.

5.2. Rock Jointing

Several aspects of minor joint formation processes in rock are still unclear. Among these, main open problems about rock jointing are hydraulic fracturing, both natural and artificial, as well as natural joint sequential filling process whose related models often appears in contrast with field observations, particularly in fine-grained rocks. Main limitations of our understanding of hydraulic fracturing are likely due to the fact that leading models illustrated in Section 3.6.2 are focused on single joint growth processes, whereas many of joint sequential filling models do not take opportunely into account the role of fluid pressure heterogeneity in interaction between growing joints.

5.2.1. Natural and induced Hydraulic Fracturing

Regarding hydraulic fracturing due to a rapid increase in pore pressure, there are two main problems: (i) fluid pressure heterogeneity and (ii) determining the increase of the latter in different fracture sets occurring in rock.

(i)

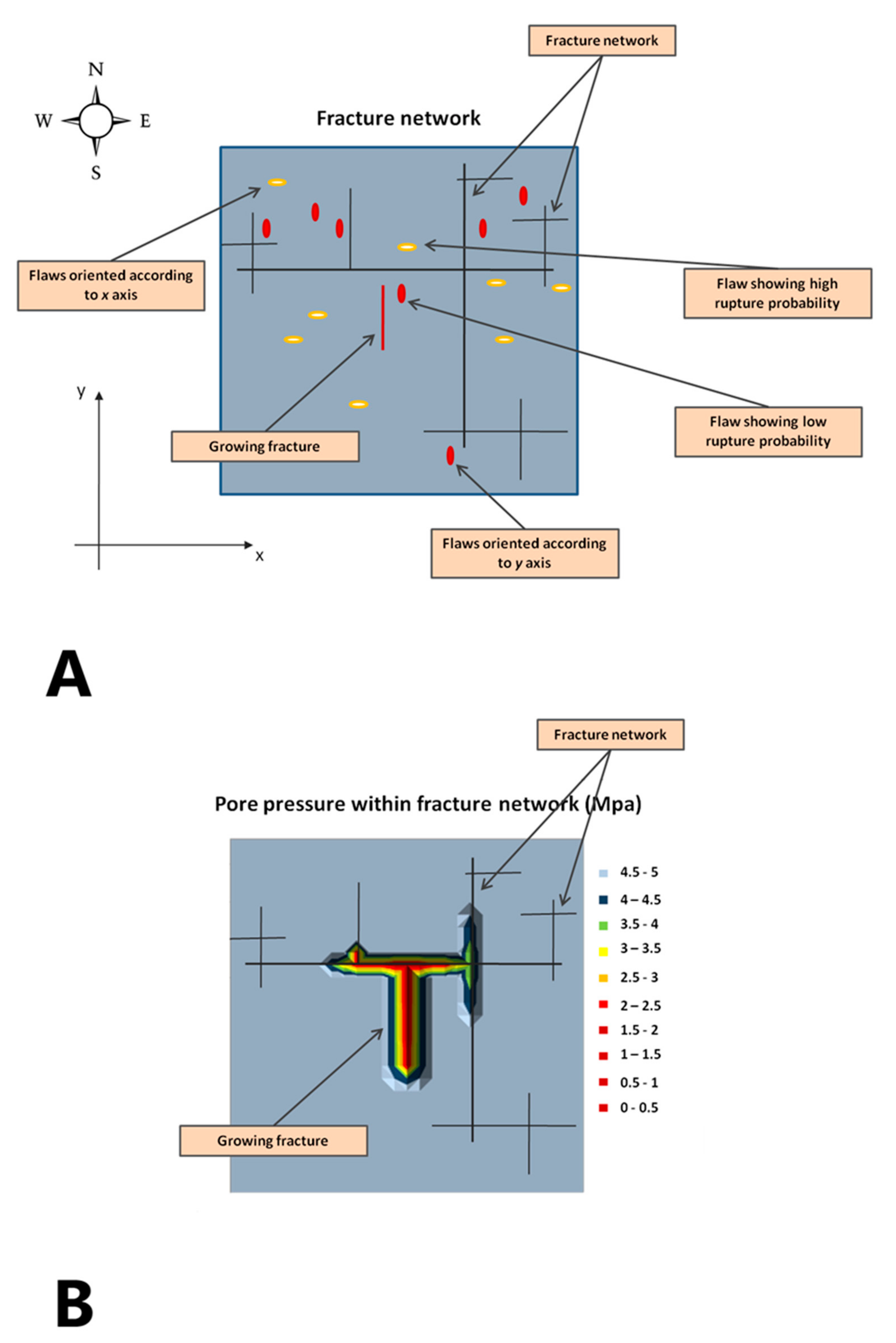
When pore pressure is markedly heterogeneous, it also varies within any generic control volume containing pores and cracks, as defined in Section 2.2; therefore ES definition is not univocal (Section 3.6.2) and, moreover, Equation (11) cannot be applied as it assumes that pore pressure is locally homogeneous within the control volume (Section 2.2). This makes it difficult to search for expressions in closed form able to describe the effect of pore pressure on fracturing processes; namely, it is complicated to predict the behaviour of saturated porous media on the basis of models involving dry media. By way of example, if we use the stress transition model proposed by Bai and Pollard [125] to analyse the joint sequential filling process (Section 3.6.3) in presence of pore pressure, there are no difficulties in the case where such pressure is homogeneous, whereas it is problematic in case it is heterogeneous. In fact, in the former case, by imagining superimposing a uniformly distributed fluid pressure over pore and external surfaces to the boundary stress, a solution is obtained which complies with Equation (11), in which the fracture tip stresses satisfy Equations (12) and (13). This allows us to reuse the solutions obtained by the authors (by means of finite element method numerical simulations) in order to evaluate the effect of stress transition on growth of new or pre-existing fractures. In case of heterogeneous fluid pressure, this operation is not allowed (Section 4.2) and the stress transition quantification would require the performance of new numerical or analytical simulations that take opportunely into account also the associated fluid dynamics.

(ii)

Pore pressure distribution evaluation within the different overlying fracture subsystems occurring in rock requires use of multiple-porosity models based on adequate geological structural models, able to characterise the different hierarchies of fracture sets ([116,149], Chapter 3.4). Nevertheless, an analysis of the available scientific literature shows as such models are scarcely utilised. Consequently, also the development of theories and methods aimed at natural or artificial hydraulic fracturing modelling in complex fracture networks still shows serious limits and several unclear aspects. Use of hierarchical fracture network models associated to appropriate multiple porosity ones may be object of future research.

5.2.2. Natural Joint Sequential Filling

With reference to natural joint sequential filling processes, there are still several unclear aspects as the proposed models cannot explain different field observations and it is still not clear how these processes are affected by the pore pressure. Odling et al. [150] have pointed out that in bedded rocks it is possible to systematically recognise, within each joint set, two overlying subsets called stratabound and nonstratabound fractures. The former are those joints that completely cut a layer, show regular spacing, which commonly appears in good agreement with the above-illustrated joint saturation models (e.g., [151,152]). It is highlighted that the works by Bai and Pollard [124,125,126,127] were mainly aimed at the study of developing of stratabound fractures (although in these works this term was not yet in use) and therefore it is unclear if such models can also be used in order to understand the evolution processes of nonstratabound joint sets.

Nonstratabound joints exhibit irregular/clustered spacing and variable aperture values over several orders of magnitude (e.g., [116,153,154,155,156,157,158,159]). This is a key point of this topic as, mainly in fine grained rocks, for nonstratabound joints the concept of fracture spacing is meaningless if a lower aperture threshold value is not preliminarily defined [155,156], as for the same outcrop different mean spacing values may be associated to different (arbitrarily chosen) lower aperture threshold values. The smaller this latter threshold value the greater the fracture intensity, up to values of thousands of fractures per metre. Micro-structural analysis has pointed out that, at the crystal scale, a maximum fracture density is observable, which depends from crystal size [116], with associated spacing values ranging from tens of centimetres scale in coarse grained rocks to submillimetre one in fine-grained rocks. Furthermore, in fine grained rocks such joints usually exhibit exponential statistical distribution of spacing values on different scales of observation (e.g., [156,157]) and also in the case of medium or coarse grained rocks, in which this distribution might be different from the exponential (e.g., Log Normal), it is usually characterised by a marked skewness. On the other hand, as observed experimentally by Rives et al. [160] and through an accurate statistical analysis of field data by Bao et al. [161], the distribution of spacing values shows a skewness gradually decreasing from high values in the early stage of sequential filling process (associated with high values of average spacing) until it vanishes when the joint saturation condition is reached (minimum average spacing).

For these reasons, the joint saturation condition envisaged by the stress transition theory—minimum spacing to bed thickness ratio equal to 0.27 [126] and zero skewness statistical distribution—is incompatible with field observations involving nonstratabound joint sets in rocks of different grain size and particularly in medium-fine grained ones.

Regarding the nucleation of new fractures in the surrounding of pre-existing stratabound fractures, i.e., at a distance less than the critical one, Bai and Pollard [125,126] point out that their model is not applicable in these cases and that this phenomenon may be attributable to heterogeneity of the local stress field near flaws or microcracks or to the effect of pore pressure.

Hooker and Katz [162] studied the effect of sin kinematic cementation on vein spacing, nevertheless they concluded that, although the resistance to fracture widening by cement can reduce such spacing, it is not sufficient to explain the systematic clustering of natural veins. An alternative model aimed at studying the development of nonstratabound joint networks could be provided by subcritical joint growth [163,164], which may explain several case studies. However, the hypothesis that all nonstratabound joint sets develop in subcritical conditions appears rather restrictive. An interesting joint sequential filling model has recently been proposed by Schopfer et al. [165], which relates joint saturation and interfacial friction between mechanical layers and, although there are limits such as e.g., bidimensional modelling, could provide the basis for interesting future research.

The main issue related to the above-illustrated models is the incompatibility among the concepts of stress shadow and the often-observed exponential distribution of spacing values between nonstratabound joints. In fact, this kind of distribution indicates a uniform random location of the fractures along an ideal orthogonal line, which may imply that fracture nucleation occurs regardless of the occurrence of other fractures in the surrounding area.

Recent studies are aimed at analysing the interaction between fluid flow and fracture mechanics, as well as to the three-dimensionality of such phenomenon, at the level of fracture network rather than single fracture (e.g., [166,167]). Aspects of the joint filling problem that may be appropriately considered and that might be object of future research are related to (i) stress relaxation due to viscous phenomena in rock, (ii) three-dimensionality of the joint filling phenomenon and (iii) fluid dynamics.

(i)

Rock elasto-viscous behaviour leads to relaxation of the internal elastic stresses. This phenomenon also affects joint related stress shadow, which, in a variable time range depending on rock properties as well as pressure and temperature conditions, can experience a significant reduction. By way of example, a recent fracture tends to close when the tensile stress that produced it is removed, whereas an ancient fracture shows residual opening even in the absence of traction. Therefore, it is presumed that, if immediately after the formation of a fracture at a certain distance from it, there is a reduction in tension stress by a certain percentage or a transition to compressive stress, after an extended time (e.g., hundreds or thousands of years) such stress reduction decreases.

(ii)

Let us consider a scan line carried out orthogonally to a certain joint set. The intercepted fractures contribute to the extensional strain along the sampling line, nevertheless, they generally have nucleation points located outside the outcrop plane. Therefore, apparently closely spaced parallel fractures on the outcrop plane may have triggered in points far enough apart to avoid significant interaction during the nucleation phase.

(iii)

Fluid dynamics is a fundamental aspect of hydraulic fracturing, as different joint subsets belonging to a fracture network, as well as other voids such as pores and microcracks, can be affected by different variations in fluid pressure [116] in non-steady-state hydraulic condition. Here it is pointed out as in case of heterogeneous pore pressure, e.g.,in the event that a fracture shows internal fluid pressure different from that present in nearby pores and fractures, it happens that this difference in fluid pressure—positive or negative—is not counterbalanced by that in the surrounding rock, thus providing the fracturing driving stress.

In order to understand the significance of the above-illustrated aspects of fracturing processes, consider the following simple two-dimensional model. Let us consider a fracture network composed by two orthogonal to bedding, as well as orthogonal each to other, joint sets (Figure 6A).

Denoting by Set 1 the joint set N-S oriented and by Set 2 that E-W oriented, let us suppose the occurrence of several randomly distributed elliptical flaws (clearly the reasoning can be extended to variously shaped elongated flaws); in Figure 6B only those showing long axis parallel to the two fracture sets are represented: red flaws are parallel to Set 1 and yellow ones to Set 2. Furthermore, let us assume that such fractures are ancient and therefore, due to viscous relaxation, the fracture associated stress shadow is significantly declined. If a microcrack starts to grow (denoted by a vertical red segment in Figure 6A) a pore pressure drop occurs within it which induces a hydraulic gradient, as well as a tensional stress release, in the surrounding rock, which hinders rupture of parallel flaws (red flaw in Figure 6). Fracture propagation velocity and internal pressure drop proceed according to the Renshaw and Harvey model [118,119]. As the effective remote stress at equilibrium is inversely proportional to the fissure length square root (e.g., [56,118,119]), this may experience notable decline. For instance, for a microcrack of millimetre initial length that reaches a 10 cm length, the equilibrium effective remote stress might be reduced of one order of magnitude; such decrease corresponds to an internal pore pressure decrease. If the growing fracture reaches the nearest joint belonging to the pre-existing network, a fluid flow starts from network to the growing fracture, which causes a pore pressure drop in the fracture network (Figure 6B). As commonly there is notable permeability difference between fractures and nonfractured host rock, we expect some relevant effects: (a) pressure drop substantially involves only the fracture network near the contact area and a sharp layer of nonfractured host rock (Figure 6B), pore pressure variations being more rapid within more permeable subsystems [116], (b) propagation velocity of the growing fracture is significantly accelerated, it does not follow anymore the Renshaw and Harvey model, being now controlled by fracture network permeability, (c) the induced fluid pressure drop within fracture network causes a notable decrease of the associated stress shadow, which has already experienced a decline as consequence of rock viscous behaviour; namely, such internal pressure drop might be sufficient to trigger a new fracture from near flaws, in an orthogonal direction with respect to the growing joint, as pictured in Figure 6B. Therefore, a growing fracture which intersects an already existing joint network may trigger new fractures in its orthogonal direction. An analogous model can be applied also to fractures or microcracks already connected to a pre-existing fracture network.

6. Concluding Remarks, Open Issues and Perspectives

Over the past century the theoretical ESP foundations have been deeply investigated and established, nevertheless some perplexities remain and these do not appear to have been always entirely perceived by many in the science community, likely as (i) many different ES formulations have been proposed and (ii) most of related theory, involving Poroelasticity and Theory of Porous Media, is very specialised.

In this work we provided a theoretical justification of ESP based on classical theory of elasticity methods. It can be proved that in a porous medium made up of isotropic linear elastic material but generally showing anisotropic nonlinear elastic behaviour in accordance to shape, orientation and distribution of voids, the local stress at a scale smaller than pores and/or clasts is given by (ψ_ij = ψ_0ij(σ_kl−δ_klp) + δ_ijp) (Equation(11)), i.e., is the sum of two contributions, one depending on Terzaghi’s ES (σ_kl−δ_klp) and one consisting of an isotopic pressure p. The former produces the often more evident strain, at microscopic as well as macroscopic scale, in terms of aggregate volume and shape change as well as of pore surface shape transformation. The latter is only responsible for a small volume reduction, according to the intrinsic bulk modulus of the solid K_s, with no shape—and pore shape—change.

This provides an explanation of the ESP for stress–strain behaviour of rock, as two identical porous bodies, one subjected to pore pressure and one in dry condition but showing the same difference (σ_ij−δ_ijp), exhibit macroscopic strains which differ only by a small uniform volume change associated to p. Furthermore, also rock strength behaviour can be explained by means of the illustrated relation, as fracture growth is controlled by forces acting in areas of high stress concentration, such as fracture tips, in which the term (δ_ijp) is negligible. Therefore, the driving stress, now given by (ψ_ij = ψ_0ij(σ_kl−δ_klp)), depends uniquely onTerzaghi’s ES which, consequently, controls rock strength behaviour.

Such considerations can be extended to soils and granular media of various nature such as e.g., metal powders, as within these materials reciprocal displacements between grains can occur (i) in the absence of significant grain deformations, as in the case of soils under load conditions in usual geotechnical applications, (ii) accompanied by grain fracturing and/or (iii) by means of a marked plastic strain of grains. In all these cases, macroscopic strain is controlled by concentrated stresses (i) at contact area, (ii) at fracture tips and/or (iii) at crystal lattice dislocations, which, likely to rock, depend on Terzaghi’s ES. Furthermore, as within each clast Equation (11) holds, also for soil under high pressure the volume strain due to pore pressure p is superimposed to macroscopic strain, so justifying the Skempton’s ES formulation, in case of high pressure.

Based on such ESP model, various ES formulations were reviewed here. The illustrated discussion highlights as the ES definition is substantially conventional and related to the problem being treated. Among various ES formulations, that proposed by Terzaghi appears often particularly appropriate, for its simplicity and as it describes a stress system directly related to the internal geometry of pores and to the mechanical characteristics of the porous medium.

Furthermore, the role of pore pressure in affecting various geological fracturing processes at several scales of observation, such as faulting and jointing, was illustrated. In such research area, we find some still open questions, mainly related to not yet fully understood character and role of heterogeneous pore pressure fields in porous media. Issues of particular relevance and complexity are the following:

• Role of coseismic overpressurisation: if it is known as it is among the competing phenomena in fault slip evolution, it is not clear what its weight is and how it varies at different depths in the Earth crust. Furthermore, the effect of fluid overpressure in enhancing faulting process instability has been questioned by recent studies and still needs confirmation.
• Natural and induced hydraulic fracturing: although the single fracture growth is now a well-established process, hydraulic fracturing modelling in complex fracture networks still shows serious limits and several unclear aspects, mainly a cause of use of often inadequate flow models. According to recent trends in modelling, pore pressure distribution evaluation within different fracture subsystems requires use of multiple-porosity models based on adequate geological structural models, able to characterise the different hierarchies of fracture subsets in rock.
• Joint sequential filling: the observed geometrical features of nonstratabound joint networks, such as natural clustering, cannot be explained by means of currently available models in literature and so these remain substantially not yet understood. Aspects of the joint filling problem that may be appropriately considered and that might be object of future research are related to (i) stress relaxation due to viscous phenomena in fractured rock, (ii) three-dimensionality of the joint filling phenomenon and (iii) characterisation of fluid flow and the associated pore pressure field within fractured rock, as well as interaction between flow and fracture mechanics.