LLUNPIY Simulations of the 1877 Northward Catastrophic Lahars of Cotopaxi Volcano (Ecuador) for a Contribution to Forecasting the Hazards

Abstract

LLUNPIY (lahar modeling by local rules based on an underlying pick of yoked processes, from the Quechua word “llunp’iy“, meaning flood) is a cellular automata (CA) model that simulates primary and secondary lahars, here applied to replicate those that occurred during the huge 1877 Cotopaxi Volcano eruption. The lahars flowing down the southwestern flanks of the volcano were already satisfactorily simulated in previous investigations of ours, assuming two possible different triggering mechanisms, i.e., the sudden and homogeneous melting of the summit ice and snow cap due to pyroclastic flows and the melting of the glacier parts hit by free-falling pyroclastic bombs after being upwardly ejected during the volcanic eruption. In a similar fashion, we apply here the CA LLUNPIY model to simulate the 1877 lahars sprawling out the Cotopaxi northern slopes and eventually impacting densely populated areas. Our preliminary results indicate that several important public infrastructures (among them the regional potable water supply system) and the Valle de Los Chillos and other Quito suburban areas might be devastated by northward-bound lahars, should a catastrophic Cotopaxi eruption comparable to the 1877 one occur in the near future.

1. Introduction

Lahars are volcanic debris flows, mixtures of water and pyroclastic sediments with high density and viscosity. They can travel great distances (even up to 250 km) before coming to a stop, after having flowed down volcanic canyons and gorges at high speed (as much as 60–70 km/h), eventually being channeled along lowland river valleys [1]. The scale of these phenomena is determined by the total available amount of melted ice, water (also from rainfalls, local springs, creeks, torrents, etc.), and volcanic sediments [2]. Although, initially, a lahar may be relatively small [1], it may enormously grow in mass and volume since, while traveling down the volcano’s flanks, it rapidly entrains huge quantities of sediments, rocks, and water, thus expanding to more than 10 times its initial size; its speed is also constantly changing along the path. In volcanic regions, lahars represent one of the most destructive and lethal natural phenomena, once infrastructure losses and human casualties are accounted for.

On the basis of their initiation modalities, lahars can be schematically subdivided into two main categories, primary and secondary lahars. Primary lahars are those originated from direct volcanic eruptive activity, such as those nes that caused the 1985 Nevado del Ruiz disaster in Colombia [3], where lava or pyroclastic flows melted the upper ice fields and/or mixed with lower wet soil, killing 22,000 persons living downstream in the town of Armero, or those triggered by the breakout of a crater lake rim or even solely by the expulsion of crater lake waters as a consequence of an eruption [4,5]. In contrast, secondary lahars may occur in post-eruptive events or quiescent periods (such as after the 1991 eruption of Mt. Pinatubo, Philippines [6]), when heavy rainwater can easily erode loose volcanic rock and soil on hillsides and in river valleys, and typhoons or lake breakouts mobilize ash and volcanic debris of previous volcanic episodes. According to Manville [4], initiation mechanisms can greatly influence lahar volumes, compositions, flow behavior, and hazards.

Cotopaxi volcano (5897 m), in the central highlands of Ecuador, is one of the biggest, most active, and most hazardous volcanos in the world. Yet, many amongst the regions nearby and around Cotopaxi are densely populated, and agricultural and industrial activities are intensively developed within these areas. This study revisits the impact of the cataclysmic lahars that sprawled out across the northern region of Cotopaxi volcano (Figure 1), immediately after the 1877 eruption and subsequent melting of the summit glacier [7,8]. Our results also offer the opportunity to contribute to the prediction of the threats that Cotopaxi lahars may pose to local populations of the present-day highlands of Ecuador.

1.1. Approaches to Numerical Simulation of Lahars

The use of computer simulations may provide a decisive contribution in assessing the hazards and forecasting the risks associated with volcanic lahars, in order to evaluate strategies and interventions useful to their mitigation. Therefore, it is of fundamental importance to develop mathematical, physical, and computational models that can reliably define the phenomenology of lahars.

Several approaches have been adopted to model the behavior of lahars and to predict the hazards posed to downstream communities [2], e.g., empirical models based on smart correlations potentially existing among the phenomenon observables [9,10], simple rheological and hydrological models that assume reasonable simplifications as a composition-independent flow behavior or a Newtonian flow regime [5,11], partial differential equations (PDE) which approximately describe the lahars’ highly complex physics and hydrodynamics [12,13], and the multicomponent cellular automata (CA) methodology [14,15] adopted here, which is briefly summarized in the next section. It is certainly worth recalling the following models, already applied to Ecuadorian lahars: LAHARZ (GIS programs for automated mapping of lahar-inundation hazard zones) is an empirical model which computes the inundation area as determined by the lahar’s volume and channel sections [10], whereas TITAN2D (software for modeling debris flow, lahars, and pyroclastic flow) simulates granular muddy debris flows and lahars adopting a physical PDE approach based upon the Coulomb mixture theory [12]; however, neither LAHARZ nor TITAN2D accounts for the erosion and bulking processes. Such processes are not contemplated in LAHARZ because of the oversimplification inherently present in the model, while, in TITAN2D, the inclusion of the erosion process would have implied unsustainable computational times to solve the corresponding and more comprehensive PDE system. The lahars that in June 1877 catastrophically outpoured into the Río Cutuchi Valley, on the southwestern areas of Cotopaxi volcano, were indeed simulated by LAHARZ [16] according to a “many sources” simplification, i.e., assuming that the same lahars were not triggered in the vicinity of the summit glacier, but “equivalently” at lower locations already within the valleys of Río Cutuchi, Río Sasquímala and Río Barrancas-Aláquez. A previous pioneering numerical simulation of the same lahars along those three main rivers was performed by Barberi et al. [17], whose results consisted of notable graphic representations such as hydrographs, maximum flow heights at several critical spots where historical data were recorded, peak discharges, and so on, yet the erosion process was not considered in the PDE system of their model.

The inclusion of the erosion process during the lahars’ downstream motion represented a numerical breakthrough delivered by the adoption of a CA approach to the development of semiempirical computational models simulating surface flows [15]. The CA approach was actually derived from the previous SCIDDICA (Simulation through Computational Innovative methods for the Detection of Debris flow path using Interactive Cellular Automata) model [18,19,20,21] for the simulation of debris flows. Moreover, it constitutes a parallel computational paradigm for modeling complex dynamical systems, whose evolution is mainly due to the interactions among their constituent parts. The present LLUNPIY model (lahar modeling by local rules based on an underlying pick of yoked processes, from the Quechua word “llunp’iy“, meaning flood) is based on the CA computational paradigm for simulating primary and secondary lahars according to a general methodology developed for surface flows [19]. LLUNPIY was applied and validated in its various versions to past volcanic events, such as the 2005 and 2008 secondary lahars of Vascún Valley, Tungurahua Volcano, Ecuador [20,21,22,23,24,25], as well as the 1877 lahars flowing along the Río Cutuchi, Cotopaxi Volcano [20], and it was also applied to forecast future probable events [26,27].

1.2. Adopted Criteria in the LLUNPIY Simulations

In this paper, we apply to the area north of the Cotopaxi Volcano the same CA approaches we adopted in the preliminary simulations of the Cotopaxi’s west and southward 1877 lahars [21,23,24,25,26], in order to get significant insights into the hazards that future similar events can cause.

One of the main working hypotheses of the approach proposed in [21] is the instantaneous melting of the glacier (IGM), which aims at improving the “many sources” assumption underlying the LAHARZ simulations [5]. IGM permits simulating the triggering of the lahars right at the top of the glacier, without any necessity of imposing values to the lahars’ initial physical parameters at the entrance of the lower major valleys. As a matter of fact, such an alternate approach would be justified when the glacier melting is mainly due to pyroclastic flows, but there is no reason to doubt the historical chronicles [7,8] that reported the 1877 volcanic activity, which clearly indicate that pyroclastic bombing occurred or even a simultaneous occurrence of pyroclastic bombs and flows.

Pyroclastic bombing implies a more gradual glacier melting (GGM) when compared to a genuine IGM, since each one of the bombs melts ice just around its point of impact, up to a depth that depends upon the size and the temperature of the bomb. However, the GGM approach adopted in [24] assumes that each cell in which the surface of the glacier is divided is labeled by an identical probability of being struck by a falling pyroclastic bomb, which in turn melts the same amount or thickness of the ice underneath the point of impact.

The CA approach and methodology of the simulations of the 1877 southwesterly Cotopaxi lahars are here applied to the region north of the volcano. To our knowledge these are the first numerical simulations that attempt to model the two possible initial triggering phases, i.e., pyroclastic bombs and immediate melting by pyroclastic flows.

We chose a duration and frequency of the pyroclastic bombing of about 10 min, after comparing this regime with the IGM one, since smaller durations coupled to bigger frequencies of bombing produced results that are practically indistinguishable from the ones obtained by the IGM simulations.

Furthermore, runout distance, inundation area, and run-up height are determined not only by the amount of available melted ice, but also by the very physical structure of the crater. As things turn out, larger quantities of melted ice favor the southward and westward runoffs. Our simulations, and not exclusively the ones we present here, show that such a complex phenomenon may not presumably be forced within any reductionistic scheme.

We are confident that this approximation is reasonable since the Cotopaxi’s crater rim is pretty regular and circular, and such a regularity has to be reflected by a certain degree of uniformity in the directions of the ballistic impacts, even allowing for a probability of impacting any given point of the glacier that is decreasing with the radial distance from the center of the crater [28]. To strengthen this assumption, however simplistic it might be considered, we remind that the radius of the Cotopaxi’s glacier is no more than 3 km in length, and we should succeed in grasping the main effect of the GGM process by assuming that each cell of the glacier is struck with the same probability by every falling bomb.

Actually, regarding the ballistic impacts of volcanic bombs, very different scenarios ought to be expected in other events, e.g., in cases such as the 2010 Stromboli eruption [29] or the 1977 Ukinrek maars [30] where the formation of new maars during the eruption affected the directions of bombing. Lastly, the historical chronicles by the eyewitnesses Sodiro and Wolf [7,8] are evidence that catastrophic lahars actually flowed down all the slopes around Cotopaxi volcano, which supports the reliability of our assumptions.

Specifically, this paper analyzes two cases of IGM and two cases of GGM, as determined by two different thicknesses of the glacier. The simulations do not aim at reproducing the totality of the trajectory of the northward-bound 1877 Cotopaxi’s lahars. These, once triggered by the melting glacier, flowed along its northern flanks, merged nearby the southeastern slopes of Pasochoa volcano, and sprawled out after invading the Valle des Los Chillos plains, to be then channeled within the deep ravine of the San Pedro River, thus bypassing the Ilaló volcano, and eventually reaching the Pacific Ocean at the estuary of the Esmeraldas River [7,8]. Instead, we stop our simulations at about 9 km “as the crow flies” north of the Ilaló volcano, just where the present town of Tumbaco lies.

We hopefully will be able to simulate the coastal course of the Cotopaxi lahars along the Guayllabamba and Esmeraldas Rivers as soon as new digital elevation model (DEM) data covering those regions are available. The aim of these preliminary simulations is to explore possible scenarios presumably prompted by a likely new catastrophic eruption of Cotopaxi volcano. The few, although precious, historical chronicles available to us cannot comprehensively answer every question and preoccupation arising within a modern scientific context. In this sense, state-of-the-art numerical simulations may constitute powerful tools when planning is required to contain or mitigate the huge risks that future Cotopaxi lahars impose on the local populations and the territories where they presently live. We hopefully assume that the diverse scenarios here explored, according to different hypotheses, permit determining their extreme (minimum and maximum) expressions and factual materializations. The results presented here will be a matter for future and more comprehensive studies, when simulations are extended to the entire trajectory of the Cotopaxi’s lahars.

This article is organized as follows: after summarizing the main features of the geographic territory hosting Cotopaxi volcano (Section 2), we briefly report the actual event of the 1877 Cotopaxi eruption, our reconstruction being inspired by the original chronicles in Sodiro [7] and Wolf [8] (Section 3). The outline of the LLUNPIY model can be found in Section 4. The core of this investigation is presented in Section 5, and the final discussion and conclusions close this article in Section 6.

2. Physiographic Overview

Cotopaxi Volcano lies in the Eastern Cordillera of the Ecuadorian Andes about 60 km south of Quito. It is a very hazardous active stratovolcano. Since 1738, Cotopaxi has erupted more than 50 times. Syn-eruptive lahars occurred frequently during the explosive activity of Cotopaxi volcano and the larger were triggered by the rapid melting of large amounts of ice during eruptions [17]. The most violent historical eruptions occurred in 1744, 1768, 1877, and 1904, all of them causing disastrous lahars [16,17].

The presence of a permanent glacier on the upper cone is one of the principal causes, together with volcanic eruptions (lava or pyroclastic flows and surges), of primary lahars, triggered by ice and snow melting [5,16,27,31]. The present Cotopaxi eruptive episode started in August 2015 and is still ongoing.

This study concentrates on the north sector of Cotopaxi Volcano. Four other notable stratovolcanoes, mainly eroded or dormant, are present in this seismically intense area, namely, Rumiñahui (4721 m), Sincholahua (4899 m), Pasochoa (4200 m), and Ilaló (3185 m), and their location defines the local orography and the flow direction of potential lahars from the nearby Cotopaxi (Figure 1). Densely inhabited areas are the towns of Sangolquí and San Rafael, and the southern peripheries of Quito, all built on deposits formed by lahars in recent geological history. The area is crossed by the San Pedro, El Salto, and Pita Rivers, whose waters are often forced to flow within narrow gorges and deep ravines, which represent preferential pathways along which the detrital flows are naturally conveyed and channeled downstream. The overall orography of the territory is typical of a rugged volcanic environment, with high volcanic cones that sharply rise from the surrounding lowlands, and whose flanks are characterized by big gradients (35°–45°) decreasing (10°–20°) toward the foothills and valleys areas (Figure 1).

3. The 1877 Eruption

On the morning of 26 June 1877, an explosive eruption started on Cotopaxi that would generate one of the most catastrophic mudflows in the volcano history. During the eruption, tephra, bombs, and lava erupted from the vent, causing ice-cap melting which in turn triggered huge and utterly destructive lahars. This eruption was marvelously described by Sodiro [7] and Wolf [8]. Their keen chronicles poignantly report the extension of lahar floods nearby human settlements and even lahar transit times, and some later field observations even carefully estimated the glacier melting at 1/10 of its total volume [8]. In Figure 2 is shown the map drawn by Wolf [8] after his reconnaissance of the event; the areas invaded by the lahars are thoroughly mapped in the southern sector, while, in the north sector, the mudflows are only partially visible.

Water, which originates from the rapidly melting glacier, was promptly mixed with the ejected pyroclastic material and with pre-existing volcanoclastic deposits outcropping along the slopes; thus, very many lahars were suddenly triggered. These laharitic flows, channeled along the regional drainage network, destroyed everything on their path, laying waste to villages and towns downstream. On the western flank of the Cotopaxi volcano, three main debris flows were generated, which descended with a conjectured speed from about 30 m/s to about 10 m/s (depending on the slope) and reached the town of Latacunga (in the southern sector of the volcano) in about one hour; approximately at the same time, lahars generated in the northern and eastern areas of the cone reached the towns of San Rafael and Sangolquí located in the Valles de los Chillos flatlands, in the northern sector of the volcano.

A detailed analysis was carried out in order to obtain the most reliable reconstruction of such a catastrophic event. As reported by Wolf [8], the glacier melting process could have been gradual indeed, due to the effect of pyroclastic bombs with a certain frequency and characteristic duration.

4. LLUNPY Model Outline

In our paper, we applied two variations of the LLUNPIY model: (i) the first is an adaptation of the basic version, where the sudden and homogeneous melting of the summit glacier of the volcano occurs at the first step of the simulation [20]; (ii) the second adds to the previous one an “external influence“ [13], i.e., the volcano’s icecap is first melted partially and locally in correspondence with landing points where the free-falling pyroclastic bombs impact the glacier during a number of LLUNPIY steps, corresponding to the “bombing“ duration; the number of bombs is constant at each step, and a stochastic function determines the drop coordinates on the icecap struck by bombs.

The following description of LLUNPIY briefly summarizes the corresponding and more comprehensive parts of paper [14]:

<R, G, X, S, P, τ, γ>,

with the variables defined below.

• R = {(x, y) | x, y ∈ ℕ, 0 ≤ x ≤ l_x, 0 ≤ y ≤ l_y} is the set of points with integer coordinates, which individuate the regular hexagonal cells, covering the finite region, where the phenomenon evolves. ℕ is the set of natural numbers.
• G ⊆ R is the set of cells corresponding to the glacier, where the lahar is triggered after the ice melting caused by the pyroclastic matter.
• X = {(0,0), (1,0), (0,1), (−1,1), (−1,0), (0,−1), (−1,−1)}, the neighborhood index, identifies the geometrical pattern of cells, which influences the change of state of the central cell: the central cell (index 0) itself and the six adjacent cells (indexes 1, …, 6).
• S is the finite set of states of the finite automaton, embedded in the cell; it is equal to the Cartesian product of the sets of the considered substates (

  Table 1. Substates.

  Names	Description
  A, D	Cell altitude, erodible soil depth
  T, X, Y, K	Debris thickness, coordinates x and y of the debris barycenter inside the cell, kinetic head
  ET, EX, EY, EK (6 components)	External debris flow normalized to a thickness, external flow barycenter: coordinates x and y and kinetic head
  IT, IX. IY, IK (6 components)	Internal debris flows normalized to a thickness, internal flow barycenter: coordinates x and y and kinetic head

  ).
• P is the set of the global physical and empirical parameters (

  Table 2. Physical and empirical parameters of the two LLUNPIY (lahar modeling by local rules based on an underlying pick of yoked processes, from the Quechua word “llunp’iy“, meaning flood) versions, adopted in simulation. CA, cellular automata.

  Parameters		Instant Melting Values	Gradual Melting Values	Unit
  Cell apothem	a	15	15	m
  Temporal correspondence of a CA step	t	6.2 × 10−2	6.2 × 10−2	s
  Mobilization threshold	tm	1.2 × 102	1.2 × 102	m
  Energy dissipation by turbulence	dt	5.0 × 10−5	1.75 × 10−8	-
  Friction coefficient	pf	4.0 × 10−2	4 × 10−2	-
  Energy dissipation by erosion	de	3 × 10−1	3 × 10−1	-
  Parameter of progressive erosion	pe	10−3	10−3	-
  Pyroclastic bombs number for each step	n	-	50	-
  Length of time of pyroclastic bombs fall	l	-	10,000/620	step/s
  Depth of the melted ice by a pyroclastic bomb	d	-	15	m

  ), which account for the general frame of the model and the physical characteristics of the phenomenon.
• τ: S⁷→ S is the cell deterministic state transition, it accounts for the components of the phenomenon, i.e., the “elementary processes” that are sketched in the next section.
• γ: ℕ×G → S (the “external influence”) is a stochastic function that determines at each step the coordinates of the G glacier cells where pyroclastic matter can strike the icecap and consequently generate the reduction of the ice thickness and lahar formation in the initial CA steps (duration of pyroclastic bombs falling). ℕ here refers to the step number. Three parameters specify g (Table 2): n = number of pyroclastic bombs for each time step, l = length of time or duration of the volcano’s eruption prompting the fall of pyroclastic bombs, and d = depth of the melted ice induced by a pyroclastic bomb.

4.1. Summary of the LLUNPIY Transition Function

The LLUNPIY state transition function is constituted by four elementary processes [14,19]: “lahar outflows from the cell”, “soil erosion”, “turbulence effect”, and “flow composition”. In what follows, the mathematical formulae do not need to be numbered and isolated in a single or more rows, since their separation from text is self-evident; multiplication is always indicated by the symbol “×”, value variation of a substate in the state transition is expressed by a Δ followed by the name of the state, and the neighborhood index is specified by a subscript in order to indicate belonging to the corresponding cell.

Note that, in the context of CA, where the area of the cells is constant, the “height” may adequately substitute the “volume” in the model specifications without loss of generality.

4.1.1. Lahar Outflows

Outflow computation is performed in two steps: determination of the outflows $f_i$ toward the neighbor $i$, $1\le i\le 6$ according to the algorithm for the minimization of differences (AMD) [14,19], and determination of the shift of the outflows [21,23,24,25,26,27].

AMD looks to capture fundamental processes in complex systems, which evolve at a local level toward minimum unbalance conditions for some quantity $q$; the system can minimize the $q$ differences in the neighborhood of each cell by flows from the central cell to the other neighbor cells. AMD calculates the conditions of local hydrostatic balance with corrections in order to account for the dynamics according to the conservation laws of energy and momentum [14,19].

The quantity $q$ regards the “height“ of the cells in the neighborhood, where $q_0=A_0+K_0$ refers to the central cell and $q_i=A_i+T_i$, $1\le i\le 6$ refers to the other neighbor cells; the flows are also expressed in terms of “height“; the amount of matter to be distributed is $T_0={\sum }_{0\le i\le 6}{f}_i$, where $f_0$ is the amount of lahar remaining in the central cell. AMD determines the flows which minimize the following equation: ${\sum }_{0\le i<j\le 6}\left|\left(q_i+f_i\right)-\left(q_j+f_j\right)\right|$.

The outflow could be represented as an ideal cylinder, tangent to the next edge of the central hexagonal cell, whose barycenter corresponds to the debris barycenter inside the central cell, directed toward the center of the neighbor cell.

The part of the outflow which overcomes the central cell constitutes the external flow, specified by external flow substates, while the remaining part, i.e., the internal flow, is specified by internal flow substates. The shift “∆$s$“ is computed according to the following simple formula, which averages the motion of the entire mass as the barycenter’s motion of a body on a constant slope-angle $\theta$ with a shift $\Delta s=v\times t+g\times \left(sin\theta -p_f\times cos\theta \right)\times t^2/2$, where “$g$“ is the gravitational acceleration and the initial velocity is $v_0=\sqrt{2\times g\times K_0}$ [13,22].

4.1.2. Flow Composition

Once the outflows and their shifts are computed, the new situation implies that external flows leave the cell, internal flows remain within the cell with different co-ordinates, and inflows (trivially derived from the values of external flows of the neighbor cells) have to be added. The new value of the debris thickness $T$ is assigned, considering the balance of inflows and outflows with the remaining debris mass in the cell. A kinetic energy reduction is considered by loss of flows, while an increase is given by inflows: the new value of the kinetic head is deduced from the computed kinetic energy. The barycenter coordinates $X$ and $Y$ are calculated as the average weight of the coordinates considering the remaining thickness in the central cell, the thickness of internal flows and the inflows.

4.1.3. Turbulence Effect

A turbulence effect is modeled by a proportional kinetic head loss at each LLUNPIY step as follows: $-\Delta K=d_t\times K$. This formula implies that a velocity limit is de facto asymptotically imposed, for a maximum slope value.

4.1.4. Soil Erosion

When the kinetic head value overcomes an opportune threshold ($K>t_m$), depending on the soil features, then a mobilization of the pyroclastic cover occurs proportionally to the quantity overcoming the threshold, and, equally proportionally, the erodible soil depth diminishes according to $\Delta T=-\Delta D=p_e\times \left(K-t_m\right)$; the corresponding kinetic head loss is $-\Delta K=d_e\times \left(K-t_m\right)$.

5. Simulations

The CA LLUNPIY model specifically explores the effects of volcanic lahars within the geological and morphological setting of the Cotopaxi Volcano north region in order to simulate the 1877 primary lahar, following the good outcome of the simulation of the 1877 lahars invading the southern region [23,26]. The propagation of a lahar along the northern sector, with magnitude similar to that of 1877, was simulated using a digital elevation model (DEM) of recent acquisition. In this way, provided with fresh data about the current regional physiography, we can predict a hazard scenario of the areas potentially most vulnerable to a future event similar to that which occurred in June 1877. More specifically, we use SRTM elevation data (Shuttle Radar Topography Mission, in orbit in February 2000) with resolution of 1 arc-second (approximately 30 m at ground level) downloaded from NASA (National Aeronautics and Space Administration) servers [32]. A uniform layer 5 m thick of erodible detrital cover was assumed.

The summit of the volcano is currently covered with a thick layer of ice that ranges between 30 and 120 m [28]. Cáceres et al. [33] estimated that the glacier volume was approximately 1.0 × 10⁹ million m³ in 1976, considering an average thickness of 50 m. Such a volume subsequently reduced to 7.32 × 10⁸ m³ in 1997, because of progressive melting, possibly due to global warming. On the basis of these considerations, we study two different scenarios, one that assumes a uniform 25 meter glacier thickness (i.e., a total volume of ice amounting to 2.99 × 10⁸ million m³) and another where the uniform glacier is 50 m thick (5.98 × 10⁸ m³). The glacier cover size was obtained from Google Earth images [34].

Both versions of LLUNPIY are implemented in in C/C++ language; the program was executed by laptop computers of different power, which required computational times ranging from 1 day to 4 days. LLUNPIY simulations permit obtaining, step by step for each cell, the values of all the substates; the values of the maximum flow height and the maximum kinetic energy of each cell are saved during the simulations. The graphic output can be cast as a “cartoon”, in order to follow in some detail the evolution of the system, a panel for each substate and for the maximum values of lahar thickness, and the corresponding kinetic energy; moreover, the simulation can be stopped at any time and then restarted, while checking all the values for each cell. The maximum lahar thickness for each cell at the end of the simulation is reported in the Figure 3e and Figure 4e.

LLUNPIY simulations, whose underlying physical parameters are reported in Table 2, can actually be performed after assuming two rather different lahar-triggering mechanisms: instant glacier melting (IGM, pyroclastic flows) and gradual glacier melting (GGM, pyroclastic bombs). The former describes the case in which the ice layer is supposed to accrete and coalesce the pyroclastic matter overflowing the crater rim and that suddenly melts the whole glacier (at the LLUNPIY first step). The latter assumes that the melting of ice and snow is produced by free-falling pyroclastic bombs after they have been ejected upwardly by the eruptive explosions; in this case, the melting of the glacier is more gradual in time, and the debris flows entrain materials proportionally to the amount of water increasingly available and the accretion process of eroded pyroclastic sediments. Such a gradual ice melting, with the mixing of pyroclastic matter and water, is generated by an opportune stochastic function.

5.1. “Instant Glacier Melting” (IGM) Simulations

In order to simulate such a kind of glacier melting, a CA “elementary process” was introduced into the model. The parameters used for “immediate glacier melting” (pyroclastic flows) simulations were based on the values reported in Table 2. The ice layer is supposed to enclose pyroclastic matter and to immediately melt (the LLUNPIY first step) the glacier. The simulations of icecap melting were based on data which correspond to the 2018 glacier extent. In the simulations, two possible scenarios were considered.

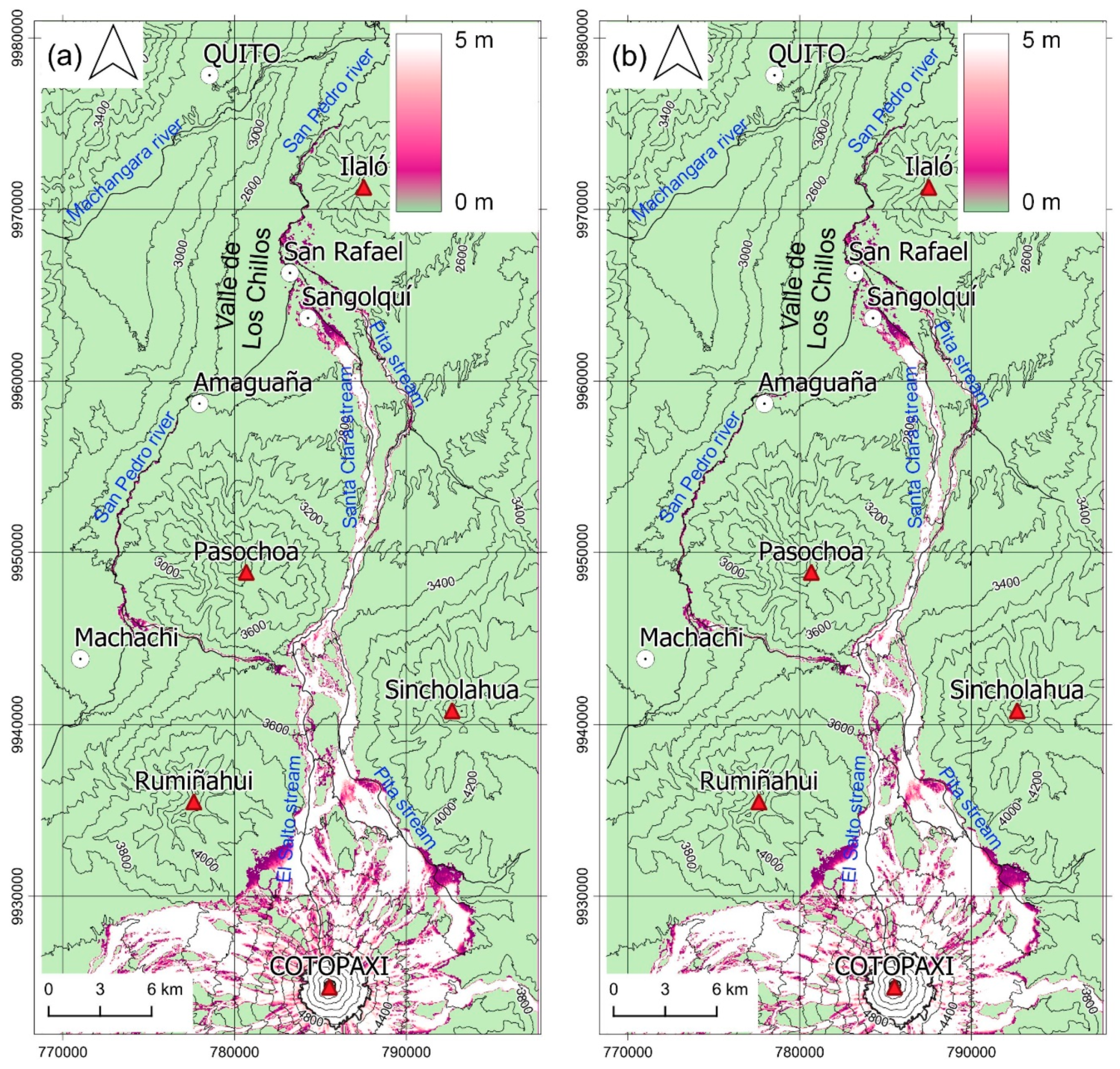
The first case (Figure 3) corresponds to the immediate melting of a 25 m uniformly thick glacier. The lahar flow sprawls out the northern flanks of the volcano and is eventually channeled along the Pita and El Salto Rivers’ upper gorges. While approaching the Pasochoa Volcano, the lahar divides into two branches. One turns westward, following the San Pedro River and coming to a stop approximately in vicinity of the town of Amaguaña. The other more voluminous branch keeps flowing northward, and then the La Caldera Canyon wall forces it to overflow the banks of the Pita River, thus diverting it into the Santa Clara River valley. The big towns of Sangolquí and San Rafael are reached, by the first lahar flows, about 50 min after the beginning of the eruption, consistently with the historical records [7,8]. Here, the debris flows break banks again and flood the Valle de los Chillos area. Finally, approximately after another 5 min, the front of the lahar enters the gorge of the San Pedro River in its path to the north, bypassing the barrier of the Ilaló volcano. In some spots, laharitic fronts several dozen meters thick are easily produced.

A similar description holds true for the second more catastrophic regime, where the totality of a 50 m uniformly thick glacier is suddenly liquefied (Figure 4). The paths of the flows are substantially similar; however, in this case, the debris thickness is systematically bigger. The westward branch of the lahar that bypasses the Pasochoa Volcano along the bed of the San Pedro River is now able to rejoin those coming from the east, i.e., from the Pita and Santa Clara River valleys.

In

Table 3. Values indicating significant features of the simulated scenarios. GGM, gradual glacier melting.

	IGM 25 m Scenario	IGM 50 m Scenario	GGM 25 m Scenario	GGM 50 m Scenario
Glacier volume	2.99 × 108 m3	5.98 × 108 m3	2.99 × 108 m3	5.98 × 108 m3
North Cotopaxi lahar volume	5.41 × 108 m3	6.79 × 108 m3	5.21 × 108 m3	7.70 × 108 m3
Invaded area	2.73 × 108 m2	2.89 × 108 m2	1.61 × 108 m2	1.98 × 108 m2
Maximum lahar length(distance from front to tail of lahar)	28,577 m	30,590 m	18,794 m	21,289 m
Maximum thickness	88.10 m	102.6 m	67 m	77 m
Travel time to slope of volcano	8 min	9 min	9 min	10 min
Travel time to Sangolquí	50 min	52 min	55 min	60 min
Travel time to San Rafael	51 min	53 min	57 min	62 min

, we report the values of a few significant observables corresponding to the different simulation scenarios, namely, the initial Cotopaxi´s glacier volume, the northward-bound lahar’s volume, the maximum thickness reached by such a lahar along its motion path, and the lapse needed by the front of the lahar to travel from its triggering site to three crucial locations, i.e., the base foothills of Cotopaxi, the town of Sangolquí, and the town of San Rafael.

The ratio between the volumes of the northward Cotopaxi lahars corresponding to the 50 m and 25 m IGM scenarios, i.e., 6.79 × 10⁸ m³/5.41 × 10⁸ m³ = 1.25, evidences that a proportionality with the original total glacier volumes (whose ratio is 2) is not systemically and rigorously maintained during the lahars’ downward motion; only a correlative lesser volume of the lahars triggered by a thicker original glacier is actually northward-bound, the remaining being diverted toward the other directions. This is corroborated by the bigger lapse required by the 50 m IGM lahar front to reach the three crucial locations—the foothills, Sangolquí, and San Rafael—due to its intrinsic much larger turbulence along streams and back streams, which causes a larger loss of energy. Note that, after 1 h of being both in motion, the 50 m IGM lahar (Figure 4c) is longer, with the longitude being measured from the front to the tail of the flow, as compared to the 25 m IGM lahar (Figure 3c).

5.2. “Gradual Glacier Melting” (GGM) Simulations

In the extended version of LLUNPIY that we name “gradual glacier melting“, the incremental melting of ice and snow is produced by pyroclastic bombs (Figure 5), which are generated according to an opportune stochastic function that mimics the progressive melting of ice/snow and mixing of pyroclastic matter with water. In this way, the ice melting is gradual, and the flows proportionally grow in time, as allowed by the increasing amount of available water and eroded pyroclastic material.

According to the firsthand report by Wolf [8], the 1877 glacier melting could have been of this type as a direct consequence of the peculiar effect of pyroclastic bombs progressively striking the glacier. The simulations of the gradual icecap melting by the effect of pyroclastic bombs are based on the parameters reported in Table 2. The underlying stochastic nature of an event like this can be visually appreciated in the three panels of Figure 5. The simulation corresponds to the case when 50 pyroclastic bombs are generated during each step for the first 10,000 steps (corresponding to about 10 min of real time). Each bomb has an equal probability of free-falling on whatever point (i.e., cell) of the glacier; the final effect is assumed to be the same for each bomb, i.e., the melting of 15 m of the ice underneath the point of impact.

Figure 6 and Figure 7 depict the results of the debris thickness values as reached by the lahar in various steps of the simulations, for glacier thickness of 25 m and 50 m, respectively. The path of the lahar is similar to the previous scenarios, in both cases; however, the lahar maximum heights are much lower now, and a secondary branch bifurcating south of the Pasochoa volcano does not form. Ten minutes after the start of the eruption, the flows have already reached the lower slopes of the volcano, and the first laharitic fronts enter the towns of Sangolquí and San Rafael in about 60 min if a 25 m thick glacier is melted (Figure 6c) and in about 55 min if a 50 m thick glacier is melted (Figure 7c). Finally, after 108 min, the lahars (Figure 6d and Figure 7d), overflowing the banks of the Pita River, have already invaded the area around San Rafael and eventually channeled into the San Pedro River’s gorge.

As in the previous analysis of the IGM scenarios, we now compare the two GGM lahar regimes as described by the observables listed in Table 3, following similar considerations. Specifically, the ratio of the volumes of the northward Cotopaxi lahars corresponding to the 50 m and 25 m GGM scenarios is 7.70 × 10⁸ m³/5.21 × 10⁸ m³ = 1.48, which implies that the GGM lahars bound to the regions north of Cotopaxi are systematically bigger when triggered by the thicker glacier. Yet, since 1.48 > 1.25, we foresee that the northward channeling of the lahars is somehow more efficient in the GGM scenario than in the IGM one. This is certainly due to the more gradual accretion process that builds up the GGM lahars as compared to the IGM lahars, which is also reflected in an overall slower motion; this can be seen in Table 3 indeed, where the lahars’ lapses are reported. Thus, while the fronts of the IGM lahars are seemingly equally fast in both scenarios (just 2 min of delay is predicted between arrival times at Sangolquí and San Rafael), 50 m GGM lahars are notably slower than the 25 m GGM lahars, with the former needing 5 min more to travel from Sangolquí to San Rafael than the latter. However, northward IGM lahars are systematically faster than the corresponding GGM lahars, indicating that the GGM lahars accrete and coalesce more gradually, despite being inherently less turbulent than the IGM ones, due to the former losing less kinetic energy along their path than the latter. Consistently, we can see that, after a lapse of 60 min, even if the 50 m GGM lahar (Figure 7c) is longer and thicker than the 25 m GGM lahar (Figure 6c) because it carries more material, it is nevertheless shorter than the 25 m IGM lahar (Figure 3c) even if it comparatively loses less of its kinetic energy.

5.3. Lahar Erosiveness

The different scenarios we assumed in our simulations consistently imply different erosional capacities of the lahars triggered in the upper cone of Cotopaxi volcano.

First, we note that the maximum height reached by the head level of the debris flow, considering the IGM simulations case, is ca. 88 m when suddenly melting the whole of the 25 m thick glacier (Figure 2e) and 103 m considering a 50 m thick icecap (Figure 4e). In the GGM case, instead, the peak height is lower, i.e., 67 m (Figure 6e) and 77 m (Figure 7e), respectively. Consistently, the areas invaded by mud and debris are considerably much wider in the IGM case (2.73 × 10⁸ m² and 2.89 × 10⁸ m², respectively, for 25 m and 50 m glacier thickness) as compared to the GGM scenario (1.61 × 10⁸ m² and 1.98 × 10⁸ m², respectively, for 25 m and 50 m glacier thickness). These values are comparable to those reported in the corresponding historical records [7,8].

In Figure 8 and Figure 9, we finally report the peculiarities of the erosive process in the different scenarios (in turn, IGM and GGM), for the two adopted thickness of glacier (25 m and 50 m, respective panels). For the village of Sangolquí, it is observed to the southeast (Figure 7a,b) that the lahars, in both IGM cases, stop their erosion and start to release the sediments that invade, in parts, the areas between the towns of Sangolquí and San Rafael, while the detritus components keep on moving along their path toward the San Pedro River ravine. Instead, in GGM cases (Figure 9a,b), the erosion activity is sustained by the GGM lahar flows, even after they invade and bypass the two towns. This can be fairly ascribed to the smaller loss of energy implied by the melting phase, since the channeled flows are produced in a less whirling and turbulent way. In fact, while the GGM lahars accrete and coalesce material more progressively and gradually than the IGM ones, at the same time, they also lose less of their kinetic energy, which is kept during the less turbulent regime, thus preserving their abrasive and erosive capacity even when invading lower and wider flatlands, such as those characteristic of the Valle de los Chillos.

6. Discussion and Conclusions

The results of the present simulations regard the northerly propagation of volcanic lahars from the vent of the Cotopaxi Volcano, Ecuador. Such results constitute a study preliminary to a more comprehensive and systematic scientific investigation program about the risks and hazards posed to local populations, whenever a future, unfortunately probable, eruption of the Cotopaxi volcano should occur. The worst-case scenarios for the two possible lahar-triggering mechanisms and two melting depths of the glacier icecap were considered, accounting for the partial geological knowledge of the areas threatened by the volcanic lahars. Some field data are scarce and need to be better known in order to obtain more reliable simulations.

We used data updated to the 2018 Cotopaxi glacier extent, today reduced by two-thirds as compared to its 1877 size, a reduction presumably due to the present global warming pulse. In addition, the thickness of the glacier was assumed the same everywhere, i.e., a maximum constant 50 m, which is probably an approximation in excess. The erodible regolith (pyroclastic soil cover) was assumed homogeneous, and 5 m deep. Geological survey, soil tomography, coring, etc. could produce not only more accurate data, but also a better value of the erosion parameters, which would no longer be global to all the study area, but would became substates, i.e., different values for different cells, according to the field measurement data.

The adopted cell dimensions are the smallest possible as allowed by the DEM accuracy; thus, the distance between two opposite sides of the hexagonal cell is 30 m, a value sufficiently large to not adequately capture in simulation the width of a relatively small stream, where the lahar can be channeled. A possible alternative, which can be applied in this context, may be found in Lupiano et al. [23], where two different altitudes can coexist in the same cell. This implies a rigorous knowledge of the areas to which to assign the two different heights of the corresponding cells; unfortunately, such knowledge is very rarely available in the present case.

Geologically, the Valles de los Chillos area was actually carved out by ancient lahar deposits of past Cotopaxi eruptions [35], and it is crossed by rivers such as Río San Pedro (west of Pasochoa Volcano), Río Pita, and Río Santa Clara (east of Pasochoa Volcano), all of them belonging to the Guayllabamba River basin, thus eventually flowing into the Esmeraldas River, which in turn reaches the Pacific Ocean. Sodiro [7] reported that the 1877 Cotopaxi lahar needed just 18 h to reach the Pacific Ocean following the course of the Esmeraldas river, and we plan to simulate the dynamic and the impact of this coastal flow of the Cotopaxi lahar in future numerical investigations.

According to historical records of the last Cotopaxi eruptive episodes, Barberi et al. [17] forecasted a probability as high as 0.7 of a novel eruption of Cotopaxi Volcano, which would currently impact the same area devastated by the 1877 northern lahars. This can be clearly seen in Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6; in any case, the Valle de los Chillos area would be buried by a laharitic front several kilometers wide (along the east–west axis), several kilometers long (along the south–north axis), and several tens of meters thick, even in the most optimistic pyroclastic bomb scenario.

In turn, the glacier-melting scenario significantly predicts that an arm of the Cotopaxi northern lahars could be able to bypass westward the Pasochoa Volcano, eventually invading the valley of the San Pedro River, a possibility never predicted by any previous study, where, among other infrastructures, the Tesalia potable water supply system is located. This is actually part of the bigger regional water system that daily supplies the Metropolitan District of Quito (MDQ), the capital of Ecuador, where about three million inhabitants live. It consists of several branches, each one of them carrying a significant part of the amount of potable water that the MDQ needs daily, and nonetheless certainly exposed to the risk of destruction in case of eruption.

More specifically, the Puengasí–Placer Hydric Zone, roughly corresponding to the central part of the MDQ, is supplied by a pipeline carrying up to 2600 L/s from the sources of the Pita River, in the upper northern slopes of the Cotopaxi. It alone guarantees about 50% of the total water supply for the capital Quito and would be completely wiped out by future Cotopaxi lahars. In addition, the Mica–Quito South Hydric Zone covers the water needs of the southern part of the MDQ and receives its water supply from the Micacocha Lagoon, about 70 km to the southeast of Quito, in proximity of the Antisana Volcano. This massive pipeline transports about 2000 L/s and is necessarily exposed to the risk of destruction since it crosses both Santa Clara and Pita Rivers, which, in case of lahar events, would channel huge thick debris flows. Lastly, the Bellavista Hydric Zone, which corresponds to the northern part of the MDQ, receives its water supply from Tumingina, Blanco Chico, and Papallacta Rivers draining from the eastern highland of Papallacta. The corresponding Bellavista main pipeline, which crosses the San Pedro River nearby Tumbaco carrying about 3000 L/s, is only marginally at risk, since it is partially protected by an underground tunnel.

All in all, of the total 8000 L/s needed to supply the MDQ, 7200 L/s, i.e., 90% of the MDQ water store per second, faces some degree of risk to be destroyed by volcanic lahars triggered by an eruptive episode of Cotopaxi Volcano.

The early warning systems put in place in the Valle de los Chillos area by local governments and social stakeholders after the most recent 2015 Cotopaxi eruptive episode, on one hand, would avoid the loss of human lives; however, on the other hand, they could not avoid the destruction of the MDQ potable water system, being impossible here to predict the unbearable suffering of about three million people without access to water for weeks or even months. As a matter of fact, future Cotopaxi lahars would heavily affect the entire region around the volcano, not only that immediately to the north of the volcano, laying waste to villages and towns, important public infrastructures, and vital agricultural lands.

These preliminary simulations will be extended to the very northern region, along the basin of the Esmeraldas River, and to the south to predict the impact of Cotopaxi lahars on the Agoyán Dam in Baños, as soon as higher-resolution DEM data are available to map these territories.

To conclude, the threat that an eruption, comparable to the 1877 one, may again occur is indeed something to consider when assessing this volcanic danger. Towns such as Quito or Latacunga would not be fully prepared to deal with the devastation that potential lahars—similar in scale to the 1877 ones—could bring about, unless reliable forecasting and prediction models are developed. In fact, it is one of the main objectives of this study to highlight to the local governments and social stakeholders the dangers that lahars can generate to the towns and villages that surround Cotopaxi and that are located along the natural drainage networks. The latter, at the same time, would need to be equipped by artificial containment and mitigation barriers at least where the most vulnerable settlements are located. We do hope that the present investigation may assist the local regional leaders in selecting such spots. The importance and the role of these kinds of engineering infrastructures cannot be overestimated, since the devastation of the laharitic fronts will not be limited to the landscape. A Cotopaxi eruption aftermath would also impact for a long time the economy and the quality of life of local populations [36], not only the physical territory of central Ecuador and the ecosystems it hosts.

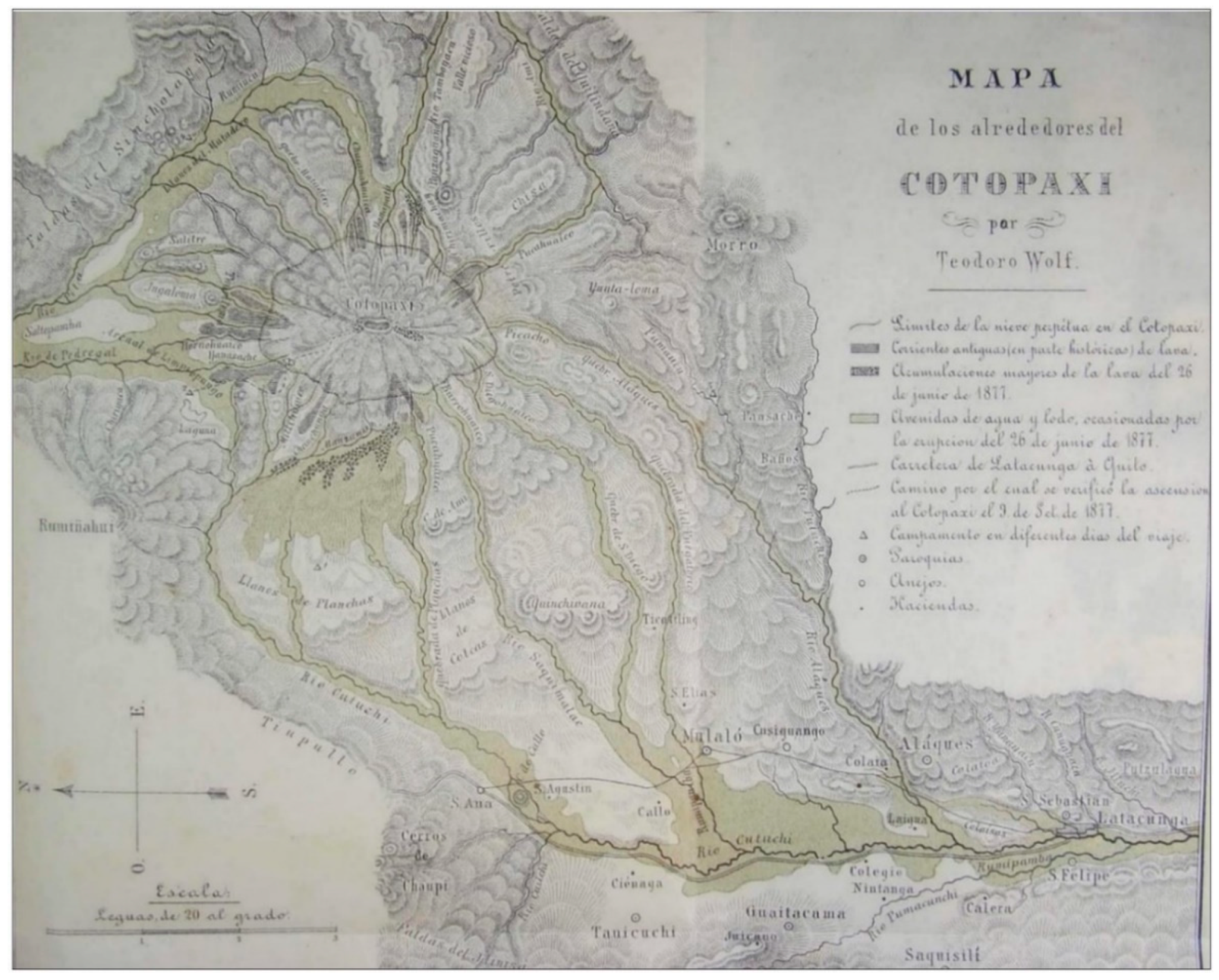
Since we necessarily enquire into present day orography and geography—even when considering the extent of the Cotopaxi glacier—the available data do not allow for an always straightforward comparison between our simulations and the actual 1877 eruptive episode. For instance, the map of the 1877 northern lahars that Wolf drew immediately after the eruption (see the left part of Figure 2, reproduced from [8]) reports the “avenues of water and mud” right up to the border of the melting glacier. In correspondence of such a border, the IGM simulations instead show much wider “avenues”, when melting a 50 m or even a 25 m ice cap. However, the GGM simulations always produce “avenues” that are fairly similar to the historical ones as depicted by Wolf (compare Figure 2 with Figure 3, Figure 4, Figure 6 and Figure 7). This indicates that, at least in the latter case, there exists the possibility of a reliable matching between historical reports and the results of our simulations, and we are confident that we just need to refine this approach to obtain hazard maps and propose mitigation solutions that are sound for the safety and wellbeing of Ecuadorian society at large.

Despite all the approximations we adopted in this study, we believe that the results of these simulations fairly indicate the areas most vulnerable to likely Cotopaxi lahar invasions and inundations. We cannot help stressing with enough urgency that the human toll and the infrastructure loss within these vulnerable areas may result to be unacceptably big, unless hazard maps, early alert systems, evacuation plans, and mitigation solutions are orderly put in place by politicians, social leaders, and local stakeholders. We are also aware that such a program transcends the resources and the knowledge available to the Ecuadorian society in general, and that it can only be carried out with the scientific and financial assistance of the international community. It is our hope that the results here presented will be useful to those objectives.