Next Article in Journal
StalGrowth—A Program to Estimate Speleothem Growth Rates and Seasonal Growth Variations
Next Article in Special Issue
Efficiency of Intensity Measures Considering Near- and Far-Fault Ground Motion Records
Previous Article in Journal
The Alps-Apennines Interference Zone: A Perspective from the Maritime and Western Ligurian Alps
Previous Article in Special Issue
Case Study of a Heavily Damaged Building during the 2016 MW 7.8 Ecuador Earthquake: Directionality Effects in Seismic Actions and Damage Assessment
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Geosciences
Volume 11
Issue 5
10.3390/geosciences11050186
geosciences-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Near-Source Simulation of Strong Ground Motion in Amatrice Downtown Including Site Effects

by
Alessandro Todrani
1,2,* and
Giovanna Cultrera
2
1
Department of Sciences, Roma Tre University, 00146 Rome, Italy
2
Istituto Nazionale di Geofisica e Vulcanologia, 00143 Rome, Italy
*
Author to whom correspondence should be addressed.
Geosciences 2021, 11(5), 186; https://doi.org/10.3390/geosciences11050186
Submission received: 8 April 2021 / Accepted: 20 April 2021 / Published: 25 April 2021
(This article belongs to the Special Issue Engineering Analysis of Near-Source Strong Ground Motion)
Browse Figures
Versions Notes

Abstract

:
On 24 August 2016, a Mw 6.0 earthquake started a damaging seismic sequence in central Italy. The historical center of Amatrice village reached the XI degree (MCS scale) but the high vulnerability alone could not explain the heavy damage. Unfortunately, at the time of the earthquake only AMT station, 200 m away from the downtown, recorded the mainshock, whereas tens of temporary stations were installed afterwards. We propose a method to simulate the ground motion affecting Amatrice, using the FFT amplitude recorded at AMT, which has been modified by the standard spectral ratio (SSR) computed at 14 seismic stations in downtown. We tested the procedure by comparing simulations and recordings of two later mainshocks (Mw 5.9 and Mw 6.5), underlining advantages and limits of the technique. The strong motion variability of simulations was related to the proximity of the seismic source, accounted for by the ground motion at AMT, and to the peculiar site effects, described by the transfer function at the sites. The largest amplification characterized the stations close to the NE hill edge and produced simulated values of intensity measures clearly above one standard deviation of the GMM expected for Italy, up to 1.6 g for PGA.

1. Introduction

In recent years, the increased number of permanent and temporary seismic stations have allowed researchers to record strong ground motions close to the seismic source, highlighting the large complexity of the waveforms due to the mixture of source, propagation, and site effects [1,2,3]. The ground motion simulation in the near field is then very difficult to perform, especially when the surface geology and morphology are highly heterogeneous. Several advanced simulation techniques have been implemented so far, to account for complex source and site effects, such as full-wavefield simulations (e.g., [4]), empirical Green’s function approaches (useful for reproducing the recorded seismograms in a large frequency band without any knowledge of the underground medium; e.g., [5]), hybrid broadband techniques (e.g., [6]), or dynamic models (e.g., [7]). Despite the increasing level of accuracy, the advanced simulation methods have limitations in frequency range and require an accurate knowledge of the propagation medium and rupture process [5,8]. All these uncertainties affect the synthetic earthquake seismograms, whose variability can be induced by the rupture behavior and errors in propagation [9], and limit the reproduction of the experienced ground motion, such as for understanding peculiar effects on the damage distribution in the near-source area. This is the case of Amatrice village (Italy), whose historic center has been destroyed by a Mw 6.0 earthquake that occurred on 24 August 2016. The so-called Amatrice earthquake started a long seismic sequence in central Italy (Figure 1), causing 299 fatalities and about 30,000 to become homeless. It was followed on 26 October by a Mw 5.9 (Visso earthquake) ∼25 km to the north, and on 30 October by a Mw 6.5 (Norcia earthquake), that nucleated in between the source regions of the two previous mainshocks; the activated zone was about 70-km-long and 10-km-thick along the central Apennine chain direction [10].
The damage in the epicentral area of the Amatrice earthquake appears rather complex and strongly dependent on the high vulnerability of the traditional dwellings, as well as on the geological conditions [11]. In particular, the historical center of Amatrice was affected by either heavy damage or total collapses reaching 85% of the whole building stock [12,13]. Its non-uniform spatial distribution may be due to the different high vulnerability of the building heritage, the ground motion variability within a few hundred meters, or possibly due to the vicinity of the seismic source and the peculiar site effects.
Source effects are claimed by several authors to have affected the resulting ground motion in Amatrice. The mainshock ruptured a WSW dipping normal fault, with prominent bilateral rupture and two well-separated slip patches [14,15,16]. In particular, ref. [7] suggested that the rupture propagation along the SE portion of the fault contributed to the ground motion amplification in Amatrice: the initial up-dip directivity caused a pulse-like ground motion at the close AMT station [14], where the recorded values reached a PGA of 8.5 m/s2 on the EW component and largely exceeded the Italian code spectrum [2,17]. The analysis of the recordings at stations belonging to the Italian accelerometric networks revealed that PGAs, PGVs, and PSAs at short periods were likely dependent on the source directivity [2,18,19,20,21].
Other effects might have accentuated locally the amplitude of the ground shaking (e.g., crustal propagation and anelastic attenuation [16,22,23,24], site effects, topographic effects), superimposing their features on the directivity pattern and contributing to the observed damage [14,19]. Most of all, local site effects probably affected the ground motion experienced in Amatrice.
The village was built on an alluvial terrace 60–80 m higher than the surrounding valley (Amatrice basin) and elongated in NW–SE direction with a length of about 2000 m and a maximum width of about 600 m [25] (Figure 1). It is bounded both at NE and SW by two river valleys and bordered by a steep slope to the north and to the west, and by a gentler slope to the south. This morphology, together with the low cohesion and the poor geotechnical properties of the covering terrain, causes a lot of landslides (collapse, overturning, sliding or falling): the landslide of the north flank is nowadays active with a fall or overturning mode, whereas the southern flank is characterized by a lot of slope instabilities in a quiescent mode [26]. The Amatrice basin is filled by about 60-m-thick Quaternary fluvial deposits, laying above the Messinian siliciclastic deposits of the Laga Formation, which play the role of seismic bedrock for the area [27,28]. They are made by conglomerates and sands alternations, few tens of meters thick, which can generate a seismic impedance contrast that, together with the topographic effects, is able to generate a strong amplification effect [25,29,30].
The analysis of earthquakes and ambient noise, recorded on the Amatrice terrace and around it for microzonation purposes, has revealed spatial variation of site effects [25,31,32,33]: the diffuse amplification of ground motion reaches its maximum values in the downtown area, at the western limit of the terrace, with a resonant frequency of about 2.0–2.5 Hz. Here, the amplification is larger in the northern sector and varies from the central part to the edge, where [25] observed a clear directionality of the resonant peak (on the contrary, [34] concluded that maximum directions are linked to the presence of noise sources). These observations suggest a lateral variability of the geological conditions, due to the spatial variation of the impedance contrast, and the presence of topographic effects, due to the morphology of the area [25,29,30].
This short review highlights that there is no single interpretation on the explanation of the ground motion experienced in Amatrice, neither on the causes of the variability of heavy damage [25,29,30,34]. Indeed, the ground motion complexity, due to a combination of near-source and site effects, is difficult to reproduce with standard simulation techniques [21,29].
To overcome the limitations in terms of frequency band, spatial resolution, and knowledge of source and propagation models, we propose a simple methodology for reproducing the ground motion in Amatrice downtown during the 24 August 2016, Mw 6.0 mainshock, in absence of recording stations in the most damaged area. Empirical transfer functions were used to recover the ground motion that could have hit the downtown during the mainshock, through the convolution with the only record available for that earthquake a few hundred meters away from the historical center (AMT station).
The applied methodology was tested on the 26 October (Mw 5.9) and 30 October (Mw 6.5) 2016 mainshocks, with the aim to highlight strengths and weaknesses of the approach. We then simulated the Mw 6.0 earthquake of 24 August by using the recordings at AMT and the empirical transfer functions at several sites in downtown. The results have been discussed in terms of time series and intensity measures (PGA, PGV, Arias intensity, significant duration).

2. Available Data

In this study, we used seismic signals of 35 earthquakes of the 2016–2017 central Italy seismic sequence (Table 1 and Figure 1A), recorded by 20 seismic stations located in the Amatrice village (Table 2 and Figure 1B).
The selected events were characterized by epicentral distances between 7 to 48 km from Amatrice downtown and magnitudes in the range ML ≥ 1.5 and Mw ≤ 6.5, including the three mainshocks of the sequence (Mw 6.0 on 24 August, Mw 5.9 on 26 October, and Mw 6.5 on 30 October 2016). The recordings were downloaded from the European Integrated Data Archive (EIDA, http://eida.ingv.it, accessed on 24 April 2021; [36]) and the Italian Strong Motion Network (RAN, http://ran.protezionecivile.it, accessed on 24 April 2021; [37]) databases. They were selected accounting for a signal-to-noise spectral ratio greater than two or three (depending on the stations) in a wide frequency band, and a clear P and S wave arrivals.
The closest seismic station to Amatrice downtown that recorded the 24 August, Mw 6.0, earthquake was AMT, belonging to the National Accelerometric Network [37] and able to record seismic events with a Ml ≥ 2.5 [17]. AMT was at an epicentral distance of about 8.5 km (Rjb = 1km; [38]) and recorded the maximum horizontal PGA for the event on the EW component (8.5 m/s2; [2]); the difference with the NS component, that recorded half of the PGA value, was probably caused by topographic effects [29], seismic amplification [25], or directivity effects [14].
Another reference station, T1299, was installed by the INGV mobile seismic network about 800 m NW of Amatrice downtown, at the base of the hill [25,39].
Moreover, to record the aftershock sequence and to investigate the local amplification effects for microzonation purposes, a total of 50 temporary seismic stations were installed by INGV in four municipalities, including Amatrice (MZ stations, belonging to the 3A network [40]; see also [25,31,32,33]). In this study, only six stations distributed along the NW-SE elongated Amatrice terrace were considered: the stations MZ10, MZ12, MZ28 were installed at the top of the sandy conglomeratic deposits of the Amatrice–Sommati units [27], whereas the stations MZ29, MZ30 were located in a NE–SW direction across the Amatrice hill.
According to [25], the station MZ08 was installed a few meters far from the AMT station, to extend the detection capability at the site towards the lower magnitude events. For events before 4 November 2016, we verified a 13° clockwise orientation difference of AMT with respect to MZ08. However, after that date, the sensor at AMT was changed and the orientation was corrected. The slight difference in the sensor’s orientation does not significantly affect the seismic recordings, showing very similar signals (see Figure S1 on Supplementary Materials).
Later on, an array of 24 seismic stations was installed for few hours of activity in the heavily damaged historical center [25]. Out of 12 stations (CS01 to CS12) that worked during 28 June 2017, only four stations (CS01 to CS04) recorded a clear seismic signal of two earthquakes with ML 1.8 and 2.2. Otherwise, 12 stations (CS13 to CS24) worked during the second day of activity, but only seven of them (CS13, CS14, CS16, CS17, CS20, CS23, CS24) recorded four seismic events with a ML between 1.5 to 3.1.

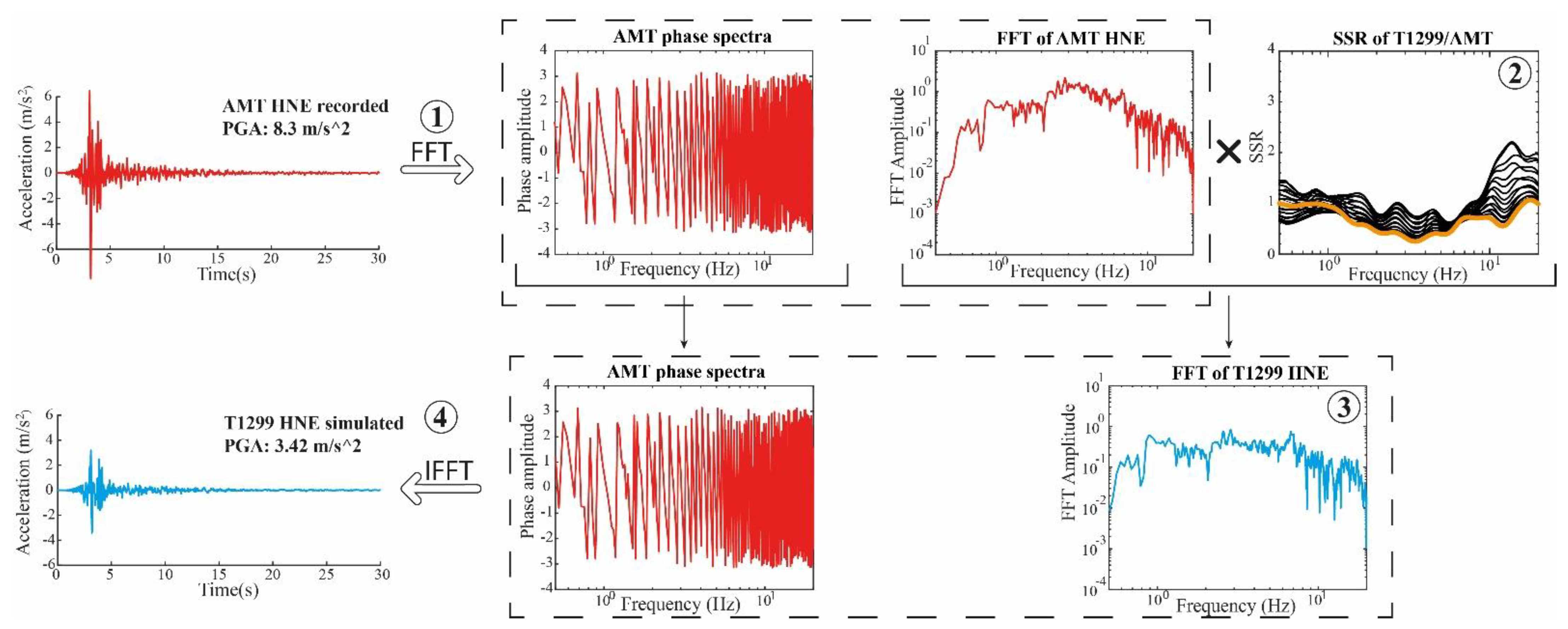
3. Simulation Method

During the Amatrice earthquake, no station was available in the historical center except for AMT. Later on, tens of temporary stations were installed in Amatrice village and they recorded many earthquakes simultaneously to the reference station.
To overcome the limits of the available data and the network geometry, we implemented a strategy for simulating a given earthquake (e.g., the Amatrice mainshock) at stations (e.g., Table 2) close to the reference one (e.g., AMT) that recorded the event. The strategy is summarized in Figure 2 and explained in the following steps:
  • The target event is recorded at a reference station, for which we calculated the Fourier transform (FFT phase and amplitude).
  • Several earthquakes are recorded simultaneously at the reference station and at the other neighboring sites (in this way we can assume similar source effects at all stations), allowing us to calculate the empirical transfer functions respect to the reference site by means of the standard spectral ratio (SSR).
  • FFT amplitude of the target event recorded at the reference station is multiplied by the SSR of each station; the result is an amplitude spectral content, modified by the contribution of a transfer function.
  • The modified FFT amplitude spectrum is back-transformed to the time domain through the IFFT, using the FFT phase of the reference station.
The proposed procedure overcomes the complexity of the source and site effects: the near-source influence is included in the strong motion recording at the reference site, whereas the relative site effects are accounted for by the site transfer functions.
However, we are aware that the use of the same phase spectrum at all stations results in an unlikely coherence at high frequencies between the signals recorded at different sites, whereas the high frequency incoherency is related to the heterogeneities of the propagation path and it is largely site dependent, but also regionally dependent [41,42,43]. Considering that the spatial coherency decreases with increasing frequency and distance between measuring points [44], the same authors showed that the coherence for high-frequency intensity measures (such as PGA) is still high within a separation distance of one to a few kilometers, which makes the stations configuration in Amatrice reliable for our methodology.
Another possible weakness, due to the use of the same phase spectrum, relates to the inability to capture the increase of the ground-motion duration for 2–3D site effects, which can act to decrease the peak amplitudes.
Finally, the small-magnitude events for the SSR computation do not account for possible nonlinear soil behavior, whose main effect would be a shift of the amplification towards lower frequencies and a decrease of the peak amplitudes [45].

4. Data Processing

The seismic recordings used for the SSR computation are listed in Table 1, together with the stations that recorded each event.
The time series have been band-pass filtered between 0.5 to 20 Hz, corrected by subtracting the mean value and the best-fit line, cut between −0.5 to 30 s with respect to the P-wave arrival (manual picking), and tapered before computing the Fourier spectra. Only the frequencies with a signal-to-noise ratio (s/n) ≥ 3 were used for the recordings at T1299 and MZ stations and (s/n) ≥ 2 for the CS stations, to maximize the information of the few low-magnitude earthquakes available.
As described in [46], the SSR were computed on 18 horizontal components, each rotated every 10° clockwise, and on the vertical component. After rotation of the time signals, their Fourier spectra were smoothed with Konno–Ohmachi algorithm [47] (b = 40 and fmax = 20 Hz) and divided by the reference ones. The spectral ratios for each station were then averaged (geometrical mean) on all the used seismic events (Figure 3).
We computed the SSR of the T1299, MZ, and CS stations with respect to AMT or MZ08 (they are equivalent), using different earthquakes (Table 1 and Figure 1)—for T1299 we used 15 earthquakes with magnitude between 2.6 and 5.4, recorded simultaneously at T1299 and AMT, whereas for the MZ stations we considered 12 events of magnitude range 3.1–5.9, using MZ08 as reference (Figure S2 in Supplementary Materials).
Regarding the CS stations in downtown, the CS13-14-16-17-20-23-24 recorded four seismic events simultaneously to AMT, but only two, with magnitude 2.6 and 3.1, were recorded by AMT and showed a signal-to-noise ratio greater than 2 in a wide frequency band (Figure 4 and Figure S3 in Supplementary Materials). Unfortunately, we could not use CS01-02-03-04 stations because they recorded two seismic events only, having too low magnitude to be recorded by the accelerometric station AMT (Table 1).
To quantify the intensity measures of the seismic signals, several parameters have been taken into account: the peak ground acceleration (PGA) and velocity (PGV), providing limited insight to the shaking at high and intermediate frequencies, respectively; the Arias intensity; the significant duration. The Arias intensity (AI) represents the cumulative energy perceived at the site, in a specific time interval during a seismic event, and it is expressed in m/s [48]; we computed it for the total duration of the seismic signal (from t = 0 to t = tmax):
A I = I a   ( 0 , t m a x ) ,   w h e r e   I a ( t 1   , t 2 ) = π 2 g ∫ t 1 t 2 a ( t ) 2 d t .
The significant duration (SID) uses Equation (1) and measures the time interval (t2–t1), in which Ia is between 5% and 95% of the total.
For the intensity measures on horizontal motion, we used the maximum between the NS and EW components. See [46] for a detailed description of the signal processing procedure.

5. Results

The proposed simulation procedure has been first tested by comparing simulated and recorded seismograms for two mainshocks (Mw 5.9 and 6.5 on 26 October and 30 October 2016, respectively) at some stations in Amatrice, using AMT and MZ08 as a reference site. Then, we simulated the expected ground motion in Amatrice downtown during the Mw 6.0 earthquake on 24 August, by means of the recordings at AMT station.

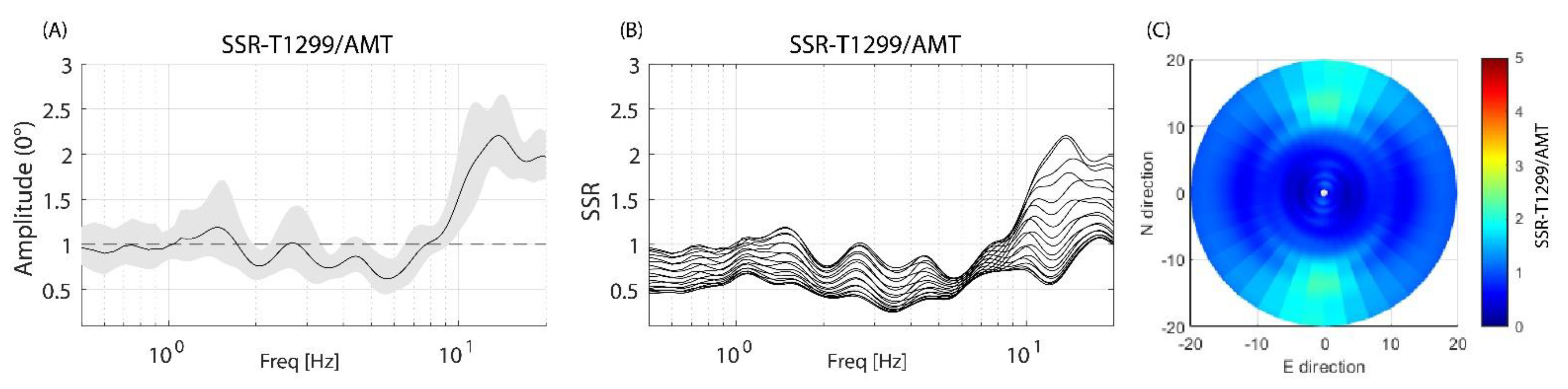
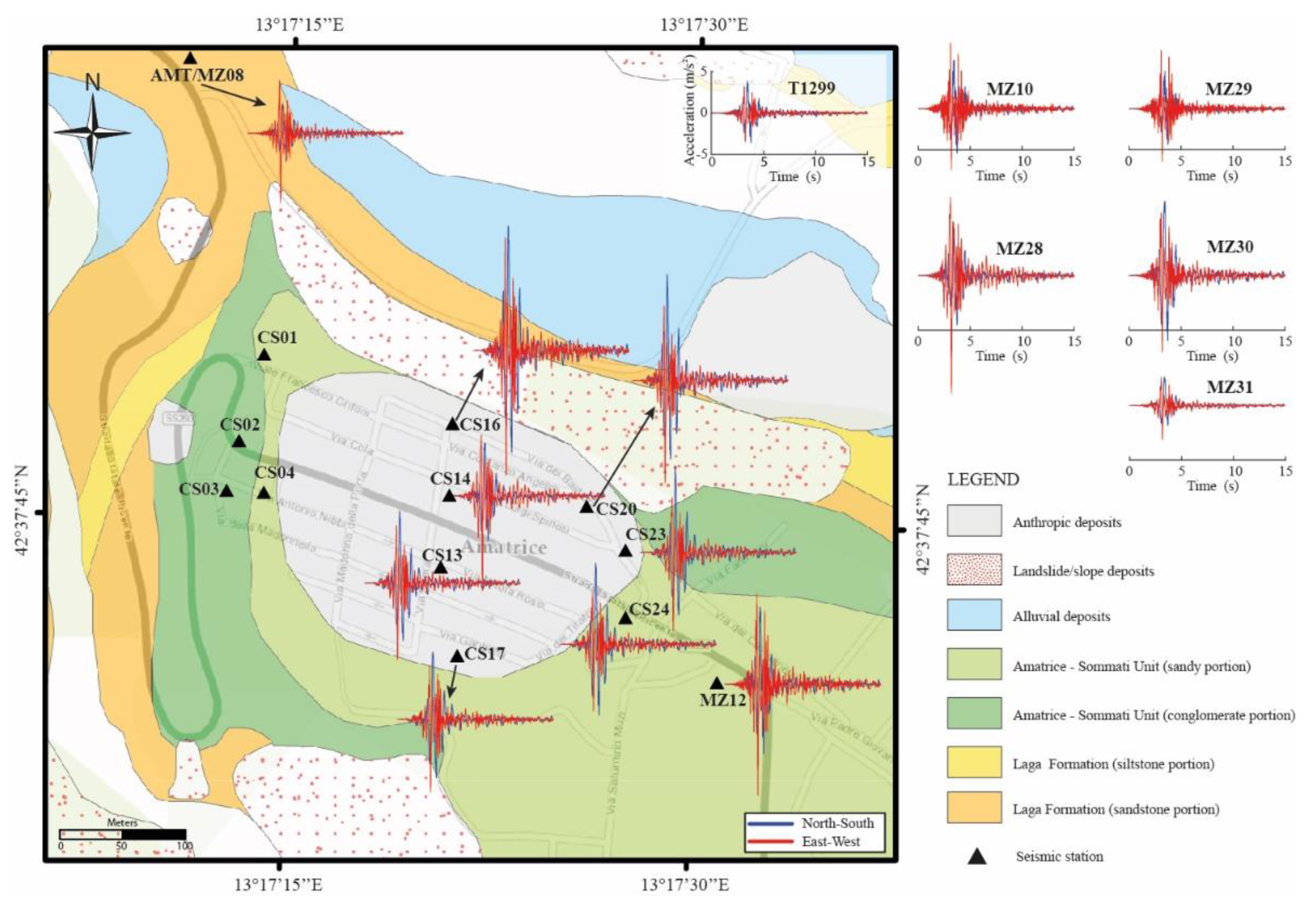
5.1. Standard Spectral Ratio (SSR)

The site effects of the Amatrice stations have been already discussed in [25,33], although their reference station was T1299; however, we list here some main findings inferred from their and our analyses (see Figure 3 and Figure 4 and Figure S2 in Supplementary Materials):
  • T1299 is affected by a slight deamplification with respect to AMT up to 10 Hz; above this value, the amplification increases by up to 2.5 (Figure 3).
  • MZ10, MZ12, and MZ28 are amplified with respect to the reference site (MZ08 or AMT): MZ10 has a strong amplification of about 7.5 above 10 Hz with a NW–SE polarization; MZ12 and MZ28 show an average amplification of about 4 and 3, respectively, along the entire frequency range and with NNW–SSE polarization; MZ29, located at the base of the terrace close to the northern edge, has a high-frequency amplification (f > 10 Hz) most likely due the slope debris, whereas MZ31, located at the base of the southern slope, does not show any amplification (Figure S2 in Supplementary Materials).
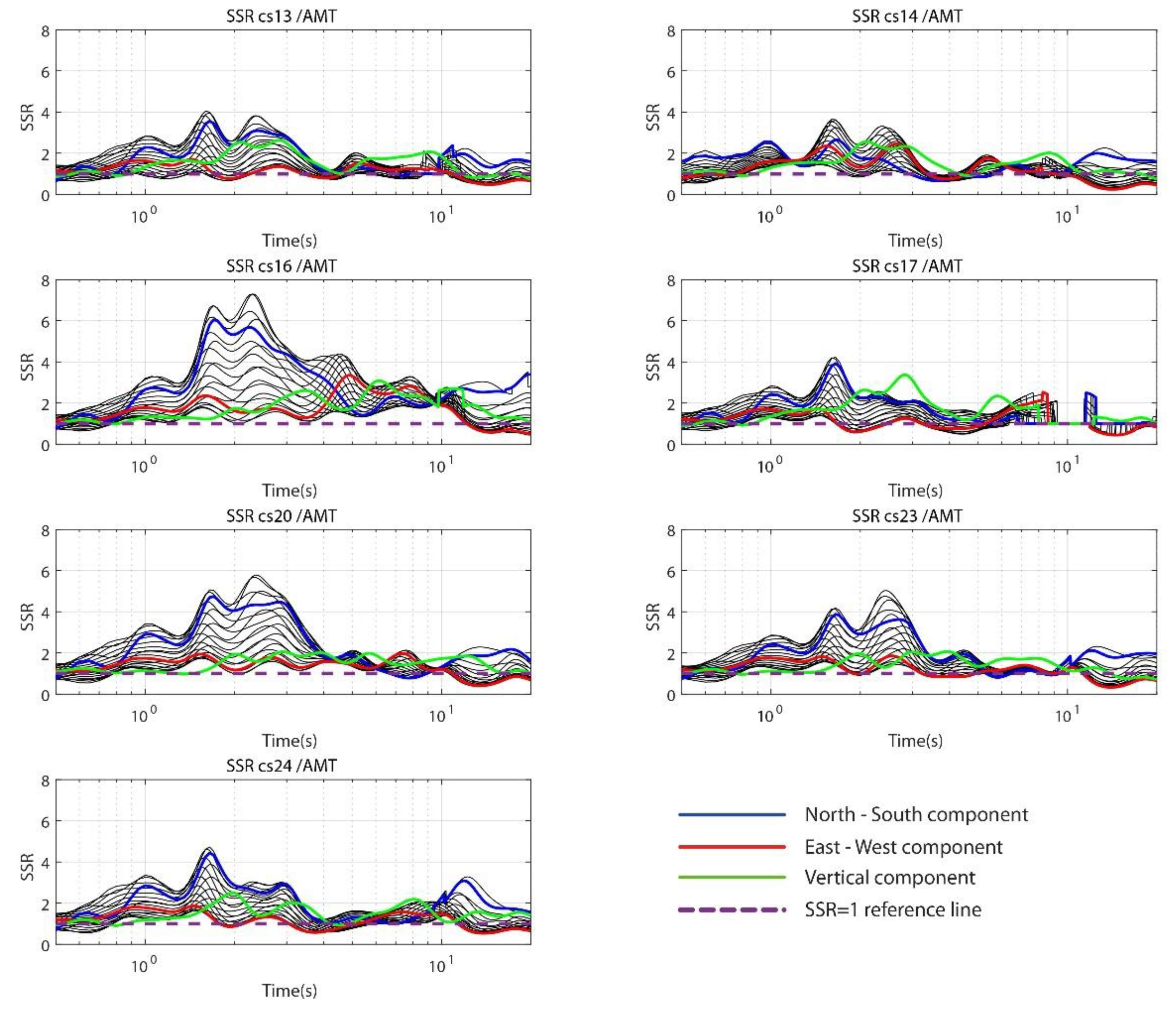
  • CS13-14-16-17-20-23-24, in Amatrice downtown, show an amplification larger than 2 in the frequency range 0.7–3.5 Hz, with a double peak between 1.5 to 2.5 Hz and a preferred NE–SW direction: the maximum amplitude of the peaks exceeds 5 at stations CS20, CS23, and CS24, and it reaches a value of about 4 at CS13, CS14, and CS17 (for this station the SSR has been evaluated only between 0.5 to about 7 Hz); CS16 appears as the most amplified seismic station in a wider frequency range (up to 10 Hz), with a maximum amplification of about 7.3 in the NE–SW direction (Figure 4 and Figure S2 in Supplementary Materials).

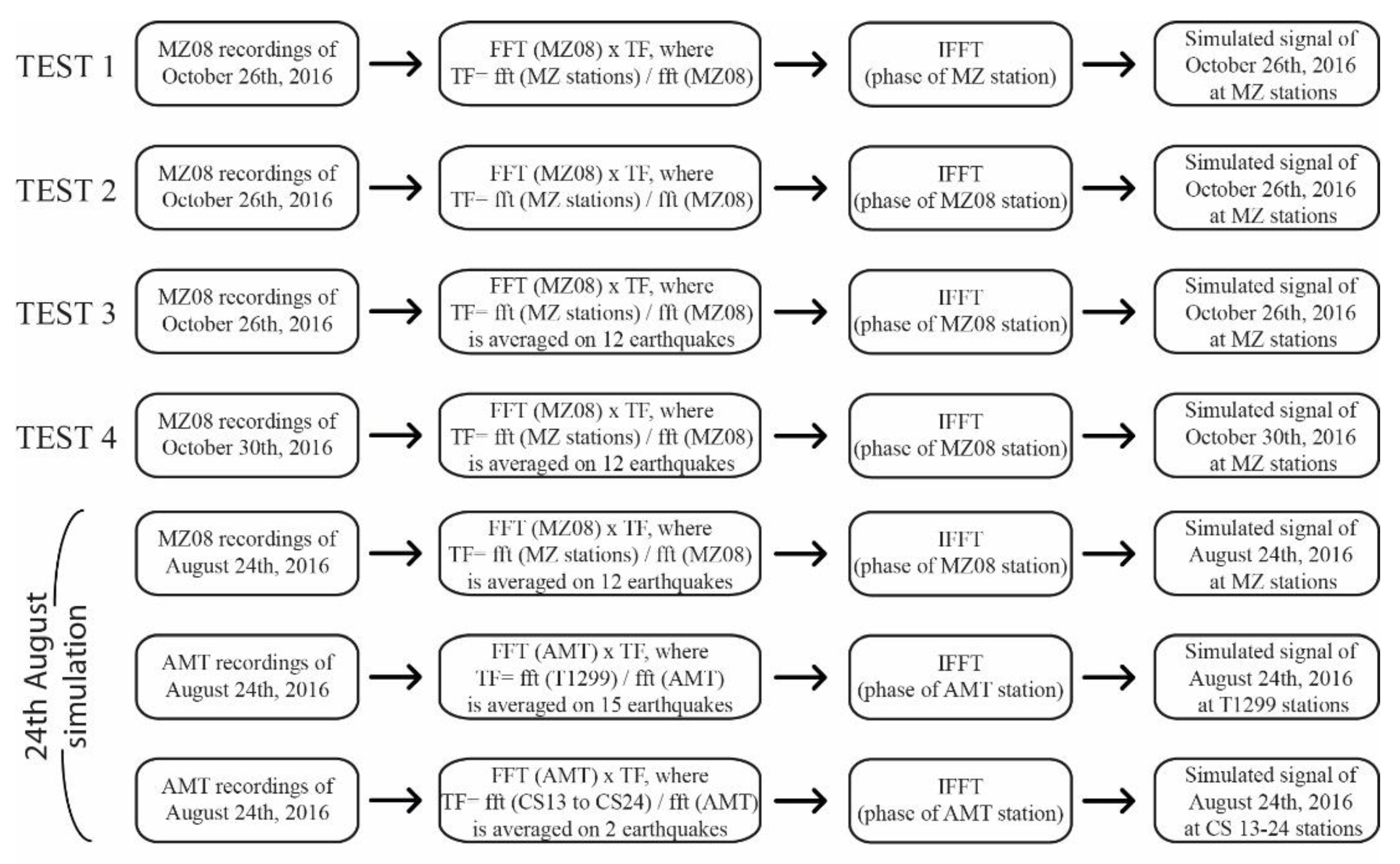
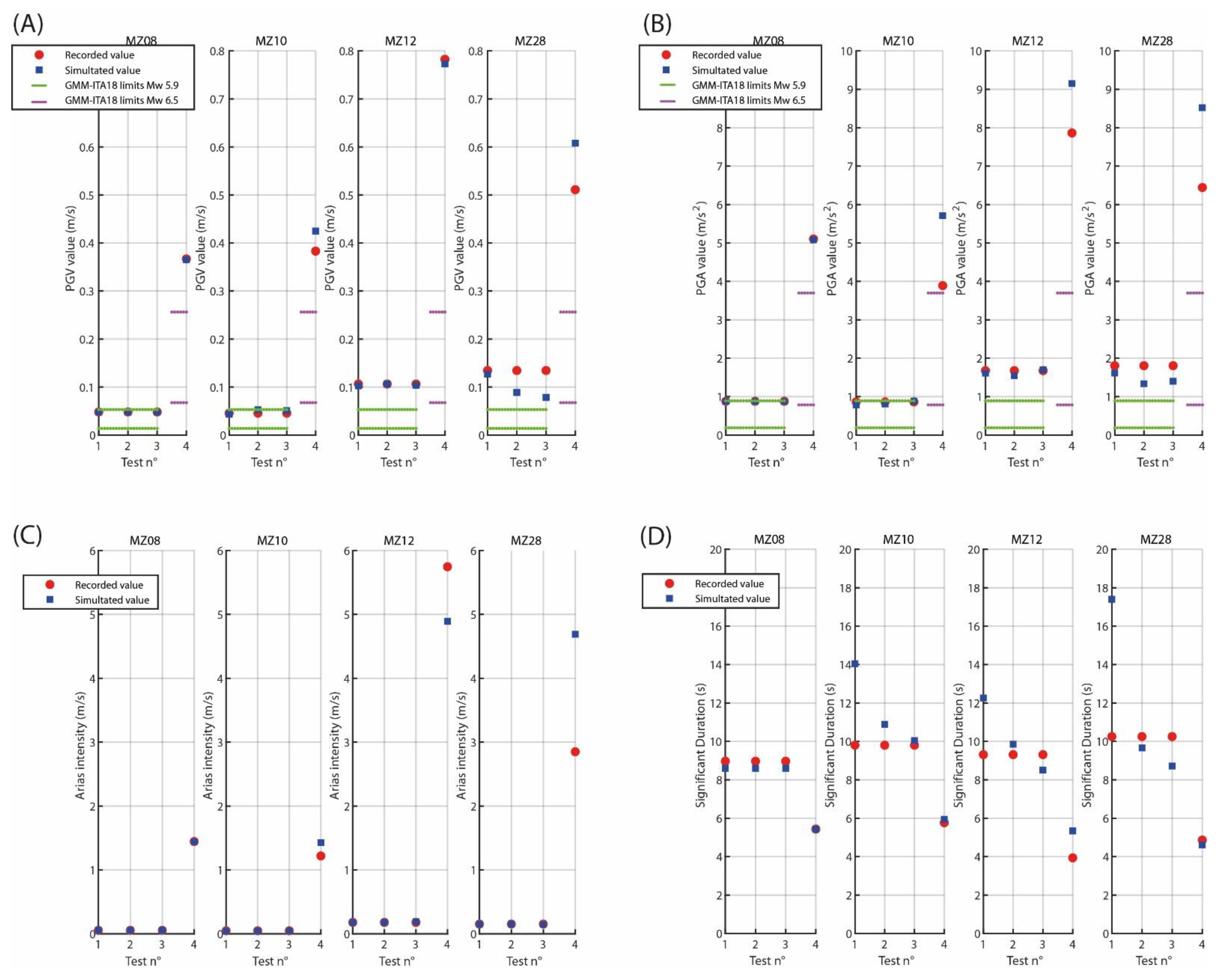
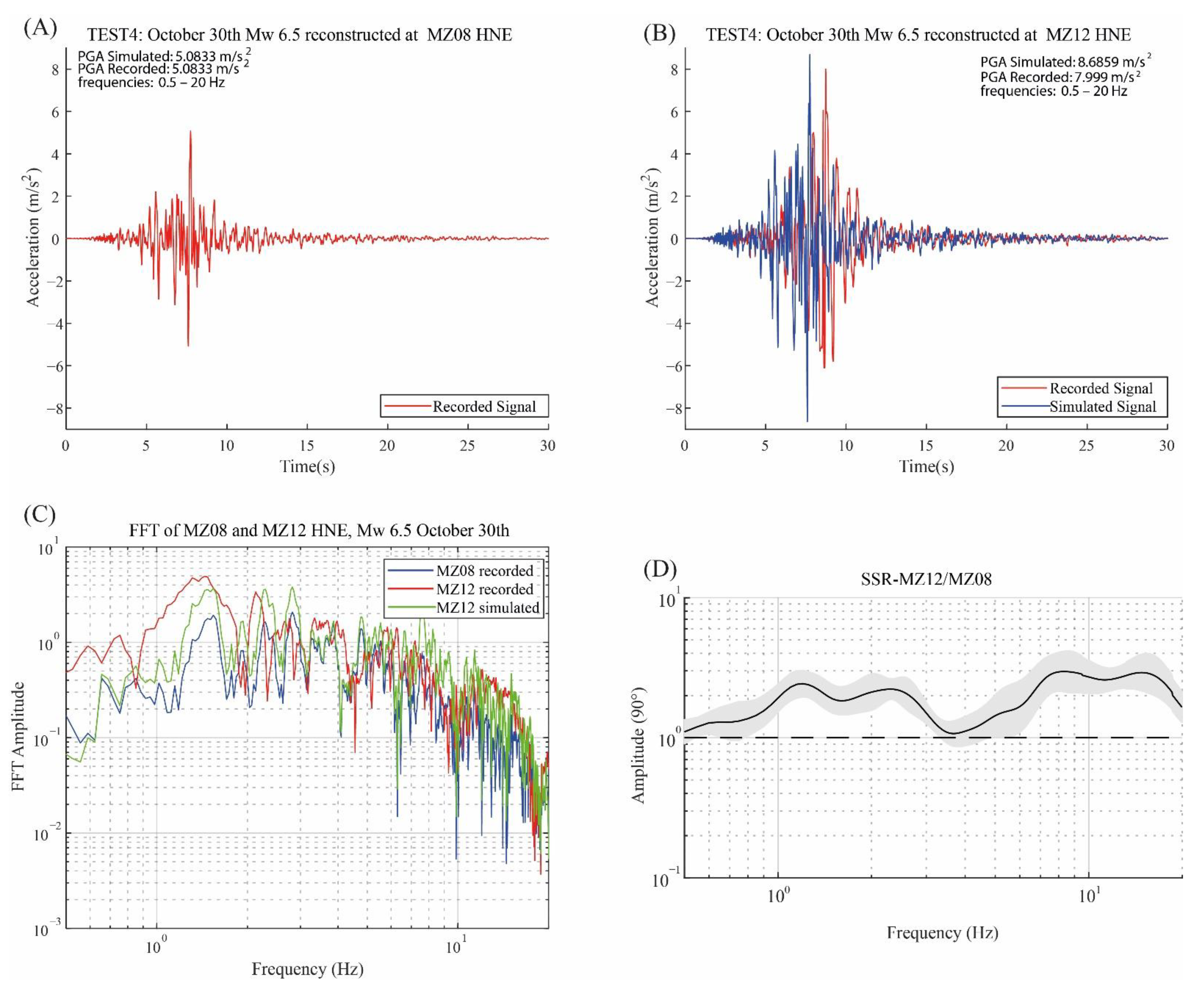
5.2. Tests

The simulation strategy has been tested to investigate the contribution of the transfer functions and the effect of the reference station phase used in the IFFT (Figure 5). We evaluated PGV, PGA, Arias intensity (AI) and signal duration (SID) of the simulated and recorded seismic signals of Mw 5.9, 26 October (Test 1 to 3), and Mw 6.5, 30 October (Test 4), at MZ08-10-12-28 stations (Figure 6).
PGA and PGV were also compared with the GMM valid for shallow crustal earthquakes in Italy (ITA18; [49]); the recorded values of the Mw 5.9 earthquake at MZ08 and MZ10 stations were close to the GMM predictions plus 1 standard deviation, while MZ12 and MZ28 showed values larger than those predicted. For the Mw 6.5 earthquake (test 4), the recordings overestimated the GMM values by a larger extent, especially for MZ12 and MZ28, where recorded values almost doubled the prediction plus 1 standard deviation.
To estimate the goodness of fit of the simulations with respect to the observations (GoF), we computed the relative difference as follow:
G o F = ( I M s i m   − I M r e c ) I M r e c
where IMsim is the intensity measure from the simulated time series and IMrec is computed from real records. The obtained values of GoF for the 4 tests can be found on Table S1 (Supplementary Materials).
The first test (TEST 1 in Figure 5) was carried out to verify the formal correctness of the procedure, whereas the second test (TEST 2 in Figure 5) aimed to investigate the use of the FFT phase of reference station (MZ08) in the IFFT process. The recorded intensity measures were well reproduced for Test 2 (Figure 6), except for MZ28 where the simulations underestimated the recorded PGV and PGA (GoF equal to −34% and −26%, respectively). As expected, the use of the reference phase in the IFFT caused a time shift of the simulated signals with respect to the recorded ones, proportional to the distance between the considered station and the reference site (Figure 7).
The third test (TEST 3 in Figure 5) was performed to investigate the use of the SSR average on 12 earthquakes (Table 1 and Figure S2, Supplementary Materials). As for Test 2, the fit was very good for all the indicators and it got better for the PGA; MZ28 was again underestimated by an amount of −42% for PGV and −22% for PGA (Figure 6 and Figure 8).
The fourth test (TEST 4 in Figure 5) mimicked Test 3 but for the Mw 6.5 earthquake, to investigate the use of small-magnitude SSR in case of possible nonlinear effects for a larger magnitude event. Figure 9 shows the different ingredients of the simulation strategy applied to MZ12: recordings of the reference station MZ08 (Figure 9A); recorded and simulated accelerations at MZ12, showing a slight amplification of the simulated signal with respect to the recorded one (Figure 9B); amplitude Fourier spectra of recorded signals at both MZ08 and MZ12, compared with the simulated FFT at MZ12 (Figure 9C); SSR used to correct the amplitude FFT spectrum of MZ08 (Figure 9D).
The comparison of the intensity measures (Figure 6) showed that the PGV at all stations were well fitted, slightly overestimating the recorded values at MZ10 and MZ28 of about 10% and 20%, respectively. The PGA values were well reproduced at MZ12, but we overestimated the recorded values of about 47% and 32% at MZ10 and MZ28. The Arias intensity values were well reproduced at MZ10 and MZ12, with a GoF of about ±15%, while at MZ28 we overestimated the recorded values of about 65%. The signal duration (SID) showed an increase of about 35% at MZ12, and ±5% at MZ10 and MZ28.

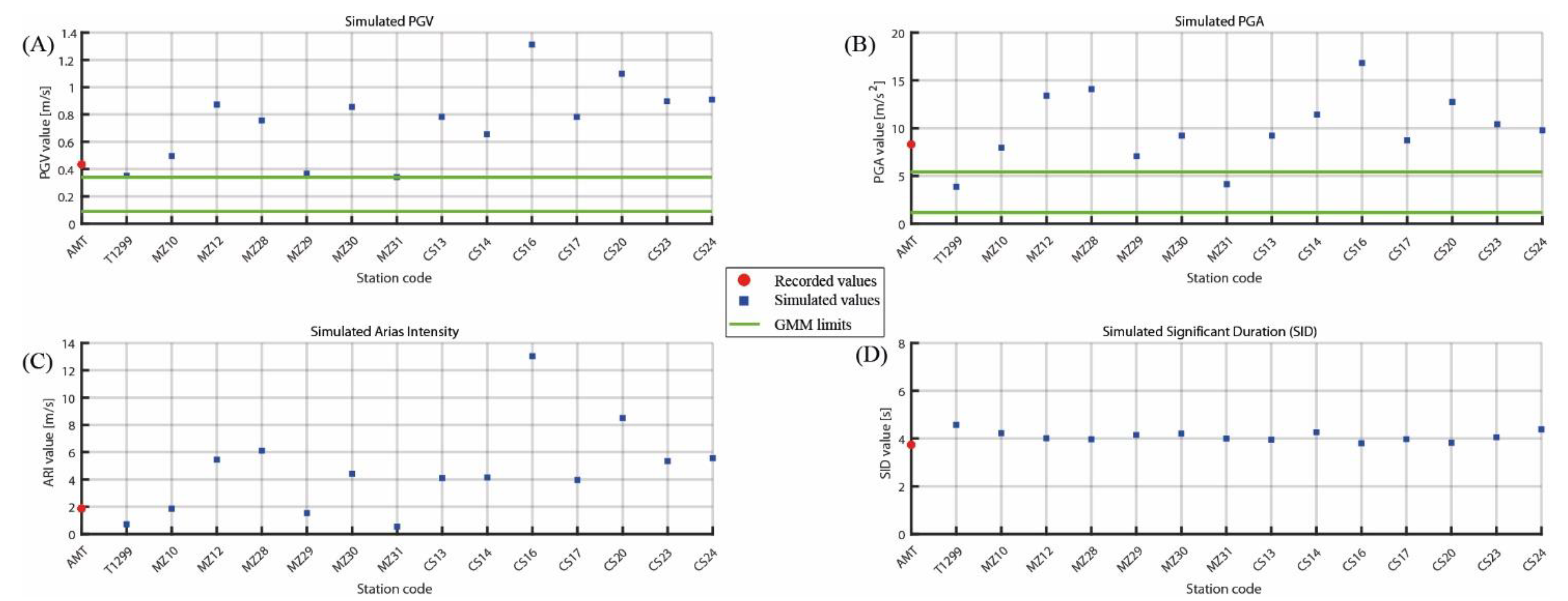
5.3. 24 August 2016 Simulation

The Mw 6.0 earthquake on 24 August 2016, was simulated at 14 seismic stations, located mainly in downtown Amatrice, using AMT as a reference site (Table 2, Figure 1). The large number of seismic events recorded by T1299 and MZ and the two events at CS13 to CS24 allowed us to reproduce reliable seismic signals in the 0.5–20 Hz frequency band (Figure 10): the highest ground shaking was concentrated in the first seconds after the P-wave arrival and the signal duration was similar at all the stations (4 to 6 s in Figure 11D).
Moreover, there was a large variability of the peak values at the different station locations (Figure 11 for the maximum of horizontal components, Figure S4 for the vertical component), and almost all the stations had PGA and PGV values up to three times the mean plus one standard deviation of the GMM valid for the area (Figure 11). During the Mw 6.0 shaking, the AMT station recorded a PGV value of 0.3 m/s (maximum on the horizontal components), slightly above one standard deviation of the GMM expected value [49]. With the exception of four stations, whose simulated PGV values were similar to AMT (GoF = −15% to −21% at T1299-MZ29-MZ31, GoF = +14% at MZ10), the other stations showed larger values with GoF ranging mostly from 50% to 100%, and with a maximum of 150% or 200% for CS20 and CS16, respectively (Figure 11A).
Regarding PGA, AMT recorded a value of about 8 m/s2, largely above one standard deviation of the GMM (Figure 11B). Again, T1299-MZ31 had smaller values (GoF about −50%), whereas CS14-CS20-MZ12-MZ28-CS16 exceeded the AMT values by more than 40% (GoF = 100% at CS16). The other stations varied between −20% to 20% of AMT values.
The Arias intensity (AI), shown in Figure 11C, was between 100% and 200% larger than AMT, with two stations reaching 350% and 600% (CS20 and CS16, respectively). T1299 and MZ31 decreased by more than 60%, whereas MZ10 and MZ29 were very similar to AMT. The significant durations (SID, Figure 11D) of the simulated signals were similar to the recorded one at AMT, characterized by a total duration of about 4 s.
Finally, the intensity measures for the vertical component (Figure S4 in Supplementary Materials) were always larger than AMT with the exception of T1299 and MZ31, and they never exceeded the 100% of AMT for PGA and PGV. Arias intensity values, instead, were larger than AMT by about 100–350%. The significant duration of the simulated signals showed a slight variation, with a maximum increase of about 1.1 s with respect to AMT.

6. Discussion

We proposed a procedure that has been tested on recorded earthquakes to evaluate the strengths and the weakness of the implemented method, checking for the contribution of the phase (Test 2) and of the average transfer functions on small earthquakes to reproduce strong shaking (Tests 3–4). The tests showed a fairly good agreement between simulations and recordings, both in terms of time series and intensity measures.
However, there are some limits due to the use of the same phase spectrum for all the stations and to the small-magnitude transfer functions. First of all, the reference site phase in the IFFT procedure implied the same P-wave arrival times at all the stations (Figure 7 and Figure 8) and it did not allow us to simulate the variation of the seismic duration due to local site response (Figure 6D). Secondly, the use of SSR produced signals whose intensity measures were lower than the recordings (Test 2 versus Test 3 in Figure 6) in the case of spectral amplification of the target event larger than the average SSR (Figure S5 in Supplementary Materials). Instead, when the transfer function is lower than the average SSR, such as for the strongest mainshock (Test 4; Figure 9 and Figure S5 in Supplementary Materials), we overestimated both the total energy AI and the PGV (Figure 6), probably because we were not accounting for possible nonlinear effects of the subsoil during the strong shaking. As a general conclusion, we can assess that our procedure evaluates an upper bound of the expected intensity measures at the target sites.
The proposed methodology has been applied to simulate the 24 August, Mw 6.0 earthquake at sites in the town of Amatrice: seven CS stations located in the historical center and seven farther sites (T1299 and six MZ stations) located on the top and at the base of the Amatrice terrace (Figure 10 and Figure 11). The largest amplification characterized the stations at the proximity of the NE hill edge and tended to decrease in the SW direction toward the central part of downtown. The lack of lateral confinement, due to the morphological escarpment, produced a NE oriented amplification of the low frequencies at the CS stations, on the direction orthogonal to the morphological elongation of the Amatrice terrace. Instead, the amplification at frequencies above 8 Hz were variable in amplitude and preferential orientation, suggesting that the top of the hill is affected by highly variable seismic amplification, due to the presence of low-velocity deposits.
The strong accelerations reproduced at the historical center of Amatrice is then related to the vicinity of the seismic source, accounted for by the ground motion at AMT, and by the local site effects, described by the SSR transfer function at the sites. The presence of layers with different impedance contrasts, together with the steep slopes bounding the Amatrice terrace, is able to generate seismic amplification effects, resulting in the increase of the intensity measures simulated on the top of the hill. The largest motion was simulated at CS16 and CS20, which showed horizontal PGA clearly exceeding the gravitational acceleration (about 16 and 12 m/s2, respectively). Similarly, the stations MZ10-12-28-30-31 were characterized by seismic amplification with respect to the reference site: MZ12 and MZ28 showed horizontal PGA of about 14 m/s2, whereas MZ10-29-30 had values between 7 to 9 m/s2. The two stations at the base of the terrace, MZ31 and T1299, were deamplified with respect to AMT and showed lower intensity measures, highlighting the high variability and the seismic behavior between the base and the top of the Amatrice hill.
Furthermore, the 24 August simulated signals showed a slight variation of the signal duration with respect to AMT (SID in Figure 11). This effect was due to the use of the reference phase spectra in the IFFT procedure, and to the near-source conditions, which concentrated the energy radiation in the direct wave arrivals. Conversely, in case of far-field conditions, as for the low-magnitude earthquakes recorded at CS stations, we verified that the seismic amplification in the Amatrice historical center was associated to an increase of SID up to three times with respect to AMT station (see also [25]).
The PGA and PGV values recorded by AMT, and the simulated ones at the stations, were clearly above one standard deviation of the GMM predictions (Figure 11), suggesting that the Amatrice historical center, especially in the eastern part of downtown, has been subjected to a severe ground shaking larger than the expected average. As already discussed, the proposed procedure did not allow us to simulate the nonlinear effects and it concentrated the energy in a time interval controlled by the reference site, suggesting that we estimated the upper limit of intensity measures in case of a seismic event characterized by similar magnitude and epicentral distance.

7. Conclusions

The proposed procedure is suitable for simulating strong ground motions of a past earthquakes recorded by at least one reference station close by. In this way, it is possible to overcome the limits of other simulation techniques for which the computation needs the description of the rupture process and propagation model from the source to the site.
This is the case of the 24 August 2016, Mw 6.0, earthquake signals which have been reproduced at the historical center of Amatrice, by using the transfer functions with respect to the closest seismic station (AMT) that recorded the event. We simulated the strong ground motion at 11 seismic stations located on the top of the Amatrice hill, out of which seven were installed in the historical center. The largest motion was reproduced at the north-eastern edge of the downtown, where the horizontal PGA values exceeded the gravitational acceleration. The simulated ground motions decreased away from the edges of the hill, suggesting that the topographic effect and the lack of lateral confinement are the predominant factors of the site effect. Two stations located at the base of the terrace showed lower intensity measures with respect to the reference site, highlighting the high variability and the seismic behavior between the base and the top of the Amatrice hill.
The strong ground motion variability during the Mw 6.0 event could help to understand the damage distribution that affected Amatrice downtown (X-XI of MCS; [50]). It is worth noting that the buildings of the historical center belonged to the most vulnerable classes [11,12] and were moderately to completely destroyed by the earthquake. The most damaged buildings were in the eastern part of the town [13], in proximity to the steep slopes of the hill, which was affected by the largest shaking.
Further studies could assess the performance of the simulation strategy for large-magnitude earthquakes having different focal mechanisms and rupture models. Moreover, it should be tested on sites with different geological and morphological conditions (such as soft sediments, fractured rock, or different topographies) and using more than one reference station close by, in order to make a robust evaluation of the simulated intensity measures.

Supplementary Materials

The following are available online at https://www.mdpi.com/article/10.3390/geosciences11050186/s1, Figure S1: Comparison of the AMT recorded time series of Mw 6.5 earthquake, NS–EW vs. 13° clockwise rotated components. Figure S2: Comparison between the time series and the FFT amplitude recorded by AMT and MZ08 for the Mw 6.5 earthquake (NS, EW, and vertical components). Figure S3: Standard spectral ratio (SSR) at the seismic stations considered in the study. Figure S4: Recorded and simulated intensity measures on the vertical component of the 24 August 2016, earthquake. Figure S5: comparison between the SSR of MZ10-12-28 averaged on 12 seismic events and the SSR on Mw 5.9 and Mw 6.5 earthquakes individually.

Author Contributions

Conceptualization, G.C.; writing—original draft preparation, A.T. and G.C.; writing—review and editing, A.T. and G.C.; supervision, G.C. All authors have read and agreed to the published version of the manuscript.

Funding

The grant of A.T. is funded by INGV and Department of Sciences, Roma Tre University (MIUR-Italy Dipartimenti di Eccellenza, Art.1, Commi 314-337 Legge 232/2016).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The signal recordings are available on the European Integrated Data Archive (EIDA, http://eida.ingv.it, accessed on 24 April 2021) and the Italian Strong Motion Network (RAN, http://ran.protezionecivile.it, accessed on 24 April 2021) databases. The simulated time-series can be requested to the corresponding author.

Acknowledgments

We would like to thank EMERSITO and SISMIKO, INGV emergency teams, for the data acquired and analyzed during and after the 2016 Central Italy seismic sequence. We are grateful to Daniela Famiani for helping us on the signal processing and for sharing useful information on data, and S. Marcucci and F. Nagashima for information regarding the AMT sensor orientation. We would like to acknowledge the editor and two anonymous reviewers for their useful comments and suggestions.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Wang, G.-Q.; Zhou, X.-Y.; Zhang, P.-Z.; Igel, H. Characteristics of amplitude and duration for near fault strong ground motion from the 1999 Chi-Chi, Taiwan Earthquake. Soil Dyn. Earthq. Eng. 2002, 22, 73–96. [Google Scholar] [CrossRef]
  2. Luzi, L.; Pacor, F.; Puglia, R.; Lanzano, G.; Felicetta, C.; D’Amico, M.; Michelini, A.; Faenza, L.; Lauciani, V.; Iervolino, I.; et al. The Central Italy Seismic Sequence between August and December 2016: Analysis of Strong-Motion Observations. Seism. Res. Lett. 2017, 88, 1219–1231. [Google Scholar] [CrossRef]
  3. Bradley, B.A.; Razafindrakoto, H.N.T.; Polak, V. Ground-Motion Observations from the 14 November 2016Mw 7.8 Kaikoura, New Zealand, Earthquake and Insights from Broadband Simulations. Seism. Res. Lett. 2017, 88, 740–756. [Google Scholar] [CrossRef] [Green Version]
  4. Magnoni, F.; Casarotti, E.; Michelini, A.; Piersanti, A.; Komatitsch, D.; Peter, D.; Tromp, J. Spectral-Element Simulations of Seismic Waves Generated by the 2009 L’Aquila Earthquake. Bull. Seism. Soc. Am. 2013, 104, 73–94. [Google Scholar] [CrossRef] [Green Version]
  5. Dujardin, A.; Causse, M.; Courboulex, F.; Traversa, P. Simulation of the Basin Effects in the Po Plain During the Emilia-Romagna Seismic Sequence (2012) Using Empirical Green’s Functions. Pure Appl. Geophys. Pageoph 2016, 173, 1993–2010. [Google Scholar] [CrossRef]
  6. Akinci, A.; Aochi, H.; Herrero, A.; Pischiutta, M.; Karanikas, D. Physics-Based Broadband Ground-Motion Simulations for Probable M w ≥7.0 Earthquakes in the Marmara Sea Region (Turkey). Bull. Seism. Soc. Am. 2017, 107, 1307–1323. [Google Scholar] [CrossRef]
  7. Gallovič, F.; Valentová, Ľ.; Ampuero, J.; Gabriel, A. Bayesian Dynamic Finite-Fault Inversion: Method and Synthetic Test. J. Geophys. Res. Solid Earth 2019, 124, 6949–6969. [Google Scholar] [CrossRef] [Green Version]
  8. Cultrera, G.; Ameri, G.; Saraò, A.; Cirella, A.; Emolo, A. Ground-motion simulations within ShakeMap methodology: Application to the 2008 Iwate-Miyagi Nairiku (Japan) and 1980 Irpinia (Italy) earthquakes. Geophys. J. Int. 2013, 193, 220–237. [Google Scholar] [CrossRef] [Green Version]
  9. Spudich, P.; Cirella, A.; Scognamiglio, L.; Tinti, E. Variability in synthetic earthquake ground motions caused by source variability and errors in wave propagation models. Geophys. J. Int. 2019, 219, 346–372. [Google Scholar] [CrossRef]
  10. Improta, L.; The Bollettino Sismico Italiano Working Group; Latorre, D.; Margheriti, L.; Nardi, A.; Marchetti, A.; Lombardi, A.M.; Castello, B.; Villani, F.; Ciaccio, M.G.; et al. Multi-segment rupture of the 2016 Amatrice-Visso-Norcia seismic sequence (central Italy) constrained by the first high-quality catalog of Early Aftershocks. Sci. Rep. 2019, 9, 1–13. [Google Scholar] [CrossRef] [PubMed]
  11. Rossi, A.; Tertulliani, A.; Azzaro, R.; Graziani, L.; Rovida, A.; Maramai, A.; Pessina, V.; Hailemikael, S.; Buffarini, G.; Bernardini, F.; et al. The 2016–2017 earthquake sequence in Central Italy: Macroseismic survey and damage scenario through the EMS-98 intensity assessment. Bull. Earthq. Eng. 2019, 17, 2407–2431. [Google Scholar] [CrossRef]
  12. Graziani, L.; Del Mese, S.; Tertulliani, A.; Arcoraci, L.; Maramai, A.; Rossi, A. Investigation on damage progression during the 2016–2017 seismic sequence in Central Italy using the European Macroseismic Scale (EMS-98). Bull. Earthq. Eng. 2019, 17, 5535–5558. [Google Scholar] [CrossRef]
  13. Fiorentino, G.; Forte, A.; Pagano, E.; Sabetta, F.; Baggio, C.; Lavorato, D.; Nuti, C.; Santini, S. Damage patterns in the town of Amatrice after August 24th 2016 Central Italy earthquakes. Bull. Earthq. Eng. 2017, 16, 1399–1423. [Google Scholar] [CrossRef] [Green Version]
  14. Tinti, E.; Scognamiglio, L.; Michelini, A.; Cocco, M. Slip heterogeneity and directivity of the ML 6.0, 2016, Amatrice earthquake estimated with rapid finite-fault inversion. Geophys. Res. Lett. 2016, 43, 10745. [Google Scholar] [CrossRef]
  15. Pizzi, A.; Di Domenica, A.; Gallovič, F.; Luzi, L.; Puglia, R. Fault Segmentation as Constraint to the Occurrence of the Main Shocks of the 2016 Central Italy Seismic Sequence. Tectonics 2017, 36, 2370–2387. [Google Scholar] [CrossRef]
  16. Cirella, A.; Pezzo, G.; Piatanesi, A. Rupture Kinematics and Structural-Rheological Control of the 2016 M w 6.1 Amatrice (Central Italy) Earthquake From Joint Inversion of Seismic and Geodetic Data. Geophys. Res. Lett. 2018, 45, 12302. [Google Scholar] [CrossRef]
  17. D’Amico, M.; Felicetta, C.; Russo, E.; Sgobba, S.; Lanzano, G.; Pacor, F.; Luzi, L. Italian Accelerometric Archive v 3.1; Istituto Nazionale di Geofisica e Vulcanologia, Dipartimento della Protezione Civile Nazionale: Rome, Italy, 2020. [Google Scholar] [CrossRef]
  18. Faenza, L.; Lauciani, V.; Michelini, A. The ShakeMaps of the Amatrice, M6, earthquake. Ann. Geophys 2016, 59. [Google Scholar] [CrossRef]
  19. Spagnuolo, E.; Cirella, A.; Akinci, A. Investigating the Effectiveness of Rupture Directivity during the August 24, 2016 Mw 6.0 Central Italy earthquake. Ann. Geophys. 2016, 59. [Google Scholar] [CrossRef]
  20. Ren, Y.; Wang, H.; Wen, R. Imprint of Rupture Directivity from Ground Motions of the 24 August 2016 M w 6.2 Central Italy Earthquake. Tectonics 2017, 36, 3178–3191. [Google Scholar] [CrossRef] [Green Version]
  21. Pischiutta, M.; Akinci, A.; Tinti, E.; Herrero, A. Broad-band ground-motion simulation of 2016 Amatrice earthquake, Central Italy. Geophys. J. Int. 2020, 224, 1753–1779. [Google Scholar] [CrossRef]
  22. Buttinelli, M.; Pezzo, G.; Valoroso, L.; De Gori, P.; Chiarabba, C. Tectonics Inversions, Fault Segmentation, and Triggering Mechanisms in the Central Apennines Normal Fault System: Insights From High-Resolution Velocity Models. Tectonics 2018, 37, 4135–4149. [Google Scholar] [CrossRef]
  23. Carannante, S.; Monachesi, G.; Cattaneo, M.; Amato, A.; Chiarabba, C. Deep structure and tectonics of the northern-central Apennines as seen by regional-scale tomography and 3-D located earthquakes. J. Geophys. Res. Solid Earth 2013, 118, 5391–5403. [Google Scholar] [CrossRef]
  24. Magnoni, F.; Casarotti, E. Kinematic finite fault and 3D seismic wave propagation of the 24 August 2016, Mw 6.0 Central Italy earthquake. Ann. Geophys. 2016, 59. [Google Scholar] [CrossRef]
  25. Milana, G.; Cultrera, G.; Bordoni, P.; Bucci, A.; Cara, F.; Cogliano, R.; Di Giulio, G.; Di Naccio, D.; Famiani, D.; Fodarella, A.; et al. Local site effects estimation at Amatrice (Central Italy) through seismological methods. Bull. Earthq. Eng. 2019, 18, 5713–5739. [Google Scholar] [CrossRef]
  26. Chiaretti, F.; Nibbi, L. Relazione Illustrativa della Microzonazione Sismica di Livello 3 del Comune di Amatrice ai sensi dell’Ordinanza del Commissario Straordinario n.24; 2017 (in Italian). Regione Lazio. Available online: http://www.regione.lazio.it/prl_ambiente/?vw=contenutidettaglio&id=238 (accessed on 25 April 2021).
  27. Vignaroli, G.; Mancini, M.; Bucci, F.; Cardinali, M.; Cavinato, G.; Moscatelli, M.; Putignano, M.; Sirianni, P.; Santangelo, M.; Ardizzone, F.; et al. Geology of the central part of the Amatrice Basin (Central Apennines, Italy). J. Maps 2019, 15, 193–202. [Google Scholar] [CrossRef] [Green Version]
  28. Vignaroli, G.; Mancini, M.; Brilli, M.; Bucci, F.; Cardinali, M.; Giustini, F.; Voltaggio, M.; Yu, T.-L.; Shen, C.-C. Spatial-Temporal Evolution of Extensional Faulting and Fluid Circulation in the Amatrice Basin (Central Apennines, Italy) During the Pleistocene. Front. Earth Sci. 2020, 8, 130. [Google Scholar] [CrossRef]
  29. Grelle, G.; Gargini, E.; Facciorusso, J.; Maresca, R.; Madiai, C. Seismic site effects in the Red Zone of Amatrice hill detected via the mutual sustainment of experimental and computational approaches. Bull. Earthq. Eng. 2020, 18, 1955–1984. [Google Scholar] [CrossRef]
  30. Miano, A.; Jalayer, F.; Forte, G.; Santo, A. Empirical fragility assessment using conditional GMPE-based ground shaking fields: Application to damage data for 2016 Amatrice Earthquake. Bull. Earthq. Eng. 2020, 18, 6629–6659. [Google Scholar] [CrossRef]
  31. Cara, F.; Cultrera, G.; Riccio, G.; Amoroso, S.; Bordoni, P.; Bucci, A.; D’Alema, E.; D’Amico, M.; Cantore, L.; Carannante, S.; et al. Temporary dense seismic network during the 2016 Central Italy seismic emergency for microzonation studies. Sci. Data 2019, 6, 1–15. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  32. Priolo, E.; Pacor, F.; Spallarossa, D.; Milana, G.; Laurenzano, G.; Romano, M.A.; Felicetta, C.; Hailemikael, S.; Cara, F.; Di Giulio, G.; et al. Seismological analyses of the seismic microzonation of 138 municipalities damaged by the 2016–2017 seismic sequence in Central Italy. Bull. Earthq. Eng. 2020, 18, 5553–5593. [Google Scholar] [CrossRef] [Green Version]
  33. Felicetta, C.; Mascandola, C.; Spallarossa, D.; Pacor, F.; Hailemikael, S.; Di Giulio, G. Quantification of site effects in the Amatrice area (Central Italy): Insights from ground-motion recordings of the 2016–2017 seismic sequence. Soil Dyn. Earthq. Eng. 2021, 142, 106565. [Google Scholar] [CrossRef]
  34. Del Gaudio, V.; Wasowski, J.; Pierri, P.; Moretti, A.; Ferrini, G. Multitemporal analysis of ambient noise polarization to characterize site response in the town of Amatrice, shattered by the 2016 central Italy earthquake. Geophys. J. Int. 2020, 224, 739–759. [Google Scholar] [CrossRef]
  35. Scognamiglio, L.; Tinti, E.; Quintiliani, M. Time Domain Moment Tensor (TDMT) [Data Set]; Istituto nazionale di Geofisica e Vulcanologia (INGV): Rome, Italy, 2006. [Google Scholar] [CrossRef]
  36. Mazza, S.; Basili, A.; Bono, A.; Luciani, V.; Mandiello, A.G.; Marcocci, C.; Mele, F.M.; Pintore, S.; Quintiliani, M.; Scognamiglio, L.; et al. AIDA—Seismic data acquisition, processing, storage and distribution the National Earthquake Center, INGV. Ann. Geophys. 2012, 55. [Google Scholar] [CrossRef]
  37. Presidency of Council Of Ministers—Civil Protection Department. Ital. Strong Motion Netw. 1972. [CrossRef]
  38. D’Amico, M.; Felicetta, C.; Schiappapietra, E.; Pacor, F.; Gallovič, F.; Paolucci, R.; Puglia, R.; Lanzano, G.; Sgobba, S.; Luzi, L. Fling Effects from Near-Source Strong-Motion Records: Insights from the 2016 Mw 6.5 Norcia, Central Italy, Earthquake. Seism. Res. Lett. 2018, 90, 659–671. [Google Scholar] [CrossRef]
  39. Moretti, M.; Pondrelli, S.; Margheriti, L.; Abruzzese, L.; Anselmi, M.; Arroucau, P.; Baccheschi, P.; Baptie, B.; Bonadio, R.; Bono, A.; et al. SISMIKO: Emergency Network Deployment and Data Sharing for the 2016 Central Italy Seismic Sequence. Ann. Geophys. 2016, 59. [Google Scholar] [CrossRef]
  40. 3A network, Seismic Microzonation Network, 2016 Central Italy. Istituto Nazionale di Geofisica e Vulcanologia (INGV), Istituto di Geologia Ambientale e Geoingegneria (CNR-IGAG), Istituto per la Dinamica dei Processi Ambientali (CNR-IDPA), Istituto di Metodologie per l’Analisi Ambientale (CNR-IMAA), Agenzia Nazionale per le nuove tecnologie, l’energia e lo sviluppo economico sostenibile (ENEA). Rete del Centro di Microzonazione Sismica (CentroMZ), Sequenza Sismica del 2016 in Italia Centrale. Istituto Nazionale di Geofisica e Vulcanologia (INGV): Italy, 2018. Available online: https://doi.org/10.13127/SD/ku7Xm12Yy9. (accessed on 8 April 2021).
  41. Imtiaz, A.; Perron, V.; Hollender, F.; Bard, P.; Cornou, C.; Svay, A.; Theodoulidis, N. Wavefield Characteristics and Spatial Incoherency: A Comparative Study from Argostoli Rock- and Soil-Site Dense Seismic Arrays. Bull. Seism. Soc. Am. 2018, 108, 2839–2853. [Google Scholar] [CrossRef] [Green Version]
  42. Sgobba, S.; Lanzano, G.; Pacor, F.; Puglia, R.; D’Amico, M.; Felicetta, C.; Luzi, L. Spatial Correlation Model of Systematic Site and Path Effects for Ground-Motion Fields in Northern Italy. Bull. Seism. Soc. Am. 2019, 109, 1419–1434. [Google Scholar] [CrossRef]
  43. Schiappapietra, E.; Douglas, J. Modelling the spatial correlation of earthquake ground motion: Insights from the literature, data from the 2016–2017 Central Italy earthquake sequence and ground-motion simulations. Earth Science Rev. 2020, 203, 103139. [Google Scholar] [CrossRef]
  44. Esposito, S.; Iervolino, I. Spatial Correlation of Spectral Acceleration in European Data. Bull. Seism. Soc. Am. 2012, 102, 2781–2788. [Google Scholar] [CrossRef]
  45. Bonilla, L.F. Nonlinear site response evidence of K-NET and KiK-net records from the 2011 off the Pacific coast of Tohoku Earthquake. Earth, Planets Space 2011, 63, 785–789. [Google Scholar] [CrossRef] [Green Version]
  46. Theodoulidis, N.; The Argostoli NERA Team; Cultrera, G.; Cornou, C.; Bard, P.-Y.; Boxberger, T.; Di Giulio, G.; Imtiaz, A.; Kementzetzidou, D.; Makra, K. Basin effects on ground motion: The case of a high-resolution experiment in Cephalonia (Greece). Bull. Earthq. Eng. 2018, 16, 529–560. [Google Scholar] [CrossRef]
  47. Konno, K.; Ohmachi, T. Ground-Motion Characteristics Estimated from Spectral Ratio between Horizontal and Vertical Components of Microtremor. Bull. Seism. Soc. Am. 1998, 88, 228–241. [Google Scholar]
  48. Arias, A. A measure of earthquake intensity. In Seismic Design for Nuclear Power Plants; Robert, J.H., Ed.; Massachusetts Institute of Technology Press: Cambridge, MA, USA, 1970; pp. 438–483. [Google Scholar]
  49. Lanzano, G.; Luzi, L.; Pacor, F.; Felicetta, C.; Puglia, R.; Sgobba, S.; D’Amico, M. A Revised Ground-Motion Prediction Model for Shallow Crustal Earthquakes in Italy. Bull. Seism. Soc. Am. 2019, 109, 525–540. [Google Scholar] [CrossRef]
  50. Galli, P.; Castenetto, S.; Peronace, E. The Macroseismic Intensity Distribution of the 30 October 2016 Earthquake in Central Italy (Mw 6.6): Seismotectonic Implications. Tectonics 2017, 36, 2179–2191. [Google Scholar] [CrossRef]
Geosciences 11 00186 g001 550
Figure 1. (A) Map of the study area with the strongest earthquakes that affected central Italy from 1997 to 2016 and the associated TDMT focal mechanisms (http://cnt.rm.ingv.it/tdmt, accessed on 24 April 2021; [35]); blue, red, and yellow dots represent the location of the seismic events used in this study. (B) Schematic geological map of the Amatrice downtown (modified after [27]) generated by GIS (base map source: Esri, user community, geographic information system. Coordinate system and projection: World Geodetic System 1984–Web Mercator Auxiliary Sphere); black triangle represents the position of seismic stations whose recordings are used for the analysis.
Figure 1. (A) Map of the study area with the strongest earthquakes that affected central Italy from 1997 to 2016 and the associated TDMT focal mechanisms (http://cnt.rm.ingv.it/tdmt, accessed on 24 April 2021; [35]); blue, red, and yellow dots represent the location of the seismic events used in this study. (B) Schematic geological map of the Amatrice downtown (modified after [27]) generated by GIS (base map source: Esri, user community, geographic information system. Coordinate system and projection: World Geodetic System 1984–Web Mercator Auxiliary Sphere); black triangle represents the position of seismic stations whose recordings are used for the analysis.
Geosciences 11 00186 g001
Geosciences 11 00186 g002 550
Figure 2. Simulation strategy proposed in this study, where numbers 1 to 4 refer to the numbered list of Section 3. Red lines represent the recorded time series and the relative phase and amplitude spectra at the reference station (AMT) for the Mw 6.5 earthquake. Number 2: orange thick line represents the standard spectral ratio (SSR) of T1299 (E–W component) with respect to AMT, thin black lines represent the 18 horizontal components of the SSR rotated every 10° and 1 vertical component. Numbers 3 and 4: blue lines represent the simulated signal at T1299 with its phase and amplitude spectra, respectively.
Figure 2. Simulation strategy proposed in this study, where numbers 1 to 4 refer to the numbered list of Section 3. Red lines represent the recorded time series and the relative phase and amplitude spectra at the reference station (AMT) for the Mw 6.5 earthquake. Number 2: orange thick line represents the standard spectral ratio (SSR) of T1299 (E–W component) with respect to AMT, thin black lines represent the 18 horizontal components of the SSR rotated every 10° and 1 vertical component. Numbers 3 and 4: blue lines represent the simulated signal at T1299 with its phase and amplitude spectra, respectively.
Geosciences 11 00186 g002
Geosciences 11 00186 g003 550
Figure 3. Standard spectral ratio (SSR) of T1299 with respect to AMT. (A) average SSR and the associated standard deviation along the N–S direction; (B) average SSR calculated along 18 horizontal directions every 10°; (C) polar plot showing the amplification along different azimuthal directions from 0 Hz (center of polar plot) to 20 Hz.
Figure 3. Standard spectral ratio (SSR) of T1299 with respect to AMT. (A) average SSR and the associated standard deviation along the N–S direction; (B) average SSR calculated along 18 horizontal directions every 10°; (C) polar plot showing the amplification along different azimuthal directions from 0 Hz (center of polar plot) to 20 Hz.
Geosciences 11 00186 g003
Geosciences 11 00186 g004 550
Figure 4. Standard spectral ratio (SSR) of the CS stations with respect to AMT between 0.5 to 20 Hz (for CS13 to CS24). Black lines represent the 18 (1) horizontal (vertical) components, blue (red) lines represent the north–south (east–west) components, green lines represent the vertical components; purple dotted lines represent the reference level of SSR = 1.
Figure 4. Standard spectral ratio (SSR) of the CS stations with respect to AMT between 0.5 to 20 Hz (for CS13 to CS24). Black lines represent the 18 (1) horizontal (vertical) components, blue (red) lines represent the north–south (east–west) components, green lines represent the vertical components; purple dotted lines represent the reference level of SSR = 1.
Geosciences 11 00186 g004
Geosciences 11 00186 g005 550
Figure 5. Flowchart of the simulation procedure for the four tests and the final simulation of 24 August 2016 earthquake. FFT, fast Fourier transform; IFFT, inverse fast Fourier transform; TF, transfer function (SSR).
Figure 5. Flowchart of the simulation procedure for the four tests and the final simulation of 24 August 2016 earthquake. FFT, fast Fourier transform; IFFT, inverse fast Fourier transform; TF, transfer function (SSR).
Geosciences 11 00186 g005
Geosciences 11 00186 g006 550
Figure 6. Comparison of the maximum horizontal intensity measures of the recorded (red) and simulated (blue) seismograms at MZ08-10-12-28 for the four tests: (A) PGV; (B) PGA; (C) Arias intensity (AI); (D) significant duration (SID). The green and magenta lines represent the GMM values ± 1 standard deviation [49], for class B site (Vs30 = 670 m/s at AMT) and for the following coupled magnitude Joyner–Boore distance (Rjb): Mw 5.9 and Rjb = 25km (26 October 2016; test 1 and 2), Mw 6.5 and Rjb = 10.1 km (30 October 2016; test 3 and 4) [38].
Figure 6. Comparison of the maximum horizontal intensity measures of the recorded (red) and simulated (blue) seismograms at MZ08-10-12-28 for the four tests: (A) PGV; (B) PGA; (C) Arias intensity (AI); (D) significant duration (SID). The green and magenta lines represent the GMM values ± 1 standard deviation [49], for class B site (Vs30 = 670 m/s at AMT) and for the following coupled magnitude Joyner–Boore distance (Rjb): Mw 5.9 and Rjb = 25km (26 October 2016; test 1 and 2), Mw 6.5 and Rjb = 10.1 km (30 October 2016; test 3 and 4) [38].
Geosciences 11 00186 g006
Geosciences 11 00186 g007 550
Figure 7. Comparison between recorded and simulated seismograms (EW component of acceleration) at MZ10 (A) and MZ28 (B) for Test 2. Red (blue) line represents the recorded (simulated) signal between 0.5–20 Hz.
Figure 7. Comparison between recorded and simulated seismograms (EW component of acceleration) at MZ10 (A) and MZ28 (B) for Test 2. Red (blue) line represents the recorded (simulated) signal between 0.5–20 Hz.
Geosciences 11 00186 g007
Geosciences 11 00186 g008 550
Figure 8. Comparison between recorded and simulated seismograms (EW component of acceleration) at MZ10 (A) and MZ28 (B) for Test 3. Red (blue) line represents the recorded (simulated) signal between 0.5–20 Hz.
Figure 8. Comparison between recorded and simulated seismograms (EW component of acceleration) at MZ10 (A) and MZ28 (B) for Test 3. Red (blue) line represents the recorded (simulated) signal between 0.5–20 Hz.
Geosciences 11 00186 g008
Geosciences 11 00186 g009 550
Figure 9. Comparison between recorded and simulated signals (EW component) at MZ12 for Test 4, in the frequency band of 0.5–20 Hz: (A) recorded signal at MZ08; (B) recorded and simulated signals at MZ12; (C) comparison of the FFT amplitudes between the signals recorded by MZ08 and MZ12, and the signal simulated at MZ12; (D) SSR ±1 standard deviation (gray) on the EW direction (MZ12 on MZ08).
Figure 9. Comparison between recorded and simulated signals (EW component) at MZ12 for Test 4, in the frequency band of 0.5–20 Hz: (A) recorded signal at MZ08; (B) recorded and simulated signals at MZ12; (C) comparison of the FFT amplitudes between the signals recorded by MZ08 and MZ12, and the signal simulated at MZ12; (D) SSR ±1 standard deviation (gray) on the EW direction (MZ12 on MZ08).
Geosciences 11 00186 g009
Geosciences 11 00186 g010 550
Figure 10. Blue (red) lines represent the north–south (east–west) components of the simulated seismograms of Mw 6.0, 24 August 2016, in Amatrice downtown at the seismic stations (black triangle). The seismograms sit on a schematic geological map of the Amatrice downtown (modified after [27]) generated by GIS (base map source: Esri, user community, geographic information system. Coordinate system and projection: World Geodetic System 1984–Web Mercator Auxiliary Sphere).
Figure 10. Blue (red) lines represent the north–south (east–west) components of the simulated seismograms of Mw 6.0, 24 August 2016, in Amatrice downtown at the seismic stations (black triangle). The seismograms sit on a schematic geological map of the Amatrice downtown (modified after [27]) generated by GIS (base map source: Esri, user community, geographic information system. Coordinate system and projection: World Geodetic System 1984–Web Mercator Auxiliary Sphere).
Geosciences 11 00186 g010
Geosciences 11 00186 g011 550
Figure 11. Comparison between the recorded (red dot) and simulated (blue square) intensity measures for Mw 6.0 (24 August 2016) at the stations in Amatrice (maximum horizontal components): (A) PGV; (B) PGA; (C) horizontal Arias intensity (AI); (D) significant duration (SID). Green lines are the GMM mean ±1 standard deviation [49] for Rjb = 1 km [38] and site class B (Vs30 = 670 m/s at AMT).
Figure 11. Comparison between the recorded (red dot) and simulated (blue square) intensity measures for Mw 6.0 (24 August 2016) at the stations in Amatrice (maximum horizontal components): (A) PGV; (B) PGA; (C) horizontal Arias intensity (AI); (D) significant duration (SID). Green lines are the GMM mean ±1 standard deviation [49] for Rjb = 1 km [38] and site class B (Vs30 = 670 m/s at AMT).
Geosciences 11 00186 g011
Table
Table 1. Location and magnitude of earthquakes whose recordings were used in this study (available at http://cnt.rm.ingv.it/, accessed on 23 April 2021). Last column lists the stations that recorded the event used for the transfer function computation (SSR).
Table 1. Location and magnitude of earthquakes whose recordings were used in this study (available at http://cnt.rm.ingv.it/, accessed on 23 April 2021). Last column lists the stations that recorded the event used for the transfer function computation (SSR).
UTC TimeLatitude
[°N]		Longitude
[°E]		Depth
[km]		Mag
Type		MagnitudeTransfer
Function
2016-08-24T01:36:3242.7013.238Mw6.0AMT
2016-10-16T09:32:3542.7513.189Mw4.0T1299,AMT
2016-10-26T17:10:3642.8813.128Mw5.4T1299,AMT
2016-10-26T19:18:0742.9113.0910Mw5.9MZ,MZ08,AMT
2016-10-26T21:42:0142.8613.1210Mw4.5T1299,AMT
2016-10-27T03:19:2742.8413.149Mw4.0T1299,AMT
2016-10-27T08:21:4542.8813.109Mw4.3T1299,AMT
2016-10-28T02:13:1943.0313.128ML3.5MZ,MZ08,AMT
2016-10-29T16:24:3342.8113.1011Mw4.1T1299,AMT
2016-10-30T06:40:1742.8313.1110Mw6.5MZ
2016-10-30T07:13:0542.6913.2311ML4.2T1299,AMT
2016-10-30T11:58:1742.8513.0610Mw4.0T1299,AMT
2016-10-31T08:37:3343.0313.088ML3.5MZ,MZ08,AMT
2016-10-31T12:30:1642.9213.0111ML2.9MZ,MZ08,AMT
2016-11-01T03:19:0542.9013.2924ML3.8MZ,MZ08,AMT
2016-11-01T04:09:1542.5913.3417ML3.0MZ,MZ08,AMT
2016-11-02T15:53:0243.0313.059ML3.4MZ,MZ08,AMT
2016-11-02T19:26:4742.9213.218ML3.1MZ,MZ08,AMT
2016-11-02T19:37:4942.8813.068Mw3.7MZ,MZ08,AMT
2016-11-03T00:35:0143.0313.058Mw4.7MZ,MZ08,AMT
2016-11-03T11:59:1742.9113.219ML3.5MZ/MZ08,AMT
2016-11-03T14:41:2942.9913.079ML3.5MZ/MZ08,AMT
2016-11-08T20:00:5642.8212.789ML3.2MZ/MZ08,AMT
2016-11-10T13:50:5942.8813.138ML3.6T1299,AMT
2016-11-10T15:57:3342.9813.057ML3.4MZ,MZ08,AMT
2016-11-12T03:54:5943.0113.078ML3.1T1299,AMT
2016-11-12T22:51:1042.9213.218ML3.2T1299,AMT
2016-11-14T01:33:4342.8613.1611ML4.1T1299,AMT
2016-11-15T22:57:5242.7513.2110ML3.3T1299,AMT
2016-06-28T10.30.0442.6213.329ML1.8-
2016-06-28T14.12.0242.9113.188ML2.2-
2017-06-29T08.52.2942.6313.2211ML2.6CS,T1299,AMT
2017-06-29T08.55.4642.6313.2111ML3.1CS,T1299,AMT
2017-06-29T09.24.2042.6413.2111ML1.5-
2017-06-29T10.24.0742.7713.1711ML1.8-
Table
Table 2. List of the seismic stations installed in the Amatrice municipality (see [25,31]). For each station, the geographic coordinates and the working periods are reported. Stations CS01–04 (in italic) were not used for the 24 August 2016 simulation.
Table 2. List of the seismic stations installed in the Amatrice municipality (see [25,31]). For each station, the geographic coordinates and the working periods are reported. Stations CS01–04 (in italic) were not used for the 24 August 2016 simulation.
Station CodeLatitude
[°N]		Longitude
[°E]		Altitude
[m]		Working Period
AMT42.632513.28629507 April 2003–today
T129942.634213.282294029 August 2016–today
MZ0842.633013.287089720 September–17 November 2016
MZ1042.625013.300097920 September–17 November 2016
MZ1242.628013.292095820 September–17 November 2016
MZ2842.621413.308099214 October–17 November 2016
MZ2942.630413.293088127 October–17 November 2016
MZ3042.626413.290695127 October–17 November 2016
MZ3142.625013.290087827 October–17 November 2016
CS0142.630413.287392928 June 2017–28 June 2017
CS0242.629713.287193528 June 2017–28 June 2017
CS0342.629413.286993328 June 2017–28 June 2017
CS0442.629413.287394028 June 2017–28 June 2017
CS1342.627013.295894629 June 2017–29 June 2016
CS1442.628813.289294929 June 2017–29 June 2017
CS1642.629913.289293029 June 2017–29 June 2017
CS1742.628213.289394829 June 2017–29 June 2017
CS2042.629313.290694029 June 2017–29 June 2017
CS2342.629013.291095129 June 2017–29 June 2017
CS2442.628513.291195329 June 2017–29 June 2017
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Todrani, A.; Cultrera, G. Near-Source Simulation of Strong Ground Motion in Amatrice Downtown Including Site Effects. Geosciences 2021, 11, 186. https://doi.org/10.3390/geosciences11050186

AMA Style

Todrani A, Cultrera G. Near-Source Simulation of Strong Ground Motion in Amatrice Downtown Including Site Effects. Geosciences. 2021; 11(5):186. https://doi.org/10.3390/geosciences11050186

Chicago/Turabian Style

Todrani, Alessandro, and Giovanna Cultrera. 2021. "Near-Source Simulation of Strong Ground Motion in Amatrice Downtown Including Site Effects" Geosciences 11, no. 5: 186. https://doi.org/10.3390/geosciences11050186

APA Style

Todrani, A., & Cultrera, G. (2021). Near-Source Simulation of Strong Ground Motion in Amatrice Downtown Including Site Effects. Geosciences, 11(5), 186. https://doi.org/10.3390/geosciences11050186

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop